Research on Fast SOC Balance Control of Modular Battery Energy Storage System
Abstract
1. Introduction
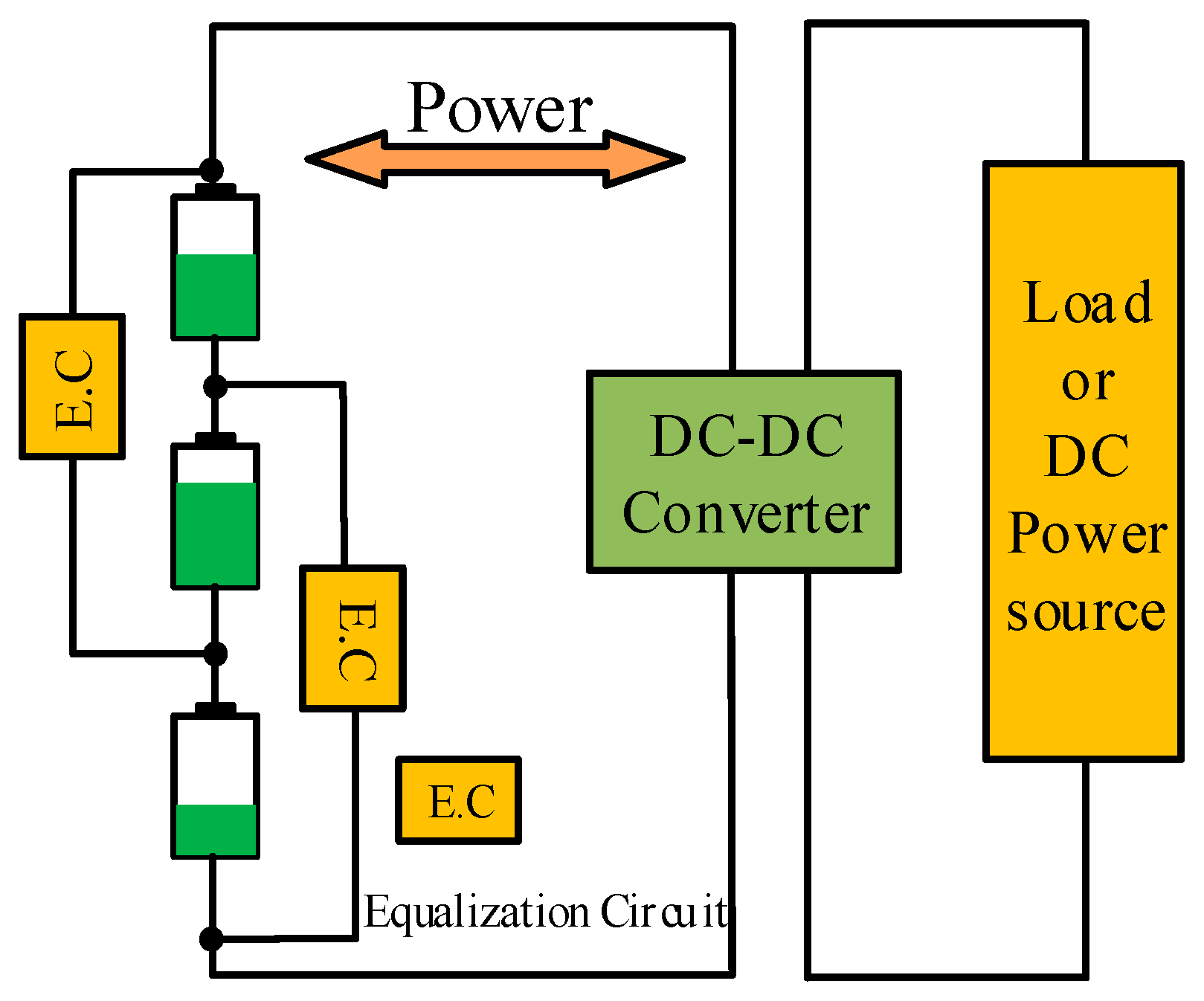
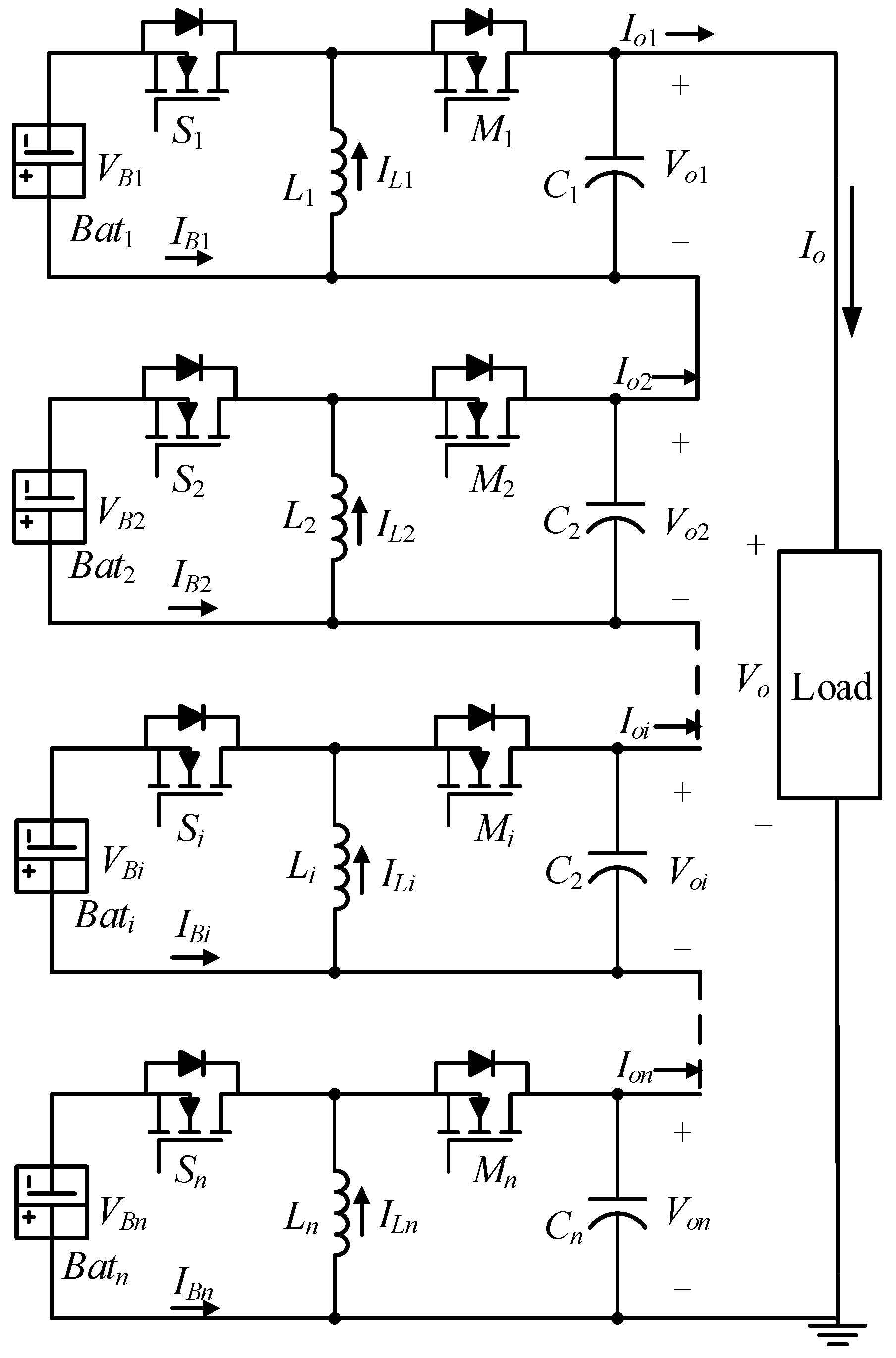
2. Modular Battery Energy Storage System
3. Fast SOC Balance and Design of Distributed Controller Control
- (1)
- Stable regulation of the DC bus voltage.
- (2)
- Effective SOC balance performance during dynamic processes.
- (3)
- A robust system fault tolerance mechanism.
3.1. SOC Estimation
3.2. Design of Centralized Controller Control
3.3. Design of Distributed Controller Control
3.4. Flow of SOC Balance Control
4. Simulation and Experiment
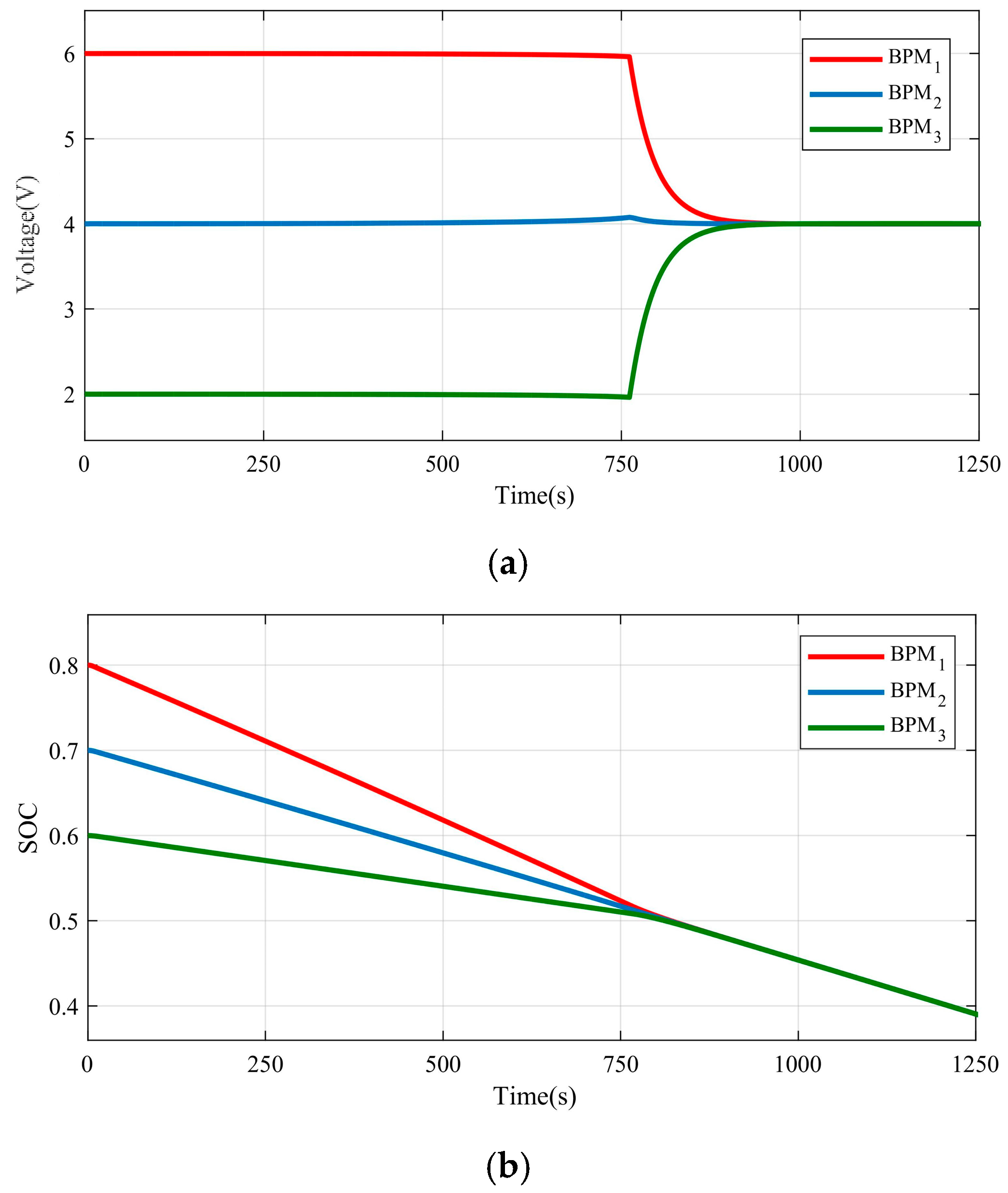
4.1. Simulation
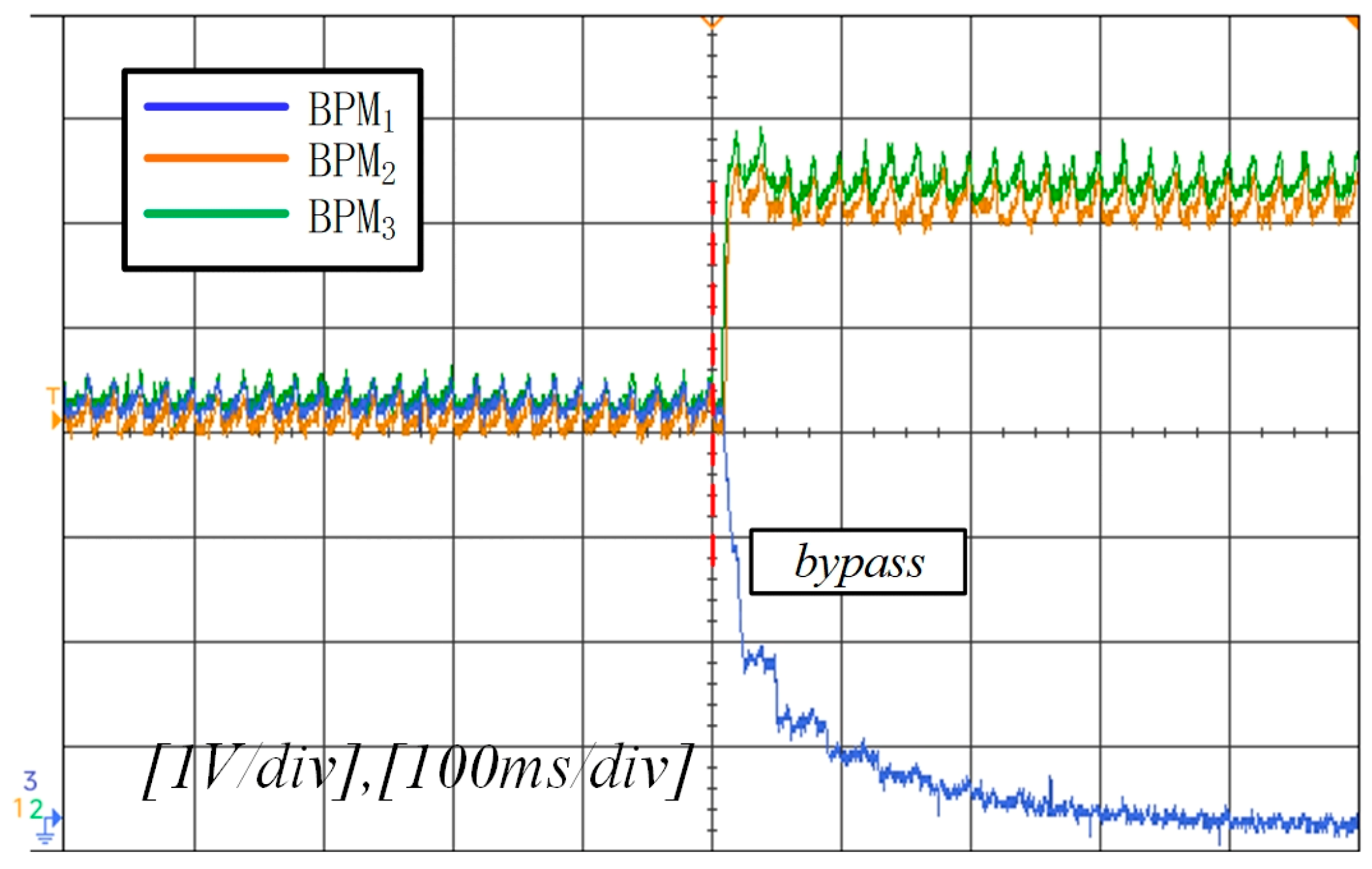
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tie, S.F.; Tan, C.W. A review of energy sources and energy management system in electric vehicles. Renew. Sustain. Energy Rev. 2013, 20, 82–102. [Google Scholar] [CrossRef]
- Hannan, M.A.; Hoque, M.M.; Hussain, A.; Yusof, Y.; Ker, P.J. State-of-the-art and energy management system of lithium-ion batteries in electric vehicle applications: Issues and recommendations. IEEE Access 2018, 6, 19362–19378. [Google Scholar] [CrossRef]
- Lawder, M.T.; Suthar, B.; Northrop, P.W.; De, S.; Hoff, C.M.; Leitermann, O.; Subramanian, V.R. Battery energy storage system (BESS) and battery management system (BMS) for grid-scale applications. Proc. IEEE 2014, 102, 1014–1030. [Google Scholar] [CrossRef]
- Lee, I.O. Hybrid PWM-resonant converter for electric vehicle on-board battery chargers. IEEE Trans. Power Electron. 2016, 31, 3639–3649. [Google Scholar] [CrossRef]
- Daowd, M.; Omar, N.; Bossche, P.V.D. Passive and Active Battery Balancing Comparison based on MATLAB Simulation. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011; pp. 1–7. [Google Scholar]
- Rehman, M.U.; Evzelman, M.; Hathaway, K.; Zane, R.; Plett, G.L.; Smith, K.; Wood, E.; Maksimovic, D. Modular approach for continuous cell-level balancing to improve performance of large battery packs. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition, Pittsburgh, PA, USA, 14–18 September 2014; pp. 4327–4334. [Google Scholar]
- Kim, J.; Shin, J.; Chun, C.; Cho, B.H. Stable configuration of a Li-ion series battery pack based on a screening process for improved voltage/SOC balancing. IEEE Trans. Power Electron. 2012, 27, 411–424. [Google Scholar] [CrossRef]
- Kim, Y.; Samad, N.A.; Oh, K.-Y.; Siegel, J.B.; Epureanu, B.I.; Stefanopoulou, A.G. Estimating state-of-charge imbalance of batteries using force measurements. In Proceedings of the American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 1500–5505. [Google Scholar]
- Lin, X.; Perez, H.E.; Siegel, J.B.; Stefanopoulou, A.G.; Li, Y.; Anderson, R.D.; Ding, Y.; Castanier, M.P. Online parameterization of lumped thermal dynamics in cylindrical lithium ion batteries for core temperature estimation and health monitoring. IEEE Trans. Control. Syst. Technol. 2013, 21, 1745–1755. [Google Scholar]
- Lozano, J.G.; Cadaval, E.R. Battery equalization active methods. J. Power Sources 2014, 246, 934–949. [Google Scholar] [CrossRef]
- Cao, J.; Schofield, N.; Emadi, A. Battery balancing methods: A comprehensive review. In Proceedings of the Vehicle Power and Propulsion Conference, Harbin, China, 3–5 September 2008; pp. 1–6. [Google Scholar]
- Zhang, X.; Liu, P.; Wang, D. The design and implementation of smart battery management system balance technology. J. Converg. Inf. Technol. 2011, 6, 108–116. [Google Scholar]
- Baronti, F.; Roncella, R.; Saletti, R.; Zamboni, W. Experimental validation of an efficient charge equalization system for Lithium-Ion batteries. In Proceedings of the IEEE 23rd International Symposium on Industrial Electronics, Istanbul, Turkey, 1–4 June 2014; pp. 1807–1812. [Google Scholar]
- Uno, M.; Tanaka, K. Single-switch multioutput charger using voltage multiplier for series-connected lithiumion battery/supercapacitor equalization. IEEE Trans. Ind. Electron. 2013, 60, 3227–3239. [Google Scholar] [CrossRef]
- Goodarzi, S.; Beiranvand, R.; Mousavi, S.M.; Mohamadian, M. A new algorithm for increasing balancing speed of switched-capacitor lithium-ion battery cell equalizers. In Proceedings of the 6th Power Electronics, Drive Systems & Technologies Conference, Tehran, Iran, 3–4 February 2015; pp. 292–297. [Google Scholar]
- Ye, Y.; Cheng, K.W.E. Analysis and design of zero-current switching switched-capacitor cell balancing circuit for series-connected battery/supercapacitor. IEEE Trans. Veh. Technol. 2018, 67, 948–955. [Google Scholar] [CrossRef]
- Sang-Hyun, P.; Ki-Bum, P.; Hyoung-Suk, K.; Gun-Woo, M.; Myung-Joong, Y. Single-magnetic cell-to-cell charge equalization converter with reduced number of transformer windings. IEEE Trans. Power Electron. 2012, 27, 2900–2911. [Google Scholar] [CrossRef]
- Mestrallet, F.; Kerachev, L.; Crebier, J.-C.; Collet, A. Multiphase interleaved converter for lithium battery active balancing. IEEE Trans. Power Electron. 2014, 29, 2874–2881. [Google Scholar] [CrossRef]
- Li, S.; Mi, C.C.; Zhang, M. A high-efficiency active battery-balancing circuit using multiwinding transformer. IEEE Trans. Ind. Appl. 2013, 49, 198–207. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, X.; Cui, Y.; Zou, J.; Yang, S. A multiwinding transformer cell-to-cell active equalization method for lithium-ion batteries with reduced number of driving circuits. IEEE Trans. Power Electron. 2016, 31, 4916–4929. [Google Scholar]
- Huang, W.; Qahouq, J.A.A. Energy sharing control scheme for state-of-charge balancing of distributed battery energy storage system. IEEE Trans. Ind. Electron. 2015, 62, 2764–2776. [Google Scholar] [CrossRef]
- Yu, L.-R.; Hsieh, Y.-C.; Liu, W.-C.; Moo, C.-S. Balanced discharging for serial battery power modules with boost converters. In Proceedings of the 2013 International Conference on System Science and Engineering, Budapest, Hungary, 4–6 July 2013; pp. 449–453. [Google Scholar]
- Li, Y.; Han, Y. Evaluation of a module-integrated distributed battery energy storage system. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition, Montreal, QC, Canada, 20–24 September 2015; pp. 1351–1358. [Google Scholar]
- Li, Y.; Han, Y. A module-integrated distributed battery energy storage and management system. IEEE Trans Power Electron 2016, 31, 8260–8270. [Google Scholar] [CrossRef]
- Yang, Q.; Xu, J.; Li, X.; Xu, D.; Cao, B. State-of-health estimation of lithium-ion battery based on fractional impedance model and interval capacity. Int. J. Electr. Power Energy Syst. 2020, 119, 105883. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zhou, S.; Mao, J. Research on Fast SOC Balance Control of Modular Battery Energy Storage System. Energies 2024, 17, 5907. https://doi.org/10.3390/en17235907
Wang J, Zhou S, Mao J. Research on Fast SOC Balance Control of Modular Battery Energy Storage System. Energies. 2024; 17(23):5907. https://doi.org/10.3390/en17235907
Chicago/Turabian StyleWang, Jianlin, Shenglong Zhou, and Jinlu Mao. 2024. "Research on Fast SOC Balance Control of Modular Battery Energy Storage System" Energies 17, no. 23: 5907. https://doi.org/10.3390/en17235907
APA StyleWang, J., Zhou, S., & Mao, J. (2024). Research on Fast SOC Balance Control of Modular Battery Energy Storage System. Energies, 17(23), 5907. https://doi.org/10.3390/en17235907





