Reliability Model of Battery Energy Storage Cooperating with Prosumer PV Installations
Abstract
1. Introduction
- Structural reliability, resulting from the design, construction, and layout of the equipment comprising the energy storage and connected with ESS failure;
- Generation reliability, resulting from the availability of stored energy.
2. Methodology
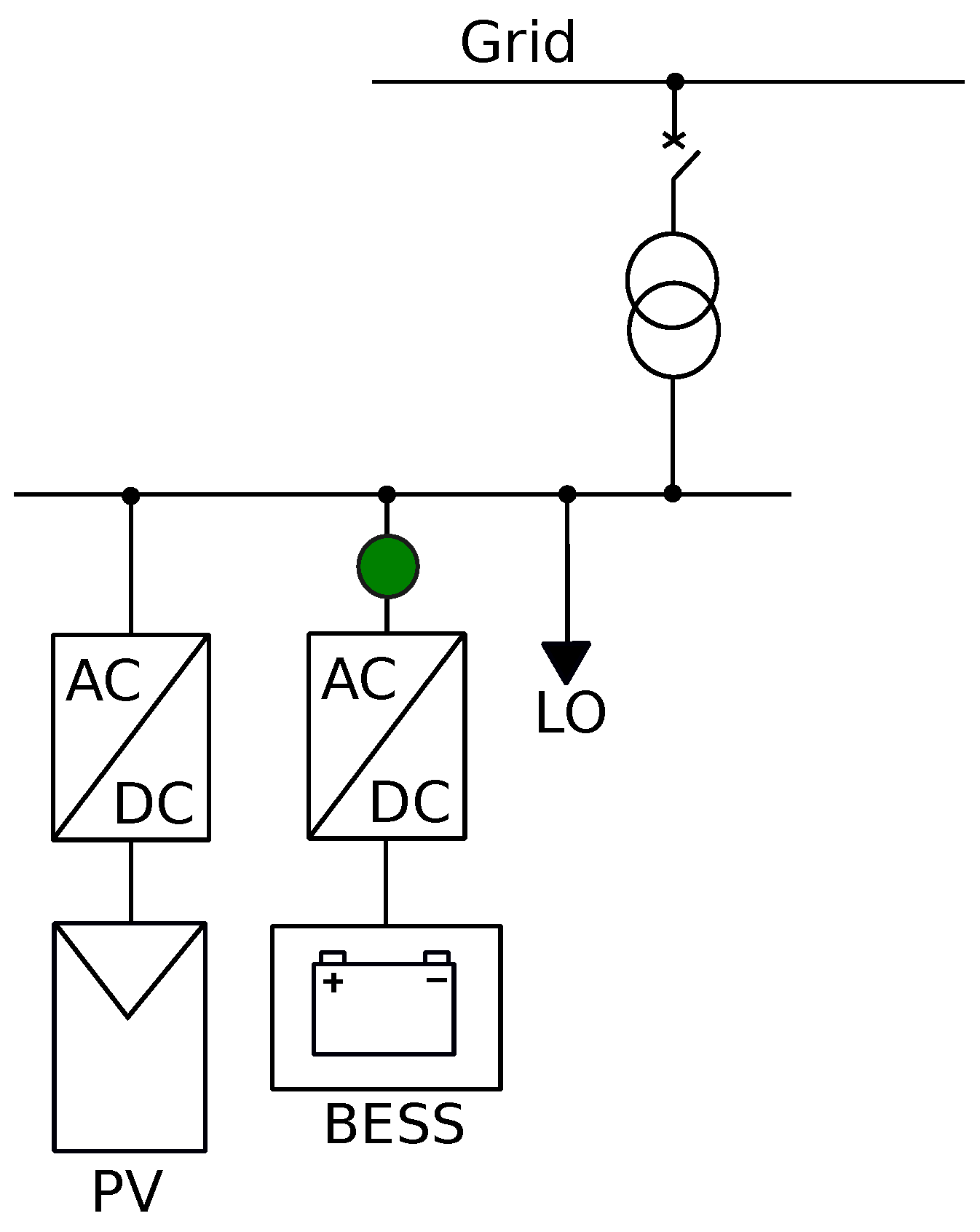
2.1. System Model
2.2. BESS Control Strategy
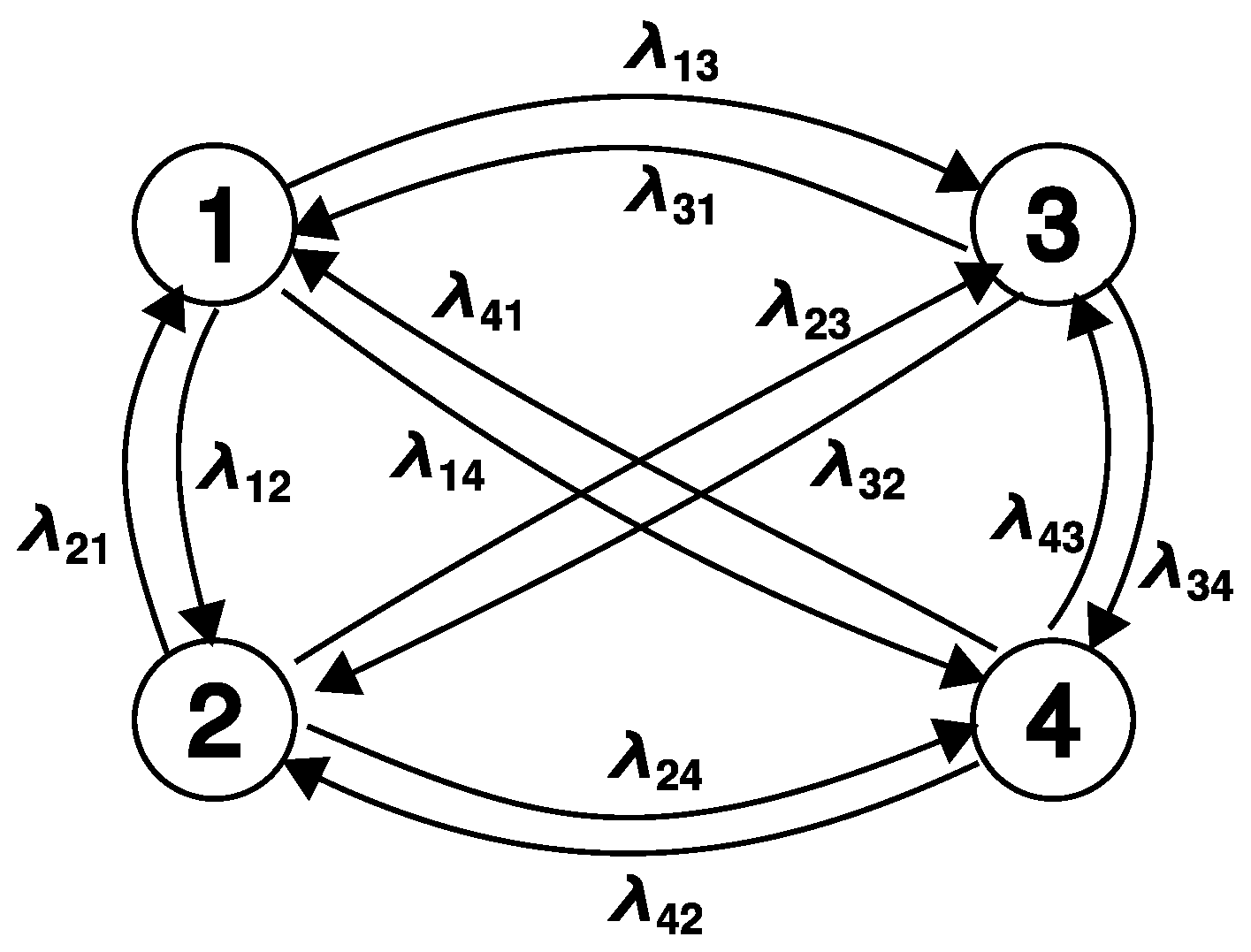
2.3. Reliability Model of BESS
- State 1—there is excess power in the system that the BESS can store ();
- State 2—there is excess power in the system, but the BESS is unable to store it (the has reached the maximum level );
- State 3—there is a shortage of power in the system, , and the BESS can supply it ();
- State 4—there is a shortage of power in the system, but the BESS is unable to supply it (the has reached the minimum level ).
2.4. Determination of Reliability Parameters
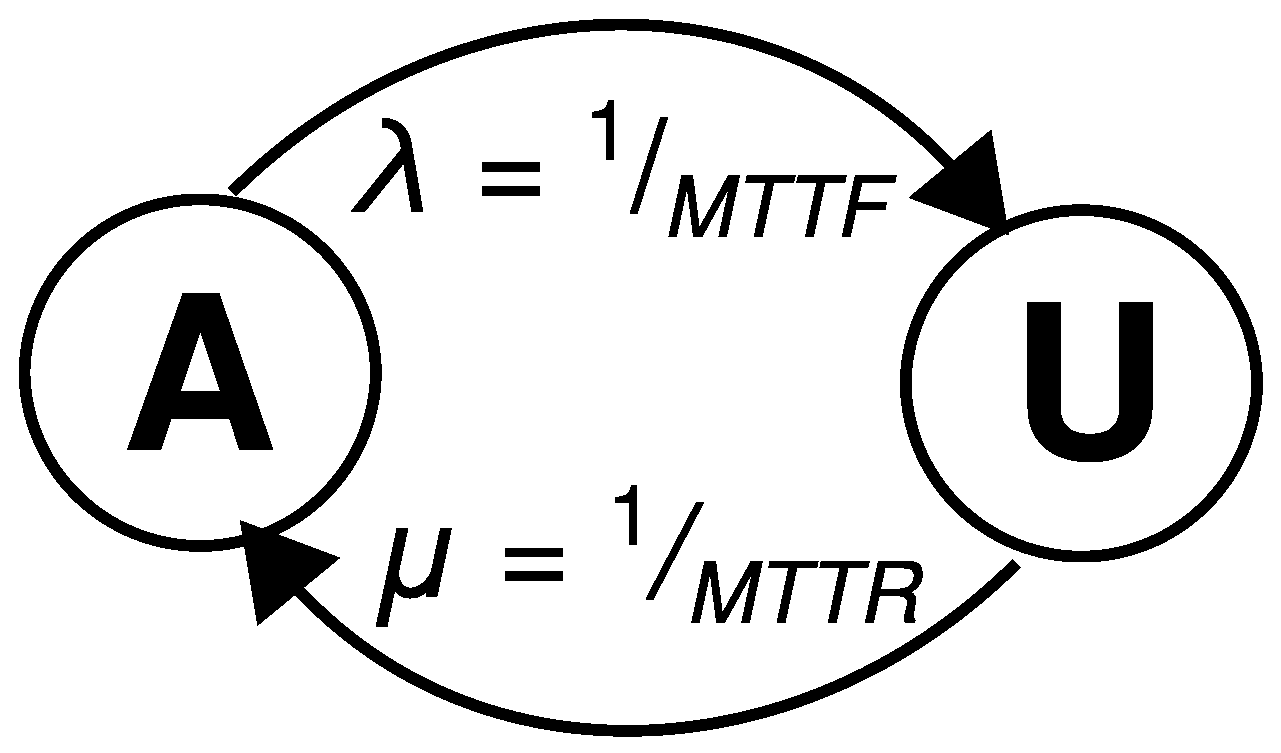
2.5. Simplified Two-State Model
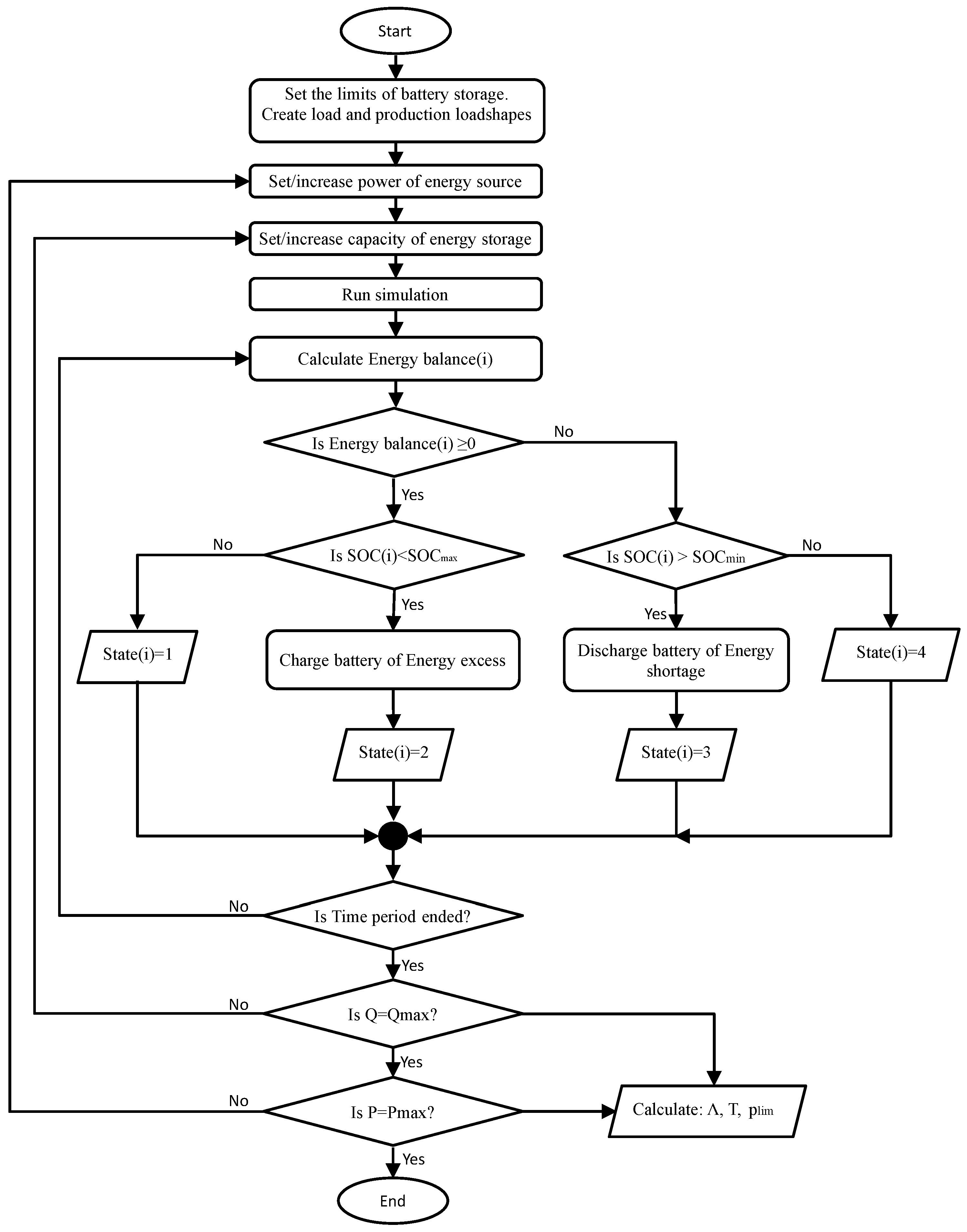
2.6. Simulation Algorithm
3. Results and Discussion
3.1. PV Model
3.2. Load Model
3.2.1. Residential Profile
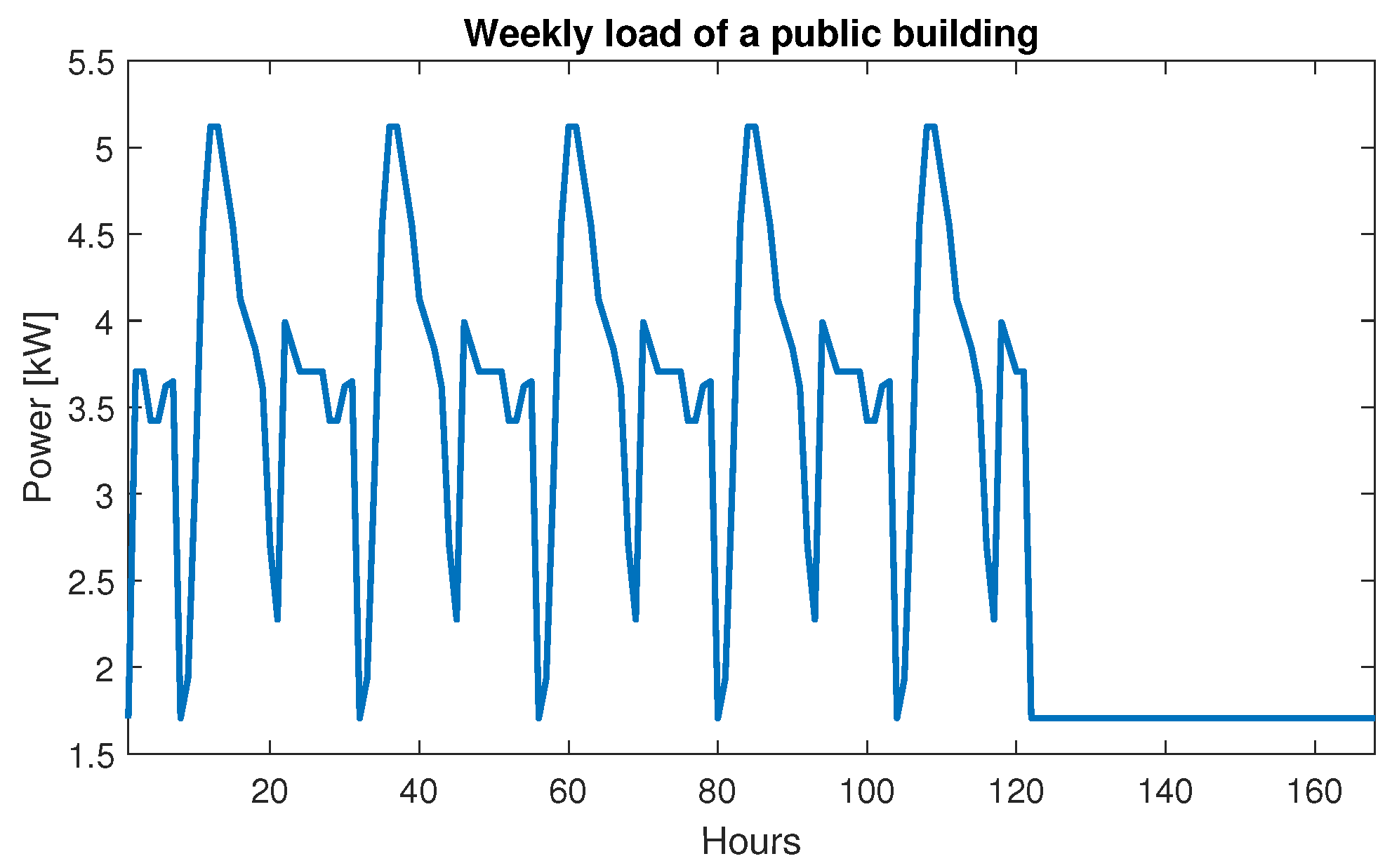
3.2.2. Public Office Profile
3.3. Battery Energy Storage Model
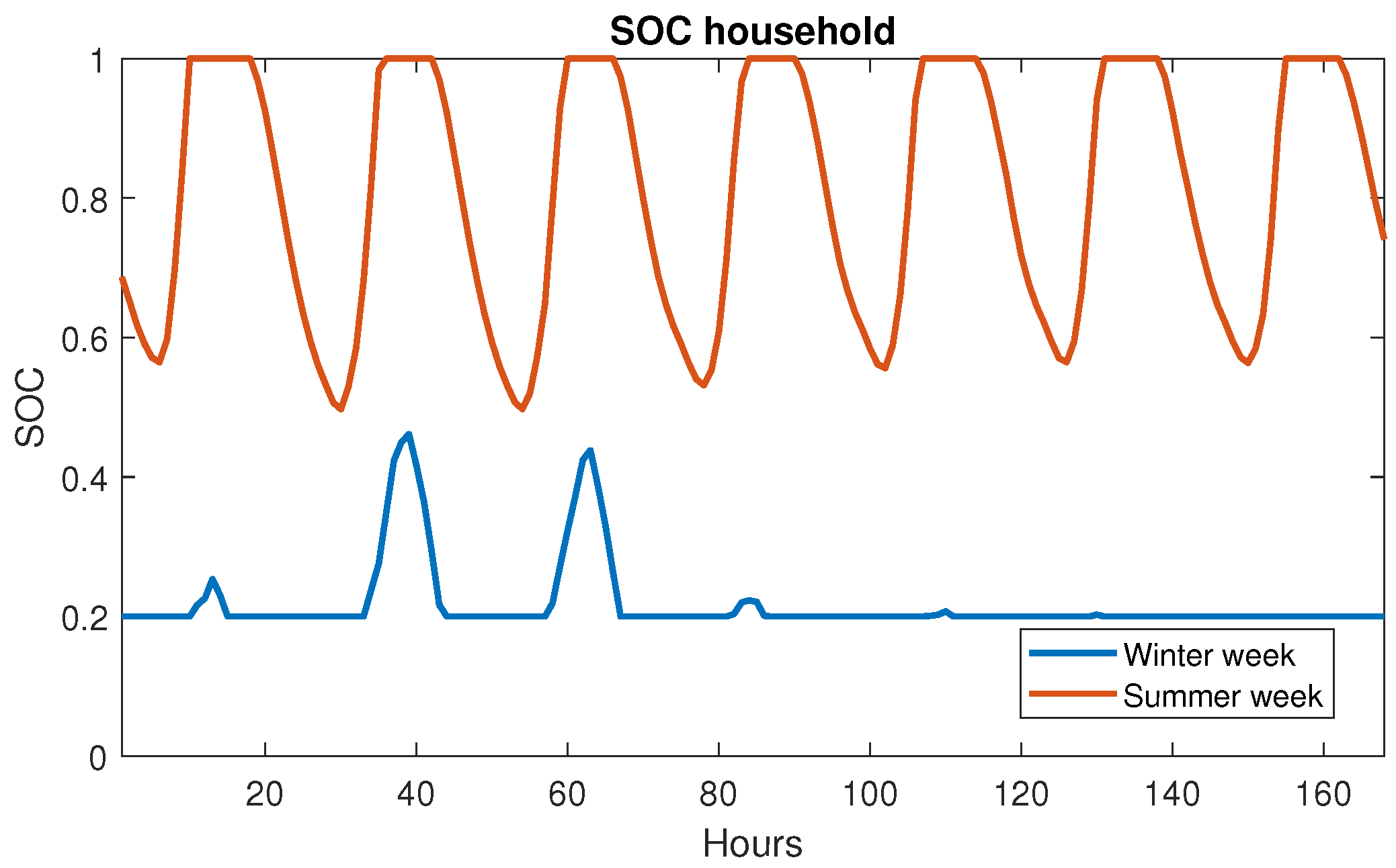
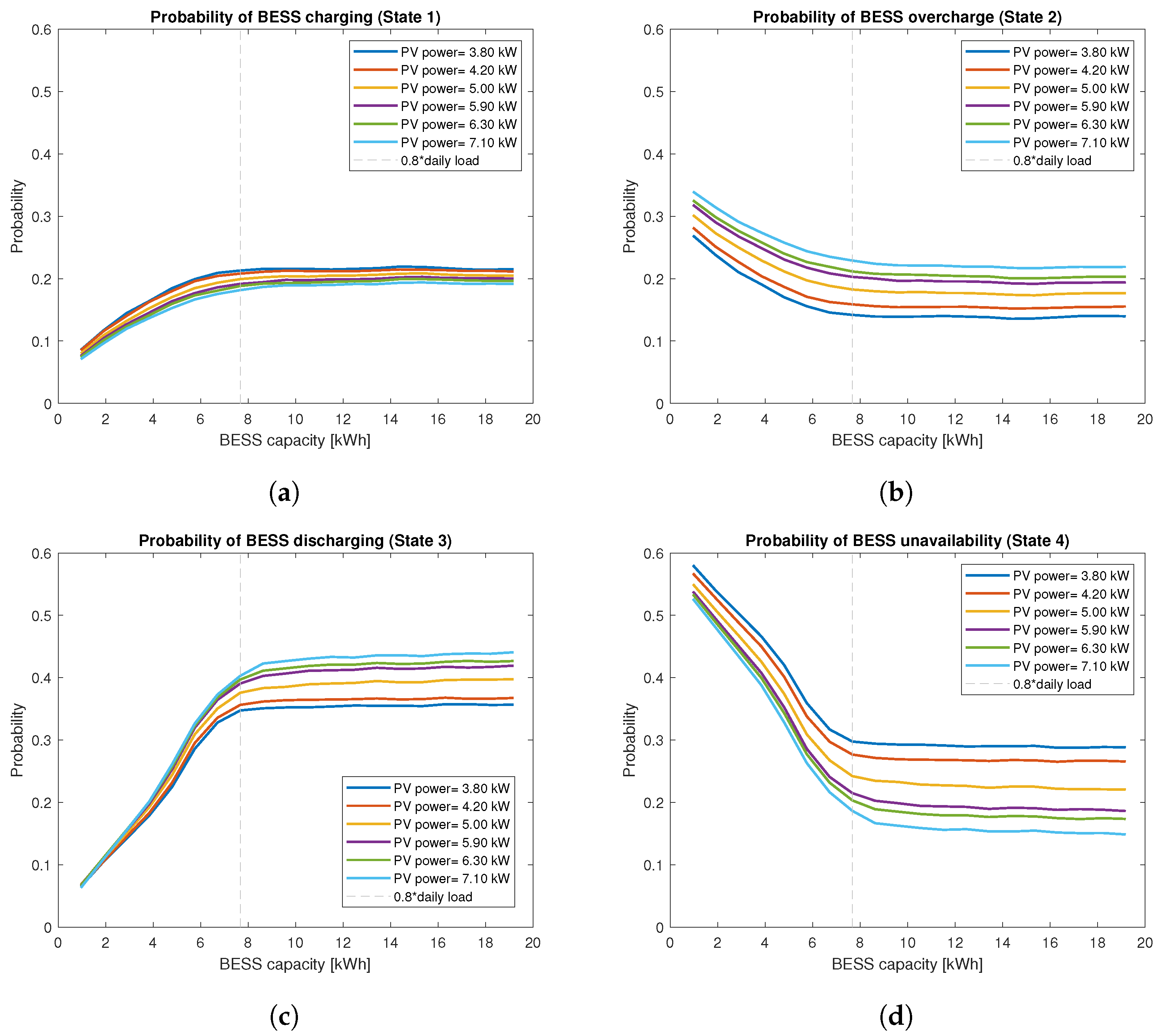
3.4. Residential Installation
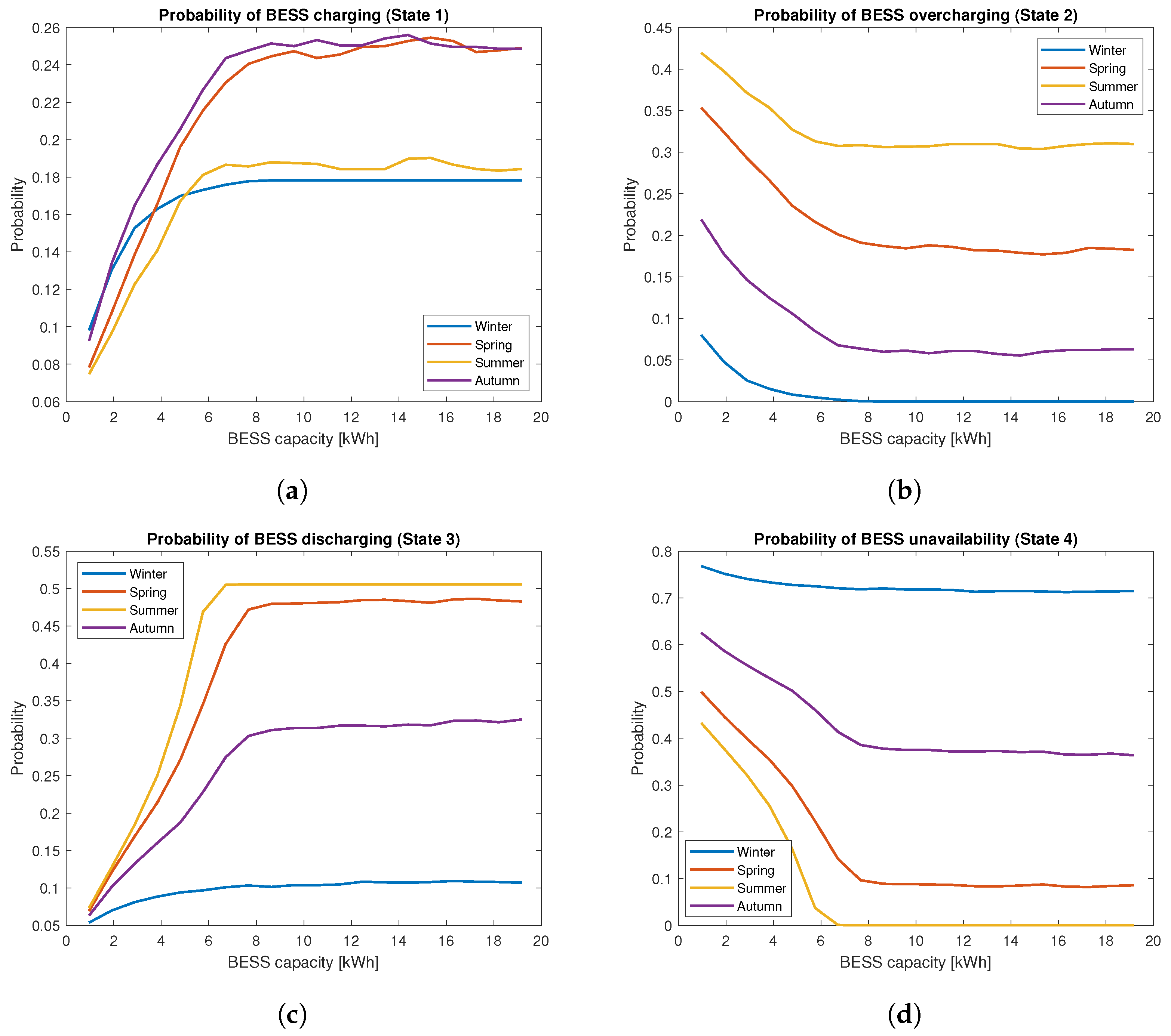
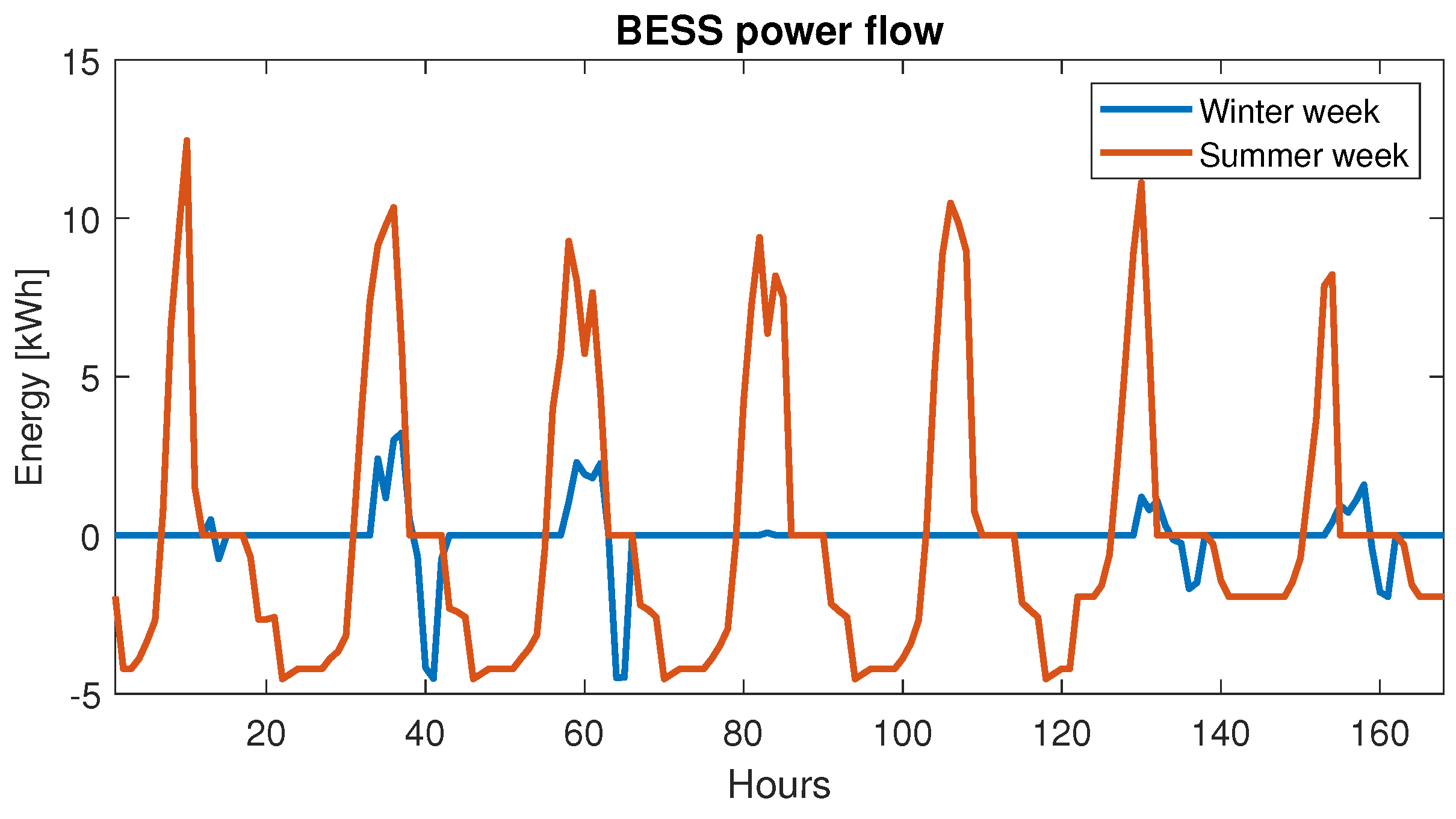
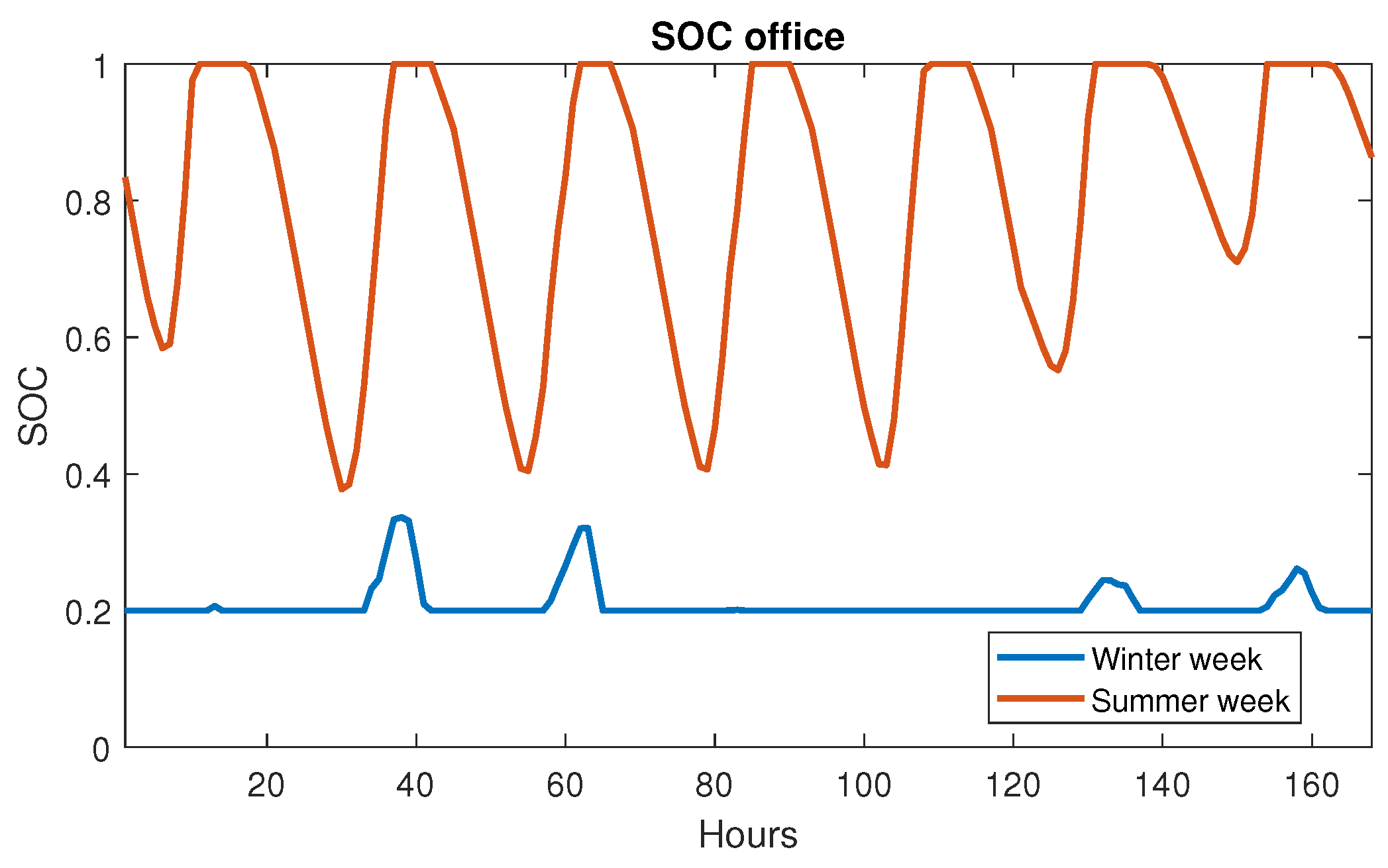
3.5. Public Office Building
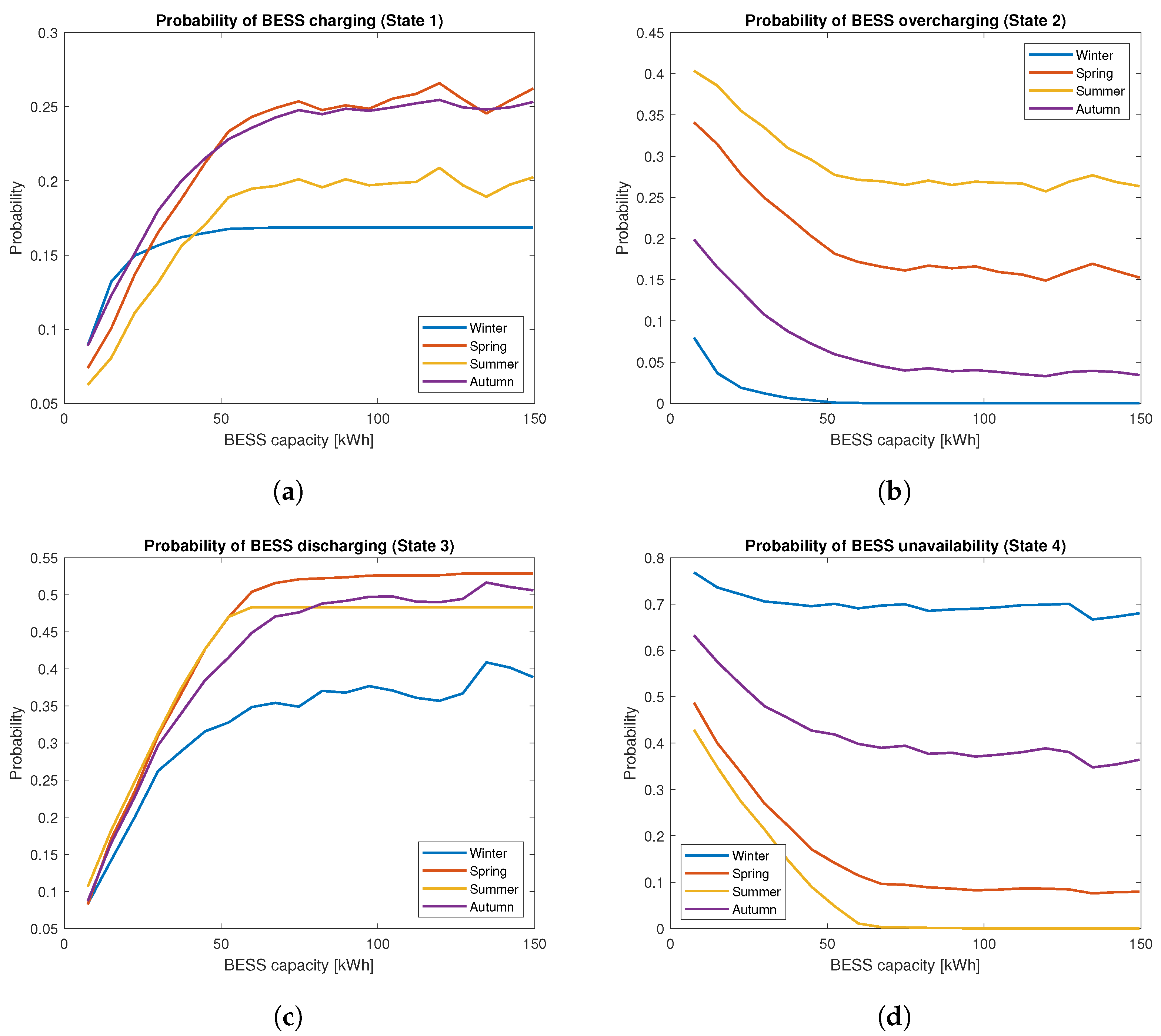
3.6. Two-State Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, P.; Li, W.; Li, S.; Wang, Y.; Xiao, W. Reliability assessment of photovoltaic power systems: Review of current status and future perspectives. Appl. Energy 2013, 104, 822–833. [Google Scholar] [CrossRef]
- Niu, M.; Xu, N.Z.; Kong, X.; Ngin, H.T.; Ge, Y.Y.; Liu, J.S.; Liu, Y.T. Reliability Importance of Renewable Energy Sources to Overall Generating Systems. IEEE Access 2021, 9, 20450–20459. [Google Scholar] [CrossRef]
- Khosravani, A.; Safaei, E.; Reynolds, M.; Kelly, K.E.; Powell, K.M. Challenges of reaching high renewable fractions in hybrid renewable energy systems. Energy Rep. 2023, 9, 1000–1017. [Google Scholar] [CrossRef]
- Meera, P.; Hemamalini, S. Reliability assessment and enhancement of distribution networks integrated with renewable distributed generators: A review. Sustain. Energy Technol. Assess. 2022, 54, 102812. [Google Scholar] [CrossRef]
- Lee, J.Y.; Ramasamy, A.; Ong, K.H.; Verayiah, R.; Mokhlis, H.; Marsadek, M. Energy storage systems: A review of its progress and outlook, potential benefits, barriers and solutions within the Malaysian distribution network. J. Energy Storage 2023, 72, 108360. [Google Scholar] [CrossRef]
- Dugan, J.; Mohagheghi, S.; Kroposki, B. Application of Mobile Energy Storage for Enhancing Power Grid Resilience: A Review. Energies 2021, 14, 6476. [Google Scholar] [CrossRef]
- Sakthivelnathan, N.; Arefi, A.; Lund, C.; Mehrizi-Sani, A.; Muyeen, S. Energy storage as a service to achieve a required reliability level for renewable-rich standalone microgrids. J. Energy Storage 2024, 77, 109691. [Google Scholar] [CrossRef]
- Boyle, J.; Littler, T.; Foley, A.M. Aggregator control of battery energy storage in wind power stations to maximize availability of regulation service. Energy Convers. Manag. X 2024, 24, 100703. [Google Scholar] [CrossRef]
- Zhang, M.; Li, W.; Yu, S.S.; Wen, K.; Muyeen, S. Day-ahead optimization dispatch strategy for large-scale battery energy storage considering multiple regulation and prediction failures. Energy 2023, 270, 126945. [Google Scholar] [CrossRef]
- Zheng, S.; Huang, G.; Lai, A.C. Techno-economic performance analysis of synergistic energy sharing strategies for grid-connected prosumers with distributed battery storages. Renew. Energy 2021, 178, 1261–1278. [Google Scholar] [CrossRef]
- Yan, X.; Li, J.; Zhao, P.; Liu, N.; Wang, L.; Yue, B.; Liu, Y. Review on reliability assessment of energy storage systems. IET Smart Grid. [CrossRef]
- Liu, M.; Li, W.; Wang, C.; Polis, M.P.; Wang, L.Y.; Li, J. Reliability Evaluation of Large Scale Battery Energy Storage Systems. IEEE Trans. Smart Grid 2017, 8, 2733–2743. [Google Scholar] [CrossRef]
- Liu, H.; Panteli, M. A Reliability Analysis and Comparison of Battery Energy Storage Systems. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe), Bucharest, Romania, 29 September–2 October 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Li, J.; Yan, X.; Liu, N. Reliability index setting and fuzzy multi-state modeling for battery storage station. J. Energy Storage 2024, 84, 110720. [Google Scholar] [CrossRef]
- Suyambu, M.; Vishwakarma, P.K. Improving grid reliability with grid-scale Battery Energy Storage Systems (BESS). Int. J. Sci. Res. Arch. 2024, 13, 776–789. [Google Scholar] [CrossRef]
- Wang, H.; Shao, Y.; Zhou, L. Reliability Analysis of Battery Energy Storage Systems: An Overview. In Proceedings of the 2022 IEEE/IAS Industrial and Commercial Power System Asia (ICPS Asia), Shanghai, China, 8–11 July 2022; pp. 2036–2040. [Google Scholar] [CrossRef]
- Bakeer, A.; Chub, A.; Shen, Y.; Sangwongwanich, A. Reliability analysis of battery energy storage system for various stationary applications. J. Energy Storage 2022, 50, 104217. [Google Scholar] [CrossRef]
- Cheng, L.; Wan, Y.; Zhou, Y.; Gao, D.W. Operational Reliability Modeling and Assessment of Battery Energy Storage Based on Lithium-ion Battery Lifetime Degradation. J. Mod. Power Syst. Clean Energy 2022, 10, 1738–1749. [Google Scholar] [CrossRef]
- Borges, C.L.T. An overview of reliability models and methods for distribution systems with renewable energy distributed generation. Renew. Sustain. Energy Rev. 2012, 16, 4008–4015. [Google Scholar] [CrossRef]
- Aien, M.; Biglari, A.; Rashidinejad, M. Probabilistic reliability evaluation of hybrid wind-photovoltaic power systems. In Proceedings of the 2013 21st Iranian Conference on Electrical Engineering (ICEE), Mashhad, Iran, 14–16 May 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Marchel, P.; Paska, J.; Zagrajek, K.; Klos, M.; Pawlak, K.; Terlikowski, P.; Bartecka, M.; Michalski, L. Reliability Models of Generating Units Utilizing Renewable Energy Sources. In Proceedings of the 2019 Modern Electric Power Systems (MEPS), Wroclaw, Poland, 9–12 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Escalera, A.; Prodanović, M.; Castronuovo, E.D. An Analysis of the Energy Storage for Improving the Reliability of Distribution Networks. In Proceedings of the 2018 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Sarajevo, Bosnia and Herzegovina, 21–25 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Tur, M.R. Reliability Assessment of Distribution Power System When Considering Energy Storage Configuration Technique. IEEE Access 2020, 8, 77962–77971. [Google Scholar] [CrossRef]
- Karngala, A.K.; Singh, C. Reliability Assessment Framework for the Distribution System Including Distributed Energy Resources. IEEE Trans. Sustain. Energy 2021, 12, 1539–1548. [Google Scholar] [CrossRef]
- Adefarati, T.; Bansal, R. Reliability assessment of distribution system with the integration of renewable distributed generation. Appl. Energy 2017, 185, 158–171. [Google Scholar] [CrossRef]
- Hussein, I.; AlMuhaini, M. Reliability assessment of integrated wind-storage systems using Monte Carlo simulation. In Proceedings of the 2016 13th International Multi-Conference on Systems, Signals and Devices (SSD), Leipzig, Germany, 21–24 March 2016; pp. 709–713. [Google Scholar] [CrossRef]
- Weng, Z.; Zhou, J.; Zhan, Z. Reliability Evaluation of Standalone Microgrid Based on Sequential Monte Carlo Simulation Method. Energies 2022, 15, 6706. [Google Scholar] [CrossRef]
- Abdulgalil, M.A.; Khalid, M.; Alshehri, J. Microgrid Reliability Evaluation Using Distributed Energy Storage Systems. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 2837–2841. [Google Scholar] [CrossRef]
- Gautam, P.; Karki, R. Quantifying Reliability Contribution of an Energy Storage System to a Distribution System. In Proceedings of the 2018 IEEE Power and Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Xie, L.; Xiang, Y.; Xu, X.; Wang, S.; Li, Q.; Liu, F.; Liu, J. Optimal Planning of Energy Storage in Distribution Feeders Considering Economy and Reliability. Energy Technol. 2024, 12, 2400200. [Google Scholar] [CrossRef]
- Chen, Y.; Zheng, Y.; Luo, F.; Wen, J.; Xu, Z. Reliability evaluation of distribution systems with mobile energy storage systems. IET Renew. Power Gener. 2016, 10, 1562–1569. [Google Scholar] [CrossRef]
- Mohamad, F.; Teh, J. Impacts of Energy Storage System on Power System Reliability: A Systematic Review. Energies 2018, 11, 1749. [Google Scholar] [CrossRef]
- Ayesha; Numan, M.; Baig, M.F.; Yousif, M. Reliability evaluation of energy storage systems combined with other grid flexibility options: A review. J. Energy Storage 2023, 63, 107022. [Google Scholar] [CrossRef]
- Karngala, A.K.; Singh, C. Impact of system parameters and geospatial variables on the reliability of residential systems with PV and energy storage. Appl. Energy 2023, 344, 121266. [Google Scholar] [CrossRef]
- Zarate-Perez, E.; Santos-Mejía, C.; Sebastián, R. Reliability of autonomous solar-wind microgrids with battery energy storage system applied in the residential sector. Energy Rep. 2023, 9, 172–183. [Google Scholar] [CrossRef]
- Rezaeimozafar, M.; Monaghan, R.F.; Barrett, E.; Duffy, M. A review of behind-the-meter energy storage systems in smart grids. Renew. Sustain. Energy Rev. 2022, 164, 112573. [Google Scholar] [CrossRef]
- Polish Act on Renewable Energy Sources. February 20th 2015, (Dz. U. 2015 Item 478). Available online: https://isap.sejm.gov.pl/isap.nsf/download.xsp/WDU20150000478/U/D20150478Lj.pdf (accessed on 1 June 2024). (In Polish)
- PVGIS Portal. Available online: http://re.jrc.ec.europa.eu/pvg_tools/en/tools.html (accessed on 1 June 2024).
- Bartecka, M.; Terlikowski, P.; Kłos, M.; Michalski, Ł. Sizing of prosumer hybrid renewable energy systems in Poland. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 721–731. [Google Scholar] [CrossRef]
- Skoplaki, E.; Palyvos, J. On the temperature dependence of photovoltaic module electrical performance: A review of efficiency/power correlations. Sol. Energy 2009, 83, 614–624. [Google Scholar] [CrossRef]
- PV Module Datasheet. Available online: https://merxu.com/media/product-index/datasheet/f338e1be-3ebe-4a41-a1c8-9f176d9e3a98 (accessed on 9 August 2024).
- Household Standard Profile of Polish DSO. Available online: https://www.stoen.pl/strona/iriesd (accessed on 9 August 2024).
- Banasiak, P.; Gorczyca-Goraj, A.; Przygrodzki, M. Analysis of load schedules of a selected segment of low-voltage customers. Energetyka 2017, 1, 23–27. [Google Scholar]
- Ayyadi, S.; Maaroufi, M.; Arif, S.M. EVs charging and discharging model consisted of EV users behaviour. In Proceedings of the 2020 5th International Conference on Renewable Energies for Developing Countries (REDEC), Marrakech, Morocco, 29–30 June 2020; pp. 1–4. [Google Scholar] [CrossRef]




| Power | Module Efficiency | Surface | System Efficiency |
|---|---|---|---|
| P | S | ||
| [W] | [%] | [m2] | [%] |
| 420 | 21.4 | 1.953 | 88 |
| kWh | h | h | h | h | - | - | - | - |
|---|---|---|---|---|---|---|---|---|
| 0.96 | 2.03 | 7.80 | 1.63 | 13.96 | 0.086 | 0.269 | 0.065 | 0.580 |
| 1.92 | 2.75 | 7.65 | 2.64 | 13.02 | 0.117 | 0.238 | 0.106 | 0.540 |
| 2.87 | 3.40 | 7.28 | 3.60 | 12.07 | 0.145 | 0.210 | 0.142 | 0.503 |
| 3.83 | 3.85 | 7.15 | 4.49 | 11.28 | 0.164 | 0.191 | 0.179 | 0.466 |
| 4.79 | 4.34 | 6.78 | 5.68 | 10.15 | 0.185 | 0.170 | 0.225 | 0.420 |
| 5.75 | 4.68 | 6.53 | 7.24 | 10.59 | 0.199 | 0.156 | 0.286 | 0.359 |
| 6.71 | 4.91 | 6.35 | 8.30 | 12.23 | 0.209 | 0.146 | 0.328 | 0.317 |
| 7.66 | 5.00 | 6.37 | 8.79 | 14.65 | 0.213 | 0.142 | 0.347 | 0.298 |
| 8.62 | 5.06 | 6.46 | 8.86 | 15.34 | 0.216 | 0.139 | 0.351 | 0.294 |
| 9.58 | 5.07 | 6.48 | 8.97 | 15.64 | 0.216 | 0.139 | 0.352 | 0.293 |
| 10.54 | 5.06 | 6.46 | 8.97 | 15.72 | 0.216 | 0.139 | 0.353 | 0.293 |
| 11.50 | 5.04 | 6.46 | 8.98 | 15.66 | 0.215 | 0.140 | 0.354 | 0.291 |
| 12.45 | 5.07 | 6.59 | 9.07 | 15.67 | 0.216 | 0.139 | 0.355 | 0.290 |
| 13.41 | 5.09 | 6.51 | 9.14 | 15.69 | 0.217 | 0.138 | 0.355 | 0.290 |
| 14.37 | 5.15 | 6.46 | 9.12 | 15.69 | 0.219 | 0.136 | 0.355 | 0.290 |
| 15.33 | 5.14 | 6.45 | 9.13 | 15.52 | 0.219 | 0.136 | 0.354 | 0.291 |
| 16.29 | 5.09 | 6.54 | 9.18 | 15.75 | 0.217 | 0.138 | 0.357 | 0.288 |
| 17.24 | 5.05 | 6.56 | 9.26 | 15.84 | 0.215 | 0.140 | 0.358 | 0.288 |
| 18.20 | 5.04 | 6.64 | 9.29 | 15.71 | 0.215 | 0.140 | 0.356 | 0.289 |
| 19.16 | 5.05 | 6.65 | 9.29 | 15.70 | 0.215 | 0.140 | 0.357 | 0.288 |
| kWh | h | h | h | h | - | - | - | - |
|---|---|---|---|---|---|---|---|---|
| 7.48 | 1.90 | 7.81 | 2.24 | 14.38 | 0.078 | 0.257 | 0.087 | 0.578 |
| 14.96 | 2.63 | 7.63 | 3.91 | 12.77 | 0.109 | 0.226 | 0.152 | 0.513 |
| 22.43 | 3.31 | 7.18 | 5.20 | 11.52 | 0.137 | 0.198 | 0.202 | 0.463 |
| 29.91 | 3.81 | 6.96 | 6.43 | 11.20 | 0.158 | 0.177 | 0.249 | 0.416 |
| 37.39 | 4.25 | 6.62 | 7.37 | 10.61 | 0.177 | 0.159 | 0.286 | 0.379 |
| 44.87 | 4.59 | 6.34 | 8.29 | 10.84 | 0.191 | 0.145 | 0.321 | 0.344 |
| 52.35 | 4.91 | 6.12 | 8.78 | 10.86 | 0.205 | 0.131 | 0.340 | 0.325 |
| 59.82 | 5.05 | 6.17 | 9.39 | 12.81 | 0.211 | 0.125 | 0.363 | 0.301 |
| 67.30 | 5.15 | 6.09 | 9.64 | 15.14 | 0.214 | 0.121 | 0.371 | 0.294 |
| 74.78 | 5.23 | 6.05 | 9.61 | 15.30 | 0.218 | 0.117 | 0.370 | 0.295 |
| 82.26 | 5.15 | 6.16 | 9.85 | 15.54 | 0.214 | 0.121 | 0.379 | 0.286 |
| 89.74 | 5.22 | 6.11 | 9.87 | 15.77 | 0.217 | 0.118 | 0.379 | 0.286 |
| 97.21 | 5.17 | 6.21 | 9.97 | 16.22 | 0.216 | 0.120 | 0.381 | 0.283 |
| 104.69 | 5.24 | 6.11 | 9.91 | 16.35 | 0.218 | 0.117 | 0.379 | 0.286 |
| 112.17 | 5.28 | 6.09 | 9.83 | 16.42 | 0.220 | 0.115 | 0.376 | 0.289 |
| 119.65 | 5.39 | 5.94 | 9.83 | 16.44 | 0.225 | 0.111 | 0.374 | 0.291 |
| 127.13 | 5.22 | 6.17 | 9.95 | 16.64 | 0.218 | 0.118 | 0.376 | 0.289 |
| 134.60 | 5.11 | 6.38 | 10.41 | 17.02 | 0.213 | 0.122 | 0.395 | 0.270 |
| 142.08 | 5.22 | 6.21 | 10.28 | 16.54 | 0.218 | 0.118 | 0.391 | 0.274 |
| 149.56 | 5.32 | 6.10 | 10.22 | 16.26 | 0.223 | 0.113 | 0.386 | 0.278 |
| P = 3.78 kW | P = 4.20 kW | P = 5.04 kW | ||||
|---|---|---|---|---|---|---|
| MTTF | MTTR | MTTF | MTTR | MTTF | MTTR | |
| [kWh] | [h] | [h] | [h] | [h] | [h] | [h] |
| 0.96 | 10.13 | 13.96 | 10.36 | 13.53 | 10.69 | 13.02 |
| 1.92 | 11.14 | 13.02 | 11.25 | 12.52 | 11.67 | 12.03 |
| 2.87 | 11.96 | 12.07 | 12.21 | 11.63 | 12.64 | 11.07 |
| 3.83 | 12.95 | 11.28 | 13.16 | 10.74 | 13.67 | 10.11 |
| 4.79 | 14.02 | 10.15 | 14.32 | 9.59 | 14.97 | 8.93 |
| 5.75 | 18.96 | 10.59 | 19.59 | 9.96 | 20.87 | 9.30 |
| 6.71 | 26.47 | 12.23 | 26.88 | 11.32 | 28.26 | 10.28 |
| 7.66 | 34.76 | 14.65 | 35.39 | 13.47 | 38.82 | 12.33 |
| 8.62 | 37.02 | 15.34 | 39.40 | 14.58 | 43.25 | 13.18 |
| 9.58 | 38.00 | 15.64 | 39.76 | 14.56 | 44.21 | 13.33 |
| 10.54 | 38.25 | 15.72 | 40.30 | 14.70 | 47.24 | 13.91 |
| 11.50 | 38.31 | 15.66 | 40.31 | 14.68 | 47.65 | 13.93 |
| 12.45 | 38.64 | 15.67 | 40.35 | 14.65 | 48.39 | 14.07 |
| 13.41 | 38.62 | 15.69 | 39.91 | 14.41 | 49.29 | 14.08 |
| 14.37 | 38.62 | 15.69 | 40.08 | 14.58 | 47.77 | 13.81 |
| 15.33 | 38.12 | 15.52 | 40.10 | 14.55 | 47.45 | 13.70 |
| 16.29 | 39.24 | 15.75 | 40.48 | 14.52 | 49.75 | 14.08 |
| 17.24 | 39.49 | 15.84 | 40.38 | 14.62 | 49.79 | 14.04 |
| 18.20 | 38.93 | 15.71 | 40.39 | 14.61 | 50.54 | 14.24 |
| 19.16 | 38.95 | 15.70 | 40.45 | 14.54 | 50.94 | 14.32 |
| P = 27.30 kW | P = 32.76 kW | P = 38.22 kW | ||||
|---|---|---|---|---|---|---|
| MTTF | MTTR | MTTF | MTTR | MTTF | MTTR | |
| [kWh] | [h] | [h] | [h] | [h] | [h] | [h] |
| 7.48 | 10.54 | 14.38 | 10.69 | 13.20 | 10.86 | 12.53 |
| 14.96 | 12.15 | 12.77 | 12.34 | 11.56 | 12.58 | 10.81 |
| 22.43 | 13.40 | 11.52 | 13.62 | 10.29 | 13.84 | 9.55 |
| 29.91 | 15.80 | 11.20 | 16.09 | 9.80 | 16.46 | 8.91 |
| 37.39 | 17.43 | 10.61 | 18.17 | 9.26 | 18.70 | 8.31 |
| 44.87 | 20.74 | 10.84 | 21.37 | 9.22 | 22.10 | 8.08 |
| 52.35 | 22.66 | 10.86 | 23.67 | 9.10 | 25.72 | 8.20 |
| 59.82 | 29.85 | 12.81 | 33.73 | 11.36 | 36.65 | 10.14 |
| 67.30 | 36.60 | 15.14 | 40.83 | 13.15 | 43.55 | 11.46 |
| 74.78 | 36.75 | 15.30 | 41.77 | 13.58 | 45.87 | 12.06 |
| 82.26 | 39.11 | 15.54 | 44.85 | 13.84 | 50.44 | 12.49 |
| 89.74 | 39.57 | 15.77 | 44.38 | 13.92 | 49.94 | 12.53 |
| 97.21 | 41.30 | 16.22 | 45.79 | 14.10 | 51.65 | 12.66 |
| 104.69 | 41.17 | 16.35 | 44.39 | 13.91 | 51.18 | 12.66 |
| 112.17 | 40.72 | 16.42 | 43.04 | 13.75 | 50.17 | 12.75 |
| 119.65 | 40.33 | 16.44 | 43.18 | 13.97 | 49.31 | 12.72 |
| 127.13 | 41.25 | 16.64 | 44.01 | 13.90 | 51.73 | 13.05 |
| 134.60 | 46.33 | 17.02 | 48.30 | 13.73 | 57.63 | 12.90 |
| 142.08 | 44.17 | 16.54 | 47.36 | 13.80 | 56.86 | 13.10 |
| 149.56 | 42.42 | 16.26 | 46.10 | 13.80 | 55.29 | 13.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bartecka, M.; Marchel, P.; Zagrajek, K.; Lewandowski, M.; Kłos, M. Reliability Model of Battery Energy Storage Cooperating with Prosumer PV Installations. Energies 2024, 17, 5839. https://doi.org/10.3390/en17235839
Bartecka M, Marchel P, Zagrajek K, Lewandowski M, Kłos M. Reliability Model of Battery Energy Storage Cooperating with Prosumer PV Installations. Energies. 2024; 17(23):5839. https://doi.org/10.3390/en17235839
Chicago/Turabian StyleBartecka, Magdalena, Piotr Marchel, Krzysztof Zagrajek, Mirosław Lewandowski, and Mariusz Kłos. 2024. "Reliability Model of Battery Energy Storage Cooperating with Prosumer PV Installations" Energies 17, no. 23: 5839. https://doi.org/10.3390/en17235839
APA StyleBartecka, M., Marchel, P., Zagrajek, K., Lewandowski, M., & Kłos, M. (2024). Reliability Model of Battery Energy Storage Cooperating with Prosumer PV Installations. Energies, 17(23), 5839. https://doi.org/10.3390/en17235839






