A Fast Variance Reduction Technique for Efficient Radiation Shielding Calculations in Nuclear Reactors
Abstract
1. Introduction
2. Methodology and Reactor Overview
2.1. MCNP
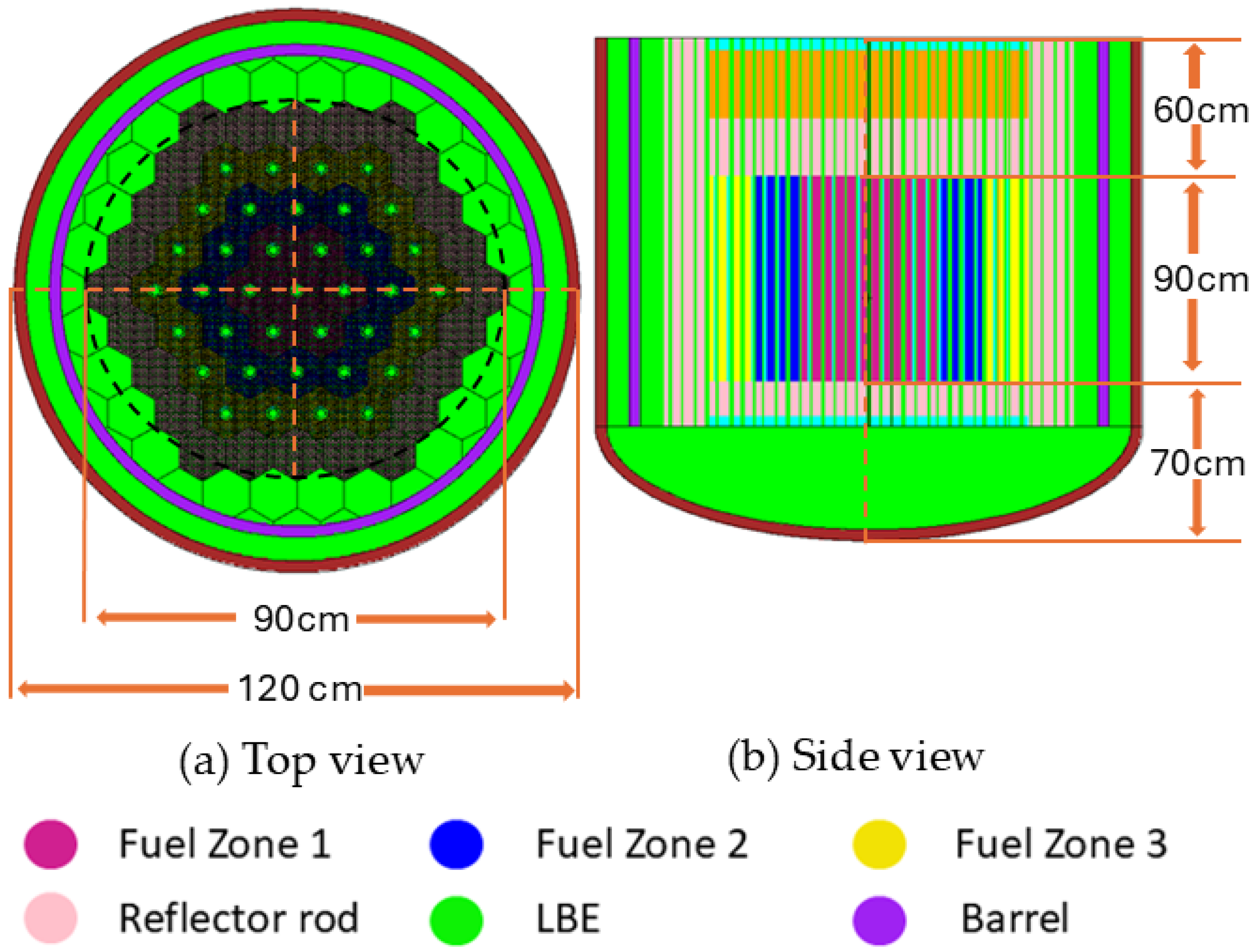
2.2. Reference Reactor Description
2.3. Variance Reduction Technique (VRT)
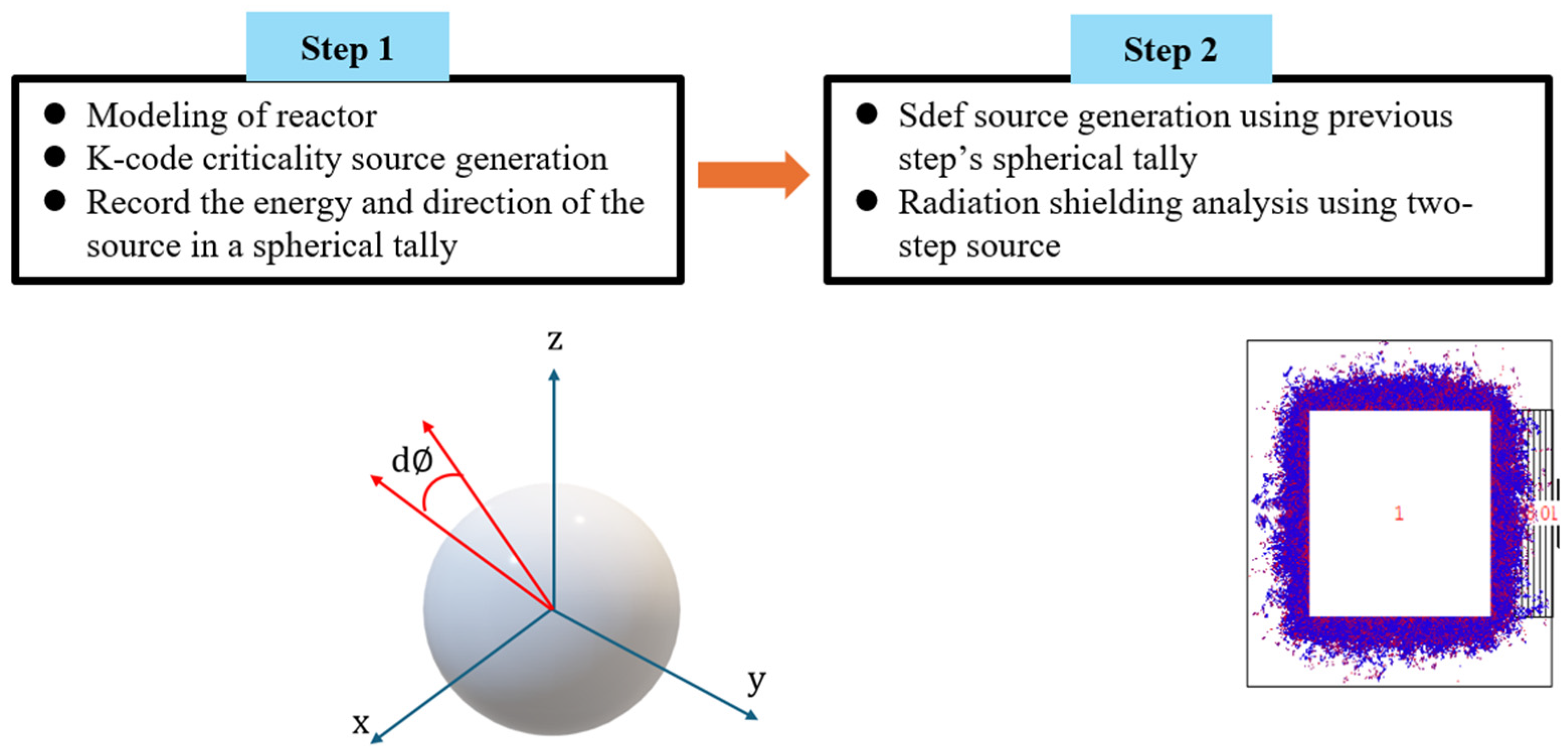
2.4. Two-Step Variance Reduction Technique
3. Results and Sensitivity Analysis
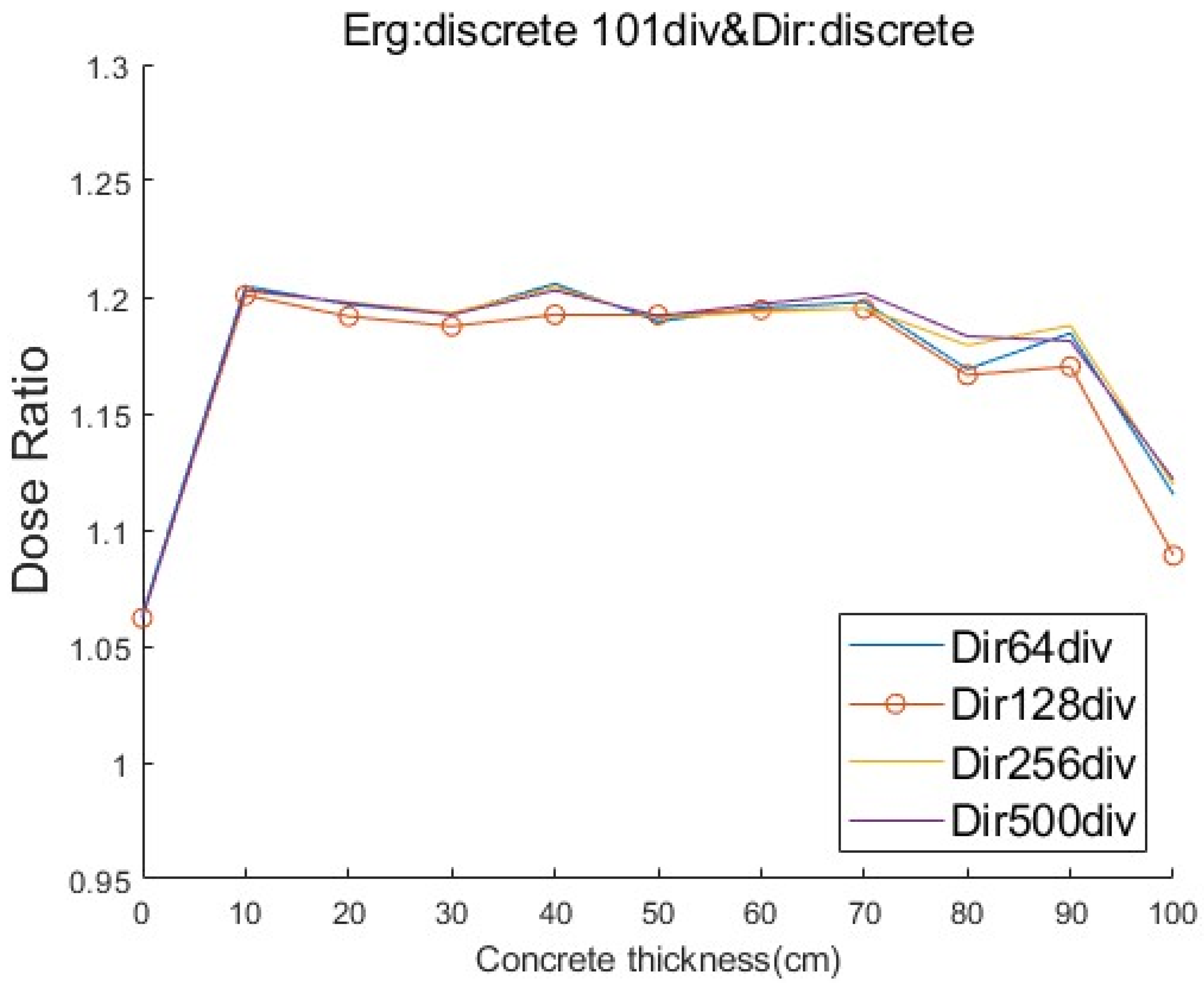
3.1. Comparison Between Direct Source Approach and Two-Step Source Approach
3.2. Efficiency of VRT
3.3. Potential Applications
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bagheri, S.; Khalafi, H. SMR, 3D source term simulation for exact shielding design based on genetic algorithm. Ann. Nucl. Energy 2023, 191, 109915. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Yan, B. The technology of shielding design for nuclear reactor: A review. Prog. Nucl. Energy 2018, 161, 104741. [Google Scholar] [CrossRef]
- Yamaji, A.; Sako, K. Shielding Design to Obtain Compact Marine Reactor. J. Nucl. Sci. Technol. 2012, 31, 510–520. [Google Scholar] [CrossRef]
- Shen, S.; Wang, W.; Chen, H.; Duan, W.; Zhang, K.; Shi, K.; Chen, Z. Core design and neutronic analysis of a long-life LBE-cooled fast reactor NCLFR-Oil. Prog. Nucl. Energy 2023, 164, 104861. [Google Scholar] [CrossRef]
- Yoo, J.-W.; Kim, Y.J.; Sungyeol, C.; Jaehyun, C.; Soon, H.I. Advanced passive design of small modular reactor cooled by heavy liquid metal natural circulation. Prog. Nucl. Energy 2014, 83, 433–442. [Google Scholar]
- Alizadeh, A.; Shirani, A.S.; Kashi, S. Neutron and gamma-ray deep penetration calculation through biological concrete shield of VVER-1000 reactor by a new technique based on variance reduction. Ann. Nucl. Energy 2013, 60, 86–92. [Google Scholar] [CrossRef]
- Judith, F.; Briesmeister. MCNPTM–A General Monte Carlo N–Particle Transport Code, 5th ed.; 2000; Available online: https://inspirehep.net/files/78c669e8d3bb59ccf6fb868a6061450chttps:/inspirehep.net/manual4d/chap2_jfb1.pdf (accessed on 7 November 2024).
- Farkas, G. wwer-440 Criticality Calculations Using mcnp5 Code, 2008. Available online: https://inis.iaea.org/collection/NCLCollectionStore/_Public/40/059/40059704.pdf (accessed on 7 November 2024).
- Yuan, X.; Cao, L.; Wu, H. Pre-conceptual study of small modular PbBi-cooled nitride fuel reactor core characteristics. Nucl. Eng. Des. 2015, 285, 23–30. [Google Scholar] [CrossRef]
- Pan, R.; Duan, W.; Wang, W.; Qin, C.; Dong, S.; Zeng, Q.; Chen, H. Design and analysis on the HP-PHRS for small modular lead-bismuth fast reactor. Nucl. Eng. Des. 2024, 426, 113371. [Google Scholar] [CrossRef]
- Rabir, M.H.; Usang, M.D. Modeling the Puspati Triga Reactor Using Mcnp Code. In Proceedings of the R and D Seminar 2012: Research and Development Seminar 2012, Bangi, Malaysia, 26–28 September 2012. [Google Scholar]
- Haghighat, A.; Wagner, J.C. Monte Carlo variance reduction with deterministic importance functions. Prog. Nucl. Energy 2003, 42, 25–53. [Google Scholar] [CrossRef]
- Thomas, E.B. A Sample Problem for Variance Reduction in MCNP; Los Alamos National Lab.: Los Alamos, NM, USA, 1985. [Google Scholar]
- Junli, L.; Li, C.; Wu, Z. An Auto-Importance Sampling Method for Deep Penetration Problems. Prog. Nucl. Sci. Technol. 2011, 2, 732–737. [Google Scholar]
- Martínez-Fernandez, E. Neural network-based source biasing to speed-up challenging MCNP simulations. Fusion Eng. Des. 2024, 202, 114406. [Google Scholar] [CrossRef]
- Trahan; John, T. MCNP Surface Source Write/Read File Format Primer. 2016. Available online: https://mcnp.lanl.gov/pdf_files/TechReport_2016_LANL_LA-UR-16-20109_Trahan.pdf (accessed on 7 November 2024).
- Hendricks, J.S.; Swinhoe, M.T.; Favalli, A. Monte Carlo N-Particle Simulations for Nuclear Detection and Safeguards; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Murata, I.; Yamamoto, H.; Miyamaru, H.; Goldenbaum, F.; Filges, D. Scattering direction biasing for Monte Carlo transport calculation. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2006, 562, 845–848. [Google Scholar] [CrossRef]
- Armstrong, J.; Mashnik, S.G.; McKinkey, G.W.; Brown, F.B.; Rising, M.E.; McMath, G.E.; Bull, J.S.; Solomon, C.; Hendricks, J.S.; Casswell, L.; et al. Mcnp® User’s Manual Code Version 6.2; Los Alamos National Security LLC: Los Alamos, NM, USA, 2017. [Google Scholar]
- Winkelman, A. Validation of the Hor Oscar4/Mcnp Model for Use in Safety Studies. 2018. Available online: https://www.rertr.anl.gov/RERTR39/pdfs/S11-P5_Winkelmanpaper.pdf (accessed on 7 November 2024).
- Lamarsh, J.R.; Baratta, A.J. Introduction to Nuclear Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Catalan, J.P. Development of radiation sources for nuclear analysis beyond ITER bio-shield: SRC-UNED code. Comput. Phys. Commun. 2022, 275, 108309. [Google Scholar] [CrossRef]
- Ko, J.H.; Park, J.H.; Jung, I.S.; Lee, G.-U.; Baeg, C.-Y.; Kim, C.-M. Shielding analysis of dual purpose casks for spent nuclear fuel under normal storage conditions. Nucl. Energy Technol. 2014, 46, 547–556. [Google Scholar] [CrossRef]
- Nicks, R.; Farinelli, U. Physics Problems of Fast Reactor Shielding. In Atomic Energy; Springer: Berlin/Heidelberg, Germany, 1979. [Google Scholar]
- Fensin, M.L.; Michael, R.; James, J.S.; Hendricks, J.T.G. The New MCNP6 Depletion Capability. In Proceedings of the Proceedings of ICAPP’12, Chicago, IL, USA, 24–28 June 2012. [Google Scholar]
- Žerovnik, G.; Podvratnik, M.; Snoj, L. On normalization of fluxes and reaction rates in MCNP criticality calculations. Ann. Nucl. Energy 2014, 63, 126–128. [Google Scholar] [CrossRef]
- Petoussi-Henss, N.; Bolch, W.E.; Eckerman, K.F.; Endo, A.; Hertel, N.; Hunt, J.; Pelliccioni, M.; Schlattl, H.; Zankl, M.; International Commission on Radiological Protection; et al. ICRP publication 116 Conversion Coefficients for Radiological Protection Quantities for External Radiation Exposures. Ann. ICRP 2010, 40, 1–257. [Google Scholar] [CrossRef] [PubMed]
- Andrianova, O.N. Application of MCNP nonanalog techniques for calculations of reaction rate measurements at the BFS facilities. Nucl. Energy Technol. 2016, 2, 197–202. [Google Scholar] [CrossRef][Green Version]
- Han, M.C.; Yeom, Y.S.; Lee, H.S.; Shin, B.; Kim, C.H.; Furuta, T. Multi-threading performance of Geant4, MCNP6, and PHITS Monte Carlo codes for tetrahedral-mesh geometry. Phys. Med. Biol. 2018, 63, 09NT02. [Google Scholar] [CrossRef] [PubMed]
- Zheng, S.; Pan, Q.; He, D.; Liu, X. Reactor lightweight shielding optimization method based on parallel embedded genetic particle-swarm hybrid algorithm. Prog. Nucl. Energy 2024, 168, 105040. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Z.; Xie, J.; Guo, Q.; Yu, T. Metaheuristic optimization method for compact reactor radiation shielding design based on genetic algorithm. Ann. Nucl. Energy 2019, 134, 318–329. [Google Scholar] [CrossRef]











| Parameters | Specification |
|---|---|
| Thermal power | 40 Mw_th |
| Fuel | UO2 |
| Enrichment (Innermost/Middle/Outermost) | 13.5 wt%/16.5 wt%/18.5 wt% |
| Cladding | T91 |
| Absorber | B4C |
| Reflector | YSZ |
| Primary coolant | LBE |
| Gap | Helium |
| Core lifetime | ≥15 years |
| Assembly geometry | Hexagonal |
| Reactivity swing | 5247 pcm |
| Secondary coolant | Rankine cycle with superheated steam |
| Core inlet temperature | 405 °C |
| Core outlet temperature | 545 °C |
| Primary cooling method | Natural circulation |
| Primary heat transfer system | Compact pool type |
| Parameters | Specification |
|---|---|
| Number of fuel assemblies | 37 |
| Number of pins per assembly | 198 |
| Equivalent core diameter | 180 (cm) |
| Active core height | 90 (cm) |
| Pitch-to-diameter ratio | 1.2 |
| Fuel pin diameter | 0.56 (cm) |
| Assembly geometry | Hexagonal |
| Number of source history N per cycle | 500,000 |
| Initial guess for the multiplication factor | 1 |
| Number of inactive cycles | 100 |
| Number of active cycles | 150 |
| Method | FOM | Recording Time (min) | Computing Time (min) |
|---|---|---|---|
| Direct | 1.336 | - | 188.58 |
| SSW/SSR | 23.995 | 1620 | 0.95 |
| Two-step | 12.097 | 16.5 | 2.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jo, S.; Kim, S.; Cho, J. A Fast Variance Reduction Technique for Efficient Radiation Shielding Calculations in Nuclear Reactors. Energies 2024, 17, 5695. https://doi.org/10.3390/en17225695
Jo S, Kim S, Cho J. A Fast Variance Reduction Technique for Efficient Radiation Shielding Calculations in Nuclear Reactors. Energies. 2024; 17(22):5695. https://doi.org/10.3390/en17225695
Chicago/Turabian StyleJo, Seungjae, Sanghwan Kim, and Jaehyun Cho. 2024. "A Fast Variance Reduction Technique for Efficient Radiation Shielding Calculations in Nuclear Reactors" Energies 17, no. 22: 5695. https://doi.org/10.3390/en17225695
APA StyleJo, S., Kim, S., & Cho, J. (2024). A Fast Variance Reduction Technique for Efficient Radiation Shielding Calculations in Nuclear Reactors. Energies, 17(22), 5695. https://doi.org/10.3390/en17225695






