Fault Diagnosis Method for Hydropower Station Measurement and Control System Based on ISSA-VMD and 1DCNN-BiLSTM
Abstract
1. Introduction
- (1)
- An improved Sparrow Search Algorithm (ISSA) is proposed, which incorporates Sine chaotic mapping and adaptive t-distribution to address the issues of local optima and premature convergence commonly encountered in traditional SSA.
- (2)
- The ISSA is employed to optimize the parameters of Variational Mode Decomposition (VMD), enhancing the decomposition accuracy. Additionally, the Pearson correlation coefficient is utilized to select intrinsic mode functions (IMFs), further improving the extraction and selection of fault signal features.
- (3)
- A fault classification method based on 1DCNN and BiLSTM is proposed, effectively extracting both spatial and temporal features of fault signals in hydropower station measurement and control system, significantly improving diagnostic accuracy.
2. Theoretical Approach
2.1. Sparrow Search Algorithm
2.2. Variational Modal Decomposition Algorithm
- (1)
- Construction of variational problems
- (2)
- Solution of the variational problem
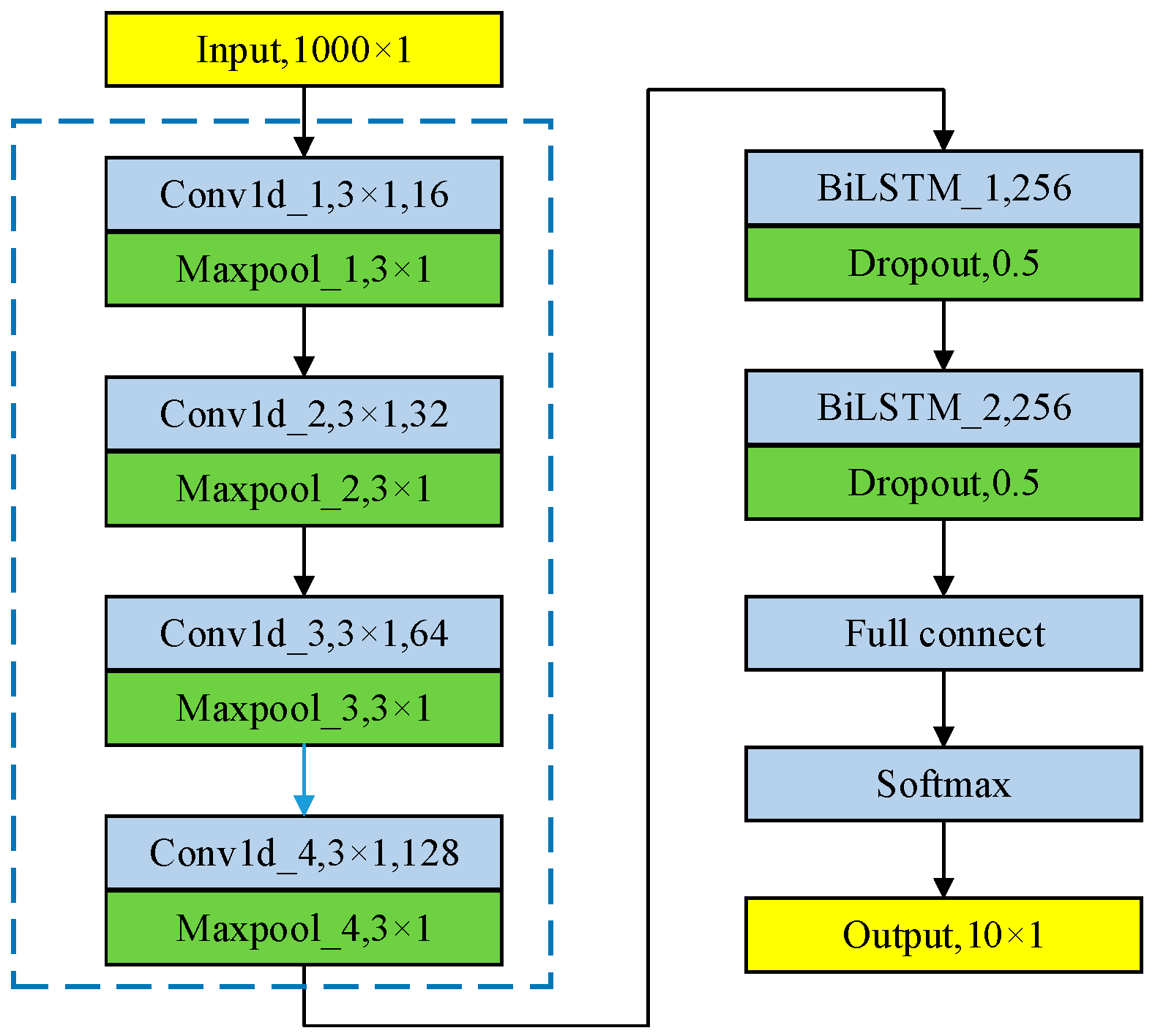
2.3. One-Dimensional Convolutional Neural Networks
2.4. Bidirectional Long and Short-Term Memory Network Theory
3. Fault Diagnosis of Hydropower Station Measurement and Control System Based on ISSA-VMD and 1DCNN-BiLSTM
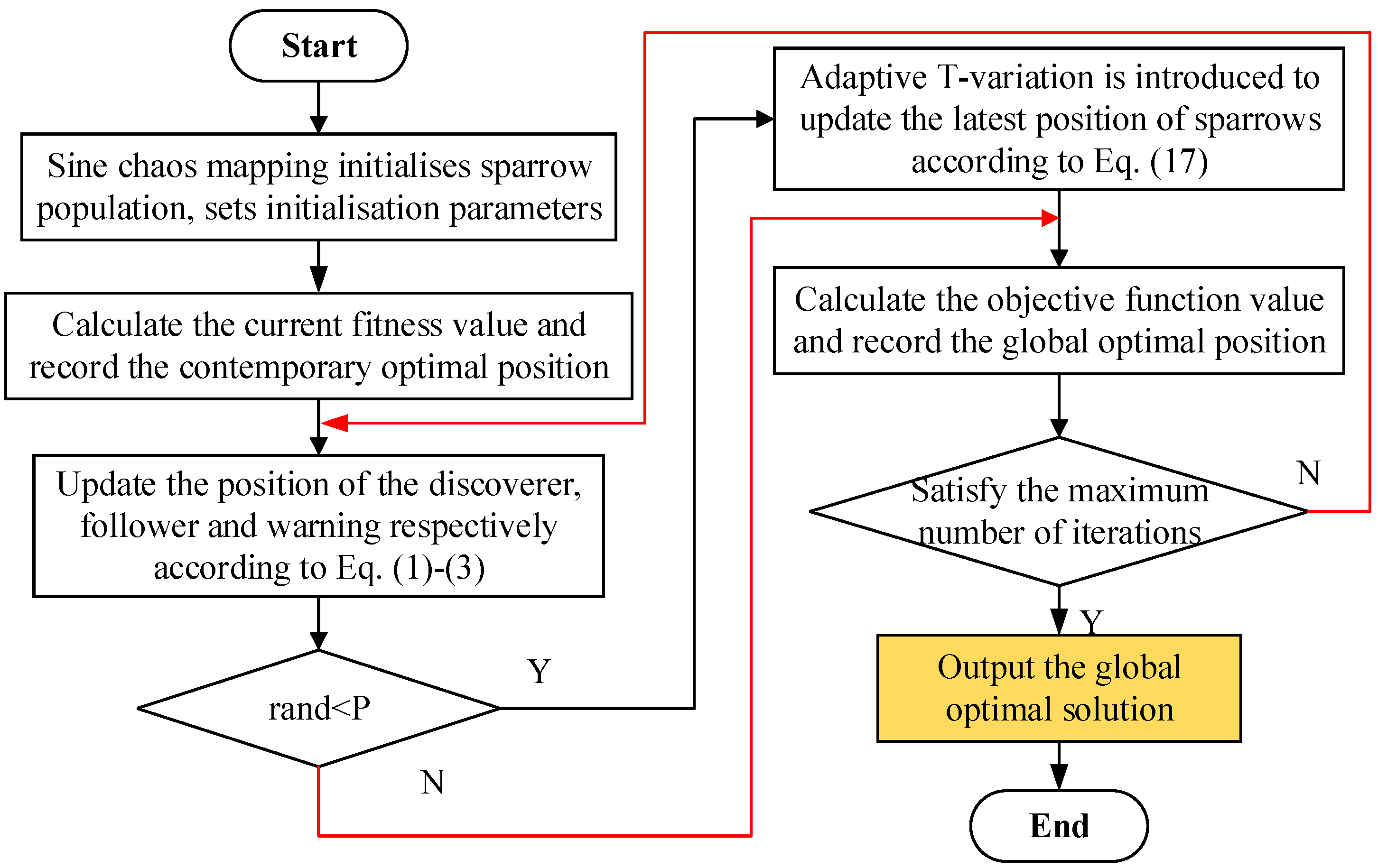
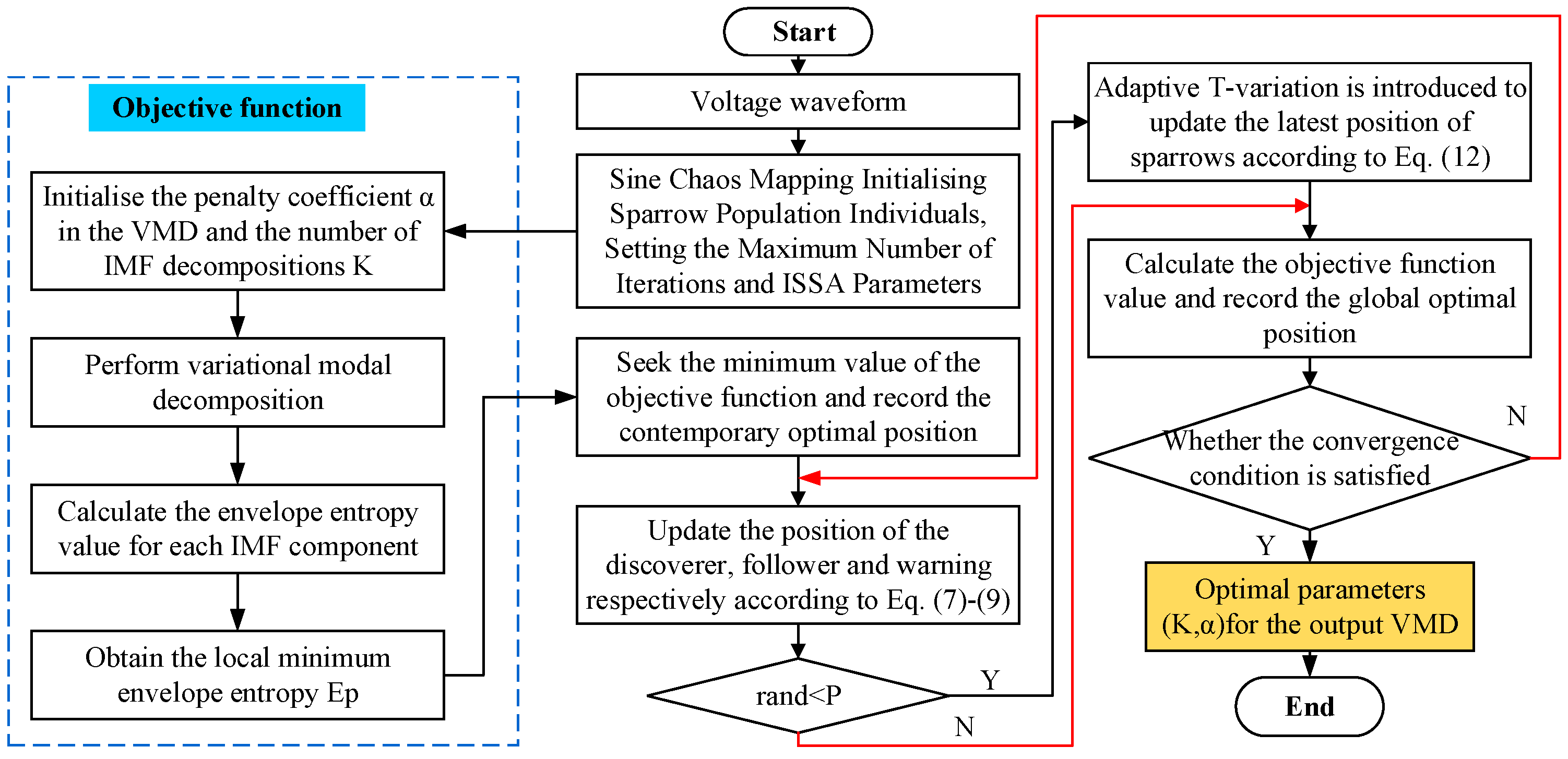
3.1. Improvement of the Sparrow Search Algorithm
3.1.1. Sine Chaotic Mapping
3.1.2. Adaptive t-Distribution
3.1.3. Improvement of the Flow of the Sparrow Search Algorithm
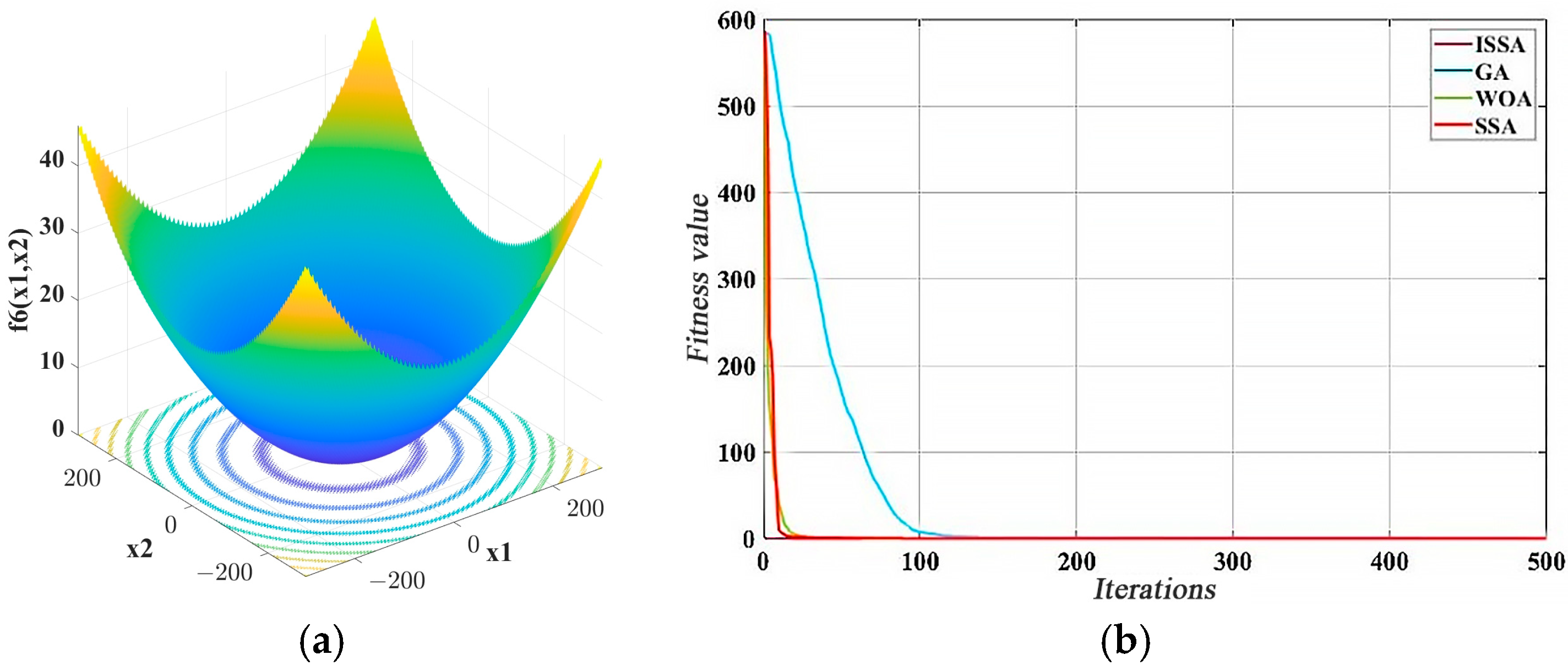
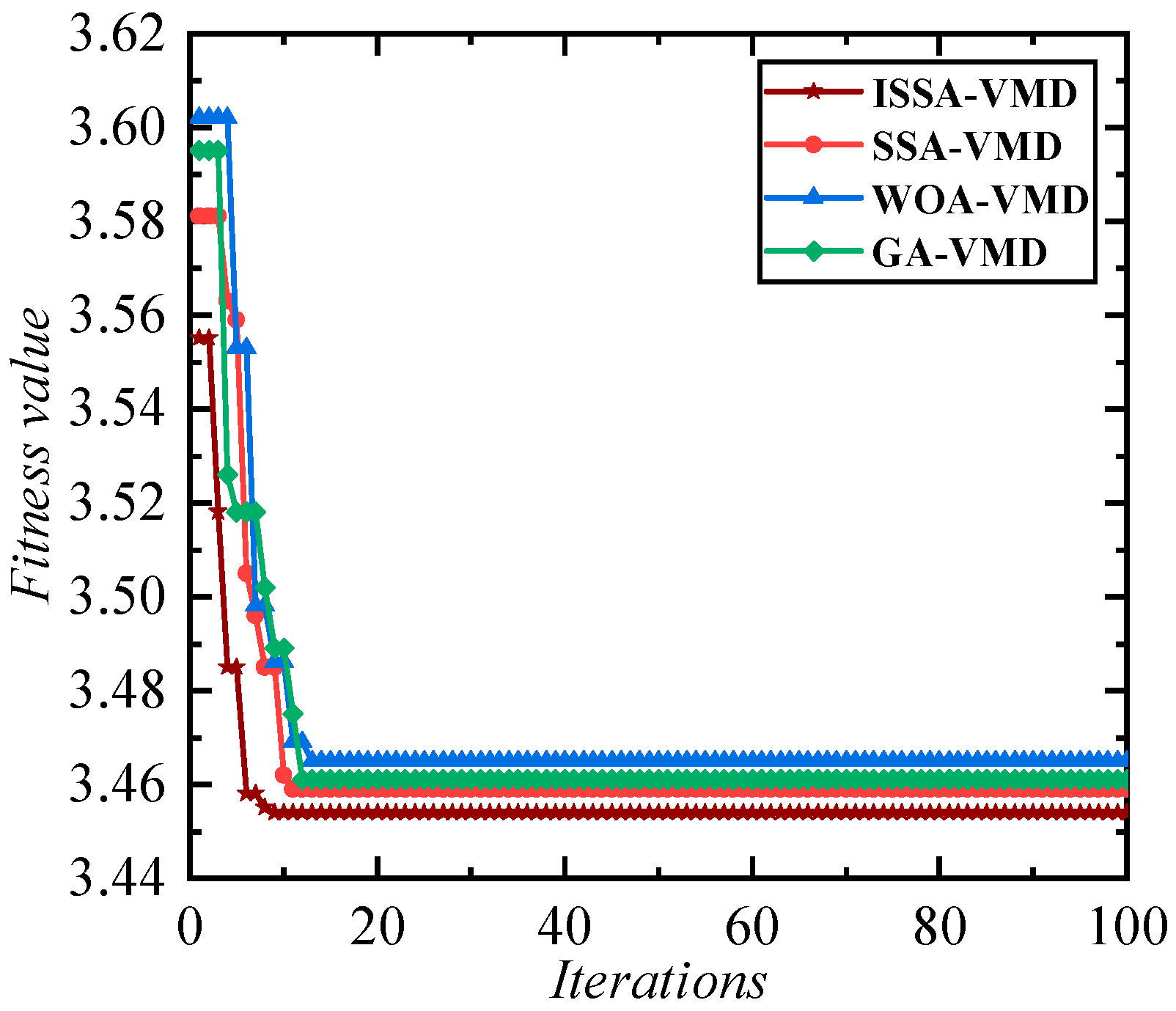
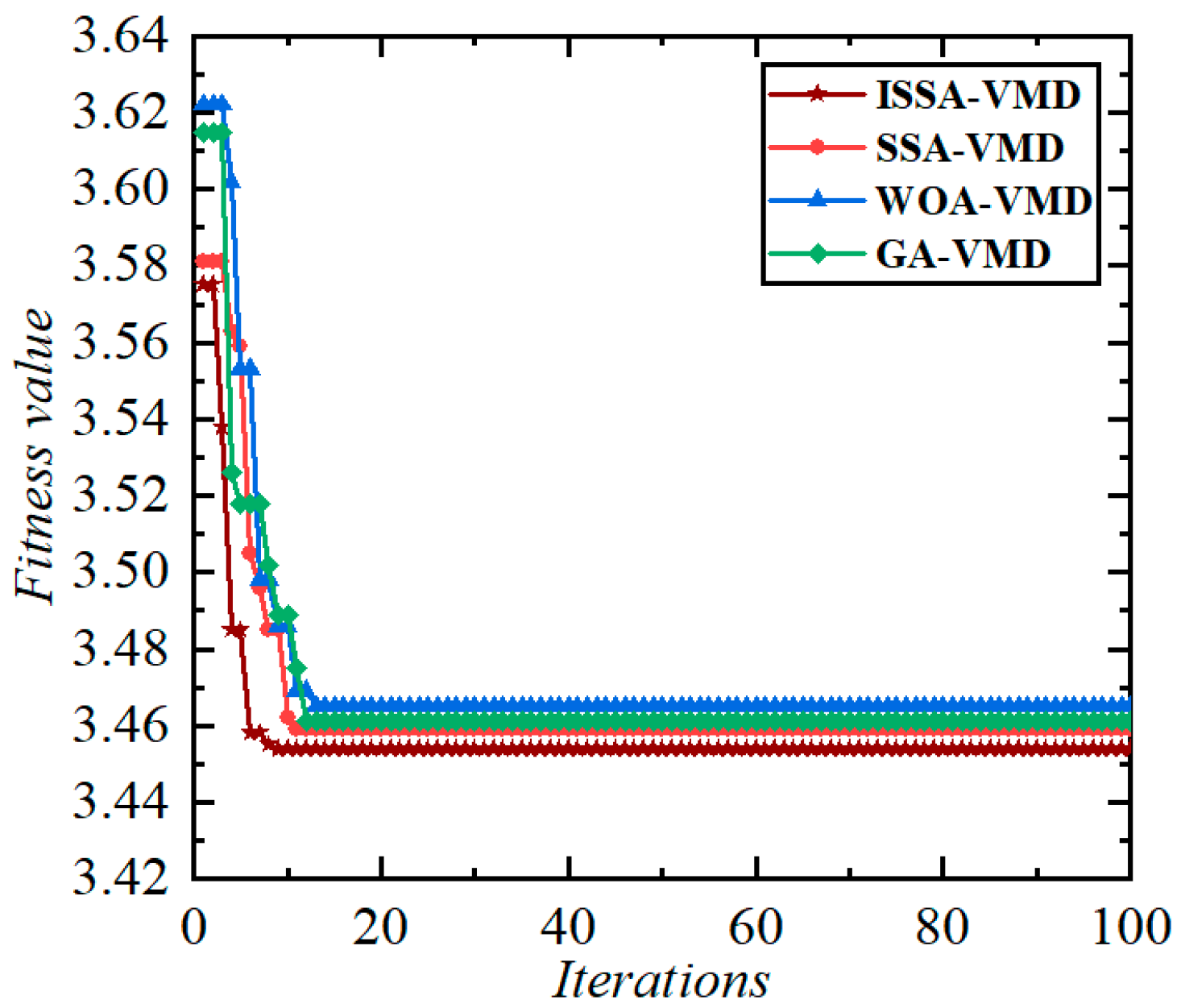
3.1.4. ISSA Performance Tests and Comparative Analyses
3.2. ISSA Optimization of the VMD Process
3.3. DCNN-BiLSTM Model
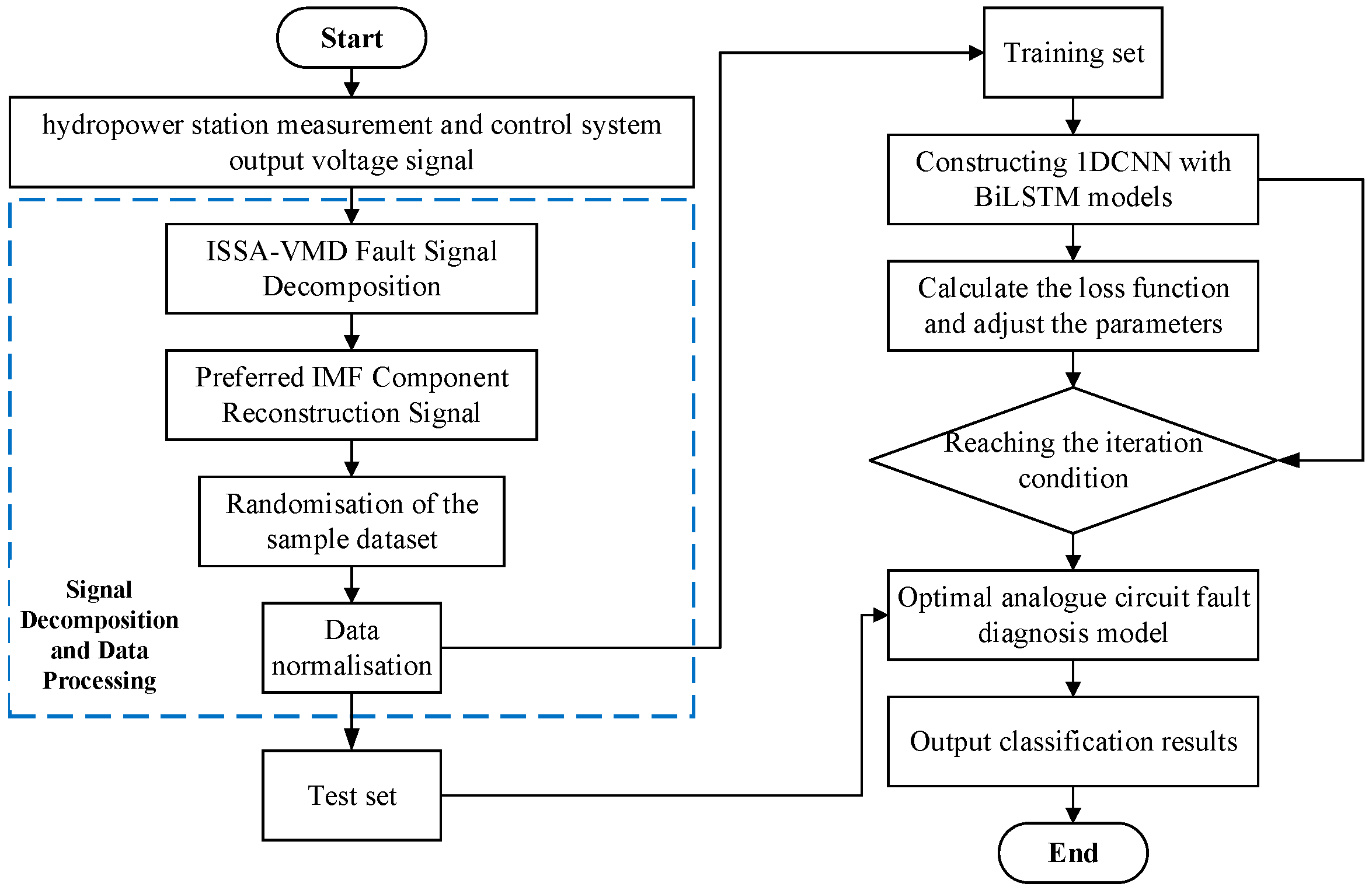
3.4. Troubleshooting Process for Hydropower Station Measurement and Control System
- (1)
- Signal acquisition: the output voltage signal of the measurement and control circuit of the hydropower station is taken as the signal input.
- (2)
- Signal decomposition: the ISSA-VMD algorithm is used to decompose the voltage signal output from the measurement and control circuit of the hydroelectric power station, and a number of IMF components are obtained.
- (3)
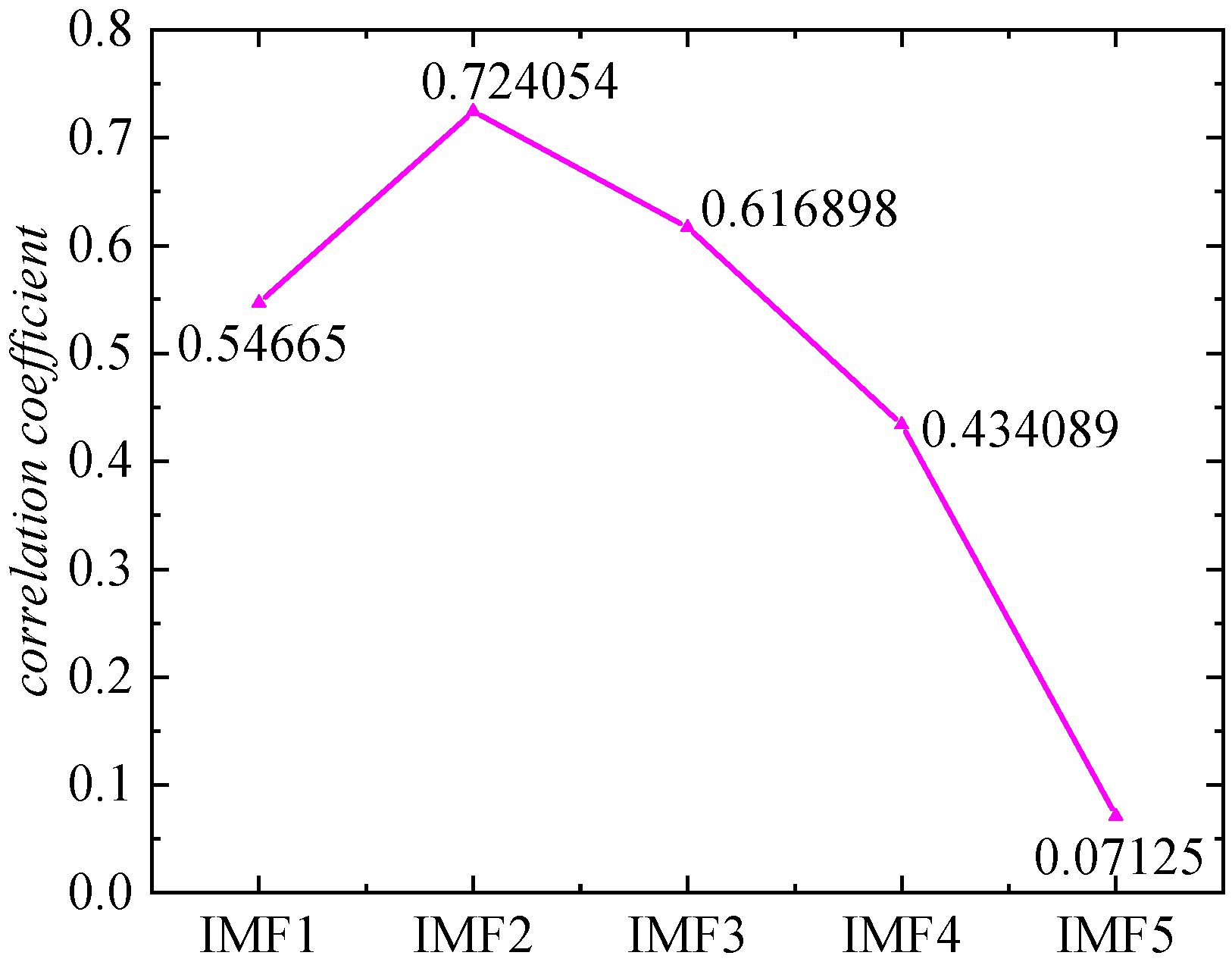
- IMF component screening: by calculating the Pearson correlation coefficient of each IMF component, in order to screen out the effective IMF components.
- (4)
- Signal reconstruction: the new fault signal sequence is obtained by signal reconstruction of the screened IMF components to extract the effective feature information.
- (5)
- Fault feature extraction: the reconstructed fault signal is input into the 1DCNN-BiLSTM model to achieve deep self-extraction of fault features, and fault feature integration is performed at the fully connected layer.
- (6)
- Fault diagnosis: the extracted fault features are inputted into the softmax layer of the 1DCNN-BiLSTM model for fault classification, in order to realise the fault diagnosis of the hydropower station measurement and control system.
4. Experimental Validation
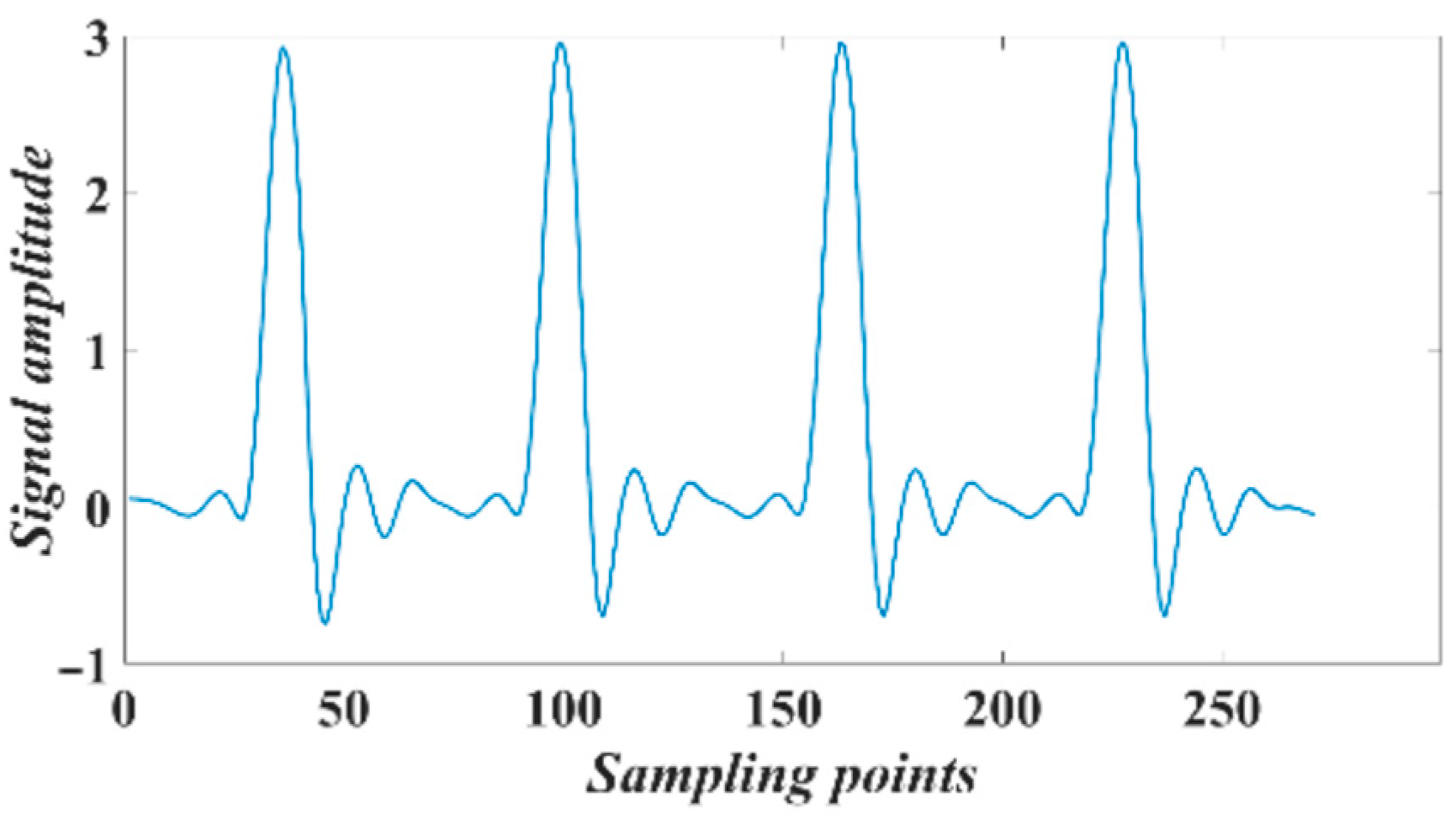
4.1. Simulation Analysis
4.2. Fault Signal Decomposition and Analysis
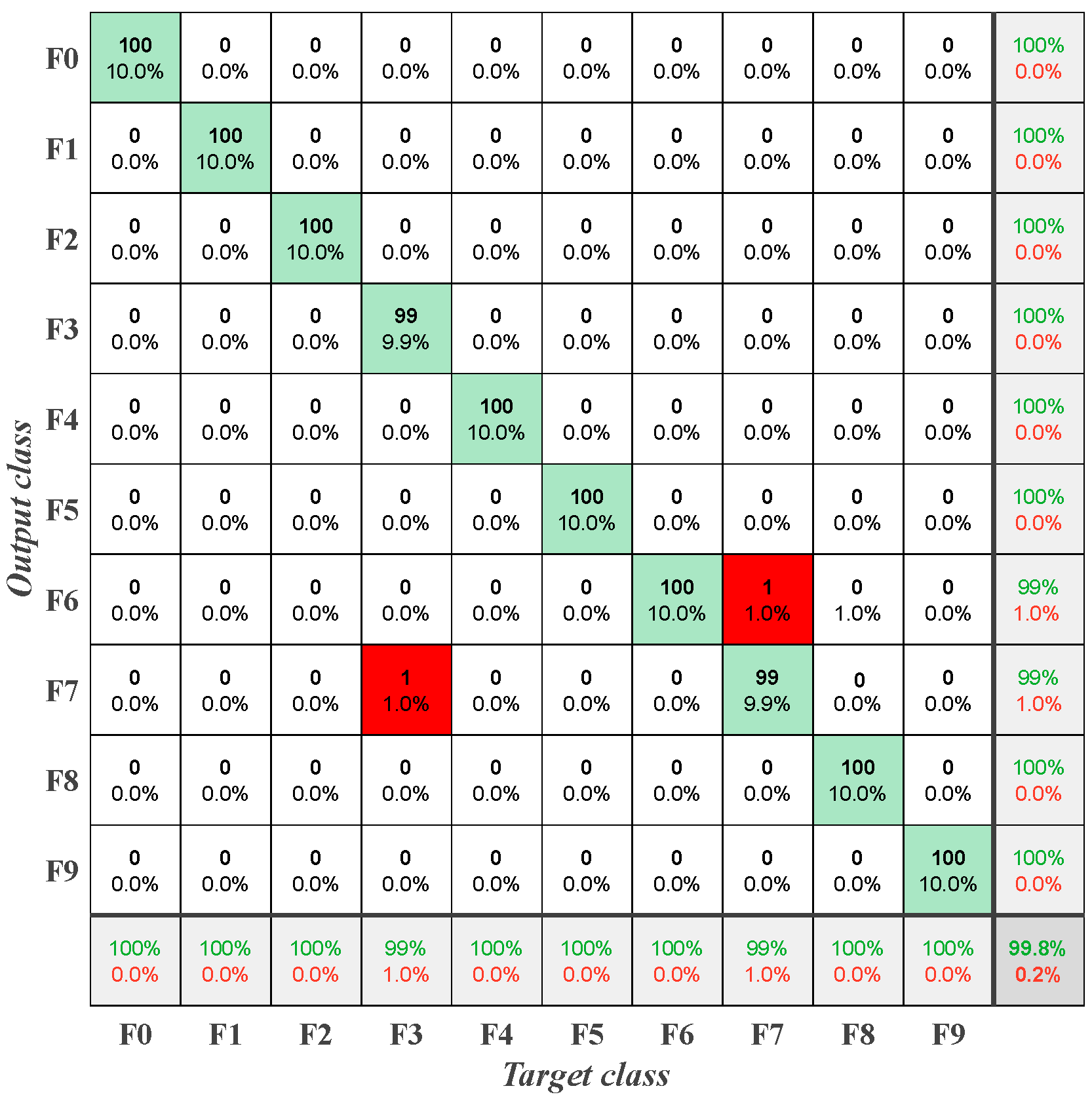
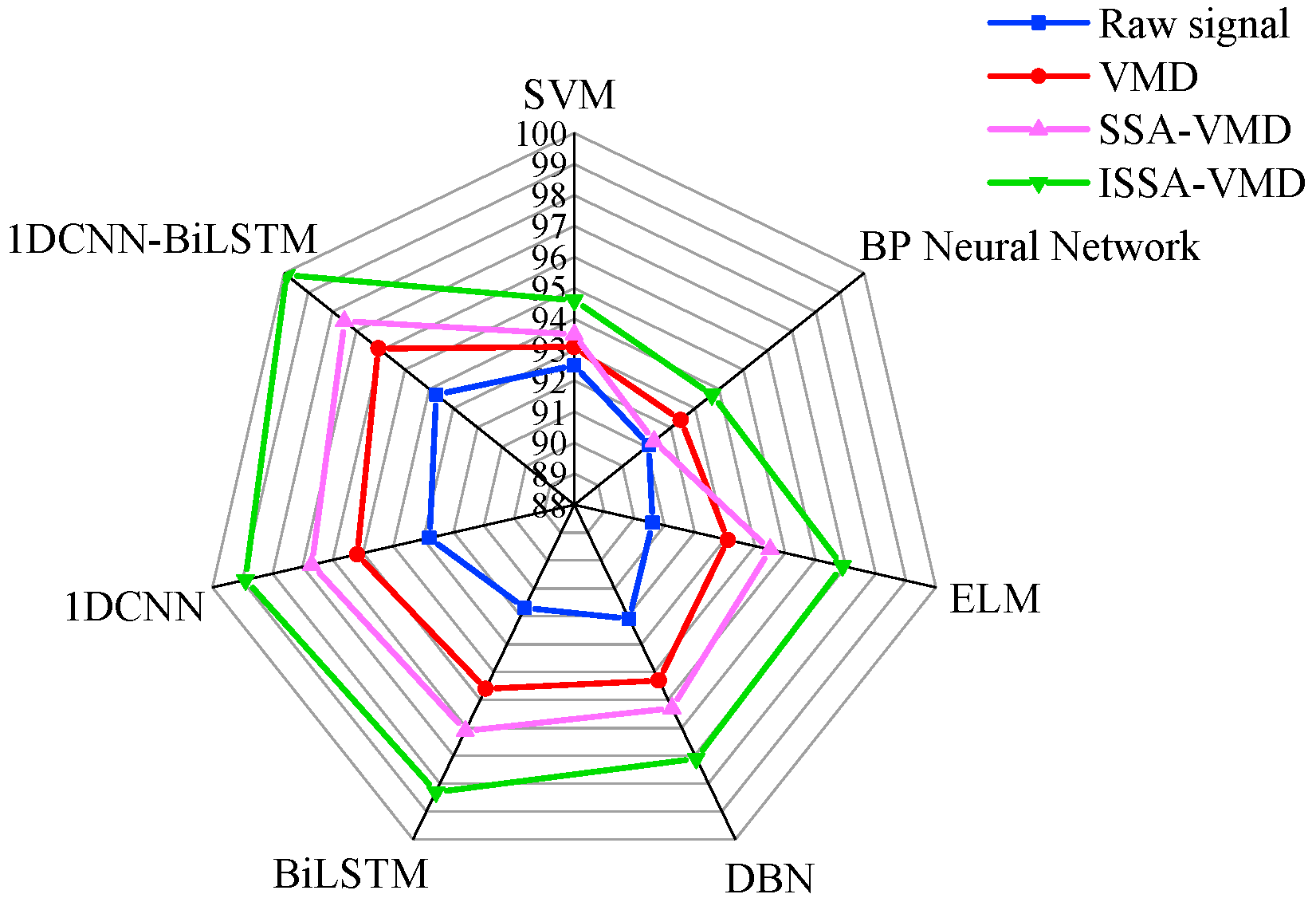
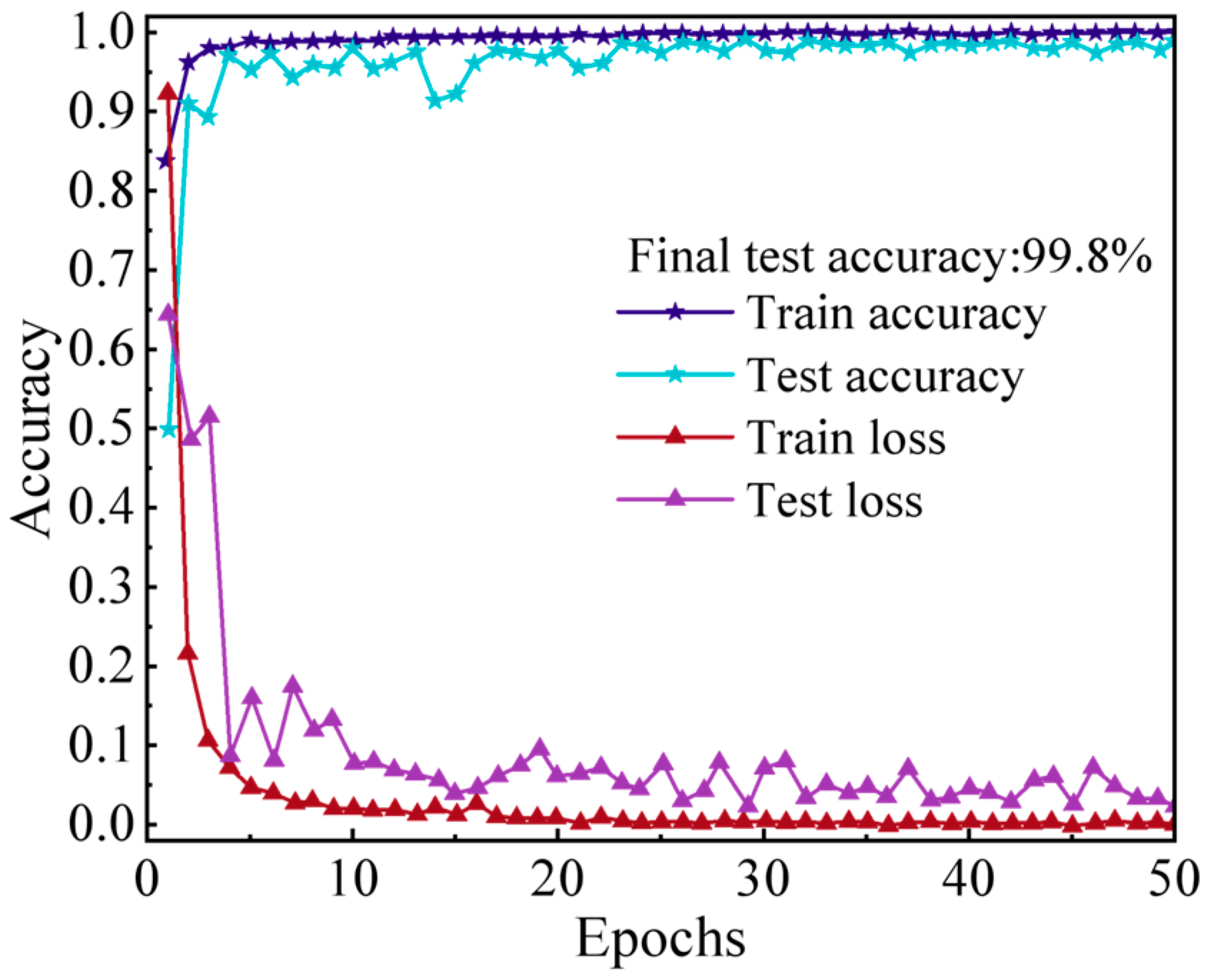
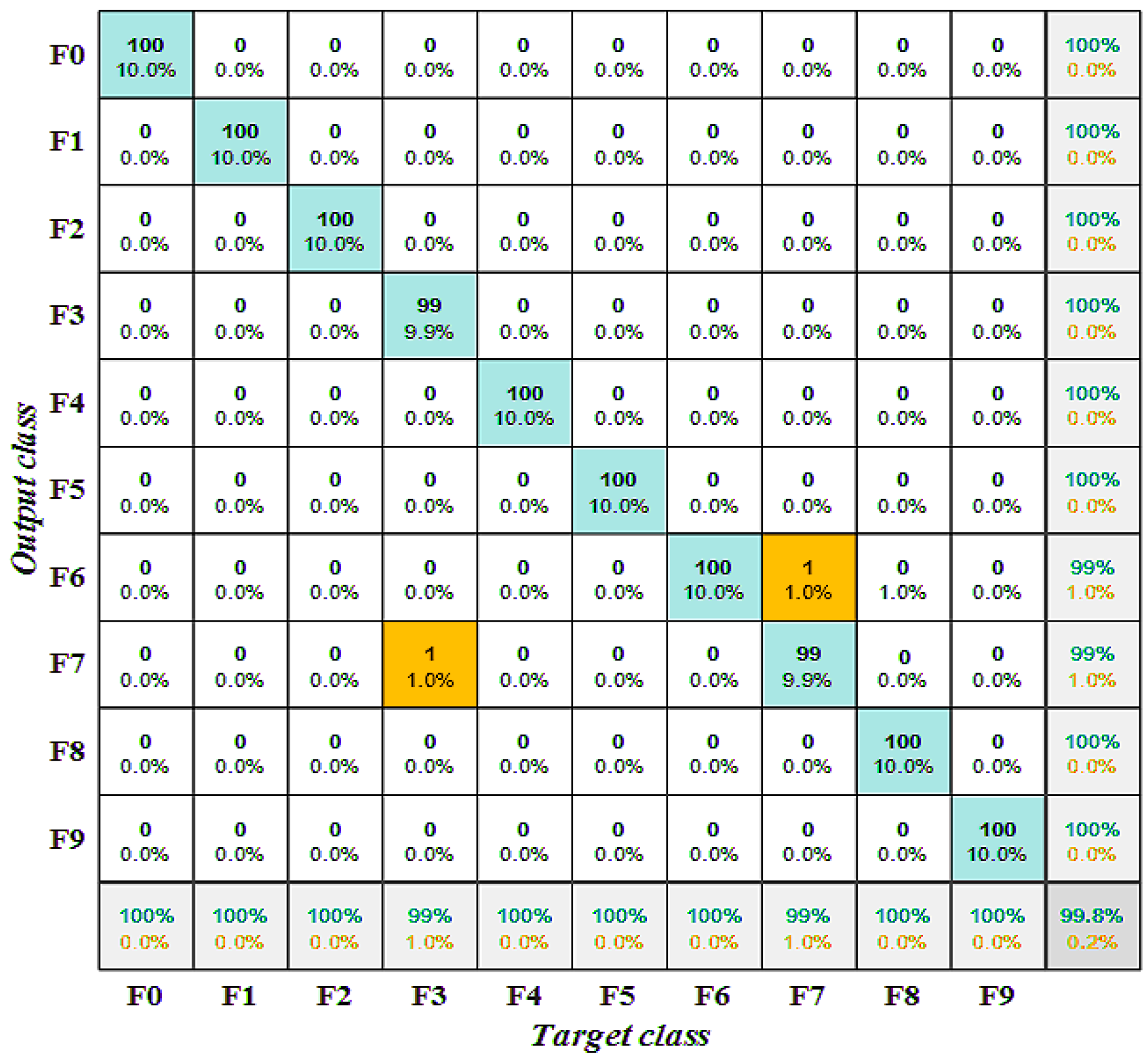
4.3. Fault Diagnosis Results and Analysis
4.4. Example Analyses
5. Conclusions
- This study introduces Sine chaotic mapping and adaptive t-distribution to improve the uniformity of the sparrow population’s distribution within the search space, enhancing global search capabilities. These improvements resolve issues of premature convergence and local optima in traditional SSA, and their effectiveness is validated through comparative experiments.
- By using ISSA to optimize VMD parameters, the accuracy and efficiency of signal decomposition are significantly enhanced. Effective IMF components are selected based on the Pearson correlation coefficient, allowing for a reconstructed signal that reduces redundant information in the sample data and produces clearer, more informative sequences.
- A comprehensive comparison of various signal decomposition and fault classification methods demonstrates that the proposed method effectively diagnoses multiple fault types in hydropower station measurement and control system circuits. The experimental results indicate that this model significantly improves diagnostic accuracy, achieving an average recognition rate of 98.8% in both simulation and real-world analyses, underscoring its high applicability and value in practical hydropower fault diagnosis tasks.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VMD | Variational Modal Decomposition |
| SSA | Sparrow Search Algorithm |
| ISSA | Improved Sparrow Search Algorithm |
| EMD | Empirical Mode Decomposition |
| SWT | Synchrosqueezing Wavelet Transform |
| ICEEMDAN | Improved Complete Ensemble Empirical Mode Decomposition With Adaptive Noise |
| GA | Genetic Algorithm |
| PSO | Particle Swarm Optimization |
| SA | Simulated Annealing |
| BA | Bat Algorithm |
| SVM | Support Vector Machine |
| ELM | Extreme Learning Machine |
| CNN | Convolutional Neural Network |
| 1DCNN | One-Dimensional Convolutional Neural Network |
| LSTM | Long and Short-term Memory Network |
| BiLSTM | Bidirectional Long and Short-term Memory Network |
| IMF | Intrinsic Mode Function |
| BiRNN | Bidirectional Recurrent Neural Network |
| WOA | Whale Optimization Algorithm |
| OPAMP | Operational Amplifier |
| BP | Back Propagation |
| DBN | Deep Belief Network |
References
- Fan, J.; Yuan, W. Review of Parametric Fault Prediction Methods for Power Electronic Circuits. Eng. Res. Express 2021, 3, 042002. [Google Scholar] [CrossRef]
- Jia, Z.; Liu, Z.; Gan, Y.; Vong, C.-M.; Pecht, M. A Deep Forest-Based Fault Diagnosis Scheme for Electronics-Rich Analog Circuit Systems. IEEE Trans. Ind. Electron. 2021, 68, 10087–10096. [Google Scholar] [CrossRef]
- Zhang, C.; He, Y.; Yuan, L.; Xiang, S. Analog Circuit Incipient Fault Diagnosis Method Using DBN Based Features Extraction. IEEE Access 2018, 6, 23053–23064. [Google Scholar] [CrossRef]
- Zhang, C.; Zha, D.; Wang, L.; Mu, N. A Novel Analog Circuit Soft Fault Diagnosis Method Based on Convolutional Neural Network and Backward Difference. Symmetry 2021, 13, 1096. [Google Scholar] [CrossRef]
- Li, J.; Chen, W.; Han, K.; Wang, Q. Fault Diagnosis of Rolling Bearing Based on GA-VMD and Improved WOA-LSSVM. IEEE Access 2020, 8, 166753–166767. [Google Scholar] [CrossRef]
- Khemani, V.; Azarian, M.H.; Pecht, M.G. Learnable Wavelet Scattering Networks: Applications to Fault Diagnosis of Analog Circuits and Rotating Machinery. Electronics 2022, 11, 451. [Google Scholar] [CrossRef]
- Du, H.; Wang, J.; Qian, W.; Zhang, X. An Improved Sparrow Search Algorithm for the Optimization of Variational Modal Decomposition Parameters. Appl. Sci. 2024, 14, 2174. [Google Scholar] [CrossRef]
- Lin, S.-L. Application Combining VMD and ResNet101 in Intelligent Diagnosis of Motor Faults. Sensors 2021, 21, 6065. [Google Scholar] [CrossRef]
- Tang, S.; Yuan, S.; Zhu, Y. Data Preprocessing Techniques in Convolutional Neural Network Based on Fault Diagnosis Towards Rotating Machinery. IEEE Access 2020, 8, 149487–149496. [Google Scholar] [CrossRef]
- Wang, Z.; Luo, Q.; Chen, H.; Zhao, J.; Yao, L.; Zhang, J.; Chu, F. A high-accuracy intelligent fault diagnosis method for aero-engine bearings with limited samples. Comput. Ind. 2024, 159, 104099. [Google Scholar] [CrossRef]
- Sob, U.M.; Bester, H.L.; Smirnov, O.M.; Kenyon, J.S.; Grobler, T.L. Radio Interferometric Calibration Using a Complex Student’s t-Distribution and Wirtinger Derivatives. Mon. Not. R. Astron. Soc. 2020, 491, 1026–1042. [Google Scholar] [CrossRef]
- Sharma, V.; Parey, A. Extraction of Weak Fault Transients Using Variational Mode Decomposition for Fault Diagnosis of Gearbox under Varying Speed. Eng. Fail. Anal. 2020, 107, 104204. [Google Scholar] [CrossRef]
- He, Z.; Chen, G.; Hao, T.; Teng, C.; Hou, M.; Cheng, Z. Weak Fault Detection Method of Rolling Bearing Based on Testing Signal Far Away from Fault Source. J. Mech. Sci. Technol. 2020, 34, 1035–1048. [Google Scholar] [CrossRef]
- Li, Y.; Huang, D.; Qin, Z. A Classification Algorithm of Fault Modes-Integrated LSSVM and PSO with Parameters’ Optimization of VMD. Math. Probl. Eng. 2021, 2021, 6627367. [Google Scholar] [CrossRef]
- Xu, Z.; Mei, X.; Wang, X.; Yue, M.; Jin, J.; Yang, Y.; Li, C. Fault Diagnosis of Wind Turbine Bearing Using a Multi-Scale Convolutional Neural Network with Bidirectional Long Short Term Memory and Weighted Majority Voting for Multi-Sensors. Renew. Energy 2022, 182, 615–626. [Google Scholar] [CrossRef]
- Yan, X.; Jia, M.; Xiang, L. Compound Fault Diagnosis of Rotating Machinery Based on OVMD and a 1.5-Dimension Envelope Spectrum. Meas. Sci. Technol. 2016, 27, 075002. [Google Scholar] [CrossRef]
- Zhou, F.; Yang, X.; Shen, J.; Liu, W. Fault Diagnosis of Hydraulic Pumps Using PSO-VMD and Refined Composite Multiscale Fluctuation Dispersion Entropy. Shock Vib. 2020, 2020, 8840676. [Google Scholar] [CrossRef]
- Yang, K.; Wang, G.; Dong, Y.; Zhang, Q.; Sang, L. Early Chatter Identification Based on an Optimized Variational Mode Decomposition. Mech. Syst. Signal Proc. 2019, 115, 238–254. [Google Scholar] [CrossRef]
- Wu, Q.; Lin, H. Short-Term Wind Speed Forecasting Based on Hybrid Variational Mode Decomposition and Least Squares Support Vector Machine Optimized by Bat Algorithm Model. Sustainability 2019, 11, 652. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A Novel Swarm Intelligence Optimization Approach: Sparrow Search Algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L. A New Two-Level Hierarchical Diagnosis Network Based on Convolutional Neural Network. IEEE Trans. Instrum. Meas. 2020, 69, 330–338. [Google Scholar] [CrossRef]
- Chen, L.; Khan, U.S.; Khattak, M.K.; Wen, S.; Wang, H.; Hu, H. An Effective Approach Based on Nonlinear Spectrum and Improved Convolution Neural Network for Analog Circuit Fault Diagnosis. Rev. Sci. Instrum. 2023, 94, 054709. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Su, J.; Sun, S.; Liu, Z.; Wang, J.; Du, M.; Liu, Z.; Zhang, Q. Compressor Fault Diagnosis System Based on PCA-PSO-LSSVM Algorithm. Sci. Prog. 2021, 104, 00368504211026110. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Xia, L.; Zhang, J. A Fault Feature Extraction Method for DC-DC Converters Based on Automatic Hyperparameter-Optimized 1-D Convolution and Long Short-Term Memory Neural Networks. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 4703–4714. [Google Scholar] [CrossRef]
- Rossi, A.; Hagenbuchner, M.; Scarselli, F.; Tsoi, A.C. A Study on the Effects of Recursive Convolutional Layers in Convolutional Neural Networks. Neurocomputing 2021, 460, 59–70. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Wang, J.; Guo, J.; Wang, L.; Yang, Y.; Wang, Z.; Wang, R. A Hybrid Intelligent Rolling Bearing Fault Diagnosis Method Combining WKN-BiLSTM and Attention Mechanism. Meas. Sci. Technol. 2023, 34, 085106. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, D.; Zhang, H.; Zhang, W.; Chen, J. Application of Relative Entropy and Gradient Boosting Decision Tree to Fault Prognosis in Electronic Circuits. Symmetry 2018, 10, 495. [Google Scholar] [CrossRef]
- Lundgren, A.; Jung, D. Data-Driven Fault Diagnosis Analysis and Open-Set Classification of Time-Series Data. Control Eng. Pract. 2022, 121, 105006. [Google Scholar] [CrossRef]
- Wang, R.; Zhan, Y.; Chen, M.; Zhou, H. Fault Diagnosis Technology Based on Wigner-Ville Distribution in Power Electronics Circuit. Int. J. Electron. 2011, 98, 1247–1257. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, X.; Yuan, H.; Zhu, X.; Yang, F.; Zhang, E.; Zhang, Q.; Yao, Y. An Adaptive T-Distribution Variation Based HS Algorithm for Power System ED. In Recent Developments in Intelligent Computing, Communication and Devices; Wu, C.H., Patnaik, S., Popentiu Vlãdicescu, F., Nakamatsu, K., Eds.; Springer: Singapore, 2021; pp. 125–133. [Google Scholar] [CrossRef]

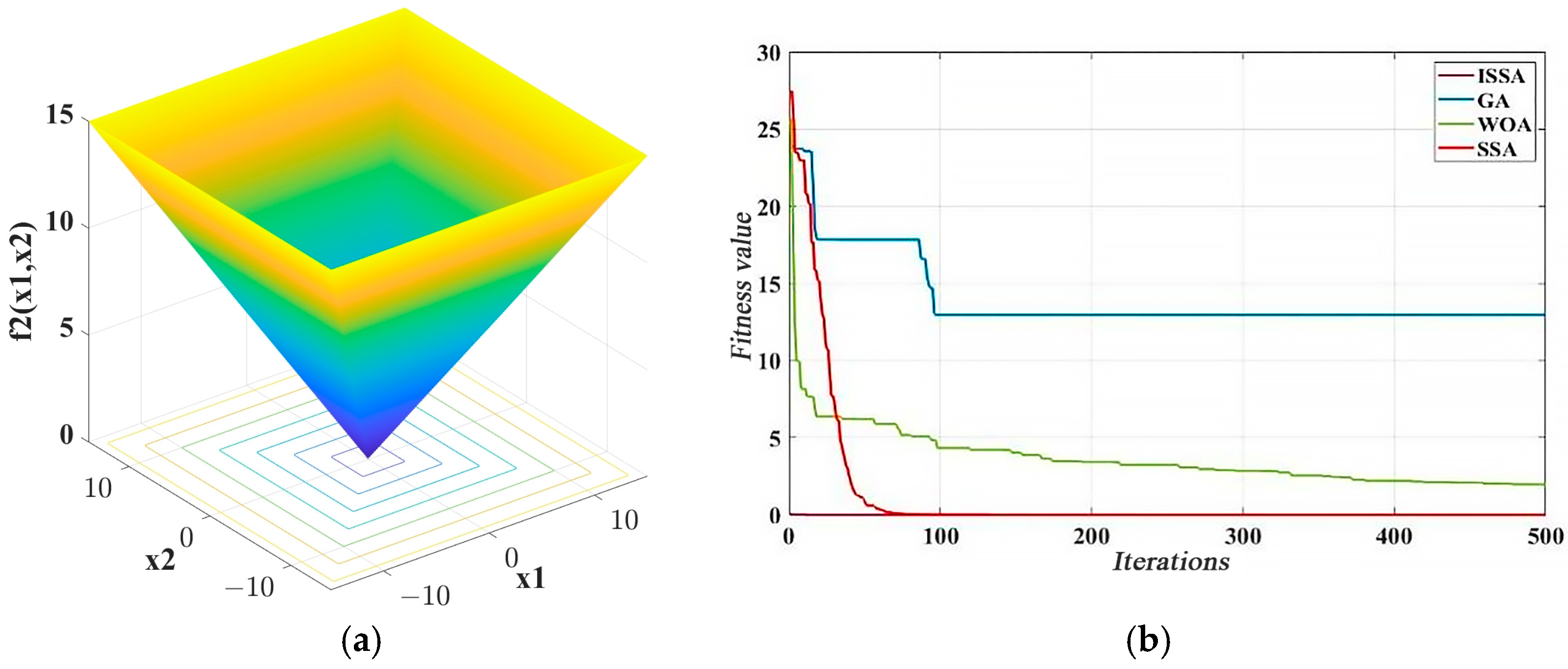
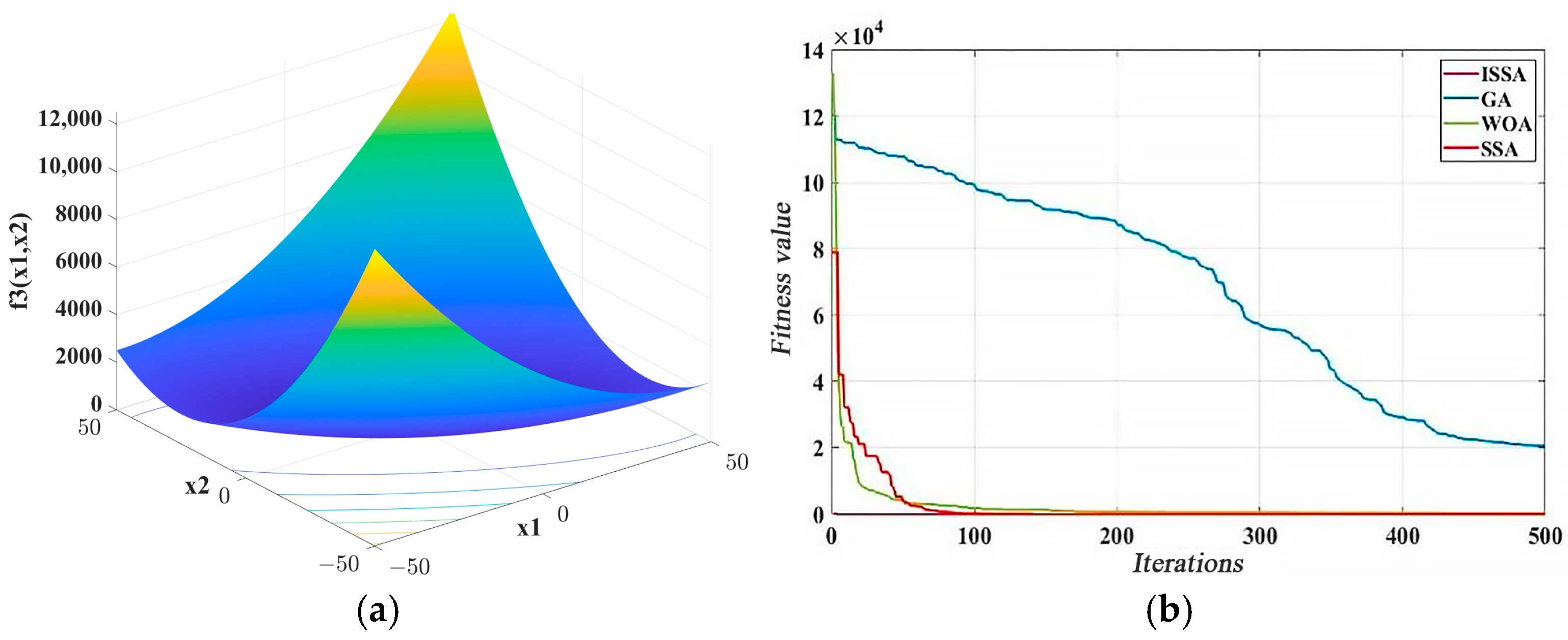
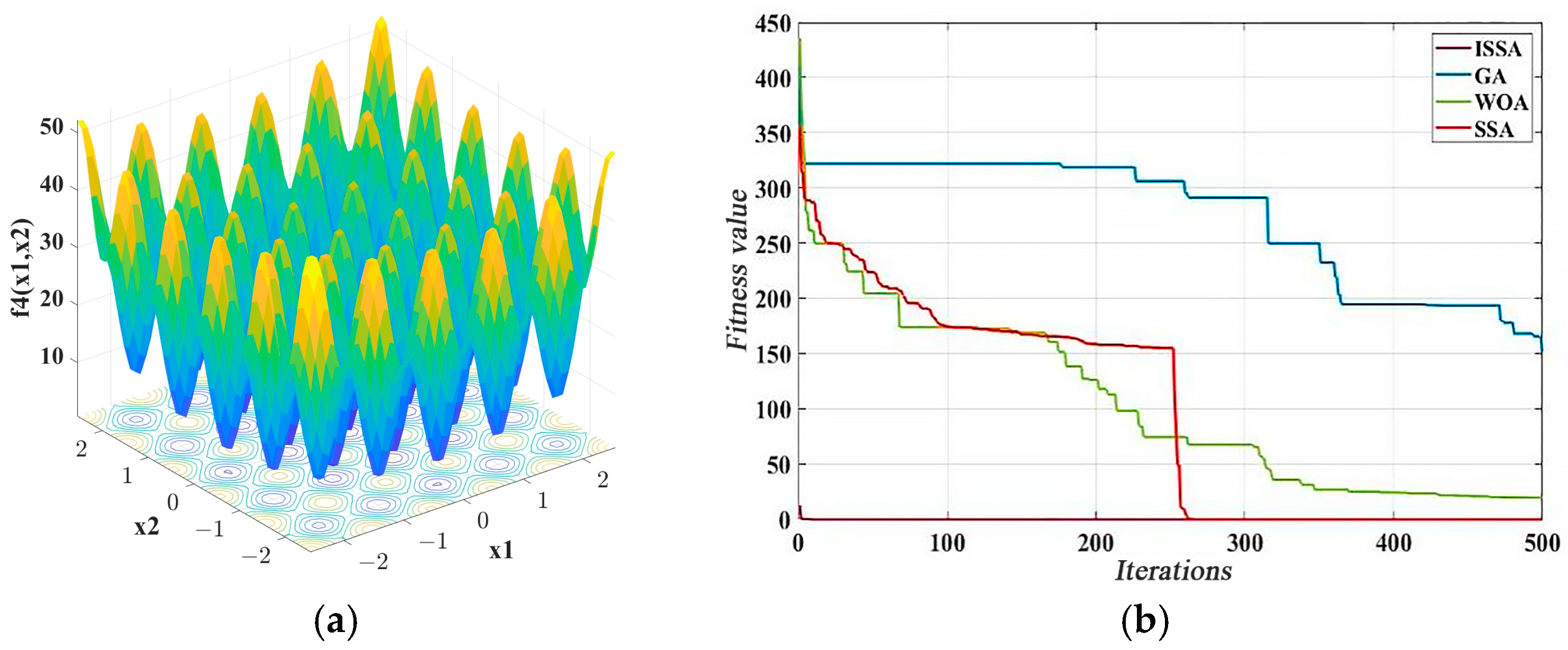









| Type | Function Expression | Dimension | Scope of the Search for Excellence | Minimum Value |
|---|---|---|---|---|
| single peak function | 30 | [−100, 100] | 0 | |
| 30 | [−100, 100] | 0 | ||
| 30 | [−100, 100] | 0 | ||
| multimax multifunction | 30 | [−5.12, 5.12] | 0 | |
| 30 | [−32, 32] | 0 | ||
| 30 | [−600, 600] | 0 |
| Algorithm Type | Parameterisation |
|---|---|
| ISSA | itermax = 500, Num = 50, ST = 0.8, PD = 0.7, SD = 0.2, P = 0.5 |
| SSA | itermax = 500, Num = 50, ST = 0.8, PD = 0.7, SD = 0.2 |
| WOA | itermax = 500, Num = 50 |
| GA | itermax = 500, Num = 50, pc = 0.8, pm = 0.05, γ = 0.01 |
| Function | Norm | ISSA | SSA | WOA | GA |
|---|---|---|---|---|---|
| f1 | Mean | 5.07 × 10−140 | 5.63 × 10−84 | 7.15 × 10−34 | 1.72 |
| Standard deviation | 2.728 × 10−139 | 2.42136 × 10−83 | 1.99205 × 10−33 | 0.702024047 | |
| f2 | Mean | 1.15 × 10−59 | 6.16 × 10−9 | 1.79 | 14.8 |
| Standard deviation | 6.2091 × 10−59 | 5.19 × 10−9 | 0.222106 | 16.14894 | |
| f3 | Mean | 5.87 × 10−91 | 3.81 × 10−8 | 132 | 2.84 × 104 |
| Standard deviation | 2.84527 × 10−90 | 1.05 × 10−7 | 51.02719 | 7877.528 | |
| f4 | Mean | 0.00 | 0.00 | 19.1 | 153 |
| Standard deviation | 0.00 | 0.00 | 9.176026 | 29.31647 | |
| f5 | Mean | 4.44 × 10−16 | 3.16 × 10−6 | 2.38 × 10−7 | 2.17 |
| Standard deviation | 1.97215 × 10−31 | 4.6892 × 10−18 | 3.6469 × 10−13 | 0.703959075 | |
| f6 | Mean | 0.00 | 8.45 × 10−3 | 5.92 × 10−3 | 8.46 × 10−2 |
| Standard deviation | 0.00 | 0.032154 | 0.010103 | 0.031793 |
| Number | Fault Type | Nominal Value | Failure Value |
|---|---|---|---|
| F0 | NF | / | / |
| F1 | C1↑ | 5 nF | 10 nF |
| F2 | C1↓ | 5 nF | 2.5 nF |
| F3 | C2↑ | 5 nF | 15 nF |
| F4 | R4↓ | 6.2 kΩ | 3 kΩ |
| F5 | R3↑ | 6.2 kΩ | 18 kΩ |
| F6 | R1↑ | 6.2 kΩ | 12 kΩ |
| F7 | R9↓ | 1.6 kΩ | 0.5 kΩ |
| F8 | R1↑C1↓ | 6.2 kΩ, 5 nF | 12 kΩ, 2.5 nF |
| F9 | R3↓R9↑C2↓ | 6.2 kΩ, 1.6 kΩ, 5 nF | 2 kΩ, 2.5 kΩ, 2.5 nF |
| Number | Fault Type | Nominal Value | Failure Value |
|---|---|---|---|
| F0 | NF | / | / |
| F1 | C1↑ | 5 nF | 10 nF |
| F2 | C1↓ | 5 nF | 2.5 nF |
| F3 | C2↓ | 5 nF | 2.5 nF |
| F4 | R2↑ | 3 kΩ | 6 kΩ |
| F5 | R2↓ | 3 kΩ | 1.5 kΩ |
| F6 | R5↑ | 2 kΩ | 4 kΩ |
| F7 | R2↑C1↓ | 3 kΩ, 5 nF | 6 kΩ, 2.5 nF |
| F8 | R2↓C1↑ | 3 kΩ, 5 nF | 1.5 kΩ, 10 nF |
| F9 | R2↓R5↑C2↓ | 3 kΩ, 2 kΩ, 5 nF | 1.5 kΩ, 4 kΩ, 2.5 nF |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Zhang, F.; Wang, J.; Ren, G.; Wang, D.; Gao, L.; Ming, X. Fault Diagnosis Method for Hydropower Station Measurement and Control System Based on ISSA-VMD and 1DCNN-BiLSTM. Energies 2024, 17, 5686. https://doi.org/10.3390/en17225686
Wang L, Zhang F, Wang J, Ren G, Wang D, Gao L, Ming X. Fault Diagnosis Method for Hydropower Station Measurement and Control System Based on ISSA-VMD and 1DCNN-BiLSTM. Energies. 2024; 17(22):5686. https://doi.org/10.3390/en17225686
Chicago/Turabian StyleWang, Lin, Fangqing Zhang, Jiefei Wang, Gang Ren, Dengxian Wang, Ling Gao, and Xingyu Ming. 2024. "Fault Diagnosis Method for Hydropower Station Measurement and Control System Based on ISSA-VMD and 1DCNN-BiLSTM" Energies 17, no. 22: 5686. https://doi.org/10.3390/en17225686
APA StyleWang, L., Zhang, F., Wang, J., Ren, G., Wang, D., Gao, L., & Ming, X. (2024). Fault Diagnosis Method for Hydropower Station Measurement and Control System Based on ISSA-VMD and 1DCNN-BiLSTM. Energies, 17(22), 5686. https://doi.org/10.3390/en17225686







