Remaining Service Life Prediction of Lithium-Ion Batteries Based on Randomly Perturbed Traceless Particle Filtering
Abstract
1. Introduction
2. Improved Particle Filtering Algorithm
3. Battery Rul Prediction Based on RP-UPF
3.1. Construction of the Battery Capacity Decline Model
3.2. Model Initialization
3.3. Battery Rul Prediction Process
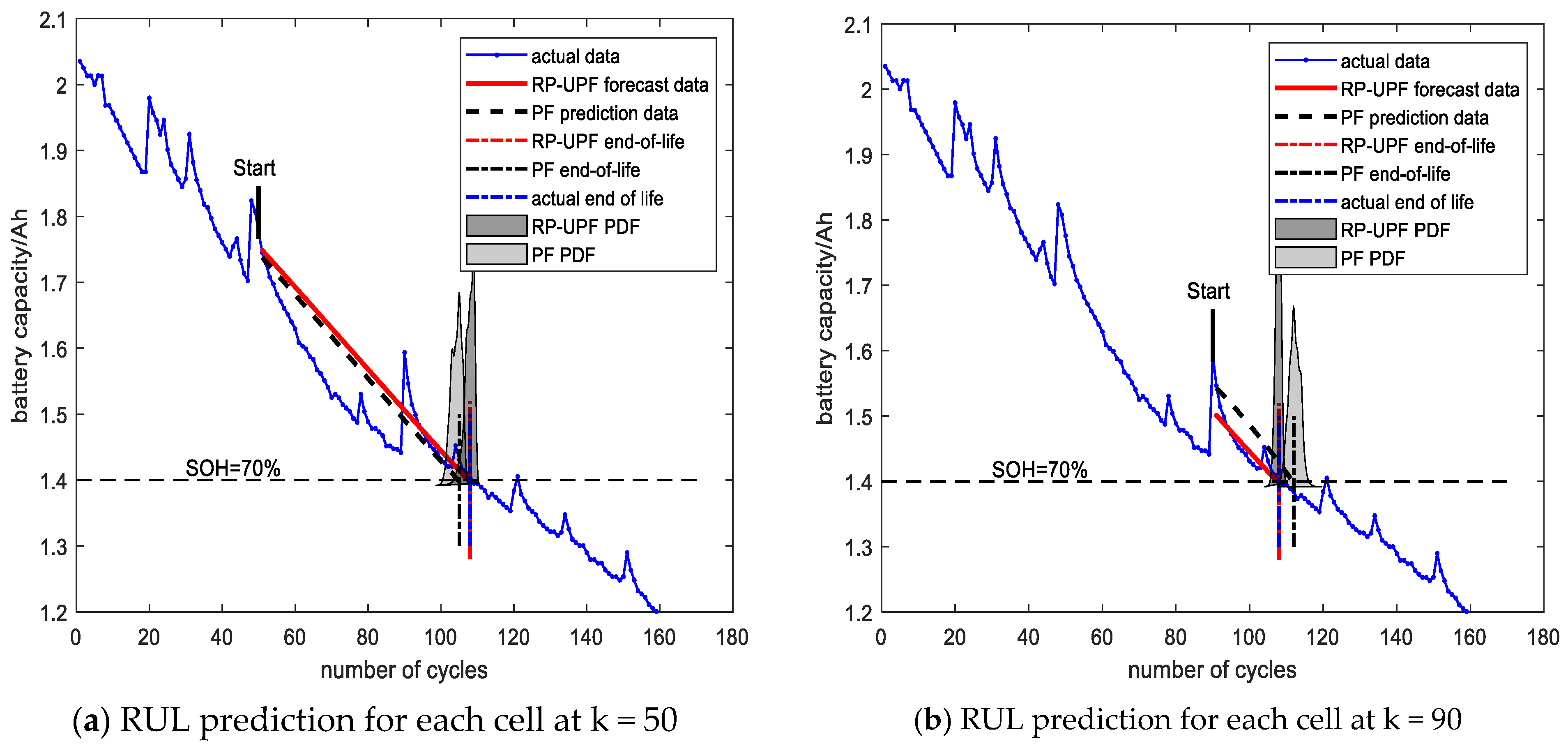
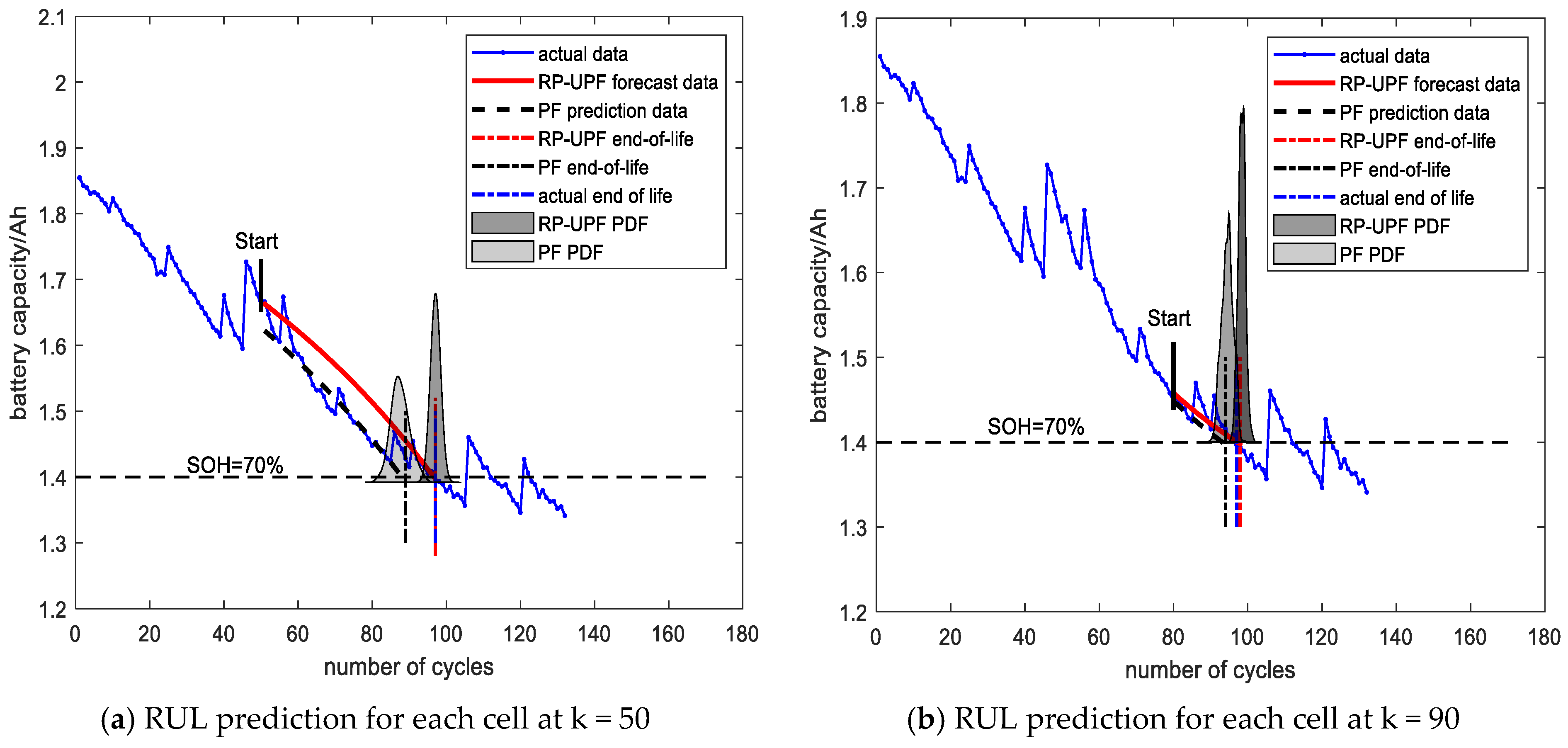
3.4. Analysis of the Battery Rul Forecast Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
References
- Ding, D.; Sun, N.; Li, A.; Li, Z.; Zhang, Y. Research on vehicle battery data cleaning method based on OOA-VMD-ATGRU-GAN. Phys. Scr. 2024, 99, 045013. [Google Scholar] [CrossRef]
- Li, Z.; Li, A.; Bai, F.; Zuo, H.; Zhang, Y. Remaining useful life prediction of lithium battery based on ACNN-Mogrifier LSTM-MMD. Meas. Sci. Technol. 2023, 35, 016101. [Google Scholar] [CrossRef]
- Li, Z.; Bai, F.; Zuo, H.; Zhang, Y. Remaining Useful Life Prediction for Lithium-Ion Batteries Based on Iterative Transfer Learning and Mogrifier LSTM. Batteries 2023, 9, 448. [Google Scholar] [CrossRef]
- Feng, S.; Wang, A.; Cai, J.; Zuo, H.; Zhang, Y. Health state estimation of on-board lithium-ion batteries based on GMM-BID model. Sensors 2022, 22, 9637. [Google Scholar] [CrossRef]
- Lyu, C.; Lai, Q.; Ge, T.; Yu, H.; Wang, L.; Ma, N. A lead-acid battery’s remaining useful life prediction by using electrochemical model in the Particle Filtering framework. Energy 2017, 120, 975–984. [Google Scholar] [CrossRef]
- Miao, Q.; Xie, L.; Cui, H.; Liang, W.; Pecht, M. Remaining useful life prediction of lithium-ion battery with unscented particle filter technique. Microelectron. Reliab. 2013, 53, 805–810. [Google Scholar] [CrossRef]
- Guha, A.; Patra, A. Online Estimation of the Electrochemical Impedance Spectrum and Remaining Useful Life of Lithium-Ion Batteries. IEEE Trans. Instrum. Meas. 2018, 67, 1836–1849. [Google Scholar] [CrossRef]
- Hong, J.; Lee, D.; Jeong, E.-R.; Yi, Y. Towards the swift prediction of the remaining useful life of lithium-ion batteries with end-to-end deep learning. Appl. Energy 2020, 278, 115646. [Google Scholar] [CrossRef]
- Chang, W. Data-Driven Prediction of Li-Ion Battery Remaining Useful Life and Optimization of Fast Charging Parameters. Master’s Thesis, East China University of Science and Technology, Shanghai, China, 2019. [Google Scholar]
- Ansari, S.; Ayob, A.; Hossain Lipu, M.S.; Hussain, A.; Saad, M.H.M. Multi-Channel Profile Based Artificial Neural Network Approach for Remaining Useful Life Prediction of Electric Vehicle Lithium-Ion Batteries. Energies 2021, 14, 7521. [Google Scholar] [CrossRef]
- Patil, M.A.; Tagade, P.; Hariharan, K.S.; Kolake, S.M.; Song, T.; Yeo, T.; Doo, S. A Novel Multistage Support Vector Machine Based Approach for Li-Ion Battery Remaining Useful Life Estimation. Appl. Energy 2015, 159, 285–297. [Google Scholar] [CrossRef]
- Zeng, W. State-Of-Health Estimation and Remaining Useful Life Prediction Method of Lithium-Ion Battery. Master’s Thesis, Anhui University of Science and Technology, Huainan, China, 2019. [Google Scholar]
- Liu, D.; Luo, Y.; Liu, J.; Peng, Y.; Guo, L.; Pecht, M. Lithium-ion battery remaining useful life estimation based on fusion nonlinear degradation AR model and RPF algorithm. Neural Comput. Appl. 2013, 25, 557–572. [Google Scholar] [CrossRef]
- Dolenc, B.; Boškoski, P.; Pohjoranta, A.; Noponen, M.; Juričić, Đ. Hybrid Approach to Remaining Useful Life Prediction of Solid Oxide Fuel Cell Stack. ECS Trans. 2017, 78, 2251–2264. [Google Scholar] [CrossRef]
- Chen, L.; Wang, H.; Chen, J.; An, J.; Ji, B.; Lyu, Z.; Cao, W.; Pan, H. A Novel Remaining Useful Life Prediction Framework for Lithium-Ion Battery Using Grey Model and Particle Filtering. Int. J. Energy Res. 2020, 44, 7435–7449. [Google Scholar] [CrossRef]
- Ju, F.; Du, W.; Zhuang, W.; Li, B.; Wang, T.; Wang, W.; Ma, H. Profit-Effective Component Sizing for Electric Delivery Trucks with Dual Motor Coupling Powertrain. Energy 2024, 296, 131055. [Google Scholar] [CrossRef]
- Su, N.K.H.; Juwono, F.H.; Wong, W.K.; Chew, I.M. Review on Machine Learning Methods for Remaining Useful Lifetime Prediction of Lithium-ion Batteries. In Proceedings of the 2022 International Conference on Green Energy, Computing and Sustainable Technology (GECOST), Miri Sarawak, Malaysia, 26–28 October 2022; pp. 286–292. [Google Scholar] [CrossRef]
- Xiong, R.; Lu, J. Preparation of Papers for IFAC Conferences & Symposia: A comparative study of remaining useful life predictions for lithium-ion battery. IFAC-Pap. 2018, 51, 268–273. [Google Scholar]
- Zan, M.; Zhou, H.; Han, D.; Yang, G.; Xu, G. Survey of Particle Filter Target Tracking Algorithms. Master’s Thesis, School of Electronic and Information Engineering, Beijing, China, 2019. [Google Scholar]
- Wang, H.; Peng, Z. Structural response reconstruction based on improved particle filter algorithm. Noise Vib. Control. 2023, 43, 31–37. [Google Scholar]
- Zhang, K.; Wang, W. EKF-PF algorithm based SOC estimation of retired power lithium batteries. Mod. Electron. Tech. 2023, 46, 145–150. [Google Scholar]
- Chen, L.; Chen, J.; Wang, H.; Wang, Y.; An, J.; Yang, R.; Pan, H. Remaining Useful Life Prediction of Battery Using a Novel Indicator and Framework With Fractional Grey Model and Unscented Particle Filter. IEEE Trans. Power Electron. 2020, 35, 5850–5859. [Google Scholar] [CrossRef]
- Chen, W.; Cai, Y.; Su, Y.; Jiang, K.; Li, A. Remaining useful life prediction for lithium-ion battery based on improved particle filtering. China Meas. Test 2021, 47, 148–153. [Google Scholar]
- Meng, F.; Yang, F.; Yang, J.; Xie, M. A power model considering initial battery state for remaining useful life prediction of lithium-ion batteries. Reliab. Eng. Syst. Saf. 2023, 237, 109361. [Google Scholar] [CrossRef]
- Shi, J.; Rivera, A.; Wu, D. Battery health management using physics-informed machine learning: Online degradation modeling and remaining useful life prediction. Mech. Syst. Signal Process. 2022, 179, 109347. [Google Scholar] [CrossRef]
- Zhang, N.; Xu, A.D.; Wang, K.; Han, X.J.; Hong, W.H.; Hong, S.H. Remaining Useful Life Prediction of Lithium Batteries Based on Extended Kalman Particle Filter. IEEJ Trans. Electr. Electron. Eng. 2021, 16, 206–214. [Google Scholar] [CrossRef]
- Mishra, A.; Subramanian, V.R.; Suthar, B. Hexic Polynomial Approximation for Spherical Diffusion to Accelerate Accurate Lithium-Ion Battery Simulation. J. Electrochem. Soc. 2022, 169, 120532. [Google Scholar] [CrossRef]
- Wang, S.; Li, Z.H.; Zhang, E.; Zhou, M.; Wang, K.L. State of Charge Estimation for Liquid Metal Batteries with Gaussian Process Regression Framework. In Proceedings of the 2022 International Power Electronics Conference, Himeji, Japan, 15–19 May 2022; pp. 1665–1669. [Google Scholar]
- He, H.; Zhang, Y.; Xiong, R.; Wang, C. A novel Gaussian model based battery state estimation approach: State-of-Energy. Appl. Energy 2015, 151, 41–48. [Google Scholar] [CrossRef]
- Duan, H.; Yi, W. Construction and optimization of EV battery capacity decline prediction model based on fusion method. Spec. Purp. Veh. 2023, 10, 8–11. [Google Scholar]
- Xiong, R.; Zhang, Y.; He, H.; Zhou, X.; Pecht, M.G. A Double-Scale, Particle-Filtering, Energy State Prediction Algorithm for Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2018, 65, 1526–1538. [Google Scholar] [CrossRef]
- Tang, X.; Wang, Y.; Yao, K.; He, Z.; Gao, F. Model migration based battery power capability evaluation considering uncertainties of temperature and aging. J. Power Sources 2019, 440, 227141. [Google Scholar] [CrossRef]
- Xia, F.; Wang, Z.; Zhang, C. State of Charge Estimation of Lithium-ion Batteries with Particle Filter Algorithm. In Proceedings of the IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 3628–3634. [Google Scholar] [CrossRef]
- Duan, W. Research on State Estimation and Remaining Useful Life Prediction of Lithium-Ion Batteries. Master’s Thesis, Jilin University, Changchun, China, 2023. [Google Scholar] [CrossRef]
- Zhao, J.; Tian, L.; Cheng, C. Review on state estimation and remaining useful life prediction methods for lithium-ion battery. Power Gener. Technol. 2023, 44, 5014. [Google Scholar] [CrossRef]
- Liao, L.; Xiao, T.; Wu, T.; Jiang, J. SOH and RUL prediction for lithium batteries based on fusion of multiple health features. Power Supply Technol. 2023, 47, 193–198. [Google Scholar]
- Shen, Y. Hybrid unscented particle filter based state-of-charge determination for lead-acid batteries. Energy 2014, 74, 795–803. [Google Scholar] [CrossRef]
- Cai, Y.; Yang, L.; Deng, Z.; Zhao, X.; Deng, H. Prediction of lithium-ion battery remaining useful life based on hybrid data-driven method with optimized parameter. In Proceedings of the 2017 2nd International Conference on Power and Renewable Energy (ICPRE), Chengdu, China, 20–23 September 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, B.; Lei, M.; Liang, J. An IPSO-GRU-Based Prediction of Remaining Useful Life of Lithium-Ion Batteries. J. Hunan Univ. Technol. 2022, 36, 23–30. [Google Scholar]
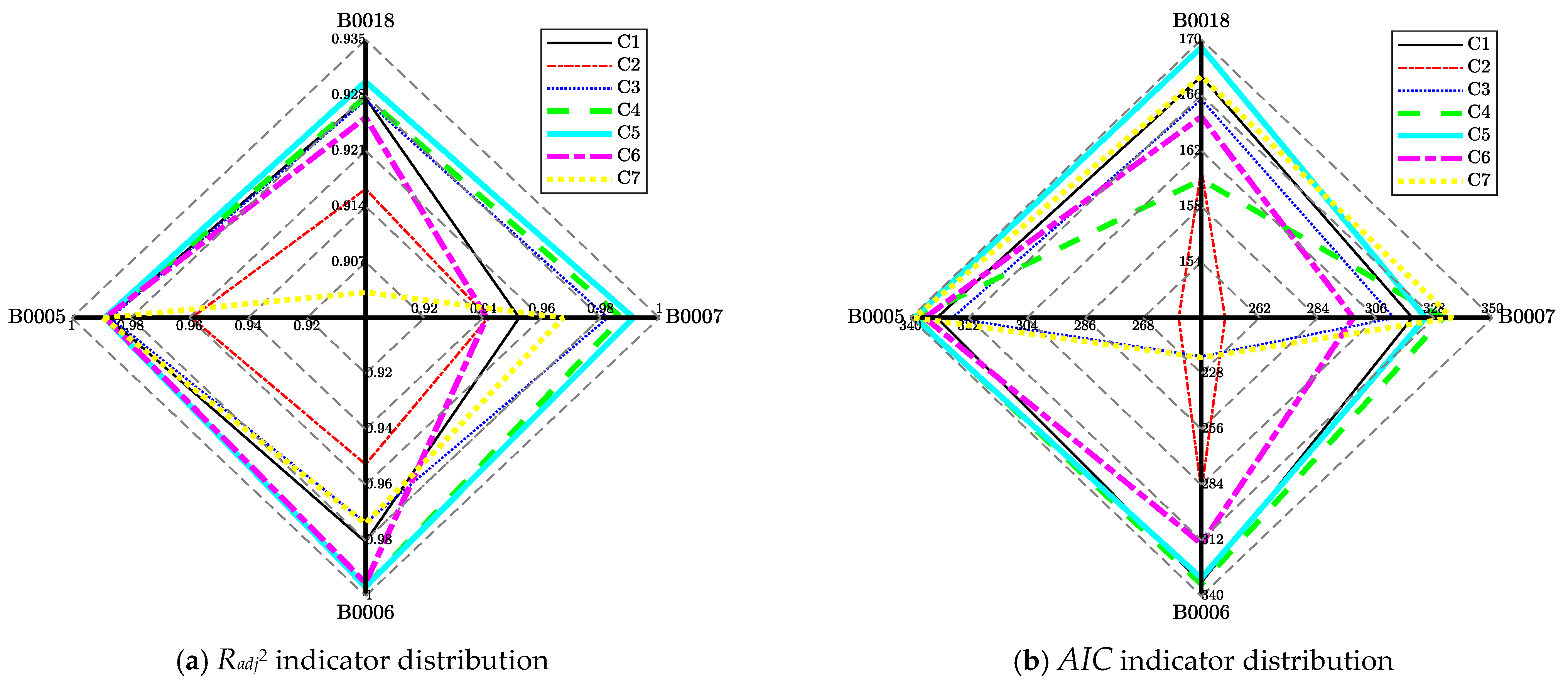

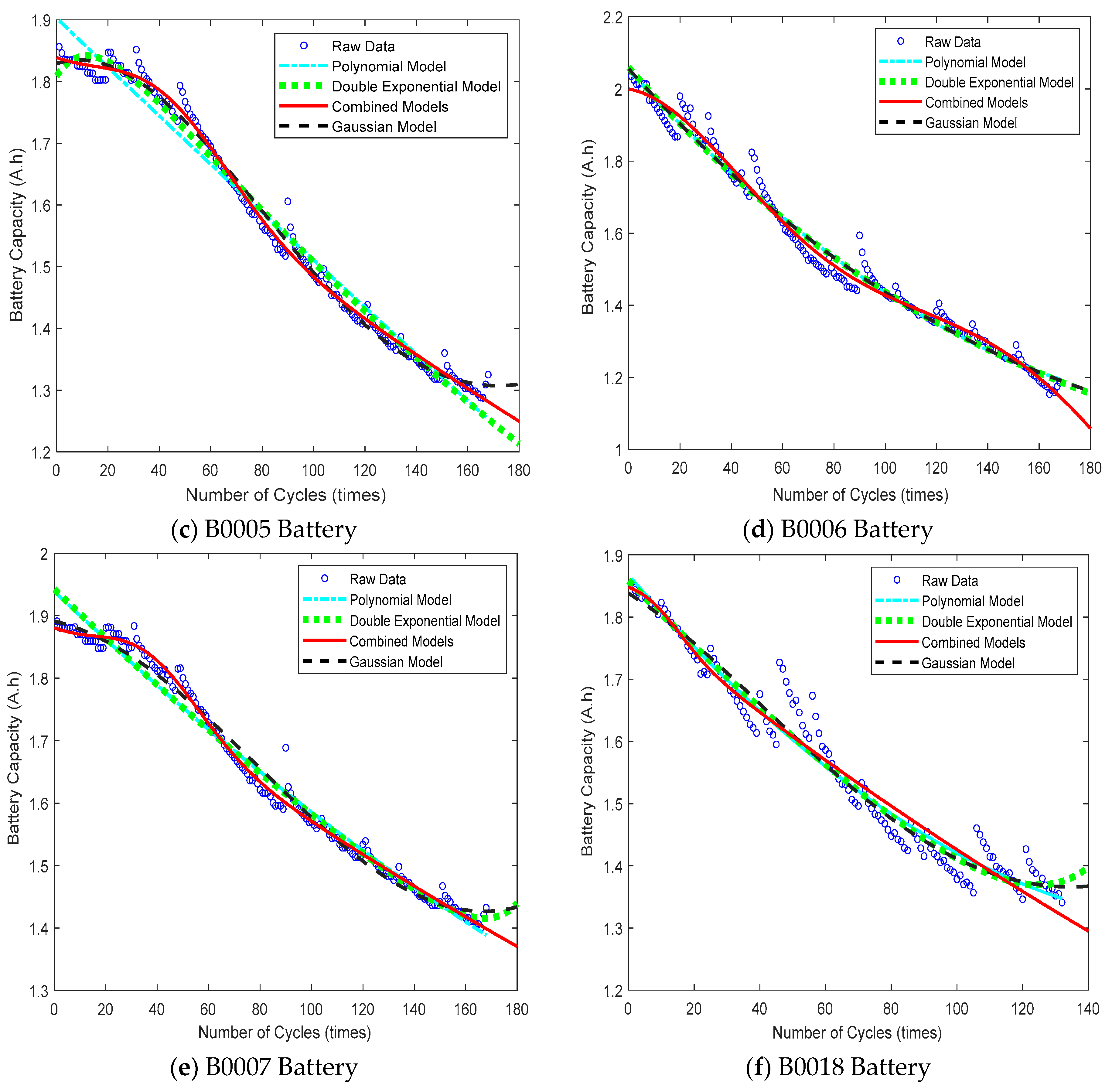
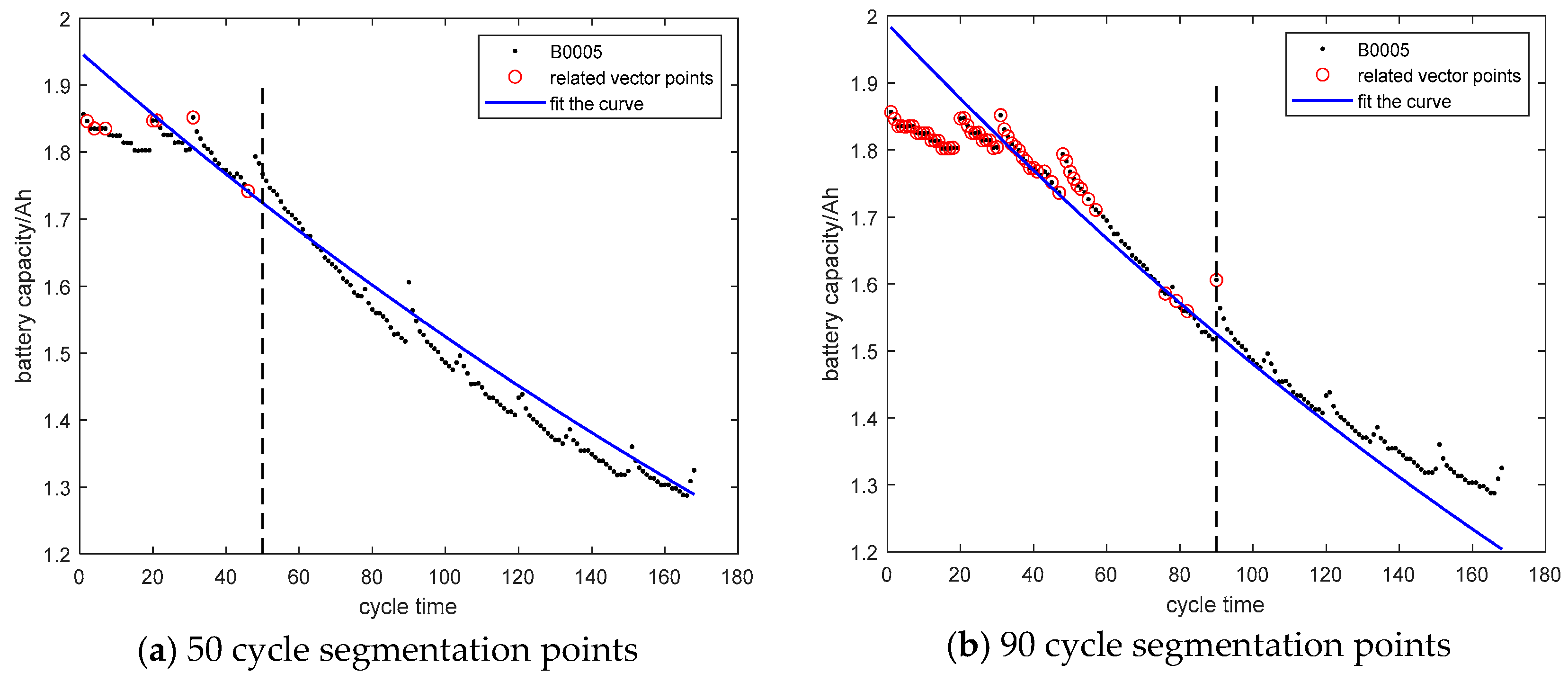
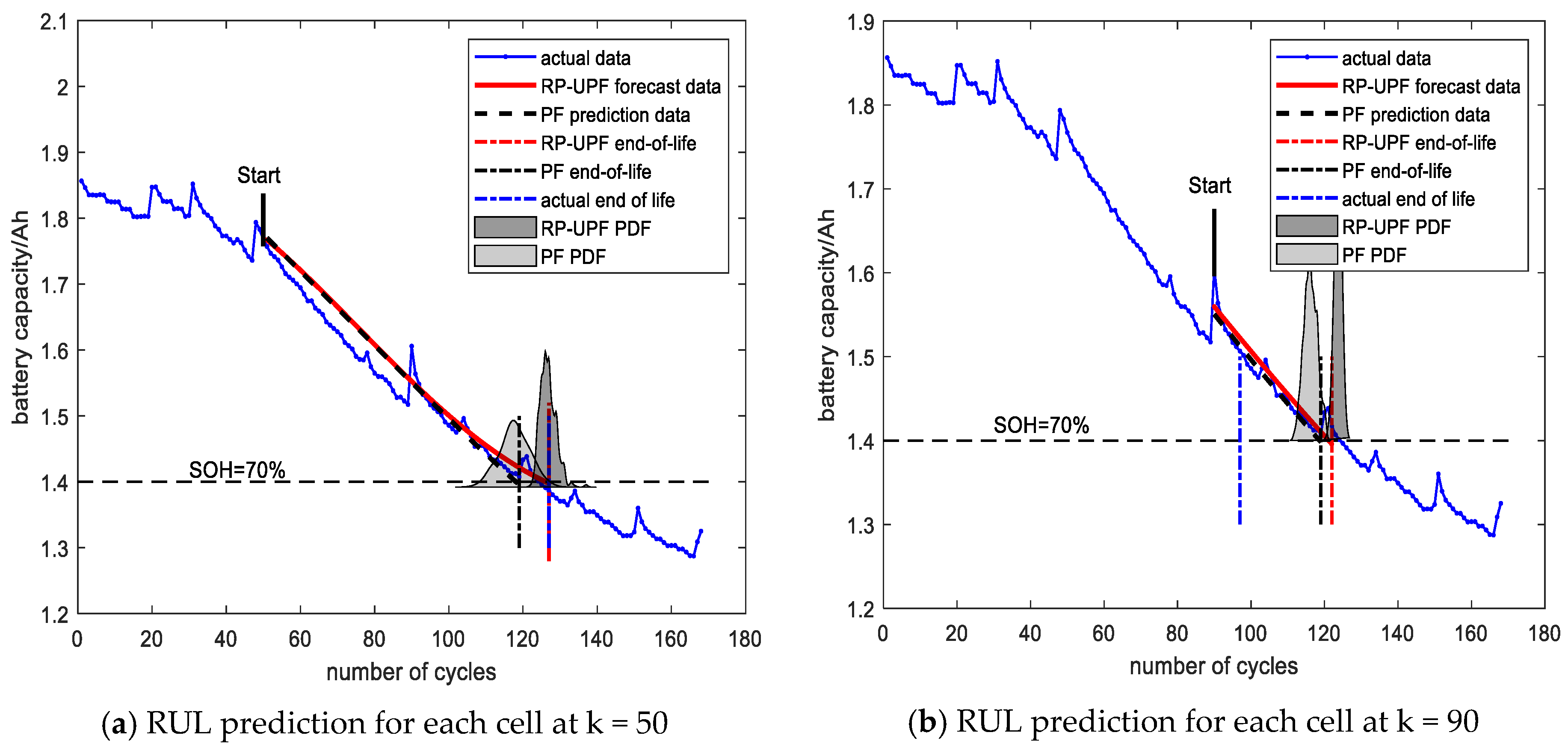
| Battery Model | Single Term of the Double Exponential Function Ce1 | Single Term of the Gaussian Function Cg1 | ||
|---|---|---|---|---|
| Radj2 | RMSE | Radj2 | RMSE | |
| B0005 | 0.9207 | 0.04189 | 0.9672 | 0.02695 |
| B0006 | 0.9409 | 0.04527 | 0.9550 | 0.03950 |
| B0007 | 0.9315 | 0.03853 | 0.9650 | 0.03150 |
| B0018 | 0.8856 | 0.04053 | 0.9013 | 0.03767 |
| Battery Model | Radj2 | ||||
|---|---|---|---|---|---|
| Polynomial Model | Biexponential Model | Gaussian Model | Building Model | ||
| NASA | B0005 | 0.9754 | 0.9859 | 0.9932 | 0.9930 |
| B0006 | 0.9808 | 0.9808 | 0.9859 | 0.9850 | |
| B0007 | 0.9785 | 0.9795 | 0.9878 | 0.9938 | |
| B0018 | 0.9587 | 0.9617 | 0.9511 | 0.9649 | |
| CALCE | A5 | 0.8776 | 0.9945 | 0.9610 | 0.9968 |
| A12 | 0.9529 | 0.9691 | 0.9874 | 0.9987 | |
| Battery Model | RMSE | ||||
| Polynomial model | Biexponential model | Gaussian model | Building model | ||
| NASA | B0005 | 0.0299 | 0.0226 | 0.0152 | 0.0150 |
| B0006 | 0.0350 | 0.0349 | 0.0300 | 0.0319 | |
| B0007 | 0.0236 | 0.0230 | 0.0182 | 0.0127 | |
| B0018 | 0.0314 | 0.0303 | 0.0342 | 0.0302 | |
| CALCE | A5 | 0.0359 | 0.0076 | 0.0205 | 0.0058 |
| A12 | 0.0581 | 0.0471 | 0.0300 | 0.0098 | |
| Battery Model | Starting Cycle | a (0) | b (0) | c (0) | d (0) |
|---|---|---|---|---|---|
| B0005 | 50 | 1.8883 | −20.6662 | 125.9084 | 0.0073 |
| 90 | 1.8730 | −21.5266 | 128.8280 | 0.0089 | |
| B0006 | 50 | 2.4047 | −101.6399 | 243.6830 | 0.0019 |
| 90 | 2.5168 | −94.0786 | 262.3111 | 0.0021 | |
| B0018 | 50 | 1.9279 | 42.4843 | 205.8986 | −0.0075 |
| 80 | 1.8546 | 37.4501 | 373.0657 | −0.0046 |
| Battery Model | Start | Filtering Algorithm | Actual RUL | Projected RUL | Absolute Error | Relative Error (%) | PDF Width |
|---|---|---|---|---|---|---|---|
| B0005 | 50 | RP-UPF | 74 | 77 | 3 | 4.05 | 9 |
| PF | 69 | 5 | 6.76 | 19 | |||
| 90 | RP-UPF | 35 | 33 | 2 | 5.71 | 6 | |
| PF | 30 | 5 | 14.29 | 9 | |||
| B0006 | 50 | RP-UPF | 59 | 58 | 1 | 1.69 | 6 |
| PF | 55 | 4 | 6.78 | 7 | |||
| 90 | RP-UPF | 19 | 18 | 1 | 5.26 | 5 | |
| PF | 22 | 3 | 15.79 | 8 | |||
| B0018 | 50 | RP-UPF | 54 | 47 | 0 | 0 | 7 |
| PF | 39 | 8 | 14.81 | 12 | |||
| 80 | RP-UPF | 24 | 22 | 2 | 8.33 | 6 | |
| PF | 20 | 4 | 16.67 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Chen, J.; Yong, J.; Yang, C.; Yan, L.; Zheng, Y. Remaining Service Life Prediction of Lithium-Ion Batteries Based on Randomly Perturbed Traceless Particle Filtering. Energies 2024, 17, 5482. https://doi.org/10.3390/en17215482
Liu Y, Chen J, Yong J, Yang C, Yan L, Zheng Y. Remaining Service Life Prediction of Lithium-Ion Batteries Based on Randomly Perturbed Traceless Particle Filtering. Energies. 2024; 17(21):5482. https://doi.org/10.3390/en17215482
Chicago/Turabian StyleLiu, Yan, Jun Chen, Jun Yong, Cheng Yang, Liqin Yan, and Yanping Zheng. 2024. "Remaining Service Life Prediction of Lithium-Ion Batteries Based on Randomly Perturbed Traceless Particle Filtering" Energies 17, no. 21: 5482. https://doi.org/10.3390/en17215482
APA StyleLiu, Y., Chen, J., Yong, J., Yang, C., Yan, L., & Zheng, Y. (2024). Remaining Service Life Prediction of Lithium-Ion Batteries Based on Randomly Perturbed Traceless Particle Filtering. Energies, 17(21), 5482. https://doi.org/10.3390/en17215482






