Energy Advantages and Thermodynamic Performance of Scheffler Receivers as Thermal Sources for Solar Thermal Power Generation
Abstract
1. Introduction
2. Organization of the Manuscript
- In this paper, first, to calculate energy performance of Scheffler-type solar receivers at part-load operating conditions, a numerical model is presented which computes all energy losses affecting the thermal transfer phase in the cavity receiver. Then, solar power collector energy efficiency obtained via the proposed numerical model could be calculated for variable sun radiation and under a wide range of working conditions.
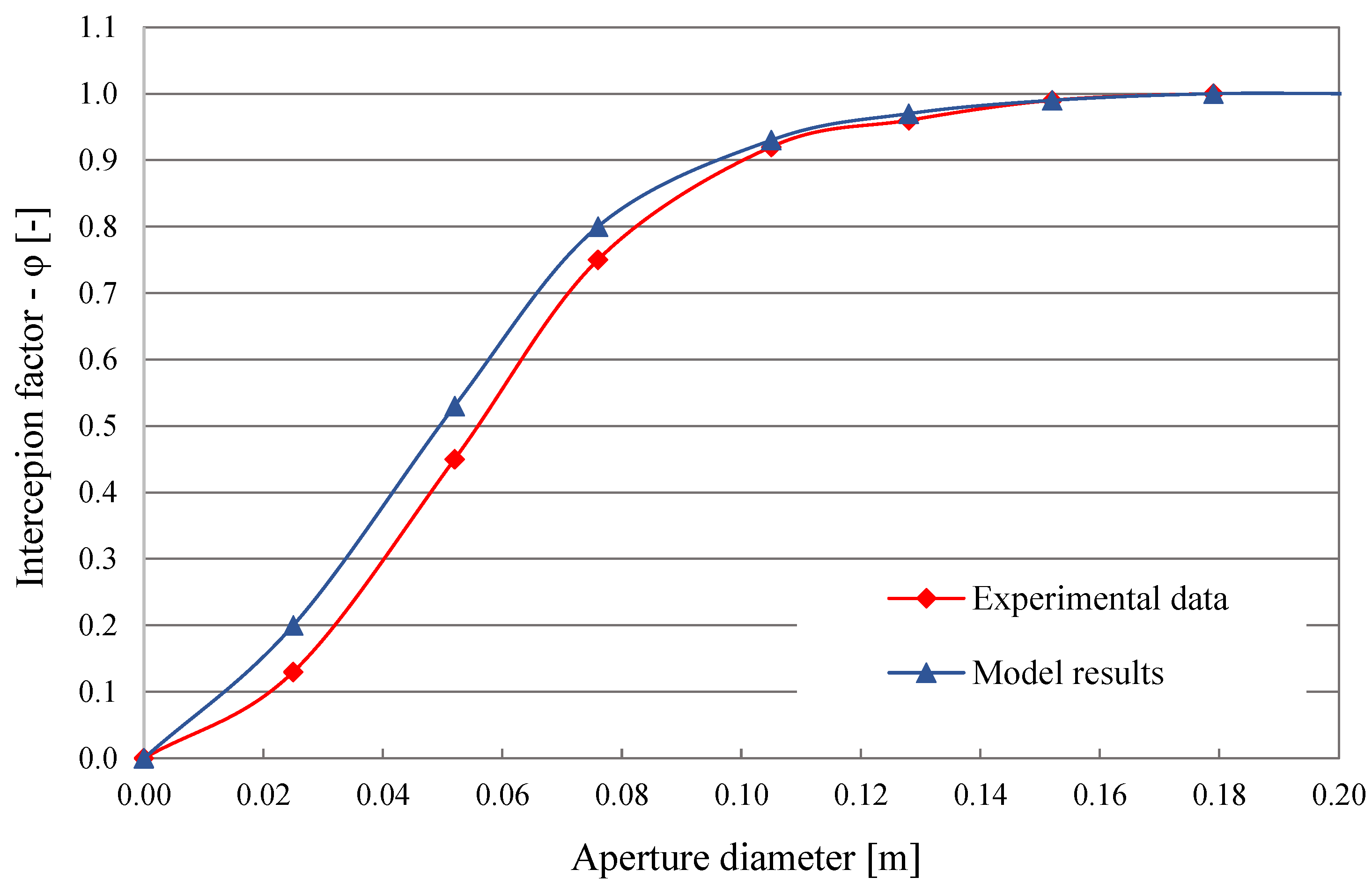
- After presenting this thermal model, its validation procedure was conducted using test data from relevant scientific literature.
- Subsequently, to evaluate a performance analysis between the Scheffler-type solar receiver and conventional PTC system, basic equations and thermodynamic models were also established on the latter solar system.
- Lastly, as a result of mathematical simulations based on such thermodynamic models, a comparison between Scheffler and PTC solar systems was conducted in relation to energy performance and solar power collector efficiency. The main results obtained for these two kinds of solar systems were then settled and compared.
3. Modelling
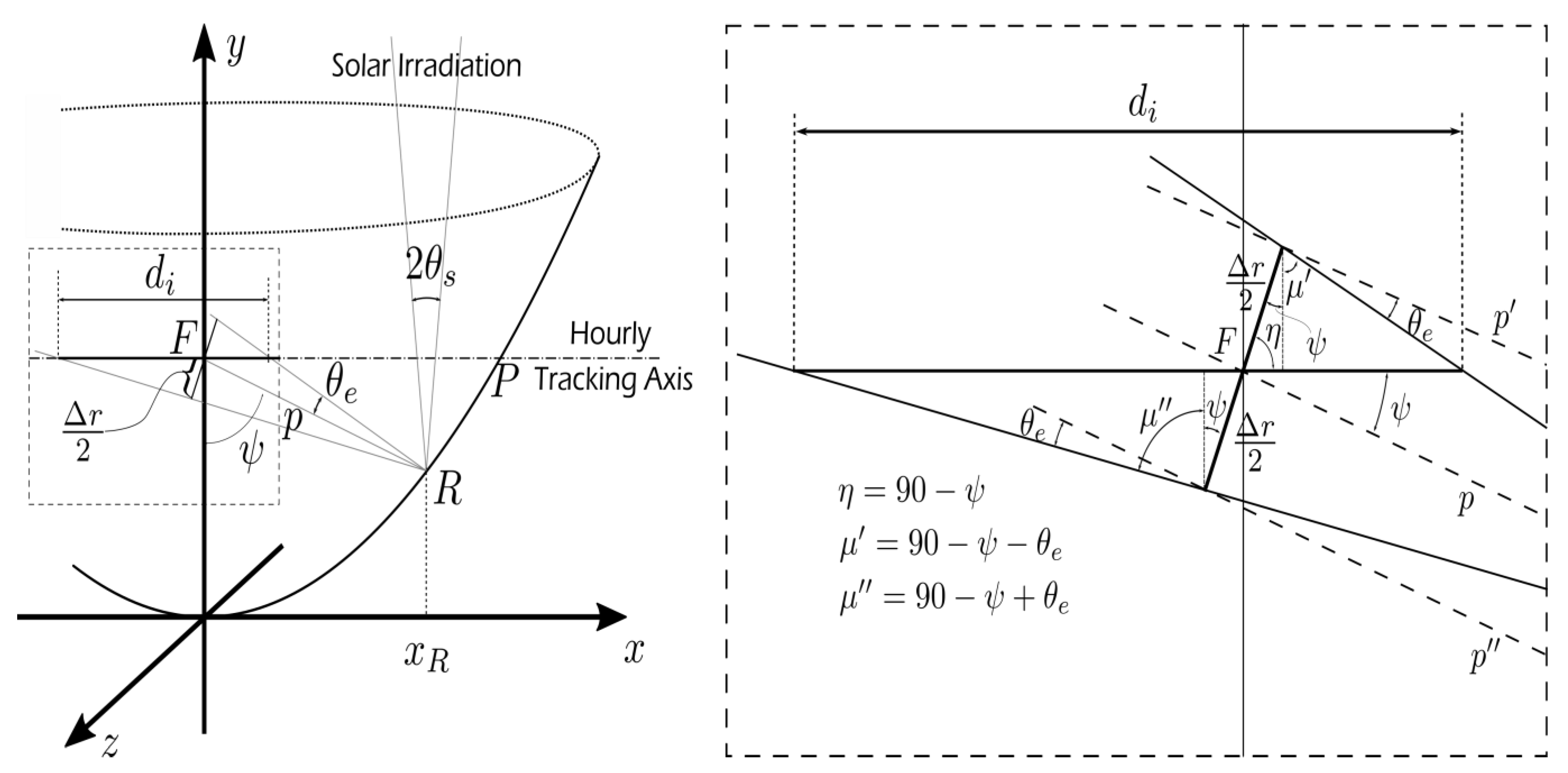
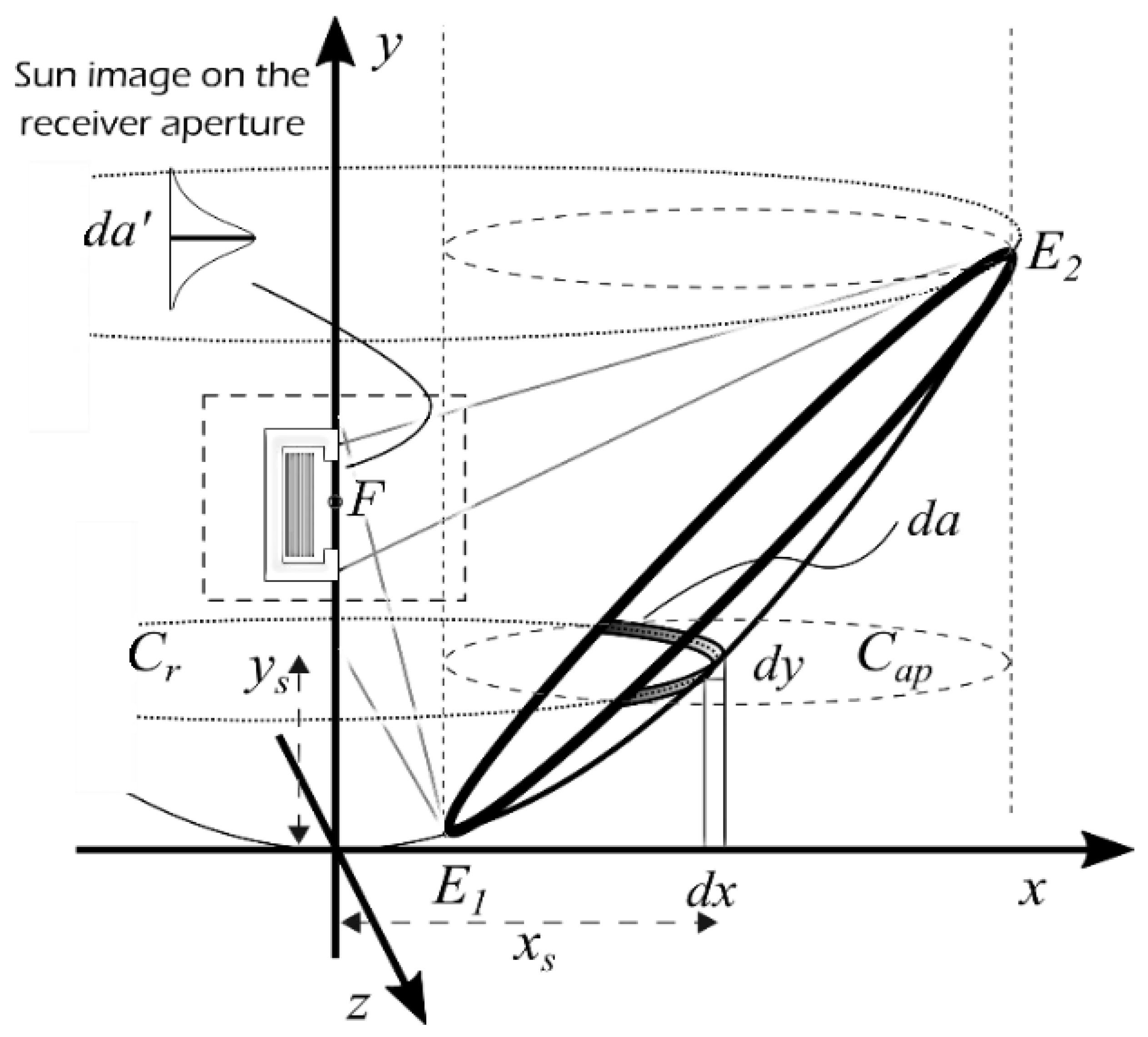
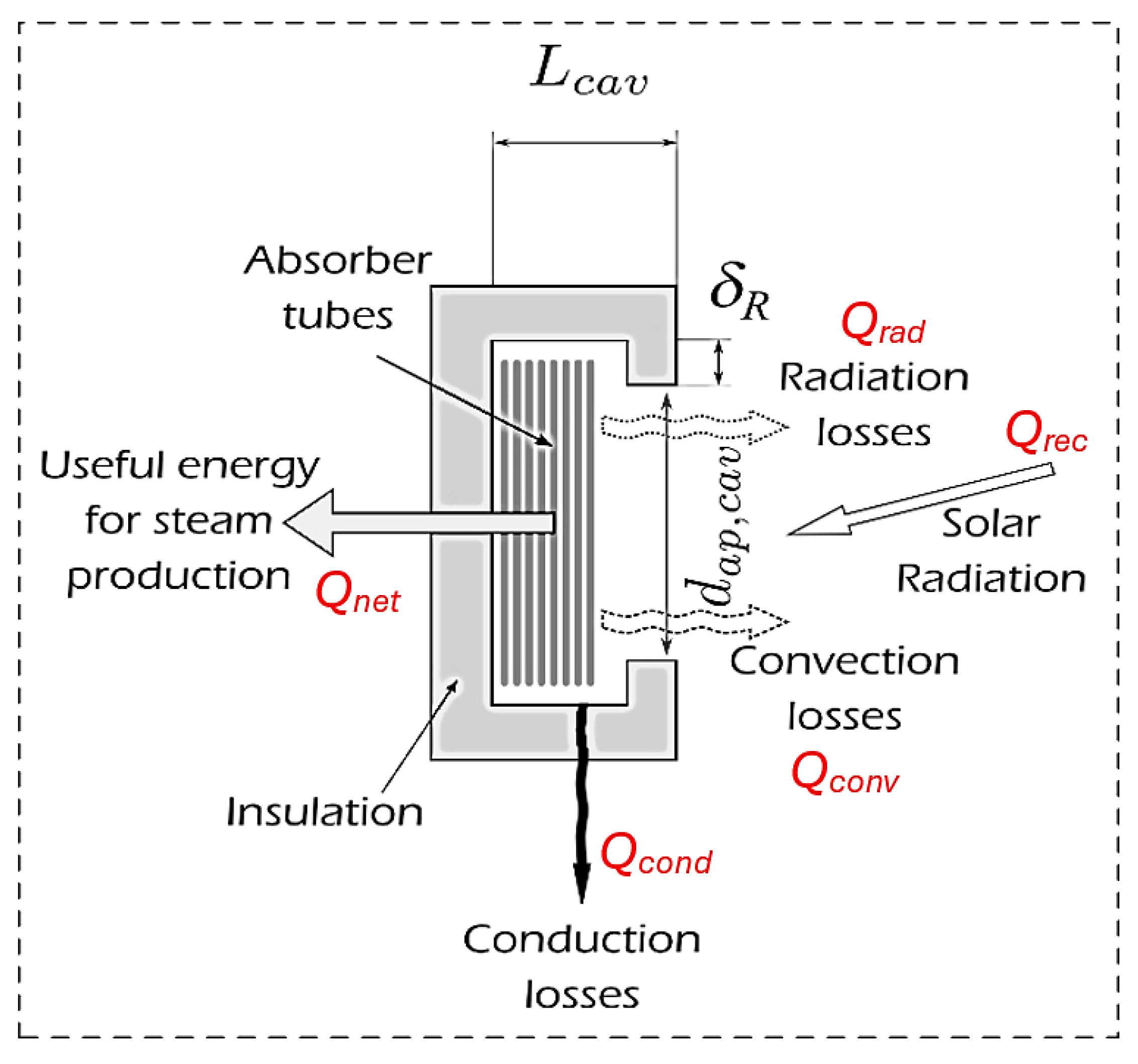
3.1. The Scheffler Reflector and Receiver
- tracking errors owing to sensors, ;
- errors caused by the width of the sun, ;
- errors caused by the inaccurate inclination of the parabolic mirror that occur during manufacturing process, ;
- imperfections in the mirror alignment of the receiver, ;
- imperfections owing to deviations in mirror reflectivity, ;
- imperfections owing to tracking guides not completely aligned, .
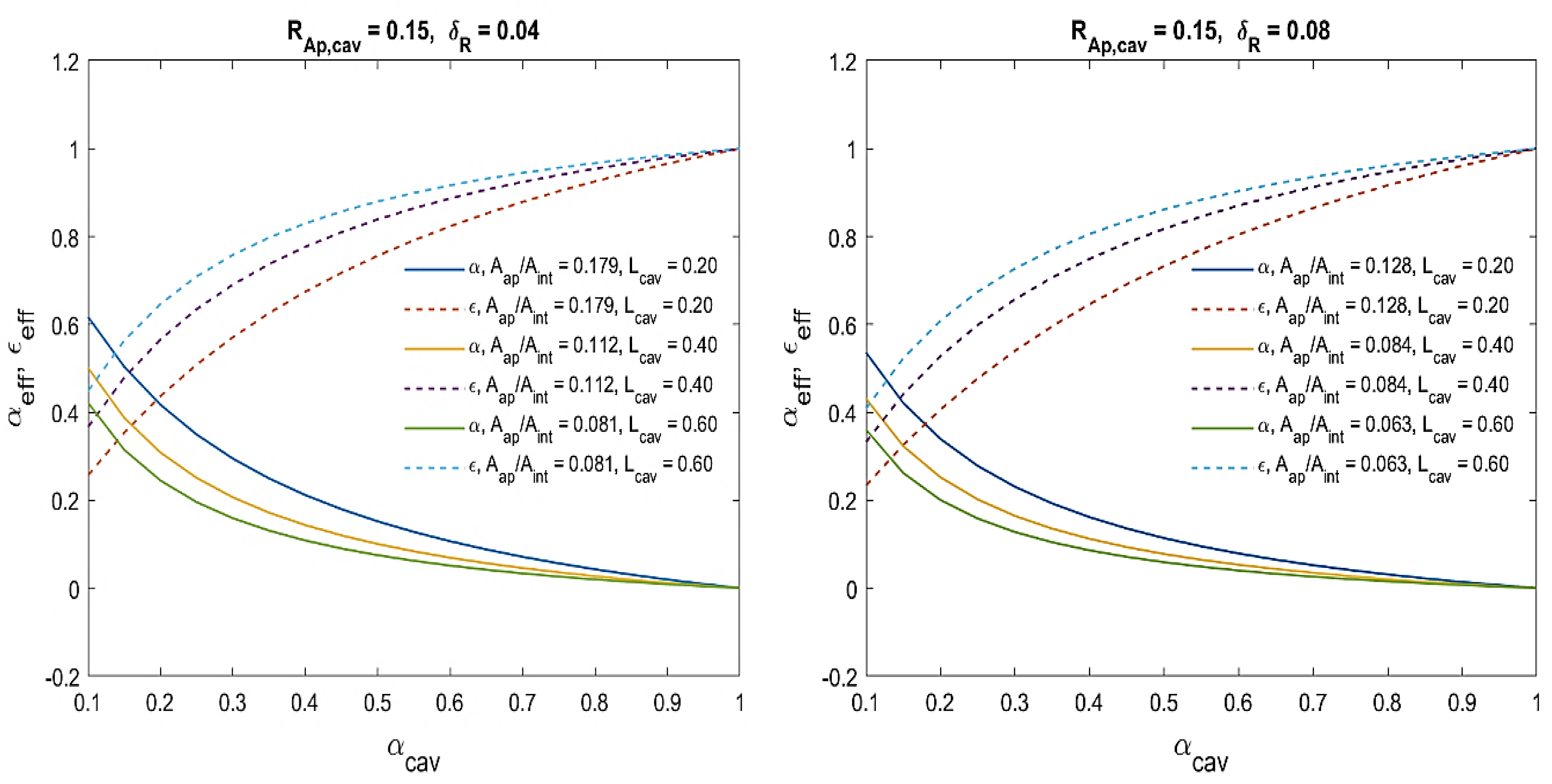
The Selection of Geometric Factors of the Scheffler Receiver System and Model Validation
3.2. The PTC Receivers
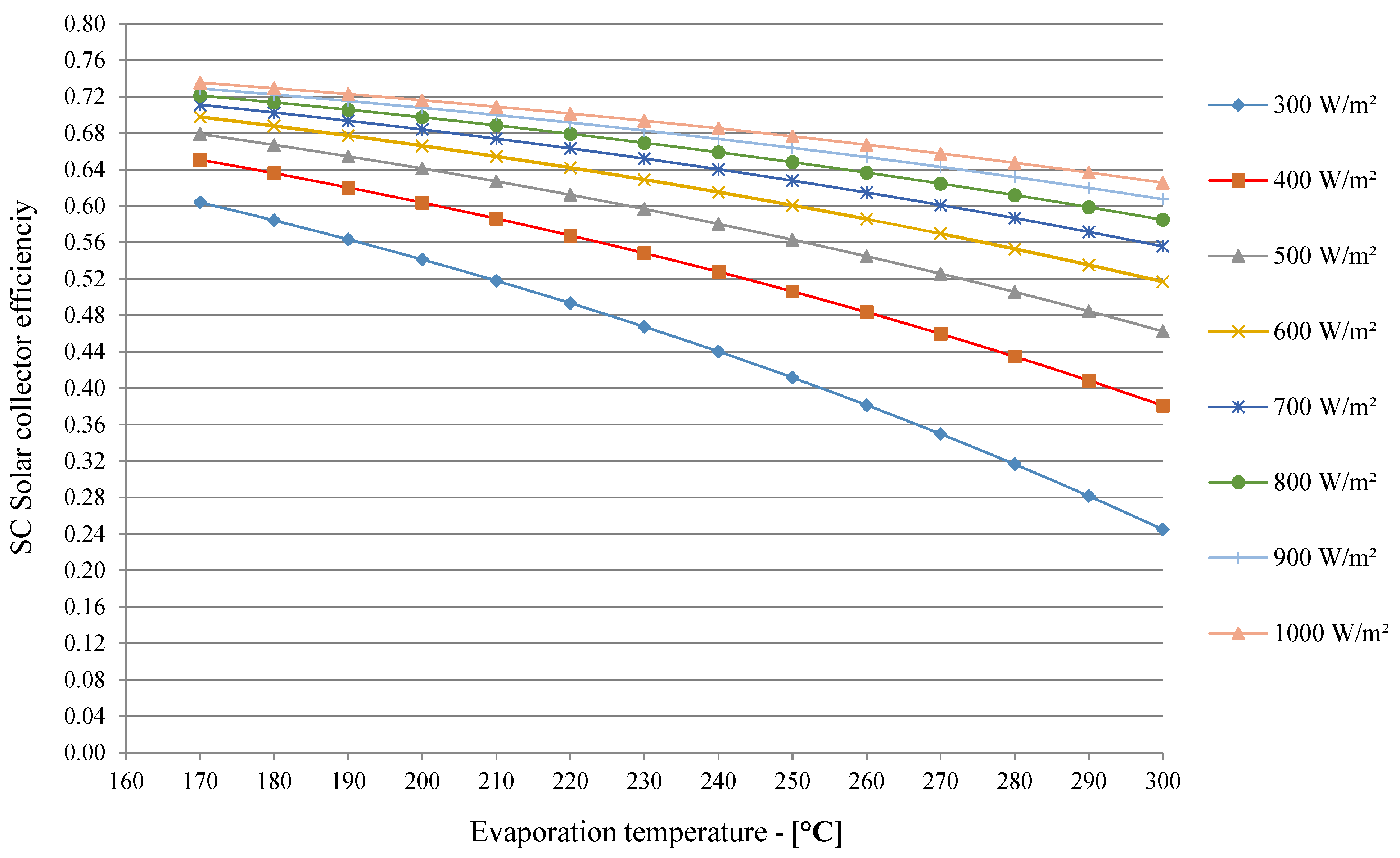
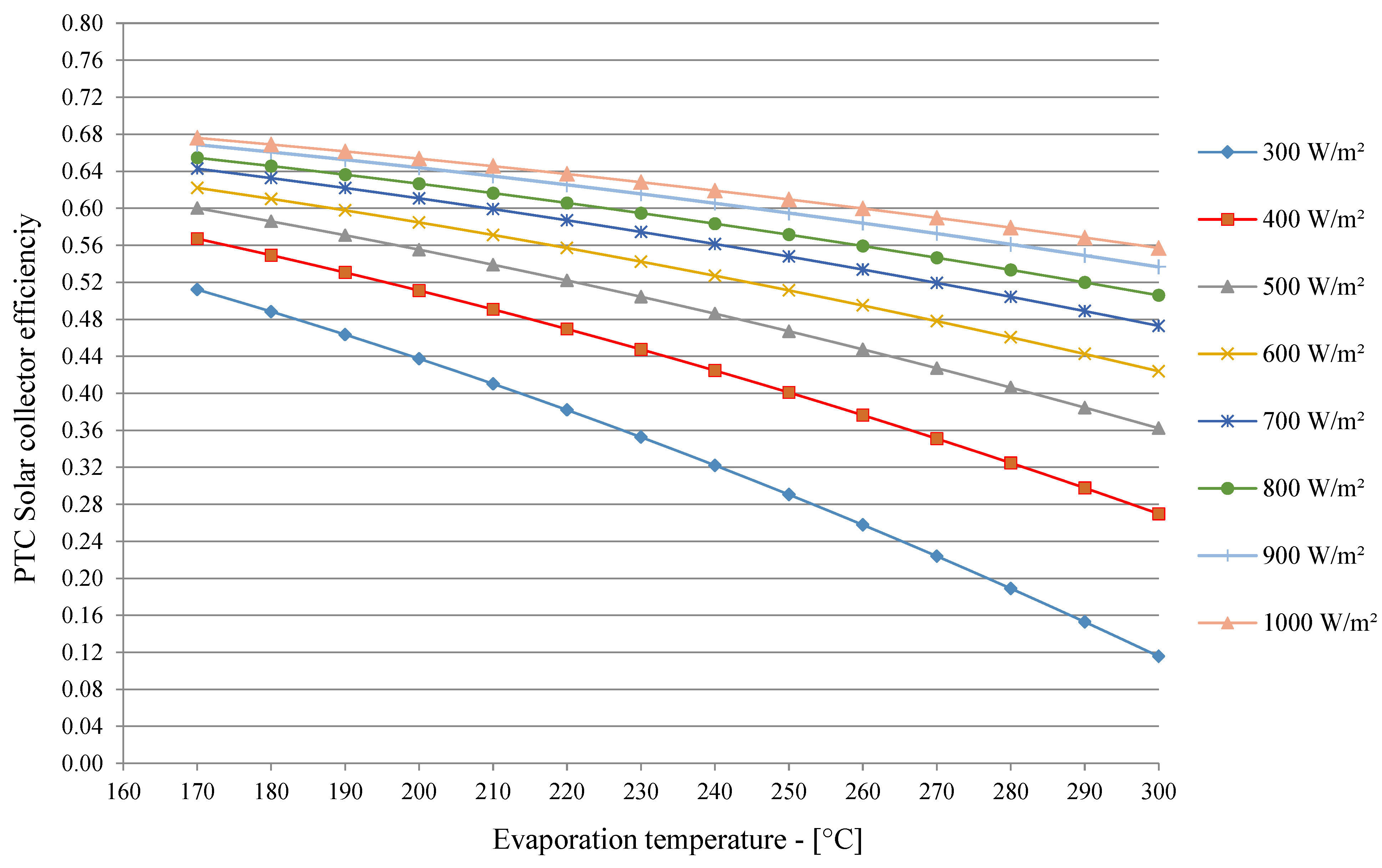
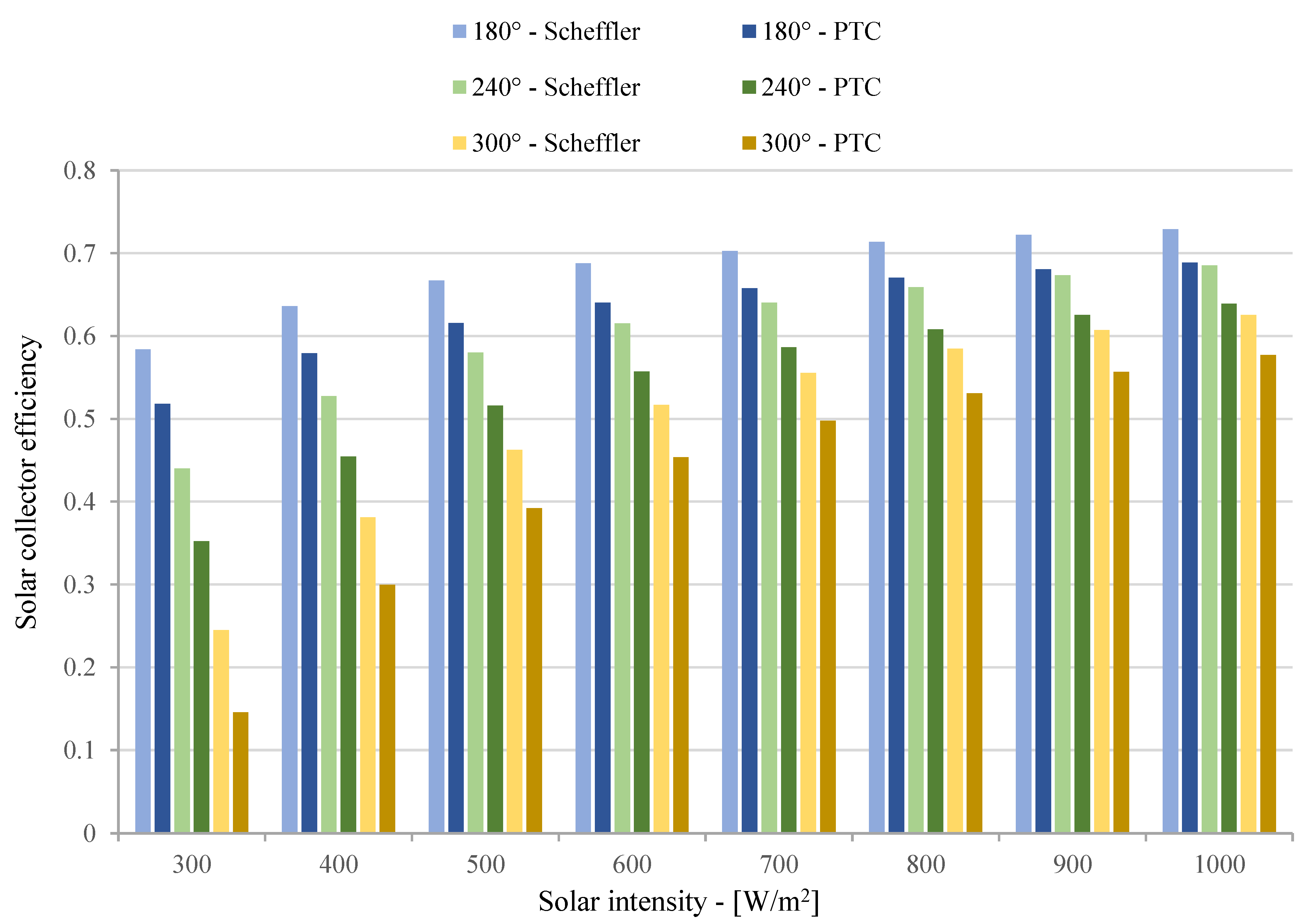
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fatigati, F.; Di Bartolomeo, M.; Cipollone, R. Dual intake rotary vane expander technology: Experimental and theoretical assessment. Energy Convers. Manag. 2019, 186, 156–167. [Google Scholar] [CrossRef]
- Li, L.; Li, Y.S.; Sun, J. Prospective fully-coupled multi-level analytical methodology for concentrated solar power plants: Applications. Appl. Therm. Eng. 2017, 118, 159–170. [Google Scholar] [CrossRef]
- Mcingani, I.; Meyer, E.L.; Overen, O.K. The Impact of Ambient Weather Conditions and Energy Usage Patterns on the Performance of a Domestic Off-Grid Photovoltaic System. Energies 2024, 17, 5013. [Google Scholar] [CrossRef]
- Saidi, S.; Abbassi, R.; Ben Hassen, W.; Chebbi, S. Solar photovoltaic energy system-based shunt active filter for electrical energy quality improvement. Int. J. Simul. Process Model. 2016, 11, 119–126. [Google Scholar] [CrossRef]
- Abbassi, R.; Saidi, S.; Urooj, S.; Alhasnawi, B.N.; Alawad, M.A.; Premkumar, M. An accurate metaheuristic mountain gazelle optimizer for parameter estimation of single- and double-diode photovoltaic cell models. Mathematics 2023, 11, 4565. [Google Scholar] [CrossRef]
- Naseri, A.; Bidi, M.; Ahmadi, M. Thermodynamic and exergy analysis of a hydrogen and permeate water production process by a solar-driven transcritical CO2 power cycle with liquefied natural gas heat sink. Renew. Energy 2017, 113, 1215–1228. [Google Scholar] [CrossRef]
- Iodice, P.; Langella, G.; Amoresano, A. Energy performance and numerical optimization of a screw expander–based solar thermal electricity system in a wide range of fluctuating operating conditions. Int. J. Energy Res. 2020, 44, 1858–1874. [Google Scholar] [CrossRef]
- Li, L.; Sun, J.; Li, Y. Thermal load and bending analysis of heat collection element of direct-steam-generation parabolic-trough solar power plant. Appl. Therm. Eng. 2017, 127, 1530–1542. [Google Scholar] [CrossRef]
- Sachdeva, J.; Singh, O. Comparative evaluation of solarized triple combined cycle for different ORC fluids. Renew. Energy 2021, 163, 1333–1342. [Google Scholar] [CrossRef]
- Petrollese, M.; Cocco, D. A multi-scenario approach for a robust design of solar-based ORC systems. Renew. Energy 2020, 161, 1184–1194. [Google Scholar] [CrossRef]
- Roumpedakis, T.C.; Loumpardis, G.; Monokrousou, E.; Braimakis, K.; Charalampidis, A.; Karellas, S. Exergetic and economic analysis of a solar driven small scale ORC. Renew. Energy 2020, 157, 1008–1024. [Google Scholar] [CrossRef]
- Li, L.; Sun, J.; Li, Y.; He, Y.L.; Xu, H. Transient characteristics of a parabolic trough direct-steam-generation process. Renew. Energy 2019, 135, 800–810. [Google Scholar] [CrossRef]
- Price, H.; Lu¨ pfert, E.; Kearney, D.; Zarza, E.; Cohen, G.; Gee, R.; Mahoney, R. Advances in parabolic trough solar power technology. J. Sol. Energy Eng. 2002, 124, 109–125. [Google Scholar] [CrossRef]
- Li, L.; Sun, J.; Li, Y.S. Prospective fully-coupled multi-level analytical methodology for concentrated solar power plants: General modelling. Appl. Therm. Eng. 2017, 118, 171–187. [Google Scholar] [CrossRef]
- Laing, D.; Bahl, C.; Bauer, T.; Lehmann, D.; Steinmann, W.D. Thermal energy storage for direct steam generation. Sol. Energy 2011, 85, 627–633. [Google Scholar] [CrossRef]
- Iodice, P.; Langella, G.; Amoresano, A. Exergetic analysis of a new direct steam generation solar plant using screw expanders. Energies 2020, 13, 720. [Google Scholar] [CrossRef]
- Li, J.; Li, P.; Gao, G.; Pei, G.; Su, Y.; Ji, J. Thermodynamic and economic investigation of a screw expander-based direct steam generation solar cascade Rankine cycle system using water as thermal storage fluid. Appl. Energy 2017, 195, 137–151. [Google Scholar] [CrossRef]
- Iodice, P.; Amoresano, A.; Langella, G.; Marra, F.S. Comprehensive assessment and energetic-exergetic performance optimization of a new solar thermal electricity system based on Scheffler-type receivers combined with screw-type volumetric machines. Int. J. ThermoFluids 2024, 24, 100881. [Google Scholar] [CrossRef]
- Ruelas, J.; Velázquez, N.; Cerezo, J. A mathematical model to develop a Scheffler-type solar concentrator coupled with a Stirling engine. Appl. Energy 2013, 101, 253–260. [Google Scholar] [CrossRef]
- Munir, A.; Hensel, O.; Scheffler, W. Design principle and calculations of a Scheffler fixed focus concentrator for medium temperature applications. Sol. Energy 2010, 84, 1490–1502. [Google Scholar] [CrossRef]
- Iodice, P.; Amoresano, A.; Langella, G.; Marra, F.S. Combined use of volumetric expanders and Scheffler receivers to improve the efficiency of a novel direct steam solar power plant. Int. J. Energy Res. 2021, 45, 21058–21081. [Google Scholar] [CrossRef]
- Li, J.; Li, P.; Pei, G.; Alvi, J.Z.; Ji, J. Analysis of a novel solar electricity generation system using cascade Rankine cycle and steam screw expander. Appl. Energy 2016, 165, 627–638. [Google Scholar] [CrossRef]
- Fraser, P.R. Stirling Dish System Performance Prediction Model. Master’s Thesis, University of Wisconsin-Madison, Madison, WI, USA, 2008. [Google Scholar]
- Stefanovic, V.P.; Pavlovic, S.R.; Bellos, E.; Tzivanidis, C.A. detailed parametric analysis of a solar dish collector. Sustain. Energy Technol. Assess. 2018, 25, 99–110. [Google Scholar] [CrossRef]
- Shubham; Kumar, P.; Kumar, S.; Kumar, R.; Mandal, S. Numerical and experimental analysis of Scheffler concentrator receiver for steam generation using phase change material. Int. J. Renew. Energy Res. 2018, 8, 1339–1345. [Google Scholar]
- Chandak, A.; Somani, S.-K.; Dubey, D. Design, development of and testing of multieffect distiller/evaporator using Scheffler solar concentrator. J. Eng. Sci. Technol. 2009, 4, 315–321. [Google Scholar]
- Ramachandran, S.; Nene, A.A. Studies on Scheffler solar concentrator to optimise thermal efficiency. Int. J. Ambient. Energy 2020, 43, 3138–3145. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A.; Worek, W.M. Solar Engineering of Thermal Processes; Wiley: New York, NY, USA, 2013. [Google Scholar]
- Dib, E.A.; Fiorelli, F.A. Analysis of the image produced by Scheffler paraboloidal concentrator. In Proceedings of the 5th International Youth Conference on Energy (IYCE), Pisa, Italy, 27–30 May 2015; pp. 1–7. [Google Scholar]
- Stine, W.B.; Harrigan, R.W. Solar Energy Fundamentals and Design with Computer Applications; WileyInterscience: New York, NY, USA, 1985. [Google Scholar]
- Shuai, Y.; Xia, X.L.; Tan, H.P. Radiation performance of dish solar concentrator/cavity receiver systems. Sol. Energy 2008, 82, 13–21. [Google Scholar] [CrossRef]
- Azzouzi, D.; Boumeddane, B.; Abene, A. Experimental and analytical thermal analysis of cylindrical cavity receiver for solar dish. Renew. Energy 2017, 106, 111–121. [Google Scholar] [CrossRef]
- Bramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables, National Bureau of Standards Applied Mathematics Series 55; Tenth Printing; U.S. Government Printing Office: Washington, DC, USA, 1972.
- Stine, W.B.; McDonald, C.G. Cavity Receiver Convective Heat Loss; International Solar Energy Society. In Proceedings of the 1989 Congress of the ISES, Kobe, Japan, 4–8 September 1989. [Google Scholar]
- Harris, J.A.; Lenz, T.G. Thermal performance of solar concentrator/cavity receiver systems. Sol. Energy 1984, 34, 135–142. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; John Wiley & Sons. Inc.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Reinalter, W.; Ulmer, S.; Heller, P.; Rauch, T.; Gineste, J.; Ferriere, A.; Nepveu, F. Detailled performance analysis of the 10 kW CNRS-PROMES dish/Stirling system. In Proceedings of the 13th SolarPACES International Symposium, Seville, Spain, 20–23 June 2006; pp. 1–9. [Google Scholar]
| a | k1 | k2 | k3 | k4 | k5 |
|---|---|---|---|---|---|
| 0.231642 | 0.31938153 | −0.35656378 | 1.78147794 | −1.8212598 | 1.33027443 |
| Geometric Factors | Value | Unit | Physical Characteristics | Value | Unit |
|---|---|---|---|---|---|
| Absorber tubes diameter | 0.0063 | m | Air conductivity | 0.028 | W/mK |
| 0.3 | m | Ambient temperature | 293 | K | |
| Capture area | 27.6 | m2 | Cavity absorbance | 0.56 | - |
| Cavity diameter | 0.46 | m | Insulation conductivity | 0.08 | W/mK |
| Cavity length | 0.46 | m | Latitude | 41 | deg |
| Cavity wall thickness | 0.05 | m | Mirror reflectance | 0.9 | - |
| Focal length | 2.1 | m | Optical errors deviation | 0.011 | rad |
| N. of absorber tubes | 71 | - | Wind velocity | 3 | m/s |
| PD Experimental Results [kW] [37] | Model-1 [kW] | Model-2 [kW] | |
|---|---|---|---|
| Captured sun radiation | 48.02 | 48.02 | 48.02 |
| Intercepted heat power | 37.75 | 35.30 | 43.64 |
| Heat loss owing to convection | 1.98 | 0.58 | 0.40 |
| Heat loss due to reflected radiation | 1.71 | 18.17 | 3.53 |
| Heat loss due to emitted radiation | 2.39 | 0.49 | 5.77 |
| Net thermal power | 31.67 | 16.05 | 33.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iodice, P.; Amoresano, A.; Langella, G.; Marra, F.S. Energy Advantages and Thermodynamic Performance of Scheffler Receivers as Thermal Sources for Solar Thermal Power Generation. Energies 2024, 17, 5393. https://doi.org/10.3390/en17215393
Iodice P, Amoresano A, Langella G, Marra FS. Energy Advantages and Thermodynamic Performance of Scheffler Receivers as Thermal Sources for Solar Thermal Power Generation. Energies. 2024; 17(21):5393. https://doi.org/10.3390/en17215393
Chicago/Turabian StyleIodice, Paolo, Amedeo Amoresano, Giuseppe Langella, and Francesco Saverio Marra. 2024. "Energy Advantages and Thermodynamic Performance of Scheffler Receivers as Thermal Sources for Solar Thermal Power Generation" Energies 17, no. 21: 5393. https://doi.org/10.3390/en17215393
APA StyleIodice, P., Amoresano, A., Langella, G., & Marra, F. S. (2024). Energy Advantages and Thermodynamic Performance of Scheffler Receivers as Thermal Sources for Solar Thermal Power Generation. Energies, 17(21), 5393. https://doi.org/10.3390/en17215393










