Development of Machine Learning-Based Production Forecasting for Offshore Gas Fields Using a Dynamic Material Balance Equation
Abstract
1. Introduction
2. Theoretical Background and Method
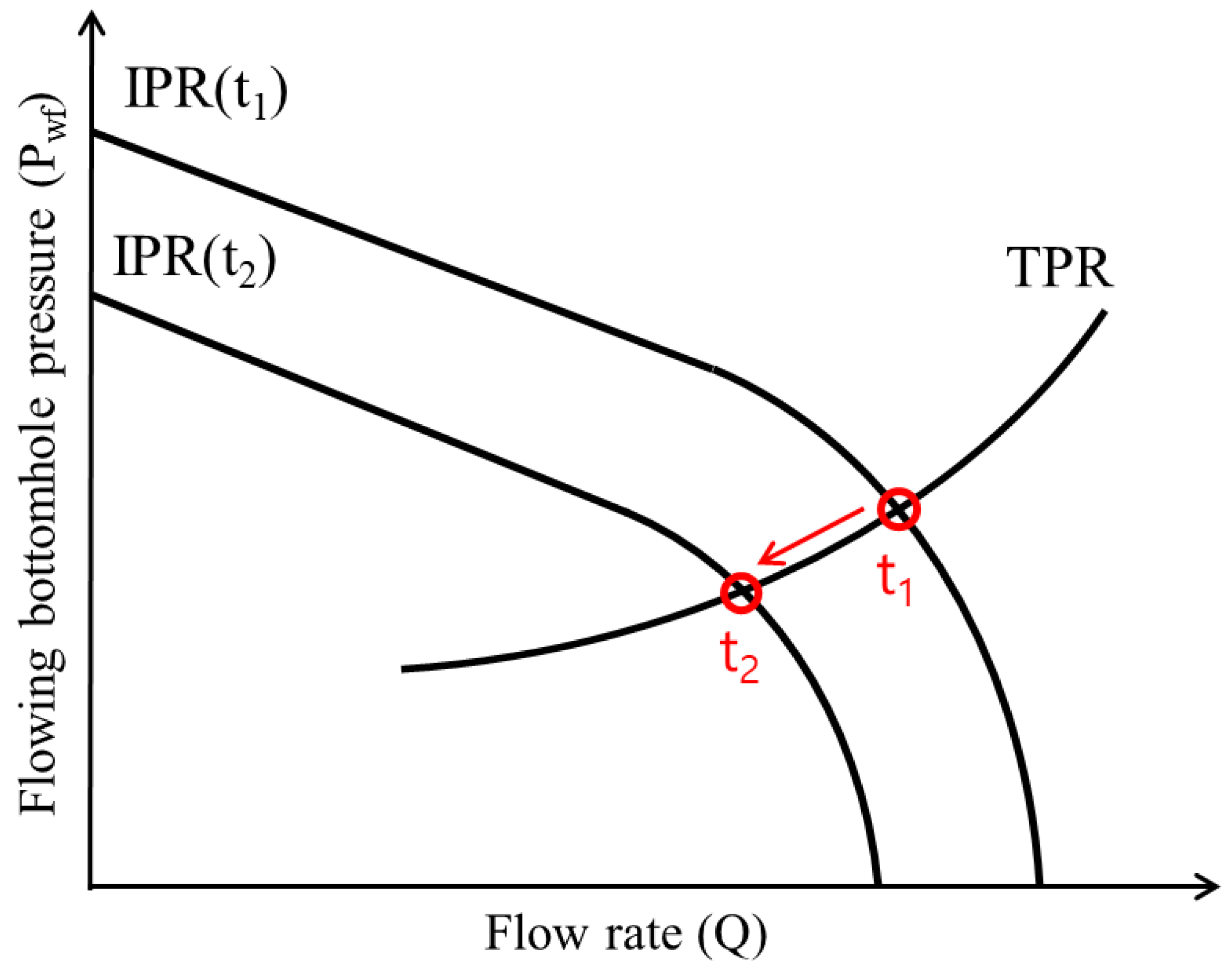
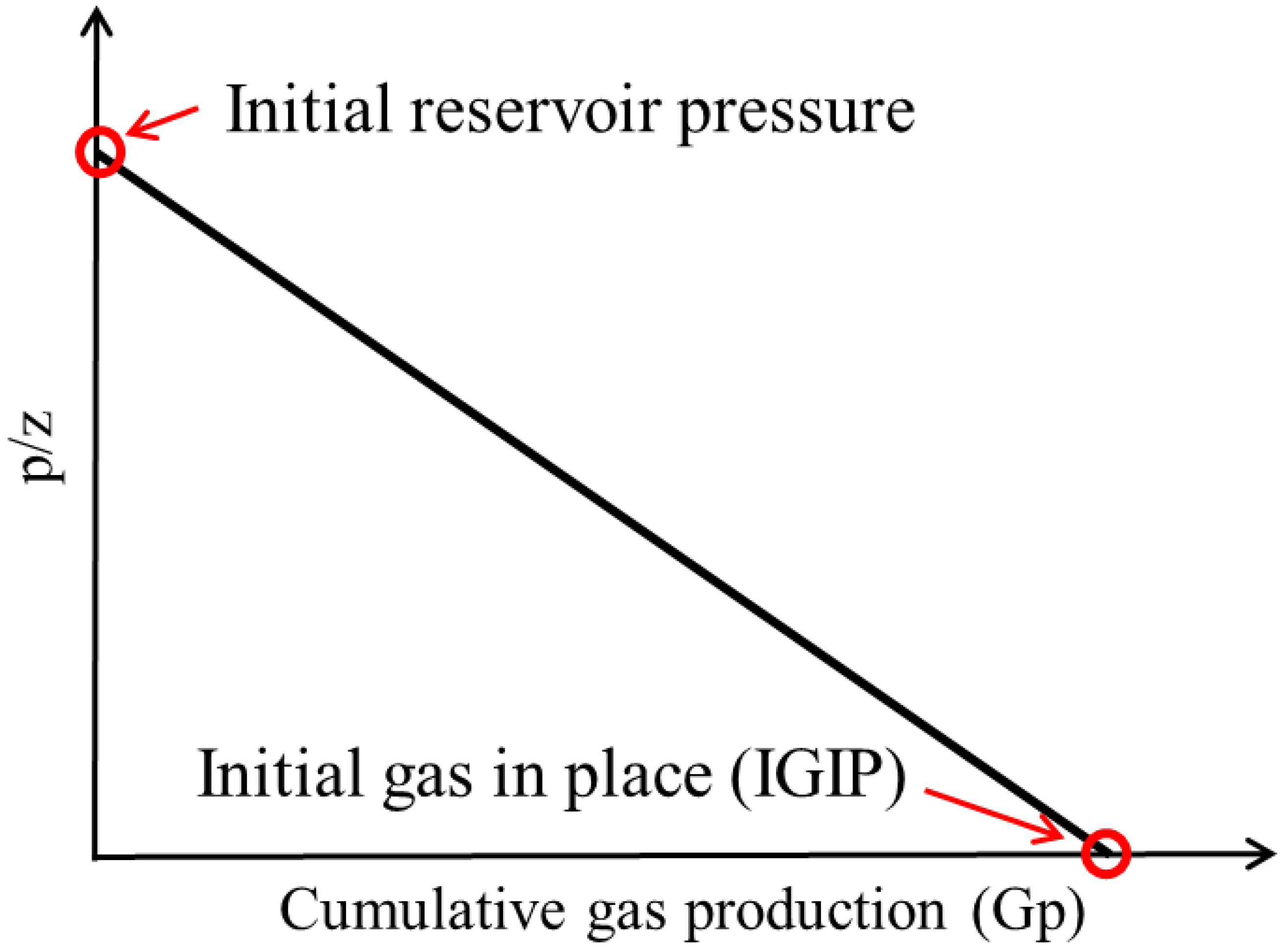
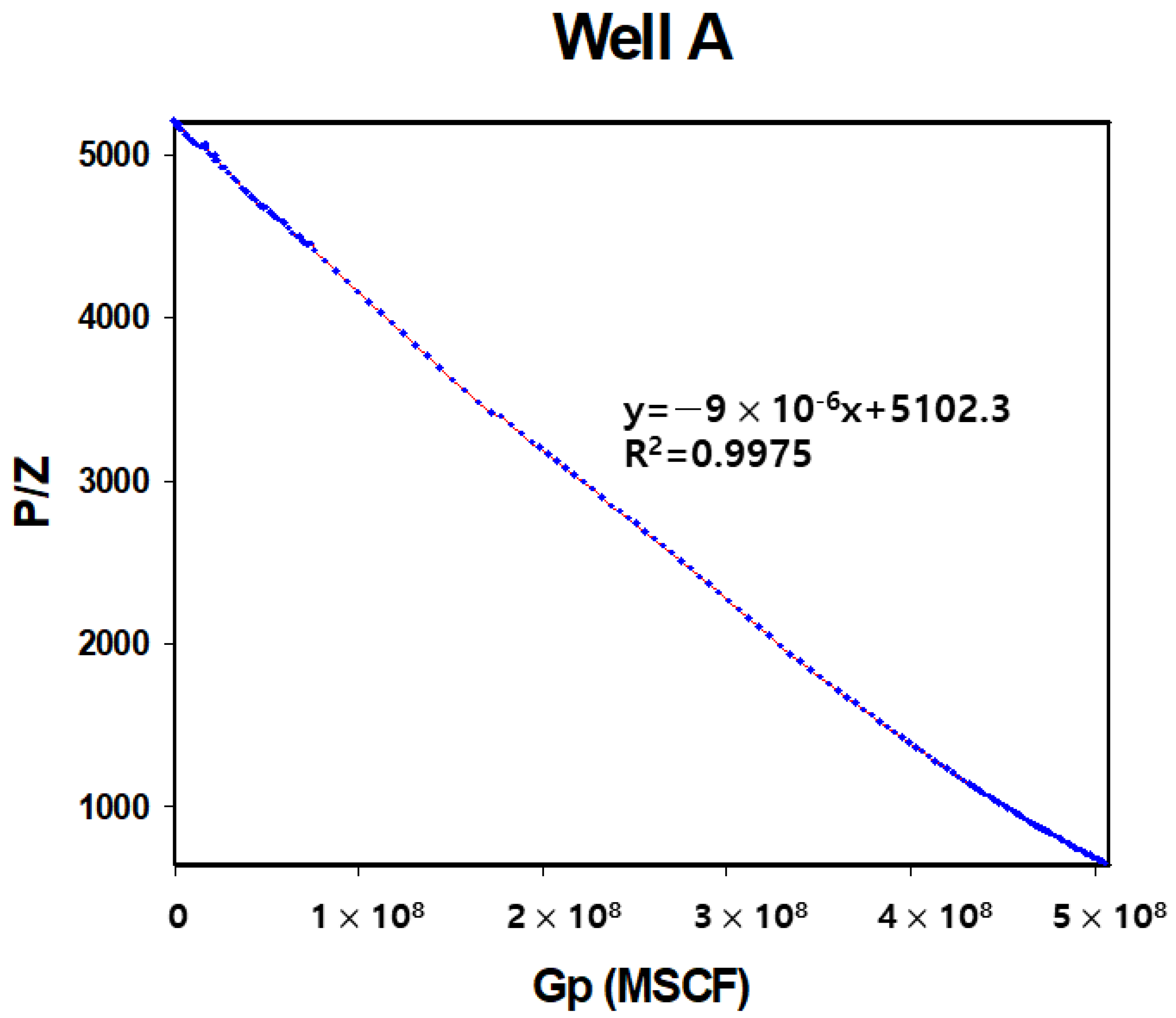
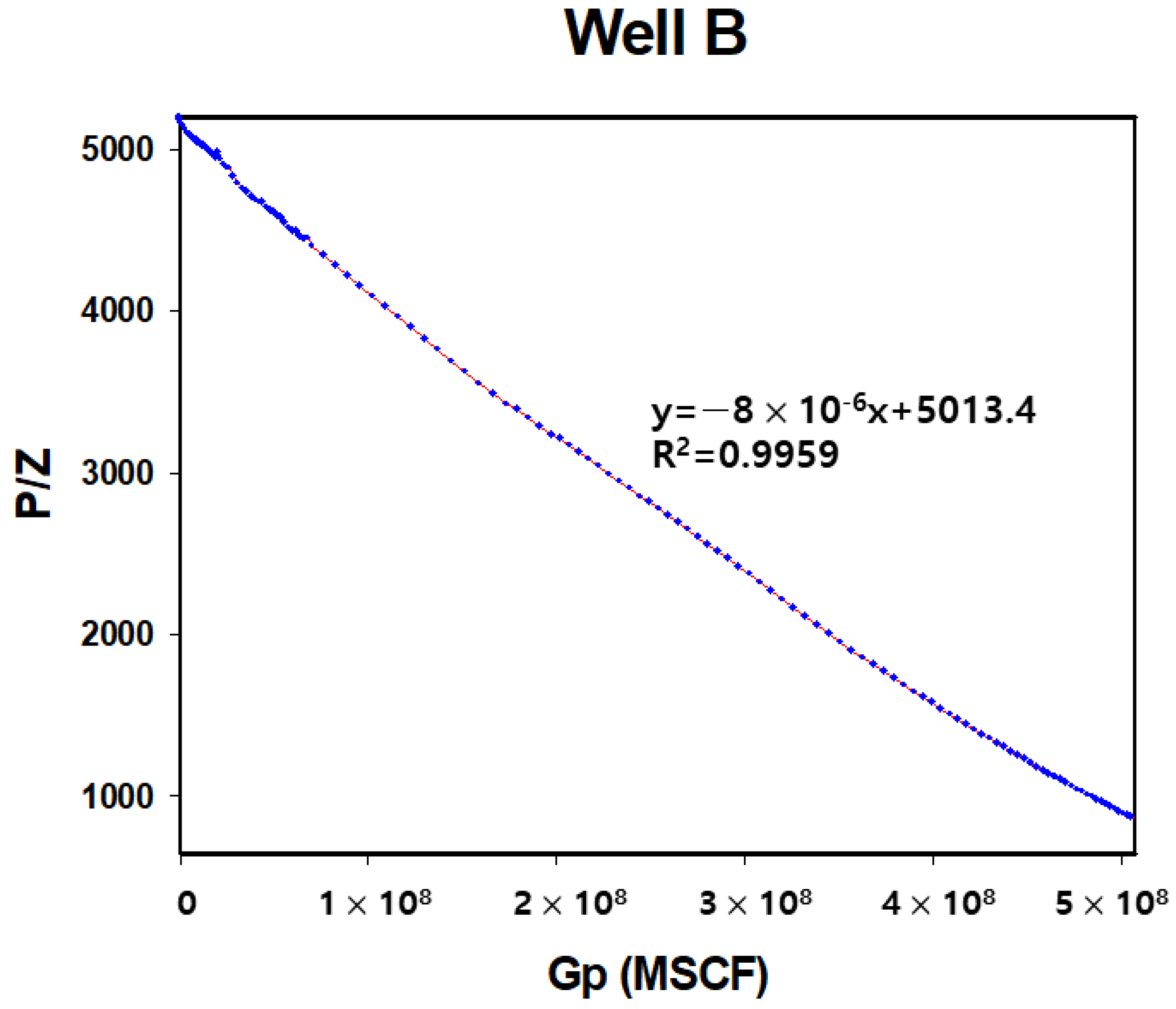
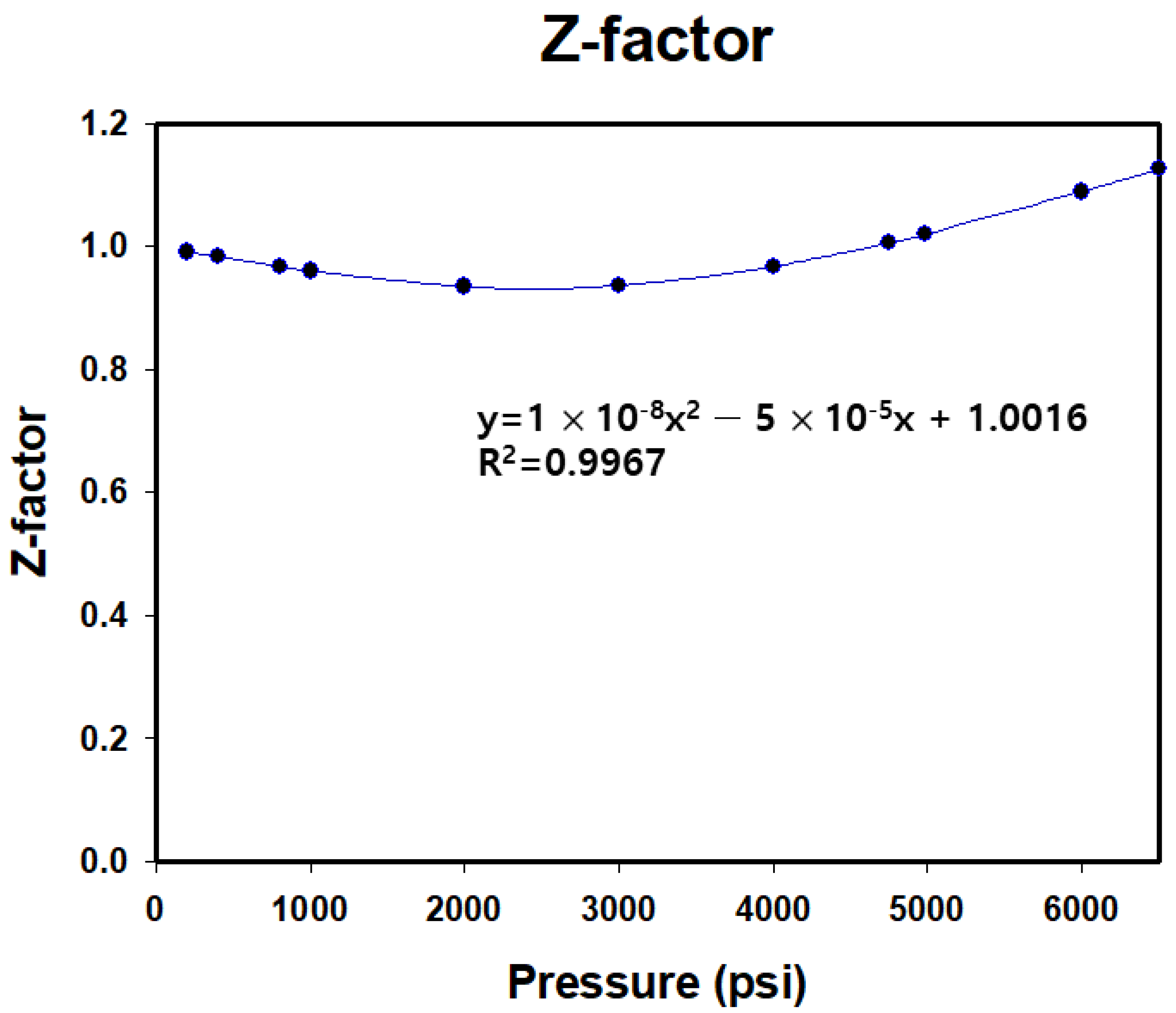
2.1. Development of Analysis Method and the Change in Production Capacity of Reservoir
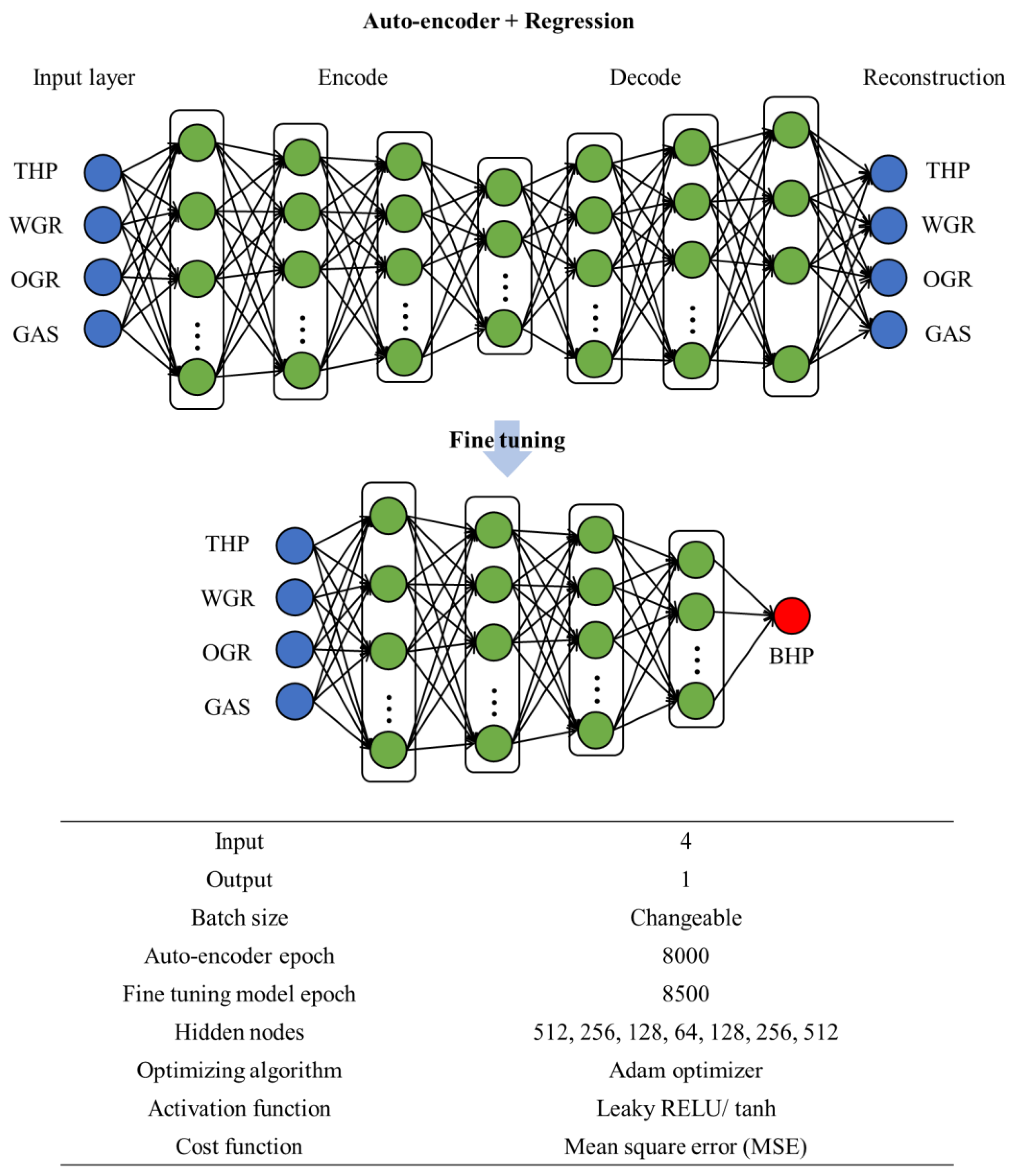
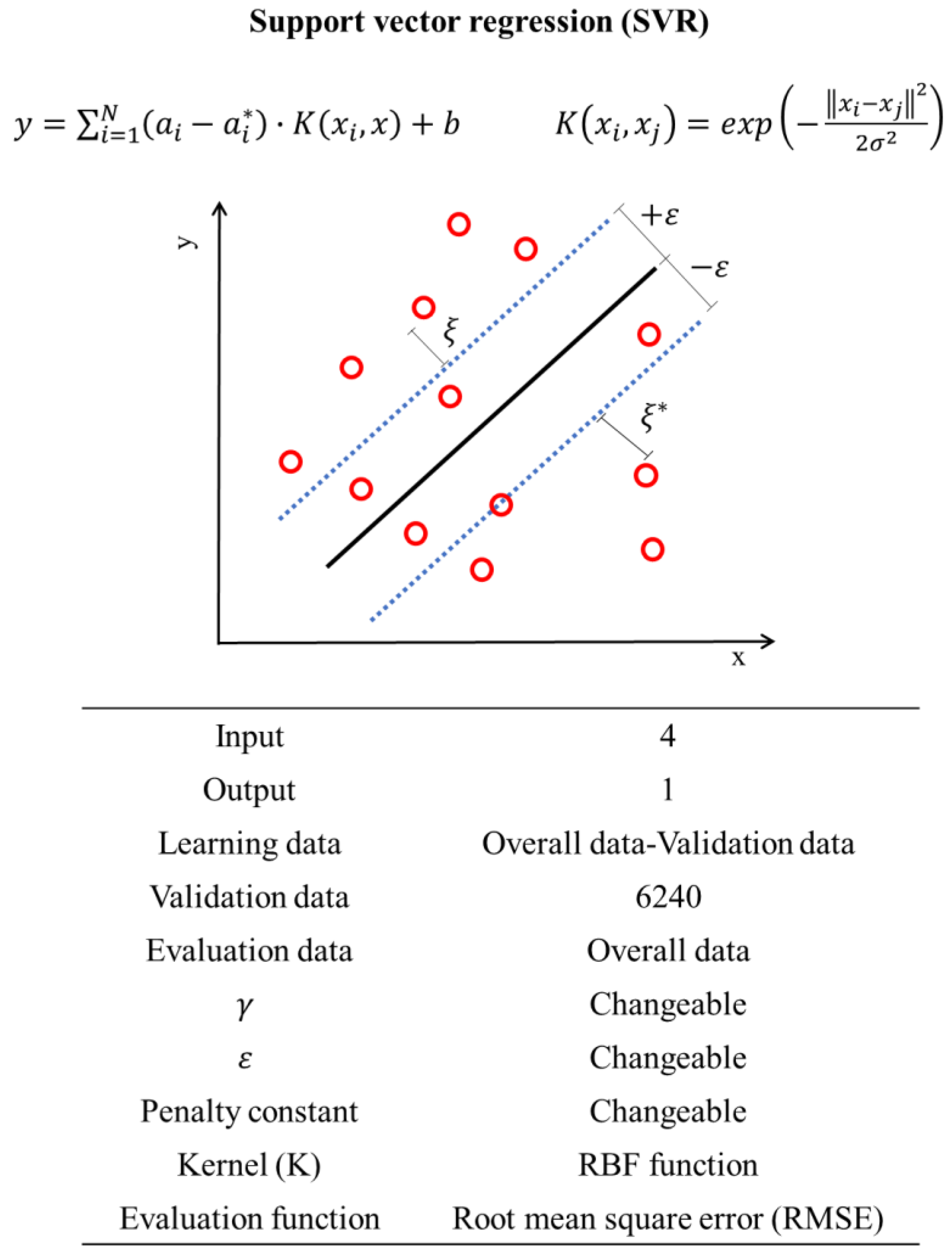
2.2. Development of In-Pipe Flow Prediction Model Using Artificial Intelligence
2.3. Building a Gas Field Optimal Operating Solution Using Rate Allocation Algorithm
3. Results and Discussion
3.1. Model Accuracy
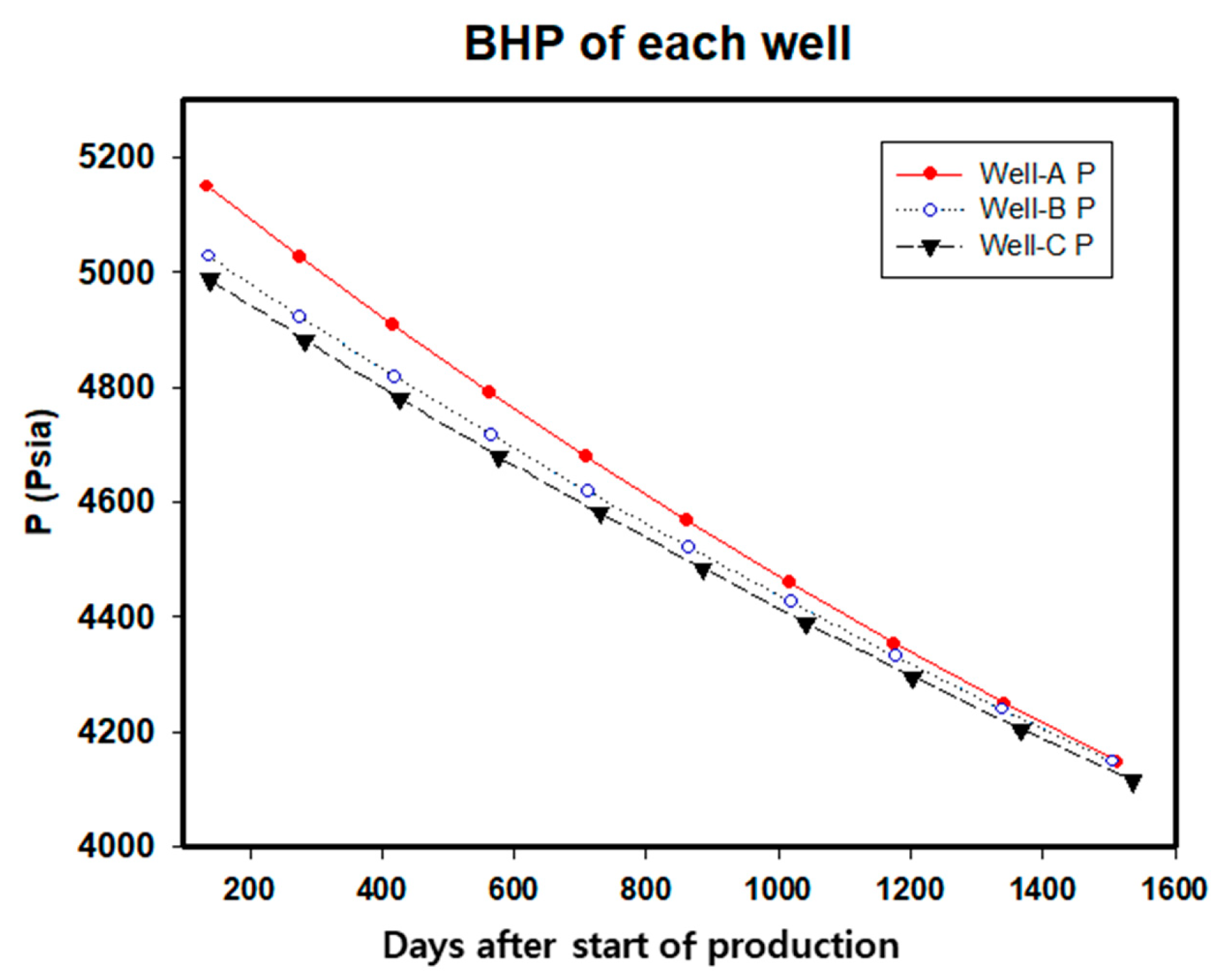
3.2. Flow Rate and Bottomhole Pressure Trends
3.3. Implications, Limitations, and Future Work
4. Conclusions
- (1)
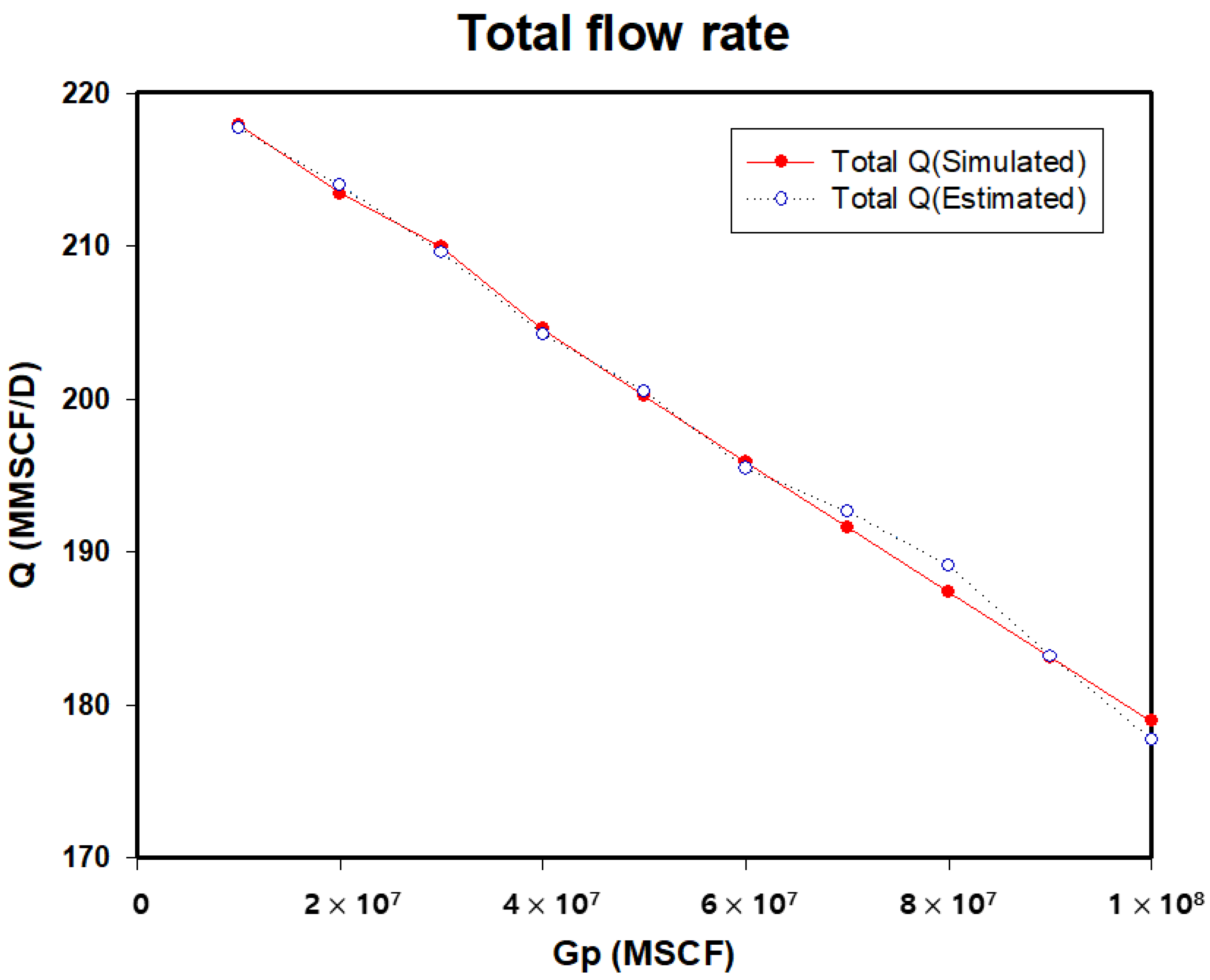
- When comparing the results of the commercial software with the deep learning model, the minimum, maximum, and average error rates of the total flow rate were 0.04%, 2.35%, and 1.5%, respectively. This indicates that the model’s predictions closely matched actual values.
- (2)
- As production progressed, different production profiles emerged based on the gas field’s IPR. This demonstrates the necessity of adjusting the top-side pressure during production to properly distribute the flow rate and achieve optimal production.
- (3)
- The findings of this study are expected to assist in the optimal allocation of production rates in future gas field operations. Using production data and BHP profiles under normal operating conditions, any real-time deviations beyond a certain threshold can be flagged as danger signals, allowing for immediate response. This can be utilized for stable plant operations and predictive maintenance of facilities, while also improving workforce efficiency in areas currently reliant on manual labor.
- (4)
- To achieve more accurate analyses, it is essential to address limitations such as the availability of diverse training data and potential overfitting issues in certain machine learning models. Increasing the volume of training data, carefully selecting AI models, and cross-validating multiple models will significantly improve predictive performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Energy Institute. Natural Gas Consumption Worldwide from 1998 to 2023 (In Billion Cubic Meters). Available online: https://www.statista.com/statistics/282717/global-natural-gas-consumption/ (accessed on 30 September 2024).
- Li, Q.; Li, Q.; Han, Y. A Numerical Investigation on Kick Control with the Displacement Kill Method during a Well Test in a Deep-Water Gas Reservoir: A Case Study. Processes 2024, 12, 2090. [Google Scholar] [CrossRef]
- Li, Q.; Li, Q.; Wang, F.; Wu, J.; Wang, Y. The Carrying Behavior of Water-Based Fracturing Fluid in Shale Reservoir Fractures and Molecular Dynamics of Sand-Carrying Mechanism. Processes 2024, 12, 2051. [Google Scholar] [CrossRef]
- Markeset, T.; Moreno-Trejo, J.; Kumar, R. Maintenance of subsea petroleum production systems: A case study. J. Qual. Maint. Eng. 2013, 19, 128–143. [Google Scholar] [CrossRef]
- Moreno-Trejo, J.; Markeset, T. Identifying Challenges in the Maintenance of Subsea Petroleum Production Systems; Springer: Berlin/Heidelberg, Germany, 2012; pp. 251–259. [Google Scholar]
- Abdalla, R. Transforming the Industry: Digitalization and Automation in Oil and Gas Wells; IntechOpen: London, UK, 2023. [Google Scholar]
- Bahari, M.; Arpaci, I.; Der, O.; Akkoyun, F.; Ercetin, A. Driving Agricultural Transformation: Unraveling Key Factors Shaping IoT Adoption in Smart Farming with Empirical Insights. Sustainability 2024, 16, 2129. [Google Scholar] [CrossRef]
- Zeba, G.; Dabić, M.; Čičak, M.; Daim, T.; Yalcin, H. Technology mining: Artificial intelligence in manufacturing. Technol. Forecast. Soc. Change 2021, 171, 120971. [Google Scholar] [CrossRef]
- Tariq, Z.; Aljawad, M.S.; Hasan, A.; Murtaza, M.; Mohammed, E.; El-Husseiny, A.; Alarifi, S.A.; Mahmoud, M.; Abdulraheem, A. A systematic review of data science and machine learning applications to the oil and gas industry. J. Pet. Explor. Prod. Technol. 2021, 11, 4339–4374. [Google Scholar] [CrossRef]
- Hussain, M.; Alamri, A.; Zhang, T.; Jamil, I. Application of Artificial Intelligence in the Oil and Gas Industry. In Engineering Applications of Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2024; pp. 341–373. [Google Scholar]
- MarketsandMarkets Digital Oilfield Market by Processes (Reservoir, Production, Drilling Optimizations, Safety-, Asset Management), Technology (loT, Al, Robotics & Automation, Big Data & Analytics, Cloud Computing), Solution, Application, Region—Global Forecast to 2029; 2024. Available online: https://www.marketsandmarkets.com/Market-Reports/digital-oilfield-market-904.html (accessed on 19 September 2024).
- Suslick, S.B.; Schiozer, D.; Rodriguez, M.R. Uncertainty and risk analysis in petroleum exploration and production. Terrae 2009, 6, 30–41. [Google Scholar]
- Elharith, M.; Huey, H.Y.; Tewari, R.D.; Claire, L.; Fawzi, N.S.M.; Schulze-Riegert, R. Integrated modeling of a complex oil rim development scenario under subsurface uncertainty. J. Pet. Explor. Prod. Technol. 2019, 9, 2417–2428. [Google Scholar] [CrossRef]
- Qiu, K.; Fan, K.; Chen, X.; Lei, G.; Wei, S.; Navik, R.; Li, J. A new approach for production prediction in onshore and offshore tight oil reservoir. J. Mar. Sci. Eng. 2023, 11, 2079. [Google Scholar] [CrossRef]
- Nikitin, N.O.; Revin, I.; Hvatov, A.; Vychuzhanin, P.; Kalyuzhnaya, A.V. Hybrid and automated machine learning approaches for oil fields development: The case study of Volve field, North Sea. Comput. Geosci. 2022, 161, 105061. [Google Scholar] [CrossRef]
- Rabczuk, T.; Bathe, K.-J. Machine Learning in Modeling and Simulation; Springer: Cham, Switzerland, 2023; Volume 10, pp. 149–178. [Google Scholar]
- Li, H.; Tan, Q.; Deng, J.; Dong, B.; Li, B.; Guo, J.; Zhang, S.; Bai, W. A Comprehensive Prediction Method for Pore Pressure in Abnormally High-Pressure Blocks Based on Machine Learning. Processes 2023, 11, 2603. [Google Scholar] [CrossRef]
- Adegboye, M.A.; Fung, W.-K.; Karnik, A. Recent advances in pipeline monitoring and oil leakage detection technologies: Principles and approaches. Sensors 2019, 19, 2548. [Google Scholar] [CrossRef] [PubMed]
- Rostamian, A.; de Sousa Miranda, M.V.; Mirzaei-Paiaman, A.; Botechia, V.E.; Schiozer, D.J. Analysis of different objective functions in petroleum field development optimization. J. Pet. Explor. Prod. Technol. 2024, 1–21. [Google Scholar] [CrossRef]
- Adeboye, Y.; Ubani, C.; Oribayo, O. Prediction of reservoir performance in multi-well systems using modified hyperbolic model. J. Pet. Explor. Prod. Technol. 2011, 1, 81–87. [Google Scholar] [CrossRef][Green Version]
- Baruah, B.; Kalita, P.; Pandey, L.; Tiwari, P. Petroleum Reservoirs and Oil Production Mechanisms. In Microbial Enhanced Oil Recovery: Principles and Potential; Springer: Singapore, 2022; pp. 1–21. [Google Scholar]
- Economides, M.J. Petroleum Production Systems; Pearson Education: Bloomington, MN, USA, 2013. [Google Scholar]
- Golan, M.; Whitson, C.H. Well Performance; Prentice Hall: Upper Saddle River, NJ, USA, 1991. [Google Scholar]
- Beggs, H.D. Production Optimization Using Nodal (TM) Analysis; Ogci: London, UK, 2003. [Google Scholar]
- Ahmed, T. Reservoir Engineering Handbook; Gulf Professional Publishing: Houston, TA, USA, 2018. [Google Scholar]
- Katz, D.L.V. Handbook of Natural Gas Engineering; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- King, G. Introduction to petroleum and natural gas engineering. 2018. Available online: https://www.e-education.psu.edu/png301/node/508 (accessed on 19 September 2024).
- Okotie, S.; Ikporo, B. Reservoir Engineering; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Mattar, L.; McNeil, R. The “flowing” gas material balance. J. Can. Pet. Technol. 1998, 37. [Google Scholar] [CrossRef]
- Mattar, L.; Anderson, D.; Stotts, G. Dynamic material balance-oil-or gas-in-place without shut-ins. J. Can. Pet. Technol. 2006, 45. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M. {TensorFlow}: A system for {Large-Scale} machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Raschka, S.; Julian, D.; Hearty, J. Python: Deeper Insights into Machine Learning; Packt Publishing Ltd.: Birmingham, UK, 2016. [Google Scholar]
- Guo, B. Petroleum Production Engineering, a Computer-Assisted Approach; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Brill, J.; Mukherjee, H. Multiphase Flow in Wells. Soc. Pet. Eng. 1999, 39, 15–21. [Google Scholar] [CrossRef]
- Wiggins, M.L. Inflow and outflow performance. In Society of Petroleum Engineers; OnePetro: Richardson, TX, USA, 2007. [Google Scholar] [CrossRef]
- Hansen, L.S.; Pedersen, S.; Durdevic, P. Multi-phase flow metering in offshore oil and gas transportation pipelines: Trends and perspectives. Sensors 2019, 19, 2184. [Google Scholar] [CrossRef] [PubMed]


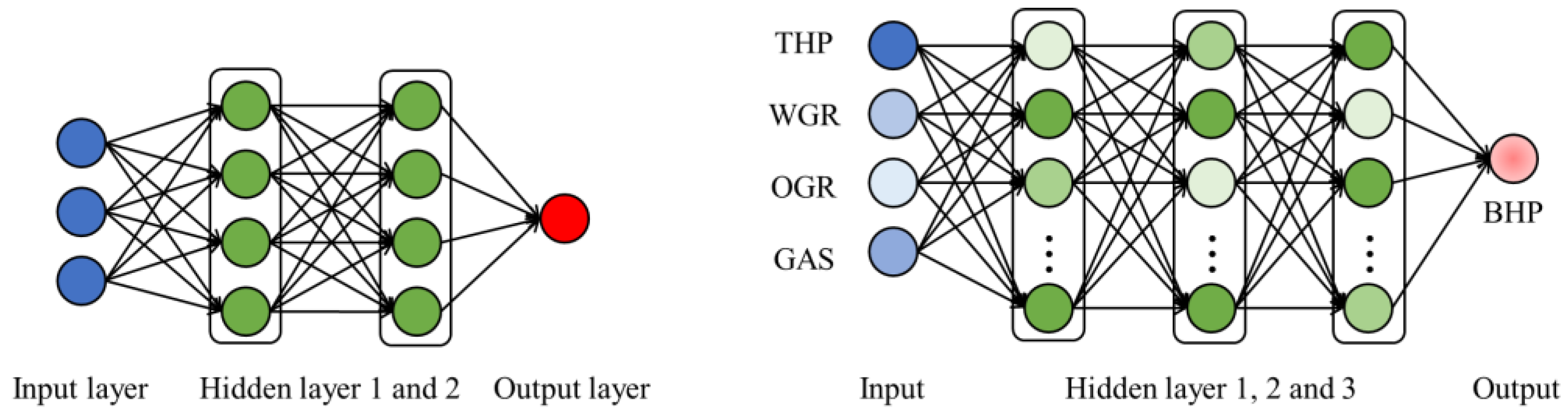
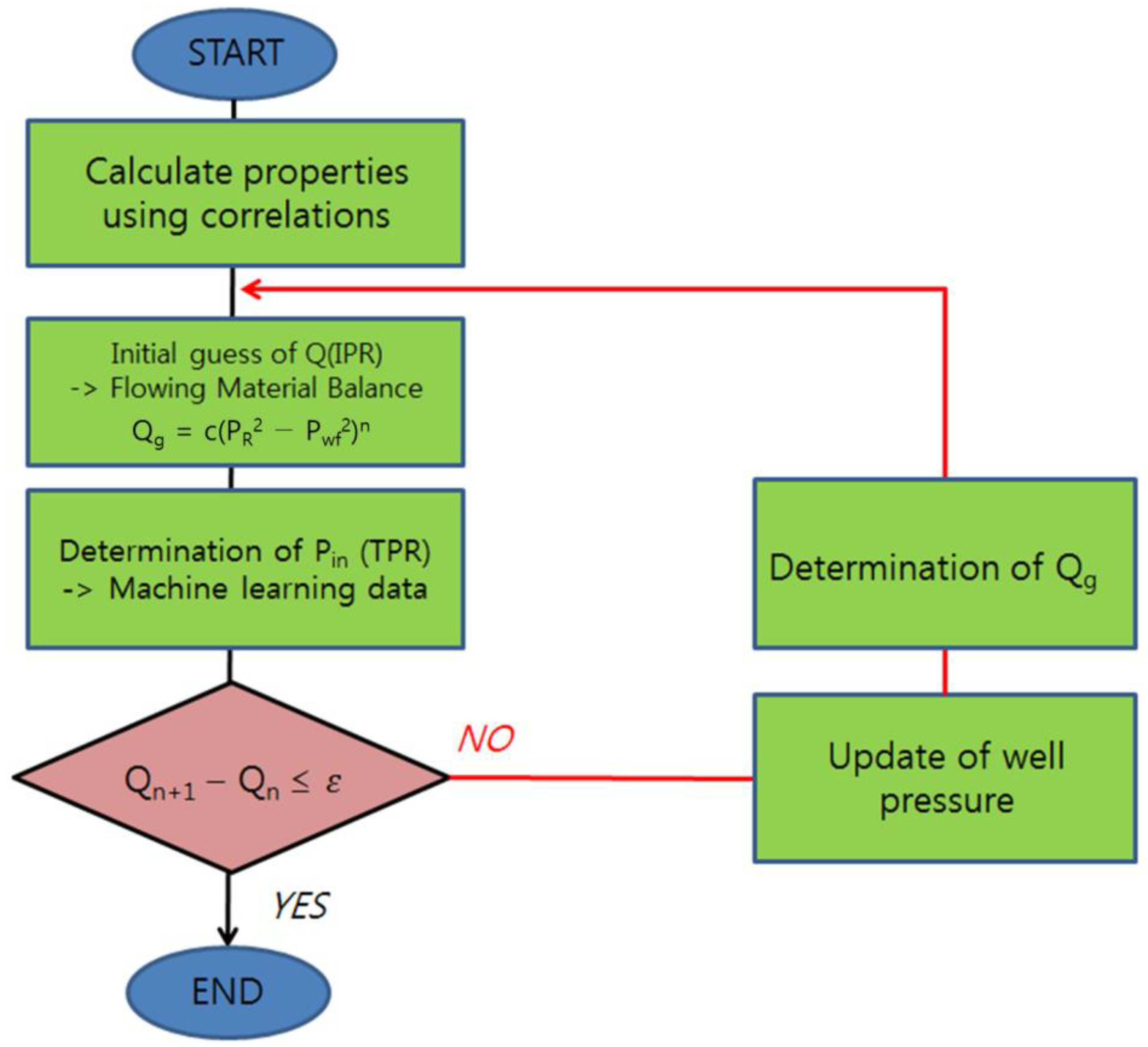
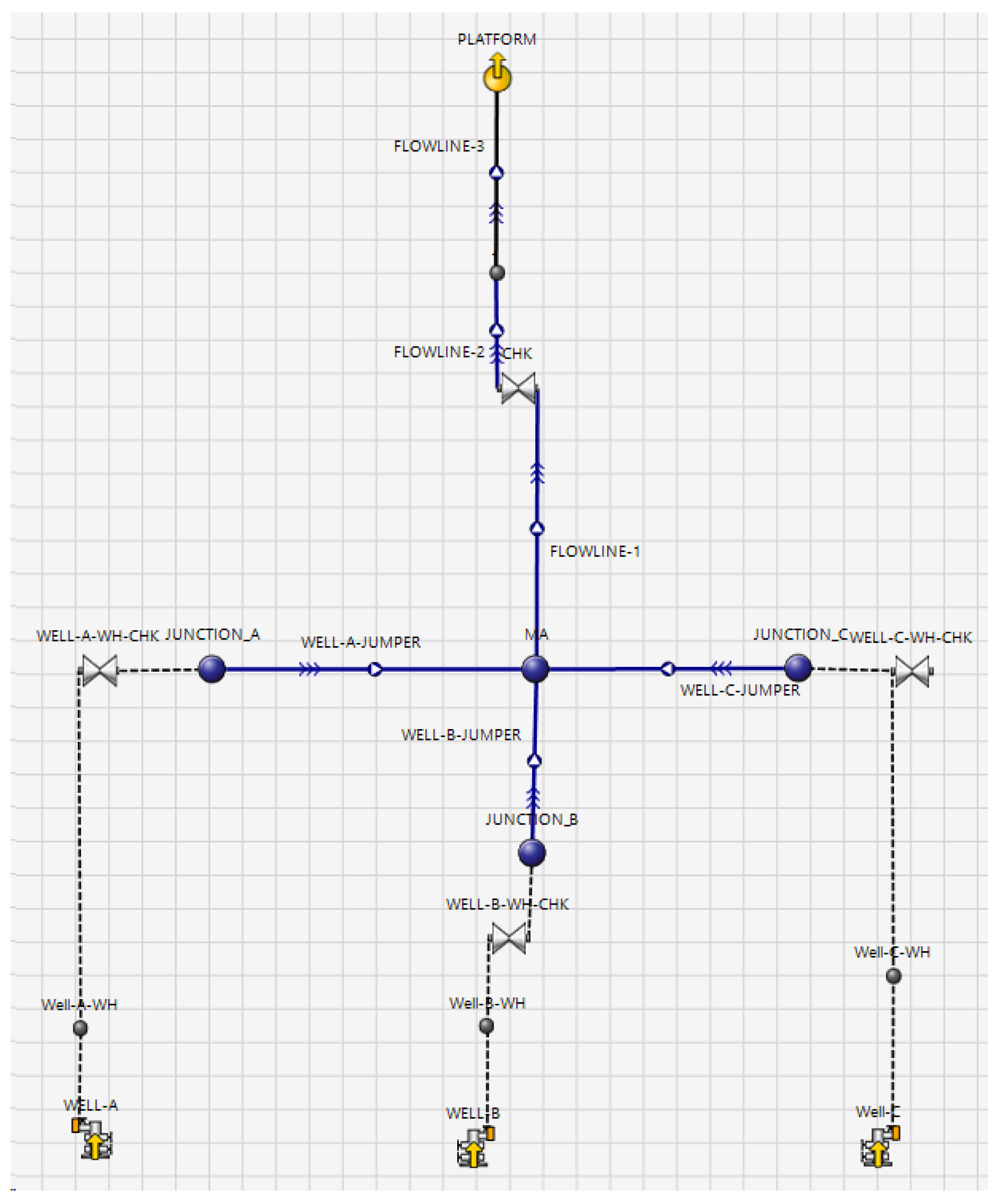
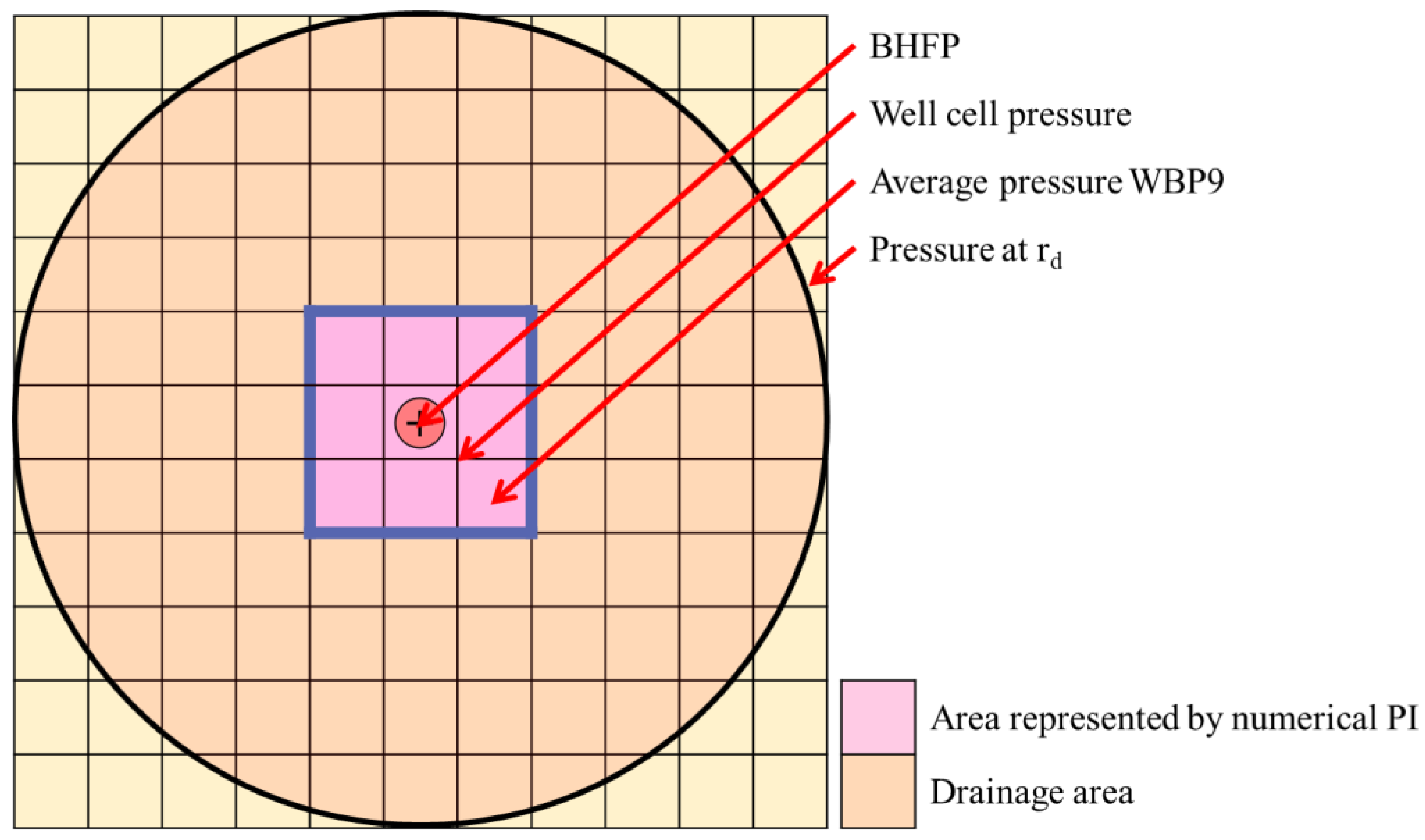


| VFP Table Index | 1st Hidden Node | 2nd Hidden Node | 3rd Hidden Node | Test Data | RMSE | ±20 Range Count | ±20 Range Count/ Total Data |
|---|---|---|---|---|---|---|---|
| 1 | 512 | 1024 | 512 | 6241 | 5.6952 | 6163 | 0.9876 |
| 2 | 6761 | 5.0745 | 6689 | 0.9893 | |||
| 3 | 7411 | 12.4004 | 6985 | 0.9425 | |||
| 4 | 4941 | 6.9936 | 4786 | 0.9688 | |||
| 5 | 7001 | 10.8435 | 6677 | 0.9538 | |||
| 6 | 6751 | 11.4112 | 6445 | 0.9548 | |||
| 7 | 6881 | 4.9926 | 6812 | 0.9901 |
| VFP Table Index | 1st Hidden Node | 2nd Hidden Node | 3rd Hidden Node | Test Data | RMSE | ±20 Range Count | ±20 Range Count/ Total Data |
|---|---|---|---|---|---|---|---|
| 1 | 512 | 1024 | 512 | 6241 | 5.6952 | 6163 | 0.9876 |
| 2 | 6761 | 5.0745 | 6689 | 0.9893 | |||
| 3 | 7411 | 12.4004 | 6985 | 0.9425 | |||
| 4 | 4941 | 6.9936 | 4786 | 0.9688 | |||
| 5 | 7001 | 10.8435 | 6677 | 0.9538 | |||
| 6 | 6751 | 11.4112 | 6445 | 0.9548 | |||
| 7 | 6881 | 4.9926 | 6812 | 0.9901 |
| VFP Table Index | Hyperparameters | Test Data | RMSE | ±20 Range Count | ±20 Range Count/ Total Data | |||
|---|---|---|---|---|---|---|---|---|
| Kernel | Gamma (γ) | Penalty (C) | Epsilon (ε) | |||||
| 1 | RBF | 1 | 0.1 | 5 × 10−3 | 6241 | 18.25427 | 1923 | 0.308124 |
| 1 | 1 | 5 × 10−3 | 16.73165 | 2098 | 0.336164 | |||
| 1 | 10 | 5 × 10−3 | 30.73826 | 1142 | 0.182983 | |||
| 1 | 100 | 5 × 10−3 | 16.33457 | 2149 | 0.344336 | |||
| 10 | 0.1 | 5 × 10−3 | 31.97001 | 1098 | 0.175933 | |||
| 10 | 1 | 5 × 10−3 | 29.62285 | 1185 | 0.189873 | |||
| 10 | 10 | 1 × 10−3 | 29.52318 | 1189 | 0.190514 | |||
| 10 | 100 | 5 × 10−3 | 15.98496 | 2196 | 0.351867 | |||
| 100 | 0.1 | 5 × 10−3 | 26.63355 | 1318 | 0.211184 | |||
| 100 | 1 | 5 × 10−3 | 30.26115 | 1160 | 0.185868 | |||
| 100 | 10 | 5 × 10−3 | 16.10967 | 2179 | 0.349143 | |||
| 100 | 1000 | 5 × 10−3 | 15.98496 | 2196 | 0.351867 | |||
| 5 | 10 | 2 × 10−4 | 30.36587 | 1156 | 0.185227 | |||
| 8 | 10 | 2 × 10−4 | 29.54800 | 1188 | 0.190354 | |||
| Well | Reservoir Pressure (psi) | C (Backpressure Eqn.) | n (Backpressure Eqn.) | Reservoir Temperature (°F) | Reservoir Depth (ft) |
|---|---|---|---|---|---|
| A | 5293 | 2.216 × 10−5 | 1 | 165.50 | 14,633 |
| B | 4800 | 3.106 × 10−5 | 1 | 165.00 | 12,253 |
| C | 5200 | 1.857 × 10−5 | 1 | 165.56 | 10,565 |
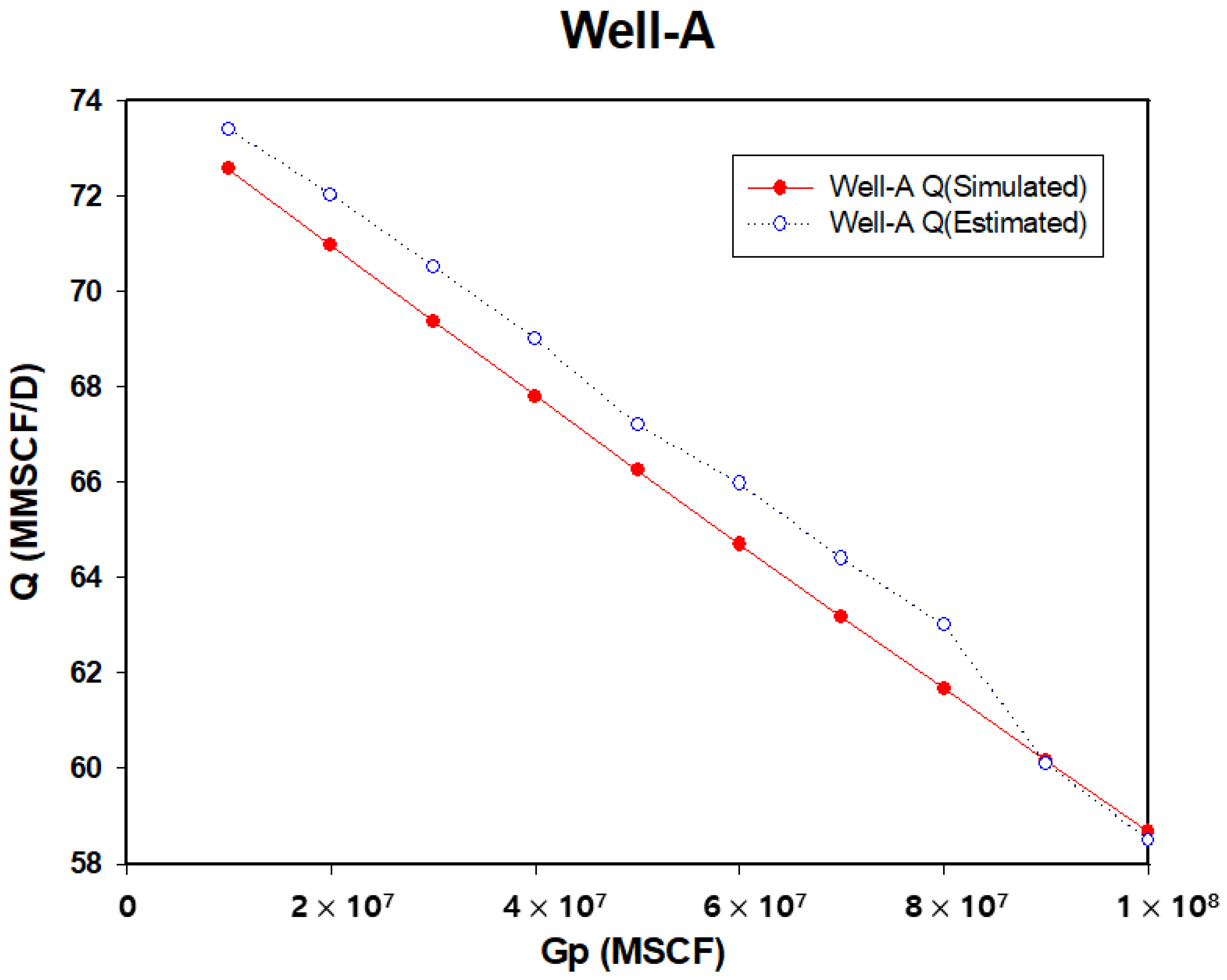
| Gp (MMSCF) | Well A Pressure (psi) | Well A Q (Simulated) (MMSCF/D) | Well A Q (Estimated) (MMSCF/D) | MAE |
|---|---|---|---|---|
| 10,000 | 5149.83 | 72.57 | 73.40 | 0.9257 |
| 20,000 | 5027.16 | 70.96 | 72.03 | |
| 30,000 | 4907.93 | 69.37 | 70.51 | |
| 40,000 | 4791.82 | 67.80 | 69.00 | |
| 50,000 | 4678.57 | 66.24 | 67.20 | |
| 60,000 | 4567.92 | 64.70 | 65.97 | |
| 70,000 | 4459.66 | 63.17 | 64.40 | |
| 80,000 | 4353.59 | 61.67 | 63.00 | |
| 90,000 | 4249.55 | 60.16 | 60.10 | |
| 100,000 | 4147.38 | 58.67 | 58.50 |
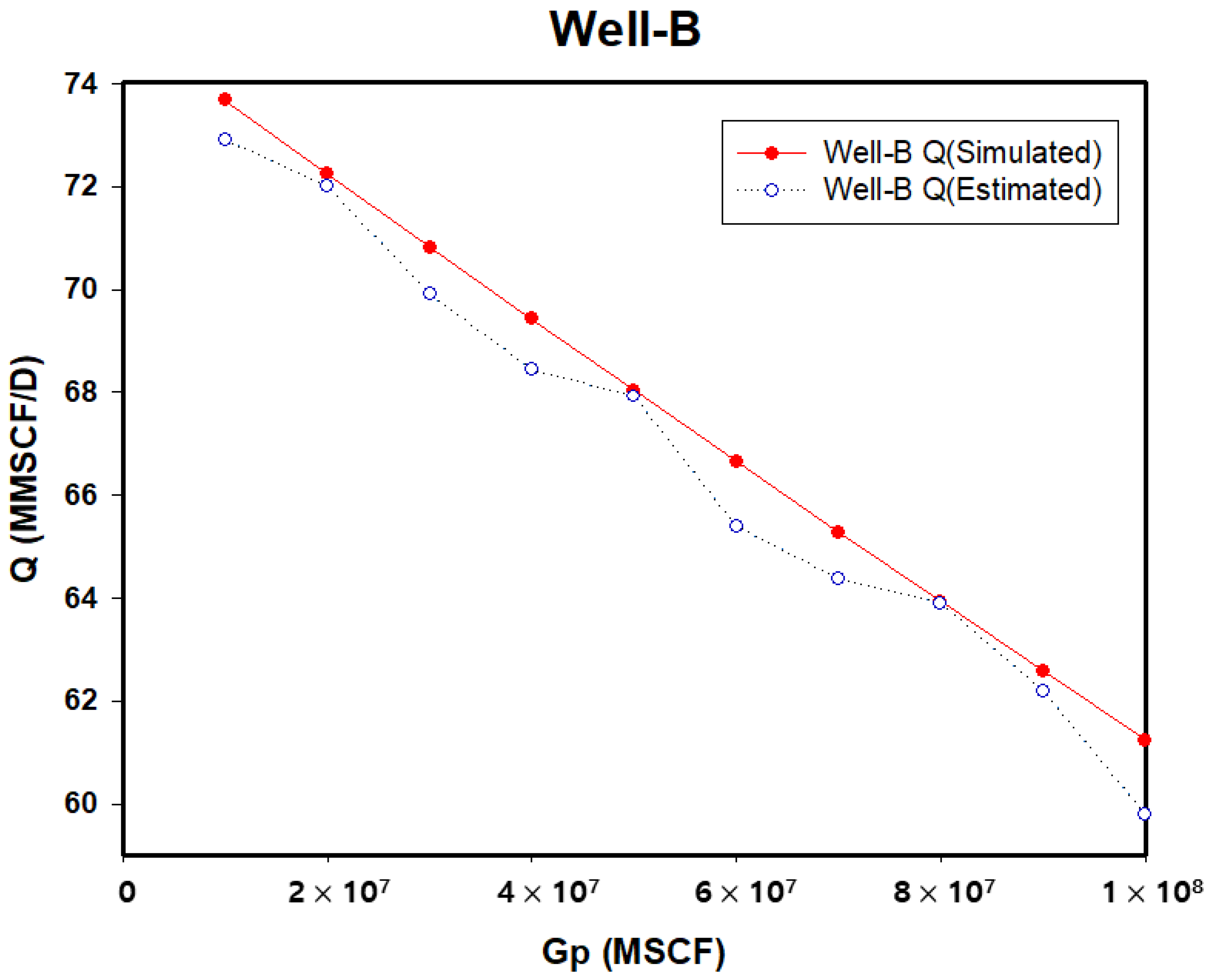
| Gp (MMSCF) | Well B Pressure (psi) | Well B Q (Simulated) (MMSCF/D) | Well B Q (Estimated) (MMSCF/D) | MAE |
|---|---|---|---|---|
| 10,000 | 5028.64 | 73.67 | 72.90 | 0.702 |
| 20,000 | 4922.46 | 72.24 | 72.01 | |
| 30,000 | 4818.78 | 70.82 | 69.90 | |
| 40,000 | 4717.40 | 69.42 | 68.44 | |
| 50,000 | 4618.14 | 68.03 | 67.92 | |
| 60,000 | 4520.84 | 66.65 | 65.40 | |
| 70,000 | 4425.37 | 65.28 | 64.37 | |
| 80,000 | 4331.58 | 63.93 | 63.90 | |
| 90,000 | 4239.37 | 62.58 | 62.20 | |
| 100,000 | 4148.62 | 61.24 | 59.80 |
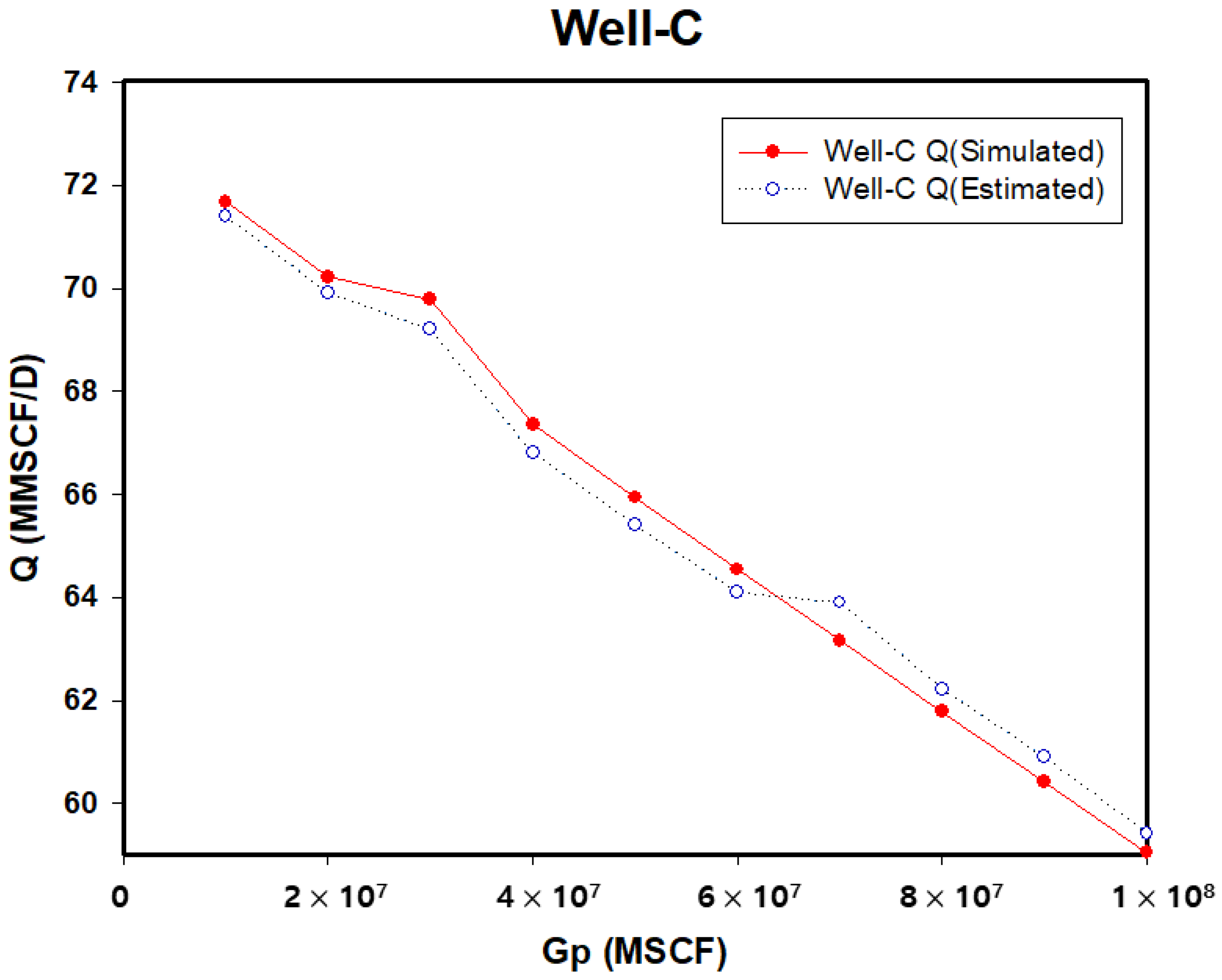
| Gp (MMSCF) | Well C Pressure (psi) | Well C Q (Simulated) (MMSCF/D) | Well C Q (Estimated) (MMSCF/D) | MAE |
|---|---|---|---|---|
| 10,000 | 4987.72 | 71.68 | 71.40 | 0.475 |
| 20,000 | 4882.52 | 70.22 | 69.91 | |
| 30,000 | 4779.74 | 69.78 | 69.20 | |
| 40,000 | 4679.19 | 67.36 | 66.80 | |
| 50,000 | 4580.70 | 65.94 | 65.40 | |
| 60,000 | 4484.12 | 64.54 | 64.10 | |
| 70,000 | 4389.30 | 63.16 | 63.90 | |
| 80,000 | 4296.13 | 61.78 | 62.22 | |
| 90,000 | 4204.49 | 60.41 | 60.90 | |
| 100,000 | 4114.27 | 59.05 | 59.42 |
| Gp (MMSCF) | Total Q (Simulated) (MMSCF/D) | Total Q (Estimated) (MMSCF/D) | MAE |
|---|---|---|---|
| 10,000 | 217.92 | 217.70 | 0.6269 |
| 20,000 | 213.42 | 213.95 | |
| 30,000 | 209.97 | 209.61 | |
| 40,000 | 204.58 | 204.24 | |
| 50,000 | 200.21 | 200.52 | |
| 60,000 | 195.89 | 195.47 | |
| 70,000 | 191.61 | 192.67 | |
| 80,000 | 187.38 | 189.12 | |
| 90,000 | 183.15 | 183.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hyoung, J.; Lee, Y.; Han, S. Development of Machine Learning-Based Production Forecasting for Offshore Gas Fields Using a Dynamic Material Balance Equation. Energies 2024, 17, 5268. https://doi.org/10.3390/en17215268
Hyoung J, Lee Y, Han S. Development of Machine Learning-Based Production Forecasting for Offshore Gas Fields Using a Dynamic Material Balance Equation. Energies. 2024; 17(21):5268. https://doi.org/10.3390/en17215268
Chicago/Turabian StyleHyoung, Junhyeok, Youngsoo Lee, and Sunlee Han. 2024. "Development of Machine Learning-Based Production Forecasting for Offshore Gas Fields Using a Dynamic Material Balance Equation" Energies 17, no. 21: 5268. https://doi.org/10.3390/en17215268
APA StyleHyoung, J., Lee, Y., & Han, S. (2024). Development of Machine Learning-Based Production Forecasting for Offshore Gas Fields Using a Dynamic Material Balance Equation. Energies, 17(21), 5268. https://doi.org/10.3390/en17215268








