A Hybrid Control-Oriented PEMFC Model Based on Echo State Networks and Gaussian Radial Basis Functions
Abstract
1. Introduction
- 1.
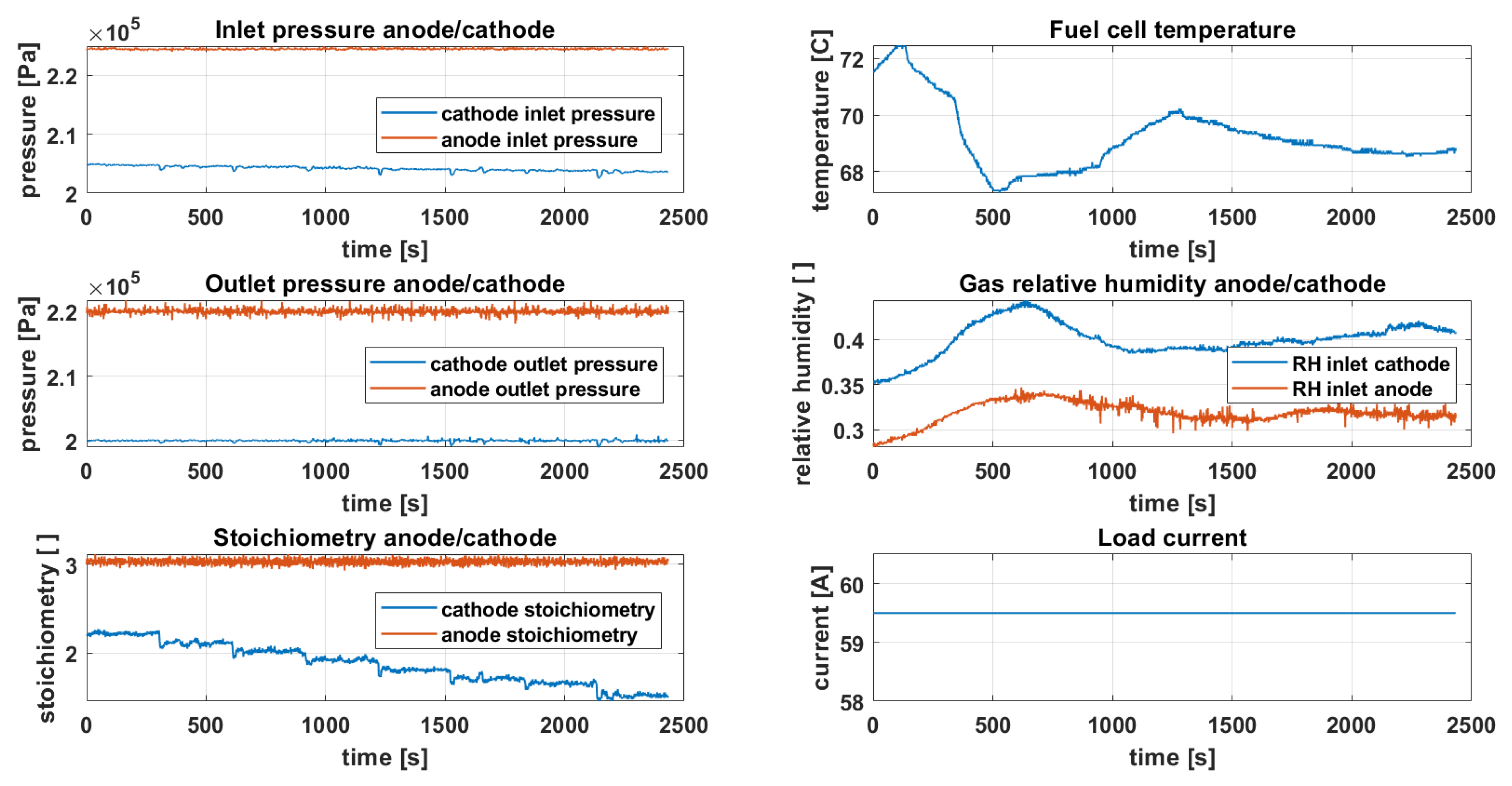
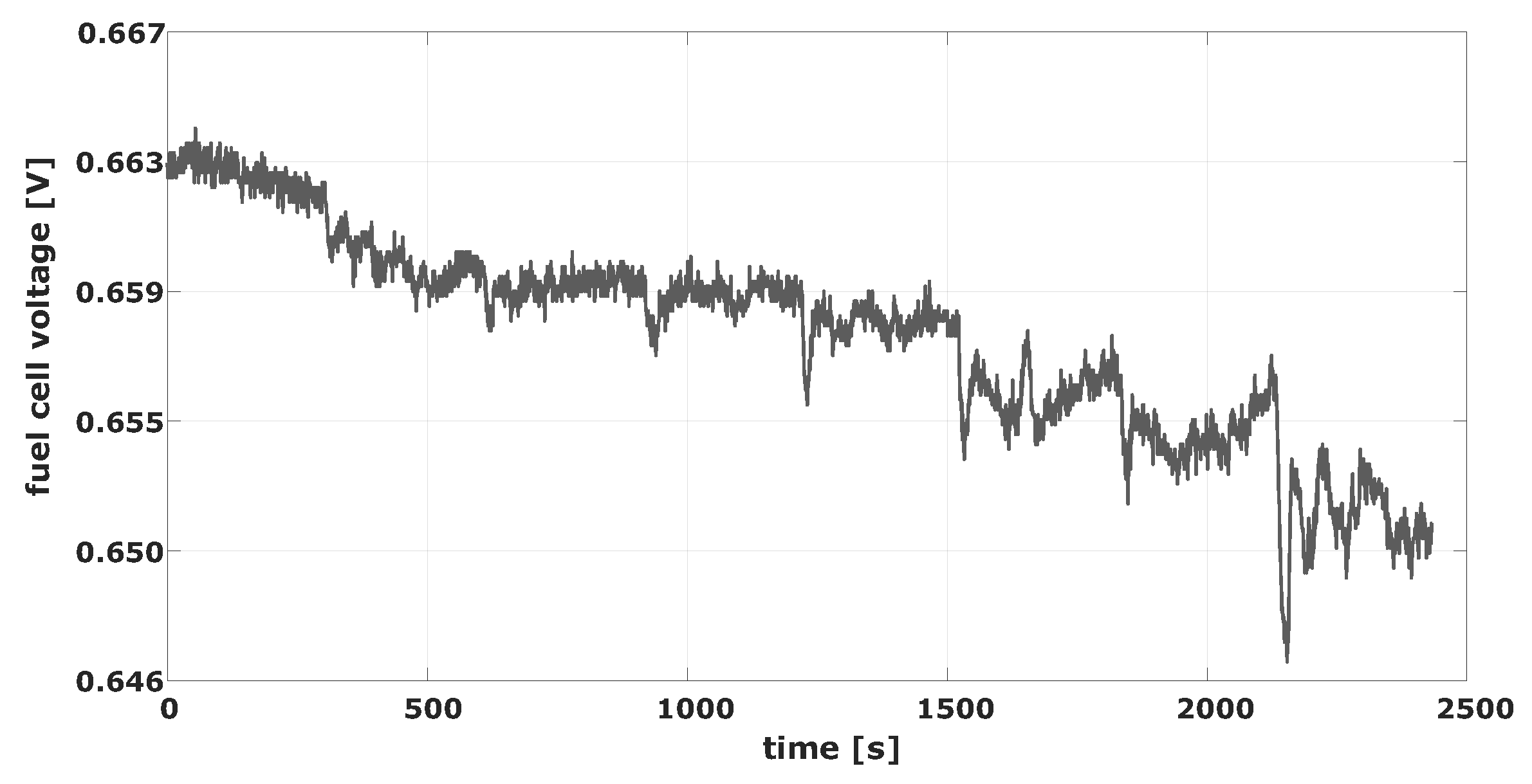
- The dataset used to train, test and validate the hybrid model comes from experiments where the operating conditions, and thus the profile of the output voltage, change dynamically, as opposed to the vast majority of datasets utilized in fuel cell modeling where the data come from static polarization curve experiments. Dynamical profiles of the operating conditions allow the showing of complex and hard-to-model behavior within the PEMFC.
- 2.
- The data-driven component of the hybrid structure is an ESN. As per the authors knowledge, this work represents the first implementation of an ESN for fuel cell modeling and voltage forecasting in a hybrid architecture.
- 3.
- A recursive GRBF is proposed for merging the contribution of each model. The GRBF recursively compares the similarity between the output of each model and the measured output of the fuel cell, assigns weights to each and computes the output of the hybrid structure.
2. Experimental Setup and Data
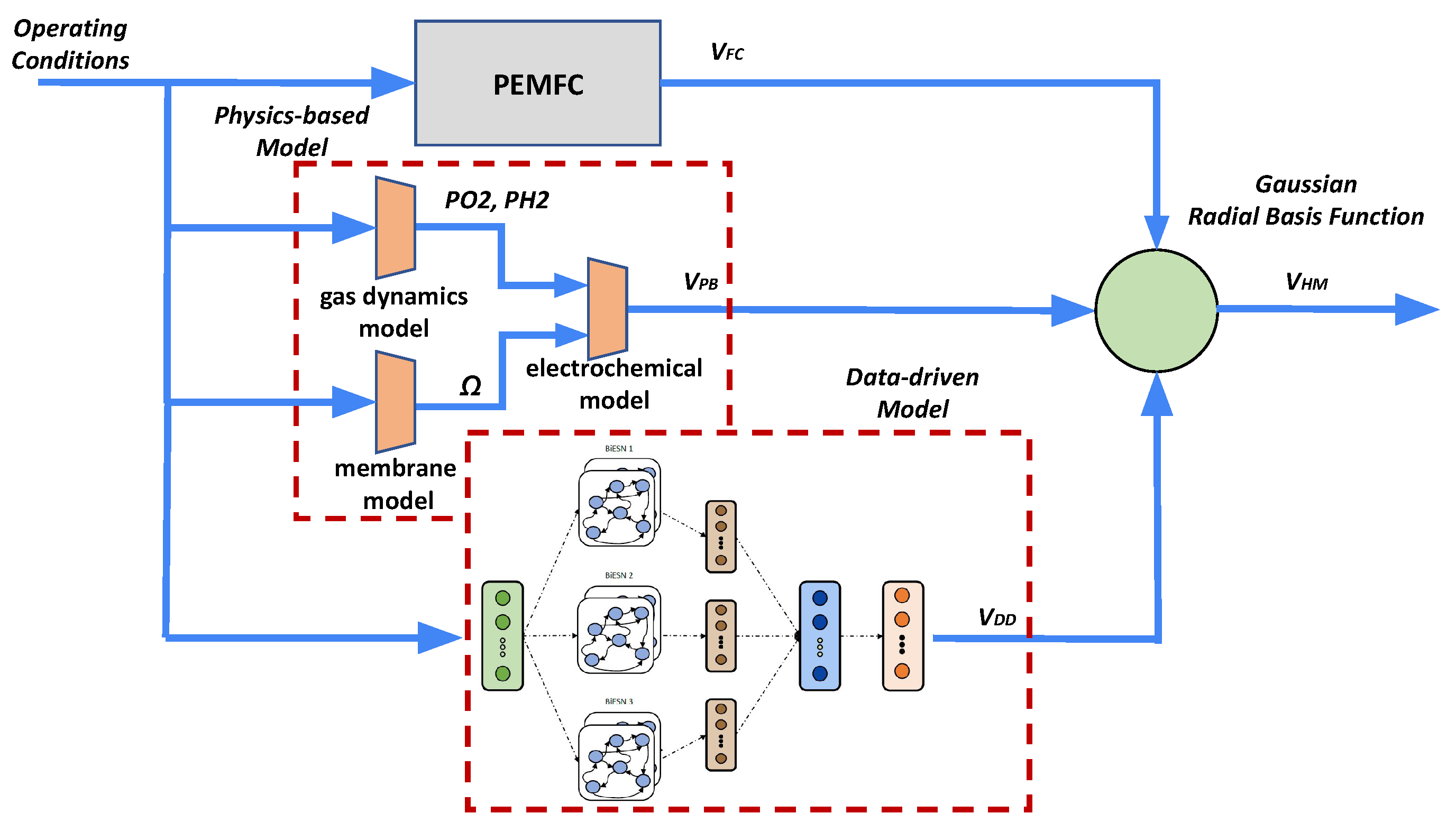
3. Physics-Based Model
3.1. Electrochemical Dynamics
3.2. Gas Channel Dynamics
3.3. Membrane Dynamics
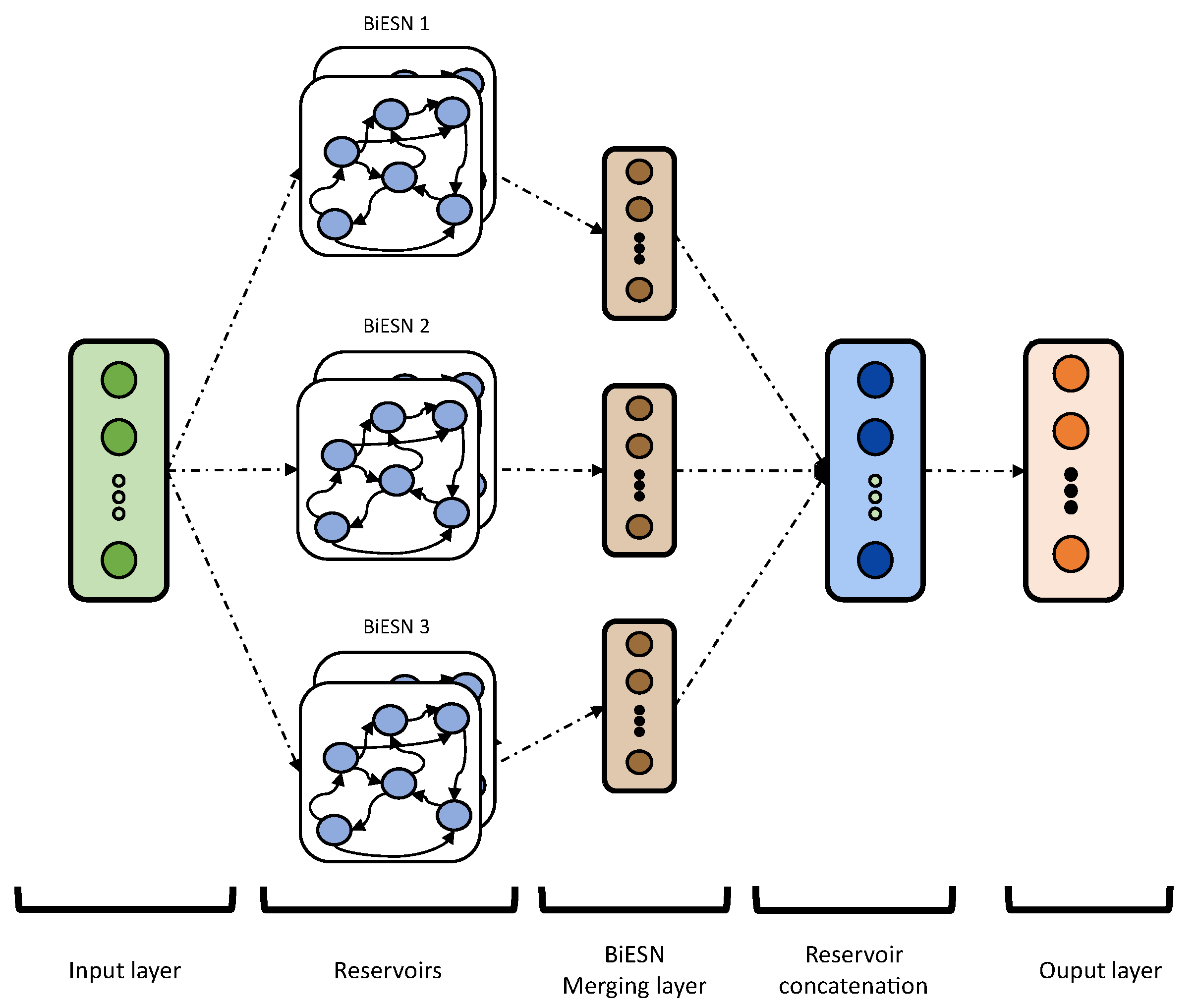
4. Data-Driven Model
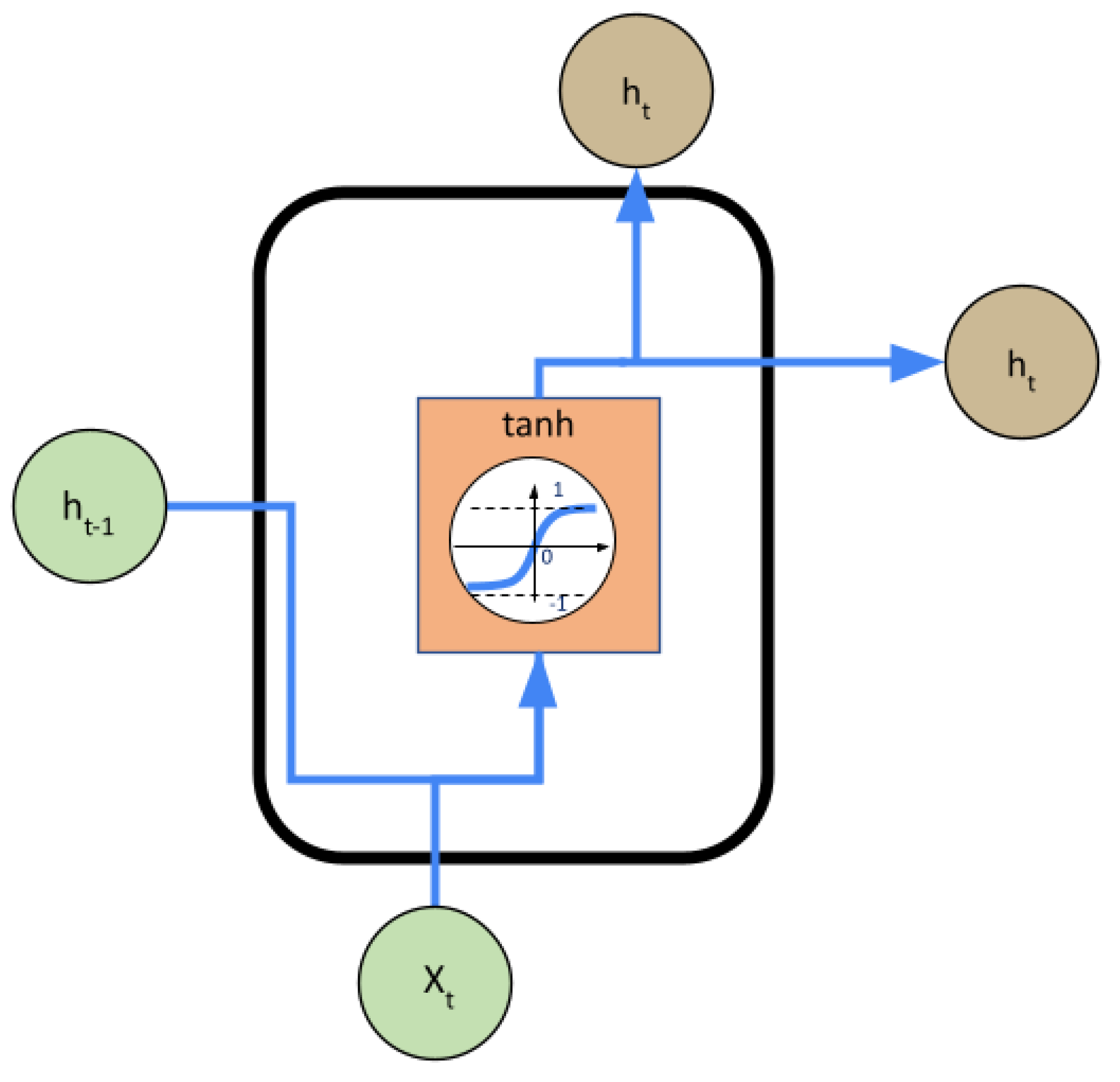
4.1. Echo State Networks
4.1.1. Equations
4.1.2. Parameters
4.1.3. Reservoir Combination
4.2. Data-Driven Model Designed
5. Hybrid Model
Merging Function
6. Results and Discussion
6.1. Physics-Based Model
6.2. Data-Driven Model
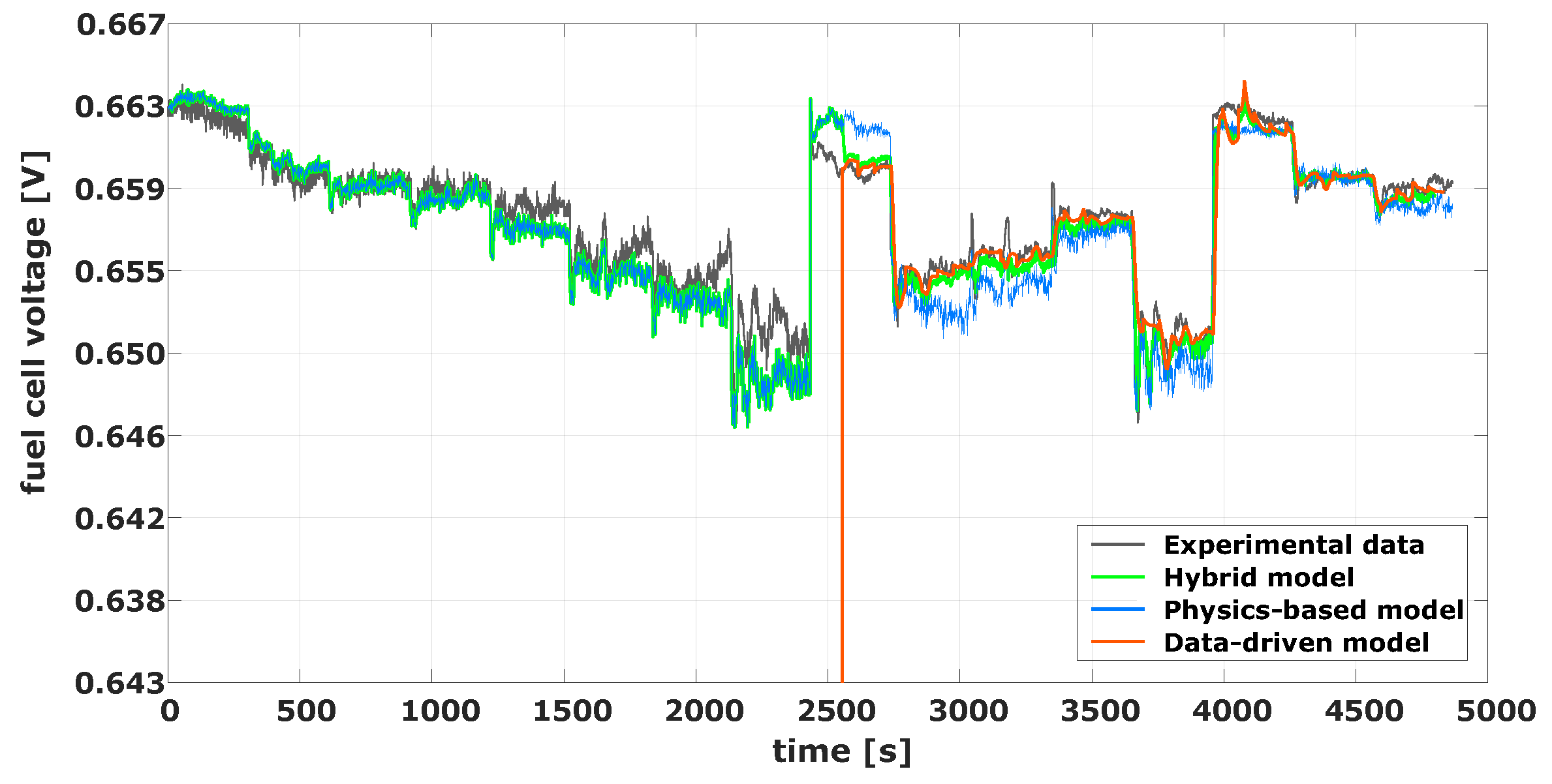
6.3. Hybrid Model
- 1.
- The physics-based part of the hybrid model has been constructed from simplifications of the main internal dynamics of the fuel cell. This results in a fewer number of parameters needed to be fitted in comparison with more complex accurate models. This allows a time-efficient model construction process.
- 2.
- The chosen data-driven model, an ESN, is an efficient neural network architecture with fast training times and simpler training algorithms than other neural networks. This results in a less time-consuming fitting process.
- 3.
- Due to the previous characteristic, the data-driven part of the hybrid model can be re-trained online, when the deviation between the system and the model is deemed too large. This would be nearly impossible with more complex architectures such as LSTM networks. The capacity to be re-trained on line is an enormous advantage with modeling systems whose parameters vary with time or suffer changes due to degradation, as is the case with important parameters in the PEM fuel cells (i.e., the amount of platinum in the catalyst layer).
- 4.
- By incorporating totally independent models in parallel, the hybrid structure is able to maintain a good approximation of the voltage during the full cycle of the fuel cell. Also, in case of failure of one the models, the hybrid model can still track the voltage with acceptable accuracy.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- U.S. Department of Energy, Fuel Cell Technologies Office. Multi-Year Research, Development, and Demonstration Plan. 2014. Available online: www.energy.gov/eere/fuelcells/downloads/hydrogen-and-fuel-cell-technologies-office-multi-year-research-development (accessed on 2 July 2023).
- Agyekum, E.B.; Ampah, J.D.; Wilberforce, T.; Afrane, S.; Nutakor, C. Research Progress, Trends, and Current State of Development on PEMFC-New Insights from a Bibliometric Analysis and Characteristics of Two Decades of Research Output. Membranes 2022, 12, 1103. [Google Scholar] [CrossRef]
- Chen, X.; Gong, G.; Wan, Z.; Luo, L.; Wan, J. Performance analysis of 5Â kW PEMFC-based residential micro-CCHP with absorption chiller. Int. J. Hydrogen Energy 2015, 40, 10647–10657. [Google Scholar] [CrossRef]
- Olabi, A.G.; Wilberforce, T.; Abdelkareem, M.A. Fuel cell application in the automotive industry and future perspective. Energy 2021, 214, 118955. [Google Scholar] [CrossRef]
- Darling, R.; Meyers, J. Kinetic Model of Platinum Dissolution in PEMFCs. J. Electrochem. Soc. 2003, 150, A1523–A1527. [Google Scholar] [CrossRef]
- Pandy, A.; Yang, Z.; Gummall, M.; Atrazhev, V.; Kuzminyh, N.Y.; Sultanov, V.; Burlatskyb, S. A Carbon Corrosion Model to Evaluate the Effect of Steady State and Transient Operation of a Polymer Electrolyte Membrane Fuel Cell. J. Electrochem. Soc. 2013, 160, F972–F979. [Google Scholar] [CrossRef]
- Schneider, P.; Sadeler, C.; Scherzer, A.; Zamel, N.; Gerteisen, D. Fast and Reliable State-of-Health Model of a PEM Cathode Catalyst Layer. J. Electrochem. Soc. 2019, 166, F322–F333. [Google Scholar] [CrossRef]
- Kneer, A.; Wagner, N. A Semi-Empirical Catalyst Degradation Model Based on Voltage Cycling under Automotive Operating Conditions in PEM Fuel Cells. J. Electrochem. Soc. 2019, 166, F120–F127. [Google Scholar] [CrossRef]
- Jia, C.; Li, K.; He, H.; Zhou, J.; Li, J.; Wei, Z. Health-aware energy management strategy for fuel cell hybrid bus considering air-conditioning control based on TD3 algorithm. Energy 2023, 283, 128462. [Google Scholar] [CrossRef]
- Jia, C.; He, H.; Zhou, J.; Li, J.; Wei, Z.; Li, K. Learning-based model predictive energy management for fuel cell hybrid electric bus with health-aware control. Energy 2024, 355, 122228. [Google Scholar] [CrossRef]
- Lechartier, E.; Laffly, E.; Péra, M.C.; Gouriveau, R.; Hissel, D.; Zerhouni, N. Proton exchange membrane fuel cell behavioral model suitable for prognostics. Int. J. Hydrogen Energy 2015, 40, 8384–8397. [Google Scholar] [CrossRef]
- Denga, Z.; Chena, Q.; Zhanga, L.; Zongb, Y.; Zhoua, K.; Fua, Z. Control oriented data driven linear parameter varying model for proton exchange membrane fuel cell systems. Appl. Energy 2020, 277, 115540. [Google Scholar] [CrossRef]
- Mohammadi, A.; Cirrincione, G.; Djerdir, A.; Khaburi, D. A novel approach for modeling the internal behavior of a PEMFC by using electrical circuits. Int. J. Hydrogen Energy 2018, 43, 11539–11549. [Google Scholar] [CrossRef]
- Nóbrega, P.H.A. A review of physics-based low-temperature proton-exchange membrane fuel cell models for system-level water and thermal management studies. J. Power Sources 2023, 558, 232585. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Gao, R.X.; Zhang, F. Hybrid physics-based and data-driven models for smart manufacturing: Modelling, simulation, and explainability. J. Manuf. Syst. 2022, 63, 381–391. [Google Scholar] [CrossRef]
- Meng, Y.; Yu, S.; Zhang, J.; Qin, J.; Dong, Z.; Lu, G.; Pang, H. Hybrid modeling based on mechanistic and data-driven approaches for cane sugar crystallization. J. Food Eng. 2019, 257, 44–55. [Google Scholar] [CrossRef]
- von Stosch, M.; Oliveira, R.; Peres, J.; de Azevedo, S.F. Hybrid semi-parametric modeling in process systems engineering: Past, present and future. Comput. Chem. Eng. 2014, 60, 86–101. [Google Scholar] [CrossRef]
- Hotvedt, M.; Grimstad, B.; Imsland, L. Developing a Hybrid Data-Driven, Mechanistic Virtual Flow Meter—A Case Study. IFAC-Pap. 2020, 53, 11692–11697. [Google Scholar] [CrossRef]
- Liang, M.; Li, S. Enhancing BNN structure learning of hybrid modeling strategy for free formulated mechanism complex systems. J. Process Control 2022, 120, 44–67. [Google Scholar] [CrossRef]
- Gaw, N.; Hawkins-Daarud, A.; Hu, L.S.; Yoon, H.; Wang, L.; Xu, Y.; Jackson, P.R.; Singleton, K.W.; Baxter, L.C.; Eschbacher, J.; et al. Integration of machine learning and mechanistic models accurately predicts variation in cell density of glioblastoma using multiparametric MRI. Sci. Rep. 2019, 9, 10063. [Google Scholar] [CrossRef]
- Hua†, F.; Hautaniemi, S.; Yokoo, R.; Lauffenburger, D.A. Integrated mechanistic and data-driven modelling for multivariate analysis of signalling pathways. J. R. Soc. Interface 2006, 3, 515–526. [Google Scholar] [CrossRef]
- Baker, R.E.; Peña, J.M.; Jayamohan, J.; Jérusalem, A. Mechanistic models versus machine learning, a fight worth fighting for the biological community? Biol. Lett. 2017, 14, 0660. [Google Scholar] [CrossRef] [PubMed]
- Liao, L.; Köttig, F. A hybrid framework combining data-driven and model-based methods for system remaining useful life prediction. Appl. Soft Comput. 2016, 44, 191–199. [Google Scholar] [CrossRef]
- Revach, G.; Shlezinger, N.; van Sloun, R.J.G.; Eldar, Y.C. KalmanNet: Data-driven Kalman filtering. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Toronto, ON, Canada, 6–11 June 2021; pp. 3905–3909. [Google Scholar]
- INN-BALANCE Project Consortium. Available online: www.innbalance-fch-project.eu (accessed on 1 December 2023).
- Dicks, A.; Rand, D. Fuel Cell Systems Explained, 3rd ed.; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Pukrushpan, J.T.; Peng, H.; Stefanopoulou, A.G. Control-Oriented Modeling and Analysis for Automotive Fuel Cell Systems. J. Dyn. Syst. Meas. Control 2004, 126, 14–25. [Google Scholar] [CrossRef]
- Barbir, F. PEM Fuel Cells: Theory and Practice; Elsevier Academic Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Jay, T.; Pukrushpan, A.G.S.; Peng, H. Control of Fuel Cell Power Systems, 1st ed.; Springer: London, UK, 2004. [Google Scholar]
- Luna, J.; Usai, E.; Husar, A.; Serra, M. Nonlinear observation in fuel cell systems: A comparison between disturbance estimation and High-Order Sliding-Mode techniques. Int. J. Hydrogen Energy 2016, 41, 19737–19748. [Google Scholar] [CrossRef]
- Kim, T.; King, B.R. Time series prediction using deep echo state networks. Neural Comput. Appl. 2020, 32, 17769–17787. [Google Scholar] [CrossRef]
- Jaeger, H. The “echo state” approach to analysing and training recurrent neural networks-with an erratum note. Bonn Ger. Ger. Natl. Res. Cent. Inf. Technol. GMD Tech. Rep. 2001, 148, 13. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 2010, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
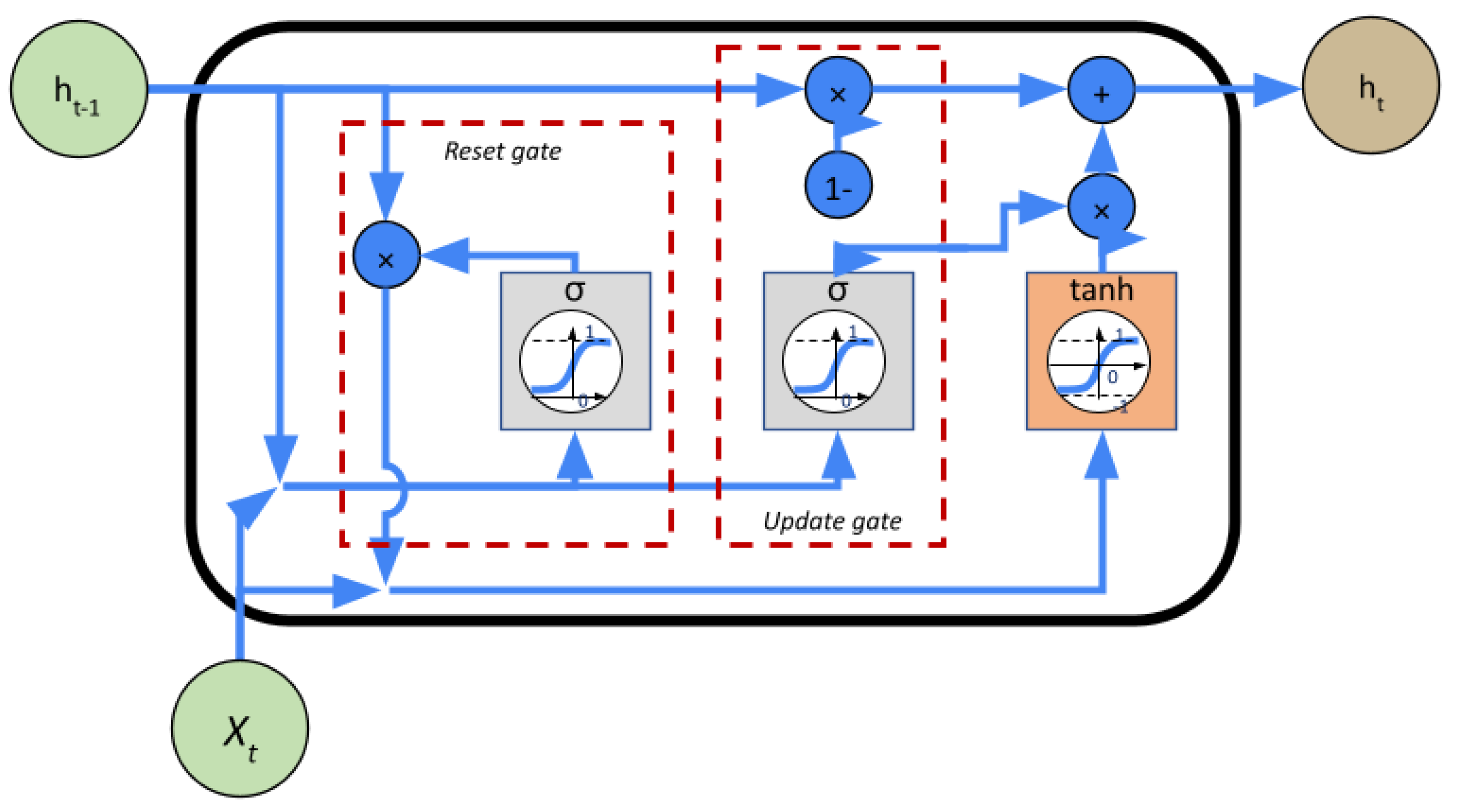
- Cho, K.; van Merrienboer, B.; Bahdanau, D.; Bengio, Y. On the Properties of Neural Machine Translation: Encoder-Decoder Approaches. arXiv 2014, arXiv:1409.1259. [Google Scholar] [CrossRef]
- Yang, S.; Yu, X.; Zhou, Y. LSTM and GRU Neural Network Performance Comparison Study: Taking Yelp Review Dataset as an Example. In Proceedings of the 2020 International Workshop on Electronic Communication and Artificial Intelligence (IWECAI), Shanghai, China, 12–14 June 2020; pp. 98–101. [Google Scholar] [CrossRef]
- Maass, W.; Natschläger, T.; Markram, H. Real-Time Computing Without Stable States: A New Framework for Neural Computation Based on Perturbations. Neural Comput. 2002, 14, 2531–2560. [Google Scholar] [CrossRef]
- Lukoševičius, M.; Jaeger, H. Reservoir computing approaches to recurrent neural network training. Comput. Sci. Rev. 2009, 3, 127–149. [Google Scholar] [CrossRef]
- Jirak, D.; Tietz, S.; Ali, H.; Wermter, S. Echo State Networks and Long Short-Term Memory for Continuous Gesture Recognition: A Comparative Study. Cogn. Comput. 2020, 15, 1427–1439. [Google Scholar] [CrossRef]
- Salmen, M.; Ploger, P. Echo State Networks used for Motor Control. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 1953–1958, ISSN: 1050-4729. [Google Scholar] [CrossRef]
- Mezzi, R.; Morando, S.; Steiner, N.Y.; Péra, M.C.; Hissel, D.; Larger, L. Multi-Reservoir Echo State Network for Proton Exchange Membrane Fuel Cell Remaining Useful Life prediction. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 1872–1877, ISSN: 2577-1647. [Google Scholar] [CrossRef]
- Morando, S.; Jemei, S.; Hissel, D.; Gouriveau, R.; Zerhouni, N. ANOVA method applied to proton exchange membrane fuel cell ageing forecasting using an echo state network. Math. Comput. Simul. 2017, 131, 283–294. [Google Scholar] [CrossRef]
- Carmichael, Z.; Syed, H.; Burtner, S.; Kudithipudi, D. Mod-DeepESN: Modular Deep Echo State Network. In Proceedings of the 2018 Conference on Cognitive Computational Neuroscience. Cognitive Computational Neuroscience, Philadelphia, PA, USA, 5–8 September 2018. [Google Scholar] [CrossRef]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Chia Laguna Resort. Sardinia, Italy, 13–15 May 2010; Volume 9, pp. 249–256. [Google Scholar]
- Lukoševičius, M. A Practical Guide to Applying Echo State Networks. In Neural Networks: Tricks of the Trade; Montavon, G., Orr, G.B., Müller, K.R., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7700, pp. 659–686. [Google Scholar] [CrossRef]
- Bianchi, F.M.; Scardapane, S.; Løkse, S.; Jenssen, R. Bidirectional deep-readout echo state networks. arXiv 2017, arXiv:1711.06509. Available online: http://xxx.lanl.gov/abs/1711.06509 (accessed on 1 October 2023).
- Sun, C.; Song, M.; Hong, S.; Li, H. A Review of Designs and Applications of Echo State Networks. arXiv 2020, arXiv:2012.02974. Available online: http://xxx.lanl.gov/abs/2012.02974 (accessed on 1 October 2023).
- Chanal, D.; Steiner, N.Y.; Chamagne, D.; Pera, M.C. Voltage prognosis of PEMFC estimated using Multi-Reservoir Bidirectional Echo State Network. In Proceedings of the 2022 10th International Conference on Systems and Control (ICSC), Marseille, France, 23–25 November 2022; pp. 352–359, ISSN: 2379-0067. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. arXiv 2017, arXiv:1711.05101. Available online: http://xxx.lanl.gov/abs/1711.05101 (accessed on 10 September 2023).
- Alitasb, G.K.; Salau, A.O. Multiple-input multiple-output Radial Basis Function Neural Network modeling and model predictive control of a biomass boiler. Energy Rep. 2024, 11, 442–451. [Google Scholar] [CrossRef]
- Kapnopoulos, A.; Kazakidis, C.; Alexandridis, A. Quadrotor trajectory tracking based on backstepping control and radial basis function neural networks. Results Control Optim. 2024, 14, 100335. [Google Scholar] [CrossRef]
- Naha, S.; Das, D.K. Radial basis function neural network controller for power control of molten salt breeder reactor of nuclear power plant. Ann. Nucl. Energy 2024, 195, 110160. [Google Scholar] [CrossRef]




| Anode Stoichiometry Set [-] | Cathode Stoichiometry Set [-] | Current Density Set [A] | Condition Number [-] |
|---|---|---|---|
| 3 | 2.2 | 200 | 0 |
| 3 | 2.1 | 200 | 1 |
| 3 | 2.0 | 200 | 2 |
| 3 | 1.9 | 200 | 3 |
| 3 | 1.8 | 200 | 4 |
| 3 | 1.7 | 200 | 5 |
| 3 | 1.65 | 200 | 6 |
| 3 | 1.5 | 200 | 7 |
| Symbol | Description | Value | Units |
|---|---|---|---|
| Fitting pressure coefficient | 30.05 | GPa | |
| Vapor energy | 36.98 | kJ mol | |
| R | Gas constant | 8.314 | J molK |
| Oxygen molar mass | 32 × 10 | kg mol | |
| Nitrogen molar mass | 28 × 10 | kg mol | |
| Water vapor molar mass | 18 × 10 | kg mol | |
| Reference exchange current density | 2.9 × 10 | mA | |
| Limiting current | 1760 | mA | |
| Charge transfer coefficient | 0.397 | kJ mol | |
| n | Number of electrons in the reaction | 2 | - |
| Parameters | Values | Comments |
|---|---|---|
| Spectral radius (ρ) | Not defined | - |
| Leaky rate (α) | 0.1/0.5/0.9 | Low/Medium/High dynamic |
| Connectivity (c) | 0.1 | - |
| Number of neurons | For each reservoir: 100 Total: 600 | - |
| Reservoir initialization | Glorot uniform | - |
| Reservoir weight scaling method | No scaling | - |
| Readout layer initialization | Glorot uniform | - |
| Merging mode of bidirectional reservoirs | Concatenation | - |
| Activation function | tanh | - |
| Optimization | AdamW | - |
| Learning rate | 0.0014 | - |
| Weight decay | 0.001 | - |
| Scheduler (learning rate + weight decay) | Exponential decay decay rate: 0.95 decay steps: 10 epochs | - |
| Batch size | 32 | - |
| Sequence length | 120 | Last 2 min (120 s) |
| Model | Training | Prediction |
|---|---|---|
| Physics-based | 2.6247 × 10 | 2.9339 × 10 |
| Data-driven | - | 1.7777 × 10 |
| Hybrid | 2.6247 × 10 | 9.5692 × 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguilar, J.A.; Chanal, D.; Chamagne, D.; Yousfi Steiner, N.; Péra, M.-C.; Husar, A.; Andrade-Cetto, J. A Hybrid Control-Oriented PEMFC Model Based on Echo State Networks and Gaussian Radial Basis Functions. Energies 2024, 17, 508. https://doi.org/10.3390/en17020508
Aguilar JA, Chanal D, Chamagne D, Yousfi Steiner N, Péra M-C, Husar A, Andrade-Cetto J. A Hybrid Control-Oriented PEMFC Model Based on Echo State Networks and Gaussian Radial Basis Functions. Energies. 2024; 17(2):508. https://doi.org/10.3390/en17020508
Chicago/Turabian StyleAguilar, José Agustín, Damien Chanal, Didier Chamagne, Nadia Yousfi Steiner, Marie-Cécile Péra, Attila Husar, and Juan Andrade-Cetto. 2024. "A Hybrid Control-Oriented PEMFC Model Based on Echo State Networks and Gaussian Radial Basis Functions" Energies 17, no. 2: 508. https://doi.org/10.3390/en17020508
APA StyleAguilar, J. A., Chanal, D., Chamagne, D., Yousfi Steiner, N., Péra, M.-C., Husar, A., & Andrade-Cetto, J. (2024). A Hybrid Control-Oriented PEMFC Model Based on Echo State Networks and Gaussian Radial Basis Functions. Energies, 17(2), 508. https://doi.org/10.3390/en17020508









