Optimizing H-Darrieus Wind Turbine Performance with Double-Deflector Design
Abstract
1. Introduction
2. Numerical Simulation
2.1. Governing Equations
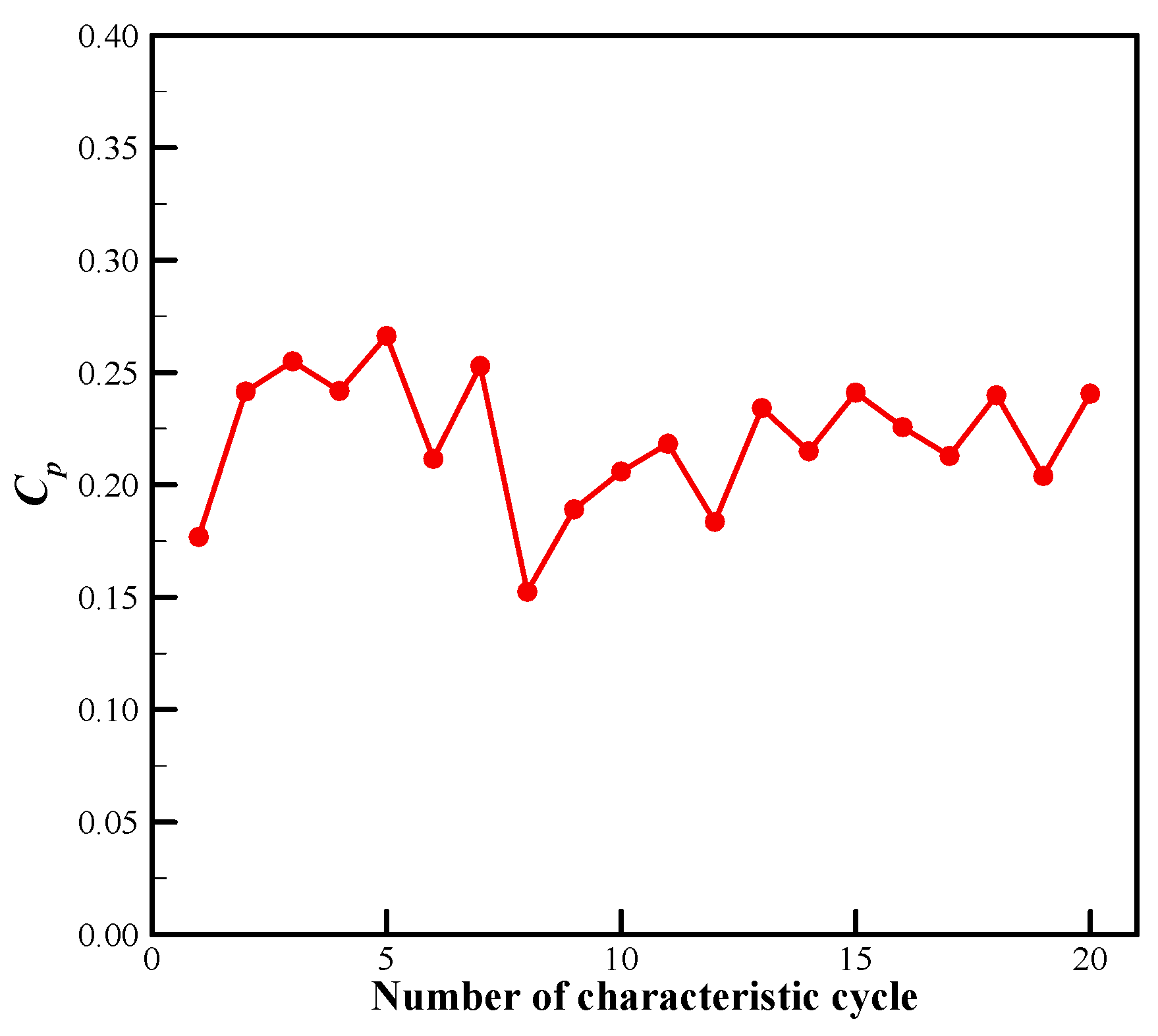
2.2. Time-Averaged Power Coefficient
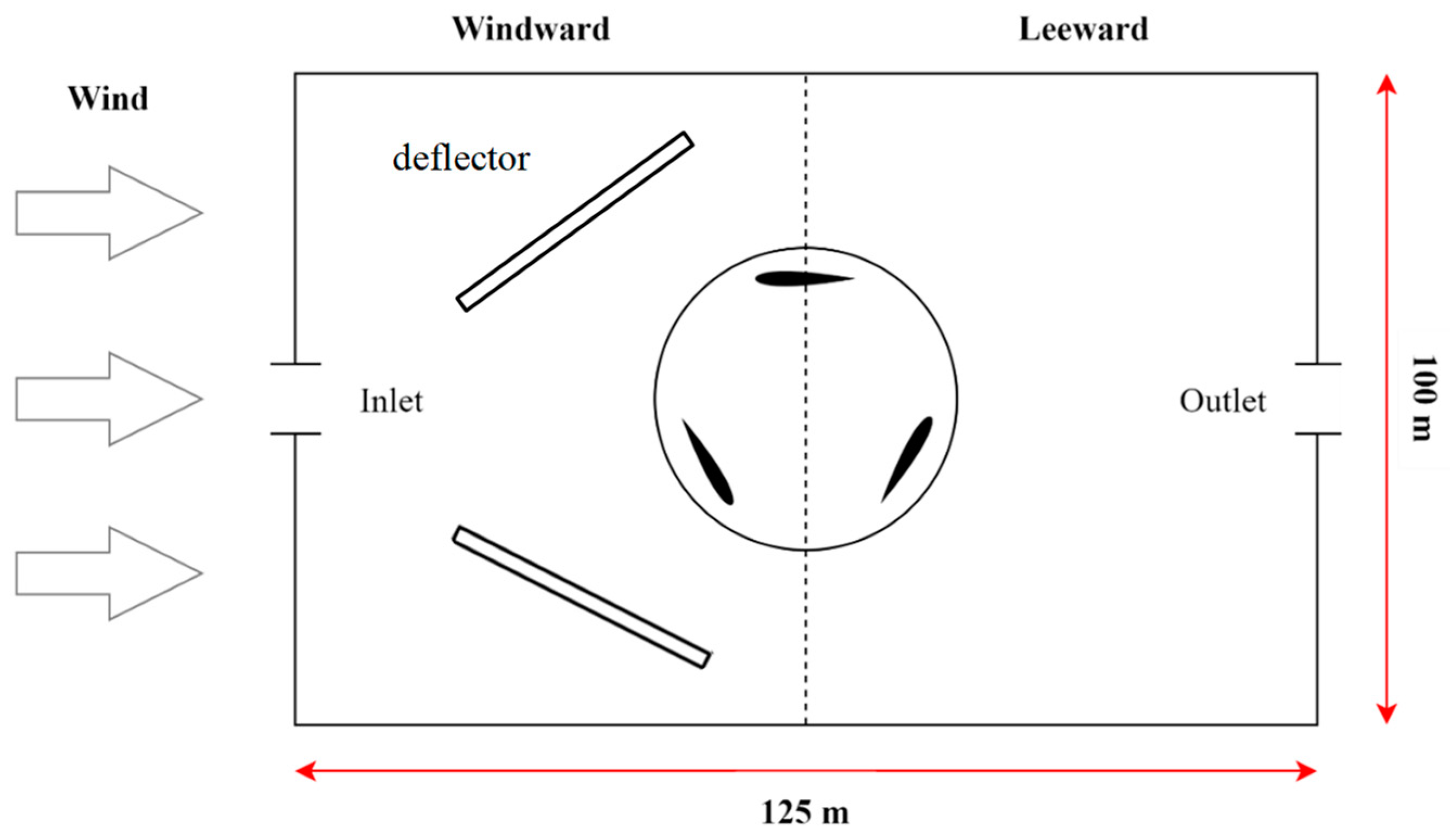
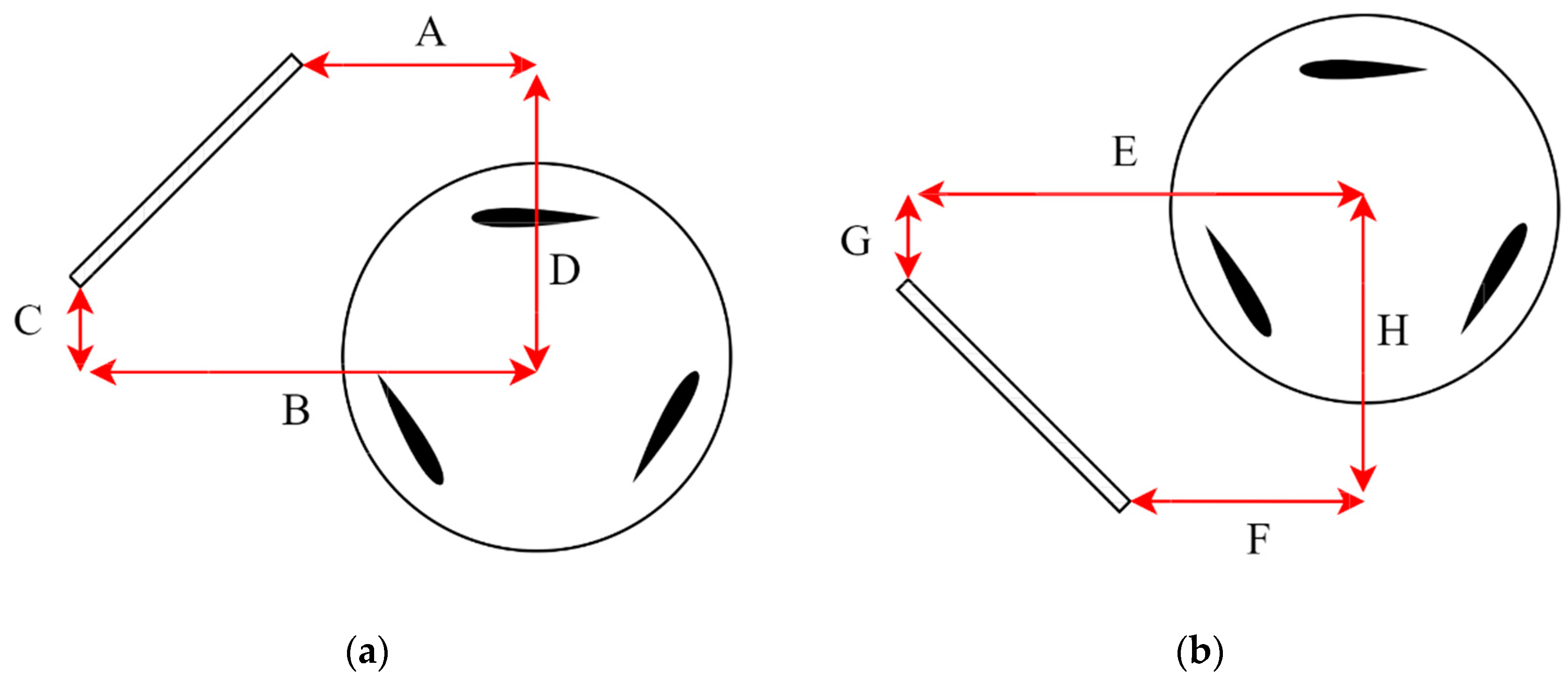
2.3. Operation Conditions with Double Deflectors
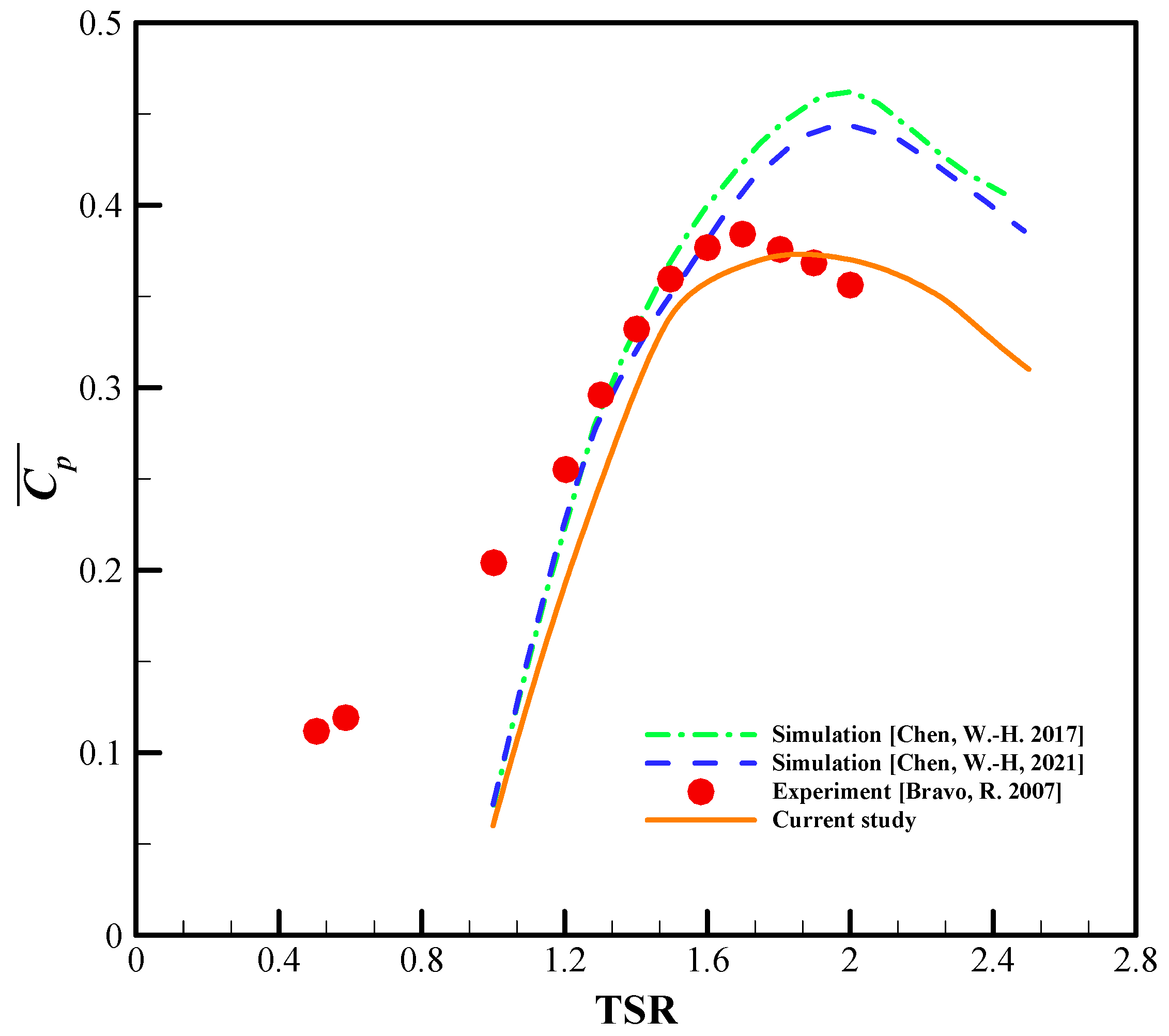
2.4. Validation and Grid-Independent Test
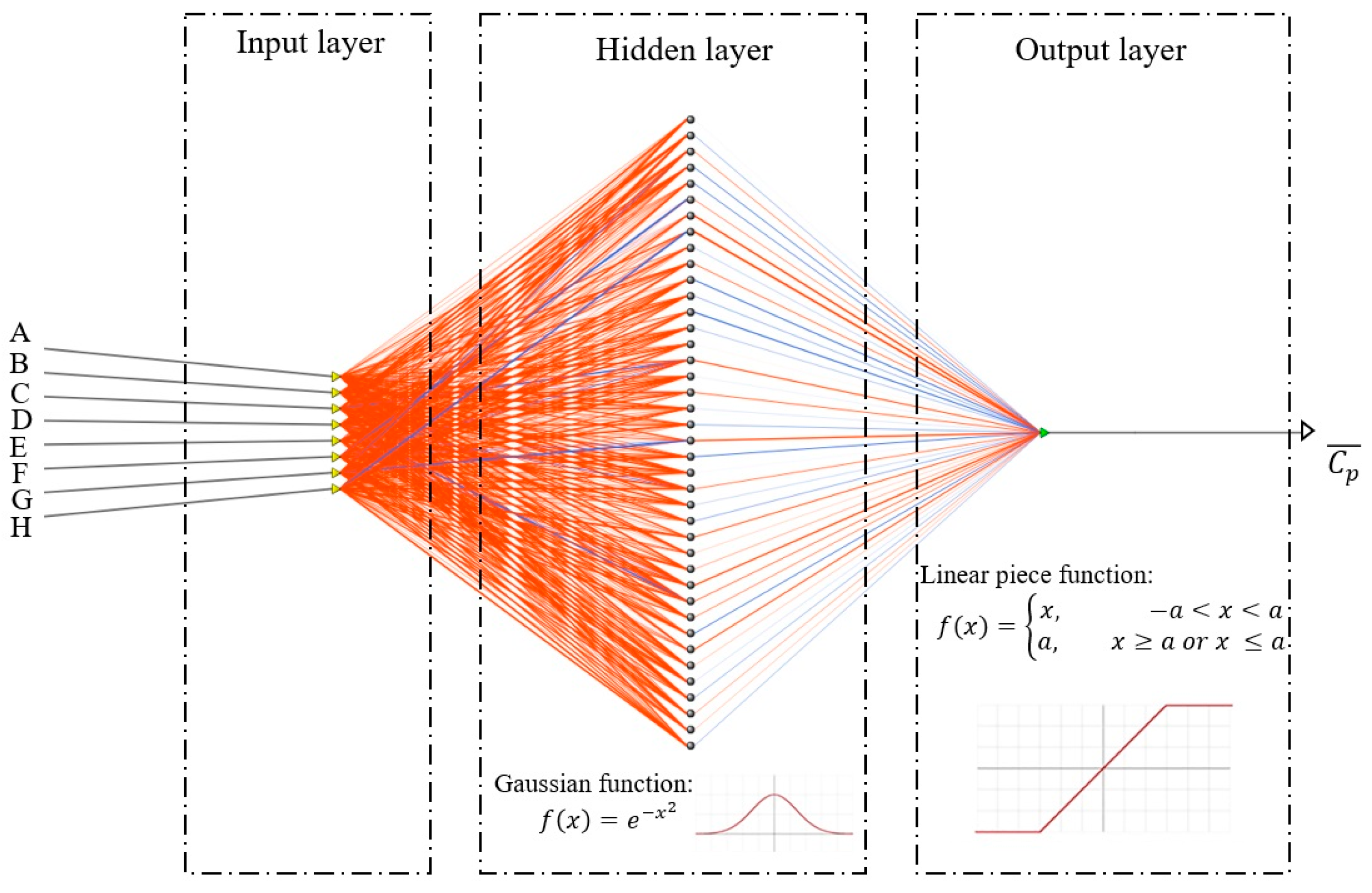
2.5. Artificial Neural Networks
3. Results and Discussion
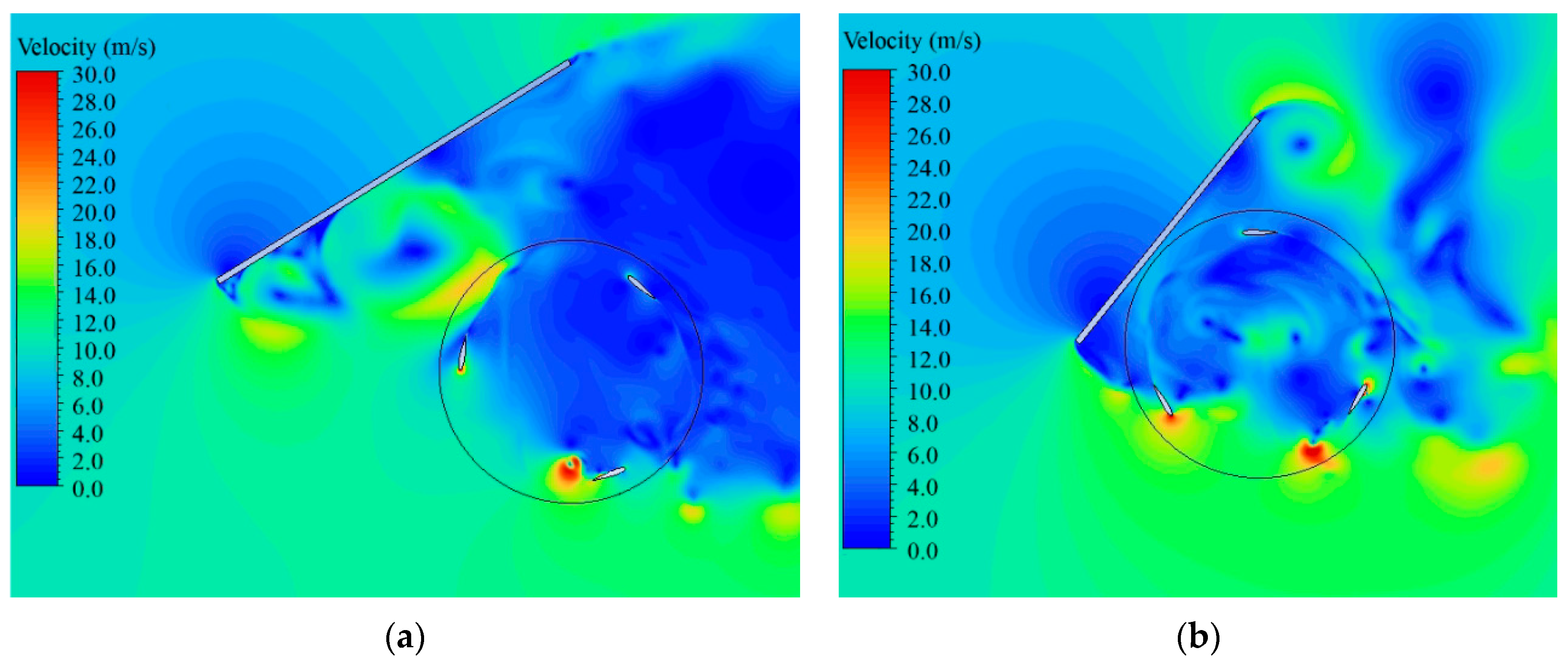
3.1. VAWT Performance with a Single Deflector
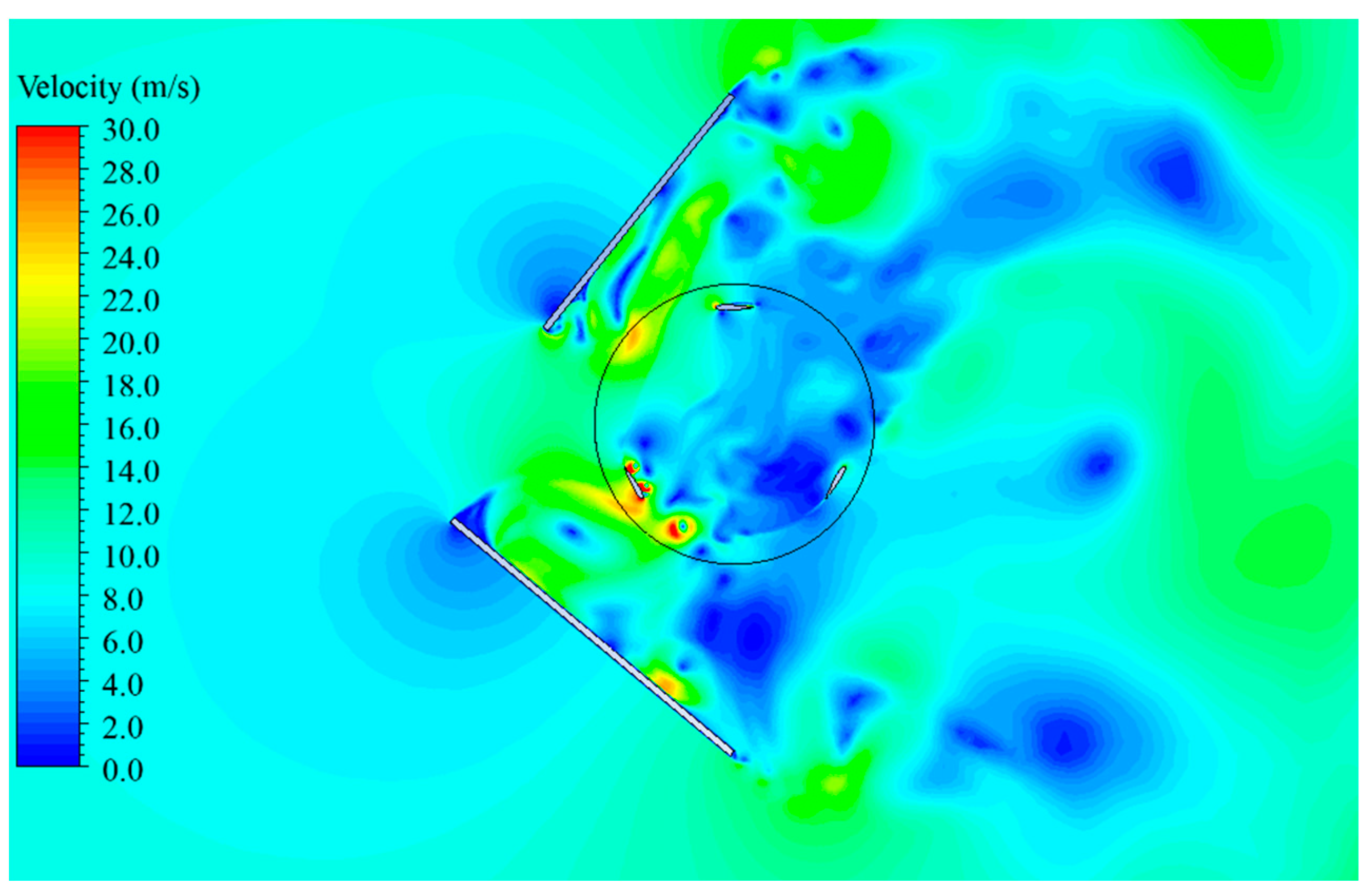
3.2. VAWT Performance with Double Deflectors
3.3. Neural Network Model Architecture and Data Training
3.4. The Optimization of VAWT Performance and CFD Confirmation
4. Conclusions
- Installing a single lower deflector positively impacts VAWT performance more than installing a single upper deflector. The major reason is that the lower deflector does not block airflow and may accelerate incoming wind velocity.
- The double-deflector design, composed of a lower deflector and an upper deflector, can greatly enhance VAWT performance. VAWT performance seems to be able to exceed the Betz limit with the proper installation of the two deflectors. However, this conclusion was found based on a 2D turbulent viscous flow model and needs to be further verified both theoretically and experimentally.
- The developed ANN model demonstrated precise prediction capability for the evaluation of the optimal for a VAWT with a double-deflector design, as evidenced by a coefficient of determination (R2) of 0.95 between the outputs and targets in the test data.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Blade swept area (m2) |
| Power coefficient | |
| Time-averaged power coefficient | |
| D | Rotor diameter (m) |
| Dω | Cross-diffusion term |
| E | Error function |
| fc | Fluctuation frequency (Hz) |
| Turbulent generation rate due to the mean flow (kg∙m−1∙s−3) | |
| Generation rate of | |
| Turbulence kinetic energy | |
| N | Number of time intervals per revolution |
| P | Average absolute pressure (Pa) |
| R | Rotor radius (m) |
| User-defined source term for | |
| User-defined source term for | |
| Current values of error derivative | |
| Previous values of error derivative | |
| T | Torque (N∙m) |
| Characteristic time (s) | |
| TSR | Tip speed ratio |
| Velocity vector (m·s−1) | |
| V = Vmean | Freestream speed (m·s−1) |
| Specific dissipation rate | |
| Current weight | |
| Previous weight | |
| Dissipation of due to turbulence | |
| Dissipation of due to turbulence | |
| Greek letters | |
| Effective diffusivity of | |
| Effective diffusivity of | |
| Kronecker delta | |
| Rotor azimuth | |
| Dynamic viscosity (kg·m−1·s−1) | |
| Eddy viscosity (kg·m−1·s−1) | |
| Density (kg·m−3) | |
| Closure coefficients of | |
| Closure coefficients of | |
| Angular velocity (rad·s−1) |
References
- Jabbar Al-Quraishi, B.; Asmuin, N.; Mohd, S.; Abd Al-Wahid, W.; Mohammed, A.; Didane, D. Review on Diffuser Augmented Wind Turbine (DAWT). Int. J. Integr. Eng. 2019, 11. [Google Scholar] [CrossRef]
- Sedaghat, A.; Hassanzadeh, A.; Jamali, J.; Mostafaeipour, A.; Chen, W.-H. Determination of rated wind speed for maximum annual energy production of variable speed wind turbines. Appl. Energy 2017, 205, 781–789. [Google Scholar] [CrossRef]
- GWEC—Global Wind Energy Council. 2023. Available online: https://gwec.net/globalwindreport2023/ (accessed on 10 December 2023).
- Shah, S.R.; Kumar, R.; Raahemifar, K.; Fung, A.S. Design, modeling and economic performance of a vertical axis wind turbine. Energy Rep. 2018, 4, 619–623. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, D.; Wang, T.; Shen, W.; Liu, H.; Chen, M. A review: Approaches for aerodynamic performance improvement of lift-type vertical axis wind turbine. Sustain. Energy Technol. Assess. 2022, 49, 101789. [Google Scholar] [CrossRef]
- Wong, K.H.; Chong, W.T.; Poh, S.C.; Shiah, Y.-C.; Sukiman, N.L.; Wang, C.-T. 3D CFD simulation and parametric study of a flat plate deflector for vertical axis wind turbine. Renew. Energy 2018, 129, 32–55. [Google Scholar] [CrossRef]
- Alom, N.; Saha, U.K. Four Decades of Research Into the Augmentation Techniques of Savonius Wind Turbine Rotor. J. Energy Resour. Technol. 2018, 140, 050801. [Google Scholar] [CrossRef]
- Golecha, K.; Eldho, T.I.; Prabhu, S.V. Influence of the deflector plate on the performance of modified Savonius water turbine. Appl. Energy 2011, 88, 3207–3217. [Google Scholar] [CrossRef]
- Jin, X.; Wang, Y.; Ju, W.; He, J.; Xie, S. Investigation into parameter influence of upstream deflector on vertical axis wind turbines output power via three-dimensional CFD simulation. Renew. Energy 2018, 115, 41–53. [Google Scholar] [CrossRef]
- Rajpar, A.H.; Ali, I.; Eladwi, A.E.; Bashir, M.B. Recent Development in the Design of Wind Deflectors for Vertical Axis Wind Turbine: A Review. Energies 2021, 14, 5140. [Google Scholar] [CrossRef]
- Zhao, P.; Jiang, Y.; Liu, S.; Stoesser, T.; Zou, L.; Wang, K. Investigation of fundamental mechanism leading to the performance improvement of vertical axis wind turbines by deflector. Energy Convers. Manag. 2021, 247, 114680. [Google Scholar] [CrossRef]
- Chen, W.-H.; Wang, J.-S.; Chang, M.-H.; Mutuku, J.K.; Hoang, A.T. Efficiency improvement of a vertical-axis wind turbine using a deflector optimized by Taguchi approach with modified additive method. Energy Convers. Manag. 2021, 245, 114609. [Google Scholar] [CrossRef]
- Kim, D.; Gharib, M. Efficiency improvement of straight-bladed vertical-axis wind turbines with an upstream deflector. J. Wind. Eng. Ind. Aerodyn. 2013, 115, 48–52. [Google Scholar] [CrossRef]
- Qasemi, K.; Azadani, L.N. Optimization of the power output of a vertical axis wind turbine augmented with a flat plate deflector. Energy 2020, 202, 117745. [Google Scholar] [CrossRef]
- Zidane, I.F.; Ali, H.M.; Swadener, G.; Eldrainy, Y.A.; Shehata, A.I. Effect of upstream deflector utilization on H-Darrieus wind turbine performance: An optimization study. Alex. Eng. J. 2023, 63, 175–189. [Google Scholar] [CrossRef]
- Jamieson, P. Generalized limits for energy extraction in a linear constant velocity flow field. Wind. Energy 2008, 11, 445–457. [Google Scholar] [CrossRef]
- Oman, R.A.; Foreman, K.M.; Gilbert, B.L. Investigation of Diffuser-Augmented Wind Turbines. Part II; Technical Report; Grumman Aerospace Corp.: Bethpage, NY, USA, 1977. [Google Scholar]
- Hansen, M.O.L.; Sørensen, N.N.; Flay, R.G.J. Effect of Placing a Diffuser around a Wind Turbine. Wind Energy 2000, 3, 207–213. [Google Scholar] [CrossRef]
- Freda, R.; Knight, B.; Pannir, S. A Theory for Power Extraction from Passive Accelerators and Confined Flows. Energies 2020, 13, 4854. [Google Scholar] [CrossRef]
- Vaz, J.R.P.; Wood, D.H. Aerodynamic optimization of the blades of diffuser-augmented wind turbines. Energy Convers. Manag. 2016, 123, 35–45. [Google Scholar] [CrossRef]
- Do Rio Vaz, D.A.T.D.; Vaz, J.R.P.; Silva, P.A.S.F. An approach for the optimization of diffuser-augmented hydrokinetic blades free of cavitation. Energy Sustain. Dev. 2018, 45, 142–149. [Google Scholar] [CrossRef]
- Keramat Siavash, N.; Najafi, G.; Tavakkoli Hashjionfn, T.; Ghobadian, B.; Mahmoodi, E. Mathematical modeling of a horizontal axis shrouded wind turbine. Renew. Energy 2020, 146, 856–866. [Google Scholar] [CrossRef]
- Chen, W.-H.; Wang, J.-S.; Chang, M.-H.; Tuan Hoang, A.; Shiung Lam, S.; Kwon, E.E.; Ashokkumar, V. Optimization of a vertical axis wind turbine with a deflector under unsteady wind conditions via Taguchi and neural network applications. Energy Convers. Manag. 2022, 254, 115209. [Google Scholar] [CrossRef]
- Svorcan, J.; Peković, O.; Simonović, A.; Tanović, D.; Hasan, M.S. Design of optimal flow concentrator for vertical-axis wind turbines using computational fluid dynamics, artificial neural networks and genetic algorithm. Adv. Mech. Eng. 2021, 13, 168781402110090. [Google Scholar] [CrossRef]
- Almohammadi, K.M.; Ingham, D.B.; Ma, L.; Pourkashan, M. Computational fluid dynamics (CFD) mesh independency techniques for a straight blade vertical axis wind turbine. Energy 2013, 58, 483–493. [Google Scholar] [CrossRef]
- Chen, W.-H.; Chen, C.-Y.; Huang, C.-Y.; Hwang, C.-J. Power output analysis and optimization of two straight-bladed vertical-axis wind turbines. Appl. Energy 2017, 185, 223–232. [Google Scholar] [CrossRef]
- ANSYS Fluent. Ansys Fluent 12.0 Theory Guide—4.5.2 Shear-Stress Transport (SST)—Model; ANSYS Inc.: Canonsburg, PA, USA, 2023. [Google Scholar]
- Oh, E.; Son, S.-Y. Energy-storage system sizing and operation strategies based on discrete Fourier transform for reliable wind-power generation. Renew. Energy 2018, 116, 786–794. [Google Scholar] [CrossRef]
- Xiao, J.; Bai, L.; Li, F.; Liang, H.; Wang, C. Sizing of energy storage and diesel generators in an isolated microgrid using discrete Fourier transform (DFT). IEEE Trans. Sustain. Energy 2014, 5, 907–916. [Google Scholar] [CrossRef]
- Ferreira, C.S. The Near Wake of the Vawt—2d and 3d Views of the Vawt Aerodynamics; TuDelf: Delf, The Netherlands, 2023. [Google Scholar]
- Reynolds number calculator. 2023. Available online: http://airfoiltools.com/calculator/reynoldsnumber (accessed on 10 December 2023).
- Bravo, R.; Tullis, S.; Ziada, S. Performance testing of a small vertical-axis wind turbine. In Proceedings of the 21st Canadian Congress of Applied Mechanics, Toronto, OT, Canada, 3–7 June 2007. [Google Scholar]
- Fahlman, S.E. An Empirical Study of Learning Speed in Back-Propagation Networks; Carnegie Mellon University, Computer Science Department: Pittsburgh, PA, USA, 1988. [Google Scholar]
- Chen, W.-H.; Ocreto, J.B.; Wang, J.-S.; Hoang, A.T.; Liou, J.-H.; Hwang, C.-J.; Chong, W.T. Two-stage optimization of three and four straight-bladed vertical axis wind turbines (SB-VAWT) based on Taguchi approach. e-Prime Adv. Electr. Eng. Electron. Energy 2021, 1, 100025. [Google Scholar] [CrossRef]
- Wong, K.H.; Chong, W.T.; Sukiman, N.L.; Shiah, Y.-C.; Poh, S.C.; Sopian, K.; Wang, W.C. Experimental and simulation investigation into the effects of a flat plate deflector on vertical axis wind turbine. Energy Convers. Manag. 2018, 160, 109–125. [Google Scholar] [CrossRef]
- Eshagh Nimvari, M.; Fatahian, H.; Fatahian, E. Performance improvement of a Savonius vertical axis wind turbine using a porous deflector. Energy Convers. Manag. 2020, 220, 113062. [Google Scholar] [CrossRef]
- Sears, W.R.; Telionis, D.P. Boundary-Layer Separation in Unsteady Flow. SIAM J. Appl. Math. 1975, 28, 215–235. [Google Scholar] [CrossRef]
- Simpson, R.L. Turbulent Boundary-Layer Separation. Annu. Rev. Fluid Mech. 1989, 21, 205–232. [Google Scholar] [CrossRef]
- Zidane, I.; Swadener, G.; Saqr, K.; Ma, X.; Shehadeh, M. CFD Investigation of Transitional Separation Bubble Characteristics on NACA 63415 Airfoil at Low Reynolds Numbers. In Proceedings of the 25th UKACM Conference on Computational Mechanics, Birmingham, UK, 12–13 April 2017. [Google Scholar]






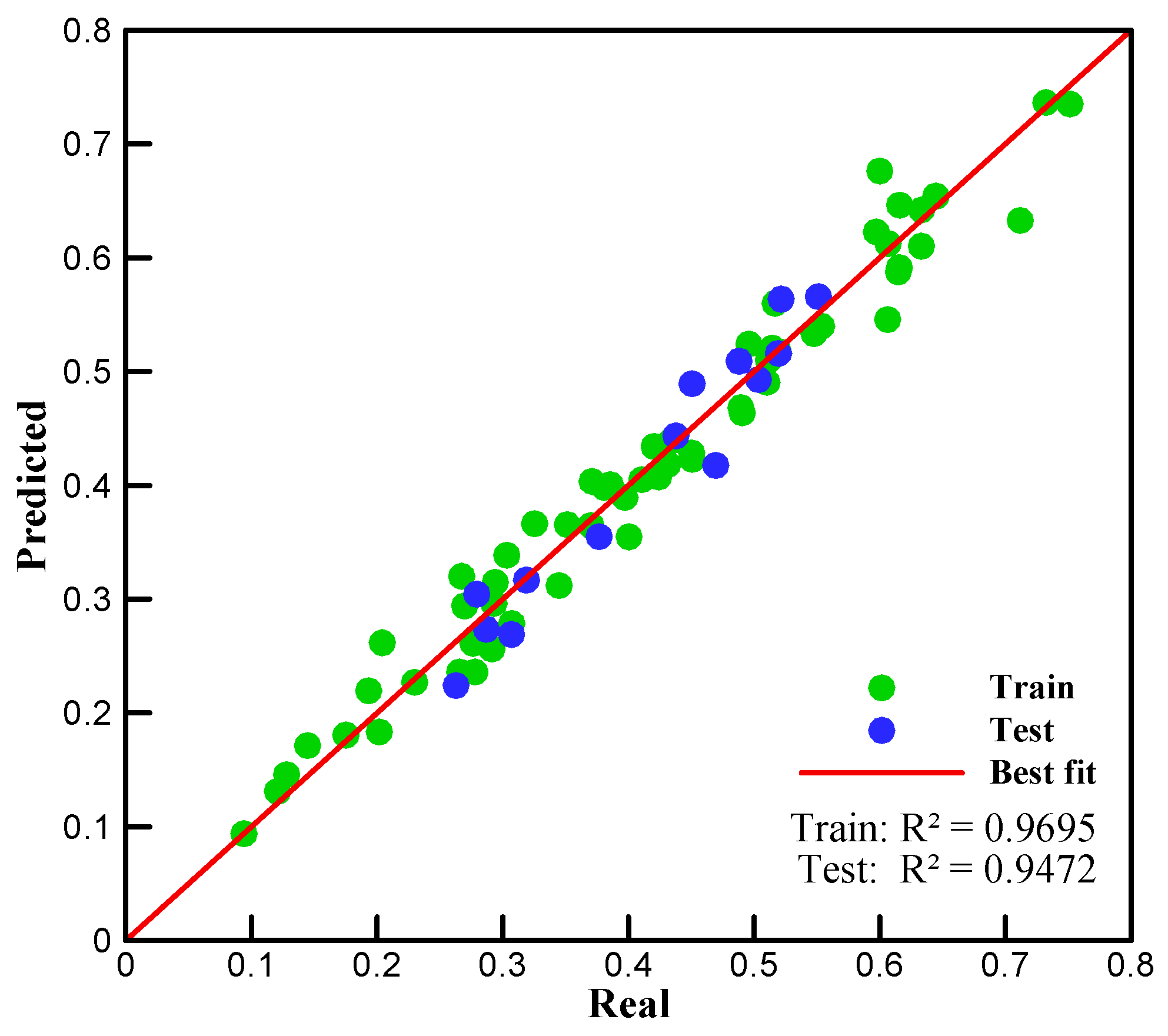

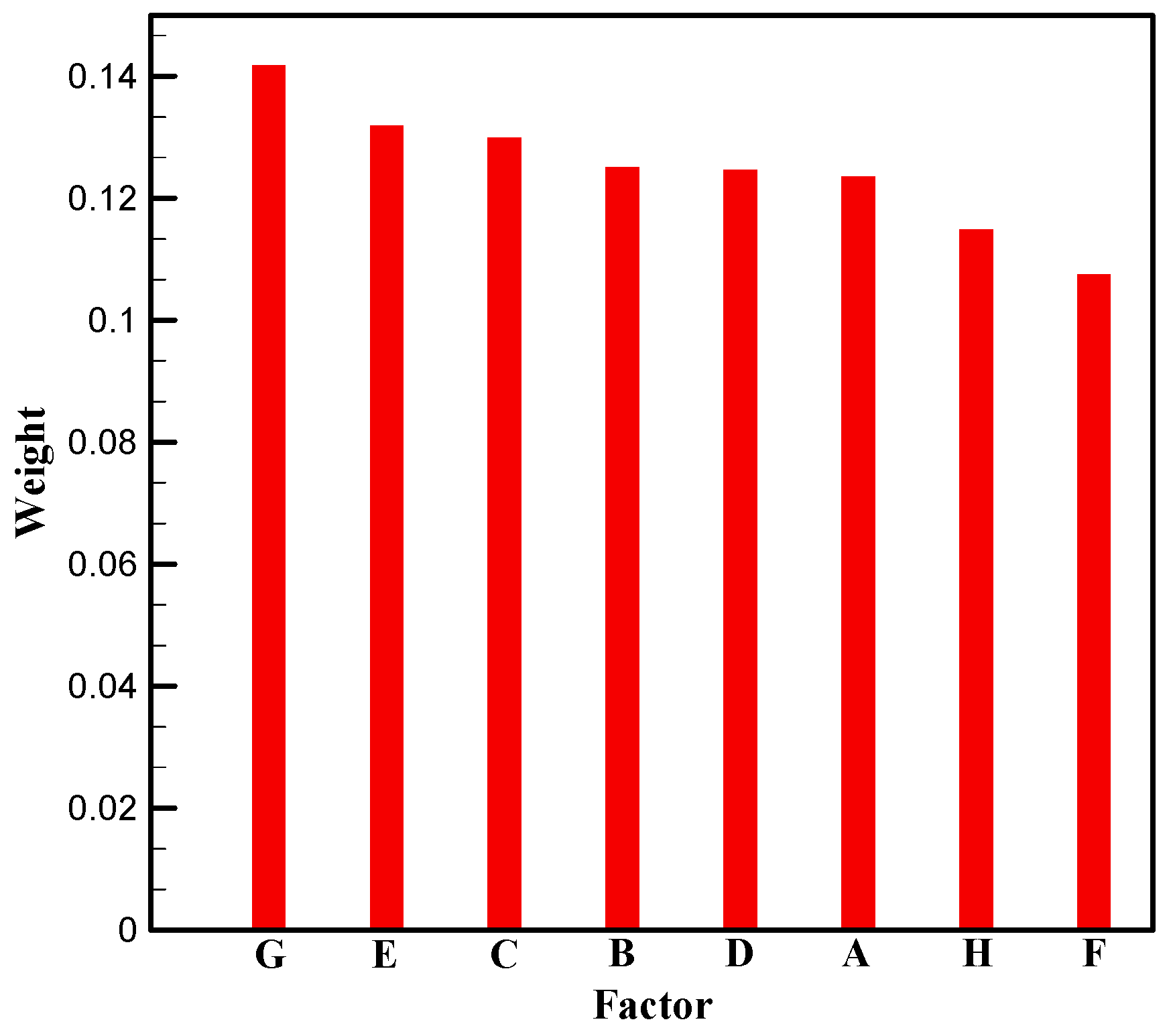
| Factor | Level (m) | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| A | 0 | 2 | 4 |
| B | 2 | 3 | 4 |
| C | 0 | 0.5 | 1 |
| D | 2.5 | 3 | 3.5 |
| E | 2 | 3 | 4 |
| F | 0 | 2 | 4 |
| G | 0.5 | 1 | 1.5 |
| H | 2.5 | 3 | 3.5 |
| Factors | ||||
|---|---|---|---|---|
| A | B | C | D | |
| U1 | 1 | 1 | 1 | 1 |
| U2 | 1 | 2 | 2 | 2 |
| U3 | 1 | 3 | 3 | 3 |
| U4 | 2 | 1 | 2 | 3 |
| U5 | 2 | 2 | 3 | 1 |
| U6 | 2 | 3 | 1 | 2 |
| U7 | 3 | 1 | 3 | 2 |
| U8 | 3 | 2 | 1 | 3 |
| U9 | 3 | 3 | 2 | 1 |
| Lower Deflector | Factors | |||
| E | F | G | H | |
| L1 | 1 | 1 | 1 | 1 |
| L2 | 1 | 2 | 2 | 2 |
| L3 | 1 | 3 | 3 | 3 |
| L4 | 2 | 1 | 2 | 3 |
| L5 | 2 | 2 | 3 | 1 |
| L6 | 2 | 3 | 1 | 2 |
| L7 | 3 | 1 | 3 | 2 |
| L8 | 3 | 2 | 1 | 3 |
| L9 | 3 | 3 | 2 | 1 |
| Experiment [32] | Simulation [12,26] | Present Study | |
|---|---|---|---|
| Wind tunnel (m) | 9.1 × 9.1 × 9.1 | _ | _ |
| Computational domain (m) | _ | 125 × 100 | 125 × 100 |
| Turbine diameter (m) | 2.5 | 2.5 | 2.5 |
| Turbine height (m) | 3 | 1 | 1 |
| Chord length (m) | 0.4 | 0.4 | 0.4 |
| Case | Difference (%) | [12] | Difference (%) | |
|---|---|---|---|---|
| U1 | 0.26 | −29.73 | 0.22 | −40.54 |
| U2 | 0.36 | −2.70 | 0.35 | −5.41 |
| U3 | 0.53 | 43.24 | 0.46 | 24.32 |
| U4 | 0.34 | −8.11 | 0.35 | −5.41 |
| U5 | 0.46 | 24.32 | 0.54 | 45.95 |
| U6 | 0.35 | −5.41 | 0.14 | −62.16 |
| U7 | 0.43 | 16.22 | 0.55 | 48.65 |
| U8 | 0.35 | −5.41 | 0.43 | 16.22 |
| U9 | 0.27 | −27.03 | 0.13 | −64.86 |
| Case | Difference (%) | |
|---|---|---|
| L1 | 0.49 | 32.43 |
| L2 | 0.58 | 56.76 |
| L3 | 0.36 | −2.70 |
| L4 | 0.57 | 54.05 |
| L5 | 0.38 | 2.70 |
| L6 | 0.41 | 10.81 |
| L7 | 0.48 | 29.73 |
| L8 | 0.45 | 21.62 |
| L9 | 0.39 | 5.41 |
| Case | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| SP1 | 2 | 3 | 3 | 3 | 2 | 1 | 2 | 3 |
| SP2 | 3 | 3 | 3 | 3 | 2 | 1 | 2 | 3 |
| SP3 | 1 | 2 | 3 | 3 | 2 | 1 | 2 | 3 |
| SP4 | 1 | 1 | 3 | 3 | 2 | 1 | 2 | 3 |
| SP5 | 1 | 3 | 3 | 2 | 2 | 1 | 2 | 3 |
| SP6 | 1 | 3 | 3 | 1 | 2 | 1 | 2 | 3 |
| SP7 | 1 | 3 | 3 | 3 | 1 | 1 | 2 | 3 |
| SP8 | 1 | 3 | 3 | 3 | 3 | 1 | 2 | 3 |
| SP9 | 1 | 3 | 3 | 3 | 2 | 2 | 2 | 3 |
| SP10 | 1 | 3 | 3 | 3 | 2 | 3 | 2 | 3 |
| SP11 | 1 | 3 | 3 | 3 | 2 | 1 | 2 | 1 |
| SP12 | 1 | 3 | 3 | 3 | 2 | 1 | 2 | 2 |
| Case | Difference (%) | Case | Difference (%) | Case | Difference (%) | Case | Differenc(%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| U1 and L1 | 0.52 | 40.54 | U2 and L2 | 0.62 | 67.57 | U3 and L3 | 0.41 | 10.81 | U4 and L4 | 0.31 | −16.22 |
| U1 and L2 | 0.45 | 21.62 | U2 and L3 | 0.37 | 0.00 | U3 and L4 | 0.63 | 70.27 | U4 and L5 | 0.29 | −21.62 |
| U1 and L3 | 0.14 | −62.16 | U2 and L4 | 0.62 | 67.57 | U3 and L5 | 0.52 | 40.54 | U4 and L6 | 0.27 | −27.03 |
| U1 and L4 | 0.16 | −56.76 | U2 and L5 | 0.26 | −29.73 | U3 and L6 | 0.29 | −21.62 | U4 and L7 | 0.38 | 2.70 |
| U1 and L5 | 0.23 | −37.84 | U2 and L6 | 0.35 | −5.41 | U3 and L7 | 0.52 | 40.54 | U4 and L8 | 0.35 | −5.41 |
| U1 and L6 | 0.12 | −67.57 | U2 and L7 | 0.20 | −45.95 | U3 and L8 | 0.52 | 40.54 | U4 and L9 | 0.13 | −64.86 |
| U1 and L7 | 0.29 | −21.62 | U2 and L8 | 0.44 | 18.92 | U3 and L9 | 0.55 | 48.65 | U5 and L1 | 0.27 | −27.03 |
| U1 and L8 | 0.55 | 48.65 | U2 and L9 | 0.18 | −51.35 | U4 and L1 | 0.55 | 48.65 | U5 and L2 | 0.50 | 35.14 |
| U1 and L9 | 0.09 | −75.68 | U3 and L1 | 0.34 | −8.11 | U4 and L2 | 0.51 | 37.84 | U5 and L3 | 0.37 | 0.00 |
| U2 and L1 | 0.49 | 32.43 | U3 and L2 | 0.56 | 51.35 | U4 and L3 | 0.27 | −27.03 | U5 and L4 | 0.49 | 32.43 |
| U5 and L5 | 0.42 | 13.51 | U7 and L1 | 0.33 | −10.81 | U8 and L6 | 0.26 | −29.73 | SP2 | 0.42 | 13.51 |
| U5 and L6 | 0.26 | −29.73 | U7 and L2 | 0.43 | 16.22 | U8 and L7 | 0.40 | 8.11 | SP3 | 0.73 | 97.30 |
| U5 and L7 | 0.49 | 32.43 | U7 and L3 | 0.39 | 5.41 | U8 and L8 | 0.54 | 45.95 | SP4 | 0.75 | 102.70 |
| U5 and L8 | 0.50 | 35.14 | U7 and L4 | 0.45 | 21.62 | U8 and L9 | 0.22 | −40.54 | SP5 | 0.60 | 62.16 |
| U5 and L9 | 0.49 | 32.43 | U7 and L5 | 0.40 | 8.11 | U9 and L1 | 0.27 | −27.03 | SP6 | 0.60 | 62.16 |
| U6 and L1 | 0.43 | 16.22 | U7 and L6 | 0.37 | 0.00 | U9 and L2 | 0.45 | 21.62 | SP7 | 0.64 | 72.97 |
| U6 and L2 | 0.47 | 27.03 | U7 and L7 | 0.41 | 10.81 | U9 and L3 | 0.33 | −10.81 | SP8 | 0.71 | 91.89 |
| U6 and L3 | 0.28 | −24.32 | U7 and L8 | 0.50 | 35.14 | U9 and L4 | 0.30 | −18.92 | SP9 | 0.62 | 67.57 |
| U6 and L4 | 0.41 | 10.81 | U7 and L9 | 0.43 | 16.22 | U9 and L5 | 0.38 | 2.70 | SP10 | 0.52 | 40.54 |
| U6 and L5 | 0.31 | −16.22 | U8 and L1 | 0.28 | −24.32 | U9 and L6 | 0.33 | −10.81 | SP11 | 0.61 | 64.86 |
| U6 and L6 | 0.37 | 0.00 | U8 and L2 | 0.43 | 16.22 | U9 and L7 | 0.30 | −18.92 | SP12 | 0.63 | 70.27 |
| U6 and L7 | 0.31 | −16.22 | U8 and L3 | 0.18 | −51.35 | U9 and L8 | 0.15 | −59.46 | |||
| U6 and L8 | 0.53 | 43.24 | U8 and L4 | 0.44 | 18.92 | U9 and L9 | 0.27 | −27.03 | |||
| U6 and L9 | 0.25 | −32.43 | U8 and L5 | 0.29 | −21.62 | SP1 | 0.50 | 35.14 |
| Case | A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|---|
| P1 | 2 | 3 | 3 | 3 | 1 | 1 | 2 | 3 | 0.48 |
| P2 | 2 | 3 | 3 | 3 | 3 | 1 | 2 | 3 | 0.55 |
| P3 | 2 | 3 | 3 | 3 | 2 | 2 | 2 | 3 | 0.51 |
| P4 | 2 | 3 | 3 | 3 | 2 | 3 | 2 | 3 | 0.51 |
| P5 | 2 | 3 | 3 | 3 | 2 | 1 | 2 | 1 | 0.43 |
| P6 | 2 | 3 | 3 | 3 | 2 | 1 | 2 | 2 | 0.50 |
| P7 | 3 | 3 | 3 | 3 | 1 | 1 | 2 | 3 | 0.28 |
| P8 | 3 | 3 | 3 | 3 | 3 | 1 | 2 | 3 | 0.48 |
| P9 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 3 | 0.43 |
| P10 | 3 | 3 | 3 | 3 | 2 | 3 | 2 | 3 | 0.45 |
| P11 | 3 | 3 | 3 | 3 | 2 | 1 | 2 | 1 | 0.29 |
| P12 | 3 | 3 | 3 | 3 | 2 | 1 | 2 | 2 | 0.35 |
| P13 | 1 | 2 | 3 | 3 | 1 | 1 | 2 | 3 | 0.73 |
| P14 | 1 | 2 | 3 | 3 | 3 | 1 | 2 | 3 | 0.66 |
| P15 | 1 | 2 | 3 | 3 | 2 | 2 | 2 | 3 | 0.68 |
| P16 | 1 | 2 | 3 | 3 | 2 | 3 | 2 | 3 | 0.60 |
| P17 | 1 | 2 | 3 | 3 | 2 | 1 | 2 | 1 | 0.54 |
| P18 | 1 | 2 | 3 | 3 | 2 | 1 | 2 | 2 | 0.68 |
| P19 | 1 | 1 | 3 | 3 | 1 | 1 | 2 | 3 | 0.69 |
| P20 | 1 | 1 | 3 | 3 | 3 | 1 | 2 | 3 | 0.66 |
| P21 | 1 | 1 | 3 | 3 | 2 | 2 | 2 | 3 | 0.68 |
| P22 | 1 | 1 | 3 | 3 | 2 | 3 | 2 | 3 | 0.57 |
| P23 | 1 | 1 | 3 | 3 | 2 | 1 | 2 | 1 | 0.52 |
| P24 | 1 | 1 | 3 | 3 | 2 | 1 | 2 | 2 | 0.64 |
| P25 | 1 | 3 | 3 | 2 | 1 | 1 | 2 | 3 | 0.70 |
| P26 | 1 | 3 | 3 | 2 | 3 | 1 | 2 | 3 | 0.63 |
| P27 | 1 | 3 | 3 | 2 | 2 | 2 | 2 | 3 | 0.61 |
| P28 | 1 | 3 | 3 | 2 | 2 | 3 | 2 | 3 | 0.55 |
| P29 | 1 | 3 | 3 | 2 | 2 | 1 | 2 | 1 | 0.46 |
| P30 | 1 | 3 | 3 | 2 | 2 | 1 | 2 | 2 | 0.61 |
| P31 | 1 | 3 | 3 | 1 | 1 | 1 | 2 | 3 | 0.66 |
| P32 | 1 | 3 | 3 | 1 | 3 | 1 | 2 | 3 | 0.55 |
| P33 | 1 | 3 | 3 | 1 | 2 | 2 | 2 | 3 | 0.56 |
| P34 | 1 | 3 | 3 | 1 | 2 | 3 | 2 | 3 | 0.47 |
| P35 | 1 | 3 | 3 | 1 | 2 | 1 | 2 | 1 | 0.34 |
| P36 | 1 | 3 | 3 | 1 | 2 | 1 | 2 | 2 | 0.50 |
| ANN | CFD | Difference (%) | |
|---|---|---|---|
| P13 | 0.73 | 0.75 | −2.67 |
| P15 | 0.68 | 0.68 | 0.00 |
| P18 | 0.68 | 0.65 | 4.62 |
| P19 | 0.69 | 0.72 | −4.17 |
| P25 | 0.70 | 0.67 | 4.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.-H.; Lam, T.T.; Chang, M.-H.; Jin, L.; Chueh, C.-C.; Augusto, G.L. Optimizing H-Darrieus Wind Turbine Performance with Double-Deflector Design. Energies 2024, 17, 503. https://doi.org/10.3390/en17020503
Chen W-H, Lam TT, Chang M-H, Jin L, Chueh C-C, Augusto GL. Optimizing H-Darrieus Wind Turbine Performance with Double-Deflector Design. Energies. 2024; 17(2):503. https://doi.org/10.3390/en17020503
Chicago/Turabian StyleChen, Wei-Hsin, Trinh Tung Lam, Min-Hsing Chang, Liwen Jin, Chih-Che Chueh, and Gerardo Lumagbas Augusto. 2024. "Optimizing H-Darrieus Wind Turbine Performance with Double-Deflector Design" Energies 17, no. 2: 503. https://doi.org/10.3390/en17020503
APA StyleChen, W.-H., Lam, T. T., Chang, M.-H., Jin, L., Chueh, C.-C., & Augusto, G. L. (2024). Optimizing H-Darrieus Wind Turbine Performance with Double-Deflector Design. Energies, 17(2), 503. https://doi.org/10.3390/en17020503








