CubeSat Mission Scheduling Method Considering Operational Reliability

Abstract

Mission scheduling is an effective method to increase the value of satellite missions and can greatly improve satellite resource management and quality of service. Based on the priority-based task scheduling model, this paper proposes a CubeSat scheduling method that takes operational reliability into account, considering the impact of scheduling results on reliable operation. In this method, the available energy and the time window are used as scheduling resources, and the average state of charge of the lithium battery and the number of task start-ups are defined as two indices to measure its reliability. To meet the mission requirements and energy availability of photovoltaic (PV) solar panel and battery constraints, the scheduling model is constructed with an objective function that includes mission priority and reliability index. The branch and bound (BB) method and analytical hierarchy process (AHP) method are used to solve the scheduling problem. The example analysis compares different scheduling results and verifies the effectiveness of the proposed scheduling method. Compared with the existing methods, it comprehensively considers the mission value and operational reliability of the CubeSat, improves the energy reserve level of the CubeSat, and reduces the surge current caused by the start-up of tasks.

1. Introduction

With the deepening of aerospace research, the demand for low-orbit space exploration missions and earth observation missions is increasing. Traditional satellites have disadvantages such as high costs and long research and development cycles. Compared with traditional satellites, CubeSats have the advantages of small size, low cost, and short development cycle and have great development potential in the aerospace field [1]. CubeSats have the basic functions of ordinary satellites, including attitude determination and control, satellite–ground communication, on-board data processing and storage, etc. [2]. Considering their short operating lifetime and limited energy-harvesting capability, it is necessary to formulate a reasonable task scheduling strategy for CubeSats.

Satellite task scheduling is when the satellite management and control department allocates time windows and on-board resources for satellite tasks and formulates satellite in-orbit operation plans to maximize the value of missions under the premise of meeting various constraints [3]. Therefore, satellite task scheduling plays an important role in improving mission value and rationally allocating on-board resources. Satellite scheduling models are mainly divided into three categories: mathematical programming models (MPMs) [4,5], graph theory models (GTMs) [6,7], and constraint satisfaction problem models (CSPMs) [8,9]. In the existing satellite mission scheduling research, the objective functions formulated include maximizing mission profit [10,11], maximizing the sum of mission priorities [12,13], maximizing data throughput [14,15], and maximizing image resolution in Earth observation (EO) missions [16].

In the research on satellite task scheduling models: Reference [17] analyzed the mission planning problem and transformed the satellite scheduling problem model into a knapsack problem model so that satellite task scheduling can be realized by solving the knapsack problem and thus the most basic mathematical model of satellite task scheduling problem is established; ref. [18] established a mission-planning model based on a general form of priority by studying the characteristics of satellite mission planning problems, without considering other indicators in the optimization direction; ref. [19] aimed at the single CubeSat mission planning problem and established a nonlinear programming model based on time window revenue without considering the constraints on the activation time and period of the satellite mission; ref. [20] studied the constraint satisfaction model for the collaborative planning of multi-satellite missions. The model can satisfy the attribute constraints of multiple satellites, extend the satellite mission scheduling model to multiple constellations, and reasonably allocate tasks according to resource attributes; ref. [21] designed a model for battery adjustment aiming at the mission planning problem of aging imaging satellites, and the satellite life was considered; ref. [22] constructed a mission-planning model for earth observation satellites that is more oriented to the scheduling of information transmission. The constraints in the model include satellite storage capacity limitations, data download rate limitations and task priorities, etc.; ref. [23] gave four criteria (value, image quality, load balance of each satellite, task number) for evaluating the scheduling results and designed a multi-objective algorithm to solve the scheduling problem of satellites, representing an improvement in the algorithm; ref. [24] constructed a scheduling model using an integer-planning approach, considered parameters such as the priority and execution time of each task, and used the input power as a constraint but did not consider the task work in the shaded area due to the lack of a battery model. Reference [25] established a mathematical model of irradiation flux on the satellite; detailed the orbit, attitude, and radiation source issues; and predicted the satellite’s life span, but the scheduling section of the battery model was also missing and the working window of the task was not considered; ref. [26] included a battery model and imposed constraints on the use of batteries, which can prolong the life of batteries, but there was no reasonable planning for the start-up sequence of tasks, and the optimization objective did not take into account factors affecting the reliable operation of satellites.

Although some literature has studied the satellite scheduling model for multi-objective optimization, the existing optimization methods do not take into account the factors that affect the reliable operation of CubeSats, and there is a lack of relevant research on satellite reliability quantification models in the direction of optimization. In this paper, reliability is defined mainly at the level of capacity standby and start-up impact, which are quantified as the state of charge and the number of start-ups, and is optimized as an objective function. In addition, considering that the initial power-up sequence of a task affects the power system operation, it is also included in the optimization of reliability. In practical applications, if the scheduling model lacks a reasonable assessment of the reliability, it will lead to an imbalance between the mission value and reliability of the CubeSat and will affect the service quality and operating life of the CubeSat.

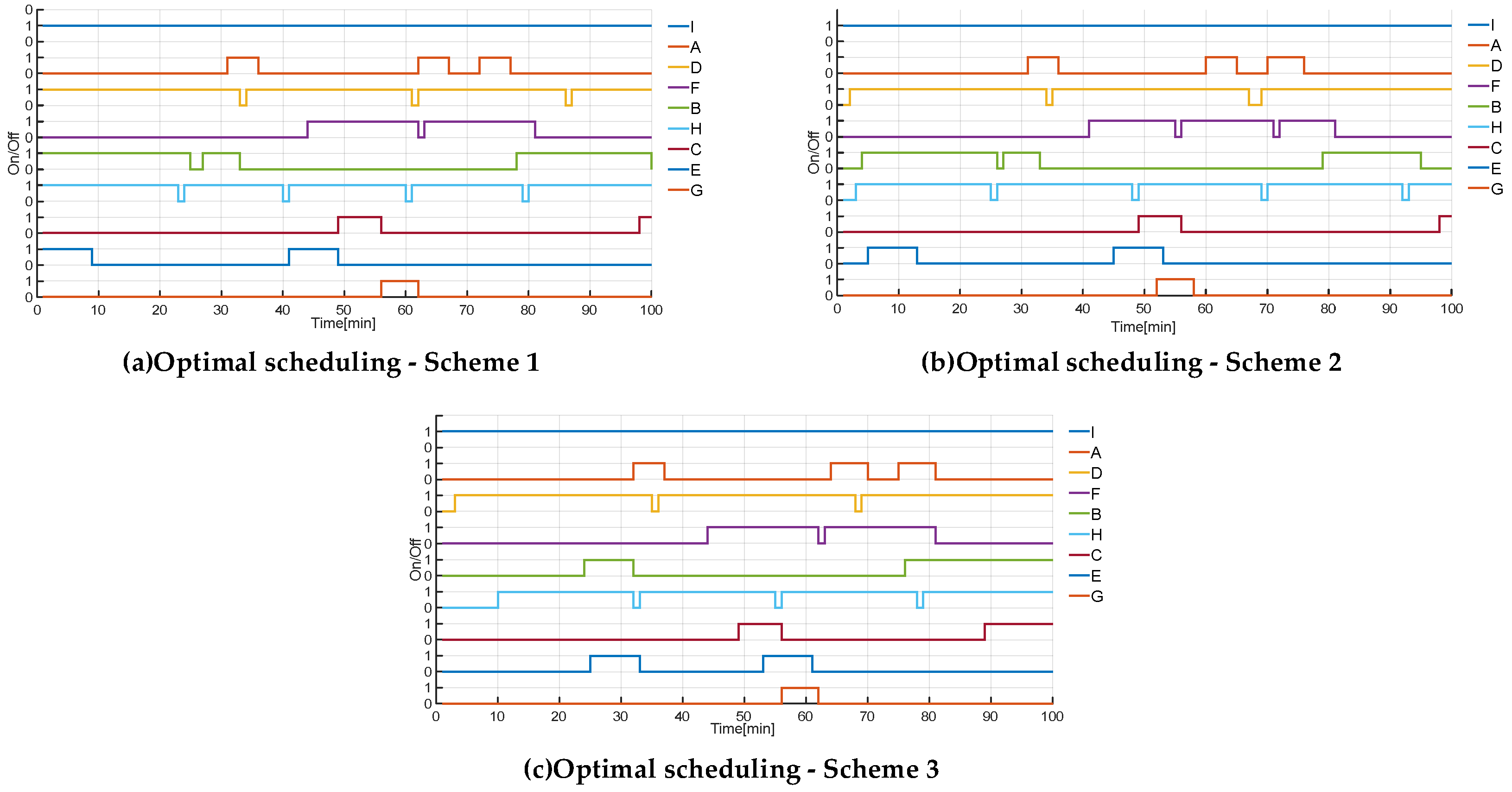
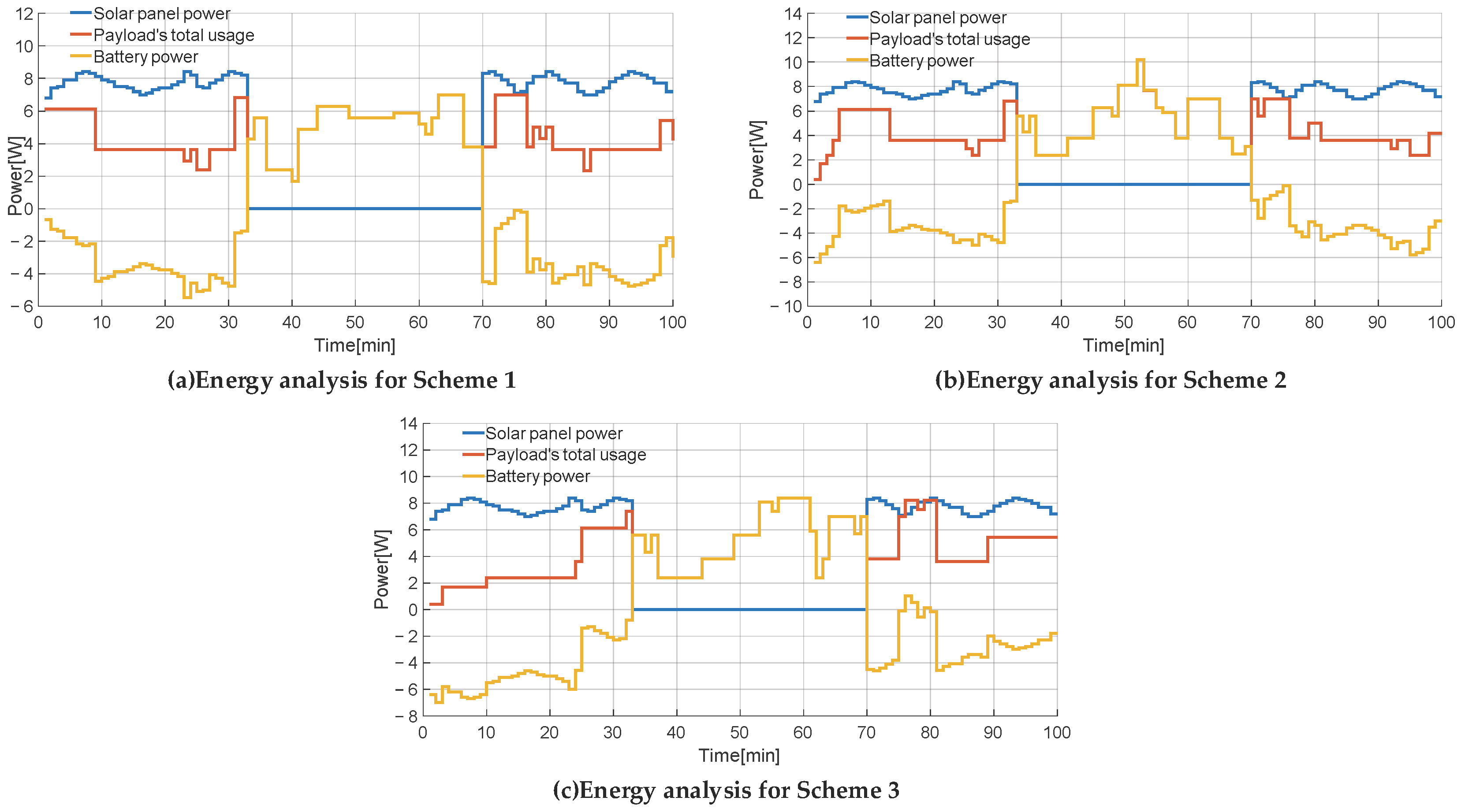
Based on [24], this paper takes the CubeSat scheduling method as the research object, establishes a mathematical model of the specific scheduling problem, designs the start-up sequence according to the influence of the CubeSat task sequence allocation on the operation results, gives the CubeSat operation a reliability quantitative index, and proposes a CubeSat scheduling method considering operational reliability. The example takes a 3U CubeSat mission as the optimization object and compares and analyzes the running results of different scheduling schemes. The results show that the CubeSat scheduling method comprehensively considers task priority and operational reliability; it can not only obtain higher mission value but also improve the level of energy storage backup and reduce the number of task start-ups under the premise of meeting task requirements, and adding step-by-step start-up to the scheduling model is more realistic.

In conclusion, the main contributions of this work include: (1) A quantitative model of CubeSat operation reliability has been established that can intuitively understand the impact of task sequence allocation in the time window on CubeSat operational reliability and provides a method for CubeSat management and control to evaluate the operational status. (2) A multi-objective optimization model that comprehensively considers the mission value and reliability is established and obtains the optimal scheduling scheme for CubeSats by solving the optimization model to realize the scheduling of the CubeSat mission. The implementation of the scheduling method can balance the mission value and reliability, improve the energy reserve level of the CubeSat, and reduce the surge current caused by simultaneous start-up of tasks. (3) A step-by-step start-up design is proposed that gives a reasonable initial start-up sequence for tasks, solving the problem of lack of step-by-step start-up design in existing scheduling methods, improving the success rate and reliability of the initial power-on of the CubeSat, and facilitating the decision-making of the satellite management and control department.

This paper is organized as follows. Section 2 describes the CubeSat scheduling problem. Section 3 presents the formula model of the CubeSat power module. Section 4 demonstrates an improvement to the existing optimization direction and establishes a CubeSat scheduling model considering reliability. Section 5 presents the comparison results of different scheduling schemes. Section 6 offers the final conclusions.

2. Problem Description

2.1. CubeSat Scheduling Problem Description

In this paper, the CubeSat task scheduling problem can be described as follows: the execution of the CubeSat task is uniformly managed by the scheduling scheme, the main task is the allocation of the CubeSat task sequence in each time period, and the optimization goal is to obtain the best scheduling method of the CubeSat task, which is the comprehensive optimization of mission value and operational reliability.

In energy scheduling, the power demand of the CubeSat mission must not exceed the maximum available energy value. At present, its power supply uses the coordination of solar panels and batteries. In the illuminated area, the PV input provides energy for the CubeSat mission while charging the lithium battery, and when the photovoltaic (PV) input power is insufficient, the PV input and lithium battery discharge provide energy for the mission; in the shadow area, only the lithium battery provides energy [27]. In this paper, we consider CubeSats operating in sun-synchronous orbits with orbital altitudes in the range of 600–800 km and orbital planes that change slightly with time [26]. In task scheduling, the formulation of the CubeSat on-orbit operation plan needs to consider the priority, number of activations, execution time, period, and execution window of each task.

2.2. Basic Assumptions

Based on the above problem description and the actual operation of CubeSat, in order to further simplify and standardize the scheduling problem, this paper makes the following assumptions and explanations for the scheduling model [28]: (1) The effect of space environmental factors (dust, particles) on the PV input power is not considered. (2) The operating state and power of the CubeSat are assumed to remain unchanged in each period; that is, the scheduling model can be discretized. (3) Assuming that the maximum power point tracking (MPPT) time is very short, the power oscillation problem near the maximum power point is not considered. (4) Parameters such as the entire orbit period of the CubeSat, the PV input power per period, the rated power consumption of each task, and the priority of the task are known quantities obtained in advance. (5) All missions, once activated, must be completed at once. (6) The CubeSat operates in the lifetime interval (within 1 year) without considering energy dissipation or additional power loss due to the aging of PV panels.

2.3. Parameter Description

To facilitate the establishment of constraints for the CubeSat scheduling problem, as shown in

Table 1. Sets and descriptions.

Constants	Definition
Sets
$\mathcal{J}$	Set of tasks to be scheduled.
$\mathcal{T}$	Set of units of time.
$\mathcal{V}$	Set of PV input power.
Indexes
$j$	Task or job index, $j\in \mathcal{J}$.
$t$	Time index, $t\in \mathcal{T}$.
$v_t$	PV input power index in period $t$, $v_t\in \mathcal{V}$.

and

Table 2. Constants and descriptions.

Constants	Definition
$J$	The number of tasks/jobs.
$T\left(\mathrm{m}\mathrm{i}\mathrm{n}\right)$	The time of the orbital cycle.
$q_j\left(\mathrm{W}\right)$	The rated power consumed by executing job $j$.
$u_j$	The priority of job $j$.
$t_j^{min}\left(\mathrm{m}\mathrm{i}\mathrm{n}\right)$	The minimum time for the job $j$ to be executed continuously.
$t_j^{max}\left(\mathrm{m}\mathrm{i}\mathrm{n}\right)$	The maximum time for the job $j$ to be executed continuously.
$y_j^{min}$	The minimum number of start-ups of job j.
$y_j^{max}$	The maximum number of start-ups of job j.
$p_j^{min}\left(\mathrm{m}\mathrm{i}\mathrm{n}\right)$	The minimum period of job $j$.
$p_j^{max}\left(\mathrm{m}\mathrm{i}\mathrm{n}\right)$	The maximum period of job $j$.
$w_j^{min}$	The start times of the available time window for the job $j$.
$w_j^{max}$	The finish times of the available time window for the job $j$.

, the sets and constants of the problem are first defined.

The decision variables and auxiliary decision variables of the scheduling model are expressed as follows:

$t$ means time $t\in \mathcal{T}$; $j$ means job $j\in \mathcal{J}$; $x_{j,t}$ is a decision variable that takes the value of 1 for each $t$ that job $j$ is executing, otherwise it assumes value 0; ${\varphi }_{j,t}$ is an auxiliary decision variable that takes the value of 1 at $t$ when job $j$ was initiated, otherwise it assumes value 0. It is used to denote the start of job $j$ at time $t$, representing this transformation of the task from not working and not consuming power to starting to work and consume power; ${\varphi }_{j,t}^{\prime }$ is an auxiliary decision variable that takes the value of 1 at $t$ when job $j$ was initiated for the first time, otherwise it assumes value 0.

3. CubeSat Power Supply Model

3.1. PV Input Power Model

The PV panels are body-mounted on the CubeSat, and the power generation by PV panels on a satellite is given by the contribution of each one of the six sides k of a standard CubeSat, as follows [25]:

$$v_t=\sum _{k=1}^6{v}_{k,t}=\sum _{k=1}^6\eta A_k{I}_{sun}{F}_{k,t\to sun}{\psi }_t$$

(1)

where $v_{k,t}$ is the PV input power of the CubeSat in the period $t$ on the side $k$; $\eta$ is the efficiency of the PV panels; $A_k$ is the layout area of the PV panels on the side $k$; $I_{sun}$ is the solar irradiance; $F_{k,t\to sun}$ is the view factor of the surface k in relation to the sun; ${\psi }_t$ is a 0–1 variable, determined by the position of the CubeSat in the period $t$, where taking 1 means it is in the illuminated area, and taking 0 means it is in the shadow area.

3.2. Lithium Battery Charge and Discharge Model

Lithium-ion batteries have become a popular choice for CubeSat energy storage sources in recent years due to their high energy density and long working life. In this paper, the battery model is added to the scheduling model, and the remaining capacity of the lithium battery is expressed as [29]:

$$E_{B,t}=E_{B,t-\Delta t}+I_{ch,t}{P}_{ch,t}\gamma \Delta t-I_{dis,t}\frac{P_{dis,t}}{\gamma }\Delta t$$

(2)

where $\gamma$ is the charging and discharging efficiency of the lithium battery; $t$ means period $t$; $E_{B,t}$ is the remaining capacity of the lithium battery; $I_{ch,t}$ is the 0–1 state variable, and when it is 1, it means that the battery is in the charging state; $I_{dis,t}$ is the 0–1 state variable, when it is 1, it means that the battery is in the discharge state; $P_{ch,t}$ is the charging power of the battery; $P_{dis,t}$ is the discharge power of the lithium battery; $\Delta t$ is the duration of each unit period.

4. CubeSat Scheduling Model

4.1. Objective Function

In this paper, the unreliability factors include three aspects: first, low energy power and insufficient energy backup, which will reduce the life of the battery and affect its performance; second, frequent payload start-ups and hidden damages that will reduce the reliability of the system equipment and increase power consumption; and third, the disordered initial start-up sequence of tasks, which will pull down the bus voltage and cause the power supply voltage to be accidentally shut down and may also potentially lead to the problem of system instability or data loss. Aiming at these unreliable factors in the operation process of the CubeSat, this paper defines the total start-up times of tasks and the average state of charge of the lithium battery as the reliability index and combines this with the task priority as a multi-objective optimization model.

• Objective function $f_1$: maximize the sum of task priorities

The value and importance of CubeSat missions are expressed by priority. For the CubeSat, the frequency and importance of communication equipment and satellite computers are higher than those of general equipment, so the priority of the antenna and CPU is higher than that of the general equipment. In addition, the attitude control equipment directly affects the satellite’s motion state, and the real-time requirement is high, so the momentum wheel has the second highest priority. The lower priority is given to scientific experiment equipment, remote sensing equipment, general loads, and so on. The mission value is positively correlated with the importance of the mission. The more high-priority tasks completed, the greater the sum of task priorities and the higher the value of the tasks that CubeSat can achieve, namely:

$$\mathit{max}{f}_1=\sum _{j=1}^J\sum _{t=1}^T{u}_j{x}_{j,t}$$

(3)

2.

Objective function $f_2$: maximize the average state of charge

To describe the reliability from the perspective of lithium battery energy backup, the energy level of batteries during the entire operating period can be expressed by the average state of charge. In the pursuit of maximizing the sum of task priorities, if the execution of tasks is not limited, the battery energy will be maximally consumed and the state of charge will be reduced to a lower level, which will reduce the battery lifetime, affect the battery’s operating performance, and reduce the reliability of the power system. The average state of charge maintains a high level, which means that the available capacity of the battery is large, the energy reserve is sufficient, and the reliability of the power system is high, namely:

$$\mathit{max}{f}_2=\sum _{t=1}^T\frac{{SOC}_t}{T}$$

(4)

3.

Objective function $f_3$: minimize the number of task start-ups

To describe reliability in terms of the impact of task activation, when the task is powered on, the capacitive components in the circuit charge quickly, resulting in a large surge current that may damage the circuit components and even affect the running instructions of other devices. Although sometimes surge current does not cause obvious damage to equipment, hidden damage can reduce the reliability of system equipment [30]. In addition, frequent start-up of tasks will consume extra time and energy, so reducing the number of task start-ups can improve the reliability of operation, namely:

$$\mathit{min}{f}_3=\sum _{j=1}^J\sum _{t=1}^T{\varphi }_{j,t}$$

(5)

Due to the inconsistency of dimensions among multiple objective functions, it is necessary to normalize each objective first and convert each objective into a dimensionless value in the range of [0, 1]. For the normalized objective function, the linear weighting method is used to convert it into a single objective function. The objective function is as follows:

$$\mathit{max}F=\sum _{i=1}^3{\lambda }_i{f}_i^{\prime }={\lambda }_1\frac{f_1-f_{1,min}}{f_{1,max}-f_{1,min}}+{\lambda }_2\frac{f_2-f_{2,min}}{f_{2,max}-f_{2,min}}+{\lambda }_3\frac{f_{3,max}-f_3}{f_{3,max}-f_{3,min}}$$

(6)

where ${\lambda }_i$ represents the weights of the corresponding sub-objective functions and $\sum _{i=1}^3{\lambda }_i=1$; $f_i^{\prime }$ is the normalized result of $f_i$, and $0\le f_i^{\prime }\le 1$; $f_{i,min}$, represents the minimum values of $f_i$; $f_{i,max}$ represents the maximum values of $f_i$.

The selection of ${\lambda }_i$ will have an impact on the final scheduling result. The larger value of ${\lambda }_1$ is to improve the task value as the main purpose. The larger values of ${\lambda }_2$ and ${\lambda }_3$ are to improve operational reliability. The distribution of weight coefficients reflects the degree of emphasis on different objectives.

4.2. Selection of Weight Coefficients by Analytical Hierarchy Process (AHP)

The existing methods for determining weight mainly include principal component analysis, AHP, fuzzy AHP, the risk preference coefficient method, etc. [31]. Considering that the hierarchical structure relationship in the AHP can make a rational judgment on the correlation between each sub-objective and there are few evaluation indicators in this example, the AHP is used to select the weight coefficient. The specific process is as follows:

(1)

Determine the index system: according to the components of the objective function, the criterion layer consists of three parts: the sum of task priorities, the average state of charge, and the total number of task start-ups.

(2)

Build a judgment matrix: The judgment matrix is composed of elements $a_{ij}$, and the weight of the criterion layer to the target layer is determined through the comparison between each element. The element $a_{ij}$ is given by the 1–9 scale method, as shown in

Table 3. The Saaty Rating Scale [32].

Scaling	Meaning	Explanation
1	The former and the latter have the same importance	Two activities contribute equally to the objective
3	The former is slightly more important than the latter	Experience and judgment slightly favor one activity over another
5	The former is obviously more important than the latter	Experience and judgment strongly favor one activity over another
7	The former is strongly more important than the latter	An activity is strongly favored and its dominance demonstrated in practice
9	The former is extremely more important than the latter	The evidence favoring one activity over another is of the highest possible order of affirmation
2,4,6,8	Intermediate values between the two adjacent judgments	When compromise is needed

. On the Saaty Rating Scale, the decision maker needs to assign a weight value to each attribute, indicating the importance of that attribute relative to other attributes.

Considering that both $f_2$ and $f_3$ are indicators to describe the operational reliability of the CubeSat, setting both of them is of equal importance [33]. After consulting with experts in standardization management, we wrote the results of the experts’ comparative judgments as the judgment matrix $A=\left[\begin{array}{ccc}1& a_{12}& a_{13}\\ a_{21}& 1& 1\\ a_{31}& 1& 1\end{array}\right]$ by introducing a suitable scale expressed numerically through the Saaty Rating Scale.

(3)

Calculate the weight vector: calculate the element product $M_i={\prod }_{j=1}^n{a}_{ij}(i=\mathrm{1,2},\dots ,n)$ of each row of the judgment matrix A, calculate the n-th root $\overline{W_i}=\sqrt[n]{M_i}$ of $M_i$, and finally, normalize $W_i=\overline{W_i}/\sum _{i=1}^n\overline{W_i}$.

(4)

Consistency check: Consistency index $CI=\frac{{\lambda }_{max}-n}{n-1}$, stochastic consistency indicator $RI=\frac{\sum _{i=1}^n{CI}_i}{n}$, consistency ratio: $CR=\frac{CI}{RI}$. When $CR<0.1$, it means that $A$ has a satisfactory consistency and can be normalized. Selection of the final weight coefficient ${\lambda }_1=0.5$,${ \lambda }_2={\lambda }_3=0.25$, and the calculation results are shown in

Table 4. Calculation results of weight coefficients.

Scaling			Consistency Check	${\mathit{\lambda }}_1$	${\mathit{\lambda }}_2$	${\mathit{\lambda }}_3$
${\mathit{a}}_{12}$	${\mathit{a}}_{13}$	${\mathit{a}}_{23}$
2	2	1	${\lambda }_{max}=2$ $CI=0$ $CR=0$	0.5	0.25	0.25

.

4.3. Restrictions

4.3.1. Task Execution Constraints

During an orbital cycle of CubeSat operation in orbit, all tasks are subject to work window constraints, execution count constraints, work time constraints, and work cycle constraints.

$$\sum _{t=1}^{w_j^{min}-1}{x}_{j,t}=0,\forall j$$

(7)

$$\sum _{t=w_j^{max}+1}^T{x}_{j,t}=0,\forall j$$

(8)

Constraint (7) means that in each period before $w_j^{min}$, the task will not be executed; constraint (8) states that during each period from $w_j^{max}+1$ to the end of the orbit, the task will not be executed.

$$y_j^{min}\le \sum _{t=w_j^{min}}^{w_j^{max}}{\varphi }_{j,t}\le y_j^{max},\forall j$$

(9)

Constraint (9) means that for each orbit, all tasks of the CubeSat should be between the minimum activation times and maximum activation times.

$$\sum _{l=t}^{t+t_j^{min}-1}{x}_{j,l}\ge t_j^{min}{\varphi }_{j,t},\forall t\in \left\{1,\dots ,T-t_j^{min}+1\right\},\forall j$$

(10)

$$\sum _{l=t}^{t+t_j^{max}}{x}_{j,l}\le t_j^{max},\forall t\in \left\{1,\dots ,T-t_j^{max}\right\},\forall j$$

(11)

$$\sum _{l=t}^T{x}_{j,l}\ge \left(T-l+1\right){\varphi }_{j,t},\forall t\in \left\{T-t_j^{min}+2,\dots ,T\right\},\forall j$$

(12)

Constraint (10) means that each time the task is started, the continuous execution time is greater than $t_j^{min}$; constraint (11) means that in any time window of size $t_j^{max}$, the continuous execution time of the task is less than $t_j^{max}$; and constraint (12) is used to constrain the task started after $T-t_j^{min}+1$. If it is started, it will be executed until the end of the orbit to ensure that the minimum execution time constraint is met.

$$\sum _{l=t}^{t+p_j^{min}-1}\left(1-{\varphi }_{j,l}\right)\ge p_j^{min}-1,\forall t\in \left\{1,\dots ,T-p_j^{min}+1\right\},\forall j$$

(13)

$$\sum _{l=t}^{t+p_j^{max}-1}\left(1-{\varphi }_{j,l}\right)\le p_j^{max}-1,\forall t\in \left\{1,\dots ,T-p_j^{max}+1\right\},\forall j$$

(14)

Constraint (13) states that in any time window of size $p_j^{min}$, the task will not be activated more than once; constraint (14) means that in any time window of size $p_j^{max}$, the task is activated at least once.

4.3.2. Energy Availability Constraints

During any period of CubeSat operation, the power balance constraints, battery energy constraints, and battery charging and discharging power constraints are satisfied.

$$\sum _{j=1}^J{q}_j{x}_{j,t}=v_t+P_{dis,t}-P_{ch,t}$$

(15)

Equation (15) is used to construct the power balance constraint. Among the variables, $P_{ch,t}$ and $P_{dis,t}$ represent the charging power and the discharge power of the battery, respectively.

$${SOC}_{min}\le {SOC}_t\le {SOC}_{max}$$

(16)

$${SOC}_1\times \left(1-0.01\right)\le {SOC}_T\le {SOC}_1\times \left(1+0.01\right)$$

(17)

Equation (16) serves to avoid overcharging and over-discharging of the battery [34], where ${SOC}_t$ is the state of charge of the battery, and ${SOC}_{min}$ and ${SOC}_{max}$ are the lower limit and the upper limit of the battery state of charge, respectively.

Considering the continuity of the orbital period of the CubeSat, for its long-term stable operation, Equation (17) ensures that the fluctuation of the state of charge of the battery should not exceed 1% at the beginning and end of each orbital scheduling period.

$$0\le P_{ch,t}\le P_{ch,max}{I}_{ch,t}$$

(18)

$$0\le P_{dis,t}\le P_{dis,max}{I}_{dis,t}$$

(19)

$$0\le I_{ch,t}+I_{dis,t}\le 1$$

(20)

Equations (18) to (20) are used to construct the charge and discharge power constraints of lithium batteries. Among the variables, $P_{ch,max}$ is the upper limit of battery charging power and $P_{dis,max}$ is the upper limit of battery discharge power.

4.3.3. Power-On Constraints

In order to rationalize the initial start-up problem of tasks, all tasks must satisfy the step-by-step start-up constraints and the start-up sequence constraints.

$${\varphi }_{j,t}\ge {\varphi }_{j,t}^{\prime }$$

(21)

$$\sum _{t=1}^T{\varphi }_{j,t}^{\prime }=1,\forall j$$

(22)

$$\sum _{l=1}^t{\varphi }_{j,l}^{\prime }=\left\{\begin{array}{c}1,\\ 0,\end{array}\right.\genfrac{}{}{0pt}{}{if\sum _{l=1}^t{\varphi }_{j,l}\ge 1,\forall t\in \left\{1\dots T\right\}}{ if\sum _{l=1}^t{\varphi }_{j,l}\le 0,\forall t\in \left\{1\dots T\right\}}$$

(23)

Constraints (21) to (23) establish an auxiliary decision variable ${\varphi }_{j,t}^{\prime }$ that ensures that the auxiliary decision variable ${\varphi }_{j,t}^{\prime }$ can detect the first start of job $j$. ${\varphi }_{j,t}^{\prime }$ takes the value of 1 only when job $j$ is first started and is 0 for the rest of the time.

$$\sum _{j=1}^J{\varphi }_{j,t}^{\prime }\le 1,\forall t$$

(24)

Constraint (24) is aimed at the initial start-up of the CubeSat and is used to constrain the initial start-up timing of tasks so as to avoid the situation that multiple high-priority tasks are powered on at the same time.

$$\sum _{l=1}^t{\varphi }_{j_1,l}^{\prime }\le \sum _{l=1}^t{\varphi }_{j_2,l}^{\prime },t\in \left\{1\dots T\right\} if u_{j_1}\le u_{j_2}$$

(25)

Constraint (25) is used to constrain the start-up sequence between multiple tasks. The start-up sequence is in the order of task priority; tasks with higher priority are started first, and tasks with lower priority are started later. No timing constraints are imposed on tasks with time window restrictions.

4.4. Solution by the Branch and Bound (BB) Method

The CubeSat task scheduling model in this paper is a mixed integer programming (MIP) model, and its standard form is as follows:

$$\left\{\begin{array}{c}\mathit{max}{c}^{T}x+h^{T}y+k^{T}z\\ s.t. A_{i}x+B_{i}y+C_{i}z\le b,\forall i\in \{\mathrm{1,2},\dots ,m\}\\ x\in \left\{\mathrm{0,1}\right\}\\ y,z\in R\end{array}\right.$$

(26)

where $\mathit{max}{c}^{T}x+h^{T}y+k^{T}z$ is the objective function; $x$ is the decision variable, which only takes 0 or 1; $A_{i}x+B_{i}y+C_{i}z\le b$ is the constraint; and $m$ is the number of constraints.

This kind of problem can be solved by the BB method, cut plane method, implicit enumeration method, etc. Considering the small scale of the model, the BB method is used to obtain the global optimal solution, which can obtain its relaxed problem by relaxing the constraints of the integer programming problem. If the optimal solution to the relaxed problem guarantees that each variable is an integer, then the original problem is solved. If the value of the variable in the optimal solution of the relaxed problem is not an integer, further “branching” and “bounding” operations are required. In this paper, the BB method is used to solve the CubeSat scheduling problem [35], and the optimal scheduling scheme of the task is obtained to realize the scheduling of the CubeSat task. The BB method in this paper is the same as the method described in [35], and the flowchart is shown in Figure 1.

As shown in Figure 1, the CubeSat scheduling model in this paper can be solved by the BB method. First, relax the constraints on $x_{j,t}$, ${\varphi }_{j,t}$, and ${\varphi }_{j,t}^{\prime }$ to solve the linear programming problem and obtain the optimal solution. If the optimal solution is a 0–1 integer and “branching” is completed, then we obtain the final result; otherwise, continue to carry out the “branching” operation until the optimal solution meets the constraints.

Compared with intelligent algorithms, this algorithm has higher solving accuracy and better ability to solve real-time problems, but when the scale of operation is large, the algorithm’s solving efficiency is relatively low.

5. Case Study

5.1. Parameter Setting

In order to verify the feasibility and effectiveness of the CubeSat optimal scheduling method proposed in this paper, 3U CubeSat mission data is used for simulation. Nine tasks participate in the scheduling allocation, named A to I respectively, and all tasks are not in the working state before the scheduling starts. Here, an orbital period is set to be 100 min, where $T=100 \mathrm{m}\mathrm{i}\mathrm{n}$. In order to simplify the scheduling model and scheduling method, an orbital period is divided into 100 time periods, which are divided in minutes, where $∆t=1 \mathrm{m}\mathrm{i}\mathrm{n}$. The input power of the solar panel is calculated minute by minute, among which 33–69 min is the shaded area, and the PV input is 0. Light and eclipse times vary from year to year, so the orbital parameters here apply only to a given orbit and are not universal. In this example, set the CubeSat mission parameters as shown in

Table 5. 3U CubeSat payload parameters.

Payload	$\mathit{j}$	${\mathit{u}}_{\mathit{j}}$	${\mathit{q}}_{\mathit{j}}\left(\mathbf{W}\right)$	${\mathit{y}}_{\mathit{j}}^{\mathit{m}\mathit{i}\mathit{n}}$	${\mathit{y}}_{\mathit{j}}^{\mathit{m}\mathit{a}\mathit{x}}$	${\mathit{t}}_{\mathit{j}}^{\mathit{m}\mathit{i}\mathit{n}}$ $\left(\mathbf{min}\right)$	${\mathit{t}}_{\mathit{j}}^{\mathit{m}\mathit{a}\mathit{x}}$ $\left(\mathbf{min}\right)$	${\mathit{p}}_{\mathit{j}}^{\mathit{m}\mathit{i}\mathit{n}}$ $\left(\mathbf{min}\right)$	${\mathit{p}}_{\mathit{j}}^{\mathit{m}\mathit{a}\mathit{x}}$ $\left(\mathbf{min}\right)$	${\mathit{w}}_{\mathit{j}}^{\mathit{m}\mathit{i}\mathit{n}}$	${\mathit{w}}_{\mathit{j}}^{\mathit{m}\mathit{a}\mathit{x}}$
A	1	5	3.2	2	3	5	6	8	32	31	80
B	2	2	1.23	2	4	6	25	18	52	1	T
C	3	1	1.8	2	6	7	20	15	49	1	T
D	4	4	1.3	3	7	4	32	25	59	1	T
E	5	1	2.5	2	5	8	35	28	62	1	60
F	6	3	1.4	2	6	3	18	15	49	41	80
G	7	1	2.1	1	7	6	30	22	56	1	T
H	8	2	0.7	1	8	7	22	15	49	1	T
I	9	6	0.4	1	1	T	T	T	T	1	T

[26]; the parameters of the battery are shown in

Table 6. Battery parameters.

Type	${\mathit{S}\mathit{O}\mathit{C}}_1$	${\mathit{S}\mathit{O}\mathit{C}}_{\mathit{m}\mathit{a}\mathit{x}}$	${\mathit{S}\mathit{O}\mathit{C}}_{\mathit{m}\mathit{i}\mathit{n}}$	$\mathit{\gamma }$	Nominal Voltage (V)	Nominal Capacity (mA·h)	Number
Lithium Battery	0.75	1.0	0.5	0.9	3.7	2500	5

, and the parameters of the orbit are shown in

Table 7. Orbital elements.

Parameters	Value
Apogee Height [km]	779
Perigee Height [km]	766
Inclination [Degrees]	98.379
Right Ascension of the Ascending Node [Degrees]	199.268
Eccentricity	0.000934
Argument of Perigee [Degrees]	24.776
Mean Anomaly [Degrees]	335.386
Mean Motion [Revs per Day]	14.358

[24,25].

In this example, tasks A to H represent the mission payload, and task I represents all the core modules of the CubeSat; this part has the highest priority. Here, it is set that task I is always in execution state and consumes 400 mW of power [26]. Payload A is an image sensor module that must take a small number of images when passing through a specific area of the Earth and has a specific time window.

5.2. Optimization Result Analysis

Applying the previously established scheduling framework, on the basis of meeting mission requirements and maintaining battery life, we must determine when the payload of the 3U CubeSat can be activated and obtain the optimal scheduling scheme for the CubeSat on a minute-by-minute basis. In order to verify the effectiveness of the scheduling method, for the following three different scheduling schemes, the MIP model is solved by the BB method, and the CubeSat power situation, task scheduling results, and start-up design results are compared and analyzed. The scheduling results are shown in Figure 2, and the energy analysis is shown in Figure 3. Table 8 and Table 9 give the comparison of the running results.

Scheme 1: CubeSat scheduling model based on task priority without step-by-step start-up design.

Scheme 2: CubeSat scheduling model based on task priority including step-by-step start-up design.

Scheme 3: CubeSat scheduling model considering operational reliability and step-by-step start-up design.

Figure 2. Scheduling results for a 3U CubeSat.

Figure 2. Scheduling results for a 3U CubeSat.

Figure 3. Energy analysis for a 3U CubeSat.

Figure 3. Energy analysis for a 3U CubeSat.

Table 8. Scheduling results of payload start-up in Schemes 1 to 3.

Scheme	Whether to Start at the Same Time	Start-Up Sequence
1	Payloads B, D, E, H and I start simultaneously	Disorderly start
2	No	The payload start-up sequence is I-D-H-B-E-C-G
3	No	The payload start-up sequence is I-D-H-B-E-C-G

Table 8. Scheduling results of payload start-up in Schemes 1 to 3.

Scheme	Whether to Start at the Same Time	Start-Up Sequence
1	Payloads B, D, E, H and I start simultaneously	Disorderly start
2	No	The payload start-up sequence is I-D-H-B-E-C-G
3	No	The payload start-up sequence is I-D-H-B-E-C-G

Table 9. Task priority and reliability indicators of Schemes 2 and 3.

Scheme	The Sum of Task Priorities	Average State of Charge	The Total Number of Tasks Starts
2	1486	0.7456	23
3	1460	0.7564	20

Table 9. Task priority and reliability indicators of Schemes 2 and 3.

Scheme	The Sum of Task Priorities	Average State of Charge	The Total Number of Tasks Starts
2	1486	0.7456	23
3	1460	0.7564	20

The specific scheduling results of the three schemes are shown in Figure 2. Since task I is a core module with the highest priority, it is eligible to be invoked preferentially during the entire scheduling time and will work continuously without interruption throughout the entire time period. Payload A will be constrained by the time window and will only be executed within its time window (31–80 min). The same is true for payloads E and F. The time distribution of the rest of the payloads also follows the task execution constraints mentioned in Section 4.3.1 above.

From the comparison results in Table 8, it can be seen that the initial start of the task of Scheme 1 is not subject to any constraints, and multiple payloads start at the same time during $t=1 \mathrm{m}\mathrm{i}\mathrm{n}$, which may generate a large surge current and lower the bus voltage. Moreover, the start-up sequence of the payload does not follow certain rules and is in a disorderly start-up mode. “Disorder” includes two situations: on the one hand, multiple payloads are started at the same time when powered on, which will lead to a large impulse current at the start of the instant, affecting the service life of electronic equipment, reducing the reliability of key components, and even pulling down the bus voltage, resulting in unexpected power shutdown; on the other hand, the power-on sequence of multiple payloads is chaotic and does not follow the priority relationship. Some devices may start to work before initialization, resulting in system instability or data loss. Therefore, it is necessary to plan the start-up priorities properly and first power on payloads with higher start-up priorities. Under this scheduling scheme, the start-up process of the CubeSat may fail or enter a permanent power-off state, so it is not advisable. Scheme 2 realizes the step-by-step start-up design through optimized scheduling, avoids the simultaneous start-up of multiple payloads, and improves the reliability and success rate of the CubeSat start-up. Except payloads A and F, which have specific time windows, the initial start-up of other tasks follows the order of priority.

The energy scheduling results are shown in Figure 3. The CubeSat is in the light area during 1–32 min and 70–100 min. At this time, the PV input provides energy for the CubeSat load mission and charges the battery at the same time; however, CubeSats orbit in space in sun-synchronous orbits around the Earth. When the CubeSat orbits to the back of the Earth, the Earth will block the sun’s rays, and the CubeSat is in the shadow zone. The PV panels have no power output, and the input power is not enough to provide energy for the mission during certain periods (e.g., 76–77 min). At this time, the lithium battery and PV input together provide energy for the mission. The CubeSat is in the shadow area at 33–69 min, and the PV input power is 0. At this time, the battery alone is used to provide energy for the payload.

It can be seen from the comparison results in Table 9 that Scheme 2 only considers the maximization of task value. Under this scheduling scheme, the relevant reliability index values are all low, and the average state of charge is lower than 75%. Scheme 3 comprehensively considers task value and reliability. The state of charge of the battery is relatively high throughout the cycle and is 1.45% higher than that of Scheme 2, indicating that the energy storage level of the battery is relatively high under this scheduling scheme. There can be more energy backup to undertake the power supply of the rest of the satellite or to deal with emergencies, so the reliability of the CubeSat power distribution system is higher. In Scheme 2, all payloads are started 23 times in one orbital period, and in Scheme 3 after optimization, all payloads are started 20 times in one orbital period, which effectively reduces the number of switching operations and possible surge currents, saves the extra time and energy consumed by frequent start-up, and improves the stability and reliability of the system.

Overall, Scheme 1 without considering the task start-up problem and does not meet the normal operation requirements of the CubeSat mission, so this scheduling scheme is not considered, and its energy profile does not need to be analyzed. Scheme 2 with improvements in the task start-up problem can meet the requirements of normal operation. Scheme 2 uses the task priority as an optimization objective and obtains the highest mission value, but the battery energy presents a low level, and the payload starts frequently, which affects the system reliability. Scheme 3 with the improvement in the mission start-up problem is the same as Scheme 2, but the reliability-related indexes are taken into account in the optimization direction, and the battery energy level is improved, so the optimization result is conducive to the safe and reliable operation of the CubeSat.

6. Conclusions

In conclusion, based on the traditional task priority scheduling model, this paper improves the state-of-the-art scheduling of CubeSats by adding a step-by-step start-up design, analyzing and proposing indicators related to the reliability of CubeSats, and establishing an optimization model considering task value and reliability comprehensively.

The scheduling results show that the CubeSat scheduling method based on task priority can obtain the highest sum of task priorities and achieve the highest task value, but it lacks a reasonable evaluation of the CubeSat’s operating status and reliability and cannot achieve comprehensive optimization. The optimal CubeSat scheduling method considering operational reliability has certain optimization effects in terms of start-up reliability, state of charge, and task start-up times. From the results, the scheduling method improves the CubeSat energy backup level, reduces the surge current caused by mission start-up, makes reasonable arrangements for the mission start-up timing, and optimizes both the energy backup and start-up impact levels. Therefore, it can reduce the unreliable factors that may occur during operation and better optimize the operation of the CubeSat.

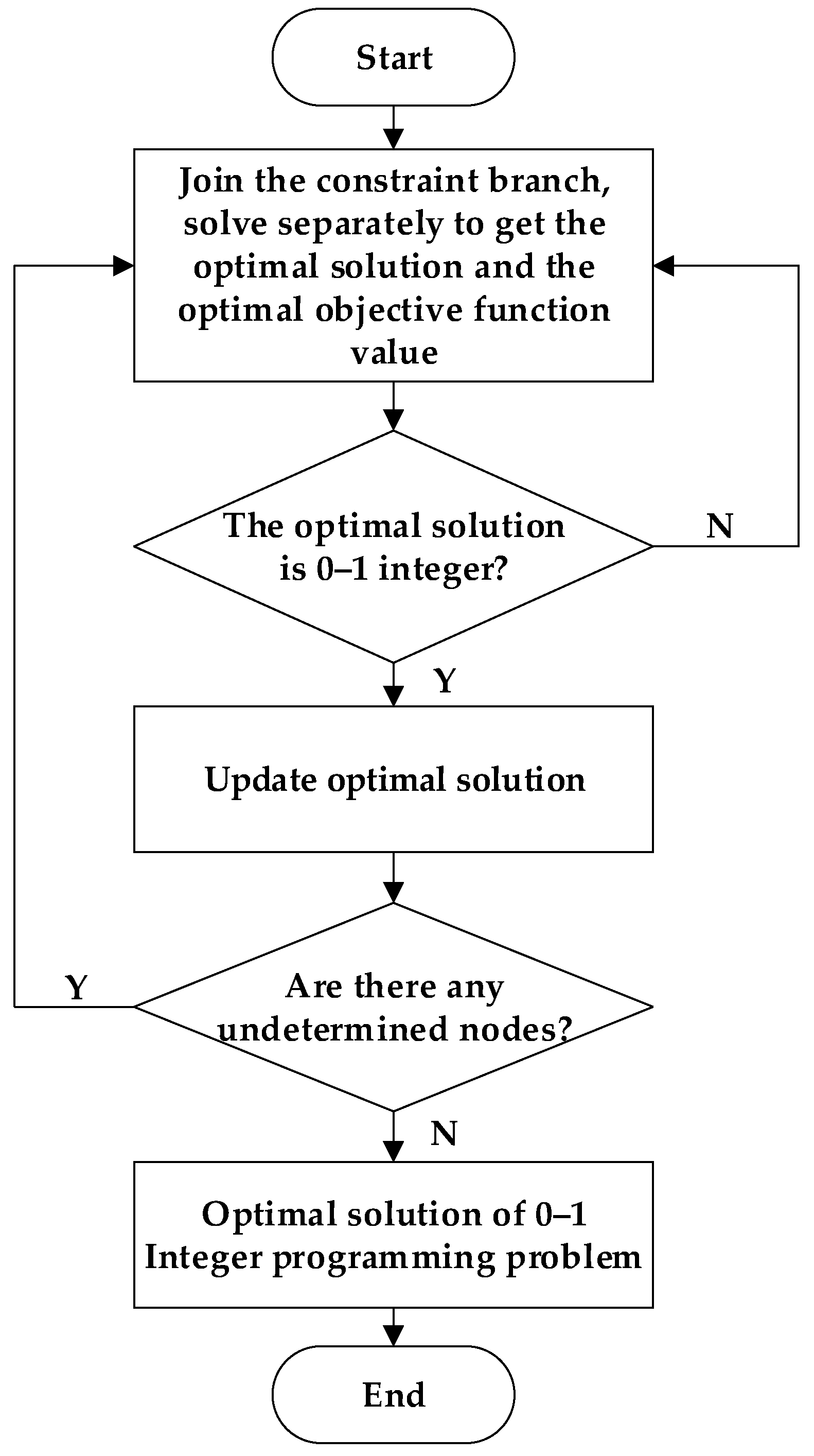
Now, the research in this paper still has some limitations, which are reflected in the following aspects. First, the scheduling model is now solved by the BB method, and when the scale of the solved model is too large, there will be a long solving time and difficulties in solving. Second, this paper uses the AHP in the process of selecting the weight coefficients, which is not a novel method and has a certain degree of subjectivity. This can be improved in the future by considering the use of more novel methods. In future research, we can further improve this scheduling model from two aspects. First, we can obtain a more refined CubeSat scheduling plan and optimize the CubeSat missions second by second, so this also puts forward higher requirements for the prediction accuracy of PV power; second, the data transmission problem between the CubeSat and the ground station can be added to the scheduling model, and the memory capacity of the CubeSat can be used as the allocation resource and constraint condition so as to schedule the information resources of the CubeSat better.