Abstract
The extension of intuitionistic fuzzy sets (IFS) to Pythagorean fuzzy sets (PFS) is a significant advancement, addressing the inherent limitations of IFS. This study introduces a novel entropy measure specifically designed for Pythagorean fuzzy sets, establishing its axiomatic definition and presenting key properties. Decision making guided by entropy is advantageous, as it effectively mitigates ambiguity with increasing entropy values. Furthermore, a numerical example is provided to facilitate a comparative assessment of our newly introduced entropy measure in contrast to existing PFS entropy measures. The validation of our findings is achieved through the application of the COPRAS method, which determines decision outcomes based on a multitude of influencing factors. Notably, the determination of weights in this method is underpinned by the utilization of our innovative entropy measure.
1. Introduction
In life, difficult and complex decision-making problems often arise, which in some cases are crucial and can significantly affect the subsequent course of events. In order to effectively deal with multicriteria decision-making problems, the field of multicriteria decision making (MCDM) is used. These techniques are often used in many areas of everyday life as well as in professional applications.
The application of these techniques has been demonstrated in a number of research studies that have considered problems in areas such as objective selection of personnel [1], supplier selection [2], selection of aircraft passage [3], innovation in the health sector regarding personnel selection [4] or evaluation in this sector [5], choice of factory location [6], evaluation of hydrogen energy storage methods [7], creation of a decision model for the development of offshore wind farms [8] or a sustainable approach to wastewater treatment technology selection [9].
There are many important problems, the solutions of which can significantly affect people’s lives or the functioning of the state. One such area is energy, which, with the advancement of civilization and technology, is attracting increasing interest. The constant drive for development results in an increased demand for electricity, the storage of which is a process fraught with inevitable loss. That is why it is important to produce energy on an ongoing basis in a sustainable manner [10]. Multicriteria decision making is often applied in the selection of different sustainable energy sources [11,12]. One interesting type of power plant is the hydropower plant, which uses a natural source to generate energy. However, it is not only the type of power plant that deserves attention, but also the choice of where its site will be located. The appropriate location of the power plant is very important, as it can affect the environment and the public sentiment, as well as carry certain risks and increased operating costs.
Given the widespread use of multicriteria decision-making methods, it can be expected that as the complexity of the decision-making problems being solved increases, there is a need for new approaches that can more accurately represent the preferences of the decision maker [13], or solve the problem by approaching its evaluation objectively. Classical approaches tend to operate on crisp values that do not allow much freedom in regard to defining the decision variants that will be considered in the problem to be solved. However, when there is uncertainty in the decision problem under consideration, a solution by the classical approach is not always possible. To this end, fuzzy sets (FS) were introduced by Zadeh [14] so that decision makers can include uncertainty through the use of a membership function and express its degree of membership and non-membership. A number of examples using fuzzy approaches to solve multicriteria problems have been developed, such as the use of fuzzy technique for order of preference by similarity to ideal solution (TOPSIS) prioritization of patients on elective surgery waiting lists, presented by Rana et al. [15].
Due to their usefulness, fuzzy sets are widely used in multicriteria decision making [5,16]. In addition, many methods for multicriteria decision making have been extended for use in a fuzzy environment. Considering the solutions presented in the last few years, we can see the development of the method resistant to the rank reversal paradox, stable preference ordering towards ideal solution (SPOTIS) presented by Shekhovtsov et al. in 2022 [17] or a fuzzy decision by opinion method (FDOSM) extension to use Pythagorean fuzzy sets presented by Al-Samarraay et al., also in 2022 [18].
However, classical fuzzy sets are not the only possible approach to problems where uncertainty and fuzzy logic arise. Another such tool was presented by Turksen in 1986, namely the interval-valued fuzzy set (IVFS), which dealt with some of the limitations arising from the use of classical fuzzy sets [19]. These sets were then subject to many improvements, for example, by using bidirectional approximate inference, which was based precisely on IVFS and was presented by Chen et al. in 1997 [20], followed by the presentation of its application to a rule-based system by Chen, Hsiao and Jong [21] in 2000. Furthermore, in 2012, Chen et al. [22] proposed fuzzy rule interpolation for interval-valued Gaussian fuzzy sets of type 2.
Classical fuzzy sets have some limitations, which were explored by Atanassov in 1986, where he proposed intuitionistic fuzzy sets (IFS) [23]. These sets, like the earlier ones, have found wide application in solving multicriteria decision-making problems. In many cases, these sets can be a suitable alternative to classical fuzzy sets or linguistic values [24]. Because of their adoption in the decision-making environment, these sets have also been used to extend multicriteria approaches to decision making. A good example is the work of Stanujkić et al. [25], in which they presented an extension of the weighted aggregated sum product assessment (WASPAS) method for this particular fuzzy set and showed its application to the website evaluation problem. In addition, the sets themselves continue to be extended to represent as many cases as possible, and extensions such as circular intuitionistic fuzzy sets [26] and continuous intuitionistic fuzzy sets [27] were presented.
Another improvement of fuzzy sets is Pythagorean fuzzy sets (PFS), which represent values using a pair of numbers that are degrees of membership and non-membership. This type of fuzzy set has also found wide application in the field of decision making. They allow for a better representation of data in uncertain, ambiguous situations, which translates into more informed decisions that better represent the decision maker’s preferences [28]. Their application in solving real-world problems has been demonstrated by Peng et al. for the evaluation of the 5G industry [29], or by Boyacı et al. for the selection of a pandemic hospital location based on PFS and a geographic information system [30]. Moreover, PFSs are constantly being studied, and new approaches are presented, such as the significance of the TOPSIS approach to multiple attribute decision making (MADM) in calculating exponential divergence measures for Pythagorean fuzzy sets presented by Arora et al. [31], directional correlation coefficient measures for Pythagorean fuzzy sets presented by Lin et al. [32], or Pythagorean fuzzy Multi-Objective Optimization on the basis of a Ratio Analysis plus the full MULTIplicative form (MULTIMOORA) method based on distance measure and score function, presented by Huang et al. [33].
In cases where the problems under consideration contain a lot of data, measures that allow us to determine their characteristics are useful. One such measure is entropy, which informs us of the uncertainty in the values under consideration, so a higher entropy value informs us that the data carry more information. The first classical entropy is Shannon entropy, which allows us to determine the degree of uncertainty in a probability distribution [34]. According to Shannon entropy, a theoretical framework based on fundamental principles for fuzzy entropy measures was presented by De Luca et al. [35]. This enabled further work on entropy and its application to fuzzy sets, such as intuitionistic fuzzy sets presented by Hung and Yang [36], interval-valued fuzzy sets presented by Zeng and Li [37], and hesitant fuzzy sets presented by Hu et al. [38].
Entropy in Pythagorean fuzzy sets is also widely used. Yang and Hussain proposed a new Pythagorean fuzzy entropy (PFE) based on probabilistic type, distance, Pythagorean index, and min–max operator [39]. In 2020, Xu et al. introduced a new PFE, which was then used to calculate the criteria weights and establish the Pythagorean fuzzy multicriteria decision-making approach [40]. Rani et al. introduced another PFE and additionally, a score function to evaluate unknown criteria weights using the COPRAS technique [41]. Abhishek introduced a new Pythagorean fuzzy entropy of R-S norms whose application was shown in a problem of hydrogen plant site selection using the VIseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR) and TOPSIS methods [42]. Biswas and Sarkar presented a new PFE measure for handling multicriteria group decision problems using TOPSIS-based methodology in a Pythagorean fuzzy environment [43]. Xue et al. proposed a PFE for decision making using a linear programming technique for a multidimensional analysis of preferences (LINMAP), which has been used in railway project investment evaluation [44]. Some researchers propose entropies for specific cases of PFS, such as the linguistic Pythagorean fuzzy-sets TOPSIS method based on correlation coefficient and entropy measure, presented by Lin et al. [45]. Over the years, many authors have continued to study entropy, which has translated into many published papers [46,47,48,49,50].
The research presented in this article proposes a new Pythagorean entropy of fuzzy sets, which has been compared with other entropies proposed by various authors. We prove that the proposed measure satisfies all conditions consistent with the axioms of valid entropy. In addition, we show the possibility of using the proposed entropy to calculate the weights of criteria in combination with a multicriteria decision-making method to solve decision-making problems, as demonstrated by the example of site selection for a hydropower plant.
The rest of the paper is structured as follows: Section 2 presents an introductory discussion that covers the basic concepts and axioms of intuitionistic fuzzy sets and Pythagorean fuzzy sets, the novel entropy of Pythagorean fuzzy sets, and the complex proportional assessment (COPRAS) approach that combines the proposed entropy with Pythagorean fuzzy data. In Section 3, an example Pythagorean fuzzy multicriteria decision problem is solved using COPRAS and the proposed entropy. Section 4 compares the proposed entropy with existing ones regarding the results obtained from their application. Additionally, Section 5 compares the used COPRAS method with two other MCDA methods, namely TOPSIS and VIKOR. Finally, Section 6 draws conclusions and discusses future directions.
2. Preliminaries
Definition 1.
Assume X is a given complete set; set S is said to be an Intuitionistic Fuzzy Set (IFS) if it can be expressed by the following formula [51]:
for which the function is the degree of membership and non-membership of , and for every Also, is the degree of uncertainty .
Definition 2.
For every two IFS K and S of the set X, we define the following relations and operations [4]:
- i.
- ii.
- iii.
- iv.
- v.
- vi.
- vii.
- viii.
- ix.
- x.
Definition 3.
Let X be a given universal set; set S is said to be a Pythagorean fuzzy set (PFS) if it can be expressed by the following formula [28]:
where the function : : if the degrees of membership and non-membership of , and .
Definition 4.
Consider three PFS: , , and ; then, we define the operations as presented below [28,52,53]:
- i.
- ii.
- iii.
- iv.
- v.
- vi.
- vii.
- viii.
- ix.
Definition 5.
Given a PFS K over X, , the score function is defined as [28]:
Definition 6.
Given a PFS K over X, , the accuracy function is given as [52]:
2.1. Novel Entropy for Pythagorean Fuzzy Set
Classical Shannon entropy, also known as information entropy, is a fundamental concept in information theory and probability theory. It is used to measure the information content or uncertainty of random variables, data, or events. The fuzzy set theory uses entropy to quantify uncertainty or vagueness within these sets, which incorporate both membership and non-membership degrees [35]. In this section, the new Pythagorean fuzzy entropy will be presented along with proof that it satisfies all the required axioms to consider the proposed measure as entropy.
Definition 7.
The function is said to be an entropy on if E has the following properties:
- 1.
- Minimality: if S is a crisp set.
- 2.
- Maximality: if for all
- 3.
- Resolution: if S is crisper than K, that is if for and for
- 4.
- Symmetry: .
In addition to the aforementioned Pythagorean measures of fuzzy entropy, we have developed the following Pythagorean measure of fuzzy entropy:
where n is the number of alternatives.
Theorem 1.
The previously mentioned function E(S) is a valid entropy measure on PFS.
Proof.
To demonstrate the theorem’s validity, it must satisfy the axioms, according to the following definitions [39].
- 1.
- Minimality: if S is a crisp set, i.e., or such that
- 2.
- Maximality: for all , if
- 3.
- Resolution: to prove the third axiom, let us assume a function f(x,y) such that:where .We can obtain the partial derivatives for x and yWe obtained that when and when , whereas when and when , then when f is increasing with respect to x when and decreasing when . Moreover, f is decreasing with respect to y for and increasing when .Based on the above function, we can say that , if S is less fuzzy than , i.e., and for or and for .
- 4.
- Symmetry:where is the complement of S.
Hence, is a valid entropy for the Pythagorean fuzzy set. □
Theorem 2.
In the universe discourse X, consider A and B to be two Pythagorean fuzzy sets. and , such that for any either or ,
and are the entropy of the fuzzy set, then
2.2. Pythagorean Fuzzy Multicriteria Decision Making Based on COPRAS Approach
The complex proportional assessment (COPRAS) approach was first proposed by Zavadskas and Kaklauskas in 1994 [54]. COPRAS has many advantages over other approaches to solving decision-making problems, such as the fact that it considers the most and least favorable solution in terms of further evaluation while keeping the calculations concise and simple, which in turn makes it fast [55]. Moreover, it ranks and estimates alternatives step by step in terms of their importance and degree of utility.
This approach is widely used in decision-making situations under uncertainty [56]. As a popular method for multicriteria decision making, it has seen many developments. Vahdani and Mousavi developed a new COPRAS approach based on interval values to solve the robot selection problem [57]. Bekar et al. integrated the COPRAS technique with grey numbers theory to create a decision support system to improve the performance of maintenance activities by evaluating total productive maintenance (TPM) strategies [58]. An extension of the COPRAS approach, which can be used with hesitant fuzzy sets, was presented by Mishra et al., where they considered evaluating the quality of service [59]. In addition, Kumari and Mishra presented an application of this method of multicriteria decision making using intuitionistic fuzzy sets to select a green supplier [60].
Figure 1 presents a general flowchart for the COPRAS approach.

Figure 1.
The COPRAS approach flowchart.
In this study, the COPRAS method is extended in such a way that it utilizes the proposed Pythagorean fuzzy entropy to calculate the weights for the problem under consideration. The steps presented in the flowchart are described in detail below.
- Step 1:
- Establish a Pythagorean fuzzy decision matrix , where denotes alternatives () and criteria ():
- Step 2:
- Calculate the entropy of Pythagorean fuzzy set for each criterion () using Equation (5) and determine the criteria weight of each criterion () by using the following formula:
- Step 3:
- Compute the weighted decision matrix using the following equation:
- Step 4:
- Determine the value of the score function using Equation (3)
- Step 5:
- Calculate maximizing and minimizing index for benefit and non-benefit criteria as follows:where stands for the collection of all non-benefit criteria and B represents the set of benefit criteria,
- Step 6:
- Determine the relative importance of each alternative for all using following equation:
- Step 7:
- Determine the priority order for all using Equation (24) and rank the alternatives in the descending order, which means that the alternative with the highest value is considered the best.
2.3. TOPSIS
TOPSIS is one of the most widely used methods for multicriteria decision making, which dates back to 1994, when it was presented by Hwang and Yoon [61]. This method, through the use of positive ideal solution (PIS) and negative ideal solution (NIS), allows the assessment of individual alternatives in the context of ideal solution. Its application has been presented in a number of papers: Alao et al. presented solving the problem of waste to energy technology selection [62], Javad et al. proposed a solution for the green supplier selection for the steel industry [63] and Konstantinos et al. designed a decision support system methodology for selecting wind farm installation locations using TOPSIS [64]. The method has seen many extensions over the years, but the most relevant to this study is the extension presented by Zhang and Xu in 2014 [65], which offers the possibility of using this method to solve problems described on Pythagorean fuzzy sets.
2.4. VIKOR
Another prevalent approach is the VIKOR method. The main difference with the TOPSIS method is that this method offers three final rankings: a S ranking, a R ranking and a compromise Q ranking. This article uses the compromise ranking, obtained by setting the compromise value to , meaning that the S ranking has the same effect on the final result as the R ranking. This method has also been used to solve various problems, such as the balanced supplier selection presented by Abdel-Baset et al. [66], or the evaluation of the service level of bike-sharing companies presented by Liang et al. [67]. In addition, it has received many extensions, for example, to group decision making based on complex spherical fuzzy sets, presented by Akram et al. [68], or the intuitionistic-fuzzy extension for solving the personnel selection problem, presented by Krishankumar et al. [69]. However, again, the most relevant extension in the context of this study is the one that allows us to operate on Pythagorean fuzzy sets, and it was presented by Bakioglu and Atahan in 2021 [70].
2.5. Ranking Similarity Coefficients
Ranking similarity coefficients are helpful when analyzing solutions to multicriteria decision-making problems offered by different methods. They allow the degree of similarity between two rankings to be determined using a single value, making the comparison more transparent and accessible. The most commonly used ranking similarity coefficients are the weighted Spearman coefficient presented by Pinto da Costa in 2005 [71] and the weighted similarity coefficient (WS) presented by Sałabun in 2020 [72]. The WS coefficient is asymmetric, so when using it, it is crucial to determine which ranking is being compared to which ranking. In addition, it allows for more accurate modeling of the change in places of individual alternatives within the podium. Both coefficients are widely used, and their application has been demonstrated by, among others, Sałabun et al., who investigated whether multicriteria decision-making methods are benchmarkable [73]; Kizielewicz et al., who used these coefficients to compare solutions in the problem supplier selection [74]; or Shekhovtsov, who examined how strongly the rank similarity coefficients vary [75]. The weighted Spearman coefficient is presented as Equation (25), while the WS coefficient is given as Equation (26).
where —position in the reference ranking; —position in the second ranking; n—number of alternatives.
where —position of reference ranking; —position of second ranking; n—number of alternatives.
3. Numerical Example
This section will present a numerical example that is solved using the procedure described in Section 2.2, namely the COPRAS approach, which integrates the proposed entropy using the numerical space of Pythagorean fuzzy sets. The presented example solves the problem of selecting the site for a hydropower plant. The exact framework for the problem under consideration is presented in Figure 2.
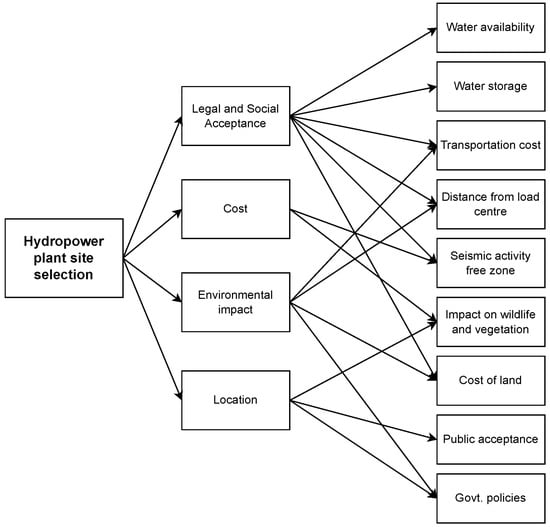
Figure 2.
Framework of site selection for Hydropower Plant.
Next, let us consider a problem in which four sites and nine criteria define our problem. The criteria are defined as availability (), water storage (), transportation cost (), distance from load centre (), seismic activity free zone (), impact on wildlife and vegetation (), cost of land (), public acceptance () and government policies (). In this study, we took , , … as benefit criteria and as non-benefit criteria. The aforementioned alternatives and criteria form our decision matrix, which is shown in Table 1.

Table 1.
Pythagorean Fuzzy matrix.
Next, we calculate the entropy for each criterion according to Equation (5). The resulting values are , , , , , , , , .
We can then calculate the weight values for each criterion using Equation (19), from which we obtain , , , , , , , , . Next, we use the calculated weight values to create a weighted decision matrix according to Equation (20). The resulting weighted decision matrix is shown in Table 2.

Table 2.
Weighted decision matrix.
The next step requires us to calculate the value of the result function using Equation (3), and the results are shown in Table 3.

Table 3.
Score function values.
The final steps to be performed are to calculate the maximizing and minimizing index using Equations (21) and (22), respectively, and then to calculate the relative importance of each alternative using Equation (23). The final importance values obtained should be ranked in descending order, that is, the alternative with the highest value should have the best position. The results are presented in Table 4. From these results, we can see that the best-ranked alternative was the second alternative, and the worst-ranked alternative was the fourth alternative.

Table 4.
Values for benefit and non-benefit criteria, relative weight and resulting ranking.
4. Comparison with Other Entropies
Since other researchers have already considered entropy creation for Pythagorean fuzzy sets, it is necessary to compare the newly obtained entropy with those already created. Such a comparison will allow us to make sure that the newly proposed approach will allow us to obtain results that do not deviate significantly from those expected, thus obtaining the accuracy and reliability of the proposed technique. The same numerical example was used to compare entropies, and the entropies considered in this comparison are as follows:
- The entropy of a Pythagorean fuzzy set proposed by Thao in 2019 [76]:
- The Pythagorean fuzzy set entropy measure proposed by Ye in 2010 [77]:
- The Pythagorean fuzzy set entropy introduced by Neeraj et al. in 2021 [46]:
The entropy values for each criterion obtained using the above formulae are shown in Table 5. The standard deviation is worth paying attention to, as it helps to show what the distribution of the obtained values looks like. As entropy returns values between 0 and 1, thus a more detailed analysis of the values obtained is possible as the range is the same in the case of all entropies. A larger standard deviation allows us to distinguish more accurately between individual values. In this case, the proposed entropy is characterized by the highest standard deviation; hence, for the problem at hand, we can conclude that the distinction between the different values will be most apparent. It should be noted that a higher standard deviation may also affect the distribution of the weights of individual criteria. The entropy presented by Thao has the smallest standard deviation, while the standard deviation for the other entropies is around a similar value.

Table 5.
Entropy values for each criterion calculated using different entropies.
Table 6 presents the results of utilization of each of the entropies in the problem under consideration. The rankings obtained using the selected entropies are exactly the same and are shown in Table 6. Obtaining the same results demonstrates the stability of the proposed entropy and that the results offered are at least similar to pre-existing entropies. Furthermore, it reinforces our belief that the newly proposed entropy offers reliable results that can be used in multicriteria decision making. Of course, the high similarity to the results offered by other entropies relates directly to the ranking, which is based on ranked data, and four alternatives are presented in the problem under study, so the characteristics of the problem create a low probability of changes in ranking. Future comparisons would require examination of other cases, especially those with more alternatives.

Table 6.
Comparative analysis of the results of presented entropy with other entropies.
5. Comparison with Other MCDA Methods
An additional comparison with other multicriteria decision-making methods allows for a more detailed analysis of the solutions offered. In this case, the COPRAS method has been compared with the TOPSIS and VIKOR methods, and the preference results obtained by using each method are presented in Table 7. In this comparison, weights for criteria were calculated only using the proposed entropy. Each method returns values of preferences in different ranges, so their direct comparison is not straightforward. It is worth noting that for the VIKOR method, the values for the fourth and first alternatives, as well as for the second and third alternatives, are similar. A similar situation occurs for the COPRAS method, where alternatives one and two obtained similar preference values. It should also be noted that prior to ranking, it is easiest to see the differences between alternatives’ preference for the COPRAS method because the standard deviation is approximately . The standard deviation for the preference values obtained using the VIKOR method is , while the standard deviation for the TOPSIS method is the smallest, at approximately . It can be concluded from this that with the TOPSIS method, it will be most difficult for the decision-maker to notice the differences between the preference values for the different alternatives.

Table 7.
Preference values for the assessed alternatives in the problem of site selection for hydropower plant.
The alternatives were then ranked, as shown in Figure 3. The order changes significantly depending on the method used. Only the ranking of the fourth alternative, which was ranked as the worst according to all methods, remained constant. For the other alternatives, the rankings change, which may be due to the large number of criteria and similar key values across the alternatives. This solution shows that a broader analysis in multicriteria decision-making problems is needed, but often introduces additional questions about which solution is better. In cases where the consensus between multiple methods is unclear, it is worth asking an expert to evaluate the individual alternatives. As the final choice rests with the decision maker, it is essential to bear in mind that the analysis is intended to identify the best options, where we could reject alternative four. It would be worthwhile to conduct similar research for a problem containing a larger number of alternatives.
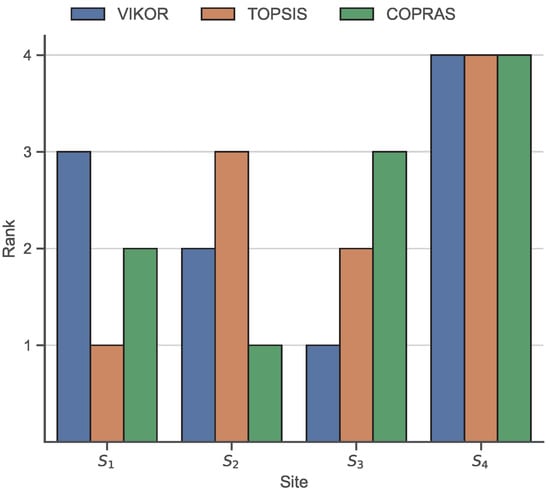
Figure 3.
Ranking visualization for the problem of site selection for hydropower plant.
In addition, it is helpful to analyze the similarity of the rankings using coefficients. In this case, the weighted Spearman coefficient was used, the values of which were calculated using Equation (25), as well as the WS coefficient, for which Equation (26) was used, and the results are presented in Table 8. In this case, the weighted Spearman coefficient returned the same value for the comparison of rankings obtained using COPRAS and VIKOR as for the comparison of COPRAS and TOPSIS rankings. This is because the weighted Spearman coefficient does not reflect the precise distance between the order of alternatives. In this case, the WS rankings’ similarity coefficient better reflects the rankings’ discrepancies, as the orders obtained by the COPRAS method are more similar to the VIKOR method, where a change of one place from first to second can be observed for alternative two. Of course, it should be remembered that the WS coefficient is asymmetric, so it is crucial that the COPRAS ranking is compared with VIKOR and not vice versa, as otherwise, a change from first to third place for alternative three would be considered.

Table 8.
Similarity of rankings of the proposed approach with other available MCDA methods.
6. Conclusions and Future Directions
As the complexity of decision-making problems increases, the demand to find new and better approaches to produce more accurate results for a given problem arises. The use of fuzzy logic and sets allows us to include the uncertainties that are so often present in real-world problems, and consequently requires further research in this direction.
This paper presents a new entropy that can be applied to Pythagorean fuzzy sets. In addition, the integration of this entropy in a multicriteria decision-making method, such as COPRAS, is presented to obtain criteria weights in the problem of selecting hydropower plant sites. In addition, a preliminary comparison of the newly proposed entropy with existing ones is made, emphasizing that the results obtained by the new entropy are stable and reliable in terms of multicriteria decision making.
In future research, it would be worthwhile to demonstrate the use of the proposed entropy in real-world problems from other areas. In addition, it would be worth extending the comparative analysis of entropies to highlight the usefulness and effectiveness of the newly proposed entropy. Furthermore, simulation studies can be carried out to obtain a more detailed picture of the distribution of weights depending on the entropy used.
Author Contributions
Conceptualization, S.K., B.P., N.G., N.S. and W.S.; methodology, S.K., B.P., N.G., N.S. and W.S.; software, S.K., B.P., N.G., N.S. and W.S.; validation, S.K., B.P., N.G., N.S. and W.S.; formal analysis, S.K., B.P., N.G., N.S. and W.S.; investigation, S.K., B.P., N.G., N.S. and W.S.; resources, S.K., B.P., N.G., N.S. and W.S.; data curation, S.K., B.P., N.G., N.S. and W.S.; writing—original draft preparation, S.K., B.P., N.G., N.S. and W.S.; writing—review and editing, S.K., B.P., N.G., N.S. and W.S.; visualization, S.K., B.P., N.G., N.S. and W.S.; supervision, S.K., B.P., N.G., N.S. and W.S.; project administration, W.S.; funding acquisition, W.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Science Center grant number 2021/41/B/HS4/01296.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MCDM | multicriteria decision making |
| MADM | multiple-attribute decision making |
| FS | fuzzy set(s) |
| IVFS | interval-valued fuzzy set(s) |
| IFS | intuitionistic fuzzy set(s) |
| PFS | Pythagorean fuzzy set(s) |
| PFE | Pythagorean fuzzy entropy |
| COPRAS | complex proportional assessment |
| SPOTIS | stable preference ordering towards ideal solution |
| LINMAP | linear programming technique for a multidimensional analysis of preferences |
| VIKOR | VIseKriterijumska Optimizacija I Kompromisno Resenje |
| TOPSIS | Technique for Order of Preference by Similarity to Ideal Solution |
| MULTIMOORA | Multi-Objective Optimization on the basis of a Ratio Analysis plus the full MULTIplicative form |
| FDOSM | fuzzy decision by opinion method |
References
- Liang, G.S.; Wang, M.J.J. Personnel selection using fuzzy MCDM algorithm. Eur. J. Oper. Res. 1994, 78, 22–33. [Google Scholar] [CrossRef]
- Önüt, S.; Kara, S.S.; Işik, E. Long term supplier selection using a combined fuzzy MCDM approach: A case study for a telecommunication company. Expert Syst. Appl. 2009, 36, 3887–3895. [Google Scholar] [CrossRef]
- Deveci, M.; Demirel, N.Ç.; Ahmetoğlu, E. Airline new route selection based on interval type-2 fuzzy MCDM: A case study of new route between Turkey-North American region destinations. J. Air Transp. Manag. 2017, 59, 83–99. [Google Scholar] [CrossRef]
- Karacan, I.; Tozan, H.; Karatas, M. Multi criteria decision methods in health technology assessment: A brief literature review. Eurasian J. Health Technol. Assess. 2016, 1, 12–19. [Google Scholar]
- Mardani, A.; Hooker, R.E.; Ozkul, S.; Yifan, S.; Nilashi, M.; Sabzi, H.Z.; Fei, G.C. Application of decision making and fuzzy sets theory to evaluate the healthcare and medical problems: A review of three decades of research with recent developments. Expert Syst. Appl. 2019, 137, 202–231. [Google Scholar] [CrossRef]
- Deveci, M.; Akyurt, I.Z.; Yavuz, S. A GIS-based interval type-2 fuzzy set for public bread factory site selection. J. Enterp. Inf. Manag. 2018, 31, 820–847. [Google Scholar] [CrossRef]
- Karatas, M. Hydrogen energy storage method selection using fuzzy axiomatic design and analytic hierarchy process. Int. J. Hydrogen Energy 2020, 45, 16227–16238. [Google Scholar] [CrossRef]
- Deveci, M.; Cali, U.; Kucuksari, S.; Erdogan, N. Interval type-2 fuzzy sets based multi-criteria decision-making model for offshore wind farm development in Ireland. Energy 2020, 198, 117317. [Google Scholar] [CrossRef]
- Priyanka; Kumar, S.; Kalia, S. MULTIMOORA-based MCDM model for sustainable ranking of wastewater treatment technologies under picture fuzzy environment. Expert Syst. 2023, e13286. [Google Scholar] [CrossRef]
- Gunnarsdóttir, I.; Davidsdottir, B.; Worrell, E.; Sigurgeirsdóttir, S. Sustainable energy development: History of the concept and emerging themes. Renew. Sustain. Energy Rev. 2021, 141, 110770. [Google Scholar] [CrossRef]
- Kumar, A.; Sah, B.; Singh, A.R.; Deng, Y.; He, X.; Kumar, P.; Bansal, R. A review of multi criteria decision making (MCDM) towards sustainable renewable energy development. Renew. Sustain. Energy Rev. 2017, 69, 596–609. [Google Scholar] [CrossRef]
- Siksnelyte, I.; Zavadskas, E.K.; Streimikiene, D.; Sharma, D. An overview of multi-criteria decision-making methods in dealing with sustainable energy development issues. Energies 2018, 11, 2754. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Goswami, S.S. A comprehensive review of multiple criteria decision-making (MCDM) Methods: Advancements, applications, and future directions. Decis. Mak. Adv. 2023, 1, 25–48. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1978, 1, 3–28. [Google Scholar] [CrossRef]
- Rana, H.; Umer, M.; Hassan, U.; Asgher, U.; Silva-Aravena, F.; Ehsan, N. Application of fuzzy TOPSIS for prioritization of patients on elective surgeries waiting list-A novel multi-criteria decision-making approach. Decis. Mak. Appl. Manag. Eng. 2023, 6, 603–630. [Google Scholar] [CrossRef]
- Kaya, I.; Colak, M.; Terzi, F. A comprehensive review of fuzzy multi criteria decision making methodologies for energy policy making. Energy Strategy Rev. 2019, 24, 207–228. [Google Scholar] [CrossRef]
- Shekhovtsov, A.; Paradowski, B.; Więckowski, J.; Kizielewicz, B.; Sałabun, W. Extension of the SPOTIS method for the rank reversal free decision-making under fuzzy environment. In Proceedings of the 2022 IEEE 61st Conference on Decision and Control (CDC), Cancun, Mexico, 6–9 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 5595–5600. [Google Scholar]
- Al-Samarraay, M.S.; Salih, M.M.; Ahmed, M.A.; Zaidan, A.; Albahri, O.S.; Pamucar, D.; AlSattar, H.; Alamoodi, A.H.; Zaidan, B.; Dawood, K.; et al. A new extension of FDOSM based on Pythagorean fuzzy environment for evaluating and benchmarking sign language recognition systems. Neural Comput. Appl. 2022, 34, 4937–4955. [Google Scholar] [CrossRef]
- Turksen, I.B. Interval valued fuzzy sets based on normal forms. Fuzzy Sets Syst. 1986, 20, 191–210. [Google Scholar] [CrossRef]
- Chen, S.M.; Hsiao, W.H.; Jong, W.T. Bidirectional approximate reasoning based on interval-valued fuzzy sets. Fuzzy Sets Syst. 1997, 91, 339–353. [Google Scholar] [CrossRef]
- Chen, S.M.; Hsiao, W.H. Bidirectional approximate reasoning for rule-based systems using interval-valued fuzzy sets. Fuzzy Sets Syst. 2000, 113, 185–203. [Google Scholar] [CrossRef]
- Chen, S.M.; Chang, Y.C.; Pan, J.S. Fuzzy rules interpolation for sparse fuzzy rule-based systems based on interval type-2 Gaussian fuzzy sets and genetic algorithms. IEEE Trans. Fuzzy Syst. 2012, 21, 412–425. [Google Scholar] [CrossRef]
- Atanassov, K.T.; Stoeva, S. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Liu, M.; Ren, H. A new intuitionistic fuzzy entropy and application in multi-attribute decision making. Information 2014, 5, 587–601. [Google Scholar] [CrossRef]
- Stanujkić, D.; Karabašević, D. An extension of the WASPAS method for decision-making problems with intuitionistic fuzzy numbers: A case of website evaluation. Oper. Res. Eng. Sci. Theory Appl. 2018, 1, 29–39. [Google Scholar] [CrossRef]
- Atanassov, K.T. Circular intuitionistic fuzzy sets. J. Intell. Fuzzy Syst. 2020, 39, 5981–5986. [Google Scholar] [CrossRef]
- Alkan, N.; Kahraman, C. Continuous intuitionistic fuzzy sets (CINFUS) and their AHP&TOPSIS extension: Research proposals evaluation for grant funding. Appl. Soft Comput. 2023, 145, 110579. [Google Scholar]
- Yager, R.R.; Abbasov, A.M. Pythagorean membership grades, complex numbers, and decision making. Int. J. Intell. Syst. 2013, 28, 436–452. [Google Scholar] [CrossRef]
- Peng, X.; Zhang, X.; Luo, Z. Pythagorean fuzzy MCDM method based on CoCoSo and CRITIC with score function for 5G industry evaluation. Artif. Intell. Rev. 2020, 53, 3813–3847. [Google Scholar] [CrossRef]
- Boyacı, A.Ç.; Şişman, A. Pandemic hospital site selection: A GIS-based MCDM approach employing Pythagorean fuzzy sets. Environ. Sci. Pollut. Res. 2022, 29, 1985–1997. [Google Scholar] [CrossRef]
- Arora, H.; Naithani, A. Significance of TOPSIS approach to MADM in computing exponential divergence measures for pythagorean fuzzy sets. Decis. Mak. Appl. Manag. Eng. 2022, 5, 246–263. [Google Scholar] [CrossRef]
- Lin, M.; Huang, C.; Chen, R.; Fujita, H.; Wang, X. Directional correlation coefficient measures for Pythagorean fuzzy sets: Their applications to medical diagnosis and cluster analysis. Complex Intell. Syst. 2021, 7, 1025–1043. [Google Scholar] [CrossRef]
- Huang, C.; Lin, M.; Xu, Z. Pythagorean fuzzy MULTIMOORA method based on distance measure and score function: Its application in multicriteria decision making process. Knowl. Inf. Syst. 2020, 62, 4373–4406. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- De Luca, A.; Termini, S. A definition of a nonprobabilistic entropy in the setting of fuzzy sets theory. In Readings in Fuzzy Sets for Intelligent Systems; Elsevier: Amsterdam, The Netherlands, 1993; pp. 197–202. [Google Scholar]
- Hung, W.L.; Yang, M.S. Fuzzy entropy on intuitionistic fuzzy sets. Int. J. Intell. Syst. 2006, 21, 443–451. [Google Scholar] [CrossRef]
- Zeng, W.; Li, H. Relationship between similarity measure and entropy of interval valued fuzzy sets. Fuzzy Sets Syst. 2006, 157, 1477–1484. [Google Scholar] [CrossRef]
- Hu, J.; Yang, Y.; Zhang, X.; Chen, X. Similarity and entropy measures for hesitant fuzzy sets. Int. Trans. Oper. Res. 2018, 25, 857–886. [Google Scholar] [CrossRef]
- Yang, M.S.; Hussain, Z. Fuzzy entropy for pythagorean fuzzy sets with application to multicriterion decision making. Complexity 2018, 2018, 2832839. [Google Scholar] [CrossRef]
- Xu, T.T.; Zhang, H.; Li, B.Q. Pythagorean fuzzy entropy and its application in multiple-criteria decision-making. Int. J. Fuzzy Syst. 2020, 22, 1552–1564. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Mardani, A. An extended Pythagorean fuzzy complex proportional assessment approach with new entropy and score function: Application in pharmacological therapy selection for type 2 diabetes. Appl. Soft Comput. 2020, 94, 106441. [Google Scholar] [CrossRef]
- Guleria, A.; Bajaj, R.K. A robust decision making approach for hydrogen power plant site selection utilizing (R, S)-Norm Pythagorean Fuzzy information measures based on VIKOR and TOPSIS method. Int. J. Hydrogen Energy 2020, 45, 18802–18816. [Google Scholar] [CrossRef]
- Biswas, A.; Sarkar, B. Pythagorean fuzzy TOPSIS for multicriteria group decision-making with unknown weight information through entropy measure. Int. J. Intell. Syst. 2019, 34, 1108–1128. [Google Scholar] [CrossRef]
- Xue, W.; Xu, Z.; Zhang, X.; Tian, X. Pythagorean fuzzy LINMAP method based on the entropy theory for railway project investment decision making. Int. J. Intell. Syst. 2018, 33, 93–125. [Google Scholar] [CrossRef]
- Lin, M.; Huang, C.; Xu, Z. TOPSIS method based on correlation coefficient and entropy measure for linguistic Pythagorean fuzzy sets and its application to multiple attribute decision making. Complexity 2019, 2019, 6967390. [Google Scholar] [CrossRef]
- Gandotra, N.; Kizielewicz, B.; Anand, A.; Bączkiewicz, A.; Shekhovtsov, A.; Wątróbski, J.; Rezaei, A.; Sałabun, W. New pythagorean entropy measure with application in multi-criteria decision analysis. Entropy 2021, 23, 1600. [Google Scholar] [CrossRef]
- Thakur, P.; Kizielewicz, B.; Gandotra, N.; Shekhovtsov, A.; Saini, N.; Sałabun, W. The Group Decision-Making Using Pythagorean Fuzzy Entropy and the Complex Proportional Assessment. Sensors 2022, 22, 4879. [Google Scholar] [CrossRef] [PubMed]
- Thakur, P.; Kaczyńska, A.; Gandotra, N.; Saini, N.; Sałabun, W. The Application of the New Pythagorean Fuzzy Entropy to Decision-Making using Linguistic Terms. Procedia Comput. Sci. 2022, 207, 4525–4534. [Google Scholar] [CrossRef]
- Kumar, R.; Gandotra, N. Novel Pythagorean Fuzzy based Information Measure using TOPSIS Technique for Application in Multi-Criteria Decision Making. In Proceedings of the 2023 10th International Conference on Computing for Sustainable Global Development (INDIACom), New Delhi, India, 15–17 March 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1271–1276. [Google Scholar]
- Kumar, R.; Saini, N.; Gandotra, N. Novel Pythagorean fuzzy entropy and its application based on MCDM for ranking the academic institutions. AIP Conf. Proc. 2022, 2357, 110005. [Google Scholar]
- Atanassov, K.T. Intuitionistic Fuzzy Sets; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Peng, X.; Yang, Y.; Song, J.; Jiang, Y. Pythagorean fuzzy soft set and its application. Comput. Eng. 2015, 41, 224–229. [Google Scholar]
- Peng, X.; Yang, Y.; Zhu, Y. Similarity measure and its application based on multiparametric intuitionistic fuzzy sets. Comput. Eng. Appl. 2015, 51, 122–125. [Google Scholar]
- Zavadskas, E.K.; Kaklauskas, A.; Šarka, V. The new method of multicriteria complex proportional assessment of projects. Technol. Econ. Dev. Econ. 1994, 1, 131–139. [Google Scholar]
- Chaurasiya, R.; Jain, D. Pythagorean fuzzy entropy measure-based complex proportional assessment technique for solving multi-criteria healthcare waste treatment problem. Granul. Comput. 2022, 7, 917–930. [Google Scholar] [CrossRef]
- Keshavarz Ghorabaee, M.; Amiri, M.; Salehi Sadaghiani, J.; Hassani Goodarzi, G. Multiple criteria group decision-making for supplier selection based on COPRAS method with interval type-2 fuzzy sets. Int. J. Adv. Manuf. Technol. 2014, 75, 1115–1130. [Google Scholar] [CrossRef]
- Vahdani, B.; Mousavi, S.M.; Tavakkoli-Moghaddam, R.; Ghodratnama, A.; Mohammadi, M. Robot selection by a multiple criteria complex proportional assessment method under an interval-valued fuzzy environment. Int. J. Adv. Manuf. Technol. 2014, 73, 687–697. [Google Scholar] [CrossRef]
- Turanoglu Bekar, E.; Cakmakci, M.; Kahraman, C. Fuzzy COPRAS method for performance measurement in total productive maintenance: A comparative analysis. J. Bus. Econ. Manag. 2016, 17, 663–684. [Google Scholar] [CrossRef]
- Mishra, A.R.; Rani, P.; Pardasani, K.R. Multiple-criteria decision-making for service quality selection based on Shapley COPRAS method under hesitant fuzzy sets. Granul. Comput. 2019, 4, 435–449. [Google Scholar] [CrossRef]
- Kumari, R.; Mishra, A.R. Multi-criteria COPRAS method based on parametric measures for intuitionistic fuzzy sets: Application of green supplier selection. Iran. J. Sci. Technol. Trans. Electr. Eng. 2020, 44, 1645–1662. [Google Scholar] [CrossRef]
- Lai, Y.J.; Liu, T.Y.; Hwang, C.L. Topsis for MODM. Eur. J. Oper. Res. 1994, 76, 486–500. [Google Scholar] [CrossRef]
- Alao, M.A.; Ayodele, T.R.; Ogunjuyigbe, A.; Popoola, O. Multi-criteria decision based waste to energy technology selection using entropy-weighted TOPSIS technique: The case study of Lagos, Nigeria. Energy 2020, 201, 117675. [Google Scholar] [CrossRef]
- Javad, M.O.M.; Darvishi, M.; Javad, A.O.M. Green supplier selection for the steel industry using BWM and fuzzy TOPSIS: A case study of Khouzestan steel company. Sustain. Futures 2020, 2, 100012. [Google Scholar] [CrossRef]
- Konstantinos, I.; Georgios, T.; Garyfalos, A. A Decision Support System methodology for selecting wind farm installation locations using AHP and TOPSIS: Case study in Eastern Macedonia and Thrace region, Greece. Energy Policy 2019, 132, 232–246. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Z. Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. Int. J. Intell. Syst. 2014, 29, 1061–1078. [Google Scholar] [CrossRef]
- Abdel-Baset, M.; Chang, V.; Gamal, A.; Smarandache, F. An integrated neutrosophic ANP and VIKOR method for achieving sustainable supplier selection: A case study in importing field. Comput. Ind. 2019, 106, 94–110. [Google Scholar] [CrossRef]
- Liang, X.; Chen, T.; Ye, M.; Lin, H.; Li, Z. A hybrid fuzzy BWM-VIKOR MCDM to evaluate the service level of bike-sharing companies: A case study from Chengdu, China. J. Clean. Prod. 2021, 298, 126759. [Google Scholar] [CrossRef]
- Akram, M.; Kahraman, C.; Zahid, K. Group decision-making based on complex spherical fuzzy VIKOR approach. Knowl.-Based Syst. 2021, 216, 106793. [Google Scholar] [CrossRef]
- Krishankumar, R.; Premaladha, J.; Ravichandran, K.; Sekar, K.; Manikandan, R.; Gao, X. A novel extension to VIKOR method under intuitionistic fuzzy context for solving personnel selection problem. Soft Comput. 2020, 24, 1063–1081. [Google Scholar] [CrossRef]
- Bakioglu, G.; Atahan, A.O. AHP integrated TOPSIS and VIKOR methods with Pythagorean fuzzy sets to prioritize risks in self-driving vehicles. Appl. Soft Comput. 2021, 99, 106948. [Google Scholar] [CrossRef]
- Pinto da Costa, J.; Soares, C. A weighted rank measure of correlation. Aust. N. Z. J. Stat. 2005, 47, 515–529. [Google Scholar] [CrossRef]
- Sałabun, W.; Urbaniak, K. A new coefficient of rankings similarity in decision-making problems. In Computational Science—ICCS 2020, Proceedings of the 20th International Conference, Amsterdam, The Netherlands, 3–5 June 2020; Part II 20; Springer: Cham, Switzerland, 2020; pp. 632–645. [Google Scholar]
- Sałabun, W.; Wątróbski, J.; Shekhovtsov, A. Are MCDA methods benchmarkable? A comparative study of TOPSIS, VIKOR, COPRAS, and PROMETHEE II methods. Symmetry 2020, 12, 1549. [Google Scholar] [CrossRef]
- Kizielewicz, B.; Więckowski, J.; Shekhovtsov, A.; Wątróbski, J.; Depczyński, R.; Sałabun, W. Study towards the time-based mcda ranking analysis—A supplier selection case study. Facta Univ. Ser. Mech. Eng. 2021, 19, 381–399. [Google Scholar] [CrossRef]
- Shekhovtsov, A. How strongly do rank similarity coefficients differ used in decision making problems? Procedia Comput. Sci. 2021, 192, 4570–4577. [Google Scholar] [CrossRef]
- Thao, N.X.; Smarandache, F. A new fuzzy entropy on Pythagorean fuzzy sets. J. Intell. Fuzzy Syst. 2019, 37, 1065–1074. [Google Scholar] [CrossRef]
- Ye, J. Two effective measures of intuitionistic fuzzy entropy. Computing 2010, 87, 55–62. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).