Spatiotemporal Evolution of Wind Turbine Wake Characteristics at Different Inflow Velocities

Abstract

In this paper, the spatiotemporal evolution of wind turbine (WT) wake characteristics is studied based on lattice Boltzmann method-large eddy simulations (LBM-LES) and grid adaptive encryption at different incoming flow velocities. It is clearly captured that secondary flow occurs in the vortex ring under shear force in the incoming flow direction, the S-wave and the Kelvin–Helmholtz instability occur in the major vortex ring mainly due to the unstable vortex ring interface with small disturbance of shear velocity along the direction of flow velocity. The S-wave and Kelvin–Helmholtz instability are increasingly enhanced in the main vortex ring, and three-dimensional disturbances are inevitable along the mainstream direction when it evolves along the flow direction. With increasing incoming flow, the S-wave and Kelvin–Helmholtz instability are gradually enhanced due to the increasing shear force in the flow direction. This is related to the nonlinear growth mechanism of the disturbance. The analysis of the velocity signal, as well as the pressure signal with a fast Fourier transform, indicates that the interaction between the vortices effectively accelerates the turbulence generation. In the near-field region of the wake, the dissipation mainly occurs at the vortex at the blade tip, and the velocity distribution appears asymmetric around the turbine centerline under shear and the mixing of fluids with different velocities in the wake zone also leads to asymmetric distributions.

1. Introduction

Wind turbine (WT) wake is a major determinant of turbulence in wind farms; it leads to load fluctuation, turbine fatigue, low-frequency noise, and performance degradation of wind farms [1]. The regulation of WT wake evolution has been undertaken by numerical simulations, and it is assumed that the appearance of the wake region will cause velocity losses and increased turbulence intensity. By revealing the wake behavior, the operational stability of WTs under different incoming flow conditions can be deeply understood, and the instability caused by eddy currents is reduced. The wake is mainly influenced by the design of the blades, the incoming flow conditions and the WT operating conditions [2]. As WT components (blades, nacelles, and towers) shed different characteristics of coherent flow structures, strong interactions can occur between them, which influences the evolutionary and stability characteristics of the wake [3]. Srensen et al. [4] reported the impact of the WT operating state on the evolution of the wake and found that changes in the blade tip velocity ratio will directly have an impact on the fusion of tip vortices and the wake expansion. In addition, the incoming flow conditions also influence the wake evolution process. Neunaber et al. [5] investigated the effect of different turbulent inflow conditions on the wake and found that changes in the turbulence characteristics of the inflow will cause changes in the turbulence intensity and mean wake velocity. Sedaghatizadeh et al. used the Large Eddy Simulation (LES) approach to calculate the WT wake flow to produce information on the flow field and wake evolution accurately and exhaustively [6]. Troldborg [7,8] and Ivanrell [9,10] combined the LES with the actuation line model to solve the wake and vortex characteristics of WTs. Xie [11] analyzed the wake of WTs under different temperature layers through large eddy simulation and found that the wind speed, humidity, and temperature changes of the wake were greatly affected by the temperature layer. Li et al. [1] dynamically simulated the flow and wake induced by MEXICO WTs by lattice Boltzmann method-large eddy simulations (LBM-LES) method, and the results show that the LBM-LES approach accurately predicts the wake structure under the WALE turbulence model. Khan et al. [12] used the LBM method to investigate the aerodynamic characteristics of a 10⁴ KW WT and found that the tip velocity significantly influences the flow field, vortex, and wake.

Based on the above discussions, the WT wake characteristics are not accurately captured due to the numerical dissipation of traditional computational fluid dynamics (CFD) methods. In the actual operating environment, WTs operate in complex conditions, and the influent conditions will impact the impeller aerodynamic properties and wake structure. The previous work mainly centered on the aerodynamic characteristics of different WTs. Therefore, it is urgent to further explore the spatiotemporal evolution characteristics and the characteristics of WT wake at various inflow conditions.

Our work aims to further explore the characteristics of WT wake near and far fields and the evolution of vortices at different incoming velocity conditions by the LBM-LES method in detail. The detailed flow field information of the wake will be captured through the adaptive mesh refinement (AMR). At first, the vortex structure and characteristics of the wake are simulated by LBM-LES at different incoming velocity conditions. In addition, the velocity and pressure signals are processed to further study the characteristics of the wake at different incoming flow conditions. Our work demonstrates that with the increase of the incoming velocity, the shear force tends to increase in the flow direction. The S-wave and Kelvin–Helmholtz instabilities are effectively enhanced, which effectively accelerates the evolution of the wake from laminar to turbulent flow. The spatial and temporal evolution characteristics of the turbulent coherent structure provide insight into the physical mechanism of the far-field WT wake, which is an advancement in improving the performance of WTs and optimizing the wind power industry.

The rest of the paper is organized as follows. Section 2 introduces the basic idea of LBM-LES, Adaptive mesh refinement. Section 3 describes the simulation setup conditions as well as the settings of the relevant parameters, and Section 4 demonstrates some numerical results of the WT wake field to illustrate the effects of vorticity, pressure, and velocity for different inflow velocities. Finally, Section 5 concludes.

2. Equation of Fluid Dynamics and Numerical Method

2.1. Lattice Boltzmann Method

The LBM is the discretization of the lattice Bhatnagar–Gross–Krook (LBGK) equations in space, time as well as velocity. The particle velocity is simplified to a finite-dimensional space of velocity {e₀, e₁, e_α, e_N}, where N denotes the type of the velocity. And f is the continuous distribution function, which is discretized accordingly as {f₀, f₁, f_α, f_N}, the discrete equation of velocity [13] can be expressed as:

$$\frac{\partial f_{\alpha }}{\partial t}+e_{\alpha }\cdot \nabla f_{\alpha }=\frac{1}{{\tau }_0}(f_{\alpha }^{eq}-f_{\alpha })+F_{\alpha },\alpha =1,\cdot \cdot \cdot ,\mathrm{N}$$

(1)

In which $f_{\alpha }$ = $f_{\alpha }$($r$,$e_{\alpha }$,$t$) is related to the quantity of velocity molecules at the point $r$ and the moment t, $e_{\alpha }$ is the discrete velocity. And $F_{\alpha }$ represents the external force in the discrete space of velocity. The evolution equations of the discrete time and space, as well as the LBGK model, are [14]:

$$f_{\alpha }(r+e_{\alpha }{\delta }_t,t+{\delta }_t)-f_{\alpha }(r,t)={\Omega }_{\alpha }+{\delta }_t{F}_{\alpha }(r,\mathrm{t})$$

(2)

In which ${\delta }_t$ represents the time step; $\tau ={\tau }_0/{\delta }_t$ denotes the dimensionless relaxation time.

In this paper, the D3Q27 model from the Dm Qn series of models introduced by Qian et al. [15] is utilized to solve the three-dimensional problem. The Dm Qn series is essentially a model that adopts the equilibrium distribution function:

$$f_{\alpha }^{eq}(r,t)=\rho {\omega }_{\alpha }[1+\frac{e_{\alpha }\cdot u}{c_s^2}+\frac{{(e_{\alpha }\cdot u)}^2}{2c_s^4}-\frac{u^2}{2c_s^2}]$$

(3)

where $\rho$, $u$, $c_s$, $e_{\alpha }$ and ${\omega }_{\alpha }$ represent the density of fluid, the macroscopic velocity, the velocity of lattice sound, the discrete velocity, and the density weighting factor, respectively.

$${\omega }_{\alpha }=\left\{\begin{array}{cc}8/27,\hfill & \hfill \alpha =0\\ 2/27,\hfill & \hfill \alpha =1,2\cdots ,6\\ 1/54,\hfill & \hfill \alpha =7,8\cdots ,18\\ 1/216,\hfill & \hfill \alpha =19,20\cdots ,26\end{array}\right.$$

(4)

There are 27 velocity vectors involved in the model of D3Q27 [16], and all the directions are taken into account. The 27 velocity vectors refer to the distribution functions ranging from f0 to f26, respectively. Thus, the distribution function can be expressed as f = (f₀, f₁, f₂,…, f₂₆)T and the discrete velocity is

$$e_{\alpha }=\left\{\begin{array}{cc}(0,0,0),\hfill & \hfill \alpha =0\\ c(\pm 1,0,0),\hspace{0.33em}c(0,0,\pm 1),c(0,\pm 1,0),\hfill & \hfill \alpha =1,2\cdots ,6\\ c(\pm 1,\pm 1,0),\hspace{0.33em}c(\pm 1,0,\pm 1),c(0,\pm 1,\pm 1)\hfill & \hfill \alpha =7,8\cdots ,18\\ c(\pm 1,\pm 1,\pm 1),\hfill & \hfill \alpha =19,20\cdots ,26\end{array}\right.$$

(5)

In which $c={\delta }_x/{\delta }_t$,${\delta }_x$ refers to the lattice step, ${\delta }_t$ is the time step. Generally, the lattice steps are the same in both $x$ and $y$ directions, and the lattice speed of sound $c_s$ can be expressed as:

$$c_s=\frac{\sqrt{3}}{3}c$$

(6)

The LBM equation in various directions [17] is

$$f_{\alpha }(r+e_{\alpha }{\delta }_t,t+{\delta }_t)-f_{\alpha }(r,t)={\Omega }_{\alpha },\alpha =0,1,\cdot \cdot \cdot ,26$$

(7)

where the collision operator ${\Omega }_{\alpha }$ can be written as

$${\Omega }_{\alpha }=-M^{-1}S[m_{\alpha }(r,t)-m_{\alpha }^{eq}(r,t)],\alpha =0,\cdot \cdot \cdot ,26$$

(8)

where $m_{\alpha }(r,t)$ represents the moment and $m_{\alpha }^{eq}(r,t)$ is the equilibrium function. $S$ is a collision matrix, $M$ stands for a 27 × 27 matrix and it converts the distribution function [18] into

$$m_{\alpha }(r,t)=M\cdot f_{\alpha }(r,t)$$

(9)

2.2. Large Eddy Simulation

In the large eddy simulation, the large-scale eddy mean component $\overline{\varphi }$ is separated from the small-scale eddy component ${\varphi }^{\prime }$ using a filter function, and for the instantaneous variable $\varphi$ we have:

$$\varphi =\overline{\varphi }+{\varphi }^{\prime }$$

(10)

The filtered variables can be represented as

$$\overline{\varphi }={\displaystyle \underset{D}{\int }\varphi G(x,x^{\prime }})d{x}^{\prime }$$

(11)

In which $D$ means the flow area, $x$ and $x^{\prime }$ represent the spatial coordinate after filtering and in the actual flow field, respectively. $G(x,x^{\prime })$ refers to the filtering function to define the spatial scale of the solvable scale turbulence, respectively.

The incompressible Navier–Stokes (N–S) equation is obtained by applying a Chapman–Enskog expansion of the Boltzmann equation [19]:

$$\nabla \cdot (\rho u)=0$$

(12)

$$\frac{\partial u}{\partial t}+(u\nabla )\cdot u=-\frac{\nabla p}{\rho }+v{\nabla }^{2}u$$

(13)

In which $\rho$, $u$, $v$ and $p$ are the density of fluid, the macroscopic velocity, the viscosity coefficient, and the pressure, respectively.

In order to account for the effect of subgrid-scale turbulence, coefficients of turbulent viscosity are included in the laminar flow, and the viscosity coefficient v consists of a grid-scale viscosity coefficient (molecular viscosity) and a subgrid-scale eddy viscosity coefficient, and in this paper, the subgrid model WALE (Wall-adapting local eddy), which is suitable for large eddy simulations in complex terrain regions, is chosen to support the LES [20].

The SGS eddy current viscosity is represented in the WALE model as follows [21]:

$$v_{SGS}={(C_W\Delta )}^2\frac{{({\overline{S}}_{ij}^d{\overline{S}}_{ij}^d)}^{3/2}}{{({\overline{S}}_{ij}{\overline{S}}_{ij})}^{5/2}+{({\overline{S}}_{ij}^d{\overline{S}}_{ij}^d)}^{5/4}}$$

(14)

where $C_W$ is the WALE model constant, 0.2 [22], and ${\overline{S}}_{ij}$ represents the tensor of strain rate after filtering [23]:

$${\overline{S}}_{ij}=\frac{1}{2}(\frac{\partial \overline{u_i}}{\partial x_j}+\frac{\partial \overline{u_j}}{\partial x_i})$$

(15)

In which ${\overline{S}}_{ij}^d$ denotes the trace-free symmetric part of the squared velocity gradient tensor.

$${\overline{S}}_{ij}^d=\frac{1}{2}({(\frac{\partial {\overline{u}}_i}{\partial x_j})}^2+{(\frac{\partial {\overline{u}}_j}{\partial x_i})}^2)-\frac{1}{3}{\delta }_{ij}{(\frac{\partial {\overline{u}}_k}{\partial x_k})}^2$$

(16)

2.3. Adaptive Mesh Refinement

The AMR is a method for dynamically changing the mesh density of an overall domain. Its advantage is that it can be refined automatically based on the specific interface positions. It primarily employs a face-oriented refinement strategy with the domain consisting of non-overlapping rectangular grids $G_{l,m}$:

$$G_l=\underset{m}{\cup }{G}_{l,m}$$

(17)

where a sequence of levels is defined

Mitchell [24] introduced the REFTREE data structure in AMR. It can be expressed as $l=0,1,\cdot \cdot \cdot ,L$

$$T(G)=\left\{\Omega ,\left\{C\left({\nu }_i\right)\right\}\right\}$$

(18)

where $\Omega ={\left\{v_i\right\}}_{i=0}^M$ denotes a group of nodes, and a bunch of children $C(v_i)$ are included in each $v_i\in \Omega$.

The computational domain is automated to be subdivided into lattices, and the precision of the physics boundaries and characteristics of the flow relies on the lattice sizes. When the WT consists of a great amount of fine lattices, the boundaries are considered smooth. Thus, the hydrodynamic calculations are precise, and the flow field is accurately characterized. For the WT boundary, the bouncing boundary conditions are assigned; this is a simple direct method applicable to both static and dynamic boundaries. In this way, the boundary node is a fluid node immediately adjacent to a solid node, with the solid boundary lying between the two. Details of the method for handling boundaries can be found in ref. [25]. Since the focus of the current work is mainly on the study of wake characterization, the AMR method [26] is recognized as an efficient method to improve the simulation accuracy of blade and wake characteristics by dynamically assigning fine meshes only where they are of interest.

The AMR is realized by means of an ochre lattice structure, which provides the possibility of utilizing a non-uniform lattice structure. Hence various spatial scales can be applied at various locations in the domain of the fluid. The width of the grid is selected as the length of the filter in the LES calculations, and the grid is modified dynamically in the wake region characterized by the vorticity magnitude. As a result, those flow vortices can be fully resolved. The fine and coarse grids have various spatial as well as temporal scales. This is specifically effective because the spatial and temporal scales remain constant throughout the domain, which enables constant Courant–Friedrichs–Lewy (CFL) condition as well as the sound velocity. In addition, an interpolation algorithm is required to provide communication between the different levels of the grid, details of which are given in the paper by Yuan et al. [27].

3. Simulation Setting

In the boundary condition setting, the boundary treatment format is designed using the boundary treatment method of the Lattice Boltzmann Method. Heuristic boundary conditions are a class of boundary treatments that work directly on the density or temperature distribution function directly from the physical nature.

The periodic format is applied to periodic boundary conditions. As an example, a mesoscopic particle on a periodic boundary exits from the left end, i.e., enters from the right end, in the case of a left-right periodic boundary condition.

This type of format should be used for solid wall boundary conditions. As an example, for the lower boundary, the macroscopic velocity should be zero for a no-slip boundary condition. For mesoscopic particles, it is collision and then rebound on the boundary. At the migration step, the second outer layer particles are emitted outward and rebound equally to the original lattice point after hitting the solid wall boundary located between the outermost and second outer layers.

Structural Modeling and Calculation Setup

The WT used in this paper is a three-bladed structure with a blade length of 6.95 m and a tower height of 12 m, as seen in Figure 1. The size of the wind tunnel used for calculations in the present work is 200 m × 60 m × 60 m. In all numerical simulations, the turbine is also located 50 m downstream from the inlet. The inlet is installed as a turbulence-free velocity inlet with a constant mean velocity profile in the vertical direction at the inlet, and the outlet is set to atmospheric pressure; the ground is set as a non-slip wall, and the remaining boundaries are symmetrical. The domain structure max level is set to 8 in order to assign fine lattices to the turbine surface and the wake region.

The computational model uses the WALE turbulence model, and the parameter Cw is 0.2. During model validation, the WT computational time step is designed to be 0.05 s, i.e., each time step, the WT rotates by 12°, and the computational time is 12 s. The maximum solution size is 8 m in the computational domain, and the solution scales in the tower, blade, and wake regions are 0.0625 m, 0.03125 m, and 0.125 m, respectively. According to the stability parameter, it can be judged that the calculation has converged when the length of calculation is 12 s, so the 12 s instantaneous state is selected for analysis in the subsequent analysis.

Figure 2 illustrates the adaptive mesh refinement of the WT wake. The mesh in the neighborhood of the turbine wake is automatically recognized based on the complexity of the flow. It is clear from the figure that the mesh is refined and encrypted in the wake computation region, thus accurately capturing the spatiotemporal characteristics of the turbine wake flow.

4. Numerical Results and Discussions

Figure 2 illustrates the adaptive mesh refinement of the WT wake. The mesh in the neighborhood of the turbine wake is automatically recognized based on the complexity of the flow. It is clear from the figure that the mesh is refined and encrypted in the wake computation region, and the spatiotemporal characterization of WT wake is accurately captured.

Figure 3 illustrates the three-dimensional vorticity equivalent surface at the instant of 12 s, where the vorticity equivalent surfaces are colored using the velocity amplitude; the vorticity equivalent face value is 7.2. As displayed in Figure 3a, it is plainly observed that the three-dimensional vortex ring structure of seven circles WT wake is smooth when the incoming velocity is 7 m/s. In the previous work of WT wake [18,28], the tip vortices are broken up by the strong deformations of the helices. Nonetheless, to obtain a better understanding, the detailed mechanism of tip vortex breakdown is reported in Figure 3. Inside the black box of Figure 3a, the secondary flow gradually appears on the main three-dimensional vortex ring, starting from the eighth vortex ring. The intensity of the secondary flow increases along the WT wake direction, and the main three-dimensional vortex ring ends up being gradually broken by the secondary flow on the main vortex ring. In the far field of the WT wake (>4D), the main vortex ring interacts, mixes, and gradually evolves into coherent structures of turbulence. A large number of turbulent low-speed areas directly appear behind the WT tow.

Inside the discrete blue box of Figure 3a, it is clearly captured that secondary flow mainly occurs in the vortex ring under shear force in the direction of incoming flow, the soft S-wave and Kelvin–Helmholtz instability occur in the main vortex ring of the near field, which gradually enhances along the direction of inflow.

As observed in Figure 3b, one can see that the three-dimensional vortex ring structure of two circles WT wake is smooth when the incoming velocity is 10 m/s. Inside the black box of Figure 3b, the strong secondary flow starting from the third vortex ring occurs on the main vortex ring; the main vortex rings are wrenched by the secondary flow. In the near field of the WT wake (>3D), these vortex rings interact, mix, and gradually evolve into turbulent coherent structures of the vortex.

Compared with Figure 3a, the intensity of secondary flow is obviously enhanced, and the crushing position of the vortex ring is advanced in Figure 3b. Meanwhile, the strong S-wave and Kelvin–Helmholtz instability occur in the main vortex ring near the field due to increasing shear force in the direction of incoming flow.

As displayed in Figure 3c, it can be seen that the three-dimensional vortex ring structure of one circle WT wake is very smooth when the incoming velocity is 13 m/s. Inside the black box of Figure 3c, the strong secondary flow starting from the second vortex ring occurs on the main vortex ring; the main vortex rings are strongly wrenched by the secondary flow. At the near field of the WT wake(>2D), these vortex rings interact, mix, and gradually evolve into turbulent coherent structures of the vortex. These very strong vortex streets behind the cylinder are mixed with the main vortex ring and quickly evolve into a turbulent flow structure.

For shorter inter-spiral distances, the instability is indeed observed to occur earlier and is captured for increasing load conditions or with gradually refined geometries consisting of increasing blades (Felli et al., 2008) [29]. Meanwhile, it was also found that when the linear growth of the S-wave reaches a certain amplitude, secondary instability is induced. Figure 3 further demonstrates that as the wake gradually develops, the vortex spacing and the vortex core radius of the tip vortex increase, the spiral vortex becomes irregular, the large-scale vortex breaks up into small-scale vortexes, gradually annihilates, and the intensity of the secondary flow gradually increases along the direction of the WT wake. As the inflow velocity increases, the turbulence generation and the coherent structure destabilization are increasingly accelerated, and the vortex ring becomes rougher earlier and breaks up at the same time. Along with the increase of the incoming velocity, the Kelvin–Helmholtz instability is gradually enhanced, which accelerates the vortex ring’s distortion and rupture. The tip vortices and the KH instability are affected by the coherent structures induced by the hub. This phenomenon reveals that the vortex of hub originates in some cases, which depends on the incoming flow conditions and the turbine geometry. Instability of tip vortex system is promoted by the coherent structures behind the hub, as demonstrated by Kang et al. (2014) [30] about a turbine.

To analyze the change of the vortex volume and coherent structure, the x-directional cross-sectional view allows us to clearly visualize and analyze the variation of the vortex volume and coherent structure at the blade tip, blade root, and behind the WT cylinder in the same position from the WT.

Figure 4 presents the vorticity magnitude contours on the central cut plane (x = 0) at 12 s, when the inflow velocity is 7 m/s, 10 m/s, and 13 m/s, respectively, and where the vortex equivalence surface is colored by the velocity magnitude.

In the black box of Figure 4a, it can be viewed that the spiral vortex structure of the WT wake is regular when the inlet velocity is 7 m/s. With the evolution of time, the blade tip vortex gradually breaks up and dissipates. In the long green delineated box in Figure 4a, the vortex shedding behind the pillar and the blade tip vortex mutual induction promotes the coherent structure. In the far field (>4D) of the WT wake, the main vortex rings interact, mix, and gradually evolve into a coherent turbulent structure. A large number of turbulent low-velocity regions appear directly behind the WT wake. In the discrete yellow box of Figure 4a, it can be seen that the vortices behind the cylinder are better preserved and transported further downstream.

As indicated in Figure 4b, it is clearly noted that when the inlet velocity is 10 m/s, the vortex intensity is significantly enhanced compared with Figure 4a. In the black box of Figure 4b, the main vortex ring is broken into smaller vortex structures starting from the third vortex ring. In the near field (>3D) of the turbine wake, these vortex rings interact, mix, and gradually evolve into a turbulent coherent structure of the vortex. Compared with Figure 4a, the turbulence intensity is significantly reinforced, and the breakup position of the regular spiral vortex rings in Figure 4b is advanced. Also, there is a very strong vortex street appearing behind the cylinder, as can be visualized in the discrete yellow box in Figure 4b.

It is obvious from Figure 4c that the vortex magnitude is further enhanced when the inlet velocity is 13 m/s. In the black box of Figure 4c, the regular spiral vortex rings start a strong secondary flow from the second vortex ring. The main vortex ring is strongly impacted by the secondary flow, and in the near field (>2D) of the fan wake, these vortex rings interact, mix, and gradually evolve into a turbulent, coherent structure of vortices. The very strong vortex street behind the cylinder can be seen in the discrete yellow box in Figure 4c, mixing with the main vortex ring and rapidly evolving into a turbulent structure.

From Figure 4, it is observed that the blade tip vortex on the vertical cross section at the inlet velocity = 10 m/s has a shorter duration compared with the incoming flow velocity of 7 m/s, the location of the destroyed is closer to the WT, and the location of the transformation into turbulence is advanced, and the blade root vortex under the condition of the inlet velocity of 13 m/s shows obvious turbulence characteristics with a larger diffusion range. With the increase of the incoming velocity, the intensity of the near vortex gradually increases.

In Figure 4, we further find that the two-dimensional vorticity distribution along the streamline can clearly capture the wake flow behind the column tower disturbing the tip separation vortices, and the intensity of the interference is gradually increasing. With the increase of inflow speed, the interference intensity of wake flow behind the column towers to the separation vortices at the blade tip increases gradually. Throughout the process of phagocytosis, the shape of the vortex N gradually becomes narrow, while the shape of the wake vortex behind the intermediate column tower remains good. This indicates that the middle large eddy structure plays a leading role during the process of blade tip separation vortexes engulfing the entire WT wake. In addition, another important phenomenon is that the wake vortices behind the center pillar tower can simultaneously engulf multiple tip vortices in the peripheral shear bands.

In order to better analyze the relationship between the magnitude of the inflow velocity and the variation characteristics of the WT wake, several points were taken within 6D distance behind the WT wake, and several sets of points were taken at different locations for more detailed analysis, as shown in Figure 5.

To investigate the influence of different positions of the WT on the wake characteristics in the initial state, three typical locations are selected to analyze the velocity fluctuation, which is illustrated in Figure 6.

Figure 6 displays the velocity fluctuation at different locations when the incoming flow velocity is 7 m/s, 10 m/s, and 13 m/s, respectively. As can be seen in Figure 6, the behavior of the velocity varies at different locations with the same initial conditions. When the inflow flow velocity is 7 m/s, the velocity fluctuation remains stable with time and maintains a uniform oscillation around the mean value. The gradient of actual velocity change above the mean value is small, and the gradient of actual velocity change below the mean value is large. When the inflow velocity is 10 m/s, the actual inflow velocity is mostly higher than the mean value in the first 2 s, and then it tends to stabilize with the smallest velocity change. When the inflow velocity is 13 m/s, the velocity gradient increasingly increases. From Figure 6a, it can be further found that the velocity fluctuation at the blade tip almost always maintains a certain regularity, which indicates that the wake flow at the blade tip behind the WT is still laminar when the incident flow velocities are 7 m/s, 10 m/s, and 13 m/s.

Compared with Figure 6a, it can be noticed that the velocity fluctuation is affected by the root of the blade, and the regularity of the fluctuation is significantly reduced. From Figure 6b, it can be presented that the mean value of the velocity fluctuation increases slightly with the increase of the inflow velocity. From Figure 6b, it can be further observed that a certain regularity is still maintained at the blade root, which indicates that the wake at the blade root behind the WT is still laminar at incoming velocities of 7 m/s, 10 m/s, and 13 m/s, respectively.

As can be seen from Figure 6c, the velocity fluctuations become irregular due to the WT axis. As the inflow velocity increases, the amplitude of the velocity fluctuation increases, and the regularity decreases. The velocity fluctuation is more regular when the inflow velocity is small. The mean value of velocity fluctuations is significantly lower than the mean value at the blade tip due to the effect of the WT axis. Compared with Figure 6a, it is found that the relationship between the velocity fluctuation range and the inflow velocity changes from positive to negative. From Figure 6c, it can be further found that the velocity fluctuation range is relatively large and remains regular at the tower back, and the inflow velocity of 7 m/s, which indicates that the wake at the back of the tower is still laminar at the inflow velocity of 7 m/s. However, at the tower back, the velocity fluctuation range is significantly lower than that at the blade tip, and the mean value of the velocity fluctuation is markedly lower than that at the blade tip. However, at the tower back, the velocity fluctuation is a random signal at inflow velocities of 10 m/s and 13 m/s, which indicates that the wake at the location behind the WT tower has developed into a turbulent state at inflow velocities of 10 m/s and 13 m/s.

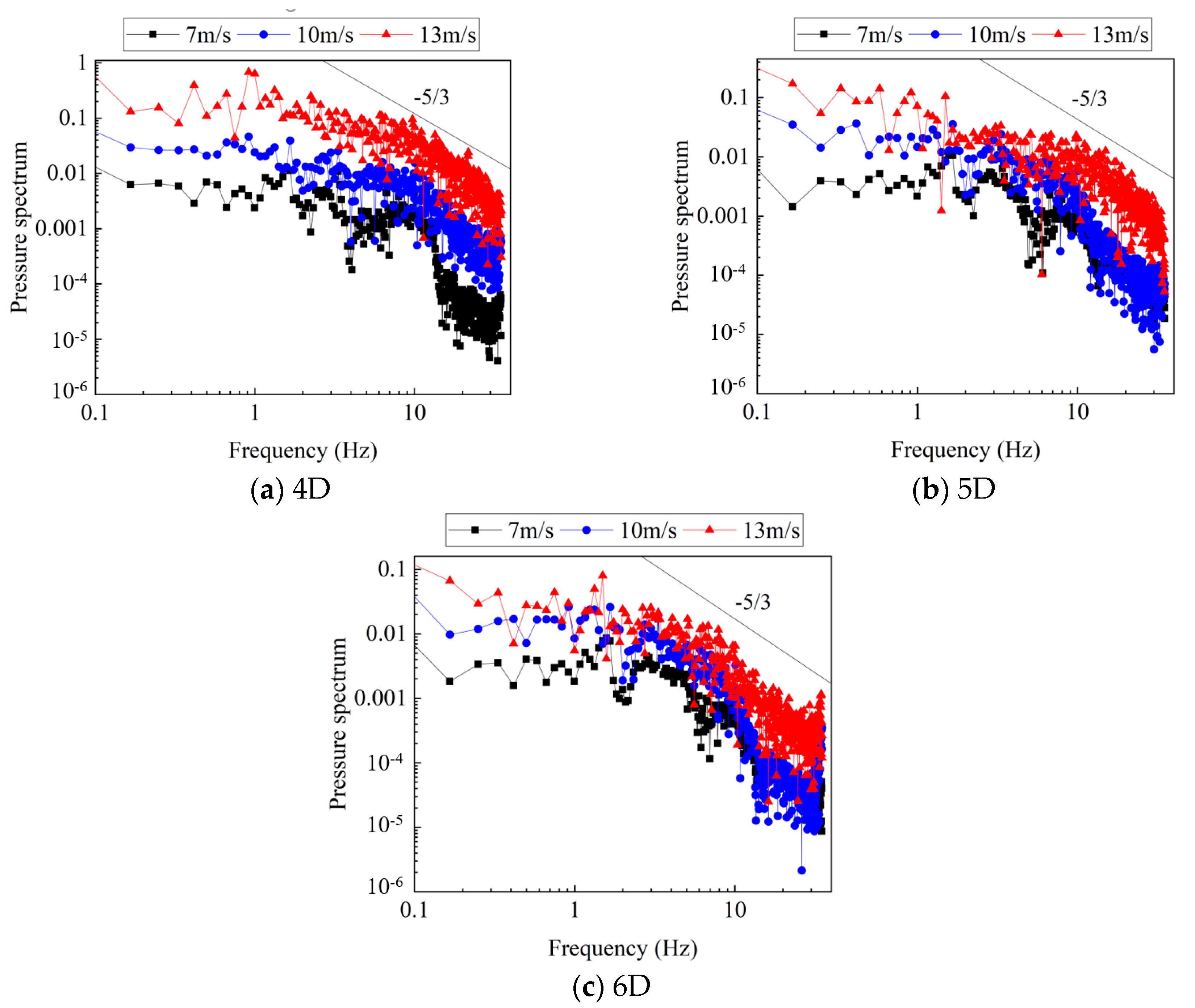
To study the wake characterization of WTs in the far field, several sets of pressure data in the far field (>4D) were selected to convert time domain signals to frequency domain signals using the Fast Fourier Transform (FFT).

Figure 7 represents the power spectrum density in the far field of the WT at the blade tip for three different incoming flow velocity conditions. In addition, the −5/3 slope of the inertial frequency range in the Kolmogorov theory of isotropic homogeneous turbulence is reported. From Figure 7, it can be found that the PSD shows an overall decreasing trend, and with the inflow velocity increases, the PSD curve converges to the −5/3 slope in Kolmogorov’s homogeneous anisotropic turbulence theory, which indicates that the far-field turbulence begins to converge to isotropy owing to the weakening coherence of the flow. The unsteady process of the blade tip vortex produces smaller-scale vortices, leading to more uniform and isotropic turbulence at the far field of the WT wake, as demonstrated by Antonio et al. (2021) [28].

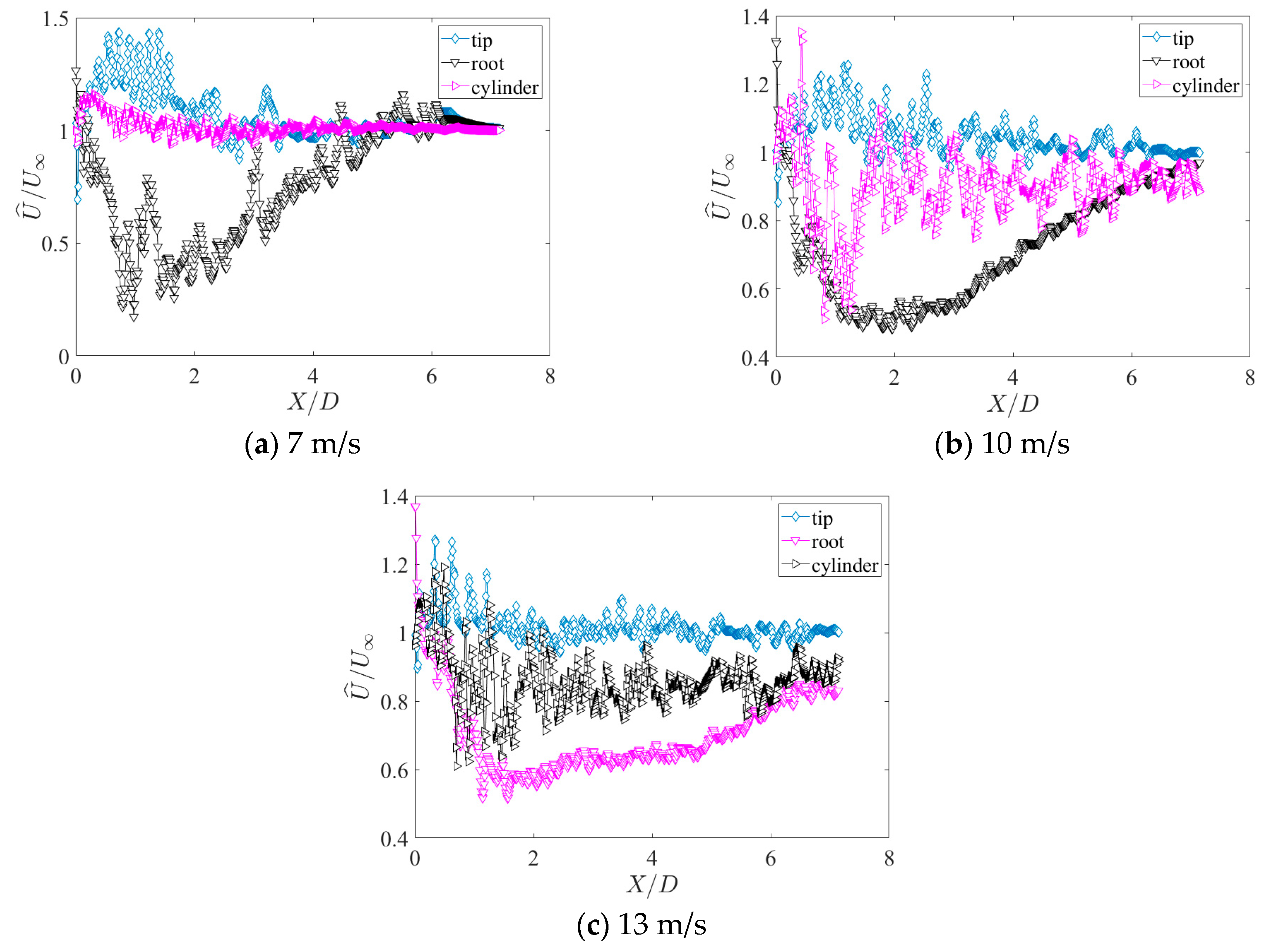
To investigate the correlation which exists between the velocity variation of the WT wake field and the magnitude of the inflow velocity, a portion of the line data in the WT wake field was selected to analyze the velocity distribution and velocity fluctuation of the WT wake field.

Figure 8 reveals the velocity distribution of the WT wake at different locations in the X-direction for different incoming velocities. From Figure 8, we can see that the average velocities at different locations in the far field of the WT show a tendency to change toward the initial velocity as the distance increases from the WT. The difference is that the blade tip and the blade root display opposite behavior in the process of changing toward the initial velocity. The magnitude of the mean velocity in the near field at the blade tip is higher than the initial wind velocity, while the magnitude of the mean velocity in the near field at the blade root is below the initial wind velocity. The mean velocity at the tower’s back position fluctuates around the initial incoming velocity with a small range of fluctuation. It can be concluded that the vortex at the tip of the blade has an enhancing effect on the velocity in the wind field, while the vortex at the root of the blade has a weakening effect on the velocity, and the effect of the vortex on the mean velocity gradually decreases over increasing distance.

As the incoming velocity increases, the mean velocity distribution changes significantly. First of all, it can be found that the overall trend of the mean velocity fluctuation at the blade tip does not change much, but it still shows the trend of fluctuation first and then flattening. The mean velocity at the blade root also remains below the initial velocity in the near field of the WT wake and then converges to the initial velocity. Most notably, the range of fluctuations in the mean velocity behind the wind column increases substantially when the inlet velocity is 10 m/s compared with Figure 8a. This is due to the fact that the vortices behind the WT pylons interact with the vortices at the top of the blades, which enhances the mutual induction and keeps the velocity fluctuating.

It can be found that the mean velocity distribution in the wake of the WT is strongly influenced by the increase of the inflow velocity and gradually deviates from the initial inflow velocity in Figure 8a–c. In particular, the mean velocity distribution behind the WT axis changes most obviously with the magnitude of the inflow velocity.

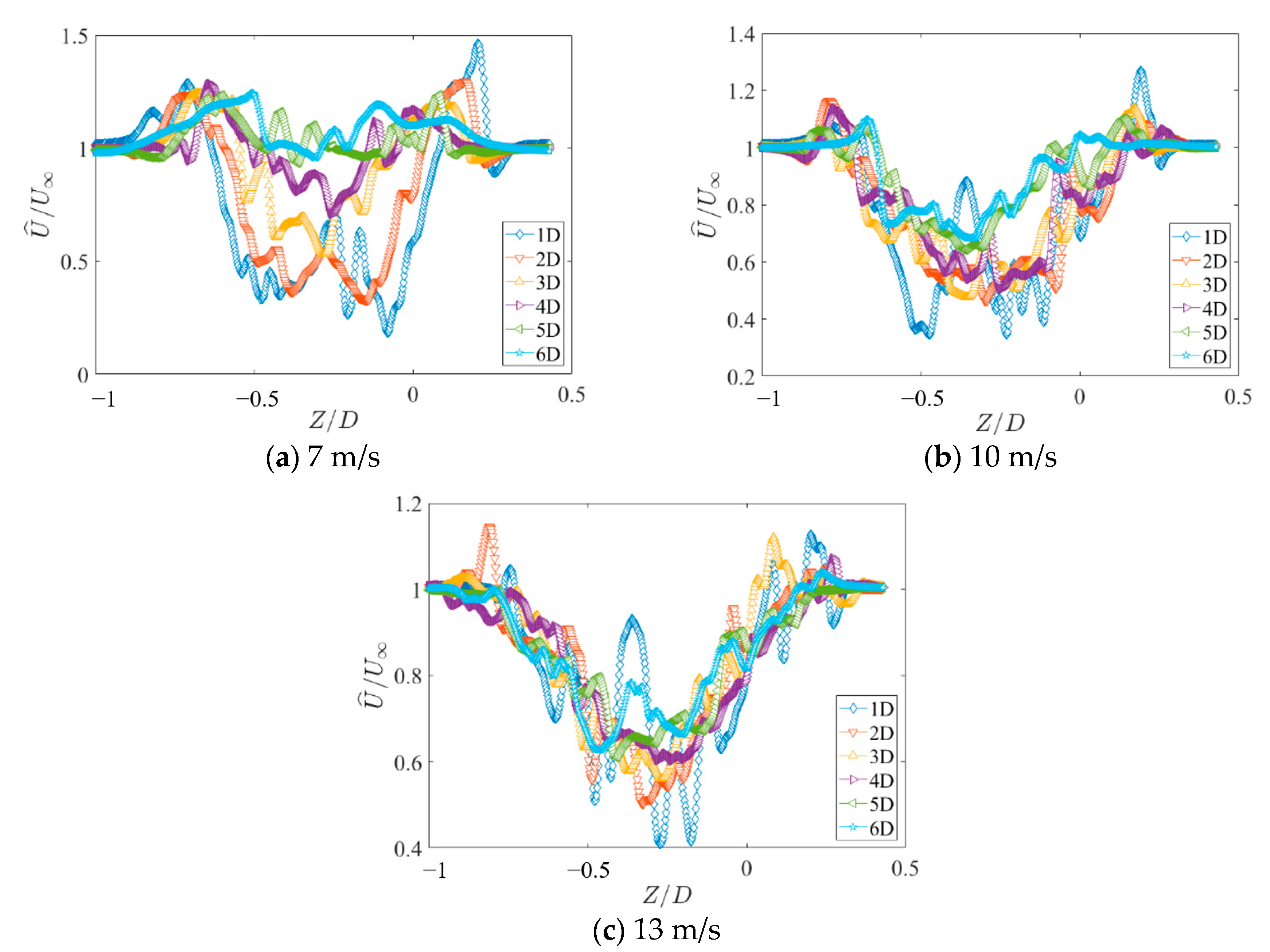
Figure 9 illustrates the velocity distribution of the WT wake in the Z-direction at different locations from the WT for different inflow velocities. From Figure 9, it is evident that the fluctuation range of the average velocity is larger in the near field of the wake stream than in the far field of the wake stream, and the fluctuation range of the average velocity decreases as the location is further away from the WT, and the average velocity tends to be the same as the initial inlet velocity. Near the WT axis center, the fluctuation range is significantly larger than the fluctuation range on both sides of the location farther from the WT axis. As observed in Figure 9, the velocity distribution asymmetrically appears and is distributed around the centerline of the WT hub. This is attributed to the vortex dissipation in the near-field wake and the mixing of fluids with different velocities in the wake area, leading to an asymmetric distribution. As the distance from the WT increases, the velocity distribution in the radial direction also changes roughly from “M” to “V” shape.

Compared with Figure 9a,b, it can be found that the increase of the inflow velocity increases the fluctuation range of the mean velocity distribution in the WT wake. The asymmetric distribution of the mean velocity distribution in the Z-direction becomes more obvious with the increase of the inflow velocity. Compared with Figure 9a–c, it is further obtained that the mean velocity distribution in the Z-direction gradually becomes compact with the increase in inflow velocity. The influence of distance on the mean velocity distribution is weakened, and the range of fluctuation is gradually reduced.

5. Conclusions

In this paper, the WT wake characteristics at different incoming velocities have been investigated, and the WT wake has been simulated by lattice Boltzmann method, large eddy simulation, and grid adaptive encryption. Some conclusions are presented.

First of all, the secondary flow occurs in the vortex ring under shear force in the direction of incoming flow; the S-wave and the Kelvin–Helmholtz instability occur in the main vortex ring, mainly due to the instability of the vortex ring interface with small disturbance of shear velocity along the direction of flow velocity. Along the mainstream direction, the S-wave and Kelvin–Helmholtz instability are gradually increasing in the main vortex ring, and three-dimensional disturbances are inevitable when it evolves along the flow direction. With increasing incoming flow, the S-wave and Kelvin–Helmholtz instability are increasingly enhanced due to increasing shear force in the flow direction.

Moreover, as time progresses, the regular spiral vortex ring is effectively broken, and secondary flow appears. The spiral vortex spacing decreases with increasing inflow velocity, and the location and time of secondary flow occurrence is advanced by increasing inflow velocity, and the mutual induction between the blade tip vortices accelerates the destabilization process. The wake flow turns turbulent earlier, and the three-dimensional disturbance of the vortex ring at the corresponding position increases.

Furthermore, the slope of the curve is close to the Kolmogorov slope of isotropic turbulence, as seen by the pressure signal power spectral density plot, and this trend is further strengthened downstream. It indicates that the WT wake has evolved into an isotropic and consistent turbulent structure in the far field.

In addition, it can be clearly observed that with the increase of inflow velocity, the dissipation of the vortex at the blade tip is accelerated, the shear effect is enhanced, and the mixing of fluids with different velocities leads to an asymmetric distribution of the mean velocity at the WT centerline.

Finally, the present results provide some insight into the evolution of the WT wake into understanding an isotropic coherent turbulent structure and the morphological changes of the vortices. The spatiotemporal evolution of the turbulent coherent structure provides insight into the physical mechanisms of wake flow in far-field WTs.