Abstract
The current limited efficiency and reliability of tidal current turbines (TCTs) have posed significant challenges in effectively harnessing tidal stream energy. To address this issue, this paper undertakes both numerical and experimental studies to explore the advantages of swept blades over conventional straight blades in terms of energy capture efficiency and cavitation resistance. It is found that both the sweep length and sweep angle of the blade can influence the power generation efficiency of the TCT. For the particular swept blade investigated in this study, the highest power coefficient is achieved when the sweep length is 0.544 m and the sweep angle is 28.88°. The research also demonstrated that the swept-blade TCT shows a higher power generation efficiency than the straight-blade TCT across a broad range of rotor speeds. To be precise, with the swept blades, the power coefficient of the TCT can be improved by 5–17%, depending on the tip speed ratio. Additionally, swept blades exhibit a superior cavitation resistance. This is evidenced by their higher cavitation numbers across all tip speed ratios in comparison to conventional straight blades.
1. Introduction
In light of the rapid depletion of traditional fossil fuels and increasing concerns about climate change, there has been significant interest in renewable energy sources in recent years, such as wind [1], wave [2], tidal current [3], solar power [4], and so on. Among the various renewable energy sources, tidal current energy emerges as a particularly attractive option as it is more sustainable and predictable and has a higher energy density compared to wind [5]. The estimates of the global potential of tidal energy generation vary, but it is widely agreed that tidal stream energy capacity could exceed 120 GW globally. It has been estimated that tidal stream energy could theoretically supply more than 150 TW/h per annum, well in excess of all domestic electricity consumption in the UK. This represents a potential total global market size of up to 90 GW of generating capacity [6]. However, due to the limited efficiency and reliability of the existing tidal current turbine (TCT) technology, today we still lack an efficient and dependable approach to tidal stream energy extraction [7].
In contrast to the extensive research conducted on enhancing the efficiency of wind turbine blades, the study on improving the energy capture efficiency of TCT blades remains relatively limited. This disparity may be attributed to the perception that TCTs operate similarly to wind turbines, leading researchers to naturally assume that established theories for designing wind turbine blades, such as Betz theory [8], blade element momentum (BEM) theory [9], Glauert theory [10], Wilson method [11], and multi-objective optimization methods [12], as well as other methods reviewed in [13] and [14], can be directly applied to TCT blade design.
In recent years, biomimetic technologies inspired by various biological characteristics have emerged as promising approaches for enhancing wind turbine blade design [15]. For example, to reduce the flow separation on blade surfaces, an owl wing-section airfoil and the non-smooth leading-edge shape of owl wings were studied in [16], finding that the power coefficient of the wind turbine can be increased by 17.7% by optimizing the wavelength and amplitude of the non-smooth leading edge of the blade. Inspired by the distinctive profile of the owl wing and the herringbone groove feature of owl feathers, the blade of a 200 W horizontal axis wind turbine was redesigned [17]. It was discovered that the incorporation of the herringbone groove structure facilitated the generation of vortices, leading to enhanced flow attachment. Consequently, this design modification effectively reduced the pressure on the leeward surface of the blade, ultimately resulting in a notable improvement in the energy capture efficiency of the blade. Taking inspiration from the leading-edge protuberances found on the pectoral fin of humpback whales, a passive fluid control device was developed in [18] for the blades of a 25 kW horizontal axis wind turbine. It was found that the leading-edge protuberances effectively stabilized and increased the power output of the turbine. For instance, at a pitch angle of , the power coefficient and the tip speed ratio (TSR) of the blade have 17.67% and 13.42% increments when it is equipped with leading-edge protuberances. When the wind speed is 8 m/s, the output power variation is reduced from 87.4% to 41.9%. In the case of the starting wind speed of 4 m/s, the output power can be increased from 786.46 W to 1.5 kW. Similar leading-edge tubercles have also been found to offer advantages in enhancing the blade performance of vertical-axis wind turbines [19]. However, a further study of this biomimetic feature revealed that the presence of leading-edge tubercles had adverse effects on turbine performance when subjected to wind speeds m/s [20]. Nevertheless, when tubercles were placed over 60% of the blade span, the adverse backflow area could be eliminated at a wind speed of m/s. This implies that biomimetic features may exhibit distinct functionalities when the turbine operates under different operating conditions. On the other hand, to mitigate the detrimental emission of infrasound from rotating wind turbine blades, a wind turbine blade with semi-cylindrical rings was studied in [21], drawing inspiration from the body features of beetles. The results from both numerical and experimental studies have shown that the application of semi-cylindrical rings not only reduced the infrasound emission by 8.3% but also led to an increase in the power coefficient of the wind turbine to varying extents at different TSRs.
In addition to the aforementioned studies that concentrated on enhancing the surface features of blades, researchers have also devoted significant efforts to studying swept wind turbine blades. This kind of research was further motivated by a pivotal discovery that swept-back bird wings can generate lift by creating leading-edge vortices [22]. For example, the investigation into the application of swept design on 750 kW, 1.5 MW, 3 MW, and 5 MW wind turbines, as detailed in [23], revealed that the amount of tip sweep had the most significant impact on blade loads and the overall power generation efficiency. The work in [24] investigated the aerodynamic characteristics of swept wind turbine blades utilizing a numerical analysis method. It unveiled that the swept-forward shape near the wing root enhanced the power coefficient at lower TSRs, while the distal swept-backward shape increased the power coefficient at higher TSRs. The relevant studies were recently extended to investigating the dynamics of swept wind turbine blades. For example, swept wind turbine blades were examined in [25] through a combined numerical and experimental approach. The research exhibited a notable increase in blade torque ranging from 10.2% to 14%. Another study [26], involving the swept-back blade for a 100 kW wind turbine, revealed that although both straight blades and swept blades have similar natural frequencies, their mode shapes are quite different due to the couplings in the flapwise-torsion directions introduced by the back-swept geometry. This coupling alters the aeroelastic response of the blade, which results in different loads in the operational conditions. The load analysis results show that the swept blade experienced significantly lower fatigue loads compared to the straight blade, with reductions of up to 29% for the flapwise bending moment and 31% for the edgewise bending moment. In terms of ultimate loads, the swept blade exhibited an almost 50% reduction in the blade root edgewise load compared to the straight blade, although the flapwise ultimate load remained similar for both blade configurations. Overall, the findings presented in these studies indicate that swept wind turbine blades offer not only enhanced efficiency but also increased durability during operation compared to straight wind turbine blades. Furthermore, to facilitate the design of swept wind turbine blades, a study was conducted recently in [27] to enable the extension of the standard BEM specifically for the design of swept blades. As a result, an efficient correction model was derived. This correction model was subsequently employed to simulate swept-blade geometries for the IEA 15 MW reference wind turbine. The results exhibited excellent agreement with lifting line simulations.
The above studies not only yield promising results for enhancing the efficiency and reliability of wind turbine blades but also inspire the design of efficient TCT blades. However, the operating environment of a TCT is completely different from that of a wind turbine. For example, the kinematic viscosity of water at is , while the kinematic viscosity of air at is . The significant disparity in kinematic viscosity between water and air necessitates that TCT blades operate under vastly different Reynolds numbers compared to wind turbine blades. Take the 1.2 GW SeaGen tidal turbine as an example, it is characterized by the unique twin rotors design, with each rotor having a rated capacity of 600 kW. Its rotor diameter is 32 m and its tip speed is 12 m/s, resulting in a corresponding Reynolds number of . In comparison, the Vestas V44 wind turbine also has a rated capacity of 600 kW. It features a larger rotor diameter of 44 m and a faster tip speed of 65 m/s. However, its corresponding Reynolds number is much lower, standing at only 9. Thus, it is imperative to undertake dedicated research specifically for the design of TCT blades, rather than simply applying the findings from wind turbine blade design to the design of TCT blades. Hence, recent endeavors have been dedicated to the exploration of design techniques tailored specifically for TCT blades. For example, in the experimental study conducted in [28], the tubercle leading-edge TCT blade was investigated, revealing the efficiency gain effect at low tip speed ratios. Furthermore, in [29], a novel concept of the TCT blade was examined through numerical analysis, where surface bumps were applied on the TCT blade surface, showing an increase in the lift-to-drag ratio with a decrease in the sound pressure level of the blade. Although the research on swept TCT blades is relatively limited, some studies have been carried out in this area as well. For example, the impact of swept blades on the performance and hydrodynamics of a bidirectional horizontal-axis TCT was numerically investigated in [30] using OpenFOAM(4.1) software. The results revealed distinct effects of forward- and backward-swept blades on the TCT’s performance and hydrodynamics. Specifically, the forward-swept blade demonstrated a 4.3% decrease in the blade load, while the back-swept blade generated 3.2% more energy at a TSR of 6. This suggests that various sweep designs can yield diverse effects on the performance and hydrodynamics of TCTs. However, which is the best sweep design for the TCT blades remains a question today.
In addition, unlike wind turbines that operate in the air, the TCTs operate entirely submerged in water. This distinction introduces unique challenges, as the varying hydrostatic pressures at different water depths (when the blades are at different azimuth positions) and the presence of moving waves on the water surface can result in significant fluctuations in hydrodynamic pressure exerted on the surfaces of the TCT blades. These fluctuations, particularly at the blade tip, can lead to unsteady cavitation, posing a significant reliability challenge for the TCT blades [31]. To address this issue, recent efforts have been undertaken in [32]. In that study, a revised theoretical analysis of hydrodynamics optimization for horizontal-axis TCTs was presented based on the improved inverse BEM theory, and the blade’s cavitation resistance performance was evaluated based on the minimum pressure on the blade surface. Then, by combining a cavitation prediction model with the improved inverse BEM theory, an anti-cavitation design for the blade was optimized. Simulation and experimental results demonstrated the effectiveness of this design approach in achieving more reliable TCT blades. However, the study reported in [32] merely focused on straight TCT blades. The influence of sweep design on the cavitation resistance performance of TCT blades remains unclear.
Hence, the novelty of this paper does not lie in developing a new concept of swept blades. Instead, its significance lies in addressing two fundamental questions regarding swept TCT blades:
- (1)
- Which sweep design is more effective in improving the energy capture efficiency of TCT blades?
- (2)
- How does the sweep design affect the cavitation resistance of TCT blades?
These two fundamental questions have remained unanswered in previous studies, highlighting the knowledge gap in the current field. By offering valuable insights and providing answers to these questions, this paper will make a significant contribution to the understanding and advancement of the design of swept TCT blades.
The remaining sections of this paper are organized as follows. Section 2 presents the establishment of a numerical model for the swept-blade TCT. In Section 3, an investigation is conducted to explore the advantages of swept blades over straight blades in terms of energy capture efficiency under various operating conditions of the TCT. The objective is to determine the optimal design for the swept blades. Section 4 focuses on calculating the cavitation number of the swept blade at different TSRs, aiming to assess the blade’s cavitation resistance capacity when operating in challenging marine environments. Section 5 presents the experimental verification of the effectiveness of the sweep design in enhancing the TCT’s power generation efficiency. Finally, the paper concludes with several key conclusions in Section 6.
2. Numerical Model of a Swept-Blade TCT
To facilitate the study, a numerical model of a swept blade is established in Ansys Fluent. In the process, the straight blade for a 10 kW TCT will be used as a reference. In this study, the hydrofoil MNU26 is utilized to establish a numerical model for the swept blade. The choice of the hydrofoil MNU26 is justified by two key factors: firstly, it demonstrates an exceptional hydrodynamic performance, particularly at high Reynolds numbers [33]; secondly, it exhibits a robust resistance to cavitation [31]. The profile of the hydrofoil MNU26 is illustrated in Figure 1. Additionally, detailed profile data of MNU26 can be also found in Appendix A.
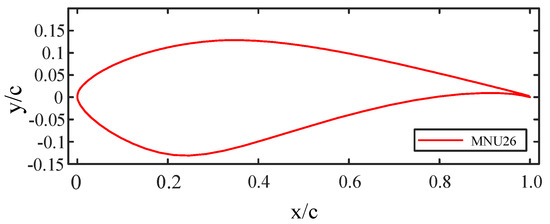
Figure 1.
The profile of the hydrofoil MNU26.
Since the energy capture efficiency of a TCT blade is heavily influenced by the lift-to-drag ratio and the angle of attack of the hydrofoil at each section of the blade, the investigation begins by examining the hydrofoil MNU26 for its optimal lift-to-drag ratio and angle of attack. To facilitate this investigation, a numerical model of a blade section is developed in ANSYS Fluent using the hydrofoil MNU26. Computational fluid dynamics (CFD) calculations are performed to estimate the hydrodynamic lift and drag forces generated by the blade section at various angles of attack. Subsequently, the lift-to-drag ratios of the hydrofoil at different angles of attack are derived from the calculated lift and drag forces. To execute this investigation, a rectangular computational domain is defined in Ansys Fluent and a blade section created using the hydrofoil MNU26 is placed in the computational domain, as shown in Figure 2. In the figure, ‘C’ represents the chord length of the hydrofoil. The computational domain spans a length of 10C, a width of 1C, and a height of 6C. The blade section’s span also measures 1C. For the calculations, the value of ‘C’ is set to 0.1 m.

Figure 2.
The fluid domain and blade section for investigating the performance of the hydrofoil MNU26.
It is well known that the accuracy of CFD calculation results is significantly affected by the number of elements used for meshing the computational domain and the object being investigated. Usually, the more elements used for meshing, the more accurate the calculation results will be. However, increasing the number of elements will increase the computational complexity. To balance the accuracy and computational burden, the lift force generated by the blade section is calculated as an indicator to examine the convergence of the CFD calculations in the following, so that an appropriate number of meshing elements can be determined.
Accordingly, we set the angle of attack of the hydrofoil to be , define the velocity of the water flow to be 4 m/s, and mesh the computational domain as depicted in Figure 3a. Then, we gradually increase the number of elements, and calculate the corresponding lift force generated by the blade section. The variation trend of the lift force with the number of elements is illustrated in Figure 3b.

Figure 3.
Convergence check for investigating the hydrofoil MNU26. (a) Meshed computational domain. (b) Lift force versus the number of elements.
Figure 3b reveals that the calculated lift force is noticeably affected by the number of elements, particularly when using coarse meshes to discretize the computational domain. However, the calculated lift force begins to converge once the number of elements surpasses . Considering these computational findings, a balance between accuracy and computational efficiency is sought, leading to a decision to utilize elements in the subsequent CFD calculations for investigating the hydrofoil MNU26.
Subsequently, we mesh the computational domain using elements and calculate the lift and drag forces generated by the blade section when the angle of attack of the hydrofoil increases from to . Then, based on the obtained lift and drag forces, the lift and drag coefficients and the corresponding lift-to-drag ratio of hydrofoil MNU26 are calculated. The calculation results are shown in Figure 4.

Figure 4.
Hydrodynamic performance of the hydrofoil MNU26. (a) Lift and drag coefficients. (b) Lift-to-drag ratio.
From Figure 4a, it is found that the drag coefficient shows a monotonically increasing trend with the increase in the angle of attack. In contrast, the lift coefficient initially increases and then decreases with the increase in the angle of attack. Since the energy capture efficiency of a hydrofoil relies on both lift and drag, determining the optimal angle of attack solely based on either of them is challenging. Thus, the lift-to-drag ratio is used as an indicator to identify the best angle of attack for the hydrofoil. Figure 4b illustrates that the lift-to-drag ratio gradually increases with the angle of attack and reaches its maximum value of 39.32 at an angle of attack of 8°. Therefore, it can be concluded that the optimal angle of attack for the hydrofoil MNU26 is 8°, which will then be utilized in the subsequent development of the numerical model for the TCT rotor using the BEM theory.
In the study, the numerical model of a straight-blade TCT is also developed for comparison. To maintain simplicity, both the straight blade and the swept-blade designs were created using the same type of hydrofoil: MNU26. The parameters of the straight blade and the specification of the TCT are listed in Table 1 and Table 2, respectively.

Table 1.
Parameters of the straight blade.

Table 2.
Specification of the TCT.
From Table 1, it is seen that along the span direction, the straight blade consists of 11 elements with varying chord lengths and twist angles. When designing the swept blade, the same hydrofoil chord lengths and twist angles as the corresponding sections of the straight blade are maintained. However, a sweep angle will be introduced at a specific span position, indicated by the sweep length L from the blade tip. From this position onwards, the corresponding hydrofoils will be parallelly displaced backwards along the sweep line defined by the sweep angle , as depicted in Figure 5.
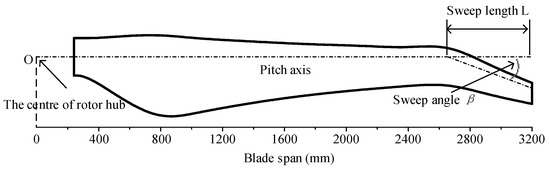
Figure 5.
Swept blade characterized by the sweep length L and sweep angle .
By modifying the values of the sweep angle and sweep length L, various blade sweep designs necessary for conducting numerical studies can be readily obtained. Then, the numerical models of the TCT’s 3-bladed rotor can be established using the straight blade and swept blade created. The rotor modelling results are shown in Figure 6, in which both types of rotors have the same diameter of 6.4 m for facilitating comparison.
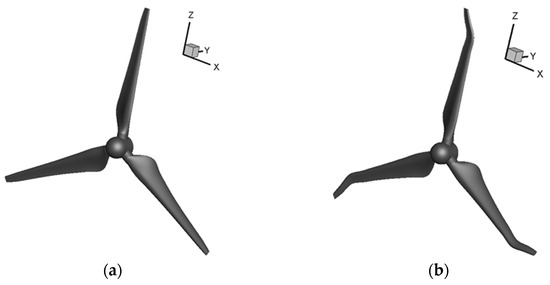
Figure 6.
Numerical models of the TCT rotors with different types of blades. (a) Rotor with straight blades. (b) Rotor with swept blades.
Subsequently, we place the 3-bladed rotors into a cylindrical computational domain for performing CFD calculations, as shown in Figure 7. To calculate the torques generated by the rotors, the computational domain consists of a stationary domain and a rotating domain that rotates at the same rotational speeds as the rotors. The stationary domain has a diameter of 12.8 m (i.e., 4R) and a length of 19.2 m (i.e., 6R). The rotating domain has a diameter of 7.2 m and a length of 0.96 m. The rotors are placed in the center of the rotating domain. The ‘inlet boundary’ of the computational domain is defined as the velocity of the water flow at infinity, while the ‘outlet boundary’ is defined as the opening pressure, which is 165,678.6 Pa as selected in [20]. The ‘inlet boundary’ is set at an upstream distance of 2R to the rotor, and the ‘outlet boundary’ is at a downstream distance of 4R from the rotor. The medium is seawater, of which the density is 1025 and the dynamic viscosity is . Hence, the TCT will operate at a high Reynolds number of . In the numerical calculations, the RNG K-epsilon (K-ɛ) turbulence model and unstructured grids are adopted.
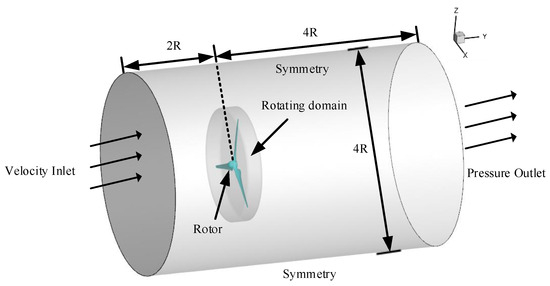
Figure 7.
The computational domain and boundary conditions of the numerical model.
As a large cylindrical computational domain will lead to a huge computational burden, the following numerical study opts for computationally efficient steady-state calculations instead of transient simulation calculations to maintain an acceptable level of computational efficiency. Herein, it should be noted that since the purpose of this study was mainly to demonstrate the superiorities of swept blades over conventional straight blades in terms of energy capture efficiency and cavitation resistance, the velocity profile of the tidal current along the water depth is not considered for simplicity.
To ensure the reliability of the numerical calculation results, several additional measures were implemented during the meshing process for both the computational domain and the numerical rotor model. These measures comprise:
- (1)
- ‘Face sizing’—Refers to the size of meshing elements on the blade surfaces. The higher the number of elements used for meshing, the smaller the face sizing. In this study, the initial size of the elements is set to 0.006 m. However, the size may be adjusted based on the number of elements;
- (2)
- ‘Body sizing’—A cylindrical region, with a diameter of 8 m and a height of 5.4 m, was defined to enclose the rotating domain. ‘Body sizing’, which is set to 0.18 m, refers to the size of the cells for meshing the cylindrical region. In the modelling, the body of influence control is utilized to create finer meshes in the cylindrical region;
- (3)
- ‘Inflation’—An inflation region is designed around the blade during the modelling process of this study. The inflation region consists of five layers. The thickness of the fifth inflation layer, representing the maximum thickness of the inflation layer, is set to 0.01 m. The thickness growth rate of these five layers in the direction of inflation is 1.2.
To ease understanding, examples of the meshing results of the rotating domain and the cylindrical region around the blade is given in Figure 8.

Figure 8.
An example of the meshing results of the rotating domain and cylindrical region. (a) Rotating domain. (b) Cylindrical region around the blade.
After successfully establishing the numerical model of the TCT rotor, the convergence check of the CFD calculation is conducted to determine the optimal number of elements for meshing the computational domain. Herein, the power coefficient of the TCT serves as an indicator for the convergence check. In the calculation, the velocity of the water flow is set to 1.2 m/s and the rotating speed of the rotor is set to 16 rpm. The power coefficient of the TCT is calculated by
where is the torque generated by the rotor (N·m), is the angular speed of the rotor (rad/s), represents the density of seawater (), is the swept area of the TCT rotor (), is the velocity of the water flow at infinity (m/s).
Since only steady-state flow is considered in this study, the flow motion will be simulated using the steady-state solver in Ansys Fluent, specifically employing a multiple reference frame (MRF) model. The MRF model serves as a steady-state approximation, allowing for the assignment of different rotational and/or translational speeds to individual cell zones. The equations governing flow within each moving cell zone are solved using the moving reference frame equations. When a zone is stationary, these equations simplify to their stationary forms. At the interfaces between cell zones, a local reference frame transformation is implemented to facilitate the utilization of flow variables from one zone for calculating fluxes at the boundary of the adjacent zone. Then, with the aid of the MRF model, the CFD calculations were performed and the trend of the obtained with the increasing number of elements is shown in Figure 9.
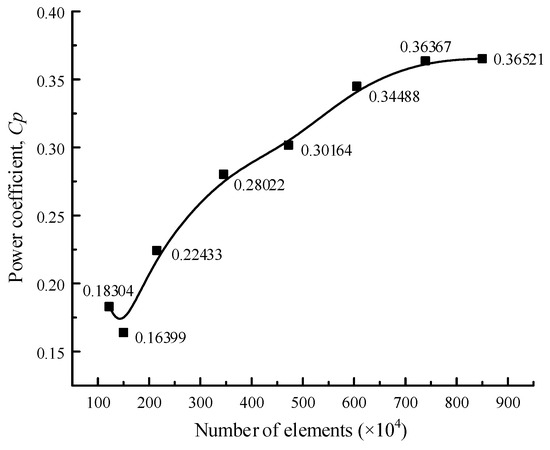
Figure 9.
Convergency check for the CFD calculation.
From Figure 9, it is found that with the increase in the number of elements, the calculated value of shows a generally increasing trend and eventually converges to 0.36521 when the number of elements reaches . Therefore, is identified as the optimal number of elements, which will be used to mesh the computational domain in the subsequent numerical studies.
3. Numerical Study of Swept Blade Efficiency
This section focuses on a numerical investigation into the energy capture efficiency of swept blades through CFD calculations. Additionally, the energy capture efficiency of straight blades is calculated as well for comparison purposes. As mentioned earlier, varying swept-blade designs can yield different energy capture efficiencies. Thus, optimizing the design of the swept blade becomes crucial to maximize the extraction of kinetic energy from tidal streams. Since the swept blade is characterized by the sweep length L and sweep angle , the power coefficient of a swept-blade TCT is calculated under different sweep lengths and sweep angles to evaluate its performance. In the present study, the sweep angle changes from to , and the sweep length L is set to 0.272 m, 0.544 m, 1.088 m, and 1.36 m, respectively, which correspond to the blade sections from elements No. 10 to 11, No. 9 to 11, No. 7 to 11, and No. 6 to 11 in Table 1. When the velocity of the water flow is 1.2 m/s and the rotor speed is 16 rpm, the power coefficients of the TCT obtained under different sweep lengths and sweep angles are shown in Figure 10, where indicates the TCT that is equipped with three conventional straight blades.
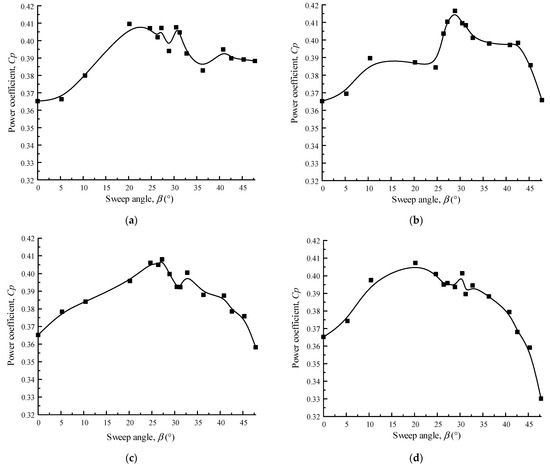
Figure 10.
The results of the TCT power coefficient under different swept designs of the blade. (a) L = 0.272 m. (b) L = 0.544 m. (c) L = 1.088 m. (d) L = 1.36 m.
From Figure 10, it is found that
- The power coefficient of the TCT with conventional straight blades (i.e., when ) is 0.36521;
- Both the sweep length and sweep angle of the blade can influence the power coefficient of the TCT;
- The power coefficient of the swept-blade TCT increases first and then decreases with the increase in sweep angle . This suggests that not all sweep designs can enhance the efficiency of the TCT. The efficiency of the TCT can be increased only when an appropriate sweep design is adopted. If either the sweep length or the sweep angle is excessively large or small, the efficiency of the TCT will significantly decline, particularly in scenarios featuring a substantial sweep length;
- Under different sweep lengths L, the power coefficient reaches the different maximum values at different sweep angles . For example, when L = 0.272 m, reaches its maximum value of 0.4096 at ; when L = 0.544 m, reaches its maximum value of 0.41654 at ; when L = 1.088 m, reaches its maximum value of 0.40801 at ; and when L = 1.36 m, reaches its maximum value of 0.40733 at ;
- Among all the scenarios examined, the maximum power coefficient that the swept-blade TCT can achieve is 0.41654, which is 14% higher than that of the TCT using three conventional straight blades.
In order to uncover the factors behind the higher energy capture efficiency of the swept blade compared to the conventional straight blade, the pressure coefficients of both types of blades are calculated using the following equation:
where refers to the reference pressure (), which is the same as the ‘outlet pressure’ in Figure 7. represents the radial distance of the blade section of interest to the hub center (m), and is the pressure on the surface of the blade section of interest ().
Part of the calculation results of obtained at different azimuth positions when L = 0.544 m and are shown in Figure 11. In the figures, the corresponding results of for the straight blade are also plotted using black solid curves. To facilitate a meaningful comparison, the x-axis of the figures is a normalized axis, indicated by the ratio of ‘X/C’. Herein, ‘C’ represents the chord length of the blade section, while ‘X’ denotes the distance from the leading edge of the blade section.

Figure 11.
Pressure coefficient curves.
It is known that the area enclosed by the pressure coefficient curve reflects the difference in the pressures acting on the pressure and suction sides of the hydrofoil. A larger enclosed area signifies a greater pressure difference, indicating that the hydrofoil can generate increased lift. From Figure 11, it is found that despite the difference in the spanwise locations of the blade section and the azimuth positions, the hydrofoils in the swept blade always show a larger area than the corresponding hydrofoils in the straight blade, although they are exactly the same in geometry. This fully proves that even with the same hydrofoil, the sweep design can result in a higher energy capture efficiency of the blade. To further comprehend this phenomenon, the areas enclosed by the pressure coefficient curves in Figure 11 are calculated and the results are tabulated in Table 3.

Table 3.
Areas enclosed by the pressure coefficient curves in Figure 11.
From Table 3, it can be seen that the swept blade sections consistently exhibit larger area values compared to their corresponding sections in the straight blade at the corresponding azimuth and location. However, the most interesting thing is that the positive contribution of the sweep design to the blade efficiency is not uniform. Instead, it is different at different spanwise locations of the blade section and the azimuth positions of the blade. Despite this, its contribution is consistently more pronounced in sections closer to the blade tip. For example, in all three azimuth scenarios, the area increments obtained at m and 3.064 m are always larger than those obtained at m.
Finally, the energy capture efficiency of the swept blade at different TSRs is investigated to understand whether the swept blade could maintain a higher efficiency over the most speed range of the TCT. In the study, the power coefficient of a three-bladed TCT is also used as the indicator of the efficiency of the swept blade. Then, when the velocity of the water flow m/s and the rotor speed of the TCT changes from 8 to 18 rpm, the corresponding values of are calculated using the following equation. The calculation results are listed in Table 4.
where R refers to the radius of the TCT rotor (m).

Table 4.
Tip speed ratio for different scenarios.
Subsequently, the power coefficient of the three-bladed TCT is calculated at various TSRs . The calculation results are shown in Figure 12a. Herein, the corresponding of the straight-blade TCT is also calculated for comparison. To facilitate analysis, the increment in generated by the swept blades is calculated as well at different TSRs, and the results are shown in Figure 12b.

Figure 12.
Power coefficients of the TCT at different tip speed ratios. (a) Power coefficient. (b) Power coefficient increment.
From Figure 12, it is clearly seen that after using the swept blades, the power coefficient of the TCT increases to varying extents, 5~17%, at all TSRs of interest. Therefore, it can be concluded that the swept-blade TCT can work more efficiently than the straight-blade TCT across a broad range of rotor speeds, spanning from 8 to 18 rpm.
4. Numerical Study of Swept-Blade Cavitation Resistance
This section focuses on conducting an additional numerical study to evaluate the influence of sweep design on the cavitation resistance capability of TCT blades. The cavitation resistance is of utmost importance in ensuring the long-term reliability of TCT blades in harsh marine environments. In the study, the cavitation number will be used as an indicator of the cavitation-resistance performance of the blade. The higher the value of , the smaller the probability that the air bubbles can be released from the water on blade surfaces, and thus the more reliable the blade will be [34].
Considering the pressures on the blade surfaces to be unevenly distributed, the pressure distributions on both the pressure side and suction side surfaces of the blade are calculated in order to obtain a dependable assessment of the anti-cavitation performance of the blades. The results obtained when the velocity of the water flow is 1.2 m/s and the rotor speed is 16 rpm are illustrated in Figure 13.

Figure 13.
Pressure distribution on the blade surfaces. (a) Pressure side—straight blade. (b) Suction side—straight blade. (c) Pressure side—swept blade. (d) Suction side—swept blade.
Observation of Figure 13 reveals that irrespective of whether straight or swept blades are used, smaller pressure areas consistently appear at the leading edge of the suction side surface in the tip section of the blade. This phenomenon implies that these specific areas are more prone to experiencing cavitation. Then, we use the minimum pressure in these areas and the following equation to calculate the cavitation number , i.e., [35]
where is the minimum pressure observed in the tip section of the blade (), and is the vapor pressure of the seawater at .
The calculation results of σ obtained when the TCT rotates at different TSRs are shown in Figure 14.
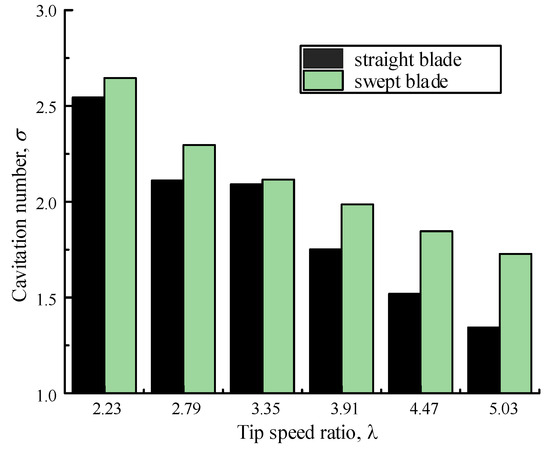
Figure 14.
Cavitation number obtained at different TSRs.
From Figure 14, it is found that
- (1)
- As expected, the calculated value of the cavitation number decreases gradually with the increase in TSR. This trend suggests that blade tip cavitation is more likely to occur at higher rotor speeds;
- (2)
- In all instances of TSRs examined, the cavitation number value for the swept blade consistently surpasses the corresponding value for the straight blade. This finding indicates that the swept blade exhibits a superior cavitation resistance capacity over the conventional straight blade when operating in harsh marine environments;
- (3)
- Finally, the increment in the cavitation number value achieved by the swept blade tends to increase with the increase in TSR. This suggests that as the rotor speed rises, the advantages of the swept blade in terms of anti-cavitation become more pronounced compared to the straight blade.
5. Verification Test
To verify the advantages of the swept blade over the straight blade in terms of energy capture efficiency, an experimental study is carried out in this section. Herein, it is worth noting that the testing of TCT blades is usually performed in a controlled water tank environment without a free surface [28]. Within such a controlled testing environment, the TCT blades’ performance, e.g., lift-to-drag ratio, energy capture efficiency, and cavitation resistance, is solely determined by the design of the blades. Therefore, conducting tests in a water tank without a free water surface is considered ideal for assessing the blade design technology. Nevertheless, neglecting the free water surface may result in imprecise predictions and unreliable evaluations of a TCT’s performance in real-life applications, where a free water surface is consistently present. Moreover, the presence of the free surface introduces additional complexities such as wave generation, wave–current interaction, and air entrainment, all of which can significantly impact the TCT’s efficiency, power output, and cavitation resistance. Therefore, testing the TCT in a water tank with a free surface can provide more accurate and reliable results, ultimately enhancing our understanding of the TCT’s true potential in practical usage.
For the above reasons, the testing of the TCT was carried out in a tidal current tank with a free water surface, as shown in Figure 15. The tank is 14.65 m long, 5.9 m wide, and 1.8 m high. The inner and outer diameters of the two ends of the tank are 2.4 m and 5.9 m, respectively. The test area is in the middle of the front channel of the tank, on the front wall of which a glass window is installed to facilitate observation, see Figure 15a. The size of the glass window is 2.7 m × 1.3 m. As shown in Figure 15b, the water in the tank is accelerated by two axial flow pumps in the rear channel, rated at 10 kW and 15 kW, respectively. The flow velocity in the tank can reach up to 2 m/s. During the test, the water depth in the tank was kept at 1 m.

Figure 15.
The tidal current tank used for the verification test. (a) Front view. (b) Side view.
To implement the experimental study, three 1:16 scale models of straight blades, and three 1:16 scale models of swept blades with the sweep design of L = 0.544 m and , as well as two TCT hubs for assembling the blades are made using photocuring 3D-printing technology. The normal layer thickness of the 3D printer is 0.1 mm, and the printing accuracy is 0.05 mm, which is good enough to ensure the correctness of the hydrofoil profile of the blade at any span position and the smooth surface of the blade. High-toughness photosensitive resin is chosen as the 3D-printing material to ensure that the ‘blades’ are strong enough to withstand the hydrodynamic loads during the test. Each printed blade is 0.185 m long and weighs 16 g. As shown in Figure 16, the printed blades and hubs are finally assembled to form two TCT rotors, mounted at a height of 0.4 m above the tank bed. The TCT rotors will drive a 220V permanent magnet (PM) synchronous generator to generate electricity.

Figure 16.
Two TCT rotors and their assemblies. (a) Rotor with straight blades. (b) Rotor with swept blades. (c) Hub. (d) 220V PM generator.
As depicted in Figure 17, the experimental setup involves the connection of a 220V PM generator to an external load bank through power cables. The total voltage across the resistors connected to the load bank serves as an indicator of the power generated by the TCT. This voltage is measured using a data acquisition system and displayed on a laptop for further analysis. Such a configuration enables power takeoff and data acquisition during the experimental study.

Figure 17.
Power takeoff and measurement system used in the test.
During the test, the velocity of the water flow in the water tank is managed by controlling the rotational speed of the axial flow pumps. In order to guarantee the accurate test of the power generation efficiency of the TCT, the ‘flow velocity versus pump speed’ curve was carefully calibrated in advance. The calibration results are shown in Figure 18. It is necessary to note that in the figure, ‘flow velocity’ refers to the average velocity of the water flow within the cross-section of the test area in the water tank.
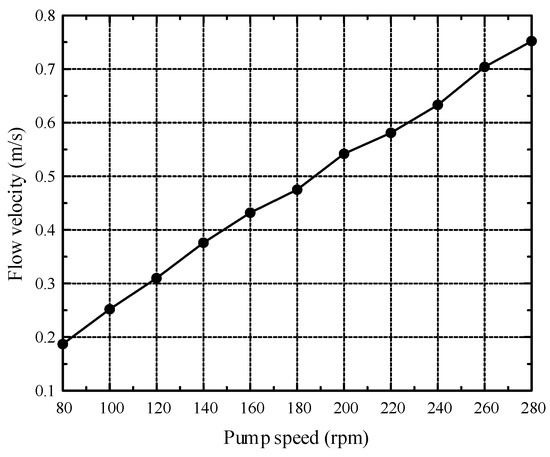
Figure 18.
Flow velocity vs. pump speed.
Then, we run the test across a range of flow velocities, spanning from 0.18 to 0.76 m/s, and collect power voltage data at each flow velocity over a duration of 2 min by using a sampling frequency of 2 kHz. The 2 min average power voltage data obtained at different flow velocities are shown in Figure 19. In the figure, the measured data for both types of TCTs are shown together for comparison.

Figure 19.
Output voltage of the TCTs at different flow velocities.
From Figure 19, it can be seen that
- (1)
- When the flow velocity is smaller than 0.252 m/s, neither the straight-blade rotor nor the swept-blade rotor rotates, indicating that both types of TCTs have a cut-in speed of about 0.252 m/s;
- (2)
- After reaching the cut-in speed, the rotors start to rotate and harness kinetic energy from tidal streams. Notably, across all corresponding flow velocities, the power voltages generated by the swept-blade TCT consistently surpass those generated by the straight-blade TCT. This suggests that the swept blade, thanks to its sweep design, exhibits a superior efficiency in capturing energy from tidal streams compared to the conventional straight blade.
6. Conclusions
To answer two fundamental scientific questions regarding the sweep design of TCT blades, numerical and experimental studies are conducted in this paper. From the work reported above, the following conclusions can be drawn:
- (1)
- Even at higher Reynolds numbers, the sweep design remains effective in enhancing the energy capture efficiency of the TCT blades. Both the sweep length and sweep angle of the blade play significant roles in influencing the power generation efficiency of the TCT. It is observed that under varying sweep lengths, the power coefficient attains its maximum value at different sweep angles. For the particular swept blade investigated in this study, the power coefficient reaches the highest at 0.41654 when the sweep length is 0.544 m and the sweep angle is , which is 14% higher than that of the TCT using conventional straight blades;
- (2)
- The contribution of the sweep design to efficiency enhancement varies with the span locations and the azimuth positions of the blade, but its contribution will become more significant in the tip section of the blade;
- (3)
- The swept-blade TCT shows a higher power generation efficiency than the straight-blade TCT across a broad range of rotor speeds, spanning from 8 to 18 rpm. To be precise, with the swept blades, the power coefficient of the TCT can be improved by 5–17%, depending on the TSR of the TCT rotor;
- (4)
- Under all TSRs examined, the cavitation number values for the swept blade are always larger than those for the straight blade. This suggests that the swept blade exhibits a superior cavitation resistance capacity over the conventional straight blade when operating in harsh marine environments. Moreover, the rise in the cavitation number associated with the swept blade tends to amplify with an increase in TSR. This implies that as the rotor speed escalates, the benefits of the swept blade in terms of anti-cavitation characteristics become more evident when contrasted with those of the straight blade.
Despite the encouraging results reported above, subsequent research will be conducted to further improve the power capture efficiency and cavitation-resistance performance of the TCT blades. This will involve a comprehensive exploration of the synergistic effects arising from the integration of multiple biomimetic features into the design of swept blades. The outcomes of this extended investigation will be reported in a separate research paper.
Author Contributions
Methodology, investigation, writing—original draft preparation, Y.Z.; conceptualization, methodology, investigation, supervision, writing—review and editing, W.Y.; supervision, funding acquisition, resources, project administration, K.W.; methodology, investigation, Y.C.; writing—review and editing, H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The work reported above was supported by the National Natural Science Foundation of China (52175089, 12002125) and the Natural Science Foundation of Hunan Province (2020JJ6020).
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to huge data size.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Profile data of the hydrofoil MNU26.
Table A1.
Profile data of the hydrofoil MNU26.
| No. of Point | Coordinates | ||
|---|---|---|---|
| x | y | z | |
| 1 | 1 | 0 | 0 |
| 2 | 0.9966 | 0.003137 | 0 |
| 3 | 0.99314 | 0.004139 | 0 |
| 4 | 0.98961 | 0.005151 | 0 |
| 5 | 0.98601 | 0.006171 | 0 |
| 6 | 0.98235 | 0.007196 | 0 |
| 7 | 0.97863 | 0.008224 | 0 |
| 8 | 0.97484 | 0.009259 | 0 |
| 9 | 0.97098 | 0.010301 | 0 |
| 10 | 0.96706 | 0.011348 | 0 |
| 11 | 0.963069 | 0.012403 | 0 |
| 12 | 0.95902 | 0.013465 | 0 |
| 13 | 0.954901 | 0.014539 | 0 |
| 14 | 0.95072 | 0.015622 | 0 |
| 15 | 0.94647 | 0.016719 | 0 |
| 16 | 0.94216 | 0.017829 | 0 |
| 17 | 0.93778 | 0.018954 | 0 |
| 18 | 0.93333 | 0.020093 | 0 |
| 19 | 0.92882 | 0.021245 | 0 |
| 20 | 0.92425 | 0.02241 | 0 |
| 21 | 0.91961 | 0.02359 | 0 |
| 22 | 0.9149 | 0.024787 | 0 |
| 23 | 0.91013 | 0.025997 | 0 |
| 24 | 0.90529 | 0.027224 | 0 |
| 25 | 0.90039 | 0.028464 | 0 |
| 26 | 0.89542 | 0.029719 | 0 |
| 27 | 0.89039 | 0.030989 | 0 |
| 28 | 0.88529 | 0.032274 | 0 |
| 29 | 0.88013 | 0.033572 | 0 |
| 30 | 0.8749 | 0.034887 | 0 |
| 31 | 0.86961 | 0.036215 | 0 |
| 32 | 0.86425 | 0.037558 | 0 |
| 33 | 0.85882 | 0.038915 | 0 |
| 34 | 0.85333 | 0.040285 | 0 |
| 35 | 0.84778 | 0.041666 | 0 |
| 36 | 0.84216 | 0.04306 | 0 |
| 37 | 0.83647 | 0.044467 | 0 |
| 38 | 0.83072 | 0.045886 | 0 |
| 39 | 0.8249 | 0.047319 | 0 |
| 40 | 0.81902 | 0.048765 | 0 |
| 41 | 0.81307 | 0.050226 | 0 |
| 42 | 0.80706 | 0.051699 | 0 |
| 43 | 0.80098 | 0.053185 | 0 |
| 44 | 0.79484 | 0.054682 | 0 |
| 45 | 0.78863 | 0.056193 | 0 |
| 46 | 0.78235 | 0.057714 | 0 |
| 47 | 0.77601 | 0.059245 | 0 |
| 48 | 0.76961 | 0.060782 | 0 |
| 49 | 0.76314 | 0.062328 | 0 |
| 50 | 0.7566 | 0.063883 | 0 |
| 51 | 0.75 | 0.065444 | 0 |
| 52 | 0.74333 | 0.067014 | 0 |
| 53 | 0.73667 | 0.068573 | 0 |
| 54 | 0.73 | 0.070128 | 0 |
| 55 | 0.72333 | 0.071676 | 0 |
| 56 | 0.71667 | 0.073216 | 0 |
| 57 | 0.71 | 0.074751 | 0 |
| 58 | 0.70333 | 0.076276 | 0 |
| 59 | 0.69667 | 0.077791 | 0 |
| 60 | 0.69 | 0.079299 | 0 |
| 61 | 0.68333 | 0.080795 | 0 |
| 62 | 0.67667 | 0.082279 | 0 |
| 63 | 0.67 | 0.083754 | 0 |
| 64 | 0.66333 | 0.085217 | 0 |
| 65 | 0.65667 | 0.086666 | 0 |
| 66 | 0.65 | 0.088103 | 0 |
| 67 | 0.64333 | 0.089527 | 0 |
| 68 | 0.63667 | 0.090934 | 0 |
| 69 | 0.63 | 0.092328 | 0 |
| 70 | 0.62333 | 0.093708 | 0 |
| 71 | 0.61667 | 0.095071 | 0 |
| 72 | 0.61 | 0.096418 | 0 |
| 73 | 0.60333 | 0.097748 | 0 |
| 74 | 0.59667 | 0.099058 | 0 |
| 75 | 0.59 | 0.100353 | 0 |
| 76 | 0.58333 | 0.101632 | 0 |
| 77 | 0.57667 | 0.10289 | 0 |
| 78 | 0.57 | 0.10413 | 0 |
| 79 | 0.56333 | 0.105351 | 0 |
| 80 | 0.55667 | 0.106549 | 0 |
| 81 | 0.55 | 0.107728 | 0 |
| 82 | 0.54333 | 0.108883 | 0 |
| 83 | 0.53667 | 0.110014 | 0 |
| 84 | 0.53 | 0.111124 | 0 |
| 85 | 0.52333 | 0.112209 | 0 |
| 86 | 0.51667 | 0.113266 | 0 |
| 87 | 0.51 | 0.114297 | 0 |
| 88 | 0.50333 | 0.115302 | 0 |
| 89 | 0.49667 | 0.116279 | 0 |
| 90 | 0.49 | 0.117228 | 0 |
| 91 | 0.48333 | 0.118151 | 0 |
| 92 | 0.47667 | 0.119044 | 0 |
| 93 | 0.47 | 0.119909 | 0 |
| 94 | 0.46333 | 0.120742 | 0 |
| 95 | 0.45667 | 0.12154 | 0 |
| 96 | 0.45 | 0.122304 | 0 |
| 97 | 0.44333 | 0.12303 | 0 |
| 98 | 0.43667 | 0.123717 | 0 |
| 99 | 0.43 | 0.124364 | 0 |
| 100 | 0.42333 | 0.124971 | 0 |
| 101 | 0.41667 | 0.125536 | 0 |
| 102 | 0.409999 | 0.126062 | 0 |
| 103 | 0.40333 | 0.126545 | 0 |
| 104 | 0.39667 | 0.126985 | 0 |
| 105 | 0.39 | 0.127382 | 0 |
| 106 | 0.38333 | 0.127732 | 0 |
| 107 | 0.37667 | 0.128032 | 0 |
| 108 | 0.37 | 0.128276 | 0 |
| 109 | 0.36333 | 0.128462 | 0 |
| 110 | 0.35667 | 0.128582 | 0 |
| 111 | 0.35 | 0.128635 | 0 |
| 112 | 0.34333 | 0.128618 | 0 |
| 113 | 0.33667 | 0.128532 | 0 |
| 114 | 0.33 | 0.128374 | 0 |
| 115 | 0.32333 | 0.128147 | 0 |
| 116 | 0.31667 | 0.12785 | 0 |
| 117 | 0.31 | 0.127486 | 0 |
| 118 | 0.30333 | 0.127054 | 0 |
| 119 | 0.29667 | 0.12656 | 0 |
| 120 | 0.29 | 0.126 | 0 |
| 121 | 0.28333 | 0.125376 | 0 |
| 122 | 0.27667 | 0.124688 | 0 |
| 123 | 0.27 | 0.123936 | 0 |
| 124 | 0.26333 | 0.12312 | 0 |
| 125 | 0.25667 | 0.122242 | 0 |
| 126 | 0.2500001 | 0.121298 | 0 |
| 127 | 0.24342 | 0.120303 | 0 |
| 128 | 0.23693 | 0.119261 | 0 |
| 129 | 0.23053 | 0.118173 | 0 |
| 130 | 0.22421 | 0.117039 | 0 |
| 131 | 0.21798 | 0.115863 | 0 |
| 132 | 0.21184 | 0.114648 | 0 |
| 133 | 0.20579 | 0.113395 | 0 |
| 134 | 0.19982 | 0.112103 | 0 |
| 135 | 0.19395 | 0.110779 | 0 |
| 136 | 0.18816 | 0.109419 | 0 |
| 137 | 0.18245 | 0.108025 | 0 |
| 138 | 0.17684 | 0.106604 | 0 |
| 139 | 0.17131 | 0.105151 | 0 |
| 140 | 0.16587 | 0.103672 | 0 |
| 141 | 0.16052 | 0.102168 | 0 |
| 142 | 0.15526 | 0.100639 | 0 |
| 143 | 0.15008 | 0.099085 | 0 |
| 144 | 0.14499 | 0.097509 | 0 |
| 145 | 0.13999 | 0.095913 | 0 |
| 146 | 0.13508 | 0.094297 | 0 |
| 147 | 0.13026 | 0.092663 | 0 |
| 148 | 0.12552 | 0.091008 | 0 |
| 149 | 0.12087 | 0.089336 | 0 |
| 150 | 0.11631 | 0.087651 | 0 |
| 151 | 0.11183 | 0.085948 | 0 |
| 152 | 0.10745 | 0.084235 | 0 |
| 153 | 0.10315 | 0.082507 | 0 |
| 154 | 0.09893 | 0.080764 | 0 |
| 155 | 0.09481 | 0.079015 | 0 |
| 156 | 0.09077 | 0.077252 | 0 |
| 157 | 0.08683 | 0.075487 | 0 |
| 158 | 0.08297 | 0.07371 | 0 |
| 159 | 0.07919 | 0.071922 | 0 |
| 160 | 0.07551 | 0.070134 | 0 |
| 161 | 0.07191 | 0.068338 | 0 |
| 162 | 0.0684 | 0.066539 | 0 |
| 163 | 0.06498 | 0.064738 | 0 |
| 164 | 0.06164 | 0.062932 | 0 |
| 165 | 0.0584 | 0.061132 | 0 |
| 166 | 0.05524 | 0.059329 | 0 |
| 167 | 0.05217 | 0.057528 | 0 |
| 168 | 0.04918 | 0.055726 | 0 |
| 169 | 0.04629 | 0.053932 | 0 |
| 170 | 0.04348 | 0.052137 | 0 |
| 171 | 0.04076 | 0.050349 | 0 |
| 172 | 0.03812 | 0.048561 | 0 |
| 173 | 0.03558 | 0.046787 | 0 |
| 174 | 0.03312 | 0.045017 | 0 |
| 175 | 0.03075 | 0.043257 | 0 |
| 176 | 0.02847 | 0.041508 | 0 |
| 177 | 0.02627 | 0.039764 | 0 |
| 178 | 0.02417 | 0.03804 | 0 |
| 179 | 0.02215 | 0.036323 | 0 |
| 180 | 0.02022 | 0.034622 | 0 |
| 181 | 0.01837 | 0.032929 | 0 |
| 182 | 0.01662 | 0.031264 | 0 |
| 183 | 0.01495 | 0.029608 | 0 |
| 184 | 0.01337 | 0.027973 | 0 |
| 185 | 0.01187 | 0.026346 | 0 |
| 186 | 0.01047 | 0.024753 | 0 |
| 187 | 0.00915 | 0.023169 | 0 |
| 188 | 0.00792 | 0.021609 | 0 |
| 189 | 0.00678 | 0.020072 | 0 |
| 190 | 0.00572 | 0.018547 | 0 |
| 191 | 0.00476 | 0.017056 | 0 |
| 192 | 0.00388 | 0.015569 | 0 |
| 193 | 0.00309 | 0.014094 | 0 |
| 194 | 0.00238 | 0.012606 | 0 |
| 195 | 0.00177 | 0.011096 | 0 |
| 196 | 0.00124 | 0.009445 | 0 |
| 197 | 0.0008 | 0.007656 | 0 |
| 198 | 0.00044 | 0.005684 | 0 |
| 199 | 0.00018 | 0.003633 | 0 |
| 200 | 0 | 0 | 0 |
| 201 | 0.000245 | −0.002549 | 0 |
| 202 | 0.000678 | −0.004584 | 0 |
| 203 | 0.000925 | −0.005491 | 0 |
| 204 | 0.006381 | −0.01743 | 0 |
| 205 | 0.016792 | −0.031576 | 0 |
| 206 | 0.031367 | −0.046492 | 0 |
| 207 | 0.049641 | −0.061655 | 0 |
| 208 | 0.07124 | −0.076713 | 0 |
| 209 | 0.09561 | −0.091093 | 0 |
| 210 | 0.122438 | −0.104309 | 0 |
| 211 | 0.151203 | −0.115726 | 0 |
| 212 | 0.181669 | −0.124578 | 0 |
| 213 | 0.213672 | −0.130235 | 0 |
| 214 | 0.247139 | −0.13131 | 0 |
| 215 | 0.283942 | −0.127757 | 0 |
| 216 | 0.323782 | −0.120293 | 0 |
| 217 | 0.367326 | −0.109093 | 0 |
| 218 | 0.414593 | −0.095249 | 0 |
| 219 | 0.465255 | −0.07966 | 0 |
| 220 | 0.518814 | −0.063236 | 0 |
| 221 | 0.574574 | −0.046894 | 0 |
| 222 | 0.631638 | −0.03152 | 0 |
| 223 | 0.688908 | −0.017904 | 0 |
| 224 | 0.745125 | −0.006688 | 0 |
| 225 | 0.798908 | 0.001698 | 0 |
| 226 | 0.84883 | 0.00707 | 0 |
| 227 | 0.893492 | 0.009517 | 0 |
| 228 | 0.931609 | 0.009395 | 0 |
| 229 | 0.962086 | 0.007279 | 0 |
| 230 | 0.983819 | 0.003889 | 0 |
| 231 | 0.996132 | 0.001014 | 0 |
| 232 | 1 | 0 | 0 |
References
- Shalby, M.; A Salah, A.; A Matarneh, G.; Marashli, A.; Gommaa, M.R. An investigation of a 3D printed micro-wind turbine for residential power production. Int. J. Renew. Energy Dev. 2023, 12, 550–559. [Google Scholar] [CrossRef]
- Shalby, M.; Elhanafi, A.; Walker, P.; Dorrell, D.G.; Salah, A.; Gomaa, M.R. Experimental investigation of the small-scale fixed multi-chamber OWC Device. Chin. J. Mech. Eng. 2021, 34, 124. [Google Scholar] [CrossRef]
- Chen, H.; Tang, T.; Ait-Ahmed, N.; Benbouzid, M.E.H.; Machmoum, M.; Zaim, M.E.-H. Attraction, challenge and current status of marine current energy. IEEE Access 2018, 6, 12665–12685. [Google Scholar] [CrossRef]
- Wang, X.; Yang, W.; Qin, B.; Wei, K.; Ma, Y.; Zhang, D. Intelligent monitoring of photovoltaic panels based on infrared detection. Energy Rep. 2022, 8, 5005–5015. [Google Scholar] [CrossRef]
- Goundar, J.N.; Ahmed, M.R. Marine current energy resource assessment and design of a marine current turbine for Fiji. Renew. Energy 2014, 65, 14–22. [Google Scholar] [CrossRef]
- EnergyBC. Estimate of Global Potential Tidal Resources. Available online: http://www.energybc.ca/cache/tidal3/tidalreserves.html (accessed on 11 December 2023).
- Zhou, Z.; Benbouzid, M.; Charpentier, J.-F.; Scuiller, F.; Tang, T. Developments in large marine current turbine technologies–A review. Renew. Sustain. Energy Rev. 2017, 71, 852–858. [Google Scholar] [CrossRef]
- Betz, A. Introduction to the Theory of Flow Machines; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Lanzafame, R.; Messina, M. Fluid dynamics wind turbine design: Critical analysis, optimization and application of BEM theory. Renew. Energy 2007, 32, 2291–2305. [Google Scholar] [CrossRef]
- Glauert, H. Aerodynamic Theory; Durand, W.F., Ed.; Chapter XI. Division, L. airplanes propellers, reprinted; Dover: New York, NY, USA, 1963; Volume 4, p. 191e5. [Google Scholar]
- Song, F.; Ni, Y.; Tan, Z. Optimization design, modeling and dynamic analysis for composite wind turbine blade. Procedia Eng. 2011, 16, 369–375. [Google Scholar] [CrossRef]
- Li, Y.; Wei, K.; Yang, W.; Wang, Q. Improving wind turbine blade based on multi-objective particle swarm optimization. Renew. Energy 2020, 161, 525–542. [Google Scholar] [CrossRef]
- Maalawi, K.Y.; Badawy MT, S. A direct method for evaluating performance of horizontal axis wind turbines. Renew. Sustain. Energy Rev. 2001, 5, 175–190. [Google Scholar] [CrossRef]
- Bavanish, B.; Thyagarajan, K. Optimization of power coefficient on a horizontal axis wind turbine using bem theory. Renew. Sustain. Energy Rev. 2013, 26, 169–182. [Google Scholar] [CrossRef]
- Siddiqui, N.A.; Asrar, W.; Sulaeman, E. Literature review: Biomimetic and conventional aircraft wing tips. Int. J. Aviat. Aeronaut. Aerosp. 2017, 4, 6. [Google Scholar] [CrossRef]
- Chen, K.; Yao, W.; Wei, J.; Gao, R.; Li, Y. Bionic coupling design and aerodynamic analysis of horizontal axis wind turbine blades. Energy Sci. Eng. 2021, 9, 1826–1838. [Google Scholar] [CrossRef]
- Gao, R.; Chen, K.; Li, Y.; Yao, W. Investigation on aerodynamic performance of wind turbine blades coupled with airfoil and herringbone groove structure. J. Renew. Sustain. Energy 2021, 13, 053301. [Google Scholar] [CrossRef]
- Lin, Y.; Chiu, P. Influence of leading-edge protuberances of fx63 airfoil for horizontal-axis wind turbine on power performance. Sustain. Energy Technol. Assess. 2020, 38, 100675. [Google Scholar] [CrossRef]
- Zhu, X.; Guo, Z.; Zhang, Y.; Song, X.; Cai, C.; Kamada, Y.; Maeda, T.; Li, Q. Numerical study of aerodynamic characteristics on a straight-bladed vertical axis wind turbine with bionic blades. Energy 2022, 239, 122453. [Google Scholar] [CrossRef]
- Ke, W.; Hashem, I.; Zhang, W.; Zhu, B. Influence of leading-edge tubercles on the aerodynamic performance of a horizontal-axis wind turbine: A numerical study. Energy 2022, 239, 122186. [Google Scholar] [CrossRef]
- Lv, J.; Yang, W.; Zhang, H.; Liao, D.; Ren, Z.; Chen, Q. A feasibility study to reduce infrasound emissions from existing wind turbine blades using a biomimetic technique. Energies 2021, 14, 4923. [Google Scholar] [CrossRef]
- Videler, J.; Stamhuis, E.; Povel, G. Leading-edge vortex lifts swifts. Science 2004, 306, 1960–1962. [Google Scholar] [CrossRef]
- Larwood, S.; Van Dam, C.P.; Schow, D. Design studies of swept wind turbine blades. Renew. Energy 2014, 71, 563–571. [Google Scholar] [CrossRef]
- Ikeda, T.; Tanaka, H.; Yoshimura, R.; Noda, R.; Fujii, T.; Liu, H. A robust biomimetic blade design for micro wind turbines. Renew. Energy 2018, 125, 155–165. [Google Scholar] [CrossRef]
- Hua, X.; Zhang, C.; Wei, J.; Hu, X.; Wei, H. Wind turbine bionic blade design and performance analysis. J. Vis. Commun. Image Represent. 2019, 60, 258–265. [Google Scholar] [CrossRef]
- Gözcü, O.; Kim, T.; Verelst, D.R.; McWilliam, M.K. Swept Blade Dynamic Investigations for a 100 kW Small Wind Turbine. Energies 2022, 15, 3005. [Google Scholar] [CrossRef]
- Fritz, E.K.; Ferreira, C.; Boorsma, K. An efficient blade sweep correction model for blade element momentum theory. Wind Energy 2022, 25, 1977–1994. [Google Scholar] [CrossRef]
- Shi, W.; Rosli, R.; Atlar, M.; Norman, R.; Wang, D.; Yang, W. Hydrodynamic performance evaluation of a tidal turbine with leading-edge tubercles. Ocean Eng. 2016, 117, 246–253. [Google Scholar] [CrossRef]
- Yang, W.; Alexandridis, T.; Tian, W. Numerical research of the effect of surface biomimetic features on the efficiency of tidal turbine blades. Energies 2018, 11, 1014. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, J.; Sun, K.; Guo, Y.; Guan, D. Influence of swept blades on the performance and hydrodynamic characteristics of a bidirectional horizontal-axis tidal turbine. J. Mar. Sci. Eng. 2022, 10, 365. [Google Scholar] [CrossRef]
- Singh, P.; Choi, Y. Shape design and numerical analysis on a 1 MW tidal current turbine for the south-western coast of Korea. Renew. Energy 2014, 68, 485–493. [Google Scholar] [CrossRef]
- Sun, Z.; Li, D.; Mao, Y.; Feng, L.; Zhang, Y.; Liu, C. Anti-cavitation optimal design and experimental research on tidal turbines based on improved inverse BEM. Energy 2022, 239, 122263. [Google Scholar] [CrossRef]
- Kim, S.; Singh, P.; Hyum, B.; Lee, Y.; Choi, Y. A study on the floating bridge type horizontal axis tidal current turbine for energy independent islands in Korea. Renew. Energy 2017, 112, 35–43. [Google Scholar] [CrossRef]
- Omelyanyuk, M.; Ukolov, A.; Pakhlyan, I.; Bukharin, N.; El Hassan, M. Experimental and numerical study of cavitation number limitations for hydrodynamic cavitation inception prediction. Fluids 2022, 7, 198. [Google Scholar] [CrossRef]
- Picanço, H.P.; Kleber Ferreira de Lima, A.; Dias do Rio Vaz, D.A.T.; Lins, E.F.; Pinheiro Vaz, J.R. Cavitation inception on hydrokinetic turbine blades shrouded by diffuser. Sustainability 2022, 14, 7067. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).