A Fast Dynamic Simulation Method of an Active Distribution Network with Distributed Generations Based on Decomposition and Coordination
Abstract
1. Introduction
2. Classification and Modeling of the Dynamic Components of the ADN
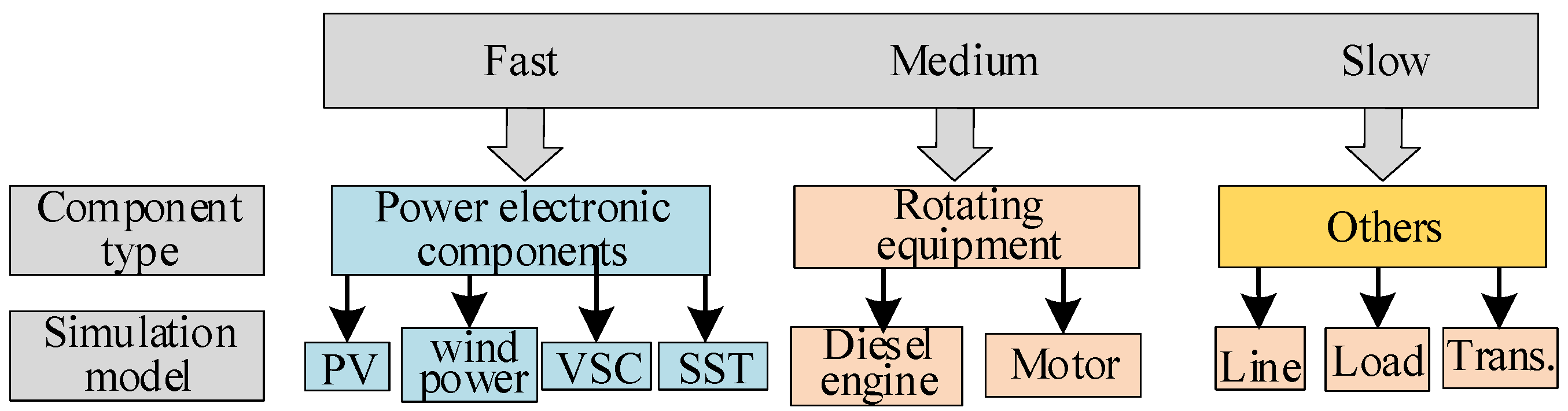
2.1. Classification of Fast/Medium/Slow Dynamic Components of the ADN
- (1)
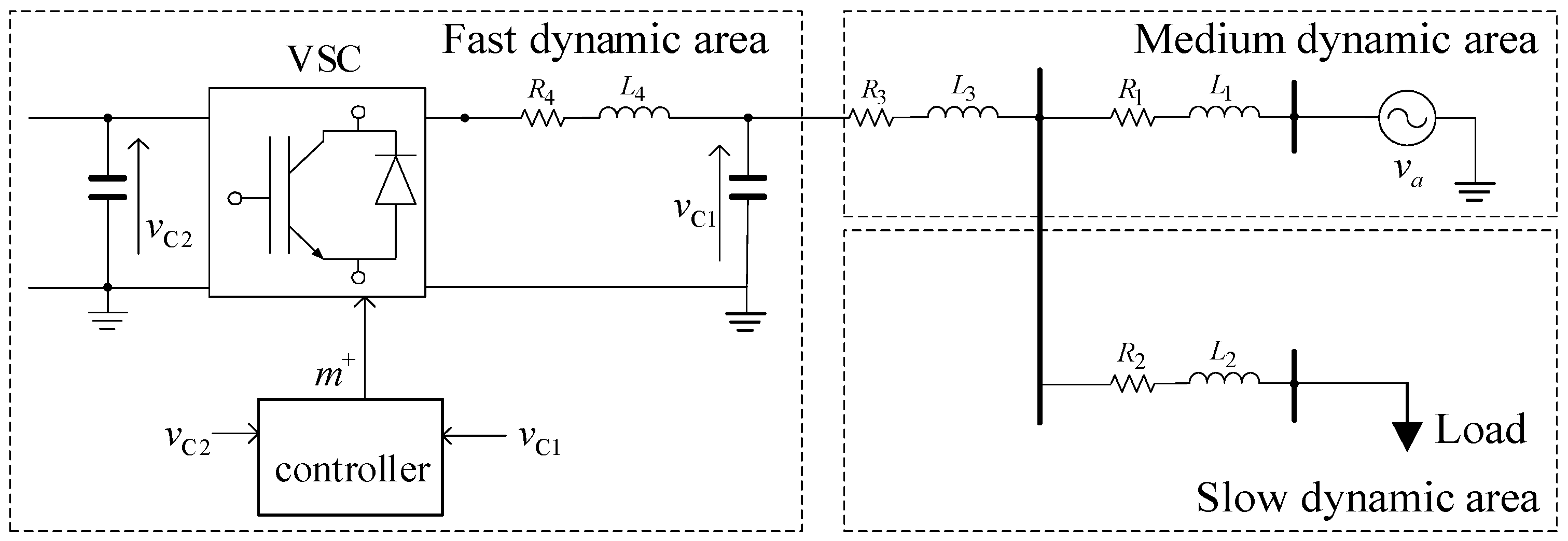
- Fast dynamic components. Typical representatives include DGs, such as photovoltaics, flexible power electronic devices, and voltage source converters. In the ADN, the switching frequency of power electronic devices is increasing from several thousand hertz to tens of thousands of hertz or even higher, making the simulation step size that meets the simulation of power electronic devices smaller and smaller. From the perspective of transient simulation, the existence of power electronic devices can cause problems such as time-varying computation matrices, switching actions between step sizes, and numerical oscillations. So, smaller simulation step size is necessary to accurately depict fast time-varying dynamic processes. More importantly, the STT is an important device in future distribution networks, since it has the ability of AC-DC conversion, high precision voltage control, power exchange, etc., which is meaningful for the AC/DC hybrid network with lots of DGs. The STT is a piece of power electronic equipment which consists of kinds of switching tubes and isolating transformers, and the principle of operation of the SST is similar to that of the VSC and PV inverter. Hence, it can be classified as a fast dynamic component, as shown in Figure 1.
- (2)
- Medium dynamic components. Typical representative components include rotating equipment represented by diesel engines and electric motors. Changes in the mechanical torque of rotating equipment have a greater impact on its operating status than sudden changes in voltage/current. The dynamic response speed of rotating equipment such as diesel engines and electric motors is slower than that of power electronics devices. Due to the fact that the transient response process of rotating equipment is mainly electromechanically transient, its electromagnetic transient process can be ignored in the simulation process, and further, its transient model can be solved using a medium time scale.
- (3)
- Slow dynamic components. Typical representative components include capacitors, reactors, transformers, control systems, and other electrical system components that do not include power electronic components. The representative components of the slow time scale do not experience sudden changes in their operating status during the transient response process and have medium- to long-term dynamic processes. They are in a slow time-varying status, and high-frequency transient effects can be neglected. Using a larger simulation step size during simulation solving will not reduce the accuracy of the simulation.
2.2. Simulation Modeling of Typical ADN Fast/Medium/Slow Equipment
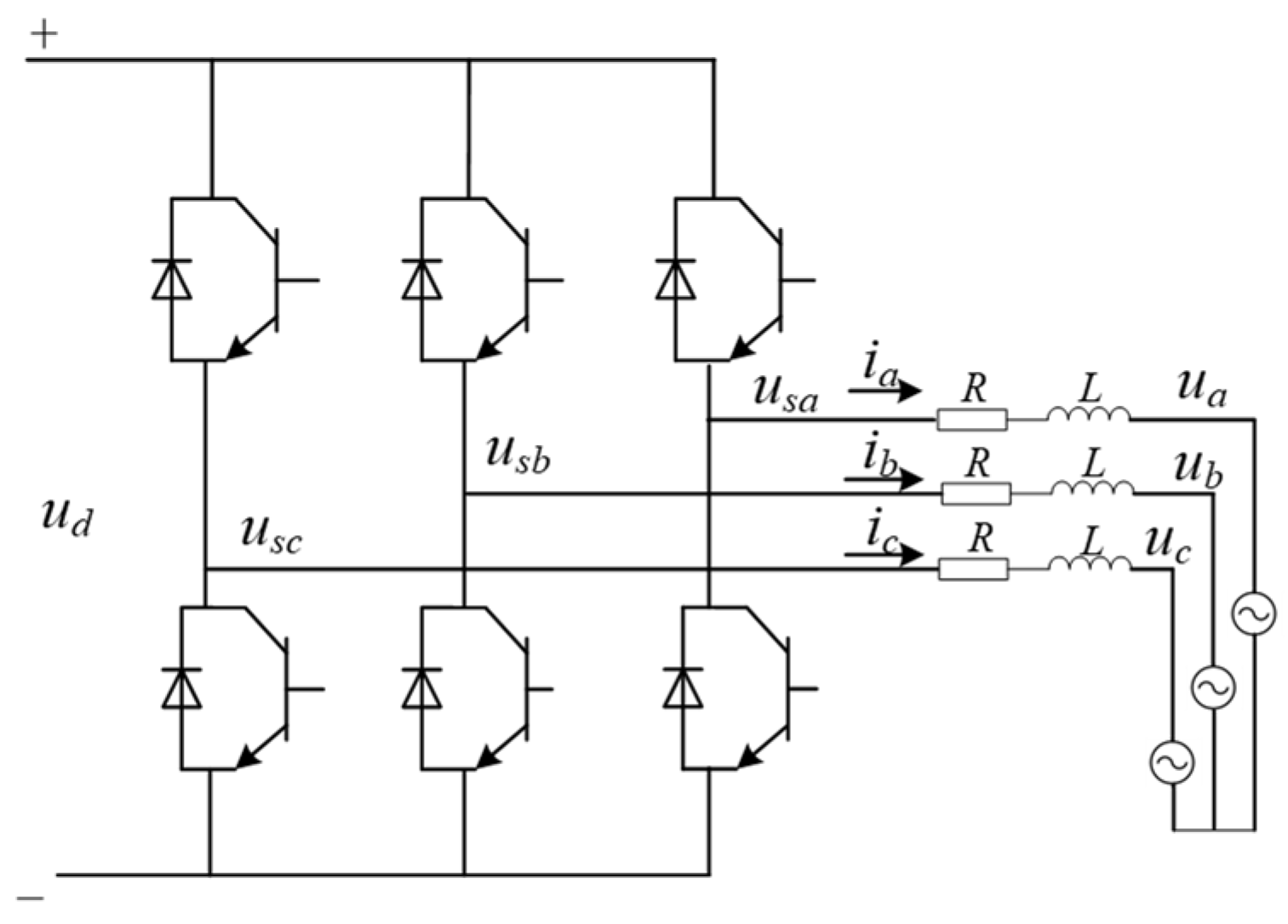
2.2.1. Fast Dynamic Modeling of DGs
2.2.2. Medium Dynamic Modeling of Diesel Generators
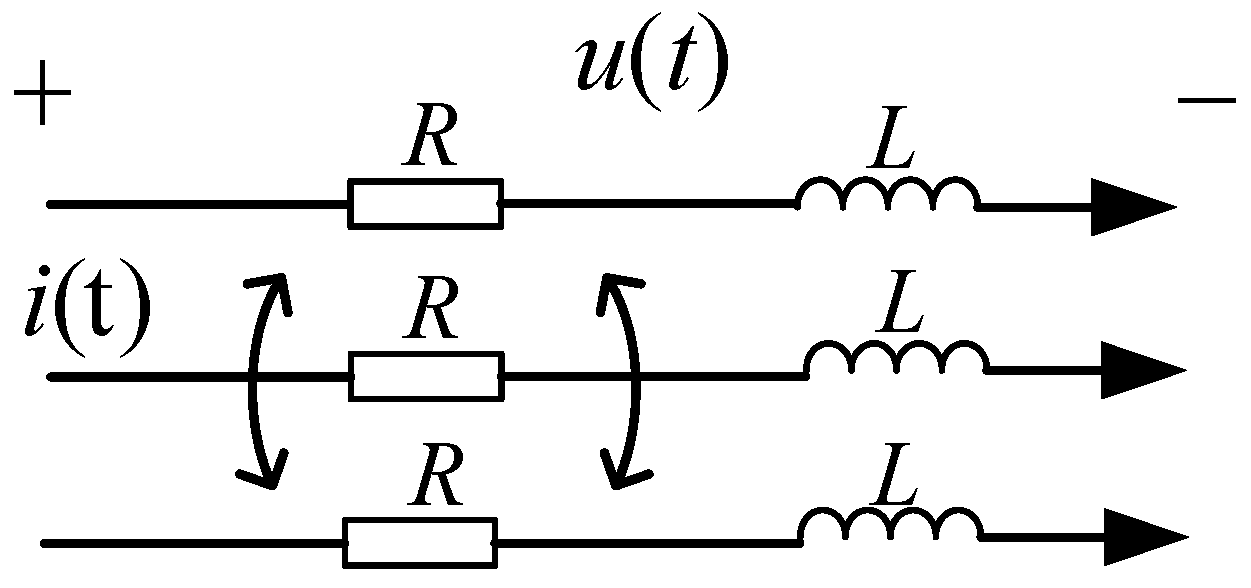
2.2.3. Slow Dynamic Modeling of Lines
3. Decoupling Method of the ADN for Dynamic Simulation
3.1. Distribution Network Partitioning Based on Fast/Medium/Slow Time Constant Clustering
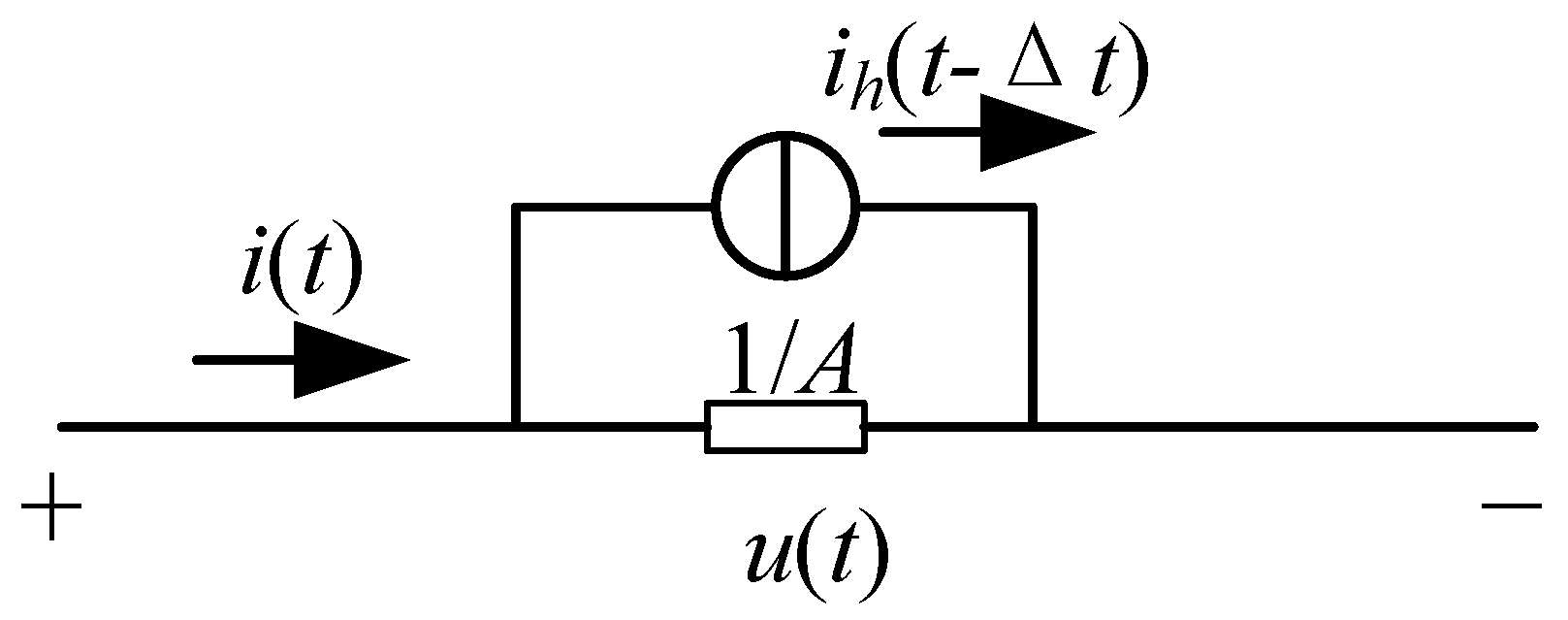
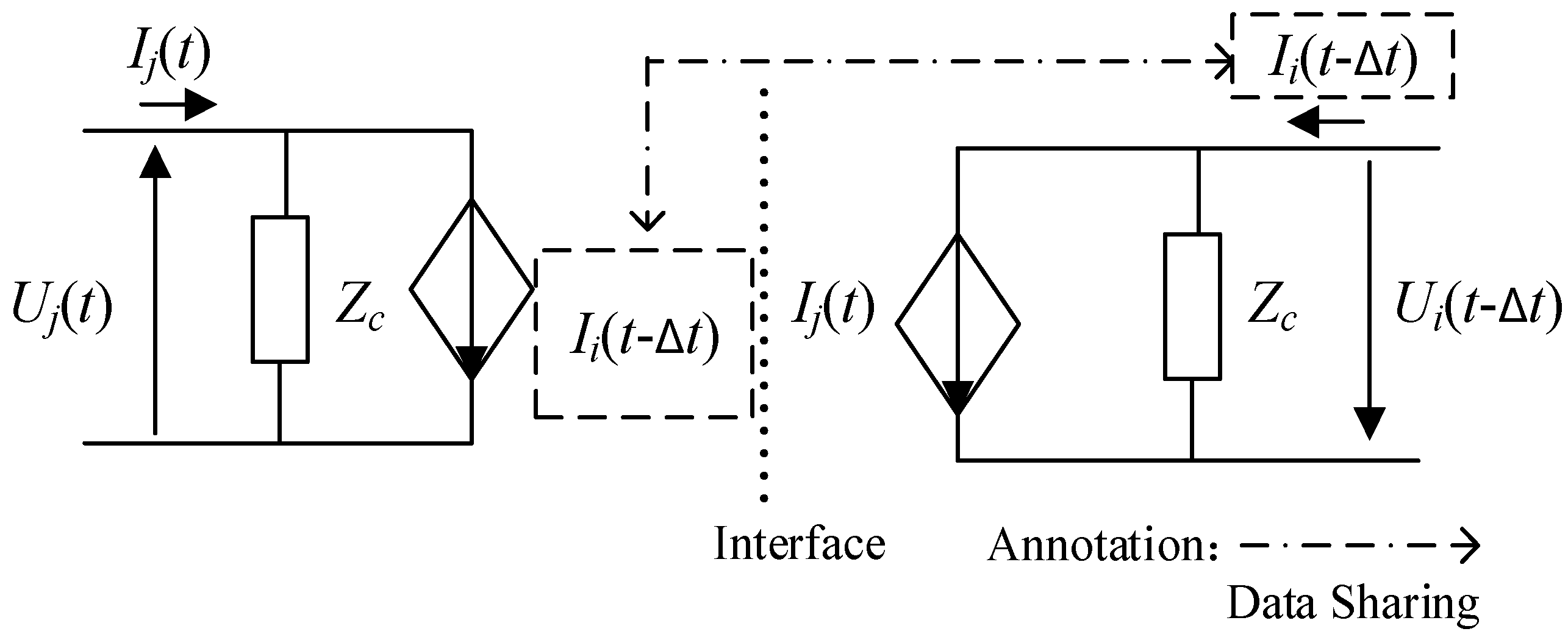
3.2. A Short-Line Characteristic Line Decoupling Method for ADNs
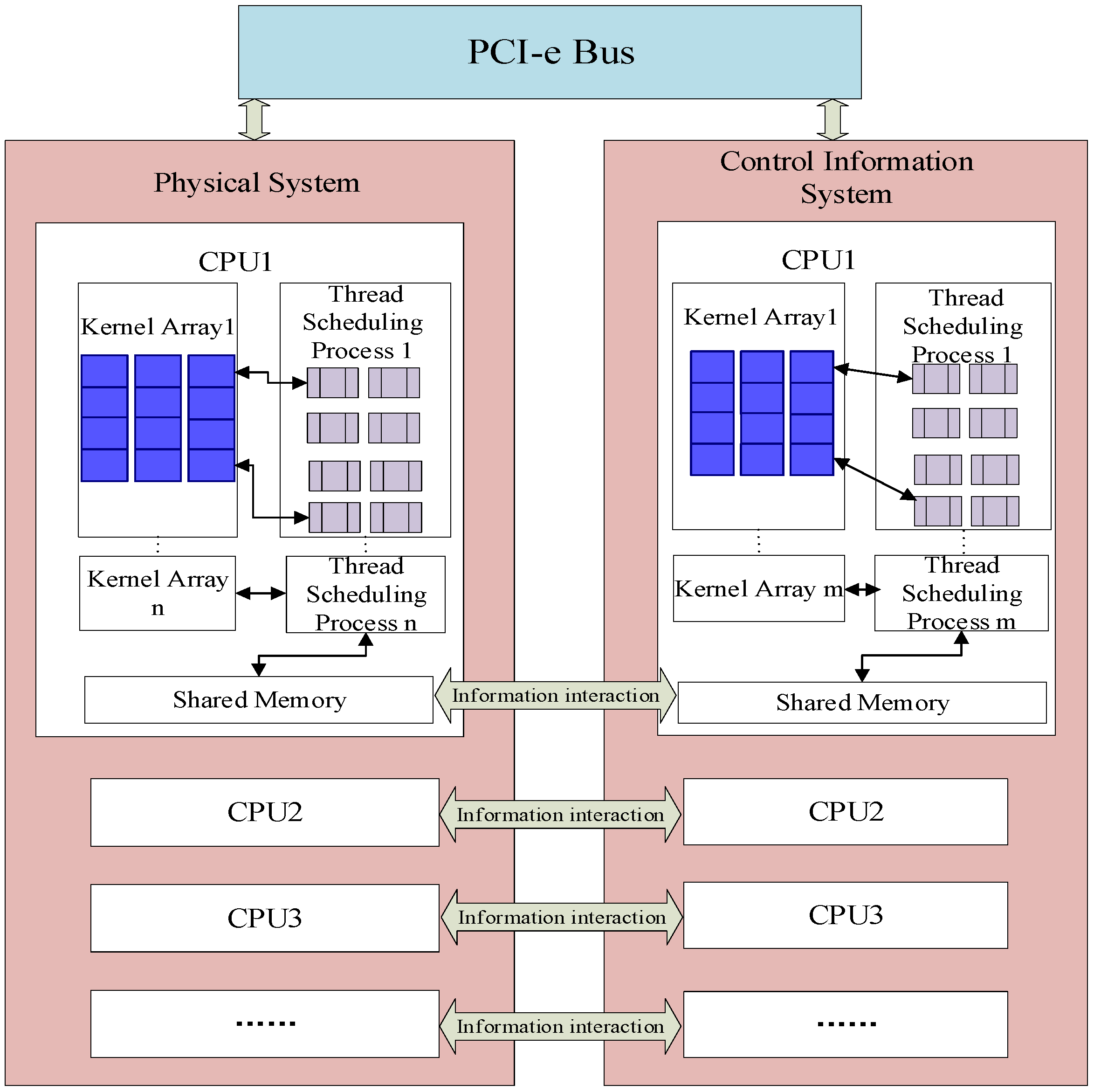
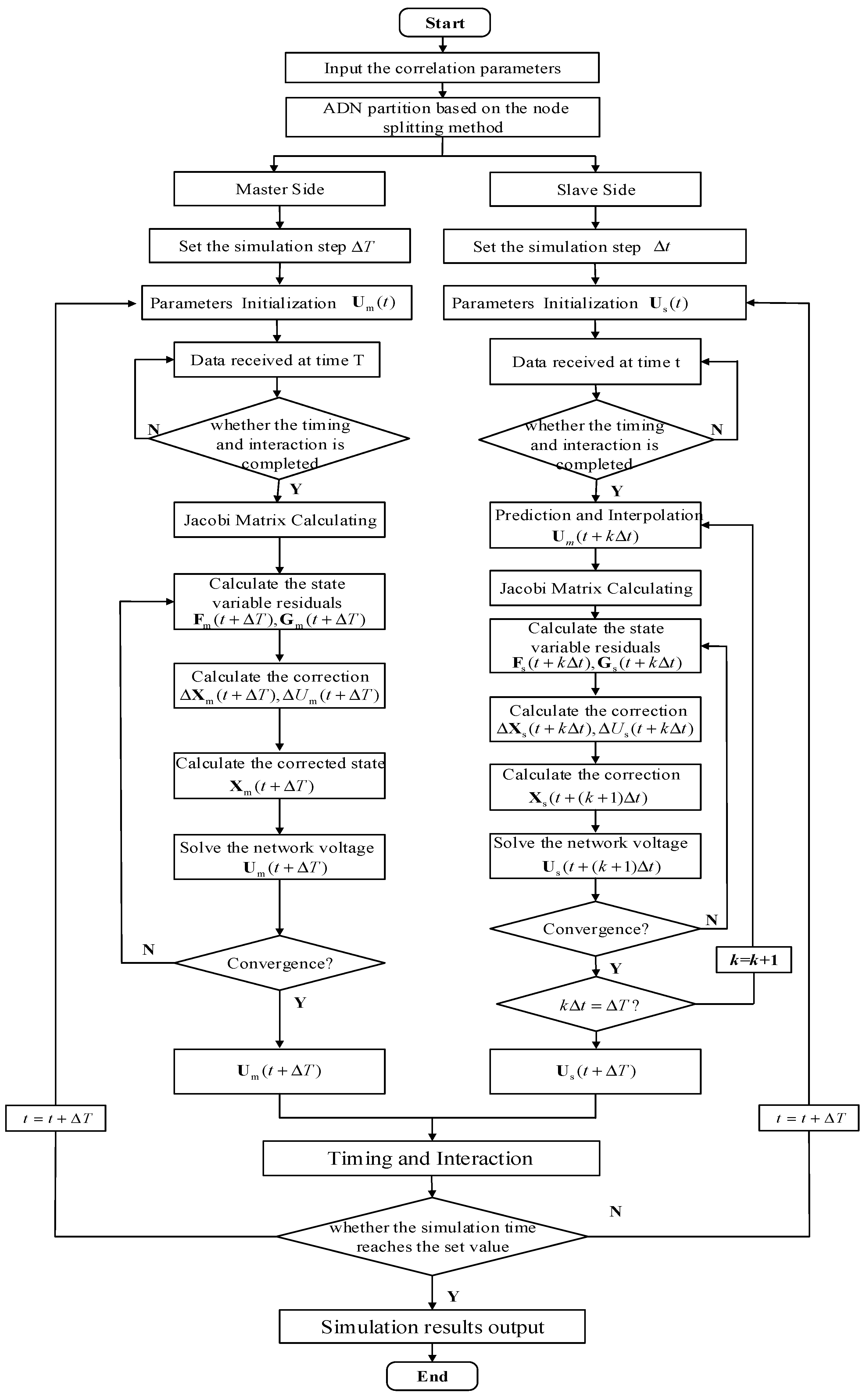
4. Multi-Rate Parallel Simulation Method of the ADN Based on Interconnected Simulator Array
5. Simulation Verification
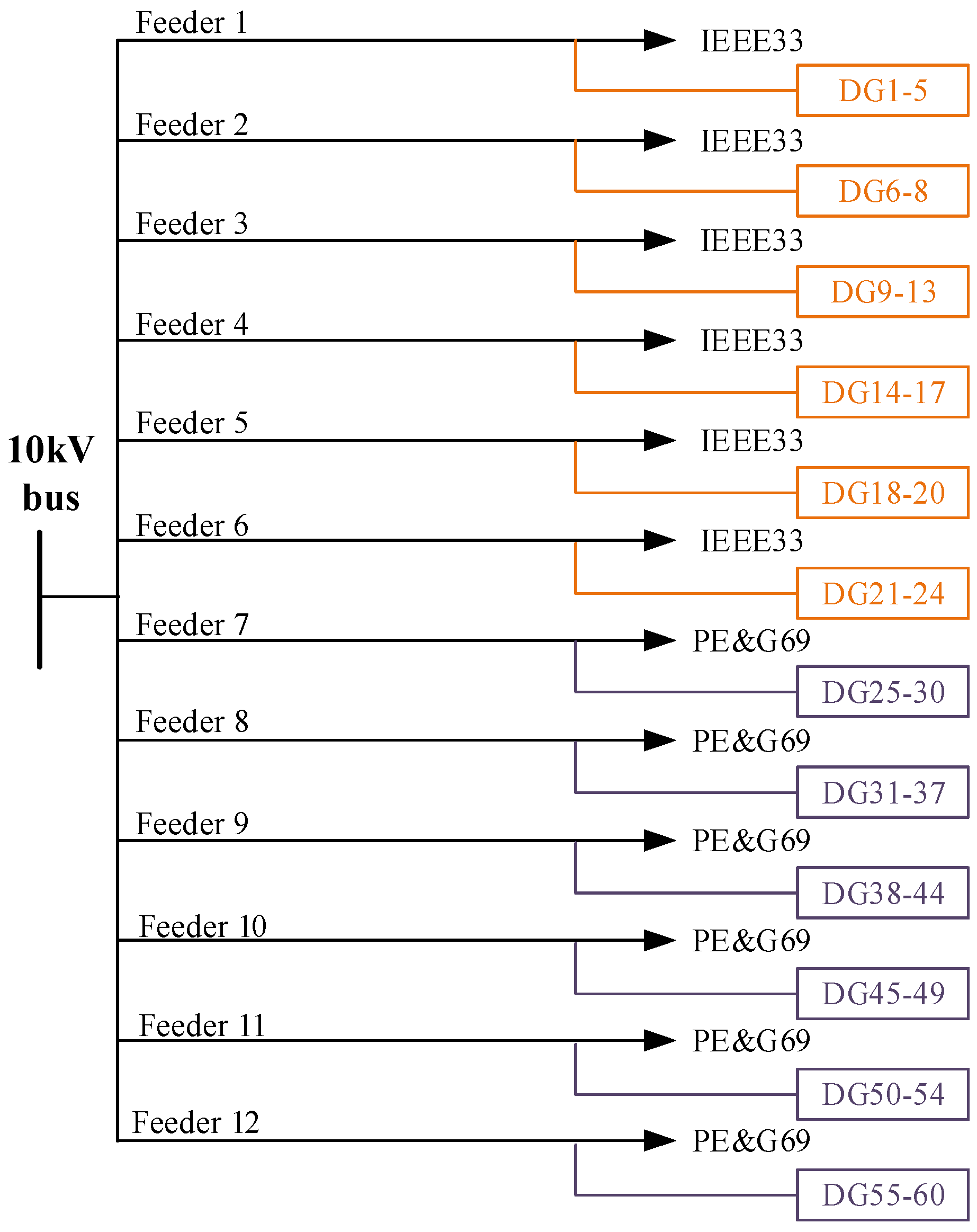
5.1. Introduction to the Example and Scenario Used in the Simulation
5.2. Simulation Speed Analysis of Partition and Coordinated Multi-Rate Parallel Simulation
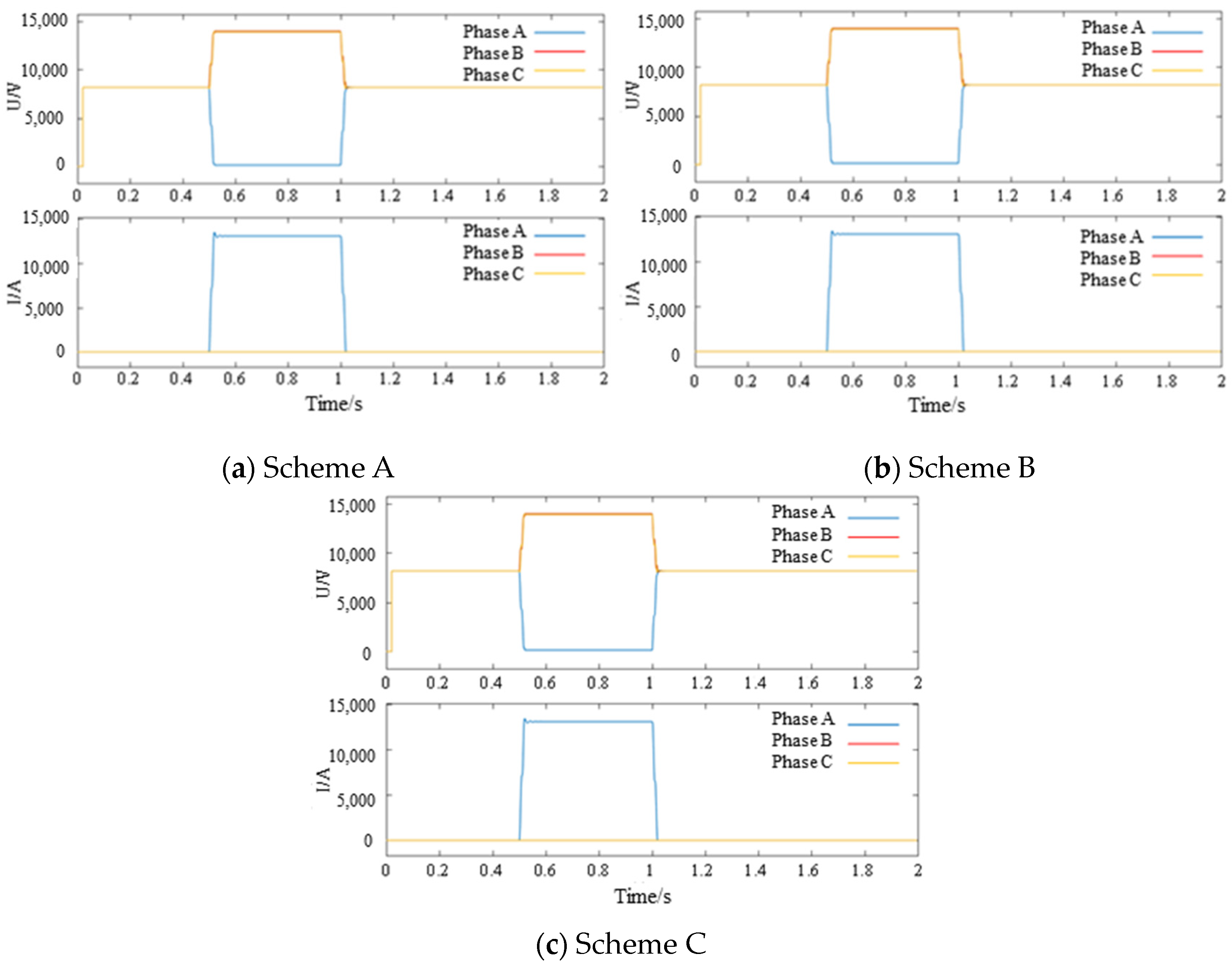
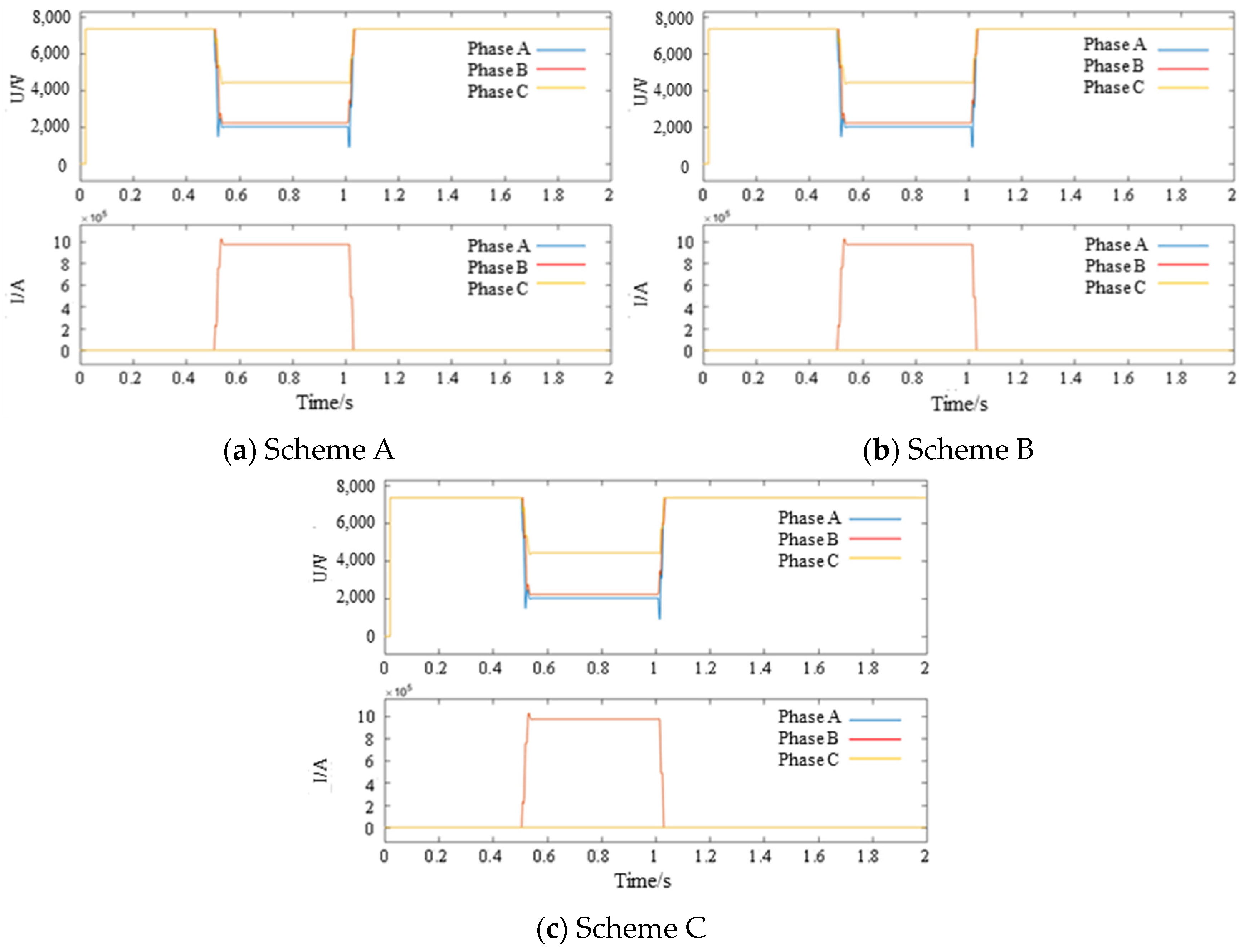
5.3. Accuracy Analysis of Partition-Coordinated Multi-Rate Parallel Simulation
- (1)
- Parallel simulation results for single-phase ground faults
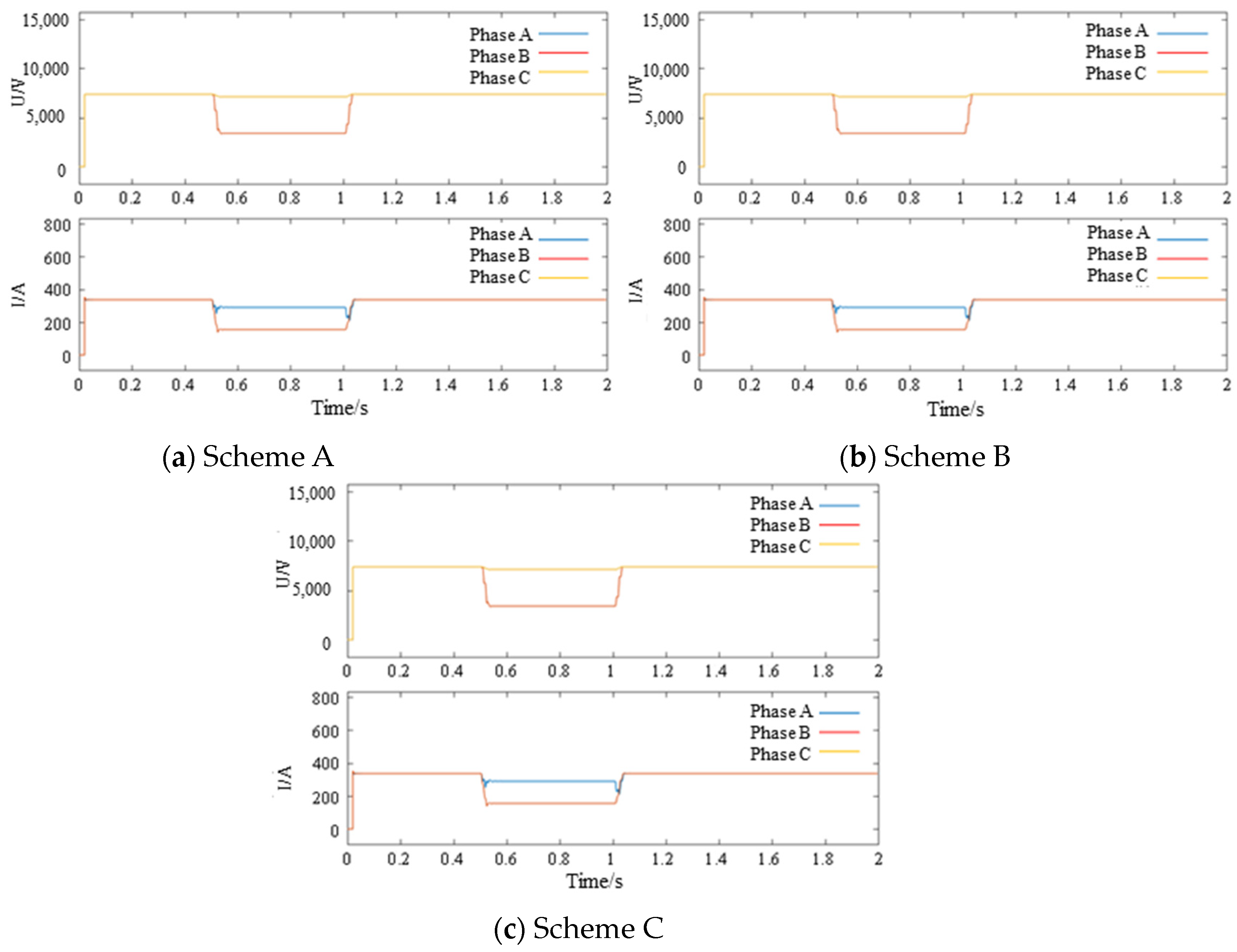
- (2)
- Parallel simulation results for two-phase short-circuit faults
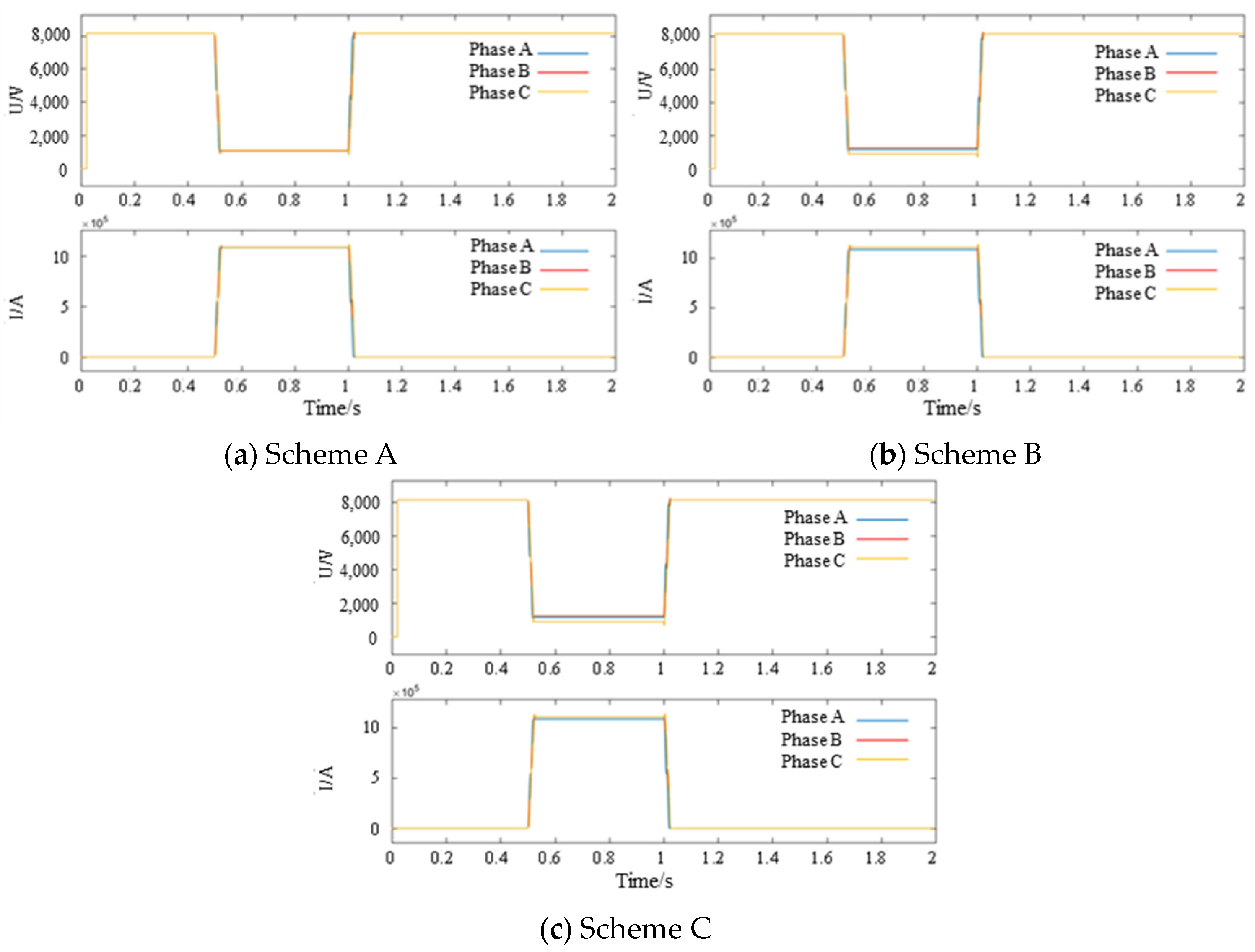
- (3)
- Parallel simulation results for two-phase short-circuit ground faults
- (4)
- Parallel simulation results for three-phase short-circuit faults
6. Conclusions
- (1)
- The transient response characteristics of fast, medium, and slow dynamic equipment components in the ADN are very different. Through multi-time-scale modeling and time constant grouping, the regions with different transient variation characteristics in the distribution network can be partitioned.
- (2)
- The ADN has a wide range of nodes and the source–grid–load–storage is tightly coupled. Through the short-line decoupling method based on the characteristic line, the decomposition and coordination between multiple regions of the distribution network can be realized so as to carry out parallel simulation.
- (3)
- The multi-rate parallel simulation of the ADN can not only effectively use the redundancy of simulation computing resources, realize parallel simulation calculation, and improve the simulation speed but also select small-step simulations in fast dynamic regions and large-step simulations in slow dynamic regions according to the fast, medium, and slow response characteristics between different partitions. A multi-rate hybrid coordinated simulation is carried out to further accelerate the simulation. The verification results of the example show that using adaptive variable-step-size multi-rate parallel simulation technology can increase the subnet computation-time balance rate and simulation acceleration ratio to 119.90% and 121.31% in the same rate-parallel mode.
- (4)
- The transient simulation is an effective means to describe the dynamic characteristics of the ADN. However, the transient simulation is greatly affected by the scale of the distribution network and the complexity of the model. The fast simulation method based on decomposition and coordination is the key to solving the problems of the slow speed and low efficiency of the transient simulation.
- (5)
- The simulation duration of the one-core simulation (i.e., the serial simulation) is 14,949.79 s, while the simulation duration of the multi-core simulation (i.e., the parallel simulation) is from 149.75 s to 155.83, which means that the parallel simulation can save about 90% of the simulation duration.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alboaouh, K.A.; Mohagheghi, S. Impact of rooftop photovoltaics on the distribution system. J. Renew. Energy 2020, 2020, 4831434. [Google Scholar] [CrossRef]
- Sheng, W.; Liu, K.Y.; Cheng, S.; Meng, X.; Dai, W. A Trust Region SQP Method for Coordinated Voltage Control in Smart Distribution Grid. IEEE Trans. Smart Grid 2016, 7, 381–391. [Google Scholar] [CrossRef]
- Azmi, K.H.M.; Radzi, N.A.M.; Azhar, N.A.; Samidi, F.S.; Zulkifli, I.T.; Zainal, A.M. Active Electric Distribution Network: Applications, Challenges, and Opportunities. IEEE Access 2022, 10, 134655–134689. [Google Scholar] [CrossRef]
- Eissa, M.M. New protection principle for smart grid with renewable energy sources integration using WiMAX centralized scheduling technology. Electr. Power Energy Syst. 2018, 97, 372–384. [Google Scholar] [CrossRef]
- Dutta, R.; Chakrabarti, S.; Sharma, A. Topology Tracking for Active Distribution Networks. IEEE Trans. Power Syst. 2021, 36, 2855–2865. [Google Scholar] [CrossRef]
- Sheng, W.; Liu, K.; Li, Z.; Ye, X. Collaborative Fault Recovery and Network Reconstruction Method for Cyber-physical-systems Based on Double Layer Optimization. CSEE J. Power Energy Syst. 2023, 9, 380–392. [Google Scholar]
- Cavraro, G.; Kekatos, V.; Veeramachaneni, S. Voltage analytics for power distribution network topology verification. IEEE Trans. Smart Grid 2019, 10, 1058–1067. [Google Scholar] [CrossRef]
- Yuan, H.; Li, F.; Wei, Y.; Zhu, J. Novel Linearized Power Flow and Linearized OPF Models for Active Distribution Networks with Application in Distribution LMP. IEEE Trans. Smart Grid 2018, 9, 438–448. [Google Scholar] [CrossRef]
- Verma, R.; Padhy, N.P. Optimal Power Flow Based DR in Active Distribution Network with Reactive Power Control. IEEE Syst. J. 2022, 16, 3522–3530. [Google Scholar] [CrossRef]
- Mitrentsis, G.; Lens, H. A Dynamic Active Distribution Network Equivalent for Enhancing the Generalization Capability of the Exponential Recovery Model in Stability Studies. IEEE Trans. Power Syst. 2021, 36, 2709–2712. [Google Scholar] [CrossRef]
- Sekhavatmanesh, H.; Rodrigues, J.; Moreira, C.L.; Lopes, J.A.P.; Cherkaoui, R. Optimal Load Restoration in Active Distribution Networks Complying with Starting Transients of Induction Motors. IEEE Trans. Smart Grid 2020, 11, 3957–3969. [Google Scholar] [CrossRef]
- Chaspierre, G.; Denis, G.; Panciatici, P.; Van Cutsem, T. An active distribution network equivalent derived from large-disturbance simulations with uncertainty. IEEE Trans. Smart Grid 2020, 11, 4749–4759. [Google Scholar] [CrossRef]
- Kontis, E.O.; Papadopoulos, T.A.; Chrysochos, A.I. On the Applicability of Exponential Recovery Models for the Simulation of Active Distribution Networks. IEEE Trans. Power Del. 2018, 33, 3220–3222. [Google Scholar] [CrossRef]
- Huang, Q.; Vittal, V. Advanced EMT and Phasor-Domain Hybrid Simulation with Simulation Mode Switching Capability for Transmission and Distribution Systems. IEEE Trans. Power Syst. 2018, 33, 6298–6308. [Google Scholar] [CrossRef]
- Chiniforoosh, S.; Jatskevich, J.; Yazdani, A.; Sood, V.; Dinavahi, V.; Martinez, J.A.; Ramirez, A. Definitions and Applications of Dynamic Average Models for Analysis of Power Systems. IEEE Trans. Power Del. 2010, 25, 2655–2669. [Google Scholar] [CrossRef]
- Daryabak, M.; Filizadeh, S.; Jatskevich, J.; Davoudi, A.; Saeedifard, M.; Sood, V.K.; Martinez, J.A.; Aliprantis, D.; Cano, J.; Mehrizi-Sani, A. Modeling of LCC-HVDC Systems Using Dynamic Phasors. IEEE Trans. Power Del. 2014, 29, 1989–1998. [Google Scholar] [CrossRef]
- Rimorov, D.; Huang, J.; Mugombozi, C.F.; Roudier, T.; Kamwa, I. Power Coupling for Transient Stability and Electromagnetic Transient Collaborative Simulation of Power Grids. IEEE Trans. Power Syst. 2021, 36, 5175–5184. [Google Scholar] [CrossRef]
- Li, C.; Wu, Y.; Zhang, H.; Ye, H.; Liu, Y.; Liu, Y. STEPS: A Portable Dynamic Simulation Toolkit for Electrical Power System Studies. IEEE Trans. Power Syst. 2021, 36, 3216–3226. [Google Scholar] [CrossRef]
- De Carne, G.; Lauss, G.; Syed, M.H.; Monti, A.; Benigni, A.; Karrari, S.; Kotsampopoulos, P.; Faruque, M.O. On Modeling Depths of Power Electronic Circuits for Real-Time Simulation—A Comparative Analysis for Power Systems. IEEE Open Access J. Power Energy 2022, 9, 76–87. [Google Scholar] [CrossRef]
- Lauss, G.; Strunz, K. Accurate and Stable Hardware-in-the-Loop (HIL) Real-Time Simulation of Integrated Power Electronics and Power Systems. IEEE Trans. Power Electron. 2021, 36, 10920–10932. [Google Scholar] [CrossRef]

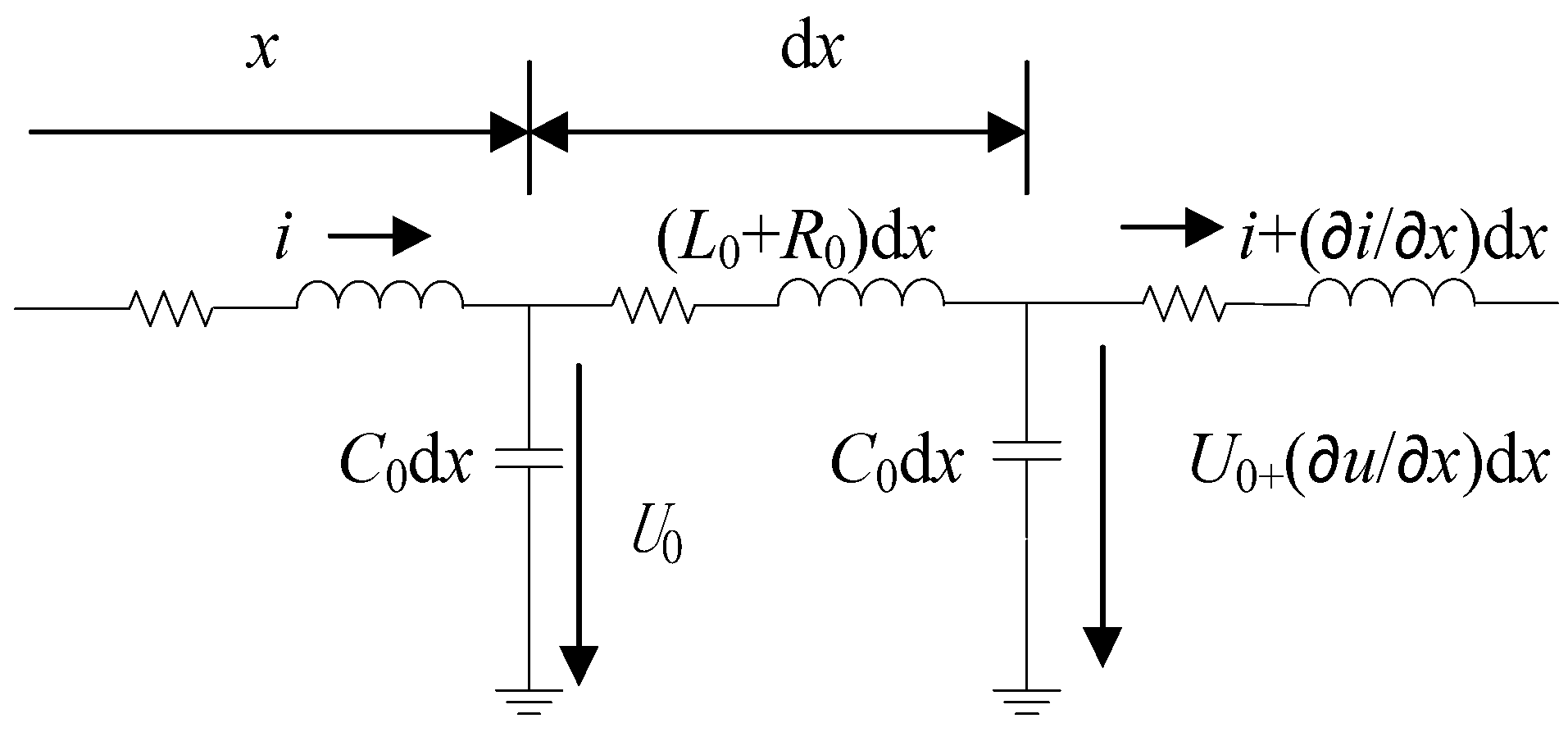
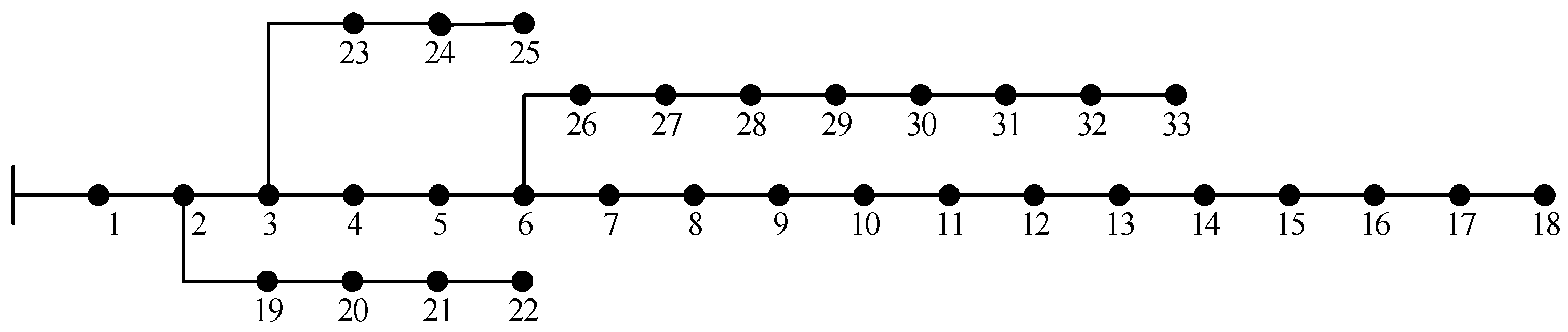

| Eigenvalues | Value |
|---|---|
| −38.02 ± 2275.44i | |
| −19.71 + 644.29i | |
| −2670.4 |
| Feeder | Total Number of Nodes | Total Number of DGs |
|---|---|---|
| 1 | 33 | 5 |
| 2 | 33 | 3 |
| 3 | 33 | 5 |
| 4 | 33 | 4 |
| 5 | 33 | 3 |
| 6 | 33 | 4 |
| 7 | 69 | 6 |
| 8 | 69 | 7 |
| 9 | 69 | 7 |
| 10 | 69 | 5 |
| 11 | 69 | 5 |
| 12 | 69 | 6 |
| 612 | 60 |
| Feeder | Node of DG Access | Capacity of DG Access | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 8 | 16 | 32 | 15 | 20 | - | - | 30 | 30 | 50 | 50 | 30 | - | - |
| 2 | 32 | 11 | 27 | - | - | - | - | 50 | 100 | 100 | - | - | - | - |
| 3 | 8 | 16 | 32 | 15 | 20 | - | - | 30 | 30 | 50 | 50 | 30 | - | - |
| 4 | 9 | 3 | 20 | 24 | - | - | - | 50 | 100 | 50 | 50 | - | - | - |
| 5 | 32 | 11 | 27 | - | - | - | - | 50 | 100 | 100 | - | - | - | - |
| 6 | 90 | 3 | 20 | 24 | - | - | - | 50 | 100 | 50 | 50 | - | - | - |
| 7 | 66 | 37 | 28 | 22 | 40 | 24 | - | 50 | 100 | 75 | 30 | 50 | 30 | - |
| 8 | 51 | 14 | 66 | 37 | 28 | 60 | 22 | 50 | 100 | 50 | 100 | 75 | 75 | 30 |
| 9 | 51 | 14 | 66 | 37 | 28 | 60 | 22 | 50 | 100 | 50 | 100 | 75 | 75 | 30 |
| 10 | 51 | 60 | 37 | 22 | 55 | - | - | 50 | 100 | 100 | 30 | 100 | - | - |
| 11 | 51 | 60 | 37 | 22 | 55 | - | - | 50 | 100 | 100 | 30 | 100 | - | - |
| 12 | 66 | 37 | 28 | 22 | 40 | 24 | - | 50 | 100 | 75 | 30 | 50 | 30 | - |
| Scheme | CPU Core Number for Traditional Load Node | CPU Core Number for DG Node | Partition Method | ||||||
|---|---|---|---|---|---|---|---|---|---|
| No. 1 | No. 2 | No. 3 | No. 4 | No. 5 | No. 6 | No. 7 | No. 8 | ||
| 1 | 612 + 60 | - | - | - | - | - | - | z | / |
| 2 | 336 | 276 | 8 | 9 | 13 | 14 | 10 | 6 | Artificially balancing the capacity of each CPU core |
| 3 | 336 | 276 | 13 | 11 | 6 | 7 | 12 | 11 | Artificially balancing the capacity of each CPU core |
| 4 | 336 | 276 | 8 | 12 | 10 | 7 | 12 | 11 | Optimized partition strategy provided in Section 3 |
| Scheme | Step Size of CPU Core for Traditional Loads (s) | Step Size of CPU Core for DGs (s) |
|---|---|---|
| 5 | 5 × 10−5 | 5 × 10−5 |
| 6 | 5 × 10−3 | 5 × 10−4 |
| 7 | 5 × 10−3 | [5 × 10−4, 5 × 10−3] |
| Scheme | Min(s) | Max(s) | |||
|---|---|---|---|---|---|
| 1 | - | - | 14,949.79 | - | 0 |
| 2 | 9.97 | 28.22 | 150.25 | 35.33% | 5.32 |
| 3 | 10.10 | 29.35 | 155.83 | 34.40% | 5.31 |
| 4 | 10.23 | 24.69 | 150.69 | 41.43% | 6.10 |
| 5 | 11.89 | 24.69 | 153.40 | 48.16% | 6.21 |
| 6 | 10.23 | 20.23 | 149.75 | 50.57% | 7.40 |
| Node | Comparsion | Average Error of Three-Phase Voltage (%) | Maximum Error of Three-Phase Voltage (%) | Average Error of Three-Phase Current (%) | Maximum Error of Three-Phase Current (%) | |
|---|---|---|---|---|---|---|
| Fault location | 1 | 4 | 0.09 | 0.15 | 0.40 | 0.45 |
| 1 | 6 | 0.12 | 0.14 | 0 | 0.10 | |
| DG next to fault location | 1 | 4 | 0.09 | 0.12 | 0.15 | 0.38 |
| 1 | 6 | 0.12 | 0.17 | 0.20 | 0.42 | |
| Feeder next to the feeder with fault node | 1 | 4 | 0.09 | 0.11 | 0.17 | 0.29 |
| 1 | 6 | 0.12 | 0.15 | 0.22 | 0.48 | |
| Node | Comparsion | Average Error of Three-Phase Voltage (%) | Maximum Error of Three-Phase Voltage (%) | Average Error of Three-Phase Current (%) | Maximum Error of Three-Phase Current (%) | |
|---|---|---|---|---|---|---|
| Fault location | 1 | 4 | 0.19 | 0.36 | 0.34 | 0.44 |
| 1 | 6 | 0.12 | 0.27 | 0.47 | 0.50 | |
| DG next to fault location | 1 | 4 | 0.19 | 0.39 | 0.15 | 0.32 |
| 1 | 6 | 0.12 | 0.33 | 0.23 | 0.34 | |
| Feeder next to the feeder with fault node | 1 | 4 | 0.19 | 0.29 | 0.17 | 0.27 |
| 1 | 6 | 0.12 | 0.41 | 0.22 | 0.41 | |
| Node | Comparsion | Average Error of Three-Phase Voltage (%) | Maximum Error of Three-Phase Voltage (%) | Average Error of Three-Phase Current (%) | Maximum Error of Three-Phase Current (%) | |
|---|---|---|---|---|---|---|
| Fault location | 1 | 4 | 0.27 | 0.35 | 0.46 | 0.62 |
| 1 | 6 | 0.31 | 0.37 | 0.57 | 0.71 | |
| DG next to fault location | 1 | 4 | 0.27 | 0.42 | 0.51 | 0.59 |
| 1 | 6 | 0.31 | 0.39 | 0.53 | 0.65 | |
| Feeder next to the feeder with fault node | 1 | 4 | 0.27 | 0.32 | 0.37 | 0.56 |
| 1 | 6 | 0.31 | 0.38 | 0.42 | 0.61 | |
| Node | Comparsion | Average Error of Three-Phase Voltage (%) | Maximum Error of Three-Phase Voltage (%) | Average Error of Three-Phase Current (%) | Maximum Error of Three-Phase Current (%) | |
|---|---|---|---|---|---|---|
| Fault location | 1 | 4 | 0.36 | 0.45 | 0.57 | 0.82 |
| 1 | 6 | 0.79 | 0.88 | 0.67 | 0.79 | |
| DG next to fault location | 1 | 4 | 0.30 | 0.51 | 0.37 | 0.49 |
| 1 | 6 | 0.67 | 0.79 | 0.73 | 0.64 | |
| Feeder next to the feeder with fault node | 1 | 4 | 0.29 | 0.39 | 0.25 | 0.47 |
| 1 | 6 | 0.38 | 0.58 | 0.35 | 0.61 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Ye, X.; Kang, T.; Li, Z.; Jia, D. A Fast Dynamic Simulation Method of an Active Distribution Network with Distributed Generations Based on Decomposition and Coordination. Energies 2024, 17, 287. https://doi.org/10.3390/en17020287
Liu K, Ye X, Kang T, Li Z, Jia D. A Fast Dynamic Simulation Method of an Active Distribution Network with Distributed Generations Based on Decomposition and Coordination. Energies. 2024; 17(2):287. https://doi.org/10.3390/en17020287
Chicago/Turabian StyleLiu, Keyan, Xueshun Ye, Tianyuan Kang, Zhao Li, and Dongli Jia. 2024. "A Fast Dynamic Simulation Method of an Active Distribution Network with Distributed Generations Based on Decomposition and Coordination" Energies 17, no. 2: 287. https://doi.org/10.3390/en17020287
APA StyleLiu, K., Ye, X., Kang, T., Li, Z., & Jia, D. (2024). A Fast Dynamic Simulation Method of an Active Distribution Network with Distributed Generations Based on Decomposition and Coordination. Energies, 17(2), 287. https://doi.org/10.3390/en17020287







