Control System for the Performance Analysis of Turbines at Laboratory Scale
Abstract
1. Introduction
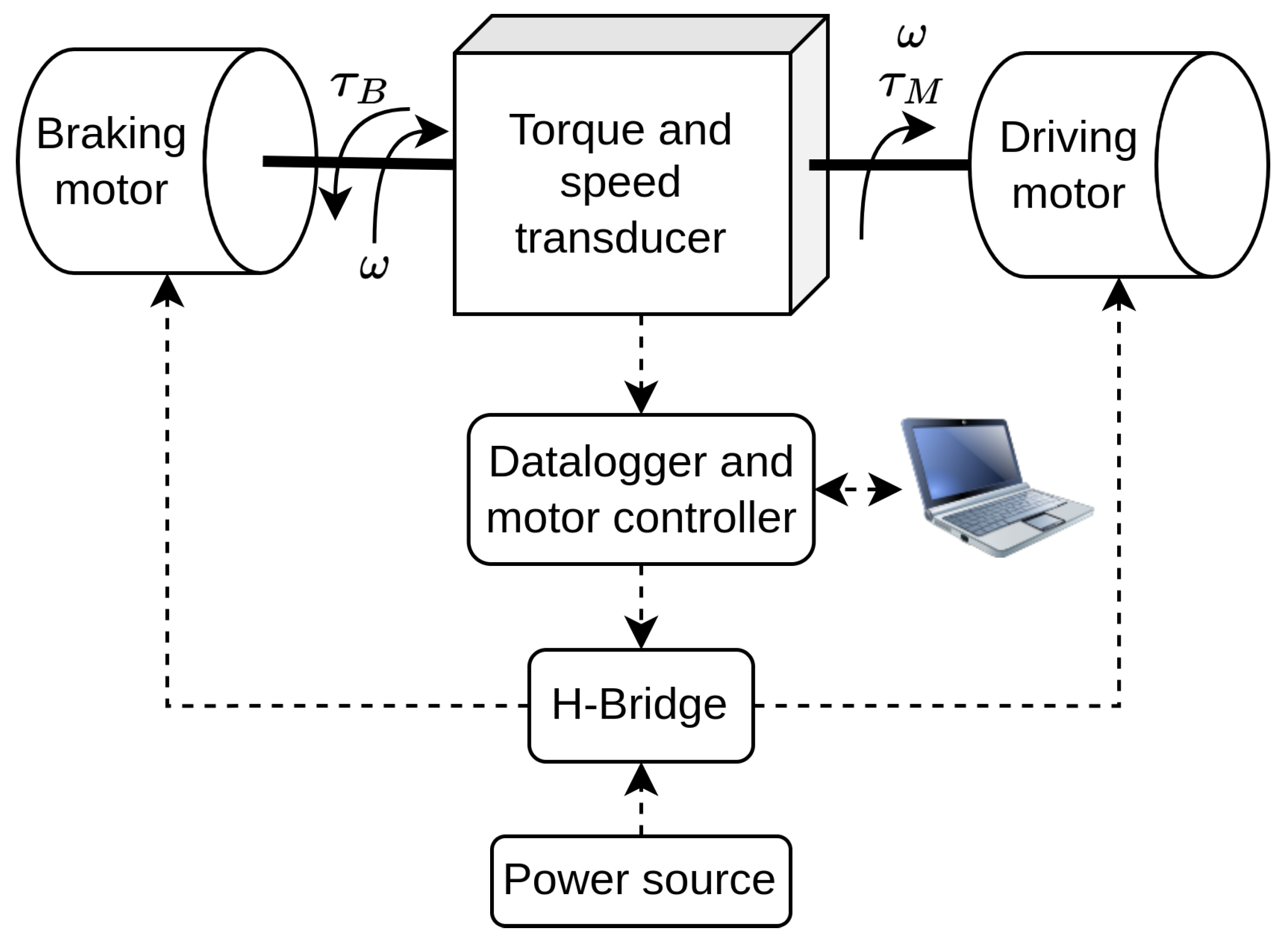
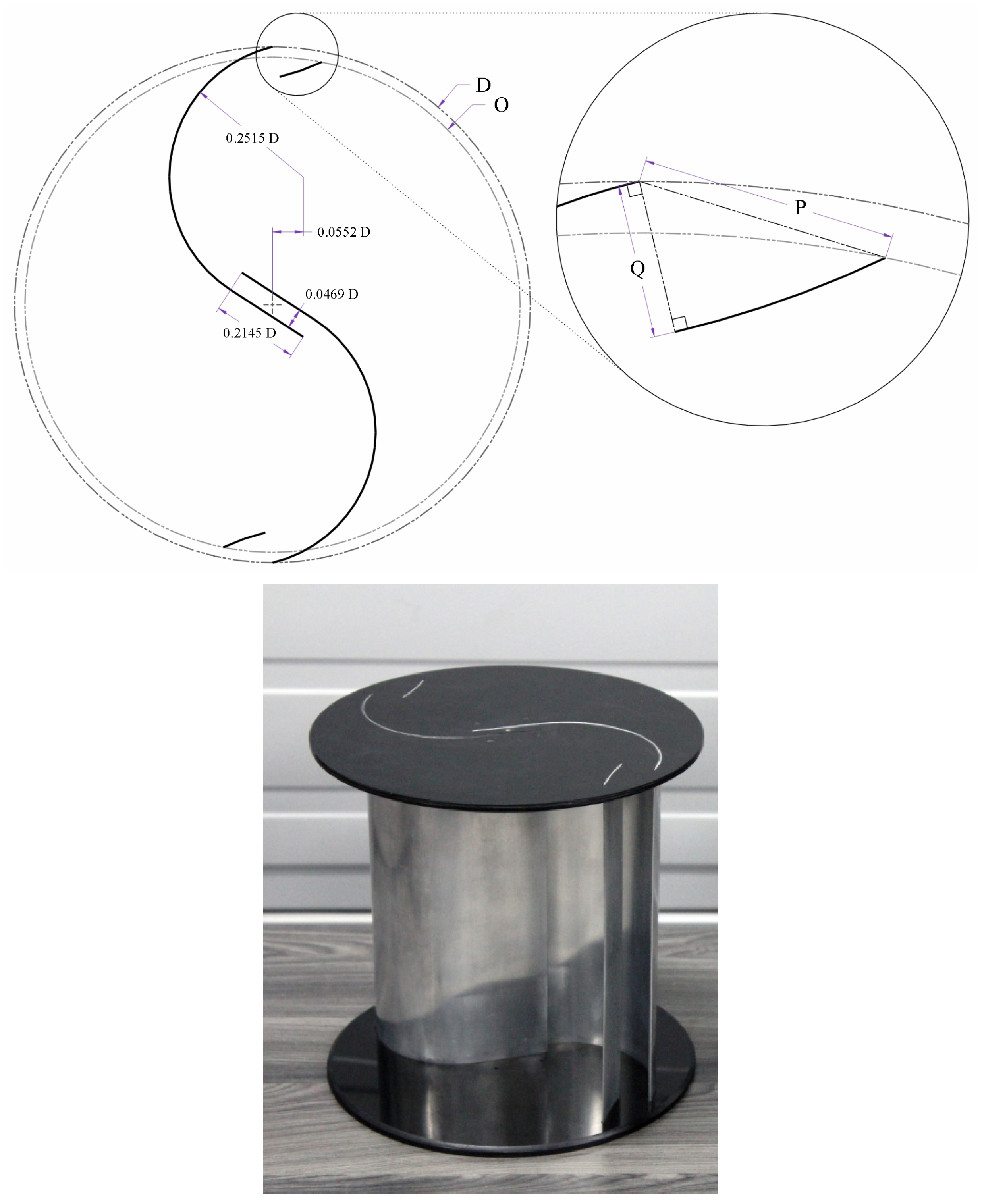
2. Materials and Methods
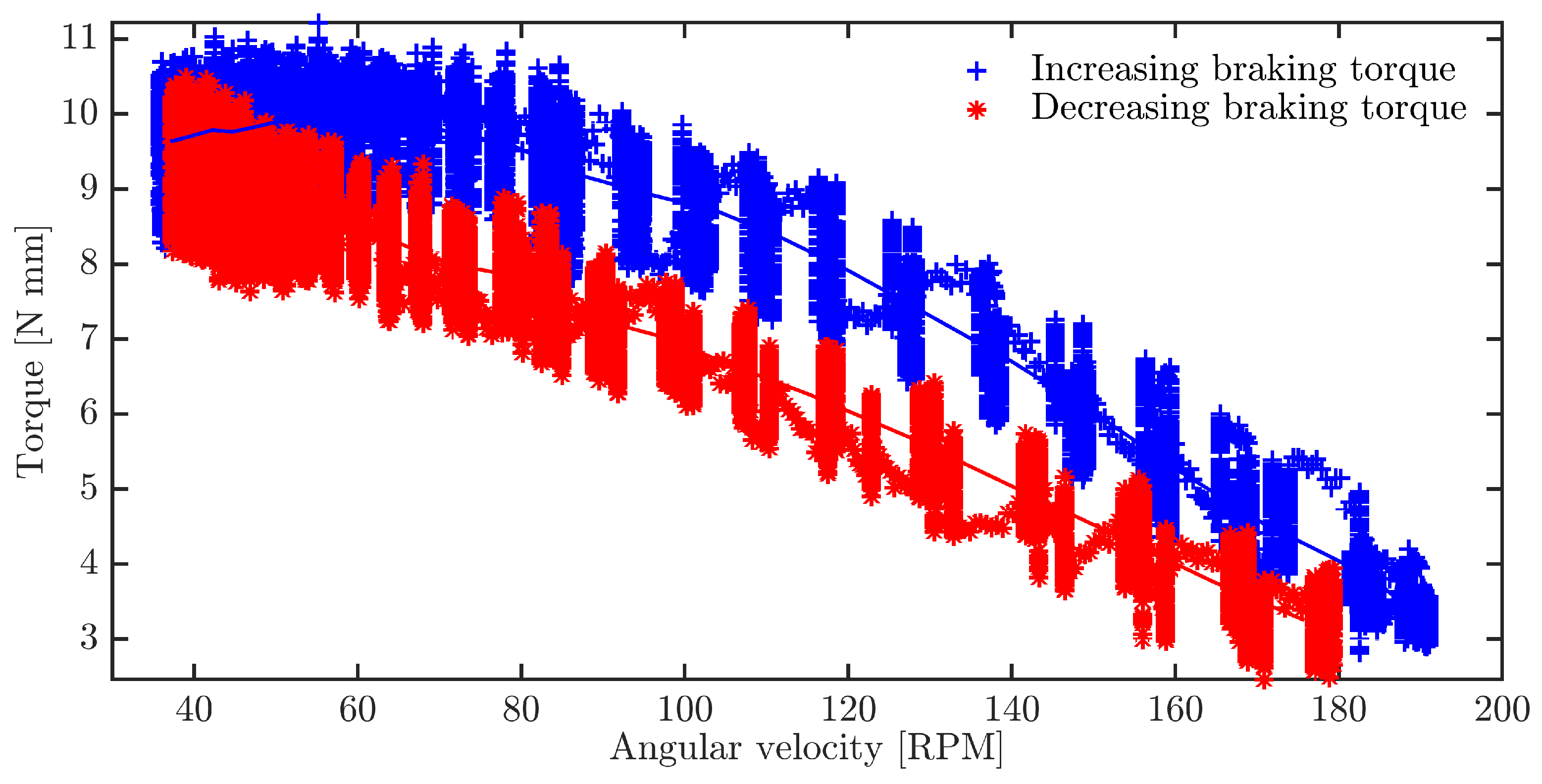
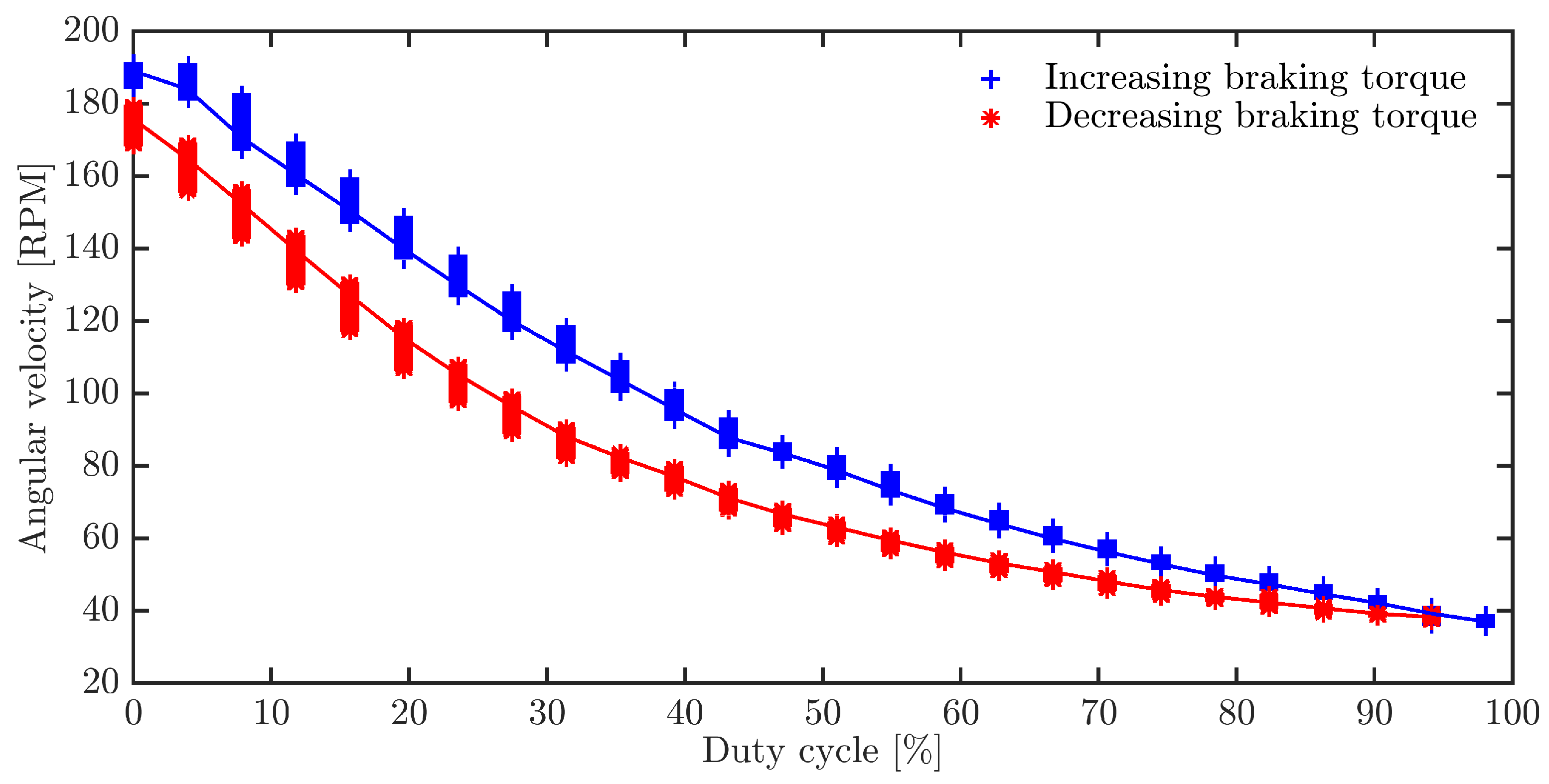
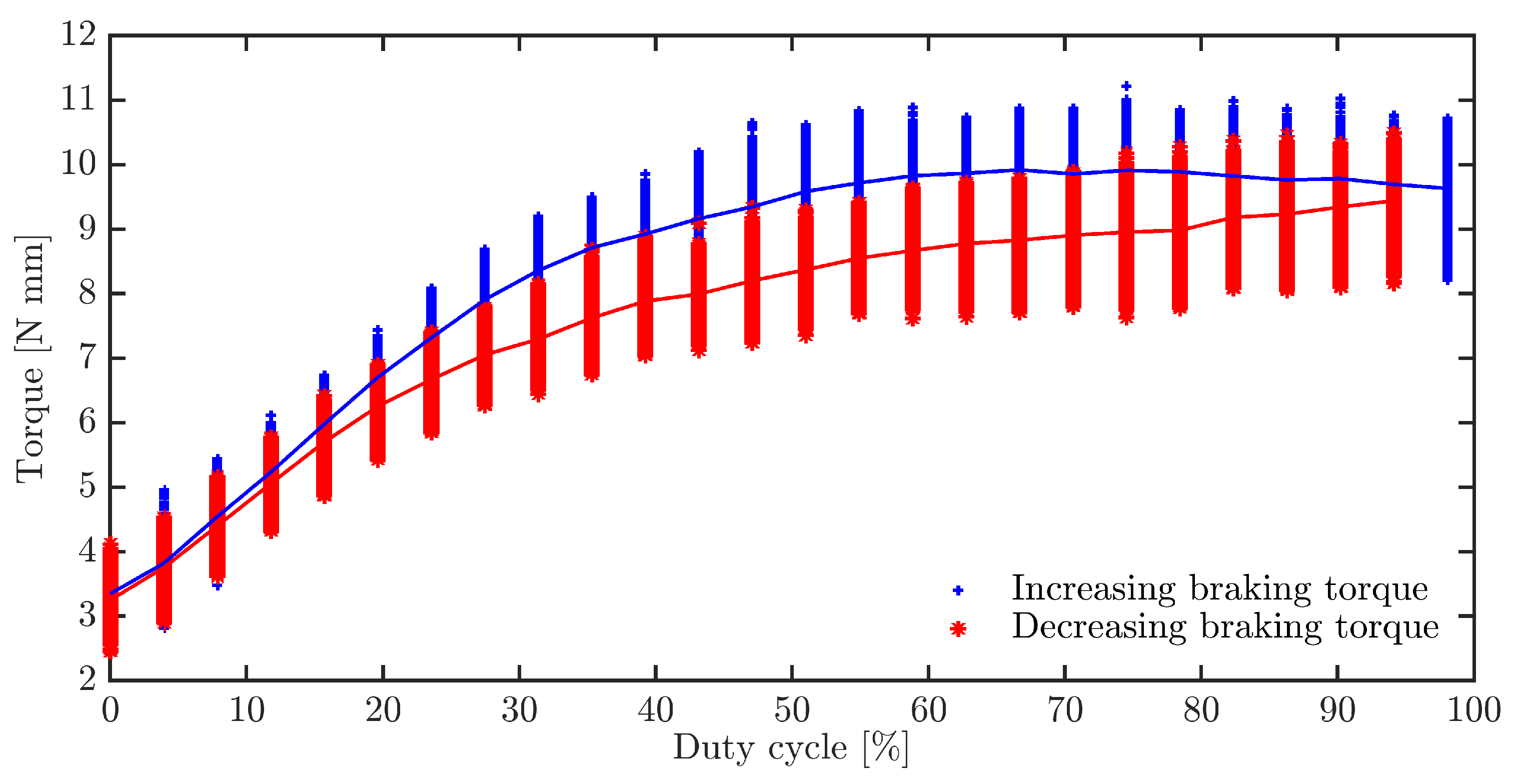
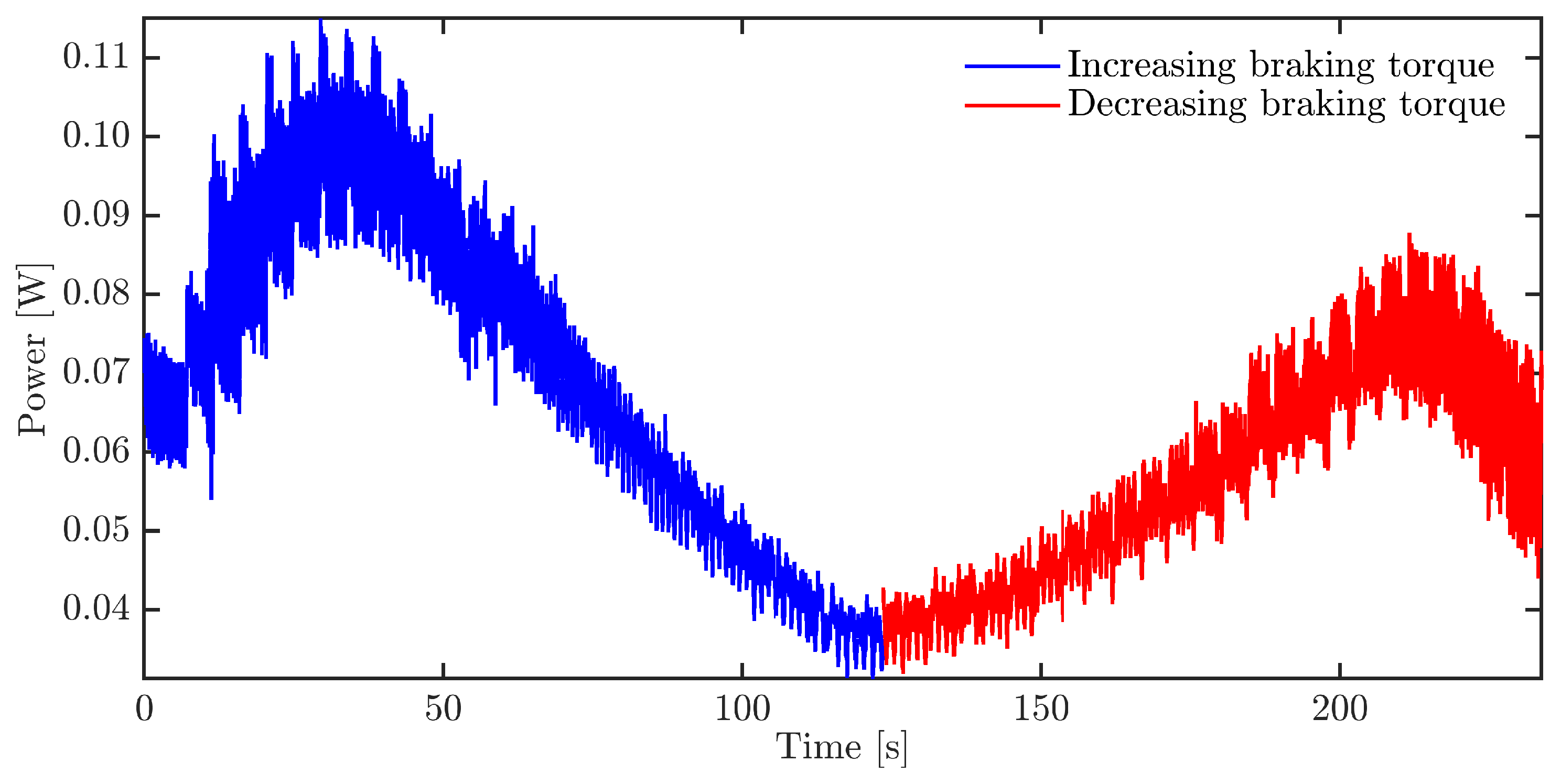
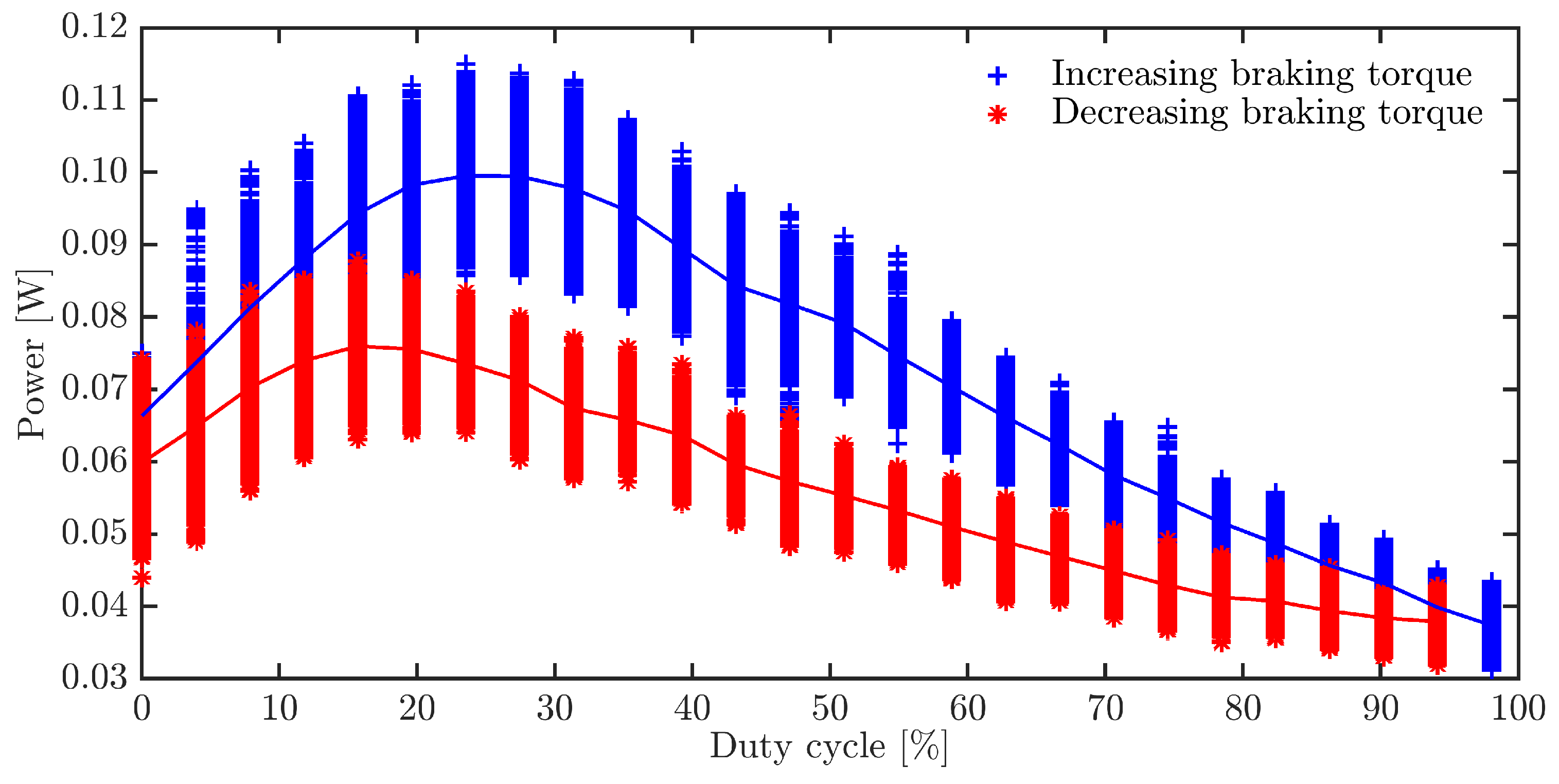
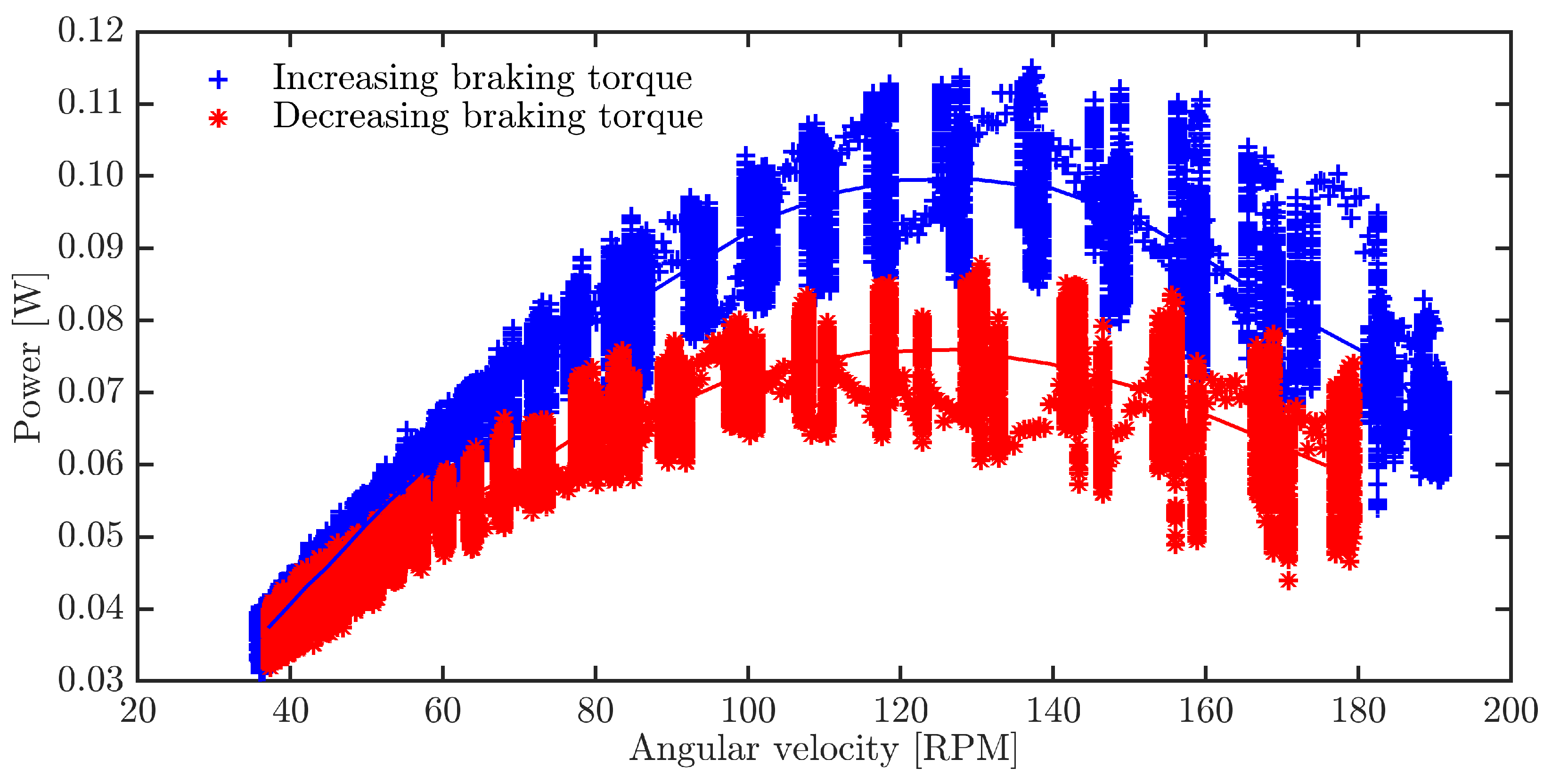
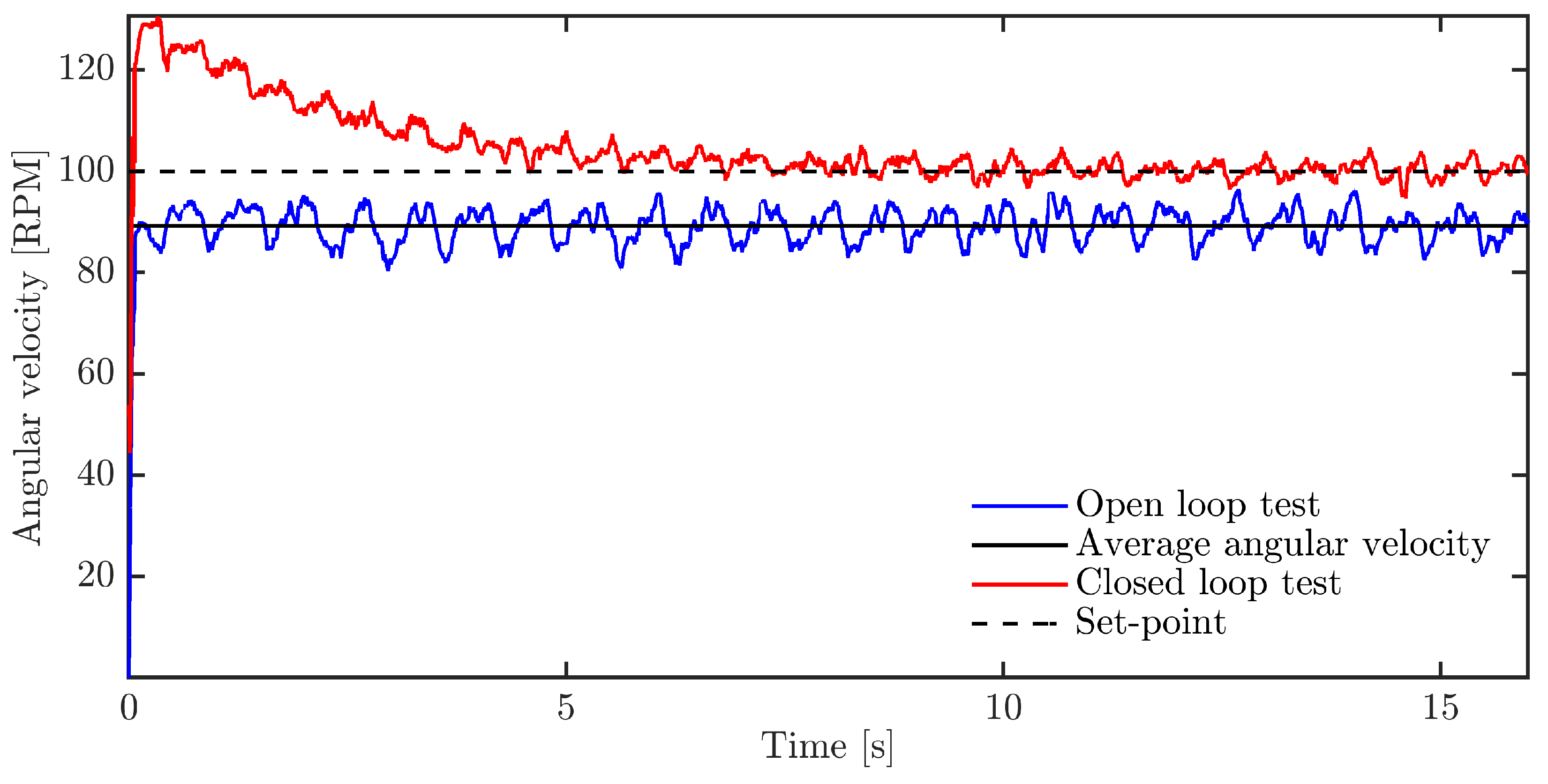
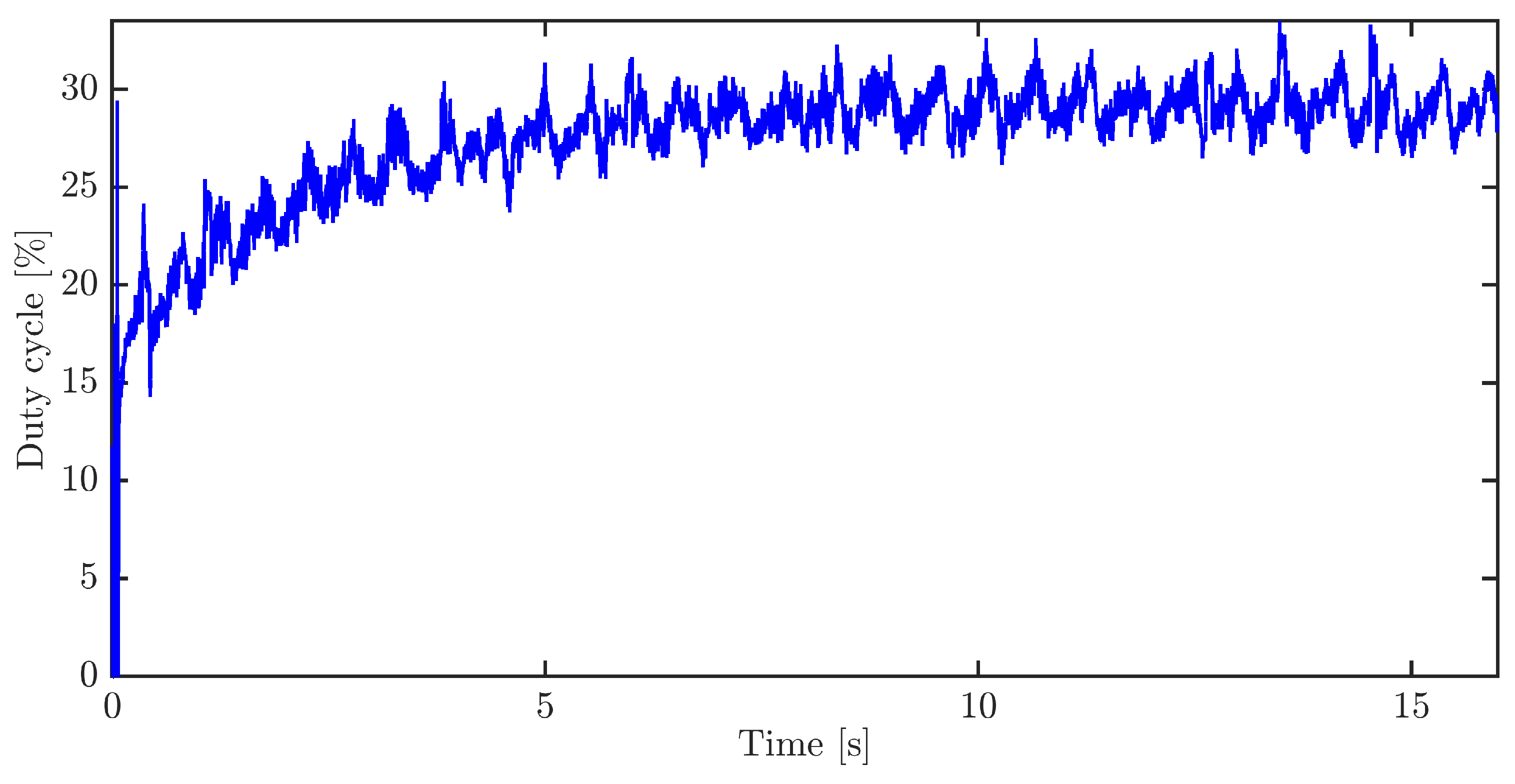
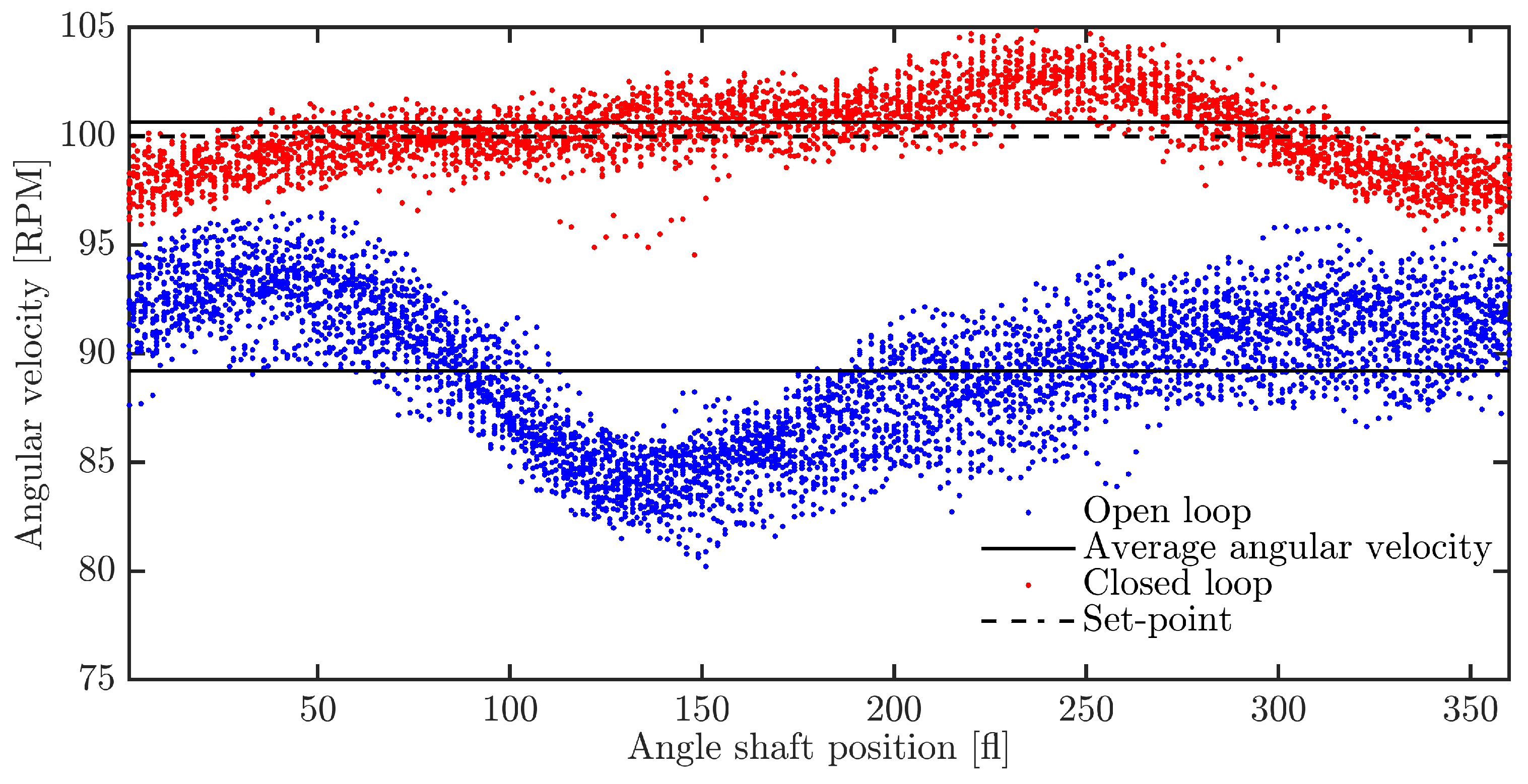
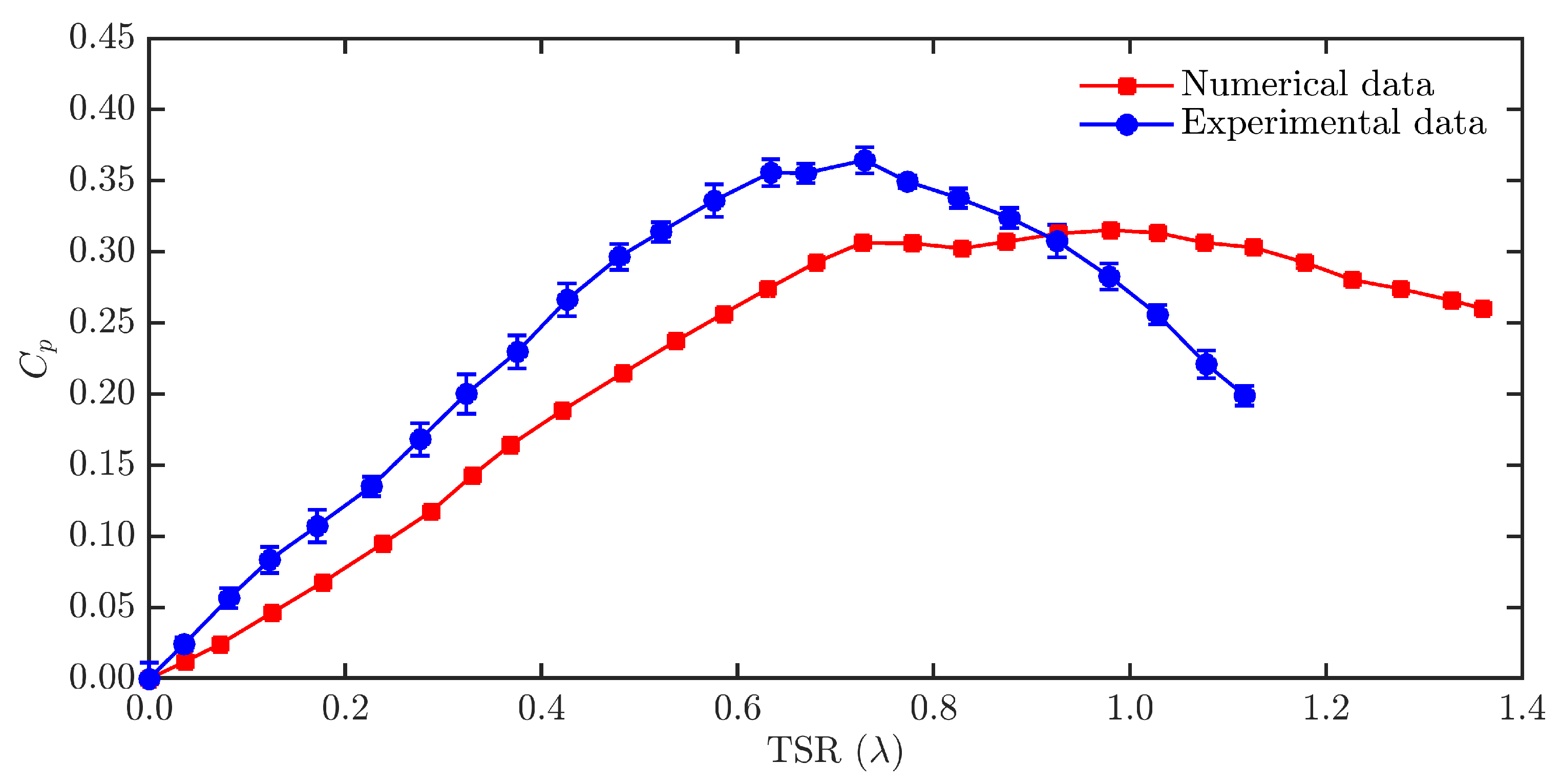
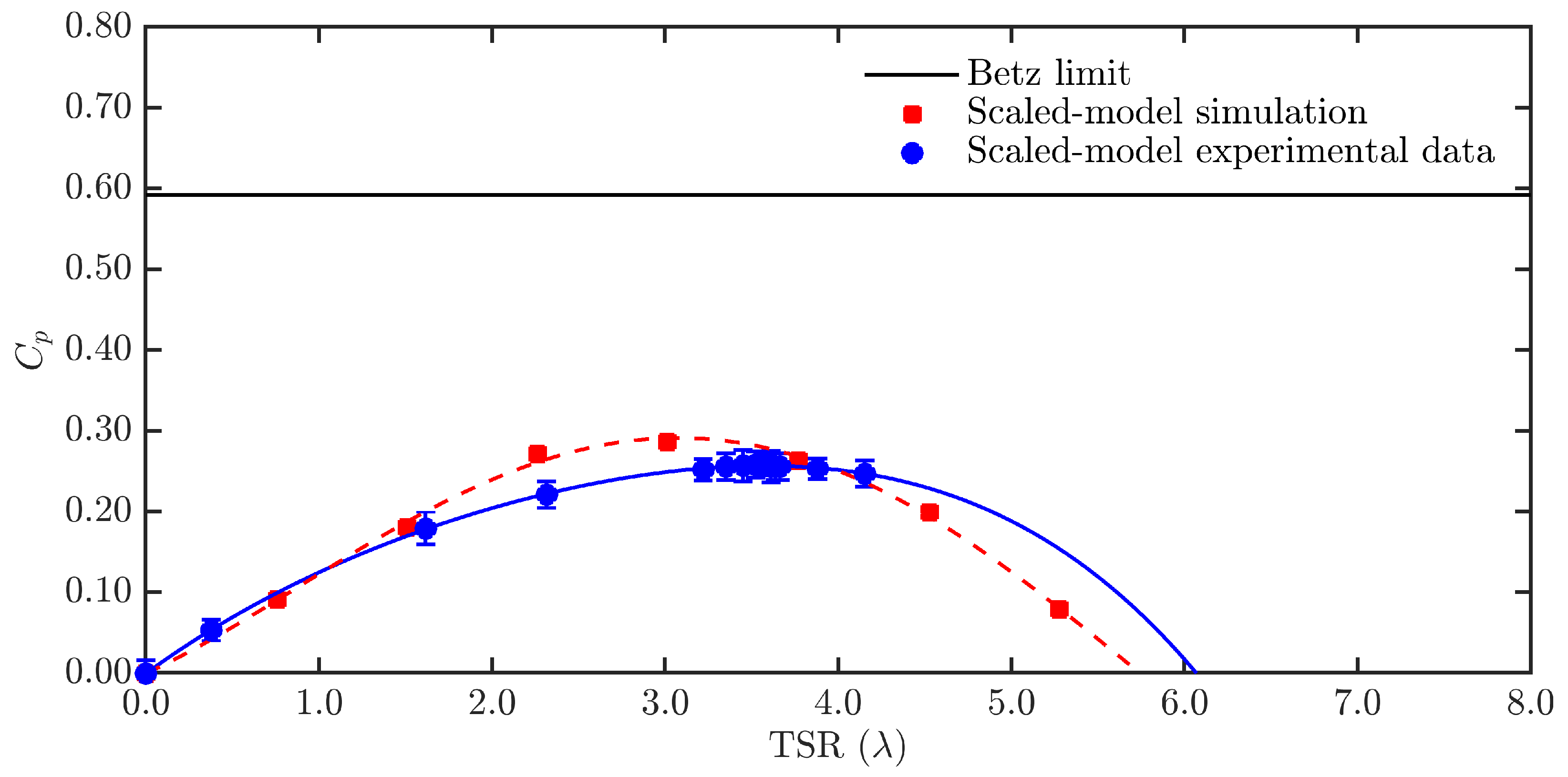
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Raihan, A. A review of the global climate change impacts, adaptation strategies, and mitigation options in the socio-economic and environmental sectors. J. Environ. Sci. Econ. 2023, 2, 36–58. [Google Scholar] [CrossRef]
- Arshad, K.; Hussain, N.; Ashraf, M.H.; Saleem, M.Z. Air pollution and climate change as grand challenges to sustainability. Sci. Total Environ. 2024, 10, 172370. [Google Scholar]
- Gayen, D.; Chatterjee, R.; Roy, S. A review on environmental impacts of renewable energy for sustainable development. Int. J. Environ. Sci. Technol. 2024, 21, 5285–5310. [Google Scholar] [CrossRef]
- Aneja, R.; Yadav, M.; Gupta, S. The dynamic impact assessment of clean energy and green innovation in realizing environmental sustainability of G-20. Sustain. Dev. 2024, 32, 2454–2473. [Google Scholar] [CrossRef]
- Mayor, B.; Rodríguez-Muñoz, I.; Villarroya, F.; Montero, E.; López-Gunn, E. The role of large and small scale hydropower for energy and water security in the Spanish Duero basin. Sustainability 2017, 9, 1807. [Google Scholar] [CrossRef]
- Amjith, L.R.; Bavanish, B. A review on biomass and wind as renewable energy for sustainable environment. Chemosphere 2022, 293, 133579. [Google Scholar] [CrossRef]
- Henao, F.; Viteri, J.P.; Rodríguez, Y.; Gómez, J.; Dyner, I. Annual and interannual complementarities of renewable energy sources in Colombia. Renew. Sustain. Energy Rev. 2020, 134, 110318. [Google Scholar] [CrossRef]
- Rueda-Bayona, J.G.; Guzmán, A.; Eras, J.J.C.; Silva-Casarín, R.; Bastidas-Arteaga, E.; Horrillo-Caraballo, J. Renewables energies in Colombia and the opportunity for the offshore wind technology. J. Clean. Prod. 2019, 220, 529–543. [Google Scholar] [CrossRef]
- Acaroğlu, H.; Güllü, M. Climate change caused by renewable and non-renewable energy consumption and economic growth: A time series ARDL analysis for Turkey. Renew. Energy 2022, 193, 434–447. [Google Scholar] [CrossRef]
- Barbarić, M.; Guzović, Z. Investigation of the possibilities to improve hydrodynamic performances of micro-hydrokinetic turbines. Energies 2020, 13, 4560. [Google Scholar] [CrossRef]
- Mat Yazik, M.H.; Wei Shyang, C.; Ishak, M.H.H.; Ismail, F. An overview of blade materials and technologies for hydrokinetic turbine application. Int. J. Green Energy 2024, 21, 476–499. [Google Scholar] [CrossRef]
- Ibrahim, W.I.; Mohamed, M.R.; Ismail, R.M.; Leung, P.K.; Xing, W.W.; Shah, A.A. Hydrokinetic energy harnessing technologies: A review. Energy Rep. 2021, 7, 2021–2042. [Google Scholar] [CrossRef]
- He, R.; Sun, H.; Gao, X.; Yang, H. Wind tunnel tests for wind turbines: A state-of-the-art review. Renew. Sustain. Energy Rev. 2022, 166, 112675. [Google Scholar] [CrossRef]
- Niebuhr, C.M.; van Dijk, M.; Neary, V.S.; Bhagwan, J.N. A review of hydrokinetic turbines and enhancement techniques for canal installations: Technology, applicability and potential. Renew. Sustain. Energy Rev. 2019, 113, 109240. [Google Scholar] [CrossRef]
- Maldar, N.R.; Ng, C.Y.; Patel, M.S.; Oguz, E. Potential and prospects of hydrokinetic energy in Malaysia: A review. Sustain. Energy Technol. Assessments 2022, 52, 102265. [Google Scholar] [CrossRef]
- Mosbahi, M.; Lajnef, M.; Derbel, M.; Mosbahi, B.; Aricò, C.; Sinagra, M.; Driss, Z. Performance improvement of a drag hydrokinetic turbine. Water 2021, 13, 273. [Google Scholar] [CrossRef]
- Mendes, R.C.; Macias, M.M.; Oliveira, T.F.; Brasil, A.C., Jr. A computational fluid dynamics investigation on the axial induction factor of a small horizontal axis wind turbine. J. Energy Resour. Technol. 2021, 143, 041301. [Google Scholar] [CrossRef]
- Bastankhah, M.; Porté-Agel, F. A new miniature wind turbine for wind tunnel experiments. Part I: Design and performance. Energies 2017, 10, 908. [Google Scholar] [CrossRef]
- Yavuz, T.; Koç, E.; Kilkiş, B.; Erol, T.; Balas, C.; Aydemir, T. Performance analysis of the airfoil-slat arrangements for hydro and wind turbine applications. Renew. Energy 2015, 74, 414–421. [Google Scholar] [CrossRef]
- Tian, W.; Mao, Z.; Ding, H. Design, test and numerical simulation of a low-speed horizontal axis hydrokinetic turbine. Int. J. Nav. Archit. Ocean Eng. 2018, 10, 782–793. [Google Scholar] [CrossRef]
- Cavagnaro, R.J.; Polagye, B. Field performance assessment of a hydrokinetic turbine. Int. J. Mar. Energy 2016, 14, 125–142. [Google Scholar] [CrossRef]
- Patel, V.; Bhat, G.; Eldho, T.I.; Prabhu, S.V. Influence of overlap ratio and aspect ratio on the performance of Savonius hydrokinetic turbine. Int. J. Energy Res. 2017, 41, 829–844. [Google Scholar] [CrossRef]
- Yuwono, T.; Sakti, G.; Aulia, F.N.; Wijaya, A.C. Improving the performance of Savonius wind turbine by installation of a circular cylinder upstream of returning turbine blade: Improving the Performance of Savonius Wind Turbine. Alex. Eng. J. 2020, 59, 4923–4932. [Google Scholar] [CrossRef]
- Roy, S.; Saha, U.K. Wind tunnel experiments of a newly developed two-bladed Savonius-style wind turbine. Appl. Energy 2015, 137, 117–125. [Google Scholar] [CrossRef]
- Talukdar, P.K.; Sardar, A.; Kulkarni, V.; Saha, U.K. Parametric analysis of model Savonius hydrokinetic turbines through experimental and computational investigations. Energy Convers. Manag. 2018, 158, 36–49. [Google Scholar] [CrossRef]
- Hughes, A. Electric Motors and Drives, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Asyraf, S.M.; Heerwan, P.; Zulhilmi, I.M.; Izhar, I.M. Plugging Brake System as a Hill Descend Control for Electric Powered Wheelchair: Experimental Analysis. In Proceedings of the 2019 IEEE 4th International Conference on Advanced Robotics and Mechatronics (ICARM), Toyonaka, Japan, 3–5 July 2019; pp. 319–324. [Google Scholar]
- Beauregard, B. Improving the Beginner’s PID—Introduction, 2011. Available online: http://brettbeauregard.com/blog/2011/04/improving-the-beginners-pid-introduction/ (accessed on 15 September 2024).
- Martins, F.G. Tuning PID Controllers using the ITAE Criterion. Int. J. Eng. Educ. 2005, 21, 867–873. [Google Scholar]
- Gallo, L.A.; Chica, E.L.; Flórez, E.G.; Obando, F.A. Numerical and experimental study of the blade profile of a Savonius type rotor implementing a multi-blade geometry. Appl. Sci. 2021, 11, 10580. [Google Scholar] [CrossRef]
- Romero-Menco, F.; Betancour, J.; Velásquez, L.; Rubio-Clemente, A.; Chica, E. Horizontal-axis propeller hydrokinetic turbine optimization by using the response surface methodology: Performance effect of rake and skew angles. Ain Shams Eng. J. 2023, 15, 102596. [Google Scholar] [CrossRef]
- Wu, K.T.; Lo, K.H.; Kao, R.C.; Hwang, S.J. Numerical and experimental investigation of the effect of design parameters on Savonius-type hydrokinetic turbine performance. Energies 2022, 15, 1856. [Google Scholar] [CrossRef]
- Aguilar, J.; Velásquez, L.; Romero, F.; Betancour, J.; Rubio-Clemente, A.; Chica, E. Numerical and experimental study of hydrofoil-flap arrangements for hydrokinetic turbine applications. J. King Saud-Univ.-Eng. Sci. 2021, 35, 577–588. [Google Scholar] [CrossRef]
- Zhu, L.; Hou, E.; Zhou, Q.; Wu, H. Numerical Experiments on Hydrodynamic Performance and the Wake of a Self-Starting Vertical Axis Tidal Turbine Array. J. Mar. Sci. Eng. 2022, 10, 1361. [Google Scholar] [CrossRef]




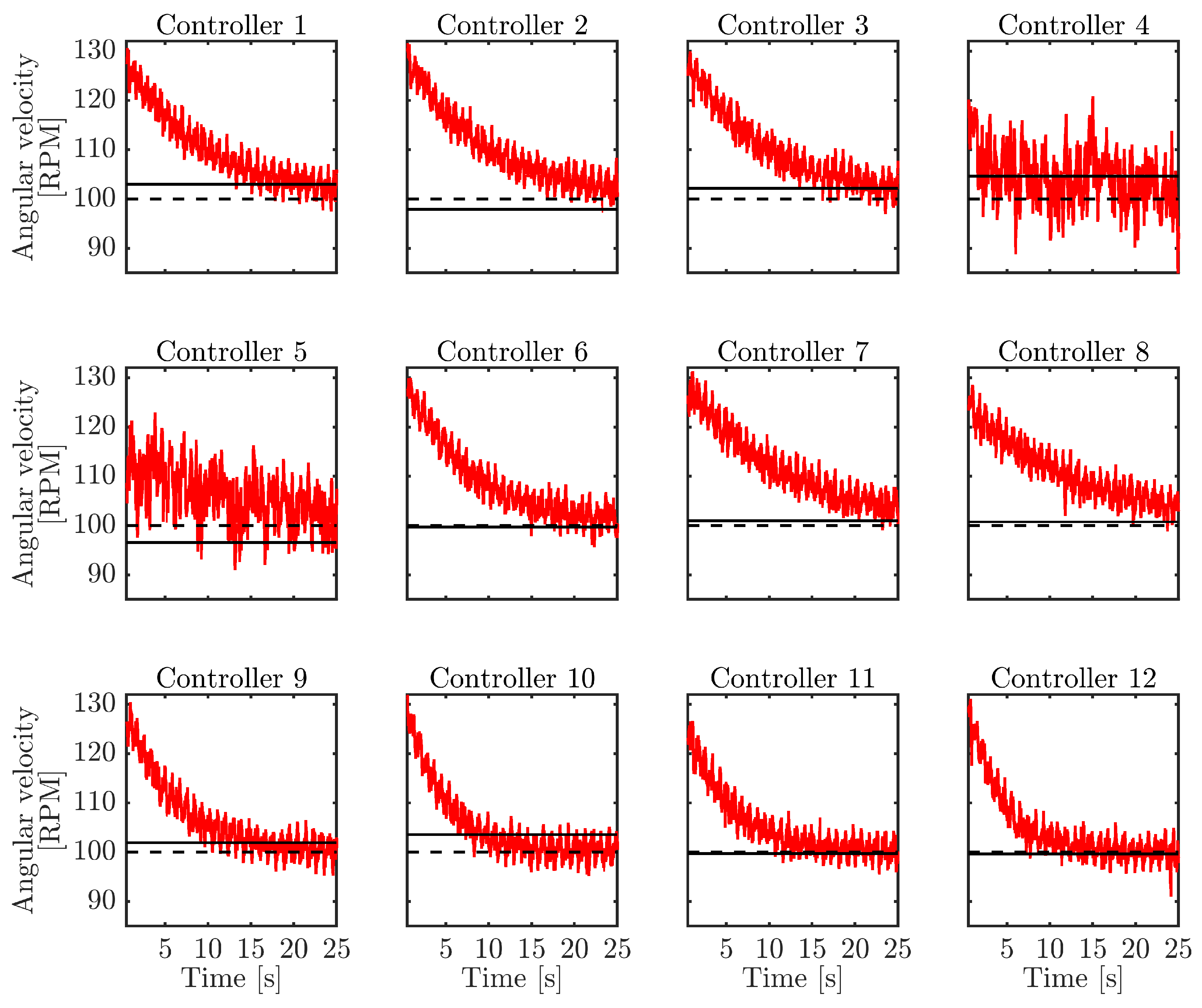
| Controller | Controller | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 0.8 | 1.2 | 0.0005 | 7 | 0.8 | 1.0 | 0.0010 |
| 2 | 0.8 | 1.2 | 0.0001 | 8 | 1.0 | 1.0 | 0.0010 |
| 3 | 0.8 | 1.2 | 0.0010 | 9 | 0.8 | 2.0 | 0.0005 |
| 4 | 0.8 | 1.5 | 0.0050 | 10 | 0.8 | 2.5 | 0.0001 |
| 5 | 0.8 | 1.2 | 0.0050 | 11 | 1.0 | 2.5 | 0.0010 |
| 6 | 0.8 | 1.5 | 0.0010 | 12 | 0.8 | 3.0 | 0.0010 |
| Controller | ITAE | Controller | ITAE | Controller | ITAE |
|---|---|---|---|---|---|
| 1 | 2391 | 5 | 2668 | 9 | 1463 |
| 2 | 2394 | 6 | 1951 | 10 | 1235 |
| 3 | 2350 | 7 | 3146 | 11 | 1218 |
| 4 | 2458 | 8 | 3158 | 12 | 1123 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Obando Vega, F.; Rubio-Clemente, A.; Chica, E. Control System for the Performance Analysis of Turbines at Laboratory Scale. Energies 2024, 17, 4950. https://doi.org/10.3390/en17194950
Obando Vega F, Rubio-Clemente A, Chica E. Control System for the Performance Analysis of Turbines at Laboratory Scale. Energies. 2024; 17(19):4950. https://doi.org/10.3390/en17194950
Chicago/Turabian StyleObando Vega, Felipe, Ainhoa Rubio-Clemente, and Edwin Chica. 2024. "Control System for the Performance Analysis of Turbines at Laboratory Scale" Energies 17, no. 19: 4950. https://doi.org/10.3390/en17194950
APA StyleObando Vega, F., Rubio-Clemente, A., & Chica, E. (2024). Control System for the Performance Analysis of Turbines at Laboratory Scale. Energies, 17(19), 4950. https://doi.org/10.3390/en17194950









