Research on Low-Carbon Building Development and Carbon Emission Control Based on Mathematical Models: A Case Study of Jiangsu Province
Abstract
1. Introduction
1.1. Background
1.2. Model Assumptions and Problems
2. Methods
2.1. Model Assumptions
- The data collected for this study are all reliable and valid. However, we do not consider the existence of other uncertain factors. The uncertain factors are limited to those mentioned in the text and do not include other potential sources of uncertainty.
- We assume that the area of doors and windows has no effect on the calculation of building energy consumption.
- We assume that extreme factors are not considered when calculating the heat loss of the building.
- We assume that when calculating the energy consumption of temperature regulation, the temperature adjustment by air conditioning will not exceed 18 °C or fall below 26 °C.
2.2. Symbol Explanation
3. Establishment and Solution of the Model
3.1. Heat Transfer Model
3.1.1. Calculate the Heat Flow
3.1.2. Calculate the Amount of Electricity Consumed per Month
3.2. Lifecycle of Buildings
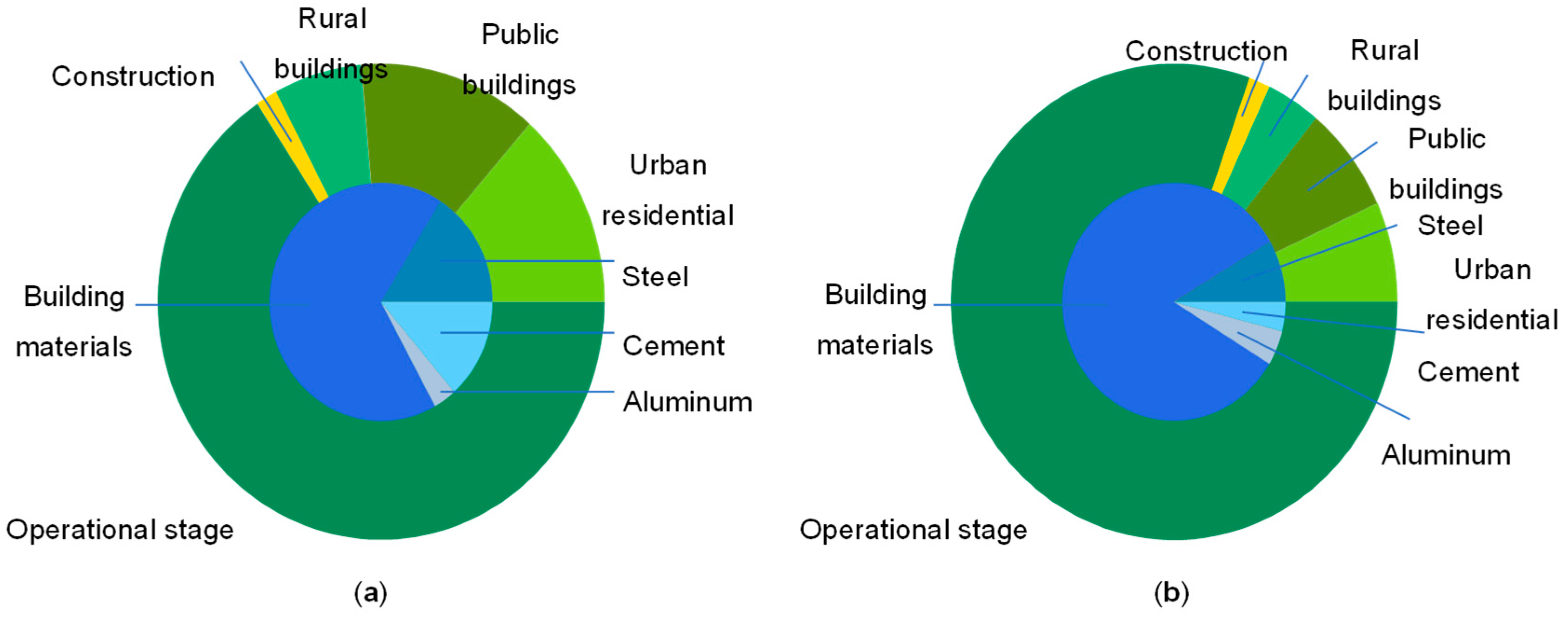
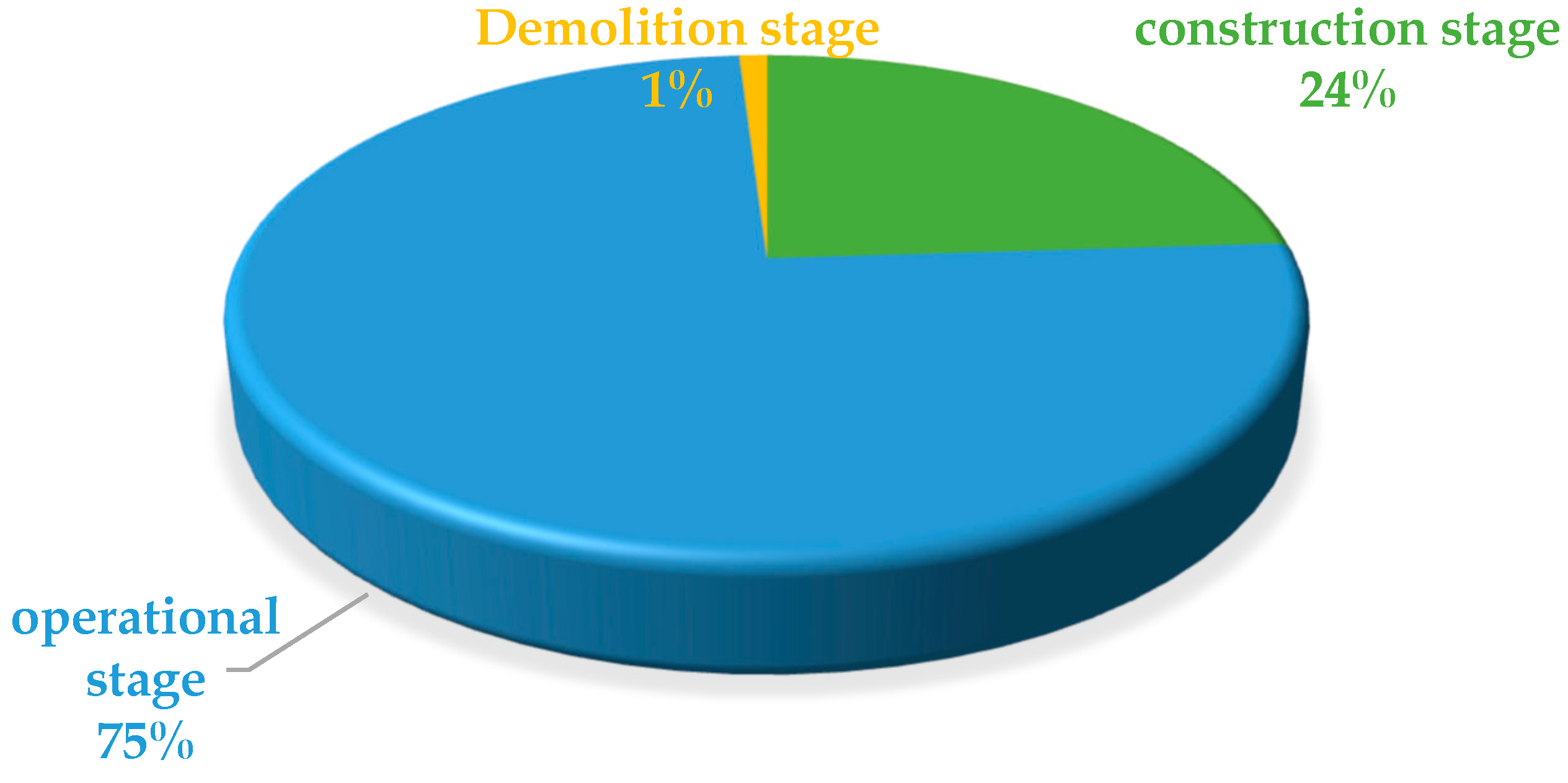
3.2.1. Analysis of Various Indicators and Data in the Lifecycle of Buildings
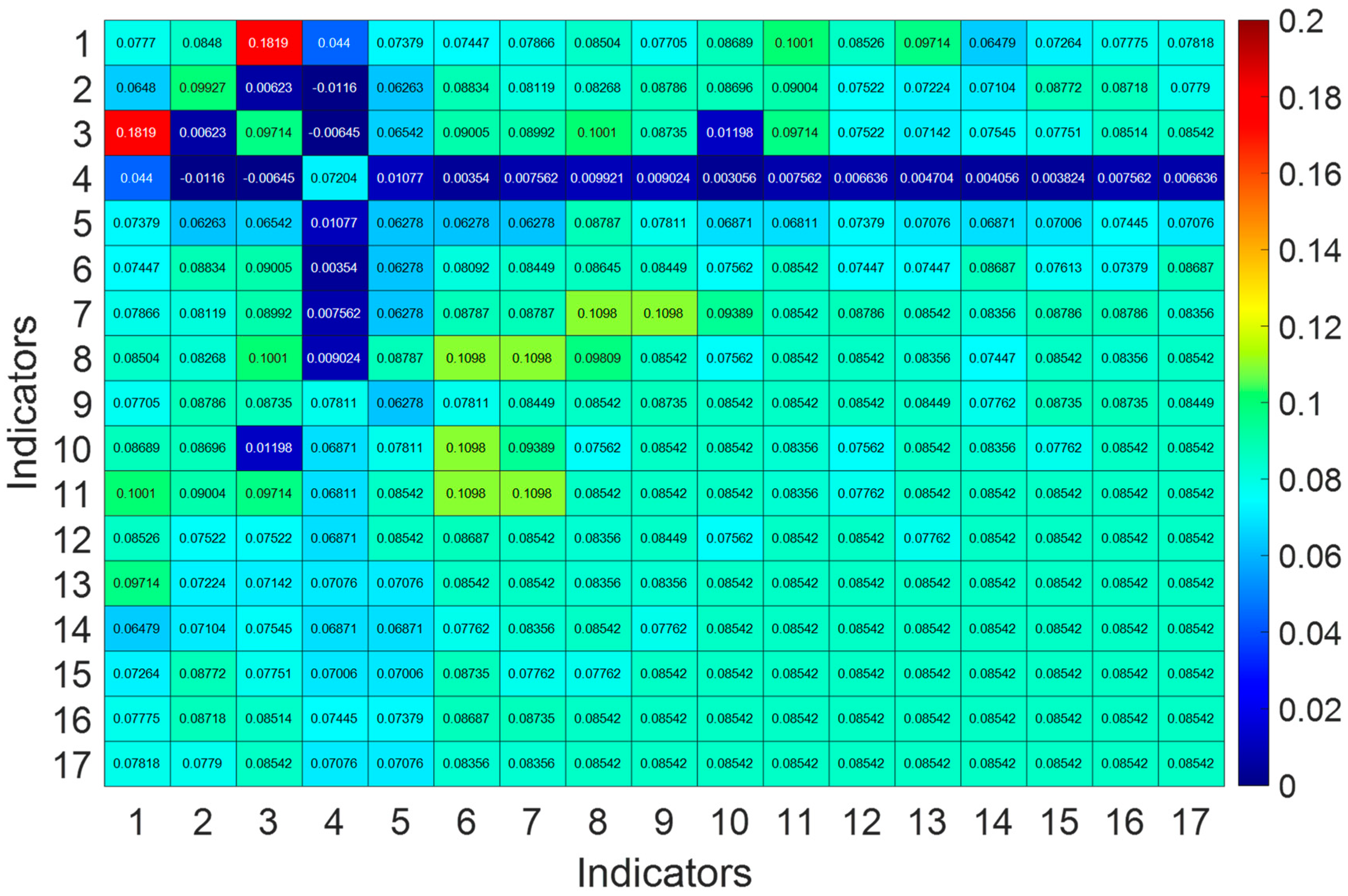
3.2.2. Correlation Analysis of Indicators
3.3. Data Collection
3.3.1. Data on Carbon Emissions
3.3.2. Establishment of Principal Component Analysis (PCA) Model
- 1.
- 2.
- Calculate eigenvalues, eigenvectors, and cumulative contribution rates.
- 3.
- Calculate the component matrix.
- 4.
- Calculate composite score coefficients.
3.4. Establishment of Grey Prediction Model
- 1.
- The Grey Prediction Model is suitable for situations with a small sample size and relatively low computational workload. This is advantageous for the case of the total carbon emissions from buildings in Jiangsu Province for the years 2016–2023, where the sample size is not large. The Grey Prediction Model establishes grey differential equations to predict future trends based on existing data, providing a reference for prediction results. Although long-term predictions may have some errors, the Grey Prediction Model still offers a quick and effective method in situations with insufficient sample size.
- (1).
- Calculate the level ratio,
- (2).
- Level ratio test graph (see Figure 7):
- 2.
- GM(1,1) Model:
- (1).
- Perform a cumulative sum on the original data,
- (2).
- Construct the data matrix B and the data vector Y
- a.
- Calculate
- b.
- Establish the differential equation and the model:
- c.
- Calculate the generated sequence values k = 1, 2, …, from the above time response function,
- 3.
- Model Verification:
- (1).
- Residual Analysis
- (2).
- Level Ratio Deviation Test
- (3).
- The calculation results of various test indicators of the model obtained using Matlab are shown in the table below (see Table 12).
- (4).
- Model Accuracy Verification:
4. Model Evaluation and Improvement
4.1. Model Evaluation Model Summary
4.2. Model Validation
4.3. Advantages of the Model
- 1.
- Thermal Conduction Model: The thermal conduction model calculates the heat transfer power of buildings using data, which has the advantages of strong objectivity and high accuracy. By measuring and analyzing the thermal conduction characteristics of buildings, the energy consumption and carbon emissions of buildings can be predicted more accurately. This method can provide actual data support, making the prediction results more reliable.
- 2.
- Principal Component Analysis (PCA): PCA can eliminate the correlation between variables, making each indicator independent. The benefit of this is to reduce redundant information and extract the most representative principal components. By assigning weights to the principal components, comprehensive evaluation and prediction can be better performed. PCA can also help us understand the relationships between various indicators and identify the main factors affecting carbon emissions.
- 3.
- Grey Prediction Model: The Grey Prediction Model is suitable for cases with small sample sizes and requires relatively little computational effort. This is advantageous in the case of the small sample size of data from 2016 to 2023 for the total carbon emissions of buildings in Jiangsu Province. The Grey Prediction Model predicts based on the development trends in existing data by establishing grey differential equations, providing a useful reference for prediction results. Although long-term predictions may have some errors, the Grey Prediction Model remains a fast and effective prediction method when sample sizes are limited.
4.4. Model Improvement
- 1.
- Addressing Data Quality Issues: If the sample size is small and data quality is low, it may lead to inaccurate prediction results. Data accuracy and completeness are crucial for the effectiveness of prediction models. Therefore, before conducting grey prediction, ensure that the data used are reliable and have been effectively cleaned and processed.
- 2.
- Addressing Model Assumptions Limitation: Grey Prediction Models are established based on certain assumptions, such as the linear relationship of data sequences and the stability of development trends. If the data sequences exhibit nonlinear relationships or unstable development trends, Grey Prediction Models may not provide accurate predictions. Therefore, when applying Grey Prediction Models, reasonable evaluation and validation of model assumptions are needed to ensure their applicability.
- 3.
- Addressing Subjectivity in Principal Component Analysis: Using contribution rates directly as weights in principal component analysis may be subjective. To assign weights more objectively, entropy weighting can be used to calculate the weights of principal components. Additionally, consulting relevant literature and assigning subjective weights based on the importance of different principal components can also be considered.
- 4.
- Addressing the Long-term Prediction Limitation of Grey Prediction Model: Grey Prediction Models are suitable for short- to medium-term predictions but may not be suitable for long-term forecasting. If long-term predictions are required, a combination of time series models and regression models can be used. Weighting the prediction results of these three models can improve prediction accuracy. This approach leverages the trend characteristics of time series and the influence factors of regression models to enhance prediction accuracy.
4.5. Methodological Limitations
- 1.
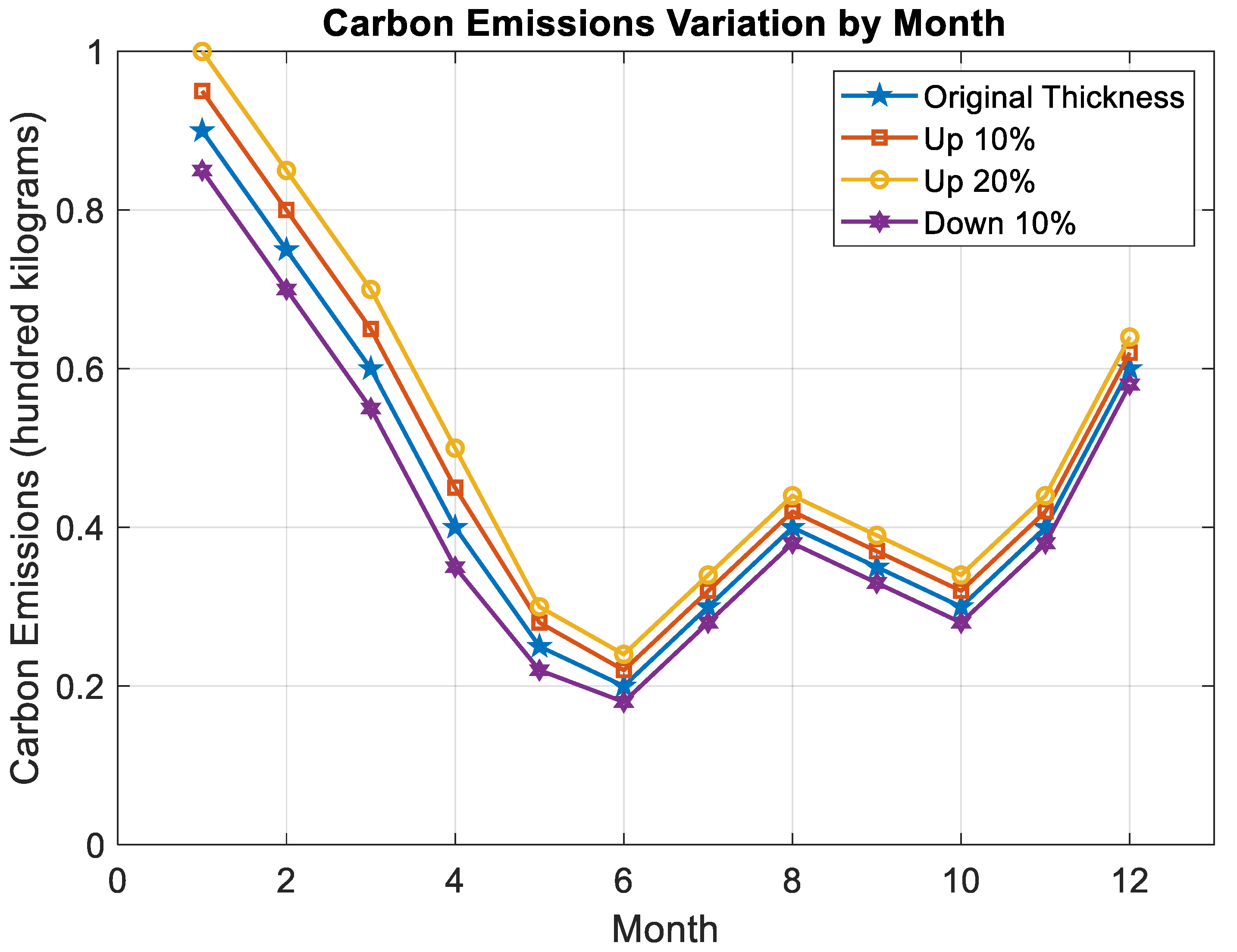
- Assumptions: The study begins by selecting a representative building unit with dimensions of 4 m in length, 3 m in width, and 3 m in height. This choice is advantageous for several reasons. Firstly, it allows for the creation of a simplified analytical model. These dimensions and structural attributes provide a model that is conducive to mathematical analysis. This simplification facilitates a clearer understanding of how various factors impact carbon emissions, thereby enabling the extension of these findings to more complex buildings. Secondly, it embodies typical characteristics of residential units and offers scalability. Finally, it represents a standard energy consumption pattern. Using a small-scale building enables precise measurement of the impact of temperature regulation, which is essential for formulating energy-saving measures that can be applied to buildings of varying sizes. Data collection in this context is generally more straightforward, and the results are easier to verify. These data can be extrapolated to larger buildings, ensuring that the research is grounded in robust empirical evidence. The study assumes a Coefficient of Performance (COP) of 3.5 and an Energy Efficiency Ratio (EER) of 2.7 for the selected air conditioning equipment. These performance metrics are consistent with the standard performance levels of most modern air conditioning systems currently available. Simplifying the analytical model in this manner aligns with energy conservation and emission reduction policies, allowing the study to better reflect the utilization of air conditioning systems in buildings across Jiangsu Province and China. This approach contributes to the development of scientifically sound and effective carbon emissions control and energy-saving strategies that are consistent with national policies. Therefore, the choice of such air conditioning equipment in this study is both representative and practically significant. Furthermore, the study deliberately excludes the impact of doors and windows, as comparative data analysis has shown that their influence is relatively minor. This simplification enhances the feasibility and accuracy of the research.
- 2.
- Model limitations: This study focused on residential buildings rather than industrial areas due to the complexities and challenges associated with obtaining energy consumption data in industrial settings. Residential buildings typically have simpler and more uniform structures, making them more amenable to study and modeling. In contrast, industrial buildings exhibit a higher degree of diversity and complexity, introducing numerous uncontrollable variables into the research process. By concentrating on residential areas, the study could better control these variables, thereby enhancing the accuracy and reliability of its findings. Additionally, energy consumption in industrial areas is often subject to stringent regulation by industry standards and policies, requiring different analytical models and methods than those applicable to residential areas. The focus on residential areas also broadens the applicability of the study’s findings to nationwide building energy conservation and carbon emission control efforts. However, it is acknowledged that the intricate and varied energy consumption structures in industrial areas may necessitate independent research methods and models, which this study does not address.
5. Conclusions
- 1.
- This paper assessed energy loss using a heat conduction model and proposed design solutions to reduce energy consumption by considering factors such as the physical properties of materials, heat conduction modes, and time. The model can assist designers in optimizing energy utilization and enhancing energy efficiency.
- 2.
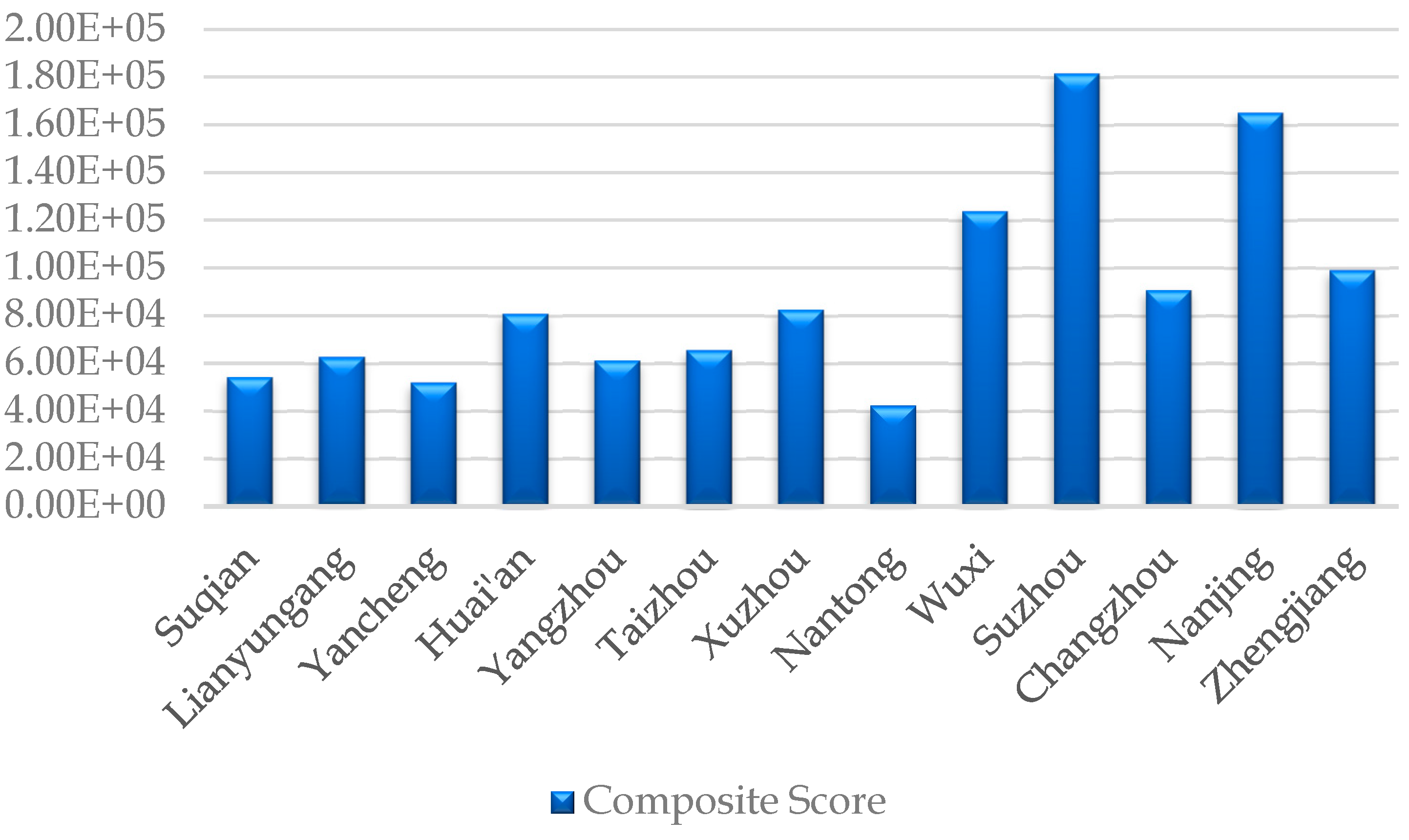
- Correlation analysis was used to estimate the correlations between indicators and to determine the applicability of Principal Component Analysis. The Principal Component Analysis model transforms highly correlated variables into linearly uncorrelated variables through orthogonal transformations. By extracting the key information, the comprehensive scores for the ten indicators were obtained, among which the building area has the most significant impact on residential building carbon emissions, with a score of 0.136. Suzhou City in Jiangsu Province has the highest comprehensive score of 1.61568, indicating that Suzhou has the highest carbon emissions from the building process, followed by Nanjing, Wuxi, and Zhenjiang. Yancheng has the lowest carbon emissions from the building process, followed by Suqian and Yangzhou.
- 3.
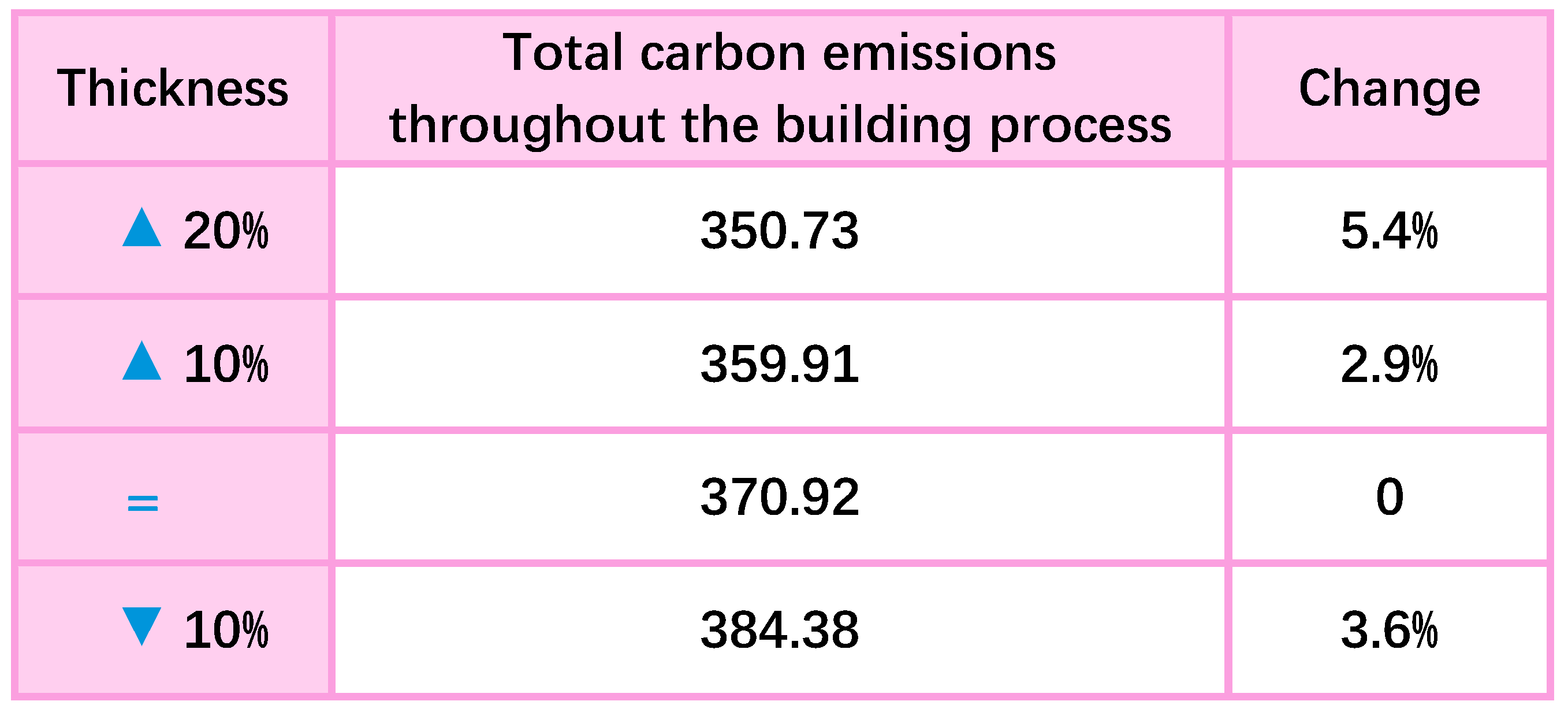
- This paper introduced a grey prediction method for carbon emissions throughout the construction process, which is effective in the presence of uncertain information. The carbon emissions for 2024 are predicted using the GM(1,1) model within the grey prediction method, based on historical data of building carbon emissions from 2016 to 2023. The forecasted total carbon emissions for buildings in Jiangsu Province in 2024 is estimated to be 1.5576 million tons. Considering variations in temperature, rainfall, building energy consumption, and industrial output among regions, the feasibility of proposals must be evaluated. Different materials exhibit significant differences in thermal conductivity, thus affecting building insulation. Since energy consumption is higher in winter, prioritizing materials with better insulation could help reduce heating energy usage. Factors such as building area and energy consumption significantly impact carbon emissions, necessitating efficient building design and resource management.
- 4.
- Significant disparities in carbon emissions exist among cities in Jiangsu Province, with southern cities emitting more than northern ones. Economic development plans should promote balance between regions, fostering green development to maintain equilibrium. Without intervention, residential building emissions are projected to double by 2031, highlighting the need for stringent control measures. By comprehensively utilizing these models and methods, decision-makers can better understand problems and enhance the accuracy and reliability of decisions.
- 5.
- This study explores effective strategies for low-carbon building development and carbon emission control in Jiangsu Province. Through a detailed analysis of carbon emissions at each stage of a residential building’s life cycle (construction, operation, and demolition), the findings show that the building’s energy consumption and carbon emissions during the operational phase account for the largest portion of total emissions. Optimizing the selection of building materials, improving construction technology, and promoting energy-saving equipment and technologies are key measures to reduce carbon emissions throughout the life cycle of buildings. In addition, the mathematical model and evaluation method proposed in this paper provide a feasible reference framework for other regions and countries, which can help promote the development of low-carbon buildings worldwide. At the same time, it was found that the energy consumption and carbon emissions in the operation phase were significantly higher than those in the construction and demolition phases, mainly focusing on the use of indoor temperature regulation (such as air conditioning systems). By using energy-efficient building materials, improving construction techniques, and promoting intelligent control systems, a building’s total carbon emissions can be significantly reduced. Therefore, we recommend that the government and relevant departments formulate and promote building energy efficiency standards, strengthen support for the research and application of green building technologies, and provide corresponding incentives.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qu, J.; Guan, S.; Qin, J.; Zhang, W.; Li, Y.; Zhang, T. Estimates of cooling effect and energy savings for a cool white coating used on the roof of scale model buildings. Mater. Sci. Eng. 2019, 479, 012024. [Google Scholar] [CrossRef]
- Valdiserri, P.; Ballerini, V.; di Schio, E.R. Interpolating functions for CO2 emission factors in dynamic simulations: The special case of a heat pump. Sustain. Energy Technol. Assess. 2022, 53, 102725. [Google Scholar] [CrossRef]
- Shen, W.; Cao, L.; Li, Q.; Zhang, W.; Li, C. Quantifying CO2 emissions from China’s cement industry. Renew. Sustain. Energy Rev. 2015, 50, 1004–1012. [Google Scholar] [CrossRef]
- Institute for Climate Change and Sustainable Development, Tsinghua University. Research on China’s Long-Term Low-Carbon Development Strategy and Transformation Pathways; Environmental Publishing House: Beijing, China, 2021; pp. 220–260. (In Chinese) [Google Scholar]
- Li, Q.; Chen, Z.; Zhang, J.; Li, X.; Zhang, X. Insights from the Future Version of China’s CCUS Technology Roadmap (Update): An Analysis Based on the Perspective of the Global CCS Roadmap. Low Carbon World 2014, 7, 7–8. [Google Scholar]
- Li, Y.; Zhang, K.; Li, J. Comparative Analysis of Carbon Emissions in the Whole Life Cycle of Residential Buildings and Carbon Reduction Strategies. J. Xi’an Univ. Archit. Technol 2021, 53, 737–745. [Google Scholar] [CrossRef]
- Huang, Z.; Zhou, H.; Miao, Z.; Tang, H.; Lin, B.; Zhuang, W. Life-cycle Carbon Emissions in the Whole Life Cycle of Buildings: Connotation, Calculation, and Reduction. Engineering 2024, 35, 115–139. [Google Scholar] [CrossRef]
- China Construction Certification Center Co., Ltd.; Zhongtan Digital Laboratory. Research Report on Carbon Peak and Carbon Neutrality in China’s Construction Industry. 2022. Available online: http://www.jccchina.com/UserFiles/upload/file/20230324/20230324093145556.pdf (accessed on 19 July 2024). (In Chinese).
- China Association of Building Energy Efficiency. 2021 China Building Energy Consumption and Carbon Emission Research Report. 2021. Available online: https://mp.weixin.qq.com/s?__biz=MzIxODcxNDEwOQ==&mid=2247484041&idx=1&sn=0d6a67b96130de524e69d14ec76502a7&chksm=97e7181ba090910d71fc1d49d57ea7b2181c4537cf1689875aa8eb19a52b96e0eed56906d7c2&scene=27 (accessed on 19 July 2024). (In Chinese).
- Jiangsu Provincial Bureau of Statistics; Jiangsu Survey Office of the National Bureau of Statistics. 2023 Jiangsu Province National Economic and Social Development Statistical Bulletin. 2023. Available online: http://tj.jiangsu.gov.cn/art/2024/3/5/art_87595_11165526.html (accessed on 19 July 2024). (In Chinese)
- Xiao, Y.; Dai, R.; Zhang, G.; Chen, W. The Use of an Improved LSSVM and Joint Normalization on Temperature Prediction of Gearbox Output Shaft in DFWT. Energies 2017, 10, 1877. [Google Scholar] [CrossRef]
- Taherahmadi, J.; Noorollahi, Y.; Panahi, M. Toward comprehensive zero energy building definitions: A literature review and recommendations. Int. J. Sustain. Energy 2021, 40, 120–148. [Google Scholar] [CrossRef]
- Lu, C.; Wang, D.; Meng, P.; Yang, J.; Pang, M.; Wang, L. Research on Resource Curse Effect of Resource-Dependent Cities: Case Study of Qingyang, Jinchang and Baiyin in China. Sustainability 2019, 11, 91. [Google Scholar] [CrossRef]
- Likos, W.J. Modeling Thermal Conductivity Dryout Curves from Soil-Water Characteristic Curves. J. Geotech. Geoenviron. Eng. 2014, 140, 04013056. [Google Scholar] [CrossRef]
- Xing, W.; Ullmann, A.; Brauner, N.; Plawsky, J.; Peles, Y. Advancing micro-scale cooling by utilizing liquid-liquid phase separation. Sci. Rep. 2018, 8, 12093. [Google Scholar] [CrossRef] [PubMed]
- Luo, Z.; Cang, Y.; Zhang, N.; Yang, L.; Liu, J. A Quantitative Process-Based Inventory Study on Material Embodied Carbon Emissions of Residential, Office, and Commercial Buildings in China. J. Therm. Sci. 2019, 28, 1236–1251. [Google Scholar] [CrossRef]
- Banti, D.C.; Tsangas, M.; Samaras, P.; Zorpas, A. LCA of a Membrane Bioreactor Compared to Activated Sludge System for Municipal Wastewater Treatment. Membranes 2020, 10, 421. [Google Scholar] [CrossRef] [PubMed]
- Kaewunruen, S.; Sresakoolchai, J.; Peng, J. Life Cycle Cost, Energy and Carbon Assessments of Beijing-Shanghai High-Speed Railway. Sustainability 2020, 12, 206. [Google Scholar] [CrossRef]
- Zou, Y.; He, Y.; Lin, W.; Fang, S. China’s regional public safety efficiency: A data envelopment analysis approach. Ann. Reg. Sci. 2021, 66, 409–438. [Google Scholar] [CrossRef]
- Sun, L.; Yu, S.; Ji, Y.; Zhou, P.; He, Y.; Weerasinghe, R. Air Environment Pollution and Management Measures at Bulk Terminals. E3S Web Conf. 2020, 143, 02037. [Google Scholar] [CrossRef]
- Binarti, F.; Koerniawan, M.D.; Triyadi, S.; Utami, S.S. Maximizing the ENVI-met Capability of Modelling the Mean Radiant Temperature of a Tropical Archaeological Site. IOP Conf. Ser. Earth Environ. Sci. 2020, 541, 012005. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, R.; Gao, H.; Zhang, Y. The New Design of Syrup Drug Delivery Device. IOP Conf. Ser. Earth Environ. Sci. 2019, 358, 032004. [Google Scholar] [CrossRef]
- Ibrahim, F.H.; Yusoff, F.M.; Fitrianto, A.; Nuruddin, A.A.; Gandaseca, S.; Samdin, Z.; Kamarudin, N.; Nurhidayu, S.; Kassim, M.R.; Hakeem, K.R.; et al. How to develop a comprehensive Mangrove Quality Index? MethodsX 2019, 6, 1591–1599. [Google Scholar] [CrossRef]
- Johnsson, M.; Henriksen, R.; Fogelholm, J.; Höglund, A.; Jensen, P.; Wright, D. Genetics and Genomics of Social Behavior in a Chicken Model. Genetics 2018, 209, 209–221. [Google Scholar] [CrossRef]
- Zheng, H.; Xia, X.; Gu, J.; Xia, Y.; Li, M.; Zhao, L.; Jin, X. Current Status, Transformation, and Countermeasures of Social Development Under the Goals of ‘Peak Carbon’ and ‘Carbon Neutrality’. Ind. Metrol. 2024, 33, 55–60+79. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y. Calculation Model of Carbon Emissions from Construction Projects Based on Whole Life Cycle. J. Eng. Manag. 2015, 29, 12–16. [Google Scholar] [CrossRef]
- Qi, X.; Shi, L.; Crockforce, K.; Zhou, M. Comparison Study on Calculation and Environmental Impact of Residential Building Lifecycle Carbon Emissions Between China and Finland. World Archit. 2024, 1, 104–109. [Google Scholar]
- Cao, Q. Research on Multispectral Dimensionality Reduction Algorithm Based on Second Order Polynomial Regression and Weighted Principal Component Analysis. Opt. Tech. 2024, 49, 250–256. [Google Scholar] [CrossRef]
- Gou, X.; Mi, C.; Zeng, B.; Li, M.; Xu, Y. New Seasonal Discrete Grey Prediction Model and Its Application from Longitudinal and Horizontal Dimensions Perspective. Chin. J. Manag. Sci. 2024, 1–12. [Google Scholar] [CrossRef]
- Ma, Q.; Li, S.; Ding, B.; Hou, M. Analysis of Precision Inspection Items of CNC Turning and Milling Compound Machine Tool. Met. Process. Cold Work. 2024, 4, 61–64. [Google Scholar]
- Zhang, S.; Wang, K. Research on Control Indicators of Carbon Emissions for Low-Carbon, Near-Zero Carbon, and Zero Carbon Residential Buildings. Build. Sci. 2024, 39, 11–19+57. [Google Scholar]
- Hu, J.; Wang, Z.; Pan, Y.; Li, P. Research on Thermal Conduction Model of Regenerative Cooling U-shaped Channel in Supercharged Pulse Detonation Engine. Propuls. Technol. 2022, 43, 152–163. [Google Scholar] [CrossRef]
- Li, Z.; Wu, X.; Yuan, T.; Mao, W. Numerical Analysis Model of Circuit Breaker Short-Circuit Closing Process and Its Application in Arcing Fault Selection. High Volt. Appar. 2022, 58, 180–187. [Google Scholar] [CrossRef]
- Sun, J.; Xin, Y.; Zhang, C.X.; Zhao, Y.; Wang, Z.F. Application of Principal Component Analysis Method in Water Quality Evaluation of Yubiao Reservoir. Tianjin Agric. For. Sci. Technol. 2024, 2, 10–12. [Google Scholar] [CrossRef]
- Li, W. Quantifying the Building Energy Dynamics of Manhattan, New York City, Using an Urban Building Energy Model and Localized Weather Data. Energies 2020, 13, 3244. [Google Scholar] [CrossRef]



| Symbols | Explanation |
|---|---|
| Indoor-outdoor temperature difference | |
| Heat transfer area | |
| Air conditioning power | |
| Heat flux | |
| Thickness of the heat transfer layer | |
| Air conditioning consumption | |
| Residual | |
| Ratio of levels | |
| Accumulate the data in turn | |
| Raw data |
| Months | Heat Flux Loss (Joules) | Month | Increase in Heat Flux (Joules) |
|---|---|---|---|
| 1 | 1551.7 | 6 | 163 |
| 2 | 1306.7 | 7 | 408.3 |
| 3 | 980 | 8 | 490 |
| 4 | 490 | ||
| 11 | 245 | ||
| 12 | 1306.7 |
| Month | Energy Consumption For Heating (Wh) | Month | Energy Consumption for Cooling (Wh) |
|---|---|---|---|
| 1 | 319.2 | 6 | 43.6 |
| 2 | 268.8 | 7 | 108.9 |
| 3 | 201.6 | 8 | 130.7 |
| 4 | 100.8 | ||
| 11 | 504 |
| Month | Carbon Emissions for Heating | Month | Carbon Emissions for Cooling (kg) |
|---|---|---|---|
| 1 | 92.3552 | 6 | 12.1956 |
| 2 | 70.2464 | 7 | 31. |
| 3 | 58.3296 | 8 | 37.8062 |
| 4 | 28.2240 | ||
| 11 | 14.1120 | ||
| 12 | 77.7728 |
| Years | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
|---|---|---|---|---|---|---|
| Per capita regional gross domestic product | 44,253 | 52,840 | 62,290 | 68,347 | 75,354 | 81,874 |
| The proportion of output from the tertiary industry | 39.6 | 41.4 | 42.4 | 43.5 | 45.5 | 47 |
| Energy consumption per unit of regional gross domestic product | 0.86 | 0.81 | 0.72 | 0.69 | 0.62 | 0.56 |
| Water consumption per unit of regional gross domestic product | 21.71 | 17.4 | 14.09 | 13.03 | 11.66 | 9.71 |
| Industrial waste gas emissions | 34,154 | 31,213 | 48,183 | 48,623 | 49,797 | 59,652 |
| Engel coefficient of urban and rural residents | 36.3 | 36.5 | 36.1 | 35.4 | 34.7 | 34 |
| Per capita disposable income of urban residents | 20,552 | 22,944 | 26,341 | 29,677 | 32,538 | 35,248 |
| Per capita park green area | 13.2 | 13.3 | 13.3 | 13.6 | 14 | 14.4 |
| Industrial wastewater discharge | 27.65 | 26.38 | 24.63 | 23.61 | 22.06 | 20.49 |
| Total energy consumption | 23,709 | 25,774 | 27,589 | 28,850 | 29,205 | 29,863 |
| Social electricity consumption | 3314.0 | 3864.37 | 4281.62 | 4580.9 | 4956.62 | 5012.54 |
| Carbon emissions (in 10,000 tons of carbon dioxide equivalent) | 115.2 | 121.6 | 128.1 | 134.5 | 132.65 | 137.6 |
| Indicators |
|---|
| Per capita regional gross domestic product |
| The proportion of output from the tertiary industry |
| Energy consumption per unit of regional gross domestic product |
| Water consumption per unit of regional gross domestic product |
| Industrial waste gas emissions |
| Engel coefficient of urban and rural residents |
| Per capita disposable income of urban residents |
| Per capita park green area |
| Industrial wastewater discharge |
| Total energy consumption |
| City Names | Per Capita Local Fiscal Revenue | Average Energy Consumption Level of Buildings |
|---|---|---|
| Suqian | 4489 | 88.23 |
| Lianyungang | 5996 | 144.99 |
| Yancheng | 2348 | 45.09 |
| Huai’an | 2830 | 126.3 |
| Yangzhou | 3282 | 129.22 |
| Taizhou | 3811 | 134.91 |
| Xuzhou | 5686 | 179.73 |
| Nantong | 3409 | 12.32 |
| Wuxi | 8529 | 269.595 |
| Suzhou | 12,509.2 | 395.406 |
| Changzhou | 6254.6 | 197.703 |
| Nanjing | 11,372 | 359.46 |
| Zhengjiang | 6823.2 | 215.676 |
| City Names | Per Capita Local Fiscal Revenue | Average Energy Consumption Level of Buildings |
|---|---|---|
| Suqian | −0.4561 | −0.7883 |
| Lianyungang | 0.0146 | −0.2832 |
| Yancheng | −1.1248 | −1.1722 |
| Huai’an | −0.9743 | −0.4495 |
| Yangzhou | −0.8331 | −0.4236 |
| Taizhou | −0.6679 | −0.3729 |
| Xuzhou | −0.0822 | 0.0259 |
| Nantong | −0.7934 | −1.4638 |
| Wuxi | 0.8058 | 0.8256 |
| Suzhou | 2.0491 | 1.9451 |
| Changzhou | 0.0954 | 0.1858 |
| Nanjing | 1.6939 | 1.6252 |
| Zhengjiang | 0.2730 | 0.3458 |
| Components | 1 | 2 | 3 | |
|---|---|---|---|---|
| Initial eigenvalues | Variance percentage | 52.2742 | 14.8430 | 14.0133 |
| Cumulative percentage | 52.2742 | 67.1172 | 81.1306 | |
| Cumulative contribution rate | 0.5227 | 0.6712 | 0.8113 | |
| Loadings Sum of squares | Variance percentage | 52.2742 | 14.8430 | 14.0133 |
| Cumulative percentage | 52.2742 | 67.1172 | 81.1306 | |
| Cumulative contribution rate | 0.5227 | 0.6712 | 0.8113 |
| Components | 1 | 2 | 3 |
|---|---|---|---|
| index1 | 3.2612 | 1.4835 | 0.3786 |
| index2 | 1.0681 | −0.3577 | 0.7418 |
| index3 | 0.0047 | −0.8499 | 0.6085 |
| index4 | −8.0916 | 3.0670 | 0.5311 |
| index5 | 0.6725 | −0.9635 | 4.1067 |
| index6 | −1.7564 | −1.5859 | 0.6761 |
| index7 | −1.8565 | −1.7575 | −0.1495 |
| index8 | −0.6674 | −0.5120 | −0.4241 |
| index9 | −2.1221 | −2.0543 | −1.1509 |
| index10 | −0.2323 | −0.1805 | −0.2169 |
| index11 | 0.7763 | −0.3014 | −0.8577 |
| index12 | 1.1221 | 0.2972 | −0.1317 |
| index13 | 2.9553 | 2.3608 | 0.0544 |
| index14 | 0.7408 | 0.2869 | −1.6175 |
| index15 | 0.2154 | −0.0338 | −2.0594 |
| index16 | 2.5291 | 1.2314 | 0.5227 |
| index17 | 1.3808 | −0.1254 | −0.9944 |
| City Names | Components 1 | Components 2 | Components 3 | Composite Score |
|---|---|---|---|---|
| Suqian | 1.1138 × 105 | 7.7466 × 104 | 2.2723 × 104 | 5.4354 × 104 |
| Lianyungang | 1.3088 × 105 | 8.3038 × 104 | 2.5300 × 104 | 6.2840 × 104 |
| Yancheng | −1.7376 × 104 | 9.7685 × 103 | 4.7785 × 103 | 5.1916 × 104 |
| Huai’an | −2.6447 × 105 | 1.6799 × 105 | 3.5142 × 104 | 8.0809 × 104 |
| Yangzhou | 1.2701 × 105 | 8.4893 × 104 | 2.2999 × 104 | 6.1296 × 104 |
| Taizhou | 1.3480 × 105 | 9.3617 × 104 | 2.5243 × 104 | 6.5532 × 104 |
| Xuzhou | 1.7486 × 105 | 1.0211 × 105 | 2.9811 × 104 | 8.2561 × 104 |
| Nantong | 8.5770 × 104 | 6.2991 × 104 | 1.8643 × 104 | 4.2345 × 104 |
| Wuxi | 2.6230 × 105 | 1.5316 × 105 | 4.4716 × 104 | 1.2385 × 105 |
| Suzhou | 3.8470 × 105 | 2.2464 × 105 | 6.5584 ×104 | 1.8164 × 105 |
| Changzhou | 1.9235 × 105 | 1.1232 ×105 | 3.2792 × 104 | 9.0819 × 104 |
| Nanjing | 3.4973 × 105 | 2.0422 × 105 | 5.9621 × 104 | 1.6513 × 105 |
| Zhengjiang | 2.0984 × 105 | 1.2253 × 105 | 3.5773 × 104 | 9.9077 × 104 |
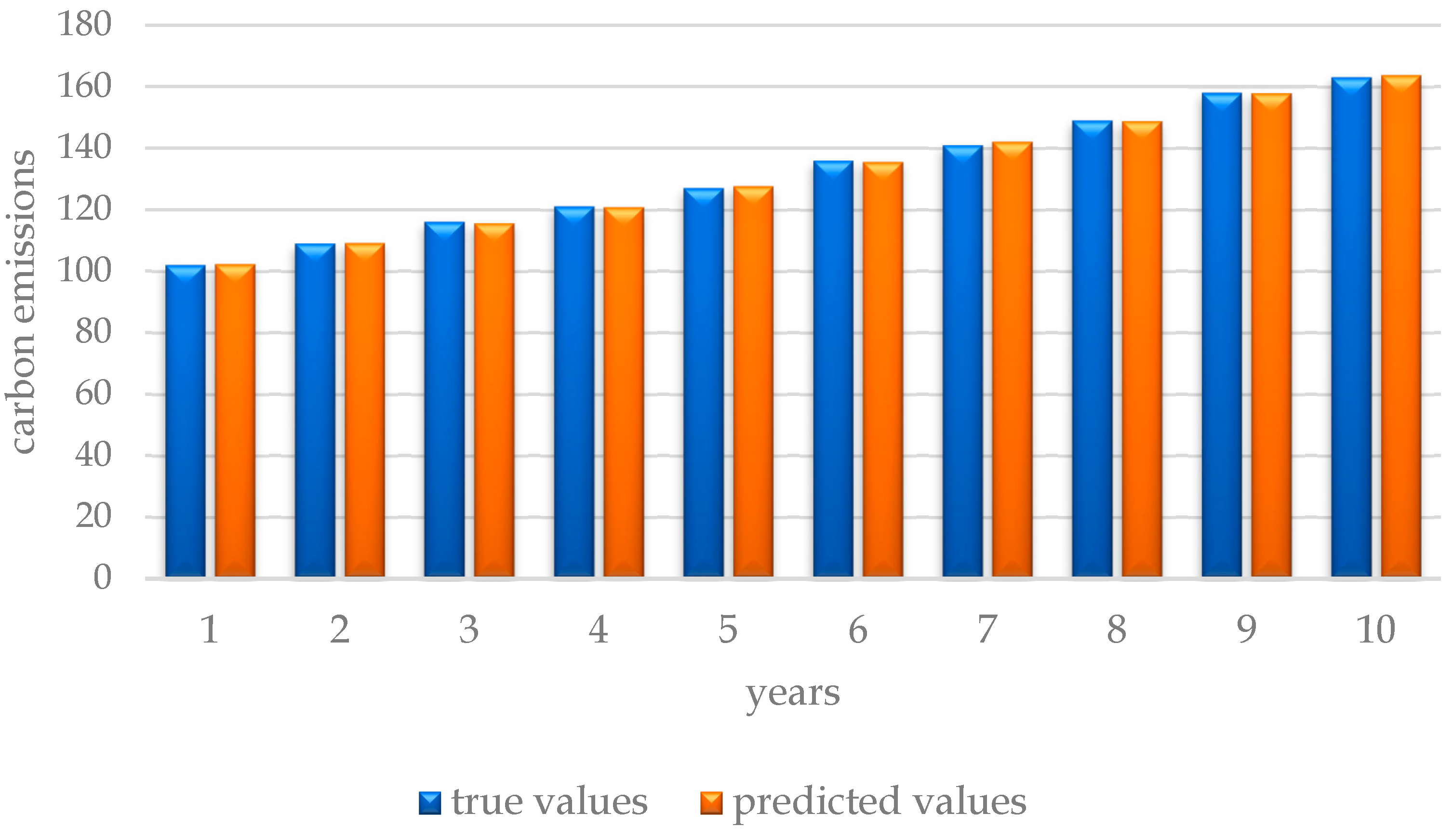
| Number | Year | Original Value | Predicted Value | Residual | Level Ratio Deviation | |
|---|---|---|---|---|---|---|
| 1 | 2015 | 102.3 | 102.3000 | 0 | 0 | — |
| 2 | 2016 | 108.7 | 109.5683 | −0.8683 | 0.0080 | 0.0104 |
| 3 | 2017 | 115.2 | 115.2151 | −0.0151 | 0.0001 | 0.0078 |
| 4 | 2018 | 121.6 | 121.1529 | 0.4471 | 0.0037 | 0.0038 |
| 5 | 2019 | 128.1 | 127.3967 | 0.7033 | 0.0055 | 0.0018 |
| 6 | 2020 | 134.5 | 133.9623 | 0.5377 | 0.0040 | −0.0015 |
| 7 | 2021 | 140.96 | 140.8663 | 0.0937 | 0.0007 | −0.0034 |
| 8 | 2022 | 147.41 | 148.1261 | −0.7161 | 0.0049 | −0.0055 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, D.; Tang, S. Research on Low-Carbon Building Development and Carbon Emission Control Based on Mathematical Models: A Case Study of Jiangsu Province. Energies 2024, 17, 4545. https://doi.org/10.3390/en17184545
Chang D, Tang S. Research on Low-Carbon Building Development and Carbon Emission Control Based on Mathematical Models: A Case Study of Jiangsu Province. Energies. 2024; 17(18):4545. https://doi.org/10.3390/en17184545
Chicago/Turabian StyleChang, Dingjun, and Shuling Tang. 2024. "Research on Low-Carbon Building Development and Carbon Emission Control Based on Mathematical Models: A Case Study of Jiangsu Province" Energies 17, no. 18: 4545. https://doi.org/10.3390/en17184545
APA StyleChang, D., & Tang, S. (2024). Research on Low-Carbon Building Development and Carbon Emission Control Based on Mathematical Models: A Case Study of Jiangsu Province. Energies, 17(18), 4545. https://doi.org/10.3390/en17184545











