Position Servo Control of Electromotive Valve Driven by Centralized Winding LATM Using a Kalman Filter Based Load Observer
Abstract
1. Introduction
- A new motorized valve structure driven by LATM is described in detail. We have fully considered the influence of motor rotor position and load current, magnetic field saturation and the cogging effect, improved the existing cogging structure LTAM model, and derived an accurate torque expression.
- Through accurate system dynamics modelling, simulation verification, and definition of the available angular range, the uncertainty in the original system is transformed into unknown but bounded uncertainty.
- The proposed approach presents an EM EGR valve servo system scheme with a dual closed-loop position and current, which achieves excellent positional accuracy and strong robustness to random shock-type disturbances through high-precision non-contact angle measurements, on-line load estimations, and feed-forward compensation.
2. Structure and Modeling
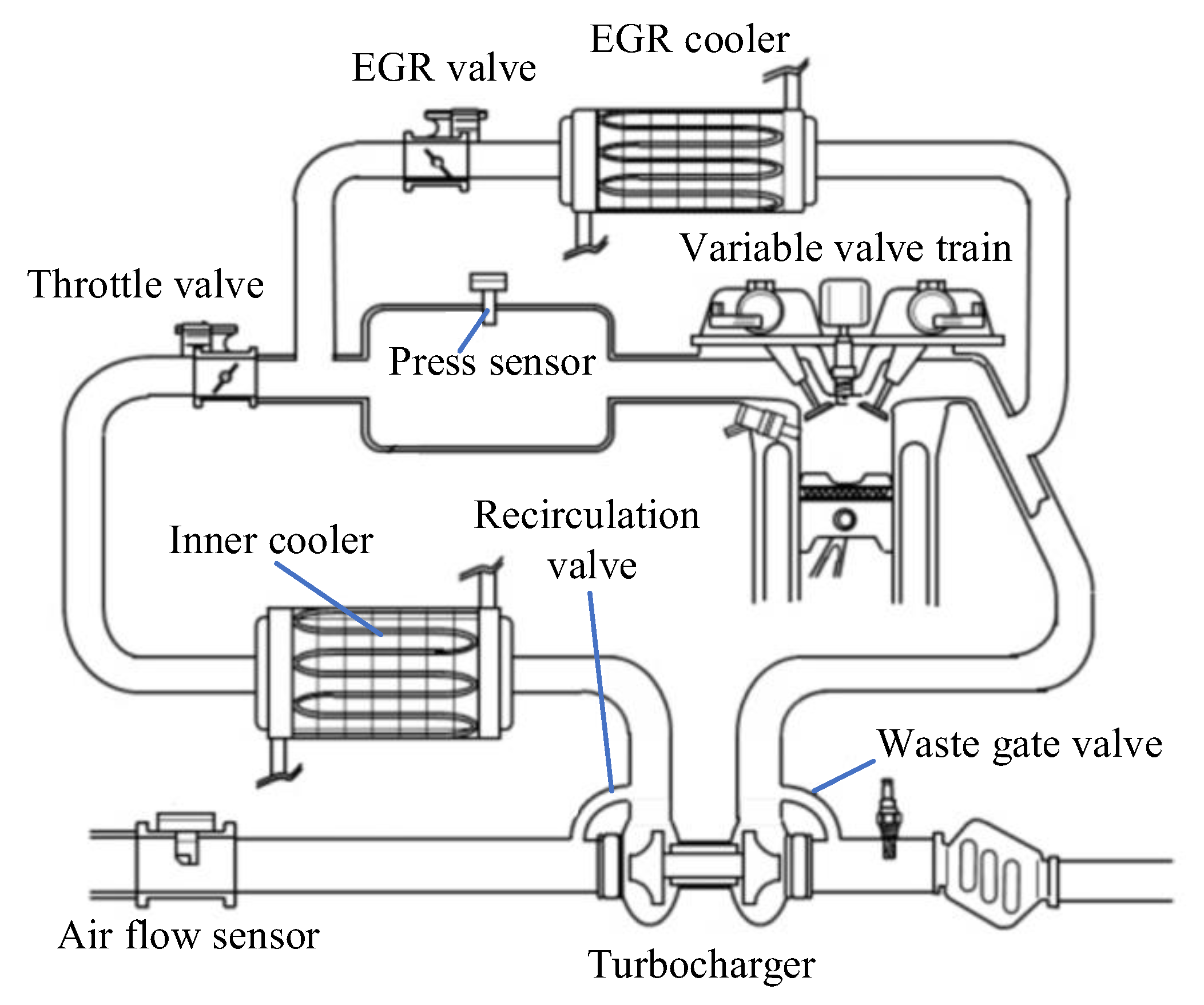
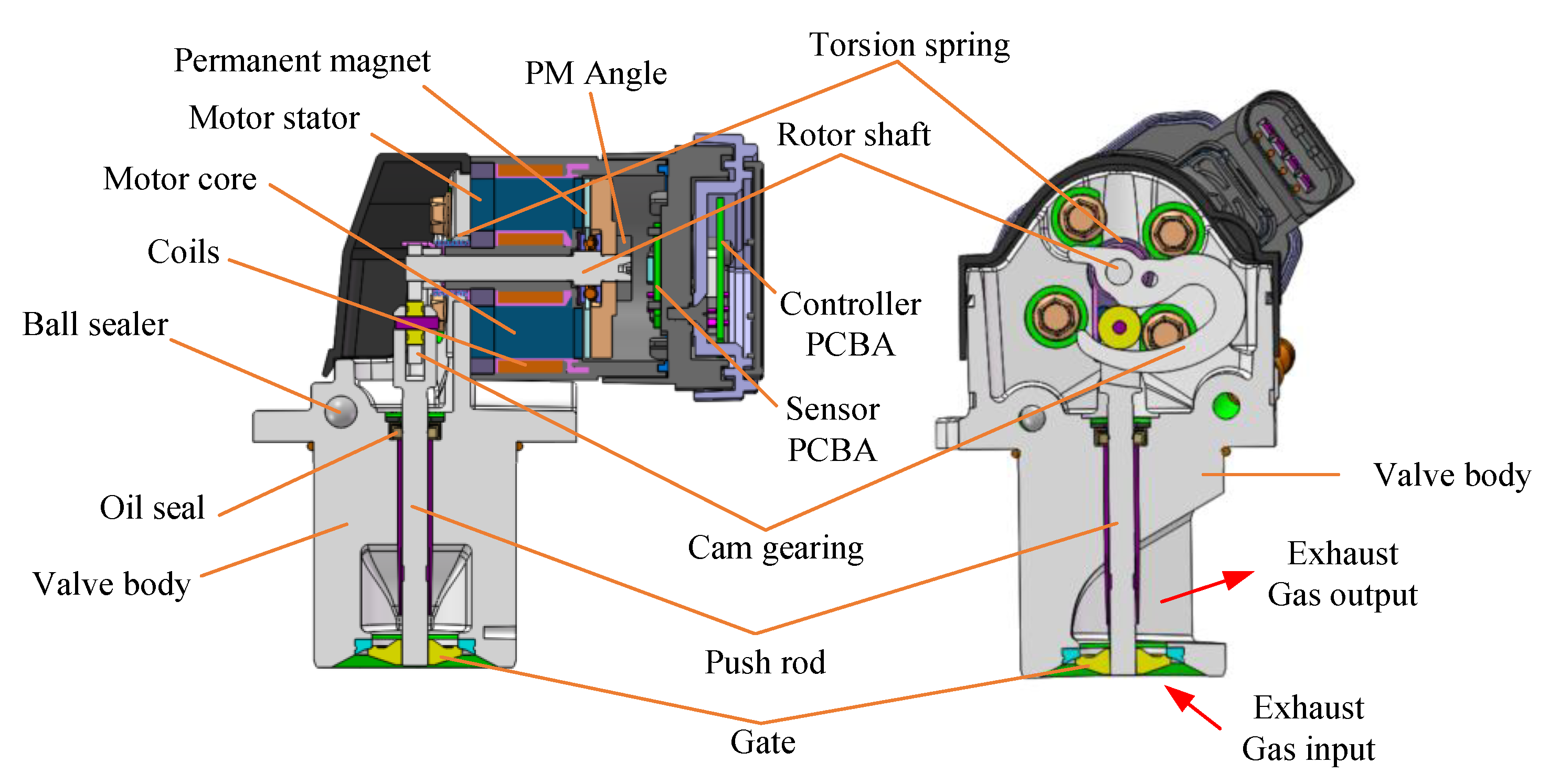
2.1. Introduction of Structure
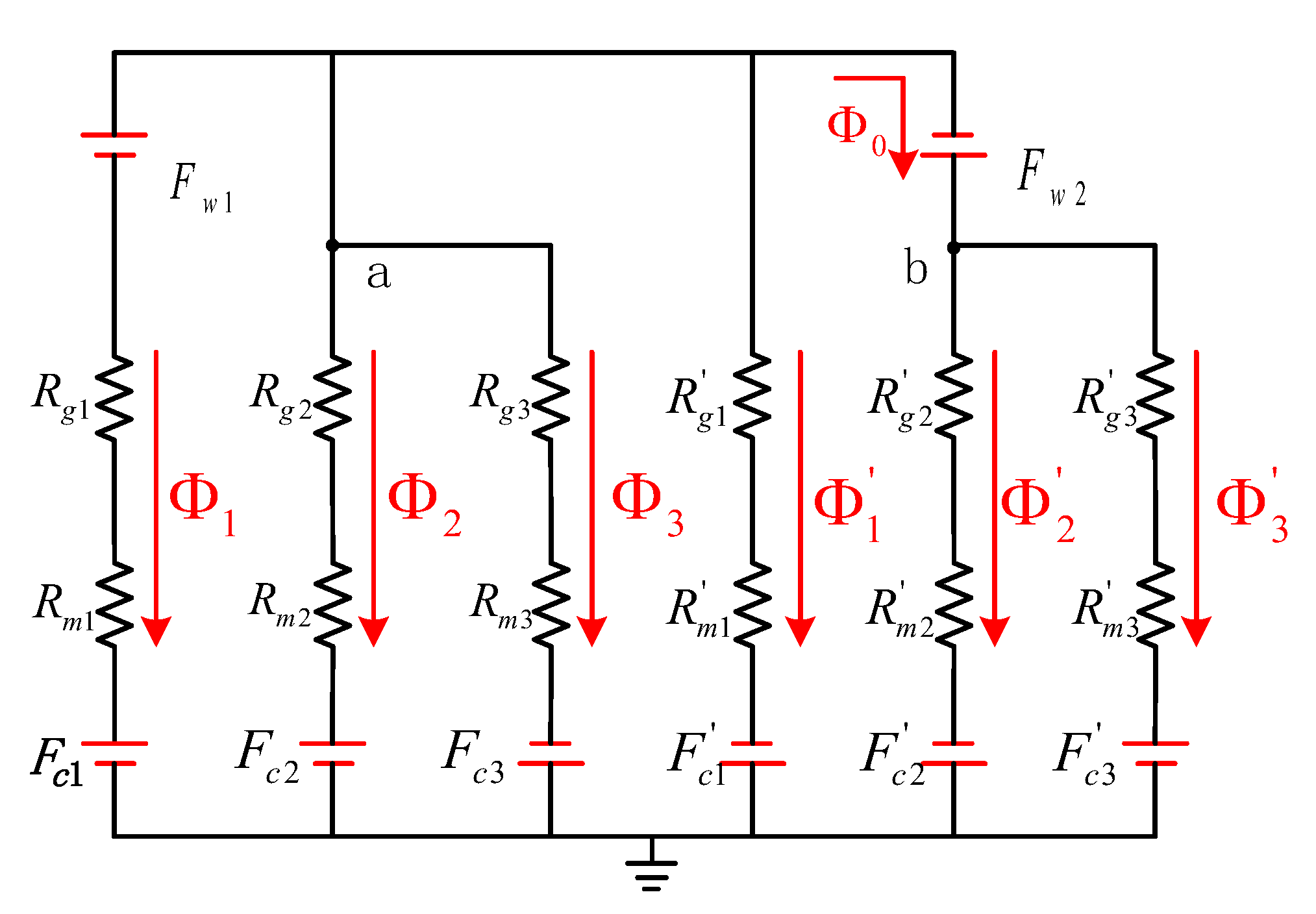
2.2. Centralized Winding LTAM Modeling
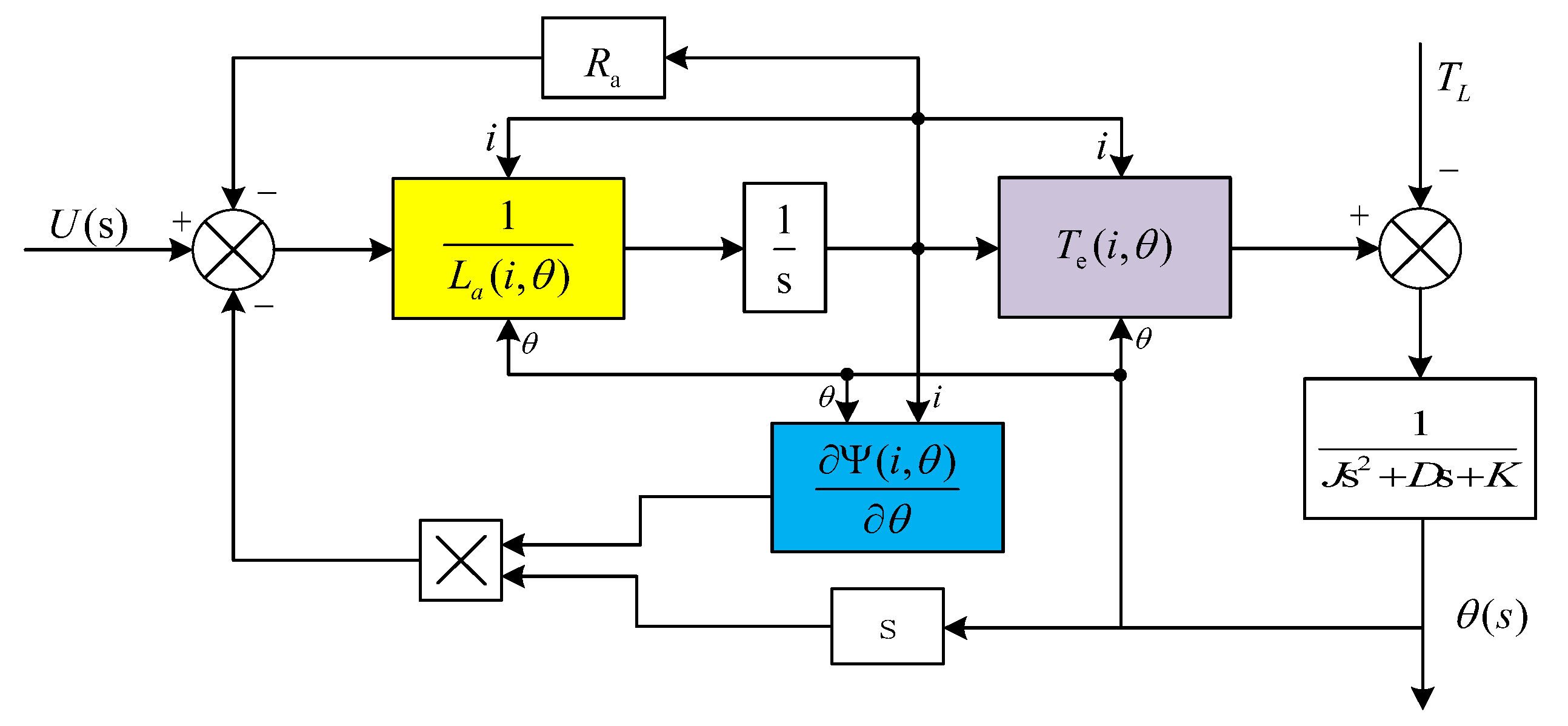
2.3. Analytical Expression of the Electromagnetic Torque
3. Position Servo Control System Using a Kalman-Filter Based Load Observer
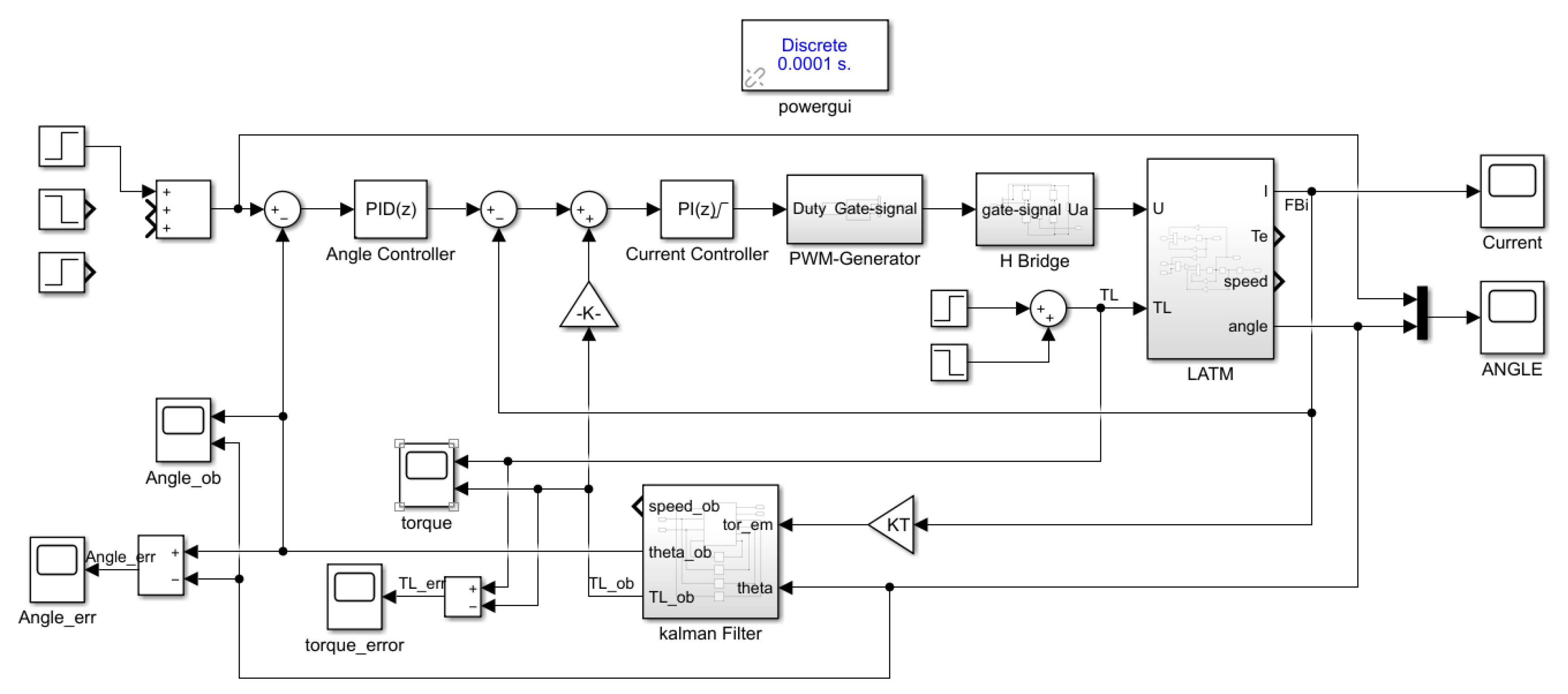
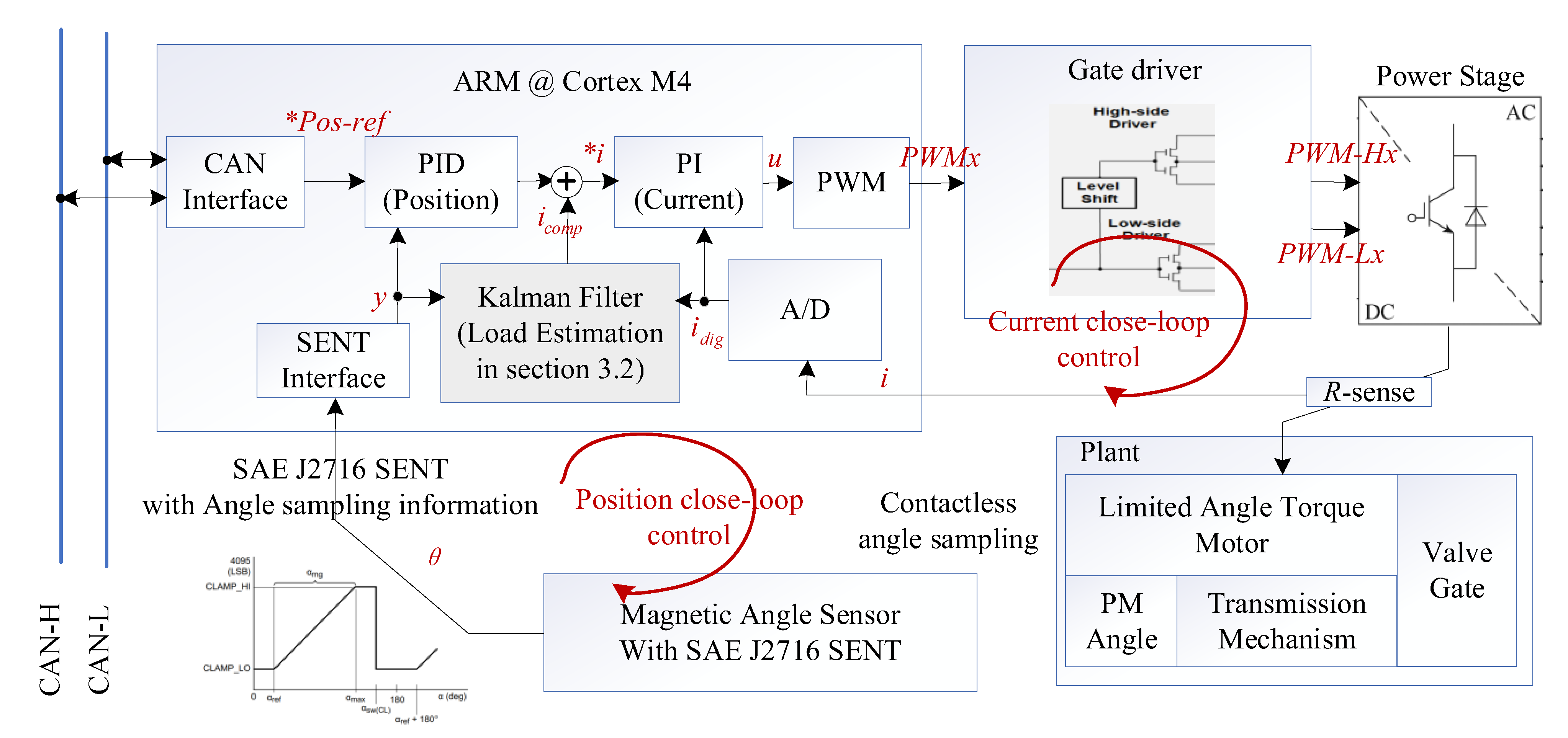
3.1. Position Servo System Structure
3.2. Kalman Filter Based Load Observer
- Calculate the a priori estimates of the state variables and the a priori estimates of the covariance matrix, as follows.
- Calculate the Kalman gain.
- The state estimation is corrected based on the measurements, and the optimal estimate of the state variable is calculated, also known as the a posteriori estimate, which is the optimized output of the algorithm.
- Calculate the posterior covariance matrix.
3.3. Simulation Verification
4. Position Servo System Implementation
5. Experimental Verification
5.1. Plant Dynamics
5.2. Positioning Accuracy
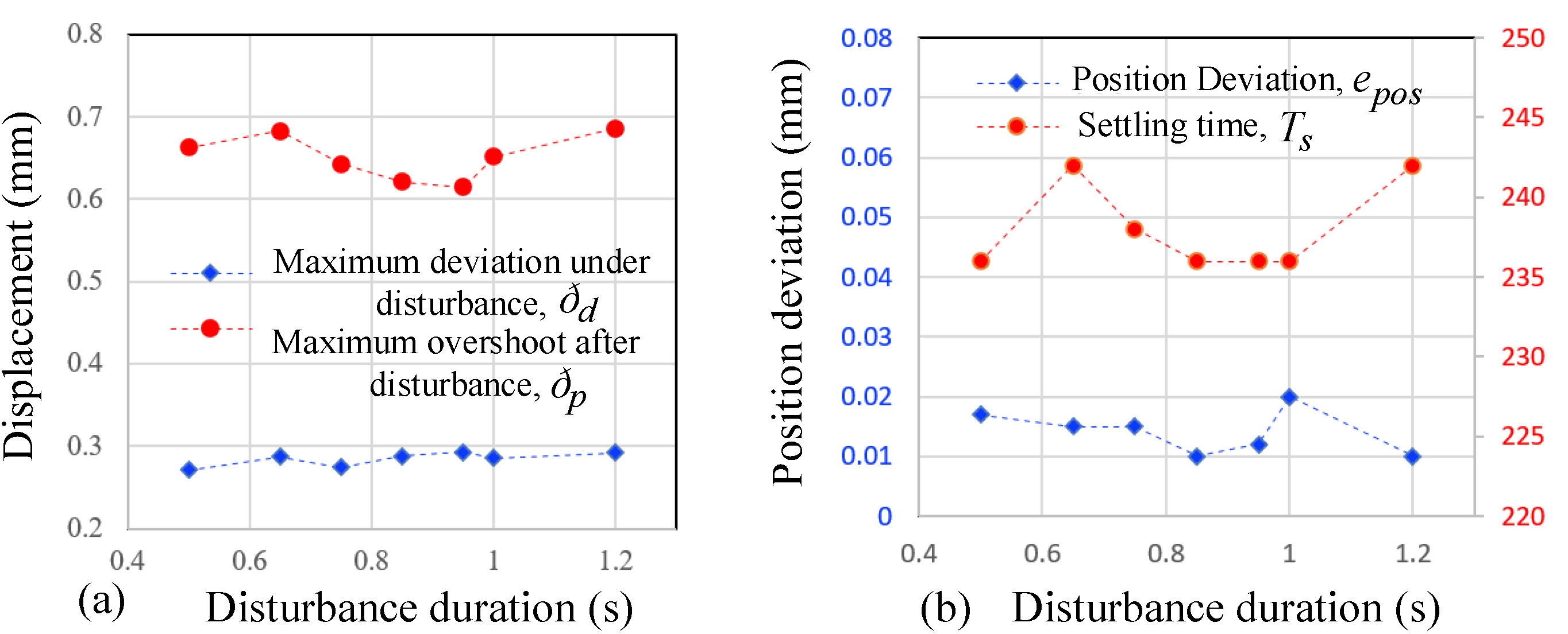
5.3. Verification of Shock-Type Disturbance Rejection
6. Conclusions
- (1)
- The servo system scheme proposed in this paper can compensate for the influence of external shock-type disturbances in real time through effective load observation and realize better valve positioning accuracy, dynamic response capabilities, and robustness.
- (2)
- The proposed Kalman filter-based load observation method can converge to the real load value within 15 ms and then realize unbiased estimations.
- (3)
- The proposed method showed a good real-time response and the ability to suppress external disturbances, and after the disappearance of the disturbance, the EM valve could be quickly restored to the reference position, with a maximum position offset of not more than 0.3 mm, a repeatable positioning error of not more than 0.002 mm after the disappearance of the disturbance, and a disturbance recovery time of not more than 250 ms. Additionally, consistent results were obtained in multiple repetitions of measurements, which demonstrates the validity and repeatability of this method.
- (4)
- The proposed method was not sensitive to the duration of the disturbance, and the values of position error, overshoot, disturbance recovery time, and other parameters caused by the disturbance of 0.5–1.2 s duration were almost at the same level.
- (5)
- Future work will be carried out in two directions: (1) Study of the influence of high temperatures on the dynamics of the plant under the actual application conditions, which could effectively improve the adaptability of the observer in different applications and further improve its observation accuracy; and (2) The failure mechanism of the observer and the constraints of the applied parameters, which could further improve the effectiveness of the application of the methods in this paper.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; Su, S.; Lai, Y.; Luo, W.; Hou, P.; Lyu, T.; Ge, Y. China 6 EGR gasoline vehicles without a GPF may struggle to meet the potential SPN10 limit. Environ. Int. 2023, 181, 108306. [Google Scholar] [CrossRef]
- Ibrahim, A.; Bari, S. An experimental investigation on the use of EGR in a supercharged natural gas SI engine. Fuel 2010, 89, 1721–1730. [Google Scholar] [CrossRef]
- Li, X.; Liu, X.; Tang, H.; Zou, Y.; Cen, W.; Zhu, T. Simultaneously accomplishing selective catalytic reduction of NO and catalytic oxidation of CO in a catalyst coupling system. Fuel 2024, 360, 130616. [Google Scholar] [CrossRef]
- Guan, B.; Zhan, R.; Lin, H.; Huang, Z. Review of the state-of-the-art of exhaust particulate filter technology in internal combustion engines. J. Environ. Manag. 2015, 154, 225–258. [Google Scholar] [CrossRef]
- Dubien, C.; Schweich, D.; Mabilon, G.; Martin, B.; Prigent, M. Three-way catalytic converter modelling: Fast-and slow-oxidizing hydrocarbons, inhibiting species, and steam-reforming reaction. Chem. Eng. Sci. 1998, 53, 471–481. [Google Scholar] [CrossRef]
- Wei, H.; Zhu, T.; Shu, G.; Tan, L.; Wang, Y. Gasoline engine exhaust gas recirculation–a review. Appl. Energy 2012, 99, 534–544. [Google Scholar] [CrossRef]
- Panni, F.S.; Waschl, H.; Alberer, D.; Zaccarian, L. Position regulation of an EGR valve using reset control with adaptive feedforward. IEEE Trans. Control Syst. Technol. 2014, 22, 2424–2431. [Google Scholar] [CrossRef]
- Hirata, M.; Hayashi, T.; Takahashi, M.; Yamasaki, Y.; Kaneko, S. A nonlinear feedforward controller design taking account of dynamics of turbocharger and manifolds for diesel engine air-path system. IFAC Pap. OnLine 2019, 52, 341–346. [Google Scholar] [CrossRef]
- Yang, C.; Wang, B.; Wang, H.; Hu, D.; Duan, B.; Wang, Y. The effect of changing EGR rate on engine performance under different ammonia/methanol ratios. J. Energy Inst. 2024, 113, 101546. [Google Scholar] [CrossRef]
- Gutfrind, C.; Dufour, L.; Liebart, V.; Vannier, J.C. An approach to the prototyping of an optimized limited stroke actuator to drive a low pressure exhaust gas recirculation valve. Sensors 2016, 16, 735. [Google Scholar] [CrossRef]
- Suzuki, K. Feasibility Study on Model Predictive Control for an EGR-Air Path System in a Turbocharged SI Engine. IFAC Pap. OnLine 2021, 54, 27–32. [Google Scholar] [CrossRef]
- Guerrier, M.; Cawsey, P. The development of model based methodologies for gasoline IC engine calibration. SAE Tech. Pap. 2004, 1, 1466. [Google Scholar] [CrossRef]
- Ohtsuka, T. A continuation/GMRES method for fast computation of nonlinear receding horizon control. Automatica 2004, 40, 563–574. [Google Scholar] [CrossRef]
- Kang, M.; Shen, T. Receding horizon online optimization for torque control of gasoline engines. ISA Trans. 2016, 65, 371–383. [Google Scholar] [CrossRef] [PubMed]
- Odachi, K.; Oyama, H.; Yamakita, M. Nonlinear model predictive control of SI engine using discrete time identification model. In Proceedings of the 2015 54th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Hangzhou, China, 28–30 July 2015; pp. 1305–1310. [Google Scholar] [CrossRef]
- Shiraishi, T.; Hirata, M.; Nishida, R.; Suzuki, M.; Muto, M.; Fujii, T.; Hikita, T. Nonlinear feedforward controller design for air-path system with transport dynamics of external EGR system. IFAC Pap. OnLine 2021, 54, 1–6. [Google Scholar] [CrossRef]
- Pashaei, S.; Badamchizadeh, M. A new fractional-order sliding mode controller via a nonlinear disturbance observer for a class of dynamical systems with mismatched disturbances. ISA Trans. 2016, 63, 39–48. [Google Scholar] [CrossRef]
- Williams, R.; Cook, S.; Woodall, K.; Clayton, C.; Gee, M.; Mulqueen, S.; Reid, J.; Rimmer, J.; Ross, A. Development of an engine test to rate the EGR deposit formation propensity of fuels in light-duty diesel engines. SAE Int. J. Adv. Curr. Pract. Mobil. 2020, 3, 337–348. [Google Scholar] [CrossRef]
- Kim, H.J.; Son, Y.D.; Kim, J.M. Improved Position Control for an EGR Valve System with Low Control Frequency. Energies 2020, 13, 457. [Google Scholar] [CrossRef]
- Bhuiyan, H.; Lee, J.H. Low cost position controller for exhaust gas recirculation valve system. Energies 2018, 11, 2171. [Google Scholar] [CrossRef]
- Ashok, B.; Denis, A.S.; Ramesh, K.C. An Integrated Pedal Follower and Torque Based Approach for Electronic Throttle Control in a Motorcycle Engine. Eng. J. 2017, 21, 63–80. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Y. An AEFA-Based Optimum Design of Fuzzy PID Controller for Attitude Control Flywheel with BLDC Motor. Aerospace 2022, 9, 789. [Google Scholar] [CrossRef]
- Heo, H.J.; Son, Y.; Kim, J.M. A Trapezoidal Velocity Profile Generator for Position Control Using a Feedback Strategy. Energies 2019, 12, 1222. [Google Scholar] [CrossRef]
- Zarghami, M.; Hosseinnia, S.H.; Babazadeh, M. Optimal control of egr system in gasoline engine based on gaussian process. IFAC Pap. OnLine 2017, 50, 3750–3755. [Google Scholar] [CrossRef]
- Zhang, L. Hopf Bifurcation and Vibration Control for a Thrust Magnetic Bearing with Variable Load Mass. Sensors 2018, 18, 2212. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Li, X. Real-Time Adaptive Control of a Magnetic Levitation System with a Large Range of Load Disturbance. Sensors 2018, 18, 1512. [Google Scholar] [CrossRef]
- Cheng, W.; Tan, Y.; Lu, Y.; Dong, R.; Tan, Q.; Chen, X. Nonlinear internal model control of EGR valve. In Proceedings of the 2019 12th Asian Control Conference (ASCC), Kitakyushu, Japan, 9–12 June 2019; pp. 1233–1236. [Google Scholar]
- Waschl, H.; Alberer, D.; del Re, L. Multi Reference Model Predictive EGR-Valve Control for Diesel Engines. In Proceedings of the International Federation of Automatic Control, Rueil-Malmaison, France, 23–25 October 2012; pp. 474–481. [Google Scholar] [CrossRef]
- Tan, Y.; Cheng, W.; Dong, R.; Tan, Q.; Cao, Q. Online optimizing positioning control with model error compensator for LEGRV system. IEEE-ASME Trans. Mechatron. 2020, 25, 594–603. [Google Scholar] [CrossRef]
- Lee, S.; Lee, Y.; Lee, Y.; Kim, M.; Shin, S.; Park, J.; Min, K. EGR prediction of diesel engines in steady-state conditions using deep learning method. Int. J. Automot. Technol. 2020, 21, 571–578. [Google Scholar] [CrossRef]
- Rajaei, N. Model Based Control of Exhaust Gas Recirculation Valves and Estimation of Spring Torque. Master’s Thesis, University of Windsor, Windsor, ON, Canada, 2010. [Google Scholar]
- Gao, J.; Feng, K.; Wang, Y.; Wu, Y.; Chen, H. Design, implementation and experimental verification of a compensator-based triple-step model reference controller for an automotive electronic throttle. Control Eng. Prac. 2020, 100, 104447. [Google Scholar] [CrossRef]
- Li, Y.; Yang, B.; Zheng, T.; Li, Y.; Cui, M.; Peeta, S. Extended-state-observer-based double-loop integral sliding-mode control of electronic throttle valve. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2501–2510. [Google Scholar] [CrossRef]
- Yu, T.; Zhang, Z.; Li, Y.; Zhao, W.; Zhang, J. Improved active disturbance rejection controller for rotor system of magnetic levitation turbomachinery. Electron. Res. Arch. 2023, 31, 1570–1586. [Google Scholar] [CrossRef]
- Cheng, X.; Yin, J.; Li, X.; Zhou, R.; Fu, C. Design and Implementation of a linear active disturbance rejection control-based position servo control system of an electromotive valve for exhaust gas recirculation. Sensors 2024, 24, 1393. [Google Scholar] [CrossRef] [PubMed]









| Symbol | Parameter | Value | Unit |
|---|---|---|---|
| R | Resistance of stator winding | 3.6 | Ω |
| Equivalent inductance of winding | 32 | mH | |
| J | Rotor moment of inertia | 0.002 | |
| D | Viscous damping coefficient | 0.0024 | |
| K | Torsion spring stiffness | 0.12 | |
| Electromagnetic torque coefficient | 0.126 | ||
| Back electromagnetic force coefficient | 0.126 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Cheng, X.; Zhou, R. Position Servo Control of Electromotive Valve Driven by Centralized Winding LATM Using a Kalman Filter Based Load Observer. Energies 2024, 17, 4515. https://doi.org/10.3390/en17174515
Yang Y, Cheng X, Zhou R. Position Servo Control of Electromotive Valve Driven by Centralized Winding LATM Using a Kalman Filter Based Load Observer. Energies. 2024; 17(17):4515. https://doi.org/10.3390/en17174515
Chicago/Turabian StyleYang, Yi, Xin Cheng, and Rougang Zhou. 2024. "Position Servo Control of Electromotive Valve Driven by Centralized Winding LATM Using a Kalman Filter Based Load Observer" Energies 17, no. 17: 4515. https://doi.org/10.3390/en17174515
APA StyleYang, Y., Cheng, X., & Zhou, R. (2024). Position Servo Control of Electromotive Valve Driven by Centralized Winding LATM Using a Kalman Filter Based Load Observer. Energies, 17(17), 4515. https://doi.org/10.3390/en17174515






