Consensus-Based Model Predictive Control for Active Power and Voltage Regulation in Active Distribution Networks
Abstract
:1. Introduction
- A Cb-MPC is adopted for active power and voltage regulation at the connection node of each DER;
- An MIMO model of the ADN is employed in the design to account for the effects of both internal and external interactions among DERs;
- An integral action MPC is implemented to counteract the effects of uncertainties in modeling parameters;
- Communication among DERs is incorporated into the numerical validation through a proper sample and hold function.
- Compared to [28], the proposed method employs an MPC algorithm capable of effectively handling current saturations and interactions among different DERs;
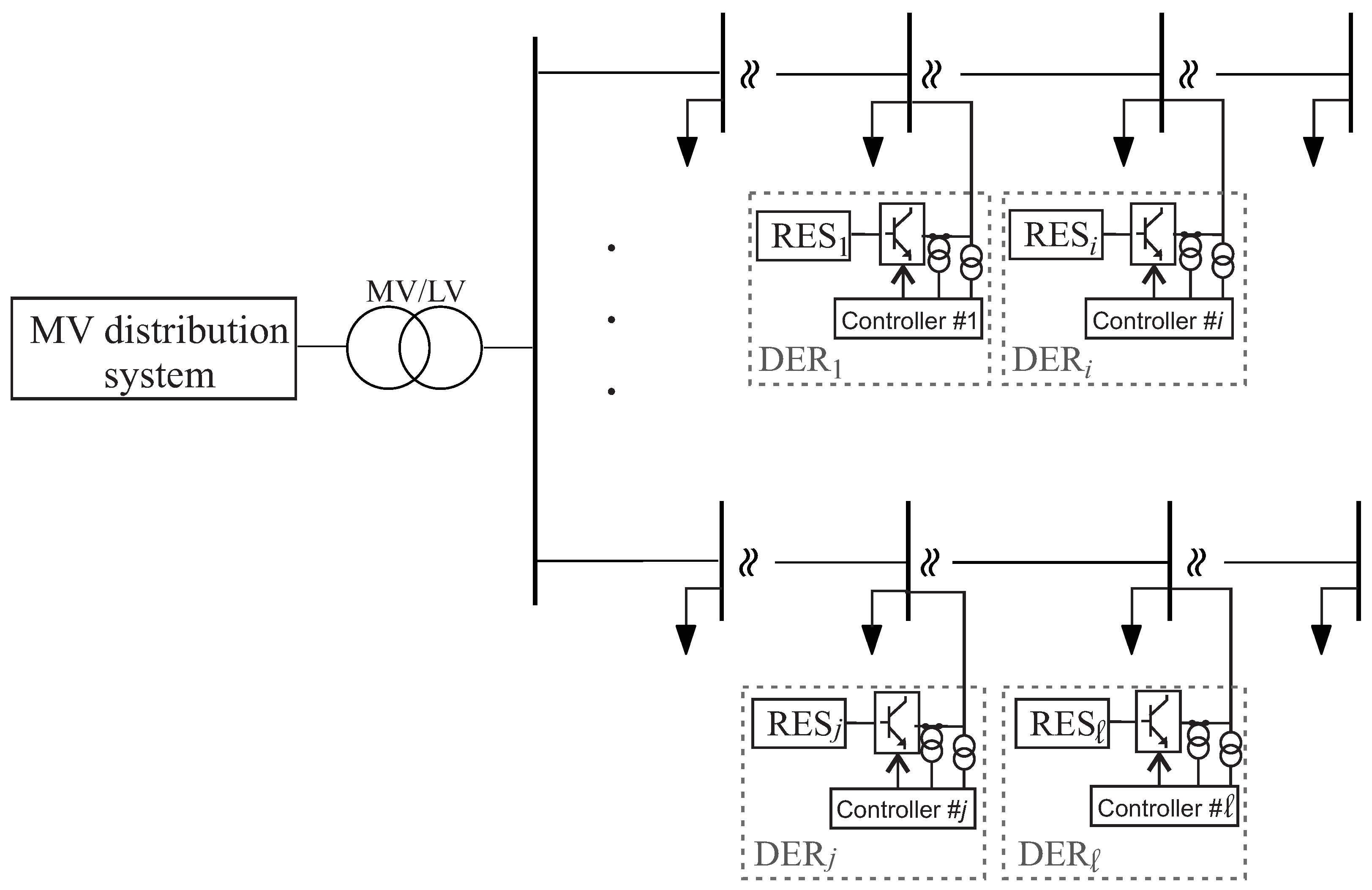
2. Model
3. Proposed Solution
3.1. Local Observer
3.2. Consensus
3.3. Control Loop
3.4. Time Constant Constraints
3.5. DER Communication Constraints
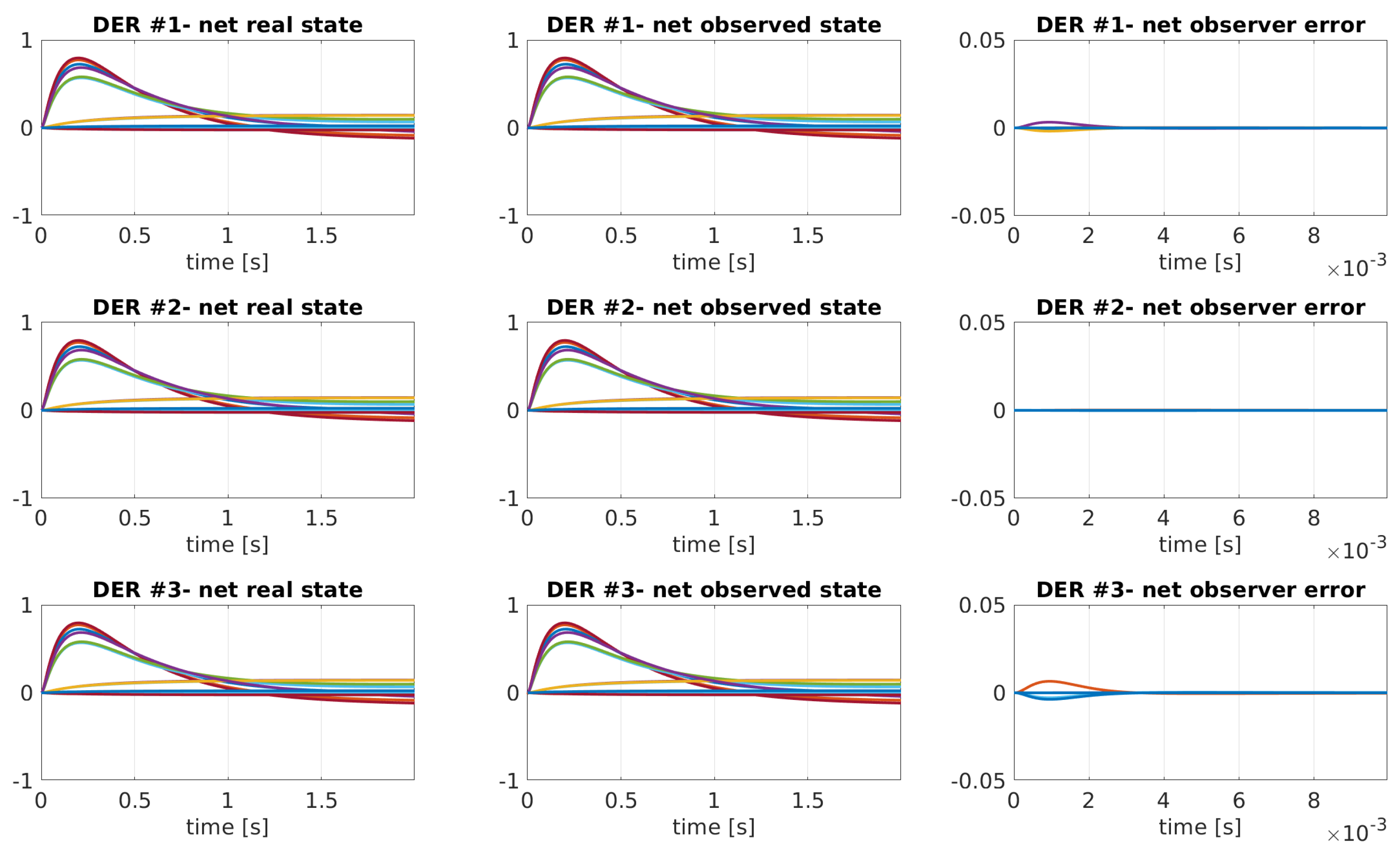
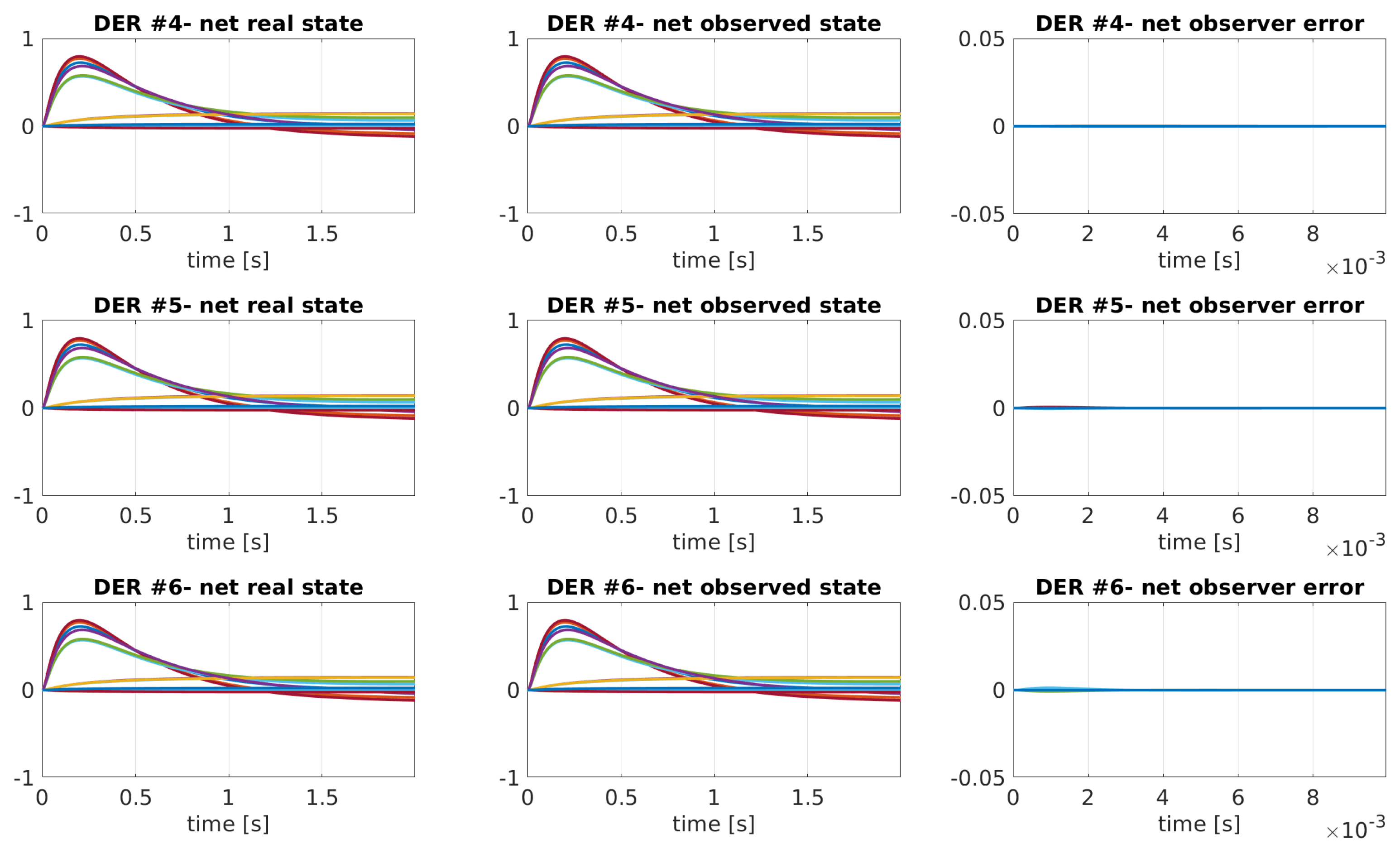
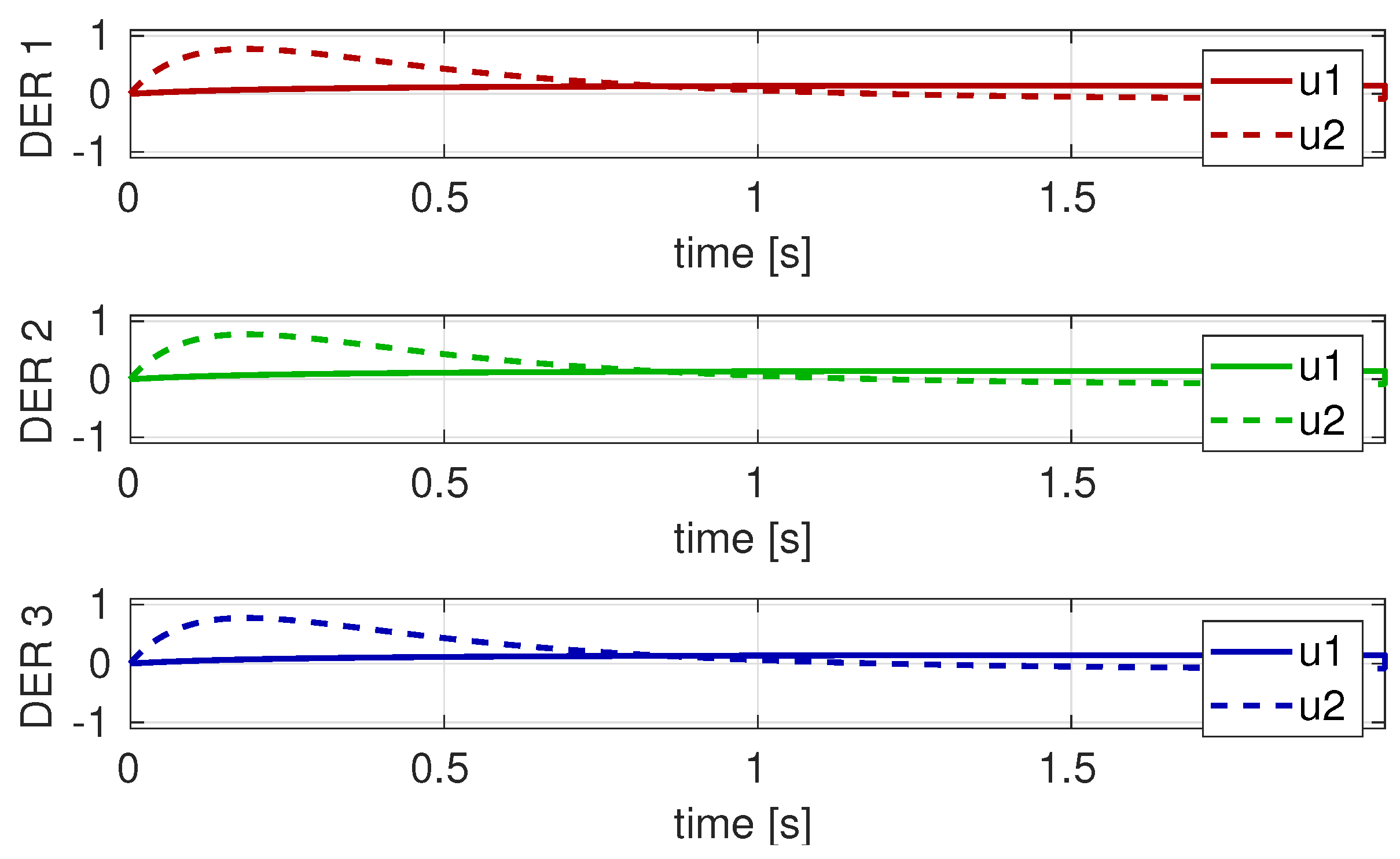
4. Numerical Validation
- Case I: nominal case, i.e., ADN operating conditions are the same as the ones used in the Cb-MPC design without simulating the communication;
- Case II: nominal case including the communication sample and hold functions;
- Case III: comparison with an integral consensus-based controller designed using the eigenvalue assignment technique in the nominal case without simulating the communication;
- Case IV: off-nominal case, i.e., different ADN operating conditions with respect to the ones assumed in the design.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tatar, S.M.; Aydin, E. Design and operation of renewable energy microgrids under uncertainty towards green deal and minimum carbon emissions. Sustain. Energy Grids Netw. 2024, 37, 101233. [Google Scholar] [CrossRef]
- Sun, H.; Guo, Q.; Qi, J.; Ajjarapu, V.; Bravo, R.; Chow, J.; Li, Z.; Moghe, R.; Nasr-Azadani, E.; Tamrakar, U.; et al. Review of Challenges and Research Opportunities for Voltage Control in Smart Grids. IEEE Trans. Power Syst. 2019, 34, 2790–2801. [Google Scholar] [CrossRef]
- Antonelli, G. Interconnected dynamic systems. An overview on distributed control. IEEE Control Syst. Mag. 2013, 33, 76–88. [Google Scholar]
- Olfati-Saber, R.; Murray, R. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.; Atkins, E. Information consensus in multivehicle cooperative control. IEEE Control Syst. Mag. 2007, 27, 71–82. [Google Scholar]
- Valverde, G.; Van Cutsem, T. Model predictive control of voltages in active distribution networks. IEEE Trans. Smart Grid 2013, 4, 2152–2161. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, Q.; Wang, J.; Liu, Z.; Shahidehpour, M.; Xue, Y. Combined Active and Reactive Power Control of Wind Farms Based on Model Predictive Control. IEEE Trans. Energy Convers. 2017, 33, 1177–1187. [Google Scholar] [CrossRef]
- Li, P.; Ji, J.; Ji, H.; Jian, J.; Ding, F.; Wu, J.; Wang, C. MPC-based local voltage control strategy of DGs in active distribution networks. IEEE Trans. Sustain. Energy 2020, 11, 2911–2921. [Google Scholar] [CrossRef]
- Dutta, A.; Ganguly, S.; Kumar, C. Coordinated control scheme for ev charging and volt/var devices scheduling to regulate voltages of active distribution networks. Sustain. Energy Grids Netw. 2022, 31, 100761. [Google Scholar] [CrossRef]
- Cabrera-Tobar, A.; Pavan, A.M.; Blasuttigh, N.; Petrone, G.; Spagnuolo, G. Real time Energy Management System of a photovoltaic based e-vehicle charging station using Explicit Model Predictive Control accounting for uncertainties. Sustain. Energy Grids Netw. 2022, 31, 100769. [Google Scholar] [CrossRef]
- Bidgoli, H.S.; Van Cutsem, T. Combined local and centralized voltage control in active distribution networks. IEEE Trans. Power Syst. 2017, 33, 1374–1384. [Google Scholar] [CrossRef]
- Wang, L.; Dubey, A.; Gebremedhin, A.H.; Srivastava, A.K.; Schulz, N. MPC-based decentralized voltage control in power distribution systems with EV and PV coordination. IEEE Trans. Smart Grid 2022, 13, 2908–2919. [Google Scholar] [CrossRef]
- Kou, P.; Liang, D.; Gao, R.; Liu, Y.; Gao, L. Decentralized model predictive control of hybrid distribution transformers for voltage regulation in active distribution networks. IEEE Trans. Sustain. Energy 2019, 11, 2189–2200. [Google Scholar] [CrossRef]
- Wen, S.; Xiong, W.; Cao, J.; Qiu, J. MPC-based frequency control strategy with a dynamic energy interaction scheme for the grid-connected microgrid system. J. Frankl. Inst. 2020, 357, 2736–2751. [Google Scholar] [CrossRef]
- Balram, P.; Tuan, L.A.; Carlson, O. Comparative study of MPC based coordinated voltage control in LV distribution systems with photovoltaics and battery storage. Int. J. Electr. Power Energy Syst. 2018, 95, 227–238. [Google Scholar] [CrossRef]
- Nguyen, H.M.; Torres, J.L.R.; Lekić, A.; Pham, H.V. MPC based centralized voltage and reactive power control for active distribution networks. IEEE Trans. Energy Convers. 2021, 36, 1537–1547. [Google Scholar] [CrossRef]
- Ouammi, A.; Achour, Y.; Zejli, D.; Dagdougui, H. Supervisory model predictive control for optimal energy management of networked smart greenhouses integrated microgrid. IEEE Trans. Autom. Sci. Eng. 2020, 17, 117–128. [Google Scholar] [CrossRef]
- Karthikeyan, N.; Pillai, J.R.; Bak-Jensen, B.; Simpson-Porco, J.W. Predictive control of flexible resources for demand response in active distribution networks. IEEE Trans. Power Syst. 2019, 34, 2957–2969. [Google Scholar] [CrossRef]
- Maharjan, S.; Khambadkone, A.M.; Peng, J.C.H. Robust constrained model predictive voltage control in active distribution networks. IEEE Trans. Sustain. Energy 2021, 12, 400–411. [Google Scholar] [CrossRef]
- Fusco, G.; Russo, M. A decentralized approach for voltage control by multiple distributed energy resources. IEEE Trans. Smart Grid 2021, 12, 3115–3127. [Google Scholar] [CrossRef]
- Yazdanian, M.; Mehrizi-Sani, A. Distributed Control Techniques in Microgrids. IEEE Trans. Smart Grid 2014, 5, 2901–2909. [Google Scholar] [CrossRef]
- Andrén, F.; Bletterie, B.; Kadam, S.; Kotsampopoulos, P.; Bucher, C. On the Stability of Local Voltage Control in Distribution Networks With a High Penetration of Inverter-Based Generation. IEEE Trans. Ind. Electron. 2015, 62, 2519–2529. [Google Scholar] [CrossRef]
- Bolognani, S.; Carli, R.; Cavraro, G.; Zampieri, S. On the Need for Communication for Voltage Regulation of Power Distribution Grids. IEEE Trans. Control Netw. Syst. 2019, 6, 1111–1123. [Google Scholar] [CrossRef]
- Zeraati, M.; Golshan, M.E.H.; Guerrero, J.M. A consensus-based cooperative control of PEV battery and PV active power curtailment for voltage regulation in distribution networks. IEEE Trans. Smart Grid 2017, 10, 670–680. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, Q.; Gao, H.; Shen, F. Distributed voltage regulation of smart distribution networks: Consensus-based information synchronization and distributed model predictive control scheme. Int. J. Electr. Power Energy Syst. 2019, 111, 58–65. [Google Scholar] [CrossRef]
- Dhulipala, S.C.; Monteiro, R.V.A.; da Silva Teixeira, R.F.; Ruben, C.; Bretas, A.S.; Guimarães, G.C. Distributed model-predictive control strategy for distribution network volt/var control: A smart-building-based approach. IEEE Trans. Ind. Appl. 2019, 55, 7041–7051. [Google Scholar] [CrossRef]
- Qi, W.; Liu, J.; Christofides, P.D. Distributed supervisory predictive control of distributed wind and solar energy systems. IEEE Trans. Control Syst. Technol. 2013, 21, 504–512. [Google Scholar] [CrossRef]
- Duan, J.; Wang, C.; Xu, H.; Liu, W.; Xue, Y.; Peng, J.C.; Jiang, H. Distributed control of inverter-interfaced microgrids based on consensus algorithm with improved transient performance. IEEE Trans. Smart Grid 2019, 10, 1303–1312. [Google Scholar] [CrossRef]
- Antonelli, G.; Arrichiello, F.; Caccavale, F.; Marino, A. A decentralized controller-observer scheme for multi-agent weighted centroid tracking. IEEE Trans. Autom. Control 2012, 58, 1310–1316. [Google Scholar] [CrossRef]
- Borrelli, F.; Bemporad, A.; Morari, M. Predictive Control for Linear and Hybrid Systems; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Kailath, T. Linear Systems; Prentice-Hall: Englewood Cliffs, NJ, USA, 1980; Volume 156. [Google Scholar]
- Hu, J.; Ye, C.; Ding, Y.; Tang, J.; Liu, S. A distributed MPC to exploit reactive power V2G for real-time voltage regulation in distribution networks. IEEE Trans. Smart Grid 2021, 13, 576–588. [Google Scholar] [CrossRef]
- Xing, X.; Lin, J.; Wan, C.; Song, Y. Model predictive control of LPC-looped active distribution network with high penetration of distributed generation. IEEE Trans. Sustain. Energy 2017, 8, 1051–1063. [Google Scholar] [CrossRef]
- Subramanian, L.; Debusschere, V.; Gooi, H.B.; Hadjsaid, N. A distributed model predictive control framework for grid-friendly distributed energy resources. IEEE Trans. Sustain. Energy 2021, 12, 727–738. [Google Scholar] [CrossRef]
- Fusco, G.; Russo, M. Robust MIMO Design of Decentralized Voltage Controllers of PV Systems in Distribution Networks. IEEE Trans. Ind. Electron. 2017, 64, 4610–4620. [Google Scholar] [CrossRef]
- Fusco, G.; Russo, M.; Casolino, G.M. Voltage and active power local PI control of distributed energy resources based on the effective transfer function method. Int. J. Electr. Power Energy Syst. 2023, 152, 109264. [Google Scholar] [CrossRef]
- Fusco, G.; Russo, M. A Procedure to Determine the Droop Constants of Voltage Controllers Coping with Multiple DG Interactions in Active Distribution Systems. Energies 2020, 13, 1935. [Google Scholar] [CrossRef]












| Method | DER Model | Network Model | Consensus Based | MPC | Integral Action | Architecture |
|---|---|---|---|---|---|---|
| in [12] | no dynamics | cluster based | no | yes | no | decentralized |
| in [16] | no dynamics | linearized | no | yes | no | centralized |
| in [19] | no dynamics | linearized | no | yes | no | centralized |
| in [25] | no dynamics | linearized | yes | yes | no | distributed |
| in [28] | time domain | micro-grid | no | no | yes | distributed |
| in [34] | time domain | energy community | yes | yes | yes | distributed |
| proposed | transfer function | linearized | yes | yes | yes | distributed |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antonelli, G.; Fusco, G.; Russo, M. Consensus-Based Model Predictive Control for Active Power and Voltage Regulation in Active Distribution Networks. Energies 2024, 17, 4490. https://doi.org/10.3390/en17174490
Antonelli G, Fusco G, Russo M. Consensus-Based Model Predictive Control for Active Power and Voltage Regulation in Active Distribution Networks. Energies. 2024; 17(17):4490. https://doi.org/10.3390/en17174490
Chicago/Turabian StyleAntonelli, Gianluca, Giuseppe Fusco, and Mario Russo. 2024. "Consensus-Based Model Predictive Control for Active Power and Voltage Regulation in Active Distribution Networks" Energies 17, no. 17: 4490. https://doi.org/10.3390/en17174490
APA StyleAntonelli, G., Fusco, G., & Russo, M. (2024). Consensus-Based Model Predictive Control for Active Power and Voltage Regulation in Active Distribution Networks. Energies, 17(17), 4490. https://doi.org/10.3390/en17174490








