Two-Dimensional Dual Jets—A Comprehensive Review of Experimental and Numerical Analyses
Abstract
1. Introduction
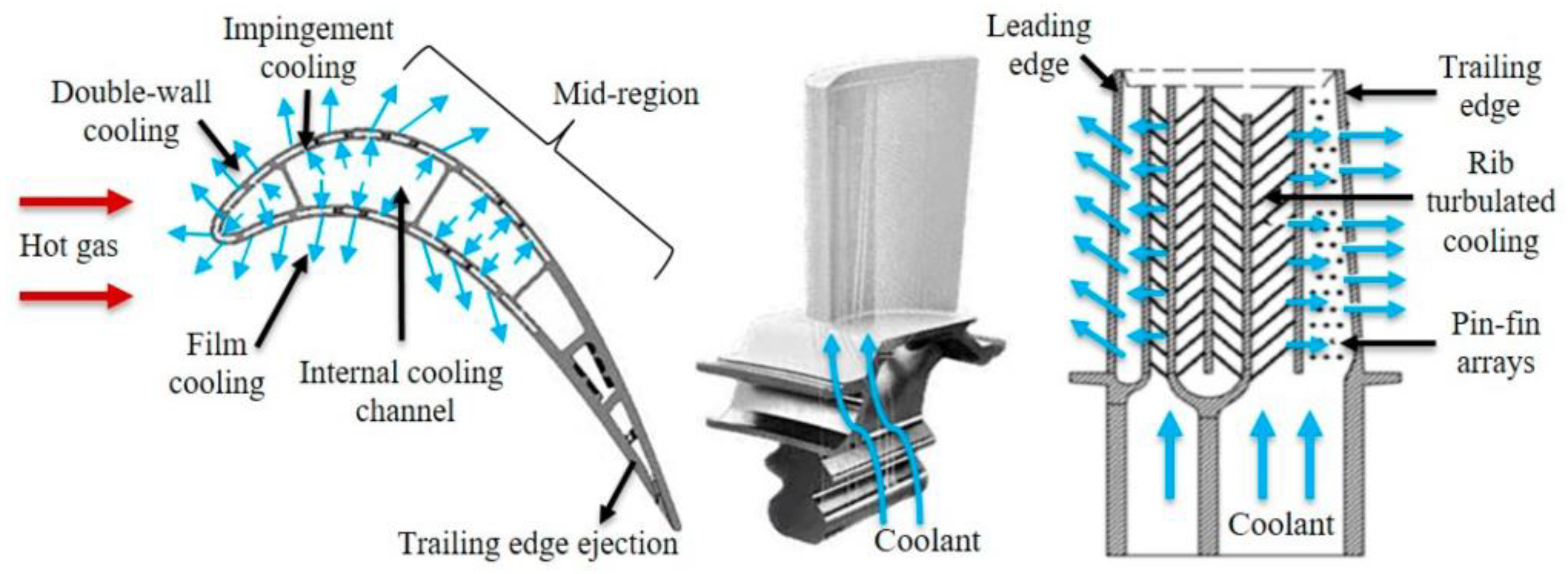
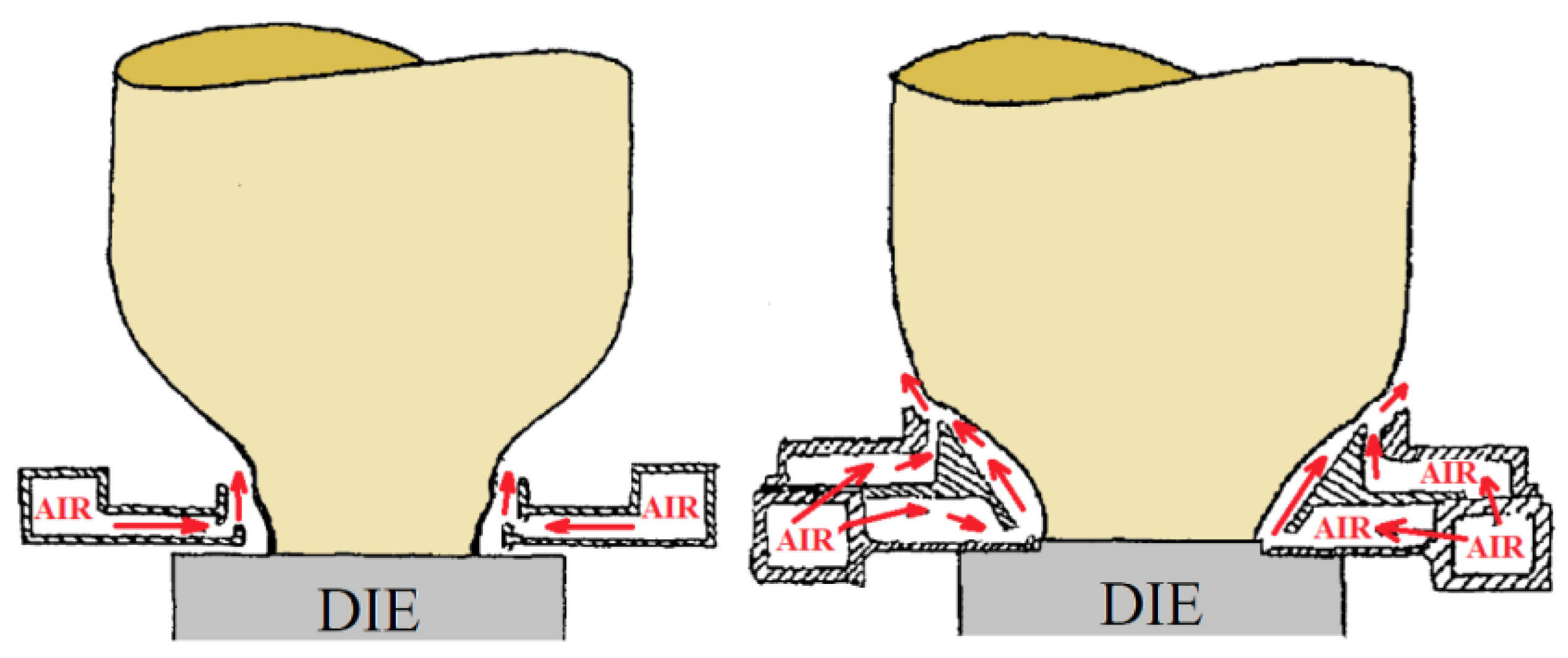
Industrial Applications of Dual Jets
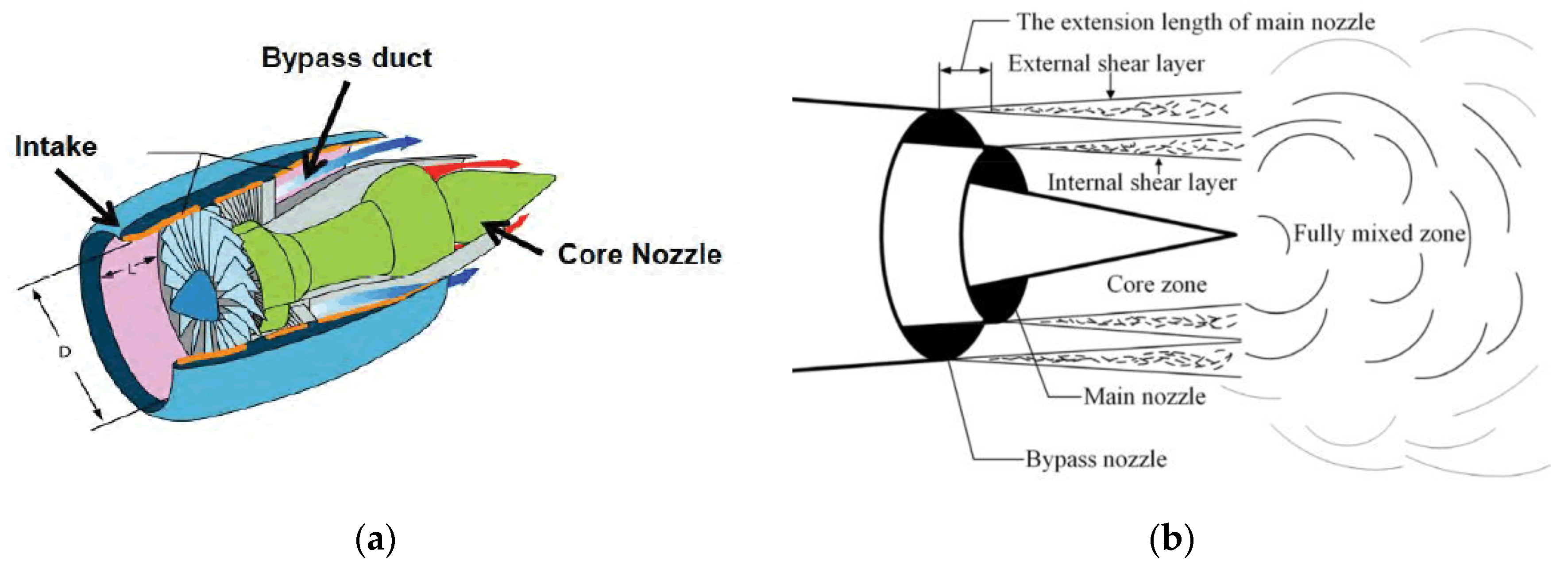
2. Comparison of Jet Flow Configurations
2.1. Turbulent Free Jets
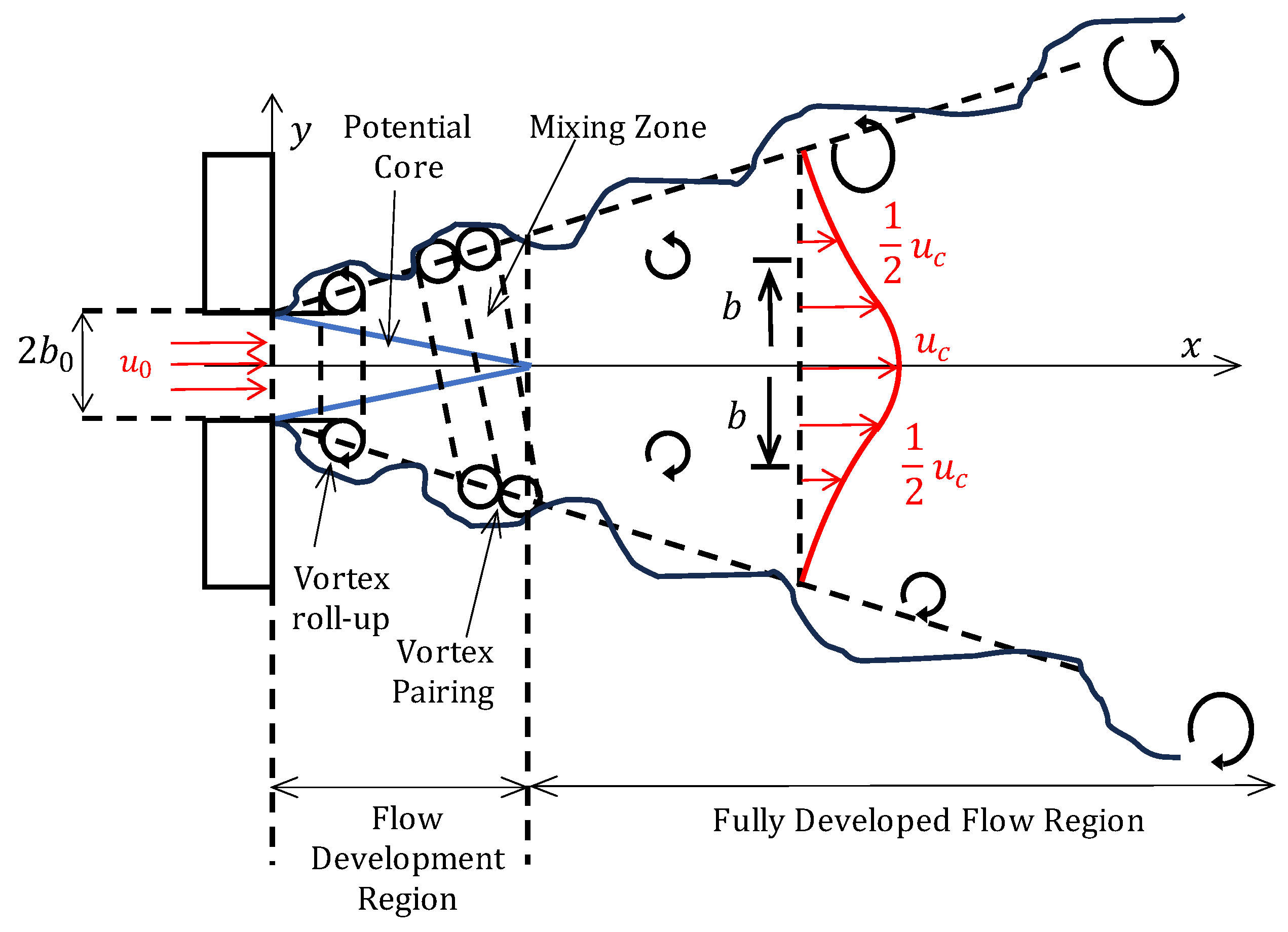
2.1.1. Single Plane Jet
2.1.2. Plane Parallel Jet
2.2. Wall-Bounded Turbulent Jets
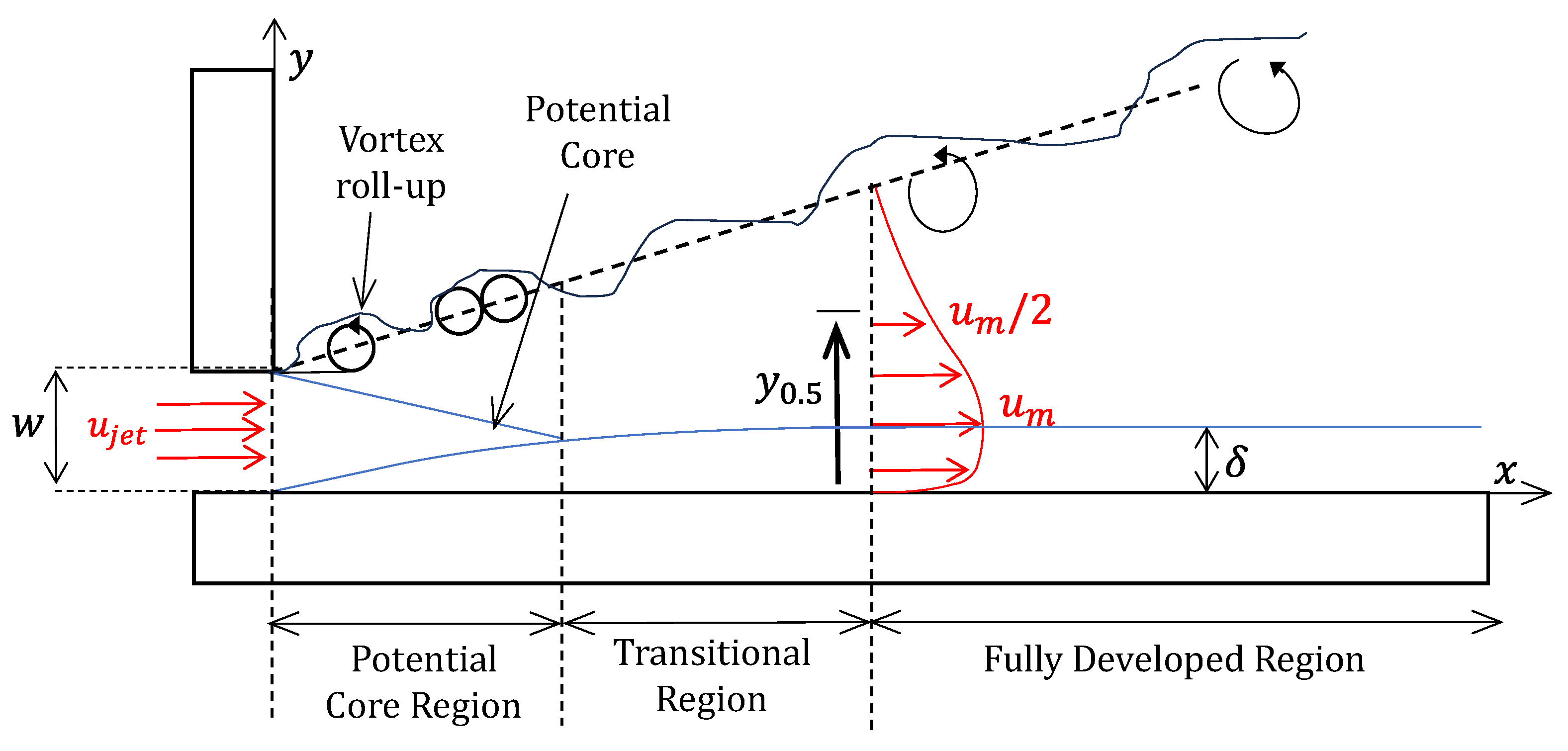
2.2.1. Wall Jets
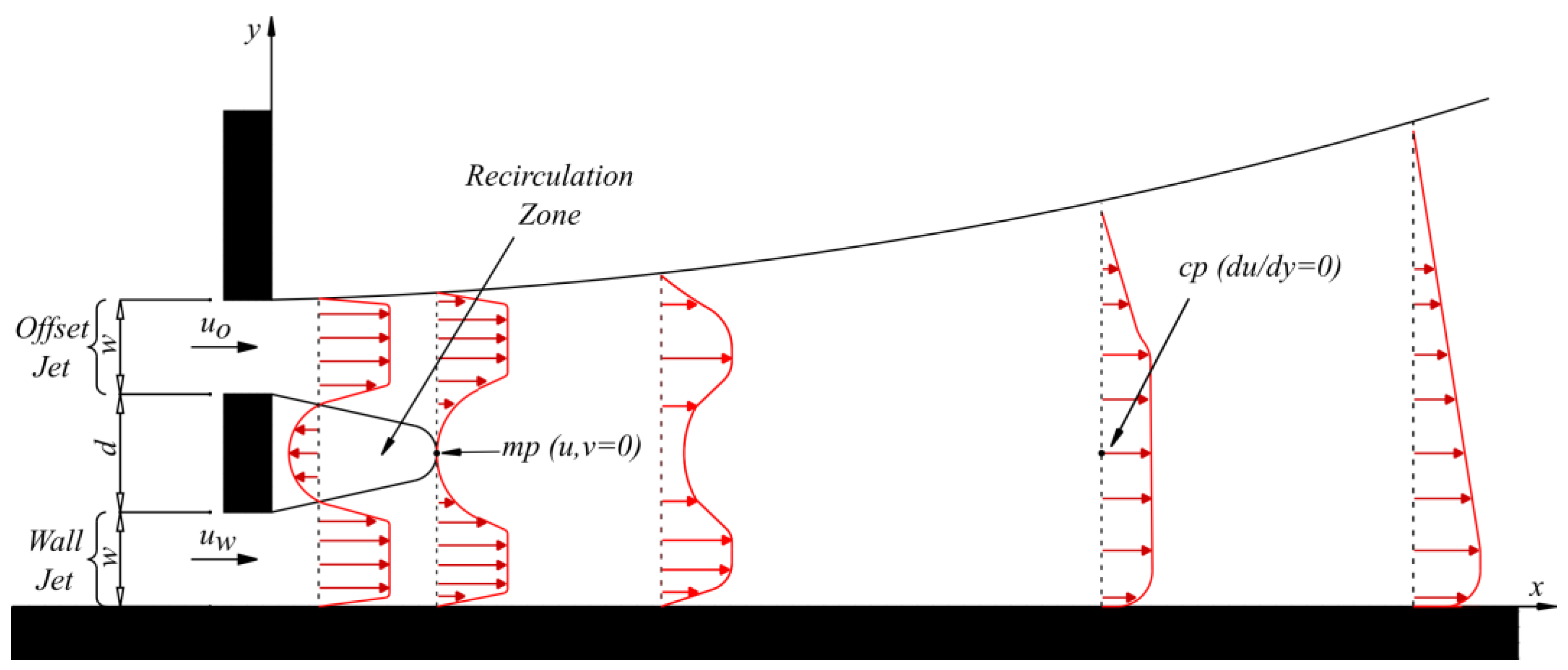
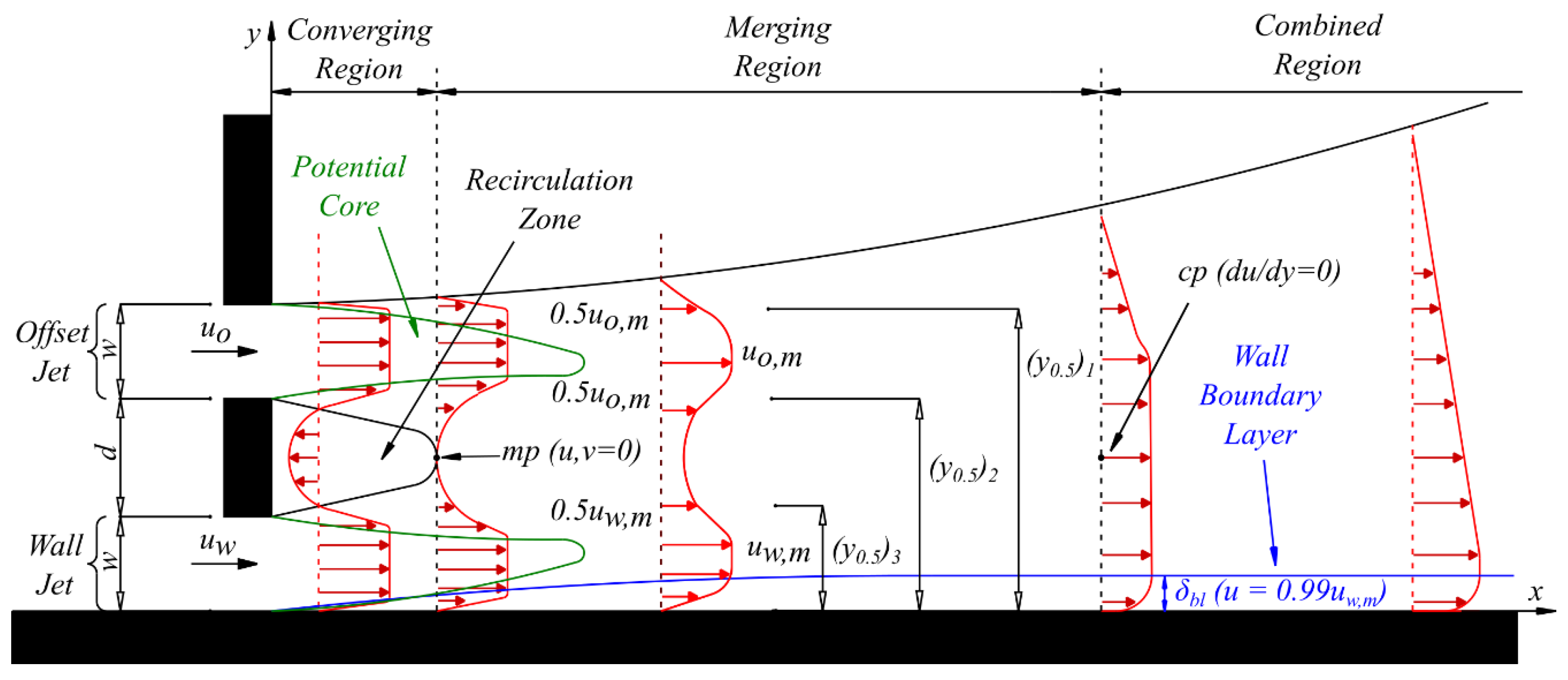
2.2.2. Offset Jets
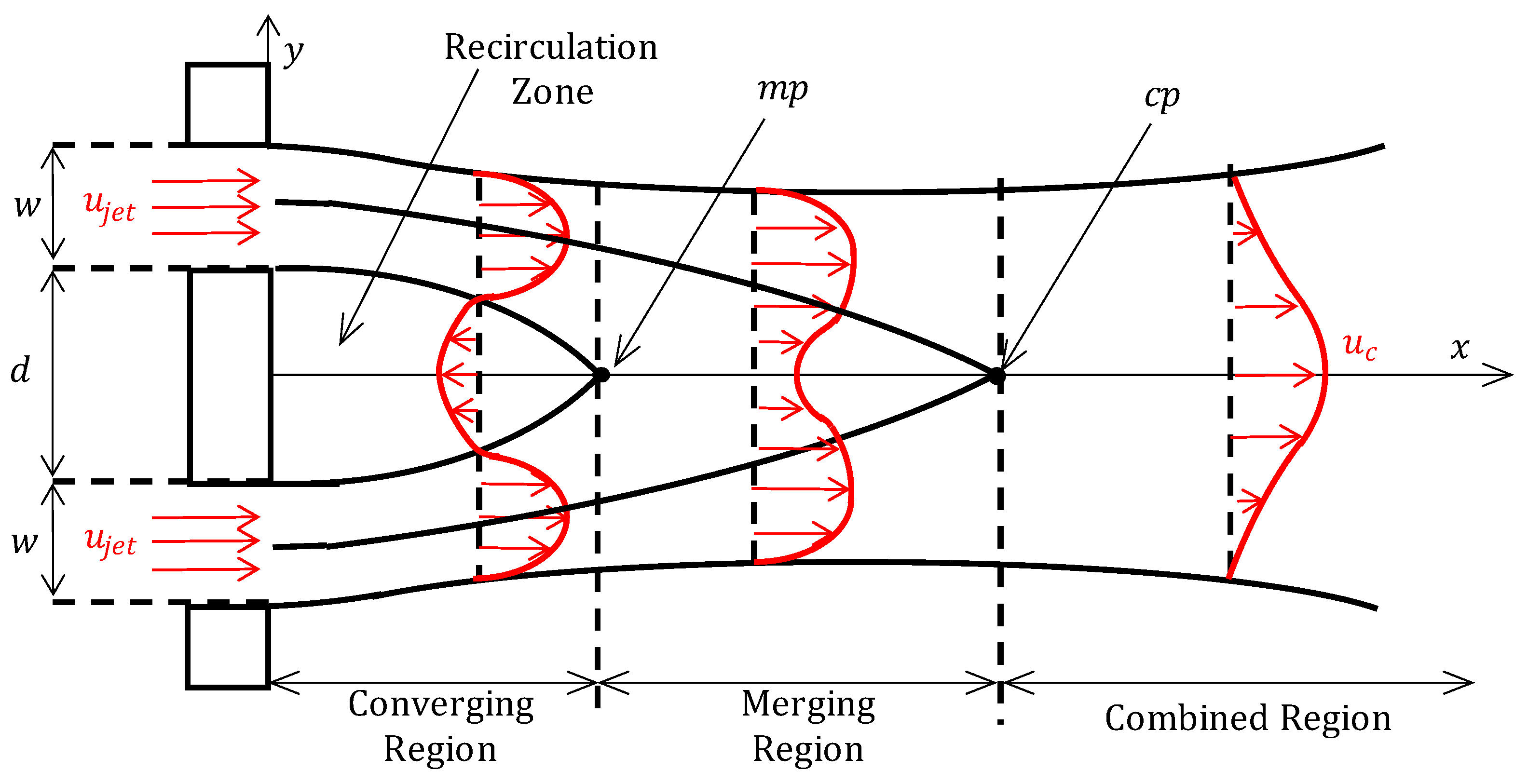
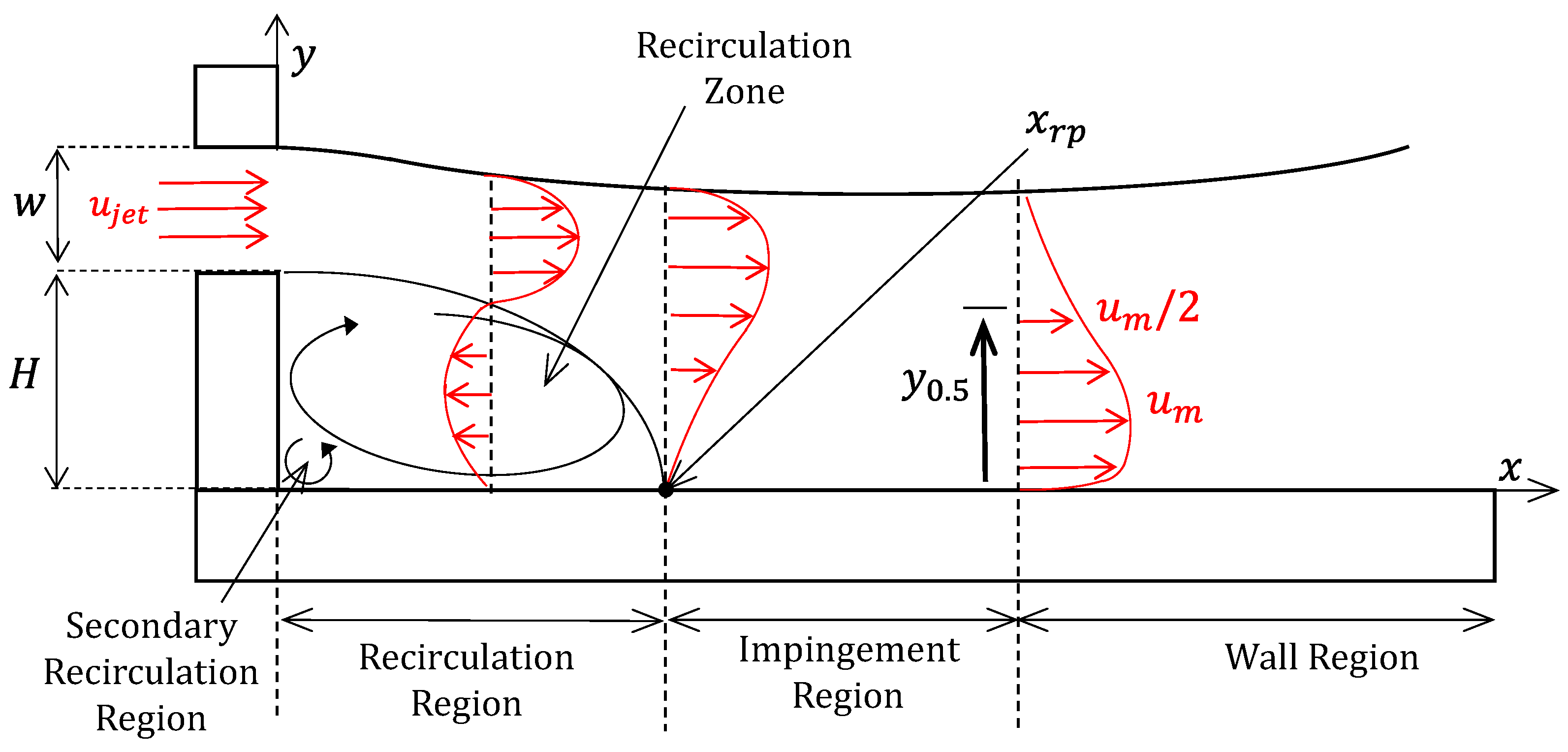
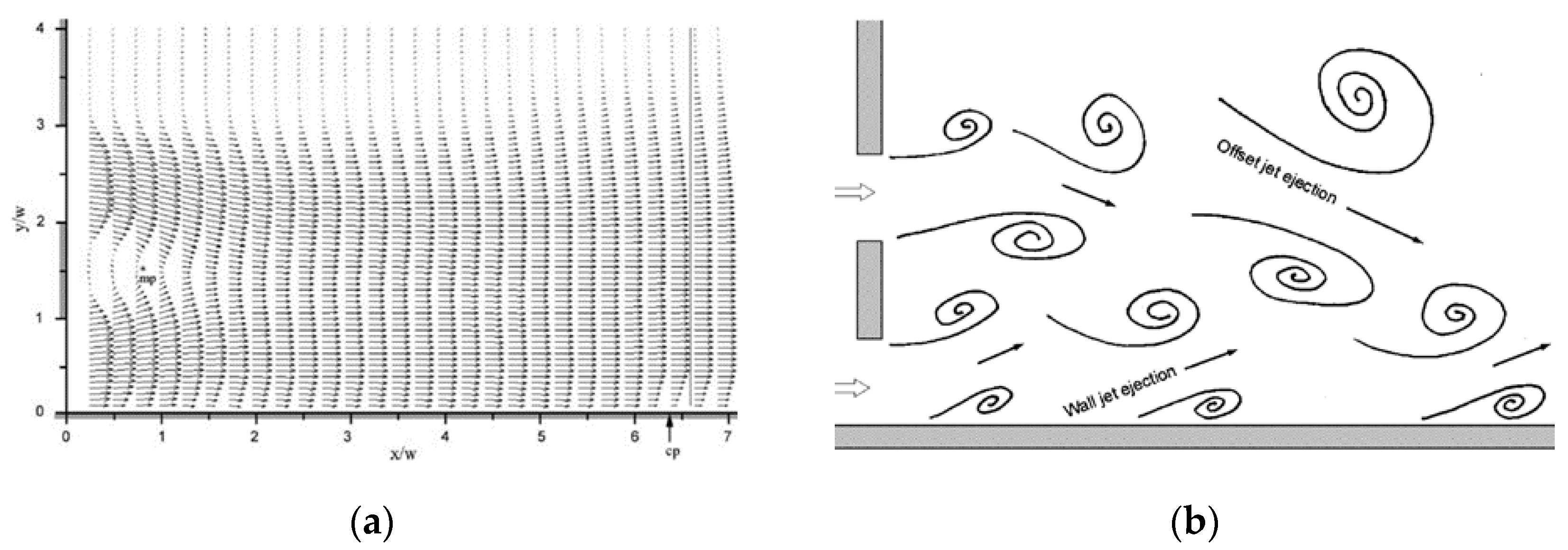
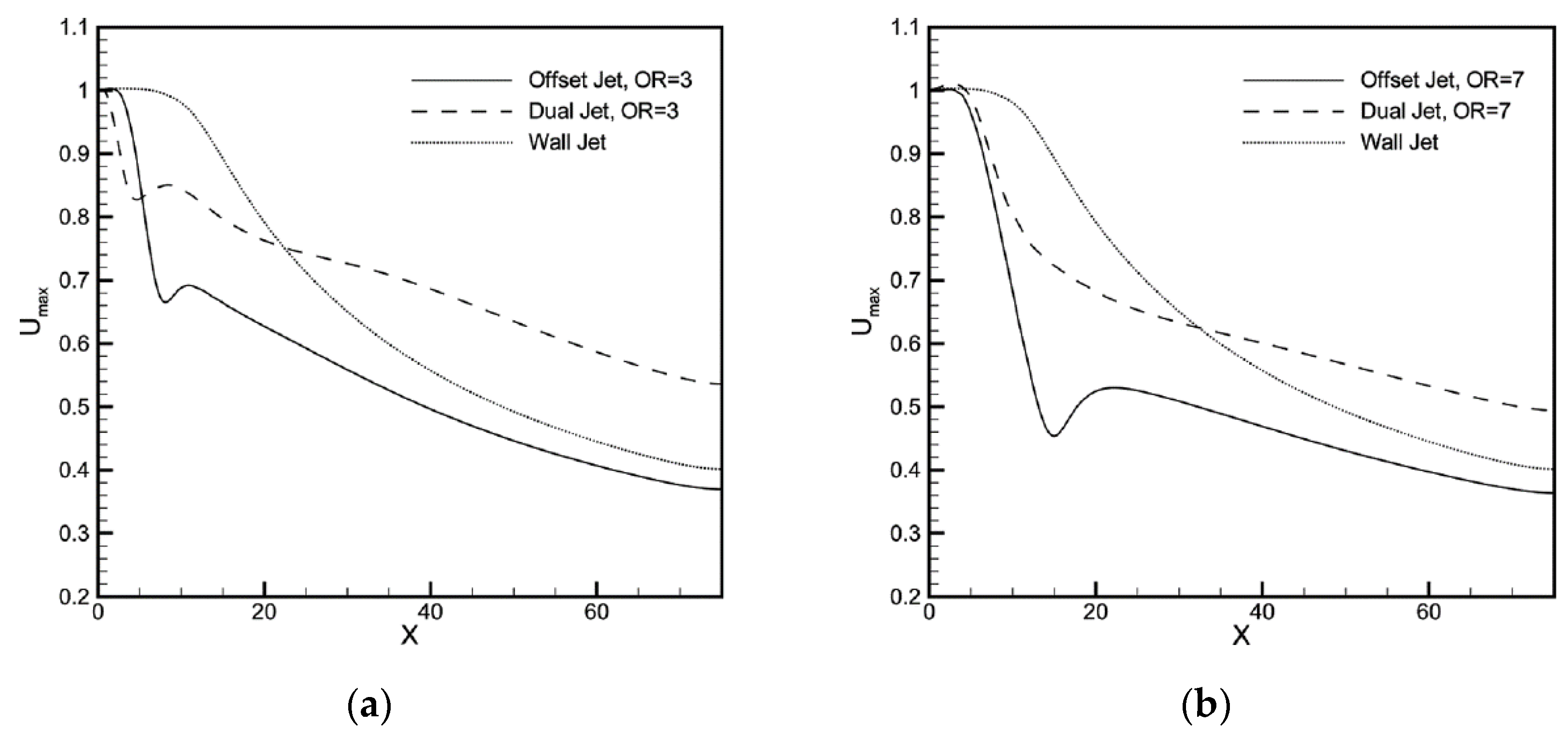
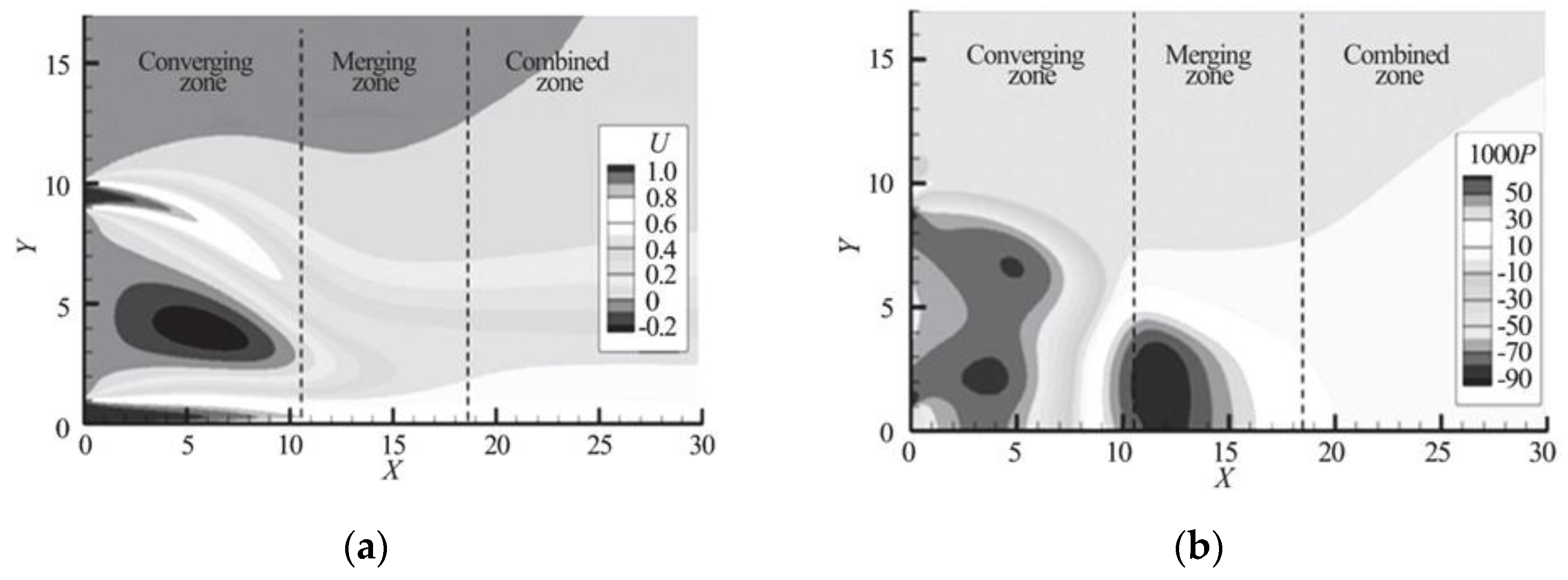
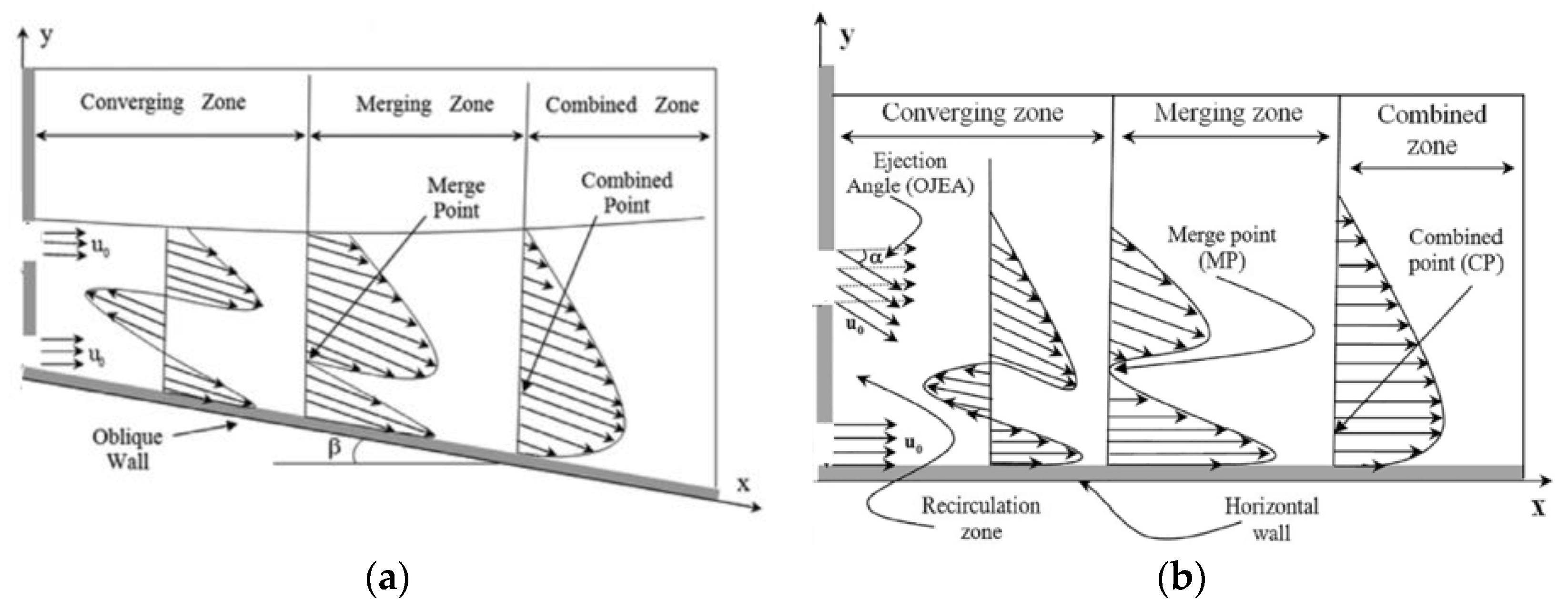
2.3. Dual Jets
3. Literature Review
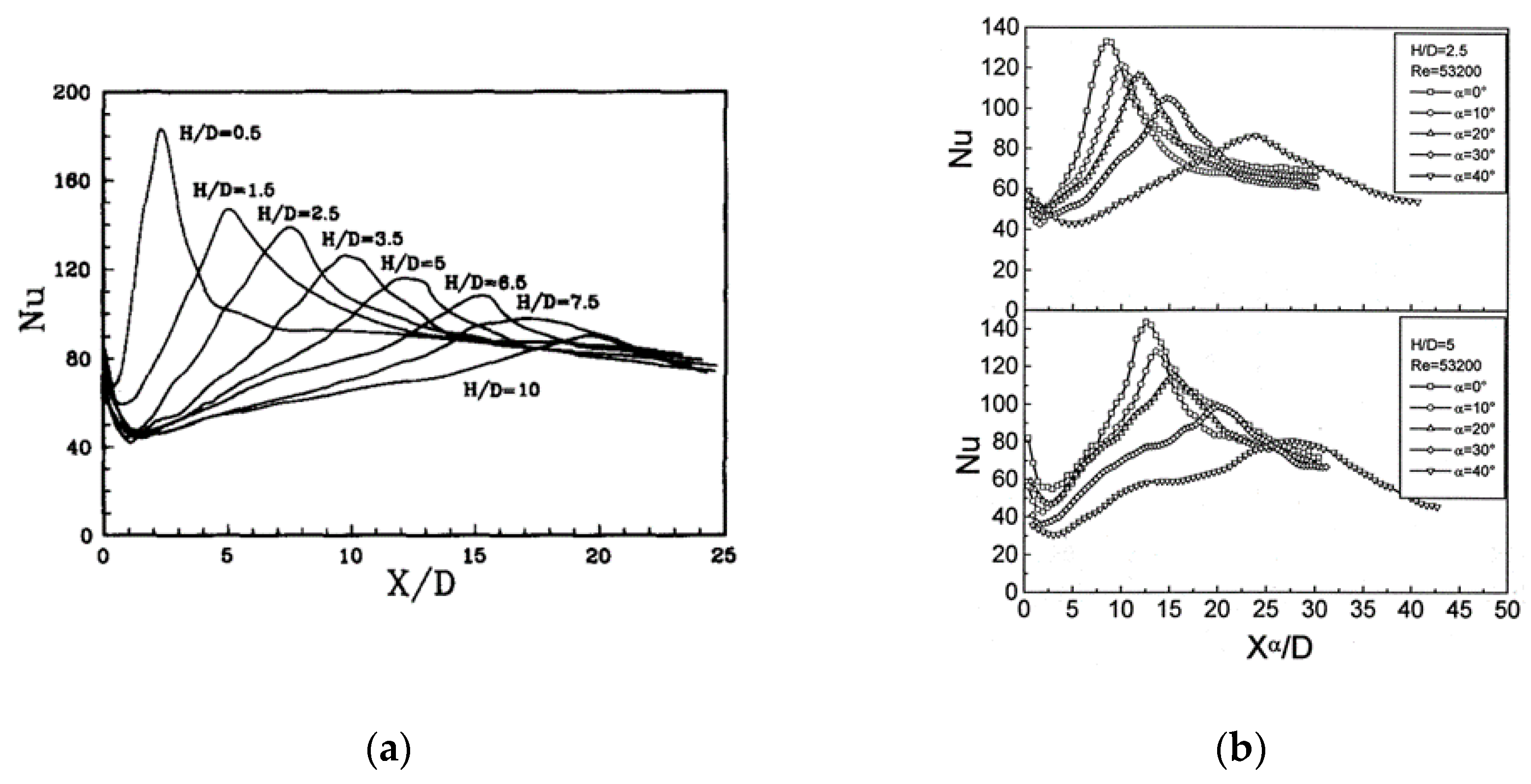
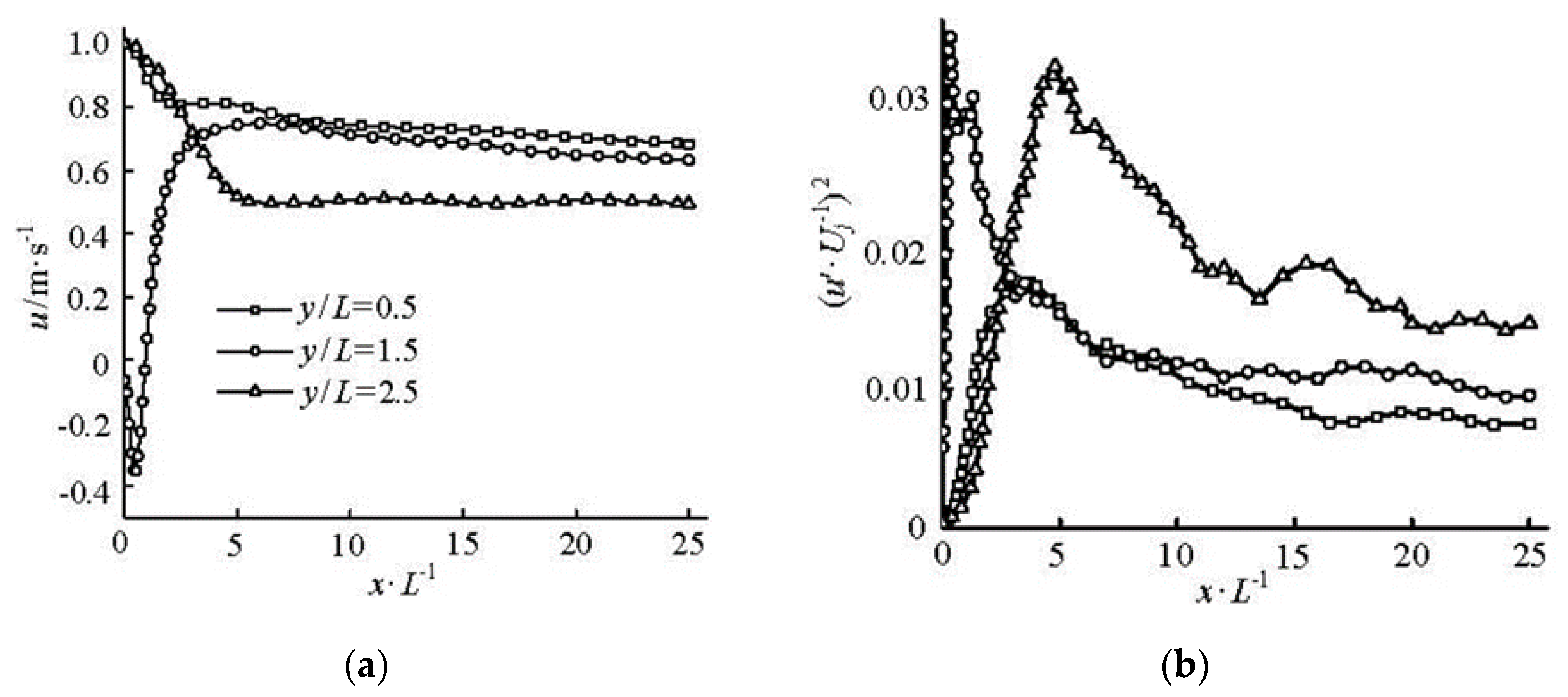
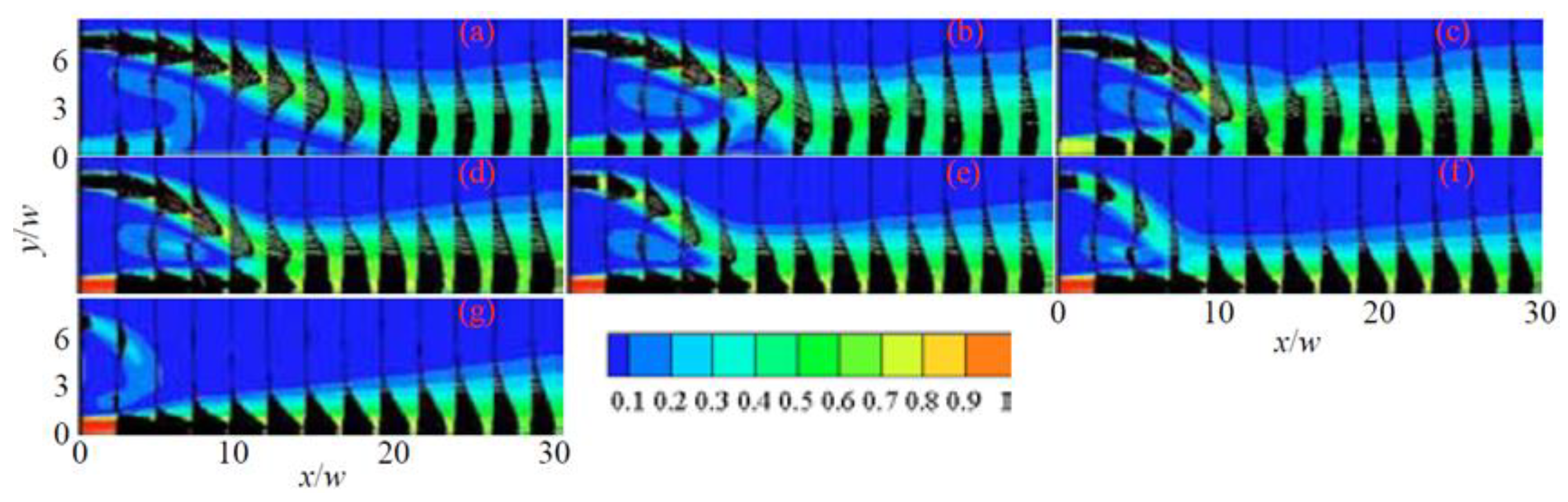
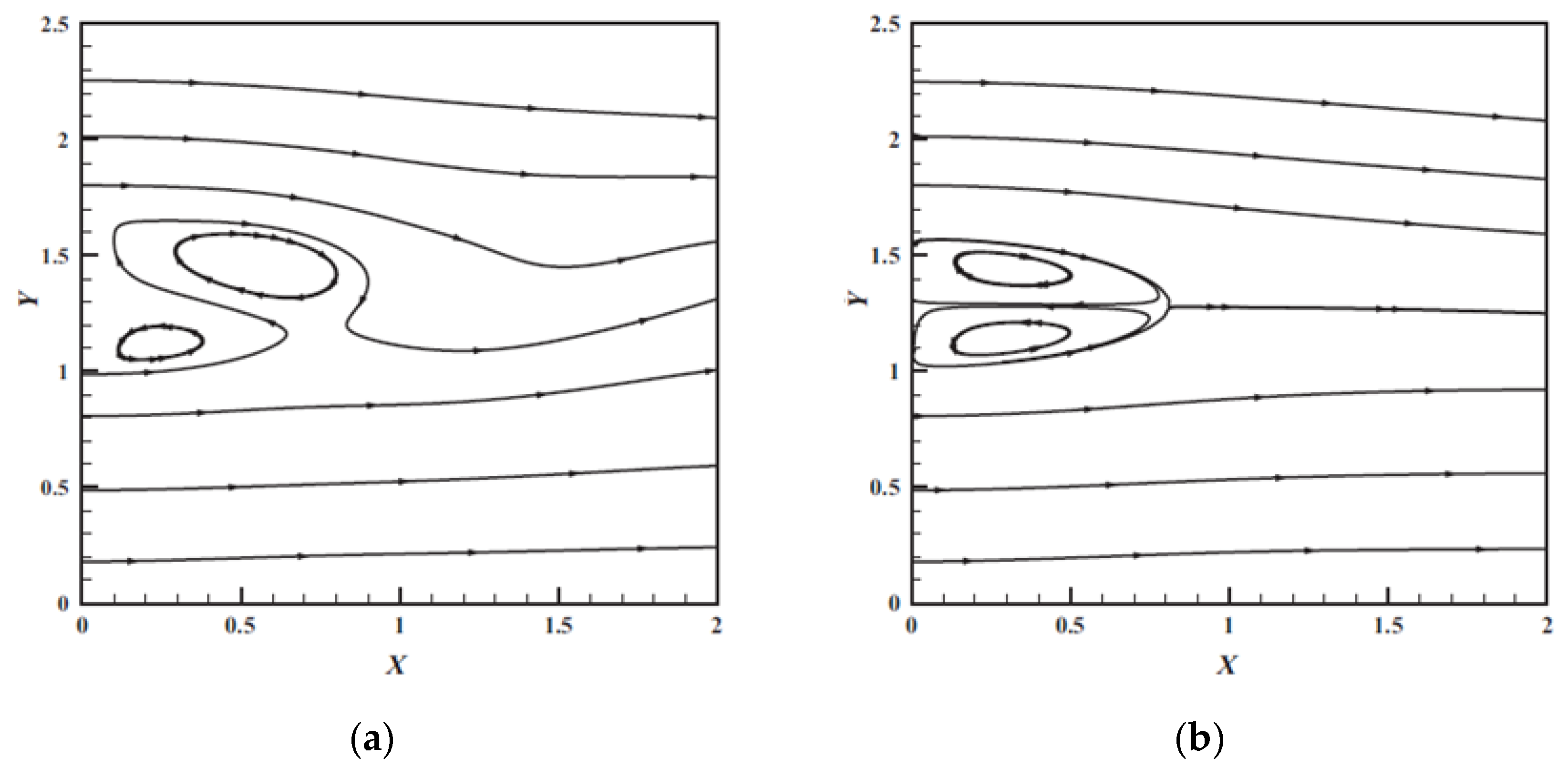
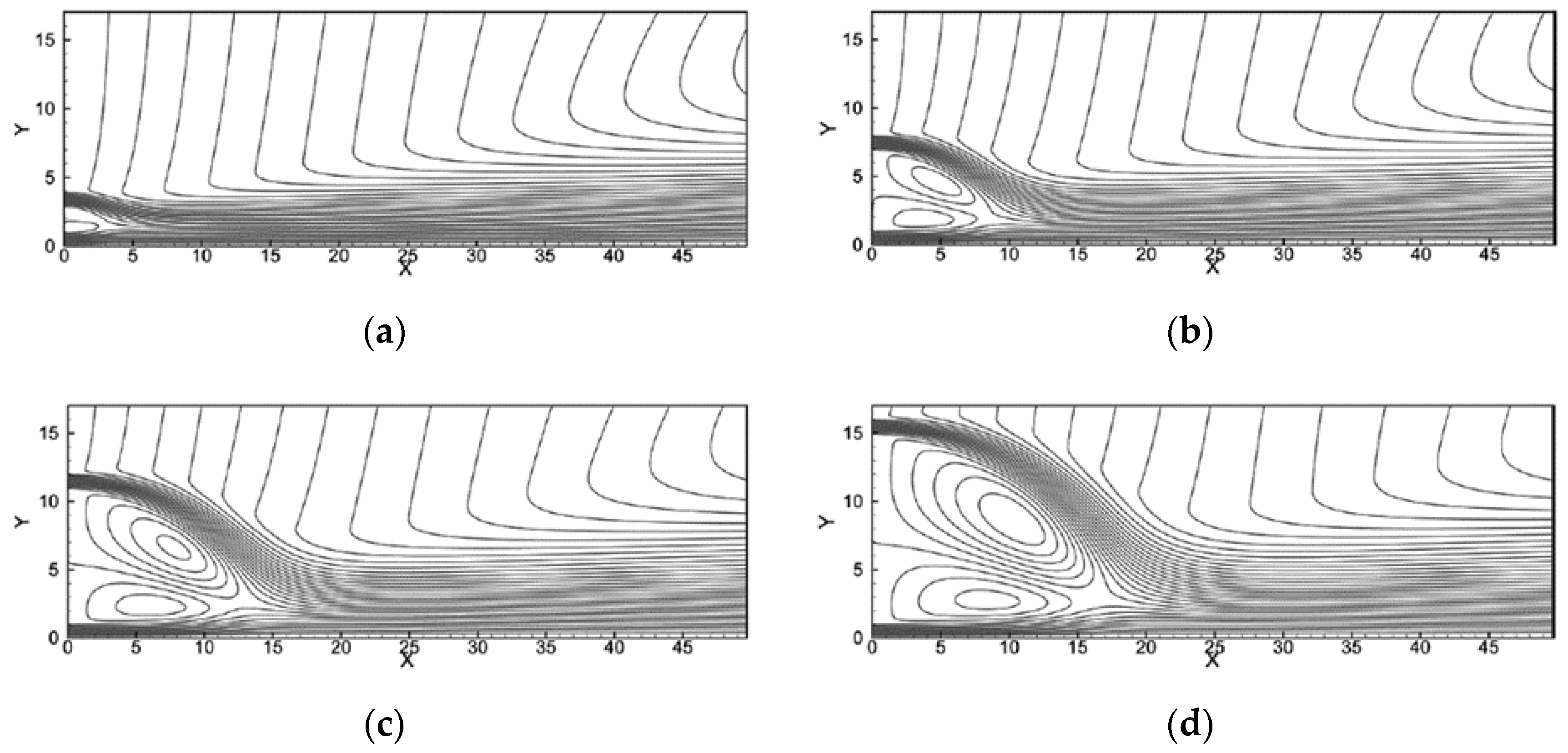
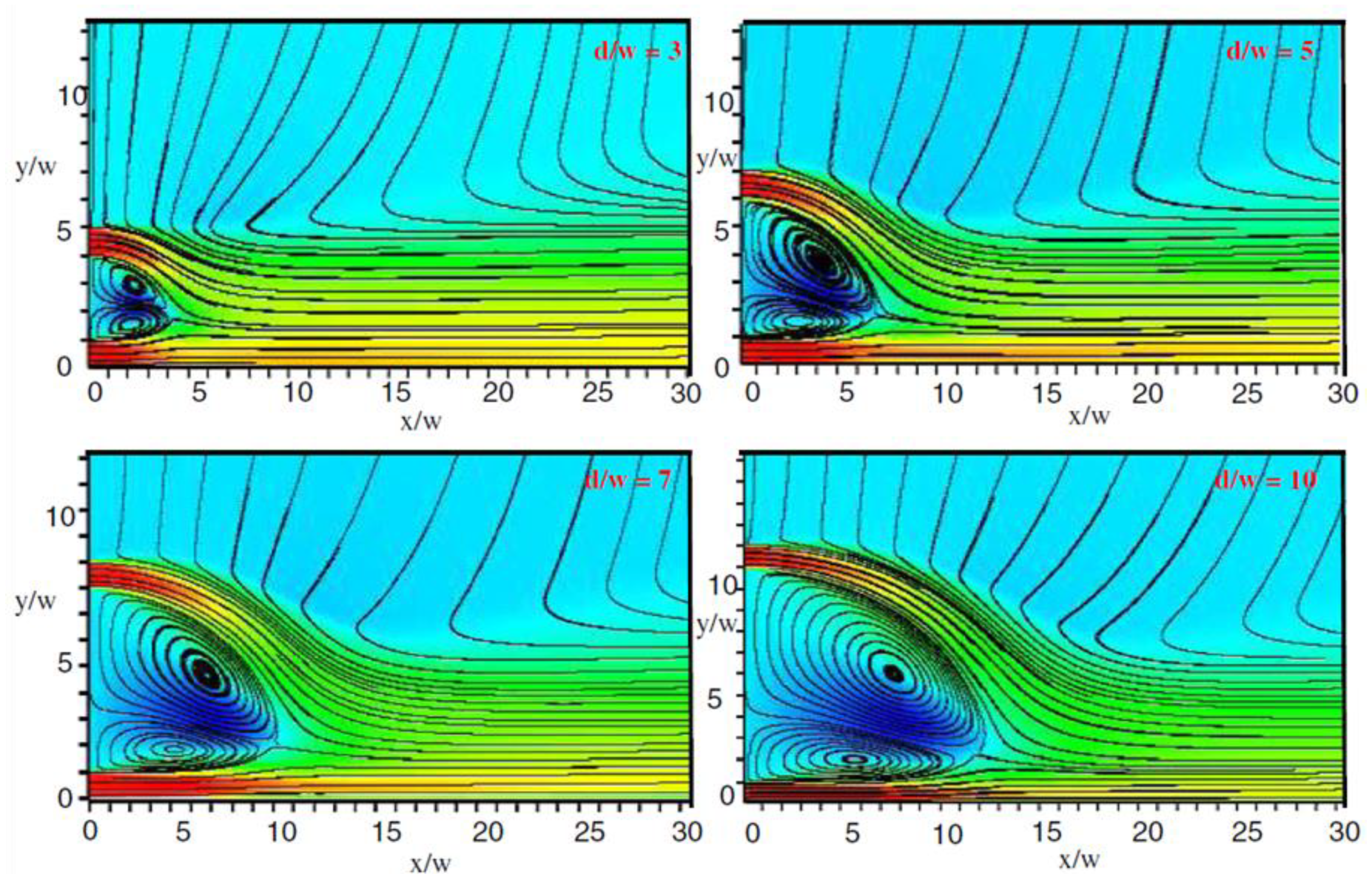
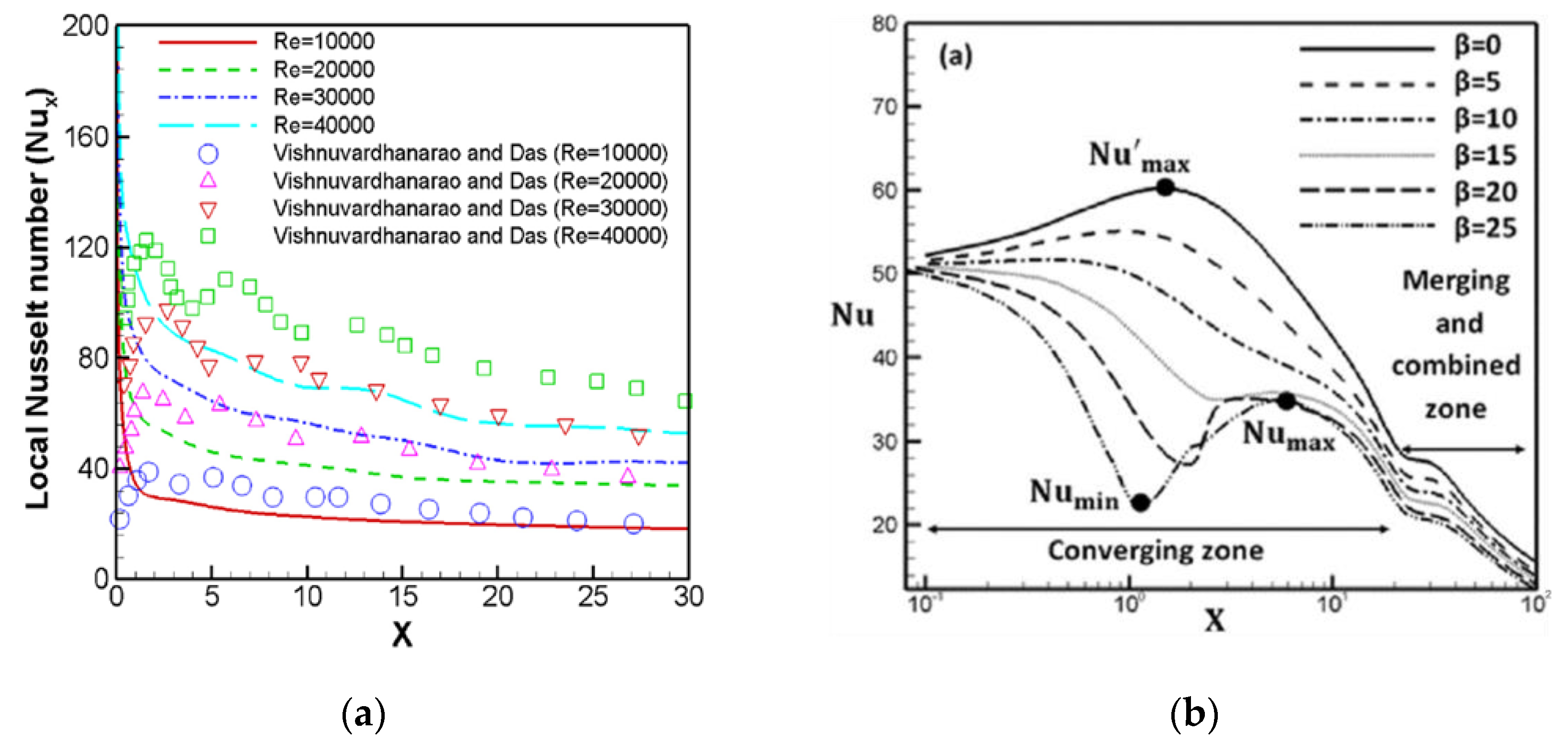
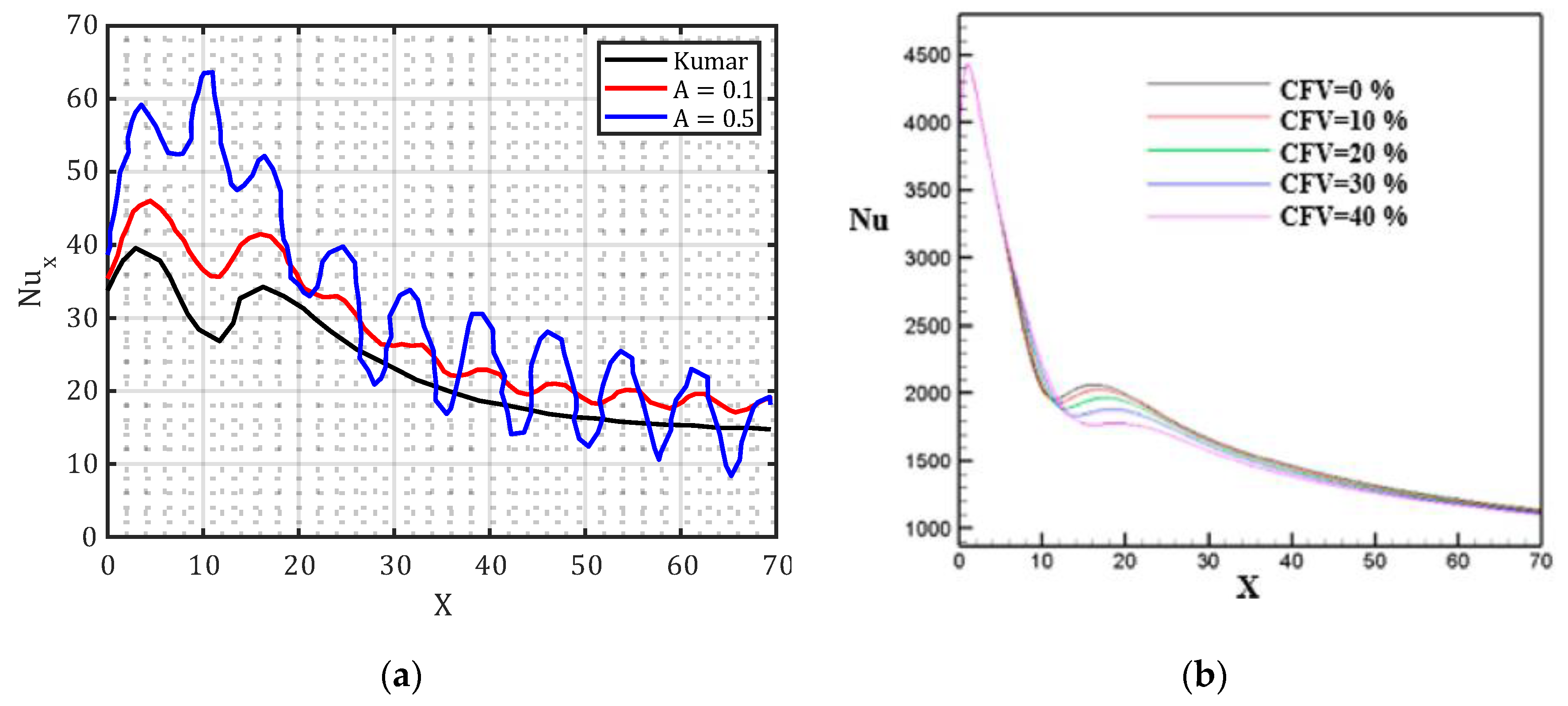
3.1. Hydrodynamic Studies of Dual Jet Flows
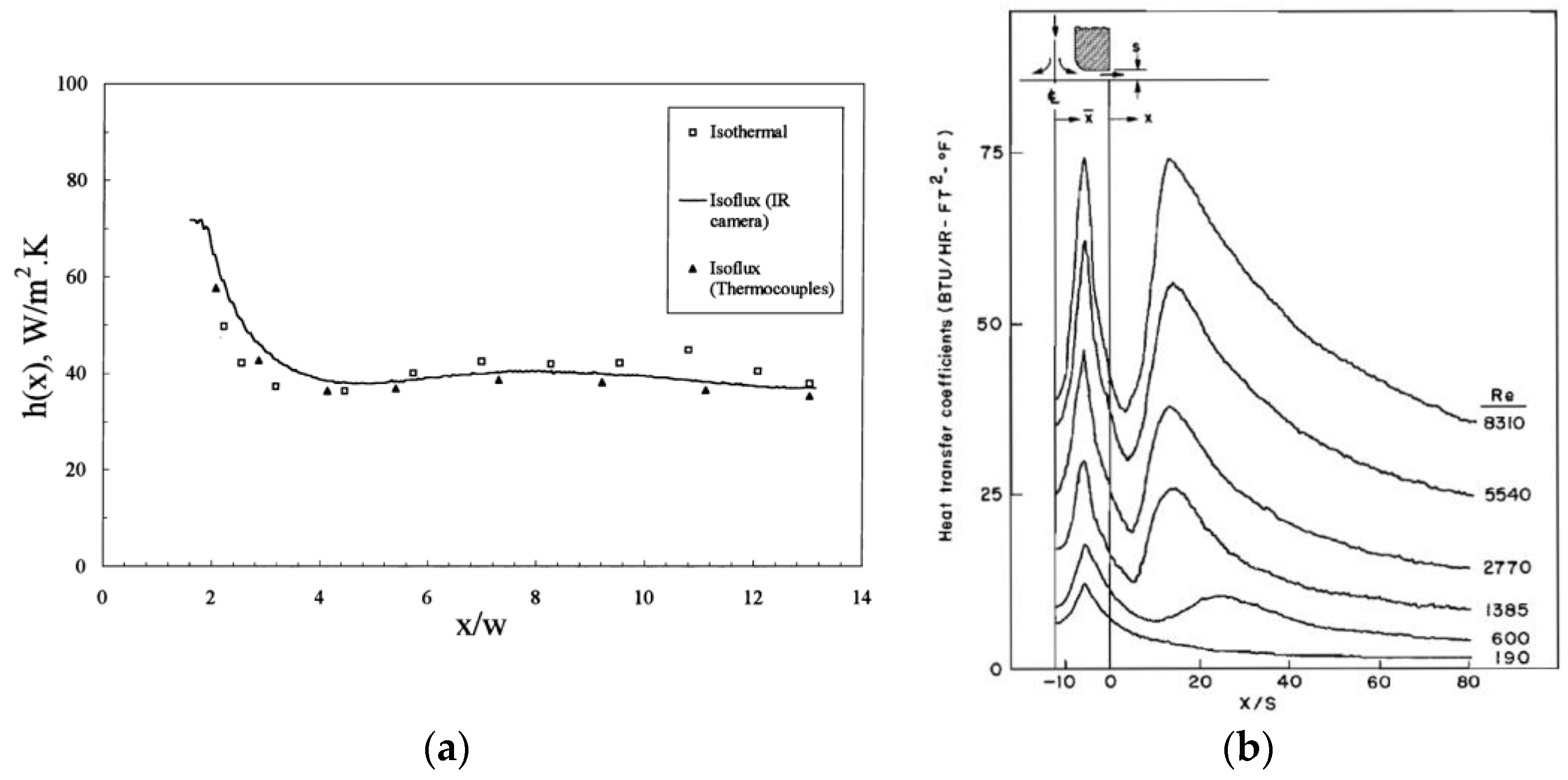
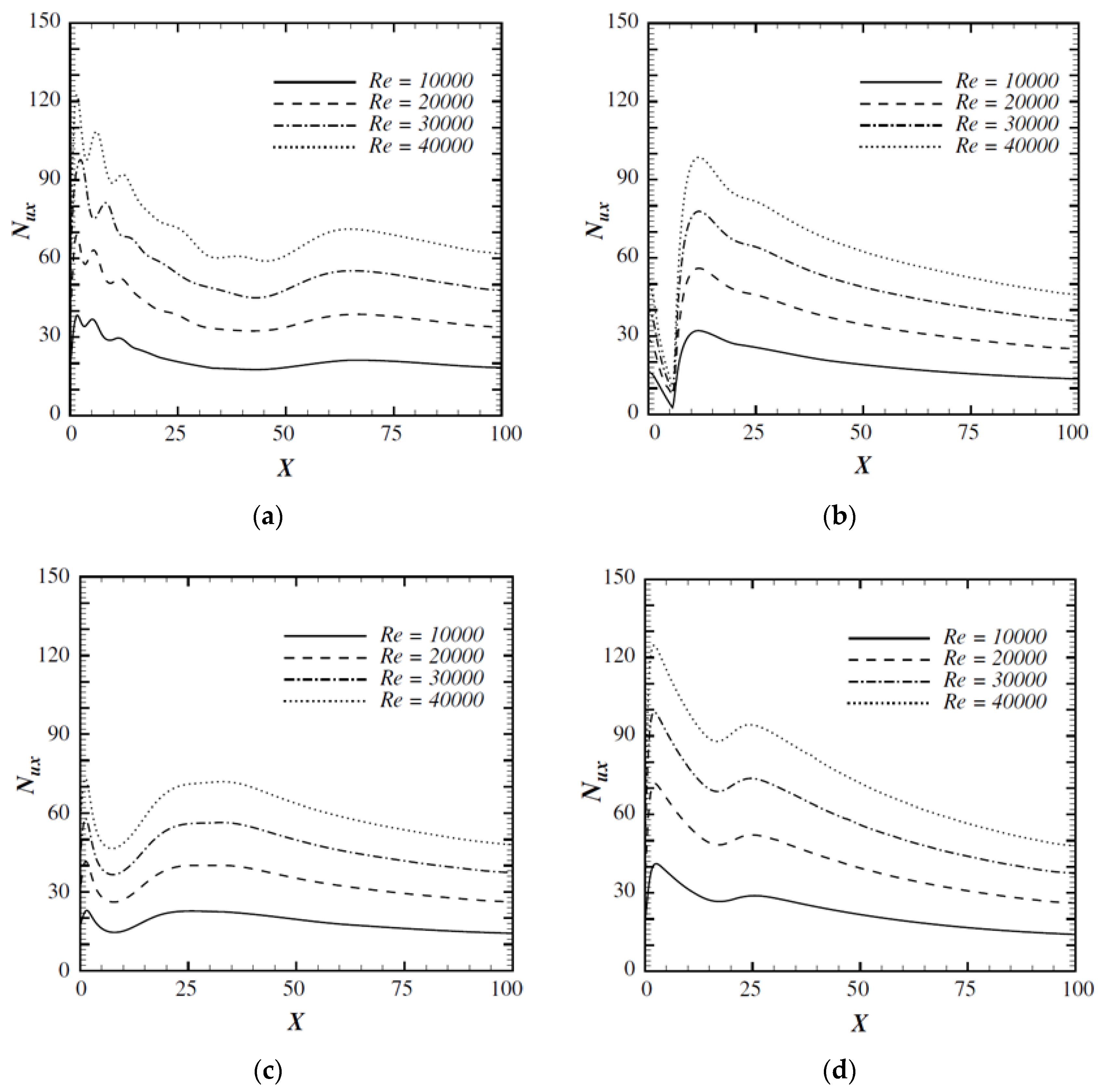
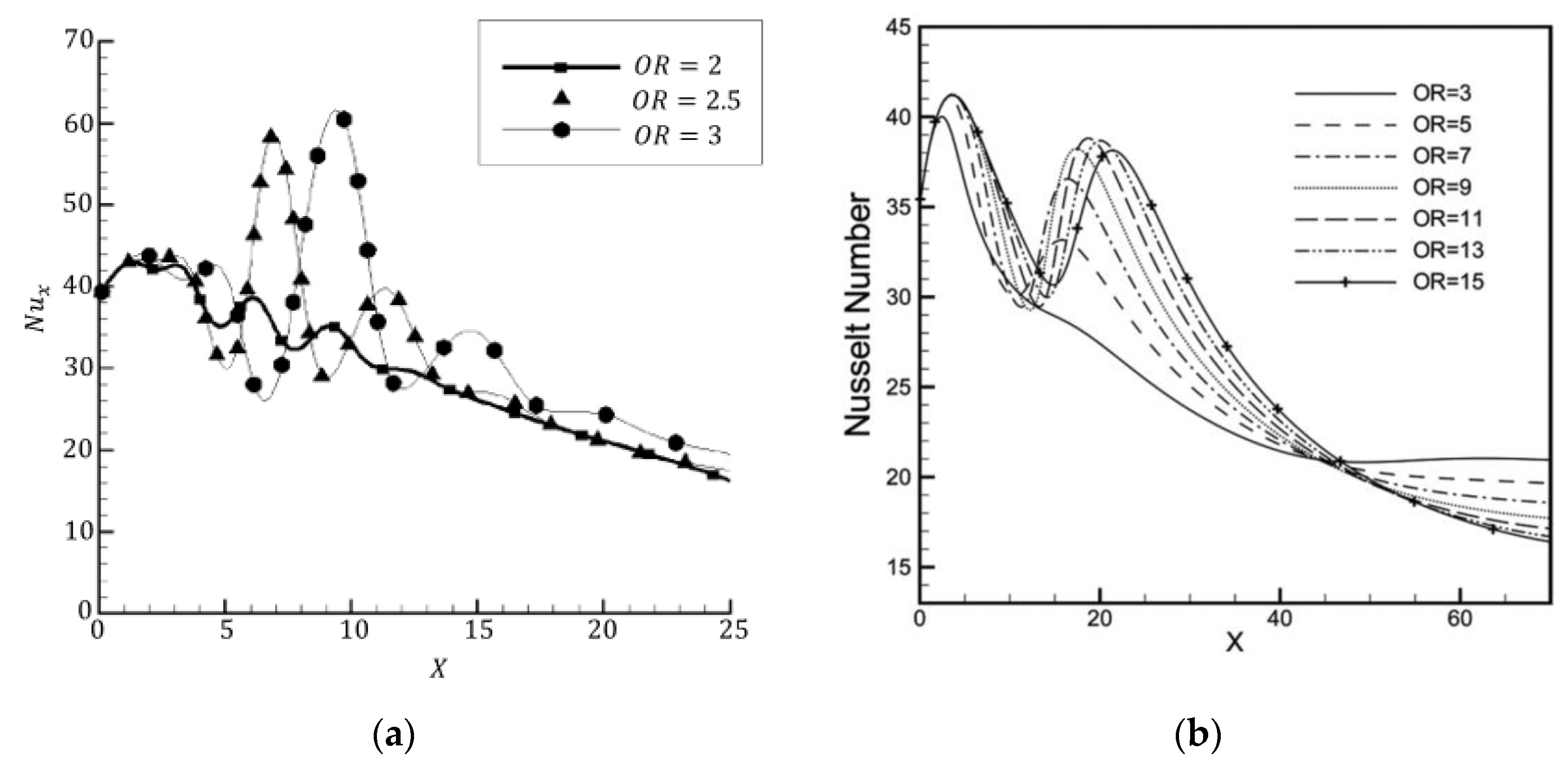
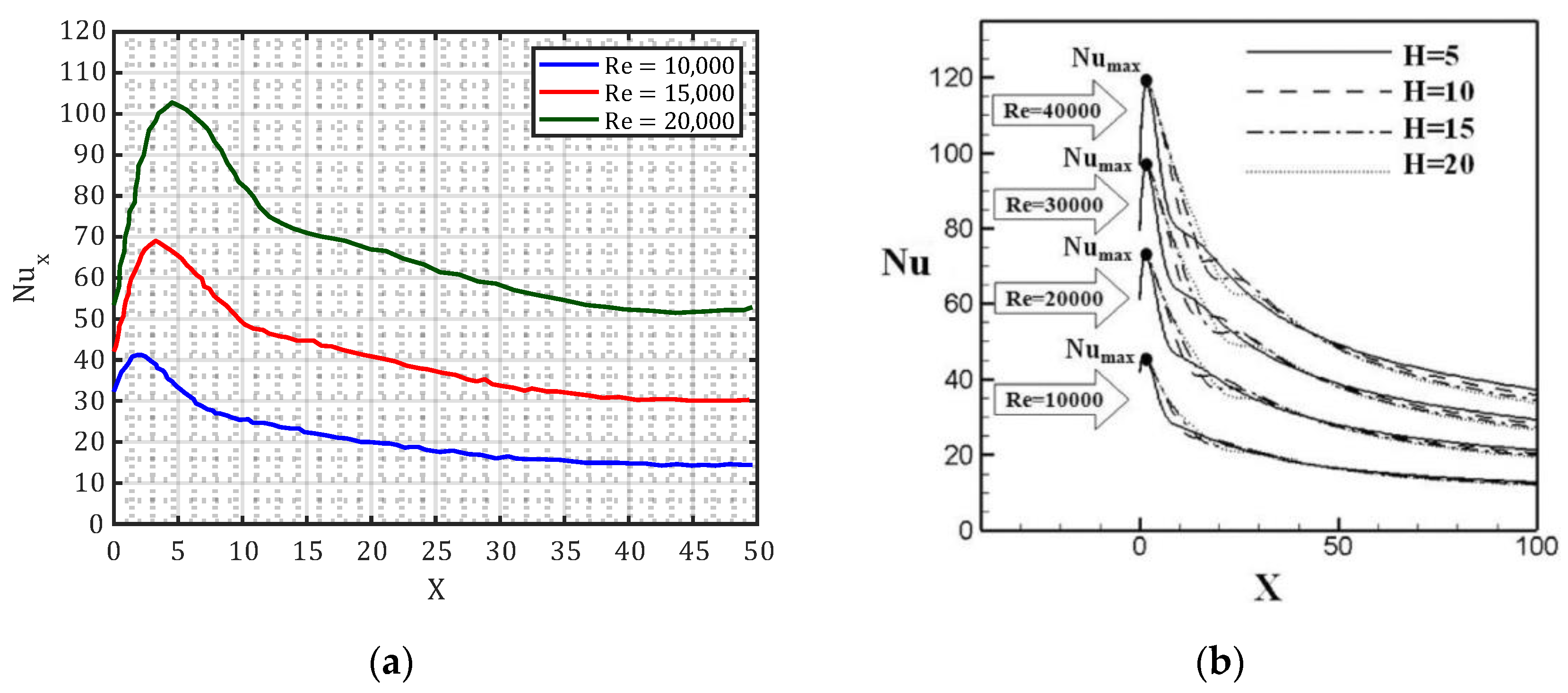
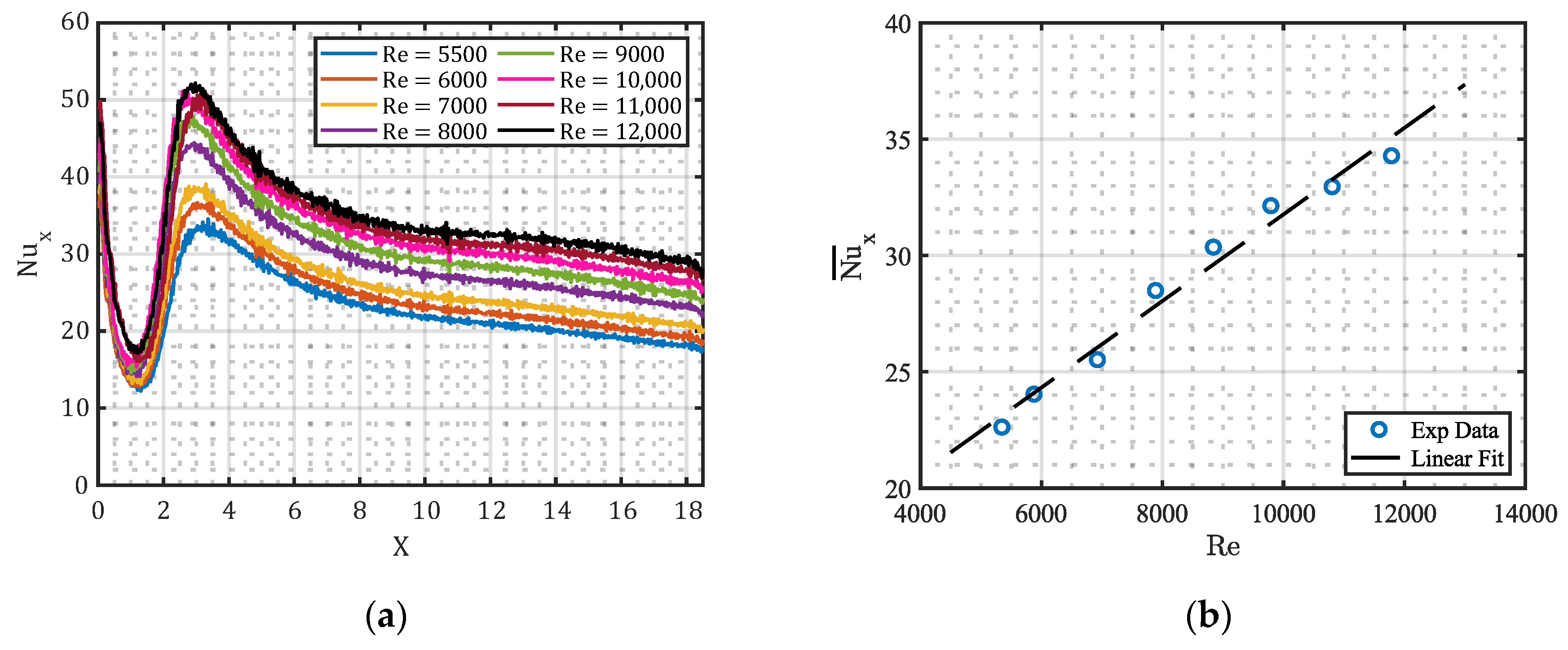
3.2. Heat Transfer Characteristics of Dual Jet Flows
4. Synthesis
5. Conclusions and Recommendations
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Authors | Method | Re (×103) | mp | cp | LVC | UVC | Main Findings | ||
|---|---|---|---|---|---|---|---|---|---|
| Experimental | |||||||||
| Wang and Tan [73] | PIV | 1 | 1 | 10 | (0.75, -n/a) | (6.4, n/a) | n/a | n/a |
|
| Murphy et al. [8] | IR Thermography | 1 | 1 | 5.5–12 | n/a | n/a | n/a | n/a |
|
| Numerical | |||||||||
| Li et al. [3] | LES | 1 | 1 | 10 | n/a | n/a | n/a | n/a |
|
| Li et al. [92] | k-ε | 0.5–8 | 0.25–4 * | 10 | n/a | n/a | n/a | n/a |
|
| Kumar and Das [2] | k-ε | 8 * | 1 | 20 | (10.5, 2.4) | (18.4, 2.8) | n/a | n/a |
|
| Mondal et al. [87] | k-ε | 0.5–2.5 | 1 | 10 | (1.4, n/a) to (1.9, n/a) | (8.3, n/a) to (36.3, n/a) | n/a | n/a |
|
| Singh and Dewan [95] | SST k-ω | 1 * | 1 | 10–40 | (1.5, 1.4) to (1.4, 1.5) | n/a | n/a | n/a |
|
| Kumar [75] and Kumar [76] | k-ε | 2–14 * | 1 | 15 | (3, 1.7) to (16.3, 3.1) | (16.3, 1.7) to (24.1, 3.8) | (1.2, 1.4) to (8.7, 2.9) | (1.3, 2.4) to (10.6, 8.6) |
|
| Kumar et al. [96] | k-ε | 3–9 | 1 | 5–20 | n/a | n/a | n/a | n/a |
|
| Mondal et al. [97] | k-ε | 1 | 0.5–2 | 10 | (1.3, 1.6) to (1.2, 1.3) | n/a | n/a | n/a |
|
| Mondal et al. [98] | k-ε | 1 | 1 | 10 | (1.5, n/a) to (1.6, n/a) | (11.5, n/a) to (18.7, n/a) | n/a | n/a |
|
| Mondal et al. [99] | k-ε | 0.5–3.33 * | 1 | 10 | (1.4, n/a) to (1.9, n/a) | (8.3, n/a) to (36.3, n/a) | n/a | n/a |
|
| Zhao and Sun [83] | BGK | 3–9 * | 1 | 56 | (3.9, 2.4) to (5.7, 5.6) | (9, 1.9) to (12.7, 5.5) | n/a | n/a |
|
| Hnaien et al. [78] | k-ω | 4–14 | 0.5–1 | 15 | (3.8, 2.4) to (14.9, 16) | (4.9, 7.4) to (15, 24.5) | (3.4, 2.2) to (7.5, 3.3) | (4.3, 5) to (9.8, 9.1) |
|
| Assoudi et al. [84] | RSM | 1–10 | 0.57–1 | 15 | (1.4, n/a) to (12.3, n/a) | (11.2, n/a) to (16, n/a) | n/a | n/a |
|
| Hnaien et al. [79] | k-ω | 8 | 1 | 15 | n/a | n/a | n/a | n/a |
|
| Hnaien et al. [80] | k-ω | 8 * | 1 | 15 | (4.8, 2.1) to (17.1, 3.2) | (13.9, 2.1) to (23.5, 3.6) | (1.9, 1.8) to (7.2, 3.2) | (2.3, 3.7) to (9.1, 9.3) |
|
| Singh et al. [81] | k-ε | 6 * | 1 | 15 | (8.2, 2.1) to (7.7, 2.2) | (15.8, 2.5) to (14.4, 2.6) | (4, 1.9) to (5.4, 1.3) | (5.1, 4.5) to (4.6, 4.3) |
|
| Mondal et al. [104] | k-ω | 4–10 * | 1 | 15 | (5.3, n/a) to (16.3, n/a) | (13.4, n/a) to (37.7, n/a) | (3, 2.1) to (3.6, 2.2) | (3.6, 5) to (4, 5.3) |
|
| Hnaien et al. [105] | k-ω | 1 | 4 | 15 | n/a | n/a | n/a | n/a |
|
| Hnaien et al. [106] | k-ω | 4–10 * | 1 | 15 | (7.6, 2.4) to (9.6, 2.7) | (15.4, 2.4) to (24.3, 3) | (3, 2.1) to (3.6, 2.22) | (3.6, 5) to (4, 5.3) |
|
| Vishnuvardhanarao and Das [86] | k-ε | 1 | 0.25–4 * | 10–40 | n/a | n/a | n/a | n/a |
|
| Farooq and Das [85] | k-ε | 2–3 | 1 | 15 | n/a | n/a | n/a | n/a |
|
| Mondal et al. [88] | k-ε | 1 | 1 | 10–20 | n/a | n/a | n/a | n/a |
|
| Hnaien et al. [77] | k-ω | 4–19 * | 1 | 10–40 | n/a | n/a | n/a | n/a |
|
| Hnaien et al. [12] | k-ω | 8 * | 1 | 15–40 | n/a | n/a | n/a | n/a |
|
| Rathore and Verma [111] | k-ε | 4–12 * | 1 | 10–25 | n/a | n/a | n/a | n/a |
|
References
- Wang, X.-K.; Tan, S.K. Environmental fluid dynamics-jet flow. J. Hydrodyn. Ser. B 2010, 22, 1009–1014. [Google Scholar] [CrossRef]
- Kumar, A.; Das, M.K. Study of a turbulent dual jet consisting of a wall jet and an offset jet. J. Fluids Eng. 2011, 133, 101201. [Google Scholar] [CrossRef]
- Li, Z.-W.; Huai, W.-X.; Jie, H. Large eddy simulation of the interaction between wall jet and offset jet. J. Hydrodyn. Ser. B 2011, 23, 544–553. [Google Scholar] [CrossRef]
- Spall, R.E.; Anderson, E.A.; Allen, J. Momentum flux in plane, parallel jets. J. Fluids Eng. 2004, 126, 665–670. [Google Scholar] [CrossRef]
- Mondal, T.; Das, M.K.; Guha, A. Periodic vortex shedding phenomenon for various separation distances between two plane turbulent parallel jets. Int. J. Heat Mass Transf. 2016, 99, 576–588. [Google Scholar] [CrossRef]
- Liu, Q.; Baccarella, D.; McGann, B.; Lee, T.; Do, H. Experimental Investigation of Single Jet and Dual Jet Injection in a Supersonic Combustor. In Proceedings of the AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; AIAA: Reston, VA, USA, 2018; p. 1363. [Google Scholar] [CrossRef]
- Aslanidou, I.; Rosic, B.; Kanjirakkad, V.; Uchida, S. Leading edge shielding concept in gas turbines with can combustors. J. Turbomach. 2013, 135, 021019. [Google Scholar] [CrossRef]
- Rathore, S.K.; Pathak, A.; Majumdar, A.; Chaudhuri, S. Computational Investigation of Mixed Convection Heat Transfer from Laminar Offset Jet and Wall Jet. In Proceedings of the Fifth International Conference on Computational Methods for Thermal Problems, Bangalore, India, 9–11 July 2018; University of Cambridge: Cambridge, UK, 2018. [Google Scholar]
- Xu, L.; Sun, Z.; Ruan, Q.; Xi, L.; Gao, J.; Li, Y. Development Trend of Cooling Technology for Turbine Blades at Super-High Temperature of above 2000 K. Energies 2023, 16, 668. [Google Scholar] [CrossRef]
- Gao, N.; Ching, C.Y.; Ewing, D.; Naughton, J.W. Flow and heat transfer measurements in a planar offset attaching jet with a co-flowing wall jet. Int. J. Heat Mass Transf. 2014, 78, 721–731. [Google Scholar] [CrossRef]
- Vlachopoulos, J.; Polychronopoulos, N.D. Understanding Rheology and Technology of Polymer Extrusion; Polydynamics Inc.: Dundas, ON, Canada, 2019. [Google Scholar]
- Hnaien, N.; Marzouk, S.; Aissia, H.B.; Jay, J. Wall inclination effect in heat transfer characteristics of a combined wall and offset jet flow. Int. J. Heat Fluid Flow 2017, 64, 66–78. [Google Scholar] [CrossRef]
- Zhao, K.; Alimohammadi, S.; Okolo, P.N.; Kennedy, J.; Bennett, G.J. Aerodynamic noise reduction using dual-jet planar air curtains. J. Sound Vib. 2018, 432, 192–212. [Google Scholar] [CrossRef]
- Zhao, K.; Okolo, P.; Neri, E.; Chen, P.; Kennedy, J.; Bennett, G.J. Noise reduction technologies for aircraft landing gear—A bibliographic review. Prog. Aerosp. Sci. 2020, 112, 100589. [Google Scholar] [CrossRef]
- Ji, R.; Huang, X.; Zhao, X. Active Jet Noise Control of Turbofan Engine Based on Explicit Model Predictive Control. Appl. Sci. 2022, 12, 4874. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Yan, Y. A review of the state-of-the-art in electronic cooling. e-Prime-Adv. Electr. Eng. Electron. Energy 2021, 1, 100009. [Google Scholar] [CrossRef]
- Nada, S.A.; El-Zoheiry, R.; Elsharnoby, M.; Osman, O. Enhancing the thermal performance of different flow configuration minichannel heat sink using Al2O3 and CuO-water nanofluids for electronic cooling: An experimental assessment. Int. J. Therm. Sci. 2022, 181, 107767. [Google Scholar] [CrossRef]
- Sarkar, S.; Gupta, R.; Roy, T.; Ganguly, R.; Megaridis, C.M. Review of jet impingement cooling of electronic devices: Emerging role of surface engineering. Int. J. Heat Mass Transf. 2023, 206, 123888. [Google Scholar] [CrossRef]
- Sadeghian, M. Technologies for aircraft noise reduction: A review. J. Aeronaut. Aerosp. Eng. 2020, 206, 123888. Available online: https://hal.science/hal-03789480 (accessed on 29 May 2024).
- Namer, I.; Ötügen, M. Velocity measurements in a plane turbulent air jet at moderate Reynolds numbers. Exp. Fluids 1988, 6, 387–399. [Google Scholar] [CrossRef]
- Ungate, C.D.; Harleman, D.R.; Jirka, G.H. Stability and Mixing of Submerged Turbulent Jets at Low Reynolds Numbers; MIT-EL 75-014; MIT Energy Lab: Cambridge, MA, USA, 1975. [Google Scholar]
- Nienow, A.W.; Edwards, M.F.; Harnby, N. Mixing in the Process Industries; Butterworth-Heinemann: Oxford, UK, 1997. [Google Scholar]
- Miller, D.R.; Comings, E.W. Static pressure distribution in the free turbulent jet. J. Fluid Mech. 1957, 3, 1–16. [Google Scholar] [CrossRef]
- Wygnanski, I.; Fiedler, H. Some measurements in the self-preserving jet. J. Fluid Mech. 1969, 38, 577–612. [Google Scholar] [CrossRef]
- Westerweel, J.; Fukushima, C.; Pedersen, J.M.; Hunt, J.C. Momentum and scalar transport at the turbulent/non-turbulent interface of a jet. J. Fluid Mech. 2009, 631, 199–230. [Google Scholar] [CrossRef]
- Gutmark, E.; Wygnanski, I. The planar turbulent jet. J. Fluid Mech. 1976, 73, 465–495. [Google Scholar] [CrossRef]
- Ball, C.; Fellouah, H.; Pollard, A. The flow field in turbulent round free jets. Prog. Aerosp. Sci. 2012, 50, 1–26. [Google Scholar] [CrossRef]
- Fitzgerald, J.A.; Garimella, S.V. A study of the flow field of a confined and submerged impinging jet. Int. J. Heat Mass Transf. 1998, 41, 1025–1034. [Google Scholar] [CrossRef]
- Oshkai, P.; Djilali, N. Multi-component high aspect ratio turbulent jets issuing from non-planar nozzles. Int. J. Hydrogen Energy 2019, 44, 15262–15277. [Google Scholar] [CrossRef]
- Faghani, E.; Maddahian, R.; Faghani, P.; Farhanieh, B. Numerical investigation of turbulent free jet flows issuing from rectangular nozzles: The influence of small aspect ratio. Arch. Appl. Mech. 2010, 80, 727–745. [Google Scholar] [CrossRef]
- Alnahhal, M.; Panidis, T. The effect of sidewalls on rectangular jets. Exp. Therm. Fluid Sci. 2009, 33, 838–851. [Google Scholar] [CrossRef]
- Rajaratnam, N. Turbulent Jets; Elsevier: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Zhang, R.; He, X.; Doolen, G.; Chen, S. Surface tension effects on two-dimensional two-phase Kelvin–Helmholtz instabilities. Adv. Water Resour. 2001, 24, 461–478. [Google Scholar] [CrossRef]
- Rosenhead, L. The formation of vortices from a surface of discontinuity. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1931, 134, 170–192. [Google Scholar] [CrossRef]
- Melander, M.V.; Zabusky, N.J.; McWilliams, J.C. Symmetric vortex merger in two dimensions: Causes and conditions. J. Fluid Mech. 1988, 195, 303–340. [Google Scholar] [CrossRef]
- Winant, C.D.; Browand, F.K. Vortex pairing: The mechanism of turbulent mixing-layer growth at moderate Reynolds number. J. Fluid Mech. 1974, 63, 237–255. [Google Scholar] [CrossRef]
- Dahm, W.; Dimotakis, P. Measurements of entrainment and mixing in turbulent jets. AIAA J. 1987, 25, 1216–1223. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Agrawal, A.; Prasad, A. Properties of vortices in the self-similar turbulent jet. Exp. Fluids 2002, 33, 565–577. [Google Scholar] [CrossRef]
- Ghosal, S.; Rogers, M.M. A numerical study of self-similarity in a turbulent plane wake using large-eddy simulation. Phys. Fluids 1997, 9, 1729–1739. [Google Scholar] [CrossRef]
- Squire, H.B. The Round Laminar Jet. Q. J. Mech. Appl. Math. 1951, 4, 321–329. [Google Scholar] [CrossRef]
- Pearce, A.F. Critical Reynolds Number for Fully-Developed Turbulence in Circular Submerged Water Jets; Hydromechanics Research Department, National Mechanical Engineering Research Institute, Council for Scientific and Industrial Research: Accra, Ghana, 1966. [Google Scholar]
- Bieber, M.; Kneer, R.; Rohlfs, W. Self-similarity of heat transfer characteristics in laminar submerged and free-surface slot jet impingement. Int. J. Heat Mass Transf. 2017, 104, 1341–1352. [Google Scholar] [CrossRef]
- Schlichting, H. Laminar spread of a jet. Z. Angew. Math. Mech. 1933, 13, 260–263. [Google Scholar] [CrossRef]
- Mollendorf, J.C.; Gebhart, B. An experimental and numerical study of the viscous stability of a round laminar vertical jet with and without thermal buoyancy for symmetric and asymmetric disturbances. J. Fluid Mech. 1973, 61, 367–399. [Google Scholar] [CrossRef]
- Hiromasa, S.; Hara, S.; Inaoka, K. The velocity and thermal fields of two parallel plane jets using simultaneous PIV and two-color LIF measurements. Int. J. Heat Fluid Flow 2023, 103, 109192. [Google Scholar] [CrossRef]
- Lin, Y.; Sheu, M. Investigation of two plane paralleltiinven ilated jets. Exp. Fluids 1990, 10, 17–22. [Google Scholar] [CrossRef]
- Miller, D.R.; Comings, E.W. Force-momentum fields in a dual-jet flow. J. Fluid Mech. 1960, 7, 237–256. [Google Scholar] [CrossRef]
- Anderson, E.A.; Spall, R.E. Experimental and Numerical Investigation of Two-Dimensional Parallel Jets. J. Fluids Eng. 2001, 123, 401–406. [Google Scholar] [CrossRef]
- Zheng, X.; Jian, X.; Wei, J.; Wenzheng, D. Numerical and Experimental Investigation of Near-Field Mixing in Parallel Dual Round Jets. Int. J. Aerosp. Eng. 2016, 2016, 7935101. [Google Scholar] [CrossRef]
- Tanaka, E. The interference of two-dimensional parallel jets: 2nd report, experiments on the combined flow of dual jet. Bull. JSME 1974, 17, 920–927. [Google Scholar] [CrossRef]
- Fujisawa, N.; Nakamura, K.; Srinivas, K. Interaction of two parallel plane jets of different velocities. J. Vis. 2004, 7, 135–142. [Google Scholar] [CrossRef]
- Nouali, N.; Amina, M. Numerical Study of Mixed Convection of Buoyant Twin Jet. ASME J. Heat Mass Transf. 2024, 146, 031001. [Google Scholar] [CrossRef]
- Lytle, D.; Webb, B. Air jet impingement heat transfer at low nozzle-plate spacings. Int. J. Heat Mass Transf. 1994, 37, 1687–1697. [Google Scholar] [CrossRef]
- Snedeker, R.S. A study of free jet impingement. Part 1. Mean properties of free and impinging jets. J. Fluid Mech. 1971, 45, 281–319. [Google Scholar] [CrossRef]
- Jambunathan, K.; Lai, E.; Moss, M.; Button, B. A review of heat transfer data for single circular jet impingement. Int. J. Heat Fluid Flow 1992, 13, 106–115. [Google Scholar] [CrossRef]
- Eriksson, J. Experimental Studies of the Plane Turbulent Wall Jet. Doctoral Dissertation, Royal Institute of Technology, Stockholm, Sweden, 2003. [Google Scholar]
- Craft, T.; Launder, B. On the spreading mechanism of the three-dimensional turbulent wall jet. J. Fluid Mech. 2001, 435, 305–326. [Google Scholar] [CrossRef]
- Nizou, P. Heat and momentum transfer in a plane turbulent wall jet. ASME J. Heat Transf. 1981, 103, 138–140. [Google Scholar] [CrossRef]
- AbdulNour, R.; Willenborg, K.; McGrath, J.; Foss, J.; AbdulNour, B. Measurements of the convection heat transfer coefficient for a planar wall jet: Uniform temperature and uniform heat flux boundary conditions. Exp. Therm. Fluid Sci. 2000, 22, 123–131. [Google Scholar] [CrossRef]
- Pramanik, S.; Das, M.K. Computational study of a turbulent wall jet flow on an oblique surface. Int. J. Numer. Methods Heat Fluid Flow 2014, 24, 290–324. [Google Scholar] [CrossRef]
- Kaffel, A.; Moureh, J.; Harion, J.-L.; Russeil, S. Experimental investigation of a plane wall jet subjected to an external lateral flow. Exp. Fluids 2015, 56, 95. [Google Scholar] [CrossRef]
- Fu, C.; Uddin, M.; Curley, A. Insights derived from CFD studies on the evolution of planar wall jets. Eng. Appl. Comput. Fluid Mech. 2016, 10, 44–56. [Google Scholar] [CrossRef]
- Akfirat, J.C. Transfer of Heat from an Isothermal Flat Plate to a Two-Dimensional Wall Jet. In Proceedings of the International Heat Transfer Conference Digital Library, Chicago, IL, USA, 7–12 August 1966; Begel House Inc.: Danbury, CT, USA, 1966. [Google Scholar] [CrossRef]
- Mabuchi, I.; Kumada, M. Studies on heat transfer to turbulent jets with adjacent boundaries: 1st report, flow development and mass transfer in plane turbulent wall jet. Bull. JSME 1972, 15, 1236–1245. [Google Scholar] [CrossRef]
- Rajesh Kanna, P.; Das, M.K. Numerical simulation of two-dimensional laminar incompressible offset jet flows. Int. J. Numer. Methods Fluids 2005, 49, 439–464. [Google Scholar] [CrossRef]
- Nasr, A.; Lai, J.C.S. A turbulent plane offset jet with small offset ratio. Exp. Fluids 1998, 24, 47–57. [Google Scholar] [CrossRef]
- Rathore, S.K.; Das, M.K. A comparative study of heat transfer characteristics of wall-bounded jets using different turbulence models. Int. J. Therm. Sci. 2015, 89, 337–356. [Google Scholar] [CrossRef]
- Gu, R. Modeling Two-Dimensional Turbulent Offset Jets. J. Hydraul. Eng. 1996, 122, 617–624. [Google Scholar] [CrossRef]
- Kim, D.S.; Yoon, S.H.; Lee, D.H.; Kim, K.C. Flow and heat transfer measurements of a wall attaching offset jet. Int. J. Heat Mass Transf. 1996, 39, 2907–2913. [Google Scholar] [CrossRef]
- Vishnuvardhanarao, E.; Das, M.K. Computation of Mean Flow and Thermal Characteristics of Incompressible Turbulent Offset Jet Flows. Numer. Heat Transf. Part A Appl. 2007, 53, 843–869. [Google Scholar] [CrossRef]
- Song, H.B.; Yoon, S.H.; Lee, D.H. Flow and heat transfer characteristics of a two-dimensional oblique wall attaching offset jet. Int. J. Heat Mass Transf. 2000, 43, 2395–2404. [Google Scholar] [CrossRef]
- Wang, X.; Tan, S. Experimental investigation of the interaction between a plane wall jet and a parallel offset jet. Exp. Fluids 2007, 42, 551–562. [Google Scholar] [CrossRef]
- Nasr, A.; Lai, J.C.S. Comparison of flow characteristics in the near field of two parallel plane jets and an offset plane jet. Phys. Fluids 1997, 9, 2919–2931. [Google Scholar] [CrossRef]
- Kumar, A. Mean flow and thermal characteristics of a turbulent dual jet consisting of a plane wall jet and a parallel offset jet. Numer. Heat Transf. Part A Appl. 2015, 67, 1075–1096. [Google Scholar] [CrossRef]
- Kumar, A. Mean flow characteristics of a turbulent dual jet consisting of a plane wall jet and a parallel offset jet. Comput. Fluids 2015, 114, 48–65. [Google Scholar] [CrossRef]
- Hnaien, N.; Marzouk, S.; Ben Aissia, H.; Jay, J. CFD investigation on the offset ratio effect on thermal characteristics of a combined wall and offset jets flow. Heat Mass Transfer 2017, 53, 2531–2549. [Google Scholar] [CrossRef]
- Hnaien, N.; Marzouk, S.; Aissia, H.B.; Jay, J. Numerical investigation of velocity ratio effect in combined wall and offset jet flows. J. Hydrodyn. 2018, 30, 1105–1119. [Google Scholar] [CrossRef]
- Hnaien, N.; Marzouk, S.; Kolsi, L.; Al-Rashed, A.; Aissia, H.B.; Jay, J. CFD Investigation on the steady interaction between an offset jet and an oblique wall jet. J. Appl. Fluid Mech. 2018, 11, 885–894. [Google Scholar] [CrossRef]
- Hnaien, N.; Marzouk, S.; Kolsi, L.; Alsagri, A.S.; Ben Aissia, H.; Jay, J. Offset jet ejection angle effect in combined wall and offset jets flow: Numerical investigation and engineering correlations. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 479. [Google Scholar] [CrossRef]
- Singh, T.P.; Kumar, A.; Satapathy, A.K. Heat transfer and fluid flow characteristics of a turbulent dual jet impinging on a wavy surface. J. Therm. Sci. Eng. Appl. 2020, 12, 041017. [Google Scholar] [CrossRef]
- Singh, T.P.; Kumar, A.; Satapathy, A.K. Role of a sinusoidal wavy surface in enhancement of heat transfer using turbulent dual jet. J. Heat Transf. 2021, 143, 032002. [Google Scholar] [CrossRef]
- Zhao, L.; Sun, J. Numerical Investigation on a Dual-jet Consisting of a Plane Wall Jet and a Parallel Offset Jet at Low-Reynolds Number. Trans. Nanjing Univ. Aeronaut. Astronaut. 2018, 35, 778–788. [Google Scholar] [CrossRef]
- Assoudi, A.; Mahjoub Saïd, N.; Bournot, H.; Le Palec, G. Comparative study of flow characteristics of a single offset jet and a turbulent dual jet. Heat Mass Transf. 2019, 55, 1109–1131. [Google Scholar] [CrossRef]
- Farooq, S.; Das, M. Simulation of Thermal Characteristics of Turbulent Dual Jets. J. Appl. Mech. Eng. 2014, 3, 2. [Google Scholar] [CrossRef]
- Vishnuvardhanarao, E.; Das, M.K. Study of the heat transfer characteristics in turbulent combined wall and offset jet flows. Int. J. Therm. Sci. 2009, 48, 1949–1959. [Google Scholar] [CrossRef]
- Mondal, T.; Das, M.K.; Guha, A. Numerical investigation of steady and periodically unsteady flow for various separation distances between a wall jet and an offset jet. J. Fluids Struct. 2014, 50, 528–546. [Google Scholar] [CrossRef]
- Mondal, T.; Guha, A.; Kumar Das, M. Analysis of conjugate heat transfer for a combined turbulent wall jet and offset jet. J. Heat Transf. 2016, 138, 051701. [Google Scholar] [CrossRef]
- Murphy, P.J.; Alimohammadi, S.; O’Shaughnessy, S.M. Experimental Analysis of Heat Transfer to a Dual Jet Flow: Effect of Reynolds Number. In Proceedings of the 28th International Workshop on Thermal Investigations of ICs and Systems (THERMINIC), Dublin, Ireland, 28–30 September 2022; IEEE: New York, NY, USA; pp. 1–6. [Google Scholar] [CrossRef]
- Murphy, P.J.; Alimohammadi, S.; O’Shaughnessy, S.M. Experimental Investigation of Heat Transfer to a Dual Jet Flow with Varying Velocity Ratio. In Proceedings of the 22nd IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), Orlando, FL, USA, 30 May–2 June 2023; IEEE: New York, NY, USA; pp. 1–8. [Google Scholar] [CrossRef]
- Murphy, P.J.; Alimohammadi, S.; O’Shaughnessy, S.M. Experimental investigation of dual jet flow past a heated surface: Effect of Reynolds number. Int. J. Heat Mass Transf. 2024, 218, 124786. [Google Scholar] [CrossRef]
- Li, Z.; Huai, W.; Yang, Z. Interaction between wall jet and offset jet with different velocity and offset ratio. Procedia Eng. 2012, 28, 49–54. [Google Scholar] [CrossRef]
- Pelfrey, J.; Liburdy, J. Mean flow characteristics of a turbulent offset jet. J. Fluids Eng. 1986, 108, 82–88. [Google Scholar] [CrossRef]
- Tanaka, E. The interference of two-dimensional parallel jets: 1st report, experiments on dual jet. Bull. JSME 1970, 13, 272–280. [Google Scholar] [CrossRef]
- Singh, T.P.; Dewan, A. Heat transfer characteristics of a periodically transient flow for turbulent wall-bounded dual jet. Eng. Sci. Technol. Int. J. 2022, 36, 101146. [Google Scholar] [CrossRef]
- Kumar, M.; Biswal, R.; Gupta, A.K.; Behera, S.K.; Sahoo, R.K. Effect of Wall Heat Flux on Fluid Flow and Thermal Characteristics of a Turbulent Dual Jet. Math. Model. Eng. Probl. 2020, 7, 127–134. [Google Scholar] [CrossRef]
- Mondal, T.; Guha, A.; Das, M.K. Computational study of periodically unsteady interaction between a wall jet and an offset jet for various velocity ratios. Comput. Fluids 2015, 123, 146–161. [Google Scholar] [CrossRef]
- Mondal, T.; Guha, A.; Das, M.K. Effect of bottom wall proximity on the unsteady flow structures of a combined turbulent wall jet and offset jet flow. Eur. J. Mech. B/Fluids 2016, 57, 101–114. [Google Scholar] [CrossRef]
- Mondal, T.; Das, M.K.; Guha, A. Transition of a steady to a periodically unsteady flow for various jet widths of a combined wall jet and offset jet. J. Fluids Eng. 2016, 138, 070907. [Google Scholar] [CrossRef]
- Singh, T.P.; Dewan, A. Transient flow and thermal transport characteristics of wall-bounded turbulent dual jet with heated undulated wall. Int. J. Therm. Sci. 2022, 182, 107800. [Google Scholar] [CrossRef]
- Singh, T.P.; Kumar, A.; Satapathy, A.K. Effect of wavy wall surface on flow structure and thermal characteristics of a turbulent dual jet comprising of a wall jet and an offset jet. Proc. Inst. Mech. Eng. Part A J. Power Energy 2021, 235, 524–545. [Google Scholar] [CrossRef]
- Singh, T.P.; Kumar, A.; Satapathy, A.K. Fluid flow analysis of a turbulent offset jet impinging on a wavy wall surface. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 544–563. [Google Scholar] [CrossRef]
- Singh, T.P.; Dewan, A. Performance assessment of different turbulence models for a dual jet flowing over a heated sinusoidal wavy surface. J. Therm. Sci. Eng. Appl. 2022, 14, 051016. [Google Scholar] [CrossRef]
- Mondal, T.; Hnaien, N.; Ajmi, M.; Ghachem, K.; Kolsi, L. CFD investigation of thermal characteristics for a dual jet with a parallel co-flow. ACS Omega 2022, 7, 27864–27875. [Google Scholar] [CrossRef] [PubMed]
- Hnaien, N.; Mondal, T.; Ajmi, M.; Aich, W.; Ayadi, B.; Kolsi, L. A CFD modelling on effects of ejection angle of a co-flow on the thermal characteristics for a combined wall and offset jet flow. Alex. Eng. J. 2023, 68, 83–91. [Google Scholar] [CrossRef]
- Hnaien, N.; Mondal, T.; Ajmi, M.; Marzouk, S.; Aich, W.; Kolsi, L. Numerical study on mean flow characteristics for a combined turbulent wall and offset jets with a parallel co-flow. J. Taibah Univ. Sci. 2022, 16, 732–748. [Google Scholar] [CrossRef]
- Mondal, T.; O’Shaughnessy, S. Numerical investigation of conjugate heat transfer to a turbulent dual offset jet. Int. J. Therm. Sci. 2022, 180, 107716. [Google Scholar] [CrossRef]
- Mondal, T.; Srivastava, N.; O’Shaughnessy, S.; Pramanik, S. Comparison of the mean flow and turbulence characteristics of a single offset jet and a dual offset jet. Eur. J. Mech. B/Fluids 2023, 98, 161–179. [Google Scholar] [CrossRef]
- Singh, T.P.; Dewan, A. Computational study of thermal and fluid mixing behaviour of a dual jet flow using LES approach. Int. Commun. Heat Mass Transf. 2024, 154, 107436. [Google Scholar] [CrossRef]
- Singh, T.P.; Dewan, A. Improvement in cooling using a sinusoidal wavy surface for a turbulent dual jet: A computational study. J. Therm. Anal. Calorim. 2023, 148, 2935–2947. [Google Scholar] [CrossRef]
- Rathore, S.S.; Verma, S.K. Computational investigation on the thermal and flow characteristics of a turbulent dual jet impinging on a heated moving surface. J. Heat Transf. 2022, 144, 092301. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murphy, P.J.; Alimohammadi, S.; O’Shaughnessy, S.M. Two-Dimensional Dual Jets—A Comprehensive Review of Experimental and Numerical Analyses. Energies 2024, 17, 4487. https://doi.org/10.3390/en17174487
Murphy PJ, Alimohammadi S, O’Shaughnessy SM. Two-Dimensional Dual Jets—A Comprehensive Review of Experimental and Numerical Analyses. Energies. 2024; 17(17):4487. https://doi.org/10.3390/en17174487
Chicago/Turabian StyleMurphy, Paula J., Sajad Alimohammadi, and Séamus M. O’Shaughnessy. 2024. "Two-Dimensional Dual Jets—A Comprehensive Review of Experimental and Numerical Analyses" Energies 17, no. 17: 4487. https://doi.org/10.3390/en17174487
APA StyleMurphy, P. J., Alimohammadi, S., & O’Shaughnessy, S. M. (2024). Two-Dimensional Dual Jets—A Comprehensive Review of Experimental and Numerical Analyses. Energies, 17(17), 4487. https://doi.org/10.3390/en17174487






