A Novel VSG with Adaptive Virtual Inertia and Adaptive Damping Coefficient to Improve Transient Frequency Response of Microgrids
Abstract
:1. Introduction
- Adapting both the VSG’s virtual inertia and damping coefficient may contribute positively to microgrids’ transient response, and only a few papers employ both adaptations in the VSG control;
- Despite the adaptations, maintaining a constant steady-state frequency droop is a required feature to preserve the VSG’s contribution in the primary frequency control;
- Relying on the grid’s frequency measurements, a phase-locked loop (PLL), for example, is an undesired feature, as the PLL itself may lead to instabilities [2];
- The control’s performance must be evaluated under off-nominal steady-state frequency operation (e.g., for islanded microgrid operation) once the adaptive strategies operate using the VSG’s frequency signal, and most of them were originally designed for operation around nominal frequency;
- The presence of SGs in microgrids is desirable for frequency regulation. These machines have fixed inertia and damping properties, so the VSG’s inertia must be carefully tuned to avoid, for example, undamped oscillatory responses in the SGs.
- The proposal of a new VSG control strategy with adaptive virtual inertia and adaptive damping coefficient (AID-VSG). The proposed AID-VSG differs from existing adaptive inertia and damping strategies as it maintains the desired steady-state frequency droop (unlike [30,31,33]) and does not rely on frequency measurements (unlike [32]) or rule-based controllers (unlike [29]);
- The validation of the proposed AID-VSG by comparison with three existing VSG control strategies (optimally tuned for off-nominal frequency operation), for a large set of initial conditions.
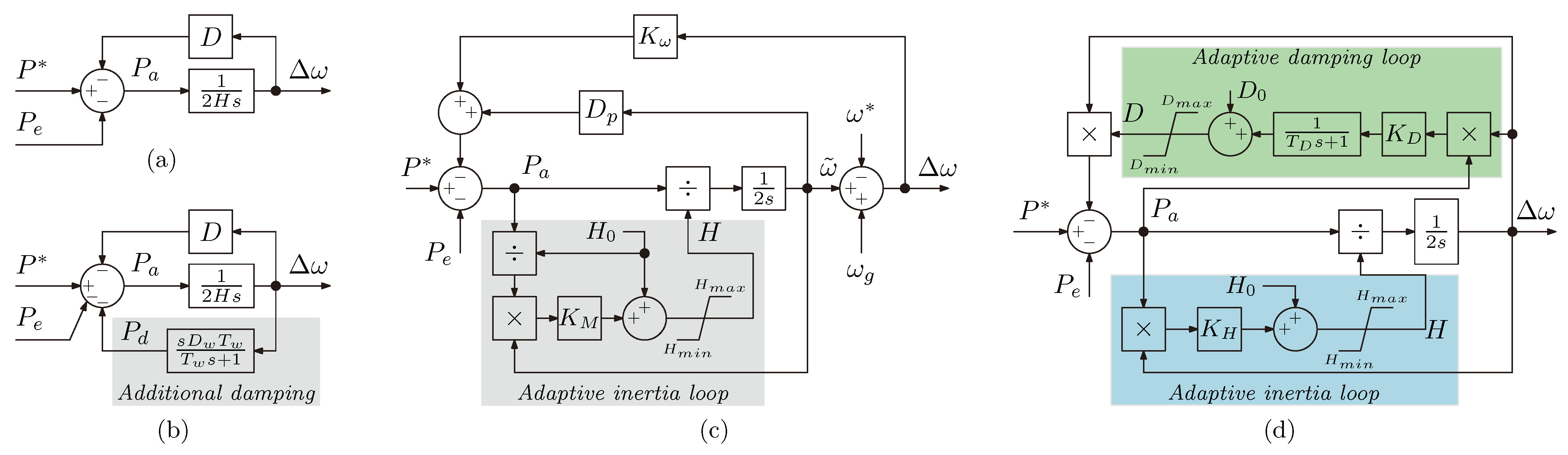
2. VSG Control Strategies for Power Converters
2.1. VSG with Fixed Parameters
2.2. VSG with Fixed Parameters and Additional Damping Loop
2.3. VSG with Adaptive Virtual Inertia
3. Proposed Adaptive Virtual Inertia and Adaptive Damping VSG Control
Steady-State Performance
Small-Signal Stability Assessment
4. Case Study
4.1. Microgrid’s Description
4.2. Microgrid’s Islanding Simulations with the Existing VSG Techniques
4.2.1. Limitations of the Existing VSG Techniques on Altering Transient Frequency Response
- To provide additional inertial support by reducing the frequency slope, the FP-VSG demands higher values of virtual inertia, which introduces a more oscillatory and possibly slower response;
- The AD-VSG allows for an improvement in the frequency nadir; however, the additional loop is less effective in reducing the frequency slope without increasing the settling time, as this loop was designed to increase damping, and no adaptive inertia was added;
- The AI-VSG provides transient additional inertial support but slightly changes the transient response time, since one of AI-VSG’s main goals was to improve transient stability instead of acting on the settling time.
4.3. Microgrid’s Islanding Simulations with the Proposed AID-VSG
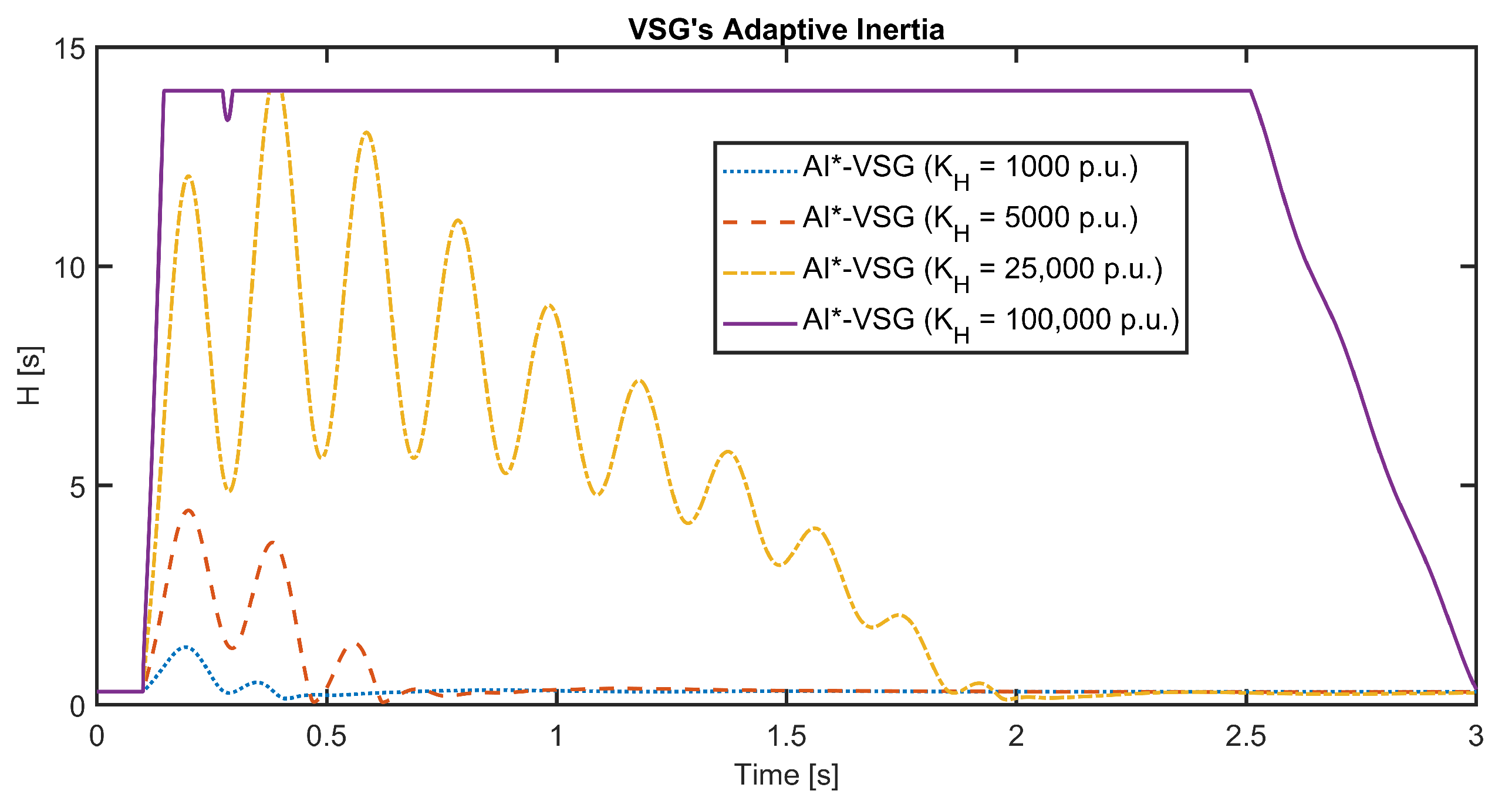
4.3.1. AI*-VSG
4.3.2. AID-VSG with Fixed
4.3.3. AID-VSG with Fixed
4.3.4. Effects of Both Adaptive Loops on the Frequency at the Microgrid’s PCC
5. Optimal Tuning of the VSG’s Parameters
Simulation Results
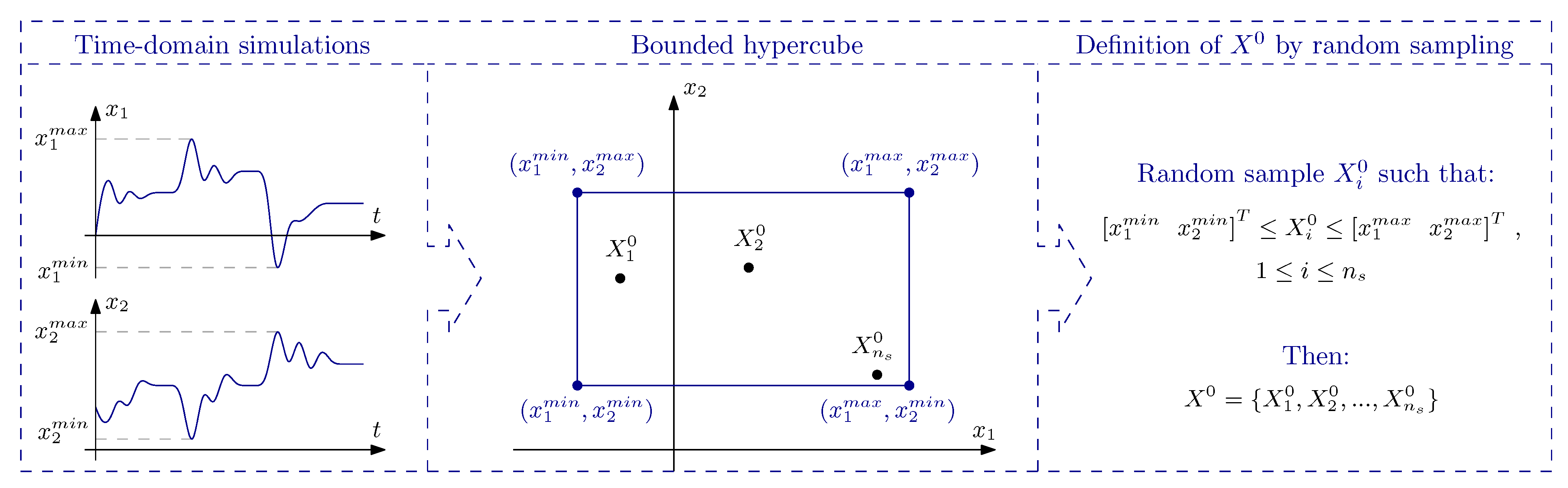
6. Performance Assessment
Definition of
- A three-phase short circuit with a duration of 150 ms at the high voltage side of TR1, followed by the opening of SW1 (i.e., microgrid islanding);
- A step of on the microgrid’s load;
- A step of +1.5 MW on the VSG’s reference power ();
- A step of MW on the VSG’s reference power ();
- A step of +1.5 MW on the VSG’s reference power ().
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AD-VSG | Virtual Synchronous Generator with Additional Damping |
| AI-VSG | Virtual Synchronous Generator with Adaptive Inertia |
| AID-VSG | Virtual Synchronous Generator with Adaptive Inertia and Adaptive Damping |
| AVR | Automatic Voltage Regulator |
| BESS | Battery Energy Storage System |
| DG | Distributed Generator |
| ENTSO-E | European Network of Transmission System Operators for Electricity |
| ESS | Energy Storage System |
| FP-VSG | Virtual Synchronous Generator with fixed parameters |
| MV | Medium Voltage |
| PCC | Point of Common Coupling |
| PLL | Phase-Locked Loop |
| PSO | Particle Swarm Optimization |
| SG | Synchronous Generator |
| VSG | Virtual Synchronous Generator |
Appendix A
| Synchronous Generator Parameters | |||||
| H | 0.3 s | D | 0 pu | 0.52% | |
| 280% | 160% | 25.5% | |||
| 25.5% | 11.7% | 3.7 s | |||
| 0.34 s | 0.018 s | 0.018 s | |||
| AVR and PF Controller Parameters | |||||
| 35 pu | 1.0 pu | 0.01 pu | |||
| 0.1 s | 1.3 s | 0.6 s | |||
| 0.001 s | 99 pu | pu | |||
| 0.001 s | 1 pu | 0 pu | |||
| 0.05 pu | 0.5 pu | 0.25 pu | |||
References
- Hu, J.; Shan, Y.; Cheng, K.W.; Islam, S. Overview of Power Converter Control in Microgrids—Challenges, Advances, and Future Trends. IEEE Trans. Power Electron. 2022, 37, 9907–9922. [Google Scholar] [CrossRef]
- Farrokhabadi, M.; Cañizares, C.A.; Simpson-Porco, J.W.; Nasr, E.; Fan, L.; Mendoza-Araya, P.A.; Tonkoski, R.; Tamrakar, U.; Hatziargyriou, N.; Lagos, D.; et al. Microgrid Stability Definitions, Analysis, and Examples. IEEE Trans. Power Syst. 2020, 35, 13–29. [Google Scholar] [CrossRef]
- Suvorov, A.; Askarov, A.; Kievets, A.; Rudnik, V. A comprehensive assessment of the state-of-the-art virtual synchronous generator models. Electr. Power Syst. Res. 2022, 209, 108054. [Google Scholar] [CrossRef]
- Shadoul, M.; Ahshan, R.; AlAbri, R.S.; Al-Badi, A.; Albadi, M.; Jamil, M. A Comprehensive Review on a Virtual-Synchronous Generator: Topologies, Control Orders and Techniques, Energy Storages, and Applications. Energies 2022, 15, 8406. [Google Scholar] [CrossRef]
- Bevrani, H.; Golpîra, H.; Messina, A.R.; Hatziargyriou, N.; Milano, F.; Ise, T. Power system frequency control: An updated review of current solutions and new challenges. Electr. Power Syst. Res. 2021, 194, 107114. [Google Scholar] [CrossRef]
- ENTSO-E. Stability Management in Power Electronics Dominated Systems: A Prerequisite to the Success of the Energy Transition; Technical Report; ENTSO-E: Brussels, Belgium, 2022. [Google Scholar]
- ESO. National Energy System Operator—Interim Report into the Low Frequency Demand Disconnection (LFDD) Following Generator Trips and Frequency Excursion on 9 Aug 2019; Technical Report, nationalgridESO; ESO: Warwick, UK, 2019. [Google Scholar]
- Lu, S.; Zhu, Y.; Dong, L.; Na, G.; Hao, Y.; Zhang, G.; Zhang, W.; Cheng, S.; Yang, J.; Sui, Y. Small-Signal Stability Research of Grid-Connected Virtual Synchronous Generators. Energies 2022, 15, 7158. [Google Scholar] [CrossRef]
- Wang, X.; Lv, Z.; Wang, R.; Hui, X. Optimization method and stability analysis of MMC grid-connect control system based on virtual synchronous generator technology. Electr. Power Syst. Res. 2020, 182, 106209. [Google Scholar] [CrossRef]
- Rahman, K.; Hashimoto, J.; Orihara, D.; Ustun, T.S.; Otani, K.; Kikusato, H.; Kodama, Y. Reviewing Control Paradigms and Emerging Trends of Grid-Forming Inverters—A Comparative Study. Energies 2024, 17, 2400. [Google Scholar] [CrossRef]
- Cheema, K.M.; Chaudhary, N.I.; Tahir, M.F.; Mehmood, K.; Mudassir, M.; Kamran, M.; Milyani, A.H.; Elbarbary, Z.S. Virtual synchronous generator: Modifications, stability assessment and future applications. Energy Rep. 2022, 8, 1704–1717. [Google Scholar] [CrossRef]
- Sang, W.; Guo, W.; Dai, S.; Tian, C.; Yu, S.; Teng, Y. Virtual Synchronous Generator, a Comprehensive Overview. Energies 2022, 15, 6148. [Google Scholar] [CrossRef]
- Gao, B.; Xia, C.; Chen, N.; Cheema, K.M.; Yang, L.; Li, C. Virtual Synchronous Generator Based Auxiliary Damping Control Design for the Power System with Renewable Generation. Energies 2017, 10, 1146. [Google Scholar] [CrossRef]
- Shuai, Z.; Huang, W.; Shen, Z.J.; Luo, A.; Tian, Z. Active Power Oscillation and Suppression Techniques Between Two Parallel Synchronverters During Load Fluctuations. IEEE Trans. Power Electron. 2020, 35, 4127–4142. [Google Scholar] [CrossRef]
- Wang, S.; Xie, Y. Virtual Synchronous Generator (VSG) Control Strategy Based on Improved Damping and Angular Frequency Deviation Feedforward. Energies 2023, 16, 5635. [Google Scholar] [CrossRef]
- Shi, R.; Lan, C.; Huang, J.; Ju, C. Analysis and Optimization Strategy of Active Power Dynamic Response for VSG under a Weak Grid. Energies 2023, 16, 4593. [Google Scholar] [CrossRef]
- Shi, R.; Lan, C.; Dong, Z.; Yang, G. An Active Power Dynamic Oscillation Damping Method for the Grid-Forming Virtual Synchronous Generator Based on Energy Reshaping Mechanism. Energies 2023, 16, 7723. [Google Scholar] [CrossRef]
- Alipoor, J.; Miura, Y.; Ise, T. Power System Stabilization Using Virtual Synchronous Generator With Alternating Moment of Inertia. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 451–458. [Google Scholar] [CrossRef]
- Meng, J.; Wang, Y.; Fu, C.; Wang, H. Adaptive virtual inertia control of distributed generator for dynamic frequency support in microgrid. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Li, J.; Wen, B.; Wang, H. Adaptive Virtual Inertia Control Strategy of VSG for Micro-Grid Based on Improved Bang-Bang Control Strategy. IEEE Access 2019, 7, 39509–39514. [Google Scholar] [CrossRef]
- Hou, X.; Sun, Y.; Zhang, X.; Lu, J.; Wang, P.; Guerrero, J.M. Improvement of Frequency Regulation in VSG-Based AC Microgrid Via Adaptive Virtual Inertia. IEEE Trans. Power Electron. 2020, 35, 1589–1602. [Google Scholar] [CrossRef]
- Fu, S.; Sun, Y.; Liu, Z.; Hou, X.; Han, H.; Su, M. Power oscillation suppression in multi-VSG grid with adaptive virtual inertia. Int. J. Electr. Power Energy Syst. 2022, 135, 107472. [Google Scholar] [CrossRef]
- Yang, X.; Li, H.; Jia, W.; Liu, Z.; Pan, Y.; Qian, F. Adaptive Virtual Synchronous Generator Based on Model Predictive Control with Improved Frequency Stability. Energies 2022, 15, 8385. [Google Scholar] [CrossRef]
- Perez, F.; Damm, G.; Verrelli, C.M.; Ribeiro, P.F. Adaptive Virtual Inertia Control for Stable Microgrid Operation Including Ancillary Services Support. IEEE Trans. Control Syst. Technol. 2023, 31, 1552–1564. [Google Scholar] [CrossRef]
- Liu, A.; Liu, J.; Wu, Q. Coupling stability analysis of synchronous generator and virtual synchronous generator in parallel under large disturbance. Electr. Power Syst. Res. 2023, 224, 109679. [Google Scholar] [CrossRef]
- Liu, H.; Yang, B.; Xu, S.; Du, M.; Lu, S. Universal Virtual Synchronous Generator Based on Extended Virtual Inertia to Enhance Power and Frequency Response. Energies 2023, 16, 2983. [Google Scholar] [CrossRef]
- Sheir, A.; Sood, V.K. Enhanced Virtual Inertia Controller for Microgrid Applications. Energies 2023, 16, 7304. [Google Scholar] [CrossRef]
- Zheng, T.; Chen, L.; Wang, R.; Li, C.; Mei, S. Adaptive damping control strategy of virtual synchronous generator for frequency oscillation suppression. In Proceedings of the 12th IET International Conference on AC and DC Power Transmission (ACDC 2016), Beijing, China, 28–29 May 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Li, D.; Zhu, Q.; Lin, S.; Bian, X.Y. A Self-Adaptive Inertia and Damping Combination Control of VSG to Support Frequency Stability. IEEE Trans. Energy Convers. 2017, 32, 397–398. [Google Scholar] [CrossRef]
- Wan, X.; Gan, Y.; Zhang, F.; Zheng, F. Research on Control Strategy of Virtual Synchronous Generator Based on Self-Adaptive Inertia and Damping. In Proceedings of the 2020 4th International Conference on HVDC (HVDC), Xi’an, China, 6–9 November 2020; pp. 1006–1012. [Google Scholar] [CrossRef]
- Shi, Q.; Du, C.; Sun, Y.; Cai, W.; Wang, A.; Chui, D. An Improved Adaptive Inertia and Damping Combination Control of Virtual Synchronous Generator. In Proceedings of the IECON 2021—47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Alghamdi, B.; Cañizares, C. Frequency and voltage coordinated control of a grid of AC/DC microgrids. Appl. Energy 2022, 310, 118427. [Google Scholar] [CrossRef]
- Ren, B.; Li, Q.; Fan, Z.; Sun, Y. Adaptive Control of a Virtual Synchronous Generator with Multiparameter Coordination. Energies 2023, 16, 4789. [Google Scholar] [CrossRef]
- Shen, C.; Shuai, Z.; Shen, Y.; Peng, Y.; Liu, X.; Li, Z.; Shen, Z.J. Transient Stability and Current Injection Design of Paralleled Current-Controlled VSCs and Virtual Synchronous Generators. IEEE Trans. Smart Grid 2021, 12, 1118–1134. [Google Scholar] [CrossRef]
- Li, Y.; Deng, F.; Qi, R.; Lin, H. Adaptive virtual impedance regulation strategy for reactive and harmonic power sharing among paralleled virtual synchronous generators. Int. J. Electr. Power Energy Syst. 2022, 140, 108059. [Google Scholar] [CrossRef]
- Teodorescu, R.; Liserre, M.; Rodríguez, P. Grid Converters for Photovoltaic and Wind Power Systems; John Wiley & Sons, Ltd.: Chichester, UK, 2011. [Google Scholar]
- Machowski, J.; Bialek, J.W.; Bumby, J.R. Power System Dynamics: Stability and Control; John Wiley & Sons, Ltd.: Chichester, UK, 2008. [Google Scholar]
- Farrokhabadi, M. Primary and Secondary Frequency Control Techniques for Isolated Microgrids. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2017. [Google Scholar]
- IEEE Std 421.5-2016 (Revision of IEEE Std 421.5-2005); IEEE Recommended Practice for Excitation System Models for Power System Stability Studies. IEEE: Piscataway, NJ, USA, 2016; pp. 1–207. [CrossRef]
- Parvizimosaed, M. Frequency and Voltage Control of Islanded Microgrids. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2020. [Google Scholar]
- Rahman, F.S.; Kerdphol, T.; Watanabe, M.; Mitani, Y. Optimization of virtual inertia considering system frequency protection scheme. Electr. Power Syst. Res. 2019, 170, 294–302. [Google Scholar] [CrossRef]
- Pournazarian, B.; Sangrody, R.; Lehtonen, M.; Gharehpetian, G.B.; Pouresmaeil, E. Simultaneous Optimization of Virtual Synchronous Generators Parameters and Virtual Impedances in Islanded Microgrids. IEEE Trans. Smart Grid 2022, 13, 4202–4217. [Google Scholar] [CrossRef]
- Mohamed, M.M.; El Zoghby, H.M.; Sharaf, S.M.; Mosa, M.A. Optimal virtual synchronous generator control of battery/supercapacitor hybrid energy storage system for frequency response enhancement of photovoltaic/diesel microgrid. J. Energy Storage 2022, 51, 104317. [Google Scholar] [CrossRef]












| Reference | Considers Adaptive Inertia | Considers Adaptive or Additional Damping | Dispenses Frequency Measurements | Considers Constant Droop Gain at Steady-State | Considers Off-Nominal Frequency | Includes Fixed-Inertia Machine |
|---|---|---|---|---|---|---|
| [21] | ✓ | ✗ | ✓ | ✓ | ✓ | ✗ |
| [18,25] | ✓ | ✗ | ✓ | ✓ | ✗ | ✓ |
| [20,23,26,27] | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ |
| [22] | ✓ | ✗ | ✗ | ✓ | ✓ | ✗ |
| [19,24] | ✓ | ✗ | ✗ | ✓ | ✗ | ✓ |
| [13] | ✗ | ✓ | ✗ | ✓ | ✗ | ✓ |
| [14,15,17] | ✗ | ✓ | ✓ | ✓ | ✓ | ✗ |
| [16,28] | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ |
| [32] | ✓ | ✓ | ✗ | ✓ | ✓ | ✓ |
| [33] | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ |
| [30,31] | ✓ | ✓ | ✓ | ✗ | ✓ | ✗ |
| [29] | ✓ | ✓ | ✓ | ✓ 1 | ✗ | ✗ |
| Proposed paper | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Transf. | Voltage | Rated Power | Impedance 1 |
|---|---|---|---|
| TR1 | 115/12.47 kV | 12 MVA | 0.08 + j9.97% |
| TR2 | 12.47/0.48 kV | 6 MVA | 3.334 + 5.773% |
| FP-VSG | AD-VSG | AI-VSG | ||||||
|---|---|---|---|---|---|---|---|---|
| 0.3 s | 59.20 Hz | 2.97 s | 5 p.u. | 59.36 Hz | 3.00 s | p.u. | 59.30 Hz | 2.97 s |
| 1.5 s | 59.43 Hz | 3.04 s | 10 p.u. | 59.48 Hz | 3.01 s | p.u. | 59.40 Hz | 2.96 s |
| 14 s | 59.56 Hz | 2.42 s | 20 p.u. | 59.55 Hz | 2.93 s | p.u. | 59.47 Hz | 2.94 s |
| 30 s | 59.56 Hz | 6.75 s | 50 p.u. | 59.56 Hz | 4.72 s | p.u. | 59.49 Hz | 2.97 s |
| AI*-VSG () | AID-VSG ( p.u.) | AID-VSG ( p.u.) | ||||||
|---|---|---|---|---|---|---|---|---|
| p.u. | 59.36 Hz | 2.95 s | 0 p.u. | 59.48 Hz | 2.92 s | 0 p.u. | 59.53 Hz | 3.00 s |
| p.u. | 59.53 Hz | 2.89 s | p.u. | 59.54 Hz | 2.88 s | p.u. | 59.56 Hz | 2.11 s |
| p.u. | 59.52 Hz | 2.69 s | p.u | 59.55 Hz | 2.72 s | p.u. | 59.56 Hz | 2.25 s |
| p.u. | 59.55 Hz | 4.16 s | p.u | 59.56 Hz | 2.11 s | p.u. | 59.56 Hz | 2.40 s |
| PSO Parameter | Setting |
|---|---|
| Individual learning rate | 1.49 |
| Global learning rate | 1.49 |
| Inertia weight | Adaptive from 0.1 to 1.1 |
| Number of particles | 100 |
| Number of maximum iterations | 100 |
| VSG Strategy | Set of Tuned Parameters | ||
|---|---|---|---|
| VSG-REF | - | 59.20 Hz | 2.97 s |
| FP-VSG | 59.55 Hz | 2.36 s | |
| AD-VSG | 59.55 Hz | 1.76 s | |
| AI-VSG | 59.49 Hz | 2.93 s | |
| AI*-VSG | 59.55 Hz | 2.42 s | |
| AID-VSG | 59.55 Hz | 1.71 s |
| VSG Strategy | Percentile of Occurrences |
|---|---|
| VSG-REF | 0.84% |
| FP-VSG | 25.47% |
| AD-VSG | 0.57% |
| AI-VSG | 1.85% |
| AI*-VSG | 10.18% |
| AID-VSG | 0.51% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gurski, E.; Kuiava, R.; Perez, F.; Benedito, R.A.S.; Damm, G. A Novel VSG with Adaptive Virtual Inertia and Adaptive Damping Coefficient to Improve Transient Frequency Response of Microgrids. Energies 2024, 17, 4370. https://doi.org/10.3390/en17174370
Gurski E, Kuiava R, Perez F, Benedito RAS, Damm G. A Novel VSG with Adaptive Virtual Inertia and Adaptive Damping Coefficient to Improve Transient Frequency Response of Microgrids. Energies. 2024; 17(17):4370. https://doi.org/10.3390/en17174370
Chicago/Turabian StyleGurski, Erico, Roman Kuiava, Filipe Perez, Raphael A. S. Benedito, and Gilney Damm. 2024. "A Novel VSG with Adaptive Virtual Inertia and Adaptive Damping Coefficient to Improve Transient Frequency Response of Microgrids" Energies 17, no. 17: 4370. https://doi.org/10.3390/en17174370
APA StyleGurski, E., Kuiava, R., Perez, F., Benedito, R. A. S., & Damm, G. (2024). A Novel VSG with Adaptive Virtual Inertia and Adaptive Damping Coefficient to Improve Transient Frequency Response of Microgrids. Energies, 17(17), 4370. https://doi.org/10.3390/en17174370







