The Impact Time Series Selected Characteristics on the Fuel Demand Forecasting Effectiveness Based on Autoregressive Models and Markov Chains
Abstract
1. Introduction
2. Brief Literature Review on Demand Forecasting Methods
3. Fuel Demand Prediction Based on ARIMA and Markov Chains Models
3.1. Basics of Forecasting with Markov Chains
3.2. Basics of Forecasting with SARIMA/ARIMA Models
- Autoregressive models (AR);
- Moving average models (MA);
- Mixed autoregressive and moving average models (ARMA).
- —the value of the variable, respectively, at the time ;
- —model parameters;
- —value of random component at the period ;
- —order lag.
- —residuals of the model, respectively, at the period ;
- —model parameters;
- —order lag.
- is the differentiated value of the time series at time , obtained after taking differences for the general and differences for the seasonal component;
- , ,… are the parameters of the autoregressive model;
- , ,… are the parameters of the moving average model;
- , ,… are the parameters of the seasonal autoregressive model;
- , ,… are the parameters of the seasonal moving average model.
4. Assumptions and Research Methodology Description
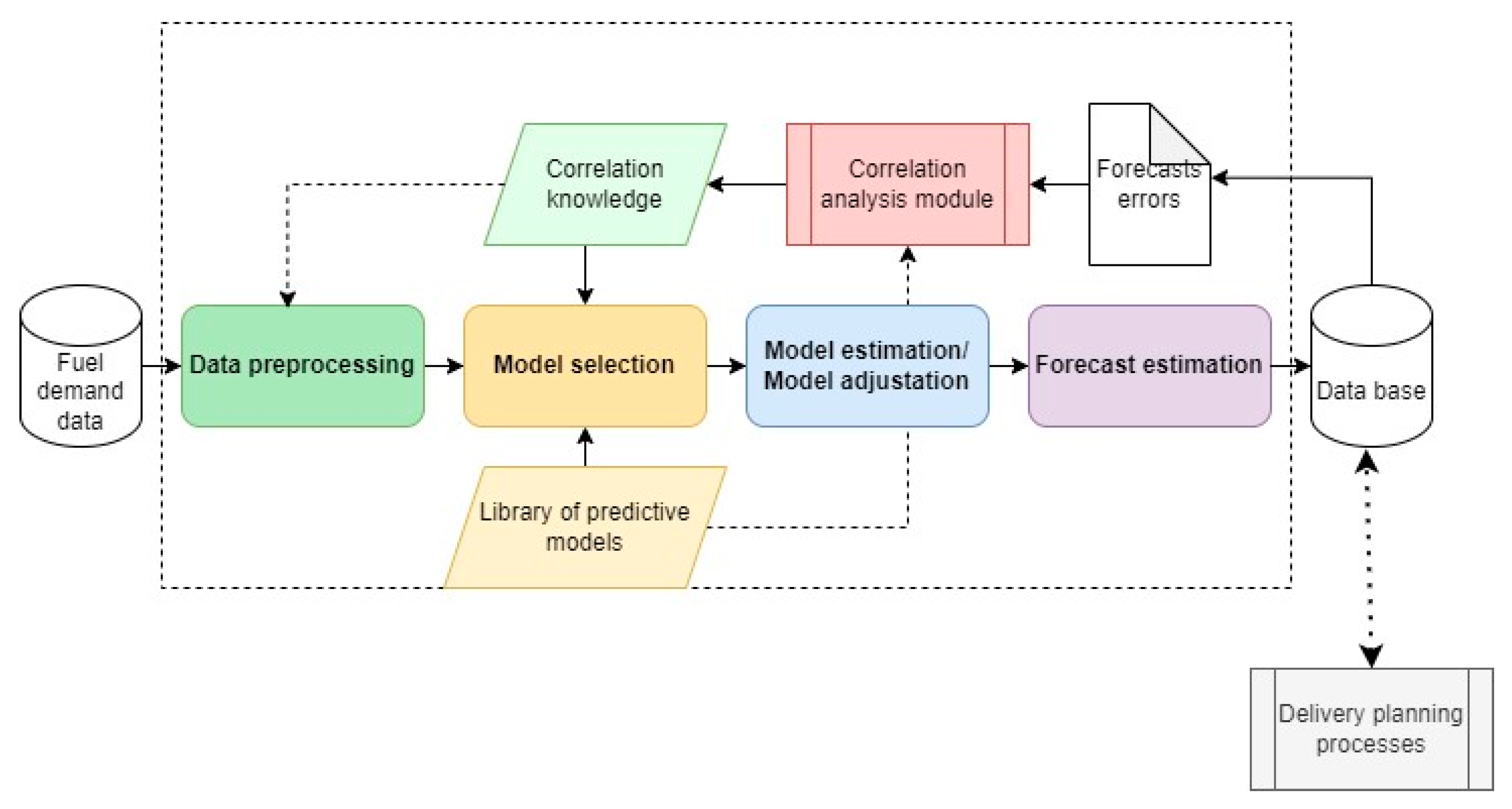
4.1. Methodology Framework
4.2. Data
4.3. Assumptions for Forecasting Models Development
4.3.1. ARIMA/SARIMA Models
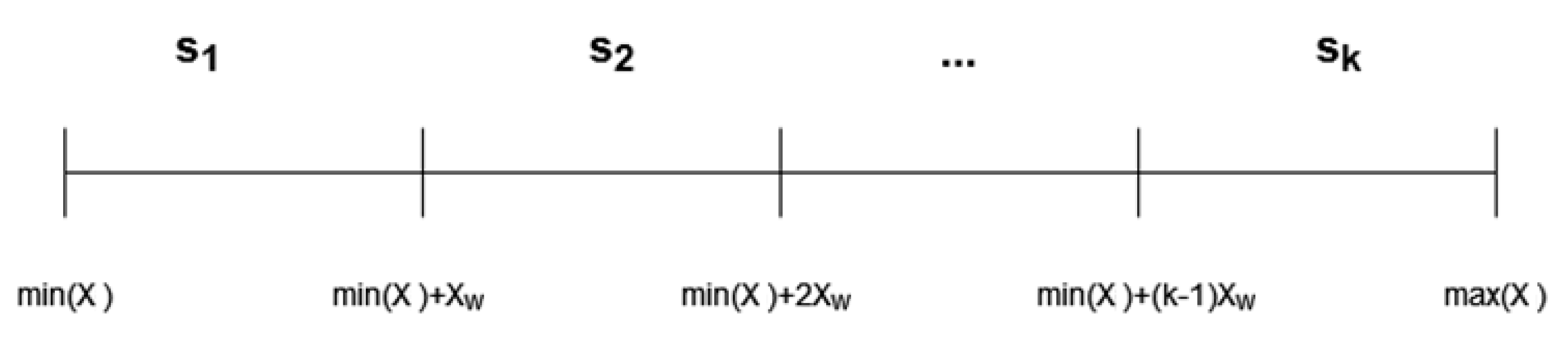
4.3.2. Markov Chain Models
- , —respectively, the maximum and minimum value of the time series ;
- —the number of observations in the time series .
- —probability value for the forecasted state of the time series;
- —the midpoint of the demand interval assigned to the -th state in the time series.
5. Numerical Experiment Results
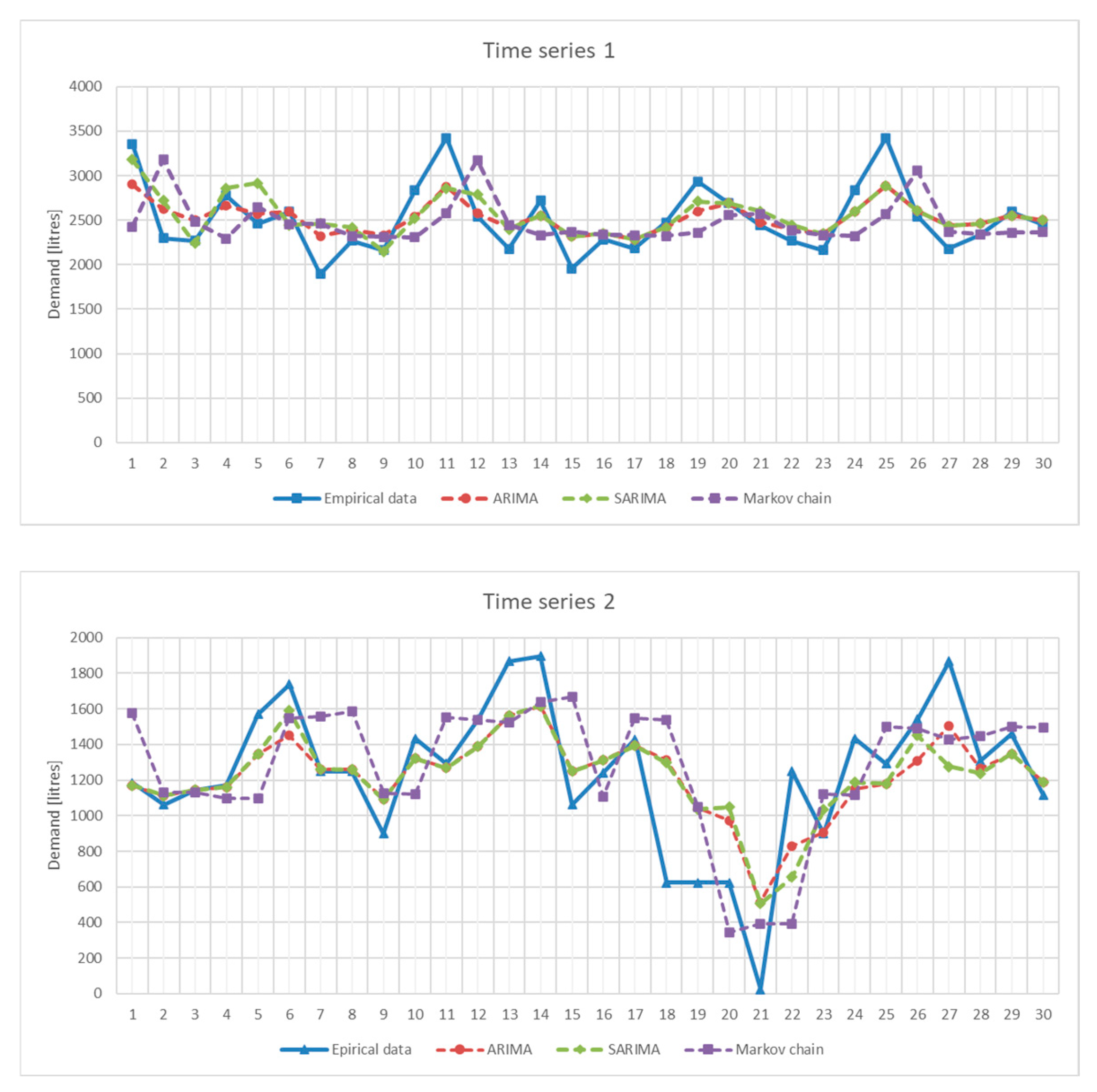
5.1. Forecast Accuracy Analysis
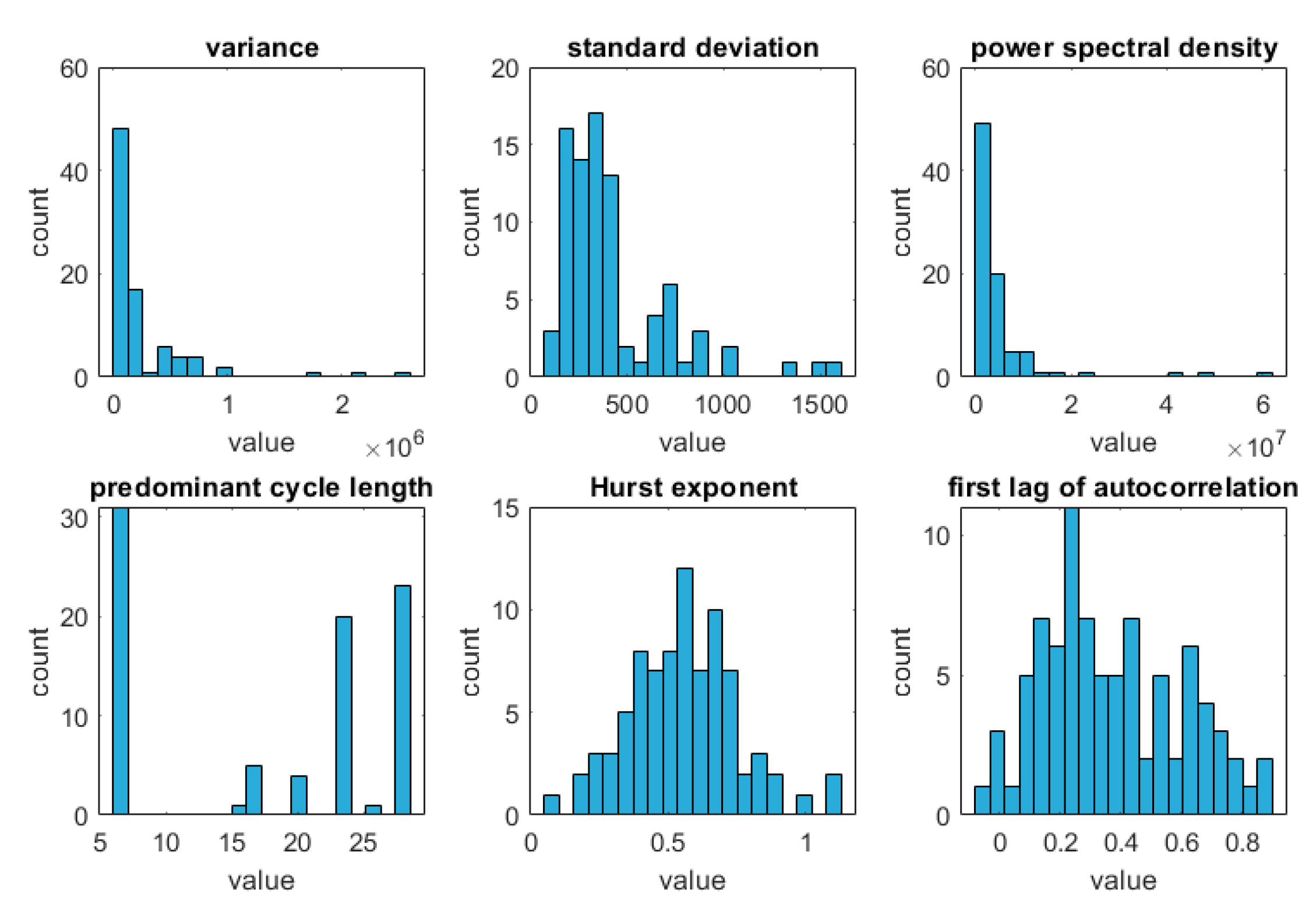
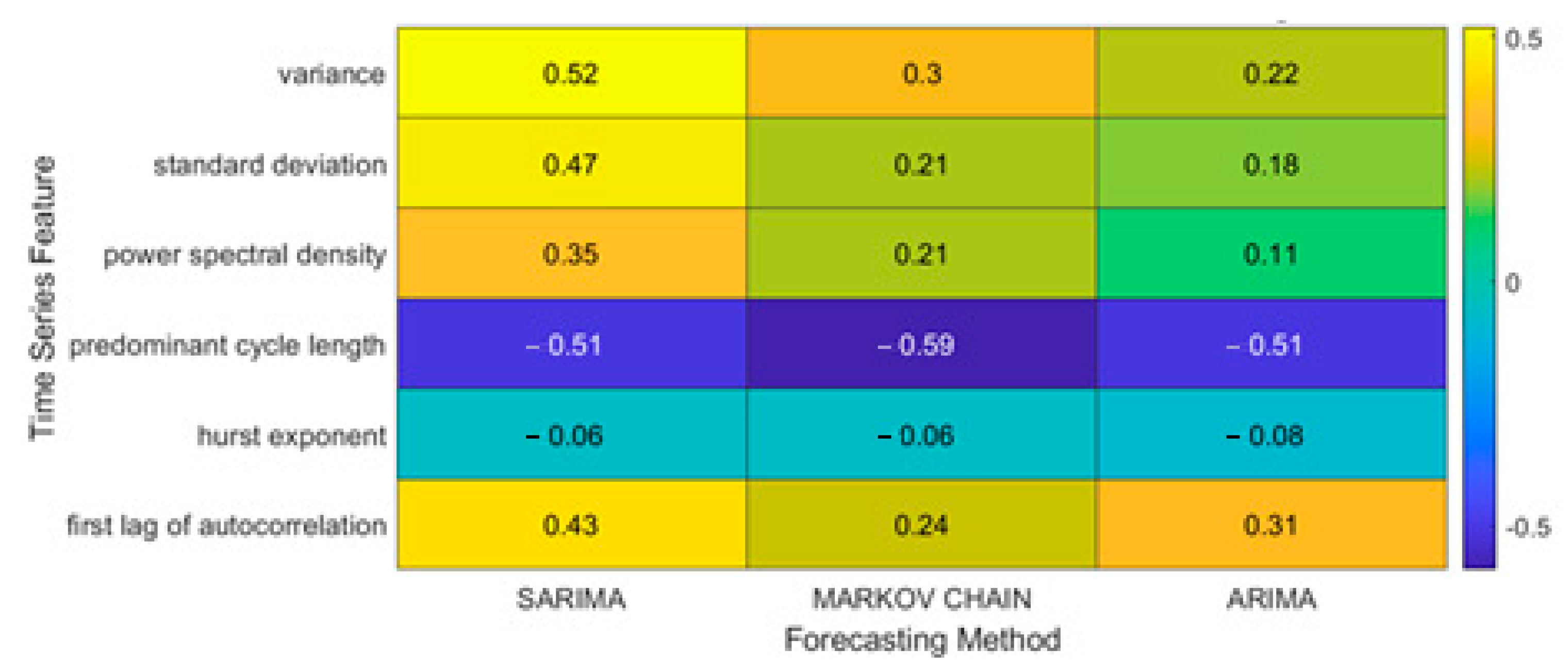
5.2. Influence of Time Series Characteristics on Forecast Accuracy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Marchi, B.; Zanoni, S. Supply chain management for improved energy efficiency: Review and opportunities. Energies 2017, 10, 1618. [Google Scholar] [CrossRef]
- Alsanad, A. Hoeffding Tree Method with Feature Selection for Forecasting Daily Demand Orders. In Proceedings of the 2020 International Conference on Technologies and Applications of Artificial Intelligence, Taipei, Taiwan, 3–5 December 2020; IEEE: Piscataway, NJ, USA, 2020; Volume 23, pp. 223–227. [Google Scholar]
- Bottani, E.; Mordonini, M.; Franchi, B.; Pellegrino, M. Demand Forecasting for an Automotive Company with Neural Network and Ensemble Classifiers Approaches; Springer International Publishing: Berlin/Heidelberg, Germany, 2021; pp. 134–142. [Google Scholar]
- Punia, S.; Nikolopoulos, K.; Singh, S.P.; Madaan, J.K.; Litsiou, K. Deep learning with long short-term memory networks and random forests for demand forecasting in multi-channel retail. Int. J. Prod. Res. 2020, 58, 4964–4979. [Google Scholar] [CrossRef]
- Balaji, K.S.; Ramasubramanian, B.; Sai Satya, V.M.; Tejesh, R.D.; Dheeraj, C.; Teja, S.K.; Anbuudayasankar, S.P. A demand-based relocation of warehouses and green routing. Mater. Today Proc. 2021, 46, 8438–8443. [Google Scholar] [CrossRef]
- Moghdani, R.; Salimifard, K.; Demir, E.; Benyettou, A. The green vehicle routing problem: A systematic literature review. J. Clean. Prod. 2021, 279, 123691. [Google Scholar] [CrossRef]
- Sar, K.; Ghadimi, P. A systematic literature review of the vehicle routing problem in reverse logistics operations. Comput. Ind. Eng. 2023, 177, 109011. [Google Scholar] [CrossRef]
- Guo, Z.X.; Wong, W.K.; Li, M. A multivariate intelligent decision-making model for retail sales forecasting. Decis. Support Syst. 2013, 55, 247–255. [Google Scholar] [CrossRef]
- Merkuryeva, G.; Valberga, A.; Smirnov, A. Demand forecasting in pharmaceutical supply chains: A case study. Procedia Comput. Sci. 2019, 149, 3–10. [Google Scholar] [CrossRef]
- Nia, A.R.; Awasthi, A.; Bhuiyan, N. Industry 4.0 and demand forecasting of the energy supply chain: A literature review. Comput. Ind. Eng. 2021, 154, 107–128. [Google Scholar]
- Van Calster, T.; Baesens, B.; Lemahieu, W. ProfARIMA: A profit-driven order identification algorithm for ARIMA models in sales forecasting. Appl. Soft Comput. 2017, 60, 775–785. [Google Scholar] [CrossRef]
- Tsiliyannis, C.A. Markov chain modeling and forecasting of product returns in remanufacturing based on stock mean-age. Eur. J. Oper. Res. 2018, 271, 474–489. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Zhong, L.; Tan, Y. A Markov Chain Based Demand Prediction Model for Stations in Bike Sharing Systems. Math. Probl. Eng. 2018, 2018, 8028714. [Google Scholar]
- Wilinski, A. Time series modelling and forecasting based on a Markov chain with changing transition matrices. Expert Syst. Appl. 2019, 133, 163–172. [Google Scholar] [CrossRef]
- Mor, B.; Garhwal, S.; Kumar, A. A Systematic Review of Hidden Markov Models and Their Applications. Arch. Comput. Methods Eng. 2021, 28, 1429–1448. [Google Scholar] [CrossRef]
- Amirkolaii, K.N.; Baboli, A.; Shahzad, M.K.; Tonadre, R. Demand Forecasting for Irregular Demands in Business Aircraft Spare Parts Supply Chains by using Artificial Intelligence (AI). IFAC-Pap. Line 2017, 50, 15221–15226. [Google Scholar] [CrossRef]
- Gonçalves, J.N.; Cortez, P.; Carvalho, M.S.; Frazăo, N.M. A multivariate approach for multi-step demand forecasting in assembly industries: Empirical evidence from an automotive supply chain. Decis. Support Syst. 2021, 142, 113452. [Google Scholar] [CrossRef]
- Falatouri, T.F.; Darbanian, P.; Brandtner, C.; Udokwu, C. Predictive analytics for demand forecasting—a comparison of sarima and LSTM in retail SCM. Procedia Comput. Sci. 2022, 200, 993–1003. [Google Scholar] [CrossRef]
- Mediavilla, M.A.; Dietrich, F.; Palm, D. Review and analysis of artificial intelligence methods for demand forecasting in supply chain management. Procedia CIRP 2022, 107, 1126–1131. [Google Scholar] [CrossRef]
- He, Q.Q.; Wu, C.; Si, Y.W. LSTM with particle Swam optimization for sales forecasting. Electron. Commer. Res. Appl. 2022, 51, 101–118. [Google Scholar] [CrossRef]
- Sun, L.; Xing, X.; Zhou, Y.; Hu, X. Demand Forecasting for Petrol Products in Gas Stations Using Clustering and Decision Tree. J. Adv. Comput. Intell. Intell. Inform. 2018, 22, 387–393. [Google Scholar] [CrossRef]
- Bandara, K.; Bergmeir, C.; Smyl, S. Forecasting across time series databases using recurrent neural networks on groups of similar series: A clustering approach. Expert Syst. Appl. 2020, 140, 112896. [Google Scholar] [CrossRef]
- Kang, Y.; Hyndmanb, R.; Smith-Miles, K. Visualising forecasting algorithm performance using time series instance spaces. Int. J. Forecast. 2017, 33, 345–358. [Google Scholar] [CrossRef]
- Petropoulos, F.; Kourentzes, N.; Nikolopoulos, K.; Siemsen, E. Judgmental selection of forecasting models. J. Oper. Manag. 2018, 60, 34–46. [Google Scholar] [CrossRef]
- Qin, L.; Shanks, K.; Philips, G.; Bernard, D. The Impact of Lengths of Time Series on the Accuracy of the ARIMA Forecasting. Int. Res. High. Educ. 2019, 4, 58–68. [Google Scholar] [CrossRef]
- Pope, E.C.D.; Stephenson, D.B.; Jackson, D.R. An Adaptive Markov Chain Approach for Probabilistic Forecasting of Categorical Events. Mon. Weather Rev. 2020, 148, 3681–3691. [Google Scholar] [CrossRef]
- Chan, K.C. Market share modelling and forecasting using Markov Chains and alternative models. Int. J. Innov. Comput. Inf. Control 2015, 11, 1205–1218. [Google Scholar]
- Gagliardi, F.; Alvisi, S.; Kapelan, Z.; Franchini, M. A Probabilistic Short-TermWater Demand Forecasting Model Based on the Markov Chain. Water 2017, 9, 507. [Google Scholar] [CrossRef]
- Brémaud, P. Non-homogeneous Markov Chains. In Markov Chains; Texts in Applied Mathematics; Springer: Berlin/Heidelberg, Germany, 2020; Volume 31, pp. 399–422. [Google Scholar]




| Forecasting Method | Min MAPE [%] | Median of MAPE [%] | Max MAPE [%] |
|---|---|---|---|
| ARIMA | 2.06 | 16.75 | 72.12 |
| SARIMA | 10.06 | 22.35 | 120.36 |
| Markov Chain | 5.88 | 15.14 | 62.99 |
| Forecasting Method | Min RMSE [l.] | Median of RMSE [l.] | Max RMSE [l.] |
| ARIMA | 42.22 | 207.94 | 902.02 |
| SARIMA | 45.85 | 208.33 | 890.51 |
| Markov Chain | 53.89 | 184.15 | 863.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Więcek, P.; Kubek, D. The Impact Time Series Selected Characteristics on the Fuel Demand Forecasting Effectiveness Based on Autoregressive Models and Markov Chains. Energies 2024, 17, 4163. https://doi.org/10.3390/en17164163
Więcek P, Kubek D. The Impact Time Series Selected Characteristics on the Fuel Demand Forecasting Effectiveness Based on Autoregressive Models and Markov Chains. Energies. 2024; 17(16):4163. https://doi.org/10.3390/en17164163
Chicago/Turabian StyleWięcek, Paweł, and Daniel Kubek. 2024. "The Impact Time Series Selected Characteristics on the Fuel Demand Forecasting Effectiveness Based on Autoregressive Models and Markov Chains" Energies 17, no. 16: 4163. https://doi.org/10.3390/en17164163
APA StyleWięcek, P., & Kubek, D. (2024). The Impact Time Series Selected Characteristics on the Fuel Demand Forecasting Effectiveness Based on Autoregressive Models and Markov Chains. Energies, 17(16), 4163. https://doi.org/10.3390/en17164163






