Research on Data-Driven Methods for Solving High-Dimensional Neutron Transport Equations
Abstract
1. Introduction
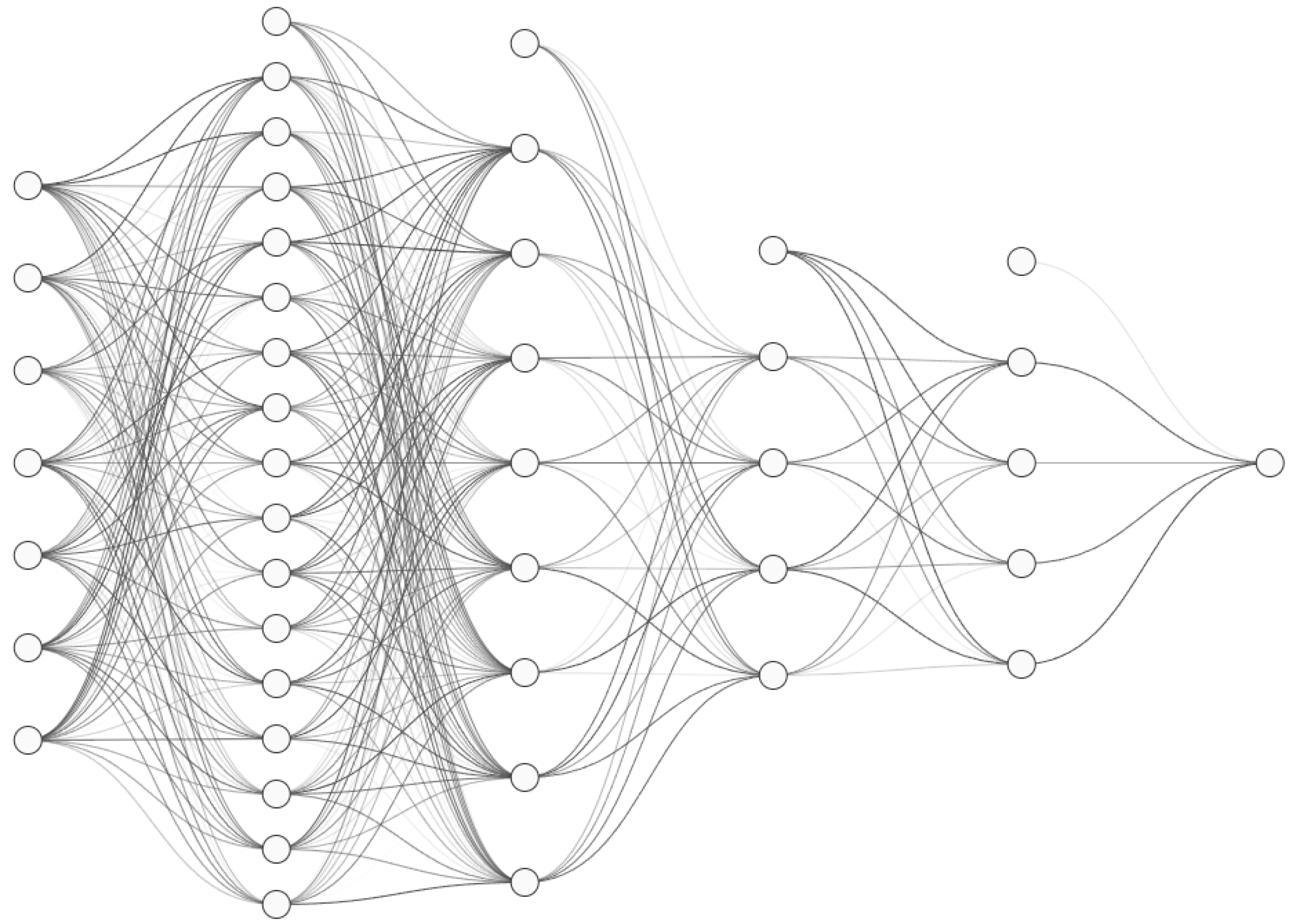
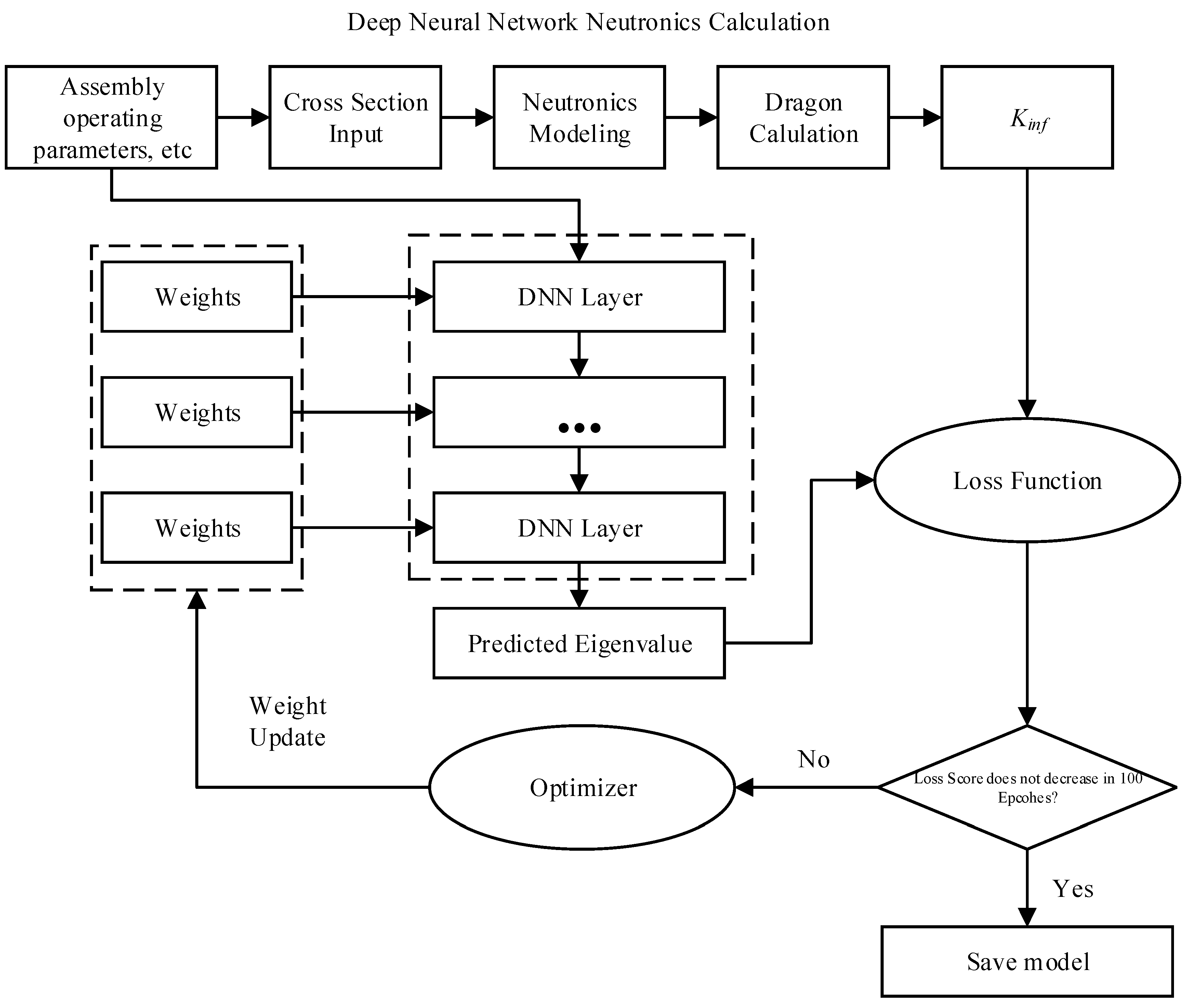
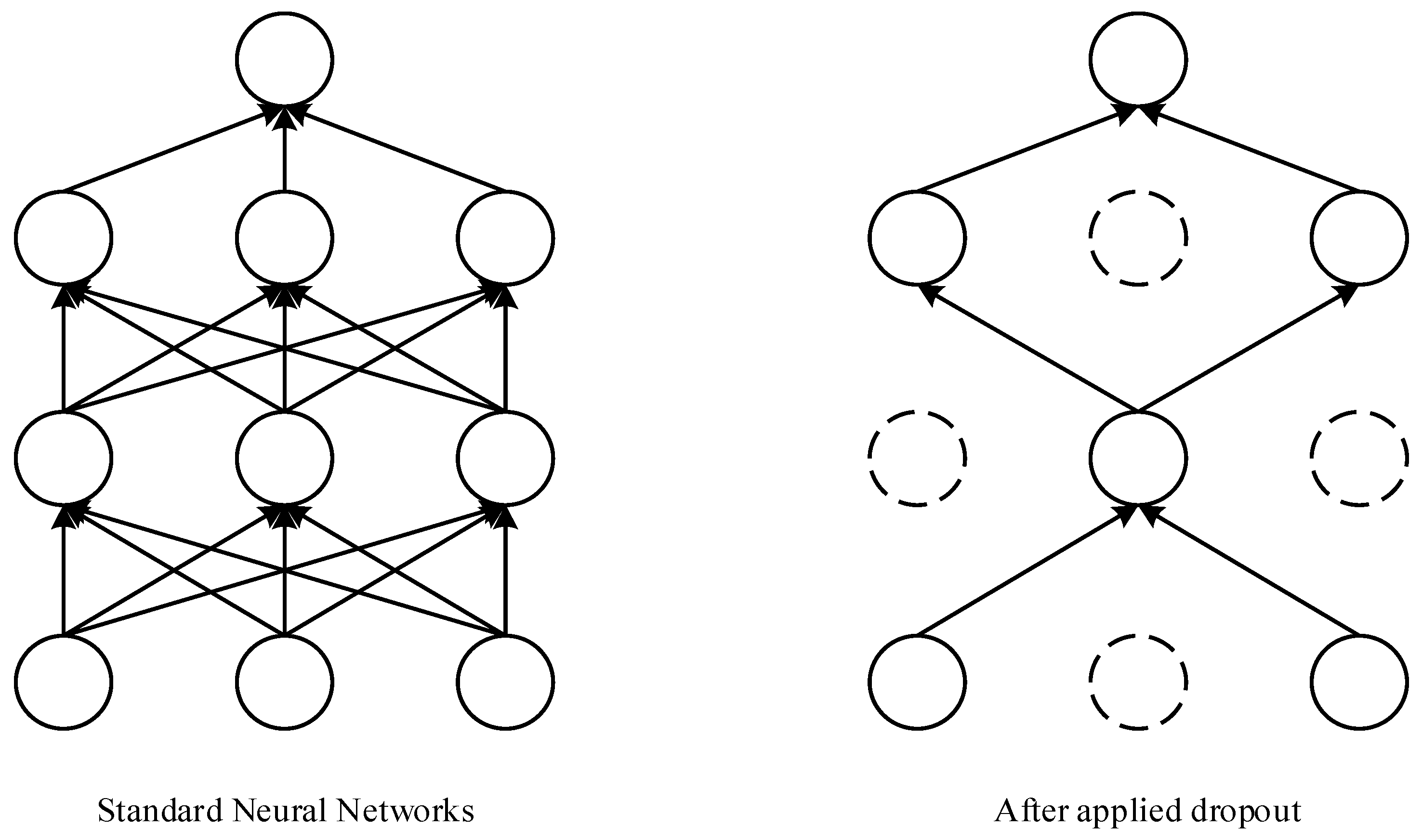
2. DNN Neural Network
3. Sample Construction
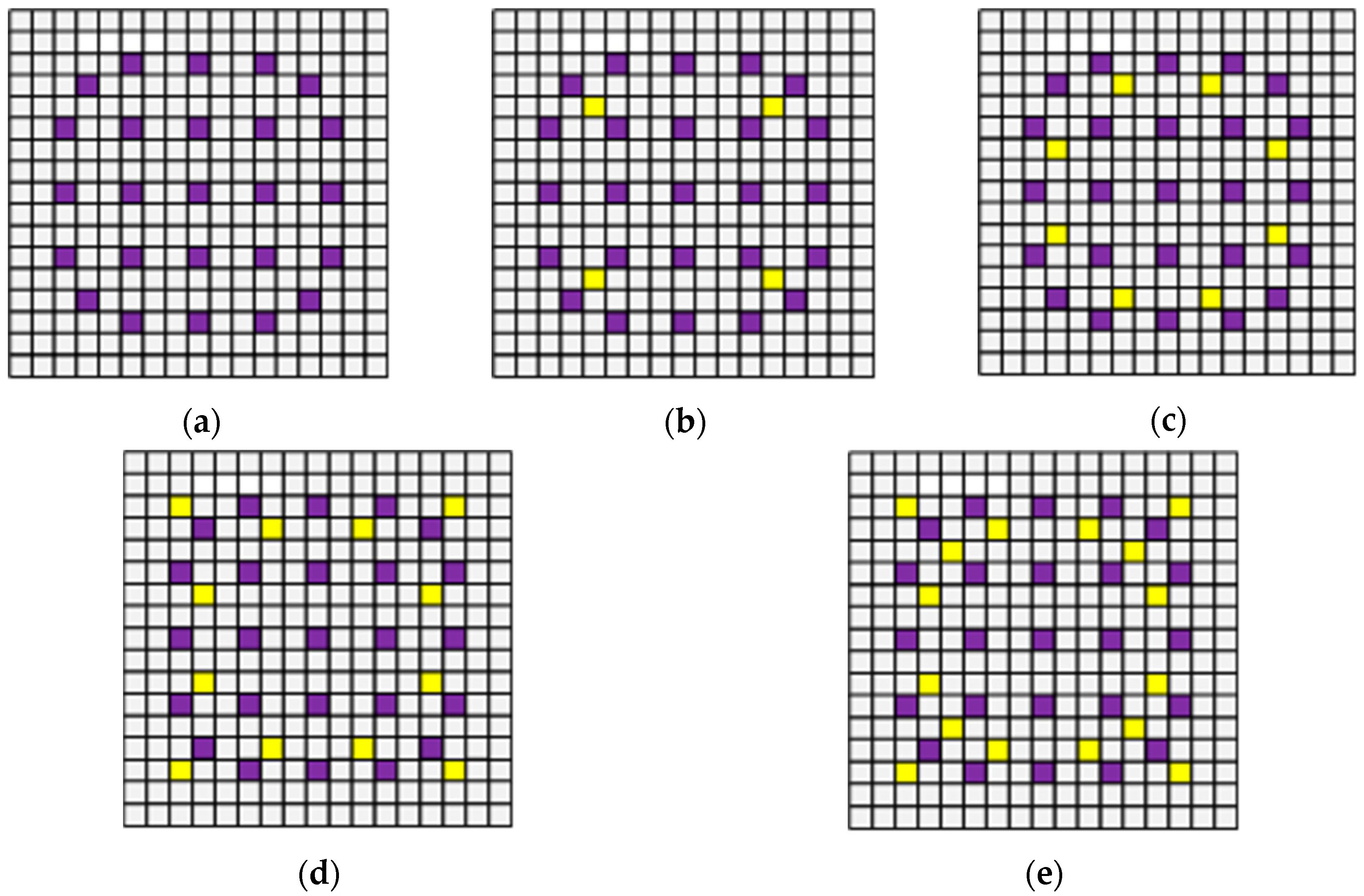
3.1. Code Introduction
3.2. Project Design
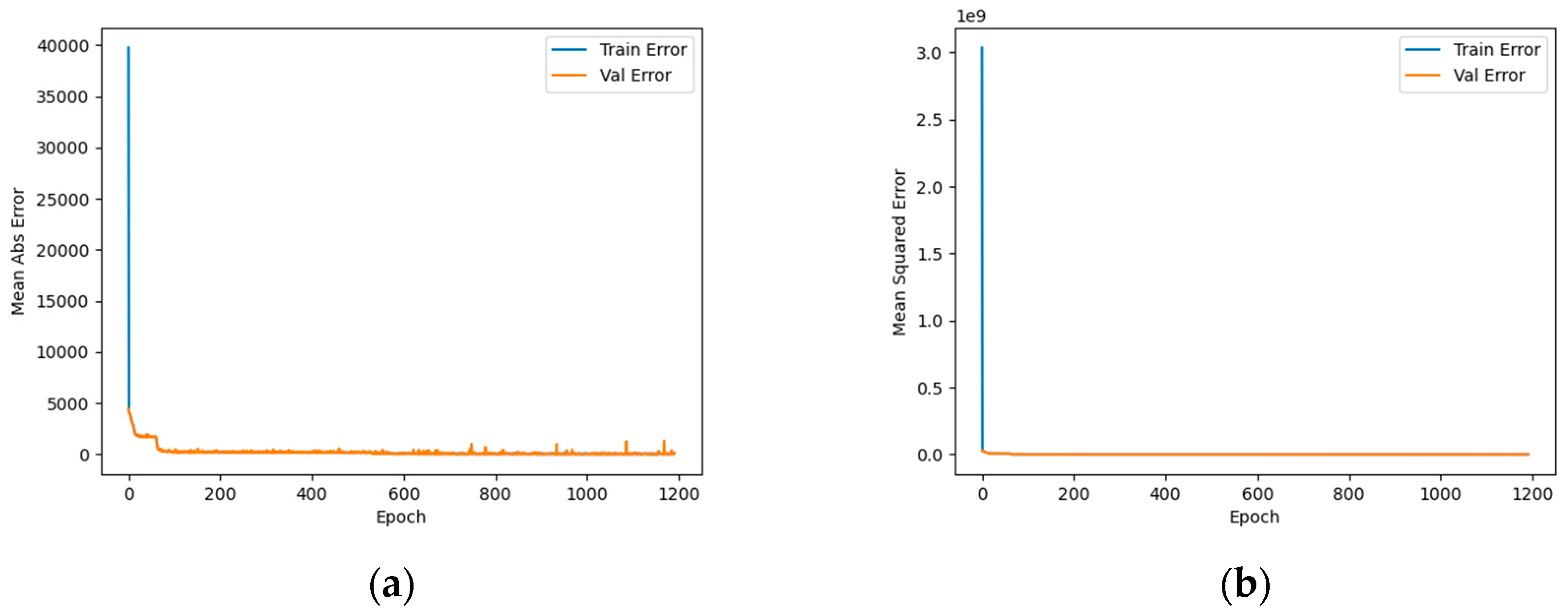
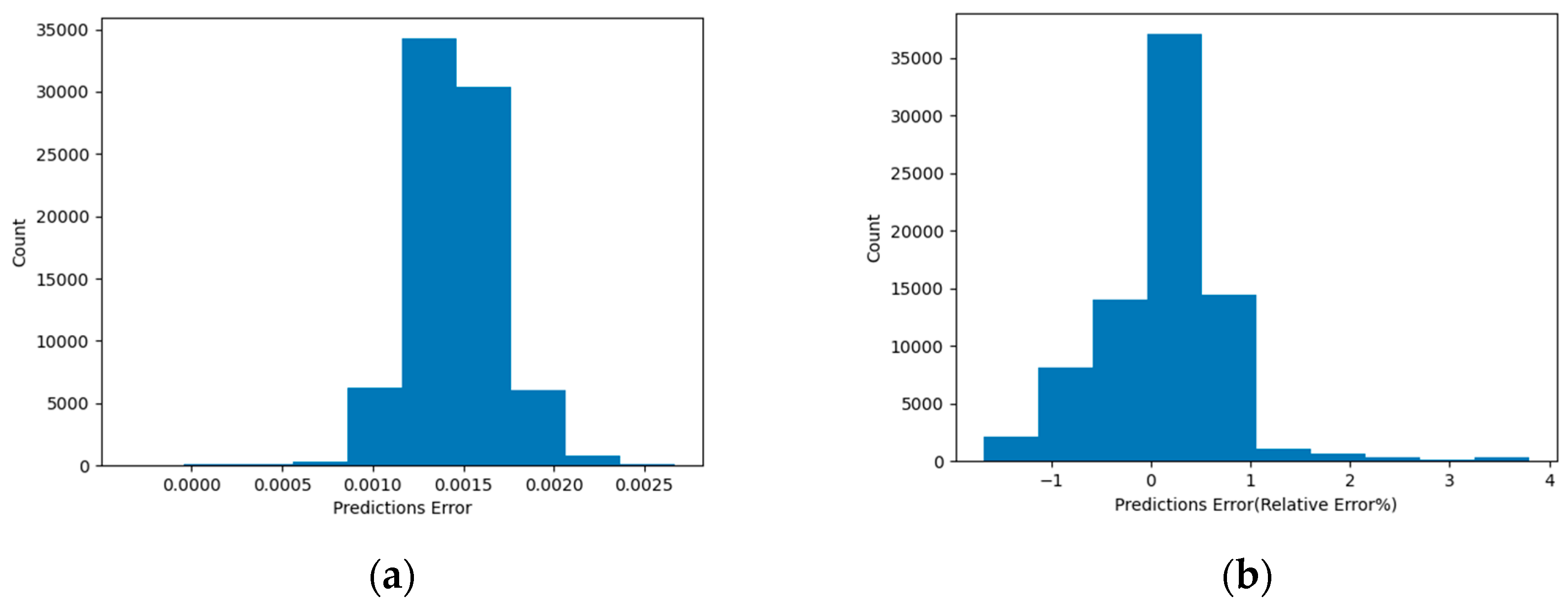
4. Results Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bethe, H.A. Nuclear physics B. Nuclear dynamics, theoretical. Rev. Mod. Phys. 1937, 9, 69. [Google Scholar] [CrossRef]
- Ren, C.; He, L.; Lei, J.; Liu, J.; Huang, G.; Gao, K.; Qu, H.; Zhang, Y.; Li, W.; Yang, X.; et al. Neutron transport calculation for the BEAVRS core based on the LSTM neural network. Sci. Rep. 2023, 13, 14670. [Google Scholar] [CrossRef]
- Lei, J.; Xie, J.; Chen, Z.; Yu, T.; Yang, C.; Zhang, B.; Zhao, C.; Li, X.; Wu, J.; Zhuang, H.; et al. Validation of Doppler Temperature Coefficients and Assembly Power Distribution for the Lattice Code KYLIN V2.0. Front. Energy Res. 2021, 9, 801481. [Google Scholar] [CrossRef]
- Capilla, M.; Talavera, C.; Ginestar, D.; Verdú, G. Validation of the SHNC time-dependent transport code based on the spherical harmonics method for complex nuclear fuel assemblies. J. Comput. Appl. Math. 2020, 375, 112814. [Google Scholar] [CrossRef]
- Zhang, G.; Li, Z. Marvin: A parallel three-dimensional transport code based on the discrete ordinates method for reactor shielding calculations. Prog. Nucl. Energy 2021, 137, 103786. [Google Scholar] [CrossRef]
- Rahman, A.; Lee, D. Incorporation of anisotropic scattering into the method of characteristics. Nucl. Eng. Technol. 2022, 54, 3478–3487. [Google Scholar] [CrossRef]
- Dunn, W.L.; Shultis, J.K. Exploring Monte Carlo Methods; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar] [CrossRef]
- Chu, T.-N.; Phan, G.T.; Tran, L.Q.L.; Bui, T.H.; Do, Q.B.; Dau, D.-T.; Nguyen, K.-C.; Nguyen, N.-D.; Nguyen, H.-T.; Hoang, V.-K.; et al. Sensitivity and uncertainty analysis of the first core of the DNRR using MCNP6 and new nuclear data libraries. Nucl. Eng. Des. 2024, 419, 112986. [Google Scholar] [CrossRef]
- Sandhu, H.K.; Bodda, S.S.; Gupta, A. A future with machine learning: Review of condition assessment of structures and mechanical systems in nuclear facilities. Energies 2023, 16, 2628. [Google Scholar] [CrossRef]
- Lei, J.; Zhou, J.; Zhao, Y.; Chen, Z.; Zhao, P.; Xie, C.; Ni, Z.; Yu, T.; Xie, J. Prediction of burn-up nucleus density based on machine learning. Int. J. Energy Res. 2021, 45, 14052–14061. [Google Scholar] [CrossRef]
- Qi, B.; Liang, J.; Tong, J. Fault diagnosis techniques for nuclear power plants: A review from the artificial intelligence perspective. Energies 2023, 16, 1850. [Google Scholar] [CrossRef]
- Lei, J.; Yang, C.; Ren, C.; Li, W.; Liu, C.; Sun, A.; Li, Y.; Chen, Z.; Yu, T. Development and validation of a deep learning-based model for predicting burnup nuclide density. Int. J. Energy Res. 2022, 46, 21257–21265. [Google Scholar] [CrossRef]
- Pikus, M.; Wąs, J. Using Deep Neural Network Methods for Forecasting Energy Productivity Based on Comparison of Simulation and DNN Results for Central Poland—Swietokrzyskie Voivodeship. Energies 2023, 16, 6632. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, Y.; Ma, Y. Boundary dependent physics-informed neural network for solving neutron transport equation. Ann. Nucl. Energy 2024, 195, 110181. [Google Scholar] [CrossRef]
- Wang, Y.; Chi, H.; Ma, Y. Nodal expansion method based reduced-order model for control rod movement. Ann. Nucl. Energy 2024, 198, 110279. [Google Scholar] [CrossRef]
- Liu, B.; Lei, J.; Xie, J.; Zhou, J. Development and Validation of a Nuclear Power Plant Fault Diagnosis System Based on Deep Learning. Energies 2022, 15, 8629. [Google Scholar] [CrossRef]
- Tran, V.D.; Lam, D.K.; Tran, T.H. Hardware-based architecture for DNN wireless communication models. Sensors 2023, 23, 1302. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, Z.; Yang, X.; Xu, L.; Chen, S.; Zhang, Y.; Zhang, J. Centroid Optimization of DNN Classification in DOA Estimation for UAV. Sensors 2023, 23, 2513. [Google Scholar] [CrossRef]
- Marleau, G.; Hébert, A.; Roy, R. A User Guide for DRAGON Version 4; Institute of Genius Nuclear, Department of Genius Mechanical, School Polytechnic of Montreal: Montreal, QC, Canada, 2011. [Google Scholar]
- Xiaohui, W. Analysis and Research on Diagnosis Methods of AFA 3G Fuel Assembly Leakage. In Proceedings of the 2017 25th International Conference on Nuclear Engineering, Shanghai, China, 2–6 July 2017; American Society of Mechanical Engineers: New York, NY, USA, 2017; Volume 57793, p. V001T01A001. [Google Scholar]
- Li, J.; Qiao, S.; Ren, J.; Yu, X.; Tian, R.; Tan, S. Detailed comparison of the characteristics of mixing and subchannel vortex induced by different spacer grids. Prog. Nucl. Energy 2023, 166, 104962. [Google Scholar] [CrossRef]
- Lei, J.; Ren, C.; Li, W.; Fu, L.; Li, Z.; Ni, Z.; Li, Y.; Liu, C.; Zhang, H.; Chen, Z.; et al. Prediction of crucial nuclear power plant parameters using long short-term memory neural networks. Int. J. Energy Res. 2022, 46, 21467–21479. [Google Scholar] [CrossRef]
- Lei, J.; Chen, Z.; Zhou, J.; Yang, C.; Ren, C.; Li, W.; Xie, C.; Ni, Z.; Huang, G.; Li, L.; et al. Research on the preliminary prediction of nuclear core design based on machine learning. Nucl. Technol. 2022, 208, 1223–1232. [Google Scholar] [CrossRef]
- Ren, C.; Li, H.; Lei, J.; Liu, J.; Li, W.; Gao, K.; Huang, G.; Yang, X.; Yu, T. CNN-lstm-based model to fault diagnosis for CPR1000. Nucl. Technol. 2023, 209, 1365–1372. [Google Scholar] [CrossRef]

| Assembly Independent Variables | Value | Feature Name |
|---|---|---|
| Burnup (Gw·d/tU) | 0–60/Step 0.5 | BURNUP |
| Enrichment (%) | 2–4/Step 0.5 | ENS |
| Power (W/cm) | 20–50/Step 10 | power |
| Temperature (°C) | 280–320/Step 10 | tem |
| Boron concentration (ppm) | 100–900/Step 200 | nb |
| Burnable poison arrangement form (rod) | 0–16/Step 4 | ngd |
| Burnable poison enrichment (%) | 6–12/Step 2 | ngdd |
| Assembly Geometry Parameter | Value |
|---|---|
| Outer surface diameter of cladding/cm | 0.95 |
| Cladding material | M5 |
| UO2 pellet diameter/cm | 0.8192 |
| Gap gas | Helium |
| Core active section height/cm | 365.8 |
| Burnable poison arrangement form (rod) | 0–16/Step 4 |
| Fuel rod center distance/cm | 1.26 |
| Number of assembly grids | 17 × 17 |
| Fuel assembly center distance/cm | 21.504 |
| Number of tubes per assembly | 25 |
| Number of UO2 fuel pins per assembly | 264 |
| UO2 pellet density/g/cm3 | 10.412 |
| Water density/g/cm3 | 0.9983 |
| M5 density/g/cm3 | 6.5 |
| Item | Value | Item | Value |
|---|---|---|---|
| Hidden Layers | 6 | Input Scaling | Max-Min |
| Nodes per layer | 512, 256, 128, 64, 4, 1 | Activation | ReLU |
| Dropout (after 1st layer) | 0.3 | Optimizer | Adam |
| Loss Function | MSE | Epochs | 5000 |
| Batch Size | 1024 | Training/Validation/Testing Samples | 6:2:2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Z.; Lei, J.; Ni, Z.; Yu, T.; Xie, J.; Hong, J.; Hu, H. Research on Data-Driven Methods for Solving High-Dimensional Neutron Transport Equations. Energies 2024, 17, 4153. https://doi.org/10.3390/en17164153
Peng Z, Lei J, Ni Z, Yu T, Xie J, Hong J, Hu H. Research on Data-Driven Methods for Solving High-Dimensional Neutron Transport Equations. Energies. 2024; 17(16):4153. https://doi.org/10.3390/en17164153
Chicago/Turabian StylePeng, Zhiqiang, Jichong Lei, Zining Ni, Tao Yu, Jinsen Xie, Jun Hong, and Hong Hu. 2024. "Research on Data-Driven Methods for Solving High-Dimensional Neutron Transport Equations" Energies 17, no. 16: 4153. https://doi.org/10.3390/en17164153
APA StylePeng, Z., Lei, J., Ni, Z., Yu, T., Xie, J., Hong, J., & Hu, H. (2024). Research on Data-Driven Methods for Solving High-Dimensional Neutron Transport Equations. Energies, 17(16), 4153. https://doi.org/10.3390/en17164153






