Advanced Deep Learning Techniques for Battery Thermal Management in New Energy Vehicles
Abstract
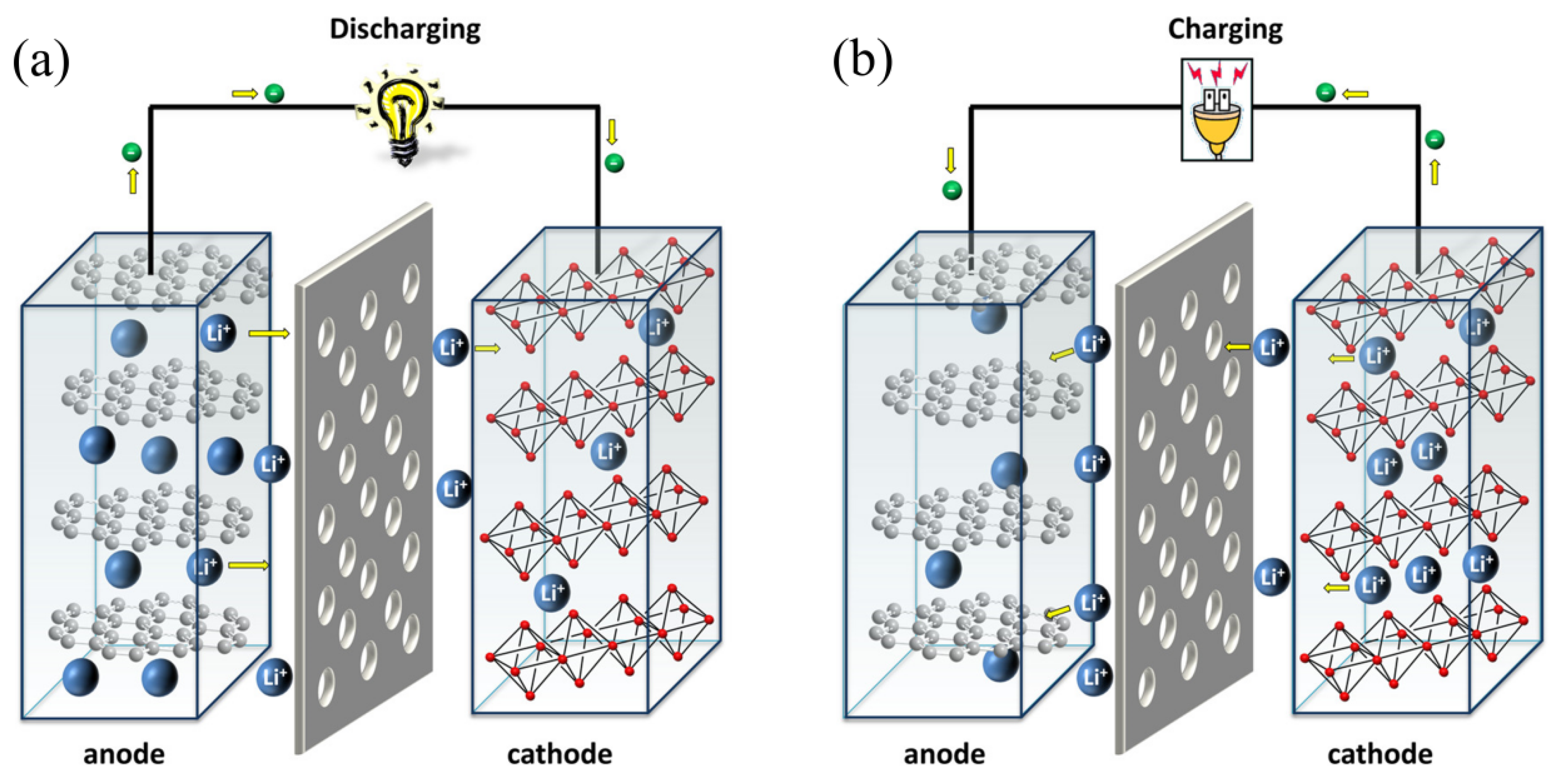
1. Introduction
2. A Basic Introduction to Deep Learning
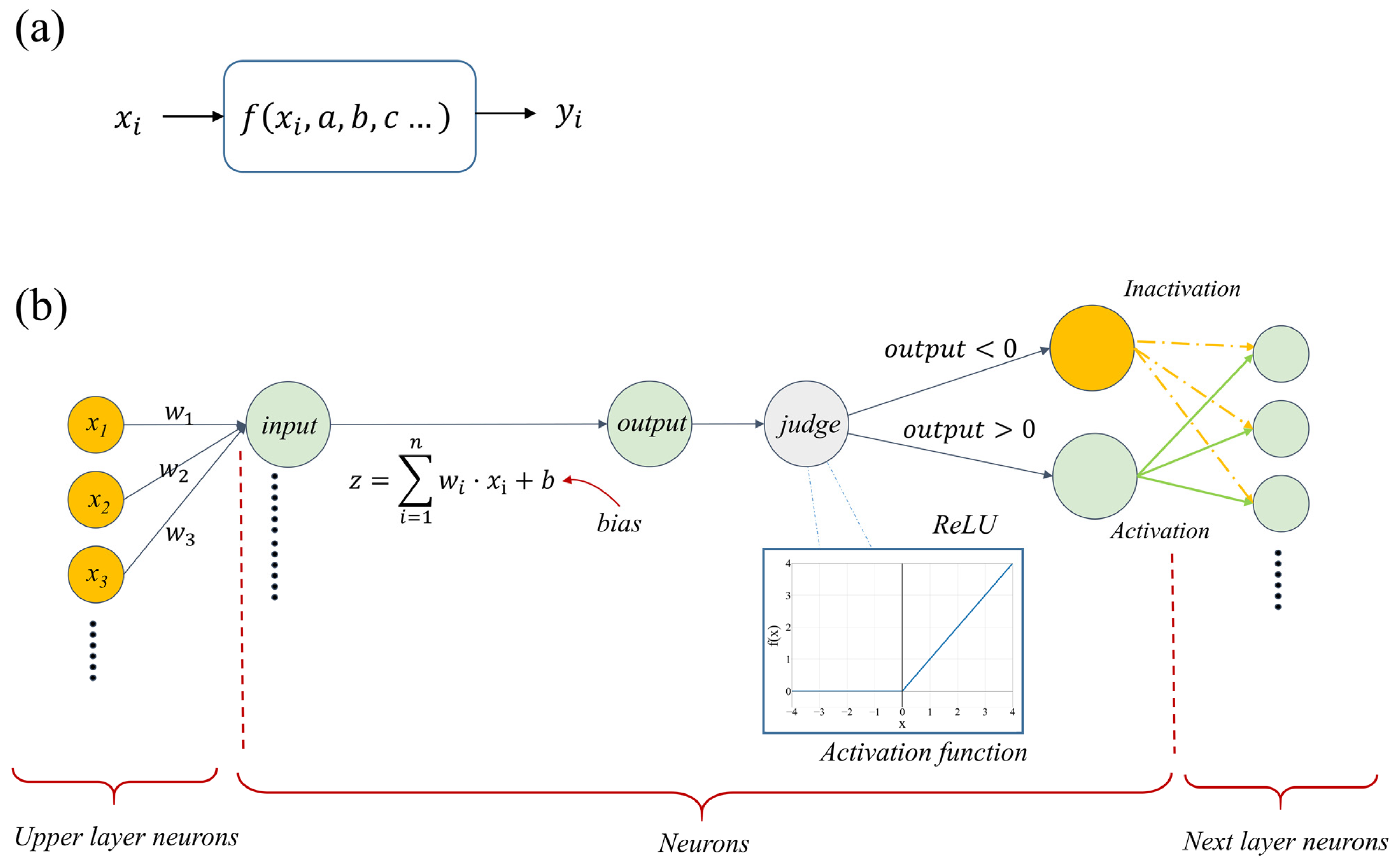
2.1. Concepts of Deep Learning
2.2. Loss Function
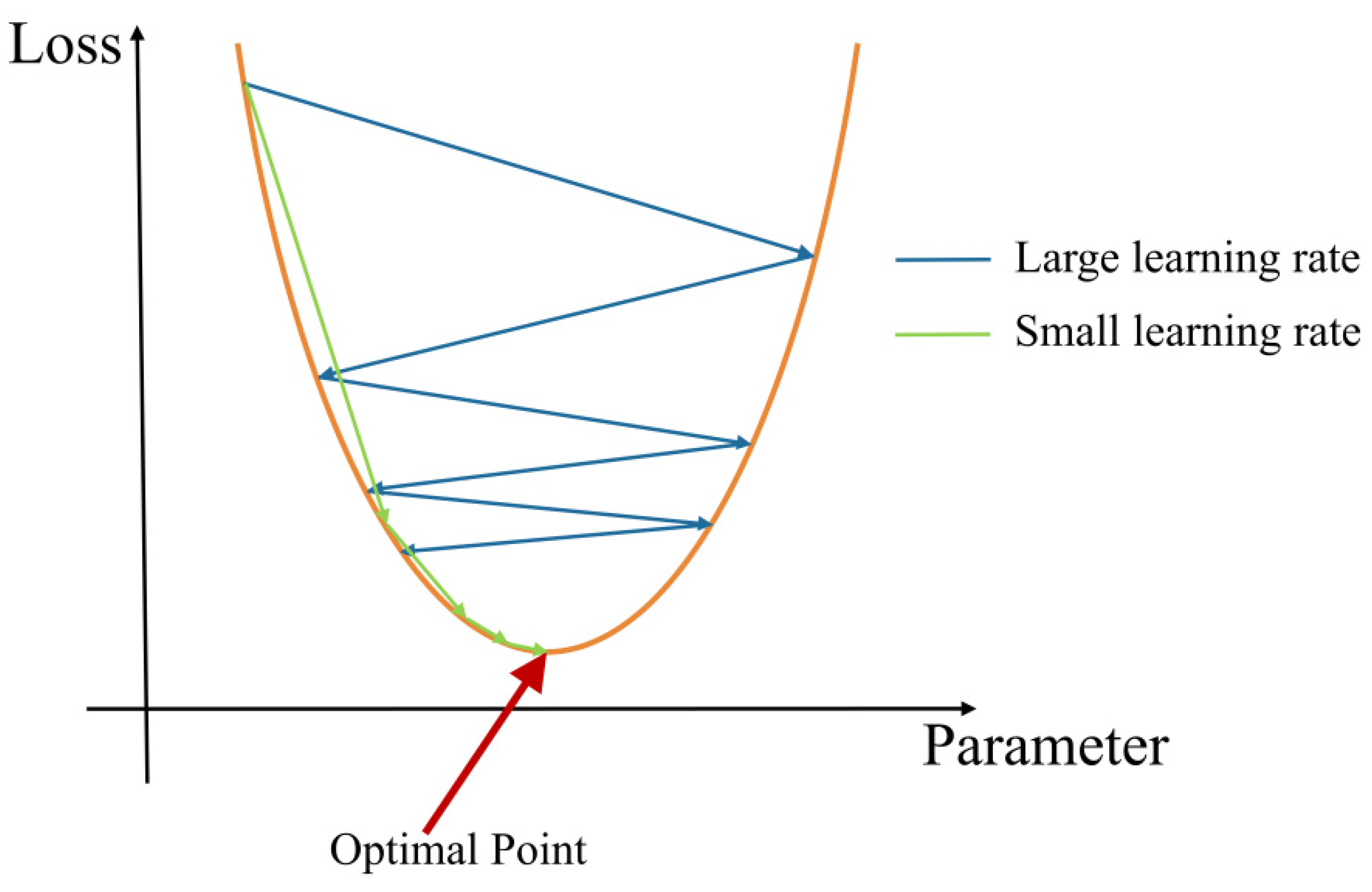
2.3. Gradient Descent
2.4. Stochastic Gradient Descent (SGD)
2.5. Backpropagation
2.6. Improved Optimization Method
2.6.1. Gradient Descent with Momentum
2.6.2. Adaptive Gradient Algorithm (AdaGrad)
2.6.3. Root Mean Square Propagation (RMSProp)
2.6.4. Adaptive Moment Estimation (Adam)
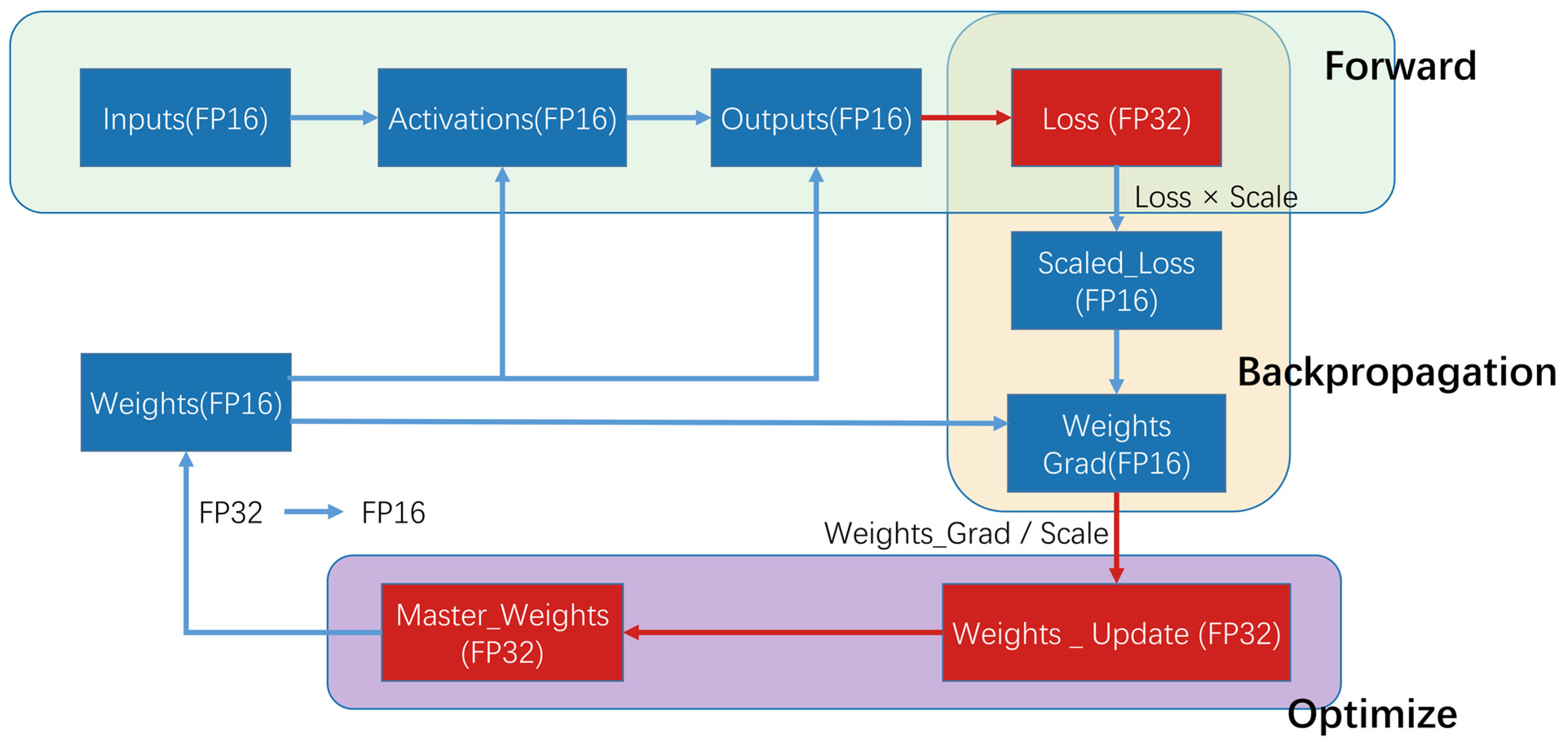
2.7. Mixed-Precision Training
3. Application of Advanced Deep Learning Algorithms in Battery Thermal Management
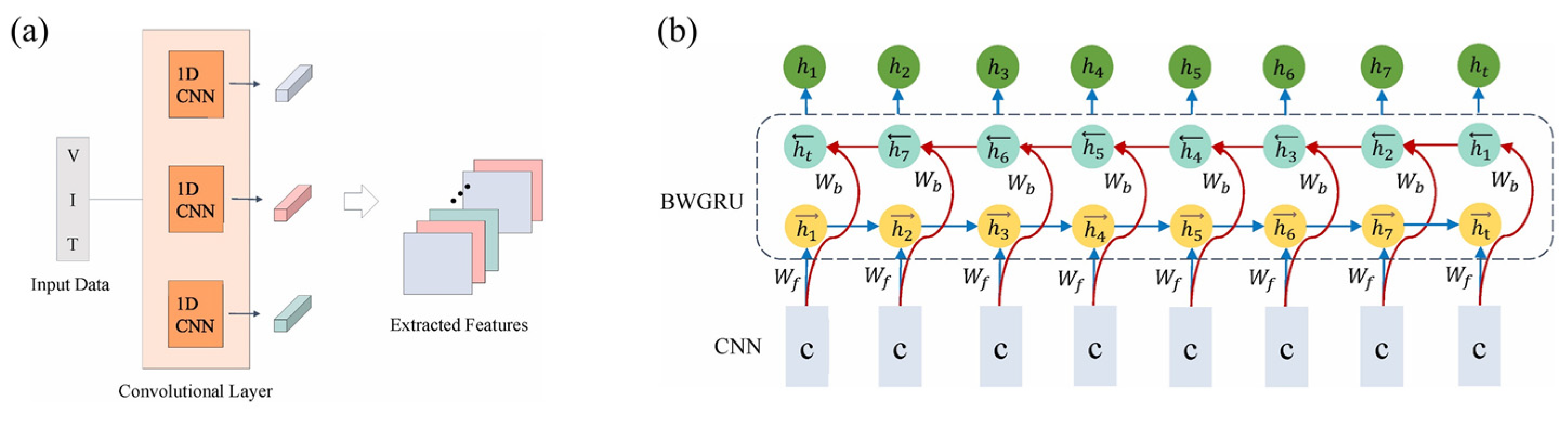
3.1. Convolutional Neural Network (CNN)
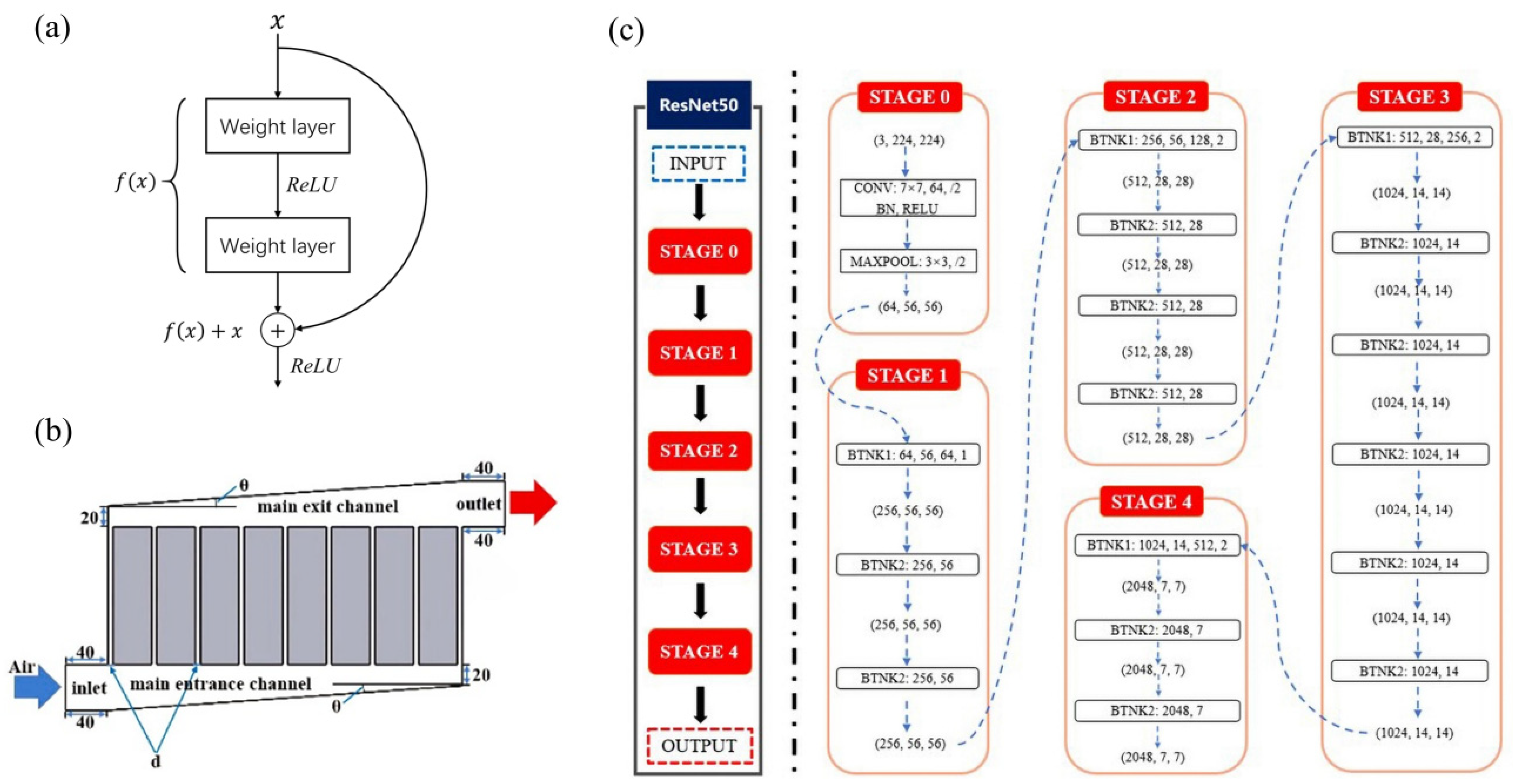
3.2. Residual Neural Network (ResNet)
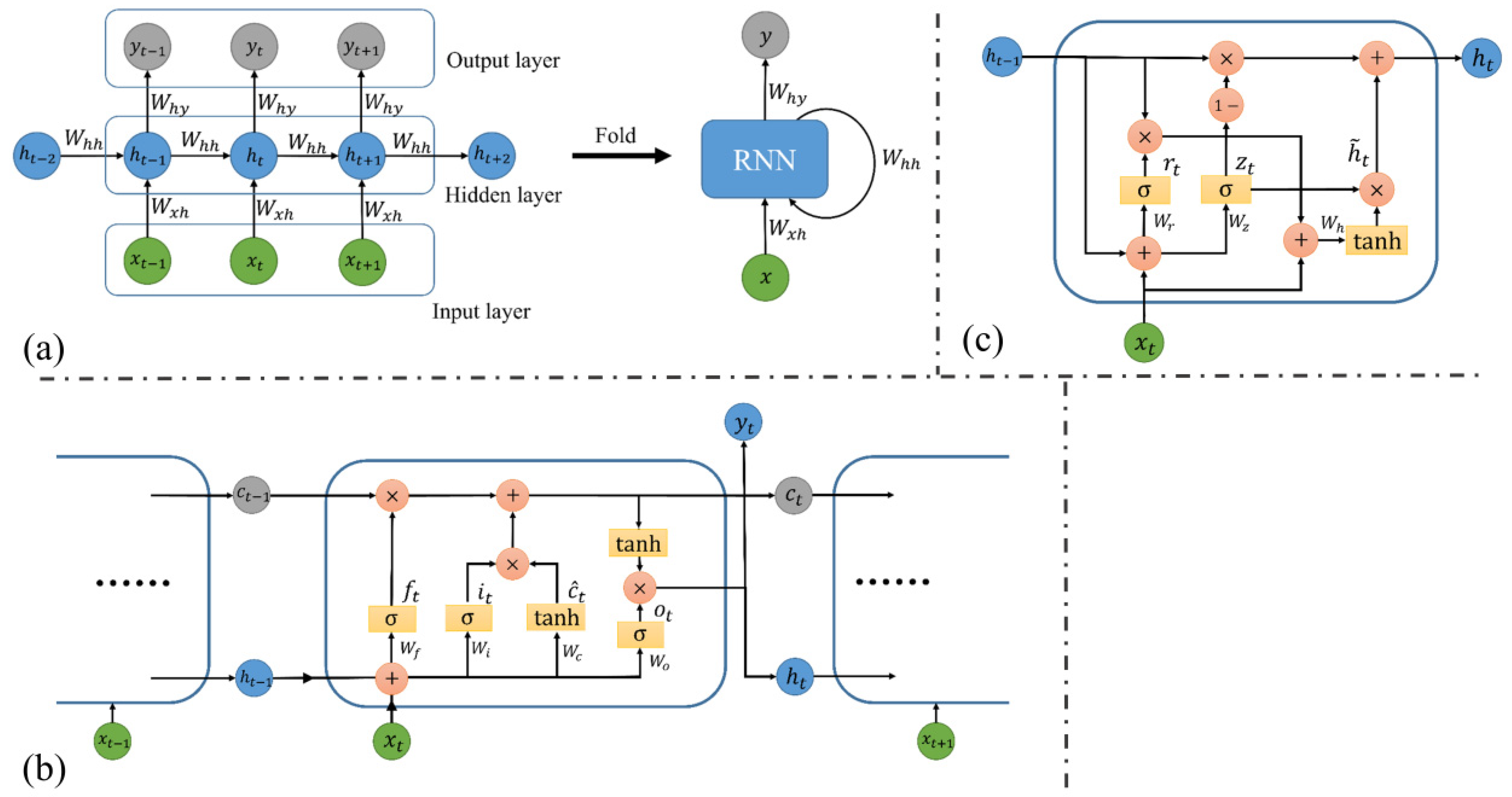
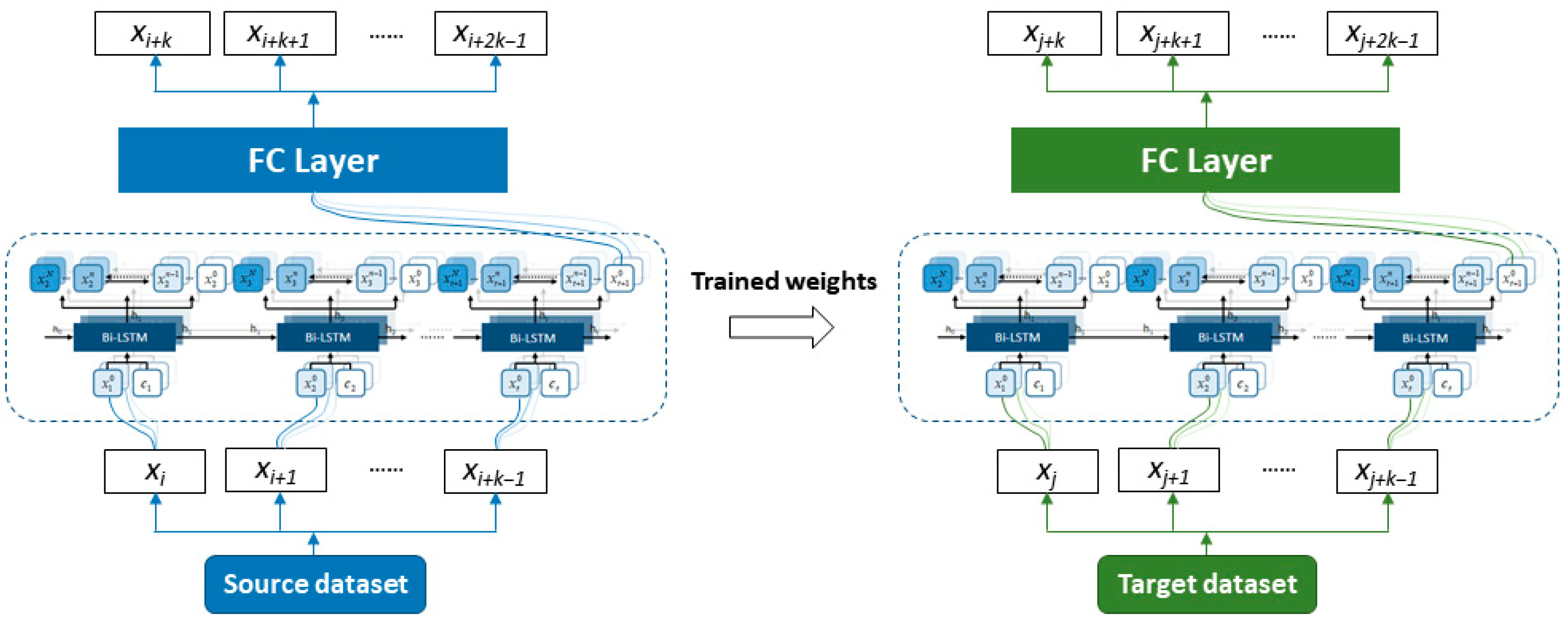
3.3. Recurrent Neural Network (RNN)
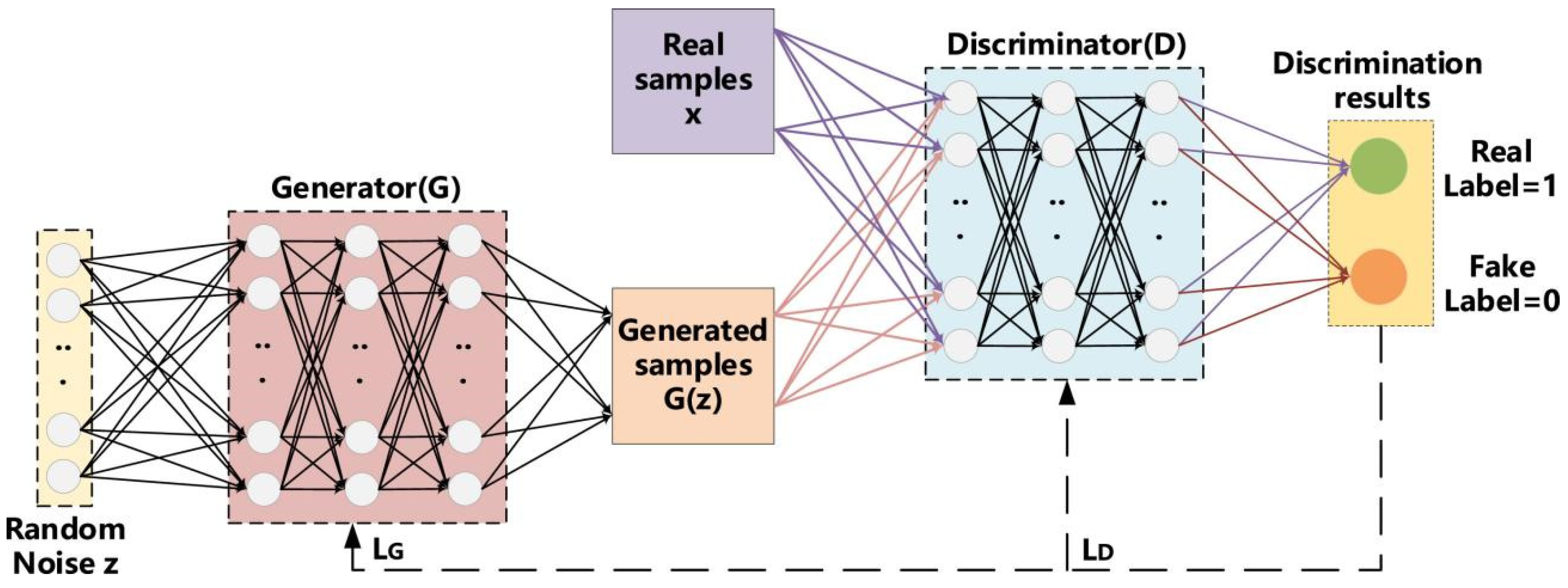
3.4. Generative Adversarial Neural Networks (GAN)
4. Emerging Deep Learning Algorithms for Battery Thermal Management
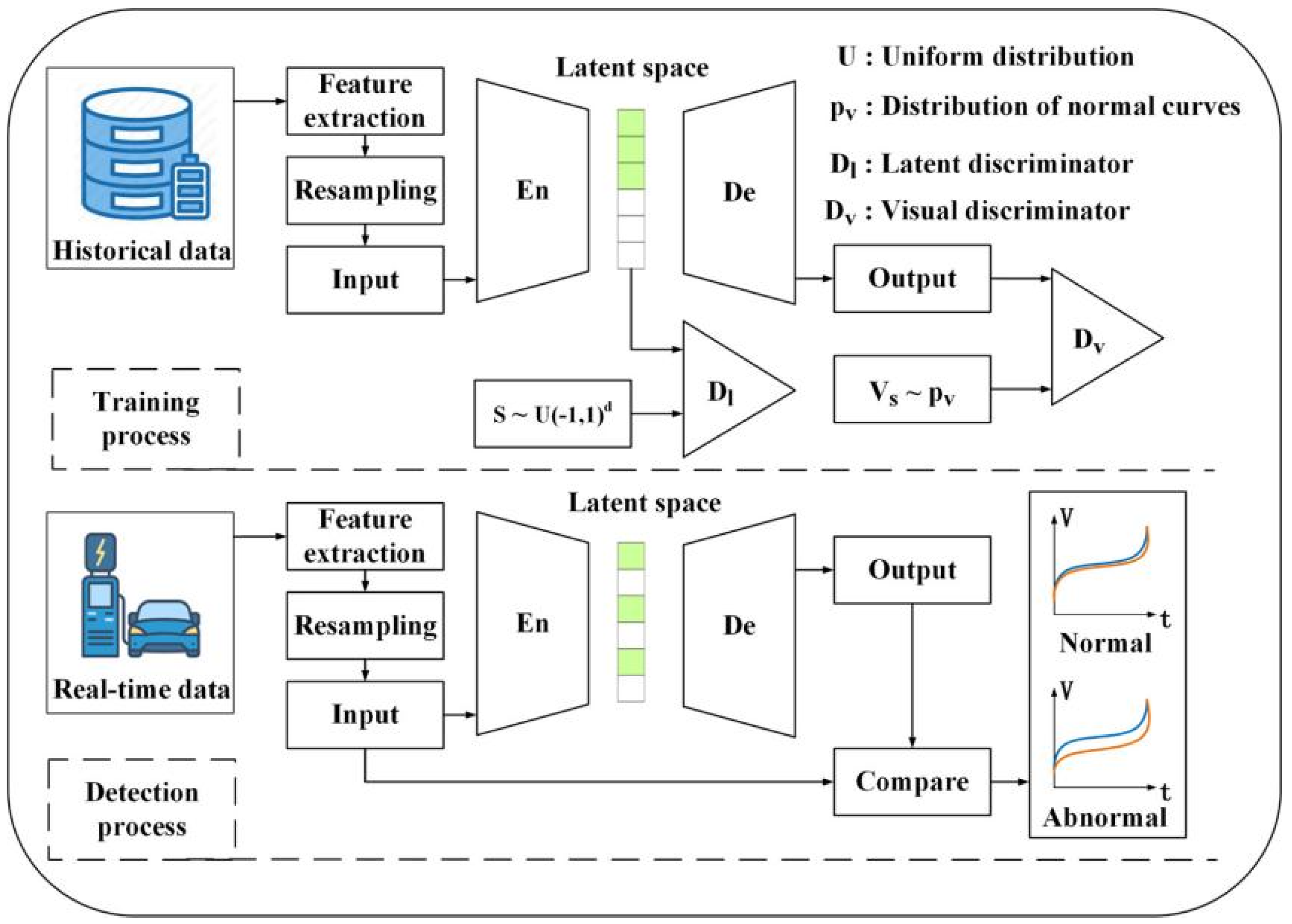
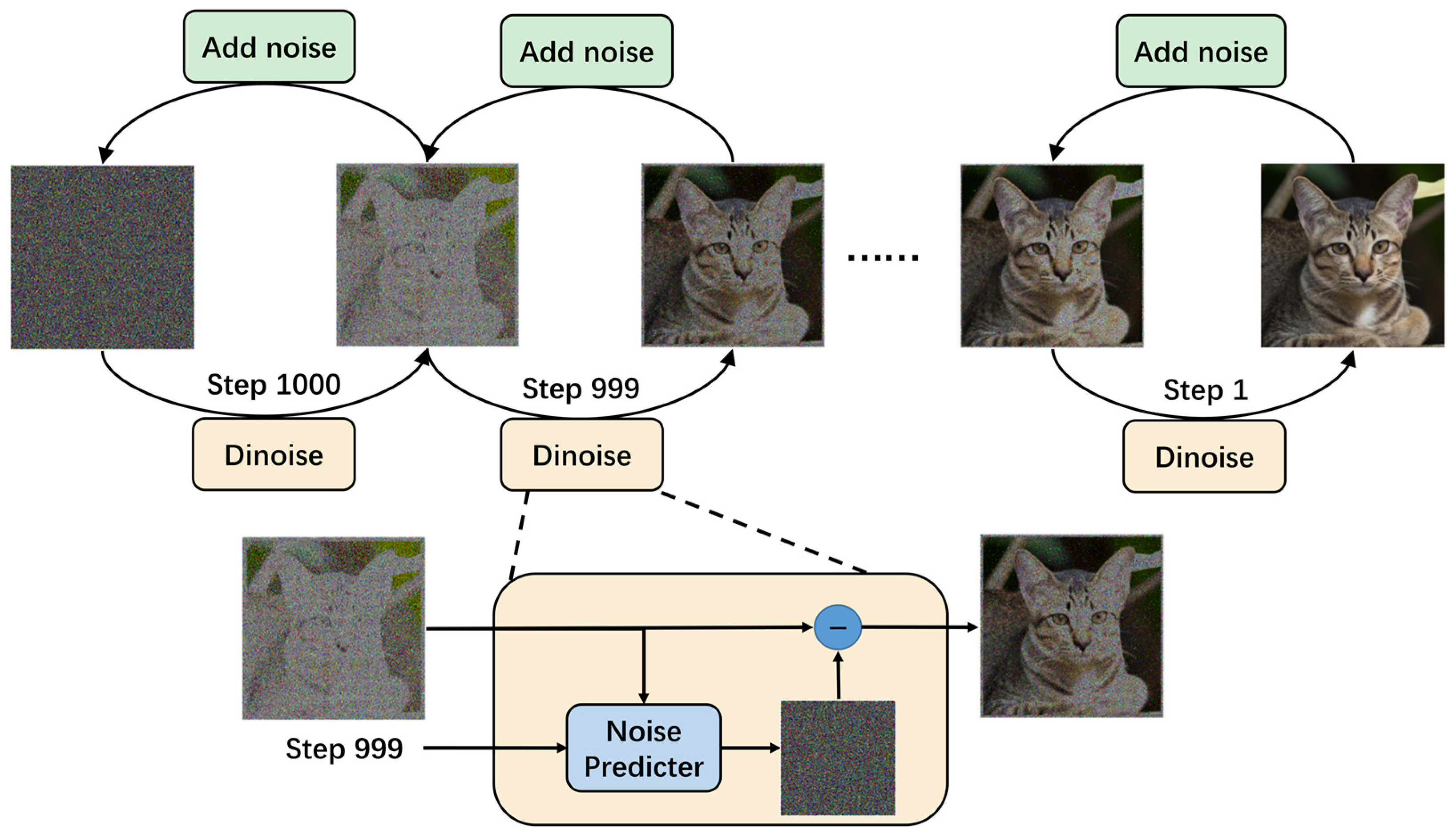
4.1. Diffusion Model (DM)
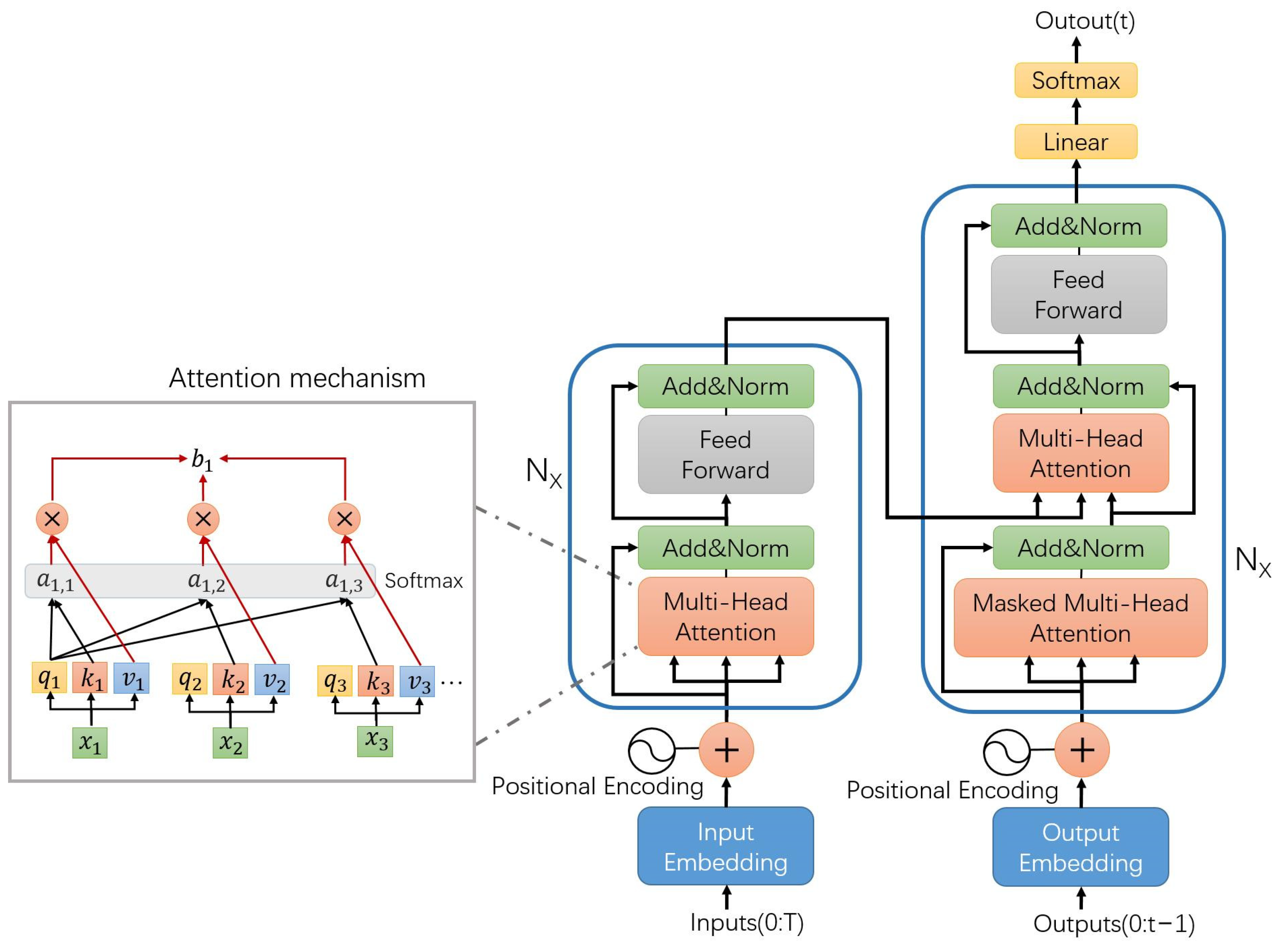
4.2. Transformer
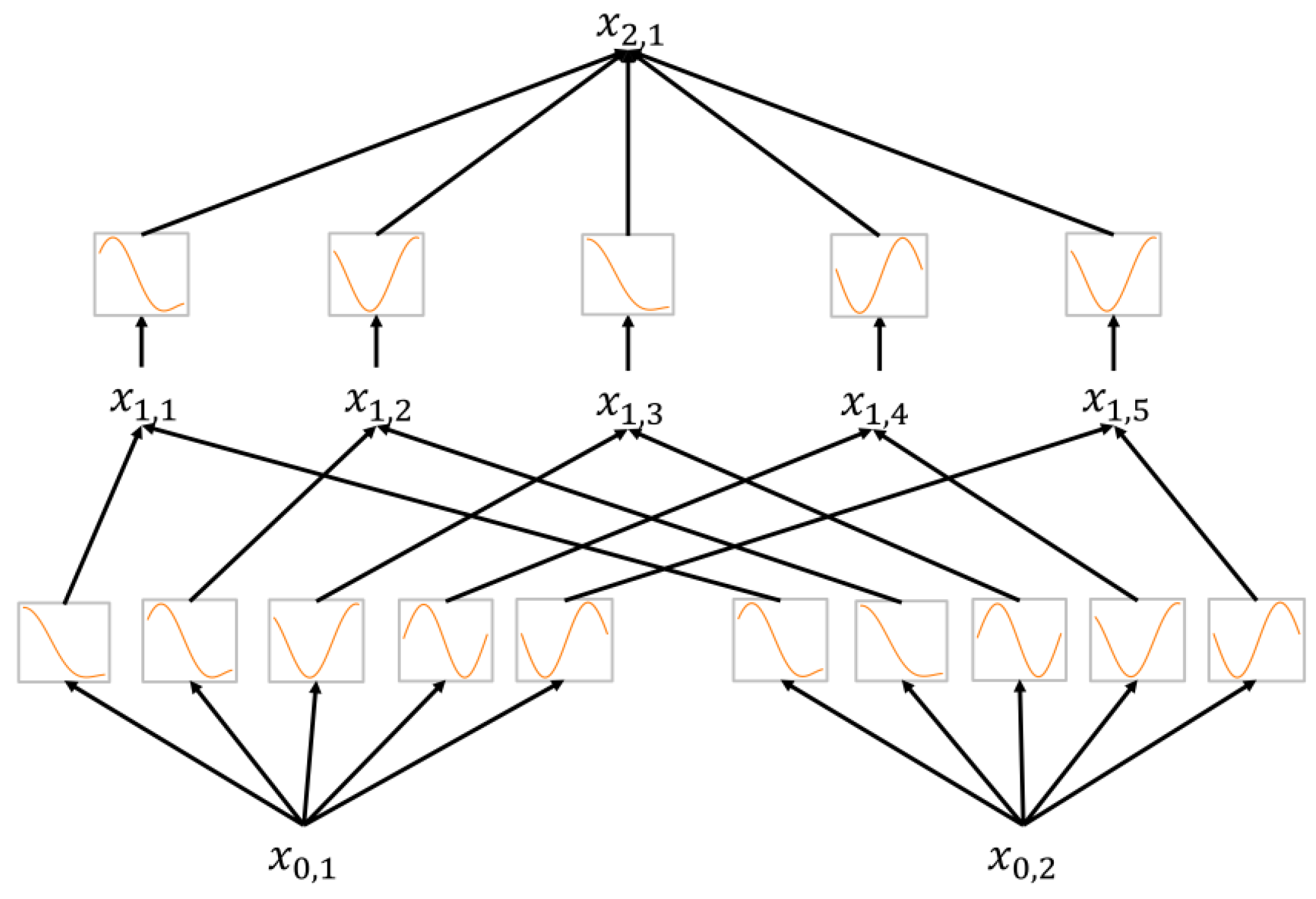
4.3. Kolmogorov–Arnold Network (KAN)
5. Summary
6. Discussion and Future Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Onn, C.C.; Chai, C.; Abd Rashid, A.F.; Karim, M.R.; Yusoff, S. Vehicle electrification in a developing country: Status and issue, from a well-to-wheel perspective. Transp. Res. Part D Transp. Environ. 2017, 50, 192–201. [Google Scholar] [CrossRef]
- Xu, B.; Lin, B.Q. Differences in regional emissions in China’s transport sector: Determinants and reduction strategies. Energy 2016, 95, 459–470. [Google Scholar] [CrossRef]
- Wang, G.; Guo, X.; Chen, J.; Han, P.; Su, Q.; Guo, M.; Wang, B.; Song, H. Safety Performance and Failure Criteria of Lithium-Ion Batteries under Mechanical Abuse. Energies 2023, 16, 6346. [Google Scholar] [CrossRef]
- Sun, S.H.; Wang, W.C. Analysis on the market evolution of new energy vehicle based on population competition model. Transp. Res. Part D Transp. Environ. 2018, 65, 36–50. [Google Scholar] [CrossRef]
- Ali, A.; Shakoor, R.; Raheem, A.; Muqeet, H.A.u.; Awais, Q.; Khan, A.A.; Jamil, M. Latest energy storage trends in multi-energy standalone electric vehicle charging stations: A comprehensive study. Energies 2022, 15, 4727. [Google Scholar] [CrossRef]
- Yuan, X.D.; Cai, Y.C. Forecasting the development trend of low emission vehicle technologies: Based on patent data. Technol. Forecast. Soc. Chang. 2021, 166, 120651. [Google Scholar] [CrossRef]
- He, W.; Li, Z.; Liu, T.; Liu, Z.; Guo, X.; Du, J.; Li, X.; Sun, P.; Ming, W. Research progress and application of deep learning in remaining useful life, state of health and battery thermal management of lithium batteries. J. Energy Storage 2023, 70, 107868. [Google Scholar] [CrossRef]
- Jaguemont, J.; Van Mierlo, J. A comprehensive review of future thermal management systems for battery-electrified vehicles. J. Energy Storage 2020, 31, 101551. [Google Scholar] [CrossRef]
- Liang, L.; Zhao, Y.; Diao, Y.; Ren, R.; Zhang, L.; Wang, G. Optimum cooling surface for prismatic lithium battery with metal shell based on anisotropic thermal conductivity and dimensions. J. Power Sources 2021, 506, 230182. [Google Scholar] [CrossRef]
- Hannan, M.A.; Hoque, M.M.; Mohamed, A.; Ayob, A. Review of energy storage systems for electric vehicle applications: Issues and challenges. Renew. Sustain. Energy Rev. 2017, 69, 771–789. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, B.; Li, B.; Yan, Y. A critical review of thermal management models and solutions of lithium-ion batteries for the development of pure electric vehicles. Renew. Sustain. Energy Rev. 2016, 64, 106–128. [Google Scholar] [CrossRef]
- Pavlovskii, A.A.; Pushnitsa, K.; Kosenko, A.; Novikov, P.; Popovich, A.A. Organic anode materials for lithium-ion batteries: Recent progress and challenges. Materials 2022, 16, 177. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Deng, J.; Robert, B.; Chen, W.; Siegmund, T. Experimental investigation on cooling of prismatic battery cells through cell integrated features. Energy 2022, 244, 122580. [Google Scholar] [CrossRef]
- Tete, P.R.; Gupta, M.M.; Joshi, S.S. Developments in battery thermal management systems for electric vehicles: A technical review. J. Energy Storage 2021, 35, 102255. [Google Scholar] [CrossRef]
- Al Miaari, A.; Ali, H.M. Batteries temperature prediction and thermal management using machine learning: An overview. Energy Rep. 2023, 10, 2277–2305. [Google Scholar] [CrossRef]
- Jay, R.P.; Manish, K.R. Phase change material selection using simulation-oriented optimization to improve the thermal performance of lithium-ion battery. J. Energy Storage 2022, 49, 103974. [Google Scholar] [CrossRef]
- Liu, H.; Wei, Z.; He, W.; Zhao, J. Thermal issues about Li-ion batteries and recent progress in battery thermal management systems: A review. Energy Convers. Manag. 2017, 150, 304–330. [Google Scholar] [CrossRef]
- Jaewan, K.; Jinwoo, O.; Hoseong, L. Review on battery thermal management system for electric vehicles. Appl. Therm. Eng. 2019, 149, 192–212. [Google Scholar] [CrossRef]
- Muench, S.; Wild, A.; Friebe, C.; Häupler, B.; Janoschka, T.; Schubert, U.S. Polymer-Based Organic Batteries. Chem. Rev. 2016, 116, 9438–9484. [Google Scholar] [CrossRef] [PubMed]
- Cui, X.; Zeng, J.; Zhang, H.; Yang, J.; Qiao, J.; Li, J.; Li, W. Simplification strategy research on hard-cased Li-ion battery for thermal modeling. Int. J. Energy Res. 2020, 44, 3640–3656. [Google Scholar] [CrossRef]
- Jin, S.-Q.; Li, N.; Bai, F.; Chen, Y.-J.; Feng, X.-Y.; Li, H.-W.; Gong, X.-M.; Tao, W.-Q. Data-driven model reduction for fast temperature prediction in a multi-variable data center. Int. Commun. Heat Mass Transf. 2023, 142, 106645. [Google Scholar] [CrossRef]
- Li, A.; Weng, J.; Yuen, A.C.Y.; Wang, W.; Liu, H.; Lee, E.W.M.; Wang, J.; Kook, S.; Yeoh, G.H. Machine learning assisted advanced battery thermal management system: A state-of-the-art review. J. Energy Storage 2023, 60, 106688. [Google Scholar] [CrossRef]
- Sandeep Dattu, C.; Chaithanya, A.; Jeevan, J.; Satyam, P.; Michael, F.; Roydon, F. Comparison of lumped and 1D electrochemical models for prismatic 20Ah LiFePO4 battery sandwiched between minichannel cold-plates. Appl. Therm. Eng. 2021, 199, 117586. [Google Scholar] [CrossRef]
- Fang, P.; Zhang, A.; Wang, D.; Sui, X.; Yin, L. Lumped model of Li-ion battery considering hysteresis effect. J. Energy Storage 2024, 86, 111185. [Google Scholar] [CrossRef]
- Lenz, C.; Hennig, J.; Tegethoff, W.; Schweiger, H.G.; Koehler, J. Analysis of the Interaction and Variability of Thermal Decomposition Reactions of a Li-ion Battery Cell. J. Electrochem. Soc. 2023, 170, 060523. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, L.; Xiao, Q.; Bai, X.; Wu, B.; Wu, N.; Zhao, Y.; Wang, J.; Feng, L. End-to-end fusion of hyperspectral and chlorophyll fluorescence imaging to identify rice stresses. Plant Phenomics 2022, 2022, 9851096. [Google Scholar] [CrossRef]
- Talaei Khoei, T.; Ould Slimane, H.; Kaabouch, N. Deep learning: Systematic review, models, challenges, and research directions. Neural Comput. Appl. 2023, 35, 23103–23124. [Google Scholar] [CrossRef]
- Bao, S.D.; Wang, T.T.; Zhou, L.L.; Dai, G.L.; Sun, G.; Shen, J. Two-Layer Matrix Factorization and Multi-Layer Perceptron for Online Service Recommendation. Appl. Sci. 2022, 12, 7369. [Google Scholar] [CrossRef]
- Zhu, F.; Chen, J.; Ren, D.; Han, Y. Transient temperature fields of the tank vehicle with various parameters using deep learning method. Appl. Therm. Eng. 2023, 230, 120697. [Google Scholar] [CrossRef]
- Xu, Y.; Zhao, J.P.; Chen, J.Q.; Zhang, H.C.; Feng, Z.X.; Yuan, J.L. Performance analyses on the air cooling battery thermal management based on artificial neural networks. Appl. Therm. Eng. 2024, 252, 123567. [Google Scholar] [CrossRef]
- O’shea, K.; Nash, R. An introduction to convolutional neural networks. arXiv 2015, arXiv:1511.08458. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the Advances in Neural Information Processing Systems 27 (Nips 2014), Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. Kan: Kolmogorov-Arnold networks. arXiv 2024, arXiv:2404.19756. [Google Scholar]
- Sohl-Dickstein, J.; Weiss, E.; Maheswaranathan, N.; Ganguli, S. Deep unsupervised learning using nonequilibrium thermodynamics. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 2256–2265. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. In Proceedings of the Advances in Neural Information Processing Systems 30 (Nips 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Angelov, P.P.; Soares, E.A.; Jiang, R.; Arnold, N.I.; Atkinson, P.M. Explainable artificial intelligence: An analytical review. WIREs Data Min. Knowl. Discov. 2021, 11, e1424. [Google Scholar] [CrossRef]
- Hossein, M.-R.; Rata, R.; Sompop, B.; Joachim, K.; Falk, S. Deep learning: A primer for dentists and dental researchers. J. Dent. 2023, 130, 104430. [Google Scholar] [CrossRef]
- Guo, C.; Liu, L.; Sun, H.; Wang, N.; Zhang, K.; Zhang, Y.; Zhu, J.; Li, A.; Bai, Z.; Liu, X. Predicting Fv/Fm and evaluating cotton drought tolerance using hyperspectral and 1D-CNN. Front. Plant Sci. 2022, 13, 1007150. [Google Scholar] [CrossRef] [PubMed]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Robbins, H.; Monro, S. A stochastic approximation method. Ann. Math. Stat. 1951, 400–407. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, Y.; Yin, W. An improved analysis of stochastic gradient descent with momentum. In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 6–12 December 2020; pp. 18261–18271. [Google Scholar]
- Sun, S.; Cao, Z.; Zhu, H.; Zhao, J. A survey of optimization methods from a machine learning perspective. IEEE Trans. Cybern. 2019, 50, 3668–3681. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Persson Hodén, K.; Hu, X.; Martinez, G.; Dixelius, C. smartpare: An r package for efficient identification of true mRNA cleavage sites. Int. J. Mol. Sci. 2021, 22, 4267. [Google Scholar] [CrossRef]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Bassiouni, M.M.; Chakrabortty, R.K.; Hussain, O.K.; Rahman, H.F. Advanced deep learning approaches to predict supply chain risks under COVID-19 restrictions. Expert Syst. Appl. 2023, 211, 118604. [Google Scholar] [CrossRef] [PubMed]
- Reyad, M.; Sarhan, A.M.; Arafa, M. A modified Adam algorithm for deep neural network optimization. Neural Comput. Appl. 2023, 35, 17095–17112. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Micikevicius, P.; Narang, S.; Alben, J.; Diamos, G.; Elsen, E.; Garcia, D.; Ginsburg, B.; Houston, M.; Kuchaiev, O.; Venkatesh, G. Mixed precision training. arXiv 2017, arXiv:1710.03740. [Google Scholar]
- Li, H.; Wang, Y.; Hong, Y.; Li, F.; Ji, X. Layered mixed-precision training: A new training method for large-scale AI models. J. King Saud Univ. Comput. Inf. Sci. 2023, 35, 101656. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.M.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the Advances in Neural Information Processing Systems 32 (Nips 2019), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M. {TensorFlow}: A system for {Large-Scale} machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Berkeley, CA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Adedigba, A.P.; Adeshina, S.A.; Aibinu, A.M. Performance Evaluation of Deep Learning Models on Mammogram Classification Using Small Dataset. Bioengineering 2022, 9, 161. [Google Scholar] [CrossRef]
- Wang, S.F.; Wang, H.W.; Perdikaris, P. Learning the solution operator of parametric partial differential equations with physics-informed DeepONets. Sci. Adv. 2021, 7, eabi8605. [Google Scholar] [CrossRef] [PubMed]
- Gu, J.X.; Wang, Z.H.; Kuen, J.; Ma, L.Y.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.X.; Wang, G.; Cai, J.F.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Long, H.X.; Liao, B.; Xu, X.Y.; Yang, J.L. A Hybrid Deep Learning Model for Predicting Protein Hydroxylation Sites. Int. J. Mol. Sci. 2018, 19, 2817. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.F.; Zhou, F.L.; Ma, L. An Automatic Detection Framework for Electrical Anomalies in Electrified Rail Transit System. IEEE Trans. Instrum. Meas. 2023, 72, 3510313. [Google Scholar] [CrossRef]
- Mahmoudi, M.A.; Chetouani, A.; Boufera, F.; Tabia, H. Learnable pooling weights for facial expression recognition. Pattern Recognit. Lett. 2020, 138, 644–650. [Google Scholar] [CrossRef]
- Wang, M.Y.; Hu, W.F.; Jiang, Y.F.; Su, F.; Fang, Z. Internal temperature prediction of ternary polymer lithium-ion battery pack based on CNN and virtual thermal sensor technology. Int. J. Energy Res. 2021, 45, 13681–13691. [Google Scholar] [CrossRef]
- Ma, H.L.; Bao, X.Y.; Lopes, A.; Chen, L.P.; Liu, G.Q.; Zhu, M. State-of-Charge Estimation of Lithium-Ion Battery Based on Convolutional Neural Network Combined with Unscented Kalman Filter. Batteries 2024, 10, 198. [Google Scholar] [CrossRef]
- Sherkatghanad, Z.; Ghazanfari, A.; Makarenkov, V. A self-attention-based CNN-Bi-LSTM model for accurate state-of-charge estimation of lithium-ion batteries. J. Energy Storage 2024, 88, 111524. [Google Scholar] [CrossRef]
- Yalçın, S.; Panchal, S.; Herdem, M.S. A CNN-ABC model for estimation and optimization of heat generation rate and voltage distributions of lithium-ion batteries for electric vehicles. Int. J. Heat Mass Transf. 2022, 199, 123486. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Cao, X.; Du, J.; Qu, C.; Wang, J.; Tu, R. An early diagnosis method for overcharging thermal runaway of energy storage lithium batteries. J. Energy Storage 2024, 75, 109661. [Google Scholar] [CrossRef]
- Wang, Z.G.; Oates, T. Imaging Time-Series to Improve Classification and Imputation. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence (IJCAI), Buenos Aires, Argentina, 25–31 July 2015; pp. 3939–3945. [Google Scholar]
- Medsker, L.R.; Jain, L. Recurrent neural networks. Des. Appl. 2001, 5, 2. [Google Scholar]
- Berman, D.S.; Buczak, A.L.; Chavis, J.S.; Corbett, C.L. A Survey of Deep Learning Methods for Cyber Security. Information 2019, 10, 122. [Google Scholar] [CrossRef]
- Zaremba, W.; Sutskever, I.; Vinyals, O. Recurrent neural network regularization. arXiv 2014, arXiv:1409.2329. [Google Scholar]
- Zhang, Y.; Li, Y.F. Prognostics and health management of Lithium-ion battery using deep learning methods: A review. Renew. Sustain. Energy Rev. 2022, 161, 112282. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, R.Q.; Qi, Y.; Wen, F. A watershed water quality prediction model based on attention mechanism and Bi-LSTM. Environ. Sci. Pollut. Res. 2022, 29, 75664–75680. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.; Lim, Y.-H.; Ha, E.; Kim, Y.; Lee, W.K. Forecasting of non-accidental, cardiovascular, and respiratory mortality with environmental exposures adopting machine learning approaches. Environ. Sci. Pollut. Res. 2022, 29, 88318–88329. [Google Scholar] [CrossRef] [PubMed]
- Yan, R.G.; Jiang, X.; Wang, W.R.; Dang, D.P.; Su, Y.J. Materials information extraction via automatically generated corpus. Sci. Data 2022, 9, 401. [Google Scholar] [CrossRef]
- Tao, S.Y.; Jiang, B.; Wei, X.Z.; Dai, H.F. A Systematic and Comparative Study of Distinct Recurrent Neural Networks for Lithium-Ion Battery State-of-Charge Estimation in Electric Vehicles. Energies 2023, 16, 2008. [Google Scholar] [CrossRef]
- Achanta, S.; Gangashetty, S.V. Deep Elman recurrent neural networks for statistical parametric speech synthesis. Speech Commun. 2017, 93, 31–42. [Google Scholar] [CrossRef]
- Dey, R.; Salem, F.M. Gate-variants of gated recurrent unit (GRU) neural networks. In Proceedings of the 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 6–9 August 2017; pp. 1597–1600. [Google Scholar]
- Cui, Z.H.; Kang, L.; Li, L.W.; Wang, L.C.; Wang, K. A hybrid neural network model with improved input for state of charge estimation of lithium-ion battery at low temperatures. Renew. Energy 2022, 198, 1328–1340. [Google Scholar] [CrossRef]
- Li, M.R.; Dong, C.Y.; Xiong, B.Y.; Mu, Y.F.; Yu, X.D.; Xiao, Q.; Jia, H.J. STTEWS: A sequential-transformer thermal early warning system for lithium-ion battery safety. Appl. Energy 2022, 328, 119965. [Google Scholar] [CrossRef]
- Bamati, S.; Chaoui, H.; Gualous, H. Virtual Temperature Sensor in Battery Thermal Management System Using LSTM-DNN. In Proceedings of the 2023 IEEE Vehicle Power and Propulsion Conference (VPPC), Milan, Italy, 24–27 October 2023; pp. 1–6. [Google Scholar]
- Yao, Q.; Lu, D.D.-C.; Lei, G. A surface temperature estimation method for lithium-ion battery using enhanced GRU-RNN. IEEE Trans. Transp. Electrif. 2022, 9, 1103–1112. [Google Scholar] [CrossRef]
- Li, D.; Liu, P.; Zhang, Z.S.; Zhang, L.; Deng, J.J.; Wang, Z.P.; Dorrell, D.G.; Li, W.H.; Sauer, D.U. Battery Thermal Runaway Fault Prognosis in Electric Vehicles Based on Abnormal Heat Generation and Deep Learning Algorithms. IEEE Trans. Power Electron. 2022, 37, 8513–8525. [Google Scholar] [CrossRef]
- Naaz, F.; Herle, A.; Channegowda, J.; Raj, A.; Lakshminarayanan, M. A generative adversarial network-based synthetic data augmentation technique for battery condition evaluation. Int. J. Energy Res. 2021, 45, 19120–19135. [Google Scholar] [CrossRef]
- Zhou, T.; Li, Q.; Lu, H.; Cheng, Q.; Zhang, X. GAN review: Models and medical image fusion applications. Inf. Fusion 2023, 91, 134–148. [Google Scholar] [CrossRef]
- Su, Y.H.; Meng, L.; Kong, X.J.; Xu, T.L.; Lan, X.S.; Li, Y.F. Generative Adversarial Networks for Gearbox of Wind Turbine with Unbalanced Data Sets in Fault Diagnosis. IEEE Sens. J. 2022, 22, 13285–13298. [Google Scholar] [CrossRef]
- Que, Y.; Dai, Y.; Ji, X.; Leung, A.K.; Chen, Z.; Jiang, Z.L.; Tang, Y.C. Automatic classification of asphalt pavement cracks using a novel integrated generative adversarial networks and improved VGG model. Eng. Struct. 2023, 277, 115406. [Google Scholar] [CrossRef]
- Wang, K.F.; Gou, C.; Duan, Y.J.; Lin, Y.L.; Zheng, X.H.; Wang, F.Y. Generative Adversarial Networks: Introduction and Outlook. IEEE/CAA J. Autom. Sin. 2017, 4, 588–598. [Google Scholar] [CrossRef]
- Qiu, X.H.; Wang, S.F.; Chen, K. A conditional generative adversarial network-based synthetic data augmentation technique for battery state-of-charge estimation. Appl. Soft Comput. 2023, 142, 110281. [Google Scholar] [CrossRef]
- Li, H.; Chen, G.H.; Yang, Y.Z.; Shu, B.Y.; Liu, Z.J.; Peng, J. Adversarial learning for robust battery thermal runaway prognostic of electric vehicles. J. Energy Storage 2024, 82, 110381. [Google Scholar] [CrossRef]
- Hu, F.S.; Dong, C.Y.; Tian, L.Y.; Mu, Y.F.; Yu, X.D.; Jia, H.J. CWGAN-GP with residual network model for lithium-ion battery thermal image data expansion with quantitative metrics. Energy Ai 2024, 16, 100321. [Google Scholar] [CrossRef]
- Rubner, Y.; Tomasi, C.; Guibas, L.J. The Earth Mover’s Distance as a metric for image retrieval. Int. J. Comput. Vis. 2000, 40, 99–121. [Google Scholar] [CrossRef]
- Chakraborty, T.; Reddy, K.S.U.; Naik, S.M.; Panja, M.; Manvitha, B. Ten years of generative adversarial nets (GANs): A survey of the state-of-the-art. Mach. Learn. Sci. Technol. 2024, 5, 011001. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, Z.; Song, Y.; Hong, S.; Xu, R.; Zhao, Y.; Zhang, W.; Cui, B.; Yang, M.-H. Diffusion models: A comprehensive survey of methods and applications. ACM Comput. Surv. 2023, 56, 1–39. [Google Scholar] [CrossRef]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 6–12 December 2020; pp. 6840–6851. [Google Scholar]
- Ramesh, A.; Dhariwal, P.; Nichol, A.; Chu, C.; Chen, M. Hierarchical text-conditional image generation with clip latents. arXiv 2022, arXiv:2204.06125. [Google Scholar]
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10684–10695. [Google Scholar]
- Saharia, C.; Chan, W.; Saxena, S.; Li, L.; Whang, J.; Denton, E.L.; Ghasemipour, K.; Gontijo Lopes, R.; Karagol Ayan, B.; Salimans, T. Photorealistic text-to-image diffusion models with deep language understanding. In Proceedings of the Advances in Neural Information Processing Systems, New Orleans, LA, USA, 28 November–9 December 2022; pp. 36479–36494. [Google Scholar]
- Bandi, A.; Adapa, P.V.S.R.; Kuchi, Y.E.V.P.K. The Power of Generative AI: A Review of Requirements, Models, Input-Output Formats, Evaluation Metrics, and Challenges. Future Internet 2023, 15, 260. [Google Scholar] [CrossRef]
- Cao, H.Q.; Tan, C.; Gao, Z.Y.; Xu, Y.L.; Chen, G.Y.; Heng, P.A.; Li, S.Z. A Survey on Generative Diffusion Models. IEEE Trans. Knowl. Data Eng. 2024, 36, 2814–2830. [Google Scholar] [CrossRef]
- Casolaro, A.; Capone, V.; Iannuzzo, G.; Camastra, F. Deep Learning for Time Series Forecasting: Advances and Open Problems. Information 2023, 14, 598. [Google Scholar] [CrossRef]
- Croitoru, F.A.; Hondru, V.; Ionescu, R.T.; Shah, M. Diffusion Models in Vision: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10850–10869. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, Z.; Zhu, S.; Li, Y. State-of-Health Prediction of Lithium-Ion Batteries Based on Diffusion Model with Transfer Learning. Energies 2023, 16, 3815. [Google Scholar] [CrossRef]
- Huang, T.; Gao, Y.; Li, Z.; Hu, Y.; Xuan, F. A hybrid deep learning framework based on diffusion model and deep residual neural network for defect detection in composite plates. Appl. Sci. 2023, 13, 5843. [Google Scholar] [CrossRef]
- Liu, N.; Yuan, Z.M.; Tang, Q.F. Improving Alzheimer’s Disease Detection for Speech Based on Feature Purification Network. Front. Public Health 2022, 9, 835960. [Google Scholar] [CrossRef] [PubMed]
- Ding, H.; Li, F.J.; Chen, X.; Ma, J.; Nie, S.P.; Ye, R.; Yuan, C.J. ContransGAN: Convolutional Neural Network Coupling Global Swin-Transformer Network for High-Resolution Quantitative Phase Imaging with Unpaired Data. Cells 2022, 11, 2394. [Google Scholar] [CrossRef] [PubMed]
- Chang, X.; Feng, Z.; Wu, J.; Sun, H.; Wang, G.; Bao, X. Understanding and predicting the short-term passenger flow of station-free shared bikes: A spatiotemporal deep learning approach. IEEE Intell. Transp. Syst. Mag. 2021, 14, 73–85. [Google Scholar] [CrossRef]
- Sajun, A.R.; Zualkernan, I.; Sankalpa, D. A Historical Survey of Advances in Transformer Architectures. Appl. Sci. 2024, 14, 4316. [Google Scholar] [CrossRef]
- Abibullaev, B.; Keutayeva, A.; Zollanvari, A. Deep Learning in EEG-Based BCIs: A Comprehensive Review of Transformer Models, Advantages, Challenges, and Applications. IEEE Access 2023, 11, 127271–127301. [Google Scholar] [CrossRef]
- Hannan, M.A.; How, D.N.T.; Lipu, M.S.H.; Mansor, M.; Ker, P.J.; Dong, Z.Y.; Sahari, K.S.M.; Tiong, S.K.; Muttaqi, K.M.; Mahlia, T.M.I.; et al. Deep learning approach towards accurate state of charge estimation for lithium-ion batteries using self-supervised transformer model. Sci. Rep. 2021, 11, 19541. [Google Scholar] [CrossRef]
- Hun, R.; Zhang, S.; Singh, G.; Qian, J.; Chen, Y.; Chiang, P.Y. LISA: A transferable light-weight multi-head self-attention neural network model for lithium-ion batteries state-of-charge estimation. In Proceedings of the 2021 3rd International Conference on Smart Power & Internet Energy Systems (SPIES), Shanghai, China, 25–28 September 2021; pp. 464–469. [Google Scholar]
- Kolmogorov, A.N. On the Representation of Continuous Functions of Several Variables by Superpositions of Continuous Functions of a Smaller Number of Variables; American Mathematical Society: Providence, RI, USA, 1961. [Google Scholar]
- Kolmogorov, A.N. On the representation of continuous functions of many variables by superposition of continuous functions of one variable and addition. Proc. Dokl. Akad. Nauk. 1957, 114, 953–956. [Google Scholar]
- Braun, J.; Griebel, M. On a Constructive Proof of Kolmogorov’s Superposition Theorem. Constr. Approx. 2009, 30, 653–675. [Google Scholar] [CrossRef]
- Yuan, L.; Chen, Y.; Tang, H.; Liu, Z.; Wu, W. DGNet: An adaptive lightweight defect detection model for new energy vehicle battery current collector. IEEE Sens. J. 2023, 23, 29815–29830. [Google Scholar] [CrossRef]

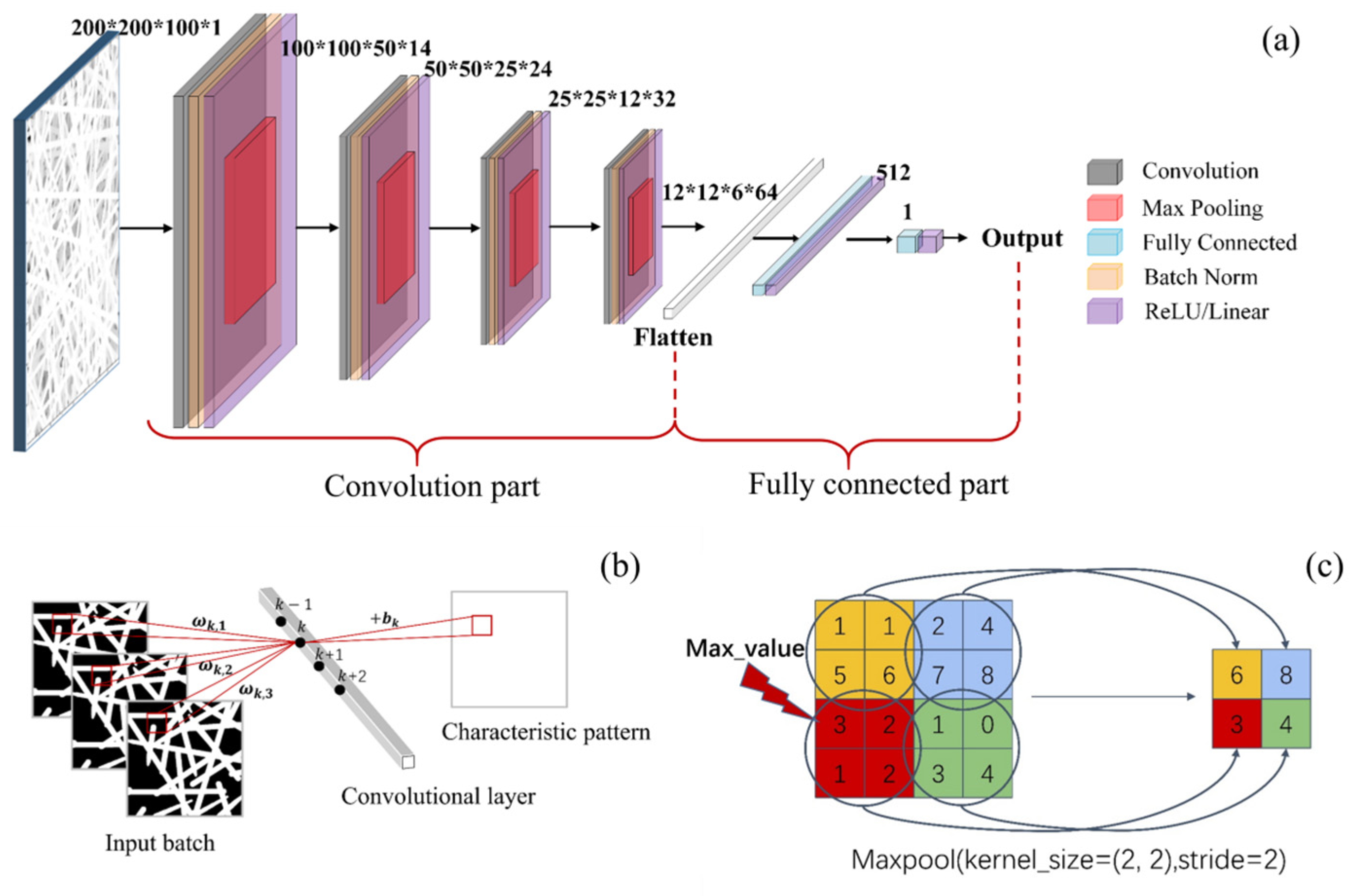
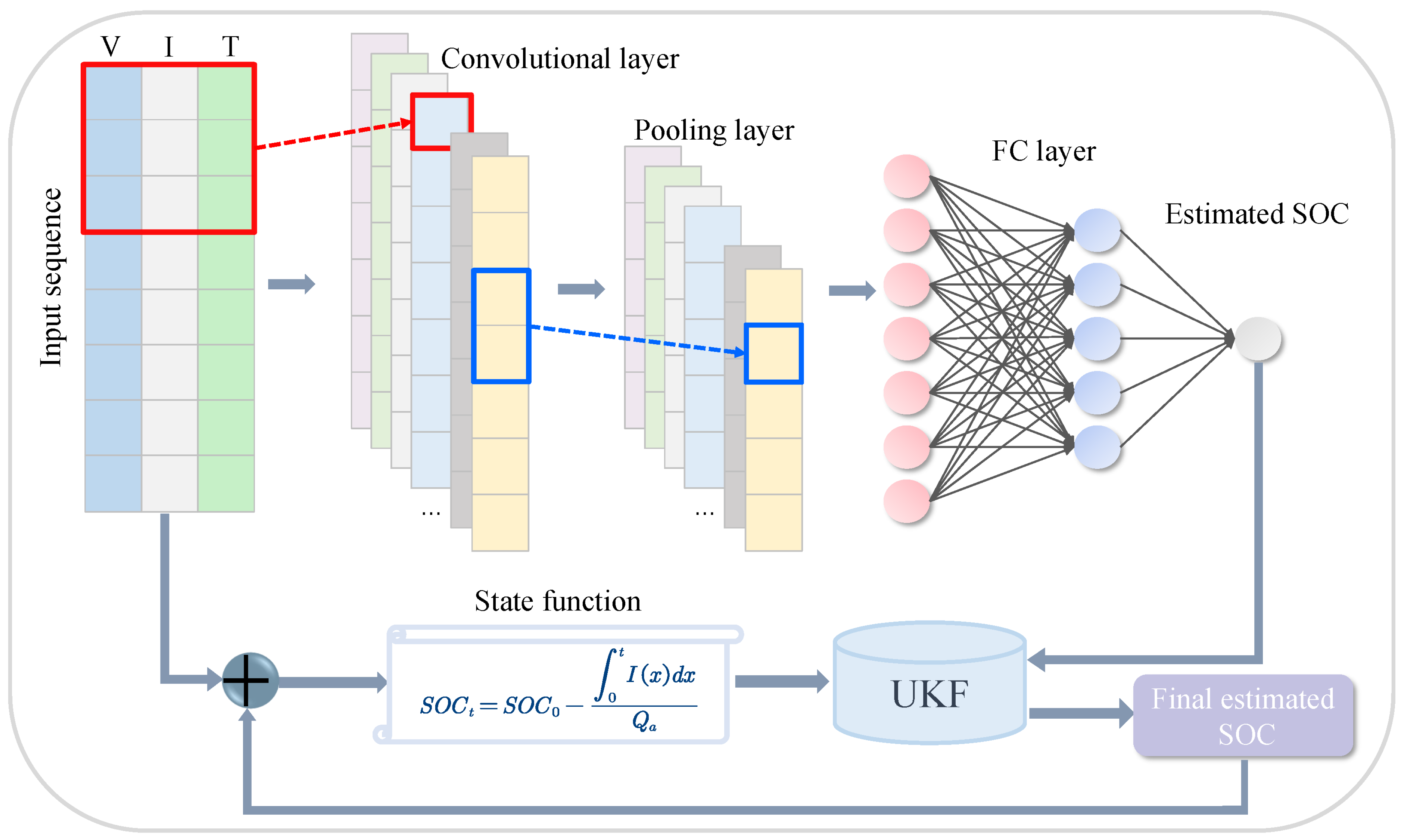
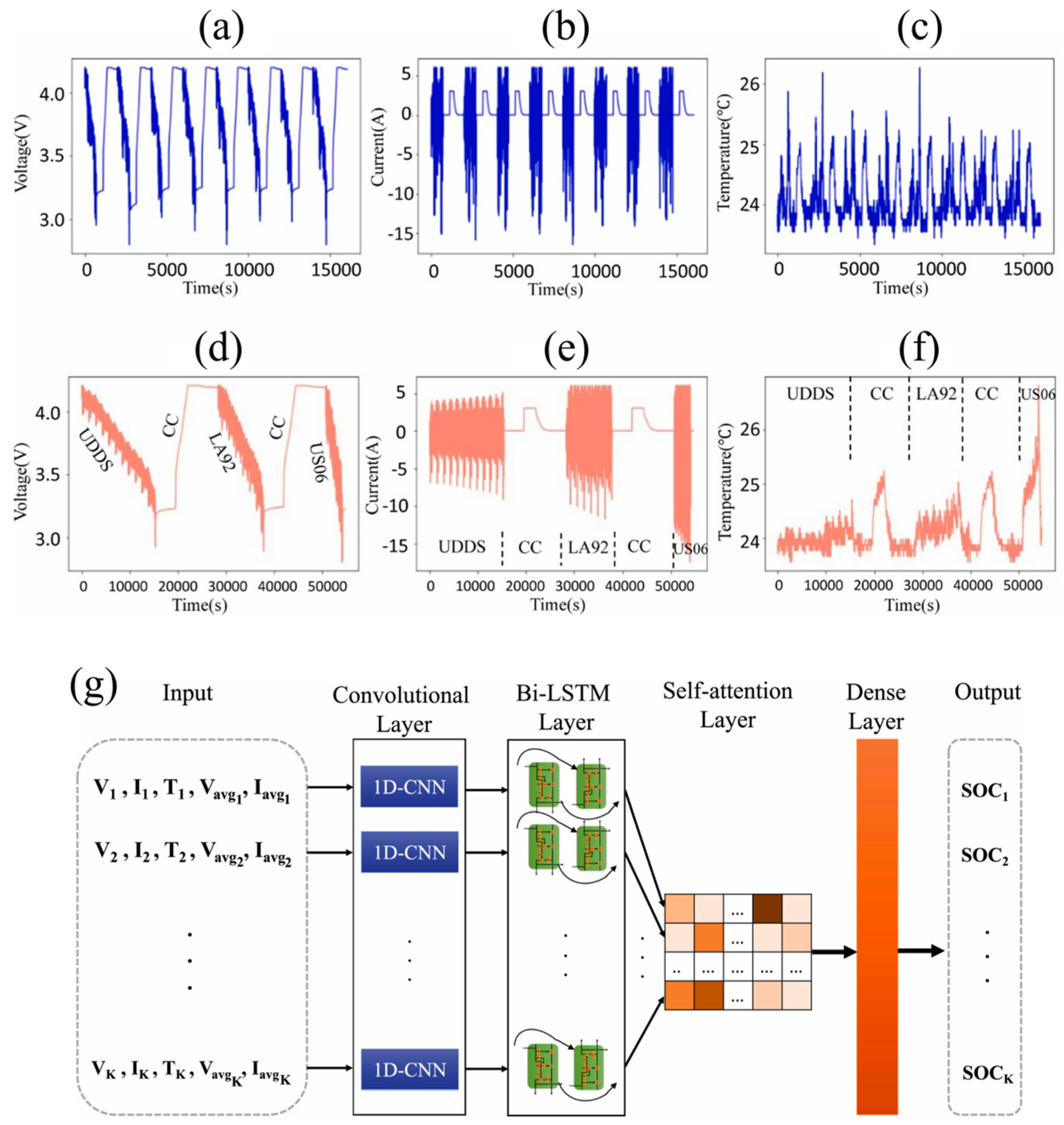
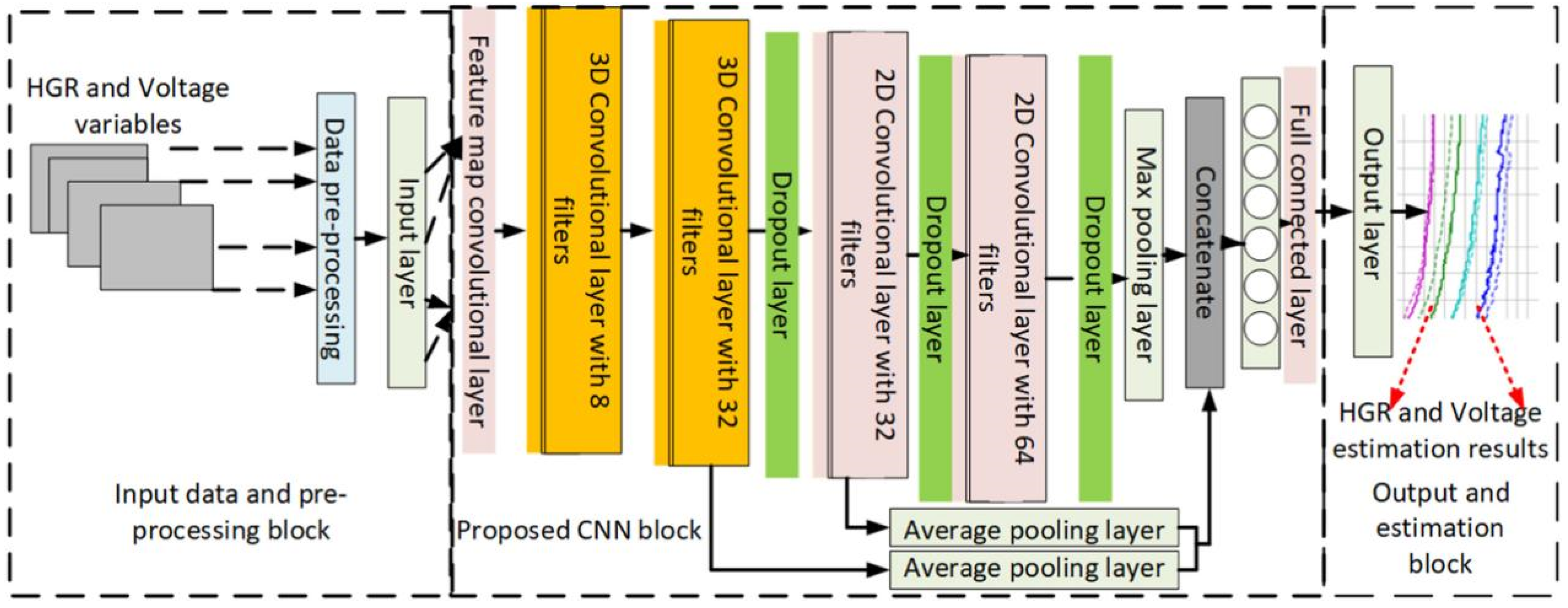


| Model | MSE | MAE | MAXE | R2 |
|---|---|---|---|---|
| LR | 0.1641 | 0.3441 | 0.3315 | 0.9823 |
| CNN | 0.047 | 0.1657 | 0.4689 | 0.9949 |
| Temperature | 10 °C | 0 °C | −10 °C | 25 °C | ||||
|---|---|---|---|---|---|---|---|---|
| RMSE (%) | MAE (%) | RMSE (%) | MAE (%) | RMSE (%) | MAE (%) | RMSE (%) | MAE (%) | |
| LSTM | 1.33 | 0.79 | 1.43 | 0.87 | 1.64 | 1.07 | 1.09 | 0.78 |
| LSTM-AM | 1.29 | 0.76 | 1.27 | 0.8 | 1.59 | 1.01 | 1.04 | 0.77 |
| Bi-LSTM | 1.31 | 0.77 | 1.25 | 0.83 | 1.61 | 1.03 | 1.08 | 0.8 |
| Bi-LSTM-AM | 1.28 | 0.77 | 1.23 | 0.78 | 1.57 | 0.93 | 1.05 | 0.76 |
| S-LSTM | 1.27 | 0.76 | 1.16 | 0.75 | 1.4 | 0.86 | 1.06 | 0.78 |
| S-LSTM-AM | 1.26 | 0.72 | 1.11 | 0.73 | 1.35 | 0.85 | 1.05 | 0.77 |
| S-Bi-LSTM | 1.26 | 0.75 | 1.1 | 0.73 | 1.29 | 0.81 | 1.05 | 0.78 |
| S-Bi-LSTM-AM | 1.25 | 0.73 | 1.08 | 0.71 | 1.28 | 0.77 | 1.05 | 0.78 |
| CNN-LSTM | 1.23 | 0.77 | 0.98 | 0.63 | 1.27 | 0.8 | 0.99 | 0.67 |
| CNN-LSTM-AM | 1.21 | 0.71 | 0.98 | 0.65 | 1.26 | 0.77 | 0.95 | 0.66 |
| CNN-Bi-LSTM | 1.23 | 0.76 | 0.99 | 0.62 | 1.25 | 0.78 | 1 | 0.72 |
| CNN-Bi-LSTM-AM | 1.2 | 0.67 | 0.97 | 0.61 | 1.19 | 0.72 | 0.92 | 0.66 |
| Temperature | 0 °C | −10 °C | −20 °C | |||
|---|---|---|---|---|---|---|
| RMSE (%) | MAE (%) | RMSE (%) | MAE (%) | RMSE (%) | MAE (%) | |
| UDDS | 0.00858 | 0.00659 | 0.0103 | 0.0075 | 0.0137 | 0.0104 |
| US06 | 0.0104 | 0.00877 | 0.0145 | 0.00987 | 0.0171 | 0.0127 |
| HWFET | 0.00813 | 0.00551 | 0.0144 | 0.0099 | 0.0133 | 0.00998 |
| LA92 | 0.00857 | 0.00687 | 0.0129 | 0.00902 | 0.0159 | 0.0126 |
| Authors, Year | Methods | Applications | Training Data | Performance | Shortcomings |
|---|---|---|---|---|---|
| Mengyi Wang et al. [63], 2021 | CNN + VTS | Predict the internal temperature of the battery. | Heat map of battery external temperature versus internal temperature | The accuracy of temperature prediction has obvious advantages over (linear regression) LR. | The robustness of the model remains to be verified. |
| Hongli Ma et al. [64], 2024 | CNN + UKF | Predict SOC. | Voltage, current and temperature, SOC | The proposed method outperforms other data-driven SOC estimation methods in terms of accuracy and robustness. | The model is sensitive to the filtering parameters, and the robustness of the model still has room for improvement. |
| Zeinab Sherkatghanad et al. [65], 2024 | CNN-Bi-LSTM-AM | Predict SOC over a wide range of temperatures. | SOC, current, voltage, temperature, average current, and average voltage | The model shows high estimation accuracy and prediction effect under different temperature conditions and has strong generalization ability. | Electrochemical information can be incorporated to expand the features, and the accuracy of the model still has room for improvement. |
| S Yalçın et al. [66], 2022 | CNN + ABC | Predict the battery HGR and voltage distribution. | Current, temperature, HGR, and voltage | The RMSE of HGR estimation is 1.38%, and the R2 is 99.72%. The RMSE of voltage estimation is 3.55%, and the R2 is 99.82%. | Validation for the prediction of battery life or other critical battery parameters is still lacking. |
| Yuan Xu et al. [30], 2024 | ResNet | Predict BTMS performance (maximum temperature and maximum temperature difference). | Cell spacing (d), main channel inclination (θ) and inlet velocity (v), Tmax, ΔTmax | The maximum temperature error of the model is 0.08%, and the maximum temperature difference error is 2.64%. | - |
| Xin Cao et al. [68], 2024 | ResNet + GASF | Early diagnosis of electrothermal runaway. | 2D thermodynamic image containing surface temperature time series information | A diagnostic accuracy of 97.7% is achieved before the battery surface temperature reaches 50 °C. | - |
| Zhenhua Cui et al. [80], 2022 | GRU + CNN | SOC estimation in low temperature environment. | Voltage, current and temperature, SOC | MAE and RMSE are less than 0.0127 and 0.0171, respectively. | - |
| Siyi Tao et al. [77], 2023 | RNN | Compare the performance of different RNN models in SOC estimation. | Current, voltage, and SOC | The BLSTM model performs best under NEDC, UDDS. and WLTP conditions with MAE values of 1.05%, 7.81%. and 1.81%, respectively. | - |
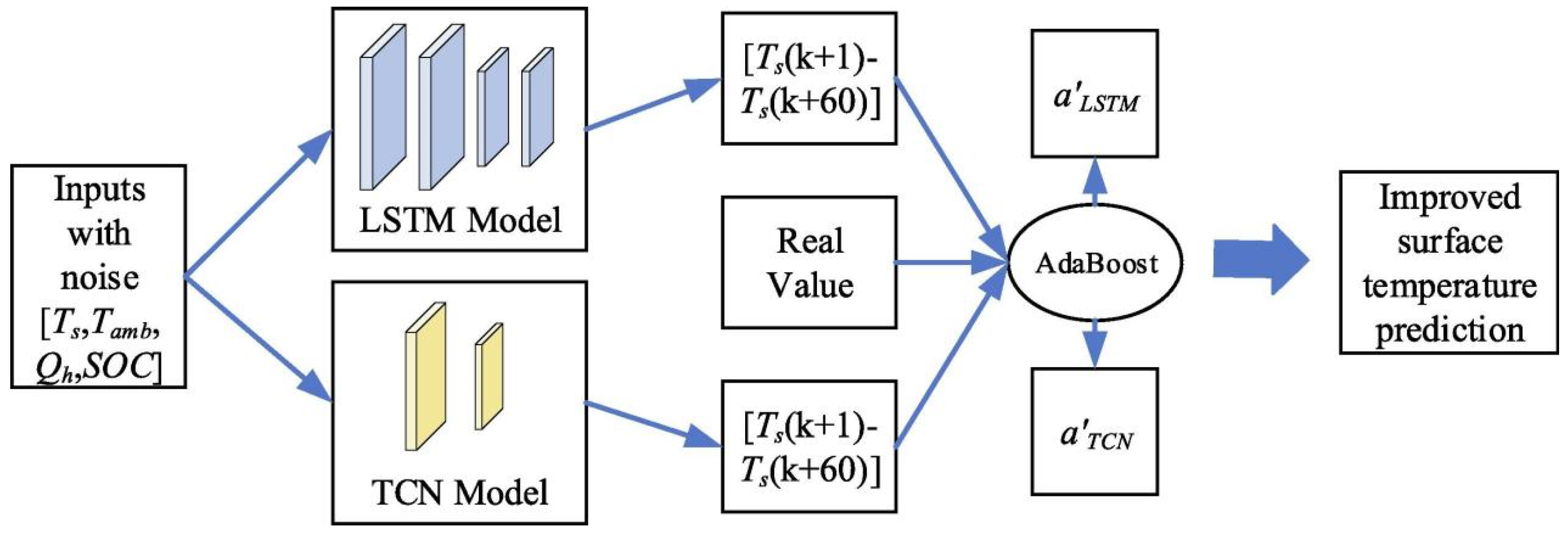
| Marui Li et al. [81], 2022 | LSTM + CNN | Estimate battery temperature trend. | Surface temperature, ambient temperature, heating rate, and SOC | The model can use 20 s of time series data to predict the surface temperature change of lithium-ion energy system in the next 60 s, and the maximum MSE reduction of the model is 0.01 compared with TCN. Compared to LSTM, the reduction can be up to 0.02. | - |
| Safieh Bamati et al. [82], 2023 | LSTM + DNN | Estimate the surface temperature of the battery. | Voltage and current time series and their average values | The proposed method can accurately estimate the surface temperature in the whole aging cycle of the battery, the prediction error range is only 0.25–2.45 °C, and it shows higher prediction accuracy in the later cycle of the battery. | - |
| Qi Yao et al. [83], 2022 | GRU | Estimate the surface temperature of the Li-ion battery. | Time series of voltage, current, SOC, and ambient temperature | It shows good performance and generalization ability under different ambient temperature conditions and different driving cycles. The MAE is less than 0.2 °C under the fixed ambient temperature condition and less than 0.42 °C under the varying ambient temperature condition. | At low temperature (−10 °C), the estimation error is higher. Under low temperature and varying temperature conditions, the estimation accuracy of the model needs to be further improved. |
| Da Li et al. [84], 2022 | LSTM + CNN | Predict battery thermal runaway, temperature. | Battery temperature, battery voltage, battery current, ambient temperature, etc | The battery temperature within the next 8 min can be accurately predicted with an average relative error of 0.28%. | The model has high complexity and depends heavily on the quality and diversity of the training data. |
| Falak Naaz et al. [85], 2021 | GAN | Broaden the dataset and enhance the SOC estimation. | Voltage, current, temperature, and SOC | It is verified on two datasets, and the model generates data with high fidelity. | - |
| Xianghui Qiu et al. [90], 2023 | C-LSTM-WGAN-GP | Conditionality broadens the dataset and enhances SOC estimation. | Class labels, temperature (T), voltage (V), and SOC series | The generated pseudo-samples are not only similar to the real samples, but also match the labels. The performance of SOC estimation models can be significantly improved by mixing synthetic data with real data for training compared to training with real data only. | The proposed model may still have room for improvement in accelerating the training convergence. |
| Heng Li et al. [91], 2024 | GAN | Early detection of electrothermal runaway. | Battery charging voltage curve | Compared with other methods, the proposed method can identify all abnormal cells before thermal runaway occurs and reduce the false positive rate by 7.54% to 31.18%. | - |
| Fengshuo Hu et al. [92], 2024 | WGAN-GP + ResNet | Directional expansion of the dataset to enhance thermal fault detection and judgment. | Fault thermal image during battery charging | After data augmentation, the fault diagnosis accuracy of the model is improved, the average accuracy is increased by 33.8%, and the average recall rate is increased by 31.9%. | There is still a clear quality gap between the generated images and the real ones. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, S.; Cheng, Y.; Li, Z.; Wang, J.; Li, H.; Zhang, C. Advanced Deep Learning Techniques for Battery Thermal Management in New Energy Vehicles. Energies 2024, 17, 4132. https://doi.org/10.3390/en17164132
Qi S, Cheng Y, Li Z, Wang J, Li H, Zhang C. Advanced Deep Learning Techniques for Battery Thermal Management in New Energy Vehicles. Energies. 2024; 17(16):4132. https://doi.org/10.3390/en17164132
Chicago/Turabian StyleQi, Shaotong, Yubo Cheng, Zhiyuan Li, Jiaxin Wang, Huaiyi Li, and Chunwei Zhang. 2024. "Advanced Deep Learning Techniques for Battery Thermal Management in New Energy Vehicles" Energies 17, no. 16: 4132. https://doi.org/10.3390/en17164132
APA StyleQi, S., Cheng, Y., Li, Z., Wang, J., Li, H., & Zhang, C. (2024). Advanced Deep Learning Techniques for Battery Thermal Management in New Energy Vehicles. Energies, 17(16), 4132. https://doi.org/10.3390/en17164132






