Optimization-Based Suppression Method of Oscillations in Photovoltaic Grid-Connected Systems with Controllable Nonlinear Loads
Abstract
1. Introduction
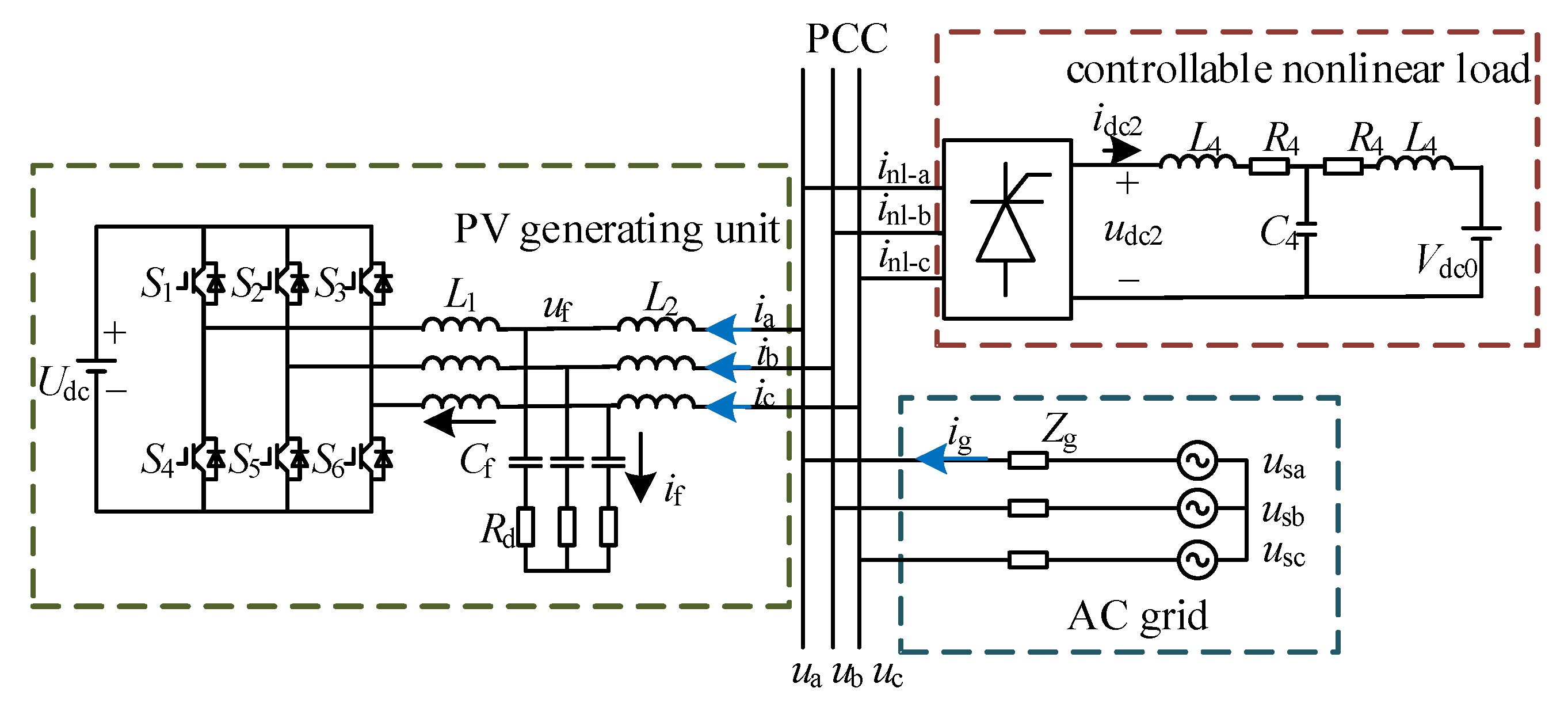
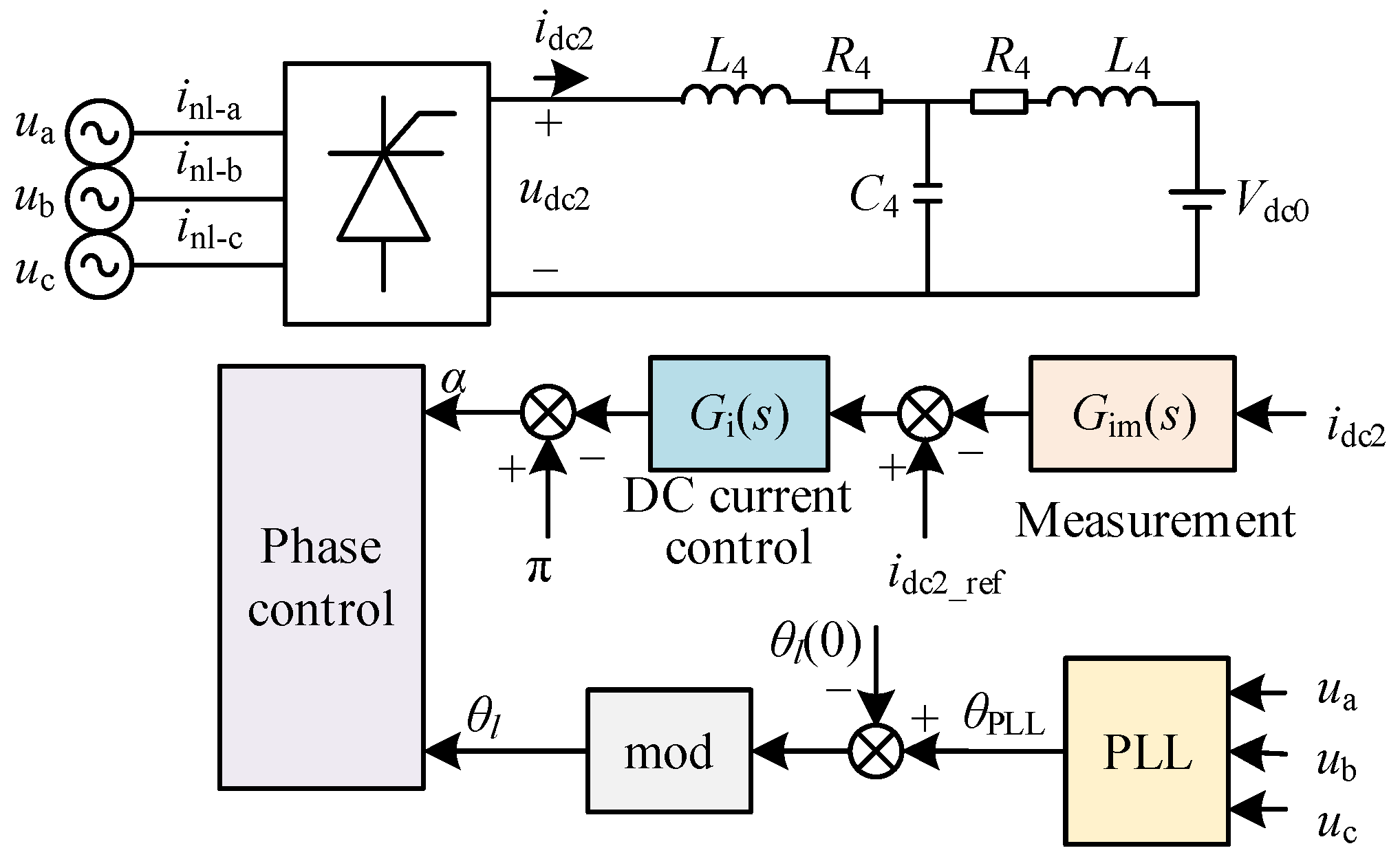
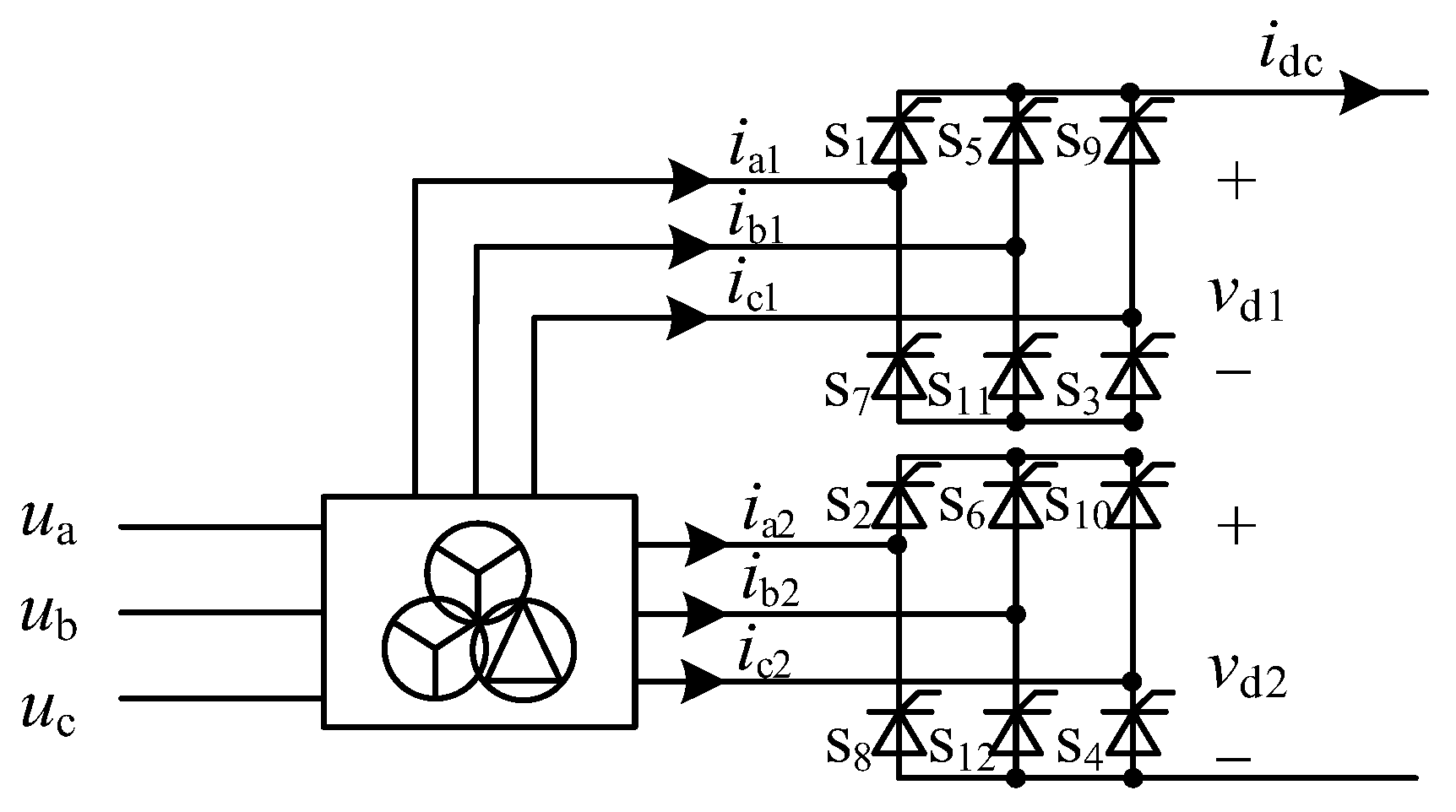
2. Impedance Modeling of the PV Grid-Connected System with Controllable Nonlinear Loads
3. Stability Analysis and Key Influencing Factor Analysis of the System
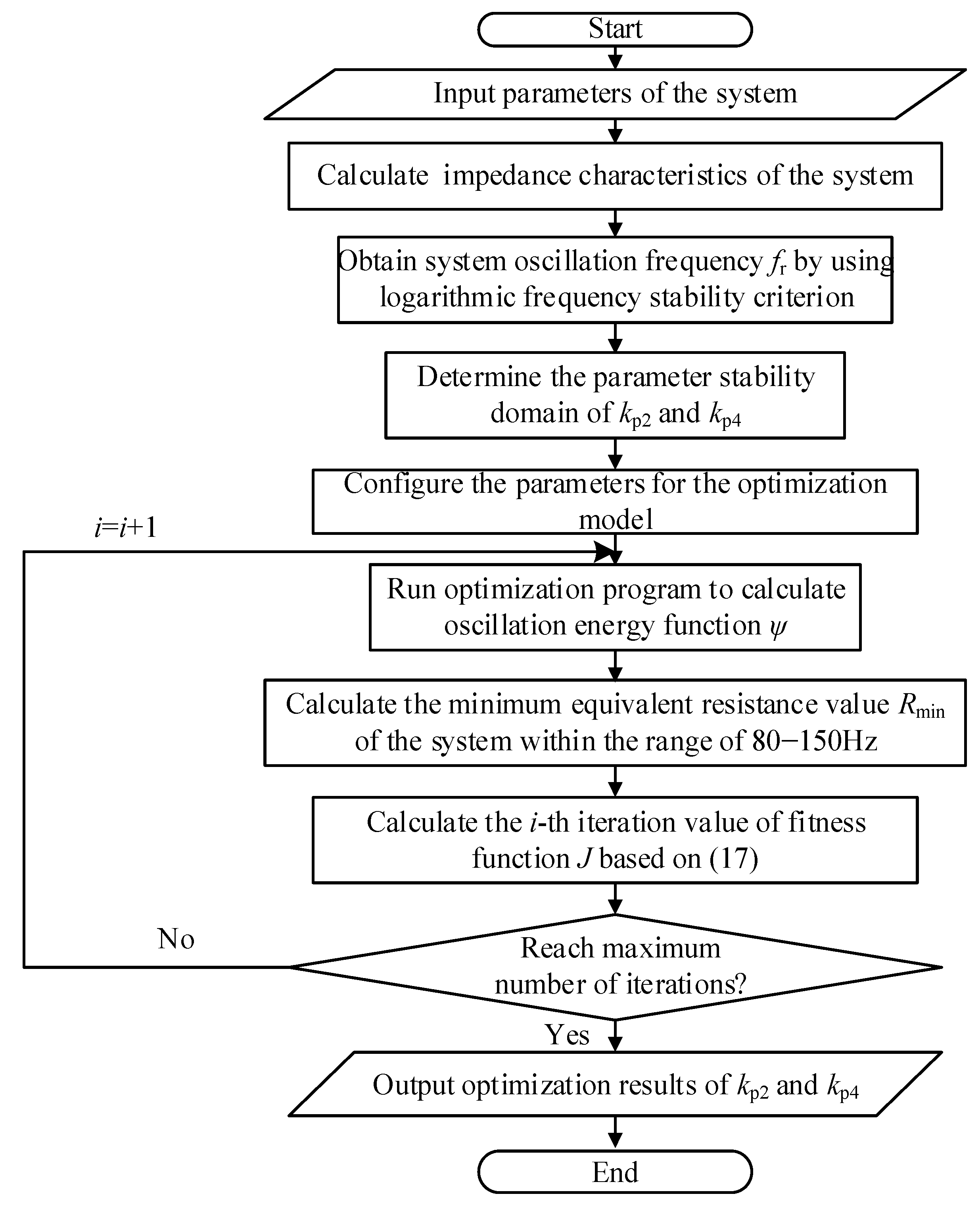
4. A Parameter-Optimization Method Balancing System Stability and Response Performance
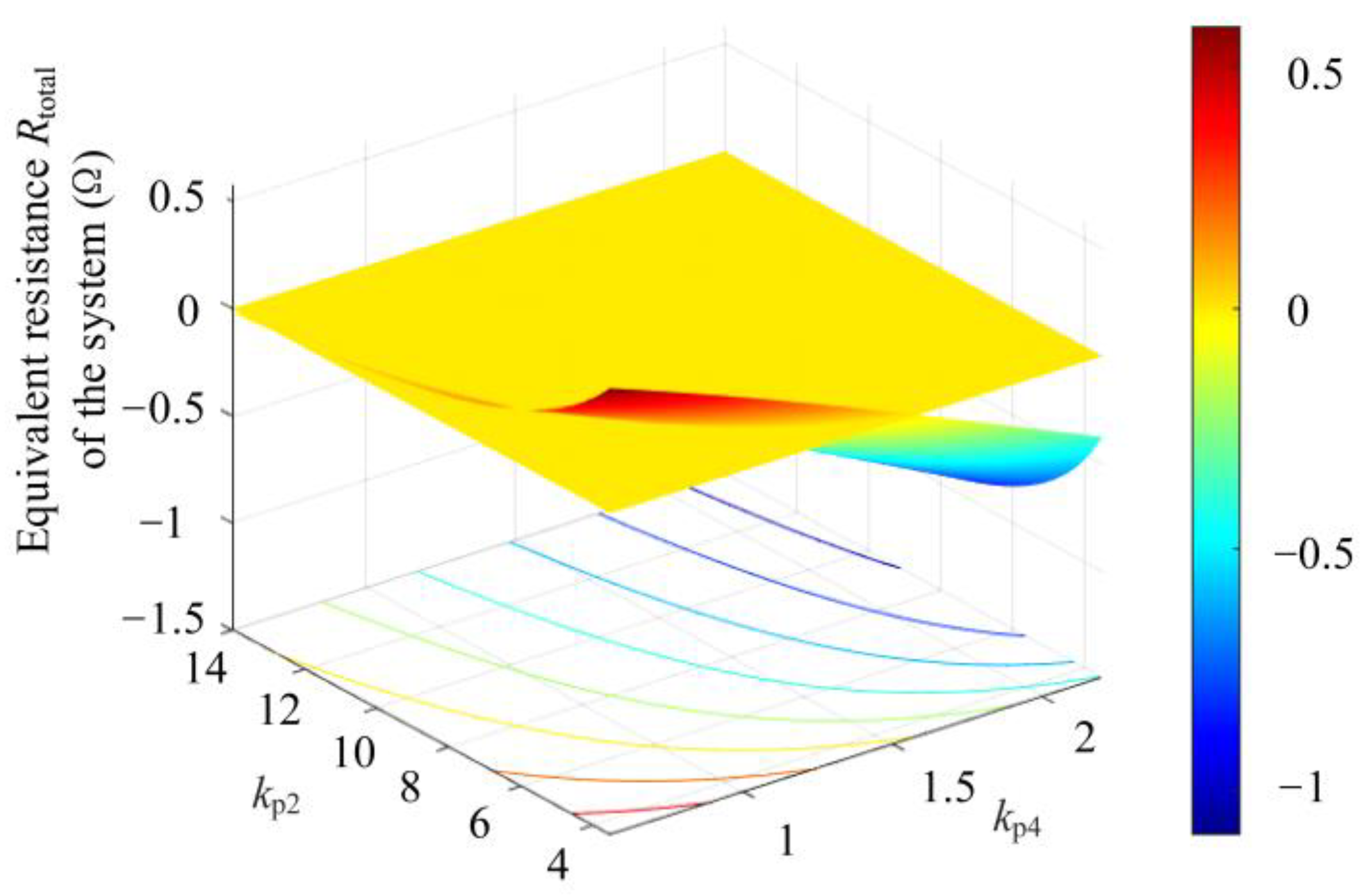
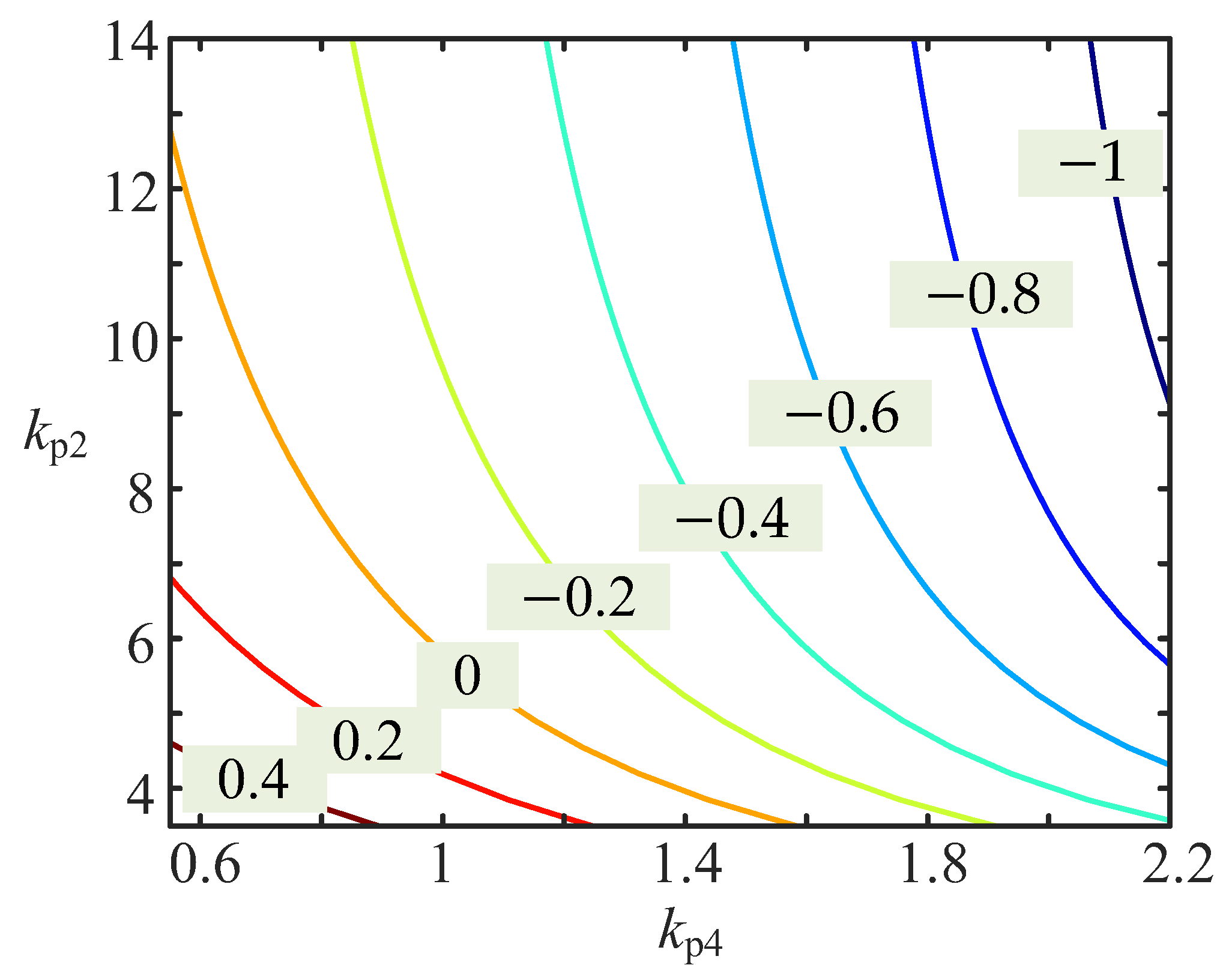
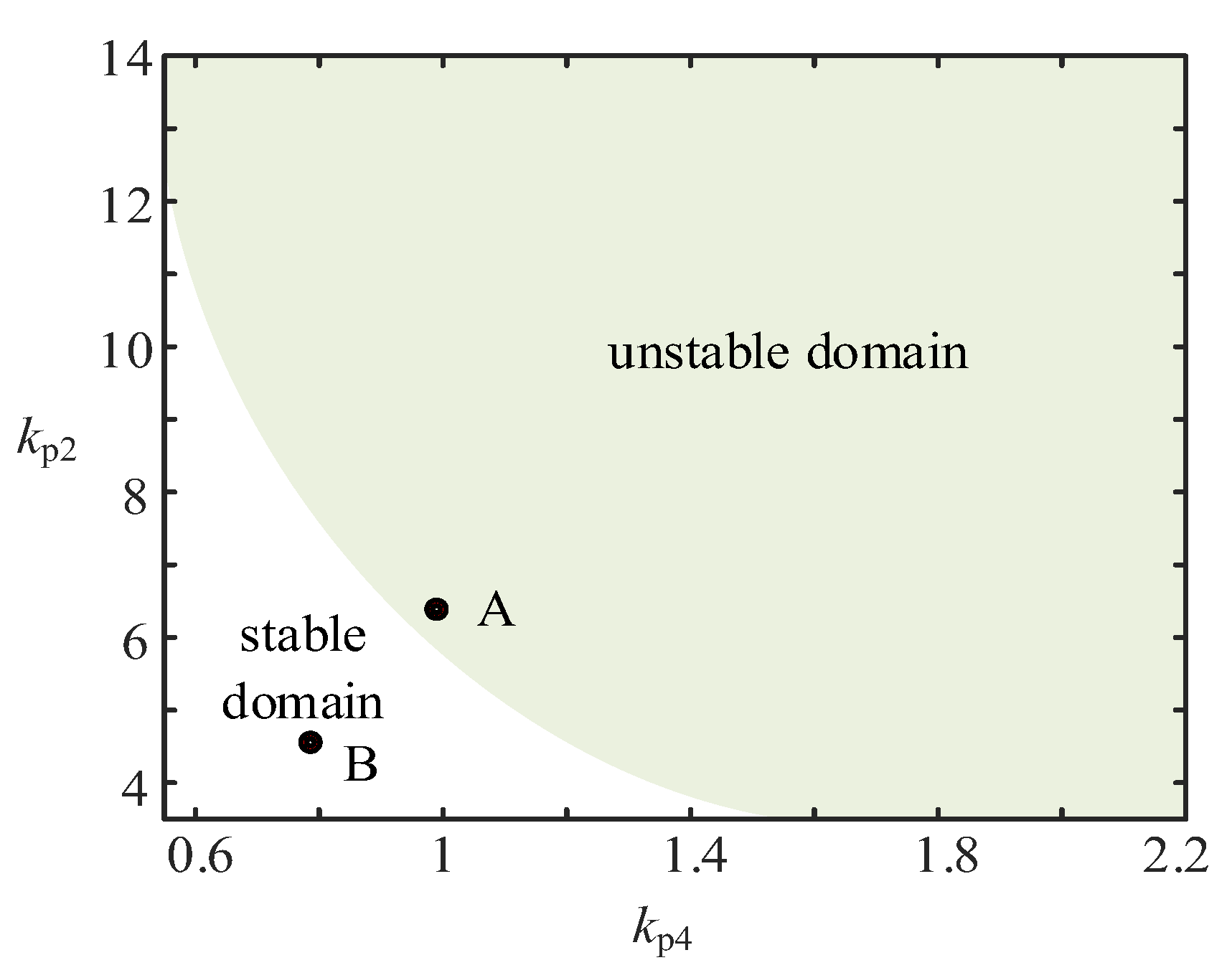
4.1. Stability Domain Analysis of Parameters
4.2. Key Parameter Optimization Based on Particle Swarm Optimization Algorithm
5. Simulation Verification
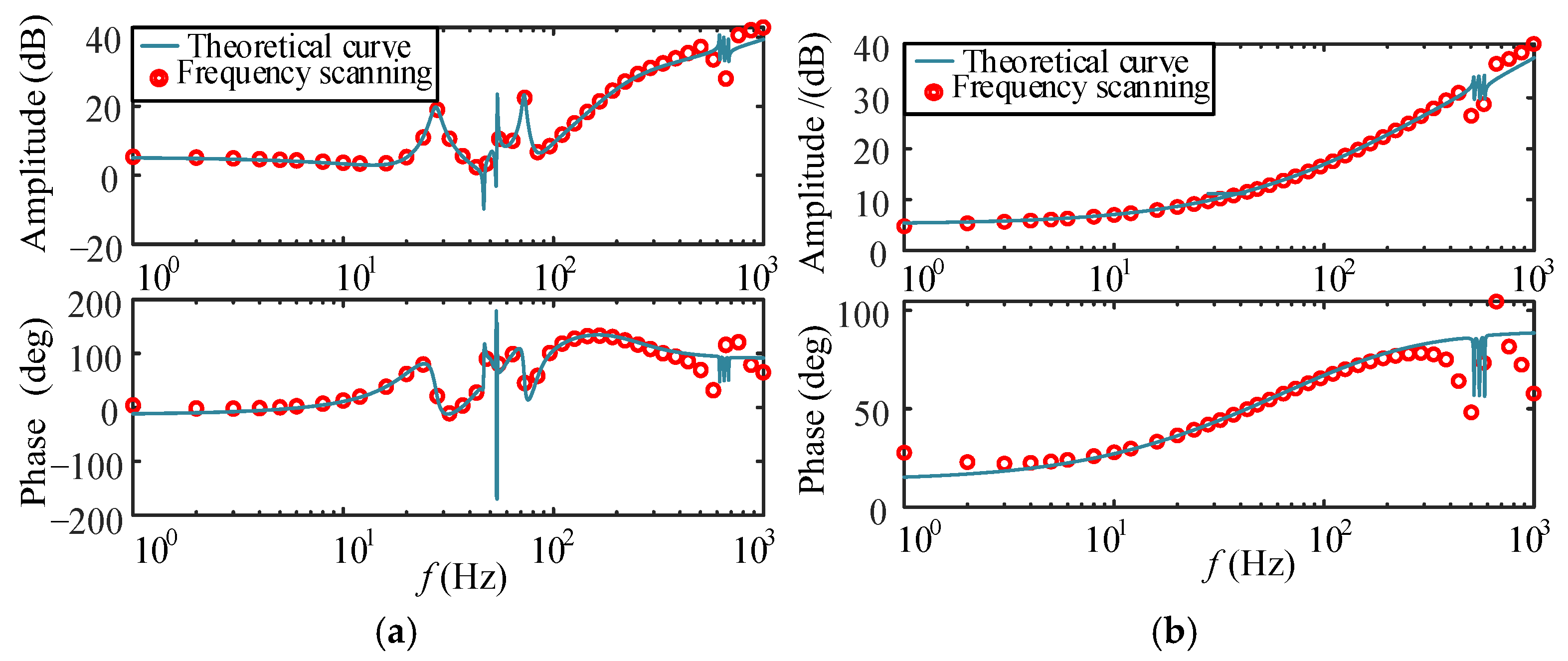
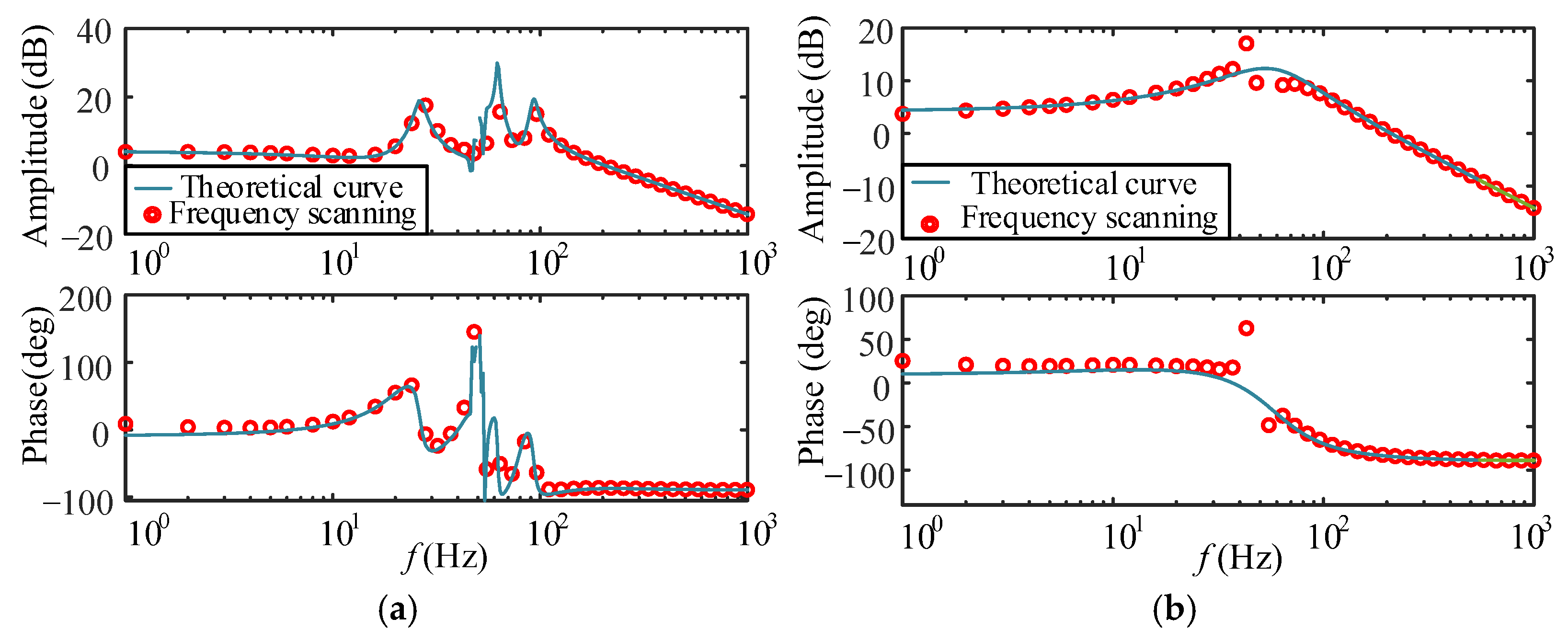
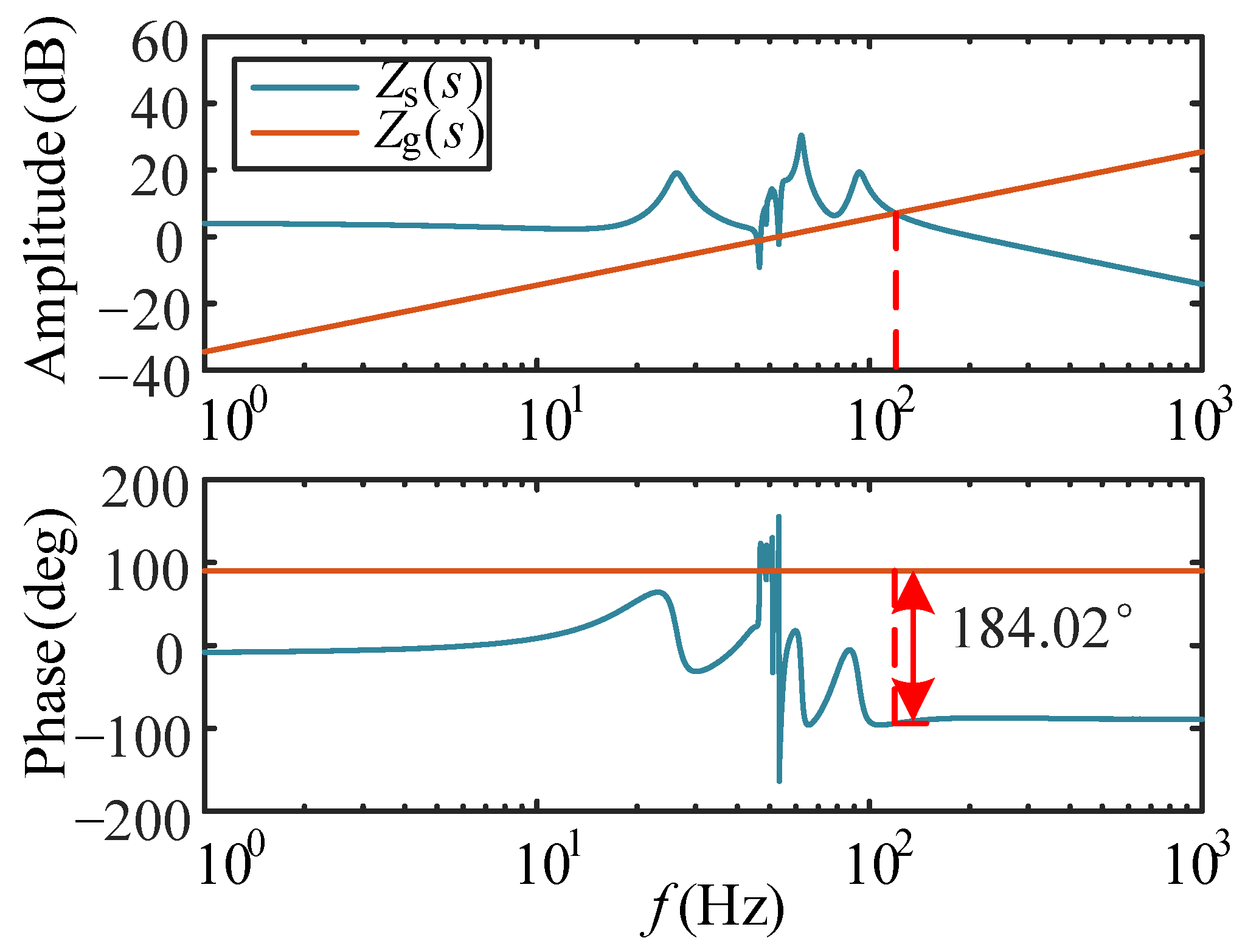
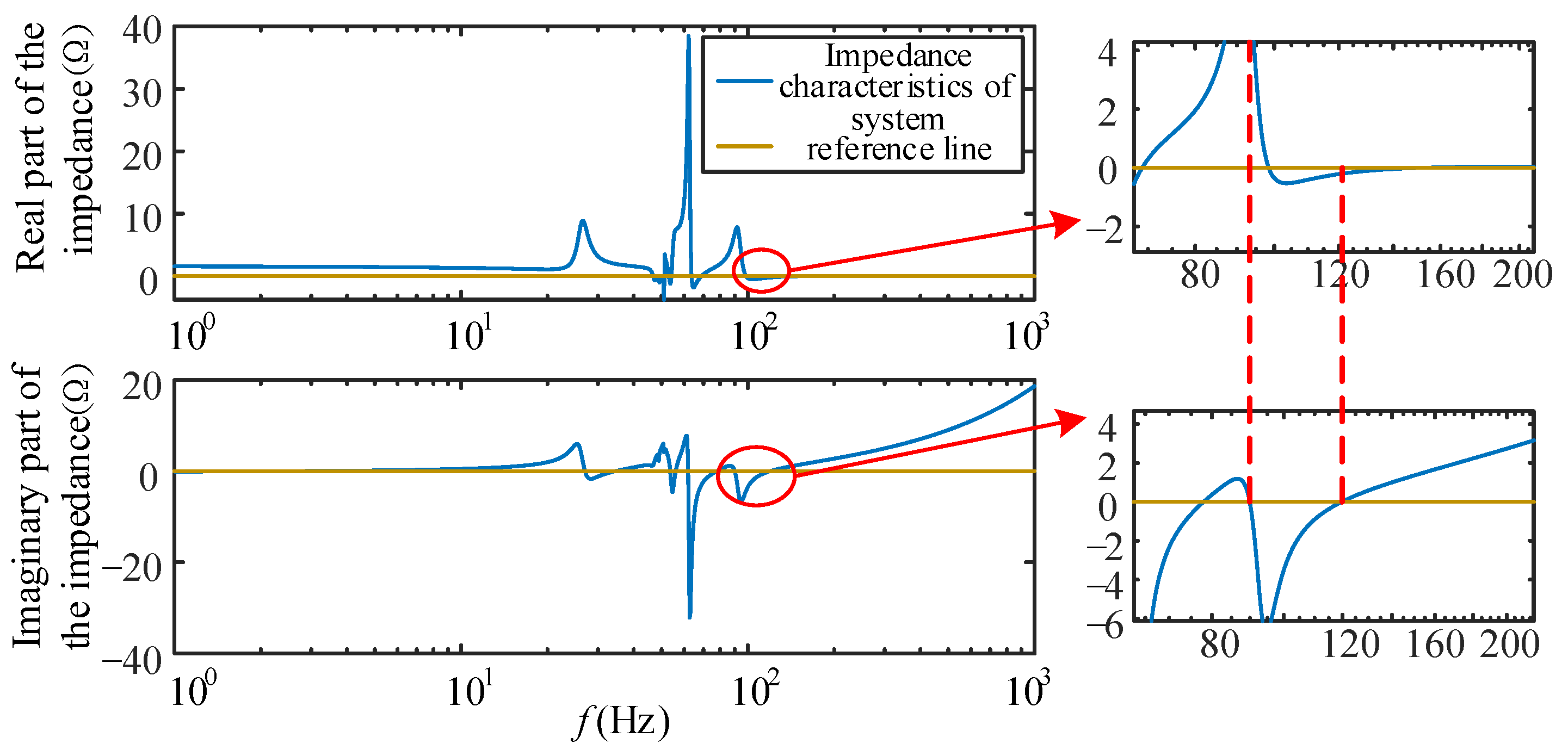
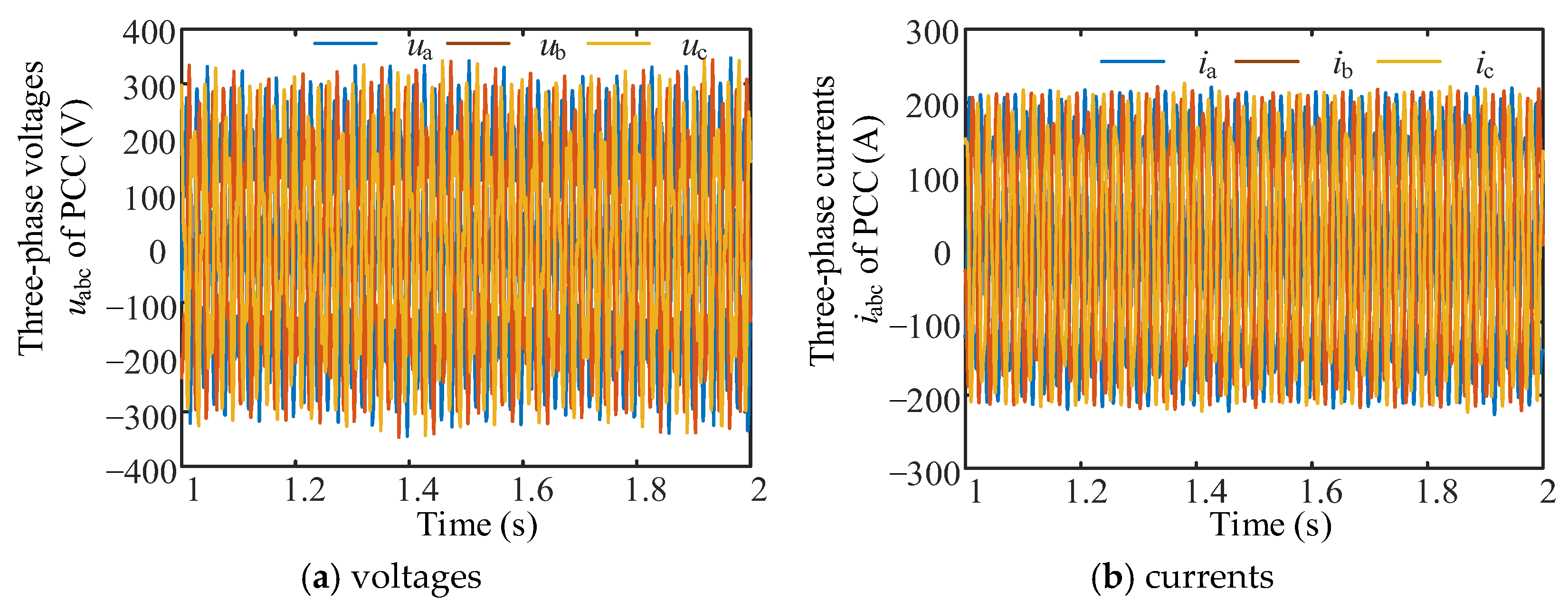
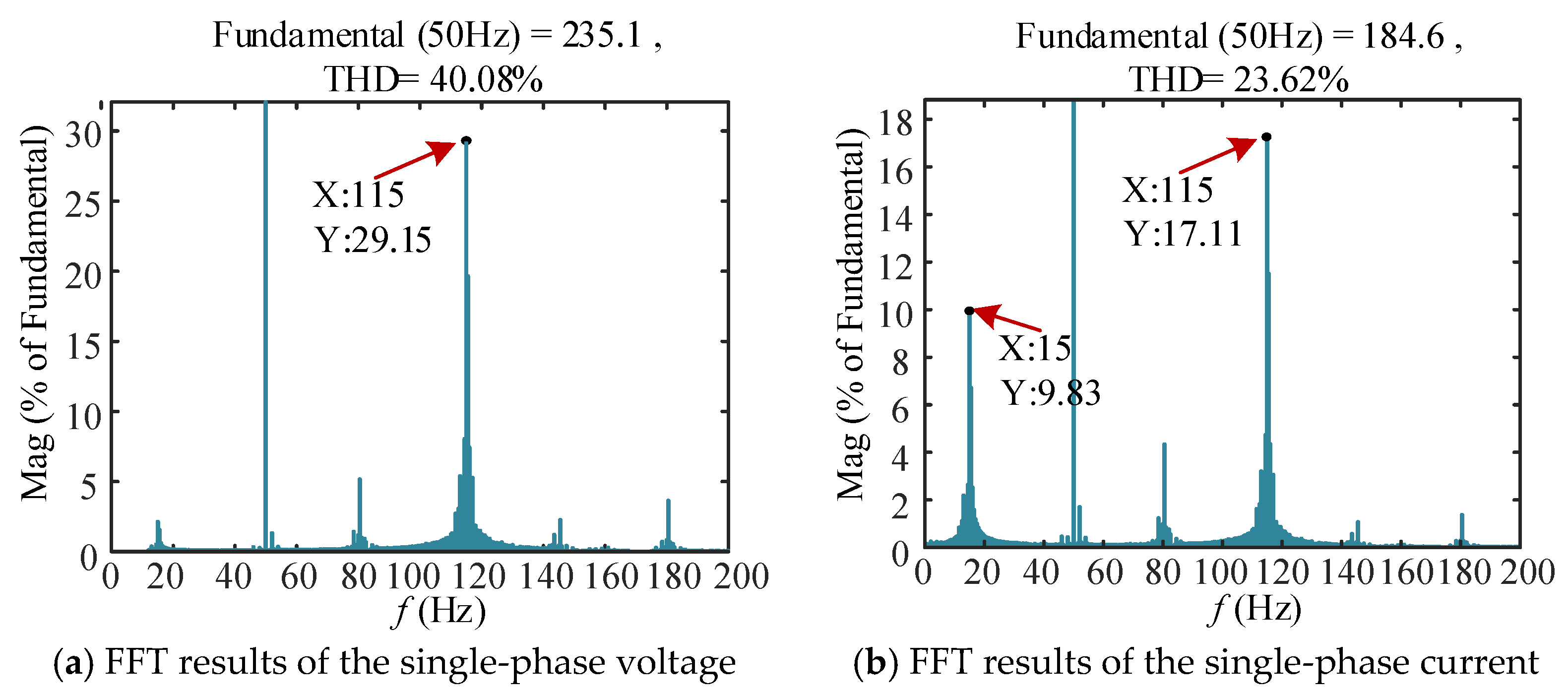
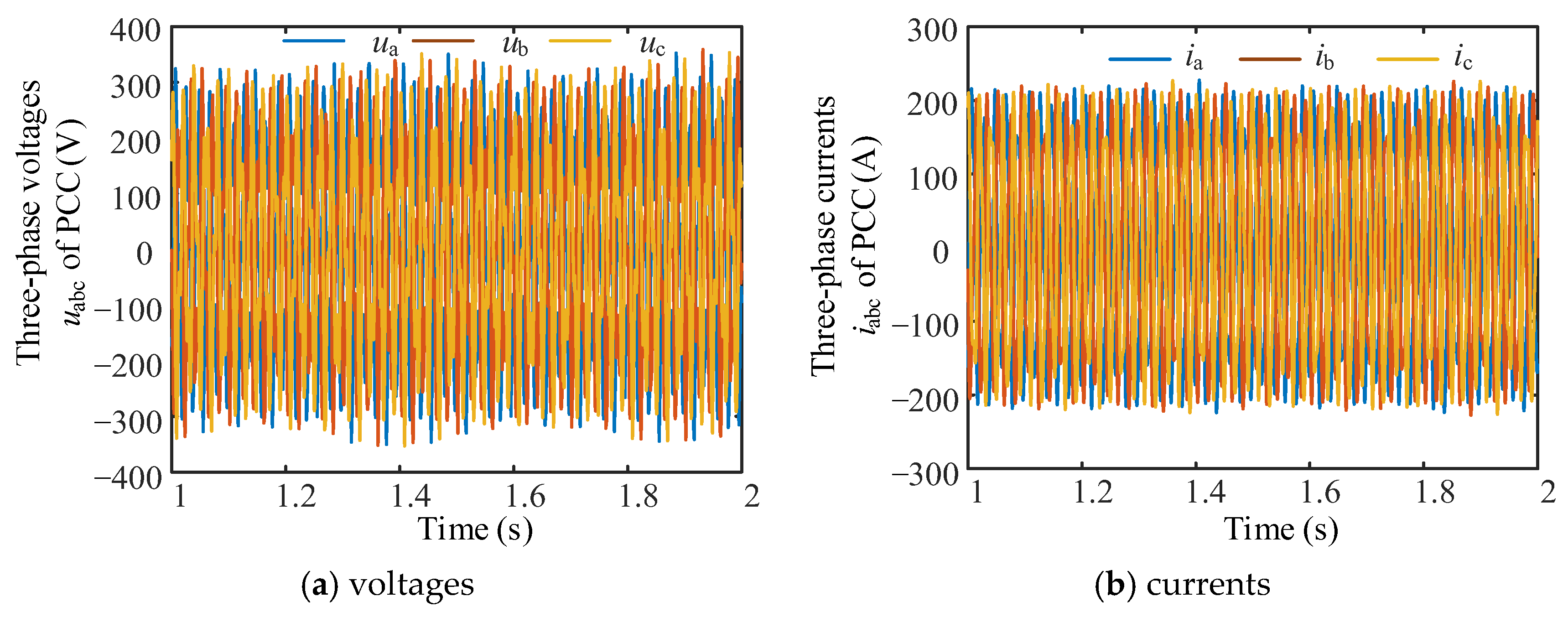
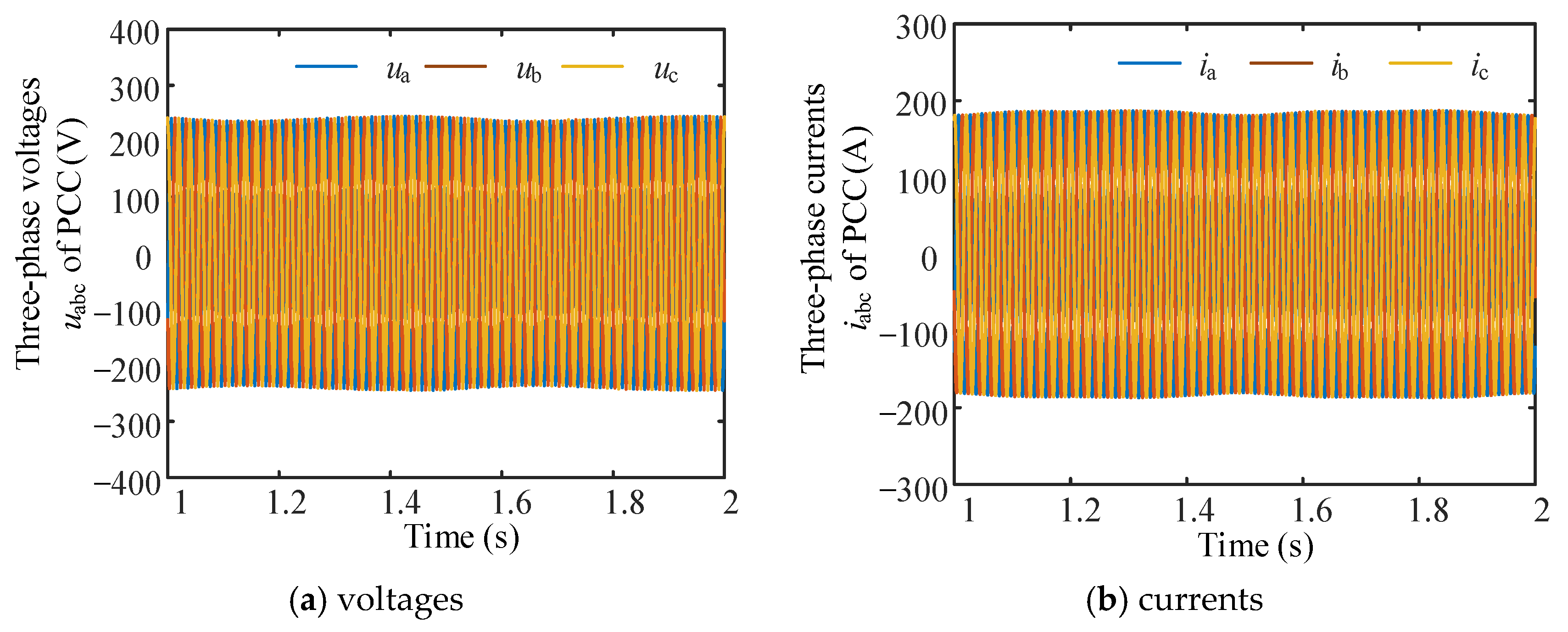
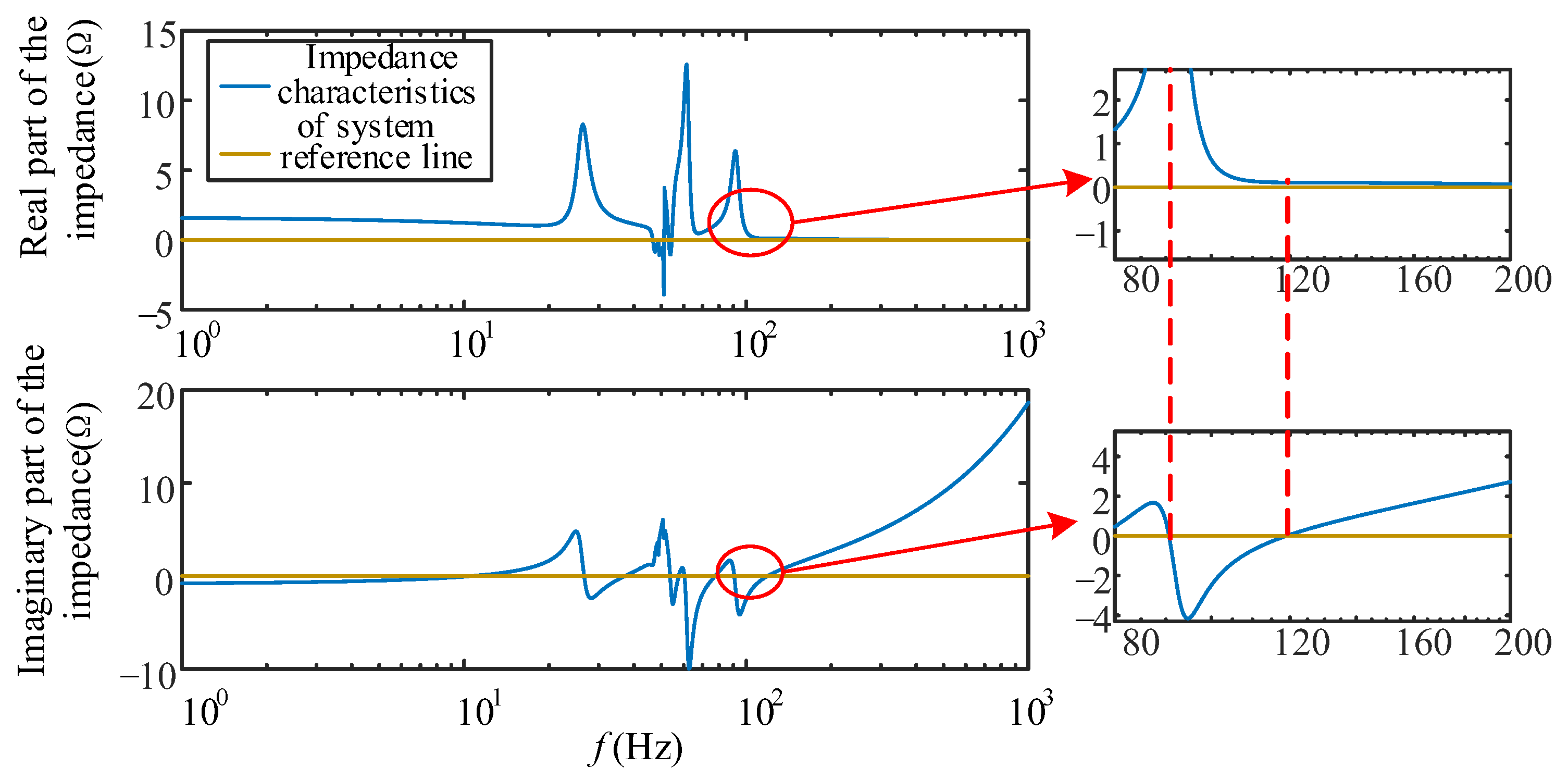
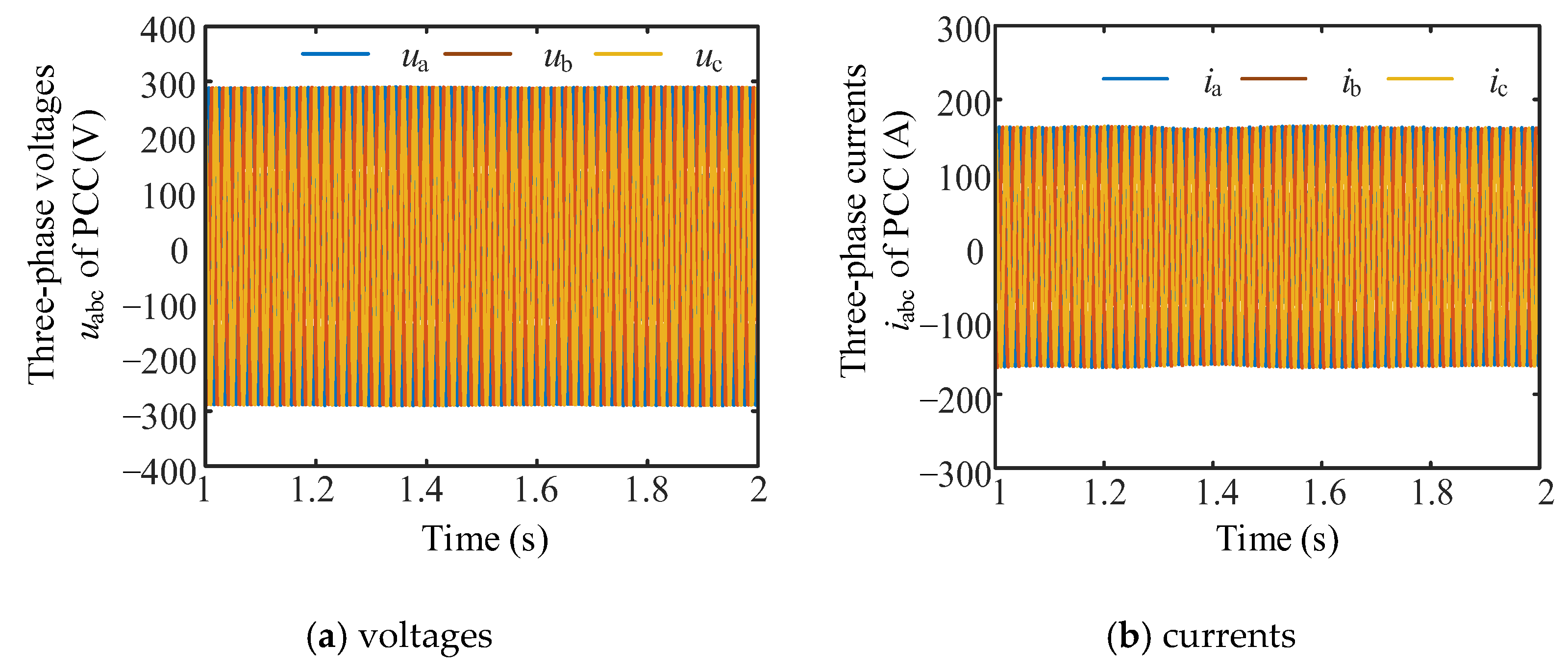
5.1. Verification of Stability Analysis
5.2. Verification of Stability Domain Analysis of Parameter
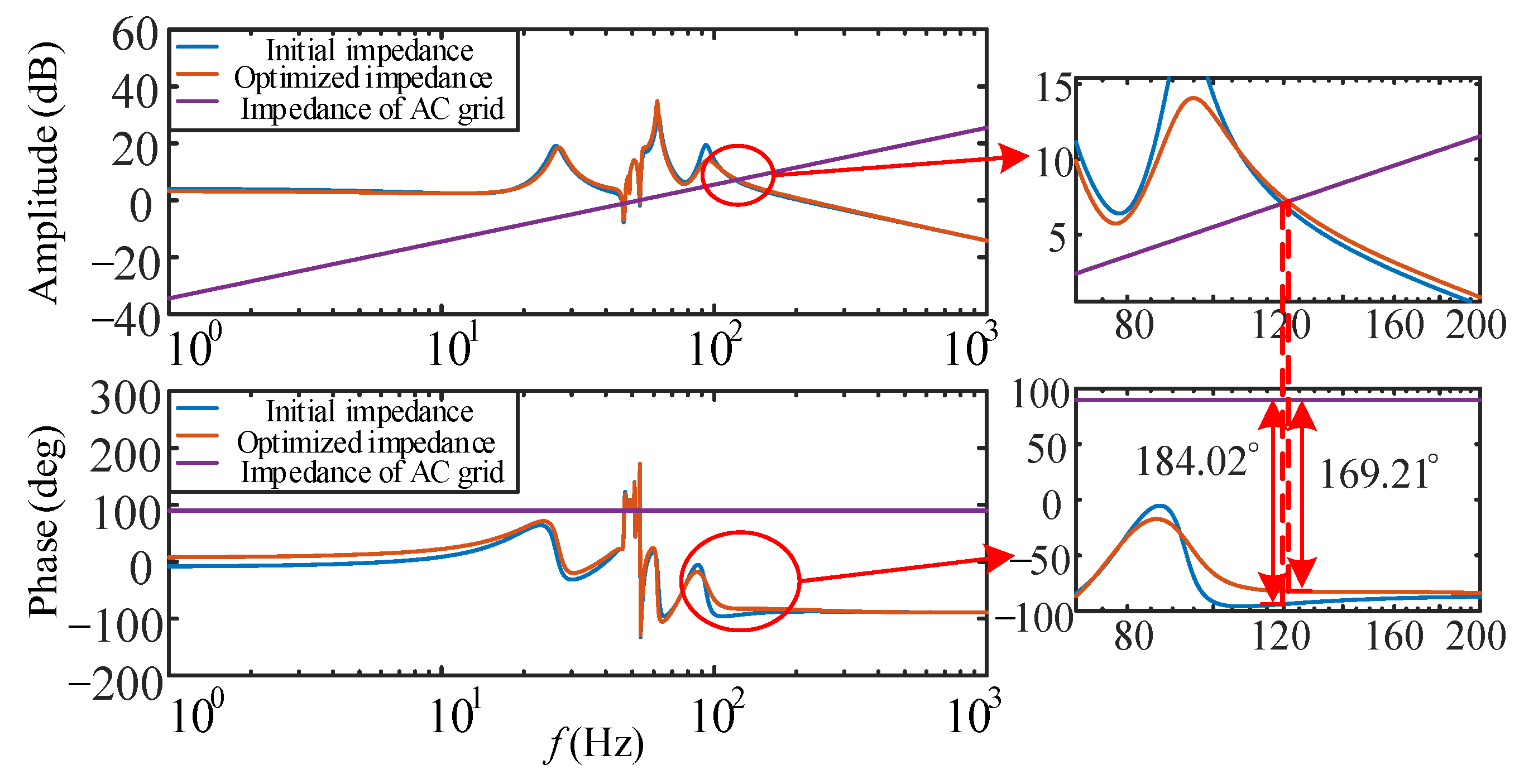
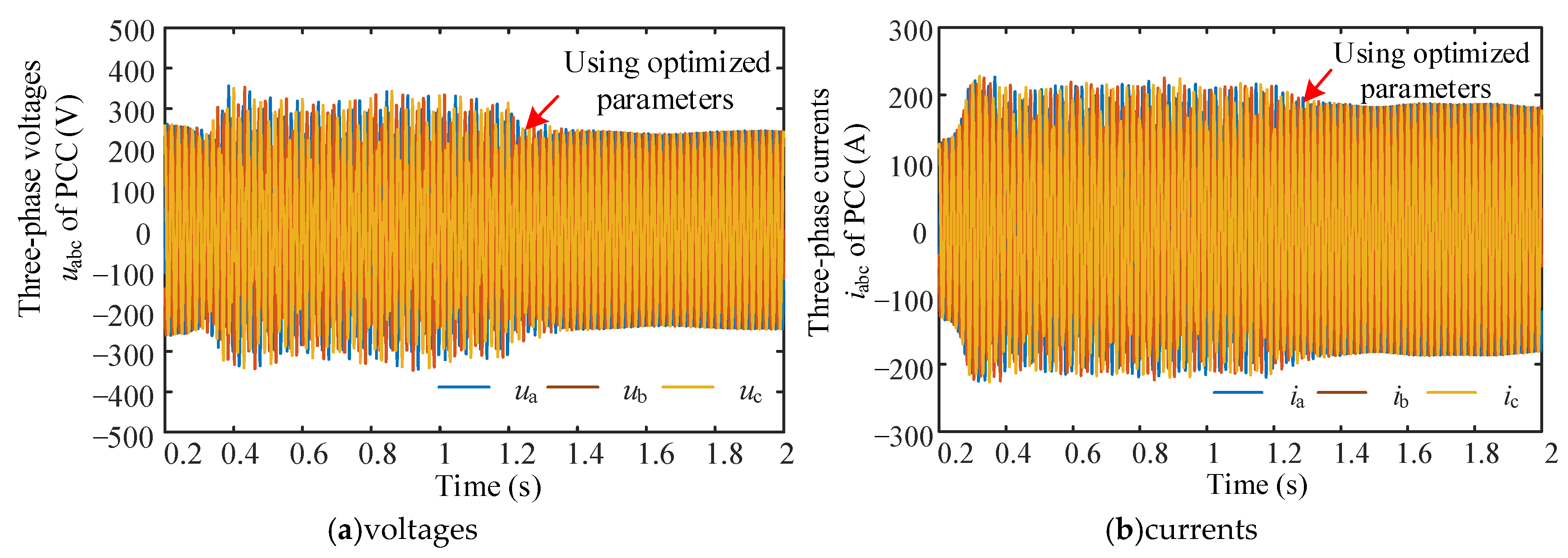
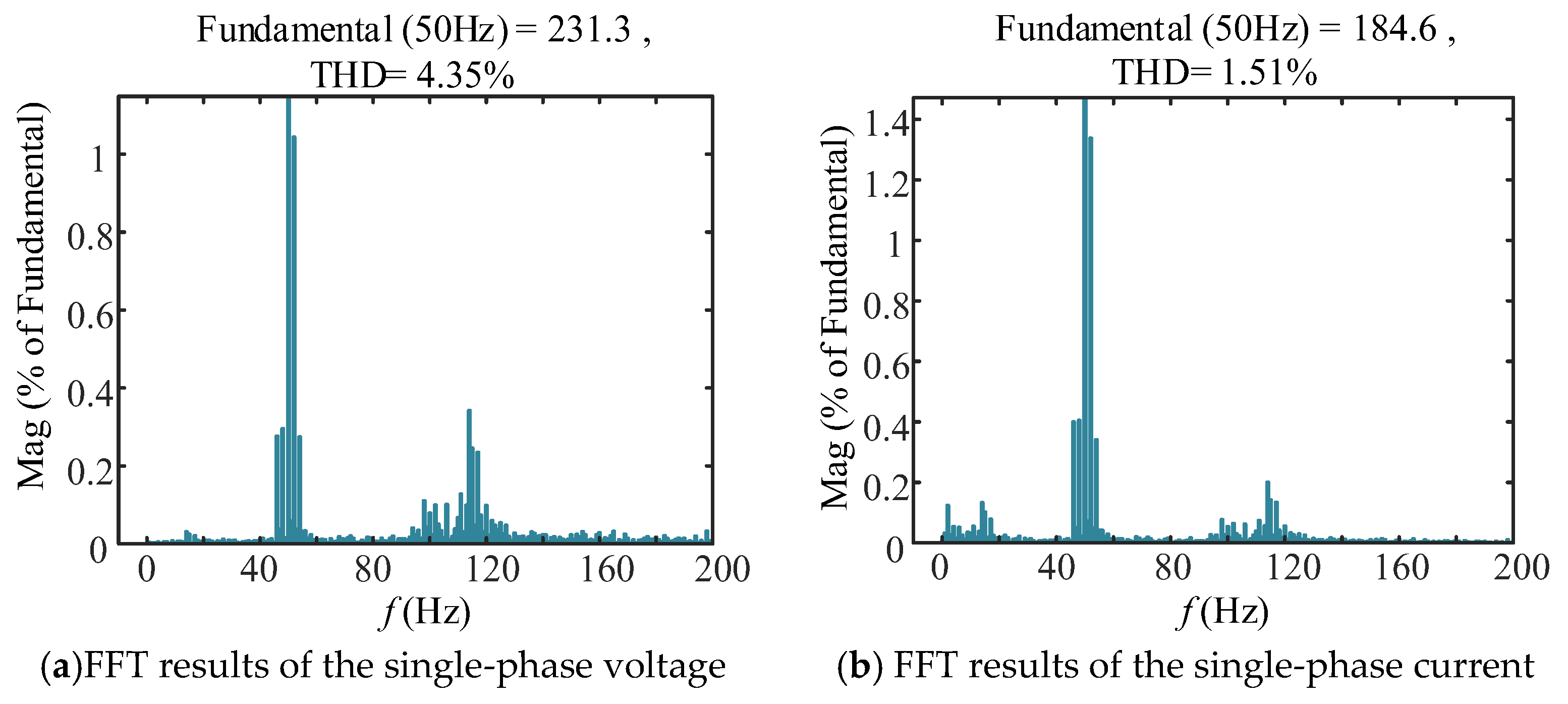
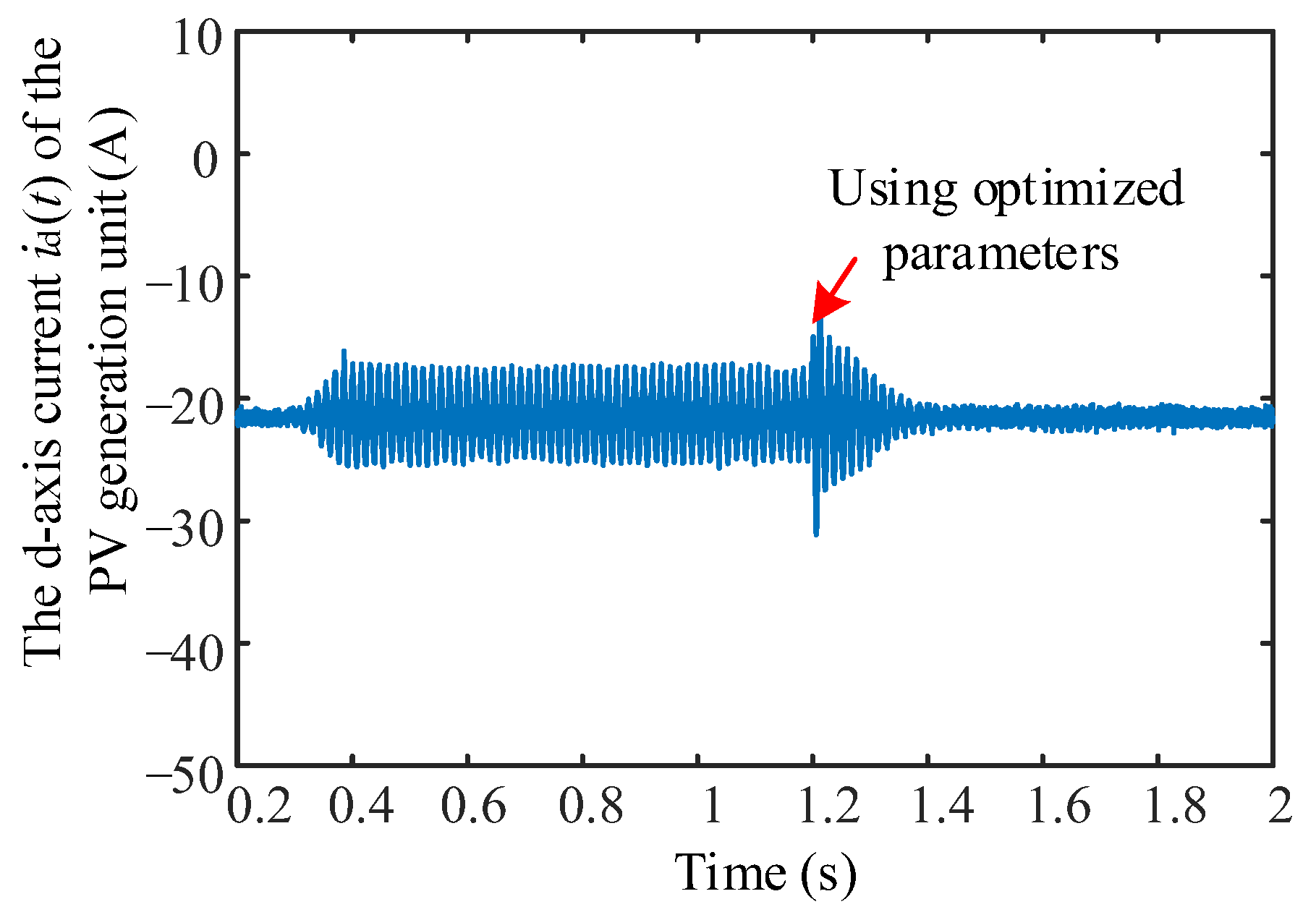
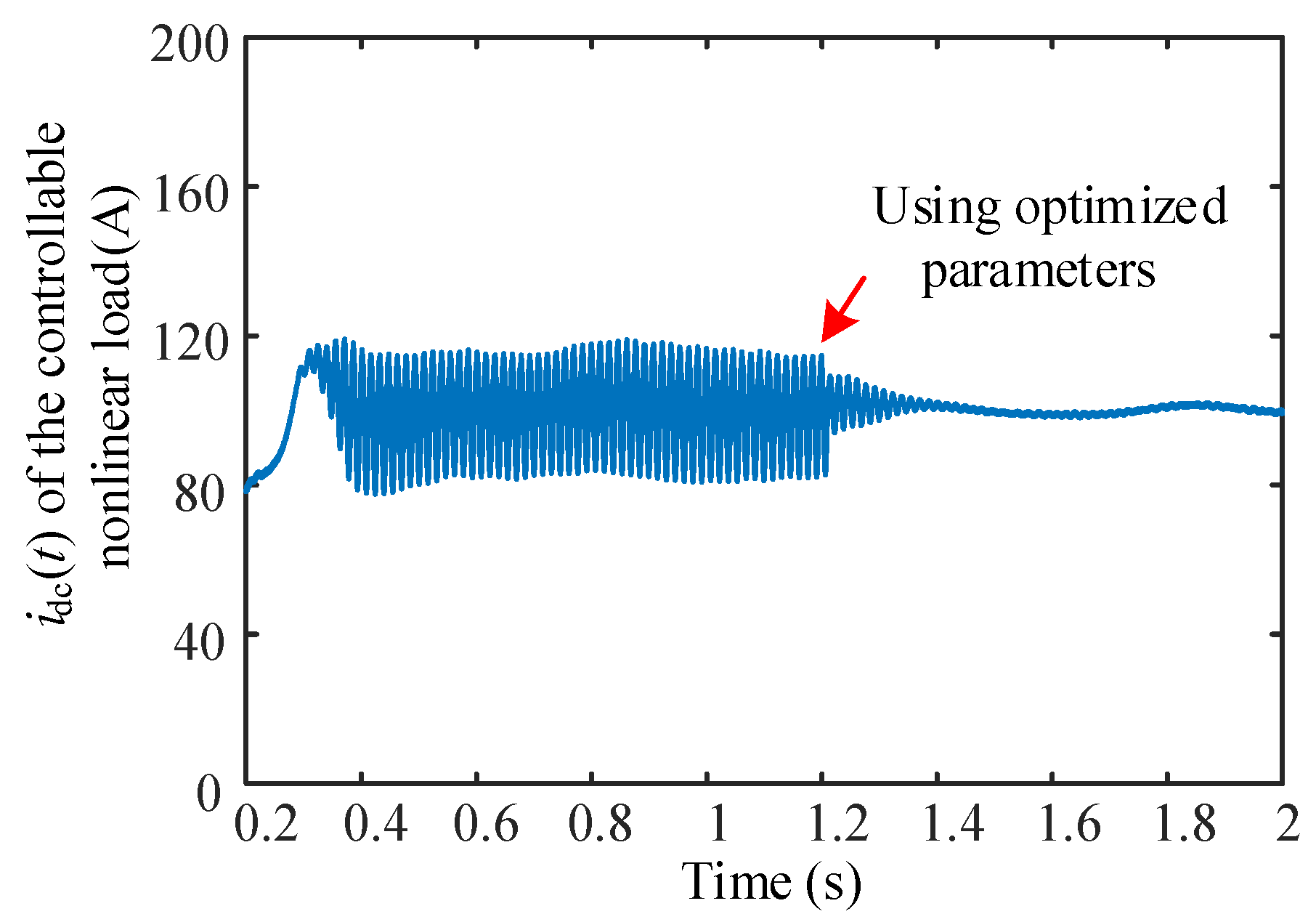
5.3. Verification of the Optimization Method
6. Conclusions
- (1)
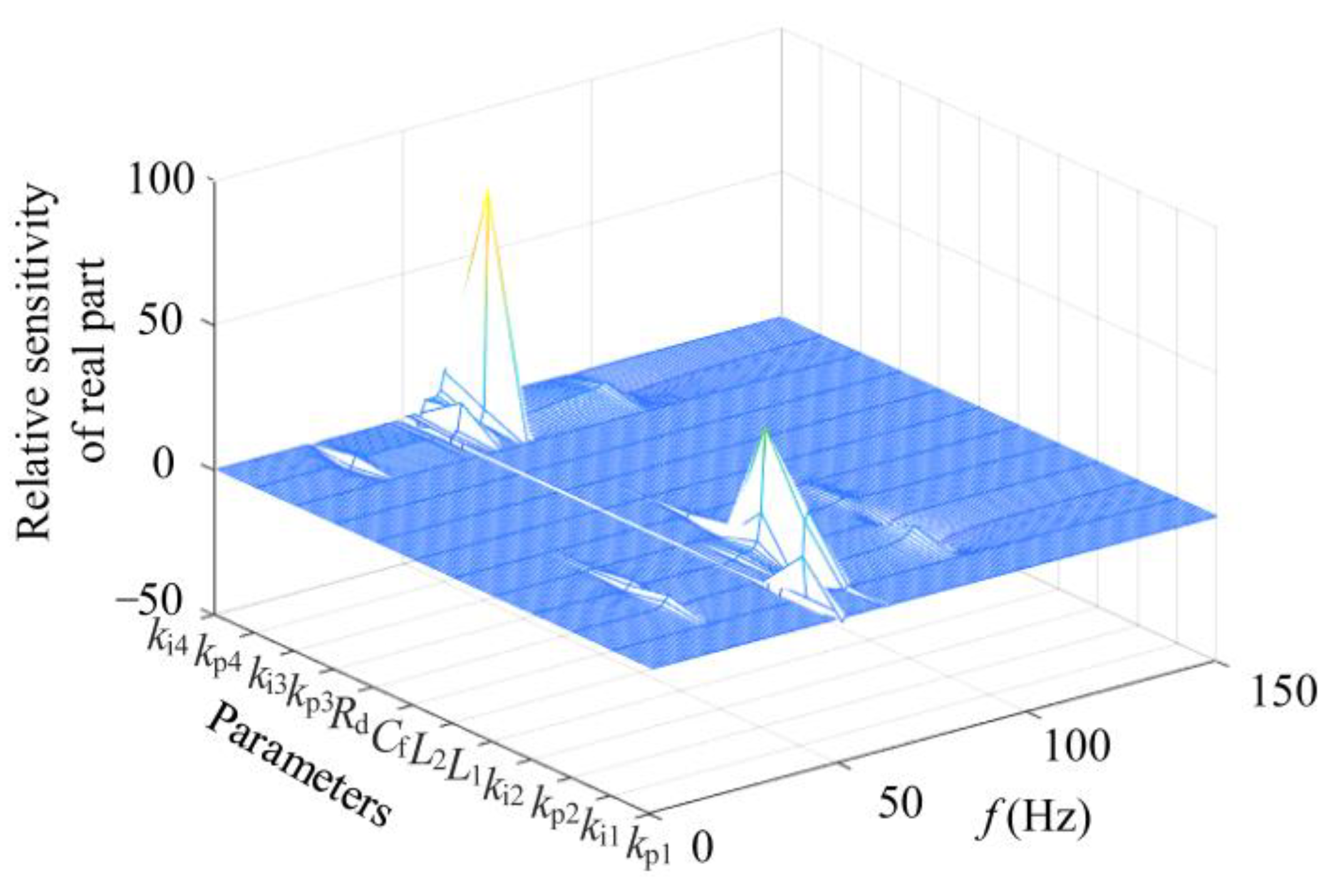
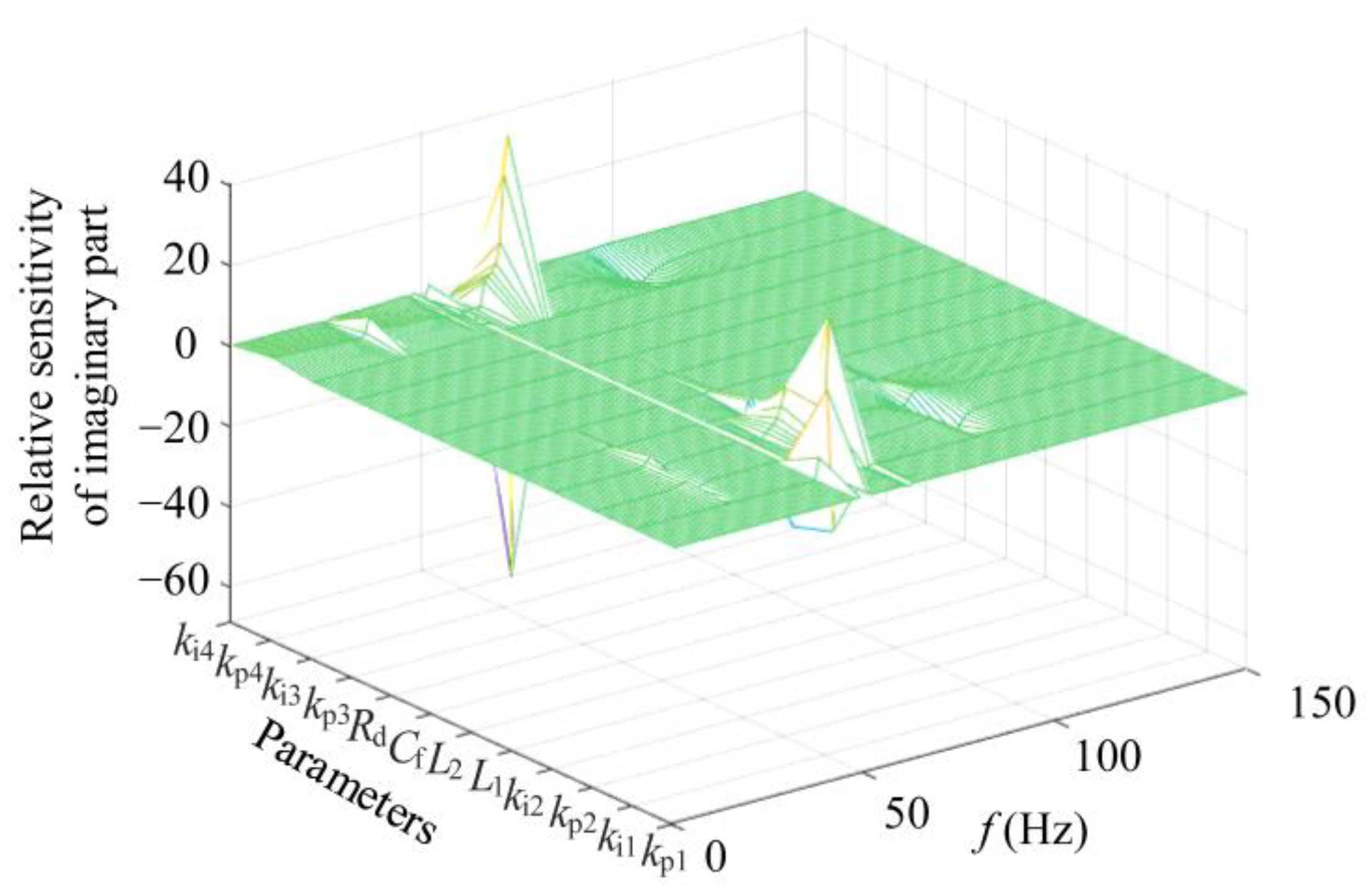
- Based on the established impedance model of the PV grid-connected system with controllable nonlinear loads, the influence of different parameters on the system impedance characteristics is analyzed using impedance relative sensitivity. This analysis reveals that the key parameters influencing system stability are the proportional coefficient kp4 of the DC current loop within the controllable nonlinear loads and the proportional coefficient kp2 of the current inner loop in the photovoltaic grid-connected inverter. By tuning these two parameters, the system impedance can be reshaped, thereby enhancing the overall stability of the system.
- (2)
- Considering the interactions between the two key parameters, the stability domain of the key parameters is analyzed. A parameter optimization method balancing system stability and response performance is then proposed, which aims to improve stability of the system while minimizing the impact on response performance. The validity of the proposed parameter-optimization algorithm is verified through comparative experiments conducted before and after the system adopts the optimized parameters. Additionally, simulation-based comparative experiments are carried out under varying conditions, specifically changes in the equivalent inductance of the power grid and alterations in load conditions. The experimental results conclusively demonstrate the robustness of the optimized parameters in suppressing system oscillations.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mohammad, A.S.; Ribal, A.; Chadi, A.; Mourad, D. Electric vehicle attack impact on power grid operation. Int. J. Electr. Power Energy Syst. 2022, 137, 107784. [Google Scholar] [CrossRef]
- Kumar, D.; Zare, F.; Blaabjerg, F. Special issue on modeling and analysis of interaction between grids and grid-connected power electronics converters in distribution networks. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2658–2661. [Google Scholar] [CrossRef]
- Wen, B.; Dong, D.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Impedance-Based Analysis of Grid-Synchronization Stability for Three-Phase Paralleled Converters. IEEE Trans. Power Electron. 2016, 31, 26–38. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.; Chen, J.; Gong, C. Analysis of Positive-sequence and Negative-sequence Impedance Modeling of Three-phase LCL-type Grid-connected Inverters Based on Harmonic Linearization. Proc. CSEE 2016, 36, 5890–5898+6033. [Google Scholar] [CrossRef]
- Zhao, S.; Li, R.; Gao, B.; Wang, Y. Analysis of Mechanism and Characteristics in Sub Synchronous Oscillation Between PV and Weak AC Networks. Proc. CSEE 2018, 38, 7215–7225+7448. [Google Scholar] [CrossRef]
- Song, S.; Wei, Z.; Lin, Y.; Liu, B.; Liu, H. Impedance modeling and stability analysis of PV grid-connected inverter systems considering frequency coupling. CSEE J. Power Energy Syst. 2020, 6, 279–290. [Google Scholar] [CrossRef]
- Liu, R.; Chen, Z.; Tang, W.; Zhu, J. Control strategy of an LCL type grid-connected inverter with the influence of a phase-locked loop under a weak power grid. Power Syst. Prot. Control 2022, 50, 178–187. [Google Scholar]
- Xia, Y.; Peng, Y.; Yang, P.; Li, Y.; Wei, W. Different Influence of Grid Impedance on Low- and High-Frequency Stability of PV Generators. IEEE Trans. Ind. Electron. 2019, 66, 8498–8508. [Google Scholar] [CrossRef]
- Mayordomo, J.G.; Beites, L.F.; Yang, X.; Xu, W. A Detailed Procedure for Harmonic Analysis of Three-Phase Diode Rectifiers Under Discontinuous Conduction Mode and Nonideal Conditions. IEEE Trans. Power Deliv. 2018, 33, 741–751. [Google Scholar] [CrossRef]
- Yang, Y.; Davari, P.; Zare, F.; Blaabjerg, F. Enhanced Phase-Shifted Current Control for Harmonic Cancellation in Three-Phase Multiple Adjustable Speed Drive Systems. IEEE Trans. Power Deliv. 2017, 32, 996–1004. [Google Scholar] [CrossRef]
- Wen, B.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Small-signal stability analysis of three-phase AC systems in the presence of constant power loads based on measured d-q frame impedances. IEEE Trans. Power Electron. 2015, 30, 5952–5963. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhao, J.; Mao, L.; Qu, K. Generalized Impedance Ratio and Stability Analysis for Grid-connected Systems. Proc. CSEE 2020, 40, 7240–7249. [Google Scholar] [CrossRef]
- Li, G.; Wang, W.; Liu, C.; Jin, Y.; He, G. Mechanism Analysis and Suppression Method of Wideband Oscillation of PMSG Wind Farms Connected to Weak Grid (Part I): Analysis of Wideband Impedance Characteristics and Oscillation Mechanism. Proc. CSEE 2019, 39, 6547–6562. [Google Scholar] [CrossRef]
- Li, Y.; Shuai, Z.; Fang, J. Application of Sensitivity in Impedance-based Stability Analysis for Converter Systems. Proc. CSEE 2021, 41, 3480–3491+3673. [Google Scholar] [CrossRef]
- Li, Y.; Shuai, Z.; Fang, J.; Wu, X. Stability improvement method for multi-converter distribution systems based on impedance sensitivity. CSEE J. Power Energy Syst. 2021, 45, 2021–2027. [Google Scholar]
- Zhang, D.; Chen, X. Overview of Broadband Oscillation Mitigation of New Energy Generation Power System Based on Impedance Perspective. Proc. CSEE 2024, 1–20. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Liu, B.; Li, Z.; Wang, H.; Dong, X.; Su, W.; Li, G.; Chen, X.; Fernando, T.; Iu, H.H.C.; Lian, X.; et al. Impedance Modeling of DFIG Wind Farms with Various Rotor Speeds and Frequency Coupling. IEEE Trans. Circuits Syst. 2021, 68, 406–410. [Google Scholar] [CrossRef]
- Wang, Y.; Ye, W.; Song, R.; Bi, J.T.; Chen, L.; Shen, J. Design of additional active damping for three-phase LCL grid connected inverter based on impedance analysis method. High Volt. Eng. 2021, 47, 2645–2656. [Google Scholar] [CrossRef]
- Liu, H.; Sun, J. Analytical mapping of harmonics and impedance through phase-controlled converters. In Proceedings of the 2012 IEEE 13th Workshop on Control and Modeling for Power Electronics (COMPEL), Kyoto, Japan, 10–13 June 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Liu, H. HVDC Converters Impedance Modeling and System Stability Analysis. Ph.D. Thesis, Rensselaer Polytechnic Institute, Troy, NY, USA, 2017. [Google Scholar]
- Wang, Y.; Cheng, Y.; Liao, J.; Wang, X. Oscillation suppression strategy of a PV grid-connected system with nonlinear loads based on improved capacitor current feedback. Power Syst. Prot. Control 2023, 51, 10–22. [Google Scholar] [CrossRef]
- Harnefors, L.; Wang, X.; Yepes, A.G.; Blaabjerg, F. Passivity-Based Stability Assessment of Grid-Connected VSCs—An Overview. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 116–125. [Google Scholar] [CrossRef]
- Wang, Y.; Min, Y.; Yu, G.; Yin, A.; Liao, J.; Zheng, Z. Parameters Coordinated Optimization of Sub-synchronous Oscillation of Doubly Fed Induction Generator System Based on Impedance Sensitivity Analysis with Sobol Method. High Volt. Eng. 2023, 49, 1703–1713. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.; Liao, J.; Wang, Y. Medium- and High-frequency Resonance Suppression Strategy in Flexible Direct Grid Connected System Based on Impedance Sensitivity Analysis. Power Syst. Technol. 2023, 47, 4311–4323. [Google Scholar] [CrossRef]
- Xing, F.; Xu, Z.; Xiao, H.; Zhang, Z. Analysis on Response Characteristics of Two-Level VSC to Disturbances and Its Oscillation Suppression Strategy. J. Electr. Eng. Technol. 2021, 16, 1389–1401. [Google Scholar] [CrossRef]

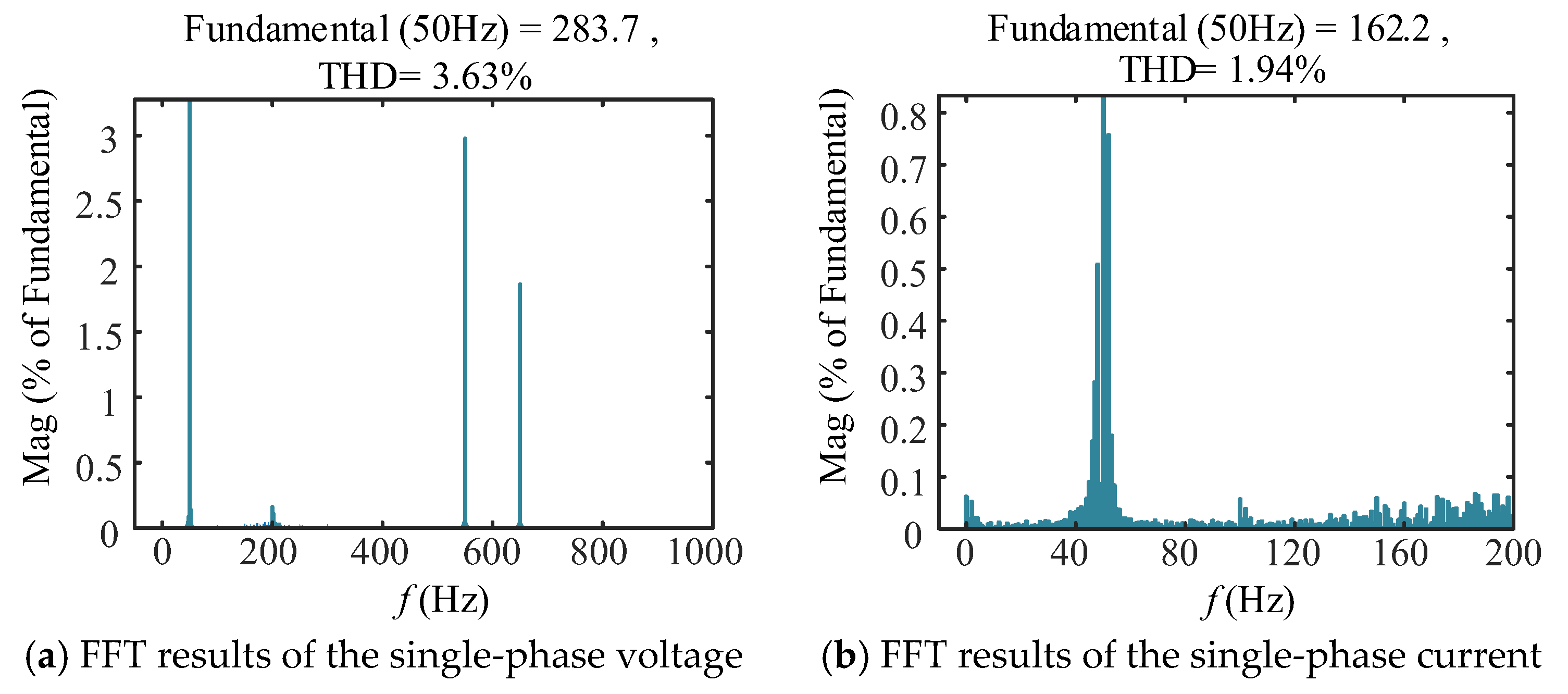
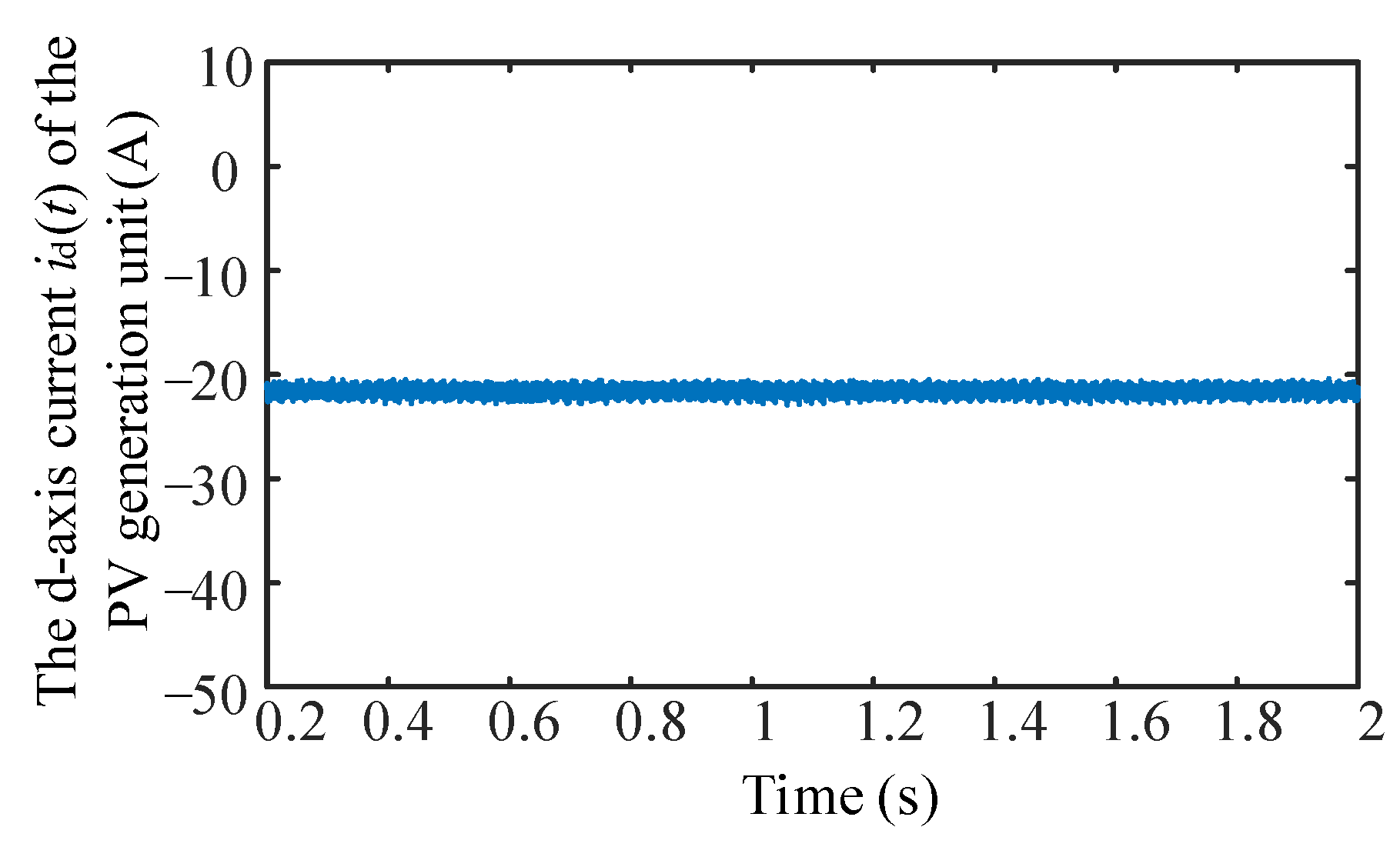
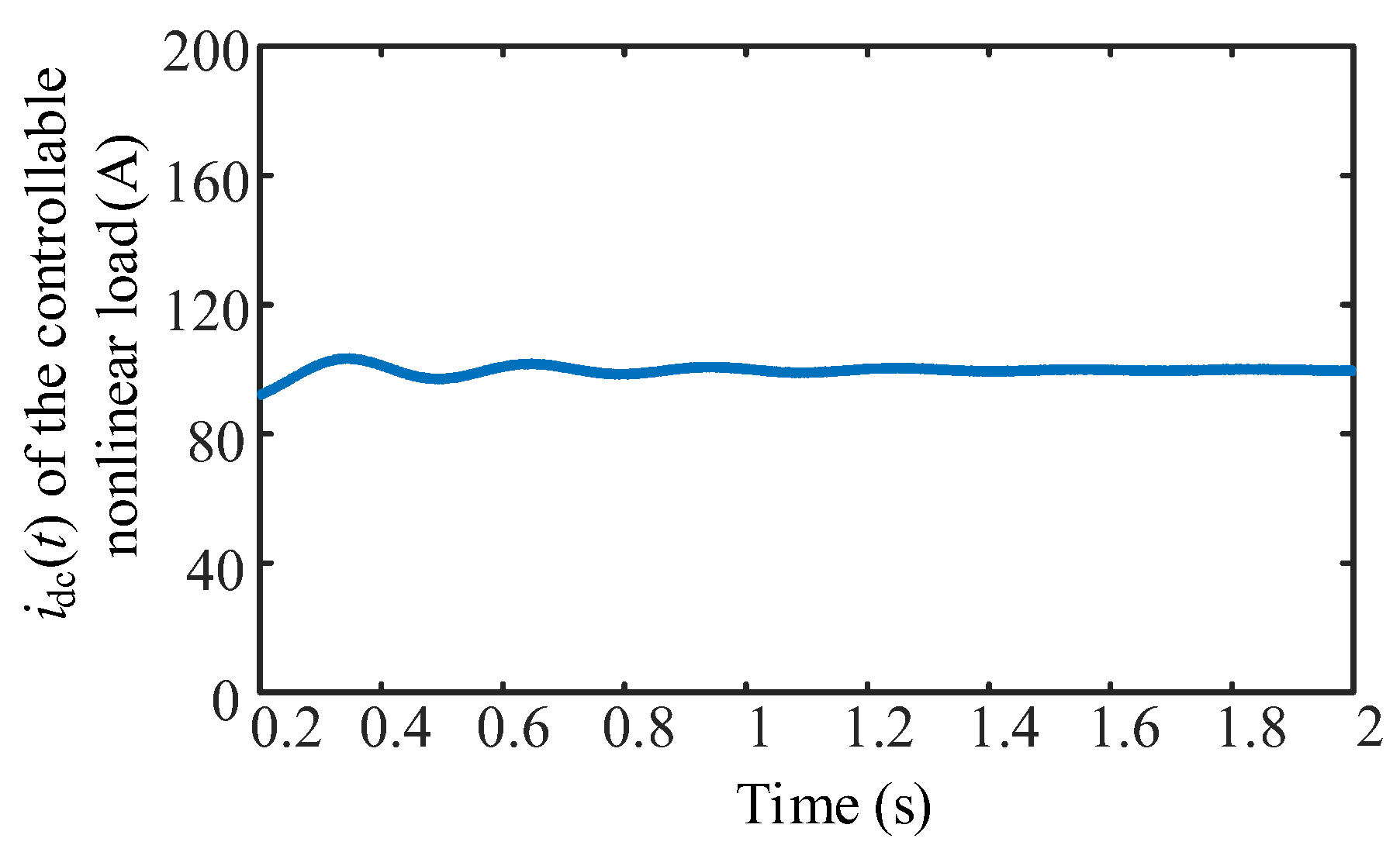
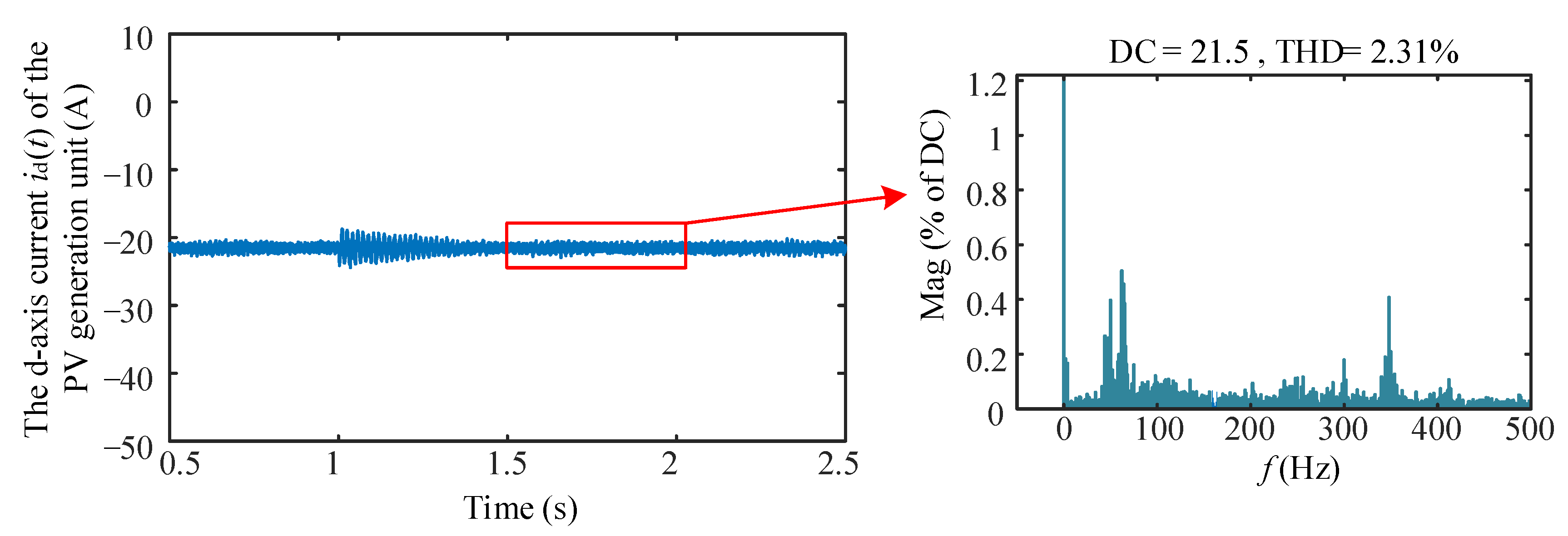
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Udc/V | 700 | L2/mH | 0.2 |
| Effective value of grid’s line voltage/V | 380 | Cf/uF | 6.8 |
| Output active power P of PV/kW | 10 | Rd/Ω | 1.8 |
| Output reactive power Q of PV/kVar | 0 | Proportional coefficient kp1 of PLL | 1.72 |
| f1/Hz | 50 | Integral coefficient ki1 of PLL | 150 |
| Switching frequency fsw/kHz | 35 | Proportional coefficient kp2 of current loop | 10 |
| L1/mH | 1.5 | Integral coefficient ki2 of current loop | 700 |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| R4/Ω | 1 | time constant Tim of the Gim(s) | 1.2 × 10−3 |
| L4/mH | 50 | Proportional coefficient kp3 of PLL | 7.64 × 10−3 |
| C4/uF | 1000 | Integral coefficient ki3 of PLL | 1.44 |
| Vdc0/V | 500 | Proportional coefficient kp4 of DC current loop | 1.1 |
| gain kim of the Gim(s) | 0.01 | Integral coefficient ki4 of DC current loop | 30 |
| Region | Name | Value |
|---|---|---|
| unstable domain | A | (0.98, 6.6) |
| stable domain | B | (0.79, 4.7) |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Spatial dimension | 2 | Population size | 100 |
| Inertial weight | 0.8 | Individual learning factor | 0.9 |
| Social learning factor | 0.9 | Maximum number of iterations | 50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, T.; Huang, G.; Ye, X.; Wang, Y.; Ouyang, X.; Zhang, W.; Cheng, Y.; Wang, Y. Optimization-Based Suppression Method of Oscillations in Photovoltaic Grid-Connected Systems with Controllable Nonlinear Loads. Energies 2024, 17, 4120. https://doi.org/10.3390/en17164120
Zhu T, Huang G, Ye X, Wang Y, Ouyang X, Zhang W, Cheng Y, Wang Y. Optimization-Based Suppression Method of Oscillations in Photovoltaic Grid-Connected Systems with Controllable Nonlinear Loads. Energies. 2024; 17(16):4120. https://doi.org/10.3390/en17164120
Chicago/Turabian StyleZhu, Tong, Gechao Huang, Xi Ye, Yanfeng Wang, Xuetong Ouyang, Weilin Zhang, Yangfan Cheng, and Yuhong Wang. 2024. "Optimization-Based Suppression Method of Oscillations in Photovoltaic Grid-Connected Systems with Controllable Nonlinear Loads" Energies 17, no. 16: 4120. https://doi.org/10.3390/en17164120
APA StyleZhu, T., Huang, G., Ye, X., Wang, Y., Ouyang, X., Zhang, W., Cheng, Y., & Wang, Y. (2024). Optimization-Based Suppression Method of Oscillations in Photovoltaic Grid-Connected Systems with Controllable Nonlinear Loads. Energies, 17(16), 4120. https://doi.org/10.3390/en17164120






