Optimizing Virtual Power Plant Management: A Novel MILP Algorithm to Minimize Levelized Cost of Energy, Technical Losses, and Greenhouse Gas Emissions

Abstract

The modern energy landscape is undergoing a significant transformation towards cleaner, decentralized energy sources. This change is driven by environmental and sustainability needs, causing traditional centralized electric grids, which rely heavily on fossil fuels, to be replaced by a diverse range of decentralized distributed energy resources. Virtual power plants (VPPs) have surfaced as a flexible solution in this transition. A VPP’s primary role is to optimize energy production, storage, and distribution by coordinating output from various connected sources. Relying on advanced communication and control systems, a VPP can balance supply and demand in real time, offer ancillary services, and support grid stability. However, aligning VPPs’ economic and operational practices with broader environmental goals and policies is a challenging yet crucial aspect. This article introduces a new VPP management and optimization algorithm designed for quick and intelligent decision-making, aiming for the lowest levelized cost of energy (LCOE), minimum grid technical losses, and greenhouse gas (GHG) emissions. The algorithm’s effectiveness is confirmed using the IEEE 33-bus grid with 10 different distributed power generators. Simulation results show the algorithm’s responsiveness to complex variables found in practical scenarios, finding the optimal combination of available energy resources. This minimizes the LCOE, technical losses, and GHG emissions in less than 0.08 s, achieving a total LCOE reduction of 16% from the baseline. This work contributes to the development of intelligent energy management systems, aiding the transition towards a more resilient and sustainable energy infrastructure.

1. Introduction

Virtual power plants (VPPs) represent a groundbreaking approach in the management and optimization of distributed energy resources (DERs) [1], enabling a more flexible, resilient, and sustainable energy system [2]. VPPs aggregate various DERs, such as solar panels, wind turbines, battery storage systems, and demand response assets, to operate as a single power plant. This integration allows for the coordinated management of these resources, optimizing their collective output and providing a range of grid services. The concept of VPPs leverages advanced software and communication technologies to monitor, control, and dispatch DERs in real time [3], thereby enhancing the efficiency and reliability of the energy grid. The growing adoption of VPPs is driven by several factors, such as the increasing use of renewable energy sources, advancements in energy storage technology, and the need for greater grid flexibility to accommodate variable demand loads [4]. Traditional power plants, which depend on large, centralized generation units, often struggle to respond quickly to changes in demand or supply. In contrast, VPPs can rapidly adjust their output by aggregating and dispatching energy from multiple, smaller sources. This capability is especially valuable in mitigating the intermittency of renewable energy, like solar and wind, subject to weather-induced fluctuations. One of the main benefits of VPPs is their ability to provide ancillary services to the grid [5]. These services include frequency regulation, voltage support [6], and spinning reserve, which are crucial for maintaining grid stability and reliability. VPPs can respond to grid imbalances faster than traditional power plants by coordinating the output of diverse DERs. For example, during high-demand periods or when there is a sudden drop in generation, VPPs can quickly dispatch stored energy from batteries or reduce demand through demand response mechanisms [7]. This rapid response helps prevent blackouts and ensures a stable electricity supply. Moreover, VPPs improve the economic efficiency of the energy system [8,9]. By optimizing the dispatch of DERs based on real-time market signals and grid conditions, VPPs can reduce the overall cost of electricity. They enable small-scale generators and consumers to participate in energy markets, allowing them to sell excess energy or provide grid services, creating new revenue streams. This democratization of the energy market can result in more competitive pricing and increased adoption of renewable energy technologies. VPPs also contribute to reducing greenhouse gas emissions [10]. By maximizing the use of renewable energy sources and improving energy storage and consumption efficiency, VPPs can significantly lower the energy sector’s carbon footprint. Additionally, VPPs facilitate the integration of electric vehicles (EVs) into the grid [11], using them as mobile storage units that provide additional grid flexibility and support. This symbiotic relationship between EVs and VPPs can accelerate the transition to a low-carbon energy system. Additionally, VPPs’ role in enhancing grid resilience is especially relevant in the context of climate change, which is increasing the frequency and severity of extreme weather events. VPPs can improve the grid’s ability to withstand and recover from disruptions by providing decentralized and distributed power sources [12]. During natural disasters, when centralized power plants and transmission lines may be compromised, VPPs can continue to supply electricity from local sources, supporting critical infrastructure and community resilience [13].

The development and deployment of VPPs are supported by advancements in digital technologies like the Internet of Things (IoT), artificial intelligence (AI), and blockchain. IoT devices enable real-time monitoring and control of DERs, ensuring optimal performance and coordination. AI algorithms can analyze vast amounts of grid and DER data to predict demand patterns, optimize energy dispatch, and identify potential issues before they escalate. Blockchain technology enhances the security and transparency of transactions within the VPP ecosystem, facilitating trust and cooperation among participants [14]. Nevertheless, despite VPPs’ numerous benefits, several challenges must be addressed to fully realize their potential. One key challenge is the integration of diverse DERs with varying characteristics and capabilities. Ensuring seamless communication and interoperability among these resources requires standardized protocols and robust communication infrastructure. Also, regulatory and market frameworks must evolve to accommodate VPPs’ unique features. This includes creating fair compensation mechanisms for the services provided by VPPs and removing barriers to market entry for small-scale participants [15]. Another significant challenge is the cybersecurity of VPPs. The energy system’s increasing digitalization and interconnectedness make it more vulnerable to cyberattacks [16]. Protecting VPPs from potential threats requires stringent cybersecurity measures and continuous monitoring for suspicious activities. Ensuring data privacy and securing communication channels are also crucial for a resilient VPP infrastructure. VPPs’ role in enhancing grid resilience is especially relevant in the context of climate change, which is increasing the frequency and severity of extreme weather events. VPPs can improve the grid’s ability to withstand and recover from disruptions by providing decentralized and distributed power sources. During natural disasters, when centralized power plants and transmission lines may be compromised, VPPs can continue to supply electricity from local sources, supporting critical infrastructure and community resilience.

Still, efficiently dispatching DERs to match supply with demand while minimizing operational costs and losses remains one of the most crucial points in the VPP’s framework. This requires advanced algorithms capable of real-time optimization based on market prices and grid conditions. VPPs must prioritize the integration and optimal use of renewable energy sources (RESs) like solar and wind. This involves balancing intermittency and ensuring that renewables are utilized to their fullest potential, which requires advanced forecasting and energy management systems. Optimizing the selection of energy sources in the context of VPPs is imperative to achieving multiple objectives: minimizing costs, enhancing the grid’s efficiency, and addressing environmental concerns. By strategically integrating diverse and RESs, VPPs can reduce reliance on expensive and polluting fossil fuels. This optimization allows for a more flexible and responsive energy system, capable of dynamically adjusting to demand fluctuations and resource availability, thereby maximizing operational efficiency. Moreover, the prioritization of cleaner energy sources within VPPs significantly mitigates GHG emissions, contributing to climate change mitigation efforts and promoting sustainable development. Thus, careful selection and management of energy sources in VPPs not only ensure economic benefits and energy security but also align with broader environmental and social responsibilities.

This article introduces a novel optimization algorithm designed to enhance the selection of energy sources within VPPs, effectively balancing supply and demand while minimizing the LCOE. The proposed algorithm not only aims to reduce energy losses but also focuses on decreasing GHG emissions, addressing critical environmental concerns. By leveraging advanced computational techniques and real-time data analytics, this optimization framework ensures efficient and sustainable energy distribution. The implementation of this algorithm promises to bolster the economic viability of VPPs and contribute significantly to the global transition towards cleaner and more resilient energy systems. The algorithm’s most significant feature is its adaptability when the power demand is lower than the available power generation capacity. It can intelligently disconnect specific energy sources or shift energy storage systems to charging mode, while ensuring the balance between the supply and demand, reducing energy costs, decreasing energy losses, and minimizing GHG emissions, thus enhancing the overall grid’s efficiency and sustainability. The presented optimization algorithm uses the MILP optimization technique, a methodology used to solve problems that involve both continuous and discrete decision variables. It combines linear programming (LP) and mixed integer (MI) programming to handle a wide range of optimization problems.

The proposed algorithm was tested using the IEEE 33-bus grid model, integrating multiple DERs at various nodes. Notably, the simulations considered several scenarios taking several factors into consideration such as the LCOE of the different power sources, the cost of GHG emissions, the spinning reserve, and the demand load. Given the intermittent nature of most DERs, rapidly changing electrical load demands, and the fluctuating electric rates in modern dynamic markets, it is essential that our algorithm can adapt quickly to these changes. It should provide the most up-to-date optimal DER combination for the VPP as swiftly as possible. Therefore, a sensitivity analysis is performed to evaluate the algorithm’s response time to rapid changes in load or market prices. Simulation results have demonstrated that the proposed algorithm is capable of providing the optimal combination of DERs every time the input values change within an average time of 0.07 s.

This article is structured to provide a comprehensive examination of the proposed optimization algorithm for VPP management. Following this introduction, the Related Works Section outlines existing research on VPP optimization and highlights the gaps that this study addresses. The MILP Optimization Algorithm Section then details the development and implementation of the optimization algorithm, including its mathematical foundations and computational techniques. Finally, in the Results Analysis Section, the performance of the algorithm is evaluated through various simulations, with a focus on balancing supply and demand, minimizing costs, and reducing greenhouse gas emissions.

2. Related Works

VPPs have emerged as a significant innovation in modern energy management, offering an advanced approach to aggregating and optimizing DERs. The latest advancements in VPP management and optimization aim to tackle various challenges and barriers associated with their deployment, such as lowering the LCOE, minimizing technical losses, reducing GHG emissions, providing the highest grid stability, and achieving the grid’s resilience and security.

However, VPPs are data-driven systems. Data play a pivotal role in the effective operation and optimization of VPPs. The integration and analysis of vast amounts of data from various sources, such as smart meters, weather forecasts, market prices, and DERs, are essential for making informed decisions. Accurate and real-time data enable precise forecasting of energy production and consumption, which is critical for balancing supply and demand. The work conducted in article [17] provides a unique perspective on the importance in the context of VPPs, as well as recent real-world projects from around the world, highlighting the most recent VPP practices. Additionally, data analytics help in identifying patterns and trends, optimizing energy dispatch, and improving the overall efficiency and reliability of the power system. Data also facilitate advanced predictive maintenance of equipment, reducing downtime and operational costs. Furthermore, in the context of regulatory compliance and sustainability, comprehensive data collection and analysis are vital for monitoring and reporting greenhouse gas emissions and other environmental impacts. Therefore, robust data management and analytics are fundamental to the success and sustainability of VPPs, enabling them to operate more efficiently, cost-effectively, and environmentally responsibly. Hence, the core of VPP management lies in the optimization algorithms that coordinate the dispatch of DERs. Recent advancements have seen the development of sophisticated algorithms utilizing artificial intelligence (AI) and machine learning (ML). These algorithms can analyze vast amounts of data in real time, enhancing the efficiency and responsiveness of VPPs. AI and ML algorithms can forecast energy demand and supply more accurately by analyzing historical data, weather patterns, and market signals. This predictive capability enables VPPs to balance supply and demand more effectively. Additionally, advanced optimization techniques, like MILP and dynamic programming, are used to solve complex scheduling problems in VPPs. These techniques consider multiple objectives to provide optimal solutions. Article [18] explores the effects of renewable production sources and storage devices on an electrical grid using an MILP optimization model to enhance the economic profitability of a VPP. Similarly, the work conducted in [19] uses an MILP-based algorithm that optimizes the daily profit of a VPP. On the other side, other researchers have adopted non-linear methodologies to deal with the intermittent and dynamic nature of VPPs. The authors in article [20] have adopted the information gap decision theory (IGDT) methodology to deal with the high level of uncertainties associated with VPPs. The IGDT is a powerful framework for making decisions under severe uncertainty, where the probability distributions of uncertainties are not well defined or are completely unknown. In the context of VPPs, IGDT can be particularly beneficial given the inherent uncertainties in renewable energy generation, market prices, and load demands. IGDT and MILP can be synergistically integrated to optimize the management of VPPs by addressing both uncertainty and operational efficiency. IGDT provides a robust framework for decision-making under uncertainty, allowing for the consideration of various scenarios and the management of risks associated with unpredictable factors such as fluctuating energy demands or supply disruptions. On the other hand, MILP offers a structured approach to optimize complex systems by formulating the problem as a set of linear equations and inequalities, which can efficiently handle operational constraints and objectives. By layering IGDT on top of MILP, VPP management can be optimized to account for the uncertainty in input parameters, such as renewable energy availability or market prices, while still adhering to operational constraints and maximizing performance metrics. This combined approach enables the development of robust strategies that balance risk and efficiency, ensuring that VPPs can effectively respond to dynamic conditions and optimize their performance across various scenarios. However, the subject article does not address the issue of uncertainty in input parameters but focuses solely on providing an optimization algorithm aimed at enhancing operational efficiency. By concentrating on this aspect, the article presents a method for optimizing the performance of VPPs based on fixed, predetermined inputs rather than exploring how variations and uncertainties in these inputs might affect the optimization process.

As the field evolved, heuristic and metaheuristic algorithms, including genetic algorithms (GAs) and particle swarm optimization (PSO), were introduced to tackle the computational complexity and scalability issues inherent in large-scale VPP optimization problems. In article [21], the authors use a GA to solve the operation issues resulting from the interaction of the VPP and the distribution network. Also, article [22] uses a genetic algorithm to manage the charge and discharge of EVs to enhance the economic and technical performance of a VPP. The authors of article [23] propose an accelerated particle swarm optimization (PSO) for optimal dispatch of renewable energy sources in a VPP context.

Stochastic and robust optimization methods have also gained prominence, addressing the fluctuations in renewable energy generation and market conditions by incorporating probabilistic and worst-case scenario analyses. The work presented in article [24] offers a multistage stochastic programming approach to model the trading of a VPP, and in article [25] the authors use a bi-level stochastic scheduling optimization model that combines day-ahead and real-time scheduling to mitigate the impact of uncertainty on VPP operations and reduce system power shortfall costs. On the other hand, the authors in article [26] apply a robust optimization method to maximize the profit of the VPP in the energy market and similarly in article [27] also a robust optimization method is applied to achieve an efficient VPP bidding technique in pool-based electricity markets. Additionally, hybrid approaches that combine multiple optimization techniques have been explored to leverage their respective strengths, resulting in more robust and efficient VPP management strategies, as applied in article [28].

Furthermore, the application of big data analytics and digital twins (DTs) has facilitated enhanced decision-making through detailed simulations and real-time data processing. The efficient management and analysis of vast amounts of data generated by VPPs are crucial for optimizing their performance. Leveraging big data analytics enables the processing and analysis of large datasets to extract valuable insights. Cloud computing provides scalable storage and processing capabilities, allowing VPPs to handle large volumes of data efficiently. The work presented in [29] proposes the use of DTs to address VPPs’ restrictions and barriers, as well as to improve their performance in a prosumer centric framework, focusing on dynamic state estimation, real-time control, and optimization.

In contrast to conventional AI techniques, recent research explores the potential of quantum computing for optimizing the operational management of VPPs, offering new avenues for addressing complex optimization problems with enhanced computational power and efficiency. The work conducted in [30] introduces a novel stochastic framework using the quantum teaching–learning-based optimization (QTLBO) algorithm for optimizing energy flow in microgrids, demonstrating its superior performance over traditional metaheuristic algorithms by addressing seasonal variations and uncertainties in distributed energy resources with improved accuracy and convergence. Similarly, article [31] presents a hybrid policy-based reinforcement learning (HPRL) approach for adaptive energy management in island energy systems with transmission constraints, using an island energy hub (IEH) model to optimize energy utilization and ensure supply, and demonstrates the effectiveness of this approach through numerical simulations.

Improving the accuracy of demand and supply forecasts enhances the efficiency and reliability of VPPs. AI algorithms, including neural networks and deep learning, can analyze historical data and external factors to provide highly accurate forecasts. Advanced weather prediction models improve the accuracy of renewable energy forecasts, particularly for solar and wind power. Therefore, artificial neural networks (ANNs) have become an integral part of optimization models for VPPs due to their ability to handle complex, non-linear relationships and process large volumes of data efficiently. ANNs are particularly effective in forecasting, optimization, and real-time management within VPP frameworks. In article [32], the authors present an ANN model for optimal scheduling and improving the cost effectiveness of a VPP. Moreover, real-time monitoring and control of DERs is also vital for the efficient operation of VPPs. Recent advancements in the Internet of Things (IoT) and communication technologies have significantly enhanced the real-time capabilities of VPPs. IoT devices and sensor networks provide real-time data on the performance and status of DERs. These data are essential for making informed decisions about resource allocation and dispatch. Edge computing allows data processing to occur closer to the source of data generation, enabling faster decision-making and enhancing the responsiveness of VPPs. The importance of IoT-based real-time management for VPPs is highlighted in article [33].

The future of VPPs is shaped by ongoing innovations and emerging trends that promise to enhance their capabilities and address existing challenges. Energy storage systems play a critical role in the functionality of VPPs [34] by storing excess energy during periods of low demand and releasing it during peak demand. Recent advancements in battery technology and energy management systems have significantly improved the efficiency and cost-effectiveness of ESS. Innovations in battery technology, like solid-state batteries and advanced lithium-ion batteries, offer higher energy density, longer lifespan, and improved safety compared to traditional batteries. Advanced energy management systems (EMSs) optimize the charge and discharge cycles of batteries, ensuring that energy storage is used efficiently. In article [35], the authors propose a GA-based smart energy resources allocation algorithm to account for depreciation of batteries resulting from discharges in the context of a VPP. Likewise, EVs are increasingly being integrated into VPPs, providing additional flexibility and storage capacity. V2G technology allows EVs to act as mobile energy storage units, providing power to the grid during peak demand and charging during low demand as highlighted in article [36]. Smart charging systems optimize the charging and discharging of EVs based on grid conditions and market signals [37]. Blockchain technology offers a decentralized and transparent platform for energy trading, enhancing the efficiency and security of VPP operations. Blockchain enables P2P energy trading, allowing consumers to buy and sell energy directly with each other. Smart contracts automate and enforce agreements between participants, ensuring transparency and reducing administrative overhead [38].

The latest advancements in VPP management and optimization are transforming the energy landscape, offering innovative solutions to mitigate the challenges and barriers associated with their deployment. By leveraging advanced algorithms, real-time monitoring, enhanced energy storage, supportive policies, and emerging technologies, VPPs are poised to lower the levelized cost of energy, minimize technical losses, and reduce greenhouse gas emissions. These advancements not only enhance the economic viability of VPPs but also contribute to a more sustainable and resilient energy future. As the energy sector continues to evolve, VPPs will play an increasingly critical role in integrating renewable energy, improving grid stability, and empowering consumers to participate actively in the energy market. Ongoing innovation and collaboration among stakeholders will ensure that VPPs remain at the forefront of the transition to a cleaner and more efficient energy system. Building on this perspective, the MILP-based VPP optimization algorithm, presented in this article, makes a significant contribution by effectively minimizing the LCOE while simultaneously accounting for carbon costs and grid technical losses. By integrating carbon pricing into the optimization model, the algorithm ensures that the economic implications of greenhouse gas emissions are considered, promoting environmentally sustainable energy production. Hence, the proposed MILP algorithm developed for minimizing the LCOE of a VPP incorporates several critical technical indicators to achieve its objective. Firstly, the algorithm meticulously accounts for the technical losses associated with the integration of DERs, ensuring that these losses are minimized to enhance overall system efficiency. This is achieved by optimizing the scheduling and dispatch of DERs to reduce energy waste and improve the reliability of energy delivery. Therefore, the cost of the total technical losses of the grid are included in the calculation of the overall LCOE. By incorporating technical losses into the grid’s operational costs, the algorithm provides a more accurate reflection of the true advantages of energy distribution, leading to more efficient resource allocation and energy dispatch. Additionally, the algorithm evaluates the cost implications of GHG emissions produced by various energy sources, integrating these costs into the optimization process to ensure that the environmental impact is considered alongside economic factors. By including both the reduction in technical losses and the cost of GHG emissions, the MILP algorithm provides a comprehensive approach to minimizing LCOE, balancing operational efficiency with environmental and economic sustainability. This multi-faceted approach ensures that the VPP operates at an optimal level while addressing both technical and ecological concerns. The algorithm’s ability to balance these complex factors underscores its potential to transform VPP management, paving the way for more sustainable and cost-effective energy systems.

3. MILP Optimization Algorithm

In order to provide an optimized cost-effective and efficient energy management for VPPs, the MILP optimization technique has been used. MILP is a mathematical optimization technique used to solve problems involving both continuous and discrete decision variables. The MILP algorithm is based on two main mathematical functions. The first function is the mixed integer (MI) element, and the second one is the linear programming function. The MI element refers to the inclusion of integer or binary decision variables, which allows for the modelling of discrete decisions within the optimization problem. The LP function is a mathematical method used to optimize a linear objective function subject to linear constraints. The key characteristics of LP are that the objective function and constraints are linear equations or inequalities, and the decision variables are continuous, meaning they can take any real value within a specified range. MILP algorithms are designed to find the best possible solution that satisfies all constraints, ensuring optimality in decision-making. MILP is widely used in fields such as energy management and scheduling, supply chain and logistics optimization, financial planning and portfolio optimization, and manufacturing and production planning. The objective function in MILP is a linear function that needs to be maximized or minimized. It typically takes the following form:

$${Min}_x(or {Max}_x)c^{T}x$$

(1)

where c is a vector of coefficients, and x is a vector of decision variables that can either be continuous or discrete. Vector c contains coefficients that represent the contribution of each decision variable to the objective function, such as cost, profit, or resource usage. Vector x consists of the decision variables, which are the elements that the optimization process will determine. These variables can be continuous, integer, or binary. Additionally, the constraints of the MILP model are expressed in the following form:

$$Ax\le b$$

(2)

where A is a matrix of constraint coefficients, x is the vector of decision variables, and b is a vector of constants representing the right-hand side of the constraints. The constraints ensure that the solution adheres to various restrictions such as resource limits, capacity constraints, or operational bounds. Through this formulation, the MILP model aims to find the optimal values for the decision variables that satisfy all constraints while optimizing the objective function.

In the context of optimizing VPPs, MILP is used to optimize the selection of energy sources and their operation schedules to achieve objectives like minimizing the LCOE, balancing supply and demand, reducing losses, and decreasing GHG emissions. The vector of coefficients includes the incurred costs of energy, GHG emissions, and technical losses, while the constraints involve load balancing, maximum emissions value in kg of CO₂ per kWh, and maximum accepted total LCOE. Hence, in our case the MILP is used to minimize the total cost of power supply of the VPP by minimizing the total LCOE of the connected DERs, minimizing the cost of emissions resulting from penalties paid for CO₂e emissions, and minimizing the cost of technical losses. Hence, the MILP formula is given by Equation (3):

$$Min Costfunction={\phi }_{LCOE}+{\phi }_{GHG}+{\phi }_{Losses}$$

(3)

where ${\phi }_{LCOE}$ is the combined LCOE of all the power sources connected to the grid including both the utility power generators and the DERs, ${\phi }_{GHG}$ is the combined cost of GHG emissions from the different power sources, and ${\phi }_{Losses}$ is the combined cost incurred by the grid’s technical losses.

The first step of the MILP algorithm is to formulate the problem as a mathematical optimization model. This involves defining the decision variables, the objective function to be minimized, and the constraints that the solution must satisfy. Thus, the first item of the MILP equation is the combined LCOE of the different considered generators. The LCOE is a measure of the average net present cost of electricity generation for a generator over its lifetime. It is a metric used to assess the average cost of producing electricity from a specific power source and it accounts for all the costs associated with the project, including initial capital costs, ongoing operation and maintenance costs, fuel costs, and financing costs. The LCOE is typically expressed in monetary terms per unit of electricity generated ($/kWh). When combining different energy sources to form a composite or blended LCOE, it is essential to consider the proportional contributions of each energy source to the total energy mix. Thus, the combine LCOE (${\phi }_{LCOE})$ is provided by Equation (4):

$${\phi }_{LCOE}={\displaystyle \frac{\sum _{i=1}^N{x}_i\times {LCOE}_i\times P_i}{\sum _{i=1}^N{x}_i\times P_i}}$$

(4)

where ${LCOE}_i$ is the levelized cost of energy of the power source $i$, $P_i$ is the power in kW provided by the power source $i$ in kW, $x_i$ is a binary decision variable (equal to 1 if the power source is selected to be connected to the grid and 0 if not), and $N$ is the set of available power sources to select among and optimize the VPP.

The second item of the MILP equation is the combined cost of GHG emissions. The cost of GHG emissions rights, also known as carbon pricing, can vary significantly depending on the specific market, regulatory framework, and geographical region. Carbon pricing, usually expressed in dollars per tonne of CO₂ ($/t CO₂), is a financial measure used to assign a cost to the emission of one metric tonne of carbon dioxide CO₂ into the atmosphere. This pricing mechanism is a key tool in climate policy aimed at reducing greenhouse gas emissions by making it more expensive to emit CO₂. In the context of a VPP that aggregates multiple energy sources, calculating the combined carbon pricing involves determining the weighted average carbon cost based on the contributions and carbon emissions of each energy source, as presented in Equation (5):

$${\phi }_{GHG}=\partial \times {\displaystyle \frac{\sum _{i=1}^N{x}_i\times {GHG}_i\times P_i}{\sum _{i=1}^N{x}_i\times P_i}}$$

(5)

where ${GHG}_i$ is the CO₂e emissions of the power source $i$ in kg of CO₂e/kWh, and $\partial$ is the carbon price of the power source $i$ in $/kg of CO₂e.

Finally, the last element of the MILP equation is to determine the cost of the technical losses in the grid. Technical losses refer to the energy losses that occur in the process of transmitting and distributing electricity from power plants to end-users. These losses are inherent to the physical and electrical properties of the transmission and distribution infrastructure and are different from non-technical losses, which result from theft, billing errors, or other non-physical causes. Technical losses in the electrical grid, such as transmission and distribution losses, are not typically included in the calculation of the LCOE. In order to account for the technical losses cost, first it is fundamental to determine the total technical losses in the grid, then calculate the cost associated with technical losses, which involves multiplying the amount of lost energy by the cost of generating that energy, and finally distribute the cost of technical losses among consumers based on their consumption. However, the trickiest part of the procedure is to calculate the grid’s technical losses. Usually, calculating the technical losses involves sophisticated and time-consuming techniques such as power flow analysis. Nevertheless, for the proper performance of our optimization algorithm, it is very important to rapidly calculate these losses. For this reason, we used the dynamic varying coefficient regression model, presented in article [39], to analytically estimate the grid’s technical losses. The aforementioned model is given by Equation (6):

$$y=f_a\left(L_i,Z_i\right)·x_i^2+f_b\left(L_i,Z_i\right)·x_i+c$$

(6)

where

$$f_a\left(L_i,Z_i\right)={\displaystyle \frac{L_i}{(642.896-45.0559\times Z_i)}}$$

(7)

$$f_b(L_i,Z_i)=0.001472\times Z_i\times L_i$$

(8)

$$c=Initial losses of the grid$$

(9)

Therefore, by using Equation (6) to calculate the contribution of each DER to the reduction in the grid’s technical losses, the cost of the technical losses (${\phi }_{Losses}$) can be calculated using Equation (10):

$${\phi }_{Losses}={\phi }_{LCOE}\times {\displaystyle \frac{[c-\sum _{i=1}^N\left(c-y_i\right)\times x_i]}{Load}}$$

(10)

where the contribution of DER to the reduction in grid technical losses is given by ($c-y_i$), the total reduction in grid technical losses from all connected DERs is given by $c-\sum (c-y_i$), and the distribution of the cost of technical losses over the load is given by ${\displaystyle \frac{[c-\sum _{i=1}^N\left(c-y_i\right)\times x_i]}{Load}}$.

The second step of the MILP algorithm, after formulating the problem as a mathematical optimization model, involves defining the constraints. The first constraint equation balances energy production with load demand, factoring in grid losses and the spinning reserve when necessary for improved grid stability. Therefore, every combination of available connected resources, including both utility grid power generation and DERs, must satisfy Equation (11):

$$\sum (x_i\times P_i)\ge Load+Losses+Spinning Reserve$$

(11)

In order to ensure that environmental objectives are met alongside economic and operational goals, a second constraint equation (Equation (12)) is added to the algorithm to make sure that the selected combination of power sources (grid and DERs) do not exceed the threshold set for ${GHG}_{Max}$.

$${\displaystyle \frac{\sum x_i\times {GHG}_i\times P_i}{\sum x_i\times P_i}}\le {GHG}_{Max}$$

(12)

Similarly, in order to ensure that the selected mix of DERs remains cost-effective, a third constraint equation (Equation (13)) is added to the algorithm. ${LCOE}_{Max }$ is a value set by the grid operator and guarantees that the optimized mix of DERs meets the economic limitations. For simulation purposes, the ${LCOE}_{Max }$ value is set to 0.21 $/kWh.

$${\displaystyle \frac{\sum x_i\times {LCOE}_i\times P_i}{\sum x_i\times P_i}}\le {LCOE}_{Max}$$

(13)

In a VPP, the power mix includes both grid power and DERs. Hence, with the aim to simulate a real-world scenario, when optimizing the DER selection within the VPP, we extended the MILP model to incorporate both sources while adhering to constraints on CO₂ emissions and LCOE. Thus, the MILP algorithm explores combinations that include the grid alone, a mix of the grid and DERs, and only DERs if they can satisfy the total load demand without additional power from the grid. However, when a mix of the grid and DERs is considered, the power provided by the grid must satisfy Equation (14):

$$P_{grid}=Load-\sum x_i\times P_i$$

(14)

In the context of optimizing VPPs using MILP, balancing multiple objectives inherently involves navigating trade-offs between conflicting goals. One of the primary trade-offs is between minimizing the LCOE and reducing greenhouse gas (GHG) emissions. Achieving a lower LCOE often involves utilizing energy sources that may have higher emissions but are cost-effective, while prioritizing lower emissions might necessitate investing in more expensive, cleaner technologies. Additionally, optimizing operational efficiency by reducing technical losses may require adjusting energy dispatch and storage strategies, which could impact both the economic performance and the reliability of the VPP. The MILP model addresses these trade-offs by employing objective functions and constraints that reflect the relative importance of each goal, allowing for a balanced solution. This process involves iterative adjustments to the model parameters and constraints, which are conducted by the grid operator and provided as inputs to the MILP algorithm to find an optimal compromise that meets the predefined performance criteria. By methodically setting the constraints, like ${LCOE}_{Max}$, ${GHG}_{Max}$, and the spinning reserve, the MILP framework facilitates informed decision-making that aligns with the strategic objectives of the VPP, ensuring that the trade-offs between cost, efficiency, and environmental impact are effectively managed.

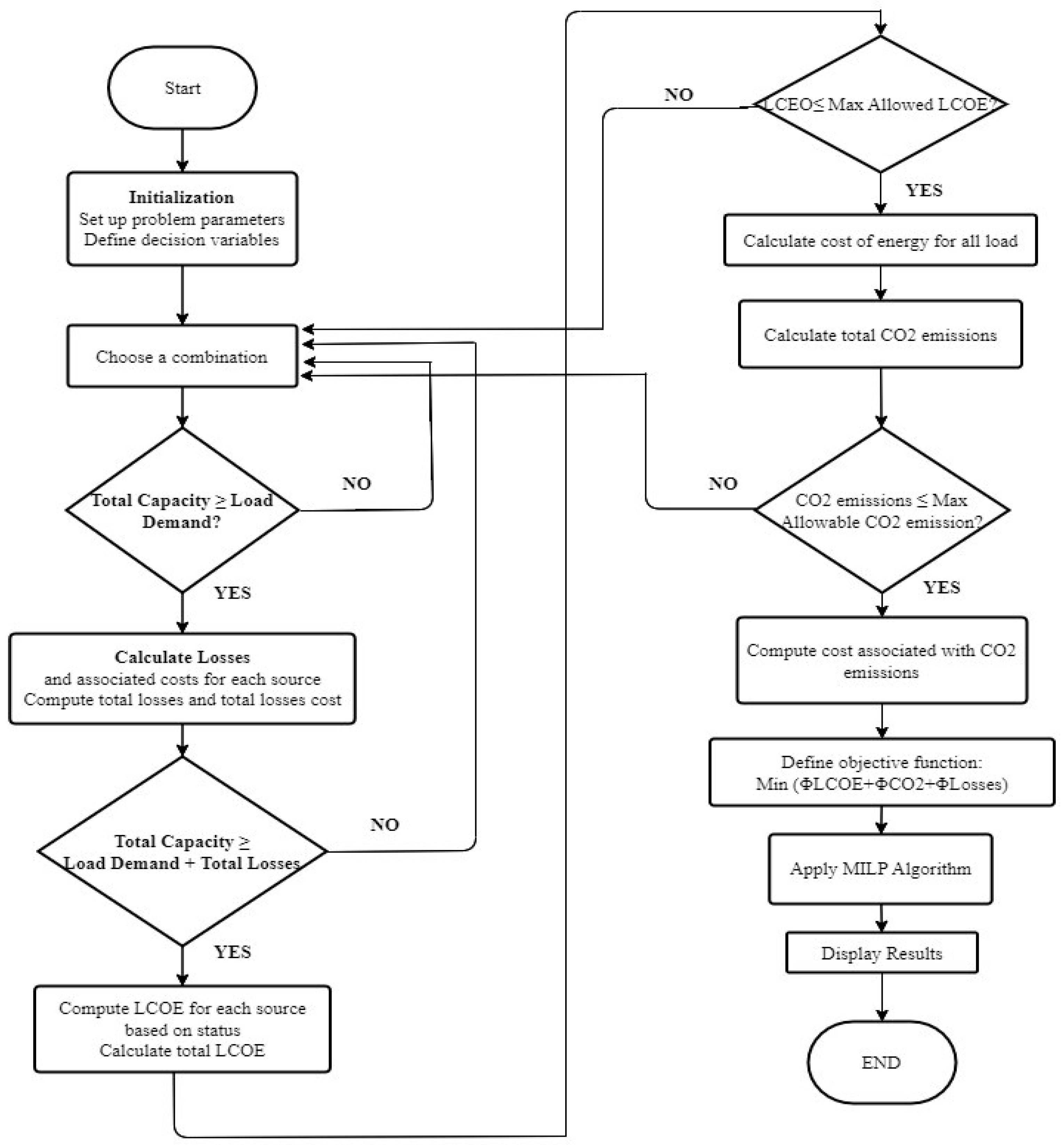
The overall process of the applied MILP algorithm is summarized in the flow diagram shown in Figure 1. In theory, optimization using the MILP technique can result in one of three outcomes: an optimal solution found, an infeasible model, or an unbounded objective. If an optimal solution is found, it means the algorithm has identified the best possible values for the decision variables that satisfy all constraints and maximize or minimize the objective function. If the model is infeasible, it indicates that no solution exists that meets all the given constraints, implying a contradiction or overly restrictive conditions. Finally, if the objective is unbounded, the algorithm determines that the objective function can be increased indefinitely (for maximization problems) or decreased indefinitely (for minimization problems) without violating any constraints, suggesting that the model lacks necessary bounds or constraints to limit the solution space. The convergence of an MILP algorithm to an optimal value is highly dependent on the set of constraints defined in the model. Constraints shape the feasible region, dictating which solutions are permissible within the problem’s context. Tight or well-defined constraints can guide the algorithm efficiently toward the optimal solution, reducing the search space and improving convergence speed. Conversely, poorly defined constraints can lead to a larger feasible region, making it more challenging for the algorithm to navigate and identify the optimal solution. Infeasible or conflicting constraints can prevent convergence entirely, while unbounded constraints can lead to an unbounded objective.

In our case, as long as $P_{Grid}$ is infinite, ${LCOE}_{Max}\ge {LCOE}_{Grid}$, and the environmental constraint exceeds the grid’s emissions limit, the model will always converge to a value. This is because one combination, for sure, can meet these conditions—connecting all the load to the grid without relying on any DER.

4. Simulation Results

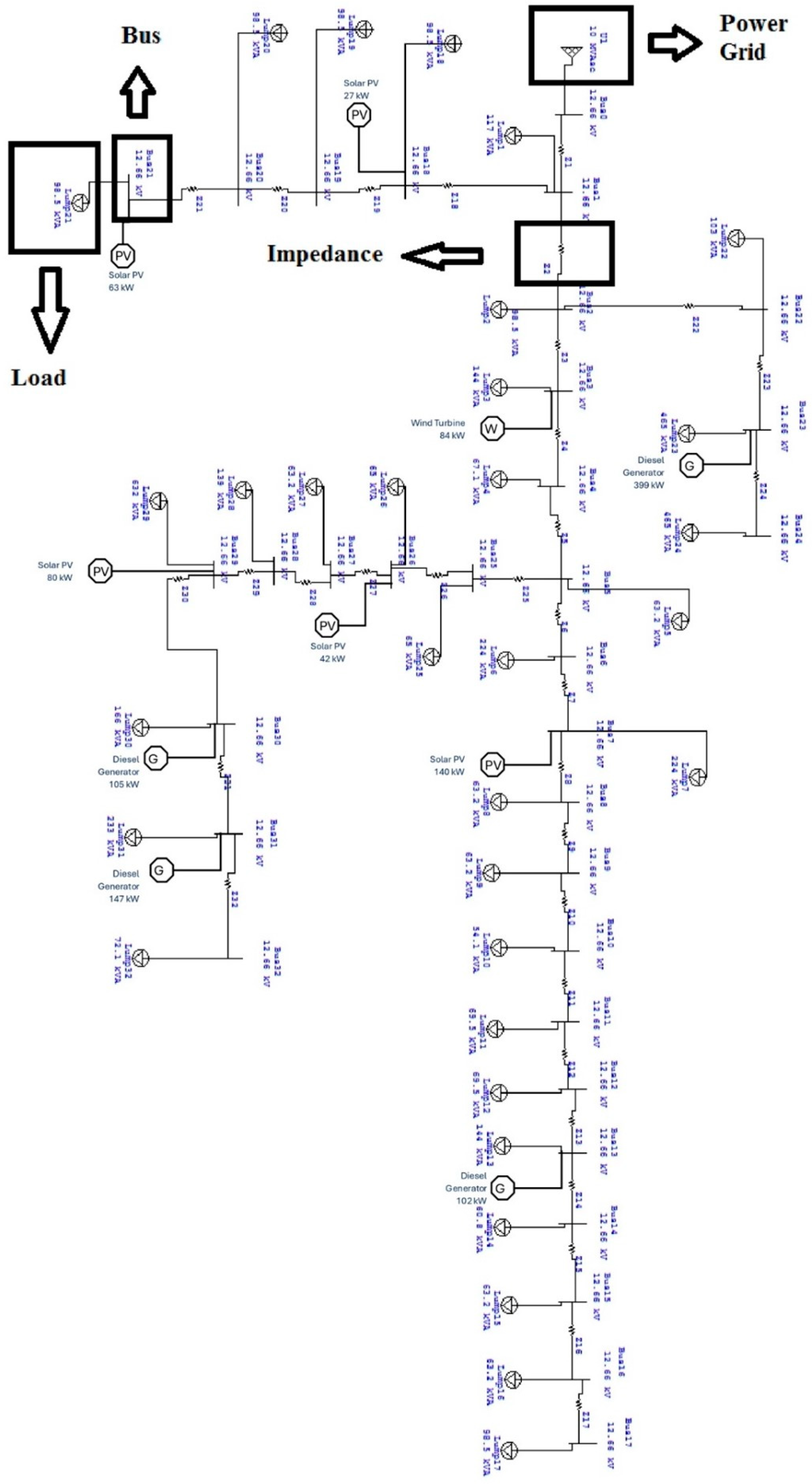
The VPP MILP-based optimization algorithm was built and tested using an Intel i7-7500U, 2.70 GHz, dual-core CPU with 16 GB RAM, operating on Windows 10. The model was tested using the IEEE 33-bus grid model with 10 different DERs. The algorithm was programmed and tested using both Microsoft 365 Excel and Matlab/Simulink R2022a version.

The IEEE 33-bus system is a standard test case in power system engineering used for studying the distribution network. This test case is commonly utilized for various purposes, such as the analysis of power flow, voltage stability, and optimization algorithms for distribution networks. The IEEE 33-bus grid model data are provided in Appendix A. The VPP is formed by 10 DERs, one wind turbine, four diesel generators, and five solar photovoltaic (PV) systems. The 10 DER generators’ connection points to the IEEE 33-bus grid, as well as the nominal power of each generator, are detailed in

Table 1. DERs connected to the IEEE 33-bus model.

Bus Number	Load Connected to the Bus (kW)	Power Generation Capacity (kW)	DER Int. (%)	Type	DER Contribution to Tech. Losses Reduction (kW)	LCOE ($/kWh)	GHG (kg of CO2e/kWh
0	0	∞	0	Grid	0	0.18	0.7
3	120	84	0.7	Wind	3	0.09	0
7	200	140	0.7	PV	13.1	0.06	0
13	120	102	0.85	Gen	13.2	0.22	0.3
18	90	27	0.3	PV	0.3	0.06	0
21	90	63	0.7	PV	4.1	0.06	0
23	420	399	0.95	Gen	15.3	0.22	0.3
26	60	42	0.7	PV	2.1	0.06	0
29	200	80	0.4	PV	7.6	0.06	0
30	150	105	0.7	Gen	12	0.22	0.3
31	210	147	0.7	Gen	17.7	0.22	0.3

.

In the simulation study, key variables and constraints are defined to assess the performance and optimization of the VPP within the IEEE 33-bus system. These variables include the power output from each DER and the power imported from the grid, as well as the total demand load and the required spinning reserve. They also consider the LCOE per unit of power generation and the environmental impact of each source, measured through the CO₂ emissions variables for each DER and grid power. By adjusting these variables and constraints, the simulation seeks to test the performance of the MILP algorithm. This algorithm aims to optimize the DER selection and operation strategy to reduce costs, satisfy demand, and comply with environmental regulations. The baseline model is considered as the scenario where all available DERs are fully used, and the grid provides the remaining necessary power. In this baseline scenario, all decision variables are set to 1. For this purpose, we have defined the following scenarios:

• Scenario #1: This scenario assumes a total demand load of 3926 kW and no spinning reserve is assumed to be provided by the VPP. The ${LCOE}_{Grid}$ is set at 0.18 $/kWh, ${LCOE}_{PV}$ at 0.06 $/kWh, ${LCOE}_{Wind}$ at 0.09 $/kWh, and ${LCOE}_{Gen}$ at 0.22 $/kWh. Additionally, it presumes that both the wind turbine and solar PV produce no GHG emissions. However, the utility grid’s emissions are set at 0.7 kg of CO₂e/kWh, and the diesel generators’ emissions are at 0.3 kg of CO₂e/kWh. The carbon price is estimated to be $0.01/kg CO₂e. In terms of constraints, ${GHG}_{Max}$ is set to 0.65 kg of CO₂e/kWh. ${LCOE}_{Max}$ is set to 0.21 $/kWh;
• Scenario #2: This scenario maintains the same conditions as scenario #1, with the sole difference being a demand load that is half of scenario #1’s load;
• Scenario #3: This scenario maintains the same conditions as scenario #1, with the sole difference being an ${LCOE}_{Grid}$ equal to 0.24 $/kWh and ${LCOE}_{Max}$ is set to 0.25 $/kWh;
• Scenario #4: This scenario maintains the same conditions as scenario #1, with the addition of 25% spinning reserve to be provided by the VPP;
• Scenario #5: This scenario maintains the same conditions as scenario #1, with the sole difference being a demand load that is one quarter of scenario #1’s load;
• Scenario #6: This scenario maintains the same conditions as scenario #5, with the sole difference being an ${LCOE}_{Grid}$ equal to 0.24 $/kWh.

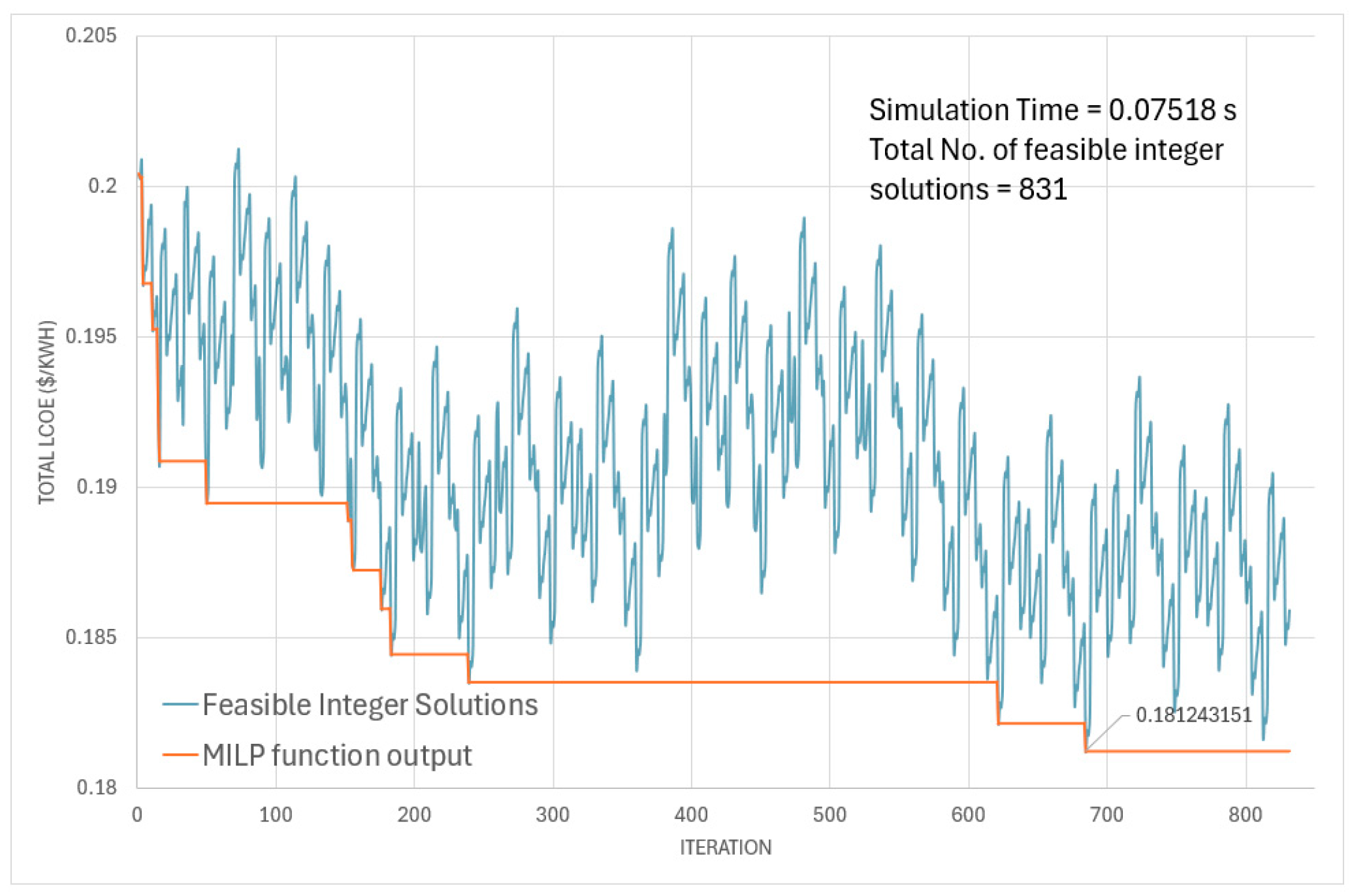
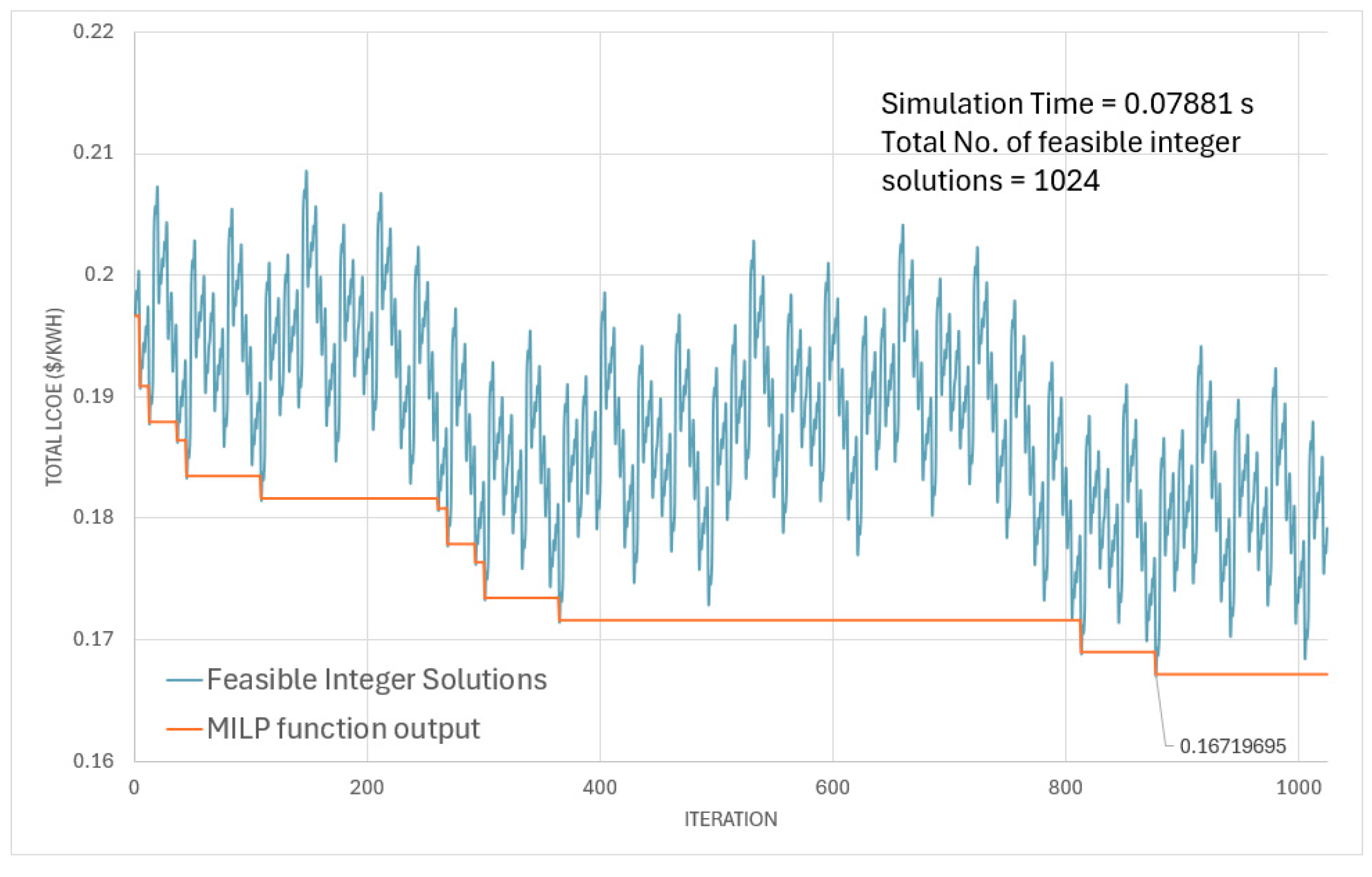
The calculated LCOE (the value of the objective function) of all feasible integer solutions which satisfy all the constraints for scenarios #1 and #2 is depicted in Figure 2 and Figure 3. From the simulations, it was observed that 831 (out of 2¹¹ possible combinations) feasible integer solutions adhered to the constraints of the MILP algorithm for scenario #1 and 1024 for scenario #2. Figure 2 and Figure 3 also illustrate the output of the MILP function (orange curve), showing the model’s convergence toward the optimal minimum LCOE. Both calculated LCOE of valid combination outputs and the MILP function output are shown on the same graph to validate the model’s convergence towards the optimal value. The simulation times for both scenarios were 0.075 and 0.078 s, respectively. Both simulations indicated that the same combination of DERs resulted in the lowest total LCOE. The selected DERs are displayed in

Table 2. Scenario #1 with a total load of 3926 kW and no spinning reserve.

Scenario #1
LCOE_Grid	0.18 $/kWh	LCOE_PV	0.06 $/kWh
LCOE_W	0.09 $/kWh	LCOE_Gen	0.22 $/kWh
GHG_Grid	0.7 kg CO2e/kWh	GHG_PV	0 kg CO2e/kWh
GHG_Gen	0.3 kg CO2e/kWh	GHG_Wind	0 kg CO2e/kWh
Grid Power	3490 kW	P_CO2e	0.01 $/kg CO2e
Total Load	3926 kW	Spinning Res.	0%
Total LCOE		0.181243 $/kWh
Total GHG emissions		0.628 kg CO2e/kWh
Baseline LCOE		0.185907 $/kWh
Bus_3 (Wind)	84 kW	Bus_23 (Wind)	0 kW
Bus_7 (PV)	140 kW	Bus_26 (PV)	42 kW
Bus_13 (Gen)	0 kW	Bus_29 (Gen)	80 kW
Bus_18 (PV)	27 kW	Bus_30 (PV)	0 kW
Bus_21 (PV)	63 kW	Bus_31 (Gen)	0 kW

and

Table 3. Scenario #2 with a total load of 1963 kW and no spinning reserve.

Scenario #2
LCOE_Grid	0.18 $/kWh	LCOE_PV	0.06 $/kWh
LCOE_W	0.09 $/kWh	LCOE_Gen	0.22 $/kWh
GHG_Grid	0.7 kg CO2e/kWh	GHG_PV	0 kg CO2e/kWh
GHG_Gen	0.3 kg CO2e/kWh	GHG_Wind	0 kg CO2e/kWh
Grid Power	1527 kW	P_CO2e	0.01 $/kg CO2e
Total Load	1963 kW	Spinning Res.	0%
Total LCOE		0.167197 $/kWh
Total GHG emissions		0.556 kg CO2e/kWh
Baseline LCOE		0.179193 $/kWh
Bus_3 (Wind)	84 kW	Bus_23 (Wind)	0 kW
Bus_7 (PV)	140 kW	Bus_26 (PV)	42 kW
Bus_13 (Gen)	0 kW	Bus_29 (Gen)	80 kW
Bus_18 (PV)	27 kW	Bus_30 (PV)	0 kW
Bus_21 (PV)	63 kW	Bus_31 (Gen)	0 kW

. The total LCOE in scenario #1 was 0.181243 $/kWh, 2.5% lower than the baseline model LCOE. However, when the demand load was halved, this LCOE dropped to 0.167197 $/kWh, nevertheless achieving 6.7% reduction from the baseline model LCOE. In the first scenario, the power supplied by the utility grid was 3490 kW, while in the second scenario, $P_{grid}$ equaled 1527 kW. Moreover, diesel generators were excluded from the selected DERs in both scenarios. This is due to the total LCOE of the generators being higher than the grid’s LCOE. The lower GHG emissions and the contribution to decreasing the grid’s technical losses from the diesel generators were insufficient to bridge this gap.

Scenario #3 demonstrates that when the LCOE provided by the grid increases to 0.24 $/kWh, compared to a diesel generator LCOE at 0.22 $/kWh, the optimization algorithm prioritizes extracting maximum power from diesel generators and other DERs. It also minimizes the power provided by the grid ($P_{grid}$ = 2737 kW). In this scenario, the total LCOE equals 0.229042 $/kWh (

Table 4. Scenario #3 with a load of 3926 kW and no spinning reserve, with ${LCOE}_{Grid}$ = 0.24 $/kWh and ${LCOE}_{Max}$ = 0.25 $/kWh.

Scenario #3
LCOE_Grid	0.24 $/kWh	LCOE_PV	0.06 $/kWh
LCOE_W	0.09 $/kWh	LCOE_Gen	0.22 $/kWh
GHG_Grid	0.7 kg CO2e/kWh	GHG_PV	0 kg CO2e/kWh
GHG_Gen	0.3 kg CO2e/kWh	GHG_Wind	0 kg CO2e/kWh
Grid Power	2737 kW	P_CO2e	0.01 $/kg CO2e
Total Load	3926 kW	Spinning Res.	0%
Total LCOE		0.229042 $/kWh
Total GHG emissions		0.545 kg COe/kWh
Baseline LCOE		0.229042 $/kWh
Bus_3 (Wind)	84 kW	Bus_23 (Wind)	399 kW
Bus_7 (PV)	140 kW	Bus_26 (PV)	42 kW
Bus_13 (Gen)	102 kW	Bus_29 (Gen)	80 kW
Bus_18 (PV)	27 kW	Bus_30 (PV)	105 kW
Bus_21 (PV)	63 kW	Bus_31 (Gen)	147 kW

), which is the same as the baseline model. The LCOEs of the different feasible integer solutions are shown in Figure 4.

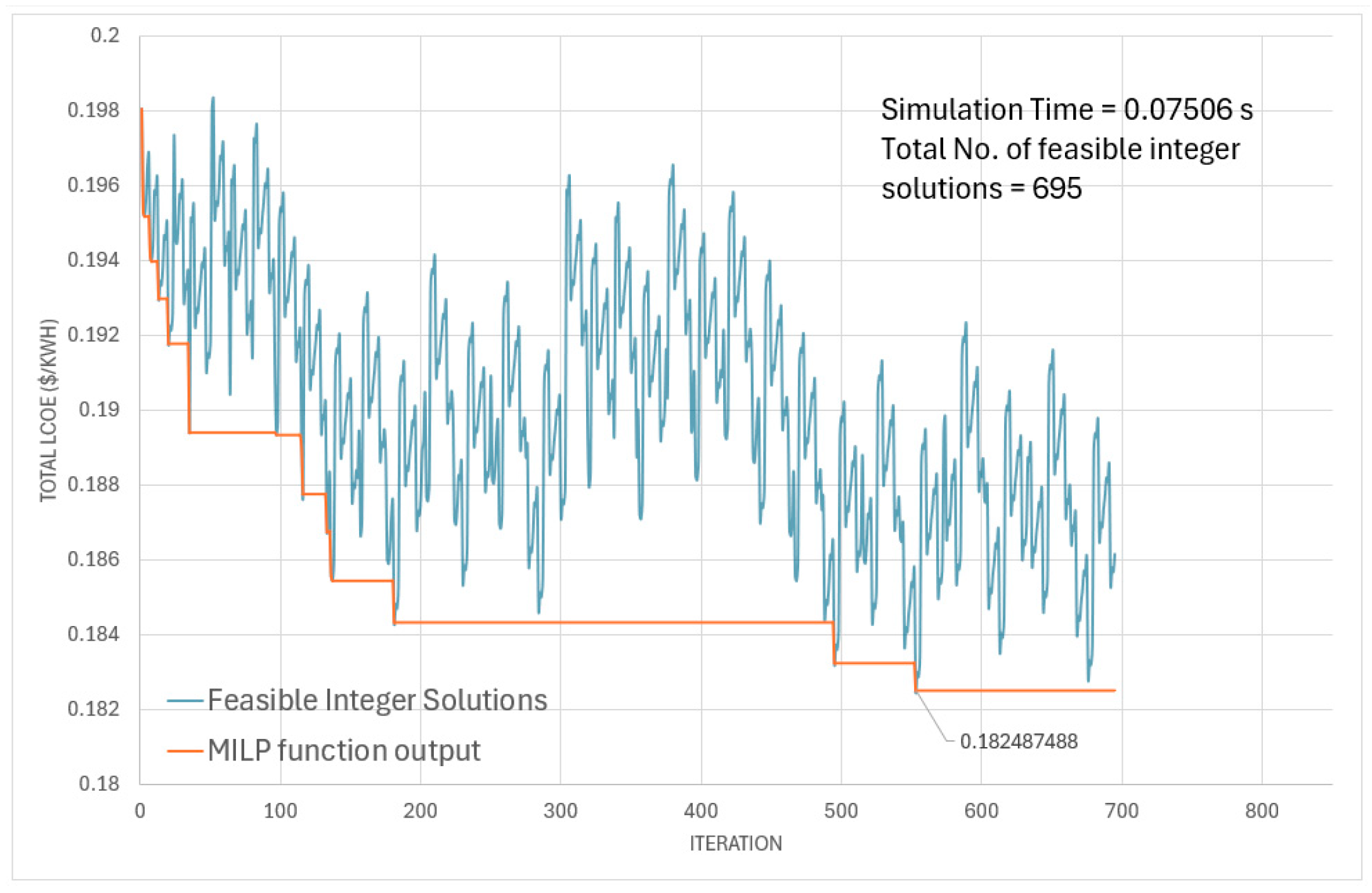
Scenario #4 examines the effect of adding a spinning reserve to the energy mix provided by the DERs. The results show that adding a spinning reserve incurs a minimal increase in the total LCOE, leading to an LCOE of 0.182487 $/kWh (

Table 5. Scenario #4 with a total load of 3926 kW and 25% spinning reserve.

Scenario #4
LCOE_Grid	0.18 $/kWh	LCOE_PV	0.06 $/kWh
LCOE_W	0.09 $/kWh	LCOE_Gen	0.22 $/kWh
GHG_Grid	0.7 kg CO2e/kWh	GHG_PV	0 kg CO2e/kWh
GHG_Gen	0.3 kg CO2e/kWh	GHG_Wind	0 kg CO2e/kWh
Grid Power	4471 kW	P_CO2e	0.01 $/kg CO2e
Total Load	3926 kW	Spinning Res.	25%
Total LCOE		0.182487 $/kWh
Total GHG emissions		0.637 kg COe/kWh
Baseline LCOE		0.186151 $/kWh
Bus_3 (Wind)	84 kW	Bus_23 (Wind)	0 kW
Bus_7 (PV)	140 kW	Bus_26 (PV)	42 kW
Bus_13 (Gen)	0 kW	Bus_29 (Gen)	80 kW
Bus_18 (PV)	27 kW	Bus_30 (PV)	0 kW
Bus_21 (PV)	63 kW	Bus_31 (Gen)	0 kW

), 2% lower than the baseline model. This is compared to 0.181243 $/kWh under the same conditions, but without a spinning reserve (scenario #1). The simulation for the 695 feasible integer solutions is 0.07506 s, as shown in Figure 5.

Scenario #5 explores the case of a demand load reduced to 25% of the baseline load. As shown in

Table 6. Scenario #5 with a total load of 982 kW and no spinning reserve.

Scenario #5
LCOE_Grid	0.18 $/kWh	LCOE_PV	0.06 $/kWh
LCOE_W	0.09 $/kWh	LCOE_Gen	0.22 $/kWh
GHG_Grid	0.7 kg CO2e/kWh	GHG_PV	0 kg CO2e/kWh
GHG_Gen	0.3 kg CO2e/kWh	GHG_Wind	0 kg CO2e/kWh
Grid Power	546 kW	P_CO2e	0.01 $/kg CO2e
Total Load	982 kW	Spinning Res.	0%
Total LCOE		0.13913 $/kWh
Total GHG emissions		0.39 kg COe/kWh
Baseline LCOE		0.16577 $/kWh
Bus_3 (Wind)	84 kW	Bus_23 (Wind)	-
Bus_7 (PV)	140 kW	Bus_26 (PV)	42 kW
Bus_13 (Gen)	0 kW	Bus_29 (Gen)	80 kW
Bus_18 (PV)	27 kW	Bus_30 (PV)	0 kW
Bus_21 (PV)	63 kW	Bus_31 (Gen)	0 kW

, the total LCOE decreases to 0.13913 $/kWh. This drop results from the DERs with low LCOE, like solar PV systems and wind turbines, serving a higher share of the load (around 40%). Consequently, the utility grid’s share decreases to 546 kW. The MILP algorithm achieved an LCOE 16% lower than the baseline model.

Like scenario #5, scenario #6 also explores the case of reduced demand load. However, this scenario assumes that the LCOE of the grid is higher than that of diesel generators. As a result,

Table 7. Scenario #6 with a load of 982 kW and no spinning reserve, with ${LCOE}_{Grid}$ = 0.24 $/kWh and ${LCOE}_{Max}$ = 0.25 $/kWh.

Scenario #6
LCOE_Grid	0.24 $/kWh	LCOE_PV	0.06 $/kWh
LCOE_W	0.09 $/kWh	LCOE_Gen	0.22 $/kWh
GHG_Grid	0.7 kg CO2e/kWh	GHG_PV	0 kg CO2e/kWh
GHG_Gen	0.3 kg CO2e/kWh	GHG_Wind	0 kg CO2e/kWh
Grid Power	0 kW	P_CO2e	0.01 $/kg CO2e
Total Load	982 kW	Spinning Res.	0%
Total LCOE		0.158897 $/kWh
Total GHG emissions		0.16 kg COe/kWh
Baseline LCOE		0.17045 $/kWh
Bus_3 (Wind)	84 kW	Bus_23 (Wind)	399 kW
Bus_7 (PV)	140 kW	Bus_26 (PV)	42 kW
Bus_13 (Gen)	0 kW	Bus_29 (Gen)	80 kW
Bus_18 (PV)	27 kW	Bus_30 (PV)	0 kW
Bus_21 (PV)	63 kW	Bus_31 (Gen)	147 kW

shows that under these conditions, the power supplied by the grid is replaced by diesel generators connected to buses 23 and 31, leading to a total LCOE of 0.158897 $/kWh, 6.7% lower than the baseline.

In order to assess the impact of the set constraints on the algorithm, we tested the model defined in scenario #1 under various constraint values for ${GHG}_{Max}$ and ${LCOE}_{Max}$ (scenarios 7–12). The results are presented in

Table 8. Various scenarios based on the conditions of scenario #1 but with different constraints.

Scenario	GHGMax (kg of CO2e/kWh)	LCOEMax ($/kWh)	No. of Feasible Integer Solutions	Total LCOE ($/kWh)	Baseline Model LCOE ($/kWh)
7	0.55	0.21	1	0.185907	0.185907
8	0.6	0.21	239	0.182306	0.185907
9	0.6	0.19	115	0.182306	0.185907
10	0.57	0.19	26	0.185053	0.185907
11	0.5	0.19	0	-	-
12	0.65	0.18	0	-	-

. When ${GHG}_{Max}$ is lowered to 0.55 kg of CO₂e/kWh, only one solution respects the constraints which is the baseline model where all DERs are online, and the grid provides the remaining power needed to serve the total load. When ${GHG}_{Max}$ and ${LCOE}_{Max}$ are both lowered, it is noticed that the number of feasible integer solutions decreases a lot compared to the same number calculated in scenario #1. Hence, it proves that a good set of tight constraints can guide the algorithm efficiently toward the optimal solution, reducing the search space and improving convergence speed. Lastly, when ${GHG}_{Max}$ or ${LCOE}_{Max}$ are extremely tightened, it leads to an infeasible solution.

In the second part of the simulation, we conducted a sensitivity analysis of the proposed MILP optimization algorithm for the VPP, focusing on examining how variations in the LCOE of the solar PV systems and the carbon price impact the total LCOE results. By systematically varying the LCOE of the solar PV system, we can evaluate the influence of changes in solar energy costs on the selection and operation of DERS within the VPP. Simultaneously, altering the carbon price allows us to assess the effect of different carbon pricing scenarios on the economic and environmental performance of the VPP. The sensitivity analysis provides insights into the robustness of the optimization algorithm, revealing how shifts in key economic parameters can affect the total cost, CO₂ emissions, and the optimal mix of energy sources. This analysis is crucial to understand the potential financial and environmental implications under varying market conditions and to make informed decisions for sustainable and cost-effective energy management. Figure 6 shows the variation in the total LCOE as a function of the variation in the solar PV’s LCOE. An increase in the solar PV’s LCOE certainly incurs an augmentation in the total LCOE. However, it is also to be noted that the proposed MILP algorithm has a rapid response time that allows it to quickly respond to fluctuations in market prices, and this is revealed in the response time (Rs_Time) shown in Figure 6. The decreasing LCOE for solar PV systems has a significant impact on the LCOE of the overall energy mix. As solar PV becomes more cost-competitive, it increasingly displaces more expensive and less environmentally friendly energy sources, like the grid power plants and the diesel generators, thus lowering the average cost of electricity generation. Similarly, Figure 7 shows the impact of the carbon price on the total LCOE. As the carbon price increases from 0.01 to 0.055 $/kg of CO₂e, the total LCOE goes from 0.181243 $/kWh to 0.209166 $/kWh. Higher prices for carbon emissions have a substantial impact on the overall LCOE. As carbon pricing mechanisms, such as carbon taxes or cap-and-trade systems, increase the cost of emitting carbon dioxide, fossil fuel-based power generation becomes more expensive. This cost pressure incentivizes a shift towards cleaner, renewable energy sources like wind, solar, and hydropower, which do not incur carbon costs. Consequently, the overall LCOE of the grid may initially rise due to the increased costs associated with fossil fuels. However, over time, as the energy mix transitions to a higher proportion of renewables, the grid’s LCOE can stabilize or even decrease due to the declining costs of renewable technologies and improved efficiencies.

5. Conclusions

Looking ahead, the continued evolution of VPPs will be shaped by technological innovations, regulatory developments, and market dynamics. The integration of advanced energy storage technologies, like solid-state batteries and hydrogen fuel cells, can enhance the storage capacity and flexibility of VPPs. Emerging technologies, like vehicle-to-grid (V2G) systems, where EVs can both draw from and supply power to the grid, hold promise for expanding VPPs’ capabilities. Additionally, the development of P2P energy trading platforms can further democratize the energy market, allowing consumers to directly trade energy with each other through VPPs. However, the optimization of the resources remains a cornerstone of any VPP. By strategically selecting and operating DERs, VPPs can efficiently balance supply and demand, minimize operational costs, and reduce greenhouse gas emissions. This optimization ensures that energy generation and consumption are managed in the most cost-effective and environmentally friendly manner. Advanced algorithms, such as MILP, play a crucial role in this process by enabling the precise allocation of resources, considering various constraints and objectives. The ability to dynamically optimize resources allows VPPs to adapt to changing market conditions, integrate renewable energy sources, and enhance the reliability and resilience of the power grid. Therefore, the continuous improvement and application of optimization techniques are fundamental to the success and sustainability of VPPs.

This article has presented an MILP-based optimization algorithm designed to enhance the operation of VPPs by minimizing the LCOE, technical losses, and GHG emissions. Through comprehensive simulations utilizing the IEEE 33-bus model, the algorithm demonstrated its effectiveness in optimizing resource allocation and operational strategies within the VPP framework. The results underscore the algorithm’s capability to achieve a low LCOE, while accounting for the grid’s technical losses and the GHG emissions of the different power sources. The rapid convergence of the MILP algorithm further highlights its practical applicability for real-time and large-scale energy management scenarios. This study confirms the potential of advanced optimization techniques in transforming the management of distributed energy resources, paving the way for more sustainable and economically viable power systems. Nevertheless, the future research direction in VPP optimization is poised to integrate real-time operational data with advanced analytical frameworks, such as chance-constrained programming (CCP) and Nash bargaining models [40], to enhance the accuracy and effectiveness of decision-making processes. By leveraging actual operational data, researchers can conduct more in-depth analyses and fine-tune VPP strategies to better accommodate dynamic conditions and improve performance. The combination of CCP with Nash bargaining models offers a promising approach to addressing the inherent uncertainties in renewable energy generation and market fluctuations. Additionally, the development of multilevel decision models can provide a comprehensive network of interactions and optimizations across various levels of VPP operations, such as using a stochastic bi-level optimal allocation model for intelligent energy storage sharing services to reduce investment and operating costs, addressing uncertainties in electricity prices [41]. Moreover, challenges such as managing the inherent uncertainties in renewable energy sources, fluctuating demand, and integration complexities will need to be addressed. These challenges require innovative approaches to data integration, model accuracy, and computational efficiency to ensure that VPPs can operate optimally in increasingly complex and variable environments.

Additionally, in a real-world scenario, several systems can induce delays in data acquisition and control of VPP resources, impacting overall operational efficiency. One primary source of delay is the communication infrastructure, including network latencies and bandwidth limitations, which can affect the timely transmission of data from DERs to the central control system. Additionally, the integration of various types of generators and storage systems, each with different communication protocols and data formats, can cause compatibility issues and slow down the data aggregation process. The data processing systems, which include data analytics and real-time monitoring tools, may also contribute to delays if they lack sufficient computational power or efficiency in processing large volumes of data. Furthermore, software and algorithmic delays can occur due to the complexity of optimization and control algorithms used for managing the VPP’s operations. Lastly, external factors such as cybersecurity measures and regulatory compliance checks can introduce additional delays, as ensuring data security and meeting regulatory requirements often involves rigorous verification processes. Collectively, these factors can lead to slower response times in controlling generators, potentially affecting the VPP’s ability to balance supply and demand effectively. However, the proposed MILP algorithm has proven to be able to provide an optimal solution very quickly, significantly reducing software and algorithmic delays.

In conclusion, virtual power plants represent a transformative approach to energy management, offering multiple benefits for grid stability, economic efficiency, and environmental sustainability. By harnessing the collective power of distributed energy resources, VPPs can provide flexible, reliable, and clean energy solutions. The successful implementation of VPPs will depend on overcoming technical, regulatory, and cybersecurity challenges, as well as fostering collaboration and innovation across the energy sector. As the energy landscape continues to evolve, VPPs will play a pivotal role in shaping a resilient, sustainable, and decentralized energy future.