Hydrodynamic Performance of a Dual-Pontoon WEC-Breakwater System: An Analysis of Wave Energy Content and Converter Efficiency
Abstract
1. Introduction
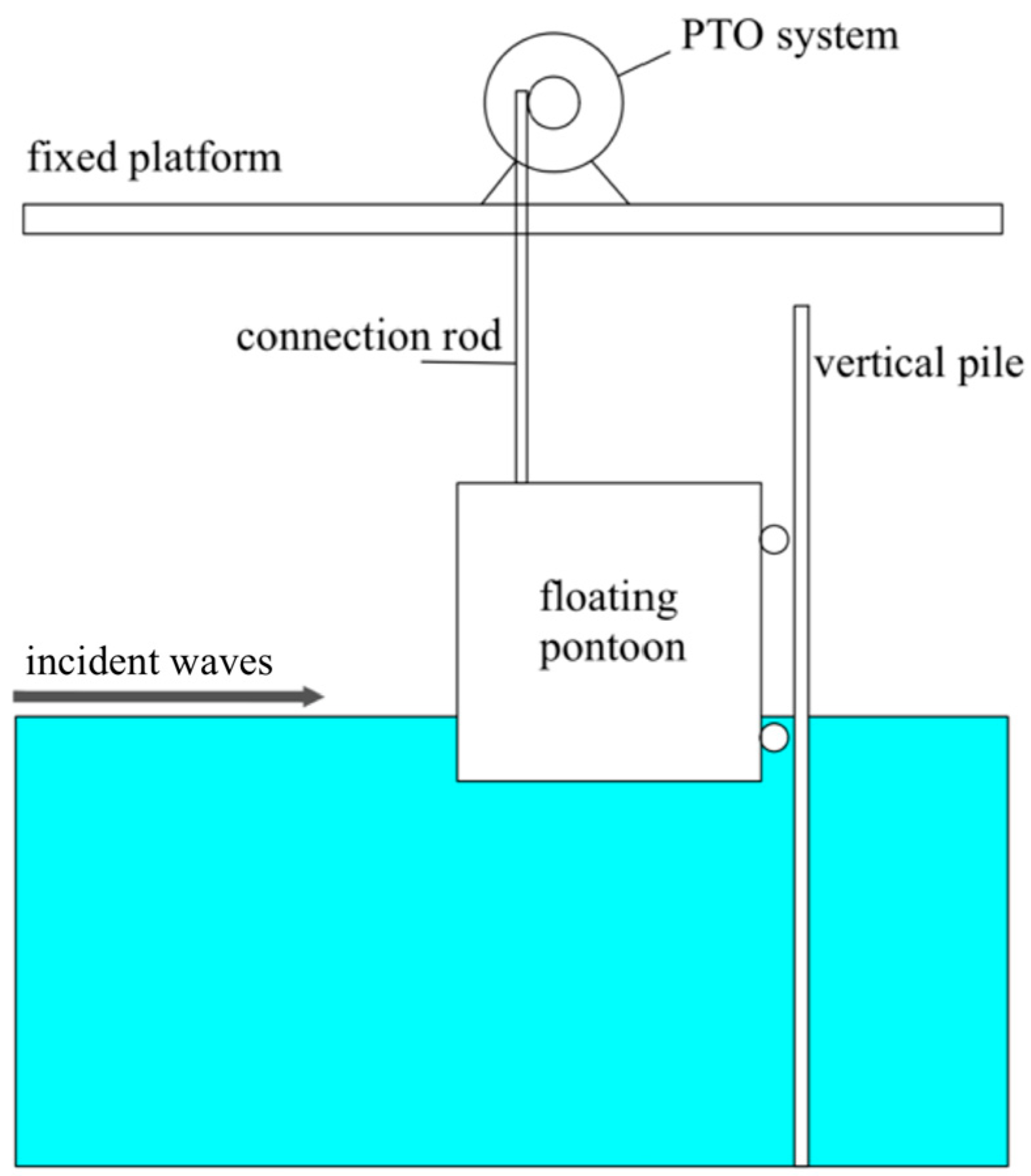
2. Numerical Model
2.1. Governing Equations
2.2. Free Surface Tracking
2.3. Wave Generation
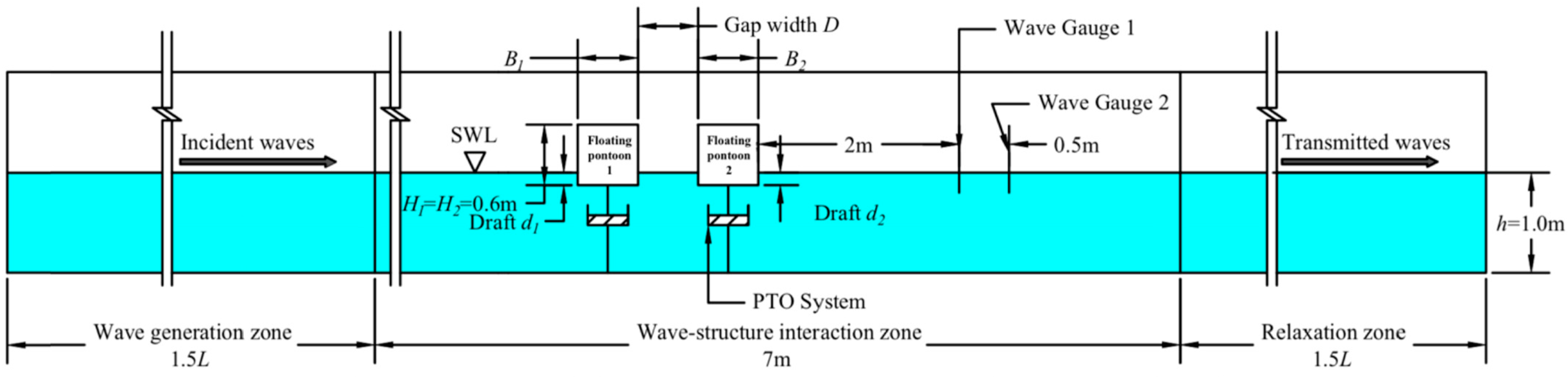
3. Numerical Setup
3.1. Numerical Wave Tank
3.2. Test Conditions
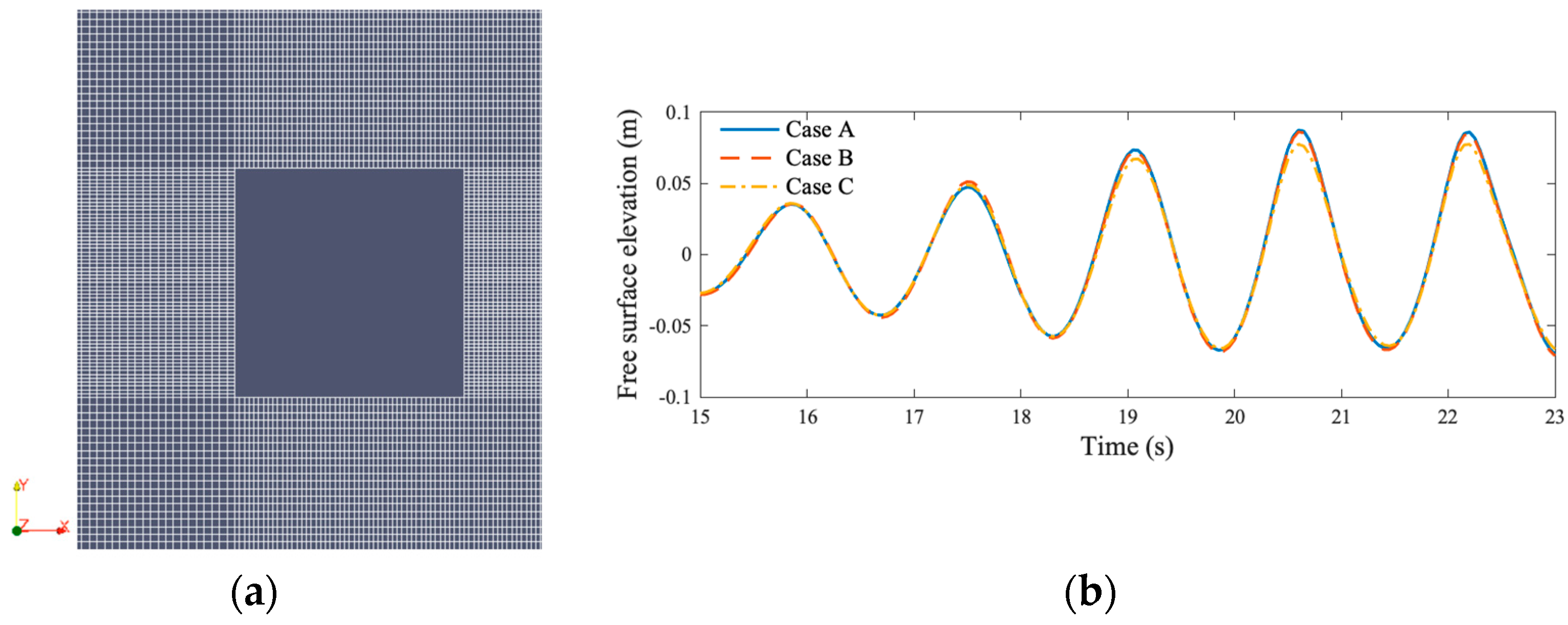
3.3. Computational Mesh
4. Model Validations
5. Numerical Results and Discussion
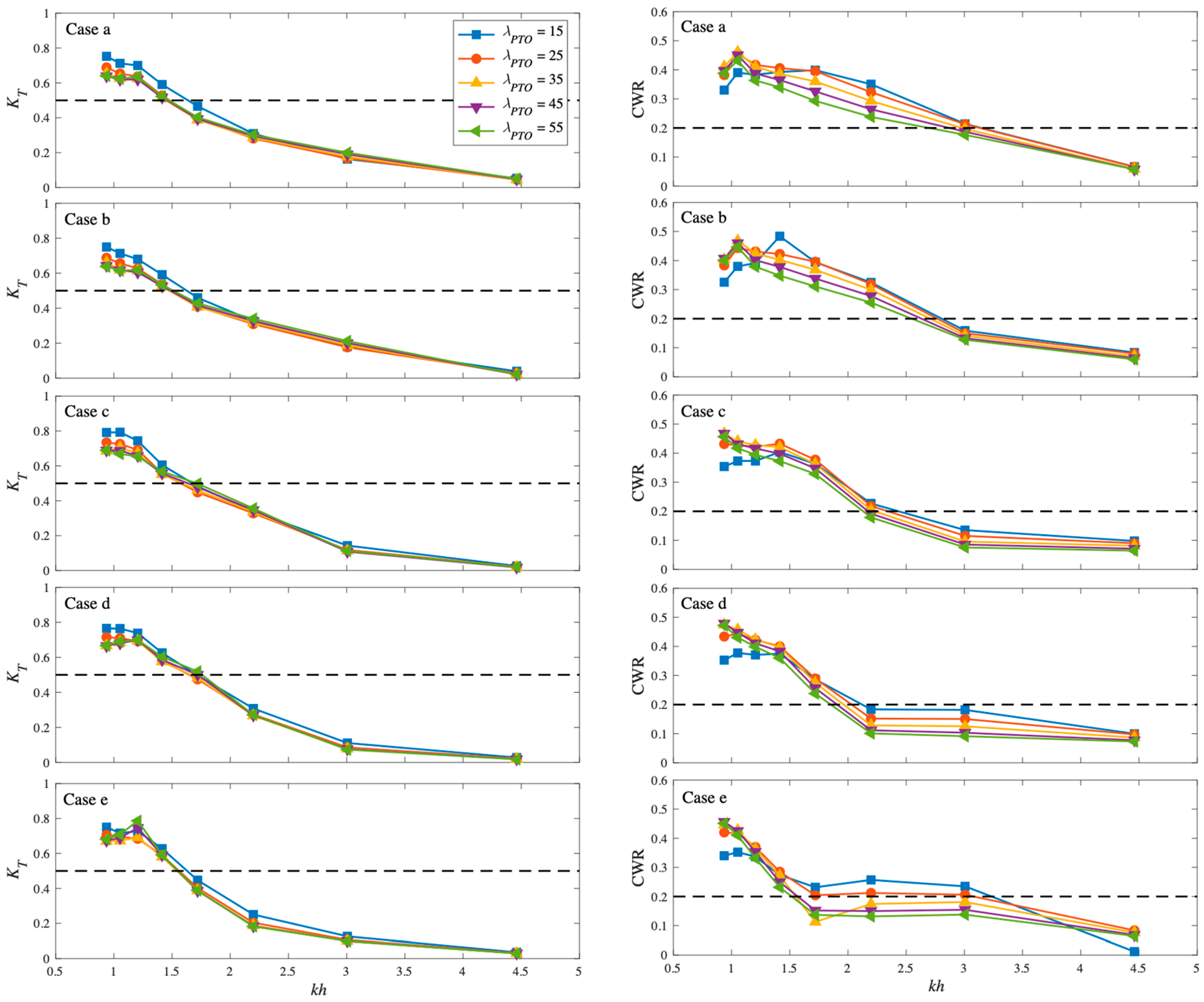
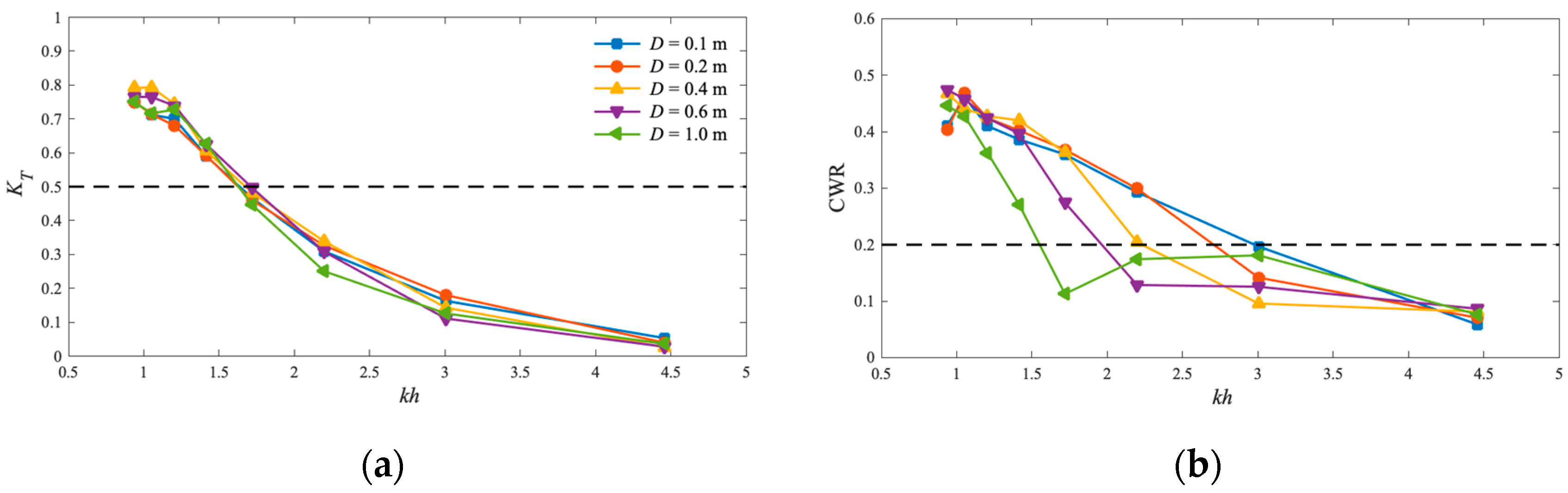
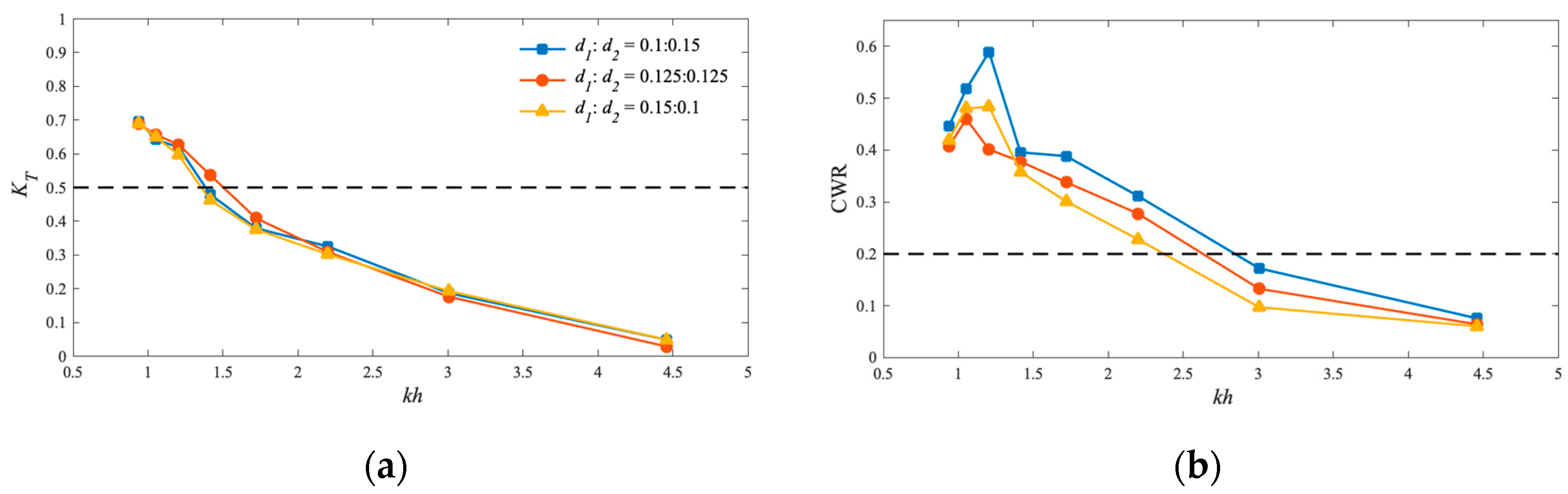
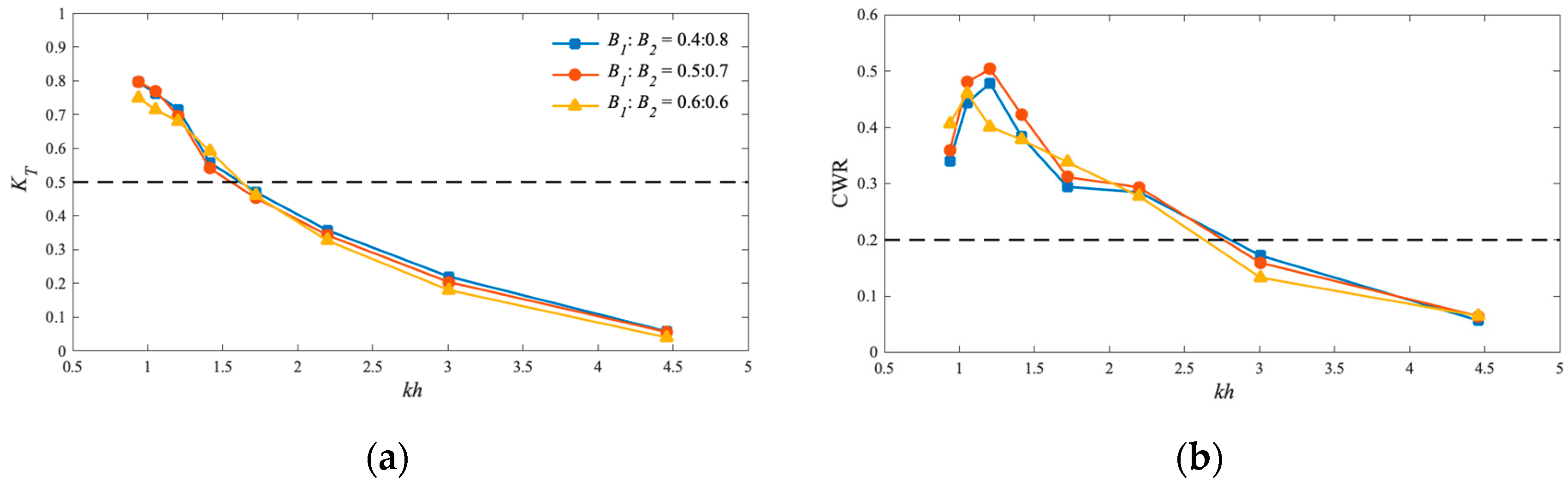
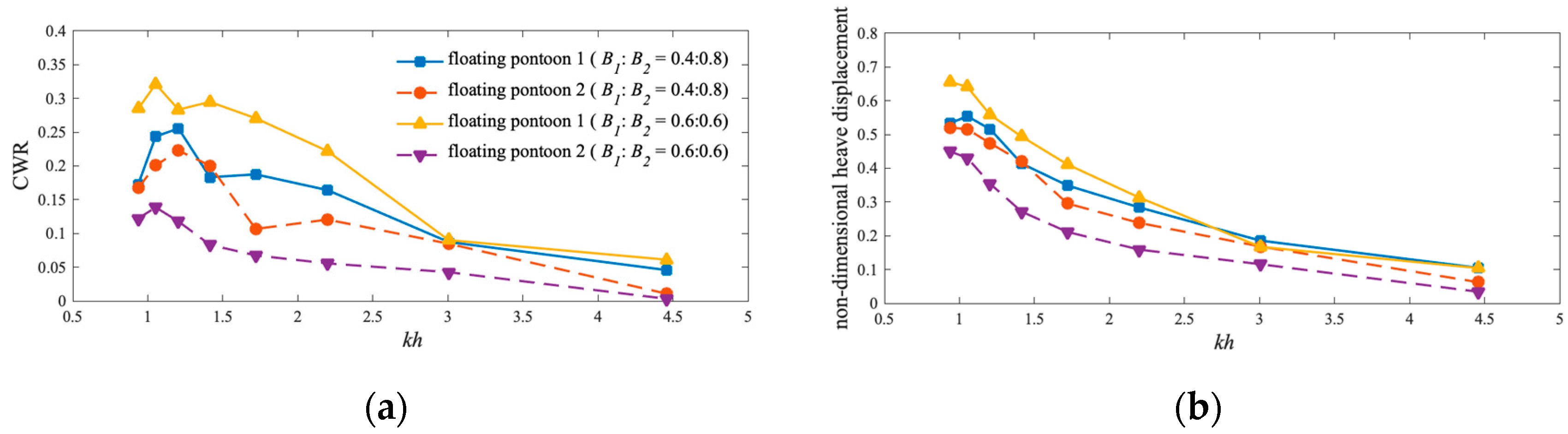
5.1. Wave Transmission Coefficient KT and Capture Width Ratio CWR
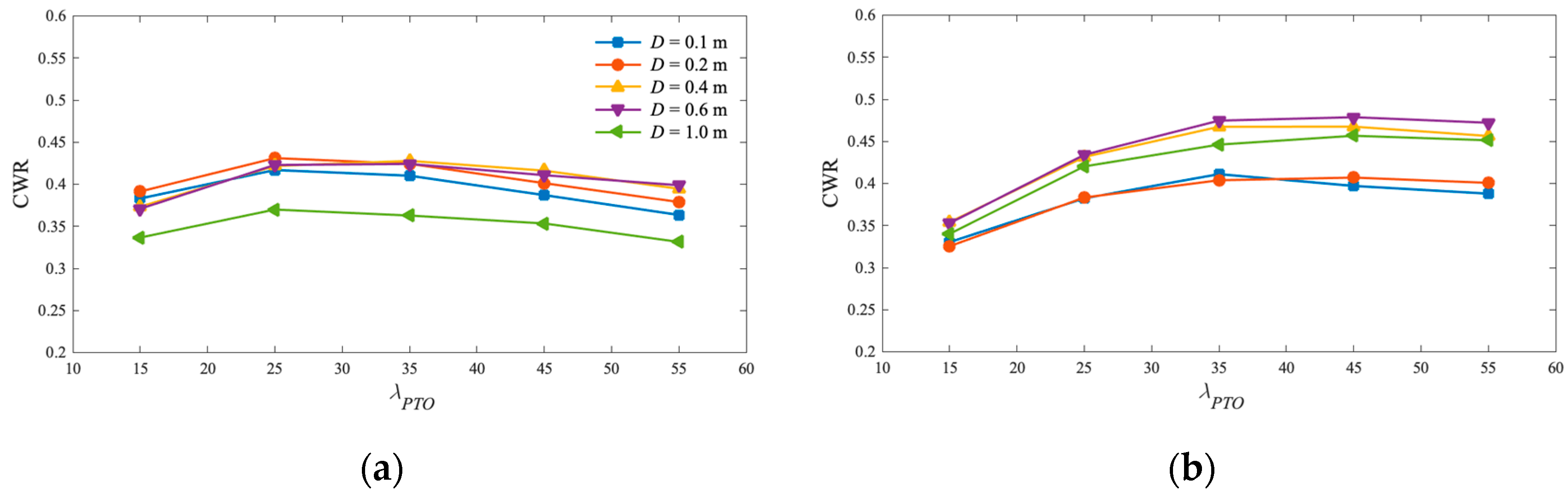
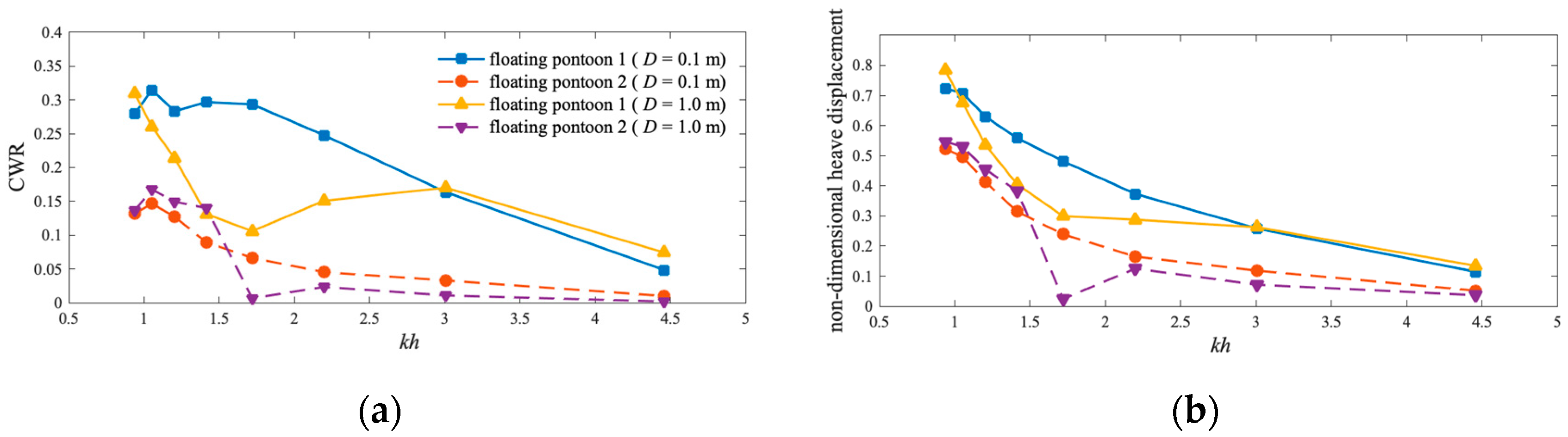
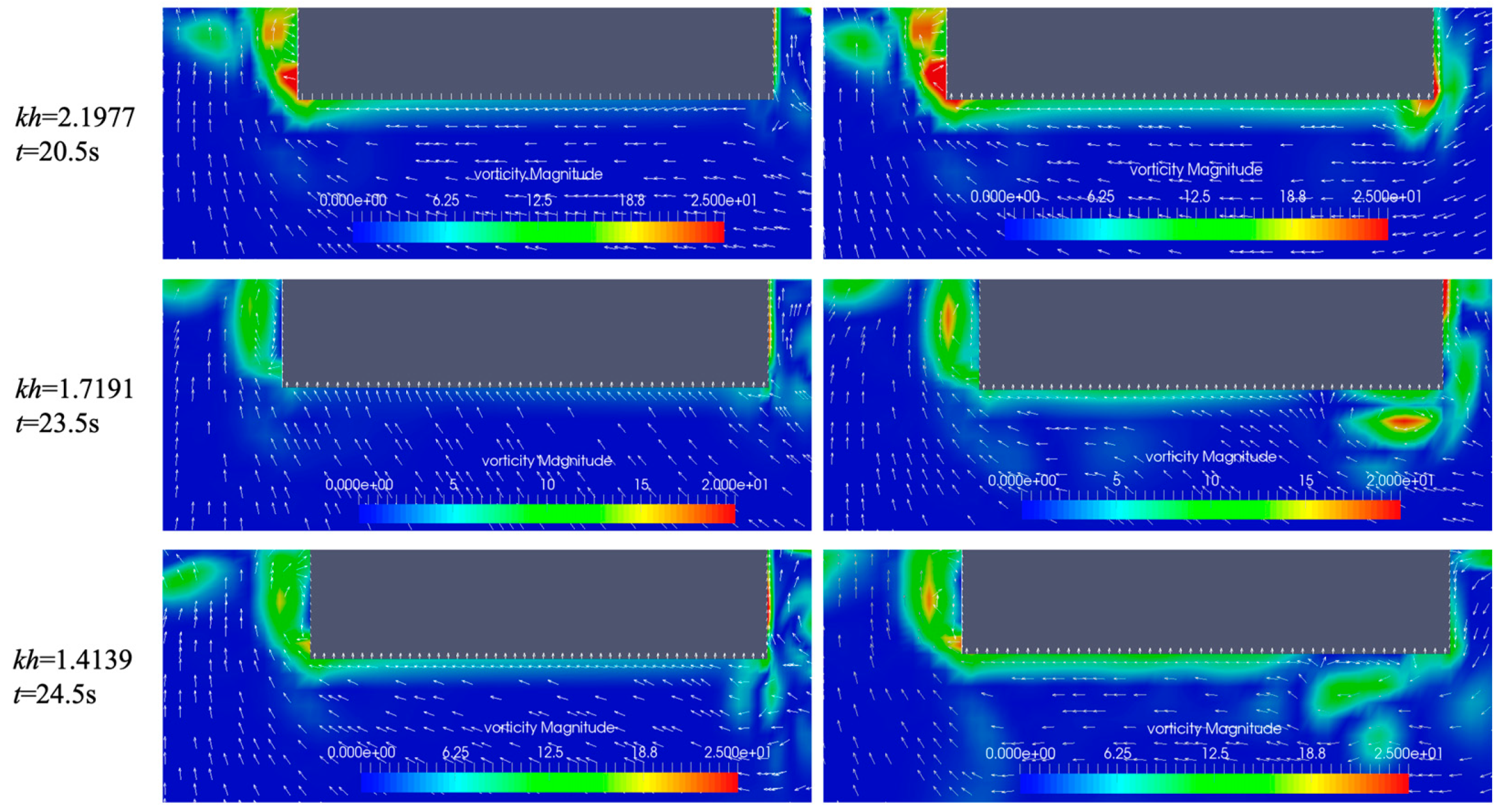
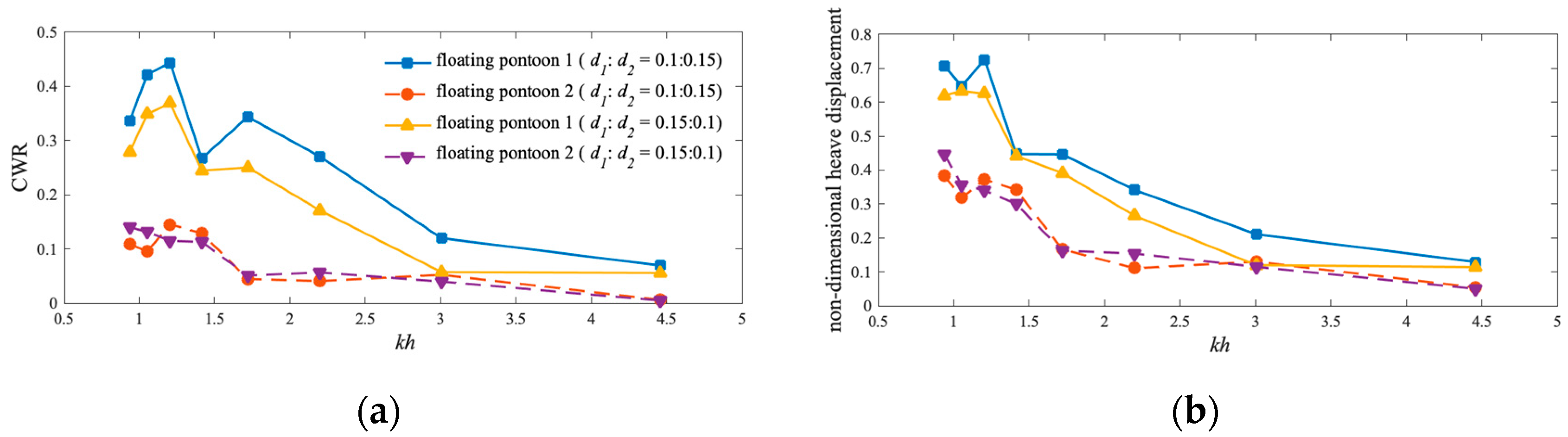
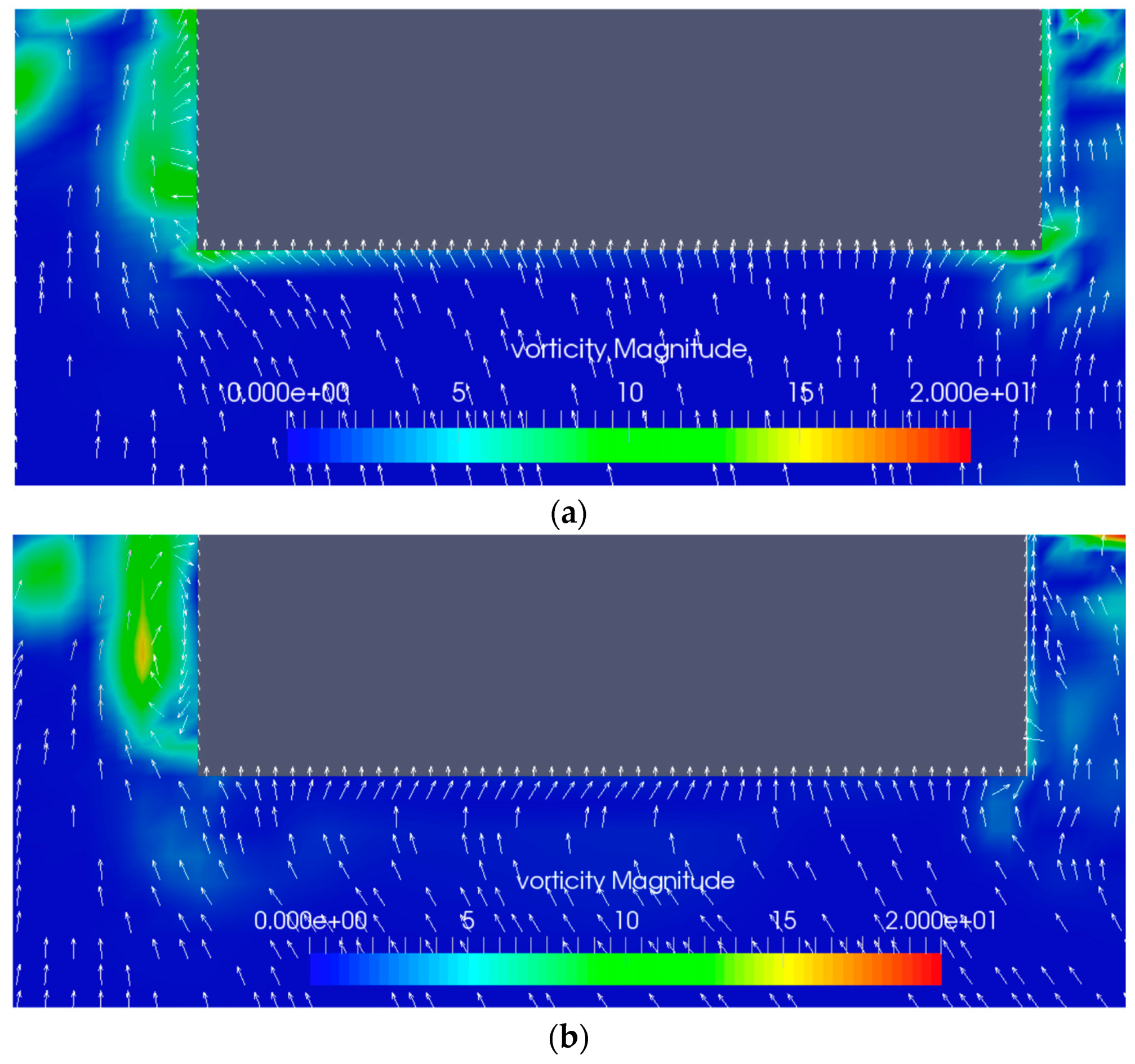
5.2. Effect of Gap Width
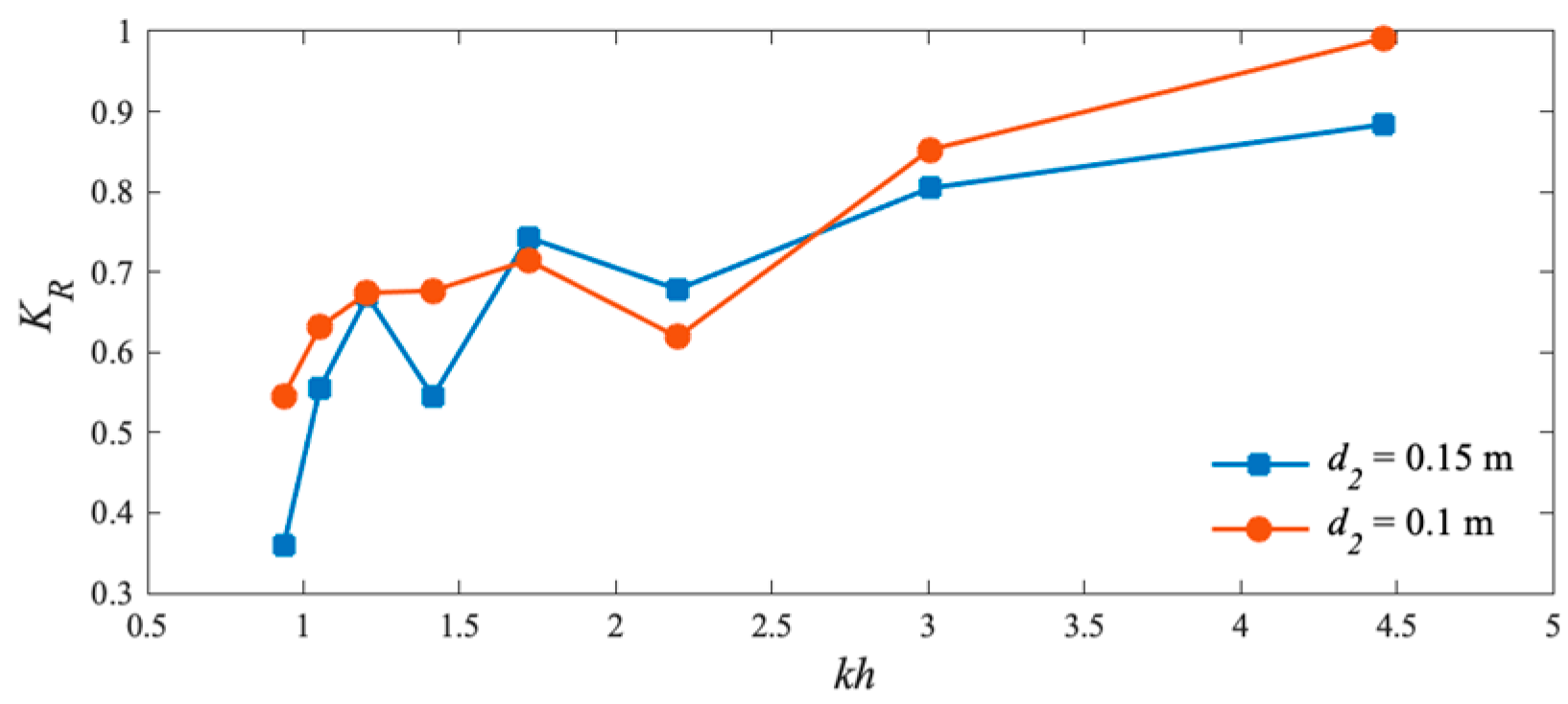
5.3. Effect of Structure Draft Ratio
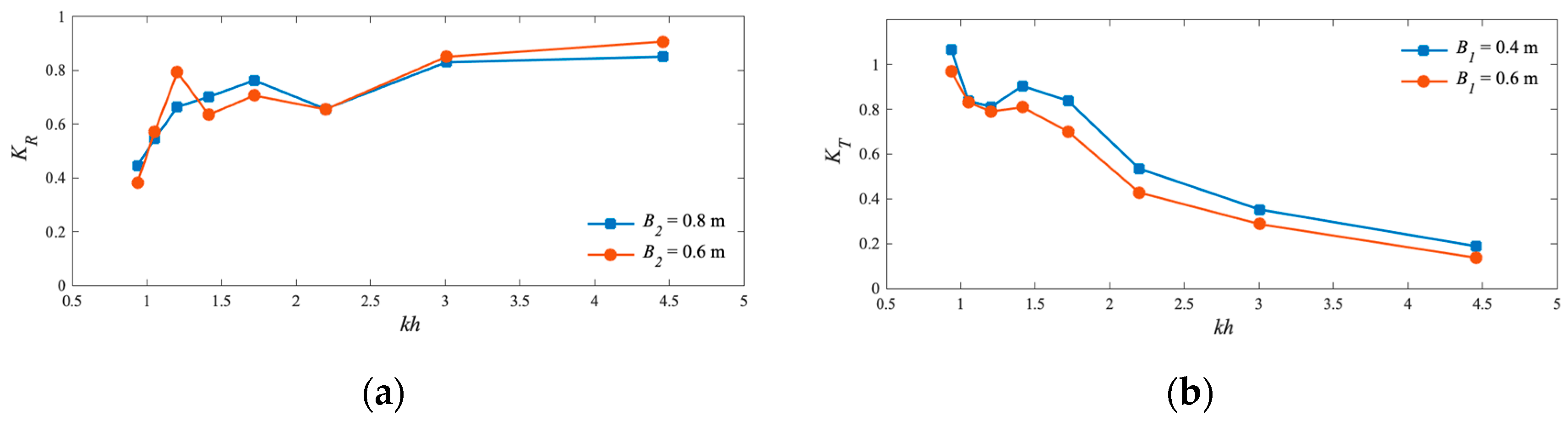
5.4. Effect of Structure Breadth Ratio
5.5. Bandwidth of Effective Frequency
6. Conclusions
- Gap width impacts the vorticity field around the floating pontoon; a smaller gap width reduces vortices, increasing heave displacement and improving functional performance. A smaller gap width (ranging from 0.1 m to 1.0 m) can improve wave energy extraction efficiency.
- Draft affects the vorticity field; a smaller draft reduces vortices and enhances performance. In this study, a smaller d1:d2 ratio improves performance. For instance, when d1:d2 = 0.1:0.15, the CWR can reach the best efficiency of 64%.
- Structure breadth influences wave reflection and transmission; a smaller B1:B2 ratio, when B1:B2 = 0.4:0.8, leads to better performance.
- Sharp changes in the high-frequency region of CWR vs. kh curves are due to Bragg reflection, which affects the effective frequency bandwidth. This factor should be considered in the design of integrated WEC and dual floating breakwaters.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vicinanza, D.; Contestabile, P.; Nørgaard, J.Q.H.; Andersen, T.L. Innovative rubble mound breakwaters for overtopping wave energy conversion. Coast. Eng. 2014, 88, 154–170. [Google Scholar] [CrossRef]
- Brooke, J. Wave Energy Conversion; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Falnes, J. Ocean Waves and Oscillating Systems: Linear Interactions Including Wave-Energy Extraction Johannes. Dev. Sedimentol. 1993, 52, 11–28. [Google Scholar] [CrossRef]
- Martinelli, L. Wave Energy Converters under mild wave climates. OCEANS’11 MTS/IEEE KONA, Waikoloa, HI, USA, 19–22 September 2011; IEEE: Washington, DC, USA, 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Güney, M.S.; Kaygusuz, K. Hydrokinetic energy conversion systems: A technology status review, Renew. Sustain. Energy Rev. 2010, 14, 2996–3004. [Google Scholar] [CrossRef]
- Waveplam Project. 2010. Available online: www.waveplam.eu (accessed on 8 August 2024).
- Takahashi, S. Hydrodynamic Characteristics of Wave-power-extracting Caisson Breakwater. Coast. Eng. 1989, 2489–2503. [Google Scholar] [CrossRef]
- Takahashi, S.; Nakada, H.; Ohneda, H.; Shikamori, M. Wave Power Conversion by a Prototype Wave Power Extracting Caisson in Sakata Port. In Proceedings of the 23rd International Conference on Coastal Engineering, Venice, Italy, 7–9 September 2015; pp. 3440–3453. [Google Scholar] [CrossRef]
- He, F.; Huang, Z.; Law, A.W.-K. Hydrodynamic performance of a rectangular floating breakwater with and without pneumatic chambers: An experimental study. Ocean Eng. 2012, 51, 16–27. [Google Scholar] [CrossRef]
- Michailides, C.; Angelides, D.C. Modeling of energy extraction and behavior of a Flexible Floating Breakwater. Appl. Ocean Res. 2012, 35, 77–94. [Google Scholar] [CrossRef]
- Zanuttigh, B.; Martinelli, L.; Castagnetti, M.; Ruol, P.; Kofoed, J.P.; Frigaard, P. Integration of wave energy converters into coastal protection schemes. Icoe 2010, 2010, 1–7. [Google Scholar]
- Zanuttigh, B.; Angelelli, E. Experimental investigation of floating wave energy converters for coastal protection purpose. Coast. Eng. 2013, 80, 148–159. [Google Scholar] [CrossRef]
- Ning, D.; Zhao, X.; Göteman, M.; Kang, H. Hydrodynamic performance of a pile-restrained WEC-type floating breakwater: An experimental study. Renew. Energy 2016, 95, 531–541. [Google Scholar] [CrossRef]
- Ning, D.Z.; Zhao, X.L.; Zhao, M.; Hann, M.; Kang, H.G. Analytical investigation of hydrodynamic performance of a dual pontoon WEC-type breakwater. Appl. Ocean Res. 2017, 65, 102–111. [Google Scholar] [CrossRef]
- Reabroy, R.; Zheng, X.; Zhang, L.; Zang, J.; Yuan, Z.; Liu, M.; Sun, K.; Tiaple, Y. Hydrodynamic response and power efficiency analysis of heaving wave energy converter integrated with breakwater. Energy Convers. Manag. 2019, 195, 1174–1186. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, B.; Vogel, C.; Willden, R.; Zang, J.; Geng, J. Hydrodynamic performance of a dual-floater hybrid system combining a floating breakwater and an oscillating-buoy type wave energy converter. Appl. Energy 2020, 259, 114212. [Google Scholar] [CrossRef]
- Zhou, B.; Huang, X.; Lin, C.; Zhang, H.; Peng, J.; Nie, Z.; Jin, P. Experimental study of a WEC array-floating breakwater hybrid system in multiple-degree-of-freedom motion. Appl. Energy 2024, 371, 123694. [Google Scholar] [CrossRef]
- Morgan, G.; Zang, J.; Greaves, D.; Heath, A.; Whitlow, C.; Young, J. Using the rasInterFoam CFD model for wave transformation and coastal modelling. In Proceedings of the 32nd Conference on Coastal Engineering, Shanghai, China, 30 June–5 July 2010. [Google Scholar]
- Morgan, G.; Zang, J. Application of OpenFOAM to Coastal and Offshore Modelling. In Proceedings of the 26th Internation Workshop on Water Waves, Athens, Greece, 17–20 April 2011; pp. 3–6. [Google Scholar]
- Jacobsen, N.G.; Fuhrman, D.R.; Fredsøe, J. A wave generation toolbox for the open-source CFD library: OpenFoams. Int. J. Numer. Methods Fluids 2012, 70, 1073–1088. [Google Scholar] [CrossRef]
- Chen, L.F.; Zang, J.; Hillis, A.J.; Morgan, G.C.J.; Plummer, A.R. Numerical investigation of wave-structure interaction using OpenFOAM. Ocean Eng. 2014, 88, 91–109. [Google Scholar] [CrossRef]
- Chen, L.F.; Zang, J.; Hillis, A.J.; Plummer, A.R. Numerical study of roll motion of a 2-D floating structure in viscous flow. J. Hydrodyn. 2016, 28, 544–563. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Issa, R.I. Solution of the Implicitly Discretised Fluid Flow Equations by Operator-Spliting. J. Comput. Phys. 1984, 62, 40–65. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.; Lewy, H. On the Partial Difference Equations of Mathematical Physics. IBM J. Res. Dev. 1967, 11, 215–234. [Google Scholar] [CrossRef]
- Greenshields, C.J. OpenFOAM Guide. 2014. Available online: https://openfoamwiki.net/index.php/OpenFOAM_guide (accessed on 8 August 2024).
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Mayer, S.; Garapon, A.; Sørensen, L.S. A fractional step method for unsteady free-surface flow with applications to non-linear wave dynamics. Int. J. Numer. Methods Fluids 1998, 28, 293–315. [Google Scholar] [CrossRef]
- He, Z.; Gao, J.; Shi, H.; Zang, J.; Chen, H.; Liu, Q. Investigation on effects of vertical degree of freedom on gap resonance between two side-by-side boxes under wave actions. China Ocean. Eng. 2022, 36, 403–412. [Google Scholar] [CrossRef]
- Gao, J.; He, Z.; Huang, X.; Liu, Q.; Zang, J.; Wang, G. Effects of free heave motion on wave resonance inside a narrow gap between two boxes under wave actions. Ocean Eng. 2021, 224, 108753. [Google Scholar] [CrossRef]
- Gao, J.L.; Lyu, J.; Wang, J.H.; Zhang, J.; Liu, Q.; Zang, J.; Zou, T. Study on transient gap resonance with consideration of the motion of floating body. China Ocean Eng. 2022, 36, 994–1006. [Google Scholar] [CrossRef]
- Gong, S.-K.; Gao, J.-L.; Mao, H.-F. Investigations on fluid resonance within a narrow gap formed by two fixed bodies with varying breadth ratios. China Ocean Eng. 2023, 37, 962–974. [Google Scholar] [CrossRef]
- Gao, J.; Mi, C.; Song, Z.; Liu, Y. Transient gap resonance between two closely-spaced boxes triggered by nonlinear focused wave groups. Ocean Eng. 2024, 305, 117938. [Google Scholar] [CrossRef]
- Gong, S.; Gao, J.; Song, Z.; Shi, H.; Liu, Y. Hydrodynamics of fluid resonance in a narrow gap between two boxes with different breadths. Ocean Eng. 2024, 311, 118986. [Google Scholar] [CrossRef]
- Ning, D.; Zhao, X.; Zang, J.; Johanning, L. Analytical and experimental study on a WEC-type floating breakwater. In Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, UK, 27 August–1 September 2017; pp. 4–9. [Google Scholar]
- Koutandos, E.; Prinos, P.; Gironella, X. Floating breakwaters under regular and irregular wave forcing: Reflection and transmission characteristics. J. Hydraul. Res. 2005, 43, 174–188. [Google Scholar] [CrossRef]
- Babarit, A.; Hals, J.; Muliawan, M.J.; Kurniawan, A.; Moan, T.; Krokstad, J. Numerical benchmarking study of a selection of wave energy converters. Renew. Energy 2012, 41, 44–63. [Google Scholar] [CrossRef]
- Gao, J.; Hou, L.; Liu, Y.; Shi, H. Influences of Bragg reflection on harbor resonance triggered by irregular wave groups. Ocean Eng. 2024, 305, 117941. [Google Scholar] [CrossRef]
- Ouyang, H.T.; Chen, K.H.; Tsai, C.-M. Investigation on Bragg reflection of surface water waves induced by a train of fixed floating pontoon breakwaters. Int. J. Nav. Archit. Ocean Eng. 2015, 7, 951–963. [Google Scholar] [CrossRef]
- Garnaud, X.; Mei, C.C. Bragg scattering and wave-power extraction by an array of small buoys. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 79–106. [Google Scholar] [CrossRef]






| Test Groups | Gap Width (D Unit: m) | Draft (d1:d2) | Structure Breadth (B1:B2) |
|---|---|---|---|
| Case a | 0.1 | 0.125:0.125 | 0.6:0.6 |
| Case b | 0.2 | ||
| Case c | 0.4 | ||
| Case d | 0.6 | ||
| Case e | 1.0 | ||
| Case f | 0.2 | 0.1:0.15 | 0.6:0.6 |
| Case g | 0.15:0.1 | ||
| Case h | 0.2 | 0.125:0.125 | 0.5:0.7 |
| Case i | 0.4:0.8 |
| Test Cases | Mesh Size in x-Axis | Mesh Size in y-Axis | Computational Time Using a Single Core (Unit: s) |
|---|---|---|---|
| Case A | L/360 | H/20 | 349,225 |
| Case B | L/290 | H/16 | 104,778 |
| Case C | L/180 | H/10 | 42,957 |
| T (s) | 1.17 | 1.22 | 1.27 | 1.33 | 1.4 | 1.5 | 1.6 | 1.7 |
| A (m) | 0.04 | 0.06 | 0.06 | 0.07 | 0.07 | 0.07 | 0.07 | 0.07 |
| kh | 2.954 | 2.726 | 2.526 | 2.318 | 2.112 | 1.874 | 1.684 | 1.528 |
| FPTO/G | 0.394 | 0.800 | 1.215 | 1.227 | 1.587 | 1.390 | 2.079 | 1.797 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, H. Hydrodynamic Performance of a Dual-Pontoon WEC-Breakwater System: An Analysis of Wave Energy Content and Converter Efficiency. Energies 2024, 17, 4046. https://doi.org/10.3390/en17164046
Ding H. Hydrodynamic Performance of a Dual-Pontoon WEC-Breakwater System: An Analysis of Wave Energy Content and Converter Efficiency. Energies. 2024; 17(16):4046. https://doi.org/10.3390/en17164046
Chicago/Turabian StyleDing, Haoyu. 2024. "Hydrodynamic Performance of a Dual-Pontoon WEC-Breakwater System: An Analysis of Wave Energy Content and Converter Efficiency" Energies 17, no. 16: 4046. https://doi.org/10.3390/en17164046
APA StyleDing, H. (2024). Hydrodynamic Performance of a Dual-Pontoon WEC-Breakwater System: An Analysis of Wave Energy Content and Converter Efficiency. Energies, 17(16), 4046. https://doi.org/10.3390/en17164046






