The Effect of Blade Angle Distribution on the Flow Field of a Centrifugal Impeller in Liquid-Gas Flow

Abstract

Operating centrifugal pumps under two-phase flow conditions presents challenges such as phase separation, cavitation, and flow instabilities, compromising reliability and performance. A specialized design is crucial to mitigate these issues. This study utilized computational fluid dynamics (CFDs) to understand two-phase flow behavior and assess the impact of different blade geometries on pump performance under such conditions. For this purpose, the inhomogeneous multiphase model was employed, wherein the momentum and continuity flow equations were individually solved for each phase across three different impellers with varying blade angle distributions. The computational results indicated higher gas concentrations on the pressure side of the blade, with gas pocket size correlating with flow rate and inlet gas concentration. The blade angle distribution’s effect was more pronounced with increased gas concentrations, while a tendency of gas bubbles to coalesce towards the impeller shroud was also observed. The presence of gas promoted flow recirculation and separation, substantially reducing impeller performance. Blade angle distribution critically influenced the flow field, affecting flow separation, stability, efficiency, and overall performance, highlighting the importance of optimized blade design for enhanced centrifugal pump performance in liquid–gas two-phase flow conditions.

1. Introduction

Centrifugal pumps are extensively used in daily life. Nowadays, with the shortage of energy resources, the performance improvement of centrifugal pumps is of the utmost importance to achieve higher efficiency and stability and reduce energy consumption. In many applications, the pumping medium is under two-phase conditions, which may have an impact on the characteristic curves of the pump, seriously affecting its performance and reliability. In such cases, and especially when the dispersed air-gas phase is at a high fraction, the impeller operation can be unstable and may even become blocked, resulting in severe consequences and accidents. The above-mentioned issues have motivated several studies in recent decades to employ numerical and experimental methods to examine the internal flow in centrifugal pumps.

One of the first scholars who studied the two-phase flow in centrifugal pumps was Murakami et al. [1], who utilized flow visualization techniques for performance evaluation in a radial pump operating with air–water flow. The authors measured the degradation of the pump performance at different gas flow rates at the intake, analyzing the contribution of different kinds of losses to the complex flow phenomena observed. They related the transitions between flow patterns in the impeller to discontinuities in the characteristic curve using images of gas distribution inside the channel between the blades of the impeller. They also investigated the influence of the number of blades and the clearance between the casing and the semi-open impeller.

In the following decades, many relevant investigations mainly focused on the detailed visualization of flow patterns, which may be categorized as an isolated bubbly flow, bubbly flow, gas pocket flow, and segregated gas flow. Changes in the above flow patterns can affect the operation of the pump, causing the performance to decline, especially under the gas pocket flow, which leads to unstable and surging phenomena. One of the first researchers to carry out testing and visual experiments was Sato et al. [2]. They pointed out that an improvement in the performance of a centrifugal pump under the conditions of a gas–liquid two-phase flow could be achieved when changes are made to the geometry of the impeller, increasing the blade outlet, or drilling the backflow holes. Pesoa et al. [3] and Bellur et al. [4] examined the influence of the stage number and inlet gas volume fraction on the performance of an ESP. The results indicated that, most importantly, the inlet gas volume fraction affected the efficiency and the pressure rise of the pump by sharply dropping when the fraction was high at the inlet. Estevan et al. [5] employed flow visualization of the gas–liquid flow inside a transparent centrifugal impeller, associated the observed surge with physical flow phenomena, and proposed a correlation to predict the onset of surging. Barrios [6] and Barrios Prado [7], with the aid of a prototype impeller, reported that decreasing the rotation speed caused an increase in the bubble size inside the impeller, followed by the deterioration of the pump’s performance. Similar observations were made with an increasing inlet gas volume fraction. The application of the similarity law under gas–liquid two-phase flow was confirmed by Matsuhita et al. [8] using a back-bent centrifugal pump and utilizing a high-speed photography technique. Also, Gamboa and Prado [9] photographed the gas–liquid flow in a modified ESP. They concluded that the first stage of a multistage pump works as a bubble breaker. At a high liquid flow rate, the dispersed bubbles left the impeller without coalescence, but at the same time, gas pockets were formed inside the channel, resulting in strong performance degradation. Paternost et al. [10] carried out an experimental investigation into the influence of the liquid’s viscosity and the inlet gas fraction on the centrifugal pump’s performance. Schaufer et al. [11,12] and Neumann et al. [13], by employing the HireCT technique, successfully estimated the average distribution of the gas fraction under steady flow conditions, changing the inlet gas volume fraction at different rotational speeds. Verde et al. [14] and Shao et al. [15] studied the flow characteristics of gas–liquid two-phase pumps using high-speed photography and confirmed the aforementioned four typical flow patterns according to the morphology of gas-–iquid medium distribution. Pirouzpanah et al. [16] conducted an experiment in order to measure the internal flow in a three-stage splitter blade ESP. Using electrical resistance tomography, they showed a direct relationship between pump performance and gas distribution patterns. Mansour et al. [17] performed an experimental analysis on both an open and closed impeller, aiming to determine the characteristics of the developed flow instabilities and their relation to different gas volume fractions. Stel et al. [18] utilized a high-speed camera in conjunction with transparent components to investigate the motion of bubbles, which allowed them to understand the coalescence effects. Finally, Cubas et al. [19] confirmed the tendency of bubble coalescence as well as the increase in bubble size.

In recent years, due to limitations in testing technology, numerical methods have provided an extremely useful and powerful tool for the study of internal flow in pumps under single-phase and multiphase conditions. Many studies have been conducted based on the Euler–Euler model.

Minemura and Murakami [20] investigated numerically the motion and the distribution of bubbles inside a radial pump channel. They concluded that the trajectories of the bubbles depended on their diameter and relative velocity between the gas and liquid phase and tended to deviate from the liquid streamlines. Caridad and Kenyeny [21] and Caridad [22] investigated numerically the effect of inlet gas volume fraction and bubble size on ESP performance using the ANSYS CFX v. 18.1 commercial software. They also analyzed the influence of the forces on the gas bubble motion, highlighting that the drag force and the force resulting from the pressure gradient are crucial in the operation of an ESP. Finally, they examined the outlet’s relative flow as a function of the liquid flow rate. As the gas pocket at the pressure side can be conceived as a modified inter-blade geometry, modifying the streamlines of the liquid, they concluded that for a constant flow rate, the outlet flow angle β₂ decreased for larger gas-void fractions. Sun and Prado [23] derived a one-dimensional momentum equation for a centrifugal pump with a high level of the gas volume fraction at the inlet, with the assumption of the ideal gas. The authors predicted the pump performance and established a shock loss model relying on empirical parameters from experimental measurements. The multiphase flow in an ESP was examined by Gamboa et al. [24,25] from both a theoretical point of view as well as an experimental standpoint. The authors confirmed the relation between the flow pattern and bubble size with the pump’s performance. Another scholar who performed multiphase CFD simulations on an ESP centrifugal pump was Barrios [26]. He examined the effect of bubble size on the prediction of pump curve operation and established a drag coefficient model. The results from numerical simulations were validated through experimental measurements. Muller et al. [27] evaluated the capability of the mono-dispersed model in ANSYS CFX to determine computationally the inner flow conditions in the channel of a radial pump. They concluded that when the inlet gas void fraction was below 3%, the head was predicted with good accuracy. Zhu and Zhang [28] utilized the CFX standard k-ε turbulence model to carry out the numerical calculation of gas and liquid two-phase flow in an ESP and compared the numerical results to test data, allowing the new bubble analysis model to be validated and improved. Yiming et al. [29] simulated and visualized the flow field of an ESP based on the population balance model (PBM) and determined the regions within the flow channel where gas accumulation and phase separation occurred by studying parametrically the effect of gas volume fraction on pump performance. Si et al. [30] highlighted that the accumulation of bubbles in the impeller of the centrifugal pump severely impacts the energy exchange in the impeller, and the impeller’s vortices also intensify the accumulation of bubbles.

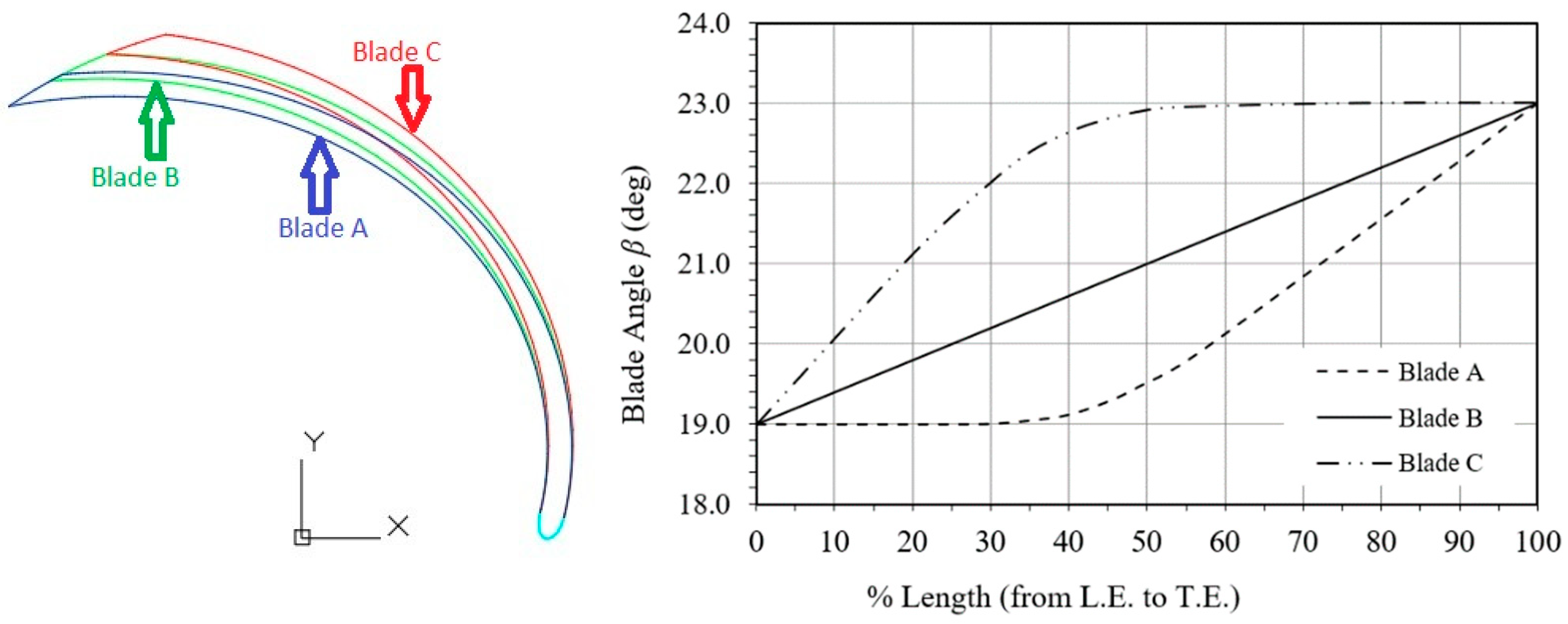
In general, from the above literature review, most researchers investigated the performance of centrifugal pumps under two-phase flow, mainly focusing on the influence of different inlet gas volume fractions at various flow rates on head and efficiency. They also found that there was a lack concerning the relationship between the geometrical shape of the blade and the operation of a radial centrifugal pump under two-phase flow. This prompted the present paper to examine the effect of different impellers on the air–water flow. A closed type of impeller with the same basic geometrical parameters but with three differently shaped blades are simulated. For this purpose, a commercial CFD code (ANSYS–CFX) was used based on the Euler–Euler method for two-phase flow, confined to a monodisperse model. Thus, the research focused on examining the potential effects of impeller configuration, specifically the blade angle distribution between the fixed blade angles of the inlet and outlet, on the pump’s overall performance. Many issues stem from gas phase accumulation within the blade channels; therefore, design improvements could positively impact the safety and operation of pumping systems in critical industrial installations.

2. Computational Domain

The geometry under consideration is a centrifugal radial impeller with five backward blades (Figure 1). Experimental results were available for this particular impeller from the previous works of Muller et al. [27,31]. The performance characteristics of this impeller are summarized in

Table 1. Performance characteristics of the impeller at design point.

Characteristic Parameter	Symbol/Units	Value
Nominal pump head	HN (m)	10.2
Nominal flow rate	QN (m3/h)	412
Nominal rotational speed	n (rpm)	540
Specific speed	nq	32.1
Flow coefficient	φ	0.030
Head coefficient	ψ	0.807
Diameter coefficient	δ	5.473

. Three different geometrical configurations were considered with different distributions of the blade angle between leading and trailing edges (Figure 2). The main geometric parameters of the pump are summarized in

Table 2. Main impeller geometry data.

Characteristic Dimension	Symbol/Units	Value
Suction diameter	d1 (mm)	260
Exit diameter	d2 (mm)	556
Blade inlet angle	βb1 (degree)	19
Blade outlet angle	βb2 (degree)	23
Blade inlet width	b1 (mm)	46
Blade outlet width	b2 (mm)	46
Blade number	Zb	5
Blade thickness	Sb (mm)	13

.

2.1. Geometry

Ideally, to simulate the flow field with increased accuracy and detect any asymmetry in the flow, all the impeller passages, as well as pump components, should be incorporated into the flow model. However, it is a common practice to take advantage of the axisymmetry of the flow and perform numerical simulations in a single impeller passage. In this way, the computational effort can be limited without serious deviations. Therefore, in the present paper, the computational domain consisted of a 72° segment with periodic boundary conditions imposed in the circumferential direction, as similarly described by Muller et al. [27]. To prevent flow separation and recirculation due to the adverse pressure gradient at the annular region at the outlet of the impeller, a converging section was placed to stabilize the numerical flow solver. This convergent arrangement reduced the final radial outlet surface to 60% outflow surface. Overall, the geometric domain, as shown in Figure 3, consisted of the inlet pipe and the outlet section subdomains and a rotating impeller subdomain, while the side chambers were not considered.

In the numerical modeling of turbomachinery, to avoid the numerical instabilities and inaccuracies caused by imposing boundary conditions close to the impeller, it is necessary to extend the domain appropriately upstream and downstream of the blade’s passage. The boundaries should be placed far enough from the entrance of the impeller and especially from the leading edge of the blade. In this way, it is possible to smooth any inconsistencies regarding flow conditions and turbulence quantities, which are usually unknown. At the same time, the enlargement of the domain also allows the capture of secondary flows and recirculation zones, especially at off-design operating conditions. To encounter this issue, the length of the suction pipe was extended to three times the diameter of the pipe in the axial direction.

2.2. Meshing

The grid of a single-blade channel was constructed for the impeller under investigation. The grid was generated via the periodic rotation around the Z-axis and consisted of a hexahedral mesh constructed using an appropriate block structure. For this purpose, the commercial meshing tool ANSYS Turbo-Grid was used.

A grid independence test was carried out to verify that the results were not dependent on the chosen grid, ensuring the required accuracy was achieved with reasonable computational cost. A reasonable number of grid points for the numerical simulation should be selected to save time and computational resources. The mesh independence analysis was carried out only for pure water, using the method proposed by Stern et al. [32], which has been shown to be an effective method to check the mesh independence by Hafizul and Guedes [33]. In the present work, the mesh was refined at each direction by a factor of $\sqrt{2}$. To ensure the accuracy of the numerical simulation, the grid quality is of the utmost importance. The structured grid used with hexahedral cells has good orthogonality, and the grid quality fulfills the requirements of the present numerical simulations.

Mesh refinement was carried out near the wall surfaces and regions of excessive curvature in the main flow components. The dimensionless wall distance y⁺ for the largest percentage of cells ranged from 11 to 155, and only a small part of them ranged between 156 and 387, ensuring that y⁺ satisfied the criterion dictated by the selected turbulence model (30 ≤ y⁺ ≤ 300). In Figure 4, the final mesh of the computational domain and a detailed view of the leading-edge area are shown, while Figure 5 shows the results of the mesh independence analysis comparing the predicted impeller head at different mesh densities. Structured hexahedral cells were used in the whole domain, with almost 222,000 cells for the inlet zone, about 320,000 cells for the impeller zone, depending on the blade’s type, and about 108,000 cells at the outlet zone.

3. Mathematical Model

In two-phase flow, each phase shows random temporal and spatial diffusion, while at the same time, phase interaction is present. To solve this complex flow problem, numerous mathematical models have been proposed. In this work, the inhomogeneous model was selected since the slip velocity and interphase force were taken into account. More specifically, the Euler–Euler two-fluid model was employed to simulate the gas–liquid two-phase flow within the centrifugal pump. This model considers the liquid phase as a continuous fluid medium and the gas phase as a dispersed fluid medium. The mass and momentum conservation equations for the liquid and gas phases were solved separately, and the two sets of equations were coupled together through the interaction between the phase interfaces. Compressibility effects resulting in the mass diffusion of the gas in the flow field were not taken into account in the present simulations.

The mass conservation equation is shown in Equation (1), and the momentum conservation equation is shown in Equation (2).

$${\displaystyle \frac{\partial \left({\rho }_{\iota }{\alpha }_{\iota }\right)}{\partial t}}+\nabla \cdot \left({\rho }_i{\alpha }_i{u}_i\right)=\underset{0}{\underbrace{S_i}}$$

(1)

$${\displaystyle \frac{\partial \left({\rho }_i{\alpha }_i{u}_i\right)}{\partial t}}+\nabla \cdot \left({\rho }_i{\alpha }_i{u}_i{u}_i\right)=-{\alpha }_i\nabla P+\nabla \cdot \left({\overline{\overline{\tau }}}_i\right)+{\alpha }_i{\rho }_{i}g+M_i+\underset{0}{\underbrace{S_{Mi}}}$$

(2)

where i represents either the liquid phase l or gas phase g. In this study, the gas–liquid two-phase working medium was air and water, respectively, where ρ_i, α_i are the density and volume fraction of the ith phase, while u_i represents the velocity component in the three directions of XYZ. The source terms S_i and S_Mi represent the transmission of the gas phase mass and momentum during bubble breakup and coalescence, which were not considered in this work. Finally, M_i represents the sum of the forces acting between the gas and liquid phase, and τ_i represents the strain force tensor of the ith phase defined by Equation (3)

$${\overline{\overline{\tau }}}_{\iota }={\alpha }_{\iota }{\mu }_{\iota }\left(\nabla u_i+\nabla u_i^T\right)+{\alpha }_i\left({\lambda }_i-{\displaystyle \frac{2}{3}}{\mu }_i\right)\nabla \cdot u_i\overline{\overline{I}}$$

(3)

The relationship between the gas volume fraction and liquid volume fraction is as follows:

$${\alpha }_g={\displaystyle \frac{Q_g}{Q_g+Q_l}}=1-{\alpha }_l$$

(4)

where α_g and α_l are the gas volume fraction and liquid volume fraction, respectively, and Q_g and Q_l represent the volume flow of air and water.

In the present study, the interphase forces considered were drag, lift, and virtual mass forces. In the gas–liquid two-phase flow, the drag force represents the interfacial momentum transfer caused by the gas–liquid phase velocity slip. The drag force model used is the Schiller and Naumann model. The formula is the following Equation (5):

$$F_D={\displaystyle \frac{3}{4}}{C}_D{\displaystyle \frac{{\rho }_l{\alpha }_g}{d_b}}\left|u_g-u_l\right|\left(u_g-u_l\right)$$

(5)

$$C_D=\{\begin{array}{ll}{\displaystyle \frac{24\left(1+0.15{\mathrm{Re}}^{0.687}\right)}{\mathrm{Re}}}\hfill & \mathrm{Re}\le 1000\hfill \\ 0.44\hfill & \mathrm{Re}>1000\hfill \end{array}$$

(6)

$$\mathrm{Re}={\displaystyle \frac{{\rho }_l\left|u_g-u_l\right|d_b}{{\mu }_g}}$$

(7)

where C_D is the drag force coefficient, d_b is the Sauter mean bubble diameter, and Re is the relative Reynolds number.

In multiphase shear flow, owing to the velocity gradient in the primary phase, the lift force is exerted on the dispersed particles and is perpendicular to the direction of relative motion between the phases. According to Drew and Lahey [34], the lift force that the primary phase exerts on the secondary phase is given by Equation (8):

$$F_{lift}=C_L{\rho }_l{\alpha }_g\left(u_l-u_g\right)\times \left(\nabla \times u_l\right)$$

(8)

where C_L is the lift force coefficient. The Legendre–Magnaudet lift force model [35] is employed, and the lift force coefficient is defined by the system of Equations (9)–(13).

$$C_L=\sqrt{C_{L.L\mathrm{Re}y}^2+C_{L.H\mathrm{Re}y}^2}$$

(9)

$$C_{L.L\mathrm{Re}y}={\displaystyle \frac{6}{{\pi }^2}}{\mathrm{Re}}_{\omega }^{-0.5}{\displaystyle \frac{2.55}{{\left(1+0.2\frac{{\mathrm{Re}}_b^2}{{\mathrm{Re}}_{\omega }}\right)}^{1.5}}}$$

(10)

$$C_{L.H\mathrm{Re}y}={\displaystyle \frac{11+16{\mathrm{Re}}_b^{-1}}{21+29{\mathrm{Re}}_b^{-1}}}$$

(11)

$${\mathrm{Re}}_b={\displaystyle \frac{{\rho }_l\left|u_g-u_l\right|d_b}{{\mu }_l}}$$

(12)

$${\mathrm{Re}}_{\omega }={\displaystyle \frac{{\rho }_l\left|\nabla \times u_l\right|d_b^2}{{\mu }_l}}$$

(13)

where Re_b is the bubble Reynolds number and Re_ω is the vorticity Reynolds number.

For multiphase flows, the virtual mass force is caused by the inertia of the surrounding fluid as the dispersed phase accelerates relative to the continuous phase. The virtual mass force is defined by the following Equation (14):

$$F_{vm}=C_{vm}{\rho }_l{\alpha }_g\left({\displaystyle \frac{d{u}_l}{dt}}-{\displaystyle \frac{d{u}_g}{dt}}\right)$$

(14)

where C_vm is the virtual mass force coefficient and equals 0.5.

Preliminary simulations showed that the homogeneous treatment of turbulence and pressure fields, i.e., both phases share the same fields, was sufficiently accurate and, at the same time, numerically stable. Therefore, homogenous treatment was preferred throughout this study.

4. Numerical Simulations

The basic assumptions for the numerical simulation of the gas–liquid two-phase pump model are as follows [36]:

• The gas–liquid two-phase flow pattern at the pump inlet is bubble flow.
• The pump inlet bubble is spherical with a diameter (d_b).
• The velocity of the gas and liquid phases at the pump inlet is uniform and equal.
• The liquid phase is an incompressible working medium, and the gas phase is a compressible ideal gas.
• The gas phase does not dissolve in the liquid phase.
• The wall of the pump model is hydraulically smooth and without slippage.
• The energy transfer is not considered in the simulation.

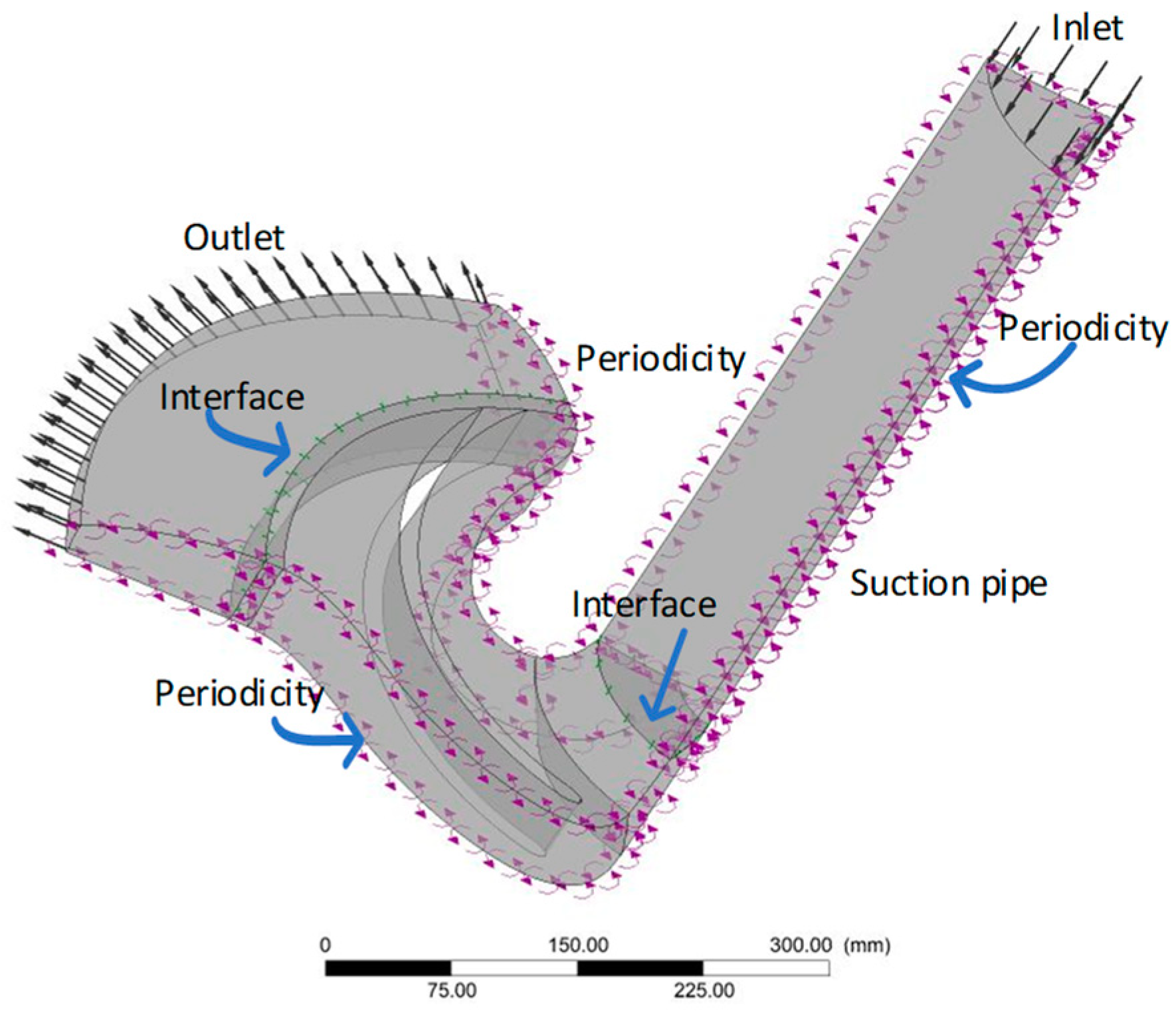
For the numerical simulation of the gas–liquid two-phase flow, the commercial 3D URANS CFD-solver ANSYS CFX version 18 was used. The Eulerian description of the dispersed phase is favored over the Lagrangian approach, as Eulerian methods are believed to have superior numerical properties concerning grid dependency [37] and are more valid in areas where the dispersed phase is dense. Furthermore, the momentum equation and continuity equation are solved in a coupled manner, while to improve convergence, the volume fraction equation is solved in a segregated manner [27,31]. Finally, second-order discretization in space and time was chosen, while double-precision accuracy numerics were considered.

In this study, the Euler–Euler inhomogeneous flow model, regardless of the influence of the temperature field, was used. The liquid phase is defined as the continuous phase (ρ_l = 998 kg/m³), and the gas phase is defined as the discrete phase (ρ_g = 1185 kg/m³), using the zero-equation theory. For turbulence modeling, the k-ω shear stress transport (SST) turbulence model by Menter [38], in conjunction with an automatic wall treatment, was selected. The wall treatment blends between a low-Reynolds approach, which integrates the governing equations up to the wall, and a wall function approach, which is deduced from the logarithmic wall law depending on the non-dimensional wall distance y⁺ of the wall-adjacent grid cell. At the entrance of the calculation domain, the gas phase is considered as uniformly distributed with equal two-phase inflow velocities. Furthermore, the gas phase is assumed as a spherical bubble with a diameter derived from experimental data (d_b = 0.5 mm) [39] while the inlet gas volume fraction is set to either 2% or 5%, respectively.

Apart from the sensitivity of the numerical results to mesh resolution, the accuracy of an unsteady simulation may be strongly influenced by the selected temporal resolution. On the one hand, the time step should be sufficiently small to capture minor changes in the flow field [40], but on the other, the simulation time may increase dramatically by selecting smaller time steps. The Courant number defined by Equation (15) is used as the criterion to judge if the time step satisfies the stability requirements of the numerical simulation. If the numerical convergence is poor, then smaller values should be used [30,40]:

$$C_o=\upsilon {\displaystyle \frac{\Delta t}{L}}<100$$

(15)

where L is the smallest size of the grid, υ is the main flow velocity, and Δt is the time step.

Therefore, considering the above, and in line with the impeller rotation speed, the time step was determined as equal to T_i = 60/(540 × 720) = 1.5432 × 10⁻⁴ s, which corresponds to a 0.5° rotating angle per time step.

The governing equations were discretized with an element-based finite volume method, while for the spatial discretization of the advection terms, a high-resolution scheme [41,42] was employed. This scheme combines first-order upwind and second-order central differencing schemes by utilizing a blending factor that varies across the computational domain according to the local solution. This variation ensures that the boundedness criterion of Barth and Jespersen [43] is satisfied. According to ref [41], the blending favors, by default, the second-order central differencing scheme to ensure accuracy. However, in regions with sharp gradients, it shifts towards the upwind scheme, thereby maintaining robustness. In turn, the Rhie–Chow interpolation [44] is employed to handle the pressure–velocity coupling.

The interface, which couples the stationary and rotating parts (between the impeller and the two other non-rotating zones at the inlet and outlet of the domain), is set to frozen or transient for the steady-state and transient numerical calculations, respectively. The convergence condition of the steady-state numerical calculation was set to an RMS value less than 10⁻⁴. The steady-state simulation results were used as the initial solution for the transient numerical calculation.

Table 3. Configuration of CFD settings.

Parameter	Conditions
Working medium	Water (ρl = 998 kg/m3)
	Air (ρg = 1.185 kg/m3, db = 0.5 mm)
Morphology	Continuous (water), dispersed phase (air)
Turbulence model	Liquid phase: k-ω (SST) with automatic wall treatment
	Gas phase: zero equation model
Inlet boundary	Mass flow water and air, IGVF
Outlet boundary	Static pressure (12 atm)
Wall boundary	Adiabatic, smooth, non-slip condition
Simulation type	Steady for initialization at transient calculation (absolute frame)
Convergence criteria	Max residuals < 1 × 10−4
	Imbalance < 1% (stability of macro head and local parameter of pressure)

summarizes the numerical setup.

5. Results

The results of the simulations include the distribution of the gas phase and how it diffuses into the continuous liquid medium, the development of agglomerates to form air pockets, and the density of the interfaces between the bubbles and the liquid. The pressure field is plotted through the iso contour’s curves, and the pressure coefficient along each blade is calculated. Additionally, snapshots of flow lines, velocity profiles at different levels, the u_y velocity component of the velocity vector, the magnitude of turbulence, and the forces exerted on each surface of the blade are shown.

5.1. Gas Phase Concentrations

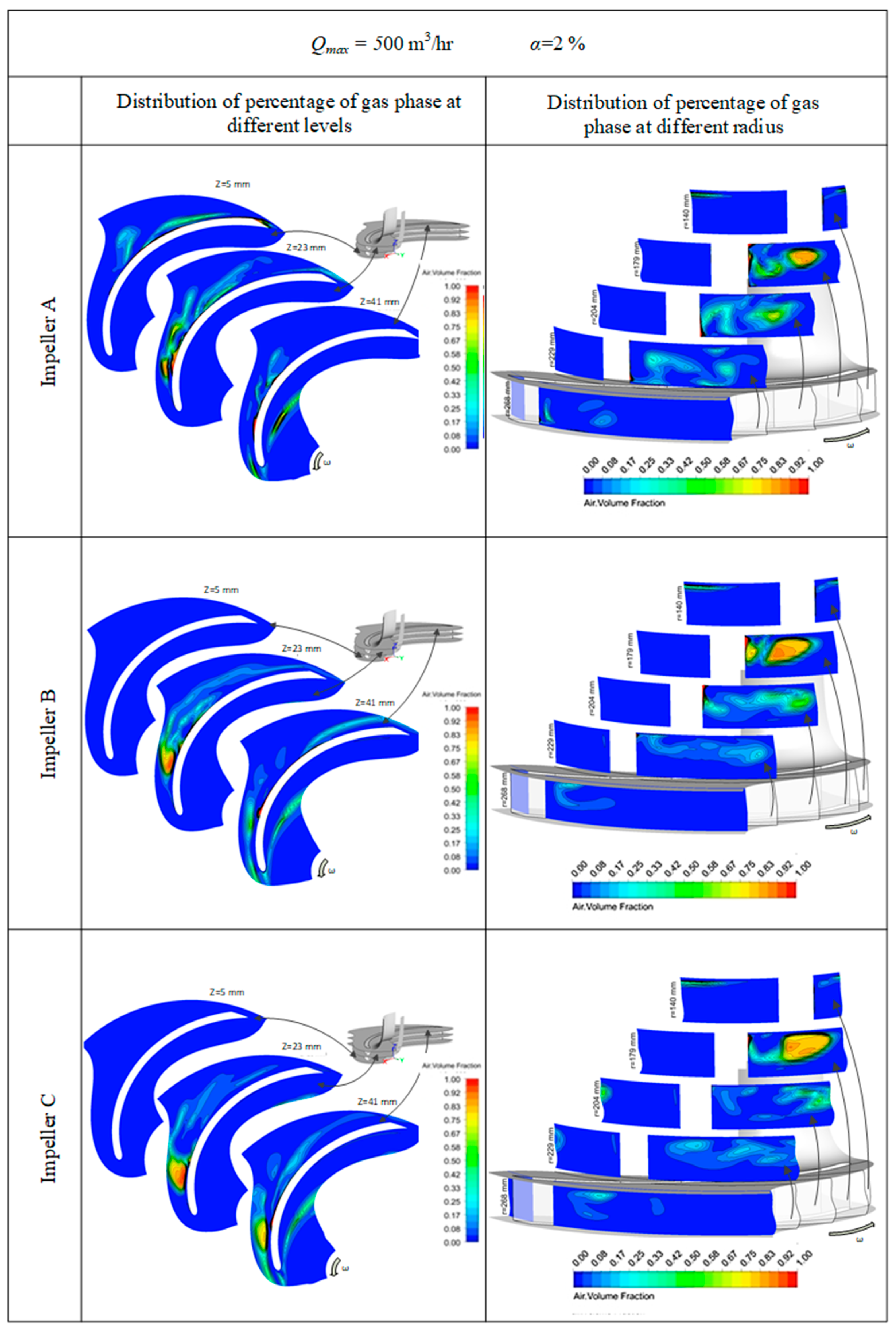
Figure 6 shows the iso-surface contours of the gas phase at different levels in the spanwise direction and different radial positions for a gas phase percentage of 2%. From this figure, it can be pointed out that, regardless of the design of the impeller, an air pocket upstream of the leading edge in the area near the shroud may be observed. Similar results for the gas phase concentration were shown in previous numerical studies [45,46]. Interestingly, there was no bubble accumulation in the area adjacent to the hub. For all impellers, the area of increased bubble concentration was located on the pressure side, close to the entrance. Almost identical findings were reported by other researchers (J. Caridad et al. [22]; T. Müller et al. [27,31]). Moving away from the shroud, towards the center of the blade passage, the starting point of bubble accumulation was observed further downstream of the inlet. Also, further downstream in the flow passage, the accumulation area seemed to expand towards the suction side of the blade, with an apparently greater diffusion of air bubbles. In this way, the bubble density was reduced and the homogenization of the mixture on the pressure side increased. At low flow rates, similarities were found between impellers B and C.

The accumulation of bubbles extends to a limited region near the shroud. Impeller A stands out with the highest concentrations of the gas phase, especially at a level near the shroud where z = 41 mm. At the flow rate of Q = 412 m³/h, impeller B behaves similarly to impeller A (Figure 6). Nonetheless, impeller C differs as the bubble aggregation areas are shown to be enlarged and with higher concentrations. The amplification of all gas phase structures, which had started to appear for Q = Q_min, is clear. For Q = Q_max, smaller air pockets were observed in impeller A in relation to the other two (Figure 7). Nevertheless, the differences between the three impellers with separate configurations (A, B, and C) were blurred, and the similarities multiplied. This was reflected in the creation of the large pocket, a fact that was recorded in radius r = 179 mm, as well as in the development of equally high concentrations and in the intermediate level of z = 23 mm, as well as the level of z = 41 mm. To summarize, increasing the flow rate to Q_max resulted in maximum concentrations of dissolved air appearing in impeller C. On the other hand, when the flow was minimal Q_min, impeller A was the one where correspondingly higher amounts of air were observed.

When the air percentage increased to 5%, the pockets that were created for Q_n were located towards the side of the upper disk, occupying almost the entire inlet space (Figure 8). The highest concentrations occurred in the form of a film in contact with the inner surfaces of the impellers. They particularly covered the inner corners, formed at the junction between the horizontal surfaces of the hub and the upper disc, with the vertical sides of the blades. At the intermediate level (z = 21 mm), the areas with the largest gas phase volume fraction moved towards the impeller discharge. At the same time, however, they expanded throughout the flow passage between successive blades. Interestingly, in the case of impeller C, larger gas phase concentrations on the blade suction side were observed, while at the same time, there was no air pocket observed in the hub. For the nominal flow Q_n, similar to the 2% inlet volume fraction case, the concentration of the gas phase at position r = 179 mm was similar for impellers A and B (Figure 8). The difference lies in the density of the bubbles that accumulated, resulting in differences in the local percentage of the gas phase, with higher values observed in impeller A.

5.2. Pressure

The pressure coefficient with respect to the surface of the impeller blades is shown in a group of diagrams in Figure 9. Most noticeable is the distinctive behavior of impeller A where, at low flows, on the pressure side and after the leading edge, the slope of the pressure coefficient curve varies considerably. In all impellers and in accordance with the findings of Yan et al. [47], there is a saddle region immediately after the rim, which varies in size, depending on the conditions and exact location. Impeller A shows the lowest values of pressure coefficient along the entire length of the blade. In particular, as the flow rate increases, contrary to the other two cases, there is an extensive area on the pressure side where the slope has zero or negative values. More specifically, for Q_n, this area extends from r/R₂ ≈ 0.15 to r/R₂ ≈ 0.25, while for Q_max, it extends to r/R₂ ≈ 0.5. For maximum flow, the pressure coefficient is higher for a large part of the pressure side of impellers B and C. For the same conditions, it is clear that impeller A shows a significant reduction in the pressure coefficient which indicates a corresponding reduction in the specific work performed by the impeller [48]. As reported by Yan et al. [47], when α = 5% and especially for impeller A, the difference in the pressure coefficient, between the pressure side and the suction along the entire length of the blade shows larger non-uniformities in relation to those resulting with α = 2%.

5.3. Velocity Profile

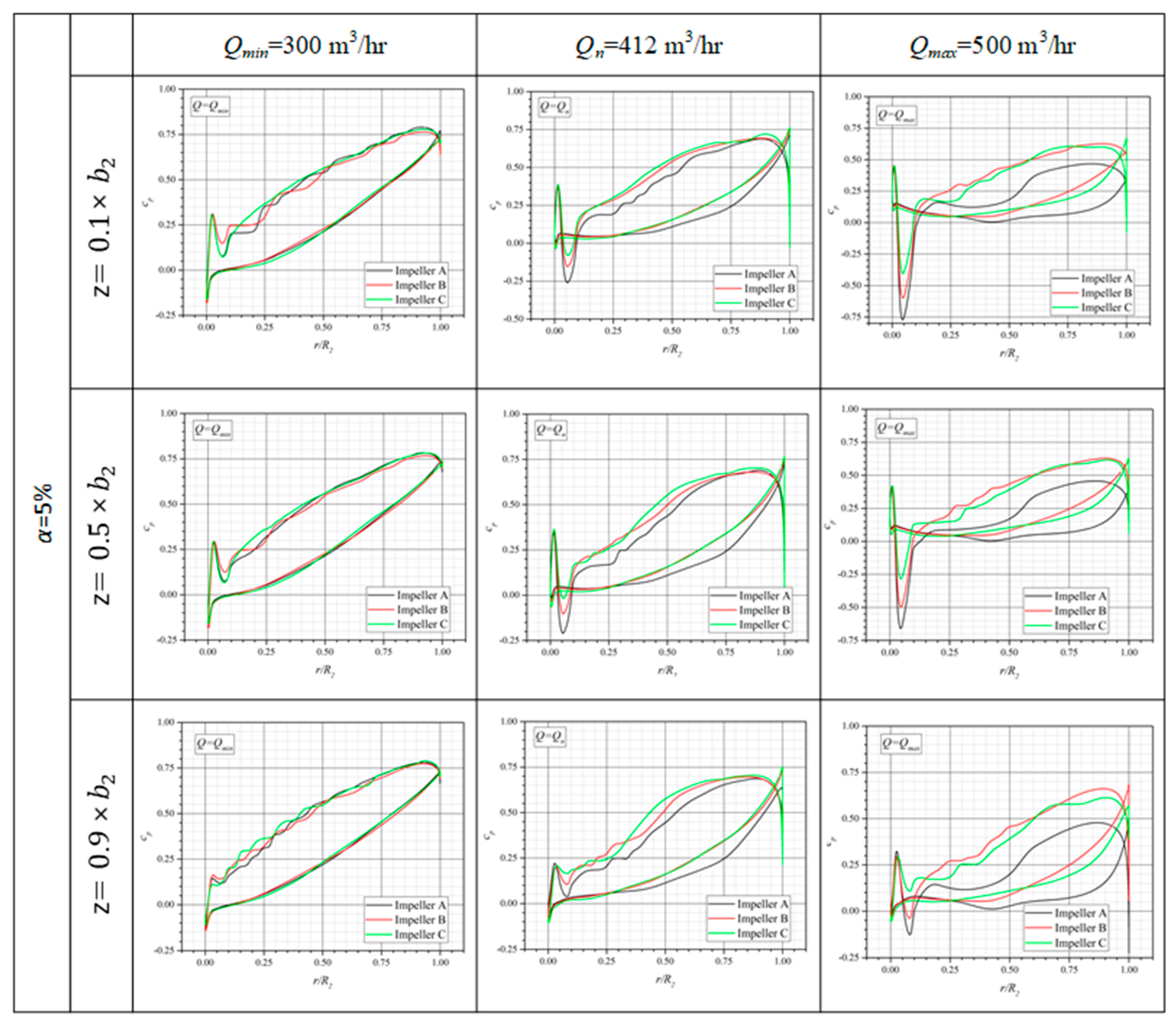
The liquid phase velocity distributions at the inlet (r = 140 mm) and outlet (r = 268 mm) of the impellers are shown in Figure 10 and Figure 11. In all the impellers studied and regardless of the flow rate after the leading edge, there was a local maximum observed on the pressure side followed by a sudden reduction in the velocity magnitude approaching almost zero values, especially in impeller B. In impeller C, this area is particularly wide relative to the other two, showing small fluctuations. As the flow increases, these differences are mitigated, with impeller C still exhibiting a distinct behavior in the area near the shroud, where velocities are lower than that in the hub area. In general, a similar flow pattern is observed in impellers A and B, while differences are observed in impeller C, located exclusively around the shroud, especially at lower flow rates.

At the outlet of the impellers where r = 268 mm (Figure 11), away from the area where the gas phase forms pockets of high air concentration, Impeller B shows a smoother velocity profile. Furthermore, the outlet velocity profile of impeller C is significantly different from the other two, showing several fluctuations along the spanwise and streamwise directions. Finally, as the flow increases, in all cases, the maximum speed is gradually shifted from the pressure side to the suction side of the blade.

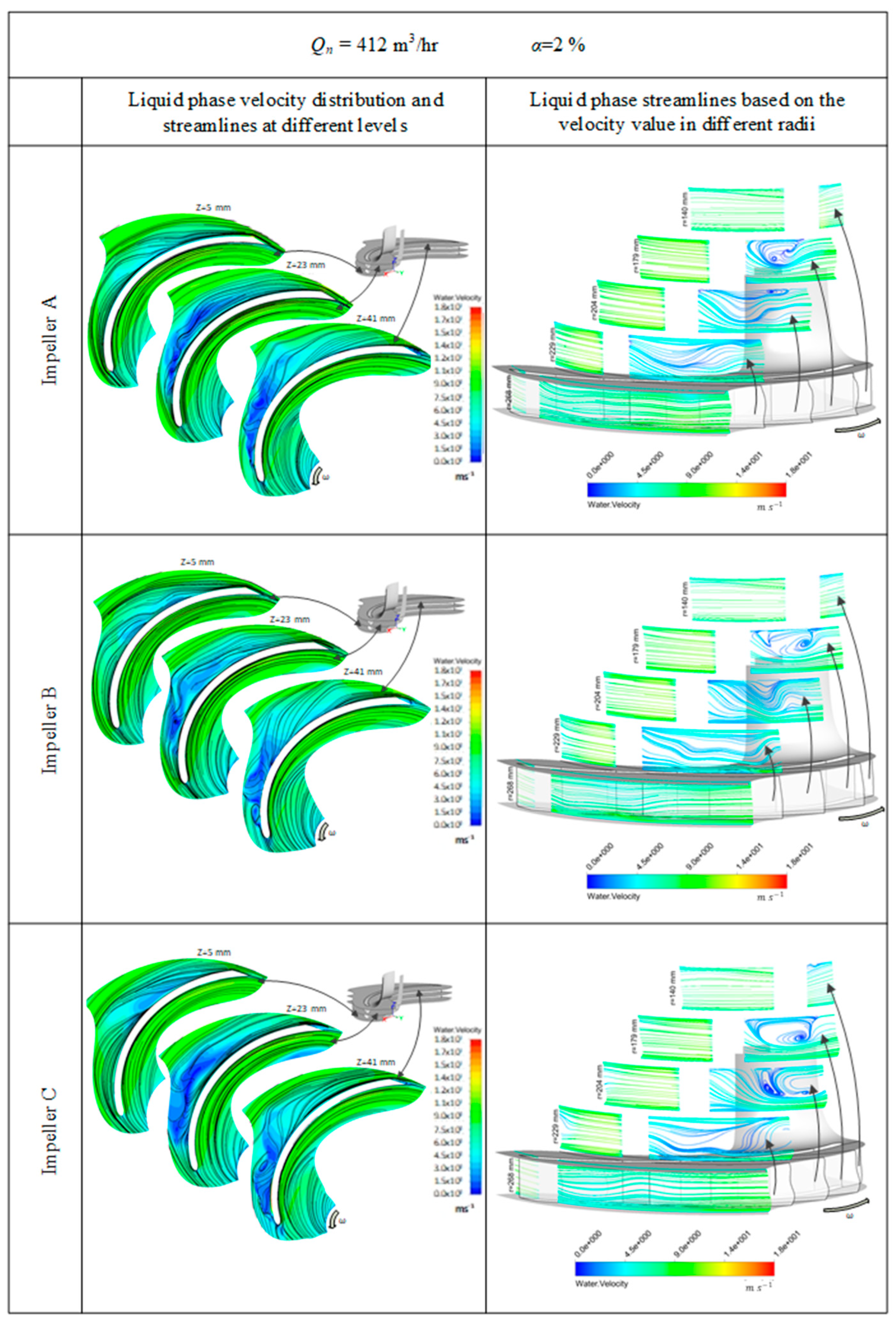
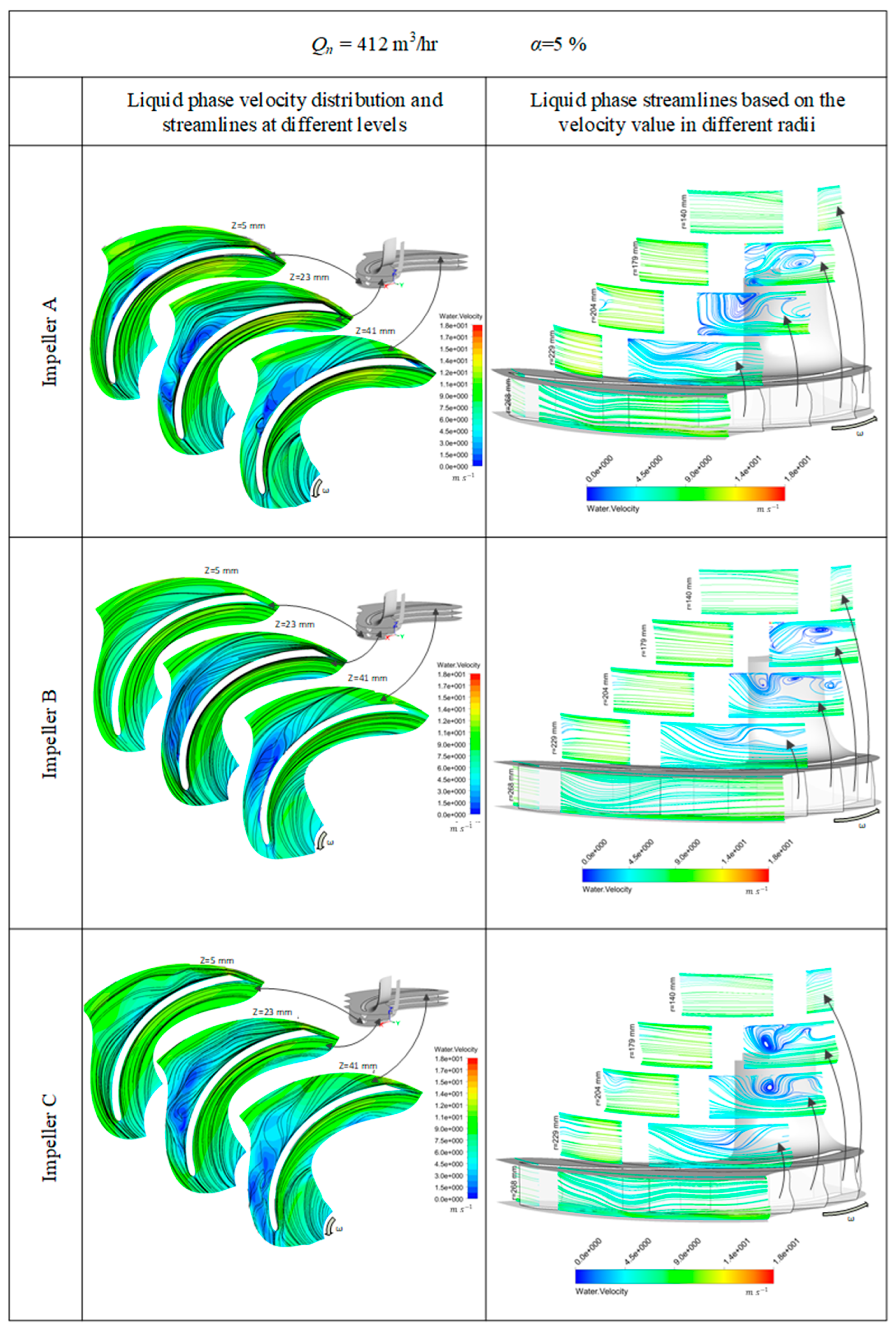
5.4. Streamlines

The introduction of bubbles resulted in increased turbulence in the flow field, facilitating the formation of vortices, as shown by the liquid flow lines in Figure 12 and Figure 13. The locations where vortices develop can be associated with bubble aggregation areas. This may be attributed to the obstruction of the free flow of the liquid, leading to even flow reversal. From the above, in combination with the local increase in speed due to the reduction in the active cross-section, this led to a reduction in the pump’s hydraulic efficiency.

From Figure 12, it can be observed that increasing the air volume fraction led to an increase in the number of larger air pockets. Similarly, with the increasing flow rate, the observed vortices became more intense while the size of the air pockets also increased. Furthermore, it can be observed that flow separation is mostly located on the pressure side of the blades near the leading edge, while the flow appears more streamlined on the suction side. Furthermore, downstream, towards the outlet of the flow passage, the flow reattaches on the pressure side, and the vortices are dispersed.

For Q_n = 412 m³/h and α = 2% and for the three different configurations of the impellers, such structures appear at approximately the same position, r = 179 mm. Especially for impeller C, the vortex structure extends further downstream. In contrast, in the case of impeller B, the vortex is quickly dissipated, while for impeller A, there is a similar structure near the shroud but with clearly limited dimensions. The developed vortices intensify with the increase in the concentration of the gas phase α = 5% at the inlet as the area where the above-mentioned structures are created and expand.

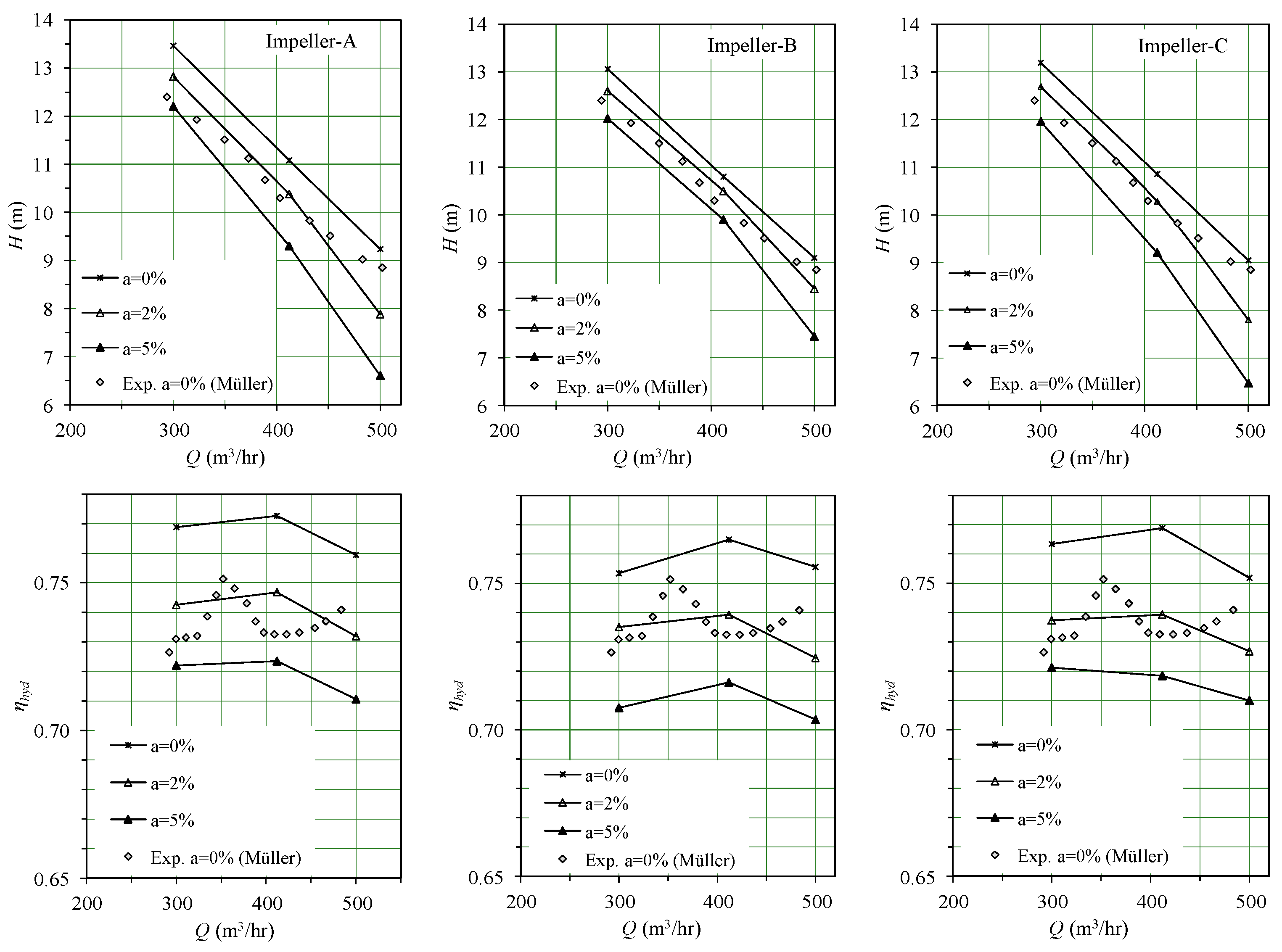
5.5. Performance Curves

The characteristic performance curves for the head and hydraulic efficiency as a function of flow were calculated by processing the simulation results according to Equations (16) and (17), which were compared to the available experimental measurements [27], in Figure 14.

$$H=(1-a_g)\cdot {\left[{\displaystyle \frac{\left(p_2-p_1\right)}{\rho g}}+{\displaystyle \frac{\left(u_2^2-u_1^2\right)}{2g}}\right]}_{liq}+a_g\cdot {\left[{\displaystyle \frac{\left(p_2-p_1\right)}{\rho g}}+{\displaystyle \frac{\left(u_2^2-u_1^2\right)}{2g}}\right]}_{gas}$$

(16)

$$\eta ={\displaystyle \frac{\left(Q_l{\rho }_l+Q_g{\rho }_g\right)gH}{{\displaystyle \sum T\omega }}}$$

(17)

Qualitatively, an expected pressure drop with the increasing flow rate was clearly visible throughout the operating range. By comparing the different impellers, it can be observed that a linear variation in the blade angle resulted in a slightly superior performance. This was more pronounced at an increased inlet air volume fraction and at higher flow rates. Furthermore, in all three different impeller configurations, the head was practically identical at design flow conditions and at an air volume fraction of α = 2%. However, as the flow rate increased, impeller B appeared to perform better. By increasing the inlet air volume fraction to α = 5%, a similar behavior was observed, with a more pronounced drop in the head with increasing flow rates for impellers A and C.

Finally, in terms of hydraulic efficiency, impeller B showed the lowest performance across all flow rate conditions, while impeller A showed the highest. The best efficiency point was observed at the rated flow rate, apart from the case of impeller C at α = 5%, where a slightly higher efficiency was observed at a lower flow rate.

Considering the present numerical set-up and results, the main limitations of the present approach and potential inaccuracies stem from the assumption of the homogeneity of the fluid–gas mixture, with the gas phase distributed in uniformly sized spherical bubbles. However, bubble sizes and distributions vary significantly, and areas with different concentrations that cannot be predetermined may well be identified. Additionally, interfacial phenomena such as bubble coalescence, breakup, and surface tension effects have not been included in the simulation and may have an impact on the accuracy of the results. Finally, the accuracy of the interfacial forces’ modeling approach on the results was not investigated. The investigation of the above uncertainties may be a matter of further research.

6. Conclusions

Based on the results presented in this work, the concentration of high percentages of gas phase on the pressure side of impellers was confirmed, as in previous studies. The size of the air pockets seems to depend on both the initial percentage of the gas phase at the inlet and the corresponding flow rate. The effect of the blade angle distribution for constant values of the inlet and outlet angles is initially small but increases with the increasing percentage of the air volume fraction. The area near the hub, as well as the suction side, are the regions with the fewest gas phase structures and with the lowest concentrations. On the contrary, the concentrations in the space between the mid-span level of z = 23 mm and the shroud are higher.

The analysis of the pressure coefficient showed a significant modification of the blade loading in two-phase flow. The comparison against the single-phase flow results showed that as the percentage of the gas phase increases, there is a distortion of the distribution of the pressure coefficient that limits the capability of the pump to transfer energy to the moving medium and produce a head. Under the presence of bubbles, a four-loaded blade design (impeller C) seems to differ from the other two, with more pronounced performance deterioration.

The continuous variation in the flow field, as a function of the percentage of the gas phase, was also confirmed. The presence of bubbles leads to the formation of vortices and large recirculation areas that are particularly pronounced in areas with pockets with high gas phase percentages. These recirculations are located shortly after the leading edge of the blades and are gradually attenuated towards the exit of the impeller. Another consequence of the formation of air pockets that are close and in contact with the surfaces of the blades is the modification of the flow passage and the ability of the impeller to transfer energy to the fluid. The flow lines are no longer streamlined and no longer follow the shape of the blade as they are forced to bypass the obstacles of existing air pockets, essentially modifying the blade profile.

Finally, by comparing the two-phase flow characteristic curves to those for single-phase flow, a reduction in both the head and efficiency can be seen with an increase in the air volume fraction. It can be concluded that the highest pressure is achieved by impeller B with a linear variation in blade angle, while the best hydraulic efficiency is achieved by an aft-loaded blade design (impeller A).

The results presented in this study enhance our understanding of the evolving two-phase flow field within the impeller, aiming to expand the range of unobstructed pump operations at higher gas phase percentages through improved impeller design.