Identifying Weak Transmission Lines in Power Systems with Intermittent Energy Resources and DC Integration
Abstract
1. Introduction
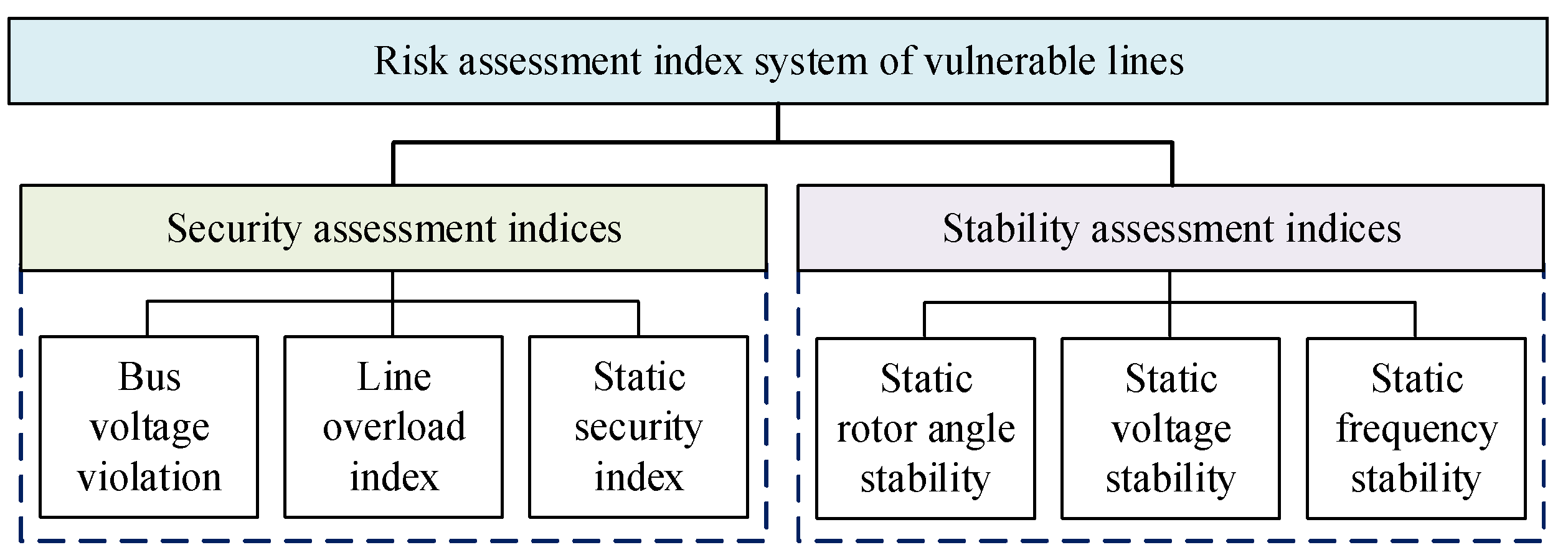
2. Risk Assessment Index System of Vulnerable Lines
3. Calculation Method for Risk Assessment Index
3.1. Bus Voltage Violation and Line Overload Index
3.2. Static Security Index
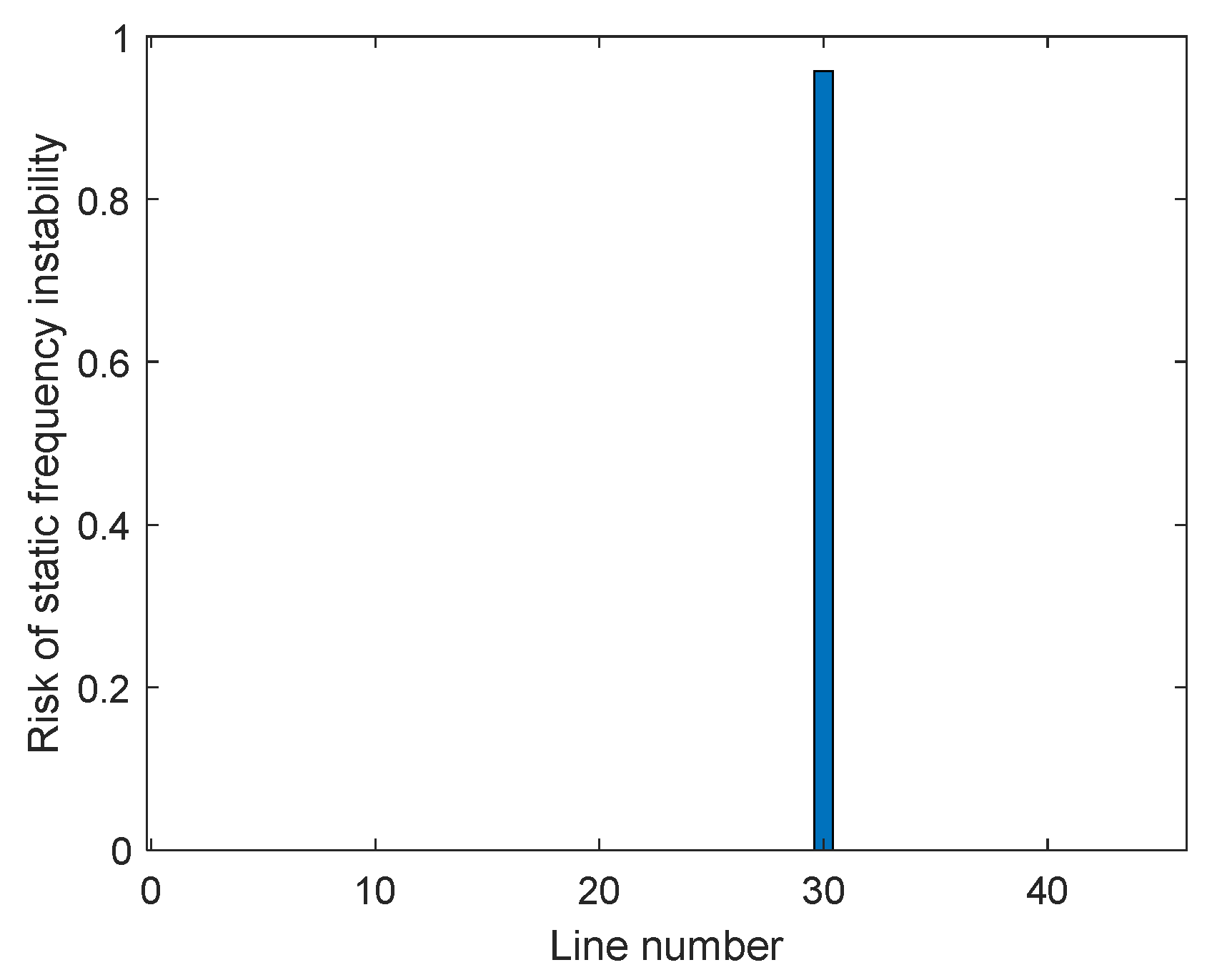
3.3. Static Frequency Stability Index
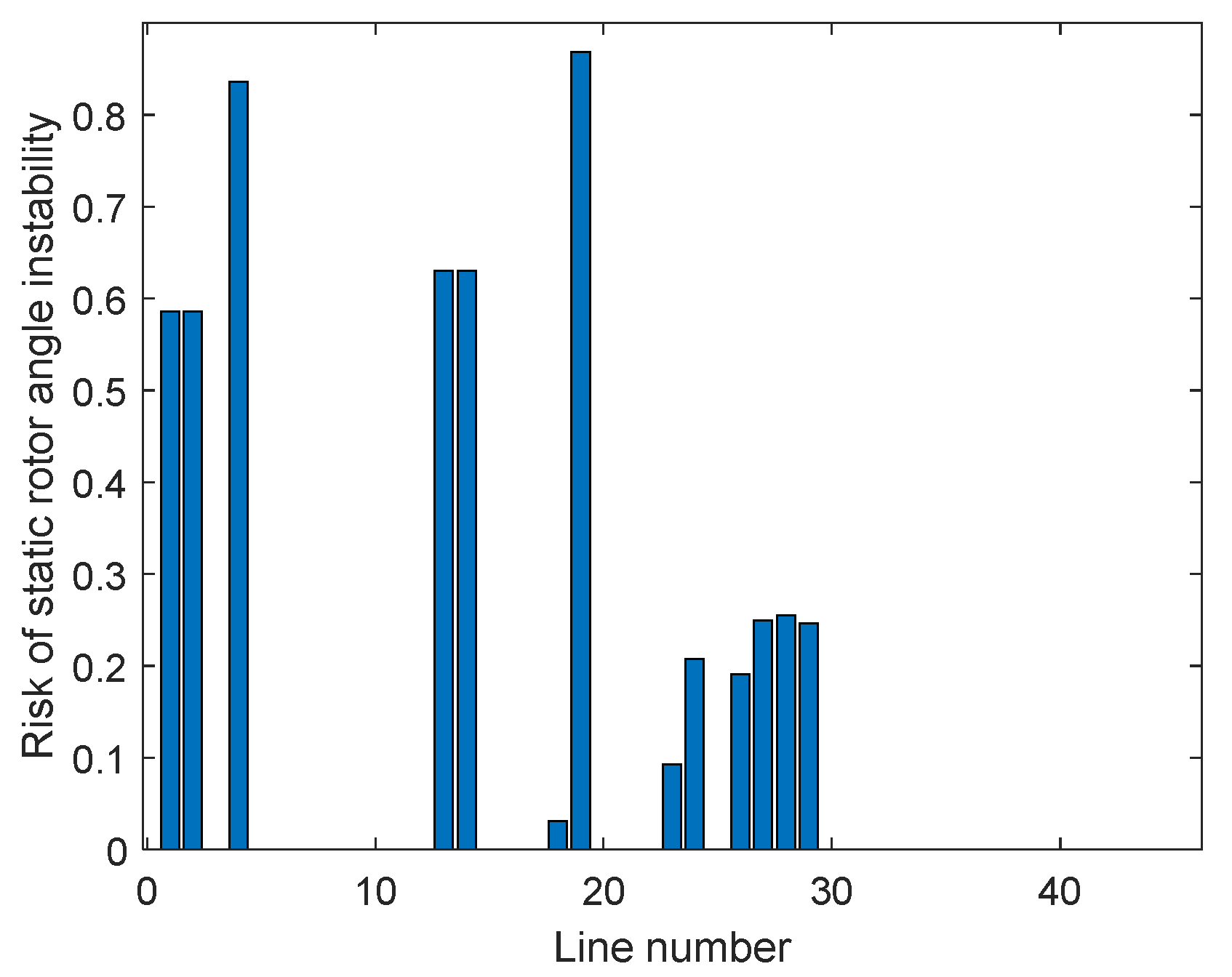
3.4. Static Rotor Angle Stability Index
3.5. Static Voltage Stability Index
4. Comprehensive Risk Assessment Index of Vulnerable Lines
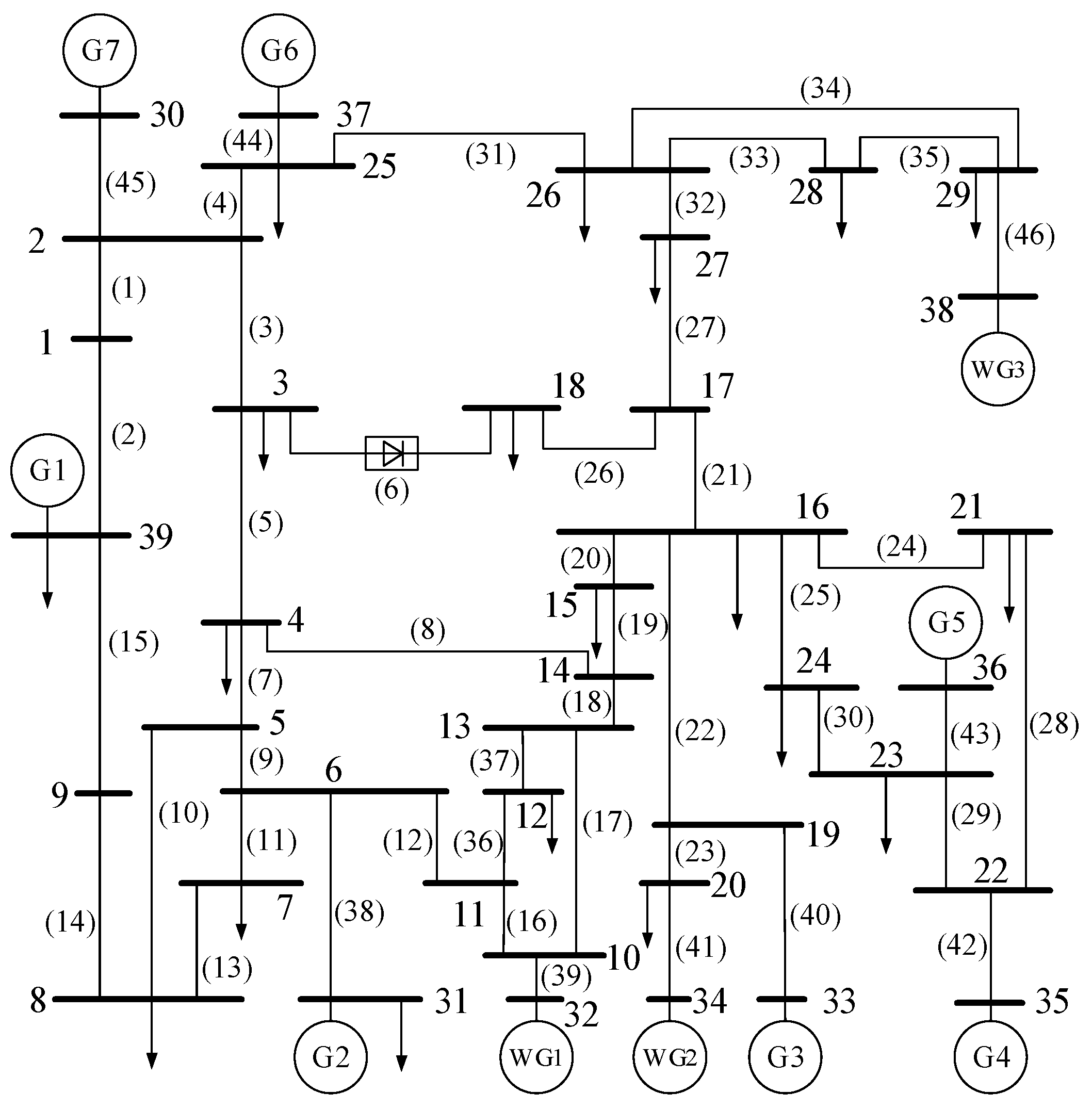
5. Simulation Tests
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kumar, S.; Pandey, A.; Goswami, P.; Pentayya, P.; Kazi, F. Analysis of Mumbai Grid Failure Restoration on Oct 12, 2020: Challenges and Lessons Learnt. IEEE Trans. Power Syst. 2022, 37, 4555–4567. [Google Scholar] [CrossRef]
- Xiang, Y.; Wang, T.; Wang, Z. Risk Prediction Based Preventive Islanding Scheme for Power System Under Typhoon Involved with Rainstorm Events. IEEE Trans. Power Syst. 2023, 38, 4177–4190. [Google Scholar] [CrossRef]
- Liu, S.; Chen, C.; Jiang, Y.; Lin, Z.; Wang, H.; Waseem, M.; Wen, F. Bi-Level Coordinated Power System Restoration Model Considering the Support of Multiple Flexible Resources. IEEE Trans. Power Syst. 2023, 38, 1583–1595. [Google Scholar] [CrossRef]
- Dobson, I.; Newman, D.E. Cascading blackout overall structure and some implications for sampling and mitigation. Int. J. Elect. Power Energy Syst. 2017, 86, 29–32. [Google Scholar] [CrossRef]
- Li, M.J.; Tse, C.K.; Liu, D.; Zhang, X. Cascading Failure Propagation and Mitigation Strategies in Power Systems. IEEE Syst. J. 2023, 17, 3282–3293. [Google Scholar] [CrossRef]
- Rajkumar, V.S.; Ştefanov, A.; Torres, J.L.R.; Palensky, P. Dynamical Analysis of Power System Cascading Failures Caused by Cyber Attacks. IEEE Trans. Ind. Informat. 2024, 20, 8807–8817. [Google Scholar] [CrossRef]
- Gao, Q.; Wang, Y.; Cheng, X.; Yu, J.; Chen, X.; Jing, T. Identification of Vulnerable Lines in Smart Grid Systems Based on Affinity Propagation Clustering. IEEE Internet Things J. 2019, 6, 5163–5171. [Google Scholar] [CrossRef]
- Liu, Y.; Lai, X.; Xin, H.; Zhu, J.; Huang, L.; Xia, S. Generalized short-circuit ratio based distributed real-time stability assessment of renewable power systems. IEEE Trans. Power Syst. 2023, 38, 5953–5956. [Google Scholar] [CrossRef]
- Shu, Y.; Tang, Y. Analysis and recommendations for the adaptability of China’s power system security and stability relevant standards. CSEE J. Power Energy Syst. 2017, 3, 334–339. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhou, Y.; Wei, W.; Zhang, L. Real-time cascading failure risk evaluation with high penetration of renewable energy based on a graph convolutional network. IEEE Trans. Power Syst. 2023, 38, 4122–4133. [Google Scholar] [CrossRef]
- Kitsak, M.; Gallos, L.K.; Havlin, S.; Liljeros, F.; Muchnik, L.; Stanley, H.E.; Makse, H.A. Identification of influential spreaders in complex networks. Nat. Phys. 2010, 6, 888–893. [Google Scholar] [CrossRef]
- Xu, L.; Wang, X.L.; Wang, X.F. Electric betweenness and its application in vulnerable line identification in power system. Chin. Soc. Electr. Eng. 2010, 30, 33–39. [Google Scholar]
- Bompard, E.; Pons, E.; Wu, D. Extended topological metrics for the analysis of power grid vulnerability. IEEE Syst. J. 2012, 6, 481–487. [Google Scholar] [CrossRef]
- Fang, J.; Su, C.; Chen, Z.; Sun, H.; Lund, P. Power system structural vulnerability assessment based on an improved maximum flow approach. IEEE Trans. Smart Grid 2018, 9, 777–785. [Google Scholar] [CrossRef]
- Chu, C.C.; Lu, H.H.C. Complex networks theory for modern smart grid applications: A survey. IEEE J. Emerg. Sel. Top. Circuits Syst. 2017, 7, 177–191. [Google Scholar] [CrossRef]
- Fan, W.; Zhang, X.; Mei, S. Vulnerable transmission line identification considering depth of K-shell decomposition in complex grids. IET Gener. Trans. Distrib. 2018, 12, 1137–1144. [Google Scholar] [CrossRef]
- Bai, H.; Miao, S. Hybrid flow betweenness approach for identification of vulnerable line in power system. IET Gener. Trans. Distrib. 2015, 9, 1324–1331. [Google Scholar] [CrossRef]
- Chen, C.Y.; Zhou, Y.; Wang, Y.; Ding, L.; Huang, T. Vulnerable Line Identification of Cascading Failure in Power Grid Based on New Electrical Betweenness. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 665–669. [Google Scholar] [CrossRef]
- Rao, S.; Tylavsky, D.; Vittal, V.; Yi, W.; Shi, D.; Wang, Z. Fast weak-bus and bifurcation point determination using holomorphic embedding method. In Proceedings of the IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar]
- Ma, Z.; Shen, C.; Liu, F.; Mei, S. Fast screening of vulnerable transmission lines in power grids: A pagerank-based approach. IEEE Trans. Smart Grid 2019, 10, 1982–1991. [Google Scholar] [CrossRef]
- Wei, X.; Zhao, J.; Huang, T.; Bompard, E. A novel cascading faults graph based transmission network vulnerability assessment method. IEEE Trans. Power Syst. 2018, 33, 2995–3000. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, M.; Hu, J.; Sun, J.; Wei, J.; Wu, Y. Research on vulnerable line identification based on PMU data and graph theory. In Proceedings of the 2022 Power System and Green Energy Conference (PSGEC), Shanghai, China, 25–27 August 2022; pp. 853–858. [Google Scholar]
- Moger, T.; Dhadbanjan, T. A novel index for identification of weak nodes for reactive compensation to improve voltage stability. IET Gener. Trans. Distrib. 2015, 9, 1826–1834. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, R.; Duan, J.; Chen, L.; Xue, B.; Cheng, W. Identification of critical transmission lines considering multiple influencing factors. Proc. CSEE 2019, 39, 5938–5947. [Google Scholar]
- Zhu, D.; Wang, R.; Duan, J.; Cheng, W. Comprehensive weight method based on game theory for identify critical transmission lines in power system. Int. J. Electr. Power Energy Syst. 2021, 124, 106362. [Google Scholar] [CrossRef]
- Yang, L.; Li, C. Identification of vulnerable lines in smart grid systems based on improved agglomerative hierarchical clustering. IEEE Access 2023, 11, 13554–13563. [Google Scholar] [CrossRef]
- Fan, W.; He, X.; Xiao, Y.; Li, Q. Vulnerability analysis of power system by modified H-index method on cascading failure state transition graph. Electr. Power Syst. Res. 2022, 209, 107986. [Google Scholar] [CrossRef]
- Li, Y.; Liu, J.; Liu, X.; Jiang, L.; Wei, Z.; Xu, W. Vulnerability assessment in power grid cascading failures based on entropy of power flow. Auto. Elect. Power Syst. 2012, 36, 11–16. [Google Scholar]
- Liu, W.; Wang, J.; Xie, C.; Wang, W. Brittleness source identification model for cascading failure of complex power grid based on brittle risk entropy. Pro. CSEE 2014, 32, 142–149. [Google Scholar]
- Lin, Z.; Wen, F.; Wang, H.; Lin, G.; Mo, T.; Ye, X. CRITIC-based node importance evaluation in skeleton-network reconfiguration of power grids. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 206–210. [Google Scholar] [CrossRef]
- Cheng, M.X.; Crow, M.; Ye, Q. A game theory approach to vulnerability analysis: Integrating power flows with topological analysis. Int. J. Electr. Power Energy Syst. 2016, 82, 29–36. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, L.; Li, G. Identification of vulnerable transmission lines in power system based on game theory. IEEE Access 2024, 12, 29607–29616. [Google Scholar] [CrossRef]
- Sun, J.; Liu, J.; Li, C.; Zhi, N. An identification method for vulnerable lines based on combination weighting method and GraphSAGE algorithm. Int. J. Electr. Power Energy Syst. 2023, 149, 109035. [Google Scholar] [CrossRef]
- Zhou, B.; Lei, Y.; Li, C.; Fang, B.; Wu, Q.; Li, L.; Li, Z. Electrical LeaderRank method for node importance evaluation of power grids considering uncertainties of renewable energy. Int. J. Electr. Power Energy Syst. 2019, 106, 45–55. [Google Scholar] [CrossRef]
- Zhang, L.; Zhu, B.; Wang, Y. Identification of vulnerable lines in power grids with wind power integration based on topological potential. Electr. Power Syst. Res. 2024, 234, 110593. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, T.; Wang, Z. Bi-level optimized emergency load/generator shedding strategy for AC/DC hybrid system following DC blocking. IET Gener. Trans. Distrib. 2020, 14, 1491–1499. [Google Scholar] [CrossRef]
- Wang, T.; Li, C.; Mi, D.; Wang, Z.; Xiang, Y. Coordinated modulation strategy considering multi-HVDC emergency for enhancing transient stability of hybrid AC/DC power systems. CSEE J. Power Energy Syst. 2020, 6, 806–815. [Google Scholar]
- Kundur, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Wang, Z.; Shen, C.; Liu, F.; Gao, F. Analytical expressions for joint distributions in probabilistic load flow. IEEE Trans. Power Syst. 2017, 32, 2473–2474. [Google Scholar] [CrossRef]
- Xiang, Y.; Wang, T.; Wang, Z. Improved Gaussian mixture model based probabilistic power flow of wind integrated power system. In Proceedings of the IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar]
- GB 38755-2019; Code on Security and Stability for Power System. Standardization Administration of China: Beijing, China, 2019.
- Bu, S.; Du, W.; Wang, H.; Chen, Z.; Xiao, L.; Li, H. Probabilistic analysis of small-signal stability of large-scale power systems as affected by penetration of wind generation. IEEE Trans. Power Syst. 2012, 27, 762–770. [Google Scholar] [CrossRef]
- Han, X.; Zhao, S.; Wei, Z.; Bai, W. Planning and overall economic evaluation of photovoltaic-energy storage station based on game theory and analytic hierarchy process. IEEE Access 2019, 7, 110972–110981. [Google Scholar] [CrossRef]



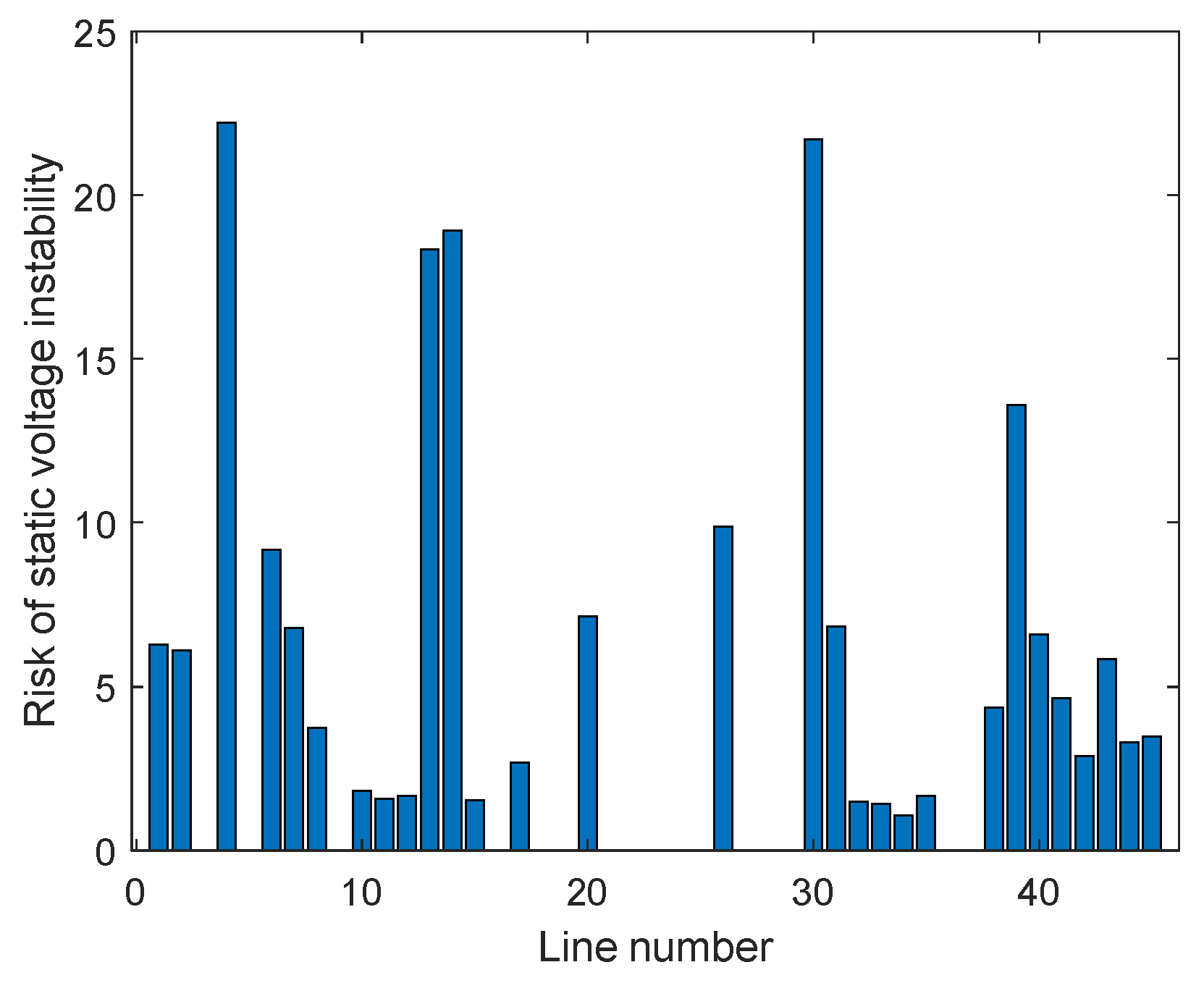
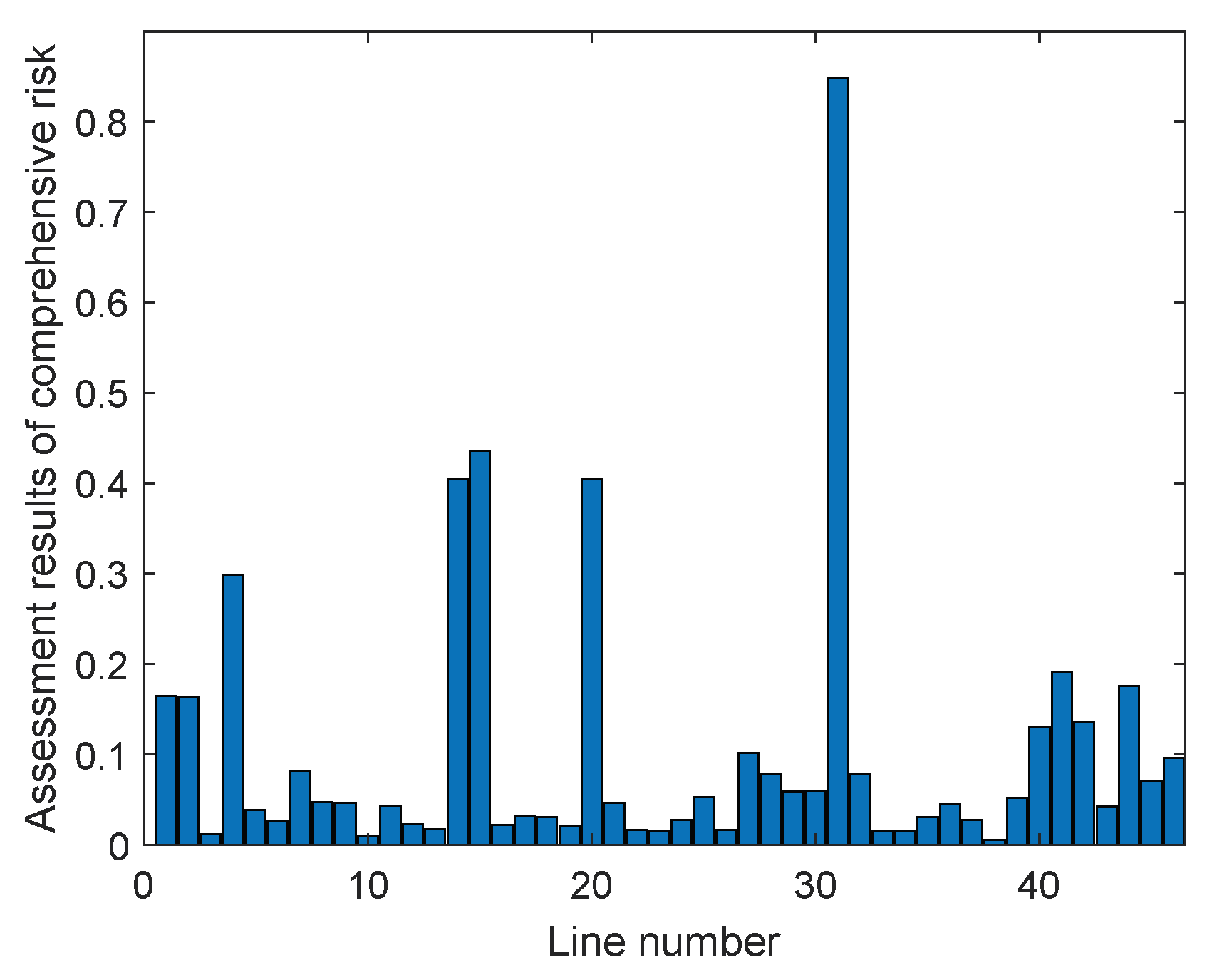
| Rank | Voltage Violation Risk | Line Overload Risk | ||
|---|---|---|---|---|
| Line Number | Risk Value | Line Number | Risk Value | |
| 1 | L15–16 | 0.1556 | L25–26 | 5.2697 |
| 2 | L25–26 | 0.1371 | L20–34 | 2.7717 |
| 3 | L9–39 | 0.1046 | L22–35 | 2.4761 |
| 4 | L8–9 | 0.0860 | L25–37 | 2.2993 |
| 5 | L25–37 | 0.0254 | L2–30 | 1.5992 |
| 6 | L20–34 | 0.0232 | L29–38 | 1.0576 |
| 7 | L12–11 | 0.0189 | L19–33 | 0.9878 |
| 8 | L4–5 | 0.0139 | L9–39 | 0.9322 |
| 9 | L12–13 | 0.0137 | L8–9 | 0.9322 |
| 10 | L6–7 | 0.0106 | L10–32 | 0.6455 |
| Rank | Line Number | Risk Value | Rank | Line Number | Risk Value |
|---|---|---|---|---|---|
| 1 | L25–26 | 7.9996 | 6 | L25–37 | 5.0127 |
| 2 | L9–39 | 6.0973 | 7 | L29–38 | 4.4849 |
| 3 | L8–9 | 5.2484 | 8 | L22–35 | 3.7451 |
| 4 | L15–16 | 5.2099 | 9 | L3–4 | 3.2632 |
| 5 | L20–34 | 5.1403 | 10 | L26–27 | 2.8230 |
| Rank | Line Number | Risk Value | Rank | Line Number | Risk Value |
|---|---|---|---|---|---|
| 1 | L15–16 | 0.8680 | 6 | L1–2 | 0.5855 |
| 2 | L2–25 | 0.8336 | 7 | L22–23 | 0.2524 |
| 3 | L9–39 | 0.6304 | 8 | L21–22 | 0.2491 |
| 4 | L8–9 | 0.6304 | 9 | L23–24 | 0.2460 |
| 5 | L1–39 | 0.5855 | 10 | L16–24 | 0.2075 |
| Rank | Line Number | Risk Value | Rank | Line Number | Risk Value |
|---|---|---|---|---|---|
| 1 | L2–25 | 22.22 | 6 | L17–27 | 9.71 |
| 2 | L25–26 | 21.71 | 7 | L4–5 | 9.18 |
| 3 | L9–39 | 18.92 | 8 | L16–17 | 6.88 |
| 4 | L8–9 | 18.22 | 9 | L26–27 | 6.82 |
| 5 | L19–33 | 13.59 | 10 | L4–14 | 6.78 |
| Rank | Line Number | Risk Value | Rank | Line Number | Risk Value |
|---|---|---|---|---|---|
| 1 | L25–26 | 0.8469 | 6 | L20–34 | 0.1897 |
| 2 | L9–39 | 0.4361 | 7 | L25–37 | 0.1738 |
| 3 | L8–9 | 0.4066 | 8 | L1–2 | 0.1691 |
| 4 | L15–16 | 0.3997 | 9 | L1–39 | 0.1671 |
| 5 | L2–25 | 0.3076 | 10 | L22–35 | 0.1360 |
| Rank | The Proposed Method | The Method of [25] |
|---|---|---|
| 1 | L25–26 | L25–26 |
| 2 | L9–39 | L2–30 |
| 3 | L8–9 | L22–35 |
| 4 | L15–16 | L10–32 |
| 5 | L2–25 | L20–34 |
| 6 | L20–34 | L29–38 |
| 7 | L25–37 | L15–16 |
| 8 | L1–2 | L25–37 |
| 9 | L1–39 | L19–33 |
| 10 | L22–35 | L6–7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, A.; Cao, J.; Li, S.; Gong, L.; Yang, M.; Hu, J. Identifying Weak Transmission Lines in Power Systems with Intermittent Energy Resources and DC Integration. Energies 2024, 17, 3918. https://doi.org/10.3390/en17163918
He A, Cao J, Li S, Gong L, Yang M, Hu J. Identifying Weak Transmission Lines in Power Systems with Intermittent Energy Resources and DC Integration. Energies. 2024; 17(16):3918. https://doi.org/10.3390/en17163918
Chicago/Turabian StyleHe, Anqi, Jijing Cao, Shangwen Li, Lianlian Gong, Mingming Yang, and Jiawei Hu. 2024. "Identifying Weak Transmission Lines in Power Systems with Intermittent Energy Resources and DC Integration" Energies 17, no. 16: 3918. https://doi.org/10.3390/en17163918
APA StyleHe, A., Cao, J., Li, S., Gong, L., Yang, M., & Hu, J. (2024). Identifying Weak Transmission Lines in Power Systems with Intermittent Energy Resources and DC Integration. Energies, 17(16), 3918. https://doi.org/10.3390/en17163918





