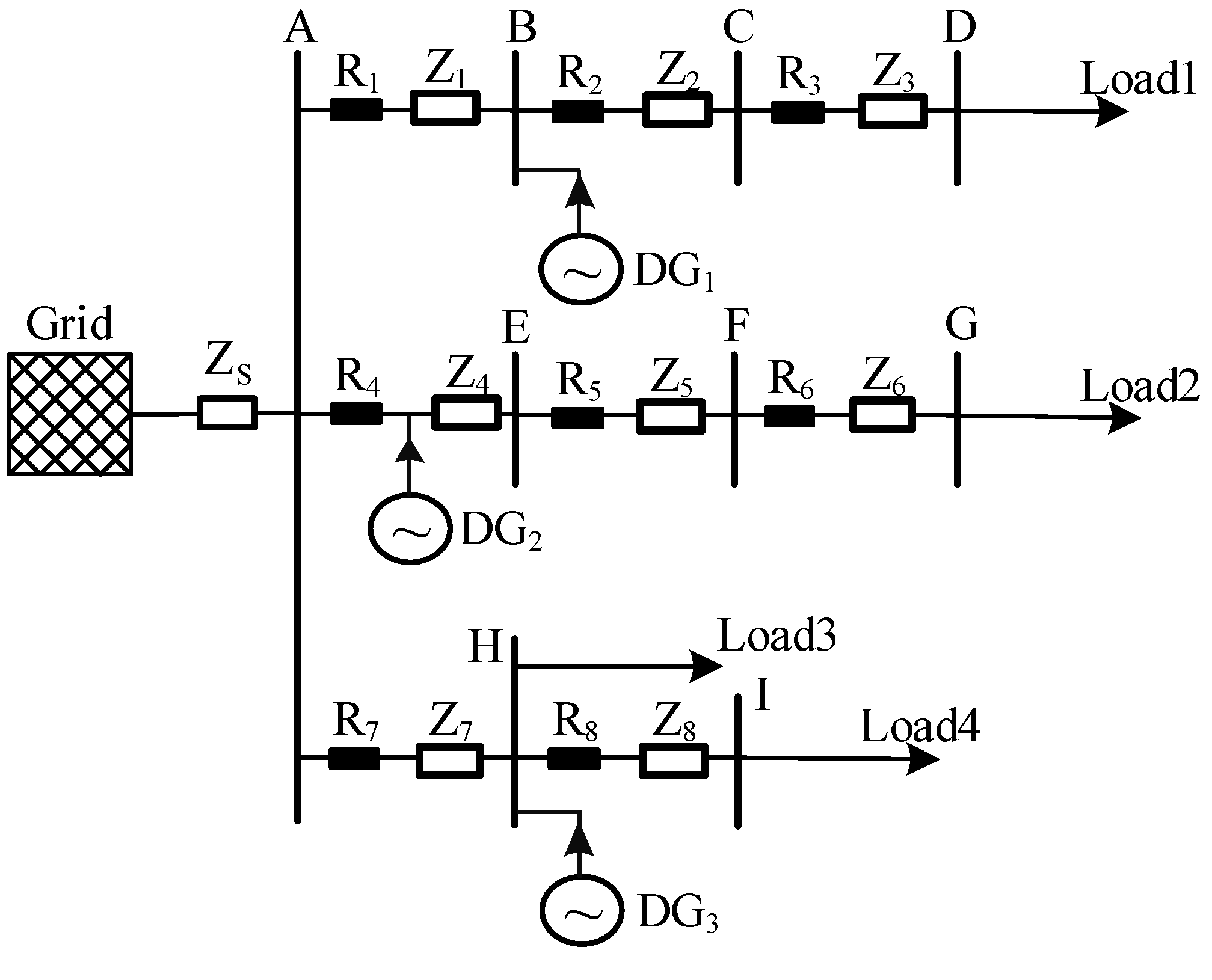
3.1. Evaluation Indicators and Calculation Models
In order to make the indicators objective, fair, and universal, the basic requirements of distribution network relay protection were analyzed and the definition of indicators was completed. Speed, sensitivity, selectivity, and reliability were selected as evaluation indicators [
29]. Combined with the traditional indicator definitions, the definition and calculation model of each indicator after DG access are as follows [
30,
31].
- (1)
Quickness index
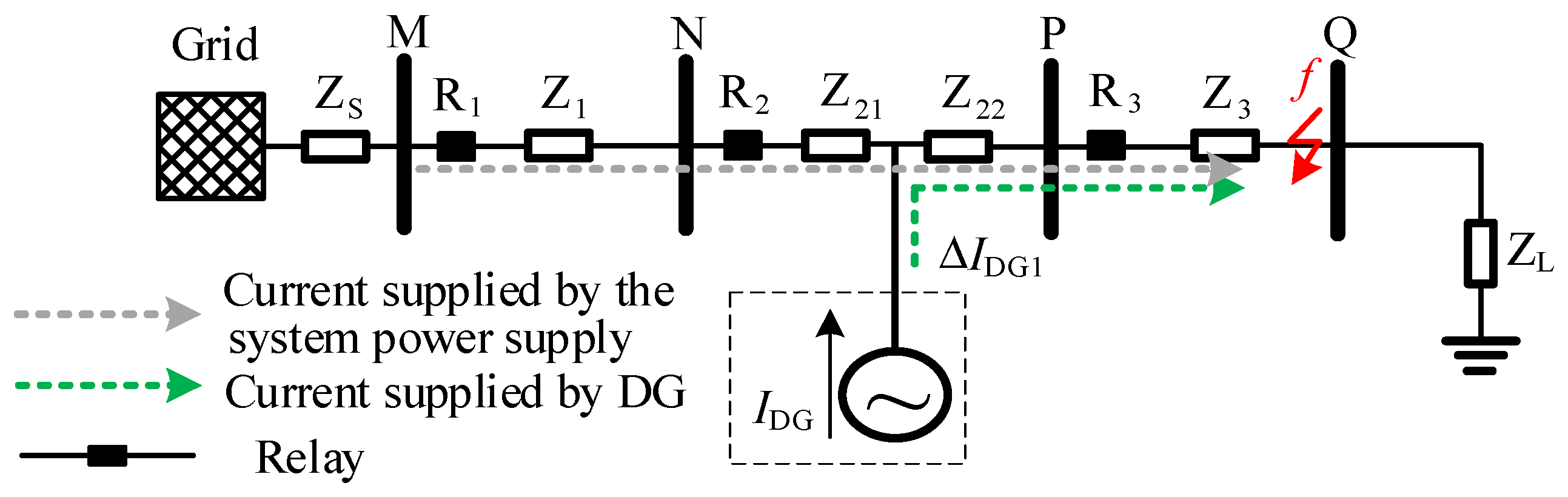
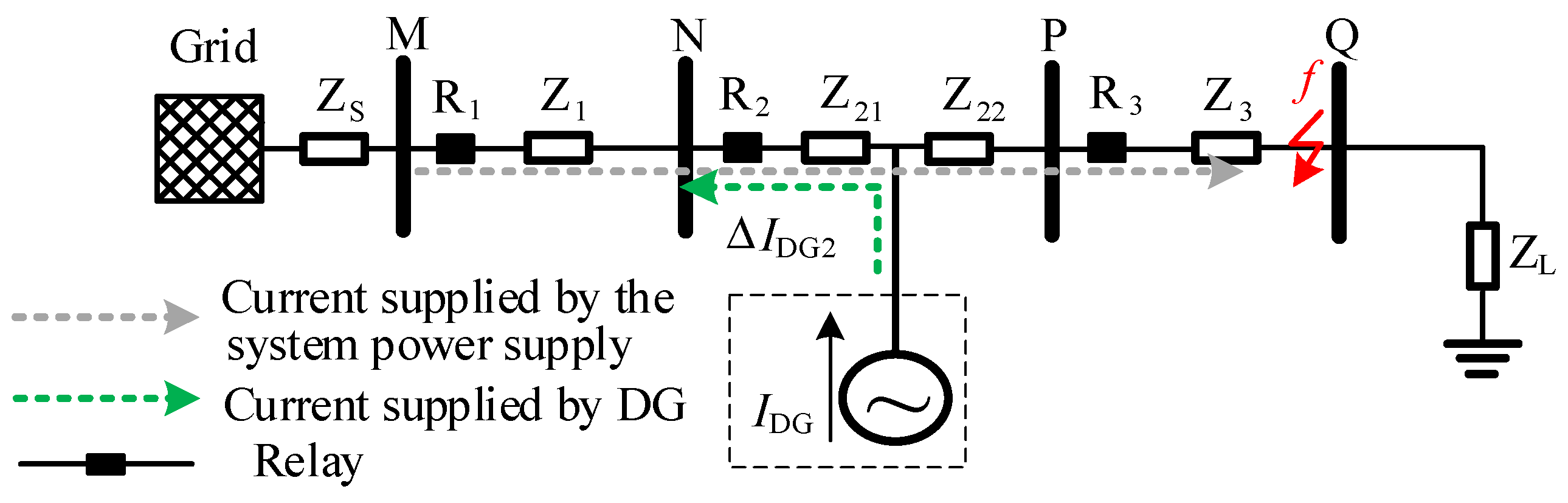
Quickness refers to the fact that when a fault occurs, the protective device is designed to act quickly to remove the fault. The operating time limits of the three-stage overcurrent protection and the adaptive overcurrent protection are set according to a stepped type. The protection action time comprises both the intrinsic action time of the device (
tmin) and the disparity between the action times of adjacent protections (
). The ratio of the protection action time after the distributed power supply is connected to the previous one is used to measure the rapidity index:
where
is the protection range of segment I without DG access and
is the protection range of segment I after DG access.
After the DG is connected, the equation of action for inverse time current protection, according to IEEE standard or the IEC 60255 [
32] equation, is shown in Equation (15):
The ratio of the protection action time after DG access to the previous one is:
where
TDS is the time coefficient,
is the start-up current of the protection, and
and
are the short-circuit currents flowing through the protection at the fault before and after the DG access, respectively. The values of characteristic parameters
a and
b are 0.14 and 0.02, respectively. The calculation method is described in
Section 2.1 and
Section 2.2.
- (2)
Sensitivity index
Sensitivity refers to the ability of a protection to react to the occurrence of faults or abnormal operating conditions within its protection area. The sensitivity coefficient
is used to measure the sensitivity index. In order to reliably protect the entire length of the line, the sensitivity value should be greater than 1.3. The calculation is usually measured by the ratio of the fault current
to the setting value
in the case of a two-phase short-circuit at the end of the protection range when the system is in the minimum mode of operation. After the DG is connected, the formula for calculating the sensitivity is as follows:
where
is the fault current value after DG access, which is calculated as shown in
Section 2.2.
- (3)
Selectivity index
Selectivity means that in the event of a fault, the faulty element should be removed from the power system by the action of the protective device nearest to the point of fault, so that the outage is minimized. The selectivity index is measured by the protection range
. The setting value
of the traditional stage current quick-break protection is:
where
is the reliability coefficient, generally 1.2~1.3,
is the equivalent phase potential of the system power supply,
is the minimum impedance from the equivalent power supply of the system to the protection installation under the maximum mode of operation, and
is the line impedance of the protection line.
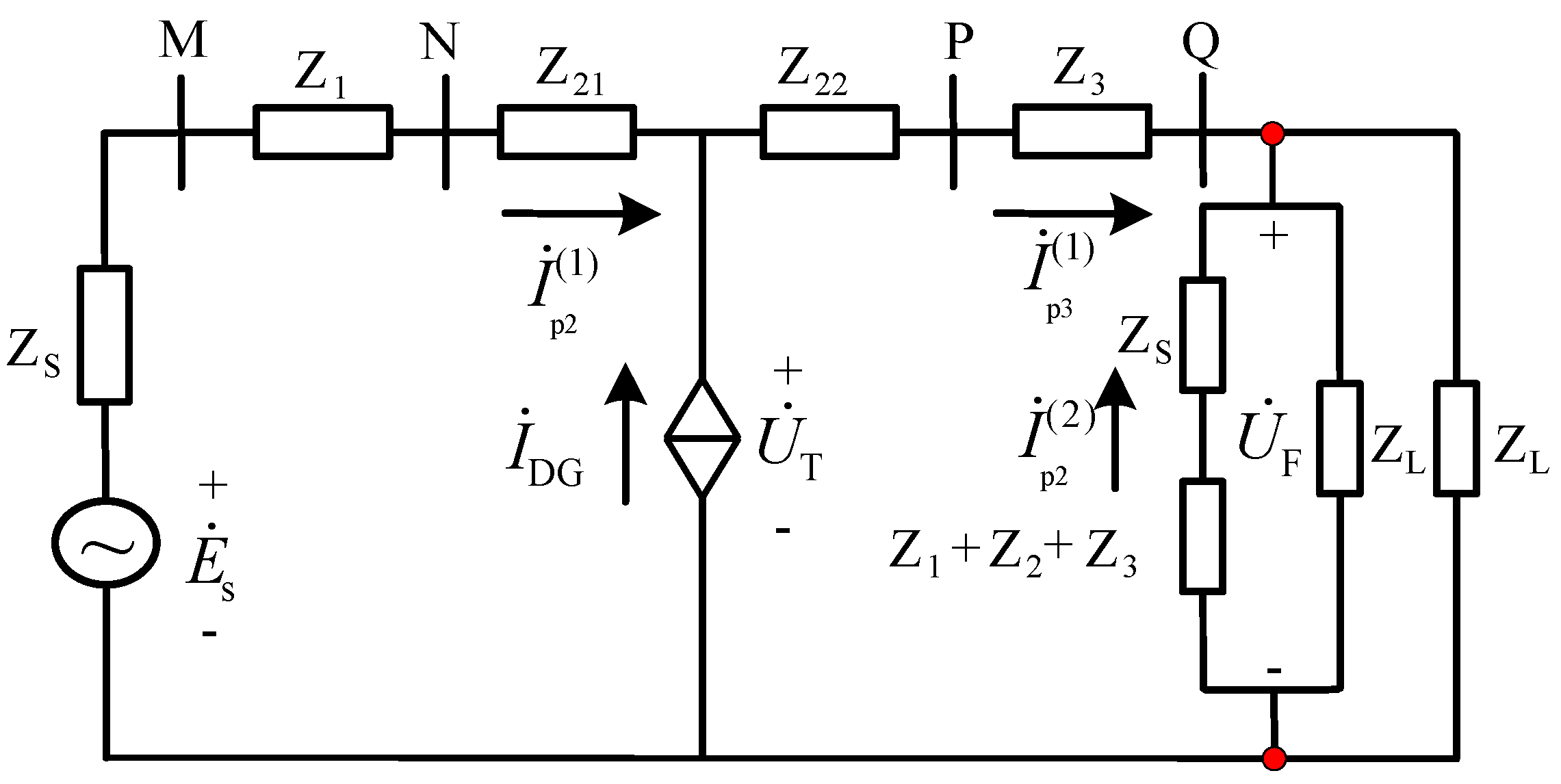
When a fault occurs at
of the line, the fault current flowing through the protection device is:
where
is the fault type coefficient, and
is the impedance from the equivalent power source of the system to the installation of the protection in any mode of operation. The value of
will be taken between
and
. According to Equations (18) and (19), the protection range of conventional current-failure protection can be obtained as:
After the DG is connected, the protection range of traditional current quick-break protection is shown in Equations (21) and (22):
In Equations (21) and (22), is the proportional coefficient of the DG access position to the total impedance of the line at this level. is the total impedance of the DG access line, and is the total impedance of the lower protection line of the DG access line. is the protection range for the case where DG access decreases the fault current magnitude, and is the protection range for the case where DG access increases the fault current magnitude.
The setting value of adaptive current quick-break protection is:
From Equations (18) and (23), the protection range of adaptive current flow disconnection protection is shown in Equation (24):
After the DG is connected, the protection range of the adaptive current flow interruption protection is shown in Equations (25) and (26):
In Equations (25) and (26), is the protection range for the case where DG access decreases the fault current magnitude, and is the protection range for the case where DG access increases the fault current magnitude.
- (4)
Reliability index
Reliability refers to the ability of the protection to operate reliably in the event of a fault within the scope of protection. The reliability of a protection system can be divided into the reliability of the equipment and the reliability of the protection function [
33]. DG access to the distribution network leads to the protection of the original fixed value under the refusal to act or false action, and the principle failure of relay protection is the main factor considered in this paper. The failure caused by the principle failure is closely related to the protection setting value and the system operation configuration program.
For three-stage overcurrent protection and adaptive overcurrent protection, a uniform distribution is used for simulation. Assuming that the length of the line is
L, the length range of the risk of relay protection refusal is
L0, and the length range of the risk of relay protection malfunction is
L1. The probability of the protection refusal/malfunction area of the line as a percentage of the total line can be expressed by Equation (27):
The reliability is defined as Equation (28):
where
is the conditional probability of protection rejection in the event of a short circuit on the protected line, and
is the probability of protection mis-operation in the event of a short circuit event on the adjacent next higher-level line.
For inverse time current protection, reliability is measured by the ratio of the difference in the action time of neighboring protections before and after DG access. The value of reliability is calculated by using the time difference when the end of the neighboring protection line fails.
3.2. Methodology for Calculating Indicator Weights
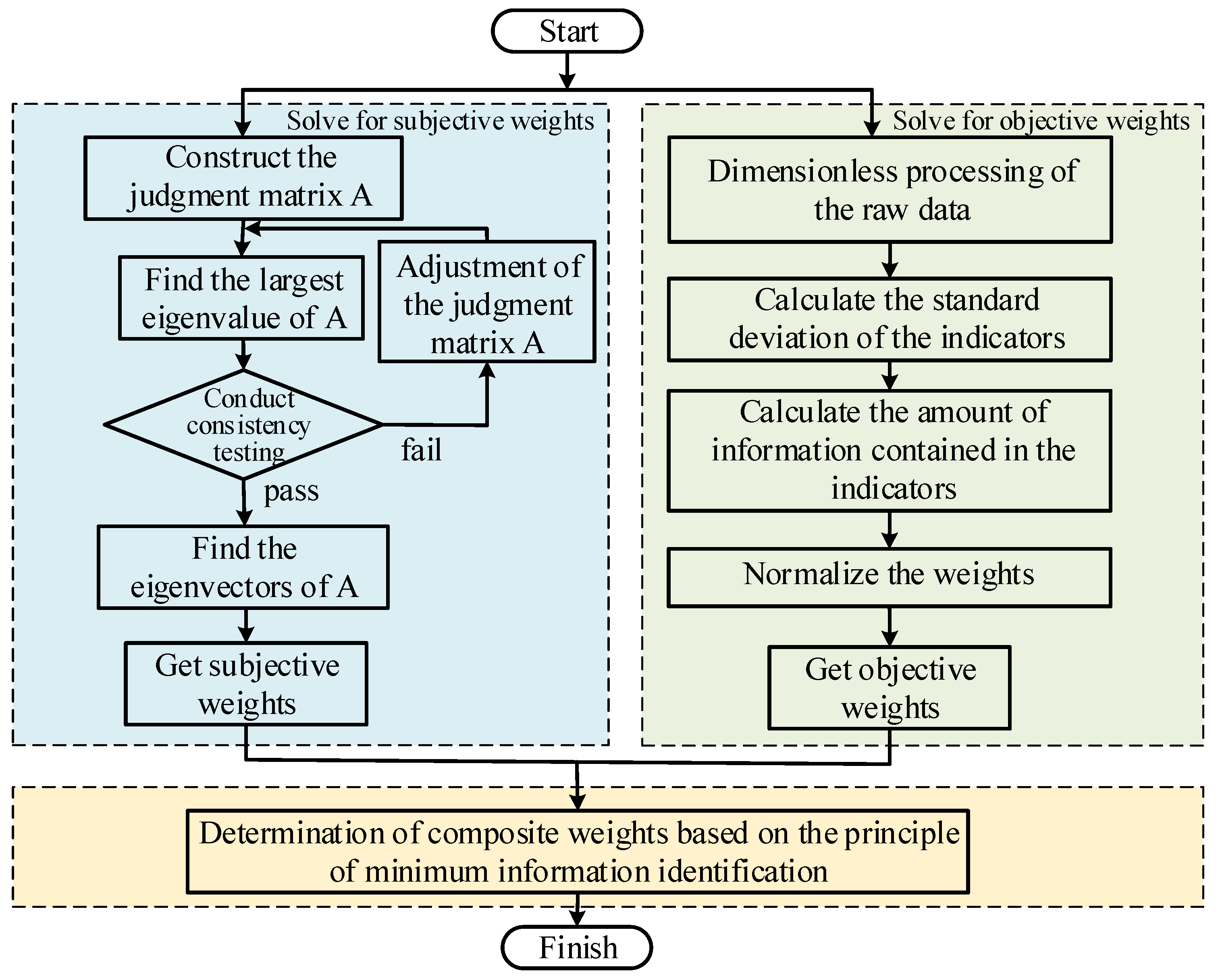
The AHP method incorporates expert experience when performing weight assignments but has some subjective limitations. The CRITIC method relies on raw data and has objective limitations. Based on the limitations of the single assignment method described in the Introduction, in order to guarantee the scientificity of the weights, this paper proposes an improved assignment method. The AHP method is used to subjectively assign weights to the indicators, while the CRITIC method is used to objectively assign weights to the indicators. The combination of subjective and objective methods is based on the principle of minimum information identification to combine the indicators to get the final weights. The calculation process is shown in
Figure 5.
3.2.1. Subjective Weighting Calculation—AHP Method
AHP is a systematic and hierarchical multi-objective decision analysis method. Based on the experience judgment of experts, it changes the judgment from directly facing multiple factors at the same time to judging only two factors. The complex problem to be solved is introduced into quantitative analysis, and mathematical methods are used to quantify the results of each expert’s empirical judgment.
The subjective weights were determined using the AHP method through the following steps:
The model usually includes the goal, criterion, and scheme layer to clarify the goal of the decision problem.
- (2)
Construct the judgment matrix
The judgment matrix indicates the relative importance of the indicators in the layer relative to the indicators in the previous layer. The values are generally given according to a nine-level scale.
- (3)
Criteria layer weight coefficients and their consistency test
The judgment matrix
A is:
where
akj is the comparison result of the
kth factor relative to the
jth factor in the judgment matrix. The largest eigenvector of the judgment matrix
A is taken for normalization, and a consistency test is performed:
where
CR is the consistency ratio of the judgment matrix,
A is the largest characteristic root of the judgment matrix, and
RI is the random consistency index. When
CR < 0.1, the judgment matrix passes the consistency check, and the obtained vector is the weight vector of the importance of the lower-level indicators relative to the upper-level indicators, that is, the weight vector of the hierarchical judgment matrix. Otherwise, it is not feasible and needs to be adjusted to construct a reasonable judgment matrix until it passes the consistency test.
3.2.2. Objective Weighting Calculation—CRITIC Method
The CRITIC method is a method capable of determining the objective weights of indicators, which combines the magnitude of variation within indicators and the conflict between indicators to determine the weights. By combining these two aspects, the CRITIC method can effectively determine the objective weights of indicators, thereby improving the accuracy of decision-making results. The calculation procedure is as follows:
- (1)
Dimensionless processing of the raw data. The raw data are processed according to Equations (32) and (33):
In Equations (32) and (33), xij is the standardized value; x′ij is the initial value of variable j; max (xj) is the maximum value of the indicator j; and min(xj) is the minimum value of the indicator j.
- (2)
Considering the vector generated by each indicator individually, the standard deviation vector σj is obtained:
- (3)
The linear correlation coefficient Rij between the two indicators is calculated as:
In Equation (35), Rij is the correlation coefficient between indicator i and indicator j; σi is the standard deviation of indicator i; σj is the standard deviation of indicator j; and n is the number of indicators.
- (4)
The amount of information is calculated, where Ci represents the amount of information contained in indicator i.
- (5)
The weights are normalized according to Equation (37):
3.2.3. Calculating the Combined Weight
Based on the principle of minimum information recognition, the subjective and objective weights obtained from the AHP and CRITIC methods are combined to minimize the distribution distance of the two weights, which is calculated as:
where
wj is the combination weight,
w1j is the subjective weight of AHP of
jth indicator,
w2j is the objective weight of the CRITIC of
jth indicator, and
j = 1, 2, …
n.