Impact of Energy-Related Properties of Cities on Optimal Urban Energy System Design
Abstract
1. Introduction
What are the main energy-related properties of cities that influence the cost-efficient composition of an urban energy system under strict carbon constraints, for different electricity import capacity levels?
2. Materials and Methods
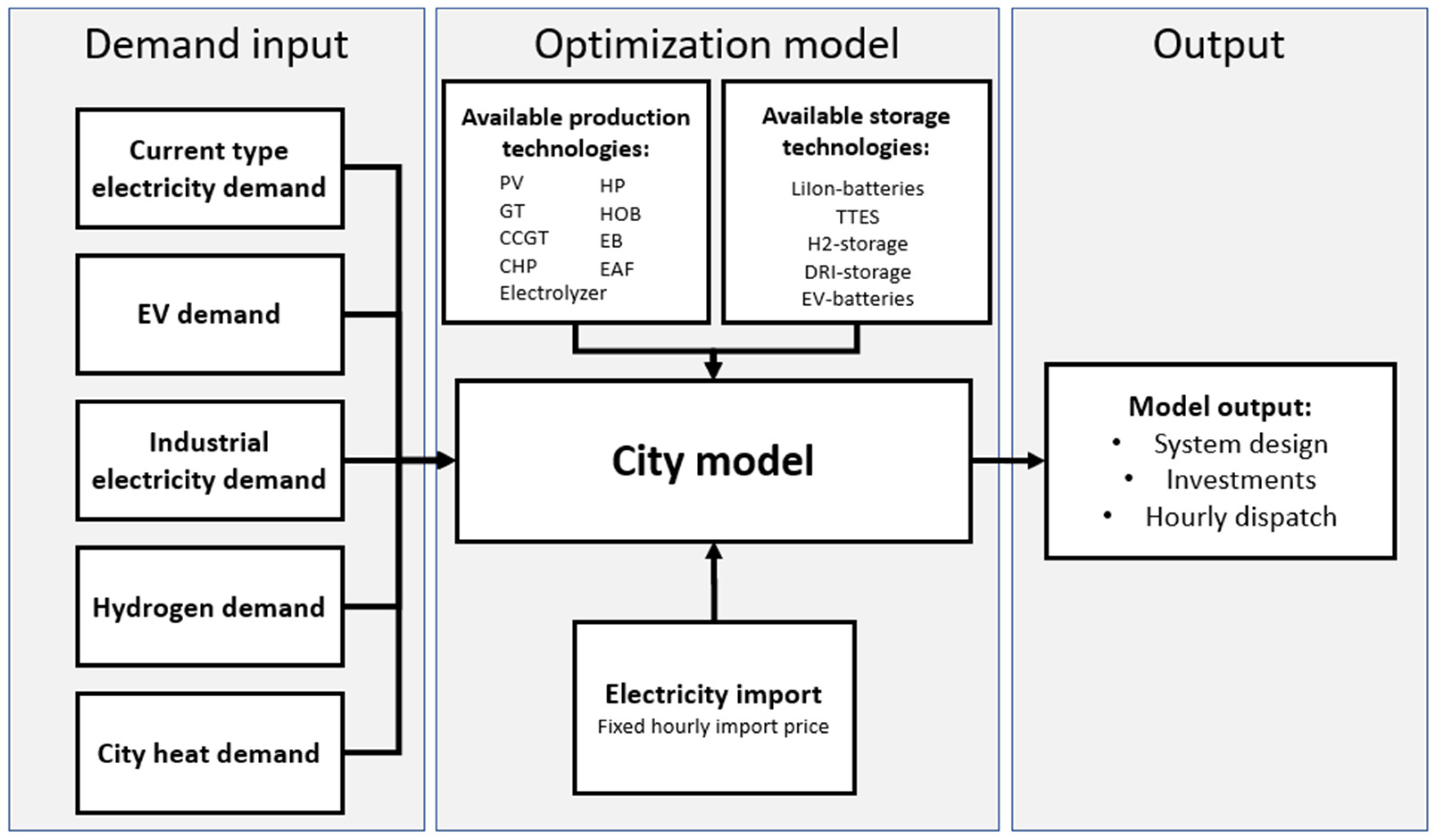
2.1. Model Description
2.2. Modeled Cities
2.3. Demand Input Data
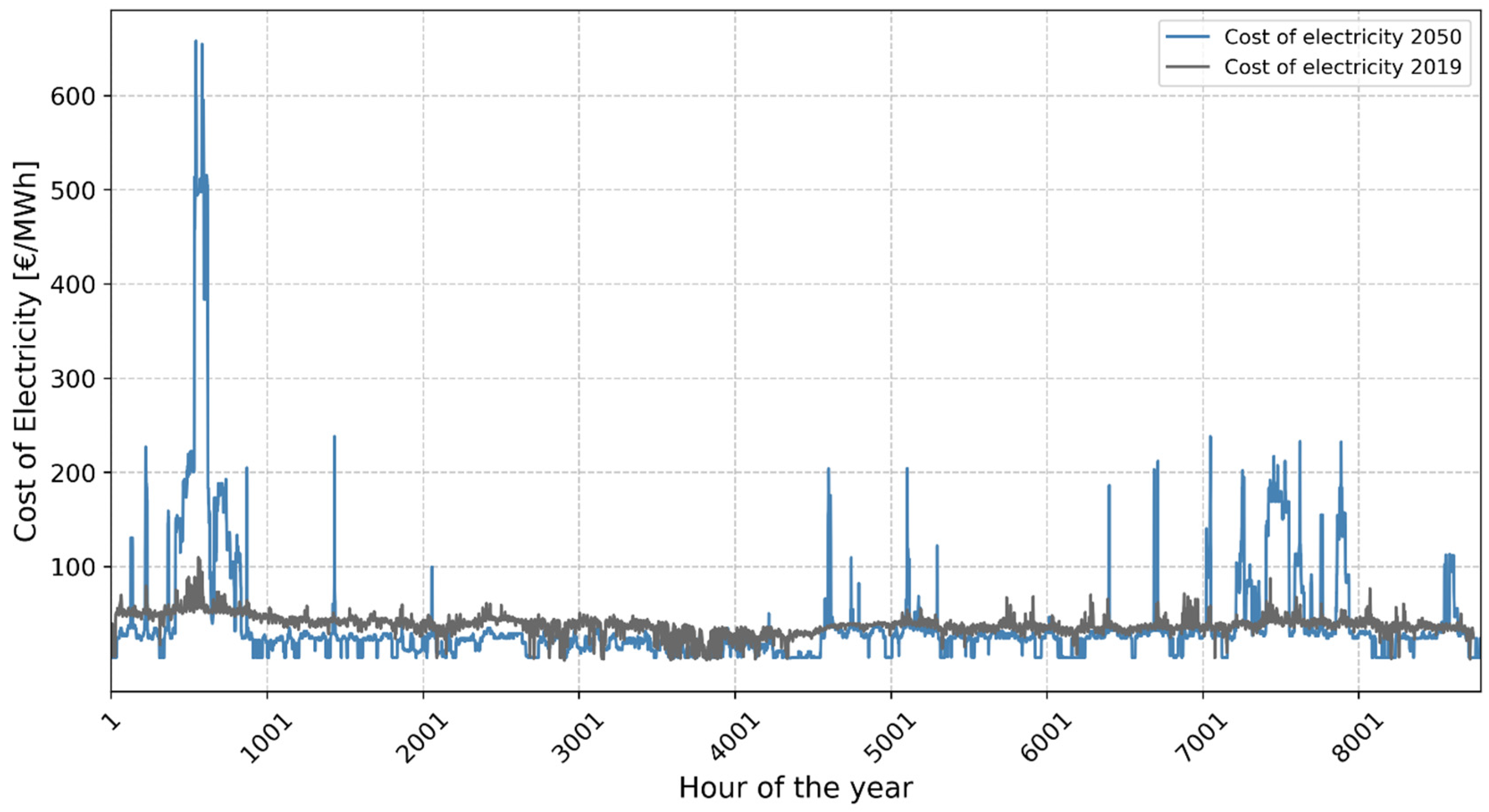
2.4. Technology Data and Electricity Import Price
2.5. Modeling Scenarios
2.6. Result Clustering
3. Results
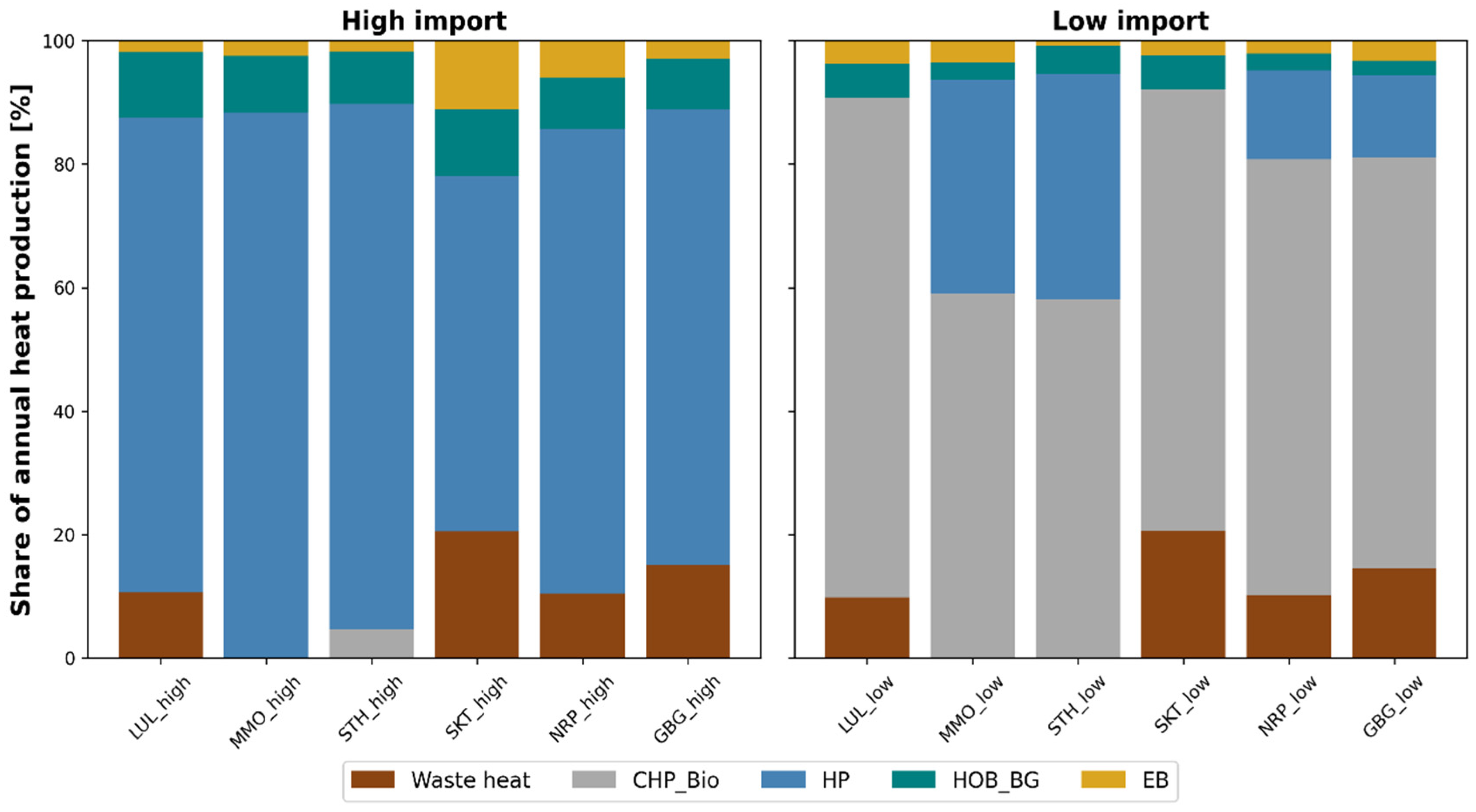
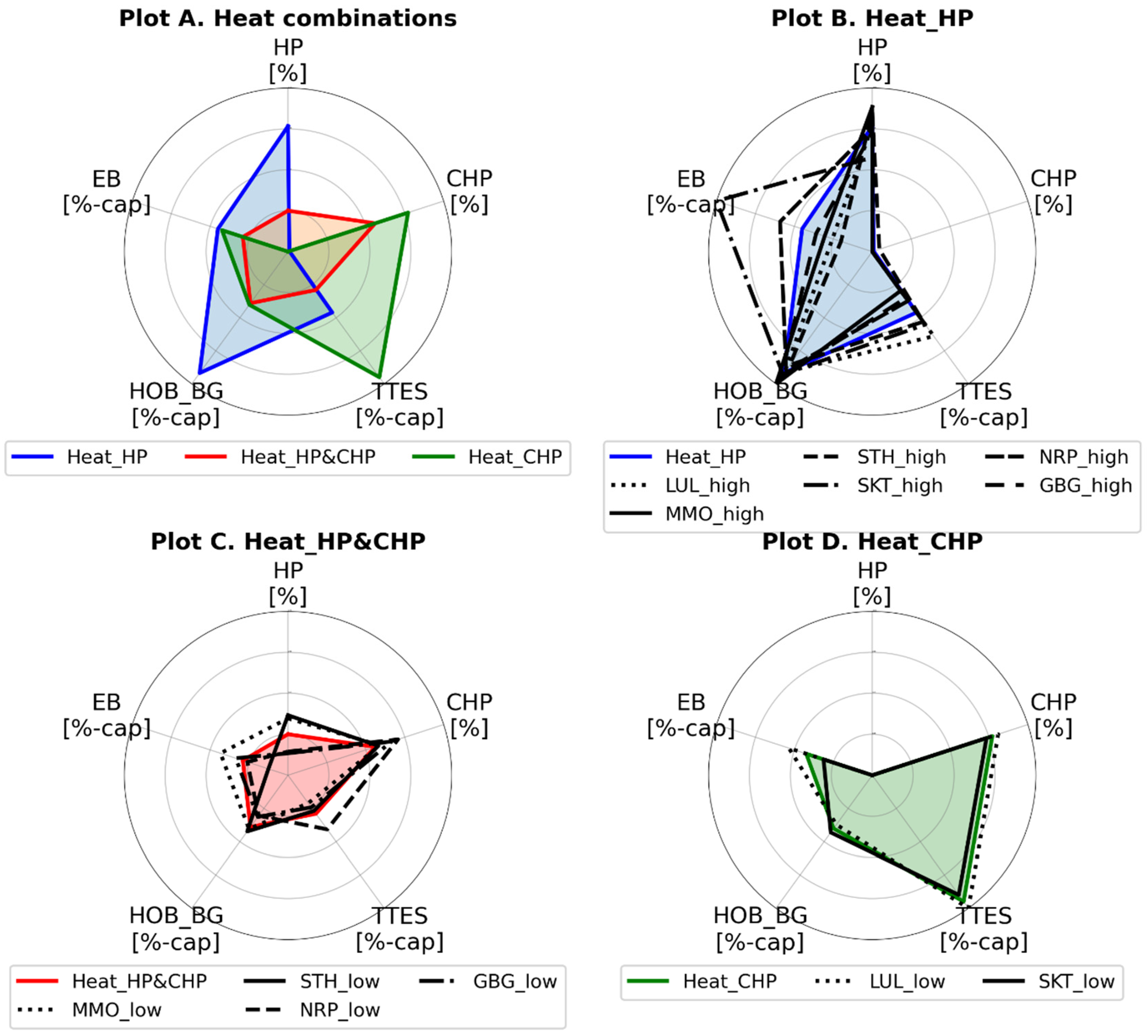
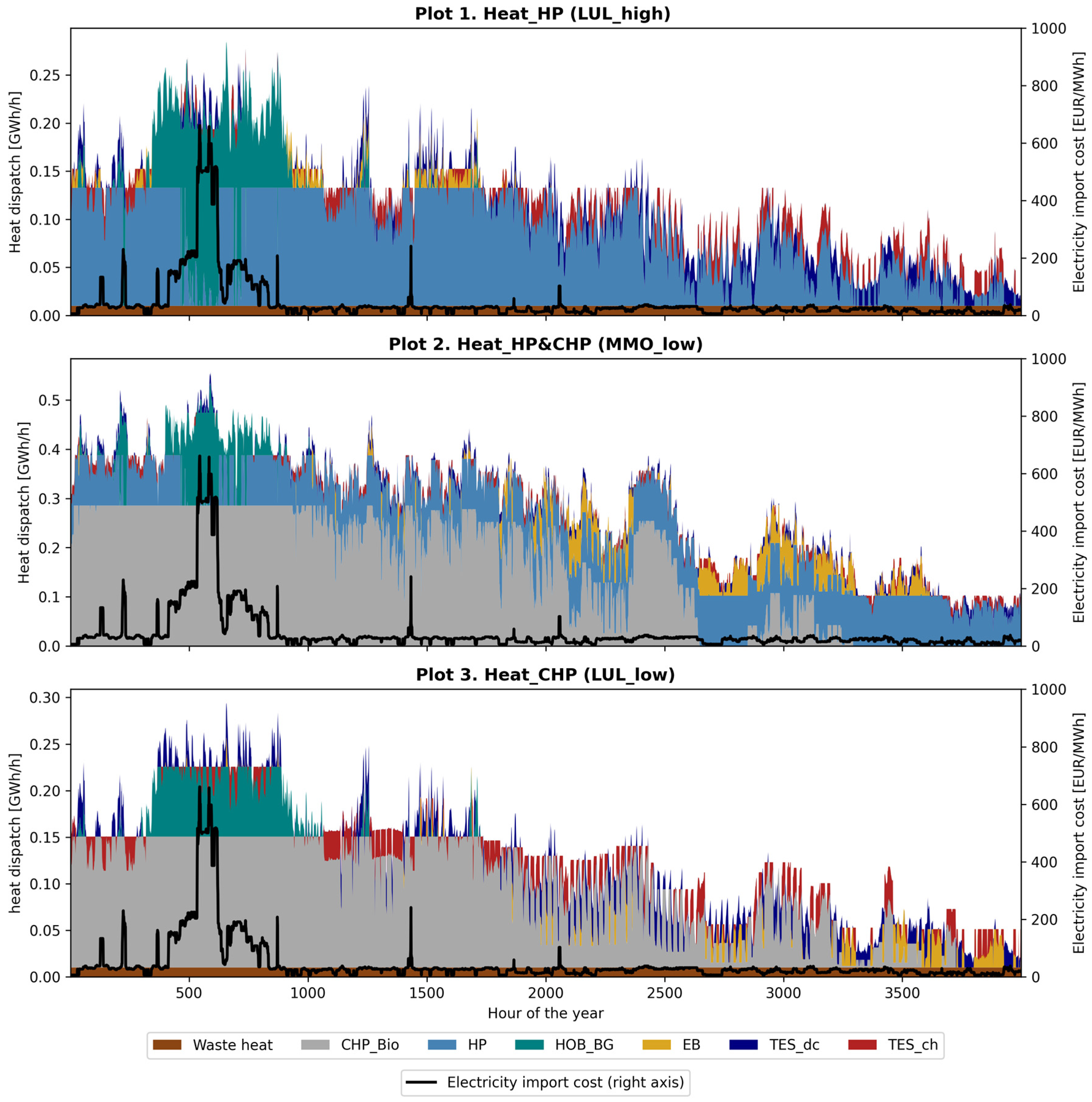
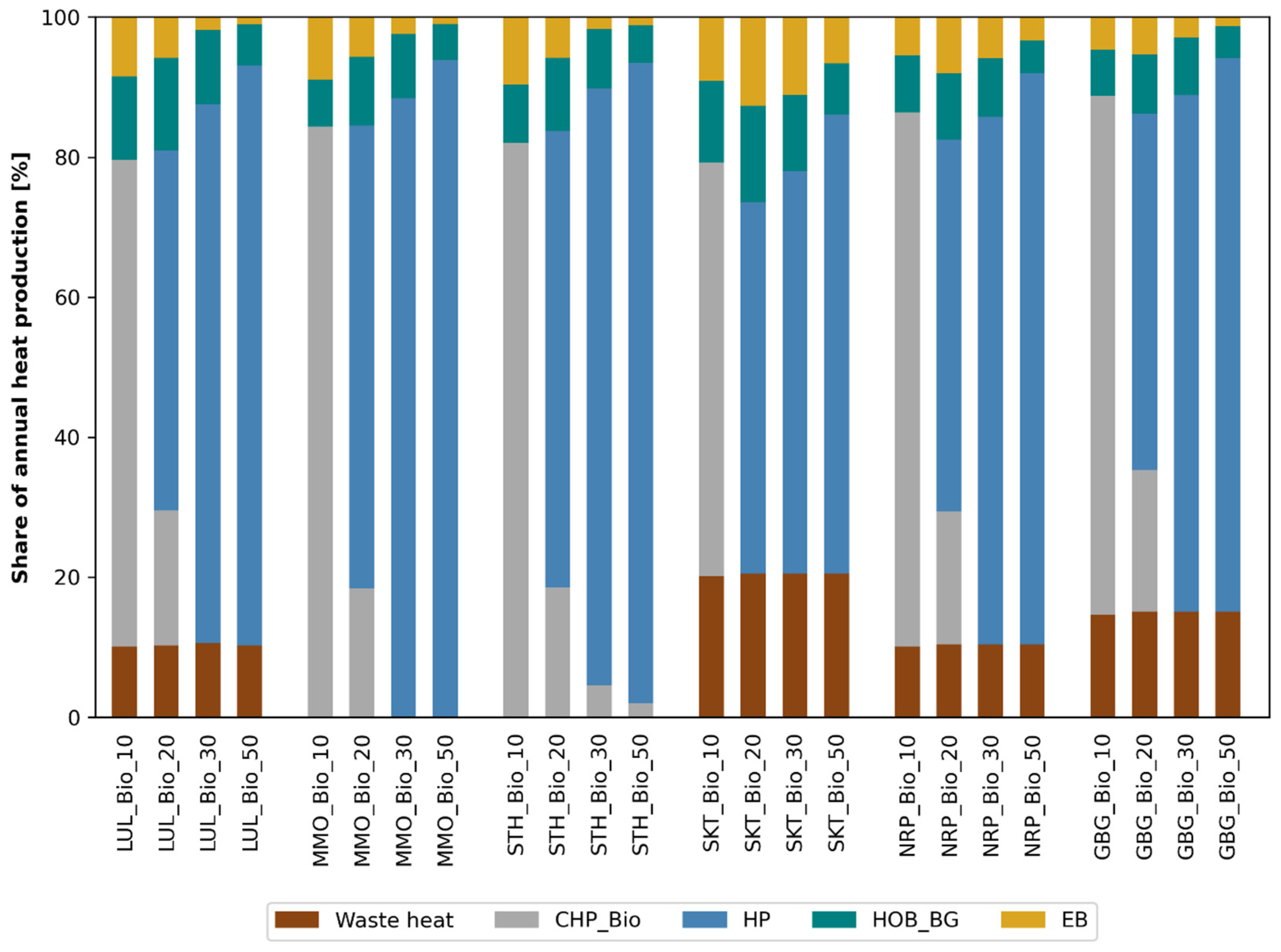
3.1. Cost-Efficient Heat-Supply Technology Combinations
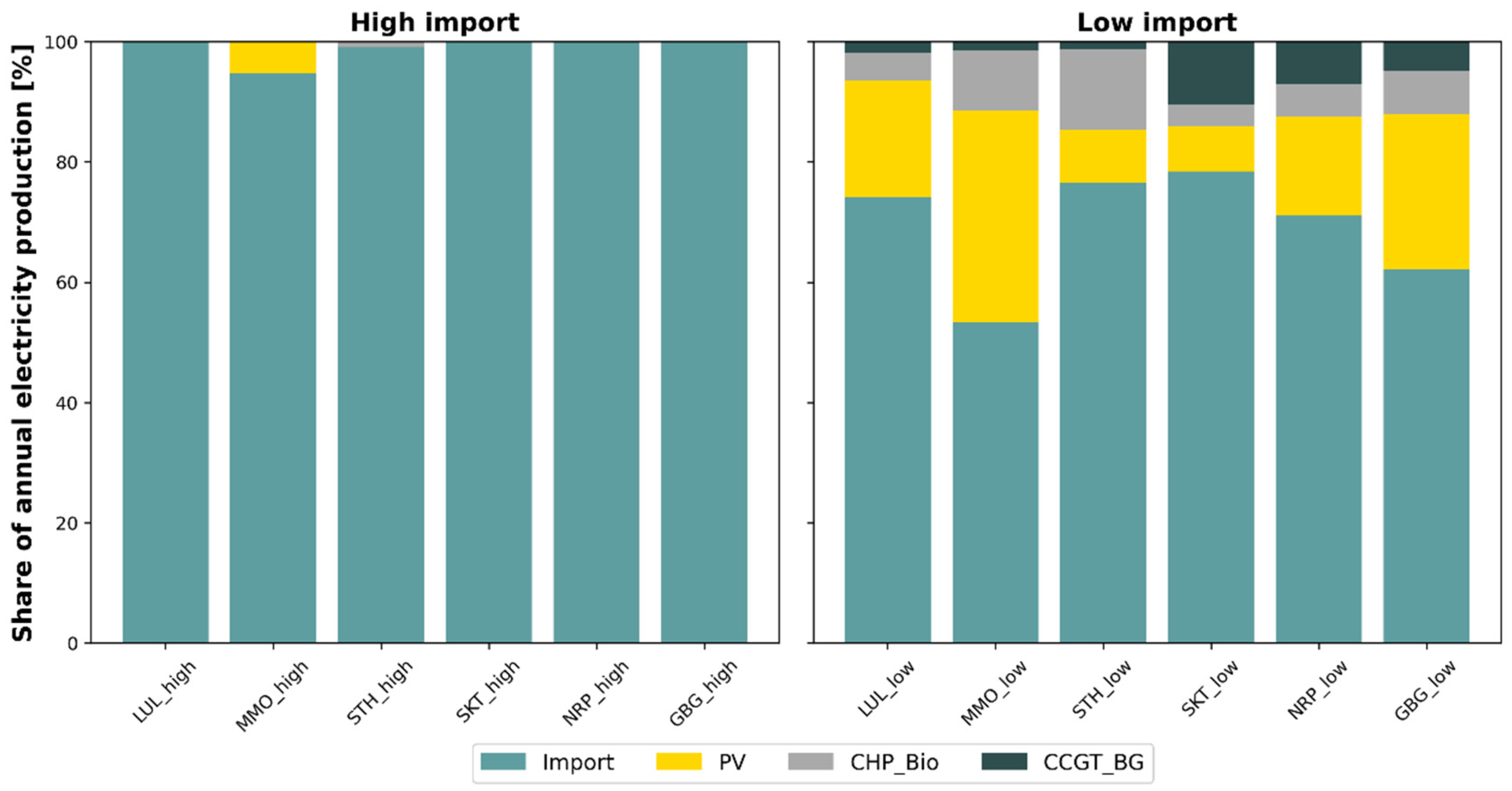
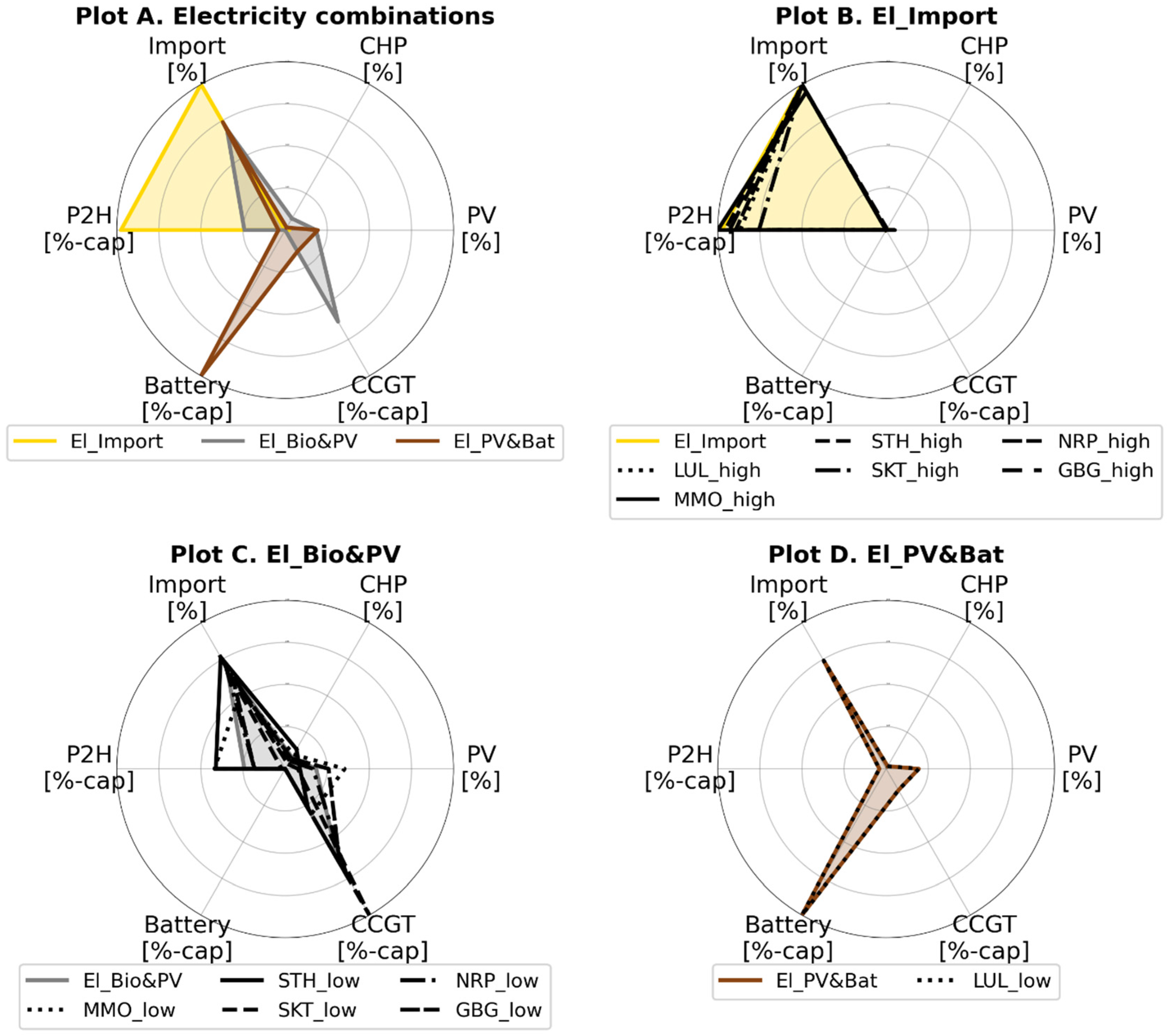
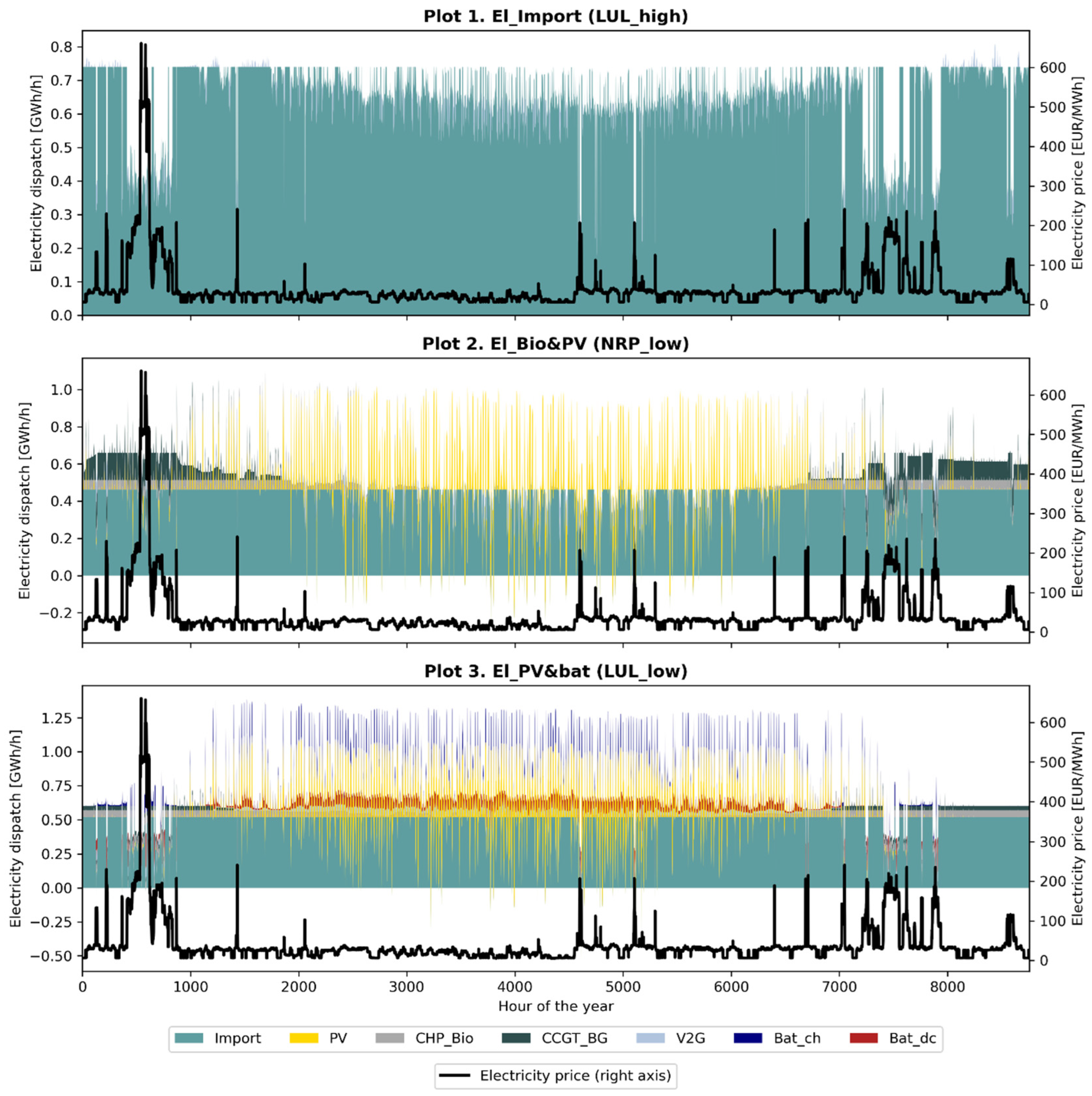
3.2. Cost-Efficient Electricity-Supply Technology Combinations
3.3. Impacts of the Energy-Related Properties of the Cities
3.4. Sensitivity Analysis of Biomass Price
4. Discussion
5. Conclusions
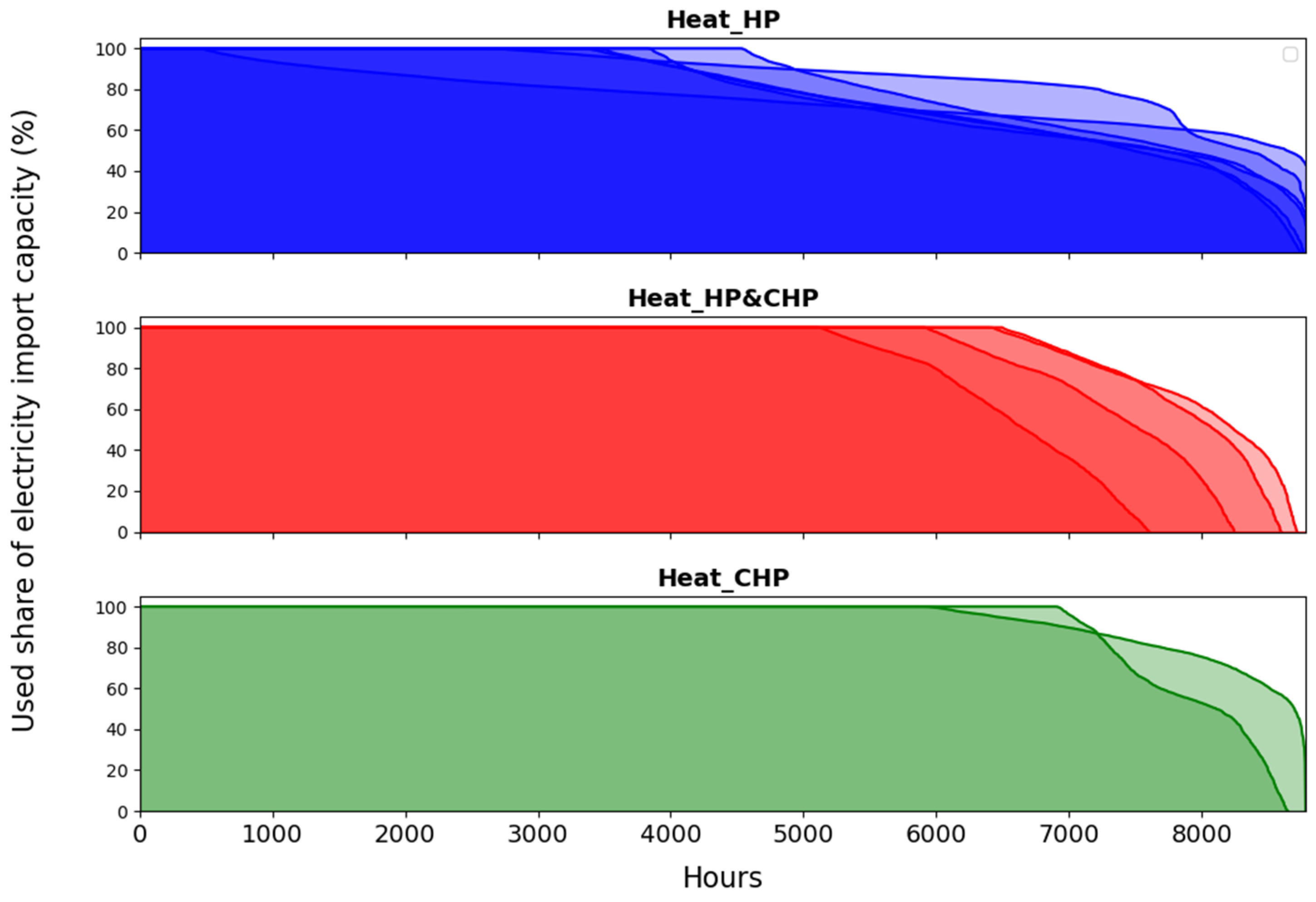
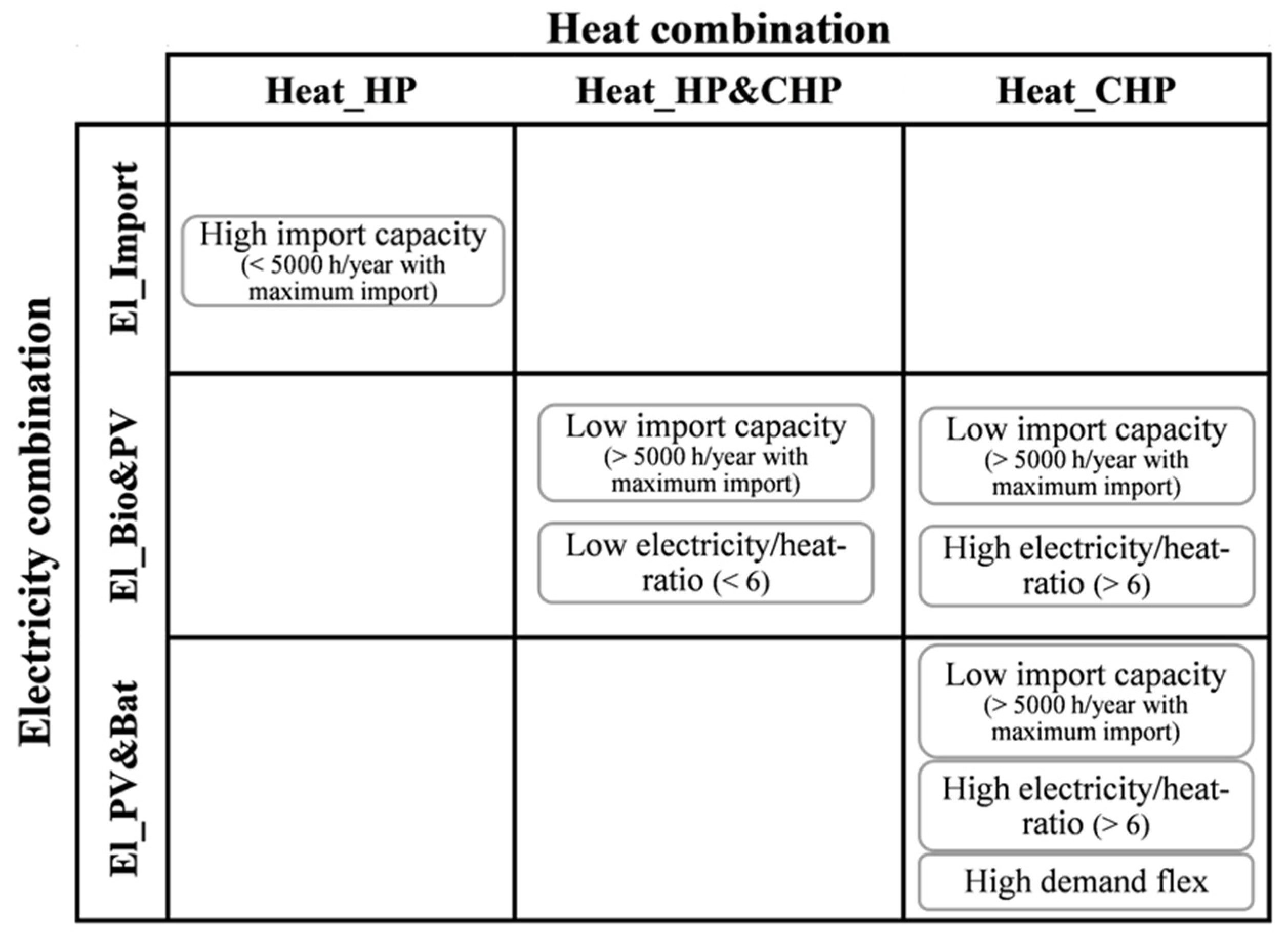
- In high electricity import capacity scenarios, the impacts of other properties in the city on the results are limited. In this scenario, electricity primarily originates from imports, which, in conjunction with the availability of urban flexibility measures, outcompete most local electricity production. Large-scale heat pumps combined with thermal energy storage and biogas boilers dominate the heating sector in all the modeled cities. Based on the assumptions outlined in this study, this assertion holds true for cities where the maximum import capacity is utilized up to 5000 h annually.
- In situations where electricity imports are more restricted, the properties of each individual city assume a more crucial role in determining the most cost-effective energy system configuration:
- o
- The electricity-to-heat ratio of a city becomes crucial in terms of determining the optimal layout of the heating sector, as cities with a large heat demand relative to their electricity demand (low electricity-to-heat ratio) tend to favor a heating system that incorporates both heat pumps and CHP. In contrast, cities with a high electricity-to-heat ratio (exceeding 6 in Table 2) tend to incorporate a heating system that is based primarily on CHP in conjunction with high levels of thermal energy storage.
- o
- High electricity demand flexibility within a city, in which loads are shiftable over seasons, enables the synergistic use of solar PV and stationary batteries as a cost-efficient alternative.
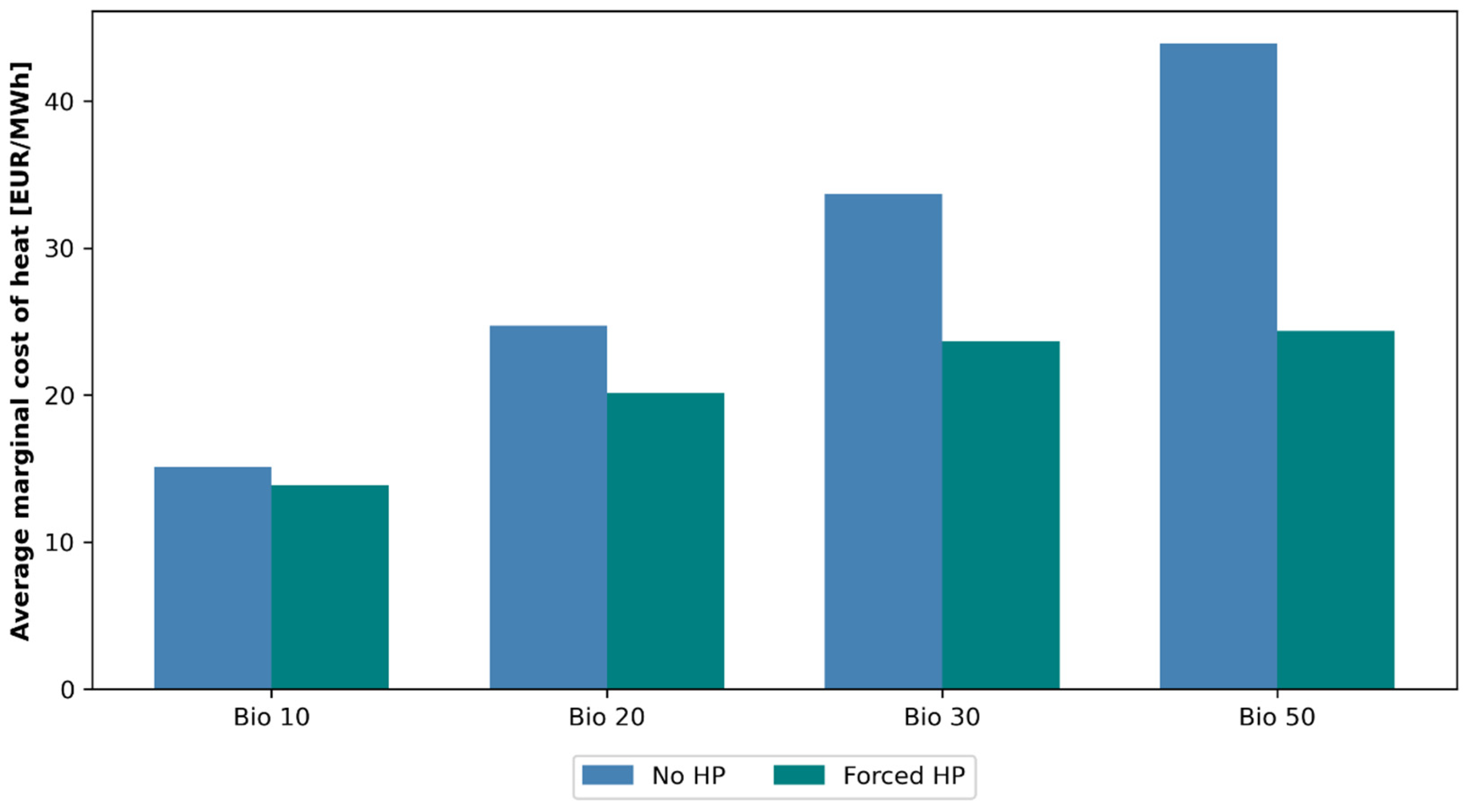
- Heating systems primarily reliant on power-to-heat emerge as the best option when biomass prices exceed 20 EUR/MWh for future electricity import costs assumed in this work. If biomass prices increase, a heating system that lacks the capacity to utilize power-to-heat through large-scale heat pumps and thermal energy storage runs the risk of encountering a substantial increase in marginal heat cost.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- International Energy Agency. Empowering Cities for a Net Zero Future; Organisation for Economic Co-Operation and Development (OECD): Paris, France, 2021. [CrossRef]
- REN21. Renewables 2019—Global Status Report 2019; REN21 Secretariat: Paris, France, 2019; Available online: https://www.ren21.net/wp-content/uploads/2019/05/gsr_2019_full_report_en.pdf (accessed on 2 November 2023).
- Puthalpet, J.R. Mitigation of Climate Change. Daunting Clim. Chang. 2022, 1454, 219–276. [Google Scholar] [CrossRef]
- International Energy Agency. World Energy Outlook; OECD/IEA: Paris, France, 2022; p. 524. Available online: https://www.iea.org/reports/world-energy-outlook-2022 (accessed on 10 September 2023).
- Perea-Moreno, M.-A.; Hernandez-Escobedo, Q.; Perea-Moreno, A.-J. Renewable Energy in Urban Areas: Worldwide Research Trends. Energies 2018, 11, 577. [Google Scholar] [CrossRef]
- Birk, S.; Brosig, C.; Waffenschmidt, E.; Schneiders, T. Influence of Sector Coupling in Future Inner City Low Voltage Grids. In Proceedings of the 2018 7th International Energy and Sustainability Conference (IESC), Cologne, Germany, 17–18 May 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Robinius, M.; Otto, A.; Heuser, P.; Welder, L.; Syranidis, K.; Ryberg, D.S.; Grube, T.; Markewitz, P.; Peters, R.; Stolten, D. Linking the Power and Transport Sectors—Part 1: The Principle of Sector Coupling. Energies 2017, 10, 956. [Google Scholar] [CrossRef]
- Heinisch, V.; Göransson, L.; Odenberger, M.; Johnsson, F. Interconnection of the electricity and heating sectors to support the energy transition in cities. Int. J. Sustain. Energy Plan. Manag. 2019, 24, 57–66. [Google Scholar] [CrossRef]
- He, G.; Mallapragada, D.S.; Bose, A.; Heuberger-Austin, C.F.; Gençer, E. Sector coupling via hydrogen to lower the cost of energy system decarbonization. Energy Environ. Sci. 2021, 14, 4635–4646. [Google Scholar] [CrossRef]
- Khalil, M.; Dincer, I. Development and assessment of integrated hydrogen and renewable energy systems for a sustainable city. Sustain. Cities Soc. 2023, 98, 104794. [Google Scholar] [CrossRef]
- Azizi, E.; Ahmadiahangar, R.; Rosin, A.; Bolouki, S. Characterizing energy flexibility of buildings with electric vehicles and shiftable appliances on single building level and aggregated level. Sustain. Cities Soc. 2022, 84, 103999. [Google Scholar] [CrossRef]
- Li, D.J.; Li, D.Y.; Huang, D.J. Optimal Scheduling of Household Appliances in Urban Smart Home: Community Approaches to Socio-Economic Aspects of Urban Energy Transition. Sustain. Cities Soc. 2023, 101, 105156. [Google Scholar] [CrossRef]
- Bartolini, A.; Comodi, G.; Salvi, D.; Østergaard, P.A. Renewables self-consumption potential in districts with high penetration of electric vehicles. Energy 2020, 213, 118653. [Google Scholar] [CrossRef]
- Wang, Q.; Hou, Z.; Guo, Y.; Huang, L.; Fang, Y.; Sun, W.; Ge, Y. Enhancing Energy Transition through Sector Coupling: A Review of Technologies and Models. Energies 2023, 16, 5226. [Google Scholar] [CrossRef]
- Ramsebner, J.; Haas, R.; Ajanovic, A.; Wietschel, M. The sector coupling concept: A critical review. WIREs Energy Environ. 2021, 10, e396. [Google Scholar] [CrossRef]
- Arabzadeh, V.; Mikkola, J.; Jasiūnas, J.; Lund, P.D. Deep decarbonization of urban energy systems through renewable energy and sector-coupling flexibility strategies. J. Environ. Manag. 2020, 260, 110090. [Google Scholar] [CrossRef]
- de Chalendar, J.A.; Glynn, P.W.; Benson, S.M. City-scale decarbonization experiments with integrated energy systems. Energy Environ. Sci. 2019, 12, 1695–1707. [Google Scholar] [CrossRef]
- Pensini, A.; Rasmussen, C.N.; Kempton, W. Economic analysis of using excess renewable electricity to displace heating fuels. Appl. Energy 2014, 131, 530–543. [Google Scholar] [CrossRef]
- Eguiarte, O.; Garrido-Marijuán, A.; de Agustín-Camacho, P.; del Portillo, L.; Romero-Amorrortu, A. Energy, environmental and economic analysis of air-to-air heat pumps as an alternative to heating electrification in Europe. Energies 2020, 13, 3939. [Google Scholar] [CrossRef]
- Bloess, A.; Schill, W.-P.; Zerrahn, A. Power-to-heat for renewable energy integration: A review of technologies, modeling approaches, and flexibility potentials. Appl. Energy 2018, 212, 1611–1626. [Google Scholar] [CrossRef]
- Heinisch, V.; Göransson, L.; Erlandsson, R.; Hodel, H.; Johnsson, F.; Odenberger, M. Smart electric vehicle charging strategies for sectoral coupling in a city energy system. Appl. Energy 2021, 288, 116640. [Google Scholar] [CrossRef]
- Huang, P.; Munkhammar, J.; Fachrizal, R.; Lovati, M.; Zhang, X.; Sun, Y. Comparative studies of EV fleet smart charging approaches for demand response in solar-powered building communities. Sustain. Cities Soc. 2022, 85, 104094. [Google Scholar] [CrossRef]
- Pastore, L.M. Combining Power-to-Heat and Power-to-Vehicle strategies to provide system flexibility in smart urban energy districts. Sustain. Cities Soc. 2023, 94, 104548. [Google Scholar] [CrossRef]
- Pilpola, S.; Arabzadeh, V.; Mikkola, J.; Lund, P.D. Analyzing National and Local Pathways to Carbon-Neutrality from Technology, Emissions, and Resilience Perspectives—Case of Finland. Energies 2019, 12, 949. [Google Scholar] [CrossRef]
- Thellufsen, J.Z.; Lund, H. Roles of local and national energy systems in the integration of renewable energy. Appl. Energy 2016, 183, 419–429. [Google Scholar] [CrossRef]
- Heinisch, V.; Göransson, L.; Odenberger, M.; Johnsson, F. The impact of limited electricity connection capacity on energy transitions in cities. Smart Energy 2021, 3, 100041. [Google Scholar] [CrossRef]
- Sneum, D.M.; González, M.G.; Gea-Bermúdez, J. Increased heat-electricity sector coupling by constraining biomass use? Energy 2021, 222, 119986. [Google Scholar] [CrossRef]
- Lund, P. Large-scale urban renewable electricity schemes—Integration and interfacing aspects. Energy Convers. Manag. 2012, 63, 162–172. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, S.; Jiang, K.; Kaghembega, W.S.-H. The gaps and pathways to carbon neutrality for different type cities in China. Energy 2021, 244, 122596. [Google Scholar] [CrossRef]
- IRENA. Sector Coupling in Facilitating Integration of Variable Renewable Energy in Cities. 2021. Available online: https://www.irena.org/publications/2021/Oct/Sector-Coupling-in-Cities (accessed on 7 November 2023).
- Arowolo, W.; Perez, Y. Rapid decarbonisation of Paris, Lyon and Marseille’s power, transport and building sectors by coupling rooftop solar PV and electric vehicles. Energy Sustain. Dev. 2023, 74, 196–214. [Google Scholar] [CrossRef]
- Göransson, L.; Goop, J.; Odenberger, M.; Johnsson, F. Impact of thermal plant cycling on the cost-optimal composition of a regional electricity generation system. Appl. Energy 2017, 197, 230–240. [Google Scholar] [CrossRef]
- Taljegard, M.; Göransson, L.; Odenberger, M.; Johnsson, F. To represent electric vehicles in electricity systems modelling—Aggregated vehicle representation vs. individual driving profiles. Energies 2021, 14, 539. [Google Scholar] [CrossRef]
- Sahlén, K.; Antonsson, E.; Bergerlind, J. Kartläggning av Hur Planerade Nätinvesteringar Avhjälper Kapacitetsbrist i Elnätet. 2020, p. 30. Available online: https://ei.se/om-oss/projekt/avslutade/kapacitetsutmaningen-i-elnatet#query/ (accessed on 10 August 2023).
- Svenska Kraftnät. Långsiktig Marknadsanalys Scenarier för Kraftsystemets Utveckling Fram till 2050. 2024. Available online: www.svk.se (accessed on 10 May 2024).
- Danish Energy Agency. Technology Data for Generation of Electricity and District Heating. 2022. Available online: https://ens.dk/en/our-services/projections-and-models/technology-data/technology-data-generation-electricity-and (accessed on 1 February 2023).
- Öberg, S.; Odenberger, M.; Johnsson, F. The cost dynamics of hydrogen supply in future energy systems—A techno-economic study. Appl. Energy 2022, 328, 120233. [Google Scholar] [CrossRef]
- Arabzadeh, V.; Pilpola, S.; Lund, P.D. Coupling variable renewable electricity production to the heating sector through curtailment and power-to-heat strategies for accelerated emission reduction. Futur. Cities Environ. 2019, 5, 1–10. [Google Scholar] [CrossRef]
- Jambagi, A.; Kramer, M.; Cheng, V. Electricity and heat sector coupling for domestic energy systems: Benefits of integrated energy system modelling. In Proceedings of the 2015 International Conference on Smart Cities and Green ICT Systems (SMARTGREENS), Lisbon, Portugal, 20–22 May 2015; pp. 66–71. [Google Scholar] [CrossRef]
- Gudmundsson, O.; Thorsen, J.E.; Brand, M. The role of district heating in coupling of the future renewable energy sectors. Energy Procedia 2018, 149, 445–454. [Google Scholar] [CrossRef]
- Staffell, I.; Pfenninger, S. Using bias-corrected reanalysis to simulate current and future wind power output. Energy 2016, 114, 1224–1239. [Google Scholar] [CrossRef]
- Pfenninger, S.; Staffell, I. Long-term patterns of European PV output using 30 years of validated hourly reanalysis and satellite data. Energy 2016, 114, 1251–1265. [Google Scholar] [CrossRef]

| Type of Constraint | Description of Constraint |
|---|---|
| Electricity import capacity |
Electricity import and export is limited by maximum capacity
|
| Electricity production |
Electricity production is always lower than the installed capacity per technology type.
|
| Heat production |
Heat production is always lower than the installed capacity per technology type.
|
| Storage level batteries |
Storage level in stationary batteries in the next timestep is equal to the level in previous timestep plus charging minus discharging.
|
| Maximum storage batteries | Storage level in stationary batteries is always lower than the installed storage capacity.
|
| Charging/discharging batteries |
The charging and discharging of stationary batteries are limited by the installed charging capacity.
|
| Storage level TES |
Storage level in TES in the next timestep is equal to the level in previous timestep plus charging minus discharging of heat.
|
| Maximum storage TES | Storage level in TES is always lower than the installed storage capacity.
|
| Charging/discharging TES |
The charging and discharging of TES are limited by a factor times the installed storage capacity.
|
| Storage level H2 |
Storage level in H2-storage in the next timestep is equal to the level in previous timestep plus charging minus discharging of H2.
|
| Maximum storage H2 |
Storage level in H2-storage is always lower than the installed storage capacity.
|
| Charging/discharging H2 |
The charging and discharging of H2 is limited by a factor times the installed storage capacity.
|
| Storage level direct reduced iron (DRI) |
Storage level in DRI-storage in the next timestep is equal to the level in the previous timestep plus charging minus discharging of DRI.
|
| Maximum storage DRI |
Storage level in DRI-storage is always lower than the installed storage capacity.
|
| Hourly DRI demand | The hourly DRI-demand is limited by the installed electric arc furnace capacity.
|
| Annual DRI demand |
The sum of DRI demand over the year must equal the supplied amount of DRI.
|
| Maximum PV capacity |
Installed capacity of PV is less than the maximum capacity based on city size.
|
| Thermal cycling | Cycling of thermal plants is limited by introducing a start-up cost when increasing production output and limited by start-up times, depending on type of technology. See [32] for details. |
| EV charging pattern | Limitations on charging patterns for electric vehicles. See [33] for details. |
| Symbol | Description of Symbol |
|---|---|
| is the charging of stationary batteries at time t. | |
| is the discharge of electricity from stationary batteries at time t. | |
| is the import cost of electricity to the city at time t. | |
| is the annualized investment cost per technology i. | |
| is the fixed operation and maintenance cost per technology i. | |
| is the additional cost of running technology i at part load at time t. | |
| is the running cost of technology i, including variable operation and maintenance cost and fuel cost. | |
| is the additional cost associated with starting technology i at timestep t. | |
| is the total annual system cost to be minimized. | |
| is the added constant industrial electricity demand. | |
| is the demand of DRI at time t. | |
| is the electricity demand in the city at time t. | |
| is the demand for hydrogen (constant). | |
| is the heat demand at time t. | |
| is the production level of DRI (constant). | |
| is the electricity demand in the EAFs at time t. | |
| is the electricity used to charge electric vehicles at time t. | |
| is the discharge of electricity from electric vehicles at time t. | |
| is the electricity demand of the electrolyzers to produce hydrogen at time t. | |
| is the production level of hydrogen in electrolyzers at time t. | |
| is the heat charged in TES at time t. | |
| is the heat discharged from TES at time t. | |
| I | is the set of all technologies allowed in the city energy system. |
| is a subset of all technologies producing electricity. | |
| is a subset of all technologies producing heat. | |
| is a subset of all technologies producing heat from electricity. | |
| is a subset of all technologies storing thermal energy. | |
| is the electricity storage level in stationary batteries at time t. | |
| is the level of DRI in the DRI storage at time t. | |
| is the level of hydrogen in the hydrogen storage at time t. | |
| is the storage level in the thermal energy storage at time t. | |
| is the electricity import capacity. | |
| is the capacity limit for solar PV in a city. | |
| is a factor limiting the charging and discharging rate from H2 storage. | |
| is a factor limiting the charging and discharging rate from TES storage. | |
| is the electricity produced from technology i at timestep t. | |
| is the heat produced from technology i at timestep t. | |
| is the installed capacity of technology i. | |
| T | is the set of all timesteps. |
| is the level of import to the city at time t. | |
| is the available industrial waste heat at time t. | |
| is the efficiency of power-to-heat technologies. This correlates to COP for HP and thermal efficiency of EB. |
| City ID | Electrification Drivers | Electricity Demand Flexibility | Electricity-to-Heat Ratio | Waste Heat Availability |
|---|---|---|---|---|
| LUL | EAF, Data centers | Very high | 6.4 | Medium |
| MMO | EV, Current industry | Low | 2.0 | No |
| STH | Data centers, EV | Low | 1.4 | No |
| SKT | Data centers, Battery factory | Very low | 7.9 | High |
| NRP | Hydrogen, Current industry | High | 5.4 | No |
| GBG | Hydrogen, Battery factory | High | 3.4 | Medium |
| Technology | Technical Lifetime (Years) | Investment Cost (EUR/kW) |
|---|---|---|
| Production technologies | ||
| Solar PV (PV) | 40 | 525 |
| Gas turbine biogas (GT_BG) | 25 | 520 |
| Combined-cycle gas turbine biogas (CCGT_BG) | 25 | 800 |
| Electric boiler (EB) | 20 | 60 |
| Heat pump (HP) | 25 | 830 |
| Heat only-boiler biomass (HOB_bio) | 20 | 400 |
| Heat only-boiler biogas (HOB_BG) | 25 | 50 |
| Combined heat and power biomass (CHP_Bio) | 25 | 3200 |
| Electric arc furnace (EAF) | 40 | 1294 |
| Electrolyzer | 25 | 500 |
| Storage technologies | ||
| Lithium ion battery storage (LiIon-bat) | 25 | 75 |
| Lithium ion battery discharge capacity (LiIon-cap) | 25 | 60 |
| Tank thermal energy storage (TTES) | 25 | 8 |
| Direct reduced iron storage (DRI-storage) | 40 | 0.1 |
| Hydrogen storage (H2-storage) | 30 | 11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bertilsson, J.; Göransson, L.; Johnsson, F. Impact of Energy-Related Properties of Cities on Optimal Urban Energy System Design. Energies 2024, 17, 3813. https://doi.org/10.3390/en17153813
Bertilsson J, Göransson L, Johnsson F. Impact of Energy-Related Properties of Cities on Optimal Urban Energy System Design. Energies. 2024; 17(15):3813. https://doi.org/10.3390/en17153813
Chicago/Turabian StyleBertilsson, Joel, Lisa Göransson, and Filip Johnsson. 2024. "Impact of Energy-Related Properties of Cities on Optimal Urban Energy System Design" Energies 17, no. 15: 3813. https://doi.org/10.3390/en17153813
APA StyleBertilsson, J., Göransson, L., & Johnsson, F. (2024). Impact of Energy-Related Properties of Cities on Optimal Urban Energy System Design. Energies, 17(15), 3813. https://doi.org/10.3390/en17153813






