Abstract
Air plate solar collectors provide a sustainable and efficient solution for building heating. The absorber plate collects solar radiation and converts it into heat. Atmospheric air is then circulated through the collector plate with perforated baffles by forced convection. The heated air is then directed through ducts into the building’s heating system. By significantly reducing reliance on fossil fuels for building heating, these collectors contribute to a lower life-cycle carbon footprint for buildings compared to conventional heating systems. While flat-plate solar collectors are widely used for renewable energy generation, their efficiency is frequently limited by the airflow path and the heat transfer efficiency within the collector. This study aims to quantify the impact of longitudinal, transverse, and perforated baffles with different hole diameters on the heat transfer characteristics and to identify the optimal design for maximizing thermal efficiency. This study also aims to integrate solar air collector in a conventional building and help reduce the overall energy demand of buildings and their associated carbon emissions. A three-dimensional numerical investigation was carried out on a flat-plate solar collector equipped with perforated transverse baffles with varying hole diameter and thickness. The results from the study predicted that perforated baffles with two holes with a diameter of 15 mm provided a maximum Nu of 79.56 and a pressure drop of 459 Pa for a Re of 8500.
1. Introduction
Carbon emission is one of the main factors that influence climate change. The world is currently moving toward net-zero carbon emission by 2050 or at least a reduction in carbon emission to 45% by 2030. Keeping the world agenda in mind, the current research focuses on harnessing renewable energy resources, namely, solar energy as a source of room heating and ventilation in a conventional building. Air solar collectors, which use air for heating applications, are a promising renewable energy source. However, improving their efficiency is crucial to maximize their potential. This article investigates the performance of air solar collectors, a type of solar collector utilizing air as the heat transfer fluid. Typically used for space heating and hot water production, air solar collectors are the focus of this study.
In response to these challenges and the pursuit of enhanced solar collector efficiency, a substantial body of research has been undertaken to summarize and synthesize the findings from these efforts.
Solar collector design and construction have seen significant advancements through decades of research and development, drawing upon diverse scientific and engineering disciplines. A persistent challenge, however, lies in stagnant air pockets within the collector. These elements impede the transfer of heat from the absorber to the air, reducing the efficiency of the collector [1], which carried a theoretical and experimental study of a flat-plate air collector equipped with artificial roughness elements placed in the airflow between the absorber and the bottom plate. In addition, a flat-plate air collector without baffles was analyzed for reference purposes. The results of the study showed that the temperature of the absorber decreases as the airflow rate increases. It was also observed that the absorber temperature, outlet temperature, and collector efficiency were higher for the collector fitted with baffles.
Other studies have shown that staggered baffles improve the thermal performance of air collectors [2]. Two cases were considered: one with a 10 cm spacing between two rows and the other with a 20 cm spacing. The convective heat transfer coefficient, almost doubled in the first case when Re > 2100, is between 4 and 45 W/m2 K for laminar flow and between 40 and 70 W/m2 K for turbulent flow, with a similar observation for the Nusselt number (Nu).
Fins were introduced into the solar air collector to improve its performance. This approach was also investigated by Fakoor Pakdaman et al. [3]. The results indicated a 20% increase in heat transfer, attributed to a 66% increase in heat exchange surface area due to the fins. Finally, the study found that the angle of inclination of the unit had a minimal impact on heat transfer. Bensaci et al. [4] evaluated the effect of different baffle placements (smooth, 50% Up, 50% Down, 50% Middle, and 100%) on the local convective heat transfer coefficient, Nusselt number, and friction factor. The study identified a 50% bottom baffle (case 2) as the most effective configuration for achieving a good balance between thermal and hydraulic performance.
The efficiency of six types of solar air heaters fitted with baffles of different shapes was compared by Sharma et al. [5] with regard to their Reynolds numbers, ranging from 3000 to 18,000. Sinusoidal baffles were found to offer the best performance, with an increase in thermal–hydraulic efficiency of up to 2.05 times at Re = 15,000.
Previous research has examined the performance of an air collector incorporating semi-circular fins and baffles [6]. It has also been shown that the finned collector offers a significant increase in air temperature, heat transfer coefficient, and thermal efficiency over the conventional flat plate solar collector. These improvements make the hollow-fin baffled solar collector a promising solution for domestic and industrial applications. In this study, the performance of an air collector incorporating fins and baffles in the form of semi-circular loops was evaluated. The aim of this evaluation was to improve the heat transfer and thermal efficiency of the collector.
Two studies on the influence of changing solar intensity on flat-plate solar collectors were analyzed by Mohammadi et al. and Rani et al. [7,8]. The results showed that solar intensity has a significant impact on the collector’s thermal parameters. These parameters include inlet and outlet temperatures, absorption temperature, and glass cover temperature. In addition, it was observed that increasing solar intensity leads to a minimal decrease in energy and effective efficiency.
Three fin-and-baffle configurations were investigated by Biswas et al. [9] to optimize heat transfer and pressure loss in a solar collector. The channel configuration was found to exhibit the best heat transfer but also the highest pressure loss. Pressure loss was reduced by the counter-flow and spiral configurations but at the expense of lower heat transfer. The 30° counter-flow configuration was determined to be the best compromise between thermohydraulic performance, pressure loss, and flow homogeneity within the collector.
The concept of an angle factor was also investigated by Promvonge and Skullog [10] and it was found that an angle of 30° resulted in the most favorable combination of heat transfer and friction factor.
An investigation into two active solar dryer designs, flat plate and evacuated tube, was conducted by Sai Kandukuri et al. [11]. The implementation of perforated baffle trays resulted in enhanced drying performance through improved air circulation and heat transfer. The evacuated tube dryer was found to achieve superior efficiency when compared to the flat plate dryer. Also, Hu et al. [12] found that perforating the deflectors in an SAC led to significant improvements. Efficiency increased by 3.6% and pressure drop reduction was observed to be 8.8%.
The crucial role of porous fins in enhancing the performance of a PCM solar collector was investigated by Khanlari et al. [13]. It was observed that an increase in the number of porous fins led to a corresponding increase in the average energy efficiency.
The study conducted by Abbas et al. [14] investigated the thermal performance of bare tube- and serpentine tube-concentrated solar collectors (CSCs). The results demonstrated that serpentine tube CSCs with a conductive material plate (C-HMA) exhibited superior thermal efficiency compared to bare tube CSCs with a non-conductive material plate (RHMA). Also, Zhang et al. [15] examined flat-plate solar collectors (FPSACs) with circular-rib absorbers that attained a thermal efficiency of 85%, surpassing the performance of other technologies evaluated. Evacuated-tube solar collectors (EVTSACs) equipped with micro-fins can achieve a thermal efficiency of 73%.
A novel triangular solar collector (TSAC) was proposed [16] to enhance the performance of air solar collectors. Three configurations of TSAC were investigated. The results of this study show that the new TSAC has improved performance in different climatic regions, especially in low-radiation regions. The optical performance of the three configurations was compared and the TSAC with a transparent plate on the side had the highest optical efficiency.
A study by Rajaseenivasan et al. [17] investigated the performance of a single-pass solar air heater (SAH) with circular and V-shaped turbulators. Two identical SAHs were tested: a conventional one and a modified one with varying Reynolds numbers (6000 to 12,000). The results indicated a direct correlation between system efficiency and both the Reynolds number and the number of turbulators employed. Notably, the thermal enhancement factor exhibited an inverse relationship with the Reynolds number across all configurations. In a similar vein, ref. [18] conducted an experimental study with V-shaped and offset rib artificial turbulators. They found that the Nusselt number and friction factor are maximized for relative offset rib lengths doubles of 3.5 and 2, respectively. Additionally, both V-shaped and offset rib artificial turbulators enhance heat transfer and the friction factor.
In another location study [19], the performances of two double-pass air solar collectors were compared. The results of the study showed that double-pass air solar collectors (DSACs) with a new type of absorbing surface, consisting of a mixture of matte black paint and graphene nanomaterial (NFAD), exhibited superior performance to conventional DSACs. DSACs with NFAD coating were a promising technology for the production of solar thermal energy. These collectors exhibited superior performance in terms of outlet temperature, thermal power, exergy efficiency, and durability index.
Another double-pass solar air heater with a porous medium was tested by [20] in Famagusta, Cyprus. The collector’s average efficiency was 53.7% at an airflow rate of 0.037 kg/s. While increasing the airflow rate improves efficiency, it reduces the temperature difference between the inlet and outlet air.
Motivated by the critical role of efficient air circulation in optimizing thermal performance, research efforts are increasingly directed toward understanding the flow dynamics within solar air collectors. This pursuit aims to refine collector designs and thereby improve overall energy conversion efficiency. Early research on air solar collectors aimed to identify the optimal airflow path to maximize collector efficiency and temperature. Different airflow configurations were examined in studies conducted by [21]. It was found that the performance of airflow exclusively under the absorber plate collector was comparable to that of airflow over the absorber plate and then returning underneath it, in the absence of baffles.
Another study by [22] showed that the collector field configuration, flow rate, inlet temperature, and working fluid have a significant impact on the resistance and efficiency characteristics of direct-return flat-plate solar collector fields. Also, an experimental study by [23] was conducted on the impact of jet shapes and absorber spacing on the heat transfer and pressure drop performance of solar air collectors. The results show that circular jet collectors offer the best overall performance. They exhibit a higher outlet temperature, a higher useful heat gain, a higher Nusselt number, and a lower friction factor than square or triangular jet collectors. Of a similar nature, another experimental and transient study by [24] was conducted on two parallel-flow solar air collectors, one without modification and one equipped with aluminum cans filled with PCM. The results showed that the integration of aluminum cans filled with PCM in a parallel-flow solar air collector can significantly improve its energy and exergy efficiency.
The Machi et al. [25] study was conducted to examine the influence of inlet duct design on the efficiency of a single-pass air solar collector (SAC). Two identical collectors were evaluated, one with a side inlet duct (SESAC) and the other with a front inlet duct (FESAC). The results of the study suggest that collectors with a front inlet duct tend to be more efficient than collectors with a side inlet duct.
Other research on the interplay between sensor manufacturing equipment and sensor performance is gaining traction across diverse scientific disciplines.
Yousif et al. [26] conducted a study to compare the performance of two types of compound parabolic concentrator (CPC) solar air flat plate collectors with paraffin wax phase change material (PCM). Both models were tested under standard conditions in Mosul, Iraq. The results showed that the normal-shape model had a higher thermal efficiency than the involute-shape model for all air mass flow rates tested but that the outlet temperature of the normal-shape model was lower than that of the involute-shape model for different air mass flow rates. The results of this study show that the phase change material and the position of the receiver have a significant impact on the performance of both CPC collector models.
Yang et al. [27] conducted an experimental study of a new model of an air solar collector that utilizes a phase change material. The findings reveal that nighttime air heating is influenced by several factors, such as the quantity of heat stored within the phase change material, the velocity of airflow, and the ambient air temperature. Additionally, the collector’s efficiency is contingent upon the start time of daytime air heating and exhibits variations between 34.51% and 44.49%. Zayed et al. [28] was implemented to assess the energy and exergy efficiencies of a wavy corrugated solar air collector (WCSAC) integrating phase change materials (PCMs), the outcomes unmistakably confirmed that the incorporation of PCMs resulted in a remarkable boost in the WCSAC’s performance, preserving the outlet air temperature above ambient temperature even after sunset.
Recently Rawat et al. [29] analyzed a solar air heater with phase change material (SAH-PCM). The study explores how the thickness-to-length ratio (t/L) of the PCM container affects performance. Findings show that increasing the t/L ratio improves energy storage, delays PCM discharge, and enhances the overall system efficiency. The research demonstrates the importance of optimizing the t/L ratio for greater energy and cost efficiency in both single-pass and double-pass flow configurations.
A thorough study was conducted to assess the thermal performance of an air solar collector (SAC) supplemented by the integration of obstacles embedded with a phase-change material (PCM) by [30]; the findings indicate that an increased solar irradiance induces a rise in the temperature gradient across the SAC simultaneously with an improved collector efficiency. However, this enhancement in efficiency is associated with a decline in the temperature difference and, recently, [31] investigated the impact of integrating a fan with an air-based solar collector (SAC) with a phase change material (PCM). The results showed that the fan significantly improved the thermal performance of the SAC, including increasing the outlet air velocity, outlet air temperature, and average indoor air temperature. The study conducted by Kumar Ahirwar and Kumar Arvind [32] investigated techniques for improving the efficiency of SAHs by disrupting the laminar sub-layer on the absorbing plate. It examines four methods: artificial roughness, jet impingement, piezo-electric fans, and phase change materials (PCMs). Research demonstrates that these techniques can significantly enhance the thermal–hydraulic performance factor of SAHs. Also, the [33] study investigated the impact of metal foam on the thermal performance and entropy generation rate of a plate heat exchanger (IB-ETC-SAH) compared to a fin-and-tube heat exchanger (SAH). The results showed that the use of metal foam can improve the thermal performance of an IB-ETC-SAH but that it also leads to an increase in pressure drop (a maximum pressure drop of 26,338 Pa (0.26 atm)). A metal foam with a lower PPI and lower porosity is preferable to minimize pressure drop while maintaining high thermal performance.
Motivation and Objective of the Study
As per the author’s knowledge, only limited studies have been carried out on optimizing the performance of perforated solar air collectors and improving their efficiency; it is clear that baffles increase solar collector efficiency but are also a key factor in increasing pressure drop. Current research is striving to improve collector efficiency while reducing the pressure drop and also reducing carbon consumption to preserve the environment.
The present study focuses on the impact of incorporating holes in the baffles to induce turbulence in the airflow; holes were introduced into the baffles to generate turbulence and reduce the pressure drop. A three-dimensional numerical simulation served to assess the performance of the cases with different configurations. The CFD simulations were carried out using ANSYS 2023 R2 at Reynolds numbers ranging from 2300 to 8500. The local convective heat transfer coefficient, thermal efficiency, Nusselt number (Nu), and pressure drop were discussed and compared.
2. Materials and Methods
2.1. Geometry
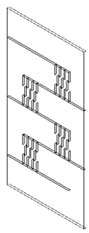
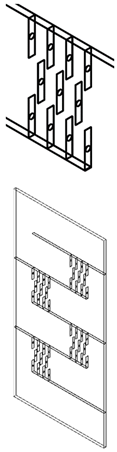
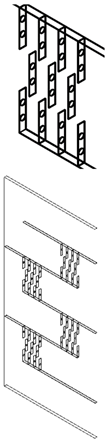
In the present work, a numerical study of a solar collector model is carried out, focusing on the airflow between the absorber plate and the insulation layer. The dimensions of the collector are fixed at 2000 mm × 1000 mm, with two types of baffles: longitudinal baffles with a length of L_LB = 800 mm and spacing of H = 333.33 mm and transverse baffles with a length of L_TB = 111.11 mm. The height of the baffles remains constant at t = 20 mm and, in part, by placing restricting baffles on the insulator to force the air to circulate through a small space left between the absorber and the baffles without touching the absorber [4], as shown in Figure 1, but with different thicknesses t = (1.0 mm, 1.5 mm, and 2.0 mm). The geometric parameters are summarized in Table 1.
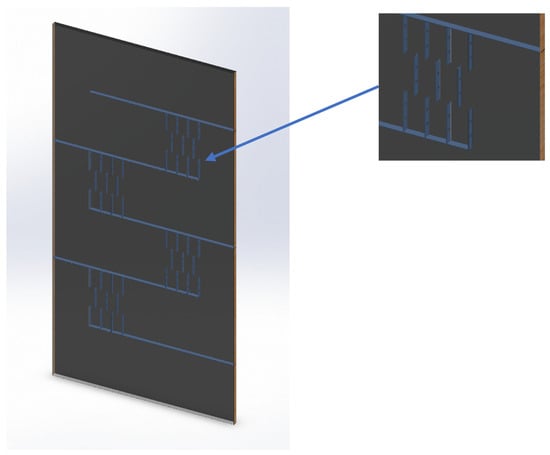
Figure 1.
Visualization of a solar air collector with internal baffles (3D).

Table 1.
The geometric parameters of conventional and perforated baffles.
The present numerical study consists of six cases:
- The first case: solar collector without baffles “Smooth“.
- The second case: solar collector with transverse and longitudinal baffles “LT”.
- The third case: a solar collector with a single hole in the middle of the transverse baffles, 10 mm of diameter “LTH 1”.
- The fourth case: a solar collector with a single hole in the middle of the transverse baffles 15 mm of diameter “LTH 1”.
- The fifth case: a solar collector with two holes in the transverse baffles, 10 mm in diameter “LTH 2”.
- The sixth case: a solar collector with two holes in the transverse baffles 15 mm in diameter “LTH 2”.
2.2. Grid Mesh
The three-dimensional numerical model of the solar air heater was discretized into a finite number of small tetrahedral elements using the finite volume approach with the Ansys workbench meshing solver. A face sizing value of 5 mm was maintained on the absorber and insulator. The inlet, outlet, and side walls were meshed with element sizes of 1 mm and 2 mm for the smooth and baffled models, respectively. An inflation technique was employed to capture the variations within the velocity and thermal boundary layers. Ten inflation layers with a total thickness of 1 mm were used on the absorber, insulator, and baffles. The total number of elements ranged from 6 million to 8.3 million, with additional Mesh sizing for longitudinal and transverse baffles as well as baffles with holes and two holes, which depends more on the baffle configuration itself rather than any other factors. The discretized model of LTH baffles with 2 holes having a diameter of 15 mm, as shown in Figure 2.

Figure 2.
Discretized model of LTH 2 holes with a diameter of 15 mm.
2.3. Grid Independence Study
The grid independence study or mesh sensitivity test was carried out to verify that numerically simulated results are independent of the mesh size. In order to carry out the grid test, a smooth surface solar air collector was used for the study and the area-weighted outlet temperature was plotted for four different body/face sizing values, namely 10 mm, 7 mm, 5 mm, and 4 mm, which is equivalent to nearly 1.3 million, 24 million, 48 million, and 69 million elements, respectively, as shown in Figure 3. The Reynolds number of 5500 was maintained as constant for this study. The outcome of the grid test predicted that when the face sizing value is nearly 7 mm and below, the outlet temperature deviation is less than 0.01% and, hence, for the upcoming numerical simulations, a face sizing value of 5 mm and below was maintained for the study.
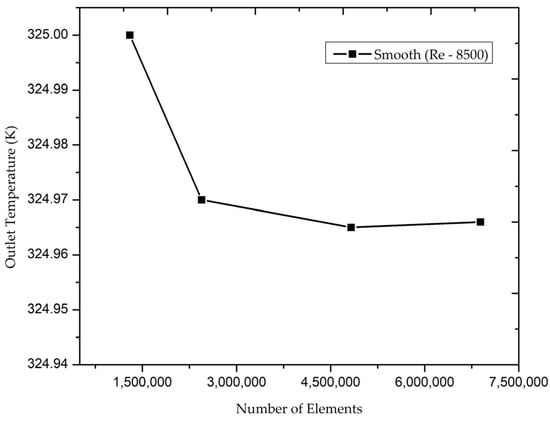
Figure 3.
Outlet temperature plot vs. number of elements for a Re 5500.
2.4. Mathematical Modeling and Solution Technique
In this study, a computational fluid dynamics (CFD) approach was used to solve the flow equations and capture the relevant geometric parameters. The CFD tool ANSYS CFD 23-R2 was used to discretize and solve the conservation of mass, momentum, and energy equations.
The flow through and under the absorber was numerically simulated by solving the mass conservation equations as well as the velocity equations for all x, y, and z directions. Turbulence, an important phenomenon in this type of flow, was modeled using the evolving wall functions of the RGN k-epsilon model, known for their accuracy in the near-wall boundary layer region.
This numerical approach accurately captured the hydrodynamic characteristics of the flow, including the distribution of velocities, pressures, and turbulence fields, in the complex geometry of the absorber. The results provided valuable information for understanding the flow behavior and optimizing the absorber design.
Continuity Equation:
Momentum Equation:
The velocity component’s scalar momentum equation in the x direction is provided by
The velocity component’s scalar momentum equation in the y direction is provided by
The velocity component’s scalar momentum equation in the z direction is provided by
Energy equation:
Transport equations for the standard k-ε model: The turbulent kinetic energy, k, and its turbulent eddy dissipation, ε, are obtained from the following transport equations:
and
The expression for the turbulent viscosity () is expressed as
The Reynolds number (Re) is based on the hydraulic diameter of the air duct, as follows:
where is kinematic.
U: The viscosity.
: The hydraulic diameter (A is the cross-section area and P is the cross-section perimeter).
The local heat transfer coefficient from the CFD results is expressed as follows:
where q is the local heat flux.
Tw,x is the local wall temperatures.
Tb,x is the bulk fluid temperatures.
The local Nusselt number can be computed based on a local heat transfer coefficient, which is obtained directly from the Fluent panel, as follows:
A user-defined function (UDF) hooked in the Fluent panel was used to calculate the average Nusselt number as [4]
The thermal efficiency of the collector is calculated by the equation
2.5. Validation
The simulation’s validation was carried out by comparing its results with experimental data [4] for different flow Re. This was performed, in particular, through a three-dimensional analysis of the airflow in a flat-plate solar collector, as shown in Figure 4. This comparison revealed a remarkable agreement between the simulated results and the experimental observations, which confirms the validity of the simulation. Also, the maximum deviation is found to be less than 10% with that of the experimental data. Hence, for the present study, the Reynolds number varies from 2300 to 8500 and a solar heat flux value of 1000 W/m2 was maintained for the entire study.
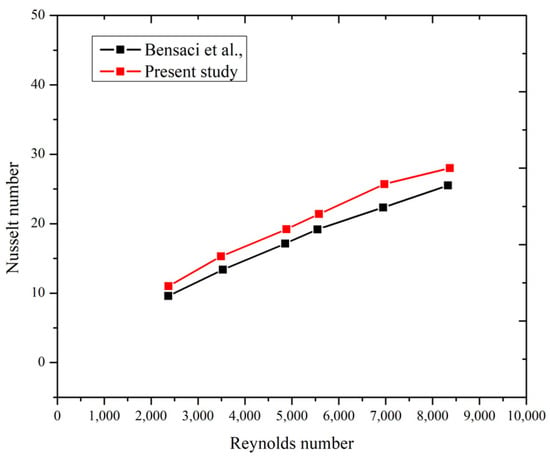
Figure 4.
Validation of numerically predicted Nu with experimental data of [4].
3. The Boundary Conditions
The present numerical investigation was carried out using the following boundary conditions. The solar air collector inlet was maintained as a mass flow inlet ranging between 0.021807 kg/s and 0.080591 kg/s, which corresponds to an Re of 2300 to 8500, respectively. The collector outlet was maintained as atmospheric, which is equivalent to 101,325 Pa. The side walls, isolator, and baffles were maintained as adiabatic walls with no-slip conditions. A solar heat flux value of nearly 1000 W/m2 was fixed to the absorber wall with a no-slip condition, as shown in Table 2. The above heat flux value was obtained from the literature [4].

Table 2.
Boundary conditions opted for in the present study.
The thermophysical properties of the air and the absorber plate and baffles are presented in Table 3, assuming that they remain constant at the mean air temperature [4].

Table 3.
Thermophysical properties of the air and the absorber plate and baffles: input data for CFD analysis.
4. Results and Discuss
4.1. Smooth Case
In this section, solar air collectors with smooth surfaces have been investigated numerically for varying Reynolds numbers ranging between 2300 and 8500. The results from the study indicated that by increasing Re from 2300 to 8500, the pressure drop increased from 0.45 Pa to 5.5 Pa, respectively. Also, the Nu was increased from 13.92 to 46.17 with an increase in Re. It is clear that an increase in Re promotes better heat transfer, as shown in Figure 5, and it also increases the pressure drop, caused by the increase in frictional resistance. The same phenomenon was observed in Figure 6, which clearly shows the pressure drop as a function of the Re. The results clearly depicted that the maximum value of the pressure drop, namely 5.5 Pa, which corresponds to the maximum value of Re (8500).
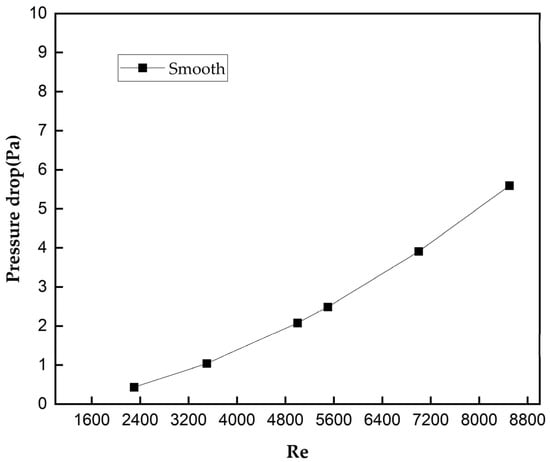
Figure 5.
Variation in Re vs. pressure drop for a smooth surface solar collector.
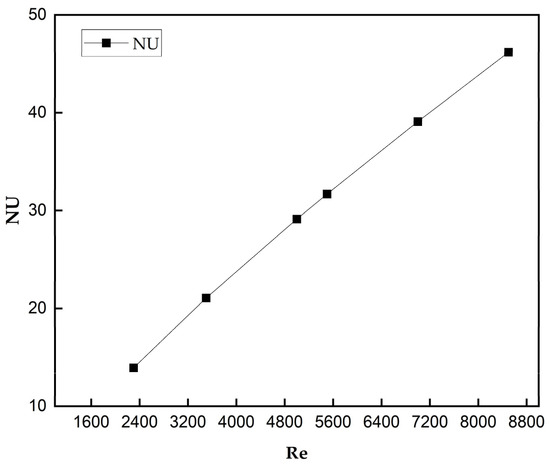
Figure 6.
Variation in Re vs. Nu for a smooth surface solar collector.
Figure 7 and Figure 8 indicate the temperature contour and pressure contour of a smooth solar air collector at the mid-plane for a Re 8500. When the temperature of the air at the inlet is maintained at 300.15 K (ambient temperature), as the air enters the solar air collector, it absorbs heat from the absorber plate where the heat flux is maintained as 1000 W/m2. The temperature rises gradually along the flow path and reaches a maximum temperature near the collector outlet. In this smooth surface, the air collector reaches about a maximum temperature of 325 K at the collector outlet for a Re 8500, as shown in Figure 7. Also, the pressure drop has increased significantly to a maximum value of 5.5 Pa from 0.45 Pa when the Re increased from 2300 to 8500, respectively, as shown in Figure 8.
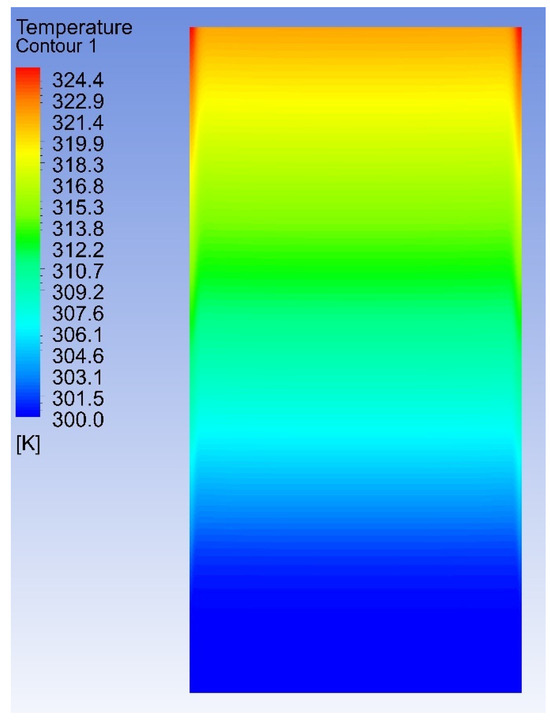
Figure 7.
Temperature contour at the mid-plane for Re 8500.
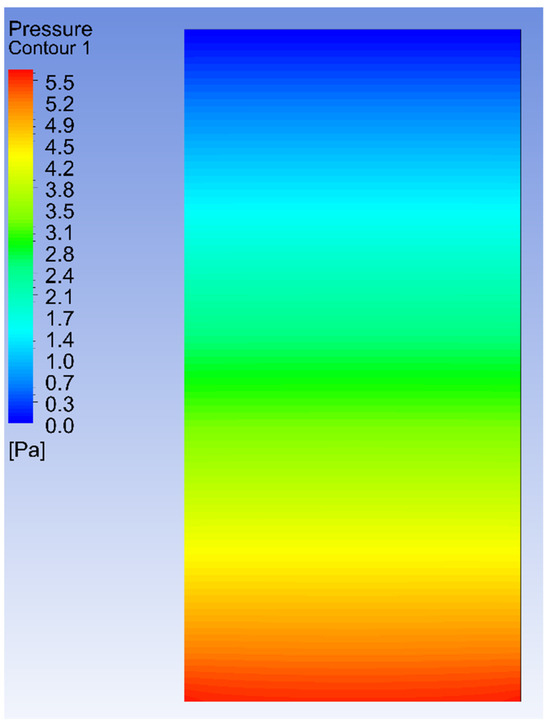
Figure 8.
Pressure contour at the mid-plane for Re 8500.
4.2. Comparison of Longitudinal and Transverse Baffles with and without Perforation
In the second phase of the study, longitudinal and transverse baffles with and without perforation were investigated numerically. The effect of the thickness of baffles and hole diameter has also been studied extensively. The thickness variations considered for the study are 1.0 mm, 1.5 mm, and 2.0 mm and the maximum number of holes in the baffle is 2, with varying diameters of 10 mm and 12.5 mm and 15 mm. The longitudinal and transverse baffles combined together are called LT, with a single hole added to it, it is called LTH 1, and with two holes added to the LT, it is called LTH 2. In total, there are three different models, namely LT, LTH1, and LTH2, in combination with three different thicknesses of the baffles, namely, 1.0 mm, 1.5 mm, and 2.0 mm, and perforation with diameters of 10 mm and 15 mm. All the above-mentioned cases were simulated for various inlet Reynolds numbers of 2300, 3500, 5000, 5500, 7000, and 8500. Thus, a total number of 105 numerical simulations were carried out in this section.
Assessment of the Nusselt Number and Pressure Drop
In the case of a solar air collector, the introduction of baffles generally (a) increases turbulence, (b) results in more contact time with the absorber plate, and (c) increases the flow path; these factors would significantly improve the thermal performance of a solar air collector. On the contrary, the same baffles would increase the resistance to fluid flow, which would result in an increase in pressure drop to a greater extent. A tradeoff must be made between the baffle configuration and pressure drop in order to obtain the maximum performance from the solar air collector. The introduction of perforated baffles provided a promising solution for the pressure drop and heat transfer characteristics. In this study, initially, longitudinal and transverse baffles with varying thicknesses were investigated and the results from the study clearly indicated that compared to the smooth alternatives, LT baffles provided a maximum Nu of 63 from 46.17 whereas the pressure drop increased from 5.5 Pa to 496 Pa for a thickness of 2 mm and Inlet Re of 8500. Though the Nu has increased moderately, the pressure drop has swept over 496 Pa, as shown in Figure 9. This larger pressure drop would greatly affect the overall performance of a solar air collector. Furthermore, the study has been extended to reduce the thickness of the baffles from 2 mm to 1.5 mm and 1.0 mm, as shown in Figure 9, Figure 10 and Figure 11.
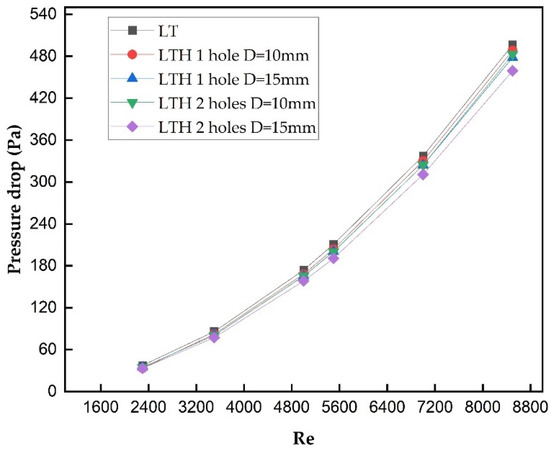
Figure 9.
Variation in pressure drop vs. Re of LT baffles with and without perforation for t = 2.0 mm.
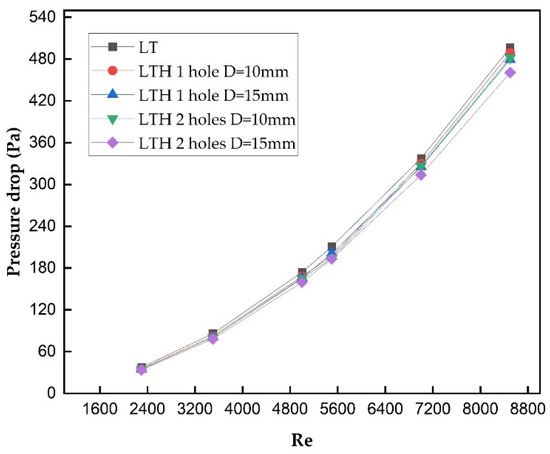
Figure 10.
Variation in pressure drop vs. Re of LT baffles with and without perforation for t = 1.5 mm.
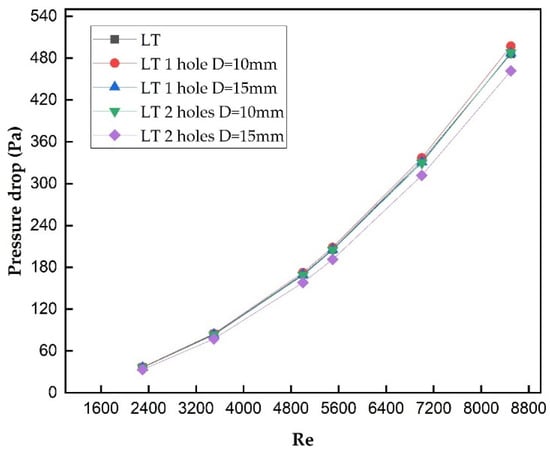
Figure 11.
Variation in pressure drop vs. Re of LT baffles with and without perforation for t = 1.0 mm.
The results predicted that Nu was increased to 64.34 from 63.25 when the thickness of baffles was reduced from 2 mm to 1 mm, as shown in Figure 12, Figure 13 and Figure 14. Similarly, the pressure drop also decreased from 496 Pa to 486 Pa when baffle thickness was reduced from 2 mm to 1 mm, respectively, as shown in Figure 9 and Figure 11.
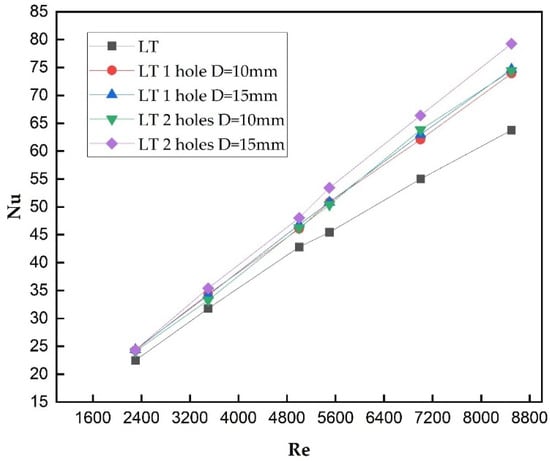
Figure 12.
Variation in Nu vs. Re of LT baffles with and without perforation for t = 1.0 mm.
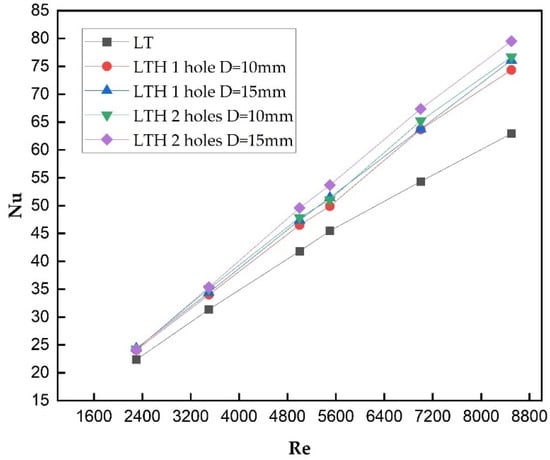
Figure 13.
Variation in Nu vs. Re of LT baffles with and without perforation for t = 1.5 mm.
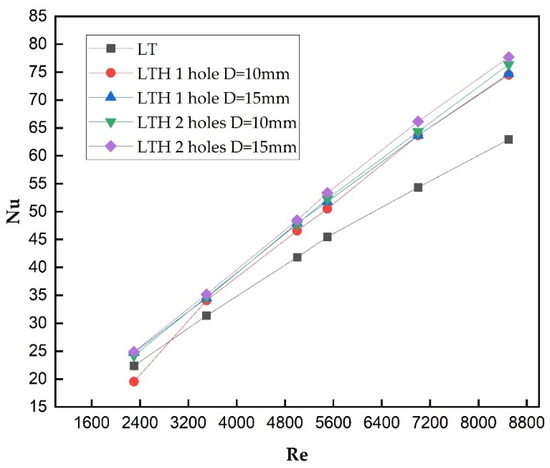
Figure 14.
Variation in Nu vs. Re of LT baffles with and without perforation for t = 2.0 mm.
The introduction of perforated baffles with 1 hole and 2 holes with diameters of 10 mm and 15 mm provided a significant improvement in heat transfer characteristics and optimal pressure drop. When the transverse baffle was perforated with 1 hole of diameter 10 mm, this provided a small increase in Nu of 74 from 63, whereas the pressure drop was reduced to 489 Pa from 496 Pa. The comparison of LT and LTH 1 (t = 2 mm) with a diameter of 10 mm, as shown in Figure 14, has not provided a significant impact on the overall performance; a notable change was observed by just perforating the baffles. Furthermore, the diameter of the hole has been increased to 15 mm and the results estimated no significant improvement in Nu and the pressure drop. Also, the thickness of the baffles was reduced from 2 mm to 1 mm and the same trend was observed for all inlet Re, as shown in Figure 12, Figure 13 and Figure 14.
Similarly, when the number of holes was increased to LTH 2 (t = 2 mm), the Nu increased to 76.71, as shown in Figure 14, and the pressure drop was reduced to 482 Pa, as shown in Figure 10. The thickness of the baffles was reduced from 2 mm to 1.5 mm and 1.0 mm, the Nu values were observed to be 77.29, 79.28, and 79.54, and the pressure drop values were observed to be 459.2, 460, and 460.1 Pa, respectively, for an Inlet Re of 8500. The results substantiated that the thickness of baffles does not provided any significant improvement to the pressure drop or the heat transfer characteristics. However, reducing the baffle thickness results in lower material costs, which makes it a cost-effective option without compromising the overall performance.
These perforated baffles allow the air to flow through the holes, as well as around the baffles, as shown in Figure 15 which reduces the airflow resistance and decreases the pressure drop. The velocity contour in the main flow direction x,y is shown in Figure 16; the velocity is highest in front of the baffles because of less resistance. Figure 17 indicates the temperature contour. As the flow moves, the temperature gradually rises, peaking at a maximum near the collector outlet.
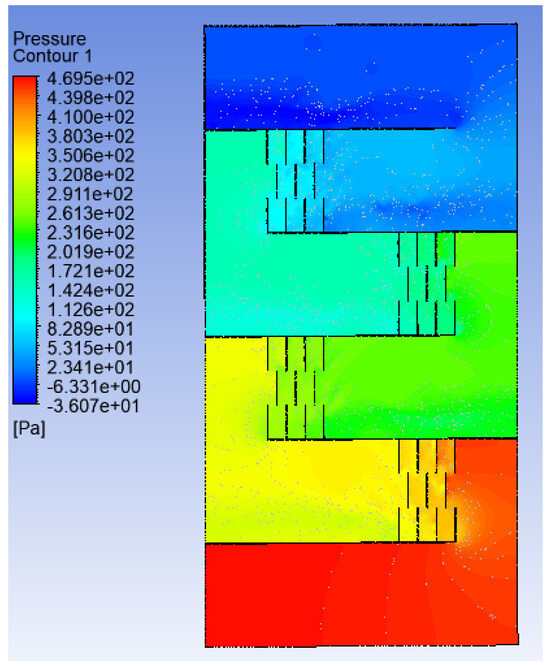
Figure 15.
Pressure contour of LTH2 with a diameter of 15 mm for a Re 8500.
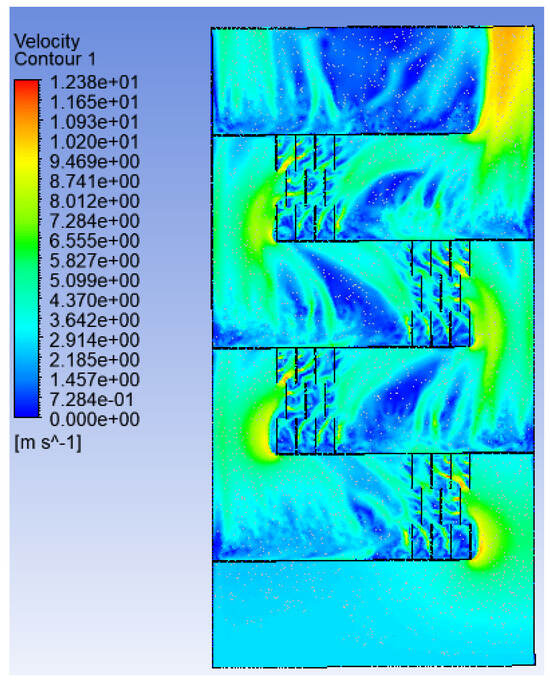
Figure 16.
Velocity contour of LTH2 with a diameter of 15 mm for a Re 8500.
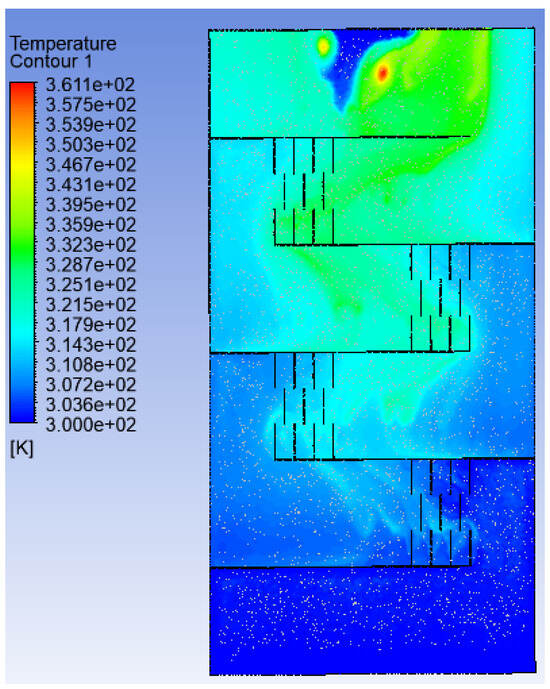
Figure 17.
Temperature contour of LTH2 with a diameter of 15 mm for a Re 8500.
5. Conclusions
As part of this study, a detailed numerical simulation of a flat solar air collector with smooth, longitudinal, and transverse baffles was carried out. Baffles, both perforated and unperforated, were tested for different thicknesses and for all inlet Reynolds numbers using a detailed numerical simulation. The outcomes of the study have been presented as follows:
- The study revealed that utilizing longitudinal and transverse baffles led to improved heat transfer characteristics compared to a smooth surface. This improvement was manifested by an increase in the Nusselt number. However, it is important to note that a significant increase in pressure drop accompanied this enhanced performance. The influence of baffle thickness on the improvement in Nusselt number or the increase in pressure drop was found to be negligible;
- On comparison of baffles with and without perforation, results clearly predicted that perforated baffles with LTH 2 holes with a diameter of 15 mm provided better heat transfer characteristics and a better estimated maximum Nu and optimal pressure drop than LTH 1 holes of diameters 10 mm and 15 mm and LT without perforation for all Re, respectively. Also, variation in the thickness of baffles has no significant improvement in terms of the Nu and pressure drop of all the models considered. Even though thickness has no impact on the thermal performance of solar air collectors, it will be a deciding factor in terms of the selection of thickness of baffles.
Among the models studied, the perforated deflectors with a thickness of 1 mm and 2 holes with a diameter of 15 mm were awarded the highest Nusselt number (Nu) in terms of the optimum pressure drop.
Author Contributions
Conceptualization, G.B., B.R. and K.A.; methodology, M.J.G. and D.R.; software, G.B. and D.R.; formal analysis, G.B. and D.R.; investigation, G.B., D.R. and M.J.G.; data curation, G.B., D.R. and A.G.; writing—original draft preparation, G.B.; writing—review and editing, D.R., G.B. and M.J.G.; visualization, G.B., B.R. and K.A.; supervision, A.G.; project administration, A.G. funding acquisition, A.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Specific heat capacity (J·kg−1·K−1) | |
| H | Heat transfer coefficient (W·m−2·K−1) |
| K | Turbulence kinetic energy (m2·s−2) |
| Nu | Nusselt number |
| Q | Absorbed heat flux (W·m−2) |
| Re | Reynolds number |
| T | Temperature (K) |
| V | Velocity (m/s) |
| P | Pressure (Pa) |
| ṁ | Air mass flow rate per meter (kg/m·s) |
| The turbulent viscosity. | |
| Absorber plate surface area (m2) | |
| Fluid density (kg·m−3) |
Abbreviations
| SAH | Solar air heater. |
| SAC | Solar air collector. |
| RHMA | Reference hot-mix asphalt. |
| C-HMA | Conductive hot-mix asphalt. |
| CSCs | Concentrated solar collectors. |
| FPSACs | Flat-plate solar air collectors. |
| TSAC | Triangular solar air collector. |
| PCM | Phase change material. |
| DSAC | Double flow solar air collector. |
| NFAD | Nano-enhanced flexible aluminum air duct. |
| FESAC | Front entrance solar air collector. |
| SESAC | Side entrance solar air collector. |
| CPC | Compound parabolic concentrator. |
| WCSAC | Wavy corrugated solar air collector. |
| IB-ETC-SAH | Inserting a baffle inside the ETC-SAH. |
| PPI | Pores per inch. |
References
- Labed, A.; Moummi, N.; Aouès, K.; Zellouf, M.; Moummi, A. Etude Théorique et Expérimentale Des Performances d’un Capteur Solaire Plan à Air Muni d’une Nouvelle Forme de Rugosité Artificielle. J. Renew. Energ. 2009, 12, 551. [Google Scholar] [CrossRef]
- Menasria, F.; Moummi, E.; Moummi, N.; Zedayria, M.; Guestal, M. Modélisation Des Échanges Convectifs Dans Le Conduit Utile d’un Capteur Solaire Plan à Air Muni de Rugosités Artificielles de Formes Rectangulaires. J. Renew. Energ. 2023, 14, 369–379. [Google Scholar] [CrossRef]
- Fakoor Pakdaman, M.; Lashkari, A.; Basirat Tabrizi, H.; Hosseini, R. Performance Evaluation of a Natural-Convection Solar Air-Heater with a Rectangular-Finned Absorber Plate. Energy Convers. Manag. 2011, 52, 1215–1225. [Google Scholar] [CrossRef]
- Bensaci, C.E.; Moummi, A.; Sanchez de la Flor, F.J.; Rodriguez Jara, E.A.; Rincon-Casado, A.; Ruiz-Pardo, A. Numerical and Experimental Study of the Heat Transfer and Hydraulic Performance of Solar Air Heaters with Different Baffle Positions. Renew. Energy 2020, 155, 1231–1244. [Google Scholar] [CrossRef]
- Sharma, S.; Kumar Das, R.; Kulkarni, K. Sustainability Analysis of Solar Air Heater Roughned with Baffles Based on Exergy Efficiency. Mater. Today Proc. 2022, 69, 75–81. [Google Scholar] [CrossRef]
- Rani, P.; Tripathy, P.P. Experimental Investigation on Heat Transfer Performance of Solar Collector with Baffles and Semicircular Loops Fins under Varied Air Mass Flow Rates. Int. J. Therm. Sci. 2022, 178, 107597. [Google Scholar] [CrossRef]
- Mohammadi, K.; Sabzpooshani, M. Appraising the Performance of a Baffled Solar Air Heater with External Recycle. Energy Convers. Manag. 2014, 88, 239–250. [Google Scholar] [CrossRef]
- Rani, P.; Tripathy, P.P. Thermal Characteristics of a Flat Plate Solar Collector: Influence of Air Mass Flow Rate and Correlation Analysis among Process Parameters. Sol. Energy 2020, 211, 464–477. [Google Scholar] [CrossRef]
- Biswas, R.; Tripathy, P.P. Finite Element Based Computational Analysis to Study the Effects of Baffle and Fin on the Performance Assessment of Solar Collector. Therm. Sci. Eng. Prog. 2024, 49, 102431. [Google Scholar] [CrossRef]
- Promvonge, P.; Skullong, S. Thermal Characteristics in Solar Air Duct with V-Shaped Flapped-Baffles and Chamfered-Grooves. Int. J. Heat Mass Transf. 2021, 172, 121220. [Google Scholar] [CrossRef]
- Sai Kandukuri, K.; Kishor Sharma, P.; Kumar Arun, R. A Comparative Assessment of Distributive Mode Active Solar Dryers: Flat Plate Collector vs Evacuated Tube Collector with Thermal Energy Storage and Perforated Baffled Trays. Sol. Energy 2024, 271, 112421. [Google Scholar] [CrossRef]
- Hu, J.; Liu, K.; Ma, L.; Sun, X. Parameter Optimization of Solar Air Collectors with Holes on Baffle and Analysis of Flow and Heat Transfer Characteristics. Sol. Energy 2018, 174, 878–887. [Google Scholar] [CrossRef]
- Khanlari, A.; Aytaç, İ.; Tuncer, A.D.; Variyenli, H.İ.; Şahin, H.N. Improving the Performance of a PCM Integrated Solar Air Collector by Adding Porous Fins over the Bottom Side of the Absorber: A Transient CFD Study. J. Energy Storage 2024, 90, 111847. [Google Scholar] [CrossRef]
- Abbas, F.A.; Alhamdo, M.H. Experimental and Numerical Analysis of an Asphalt Solar Collector with a Conductive Asphalt Mixture. Energy Rep. 2024, 11, 327–341. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, T. Systematic Review of Solar Air Collector Technologies: Performance Evaluation, Structure Design and Application Analysis. Sustain. Energy Technol. Assess. 2022, 54, 102885. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, H.; Zhao, R.; Liu, Z.; Wang, Y.; You, S.; Wu, Z.; Wei, S. Thermal and Optical Performance Analysis of Triangular Solar Air Collectors and Regional Applicability in China. Sol. Energy 2023, 249, 288–300. [Google Scholar] [CrossRef]
- Rajaseenivasan, T.; Srinivasan, S.; Srithar, K. Comprehensive Study on Solar Air Heater with Circular and V-Type Turbulators Attached on Absorber Plate. Energy 2015, 88, 863–873. [Google Scholar] [CrossRef]
- Patel, S.S.; Lanjewar, A. Experimental Analysis for Augmentation of Heat Transfer in Multiple Discrete V-Patterns Combined with Staggered Ribs Solar Air Heater. Renew. Energy Focus 2018, 25, 31–39. [Google Scholar] [CrossRef]
- Öztürk, M.; Çiftçi, E. Upgrading the Performance of a Solar Air Collector with Flexible Aluminum Air Ducts and Graphene Nanoplatelet-Enhanced Absorber Coating. Therm. Sci. Eng. Prog. 2023, 40, 101760. [Google Scholar] [CrossRef]
- Nowzaria, R.; Aldabbagh, L.B.Y.; Mirzaei, N. Experimental Study on Double Pass Solar Air Heater with Mesh Layers as Absorber Plate. Int. J. Electron. Mech. Mechatron. Eng. 2011, 3, 673–682. [Google Scholar]
- Bhargava, A.K.; Garg, H.P.; Sharma, V.K. Evaluation of the Performance of Air Heaters of Conventional Designs. Sol. Energy 1982, 29, 523–533. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, R.; Liu, Y.; Zhang, X.; Fan, J. Optimization of the Flow Resistance Characteristics of the Direct Return Flat Plate Solar Collector Field. Sol. Energy 2021, 215, 388–402. [Google Scholar] [CrossRef]
- Elwekeel, F.N.; Nasr, A.A.E.; Radwan, M.I.; Aly, W.I. Influence of Impingement Jet Designs on Solar Air Collector Performance. Renew. Energy 2024, 221, 119757. [Google Scholar] [CrossRef]
- Tuncer, A.D.; Amini, A.; Khanlari, A. Experimental and Transient CFD Analysis of Parallel-Flow Solar Air Collectors with Paraffin-Filled Recyclable Aluminum Cans as Latent Heat Energy Storage Unit. J. Energy Storage 2023, 70, 108009. [Google Scholar] [CrossRef]
- Machi, M.H.; Farkas, I.; Buzas, J. Enhancing Solar Air Collector Performance through Optimized Entrance Flue Design: A Comparative Study. Int. J. Thermofluids 2024, 21, 100561. [Google Scholar] [CrossRef]
- Yousif, M.N.; Alomar, O.R.; Saleem, A.M. Performance of Compound Parabolic Concentrator Solar Air Flat Plate Collector Using Phase Change Material. Appl. Therm. Eng. 2024, 240, 122224. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, N.; Yuan, Y.; Cao, X.; Qian, B.; Zeng, C. A New Operating Model for Improving Thermal Efficiency of Double-Glazed Solar Air-Phase Change Material Collector: An Experimental Study. J. Energy Storage 2023, 58, 106448. [Google Scholar] [CrossRef]
- Zayed, M.E.; Kabeel, A.E.; Shboul, B.; Ashraf, W.M.; Ghazy, M.; Irshad, K.; Rehman, S.; Zayed, A.A.A. Performance Augmentation and Machine Learning-Based Modeling of Wavy Corrugated Solar Air Collector Embedded with Thermal Energy Storage: Support Vector Machine Combined with Monte Carlo Simulation. J. Energy Storage 2023, 74, 109533. [Google Scholar] [CrossRef]
- Rawat, P.; Ashwni; Sherwani, A.F. Optimization of Single and Double Pass Solar Air Heater-Phase Change Material (SAH-PCM) System Based on Thickness to Length Ratio. Int. J. Heat Mass Transf. 2024, 224, 125356. [Google Scholar] [CrossRef]
- Fadhil, A.M.; Jalil, J.M.; Bilal, G.A. Experimental and Numerical Investigation of Solar Air Collector with Phase Change Material in Column Obstruction. J. Energy Storage 2024, 79, 110066. [Google Scholar] [CrossRef]
- Bo, R.; Fu, W.; Meng, X.; Zhang, G. Employing a Fan to Improve the Wintery Heating Performance of Solar Air Collectors with Phase-Change Material: An Experimental Comparison. Case Stud. Therm. Eng. 2023, 50, 103425. [Google Scholar] [CrossRef]
- Kumar Ahirwar, B.; Kumar, A. Review on Different Techniques Used to Enhance the Thermal Performance of Solar Air Heater. Int. J. Heat Mass Transf. 2024, 220, 124979. [Google Scholar] [CrossRef]
- Abrofarakh, M.; Moghadam, H. Investigation of Thermal Performance and Entropy Generation Rate of Evacuated Tube Collector Solar Air Heater with Inserted Baffles and Metal Foam: A CFD Approach. Renew. Energy 2024, 223, 120022. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).