Short-Circuit Current Calculation of Flexible Direct Current Transmission Lines Considering Line Distribution Parameters
Abstract
1. Introduction
2. Transmission Line Equation
3. Line Equivalent Model with Distributed Parameters
3.1. Equivalent Model of Transmission Line Correction Coefficient
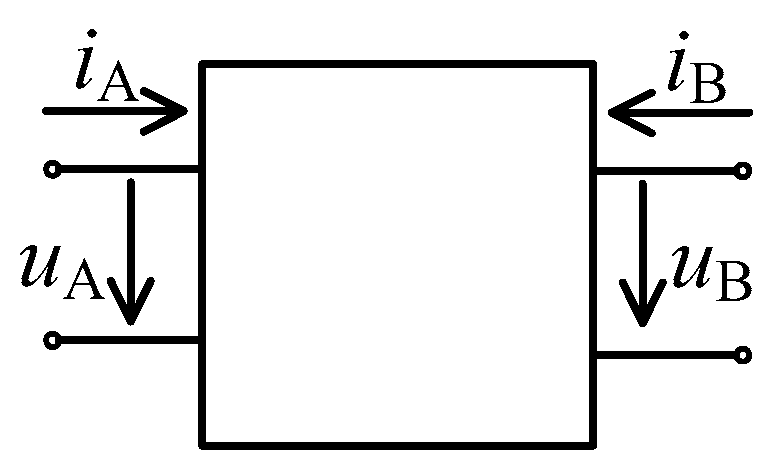
3.2. Gorev Equivalent Model of Transmission Line
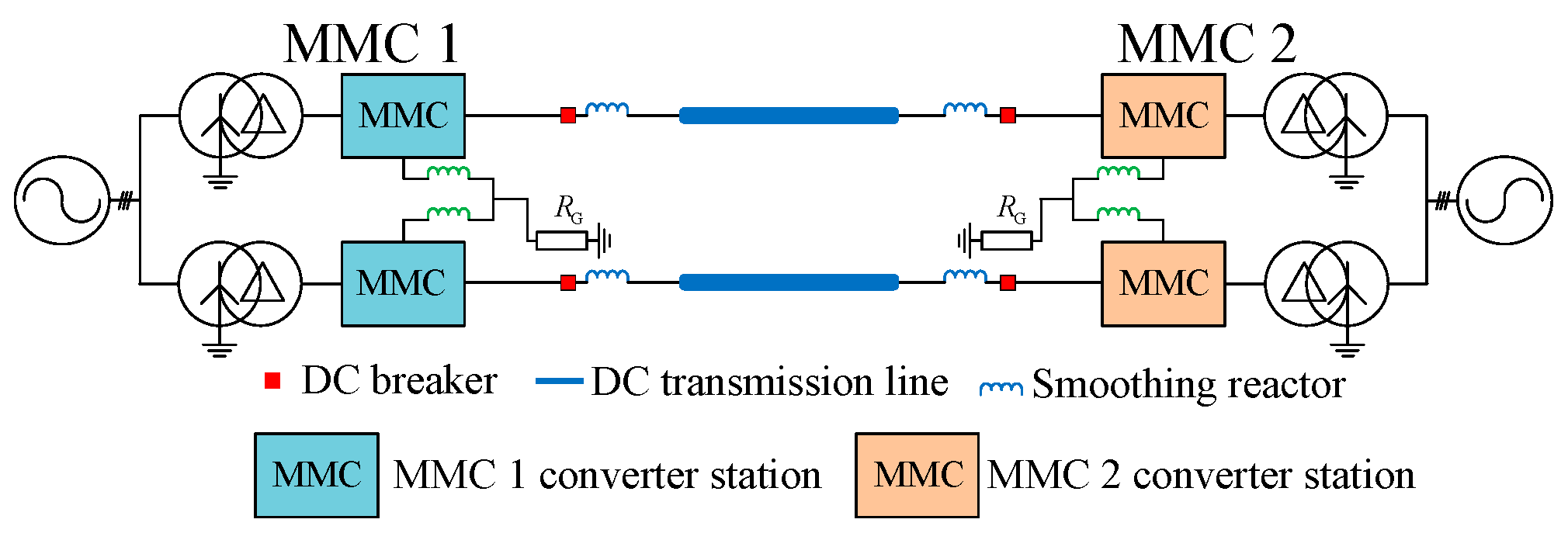
4. Short-Circuit Current Calculation Method for Flexible DC Transmission System with Distributed Parameters
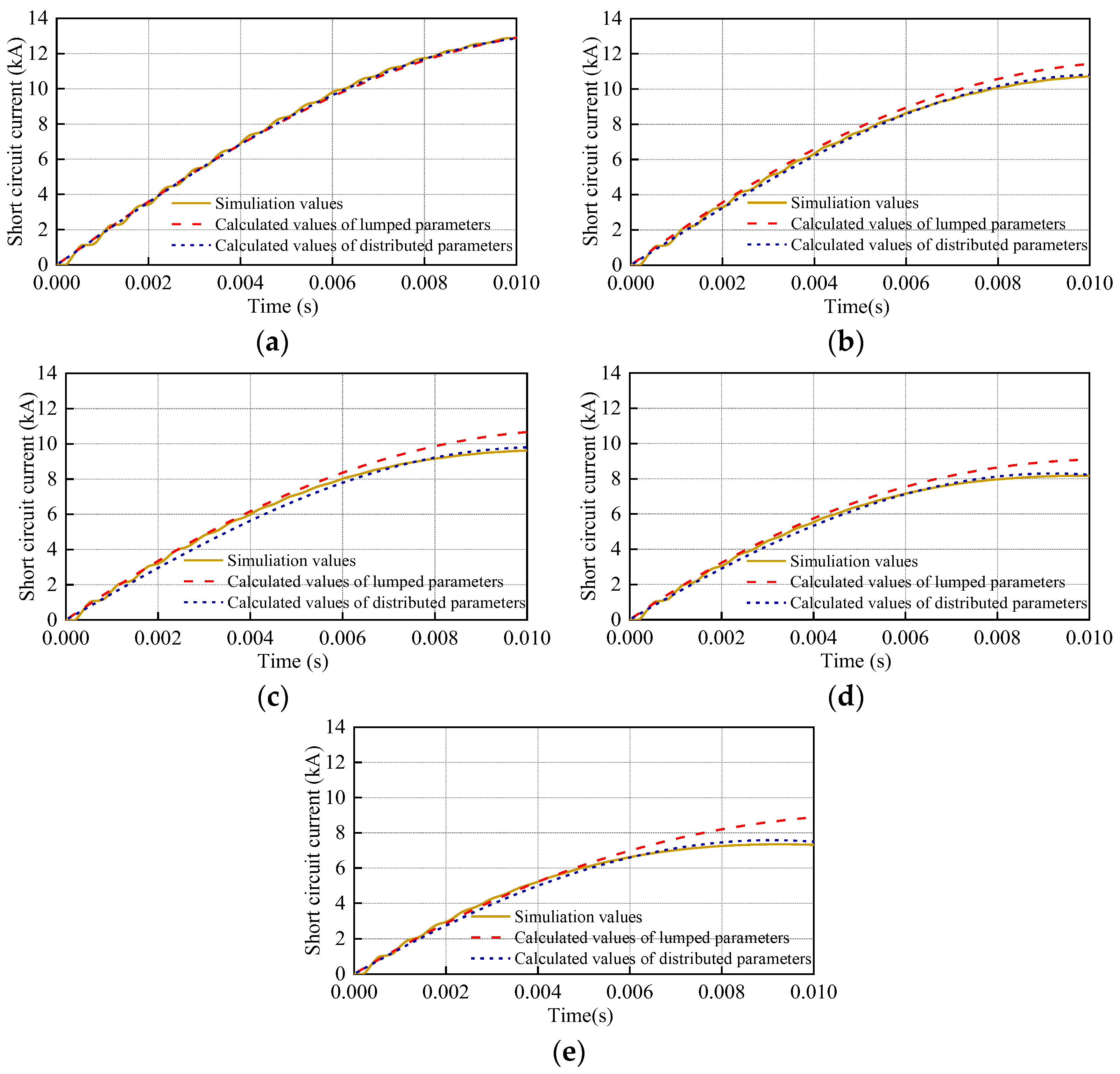
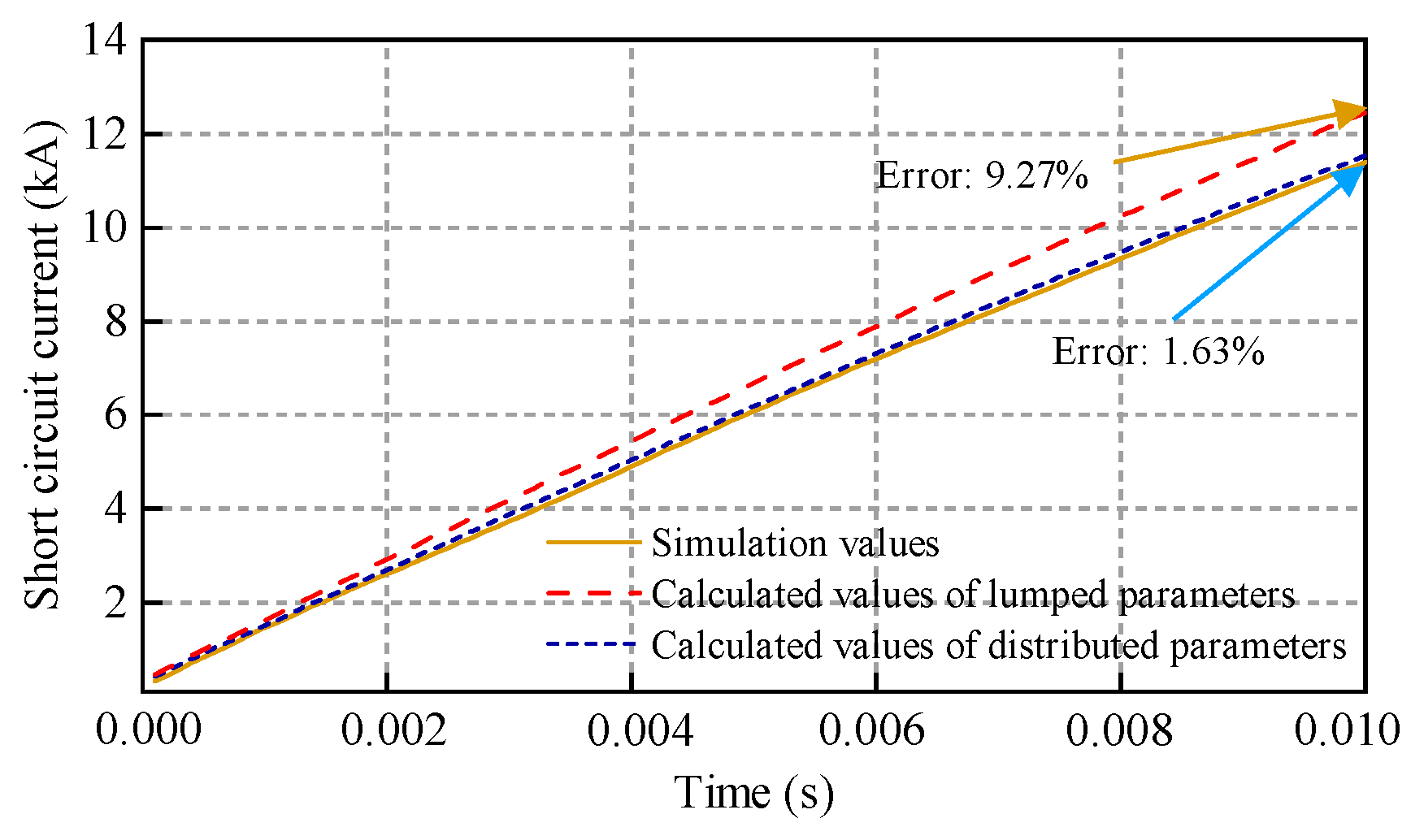
5. Simulation Verification
6. Conclusions and Limitations
- With an increase in the transmission line length, the error between the equivalent impedance calculated with the lumped parameter model and the equivalent impedance calculated with the distributed parameter model increases significantly. When the line length is less than 300 km, the equivalent reactance calculated with the lumped parameter model and the distributed parameter model is basically equal; when the line length exceeds 350 km, the equivalent reactance calculated with the lumped parameter model and the distributed parameter model is basically equal. The deviation in the equivalent reactance of the two models increases gradually with an increase in the line and reaches about twice the error at 1000 km.
- When the line length is less than 300 km, the lumped parameter model can be used for direct calculation; when the line length is 300–500 km, the circuit impedance is calculated with the modified coefficient method to solve the short-circuit current. When the line length is greater than 500 km, the Gorev method line equivalent model is used for calculation.
- Upon comparing the simulation and analytical calculation values for different fault distances, the results show that the analytical calculation values can better characterize the fault current characteristics and effectively reduce the error of the lumped parameter model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liao, Y.; Jin, L.; You, J.; Xu, Z.; Liu, K.; Zhang, H.; Shen, Z.; Deng, F. A Novel Voltage Sensorless Estimation Method for Modular Multilevel Converters with a Model Predictive Control Strategy. Energies 2024, 17, 61. [Google Scholar] [CrossRef]
- Wang, Z.; Hao, L.; He, J. Short-circuit current calculation on DC side of MMC-HVDC system with long distance transmission lines. In Proceedings of the 2023 3rd International Conference on Electrical Engineering and Control Science (IC2ECS), Hangzhou, China, 29–31 December 2023; pp. 300–306. [Google Scholar]
- Sun, Y.; Li, Z.; Zhang, Y.; Li, Y.; Zhang, Z. A Time-Domain Virtual-Flux Based Predictive Control of Modular Multilevel Converters for Offshore Wind Energy Integration. IEEE Trans. Energy Convers. 2022, 37, 1803–1814. [Google Scholar] [CrossRef]
- Wei, N.; Zhou, N.; Liao, J.; Luo, Y.; Wang, Q. A Parameters Optimal Method for Fault Current Limiting Devices of MMC Based on Fault Current Amplitude and Energy Limiting Contribution. Proc. CSEE 2021, 41, 3751–3764. [Google Scholar]
- Hu, K.; Mao, M.; He, Z.; Cheng, D.; Lu, H. Optimization of inductance parameters of main circuit for MMCHVDC grid based on transient energy suppression under DC short-circuit faults. Proc. CSEE 2022, 42, 1680–1690. [Google Scholar]
- Wang, Z.; Hao, L.; Wang, L.; He, J. Analysis and general calculation of DC fault currents in MMC-MTDC grids. Electr. Power Syst. Res. 2023, 224, 1809–1817. [Google Scholar] [CrossRef]
- Lin, S.; Li, X.; Lei, X.; Xie, G.; He, Y. Risk Analysis and Prevention Measures of Operation Mode Transformation for Zhangbei VSC-based DC Grid. Power Sys. Technol. 2023, 47, 4017–4025. [Google Scholar]
- Li, J.; Zhang, Z.; Li, Z.; Babayomi, O. Predictive Control of Modular Multilevel Converters: Adaptive Hybrid Framework for Circulating Current and Capacitor Voltage Fluctuation Suppression. Energies 2023, 16, 5772. [Google Scholar] [CrossRef]
- Lewis, P.; Grainger, B.; Hassan, H.; Barchowsky, A.; Reed, G. Fault Section Identification Protection Algorithm for Modular Multilevel Converter Based High Voltage DC with a Hybrid Transmission Corridor. IEEE Trans. Ind. Electron. 2016, 63, 5652–5662. [Google Scholar] [CrossRef]
- Deng, F.; Tian, Y.; Zhu, R.; Chen, Z. Fault-Tolerant Approach for Modular Multilevel Converters Under Submodule Faults. IEEE Trans. Ind. Electron. 2016, 63, 7253–7263. [Google Scholar] [CrossRef]
- Wang, Z.; Hao, L.; He, J. Research on Influence Factors in MMC-HVDC Short-Circuit Current Based on Improved Calculation Method. In Proceedings of the 2023 The 8th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 22–25 September 2023; pp. 44–50. [Google Scholar]
- Li, B.; Zhou, S.; Xu, D.; Yang, R.; Xu, D.; Buccella, C.; Cecati, C. An Improved Circulating Current Injection Method for Modular Multilevel Converters in Variable-Speed Drives. IEEE Trans. Ind. Electron. 2016, 63, 7215–7225. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Z. Short-circuit current calculation and performance requirement of HVDC breakers for MMC-MTDC systems. IEEJ Trans. Electr. Electron. Eng. 2016, 11, 168–177. [Google Scholar] [CrossRef]
- Wang, Z.; Hao, L.; Wang, L.; He, J. Calculation method of nonmetallic fault short circuit current in DC side of MMC-HVDC. Electr. Power Auto Equip. 2024, 44, 187–194. [Google Scholar]
- Li, M.; Luo, Y.; He, J.; Zhang, Y.; Meliopoulos, A. Analytical estimation of MMC short-circuit currents in the AC in-feed steady-state stage. IEEE Trans. Power Deliv. 2021, 37, 431–441. [Google Scholar] [CrossRef]
- Han, X.; Sima, W.; Yang, M.; Li, L.; Yuan, T.; Si, Y. Transient Characteristics Under Ground and Short-circuit Faults in a ±500 kV MMC-Based HVDC System with Hybrid DC Circuit Breakers. IEEE Trans. Power Deliv. 2018, 33, 1378–1387. [Google Scholar] [CrossRef]
- Xu, J.; Zhu, S.; Li, C.; Zhao, C. The Enhanced DC Fault Current Calculation Method of MMC-HVDC Grid with FCLs. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 1758–1767. [Google Scholar] [CrossRef]
- Li, C.; Zhao, C.; Xu, J.; Ji, Y.; Zhang, F. A Pole-to-pole short-circuit fault current calculation method for DC grids. IEEE Trans. Power Syst. 2017, 32, 4943–4953. [Google Scholar] [CrossRef]
- Langwasser, M.; Giobanni, D.; Liserre, M.; Biskoping, M. Improved Fault Current Calculation Method for Pole-to-Pole Faults in MMC Multi-Terminal HVDC Grids Considering Control Dynamics. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018. [Google Scholar]
- Langwasser, M.; Giobanni, D.; Liserre, M.; Biskoping, M. Fault Current Estimation in Multi-Terminal HVDC Grids Considering MMC Control. IEEE Trans. Power Syst. 2019, 34, 2179–2189. [Google Scholar] [CrossRef]
- Torwelle, P.; Bertinato, A.; Raison, B.; Le, T.; Petit, M. Fault current calculation in MTDC grids considering MMC blocking. Electr. Power Syst. Res. 2022, 207, 1–12. [Google Scholar] [CrossRef]
- Sun, P.; Jiao, Z.; Gu, H. Calculation of Short-Circuit Current in DC Distribution System Based on MMC Linearization. Front. Energy Res. 2021, 9, 634232. [Google Scholar] [CrossRef]
- Gu, J.; Hu, J.; Jiang, L.; Wang, Z.; Zhang, X.; Xu, Y.; Zhu, J.; Fang, L. Research on Object Detection of Overhead Transmission Lines Based on Optimized YOLOv5s. Energies 2023, 16, 2706. [Google Scholar] [CrossRef]
- Man, J.; Xie, X.; Tang, J.; Wang, Y.; Luo, Y. Transmission line modeling for high frequency resonance analysis of MMC-HVDC systems. Power Syst. Technol. 2021, 45, 1782–1789. [Google Scholar]
- Li, Z.; Dai, Z.; Shi, X.; Yang, M. Approximate Calculation Method of Short-Circuit Current of Multi-Terminal Hybrid DC Transmission System Considering Control Strategy. Trans. China Electrotechnol. Soc. 2024, 39, 2810–2824. [Google Scholar]
- Souza, N.; Carvalho, C.; Kurokawa, S.; Pissolato, J. A Distributed-parameters Transmission Line Model Developed Directly in the Phase Domain. Electr. Mach. Power Syst. 2013, 41, 1100–1113. [Google Scholar] [CrossRef]
- Xie, R.; Zhang, G.; Xie, B. Analysis and Suppression of Harmonic Instability for Grid-connected Inverter System Considering Characteristics of Long Transmission Cable. Auto Electr. Power Syst. 2024, 48, 128–139. [Google Scholar]
- Ma, J.; Shi, Y.; Ma, W.; Wang, Z. Location Method for Interline and Grounded Faults of Double-Circuit Transmission Lines Based on Distributed Parameters. IEEE Trans. Power Deliv. 2015, 30, 1307–1316. [Google Scholar] [CrossRef]
- Nie, Y.; Liu, Y.; Pan, R.; Lu, D.; Fan, R. Convolution Based Time Domain Fault Location Method for Lines in MMC-HVDC Grids with Distributed and Frequency Dependent Line Model. IEEE Trans. Power Deliv. 2023, 38, 3860–3874. [Google Scholar] [CrossRef]
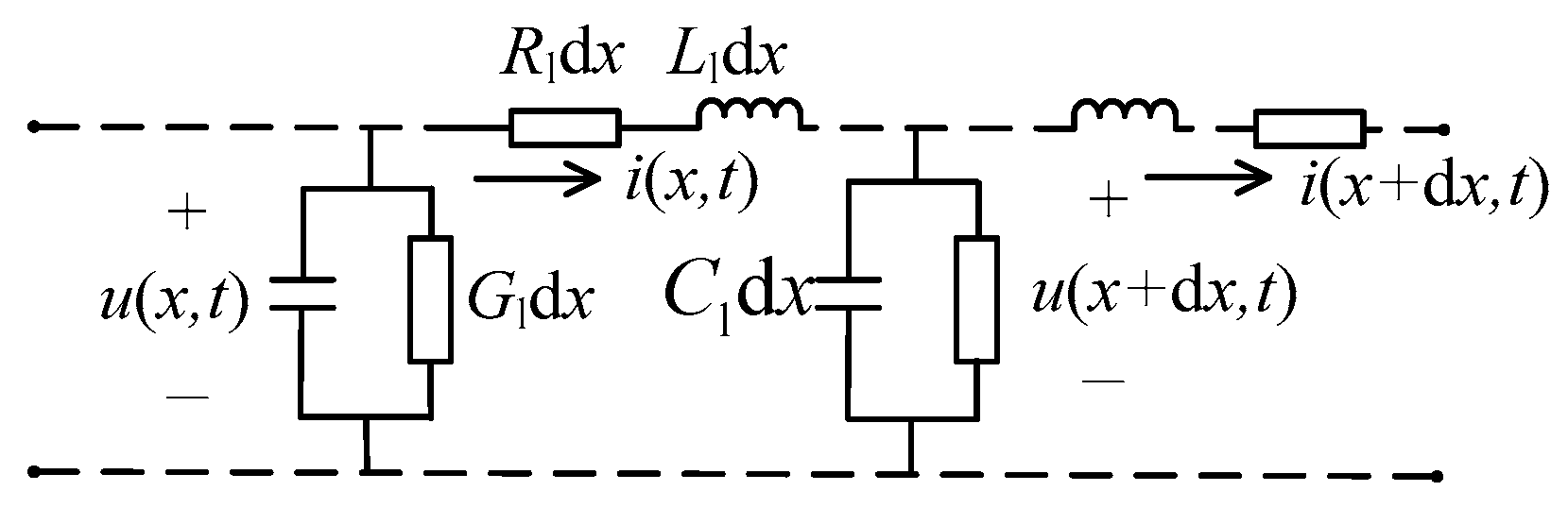
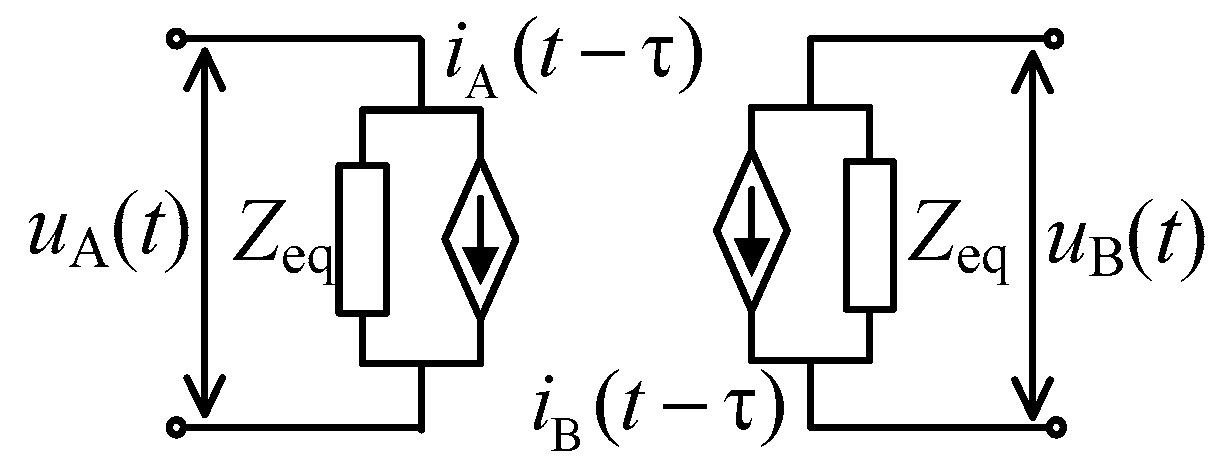

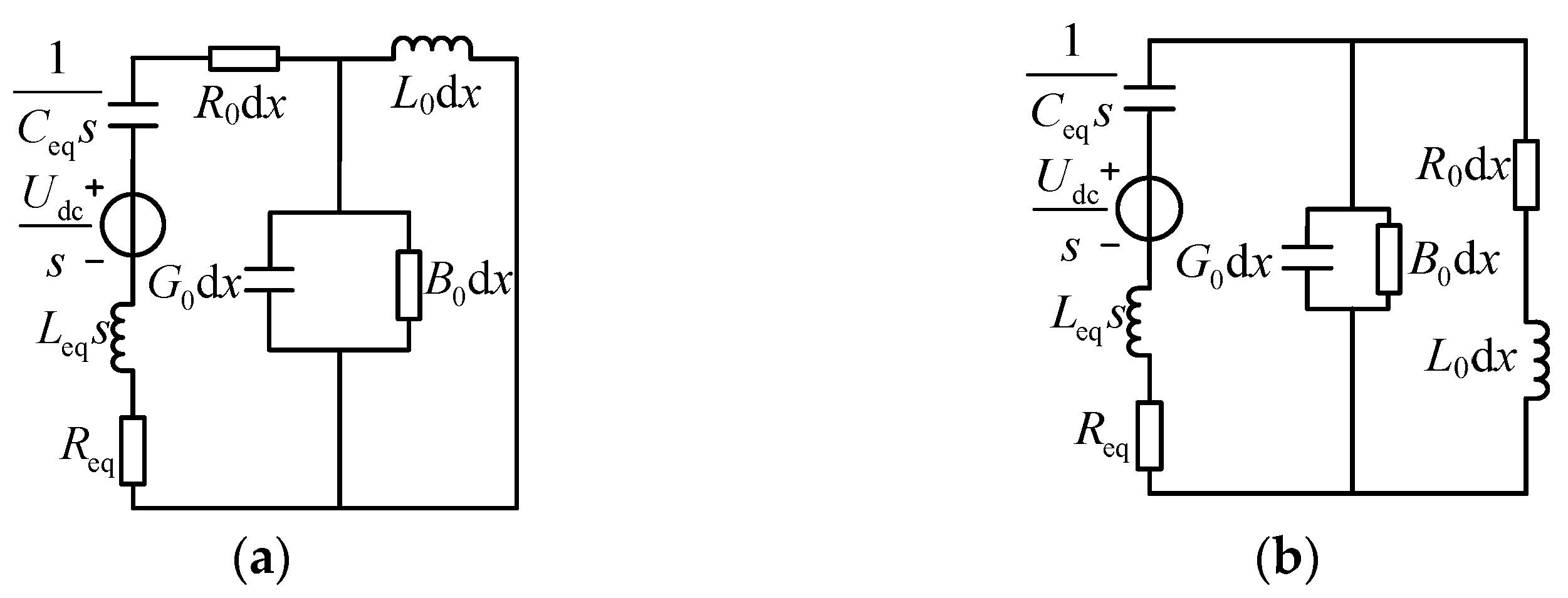



| Line Length | kr | kx | kb |
|---|---|---|---|
| 50 km | 0.99905 | 0.99953 | 1.00024 |
| 100 km | 0.99622 | 0.99812 | 1.00095 |
| 150 km | 0.99151 | 0.99577 | 1.00213 |
| 200 km | 0.98493 | 0.99250 | 1.00380 |
| 250 km | 0.97650 | 0.98829 | 1.00595 |
| 300 km | 0.96624 | 0.98316 | 1.00859 |
| 350 km | 0.95418 | 0.97712 | 1.01174 |
| 400 km | 0.94034 | 0.97018 | 1.01590 |
| 450 km | 0.92477 | 0.96236 | 1.01950 |
| 500 km | 0.90548 | 0.95274 | 1.02363 |
| 550 km | 0.88563 | 0.94282 | 1.04881 |
| Parameters | Values |
|---|---|
| Bridge arm reactor | 100 mH |
| Rated voltage of submodule | 2.05 kV |
| Submodule capacitance | 10 mF |
| Number of submodule | 244 |
| Arm loss equivalent resistance | 0.5 Ω |
| Rated capacity | 850/3 MVA |
| Parameters | Values |
|---|---|
| Line resistance | 0.00995 Ω/km |
| Line inductance | 0.86 mH/km |
| Smoothing reactor | 200 mH |
| Rated voltage of DC side | ±500 kV |
| Distance from the Fault Point | Lumped Parameter Calculation Error | Distribution Parameters Calculation Error |
|---|---|---|
| 0 km | 0.06% | 0.25% |
| 600 km | 6.67% | 0.93% |
| 1000 km | 10.1% | 1.92% |
| 1600 km | 11.36% | 0.74% |
| 2000 km | 10.27% | 0.66% |
| Parameters | MMC 1, MMC 2 | MMC 3, MMC 4, MMC 5, MMC 6 |
|---|---|---|
| Bridge arm reactor | 100 mH | 50 mH |
| Submodule capacitance | 10 mF | 15 mF |
| Number of submodule | 244 | 244 |
| Arm loss equivalent resistance | 0.5 Ω | 0.5 Ω |
| Rated capacity | 1500 MW | 3000 MW |
| Parameters | Values |
|---|---|
| Line resistance | 0.00995 Ω/km |
| Line inductance | 0.86 mH/km |
| Smoothing reactor | 200 mH |
| Length of cable 12 | 1500 km |
| Other cable lengths except cable 12 | 200 km |
| Rated voltage of DC side | ±500 kV |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Hao, L.; Wang, Z. Short-Circuit Current Calculation of Flexible Direct Current Transmission Lines Considering Line Distribution Parameters. Energies 2024, 17, 3800. https://doi.org/10.3390/en17153800
Wang Z, Hao L, Wang Z. Short-Circuit Current Calculation of Flexible Direct Current Transmission Lines Considering Line Distribution Parameters. Energies. 2024; 17(15):3800. https://doi.org/10.3390/en17153800
Chicago/Turabian StyleWang, Zhuoya, Liangliang Hao, and Zemin Wang. 2024. "Short-Circuit Current Calculation of Flexible Direct Current Transmission Lines Considering Line Distribution Parameters" Energies 17, no. 15: 3800. https://doi.org/10.3390/en17153800
APA StyleWang, Z., Hao, L., & Wang, Z. (2024). Short-Circuit Current Calculation of Flexible Direct Current Transmission Lines Considering Line Distribution Parameters. Energies, 17(15), 3800. https://doi.org/10.3390/en17153800






