Abstract
This paper introduces an innovative approach to address the distribution network reconfiguration (DNR) challenge, aiming to reduce power loss through an advanced hyperbolic tangent particle swarm optimization (HT-PSO) method. This approach is distinguished by the adoption of a novel hyperbolic tangent function, which effectively limits the rate of change values, offering a significant improvement over traditional sigmoid function-based methods. A key feature of this new approach is the integration of a tunable parameter, , into the HT-PSO, enhancing the curve’s adaptability. The careful optimization of ensures superior control over the rate of change across the entire operational range. This enhanced control mechanism substantially improves the efficiency of the search and convergence processes in DNR. Comparative simulations conducted on 33- and 94-bus systems show an improvement in convergence, demonstrating a more exhaustive exploration of the search space than existing methods documented in the literature based on PSO and variations where functions are proposed for the rate of change of values.
1. Introduction
In electric energy distribution systems (EEDSs) with a radial topology, strategically placed medium-voltage switches are crucial for operational and maintenance efficiency. The actuation of these switches, either by opening or closing, alters the network topology, thereby affecting energy losses predominantly due to the Joule effect. This energy loss presents a significant challenge for distribution companies. In order to mitigate it, several strategies are employed, including the installation of step-up transformers and phase shifters to improve voltage profiles, the replacement of electrical cables, the integration of capacitor banks and distributed generation, and the strategic adjustment of switch states. These methods aim to optimize network configurations, reducing Joule effect losses, as detailed in the studies referenced in [1,2].
Distribution network reconfiguration (DNR), a technique involving the strategic opening and closing of switches, stands as one of the most cost-effective methods for reducing energy losses in electric distribution networks. In the realm of optimization within these networks, there are five methodologies [3], but three primary approaches are distinguished [4]. The first, which is a classical approach, encompasses methods such as linear, nonlinear, and dynamic programming. However, these traditional techniques have been found to lack efficiency [5]. Heuristic-based approaches always give fast reconfiguration results and are based on distribution network operational experience; hence, they are simple to formulate. However, these methods do not necessarily always give the global optimum values [4]. In contrast, the third approach, rooted in metaheuristics, represents a more recent development and guaranteed global optimal results [4]. This approach has demonstrated promising results in solving complex optimization problems, marking a significant advancement in the field.
In the domain of metaheuristics for optimization in power systems and DNR, the technical literature presents a diversity of innovative approaches. Y. Shan. [6] proposed a holistic energy optimization and control strategy for microgrids. In addition, they designed an evolutionary PSO algorithm to generate the optimal active and reactive power setpoints, which are then sent to the device level for controlling inverters. Subsequently, Y. Shan. [7] presented a model of a hybrid microgrid that comprises both AC and DC subgrids, and the optimal power guidance value was determined using the PSO algorithm. Pegado R. [8] employed improved selective binary particle swarm optimization (IS-BPSO), introducing a novel sigmoidal function that enhances particle rate of change control and convergence efficiency. Gerez C. [1] adopted a selective firefly algorithm, uniquely incorporating a load flow analysis criterion (LFAC) to refine and reduce the search space for DNR optimization. Thanh N. [9] explored the initial search point (ISP) method to augment the efficiency of the continuous genetic algorithm (CGA), focusing on minimizing energy loss in DNR. Silva L. [10] utilized PSO in conjunction with mesh analysis, a technique aimed at narrowing the search space in DNR problems. Lastly, Thuan T. [11] proposed an enhanced binary cuckoo search algorithm (EBCSA), which is a novel adaptation of the continuous cuckoo search algorithm (CSA) into a binary format complemented with a local search mechanism.
In the sphere of recent advancements, Wu, Y. [12] proposed an algorithm named chaotic particle swarm chicken swarm fusion optimization (CPSCSFO), which was used to optimize the DNR using distributed generation (DG). They used the chaotic formula to improve the initialization of particles and optimize the optimal position. In order to improve the availability and robustness of the solutions, Li, X. [13] proposed an improved discrete multi-mode multi-objective particle swarm optimization (IDMMPSO) algorithm to solve the distribution network fault reconfiguration problem. Alanazi, A. [14] used improved particle swarm optimization (IPSO) for improving distribution system performance by concurrently deploying remote-controlled sectionalized switches to solve the problem effectively and, at the same time, to improve conventional PSO exploration and exploitation capabilities; they developed a novel chaotic inertia weight and cross-operation mechanism. Other works, such as those of Fathi, R. [15], present an optimal and simultaneous allocation of photovoltaic panels and wind turbines with DNR to reduce the cost of energy losses and improve reliability. They developed an improved salp swarm algorithm (ISSA). They also used differential evolutionary algorithm operators to improve the performance of the conventional salp swarm algorithm (SSA) to avoid trapping in local optima and increase the speed of convergence to achieve the global optimal solution. A. Azizi [16] presented an active distribution networks (ADNs) reconfiguration approach that includes distributed generation (DG) sources, soft open points (SOPs), and protection devices. This approach selects the ideal configuration, DG output, and SOP placement and control by employing PSO to minimize power loss while ensuring the correct operation and protection of devices under normal and fault conditions. Vargas, G.A.D. [17] addressed a comprehensive analysis of power electrical systems by using a combined approach of genetic algorithms and mathematical optimization through discontinuous nonlinear programming (DNLP) in GAMS. The main objective was to minimize the economic losses and associated costs faced by the network operator after disruptive events as well as DNR addresses.
Amirreza N. [18] contributed a novel perspective to the DNR challenge by employing the immune herd optimizing algorithm (ICHIOA), a metaheuristic inspired by herd immunity strategies against COVID-19. This approach uniquely incorporates social distancing concepts and an innovative strategy for determining a nonlinear decreasing inertial weight, significantly enhancing both local and global exploration capabilities in DNR. Meanwhile, Hong-Jiang W. [19] tackled the DNR problem, specifically in networks with distributed generation, through the application of the parallel slime mold algorithm (PSMA). This method represents an evolution in metaheuristic techniques, offering new dimensions of efficiency and effectiveness in addressing DNR complexities.
Metaheuristic techniques, while potent in yielding favorable outcomes, hinge critically on the precise tuning of their parameters. This calibration is particularly crucial in PSO, where optimizing the exploration of the search space is a key determinant of success. Consequently, this area presents a substantial opportunity for groundbreaking research. Future studies that delve into innovative ways to enhance PSO search space exploration hold the promise of uncovering superior solutions, further advancing the field.
In tackling the intricate task of network reconfiguration in distribution systems, metaheuristic techniques emerge as prominent solutions. Specifically, PSO is used frequently [7,20], and its efficacy in addressing various challenges within the electrical sector has been demonstrated. With pertinent enhancements, this metaheuristic holds the potential to yield even more efficient results for resolving the network reconfiguration problem.
This paper presents a new and improved method to address the DNR problem: the hyperbolic tangent particle swarm optimization (HT-PSO) approach. This method uses the hyperbolic tangent function, which serves to better constrain the rate of change values, , within the range [0.0–1.0]. This approach changes the traditional sigmoid transfer function commonly employed in PSO, as documented in previous studies [8,10]. Furthermore, the method incorporates a parameter, , specifically introduced to adjust the steepness of the curve, demonstrating a more exhaustive exploration of the search space than existing methods documented in the literature based on PSO and variations where functions are proposed for the rate of change of values.
This paper applies the proposed HT-PSO method to two distribution systems frequently referenced in the existing literature, setting the stage for a comparative analysis with other modified PSO-based methods. The key contributions of this study are outlined as follows:
- The introduction of a novel hyperbolic tangent function allows for more precise control over the rate of change values, , within the range of [0.0–1.0]. This enhanced control facilitates the discovery of optimal solutions in particles’ behavior.
- By integrating the parameter, the method significantly improves the exploration of the search space, thereby enabling faster identification of the best solutions. This enhancement is directly attributable to the nuanced adjustability offered by the parameter.
- The optimal value of is efficiently determined through a novel algorithm that utilizes the sum of least squares method, applied selectively across different switch spaces (number of switches). This approach eliminates the need for extensive trial-and-error testing to establish the parameter’s optimal value.
- The proposed HT-PSO method notably enhances the convergence rate of the population and reduces the number of iterations required to reach the optimal solution, thereby increasing the overall efficiency of the problem-solving process.
The structure of this paper is systematically organized into several sections to provide comprehensive coverage of the topic. Section 2 introduces the mathematical formulation of the DNR problem. In Section 3, we present the newly proposed HT-PSO method, elaborating on its conceptual framework and operational mechanics. Section 4 is dedicated to the application of the HT-PSO method to the reconfiguration problem, showcasing its practical implementation. Provides a detailed analysis of the results obtained from applying the proposed method to 33- and 94-bus systems, including a comparative assessment with other existing methods.
2. Distribution Network Reconfiguration (DNR)
DNR plays a pivotal role in distribution automation. Under standard operational conditions, DNR enables the network to be configured in a manner that minimizes total power losses, primarily attributed to the Joule effect. This reconfiguration facilitates the adaptation of network topology to achieve specific objectives, such as alleviating any critical load sections of the network through effective load balancing.
In scenarios where multiple objectives are considered, DNR becomes even more significant. It prominently addresses various goals, including but not limited to the minimization of power losses, transformer load balancing, feeder load equalization, maximizing feeder capacity, and voltage profile enhancement. Despite these diverse objectives, the principal aim of DNR remains the reduction of active power losses within the system. This objective must be achieved while adhering to crucial operational constraints, such as maintaining voltage limits, ensuring radial network structure, and respecting the current carrying capacities of the network branches.
2.1. Fitness Function
In the context of DNR, the effectiveness of the optimization process hinges critically on the predefined fitness function, also known as the evaluation function. This function, which was tailored to suit the specific requirements of the problem at hand, is a key determinant of both the search space’s nature and the problem’s inherent complexity. This function must be optimized to facilitate accurate and efficient problem-solving. For the critical task of power flow calculation, this study utilizes the OpenDSS software, Version 10.0.0.2—Columbus, a proven tool in the field of power distribution analysis.
The fitness function, designed with the primary goal of minimizing system losses, is articulated in Equation (1).
where
- represents the total number of lines;
- denotes the resistance of line l;
- is the current flowing through line l.
2.2. Operational Limitations
In the process of DNR, it is crucial to adhere to three primary operational constraints: (a) voltage limits, (b) the current limits of the lines, and (c) the radiality of the network.
(a) Voltage Limits: The voltage levels at the buses must be maintained within the thresholds prescribed by regulatory standards. Adhering to these voltage limits is crucial for ensuring the stability and reliability of the power system. These limits are mathematically represented by the following equation (see Equation (2)):
where
- represents the minimum permissible voltage at bus k;
- denotes the maximum permissible voltage at bus k.
These limits typically correspond to a range of up to 5% for overvoltage and 7% for undervoltage conditions.
(b) Current Limits: In a power system, it is crucial to ensure that the current flowing through any conductor does not exceed its maximum allowable limit, as defined by Equation (3). Exceeding this limit can result in the excessive heating of the conductor, leading to increased network losses due to Joule heating. Furthermore, it can potentially reduce the lifespan of the conductor due to thermal stress and material degradation.
where
- represents the current flowing through conductor l;
- denotes the maximum permissible current for conductor l beyond which the safety and efficiency of the power system may be compromised.
(c) Radiality of the Network: The distribution network must maintain its radial structure, which ensures that there is a single power path from any bus to its substation. This condition is achieved by appropriately managing the opening and closing states of switches. Maintaining a radial structure prevents the formation of loops within the network, ensuring that all loads are connected and energized by the substation. This requirement is mathematically represented by Equations (4) and (5) [21].
The total number of lines in the system should be [22]
- M is the total number of active lines;
- is the number of buses;
- is the number of sources.
The total number of meshes obtained by closing all interlocking switches must be
- is the number of meshes;
- is the total number of interconnection switches.
It is important to note that maintaining a radial structure requires that only one switch be opened in each mesh. This ensures network reliability and efficiency, aligning with the overarching goal of optimizing power system operations [23].
3. Proposed Method
3.1. Hyperbolic Tangent Particle Swarm Optimization (HT-PSO)
The hyperbolic tangent function (HTF), widely utilized as an activation function in artificial neural networks (ANNs) [24], has recently been adopted as a transfer function in nature-inspired swarm algorithms such as the tunicate swarm algorithm (TSA) [25]. This function’s tunable parameters render it highly suitable for optimization applications.
In power system research, particularly in transmission network expansion planning, heuristic and metaheuristic algorithms are prevalent due to the binary nature of decision-making. A novel approach in this domain involves the adjustment of the HTF slope within the optimization process, enhancing the generation of sensitive, high-quality candidate solutions [26].
Y. Lee’s research [27] employs the HTF, along with various bounded functions for , in the PSO method to regulate global particle exploration. Their findings suggest that bounding with the HTF produces superior results compared to the sigmoid function.
The proposed HT-PSO method leverages the HTF to constrain the rate of change within the range [0.0–1.0]. Unlike previous studies [1,8,10] that utilized the sigmoid function, this approach incorporates a parameter to adjust the curve’s steepness. This modification effectively controls the rate of change of , thereby improving the search process’s efficiency and convergence. The new function is defined in Equations (6) and (7).
The HTF introduced in the HT-PSO method exhibits an “S”-shaped curve, similar to the sigmoid function. Despite this similarity, the addition of the parameter in the hyperbolic tangent function preserves its “S”-shaped characteristic. A critical comparison between the sigmoid function and HTF reveals notable differences in their impact on the algorithm’s exploration capabilities.
For the sigmoid function, as depicted in Figure 1a, smaller values of result in a constrained rate of change, typically ranging between [0.14–0.88]. This restriction limits the range of probabilities for , potentially impeding effective exploration. In contrast, the HTF, as shown in Figure 1b, maintains a probability range between [0.0–1.0], even with smaller values of . This extended range enhances the algorithm’s exploration capacity and increases the likelihood of assuming new values, thereby improving the search for optimal solutions. These differences are illustrated in Figure 1.
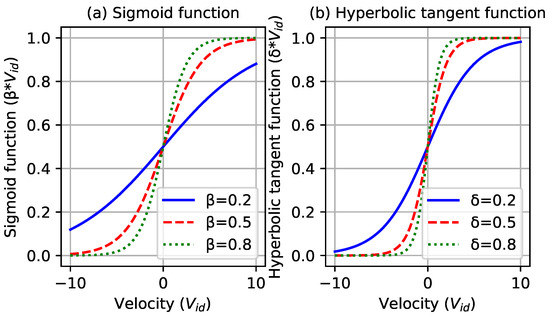
Figure 1.
Behavior comparison of the functions at different values of and .
The broader probability range of the HTF underscores its superiority in ensuring comprehensive exploration within the HT-PSO framework. This feature renders it a more robust and efficient choice for tackling complex optimization problems.
The parameter in the HT-PSO method is pivotal for optimizing the function’s behavior. In order to ascertain the optimal value of , an algorithm is utilized that focuses on minimizing the sum of least squares between the data points generated by the HT-PSO function, defined in Equation (6), and a standard linear model, the equation of which is presented in (8). This minimization process is executed within each selective space , ensuring that is fine-tuned to the specific dynamics of each space.
The optimal algorithm finds and evaluates each HT-PSO curve with different values of . The result will be the HT-PSO curve that has a minimum value of (Figure 2).
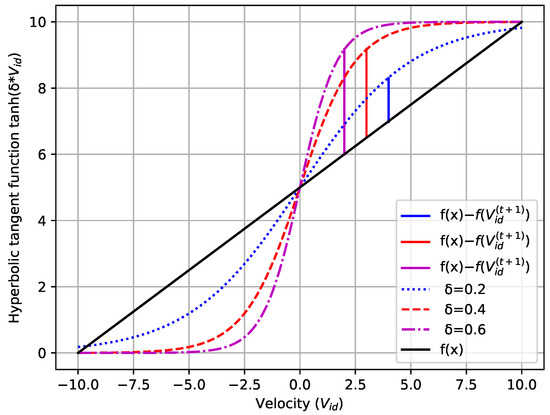
Figure 2.
Method to determine the optimal .
The parameter plays a critical role in the HT-PSO method, particularly in determining the extent of exploration for new values within each selective space of the mesh, defined by the number of switches. The optimal values of are determined by the algorithm for various selective spaces , reflecting how this parameter influences the search process in different scenarios. Table 1 presents the optimal values obtained for different selective spaces :

Table 1.
Optimal values.
3.2. Application of the Proposed HT-PSO Algorithm in DNR
The data presented in Table 1 elucidates an interesting trend regarding the values of concerning the size of the selective spaces in the HT-PSO method. It is observed that the values of tend to decrease as the size of the selective space increases, with a minimum threshold set at 0.1. This trend suggests that smaller values of are more effective in larger selective spaces.
This phenomenon can be attributed to the increased probability of the variable taking on new values in larger selective spaces when is smaller. Such a setting is advantageous in scenarios where a wide range of potential solutions exists, as it enhances the exploration capabilities of the HT-PSO algorithm in these extensive selective spaces.
The HT-PSO algorithm is applied in the DNR process as follows:
- Input data, network configuration (line data), inertial weight limits (), social and cognitive learning parameters (), maximum number of iterations , the particle population (m), and search limits ().
- Declare the search spaces () and dimensions (). The search space comprises branches that are part of a mesh, and represents the number of meshes.
- Generate the initial population and velocities randomly, along with and .
- Increment iteration count: iter = iter + 1.
- Calculate the fitness function for each particle using load flow calculations, which are typically performed using tools such as OpenDSS.
- Update and with new values.
- The stopping criterion: if the number of iterations reaches , terminate; otherwise, return to step 5.
- Displays the results.
The complete flowchart of the HT-PSO algorithm in DNR is presented in Figure 3.
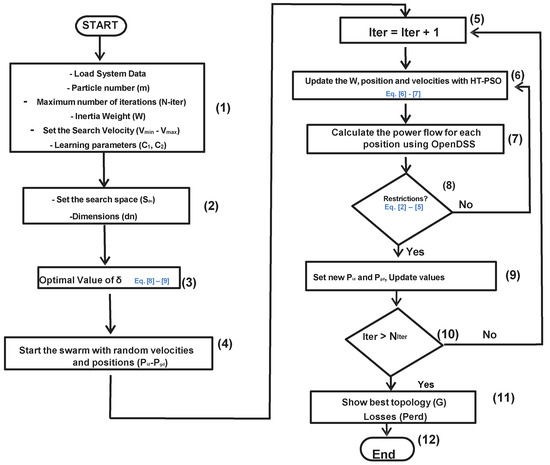
Figure 3.
Flow chart of the proposed method.
4. Simulation and Results
The HT-PSO method was deployed to address the DNR challenges within the extensively benchmarked 33-bus and 94-bus distribution systems. The HT-PSO algorithm was developed using Python 3.12 and facilitated through the Visual Studio Code environment, with OpenDSS Software, Version 10.0.0.2 - Columbus, serving as the interface for executing power flow calculations. The configuration of the implemented parameters of HT-PSO was meticulously chosen based on authoritative sources within the field; both cognitive learning factors, and , were set to 2, as recommended by Kennedy [28], while the inertial weight bounds were designated as and , following the guidance of Pegado [8] for radial distribution systems. These parameter settings are considered optimal within the existing literature, ensuring that the HT-PSO approach aligns with best practices for solving DNR problems.
On the other hand, to ensure the fairness of the comparative experiments across the five methods evaluated (HT-PSO, IS-BPSO [4], SPSO [16], N.H.A. Rahman [23], and J. Dong [24]), we adhered to a consistent experimental framework. All methods were implemented within the same software environment (Python in Visual Studio Code), utilizing an identical interface for the power flow calculations facilitated by OpenDSS. In order to maintain comparability, the experiments were standardized in terms of the number of iterations and particle sizes across the different methods. Specifically, for the 33-bus system tests, a maximum of 40 iterations with a particle count of 30 was employed, whereas for the 94-bus system tests, the parameters were adjusted to a maximum of 60 iterations and a particle count of 60. This consistency in experimental setup ensured that the comparative analysis of the methods was conducted on an equitable basis, allowing for a fair evaluation of their respective performances.
4.1. Case Study: 33-Bus System
The first case study involves the 33-bus system proposed by E. Baran and F. Wu in 1989 [29]. This system comprises 33 busbars, 32 fixed lines, five switchable lines, and no reactive compensation unit. Five meshes with 32 closed switches (s1 to s32) and five open switches (s33, s34, s35, s36, and s37) were considered for the case study [8]. The one-line diagram of this system is shown in Figure 4. The initial conditions include a total active load of 3715 kW, a reactive load of 2300 kvar, and total system losses of 202.67 kW. The maximum number of iterations for the system tests was set to 40, and the number of particles used was 30.
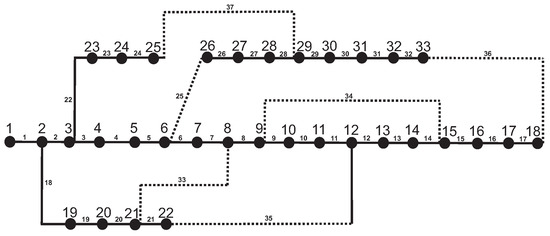
Figure 4.
Diagram of the distribution system test case 1.
In the literature, the optimal solution for this case involved opening switches S7, S9, S14, S32, and S37 [8,30]. The proposed HT-PSO method successfully found this optimal solution, resulting in a minimum active loss of 139.32 kW. Simulations were conducted to compare the computational performance and efficiency of the proposed method with other approaches, as summarized in Table 2.

Table 2.
Comparison between the results of the system of case study 1 for different methods in 100 trials.
Table 2 shows that using the proposed HT-PSO method and the IS-BPSO method (it should be noted that with the IS-BPSO method, tests have to be carried out for different values of ranging from 0.1 to 2.0 in 100 random trials [8]. These tests make the process of finding the best solution take 10 times longer than HT-PSO), the best solution is obtained in all tests (standard deviation equal to 0), and, at the same time, better convergence characteristics concerning the other implemented methods were obtained. The use of the hyperbolic tangent function and the parameter makes the proposed method more efficient than the others. It is superior to IS-BPSO due to the algorithm being implemented to find the optimal value of without the need to perform tests (see Figure 2), leading to the repeatability of the results and convergence in a few iterations (Figure 5).
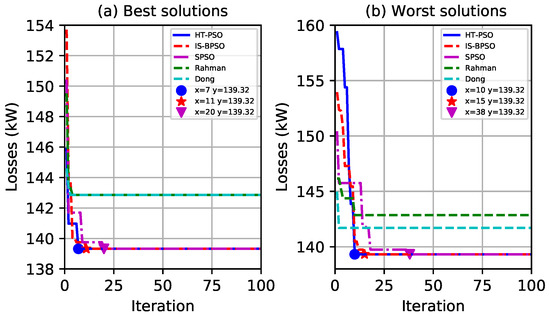
Figure 5.
Convergence of methods for the case study of a 33-bus system.
When analyzing Figure 5a,b, it is evident that the proposed HT-PSO method exhibits superior convergence compared to the other methods when considering a maximum of 100 iterations. In Figure 5a, the optimal solution is achieved at iteration 7 using HT-PSO, while the IS-BPSO method [8] and SPSO [31] converge at iterations 11 and 20, respectively. Similarly, in Figure 5b, the optimal solution is obtained in 10 iterations using HT-PSO, 13 iterations using IS-BPSO, and 38 iterations using SPSO. Notably, Figure 5a,b also demonstrate that the Rahman algorithms [32] and Dong [33] fail to achieve convergence with the optimal solution.
4.2. Case Study: 94-Bus System
For the second case study, the 94-node system was utilized, and the line and bus data were sourced from Ching-Tzong Su [34]. This 11.4 kV, three-phase system comprises 11 feeders, 83 normally closed, and 13 normally open switches, as illustrated in Figure 6. The voltage constraints were set using Vmax = 11.97 kV and Vmin = 10.83 kW. The total active losses calculated before reconfiguration amount to 531.99 kW [34]. The system tests employed a maximum of 60 iterations and a particle count of 60.
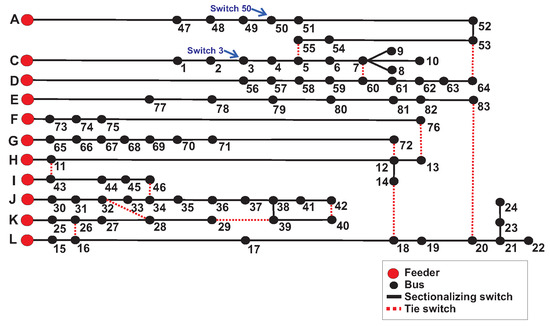
Figure 6.
Diagram of the distribution system for test case 2.
In the existing literature, the optimal solution configuration involved opening switches 55, 7, 86, 72, 13, 89, 90, 83, 92, 39, 34, 42, and 62 [8]. The proposed HT-PSO method successfully identified this optimal configuration, resulting in a minimum active loss of 470.95 kW. Comparative simulations were conducted to evaluate the performance and efficiency of the proposed method, alongside other existing methods, as summarized in Table 3.

Table 3.
Comparison between the results of the system of case study 2 for different methods in 100 trials.
Table 3 illustrates that the newly proposed HT-PSO method consistently delivers the best solution in all tests, characterized by a standard deviation of 0. The IS-BPSO method follows as the second-best solution with a standard deviation of 2.307, while the SPSO method ranks third with a standard deviation of 4.49. In contrast, the N.H.A. Rahman algorithm fails to converge to the optimal result in all tested scenarios. As a result, the HT-PSO method demonstrates superior convergence characteristics compared to the other implemented methods.
When analyzing Figure 7a,b, the proposed HT-PSO method demonstrates superior convergence performance compared to other methods within a maximum of 100 iterations. In Figure 7a, HT-PSO achieves the optimal solution by iteration 18, whereas the IS-BPSO method [8] and SPSO [31] converge at iterations 25 and 32, respectively. Similarly, in Figure 7b, HT-PSO finds the optimal solution in 25 iterations, compared to 30 iterations for IS-BPSO and 38 iterations for SPSO. Notably, Figure 7a,b also reveal that the Rahman algorithms [32] fail to converge to the optimal solution. These results highlight the enhanced efficiency and reliability of the HT-PSO method in achieving faster convergence to optimal solutions in comparison to traditional methods.
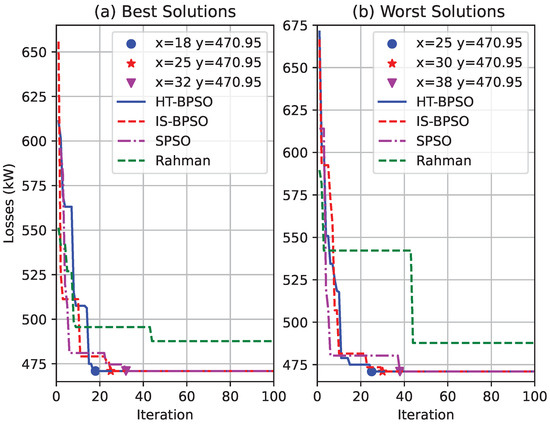
Figure 7.
Convergence of methods for the 94-bus system case study.
5. Conclusions
This paper introduces the HT-PSO method, a novel approach that employs the HTF to restrict the rate of change within the range [0.0–1.0], departing from the commonly used sigmoid function. This modification enhances the probability of assuming new values, facilitating increased exploration within the search space.
Furthermore, the addition of a tunable parameter to adjust the curve’s accentuation further improves search space exploration, expedites the discovery of optimal solutions, and reduces active power losses. An algorithm was developed to determine the optimal value of based on the sum of least squares, eliminating the need for exhaustive testing.
Simulation results across 33- and 94-bus distribution networks demonstrate that the HT-PSO method effectively minimizes active power losses. When compared to existing methods in the literature based on PSO and variations where functions are proposed for the rate of change of values, HT-PSO exhibits superior exploration capabilities, population convergence, and reduces the number of iterations required to obtain optimal solutions.
Author Contributions
Conceptualization, D.W.P.; methodology, D.W.P. and Y.P.M.; validation, D.W.P. and Y.P.M.; investigation, D.W.P. and Y.P.M.; writing—review and editing, D.W.P. and B.A.A.; visualization, Z.Ñ. and J.E.L.; supervision, Y.P.M. All authors have read and agreed to the published version of the manuscript.
Funding
The publication of this article was solely funded by the authors and co-authors, with no direct financial contribution from other entities.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
I thank the National Council of Science and Technology and Technological Innovation (CONCYTEC) for the PhD study scholarship. We thank the National University of Engineering, Technological University of Peru and Federal University of Paraiba for the support provided for this research work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gerez, C.; Silva, L.I.; Belati, E.A.; Sguarezi Filho, A.J.; Costa, E.C.M. Distribution Network Reconfiguration Using Selective Firefly Algorithm and a Load Flow Analysis Criterion for Reducing the Search Space. IEEE Access 2019, 7, 67874–67888. [Google Scholar] [CrossRef]
- Helmi, A.M.; Carli, R.; Dotoli, M.; Ramadan, H.S. Efficient and Sustainable Reconfiguration of Distribution Networks via Metaheuristic Optimization. IEEE Trans. Autom. Sci. Eng. 2022, 19, 82–98. [Google Scholar] [CrossRef]
- Behbahani, M.R.; Jalilian, A.; Bahmanyar, A.; Ernst, D. Comprehensive Review on Static and Dynamic Distribution Network Reconfiguration Methodologies. IEEE Access 2024, 12, 9510–9525. [Google Scholar] [CrossRef]
- Mishra, S.; Das, D.; Paul, S. A comprehensive review on power distribution network reconfiguration. Energy Syst. 2017, 8, 227–284. [Google Scholar] [CrossRef]
- Jordehi, A.R. Optimisation of electric distribution systems: A review. Renew. Sustain. Energy Rev. 2015, 51, 1088–1100. [Google Scholar] [CrossRef]
- Shan, Y.; Hu, J.; Liu, H. A Holistic Power Management Strategy of Microgrids Based on Model Predictive Control and Particle Swarm Optimization. IEEE Trans. Ind. Inform. 2022, 18, 5115–5126. [Google Scholar] [CrossRef]
- Shan, Y.; Ma, L.; Yu, X. Hierarchical Control and Economic Optimization of Microgrids Considering the Randomness of Power Generation and Load Demand. Energies 2023, 16, 5503. [Google Scholar] [CrossRef]
- Pegado, R.; Ñaupari, Z.; Molina, Y.; Castillo, C. Radial distribution network reconfiguration for power losses reduction based on improved selective BPSO. Electr. Power Syst. Res. 2019, 169, 206–213. [Google Scholar] [CrossRef]
- Thanh Nguyen, T.; Nguyen, T.T.; Nguyen, N.A. Optimal network reconfiguration to reduce power loss using an initial searching point for continuous genetic algorithm. Complexity 2020, 2020, 2420171. [Google Scholar] [CrossRef]
- Silva, L.I.; Belati, E.A.; Gerez, C.; Silva Junior, I.C. Reduced search space combined with particle swarm optimization for distribution system reconfiguration. Electr. Eng. 2021, 103, 1127–1139. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, T.T.; Le, B. Optimization of electric distribution network configuration for power loss reduction based on enhanced binary cuckoo search algorithm. Comput. Electr. Eng. 2021, 90, 106893. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, J.; Wang, L.; An, Y.; Zhang, X. Distribution Network Reconfiguration Using Chaotic Particle Swarm Chicken Swarm Fusion Optimization Algorithm. Energies 2023, 16, 7185. [Google Scholar] [CrossRef]
- Li, X.; Li, M.; Yu, M.; Fan, Q. Fault Reconfiguration in Distribution Networks Based on Improved Discrete Multimodal Multi-Objective Particle Swarm Optimization Algorithm. Biomimetics 2023, 8, 431. [Google Scholar] [CrossRef] [PubMed]
- Alanazi, A.; Alanazi, T.I. Multi-Objective Framework for Optimal Placement of Distributed Generations and Switches in Reconfigurable Distribution Networks: An Improved Particle Swarm Optimization Approach. Sustainability 2023, 15, 9034. [Google Scholar] [CrossRef]
- Fathi, R.; Tousi, B.; Galvani, S. Allocation of renewable resources with radial distribution network reconfiguration using improved salp swarm algorithm. Appl. Soft Comput. 2023, 132, 109828. [Google Scholar] [CrossRef]
- Azizi, A.; Vahidi, B.; Nematollahi, A.F. Reconfiguration of Active Distribution Networks Equipped with Soft Open Points Considering Protection Constraints. J. Mod. Power Syst. Clean Energy 2023, 11, 212–222. [Google Scholar] [CrossRef]
- Vargas, G.A.D.; Mosquera, D.J.; Trujillo, E.R. Optimization of Topological Reconfiguration in Electric Power Systems Using Genetic Algorithm and Nonlinear Programming with Discontinuous Derivatives. Electronics 2024, 13, 616. [Google Scholar] [CrossRef]
- Naderipour, A.; Abdullah, A.; Marzbali, M.H.; Arabi Nowdeh, S. An improved corona-virus herd immunity optimizer algorithm for network reconfiguration based on fuzzy multi-criteria approach. Expert Syst. Appl. 2022, 187, 115914. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.J.; Pan, J.S.; Nguyen, T.T.; Weng, S. Distribution network reconfiguration with distributed generation based on parallel slime mould algorithm. Energy 2022, 244, 123011. [Google Scholar] [CrossRef]
- Atoccsa, B.A.; Puma, D.W.; Mendoza, D.; Urday, E.; Ronceros, C.; Palma, M.T. Optimization of Ampacity in High-Voltage Underground Cables with Thermal Backfill Using Dynamic PSO and Adaptive Strategies. Energies 2024, 17, 1023. [Google Scholar] [CrossRef]
- Niknam, T.; Azadfarsani, E.; Jabbari, M. A new hybrid evolutionary algorithm based on new fuzzy adaptive PSO and NM algorithms for distribution feeder reconfiguration. Energy Convers. Manag. 2012, 54, 7–16. [Google Scholar] [CrossRef]
- Lavorato, M.; Franco, J.F.; Rider, M.J.; Romero, R. Imposing radiality constraints in distribution system optimization problems. IEEE Trans. Power Syst. 2011, 27, 172–180. [Google Scholar] [CrossRef]
- Prieto, L.P.V. Uma Eficiente Metodologia para Reconfiguração de Redes de Distribuição de Energia eléTrica Usando Otimização por Enxame de Partículas. Master’s Thesis, Universidade Federal do ABC, Santo André, Brazil, 2015. [Google Scholar]
- Dennis, C.; Engelbrecht, A.P.; Ombuki-Berman, B.M. An analysis of activation function saturation in particle swarm optimization trained neural networks. Neural Process. Lett. 2020, 52, 1123–1153. [Google Scholar] [CrossRef]
- Laishram, R.; Rabidas, R. Optimized hyperbolic tangent function-based contrast-enhanced mammograms for breast mass detection. Expert Syst. Appl. 2023, 213, 118994. [Google Scholar] [CrossRef]
- da S. Oliveira, E.; Silva Junior, I.C.; de Oliveira, L.W.; de Mendonça, I.M.; Vilaça, P.; Saraiva, J.T. A two-stage constructive heuristic algorithm to handle integer investment variables in transmission network expansion planning. Electr. Power Syst. Res. 2021, 192, 106905. [Google Scholar] [CrossRef]
- Lee, Y.; Shamsuddin, S.; Hamed, H. Bounded PSO Vmax function in neural network learning. In Proceedings of the 2008 Eighth International Conference on Intelligent Systems Design and Applications, Kaohsuing, Taiwan, 26–28 November 2008; IEEE: Piscataway, NJ, USA, 2008; Volume 1, pp. 474–479. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Baran, M.; Wu, F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
- Goswami, S.; Basu, S. A new algorithm for the reconfiguration of distribution feeders for loss minimization. IEEE Trans. Power Deliv. 1992, 7, 1484–1491. [Google Scholar] [CrossRef]
- Khalil, T.; Gorpinich, A. Selective particle swarm optimization. Int. J. Multidiscip. Sci. Eng. (IJMSE) 2012, 3, 2045–7057. [Google Scholar]
- Abd Rahman, N.H.; Zobaa, A.F. Integrated mutation strategy with modified binary PSO algorithm for optimal PMUs placement. IEEE Trans. Ind. Inform. 2017, 13, 3124–3133. [Google Scholar] [CrossRef]
- Dong, J.; Li, Q.; Deng, L. Design of fragment-type antenna structure using an improved BPSO. IEEE Trans. Antennas Propag. 2017, 66, 564–571. [Google Scholar] [CrossRef]
- Su, C.T.; Lee, C.S. Network reconfiguration of distribution systems using improved mixed-integer hybrid differential evolution. IEEE Trans. Power Deliv. 2003, 18, 1022–1027. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).