Abstract
Inductive power transfer (IPT) systems often encounter limitations in efficiency and transmission distance due to near-field magnetic coupling characteristics. Increasing the inductance can enhance the transmission distance, but it also raises the system’s Q factor, leading to several issues. This study aimed to optimize the magnetic core design of helical coils to enhance magnetic coupling in IPT systems while minimizing the increase in self-inductance. Through finite element analysis, various core placements were evaluated, leading to a proposed core design process that integrates inner and lower cores at optimal angles. The proposed design was compared with conventional cores, and its performance was validated in an IPT system. The results demonstrate that the proposed core design significantly enhances the coupling coefficient (k) and extends power transmission distance compared with conventional planar and U-shaped core structures without substantially increasing self-inductance (L). This design effectively balances the trade-off between increasing inductance and maintaining system stability, thereby improving transmission efficiency while minimizing frequency instability and voltage stress.
1. Introduction
Wireless power transfer (WPT) technologies can be broadly categorized into capacitive, inductive, and electromagnetic wave methods. Currently, most commercially available WPT systems use inductive power transfer (IPT) via magnetic fields. However, IPT systems using magnetic coupling face inherent limitations in efficiency and transmission distance due to near-field characteristics, which are inversely proportional to the cube of the distance. Consequently, extensive research is being conducted to overcome these limitations.
Although research on inductive WPT systems utilizing magnetic coupling has been ongoing for many years, significant attention was drawn by MIT’s research in 2007. This system achieved a 60 W power transfer with a 40% efficiency over a distance of 2.1 m [1,2]. However, the measured quality factor (Q) of the resonant coil in this study was about 950 (the theoretical value is about 2500), indicating that a 0.05% frequency shift reduces the output by less than half at a resonant frequency of 10 MHz. Thus, increasing the Q factor to enhance transmission distance also raises system instability.
In 2014, KAIST developed a dipole coil resonance system (DCRS) using bar-shaped ferrite cores. This system achieved power transfers of 1403 W, 471 W, and 209 W over distances of 3, 4, and 5 m, respectively [3,4,5]. This allowed for stable power transfer with a Q factor of below 100 at a relatively low frequency of 20 kHz and offered a smaller volume advantage over circular coils. In this way, it is possible to utilize magnetic cores to improve coil coupling, but most magnetic core research has focused on designing cores for specific coil shapes (spiral coils, solenoids) or for shielding purposes.
Other studies to improve efficiency and transmission distance include metamaterials [6,7,8,9] and relay coils [10,11,12,13], but these require additional devices between the transmitter and receiver. Superconducting coils can also be considered. However, as described earlier, this method reduces bandwidth by increasing the Q factor and causes high-voltage stress issues.
To address these limitations, this study focused on optimizing the magnetic core design of helical coils to enhance magnetic coupling while minimizing the increase in inductance in IPT systems. Due to various factors, the optimal design values may differ for each model. However, the design process described in this study is expected to be applicable to the optimal design of specific models.
2. Methodology and System Configuration
In inductive power transfer (IPT) systems, magnetic cores are primarily used to increase self-inductance (L), enhance the coupling coefficient (k), or provide shielding. Magnetic cores can elevate L by increasing the magnetic field in the coils, which depends on the magnetic permeability (μ). Simultaneously, they can modify the magnetic flux path to enhance k based on their configuration. Elevating both L and k is a primary method to boost mutual inductance (M), which enables higher efficiency and extended power transmission distances. However, increasing L not only causes the aforementioned issues but also increases eddy current and hysteresis losses in the core, resulting in a potential decrease in the efficiency of the system.
Therefore, this study aimed to design a magnetic core that maximizes k with minimal core usage to minimize frequency instability and voltage stress on coils and capacitors. This study began by investigating the impact of two commonly used core structures. It then analyzed how the placement of cores around the coils affected their magnetic coupling. Subsequently, it designed an optimal core structure by integrating suitable core positions and sizes. Finally, this optimized design was applied to an IPT system to validate its effectiveness.
The selected core for this research was the Mn-Zn ferrite core PL-13, with a relative permeability (μr) of 3200. Core losses were not considered in this study. The coils used were a pair of helical coils with a diameter of 300 mm (80 turns) and a cross-sectional area of 40 mm by 8 mm. In an IPT system without cores, the original coil’s optimal transmission distance was 402 mm at 50 kHz resonance and 523 mm at 100 kHz resonance. To include this, the core design was evaluated by comparing the coupling coefficient k, mutual inductance M, and self-inductance L for transmission distances of 300 mm and 600 mm. The analysis was conducted using the commercial finite element analysis software ANSYS Maxwell 2023 R1.
3. Core Effect Analysis
3.1. Analysis of Commonly Used Cores
Due to limited research on the application of cores to helical coil forms, we first analyzed the effects of two commonly used core structures, as depicted in Figure 1. Planar cores, positioned flat at the bottom of the coil as shown in Figure 1a–c, are commonly used alongside spiral coils in most wireless charging applications [14,15,16]. These cores are sometimes composed of multiple rectangular prisms arranged radially to fill the entire bottom of the coil, considering cost factors. On the other hand, U-shaped cores, wrapping around the inside, outside, and bottom of the coil, as depicted in Figure 1d–f, are typically used with straight conductors in power supply systems like online electric vehicles (OLEVs) and high-speed trains [17,18,19].

Figure 1.
Two types of core structures commonly used in WPT systems: (a) planar core; (b) cross-section of the planar core; (c) quarter geometry of the planar core; (d) U-shaped core; (e) cross-section of the U-shaped core; (f) quarter geometry of the U-shaped core.
These cores were applied to helical coils, and their effects were compared. Two core structures were designed with the same volume of 1,238,412 mm3 and cross-sectional area with 45 mm × 10 mm rectangular sections. Their effects were analyzed, and the results were compared with the case of no core usage in Table 1.

Table 1.
Results of analyzing the inductance and coupling coefficient of two commonly used cores.
The analysis results indicate that both types of cores increase the mutual inductance (M). For the planar core, there is little change in the coupling coefficient (k), but an increase in inductance (L) leads to a higher M. In contrast, the U-shaped core shows a halving of k, while L more than doubles, resulting in a higher M. Consequently, while L is over twice as high for the U-shaped core compared with the planar core, there is not a significant difference in M between the two core structures.
As this is not an analysis based on optimized shapes, we cannot conclusively determine the performance of both core shapes. However, it is expected that a WPT system using a U-shaped core will achieve higher magnetic coupling efficiency, longer transmission distances, and narrower bandwidth compared with a system using a planar core.
3.2. Effect of Core Placement
In the geometric design of cores around the coil, there are numerous variables that can be adjusted, such as core shape, size, and position. Therefore, we first analyzed the influence of cores positioned inside, outside, and at the bottom of the coil separately in the surrounding space. Subsequently, we proceeded with the design by adjusting design variables to derive the optimal core structure that maximizes the coupling coefficient. All analyses were conducted with the two coil and core sets arranged symmetrically above and below, with only the lower side shown in the subsequent figures.
3.2.1. Inner Core
For the analysis of the effect caused by the inner core, we varied the width of the inner core (), which is spaced 5 mm apart from the coil as shown in Figure 2, from 2 mm to a maximum of 137 mm. The changes in k, M, and L were analyzed, and the results for transmission distances of 600 mm and 900 mm are shown in Figure 3. Here, the increase in corresponds to a decrease in the inner diameter of the core.

Figure 2.
Core structures according to inner core width.

Figure 3.
Analysis results of k, M, and L according to inner core width: (a) d = 600 mm; (b) d = 900 mm.
As the width (volume) of the inner core increases, k rises until the core is completely filled, but the rate of increase gradually diminishes. In contrast, L experiences a significant rise compared with the case without a core, but it is not substantially affected by the core’s volume. In this way, filling the coil with the core maximizes k, but increasing the core’s volume also raises costs, losses, and system weight. Therefore, it is essential to use the core minimally. To achieve this, one can select the minimum core width that prevents the magnetic field inside the core from reaching the saturation point on the B–H curve.
For example, when aiming to transmit 3 kW of power with a supplied current of 70 A, the saturation level of the flux density varies with the core width, as shown in Figure 4. To ensure that the system operates within the linear range of the B–H curve shown in Figure 5a, the maximum internal flux density B within the core should not exceed approximately 400 mT. Therefore, from the graph of core center flux density versus core width shown in Figure 5b, we can select a minimum core width of 10 mm that does not exceed this limit.

Figure 4.
Magnetic flux density and flux line distribution inside the core according to the inner core width: (a) wci = 6 mm; (b) wci = 8 mm; (c) wci = 10 mm; (d) wci = 12 mm.
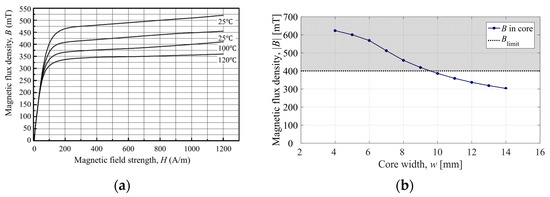
Figure 5.
Magnetic characteristics of the core: (a) B–H curve; (b) flux density at the core center as a function of core width.
In the following steps, the gap between the coil and the inner core can be considered. L tends to increase as the core gets closer to the coil, but k can decrease because of the proximity of the core to the coil, as seen in the case of the U-shaped core structure. When the gap (gci) between the inner core (with a width of 10 mm) and the coil is varied as shown in Figure 6, the changes in k, M, and L are illustrated in Figure 7.

Figure 6.
Core structures according to the distance between the inner core and coil.

Figure 7.
Analysis results of k, M, and L according to the distance between the inner core and coil (top) with an enlarged view of k (bottom): (a) d = 600 mm; (b) d = 900 mm.
The analysis reveals the existence of an optimal gap between the inner core and the coil that maximizes k. For a transmission distance of 600 mm, an optimal gap of = 25 mm is found, whereas for 900 mm, = 20 mm provides optimal results. This indicates that varies with transmission distance. Additionally, also varies with the width of the inner core . For example, with = 40 mm, is found to be 20 mm and 15 mm for transmission distances of 600 mm and 900 mm, respectively. Therefore, to achieve maximum k, it is evident that the core should be positioned at a specific distance from the coil depending on the core width.
The distribution of magnetic flux density and flux line according to the gap is shown in Figure 8. The inner core enhances magnetic coupling by concentrating the magnetic field around the coil cross-section towards the center of the coil. However, if the core is too close to the coil, the magnetic field becomes concentrated only around the periphery of the coil, leading to adverse effects. For this reason, it can be understood that an optimal gap exists.

Figure 8.
Magnetic flux density and flux line distribution according to the separation distance between the inner core and coil: (a) gci = 5 mm; (b) gci = 20 mm; (c) gci = 40 mm; (d) gci = 80 mm.
3.2.2. Outer Core
Secondly, we repeated the same process for the outer core, as shown in Figure 9, to analyze the variations in k, M, and L. When a core is placed outside the coil, L increases, but M and k significantly decrease. Additionally, as depicted in Figure 10a, as the width of the outer core () increases, M and k decrease further, while L remains relatively unchanged. Conversely, increasing the gap between the outer core and the coil (), as shown in Figure 10b, causes L to gradually decrease, while M and k increase until they converge to the values observed when no outer core is present.

Figure 9.
Core structures according to the outer core width and gap between the outer core and the coil.

Figure 10.
Analysis results of k, M, and L based on the variation of the two variables of the outer core (d = 600 mm): (a) width of the outer core; (b) gap between the outer core and the coil.
In other words, beyond a certain transmission distance, if the core is located outside the coil, k decreases regardless of the width or gap. This is because an outer core positioned outside the coil, as shown in Figure 11, shields the magnetic field, thereby reducing the induced magnetic flux reaching the opposite coil. Therefore, for medium-distance power transmission, unless it is for increasing k or for the purpose of magnetic shielding, the core should not be positioned outside the coil. Accordingly, the outer core was excluded from the subsequent process.

Figure 11.
Magnetic flux density and flux line distribution according to the gap between the outer core and coil: (a) gco = 5 mm; (b) gco = 50 mm; (c) without core.
3.2.3. Lower Core
Thirdly, the influence of the lower core beneath the coil, commonly used in both planar cores and U-shaped cores, was analyzed. In accordance with Figure 12, the analysis proceeded by increasing the internal length () or external length () of the core located under the coil as observed in the cross-section. The increase in these lengths indicates a decrease in the core’s inner diameter and an increase in its outer diameter, respectively.

Figure 12.
Core structures according to the inner and outer lengths of the lower core.
In the cross-section view, these lengths indicate how far the core extends beyond the coil boundary. Thus, when = 0 mm, the actual width of the core matches the coil width of 8 mm. Additionally, in the cross-section, a positive length signifies an increase in the outer diameter of the lower core, while a negative length indicates a decrease in the inner diameter. By varying the length of the lower core located 5 mm beneath the coil, interpretations of changes in k, M, and L yield results similar to those shown in Figure 13.

Figure 13.
Analysis results of k, M, and L according to the inner and outer lengths of the lower core (top) with an enlarged view of k (bottom): (a) d = 600 mm; (b) d = 900 mm.
As the lower core extends internally or externally, k shows a tendency to decrease initially and then increase again. For a transmission distance of 600 mm, when the internal length of the core reaches approximately 40 mm, k increases compared with the case where there is no core. In the opposite case, the external length must exceed 60 mm for k to be greater than in the case without a core.
Similar to the influence of inner and outer cores, the effect of this lower core also results from changes in the magnetic flux path. Depending on the length of the lower core, the distribution of magnetic flux density and flux lines varies as depicted in Figure 14.

Figure 14.
Magnetic flux density and flux line distribution according to the length of the lower core: (a) lcu = 10 mm; (b) lcu = 40 mm; (c) lcu = 80 mm.
Thus, when using a lower core for improving the magnetic coupling efficiency, it can be concluded that the lower core’s length (outer diameter) should be designed to meet at least a certain minimum length. Furthermore, for power transmission over a certain distance, it becomes evident that the planar core structure beneath the coil is not the optimal configuration.
3.3. Summary
The analysis of the effects of inner, outer, and lower cores on the coil yields the following conclusions. Firstly, the inner core enhances k as it occupies more space within the coil. However, optimizing the width while considering the magnetic saturation is essential to minimize costs and losses. Additionally, there exists an optimal gap between the coil and the core for maximizing efficiency. Next, regarding outer cores, they consistently reduce k regardless of width or gap, suggesting that it is preferable not to use them when aiming to enhance magnetic coupling, except for increasing L or for shielding purposes. Lastly, concerning the lower core, when it is positioned within a specific area beneath the coil, it reduces k. However, reducing the inner diameter further or increasing the outer diameter beyond this area has the effect of increasing the decreased k once again. Therefore, in subsequent core designs, we aimed to maximize k by utilizing a combination of inner and lower cores beneath the coil.
It is noted that in this study, we assumed limited space and only utilized up to 15 cm below the coil, with no use of the area beyond that. However, if this space is not restricted, it is feasible to design the inner core with an increased length downward. As the inner core length increases downward, k, M, and L all show a continuous upward trend. Thus, in scenarios where the space beneath the coil is not restricted by circuits or shielding plates, designing the inner core as long as possible enables more effective magnetic coupling.
4. Optimization of Core Structure
Based on the previously analyzed effects of core positioning, we designed the overall core structure to maximize magnetic coupling while minimizing the increase in self-inductance L. However, due to the numerous spatial and structural variables and their diverse combinations, it is not feasible to consider all of them simultaneously. Therefore, this study performed stepwise optimization beginning with the most effective variables to derive the most reasonable results. It is important to note that these optimal values may vary depending on the target specifications and constraints of the system, and thus, they should not be regarded as definitive solutions.
4.1. Combination of Inner and Lower Cores
In the previous analysis, the effects of the cores located inside, outside, and at the bottom of the coil were examined. However, the trends may differ when using more than one core. Therefore, the design was conducted by fixing the inner core and adding a bottom core, then adjusting the design variables accordingly. When used in conjunction with the inner core, the effects of the bottom core’s inner length and outer length are shown in Figure 15. Here, the distance between the internal core and the coil was the optimal value of 20 mm when used independently.

Figure 15.
Effect of lower core length when combined with the inner core: (a) core structure; (b) analysis results of k, M, and L (d = 600 mm).
Compared with Figure 13, which shows the effect of the lower core alone, Figure 15b shows that k increases rapidly until , where the inner diameters of the lower and inner cores become equal. This is because the magnetic flux path continues through both cores as they come closer together. To maximize this effect, in subsequent designs, the length of the internal core was increased by 5 mm downwards, and the two cores were integrated into a unified structure.
In the analysis above, the optimal distance between the internal core and the coil was determined; however, this distance can vary depending on the presence of the bottom core. Furthermore, because the two cores are connected, there also exists an optimal length of the bottom core corresponding to . As shown in Figure 16, can be obtained by varying the length of the lower of the two connected cores. The analysis results show that mm at mm ( mm at mm).

Figure 16.
Effect of the length of the lower core integrated with the inner core: (a) core structure; (b) analysis results of k, M, and L (d = 600 mm).
The length varies depending on the transmission distance, gradually decreasing as the distance increases, converging to approximately 45 mm. Therefore, the optimal length of the bottom core can be selected as mm, which is between the optimal value at d = 600 mm and the converging value. At this point, the distance between the internal core and the coil is mm. In practical design, and can be chosen based on the target transmission distance, or can be appropriately selected to adjust L. If designing for maximum M instead of k, should be designed close to zero to place the internal core as close as possible to the coil.
Similar to the case of single-core usage, the bottom core, when used in conjunction with both cores connected, exhibits a complex trend in k as its length outward from the coil increases. As illustrated in Figure 17, positioning the internal core at the optimal distance mm while gradually increasing the length of the bottom core outward results in k, M, and L showing trends similar to those depicted in Figure 18 at transmission distances of d = 300 mm, d = 600 mm, d = 900 mm, and d = 1200 mm.

Figure 17.
Core structures according to the length of the lower core when the inner core is located at the optimal distance: (a) core structure; (b) optimal length when d = 600 mm; (c) optimal length when d = 900 mm.

Figure 18.
Analysis results of k, M, and L according to the length of the lower core when the inner core is located at the optimal distance: (a) d = 300 mm; (b) d = 600 mm; (c) d = 900 mm; (d) d = 1200 mm.
As shown in Figure 18a, for short transmission distances, increases, leading to a continuous increase in k. Therefore, in near-field magnetic coupling systems, it is appropriate to design the bottom core to extend beyond the coil radius (e.g., planar core). However, for longer transmission distances, k exhibits an increase–decrease–increase pattern as the length of the bottom core increases, as shown in Figure 18b–d. The length of the bottom core at which k first reaches its maximum value is denoted as , and this value ranges from approximately 40 to 45 mm depending on the distance d. Figure 17 shows that this value corresponds to the circumference of the bottom core being located directly beneath the coil. Therefore, to achieve magnetic coupling over a certain distance, the outer diameter of the bottom core should be designed so that it does not exceed the inner diameter of the coil.
4.2. Adjusting the Core Angle
Based on the results of core placement and combination, it can be observed that k decreases and then increases as the lower core extends beyond the outer diameter of the coil. Specifically, within a certain range at the bottom of the coil, the core tends to decrease the coupling coefficient. This phenomenon is attributed to the core altering the path of the magnetic field, which increases the leakage flux. Thus, to enhance transmission distance, it is essential to design the core outside the inner diameter of the coil, considering the flux path. Therefore, to improve magnetic coupling, it is necessary to design the core outside the coil’s inner diameter, considering the magnetic flux path.
As shown in Figure 19, the portion of the lower core extending outside the coil radius is redefined as the outer core. By adjusting the angle of the core, positions that cause adverse effects can be avoided. As the angle of the outer core changes from −80 degrees to 90 degrees, k, M, and L change, as shown in Figure 20.

Figure 19.
Core structures according to the angle of the outer core: (a) upward; (b) downward.

Figure 20.
Analysis results of k, M, and L according to the angle of the outer core: (a) −80~90°; (b) enlarged view of 0~90°.
As the core angle approaches , both k and M decrease, which aligns with previous analysis of the effects caused by the external core. Conversely, when the core angle is increased to move away from the coil, k reaches its maximum at the optimal core angle and then starts to decrease. Additionally, as the core angle increases, the distance between the core and the coil increases, leading to a decrease in L. Consequently, M reaches its maximum at around , which is less than .
The optimal core angle, , also varies with the transmission distance. For a distance d = 900 mm, the is 70 degrees. For distances beyond 900 mm, tends to converge to approximately 75 degrees. Therefore, similar to selecting the lower core length , can be selected as 70 degrees, which is the midpoint between the optimal value at 600 mm and the convergent value.
The effect of the core angle varies depending on the coil shape, transmission distance, and position and size of the core. Thus, it is impossible to generalize the optimal core angle . To understand the general trends, the optimal core angle and the influence on the coupling coefficient for different core positions can be simulated as shown in Figure 21 and Table 2. The data for core positions and angles that decrease k below 0.6004 (the value of k without a core) were excluded.

Figure 21.
Optimal placement angle of the core depending on position and its influence on the coupling coefficient: (a) analysis range of core positions and angles; (b) magnetic flux distribution of a coil without a core and the changes in the optimal angle and coupling coefficient with respect to core position (d = 600 mm).

Table 2.
Optimal core angle and maximum coupling coefficient for different core positions based on distance x and y from the coil (d = 600 mm).
The analysis results indicate that the core within the coil radius primarily increases the coupling coefficient, k, and there is an optimal angle for this effect. However, due to the characteristics of the IPT system, positioning a core above the coil is not feasible and was therefore excluded from the design considerations. Additionally, adjusting the angle of the internal core at x = 0 shows a less than 1% increase in k, and therefore, it was also excluded in the design.
4.3. Core Design Result
The final core design results are shown in Figure 22, and the outcomes of each design variable are summarized in Table 3.

Figure 22.
Optimal core design result: (a) design variables and optimal values; (b) configuration.

Table 3.
Optimal core design variables and changes in k at each design step.
Applying the designed core results in an increase in the coupling coefficient by approximately 41–52% compared with the case without the core, as shown in Figure 23. At very close distances, the influence of the opposite coil significantly increases the coupling coefficient. Excluding these extreme cases and comparing within the design conditions between d = 600 mm and d = 900 mm, the coupling coefficient increases by an average of about 46.9% due to the core application. The cause of this effect can be explained by Figure 21. Examining the flux distribution and optimal core angle in Figure 21 indicates that the optimal angle allows the coil’s flux to rotate at a larger radius. Consequently, the flux distribution before and after applying the designed core changes as shown in Figure 24.
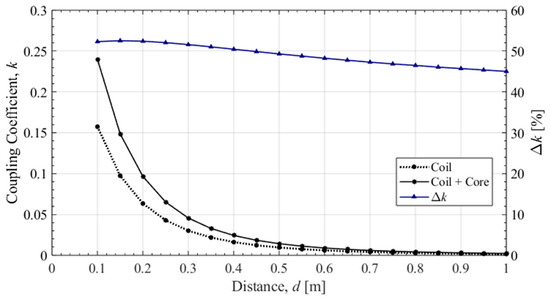
Figure 23.
Change in the coupling coefficient before and after core application as a function of distance.

Figure 24.
Changes in magnetic flux density and flux distribution before and after using the designed core (d = 300 mm, identical L): (a) receiving coil; (b) receiving coil with core; (c) transmitting coil; (d) transmitting coil with core.
5. Analysis of the Design Result
To evaluate the effectiveness of the designed core compared with conventional core structures, we conducted a comparison and analysis with planar and U-shaped cores of the same volume, as shown in Figure 25.

Figure 25.
Core structures used for comparison/analysis: (a) planar core; (b) U-shaped core; (c) proposed core.
Under the condition that the volumes of the three cores are the same, the thickness of the planar core in Figure 25a was adjusted to 16.16 mm. Based on the analysis results of the lower core length , the core was restricted to ensure it did not extend beyond the outer diameter of the coil. The U-shaped core in Figure 25b was adjusted to have a uniform thickness while maintaining the same volume as the other cores. Accordingly, the gap between all parts of the core and the coil was set to 3.26 mm. The results of comparing the coupling coefficients based on the distance of the three cores are shown in Figure 26. For comparison, the y-axis, representing the coupling coefficients, is displayed on a logarithmic scale.

Figure 26.
Comparison of coupling coefficients for coil without core and coil with three types of cores at varying distances.
The planar core increases the coupling coefficient k by approximately 13.5% at close distances, but this increase rate diminishes as the distance increases. Within the 600–900 mm range, it shows an average increase in k of about 4.52%. Conversely, the U-shaped core decreases the coupling coefficient more significantly as the distance increases, with a reduction ranging from a minimum of 45% to a maximum of 70%. The proposed core increases the coupling coefficient by approximately 52.3% at close distances and by about 46.9% within the target distance range. Increasing the coupling coefficient at the same distance implies achieving the same magnetic coupling efficiency at a greater distance. In other words, under the same conditions such as self-inductance L, the proposed core allows for the same power transmission efficiency at distances that are approximately 45 to 125 mm farther. However, the actual power transmission distance is determined by the mutual inductance M, which is influenced by the self-inductance L that varies with each core shape. Therefore, to make an accurate comparison, three different cores were applied to the IPT system, and power transmission was simulated. A simple series LC resonant IPT system was used, with the system specifications being detailed in Table 4. The inductance and compensation capacitor sizes for each model with their respective cores are shown in Table 5.

Table 4.
Specifications of the system used in the simulation.

Table 5.
The inductance and compensation capacitor sizes for each model.
Figure 27 illustrates the power transmission as a function of distance for each core used in the IPT system. In a 50 kHz resonant system, the power transmission distances for the planar core and U-shaped core are 594 mm and 660.5 mm, respectively. Compared with the case without a core (549 mm), this results in an increase in transmission distance of 45 mm and 111.5 mm, respectively.

Figure 27.
Change in the power transmission distance of the IPT system with each core used.
Despite reducing the coupling coefficient, the U-shaped core increases the power transmission distance due to its high self-inductance L. However, the very high L increases the system’s quality factor (Q), thereby narrowing the bandwidth. Consequently, systems utilizing a U-shaped core will experience a significant reduction in output with even a slight frequency misalignment. Considering these points, it can be concluded that the proposed core is an effective design that maximizes the increase in power transmission distance by enhancing k without causing a significant rise in L.
6. Conclusions
In this study, we optimized the design of magnetic cores for helical coils in inductive power transfer (IPT) systems to improve efficiency and transmission distance. Using finite element analysis, the effects of inner, outer, and lower cores were analyzed, leading to the development of a new core design process that integrates inner and lower cores at optimal angles.
The proposed core design significantly enhances the coupling coefficient (k) without substantially increasing self-inductance (L), compared with conventional planar and U-shaped cores. Additionally, when applied to wireless power transfer, the designed core demonstrates a significant improvement in transmission distance due to its higher magnetic coupling efficiency. The lower self-inductance compared with the U-shaped core allows the system to have lower frequency instability and voltage stress.
The proposed core design can also be applied to increase output or efficiency at the same transmission distance. Therefore, the study results are expected to enhance IPT performance in various aspects.
Author Contributions
Conceptualization, H.-Y.L.; methodology, H.-Y.L.; software, H.-Y.L. and S.-A.C.; validation, H.-Y.L. and G.-S.P.; formal analysis, H.-Y.L.; investigation, H.-Y.L., S.-A.C. and M.-S.S.; resources, G.-S.P.; data curation, H.-Y.L. and M.-S.S.; writing—original draft preparation, H.-Y.L.; writing—review and editing, H.-Y.L. and S.-A.C.; visualization, H.-Y.L.; supervision, G.-S.P.; project administration, H.-Y.L.; funding acquisition, H.-Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education (2022R1I1A1A01071307).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljačić, M. Wireless power transfer via strongly coupled magnetic resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef] [PubMed]
- Karalis, A.; Joannopoulos, J.; Soljačić, M. Efficient wireless non-radiative mid-range energy transfer. Ann. Phys. 2008, 323, 34–48. [Google Scholar] [CrossRef]
- Park, C.; Lee, S.; Cho, G.-H.; Rim, C.T. Innovative 5-m-off-distance inductive power transfer systems with optimally shaped dipole coils. IEEE Trans. Power Electron. 2015, 30, 817–827. [Google Scholar] [CrossRef]
- Choi, B.H.; Thai, V.X.; Lee, E.S.; Kim, J.H.; Rim, C.T. Dipole-coil-based wide-range inductive power transfer systems for wireless sensors. IEEE Trans. Ind. Electron. 2016, 63, 3158–3167. [Google Scholar] [CrossRef]
- Choi, B.-G.; Lee, E.S.; Kim, Y.-S. Optimal structure design of ferromagnetic cores in wireless power transfer by reinforcement learning. IEEE Access 2020, 8, 179295–179306. [Google Scholar] [CrossRef]
- Chabalko, M.J.; Besnoff, J.; Ricketts, D.S. Magnetic Field Enhancement in Wireless Power with Metamaterials and Magnetic Resonant Couplers. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 452–455. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, B.; Deng, B.; Wei, X.; Wang, J. Opportunities and challenges of metamaterial-based wireless power transfer for electric vehicles. Wirel. Power Transf. 2017, 5, 9–19. [Google Scholar] [CrossRef]
- Shaw, T.; Mitra, D. Wireless Power Transfer System Based on Magnetic Dipole Coupling with High Permittivity Metamaterials. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1823–1827. [Google Scholar] [CrossRef]
- Zeng, Y.; Lu, C.; Rong, C.; Tao, X.; Liu, X.; Liu, R.; Liu, M. Analysis and Design of Asymmetric Mid-Range Wireless Power Transfer System with Metamaterials. Energies 2021, 14, 1348. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, G.-X. Middle range wireless power transfer systems with multiple resonators. J. Cent. South Univ. 2015, 22, 2127–2136. [Google Scholar] [CrossRef]
- Dong, Z.; Liu, S.; Li, X.; Xu, Z.; Yang, L. A Novel Long-Distance Wireless Power Transfer System with Constant Current Output Based on Domino-Resonator. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 2343–2355. [Google Scholar] [CrossRef]
- Kaczmarczyk, Z.; Bodzek, K.; Frania, K.; Ruszczyk, A. Chart Design Method for Multicoil Resonant Wireless Power Transfer Systems. IEEE Trans. Power Electron. 2021, 36, 795–804. [Google Scholar] [CrossRef]
- Lee, K.; Chae, S.H. Comparative Analysis of Frequency-Selective Wireless Power Transfer for Multiple-R Understood x Systems. IEEE Trans. Power Electron. 2020, 35, 5122–5131. [Google Scholar] [CrossRef]
- Kim, J.H.; Choi, B.G.; Jeong, S.Y.; Han, S.H.; Kim, H.R.; Rim, C.T.; Kim, Y.-S. Plane-Type Receiving Coil with Minimum Number of Coils for Omnidirectional Wireless Power Transfer. IEEE Trans. Power Electron. 2020, 35, 6165–6174. [Google Scholar] [CrossRef]
- Mohammed, M.H.; Ameen, Y.M.Y.; Mohamed, A.A.S. Dish-Shape Magnetic Flux Concentrator for Inductive Power Transfer Systems. Int. J. Electr. Electron. Eng. Telecommun. 2020, 9, 455–461. [Google Scholar] [CrossRef]
- Xu, H.; Song, H.; Hou, R. Central Bulge Ferrite Core for Efficient Wireless Power Transfer. Energies 2021, 14, 5111. [Google Scholar] [CrossRef]
- Shin, J.; Shin, S.; Kim, Y.; Ahn, S.; Lee, S.; Jung, G.; Jeon, S.-J.; Cho, D.-H. Design and Implementation of Shaped Magnetic-Resonance-Based Wireless Power Transfer System for Roadway-Powered Moving Electric Vehicles. IEEE Trans. Ind. Electron. 2014, 61, 1179–1192. [Google Scholar] [CrossRef]
- Li, Y.; Mai, R.; Lu, L.; He, Z. A Novel IPT System Based on Dual Coupled Primary Tracks for High Power Applications. J. Power Electron. 2016, 16, 111–120. [Google Scholar] [CrossRef]
- Dai, Z.; Wang, J.; Li, Y.; He, Y.; Fang, Z.; Hou, H. Optimal Design of Magnetic Coupling Wireless Power Supply System for Monitoring Equipment. IEEE Access 2018, 6, 58600–58608. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).