Abstract
Virtual power plants (VPPs) integrate diverse energy resources using advanced communication technologies and intelligent control strategies. This integration enhances the utilization and efficiency of distributed generation. This paper explores the incorporation of VPPs into load frequency control (LFC) systems. It includes an analysis of VPP-aggregated resources’ frequency regulation characteristics and a VPP-inclusive LFC model. Additionally, a decentralized automatic generation control strategy is proposed to distribute power outputs effectively, enabling swift grid frequency adjustments. This study uses MATLAB simulations to demonstrate the benefits and efficacy of VPPs in LFC, underscoring their role in advancing grid management and stability.
1. Introduction
As the global energy paradigm shifts towards sustainable development, the widespread integration of renewable energy sources and distributed generation systems (DGs) is fundamentally transforming traditional power systems. This transition offers unprecedented opportunities but also introduces significant challenges, particularly in terms of grid stability and frequency control. In response to these challenges, the concept of virtual power plants (VPPs) has emerged as a crucial innovation in modern energy management. VPPs utilize advanced information technology to integrate various forms of DERs into a unified, controllable entity, effectively simulating the functionality of traditional power plants but with greater flexibility and rapid response capabilities [1]. This technological advancement not only optimizes resource utilization and enhances the generation efficiency but also plays a vital role in maintaining grid stability amid fluctuations in renewable energy outputs.
The role of VPPs in grid regulation has been extensively studied, particularly in the contexts of energy market transactions [2] and multi-timescale economic dispatch [3,4,5]. Ref. [6] explores internal comprehensive profit distribution strategies when VPPs participate in wholesale electricity markets. Ref. [7] has proposed profit maximization models for VPPs that include renewable sources, battery energy storage systems (BESSs), and conventional power facilities in day-ahead and balancing markets. Ref. [8] has examined the use of 5G RAN slicing technologies to assist VPPs in frequency regulation markets, aiming to reduce risks and profit losses. Ref. [9] has dynamically clustered distributed photovoltaic systems containing BESSs within microgrids into two heterogeneous VPPs, designated for power supply and frequency regulation services. Ref. [10], based on photovoltaic and variable frequency loads in distribution networks, has constructed VPPs that adjust the power output of individual DER devices through VPP controllers to precisely track transmission system frequency signals or dispatch commands. Ref. [11] has discussed the direct control of VPPs during peak load periods, involving only household air conditioners, while ref. [12] has shown that VPPs can aggregate a large number of distributed renewable resources, optimizing their utilization. Ref. [13] has investigated strategies for VPPs covering distributed BESSs and heat pump water heaters in automatic generation control.
As the number and variety of devices within VPPs increase, maintaining a stable and high-quality power supply through load frequency control (LFC) is imperative. Ensuring that the frequency within the VPP-integrated power system remains at a nominal value is essential for the integrity of a system [13]. Enhancing the disturbance rejection capability of LFC within VPP-integrated power systems and determining how VPPs can effectively participate in the frequency regulation of the entire power system have become focal points of current research.
Load frequency control lies at the heart of VPP-integrated power system design, striving to maintain steady system frequency and power exchanges. Over the recent few decades, researchers have extensively investigated LFC issues, establishing effective LFC as a critical component for ensuring a high-quality power supply [14]. As wind and solar power have become increasingly integrated on a large scale, scholars have delved deeply into the LFC challenges within wind- and solar-power-integrated power systems, achieving noteworthy results [14,15,16,17,18,19,20]. Ref. [14] proposed an innovative algorithm for optimizing the PI controller settings within the LFC of hybrid power systems comprising photovoltaic and thermal units. Ref. [15] developed a dynamic model for LFC with wind farms, introducing an optimal frequency control method effective under various conditions. A multi-agent deep reinforcement learning approach for LFC in multi-regional power systems was put forward in [16], while ref. [17] examined the influence of photovoltaic systems on frequency regulation under different environmental conditions, proposing an enhanced optimization algorithm. Ref. [21] introduced a predictive controller for interconnected power systems, optimizing the frequency response of the LFC model.
However, with the ongoing rise in distributed resource integration, AGC systems confront several new challenges. These include integrating traditional power generation with a growing array of distributed resources and managing generation schedules in an environmentally sustainable manner. VPPs offer unique advantages in addressing these challenges. They not only provide essential frequency support services but also significantly reduce the carbon footprint of power systems by aggregating numerous distributed generation resources. Furthermore, recent research has highlighted the auxiliary service capabilities of VPPs in frequency regulation, particularly their potential role in enhancing AGC. However, much of the existing literature has yet to fully exploit the capabilities of VPPs. Within VPPs, diverse resources such as wind, storage, and electric vehicles can respond adeptly to AGC signals through varied strategies, enabling precise control over power outputs.
Accordingly, this paper proposes an innovative multiarea LFC model that incorporates VPP functionalities to optimize the grid frequency response and regulation performance. By embedding VPPs into the model, they not only act as active participants in AGC but also refine the scheduling of internal generation resources, enhancing responsiveness to electrical disturbances and bolstering the overall stability and economic efficiency of multiarea power systems.
This research aims to delve into the potential applications of VPPs in multiarea LFC systems, demonstrating how VPPs can elevate grid frequency performance and facilitate a broader integration of renewable energy. We endeavor to provide robust strategies and technical solutions that support the stable and sustainable operation of global power systems, thereby fostering further innovations in grid management and advancing towards a more sustainable energy future.
The remaining sections of this paper are as follows. Section 2 outlines how the model of adaptive memory-event-triggered LFC with EVs is built. The main theoretical results based on the linear matrix inequality are presented in Section 3. Numerical simulations and conclusions are given in Section 4 and Section 5, respectively.
2. Description of the System Model
2.1. Modeling VPPs
VPPs possess the capability to flexibly schedule and rapidly respond with resources composed of energy storage systems, power generation units, and communication technologies. This paper focuses on a VPP that integrates a combination of wind, solar, and storage systems to participate in the frequency regulation of a power system. The VPP designed in this study employs a controlled model for the involvement of diverse resources in the secondary frequency regulation of regional systems, as depicted in Figure 1. Detailed models for each resource type are presented.
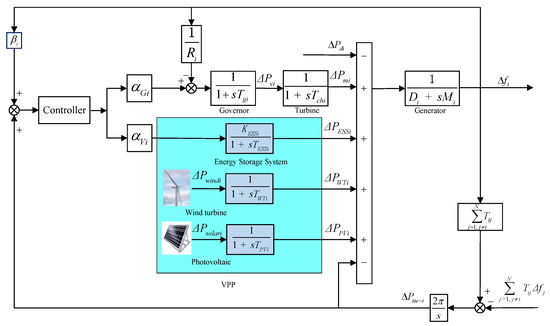
Figure 1.
The model of area i LFC system with virtual power plant participation.
2.1.1. Modeling of Wind Power
The first-order dynamic model for wind power generation is employed to analyze LFC issues. Due to the substantial influence of meteorological factors, such as wind speed and direction, on the power output from wind turbines, these elements are treated as disturbances in the study discussed in this section. This approach allows for a more accurate assessment of the impact of variable wind conditions on the stability and performance of LFC systems.
where refers to the deviation in output power from the wind power generation system, and represents the time constant associated with the wind turbine, reflecting its dynamic response to changes in wind conditions. is the wind power change.
2.1.2. Modeling of Photovoltaic Systems
In distributed photovoltaic systems, which typically operate using maximum power point tracking (MPPT), inverters are set to maintain a constant power output. The dynamic active power characteristics of these systems can be modeled as a first-order inertial element:
where indicates the change in active power output from the i photovoltaic inverter, refers to the deviation in solar power, and represents the inertia time constant of the inverter. Considering photovoltaic systems as non-adjustable resources, this study does not account for the impact of their spatial distribution on control strategies. Instead, all PV units within the VPP are aggregated and modeled as a single equivalent photovoltaic station. For analytical simplicity, it is assumed that all distributed PV inverters share a uniform time constant, which is considerably shorter than the cycle for secondary frequency control.
2.1.3. Modeling of Energy Storage Systems
The energy storage system (ESS) serves as an efficient auxiliary device for frequency regulation, enhancing the power system’s dynamic response to frequency deviations while alleviating transient stresses on traditional thermal power plants. The operational dynamics of an ESS, particularly its charging and discharging processes, necessitate a controlled response time. To accurately model these dynamics within the context of LFC in hybrid power systems, a first-order lag model is employed. The model is formulated as follows:
where denotes the response time constant of the ESS.
2.2. Modeling Multiarea Power Systems with VPP
VPPs engage in LFC, leveraging AGC signals to contribute to the frequency regulation efforts within power systems. The power system framework is structured into interconnected LFC areas, linked by tie-lines. The implementation of the LFC framework, which incorporates a VPP, is depicted for the i-th area in Figure 1. It can be described as
where .
Using inverse Laplace transformation and defining , , and , it has
where
We have the LFC model as follows:
where , , and are the state vector, the measurement output, the control input, and the disturbance, respectively. , , , . We assume that not all states of are accessible, and the matrix C is of a full row rank.
3. Design of the LFC Scheme for Power Systems with VPPs
The controller is designed as follows:
where with remain to be designed. The dynamic model is reconstructed as
The purpose of this paper is to provide a load frequency controller design method to make the power systems (2) with VPP satisfying:
- (1)
- System (2) with is asymptotically stable;
- (2)
- Under the zero initial condition, for any nonzero and a prescribed .
3.1. Stability Analysis
Theorem 1.
For given parameters and a matrix K, the system (6) is asymptotically stable with a prescribed disturbance attenuation level γ if there exists a matrix , such that
where , , .
Proof.
Consider the Lyapunov function defined as follows:
From (12), if , it follows that
Since is continuous over the interval , integrating both sides from 0 to t yields the following:
With zero initial conditions , this leads to
This implies that for any nonzero , there exists . When , there exists a positive constant such that for , from which we can confirm that the system (11) is asymptotically stable with an performance. □
3.2. Controller Design
Theorem 2.
For given parameters and a matrix K, the system (6) is asymptotically stable with a prescribed disturbance attenuation level γ if there exist matrix , such that
where , , .
where , , , , , .
Proof.
Define , pre- and post-multiplying both sides as in (15) with diag . By using the Schur complement, one can obtain (16).
Notice that Theorem 2 is difficult to be solved directly since there are many coupling nonlinear items . Moreover, C is full row rank; therefore, the general method to obtain the controller gain—which comprises setting and then obtaining —is infeasible due to the fact that C is a singular matrix in this work. For any matrices N and M with appropriate dimensions, we also define and . Notice that there is no feasible solution since is not a strict inequality. Then, the problem to solve the coupling items in Theorem 2 can be converted into a . As an alternative resolution, from , one can calculate that , which can be further converted into the following optimization problem by using the Schur complement, as follows:
where i.a. a small enough positive scalar. Since C is full row rank, it follows from and that M is a full rank matrix. Thus, M is invertible. Then, one can assume that the controller gain can be written as . □
4. Simulation
To verify the effectiveness of the proposed VPP-based secondary frequency control strategy, a simulation study was conducted within a two-area LFC system (see Figure 2). The parameters are listed in Table 1 [20,22].
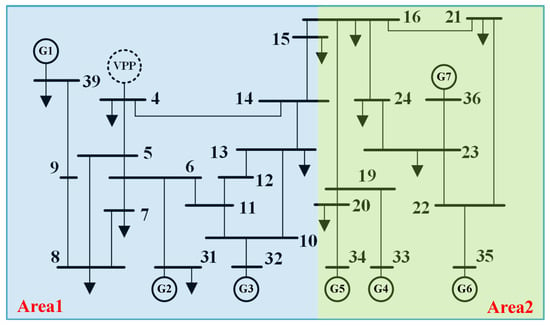
Figure 2.
Two-area interconnected power system with a VPP.

Table 1.
The parameters of the power system with a VPP.
We provide a detailed analysis of the waveforms depicted in Figure 3, Figure 4, Figure 5 and Figure 6, emphasizing the comparative dynamics of the system with and without the inclusion of a virtual power plant (VPP). Each figure contrasts the responses with a VPP (blue line) against those without a VPP (green line).
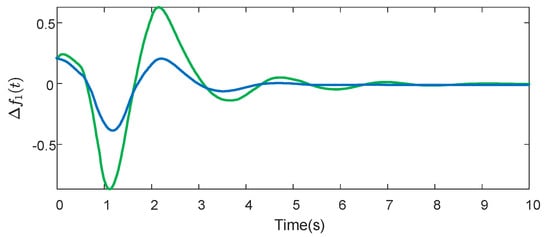
Figure 3.
Responses of .
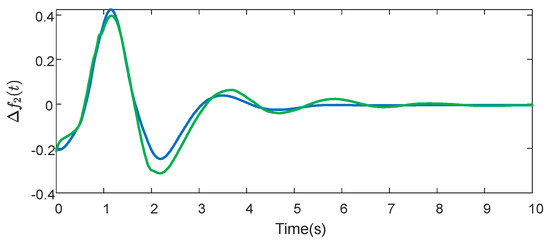
Figure 4.
Responses of .
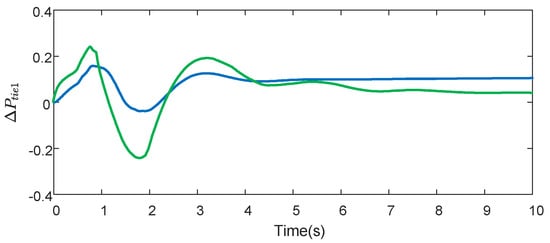
Figure 5.
Responses of .
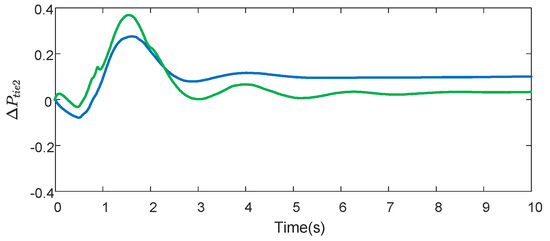
Figure 6.
Responses of .
In Figure 3, the waveform with VPP (blue) quickly rises and peaks at about 0.5 s, followed by a swift decline and subsequent stabilization within approximately 4 s. This rapid stabilization contrasts significantly with the waveform without a VPP (green), which shows larger oscillations and takes about 5 s to stabilize. This comparison demonstrates that a VPP significantly enhances the system’s ability to quickly dampen fluctuations and return to a steady state after a disturbance, indicating effective control in managing frequency deviations.
The responses of in Figure 4 further support the effectiveness of the VPP. The waveform with a VPP (blue) reaches its peak more swiftly at 1.5 s and shows a rapid decrease with damped oscillations that stabilize around 4 s. Conversely, the waveform without a VPP (green) experiences prolonged and larger oscillations before stabilizing, underscoring the VPP’s role in facilitating faster and more stable frequency control.
Figure 5 shows the response of , where the inclusion of a VPP (blue) results in a peak at 1.5 s and a subsequent quick decline to stability at about 5 s. The waveform without a VPP (green) displays a slower response with larger oscillations, emphasizing the VPP’s ability to provide quicker stabilization and a reduced oscillation amplitude, which is crucial in maintaining system stability amidst tie-line power perturbations.
In Figure 6, the waveform of with a VPP (blue) peaks quickly and stabilizes within 4 s, showing an efficient reduction in oscillations. In contrast, the scenario without a VPP (green) displays extended oscillations that stabilize much later, further highlighting the benefits of integrating a VPP into the system for improved frequency regulation and response time under varying load conditions.
The comparison of the waveforms in Figure 3, Figure 4, Figure 5 and Figure 6 clearly demonstrates that the inclusion of a VPP significantly improves the frequency stability of the power system. The VPP-enabled scenarios exhibit faster response times, reduced oscillation amplitudes, and quicker stabilization compared to scenarios without a VPP. These benefits underscore the practical advantages of integrating VPPs into power systems for effective frequency regulation.
5. Conclusions
This paper has analyzed the frequency regulation capabilities of resources integrated within VPPs and has developed a comprehensive framework that incorporates VPPs into LFC systems. The decentralized automatic generation control strategy formulated in this study efficiently manages power distribution, ensuring timely and necessary adjustments to grid frequency. Empirical validations conducted through MATLAB simulations substantiate the effectiveness of VPP integration in LFC systems, highlighting significant improvements in grid stability and responsiveness to frequency fluctuations. Conclusively, the integration of VPPs into LFC systems emerges as a progressive approach to modernize grid management and augment stability. This strategy promotes the transition toward more sustainable and flexible power systems, showcasing the potential to optimize frequency control and minimize reliance on traditional generation methods, thereby paving the way for a more sustainable and efficient energy future. Future research should focus on optimizing participation factors to enhance system stability and on investigating the robustness and resilience of power systems in the face of cyber threats.
Author Contributions
Conceptualization, Z.W., Y.W. and L.X.; methodology, Z.W.; software, L.X.; validation, D.P. and H.S.; formal analysis, Z.W. and Y.W.; investigation, H.Z.; resources, H.Z.; data curation, L.X.; writing—original draft preparation, Z.W. and Y.W.; writing—review and editing, Z.W. and Y.W.; visualization, L.X.; supervision, L.X. and Y.W.; project administration, Z.W.; funding acquisition, Z.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the State Grid Jilin Electric Power Company under the “Unveiling and Commanding” Science and Technology Project, “Key Technologies Research and Application for Coordinated Operation of Integrated Source-Load-Storage in Smart Medium and Low Voltage Distribution Network of State Grid Changchun Power Supply Company in 2024” (Project Number: 2023JBGS-01).
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
Authors Zeyi Wang, Yao Wang, Dan Peng and Hao Shi were employed by the company Changchun Power Supply Company of State Grid Jilin Electric Power Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Mashhour, E.; Moghaddas-Tafreshi, S.M. Bidding Strategy of Virtual Power Plant for Participating in Energy and Spinning Reserve Markets—Part I: Problem Formulation. IEEE Trans. Power Syst. 2011, 26, 949–956. [Google Scholar] [CrossRef]
- Koraki, D.; Strunz, K. Wind and Solar Power Integration in Electricity Markets and Distribution Networks Through Service-Centric Virtual Power Plants. IEEE Trans. Power Syst. 2018, 33, 473–485. [Google Scholar] [CrossRef]
- Pandžić, H.; Kuzle, I.; Capuder, T. Virtual power plant mid-term dispatch optimization. Appl. Energy 2013, 101, 134–141. [Google Scholar] [CrossRef]
- Yi, Z.; Xu, Y.; Gu, W.; Wu, W. A multi-time-scale economic scheduling strategy for virtual power plant based on deferrable loads aggregation and disaggregation. IEEE Trans. Sustain. Energy 2019, 11, 1332–1346. [Google Scholar] [CrossRef]
- Wang, Y.; Ai, X.; Tan, Z.; Yan, L.; Liu, S. Interactive dispatch modes and bidding strategy of multiple virtual power plants based on demand response and game theory. IEEE Trans. Smart Grid 2015, 7, 510–519. [Google Scholar] [CrossRef]
- Rahmani-Dabbagh, S.; Sheikh-El-Eslami, M.K. A profit sharing scheme for distributed energy resources integrated into a virtual power plant. Appl. Energy 2016, 184, 313–328. [Google Scholar] [CrossRef]
- Pandžić, H.; Morales, J.M.; Conejo, A.J.; Kuzle, I. Offering model for a virtual power plant based on stochastic programming. Appl. Energy 2013, 105, 282–292. [Google Scholar] [CrossRef]
- Feng, C.; Chen, Q.; Wang, Y.; Ma, J.; Wang, X. Frequency regulation service provision for virtual power plants through 5G RAN slicing. IEEE Trans. Smart Grid 2022, 13, 4943–4956. [Google Scholar] [CrossRef]
- Zhang, R.; Hredzak, B. Distributed dynamic clustering algorithm for formation of heterogeneous virtual power plants based on power requirements. IEEE Trans. Smart Grid 2020, 12, 192–204. [Google Scholar] [CrossRef]
- Dall’Anese, E.; Guggilam, S.S.; Simonetto, A.; Chen, Y.C.; Dhople, S.V. Optimal regulation of virtual power plants. IEEE Trans. Power Syst. 2017, 33, 1868–1881. [Google Scholar] [CrossRef]
- Ruiz, N.; Cobelo, I.; Oyarzabal, J. A direct load control model for virtual power plant management. IEEE Trans. Power Syst. 2009, 24, 959–966. [Google Scholar] [CrossRef]
- Wei, C.; Xu, J.; Liao, S.; Sun, Y.; Jiang, Y.; Ke, D.; Zhang, Z.; Wang, J. A bi-level scheduling model for virtual power plants with aggregated thermostatically controlled loads and renewable energy. Appl. Energy 2018, 224, 659–670. [Google Scholar] [CrossRef]
- Oshnoei, A.; Kheradmandi, M.; Blaabjerg, F.; Hatziargyriou, N.D.; Muyeen, S.; Anvari-Moghaddam, A. Coordinated control scheme for provision of frequency regulation service by virtual power plants. Appl. Energy 2022, 325, 119734. [Google Scholar] [CrossRef]
- Wen, S.; Yu, X.; Zeng, Z.; Wang, J. Event-triggering load frequency control for multiarea power systems with communication delays. IEEE Trans. Ind. Electron. 2015, 63, 1308–1317. [Google Scholar] [CrossRef]
- Gholamrezaie, V.; Dozein, M.G.; Monsef, H.; Wu, B. An optimal frequency control method through a dynamic load frequency control (LFC) model incorporating wind farm. IEEE Syst. J. 2017, 12, 392–401. [Google Scholar] [CrossRef]
- Yan, Z.; Xu, Y. A multi-agent deep reinforcement learning method for cooperative load frequency control of a multi-area power system. IEEE Trans. Power Syst. 2020, 35, 4599–4608. [Google Scholar] [CrossRef]
- Khadanga, R.K.; Kumar, A.; Panda, S. A novel modified whale optimization algorithm for load frequency controller design of a two-area power system composing of PV grid and thermal generator. Neural Comput. Appl. 2020, 32, 8205–8216. [Google Scholar] [CrossRef]
- Qian, D.; Tong, S.; Liu, H.; Liu, X. Load frequency control by neural-network-based integral sliding mode for nonlinear power systems with wind turbines. Neurocomputing 2016, 173, 875–885. [Google Scholar] [CrossRef]
- Qian, D.; Fan, G. Neural-network-based terminal sliding mode control for frequency stabilization of renewable power systems. IEEE/CAA J. Autom. Sin. 2018, 5, 706–717. [Google Scholar] [CrossRef]
- Shangguan, X.C.; Zhang, C.K.; He, Y.; Jin, L.; Jiang, L.; Spencer, J.W.; Wu, M. Robust load frequency control for power system considering transmission delay and sampling period. IEEE Trans. Ind. Informatics 2020, 17, 5292–5303. [Google Scholar] [CrossRef]
- Ersdal, A.M.; Imsland, L.; Uhlen, K. Model predictive load-frequency control. IEEE Trans. Power Syst. 2015, 31, 777–785. [Google Scholar] [CrossRef]
- Farivar, F.; Bass, O.; Habibi, D. Memory-Based Adaptive Sliding Mode Load Frequency Control in Interconnected Power Systems With Energy Storage. IEEE Access 2023, 11, 102515–102530. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).