Adaptability Evaluation of Power Grid Planning Scheme for Novel Power System Considering Multiple Decision Psychology
Abstract
1. Introduction
- (1)
- A comprehensive evaluation index system of power grid planning adaptability is established, which comprehensively addresses the emerging requirements of grid planning for the novel power system, including economy adaptability, energy structure adaptability, power grid structure adaptability, reliability adaptability, and environment adaptability.
- (2)
- An improved cumulative prospect theory (ICPT) is introduced into the evaluation model to effectively characterize the different decision-making psychologies, which enhances the adaptability to the uncertainty of renewable energy and makes the evaluation results more realistic.
- (3)
- A combination evaluation method based on a cooperative game (CG) is constructed, fully contributing to the advantages of different evaluation models to make the evaluation results fairer.
2. Adaptive Requirements of Grid Planning for Novel Power System
2.1. Adaptive Requirements for Economic
2.2. Adaptive Requirements for Energy Structure
2.3. Adaptive Requirements for Grid Structure
2.4. Adaptive Requirements for Reliability
2.5. Adaptive Requirements for Environment
3. Construction of Evaluation Index System
3.1. Economic Adaptability
3.2. Energy Structure Adaptability
3.3. Grid Structure Adaptability
3.4. Reliability Adaptability
3.5. Environment Adaptability
4. Construction of Evaluation Method Considering Multiple Decision Psychology
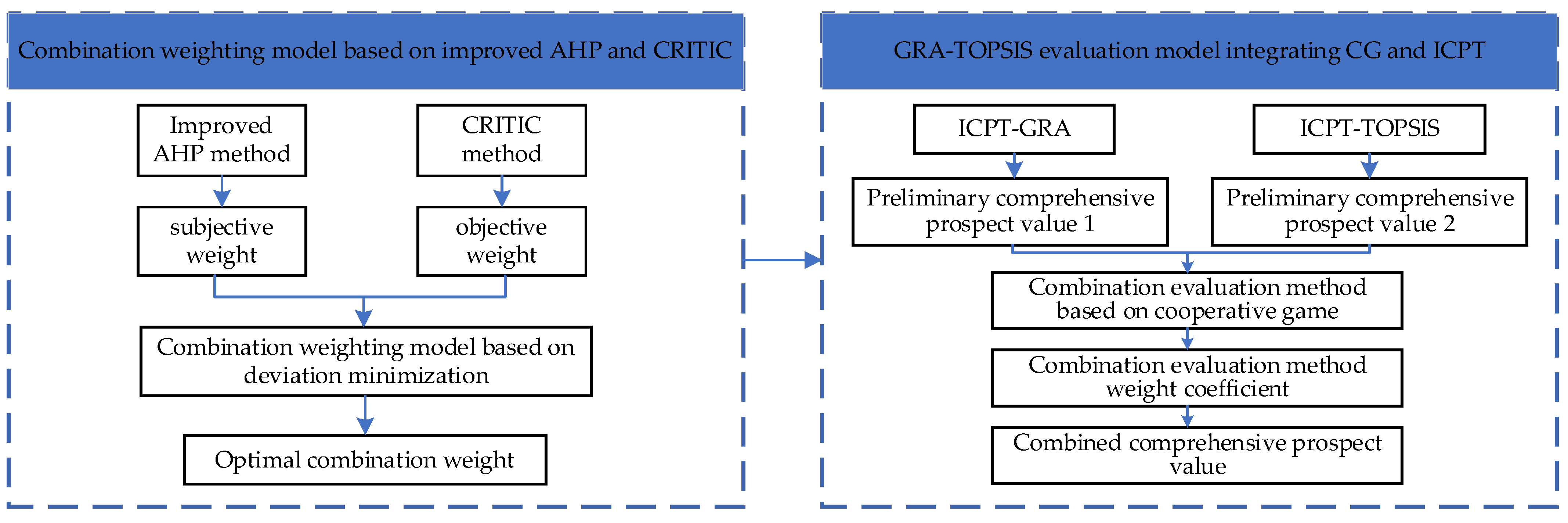
4.1. Framework of the Evaluation Method
4.2. Weighting Method Based on Improved AHP-CRITIC
4.2.1. Subjective Weight Calculation Based on Improved AHP
- (1)
- Improved judgment matrix
- (a)
- Experts select the importance of each indicator;
- (b)
- Based on the opinions of experts, a judgment matrix is formed, with the following parameters:
- (2)
- Improve matrix consistency
- (3)
- Construct an antisymmetric matrix
- (4)
- Solve the optimal transfer matrix
- (5)
- Solve the consistency matrix
- (6)
- Calculate the weight value
- (a)
- The th root of the product for the elements in each row of are calculated.
- (b)
- The values of the elements of each row are processed to the th power and recorded as vectors
- (c)
- Through the step of normalizing , the weight obtained:
4.2.2. Objective Weight Calculation Based on CRITIC
4.2.3. Combination Weight Calculation Based on Deviation Minimization
4.3. Adaptability Evaluation Model Based on GRA-TOPSIS Integrating CG and ICPT
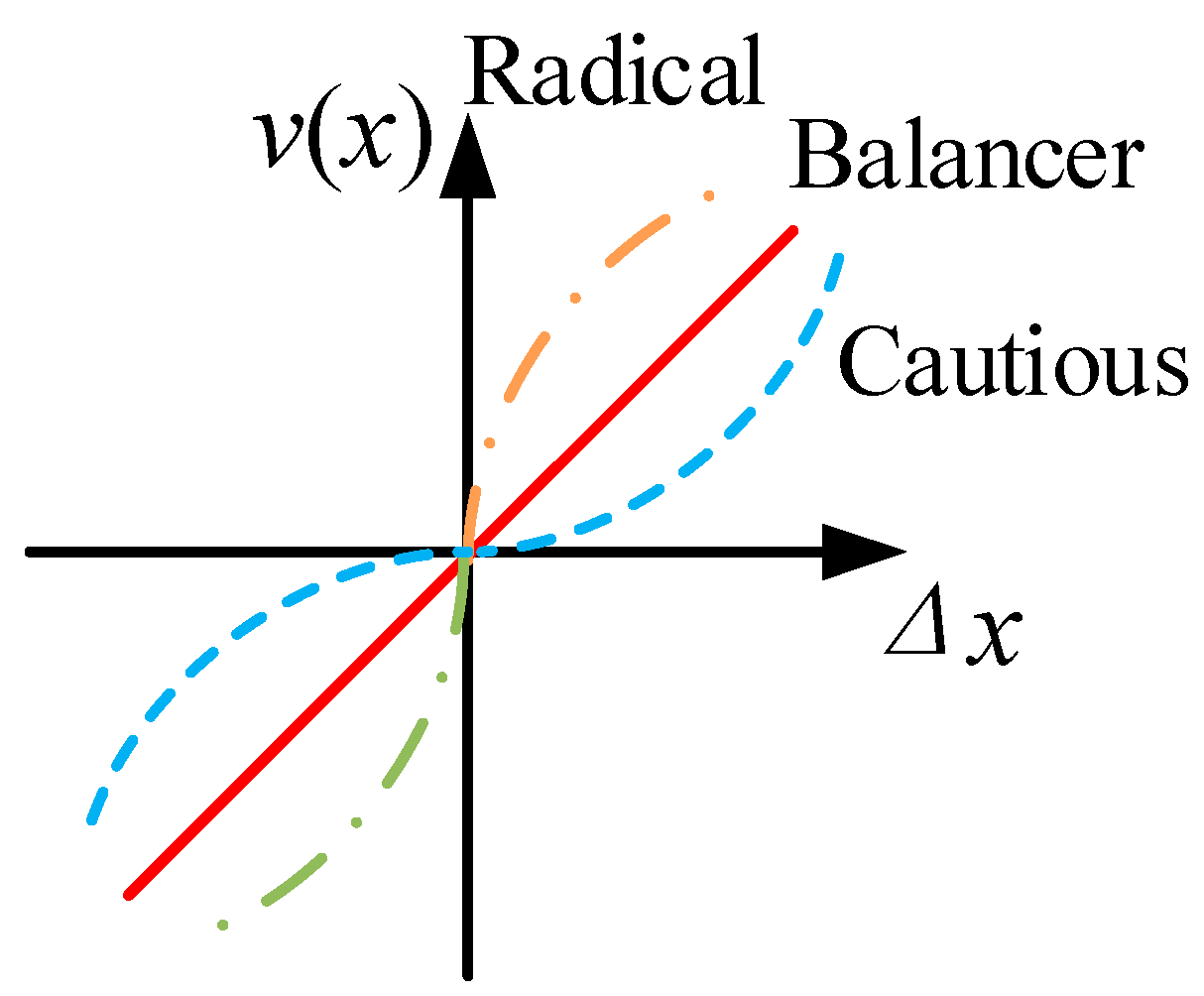
4.3.1. ICPT Method
4.3.2. ICPT-GRA Method
4.3.3. ICPT-TOPSIS Method
4.3.4. Integrating CG and ICPT GRA-TOPSIS Method
5. Example Analysis
5.1. Basic Data and Standardized Processing
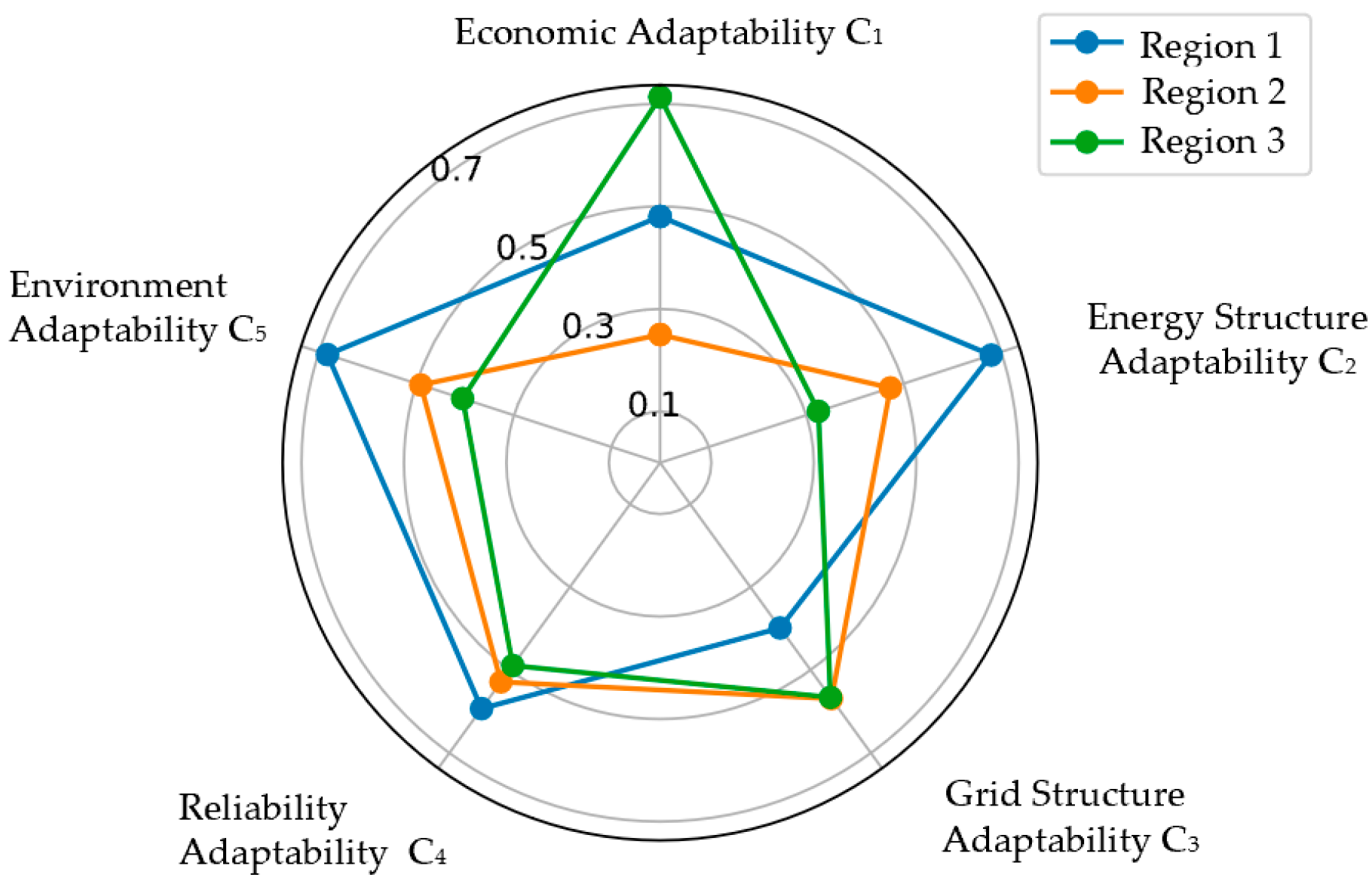
5.2. Weighting of Indicators
5.3. Adaptability Evaluation of Grid Planning Scheme for Novel Power System Based on GRA-TOPSIS Integrating CG and ICPT
5.3.1. Evaluating Based on ICPT-GRA
5.3.2. Evaluating Based on ICPT-TOPSIS
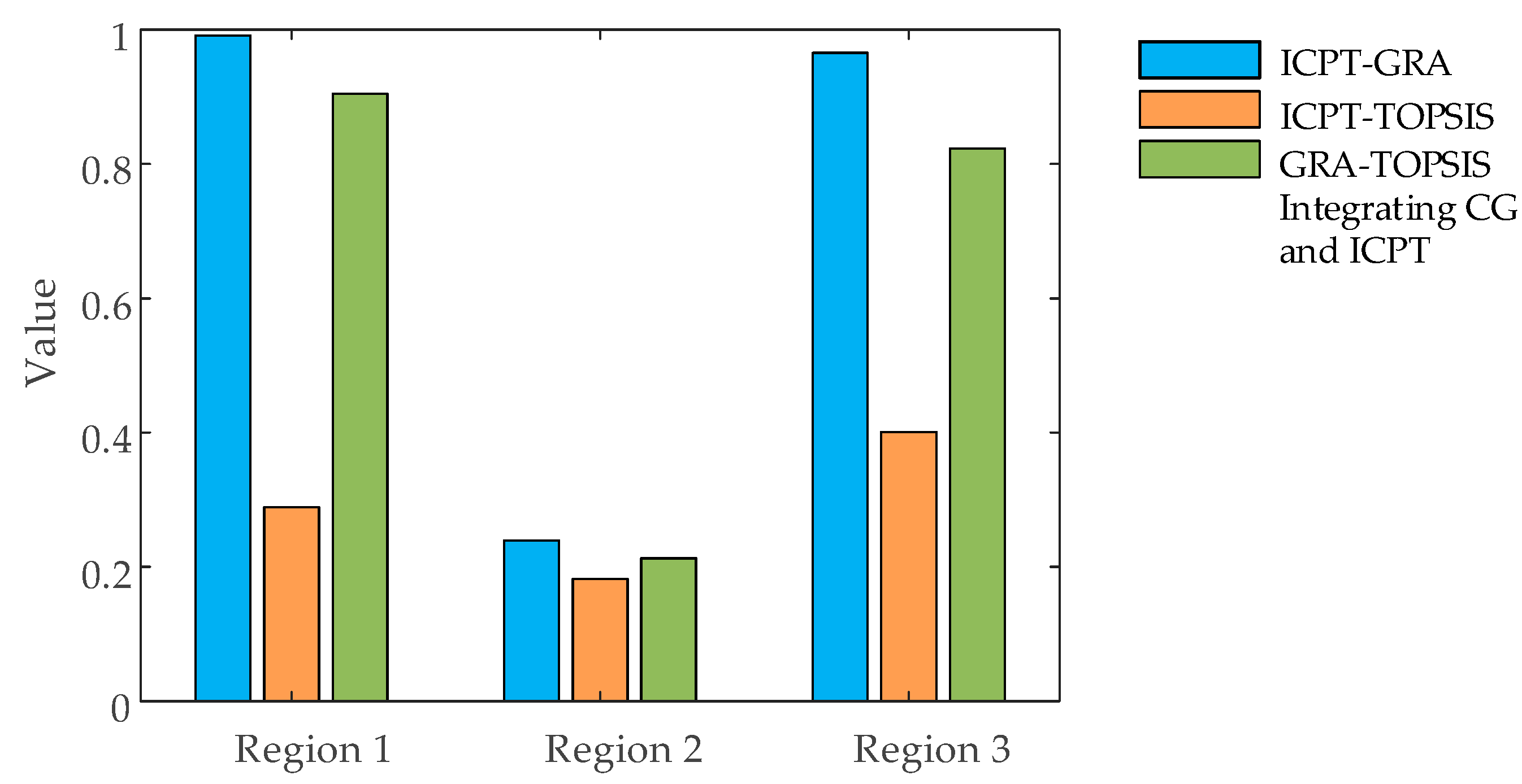
5.3.3. Combination Evaluation Based on CG
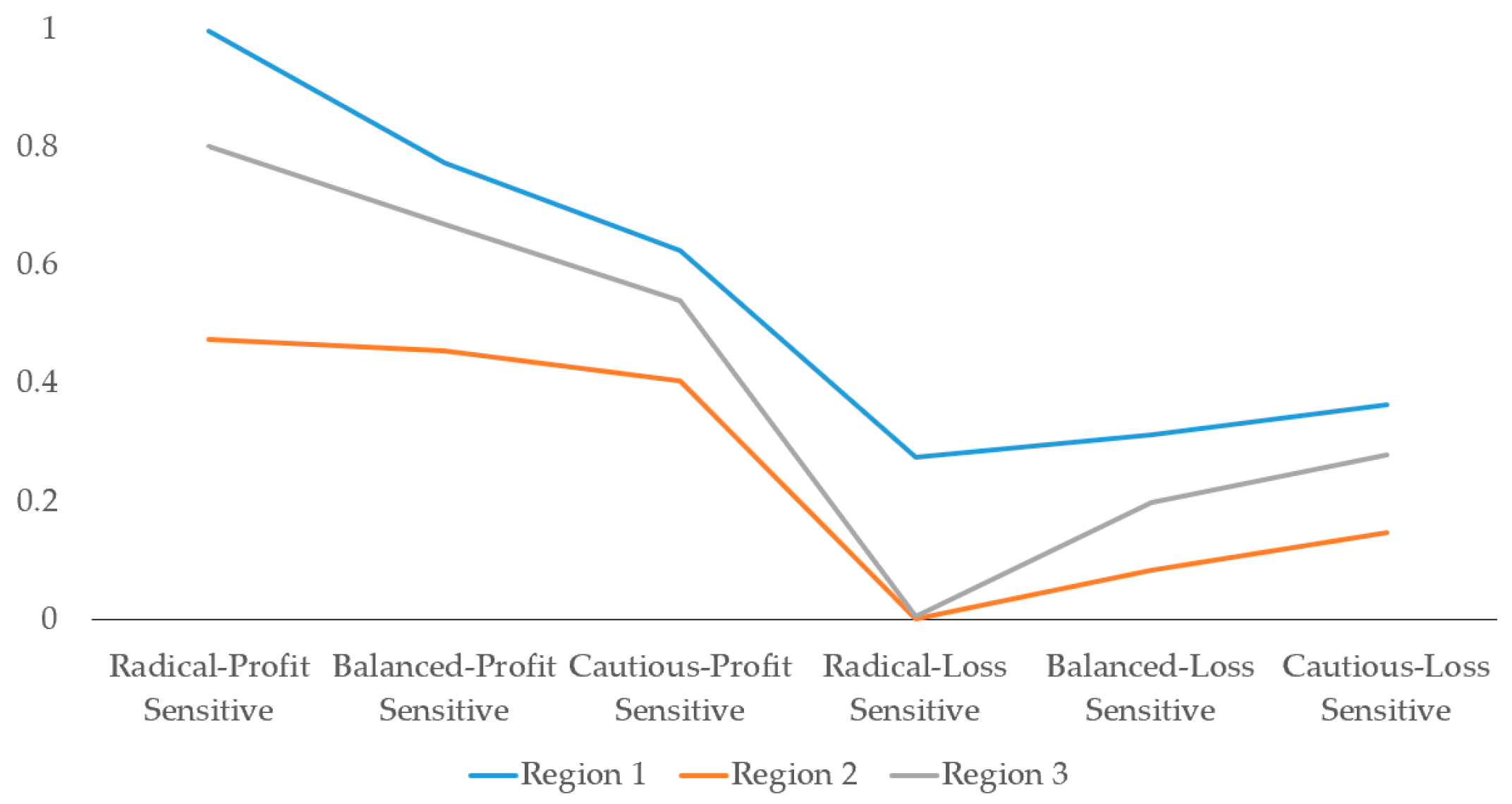
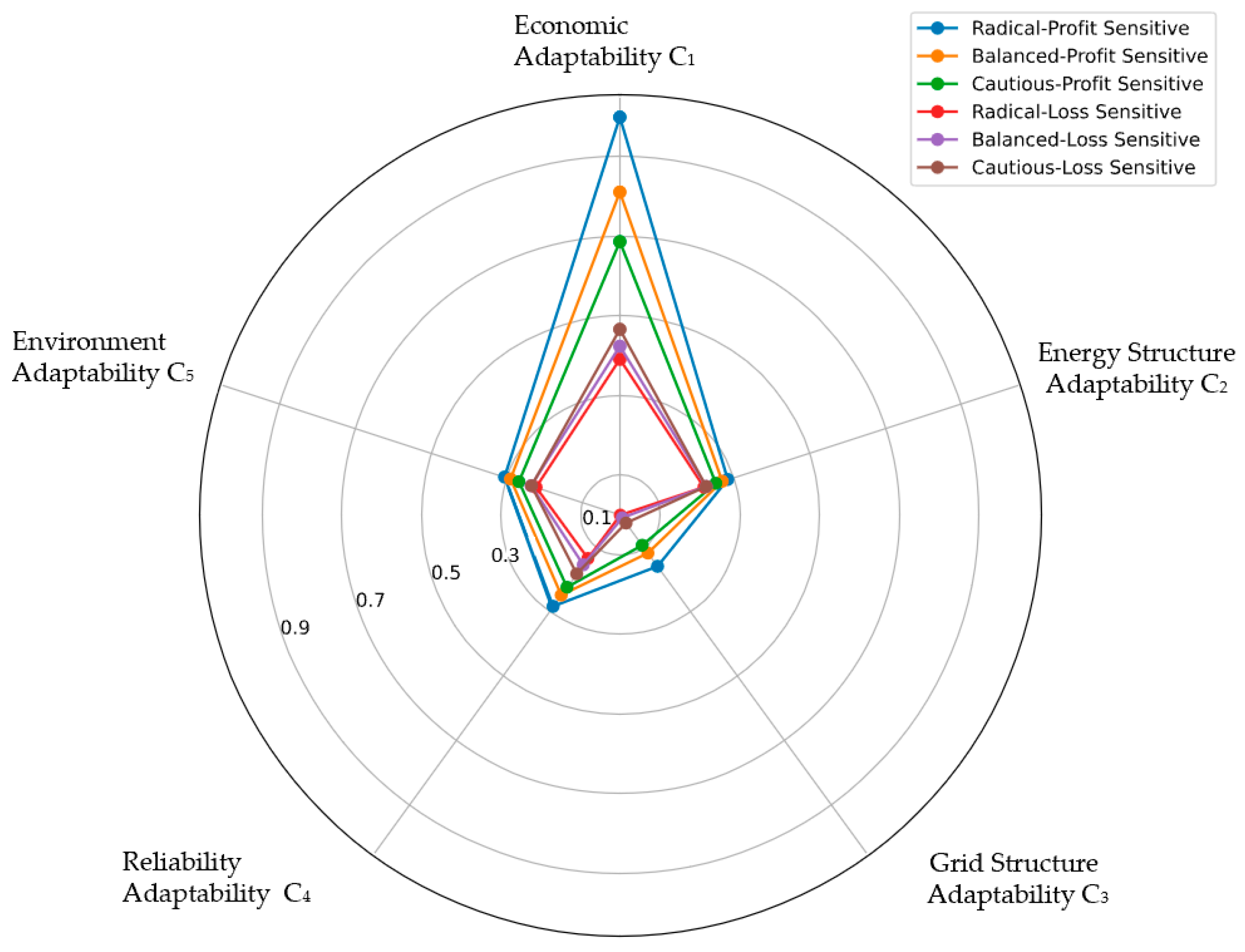
5.4. Sensitivity Analysis Based on Multiple Psychology of Decision-Maker on the Evaluation of Planning Schemes
6. Conclusions
- (1)
- In the evaluation of the adaptability of grid planning for novel power system, grid structure adaptability and reliability adaptability have a greater impact.
- (2)
- It is considered that the different risk and loss attitudes of decision-makers can effectively improve the accuracy of the evaluation results, and radical profit-sensitive decision-making psychology pays more attention to economic adaptability.
- (3)
- The ICPT-TOPSIS method can better identify the weakness of the evaluation scheme, while the ICPT-GRA method can distinguish the better overall scenario more intuitively, and the combination evaluation method based on CG effectively combines the advantages of these two different methods.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, J.; Chen, Y.; Yu, L.; Li, G.; Li, J. Has the evolution of renewable energy policies facilitated the construction of a new power system for China? A system dynamics analysis. Energy Policy 2023, 183, 113798. [Google Scholar] [CrossRef]
- Li, R.; Hu, Y.; Wang, X.; Zhang, B.; Chen, H. Estimating the impacts of a new power system on electricity prices under dual carbon targets. J. Clean. Prod. 2024, 438, 140583. [Google Scholar] [CrossRef]
- Bo, H.; Xie, K.G.; Shao, C.Z.; Pan, C.; Lin, C.; Zhao, Y. Commentary on Risk of New Power System Under Goals of Carbon Emission Peak and Carbon Neutrality: Characteristics, indices and Assessment Methods. Autom. Electr. Power Syst. 2023, 47, 1–15. [Google Scholar]
- Liao, Z.; Kally, J.; Ru, S. Probabilistic modeling of renewable energy sources in smart grids: A stochastic optimization perspective. Sustain. Cities Soc. 2024, 109, 105522. [Google Scholar] [CrossRef]
- Wu, Y.; Fang, J.; Ai, X.; Xue, X.; Cui, S.; Chen, X.; Wen, J. Robust co-planning of AC/DC transmission network and energy storage considering uncertainty of renewable energy. Appl. Energy 2023, 339, 120933. [Google Scholar] [CrossRef]
- Li, F.; Yang, J.; Shen, S.; Zhu, K.; Qian, J.; Yan, C. Adaptability Evaluation of Power Grid Planning Scheme Based on Improved AHP-CRITIC-TOPSIS with High Proportion of Renewable Energy. In Proceedings of the 2023 IEEE International Conference on Power Science and Technology (ICPST), Kunming, China, 5–7 May 2023; pp. 623–630. [Google Scholar] [CrossRef]
- Yin, L.; Wei, X. Multigroup differential evolutionary and multilayer Taylor dynamic network planning for zero-carbon grid extension model with user satisfaction. Energy Convers. Manag. 2023, 297, 117753. [Google Scholar] [CrossRef]
- Huang, Y.S.; Jiang, Y.Q.; Wang, J. Research on Adaptability Evaluation of Distribution Network Based on Improved TOPSIS-PSO-SVM. Electron. Sci. Technol. 2022, 35, 54–63. [Google Scholar]
- Lu, X.Q.; Ye, Y.; Cao, C.; Meng, J.H.; Tang, H.; He, J. Comprehensive evaluation method of distribution network planning for distributed photovoltaic access. J. North China Electr. Power Univ. (Nat. Sci. Ed.) 2022, 51, 1–10. [Google Scholar]
- Zhang, Z.; Yang, H.Y.; Gao, X.T.; Wang, J.; Wang, Q. Research on Evaluation Method of Distribution Network Planning Scheme Adaptability Based on BPNN Model. Distrib. Util. 2021, 38, 56–63+88. [Google Scholar]
- He, X.; Gao, C.; Cao, H.Z.; Li, Y.; Yu, T. Index evaluation of distribution network based on improved analytic hierarchy process. Electr. Meas. Instrum. 2022, 59, 93–99. [Google Scholar]
- An, Z.; Wei, N.; Liu, S.; Chen, Q.F.; Xing, D. An Efficiency and Benefit Evaluation Method for New Transmission Network Planning Based on Production Simulation. Power Syst. Clean Energy 2024, 40, 73–83. [Google Scholar]
- Zhang, J.; Gao, C.; Wang, T.; Duan, Y.; Xu, M.; Guo, Z. A Dynamic Evaluation Method for High-Permeability New Energy Distribution Network Planning Considering Multistage Development Trends. Front. Energy Res. 2022, 10, 958892. [Google Scholar] [CrossRef]
- Lu, L.; Zhou, H.; Cai, S.; Liao, Y.; Jiang, L.; Wang, Y. Comprehensive Evaluation of Transmission Network Planning Schemes Based on IFAHP. In Proceedings of the 2020 4th International Conference on HVDC (HVDC), Xi’an, China, 6–9 November 2020; pp. 375–381. [Google Scholar]
- Si, J.D.; Wu, X.; Guo, Q.S.; Cai, H.; Cheng, L. Review of Flexible Interconnection of Regional Grids Interconnection Planning and Operation Techniques for High Percentage of Renewable Energy Consumption. Power Syst. Technol. 2024, 48, 2272–2286. [Google Scholar]
- Gao, Y.; Gao, Q.C. Serve the high-quality development of the power grid with standard digital innovation. State Grid News China 2024, 1. [Google Scholar] [CrossRef]
- Fan, W.; Fan, Y.; Tan, Z.; Ju, L.; Yao, X. Distributionally robust optimization model for virtual power plant participation in electricity carbon market based on multi-layer benefit sharing. Syst. Eng.-Theory Pract. 2024, 44, 661–683. [Google Scholar]
- Wang, Z.; Lu, X.; Zhuang, M.; Zhang, C.; Chen, S. Spatial Optimization of Wind-PV Hybrid Energy Systems for the Three-North Region in China. J. Glob. Energy Interconnect. 2020, 3, 97–104. [Google Scholar]
- Gu, J.M.; Song, Y.T.; Liu, X.Y.; Zhu, S.X.; Lei, Y. Design of Security Defense System for UHV Power Grids under the Dual Carbon Background. Electr. Drive 2024, 1–6. [Google Scholar] [CrossRef]
- Tian, C.; Liu, Y.; Zhang, G.; Yang, Y.; Yan, Y.; Li, C. Transfer learning based hybrid model for power demand prediction of large-scale electric vehicles. Energy 2024, 300, 131461. [Google Scholar] [CrossRef]
- Wang, J.H. Exploration of Power Grid Planning Method Based on New Energy Consumption Under the “Dual Carbon” Goal. Electr. Eng. 2023, S1, 237–239. [Google Scholar]
- Zhang, Y.; Xiang, R.M.; Zheng, Z.H. Industrial User Decision Model Considering Differentiated Power Quality Services in the Context of Carbon Market. Proc. CSEE 2024, 1–14. [Google Scholar]
- Lu, Y.F.; Liu, D.; Zhang, Y. Construction Sequence Planning of Power Transmission and Transformation Projects Based on Game Theory Combined Weighting and Improved Technique for Order Preference by Similarity to Ideal Solution. Sci. Technol. Eng. 2024, 24, 4124–4131. [Google Scholar]
- Fang, H.; Shang, L.; Dong, X.; Tian, Y. High Proportion of Distributed PV Reliability Planning Method Based on Big Data. Energies 2023, 16, 7692. [Google Scholar] [CrossRef]
- Zhang, K.; Zhao, Q.; Wang, S.; Liang, F.; Ni, J.F. Construction and calculation method of comprehensive evaluation index reflecting distributed photovoltaic hosting capacity of distribution network. Distrib. Util. 2024, 41, 3–11. [Google Scholar]
- Zhao, S.Q.; Tang, S.F. Comprehensive evaluation of transmission network planning scheme based on improved analytic hierarchy process, CRITIC method and TOPSIS. Electr. Power Autom. Equip. 2019, 39, 143–148+162. [Google Scholar]
- Ilbahar, E.; Kahraman, C.; Cebi, S. Risk assessment of renewable energy investments: A modified failure mode and effect analysis based on prospect theory and intuitionistic fuzzy AHP. Energy 2022, 239, 121907. [Google Scholar] [CrossRef]
- Cao, Y.; Li, G.J. Comprehensive evaluation of island isolated microgrid dispatch considering multiple decision psychology. Control Decis. 2022, 37, 1591–1600. [Google Scholar]
- Liu, Y.; Gaun, X.; Li, Y.C. Multi-attribute decision making based on comprehensive hesitation fuzzy entropy. Control Decis. 2024, 39, 2022–2030. [Google Scholar]
- Qu, K.Q.; Qiao, J.M.; Mao, L.; Zhu, S.J.; Zhao, J.B. Optimal Configuration and Site-selection Evaluation Method for Shared Energy Storage Stations. Mod. Electr. Power 2024, 1–9. [Google Scholar] [CrossRef]
- He, L.J.; Li, W.F.; Zhang, Y. Multi-objective optimization method based on grey synthetic incidence analysis. Control Decis. 2020, 35, 1134–1142. [Google Scholar]
- Zhao, H.; Hao, X. Location decision of electric vehicle charging station based on a novel grey correlation comprehensive evaluation multi-criteria decision method. Energy 2024, 299, 131356. [Google Scholar] [CrossRef]
- Wang, L.; Yang, J.; Qu, B.; Pang, C. Multi-Objective Optimization of an Organic Rankine Cycle (ORC) for a Hybrid Solar–Waste Energy Plant. Energies 2024, 17, 1810. [Google Scholar] [CrossRef]
- Akram, F.; Ahmad, T.; Sadiq, M. An integrated fuzzy adjusted cosine similarity and TOPSIS based recommendation system for information system requirements selection. Decis. Anal. J. 2024, 11, 100443. [Google Scholar] [CrossRef]
- Aiello, G.; Quaranta, S.; Inguanta, R.; Certa, A.; Venticinque, M. A Multi-Criteria Decision-Making Framework for Zero Emission Vehicle Fleet Renewal Considering Lifecycle and Scenario Uncertainty. Energies 2024, 17, 1371. [Google Scholar] [CrossRef]
- Çakiroğlu, R.; Çinici, O.K.; Asal, Ş.; Acır, A. Multi-objective optimization of the hydrogen fuel production of a solar-based cobalt-chlorine (Co–Cl) thermochemical cycle with grey relational analysis. Int. J. Hydrogen Energy 2024, 68, 360–373. [Google Scholar] [CrossRef]
- Zhang, X.; Duan, X. Evaluating water resource carrying capacity in Pearl River-West River economic Belt based on portfolio weights and GRA-TOPSIS-CCDM. Ecol. Indic. 2024, 161, 111942. [Google Scholar] [CrossRef]
- Chen, Y.T.; Chen, G.H.; Li, M.J. Research on Determining Weights of Combination Evaluation Method Using Cooperative Games. Chin. J. Manag. Sci. 2005, 13, 89–94. [Google Scholar]
- Więckowski, J.; Kizielewicz, B.; Shekhovtsov, A.; Sałabun, W. RANCOM: A novel approach to identifying criteria relevance based on inaccuracy expert judgments. Eng. Appl. Artif. Intell. 2023, 122, 106114. [Google Scholar] [CrossRef]


| First-Level Indicators | Second-Level Indicators |
|---|---|
| Economic Adaptability (C1) | Elasticity coefficient of power production (C11) |
| Investment revenue expansion ratio (C12) | |
| Additional load capacity per unit investment (C13) | |
| Additional electricity supply per unit investment (C14) | |
| Energy Structure Adaptability (C2) | Proportion of clean energy (C21) |
| Capacity to accommodate renewable energy (C22) | |
| Grid Structure Adaptability (C3) | Substation full stop and turn rate (C31) |
| Capacity ratio of transformer (C32) | |
| Capacity expansion margin of substation (C33) | |
| Remaining interval ratio (C34) | |
| Line capacity-to-load ratio (C35) | |
| Line loss rate (C36) | |
| Reliability Adaptability (C4) | N-1 pass rate of power lines (C41) |
| N-1 pass rate of transformers (C42) | |
| Voltage compliance rate (C43) | |
| Mean power supply reliability (C44) | |
| Environment Adaptability (C5) | CO2 emission reduction (C51) |
| NOX emission reduction (C52) | |
| SO2 emission reduction (C53) |
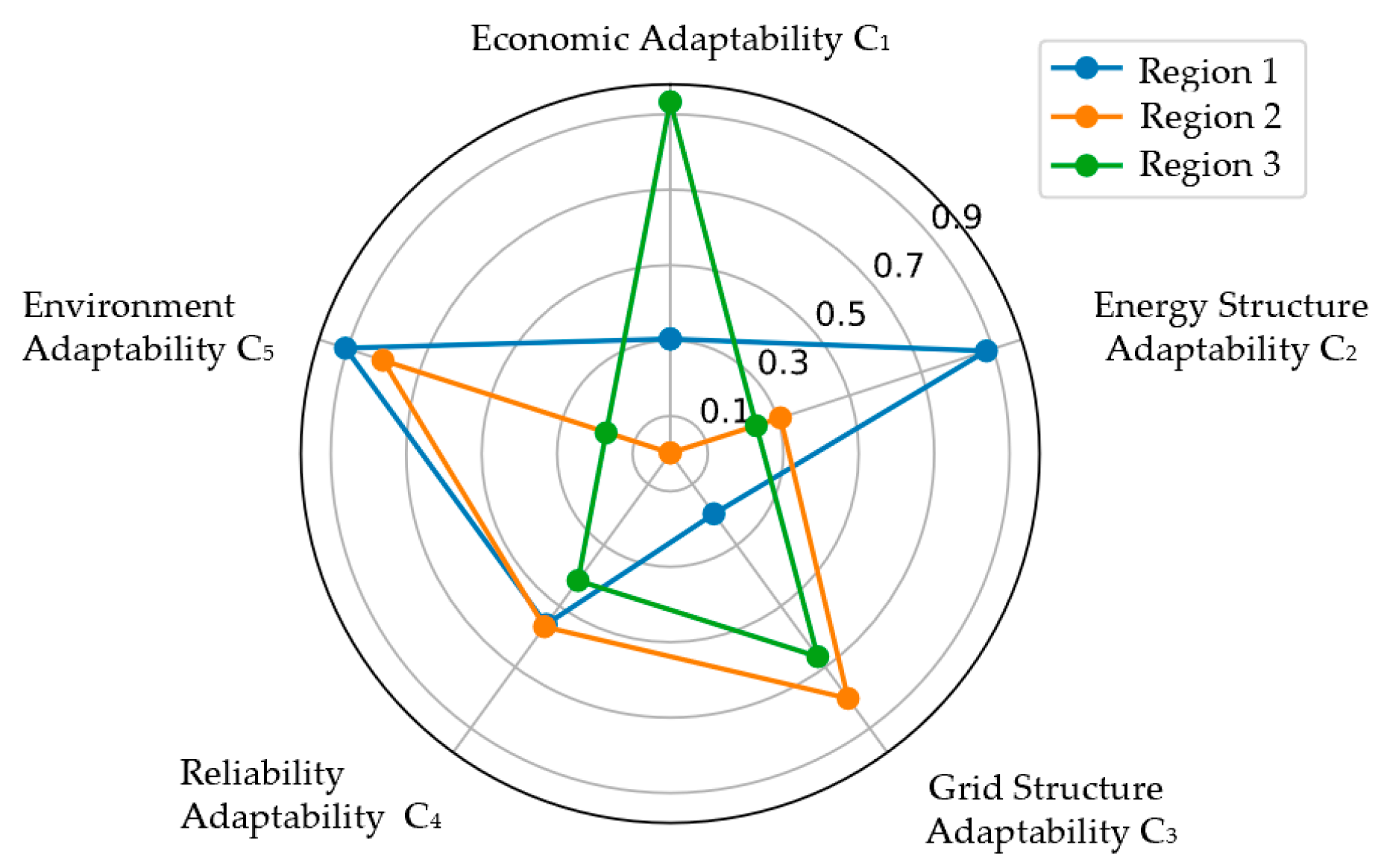
| Indicators | Region 1 | Region 2 | Region 3 |
|---|---|---|---|
| C11 | 0.6200 | 0.6000 | 0.9800 |
| C12 | 0.8627 | 0.8013 | 0.8480 |
| C13 | 0.8460 | 0.5331 | 0.7840 |
| C14 | 0.7578 | 0.6525 | 0.8867 |
| C21 | 0.6421 | 0.5262 | 0.5575 |
| C22 | 0.5846 | 0.6048 | 0.5408 |
| C31 | 0.7541 | 0.8230 | 0.6997 |
| C32 | 0.4710 | 0.9058 | 0.7609 |
| C33 | 1.0000 | 0.6750 | 0.9300 |
| C34 | 1.0000 | 0.9555 | 1.0000 |
| C35 | 0.8036 | 0.8794 | 0.7851 |
| C36 | 0.6584 | 0.6569 | 0.6996 |
| C41 | 0.9000 | 1.0000 | 0.8300 |
| C42 | 0.7456 | 0.6616 | 0.7144 |
| C43 | 0.7546 | 0.8750 | 0.8449 |
| C44 | 0.9709 | 0.7750 | 0.9340 |
| C51 | 0.6121 | 0.5538 | 0.5645 |
| C52 | 0.6411 | 0.6554 | 0.3992 |
| C53 | 0.5839 | 0.5209 | 0.6227 |
| Evaluation Indicators | Evaluation Indicators | ||||
|---|---|---|---|---|---|
| C11 | 0.8402 | 0.0498 | C35 | 1.3243 | 0.0785 |
| C12 | 0.6686 | 0.0397 | C36 | 0.8448 | 0.0501 |
| C13 | 0.6666 | 0.0395 | C41 | 1.2951 | 0.0768 |
| C14 | 0.7340 | 0.0435 | C42 | 0.6796 | 0.0403 |
| C21 | 0.7453 | 0.0442 | C43 | 1.2499 | 0.0741 |
| C22 | 1.2320 | 0.0731 | C44 | 0.6662 | 0.0395 |
| C31 | 0.6853 | 0.0406 | C51 | 0.7662 | 0.0454 |
| C32 | 1.2692 | 0.0753 | C52 | 1.1607 | 0.0688 |
| C33 | 0.6674 | 0.0396 | C53 | 0.6995 | 0.0415 |
| C34 | 0.6653 | 0.0395 |
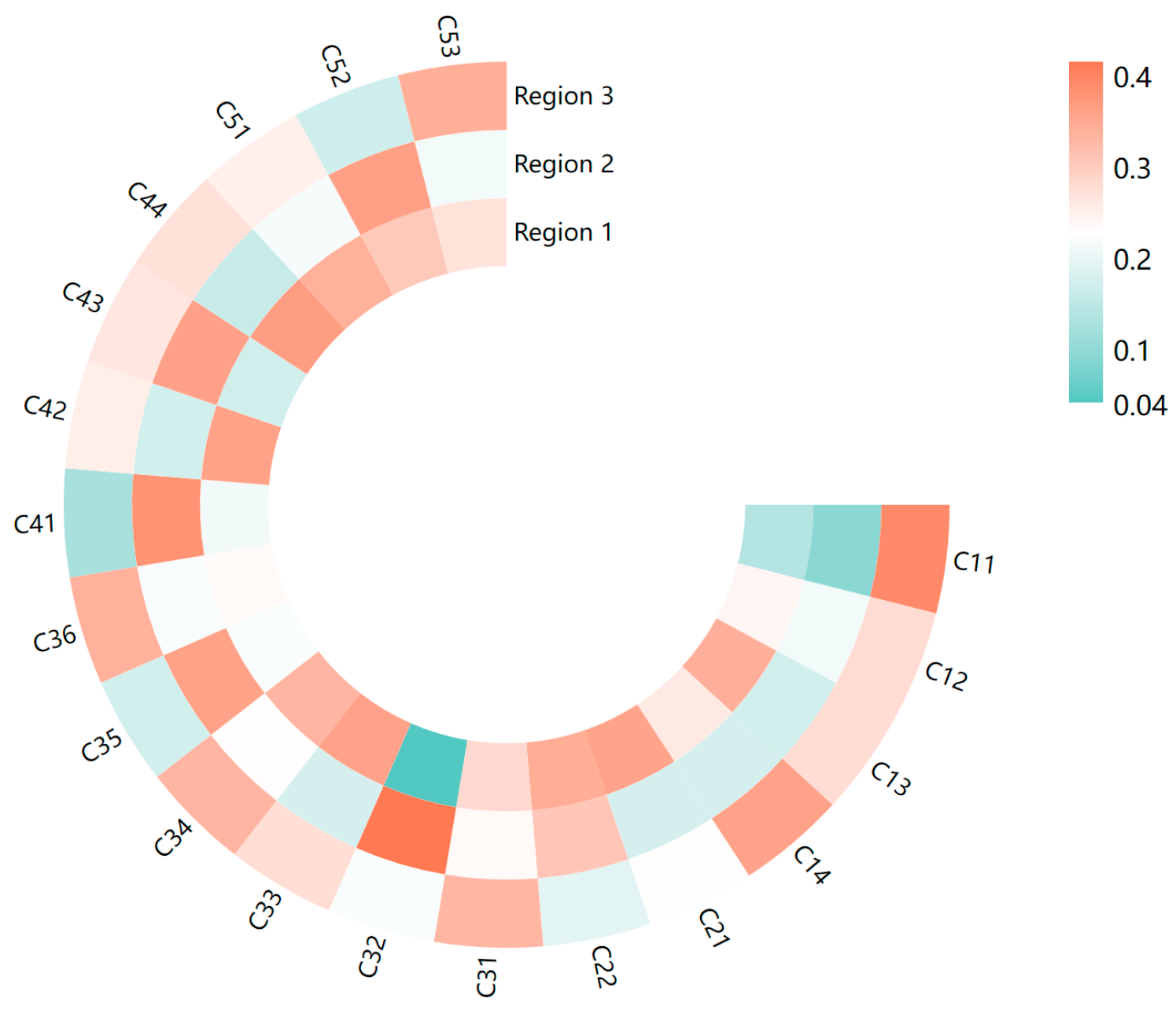
| First-Level Indicators | Combined Weights | Second-Level Indicators | Combined Weights |
|---|---|---|---|
| C1 | 0.1969 | C11 | 0.0601 |
| C12 | 0.0383 | ||
| C13 | 0.0476 | ||
| C14 | 0.0509 | ||
| C2 | 0.1210 | C21 | 0.0492 |
| C22 | 0.0718 | ||
| C3 | 0.2936 | C31 | 0.0388 |
| C32 | 0.0873 | ||
| C33 | 0.0364 | ||
| C34 | 0.0341 | ||
| C35 | 0.0548 | ||
| C36 | 0.0422 | ||
| C4 | 0.03065 | C41 | 0.0825 |
| C42 | 0.0672 | ||
| C43 | 0.0764 | ||
| C44 | 0.0804 | ||
| C5 | 0.07940 | C51 | 0.0315 |
| C52 | 0.0235 | ||
| C53 | 0.0244 |
| Sample | Positive Ideal Solution Distance | Negative Ideal Solution Distance | Comprehensive Prospect Value of ICPT-GRA | Ranking Results in ICPT-GRA |
|---|---|---|---|---|
| Region 1 | 0.6555 | 0.5990 | 1.7874 | 1 |
| Region 2 | 0.5998 | 0.6037 | 0.5395 | 3 |
| Region 3 | 0.6312 | 0.5659 | 1.6623 | 2 |
| Sample | Positive Ideal Solution Distance | Negative Ideal Solution Distance | Comprehensive Prospect Value of ICPT-TOPSIS | Ranking Results in ICPT-TOPSIS |
|---|---|---|---|---|
| Region 1 | 0.6138 | 0.6873 | 0.33364 | 2 |
| Region 2 | 0.46540 | 0.5548 | 0.1974 | 3 |
| Region 3 | 0.6973 | 0.4213 | 0.4064 | 1 |
| Sample | Comprehensive Prospect Value of GRA-TOPSIS Integrating CG and ICPT Method | Ranking Results in GRA-TOPSIS Integrating CG and ICPT Method |
|---|---|---|
| Region 1 | 0.9879 | 1 |
| Region 2 | 0.2983 | 3 |
| Region 3 | 0.9100 | 2 |
| Sequence | Risk Attitudes of Decision-Maker | Profit–Loss Attitude of Decision-Maker | ||||
|---|---|---|---|---|---|---|
| 1 | 0.4 | 0.4 | 1 | 2.25 | Radical | Loss-sensitive |
| 2 | 1 | 1 | 1 | 2.25 | Balanced | |
| 3 | 1.9 | 1.9 | 1 | 2.25 | Cautious | |
| 4 | 0.4 | 0.4 | 2.25 | 1 | Radical | Profit-sensitive |
| 5 | 1 | 1 | 2.25 | 1 | Balanced | |
| 6 | 1.9 | 1.9 | 2.25 | 1 | Cautious |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yan, C.; Wang, Z.; Wang, J. Adaptability Evaluation of Power Grid Planning Scheme for Novel Power System Considering Multiple Decision Psychology. Energies 2024, 17, 3672. https://doi.org/10.3390/en17153672
Wang Y, Yan C, Wang Z, Wang J. Adaptability Evaluation of Power Grid Planning Scheme for Novel Power System Considering Multiple Decision Psychology. Energies. 2024; 17(15):3672. https://doi.org/10.3390/en17153672
Chicago/Turabian StyleWang, Yuqing, Chaochen Yan, Zhaozhen Wang, and Jiaxing Wang. 2024. "Adaptability Evaluation of Power Grid Planning Scheme for Novel Power System Considering Multiple Decision Psychology" Energies 17, no. 15: 3672. https://doi.org/10.3390/en17153672
APA StyleWang, Y., Yan, C., Wang, Z., & Wang, J. (2024). Adaptability Evaluation of Power Grid Planning Scheme for Novel Power System Considering Multiple Decision Psychology. Energies, 17(15), 3672. https://doi.org/10.3390/en17153672





