Investigation on Cryogenic Cavitation Characteristics of an Inducer Considering Thermodynamic Effects
Abstract
1. Introduction
2. Research Objects and Numerical Calculation Methods
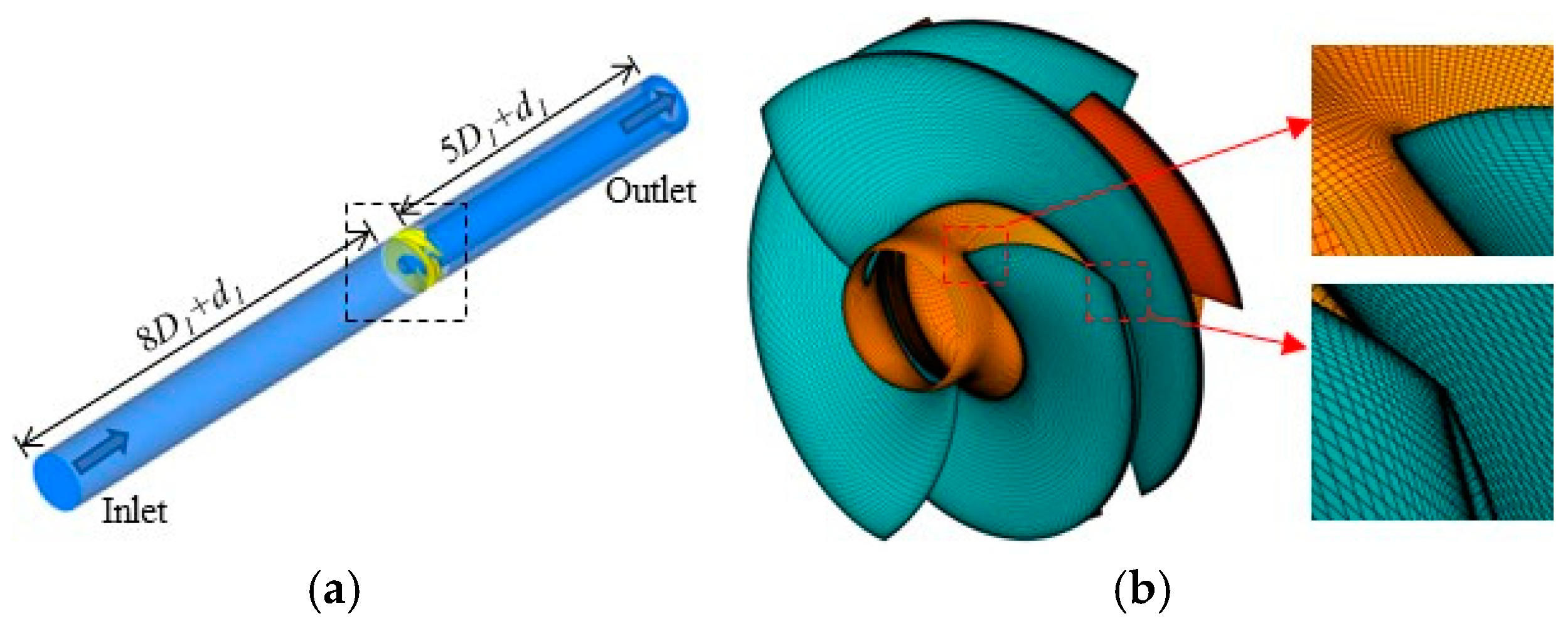
2.1. Research Objects
2.2. Governing Equations
2.3. The Cavitation Model
2.4. Turbulence Model
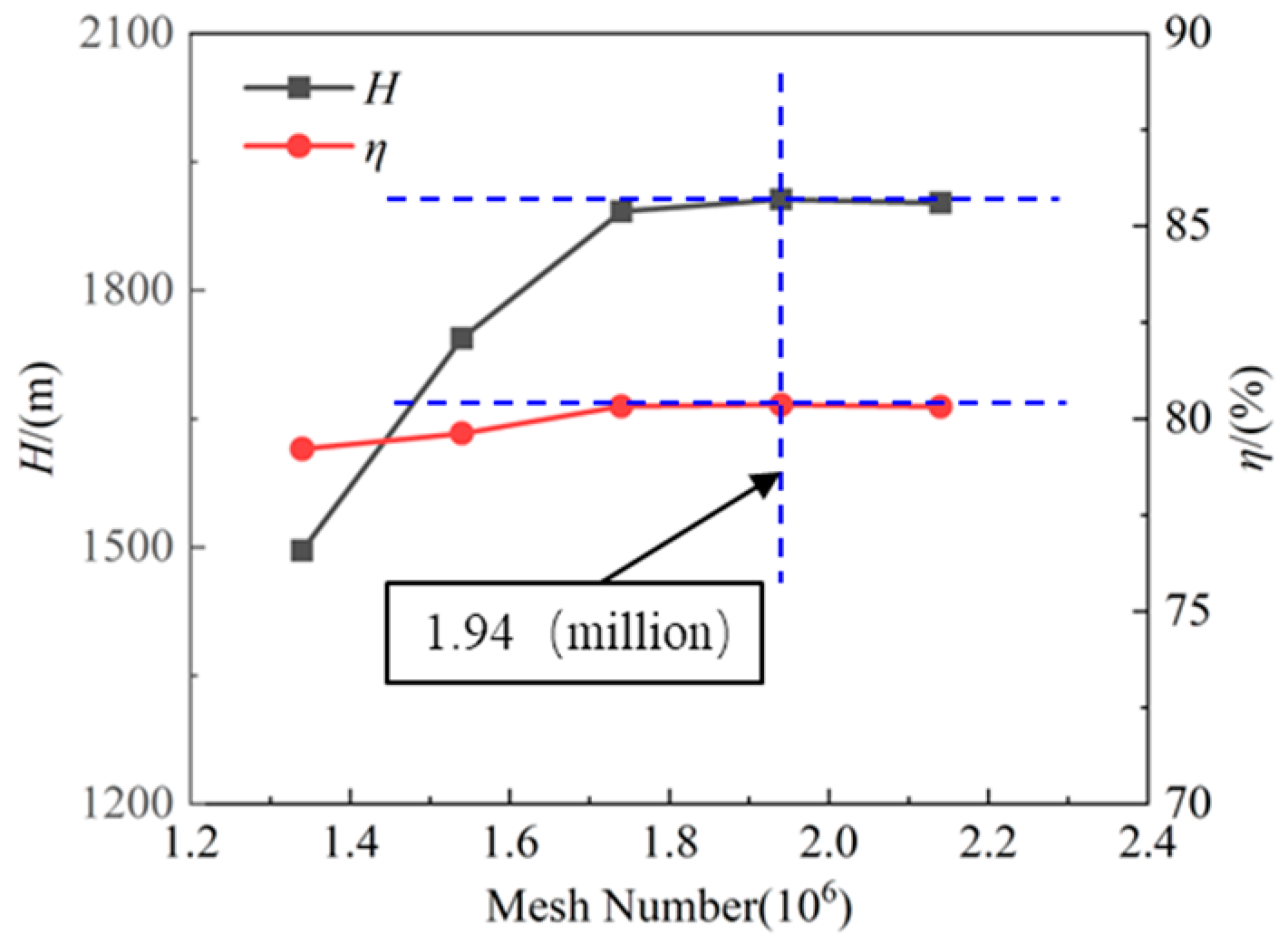
2.5. Computing Domain and Grid Independence Verification
2.6. Boundary Condition Settings
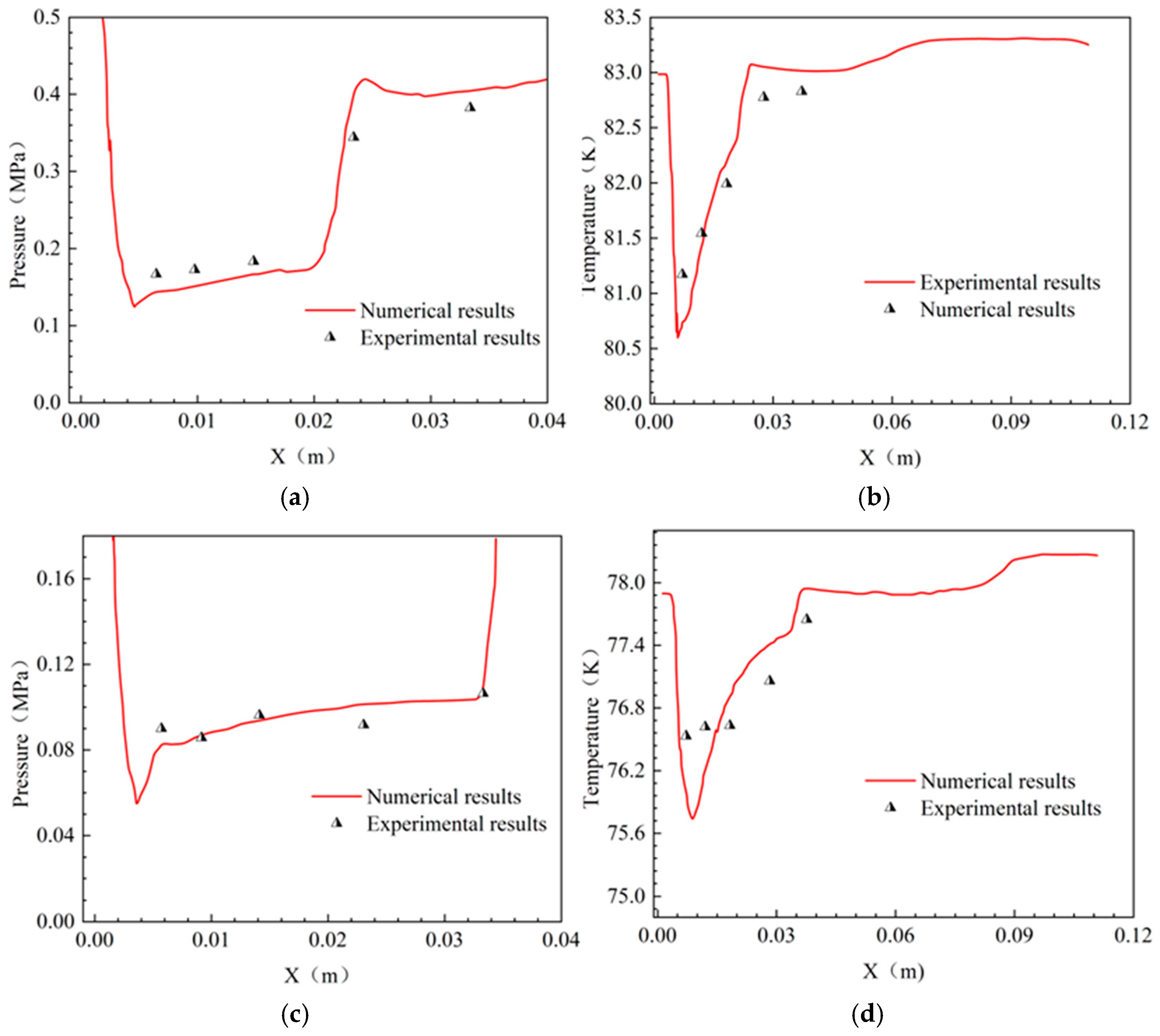
2.7. Cavitation Model Verification
3. Analysis of Calculation Results
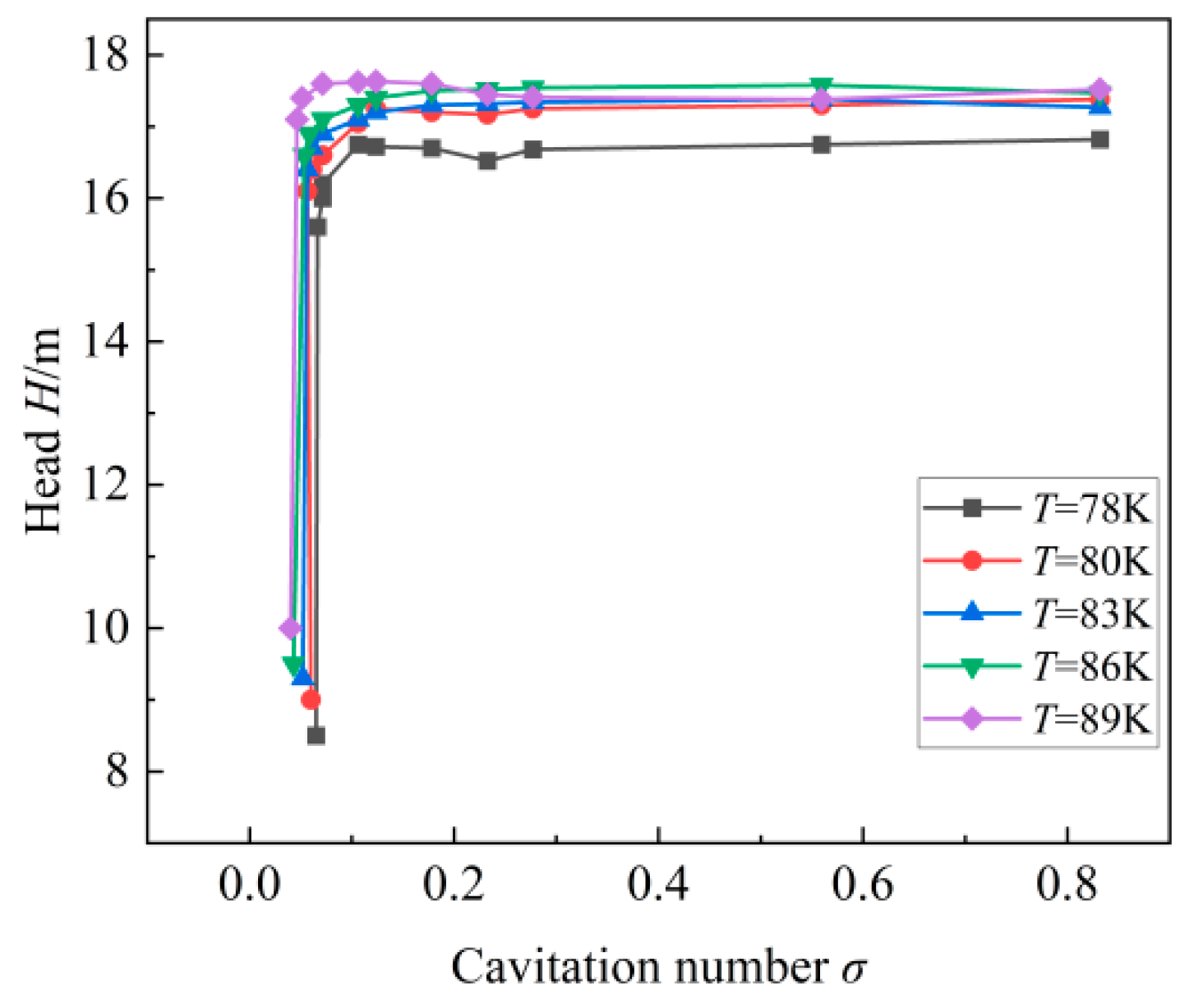
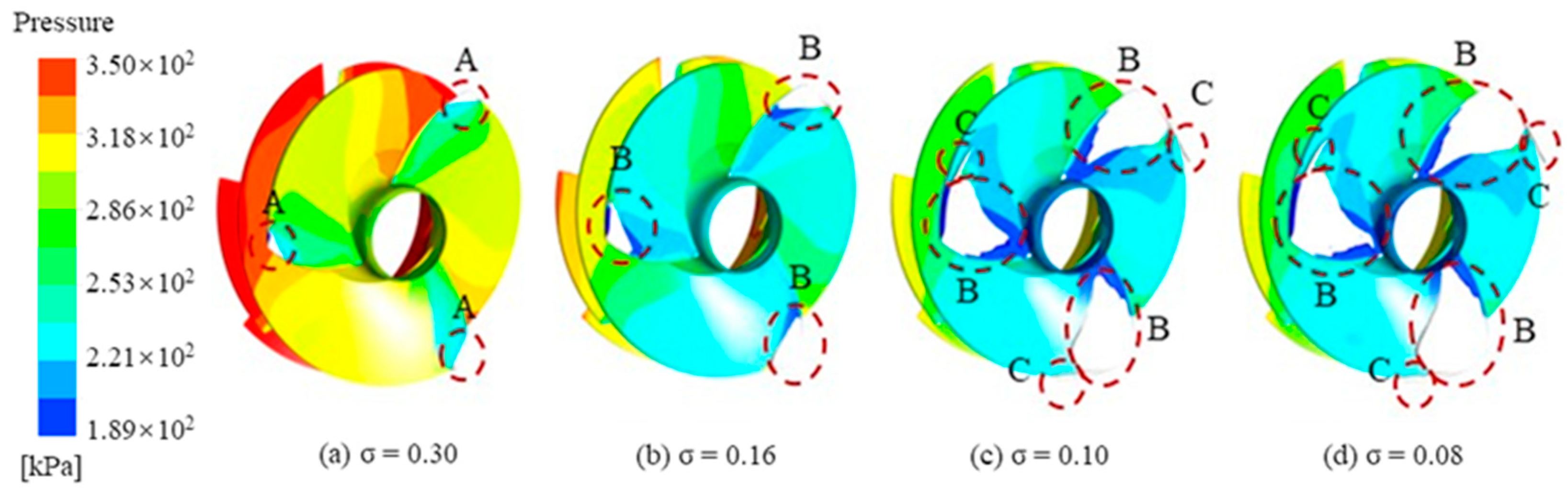
3.1. Study on Cavitation Performance of the Inducer at Different Temperature Conditions
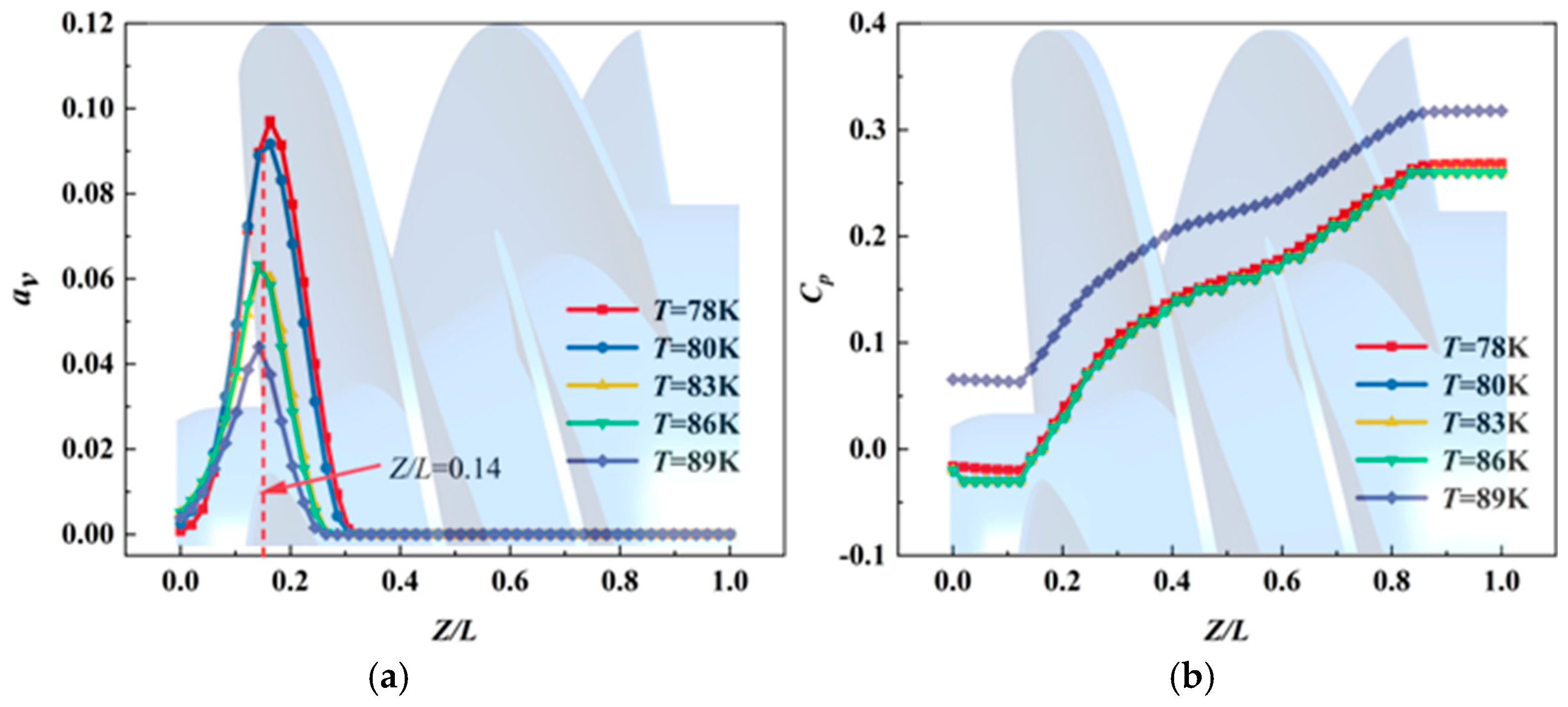
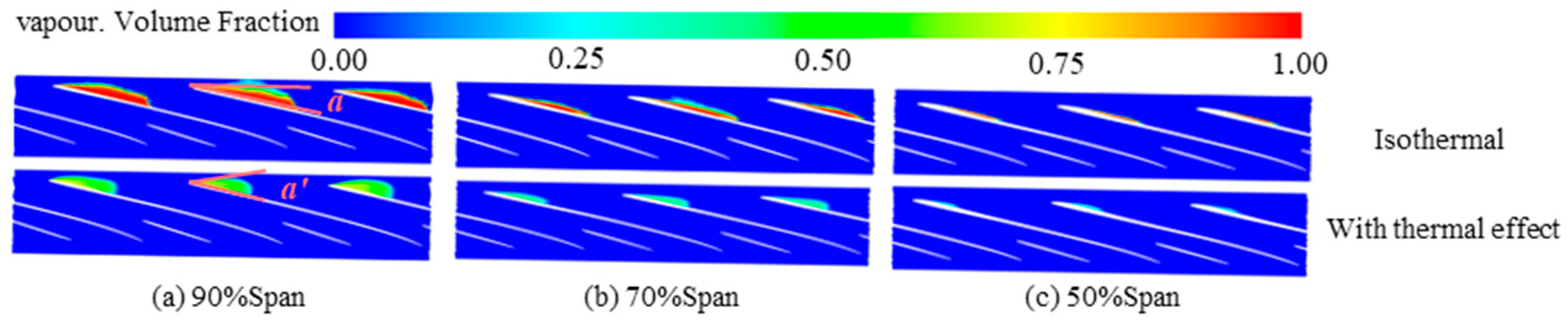
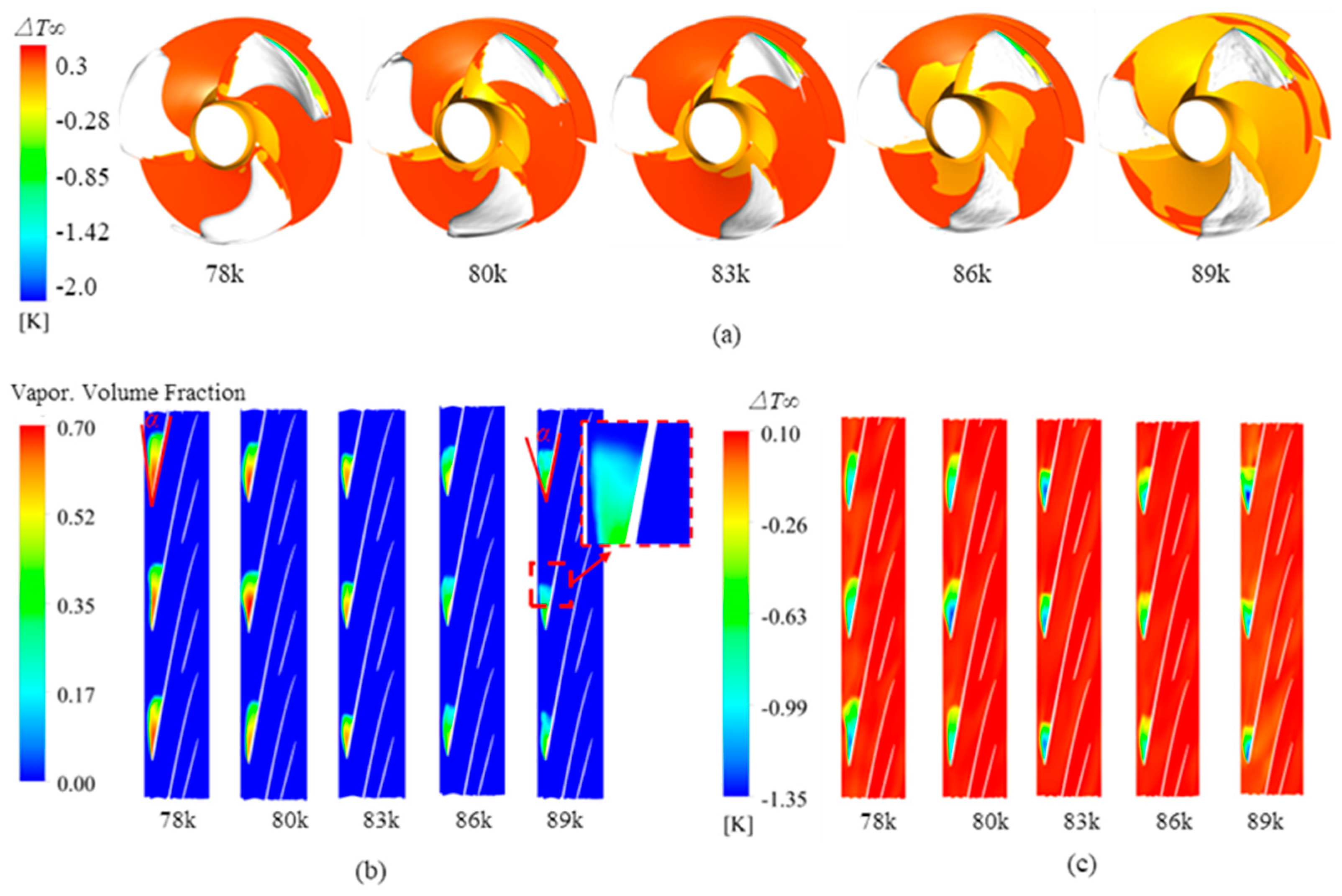
3.2. Cavitation Flow Characteristics in the Inducer at Different Temperature Conditions
4. Conclusions
- The spatio-temporal evolution of cryogenic cavitation in the inducer is clarified. Cavitation initially occurs at the outer edge of the long blade. Then, the cavities take on a triangular shape, and the cavitation area continues to grow, spreading along the direction of fluid flow. When cavitation reaches a certain level, the wake phenomenon is observed.
- Cavities production and collapse are accompanied by energy changes that affect the work capacity of the blades. The incipient cavitation is of a low intensity and area, with a small effect on the performance of the inducer. When the inlet of the inducer begins to show obvious flake cavitation, the pump performance is affected, but can still work normally. As the cavitation region expands further, the vortex cavitation become intense, causing the pump to fail to work properly.
- The relationship between thermodynamic effects and tip leakage vortex is revealed. The cavitation area of the inducer wheel is mainly composed of tip leakage vorticity, and the cavity completely covers the leakage vorticity of the inducer wheel. As the temperature decreases, the area of the leakage vorticity gradually increases. The leakage vorticity is more serious at 78.00 K and 80.00 K, which causes the attached vorticity that falls off from the tip leakage vorticity and moves towards the wheel hub.
- Thermodynamic effects have less influence on the position at which cryogenic cavitation occurs in the inducer, but there is a significant inhibition of cavitation. Temperature has little influence on the position of cavitation under different temperature conditions. The increase in temperature enhances the thermodynamic effects, the boundaries of the cavities become more ambiguous and the tiny bubble groups at the vapor–liquid interface are more easily diffused, thus effectively suppressing cavitation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, G.; Zuo, Z.; Sun, Y.; Liu, D.; Tsujimoto, Y.; Liu, S. Experimental evidence of cavitation influences on the positive slope on the pump performance curve of a low specific speed model pump-turbine. Renew. Energy 2017, 113, 1539–1550. [Google Scholar] [CrossRef]
- Zhang, M.; Huang, B.; Wu, Q.; Zhang, M.; Wang, G. The interaction between the transient cavitating flow and hydrodynamic performance around a pitching hydrofoil. Renew. Energy 2020, 161, 1276–1291. [Google Scholar] [CrossRef]
- Zhu, D.; Xiao, R.; Liu, W. Influence of leading-edge cavitation on impeller blade axial force in the pump mode of reversible pump-turbine. Renew. Energy 2021, 163, 939–949. [Google Scholar] [CrossRef]
- Cheng, X.; Li, Y.; Zhang, S. Effect of inlet sweepback angle on the cavitation performance of an inducer. Eng. Appl. Comp. Fluid 2019, 13, 713–723. [Google Scholar] [CrossRef]
- Morii, T.; Tanaka, Y.; Watanabe, S.; Ohashi, S.; Matsunaga, Y. Suction performance and cavitation instabilities of turbopumps with three different inducer designs. Int. J. Fluid Mach. Syst. 2019, 12, 128–135. [Google Scholar] [CrossRef]
- Kim, J.; Song, S.J. Visualization of rotating cavitation oscillation mechanism in a turbopump inducer. J. Fluid Eng.-Trans. ASME 2019, 141, 091103. [Google Scholar] [CrossRef]
- Zhai, L.; Li, Y.; Cui, B.; Guo, J.; Li, X.; Zhu, Z. Studies of cavitation characteristics of inducers with different blade numbers. AIP Adv. 2021, 11, 085216. [Google Scholar] [CrossRef]
- Karakas, E.S.; Watanabe, H.; Aureli, M.; Evrensel, C.A. Cavitation performance of constant and variable pitch helical inducers for centrifugal pumps: Effect of inducer tip clearance. J. Fluids Eng. 2020, 142, 021101. [Google Scholar] [CrossRef]
- Hashimoto, T.; Yoshida, M.; Watanabe, M.; Kamijo, K.; Tsujimoto, Y. Experimental study on rotating cavitation of rocket propellant pump inducers. J. Propul. Power 1997, 13, 488–494. [Google Scholar] [CrossRef]
- Franc, J.-P.; Rebattet, C.; Coulon, A. An experimental investigation of thermal effects in a cavitating inducer. J. Fluid Eng.-Trans. ASME 2004, 126, 716–723. [Google Scholar] [CrossRef]
- Kim, D.-J.; Sung, H.J.; Choi, C.-H.; Kim, J.-S. Cavitation instabilities of an inducer in a cryogenic pump. Acta Astronaut. 2017, 132, 19–24. [Google Scholar] [CrossRef]
- Ito, Y.; Tsunoda, A.; Kurishita, Y.; Kitano, S.; Nagasaki, T. Experimental visualization of cryogenic backflow vortex cavitation with thermodynamic effects. J. Propul. Power 2016, 32, 71–82. [Google Scholar] [CrossRef]
- Ito, Y. The world’s first test facility that enables the experimental visualization of cavitation on a rotating inducer in both cryogenic and ordinary fluids. J. Fluid Eng.-Trans. ASME 2021, 143, 121105. [Google Scholar] [CrossRef]
- Kikuta, K.; Yoshida, Y.; Watanabe, M.; Hashimoto, T.; Nagaura, K.; Ohira, K. Thermodynamic effect on cavitation performances and cavitation instabilities in an inducer. J. Fluid Eng.-Trans. ASME 2008, 130, 111302. [Google Scholar] [CrossRef]
- Yoshida, Y.; Nanri, H.; Kikuta, K.; Kazami, Y.; Iga, Y.; Ikohagi, T. Thermodynamic effect on subsynchronous rotating cavitation and surge mode oscillation in a space inducer. J. Fluid Eng.-Trans. ASME 2011, 133, 061301. [Google Scholar] [CrossRef]
- Fan, Y.; Chen, T.; Liang, W.; Wang, G.; Huang, B. Numerical and theoretical investigations of the cavitation performance and instability for the cryogenic inducer. Renew. Energy 2022, 184, 291–305. [Google Scholar] [CrossRef]
- Ehrlich, D.A.; Murdock, J.W. A dimensionless scaling parameter for thermal effects on cavitation in turbopump inducers. J. Fluid Eng.-Trans. ASME 2015, 137, 041103-1–041103-8. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, S.; Li, X.; Li, Y.; Li, L. Investigation on leakage vortex cavitation and corresponding entropy characteristics in a liquid nitrogen inducer. Cryogenics 2023, 129, 103606. [Google Scholar] [CrossRef]
- Xiang, L.; Tan, Y.; Chen, H.; Xu, K. Numerical simulation of cryogenic cavitating flow in LRE oxygen turbopump inducer. Cryogenics 2021, 126, 103540. [Google Scholar] [CrossRef]
- Alavi, A.; Roohi, E. Large eddy simulations of cavitation around a pitching–plunging hydrofoil. Phys. Fluids 2023, 35, 125102. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Roohi, E. On the effects of hybrid surface wettability on the structure of cavitating flow using implicit large eddy simulation. J. Taiwan Inst. Chem. Eng. 2023, 104828, 148. [Google Scholar] [CrossRef]
- Ji, B.; Luo, X.W.; Arndt, R.E.A.; Peng, X.; Wu, Y. Large eddy simulation and theoretical investigations of the transient cavitating vortical flow structure around a NACA66 hydrofoil. Int. J. Multiphas. Flow 2015, 68, 121–134. [Google Scholar] [CrossRef]
- Li, X.; Li, B.; Yu, B.; Ren, Y.; Chen, B. Calculation of cavitation evolution and associated turbulent kinetic energy transport around a NACA66 hydrofoil. J. Mech. Sci. Technol. 2019, 33, 1231–1241. [Google Scholar] [CrossRef]
- Shen, T.; Li, X.; Li, L.; Wang, Z.; Liu, Y. Evaluation of vorticity forces in thermos-sensitive cavitating flow considering the local compressibility. Int. Commun. Heat Mass Transf. 2021, 120, 105008. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Hu, B.; Liu, Y.; Zhu, Z. Numerical investigation of attached cavitating flow in thermo-sensitive fluid with special emphasis on thermal effect and shedding dynamics. Int. J. Hydrogen Energy 2018, 11, 224. [Google Scholar] [CrossRef]
- Li, X.; Shen, T.; Li, P.; Guo, X.; Zhu, Z. Extended compressible thermal cavitation model for the numerical simulation of cryogenic cavitating flow. Int. J. Hydrogen Energy 2020, 45, 10104–10118. [Google Scholar] [CrossRef]
- Zhang, S.F.; Li, X.J.; Zhu, Z.C. Numerical simulation of cryogenic cavitating flow by an extended transport-based cavitation model with thermal effects. Cryogenics 2018, 92, 30352. [Google Scholar] [CrossRef]
- Hord, J. Cavitation in Liquid Cryogens. 2: Hydrofoil; NASA: Washington, DC, USA, 1973.
- Utturkar, Y.; Wu, J.; Wang, G.; Shyy, W. Recent progress in modeling of cryogenic cavitation for liquid rocket propulsion. Prog. Aerosp. Sci. 2005, 41, 558–608. [Google Scholar] [CrossRef]




| Parameters | Values |
|---|---|
| Imported hub diameter dh1 | 54 mm |
| Imported hub diameter dh2 | 129.3 mm |
| Inducer diameter D1 | 192.5 mm |
| Blade inlet angle βb1 | Long blade: 10.1° Short blade: 23.1° |
| Blade outlet angle βb2 | Long blade: 23.1° Short blade: 22.4° |
| Wrap angle φ | 217.8° |
| Tip clearance d1 | 1.1 mm |
| Number of blades z | Long blade: 3 Short blade: 3 |
| Operating Conditions | T = 78 K | T = 80 K | T = 83 K | T = 86 K | T = 89 K |
|---|---|---|---|---|---|
| Density (kg/m3) | 803.1482 | 793.9471 | 779.7973 | 765.2261 | 750.1647 |
| Dynamic Viscosity (10−5 Pa·s) | 15.6643 | 14.5110 | 13.0074 | 11.7246 | 10.6178 |
| Saturation Pressure (kPa) | 109.2552 | 136.8718 | 187.79884 | 251.7359 | 330.5505 |
| Latent Heat of Vaporization (kJ/kg) | 198.3391 | 195.6756 | 191.4698 | 186.9806 | 182.1696 |
| Specific Heat Capacity at Constant Pressure (kJ·kg−1·K−1) | 2.0447 | 2.0555 | 2.0751 | 2.0993 | 2.1292 |
| Thermal Conductivity (W·m−1·K−1) | 0.1435 | 0.1395 | 0.1336 | 0.1277 | 0.1218 |
| Operating Conditions | Inlet Temperature T∞ (K) | Inlet Velocity V∞ (m/s) | Cavitation Number σ | Gasification Latent Heat L (J/kg) |
|---|---|---|---|---|
| A | 83.06 | 23.9 | 1.7 | 1.91 × 105 |
| B | 77.9 | 23.9 | 1.7 | 1.98 × 105 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Yang, M.; Li, F.; Zhu, Z.; Cui, B. Investigation on Cryogenic Cavitation Characteristics of an Inducer Considering Thermodynamic Effects. Energies 2024, 17, 3627. https://doi.org/10.3390/en17153627
Guo X, Yang M, Li F, Zhu Z, Cui B. Investigation on Cryogenic Cavitation Characteristics of an Inducer Considering Thermodynamic Effects. Energies. 2024; 17(15):3627. https://doi.org/10.3390/en17153627
Chicago/Turabian StyleGuo, Xiaomei, Mingyu Yang, Fengqin Li, Zuchao Zhu, and Baoling Cui. 2024. "Investigation on Cryogenic Cavitation Characteristics of an Inducer Considering Thermodynamic Effects" Energies 17, no. 15: 3627. https://doi.org/10.3390/en17153627
APA StyleGuo, X., Yang, M., Li, F., Zhu, Z., & Cui, B. (2024). Investigation on Cryogenic Cavitation Characteristics of an Inducer Considering Thermodynamic Effects. Energies, 17(15), 3627. https://doi.org/10.3390/en17153627






