Equilibrium Interaction Strategies for Integrated Energy System Incorporating Demand-Side Management Based on Stackelberg Game Approach
Abstract
1. Introduction
2. Materials and Methods
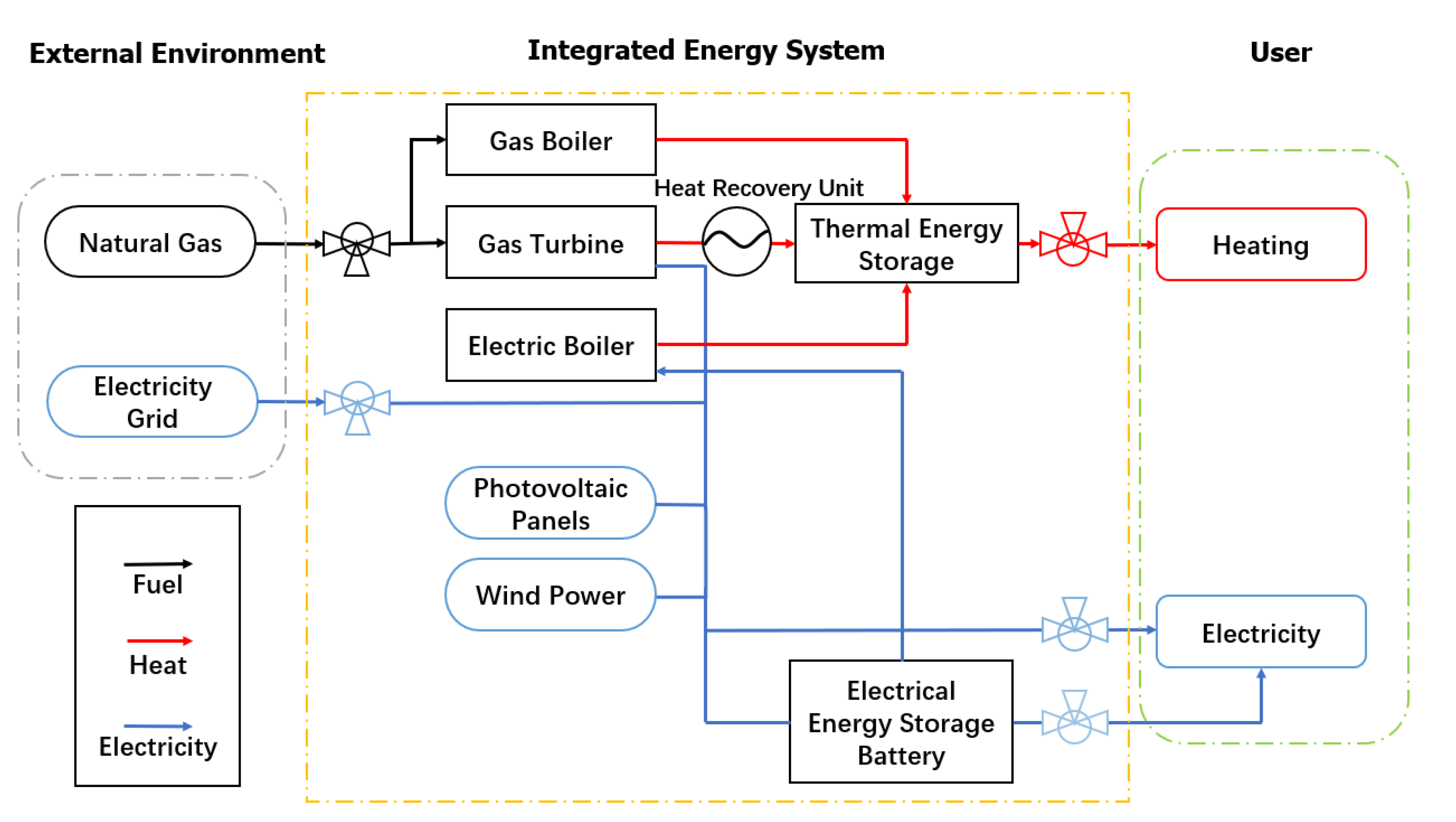
2.1. Modeling of the IES
2.1.1. Objective Function of the IES
2.1.2. Constraints of the IES
2.2. Modeling of Users
2.2.1. Objective Function of Demand-Side Users
2.2.2. Constraints of Demand-Side Users
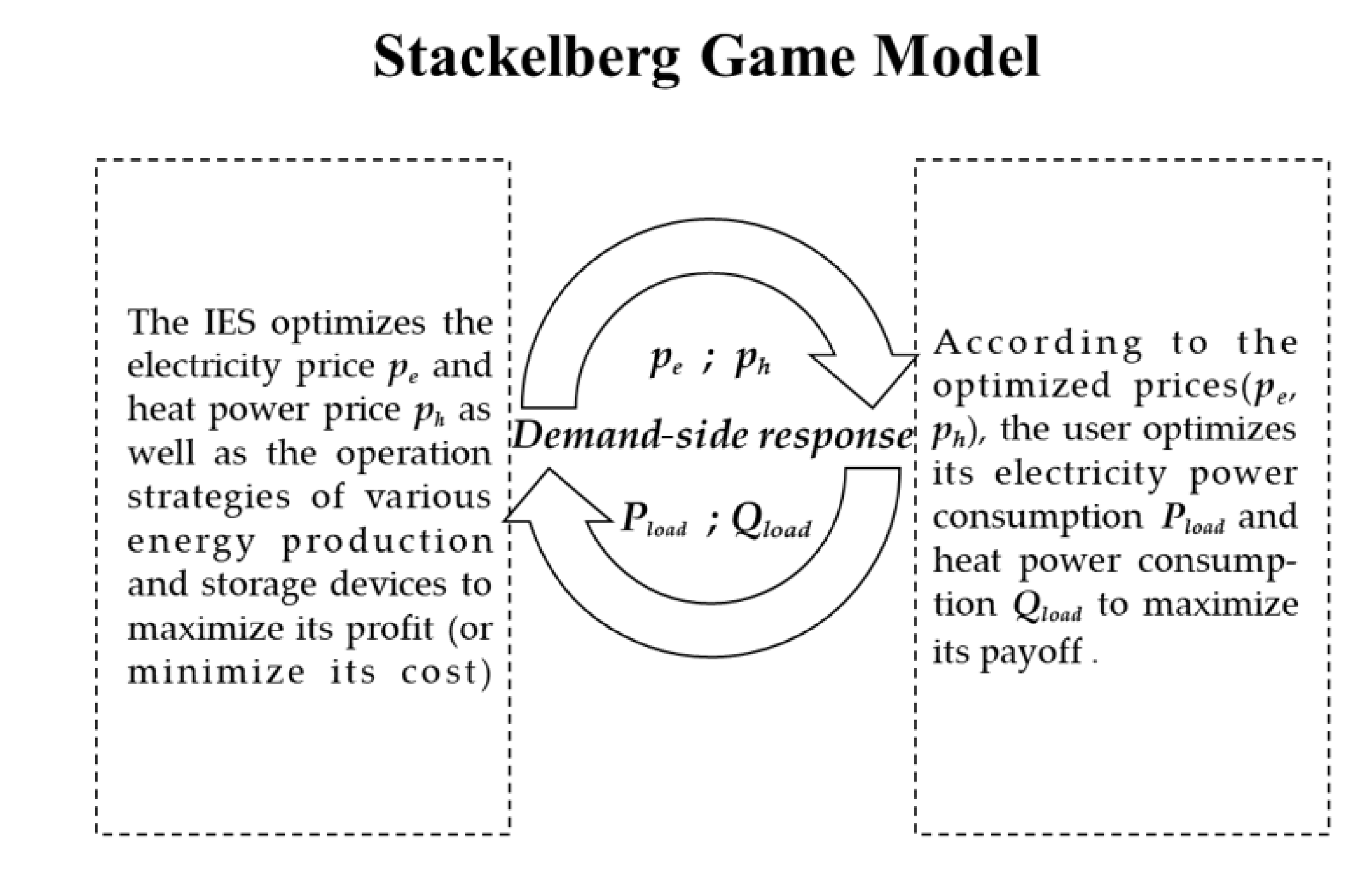
3. Game Theory Analysis for IES–Demand-Side User Interaction
3.1. Establishment of IES–Demand-Side User Interaction Using Stackelberg Game
3.2. Equilibrium Analysis
3.3. Solving the Stackelberg Game by Branch-and-Bound Method
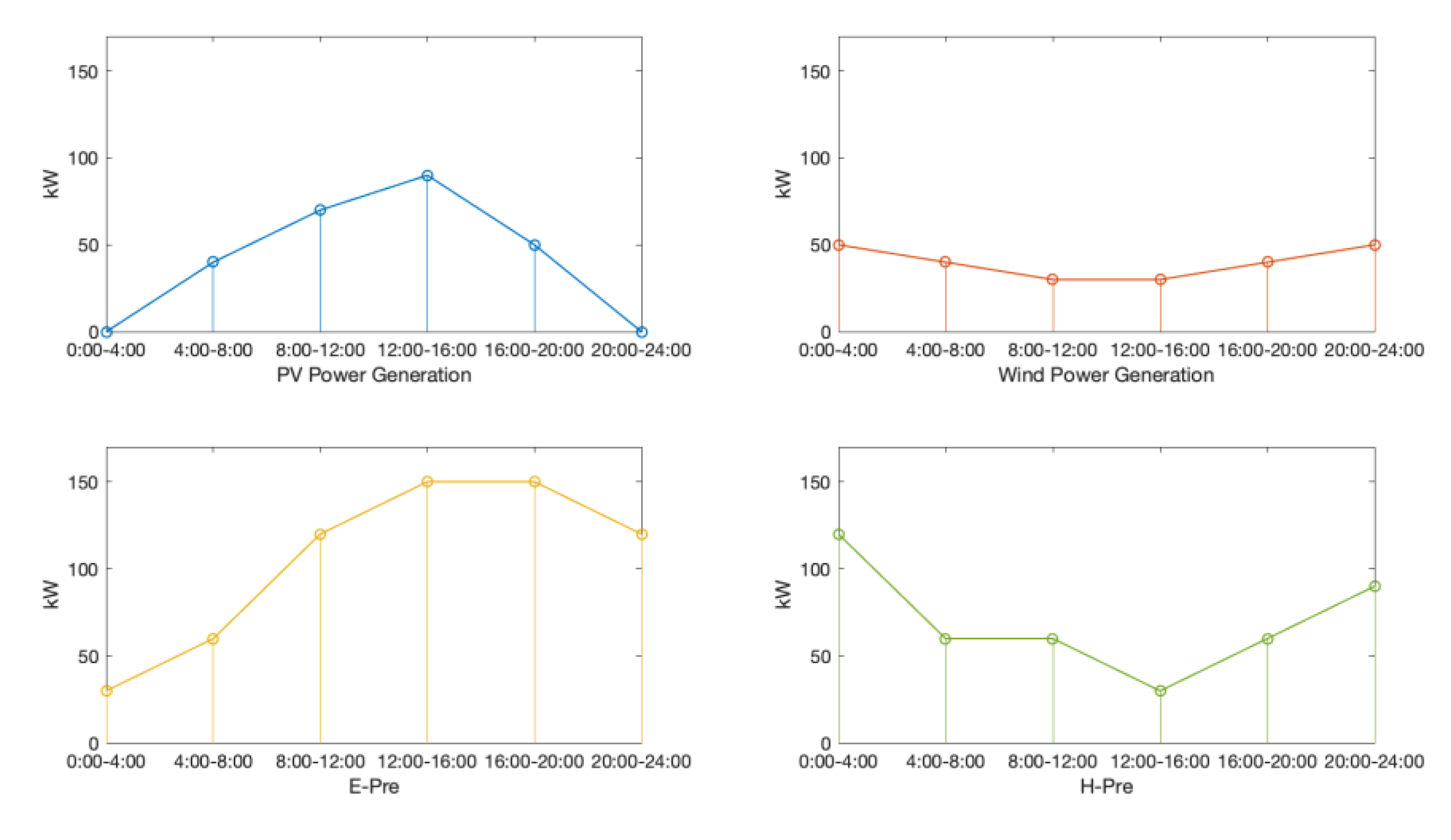
4. Initialization of Parameters
5. Simulation Results
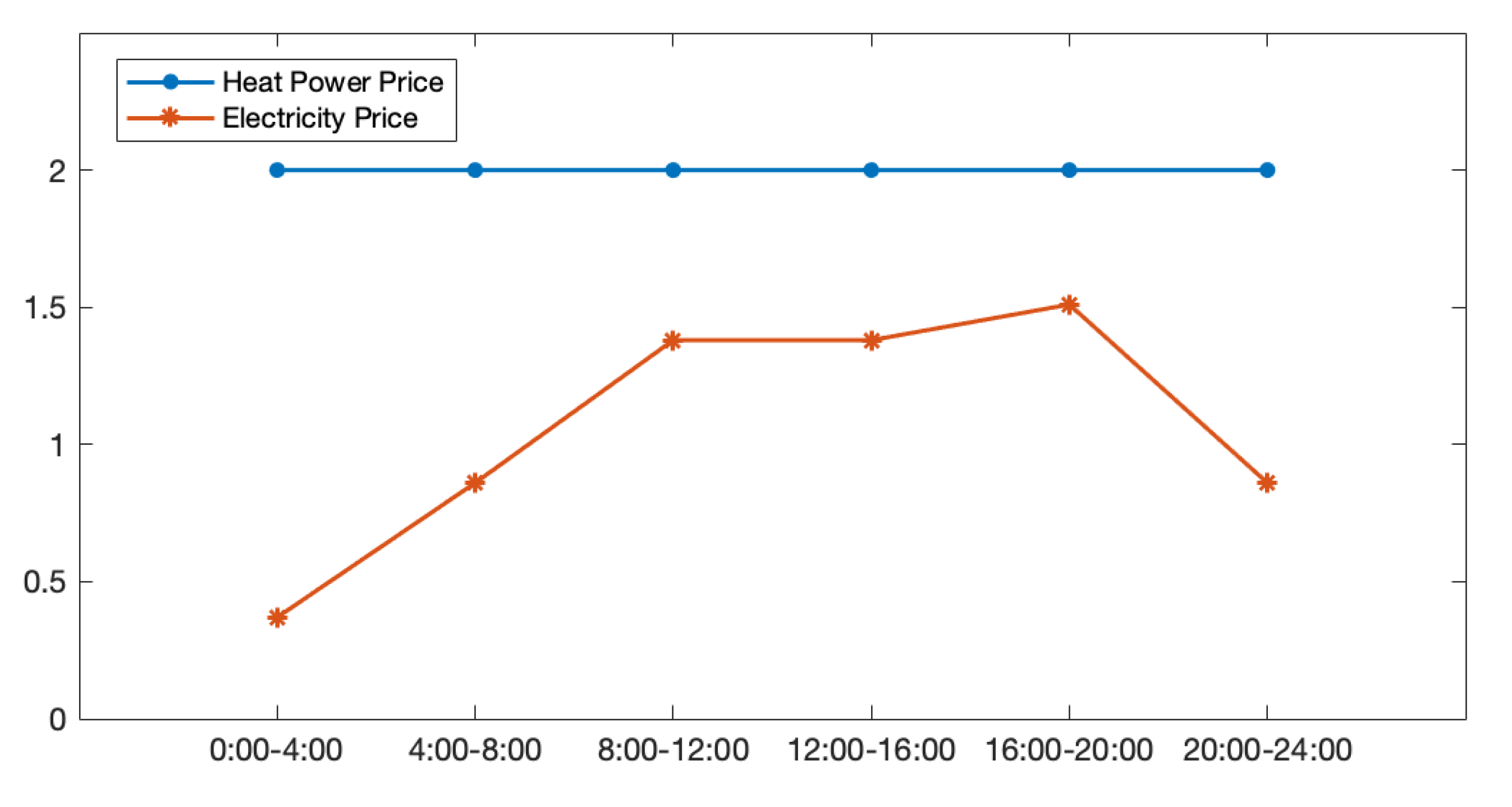
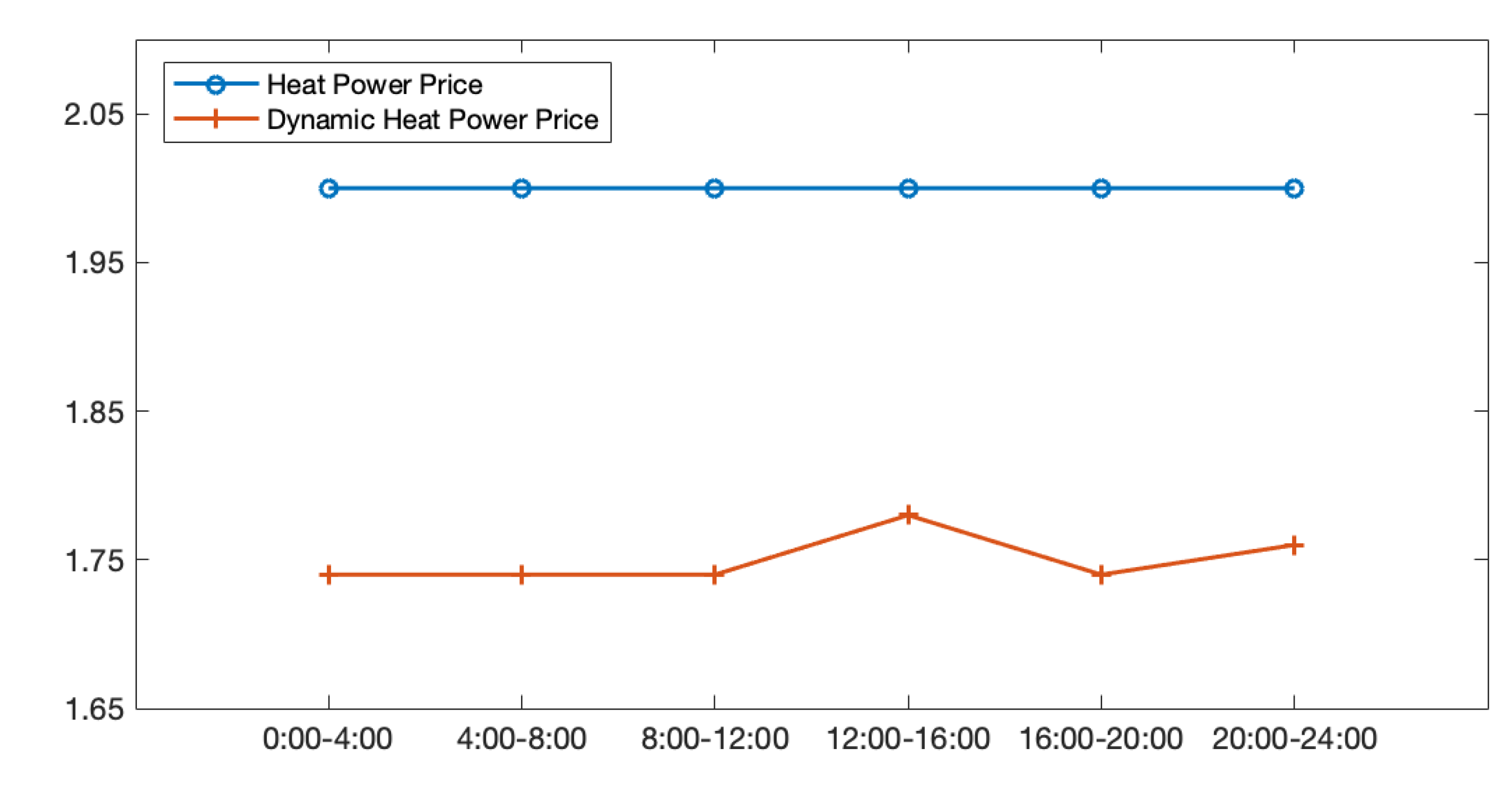
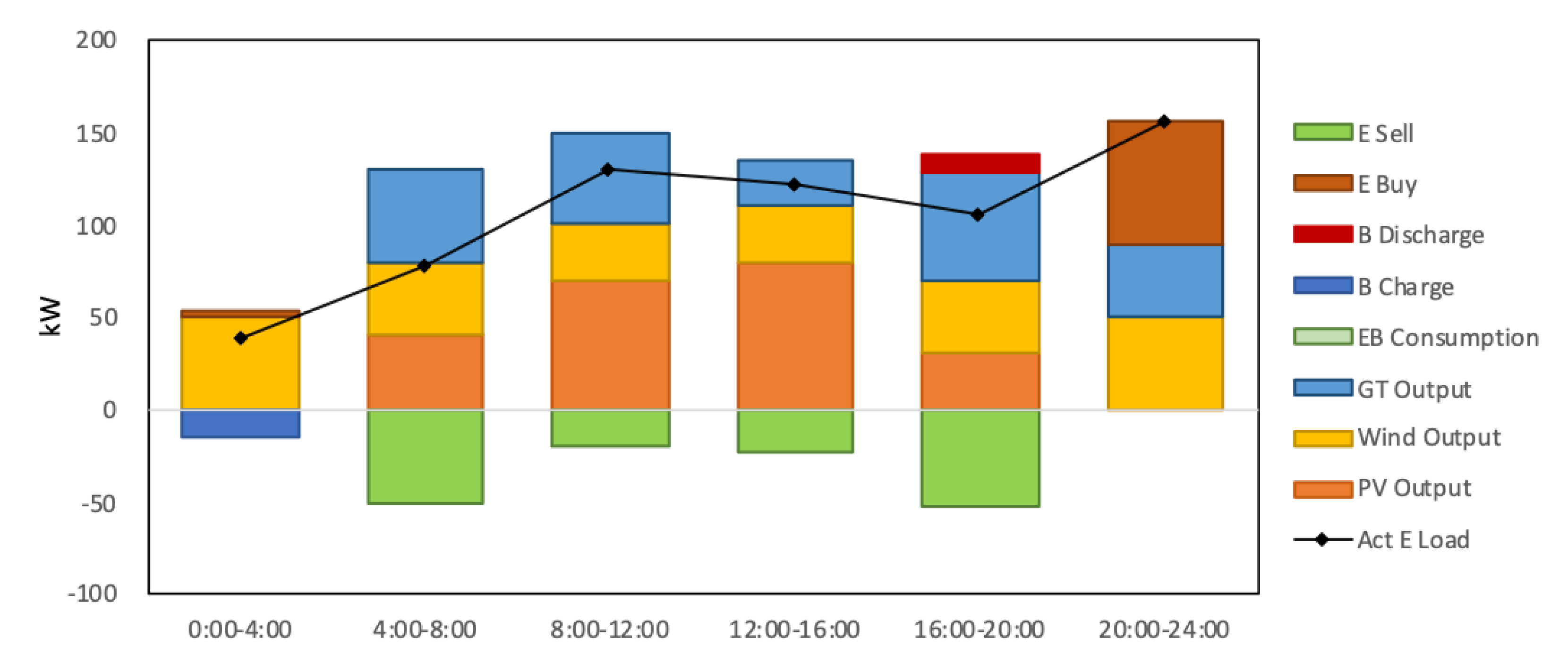
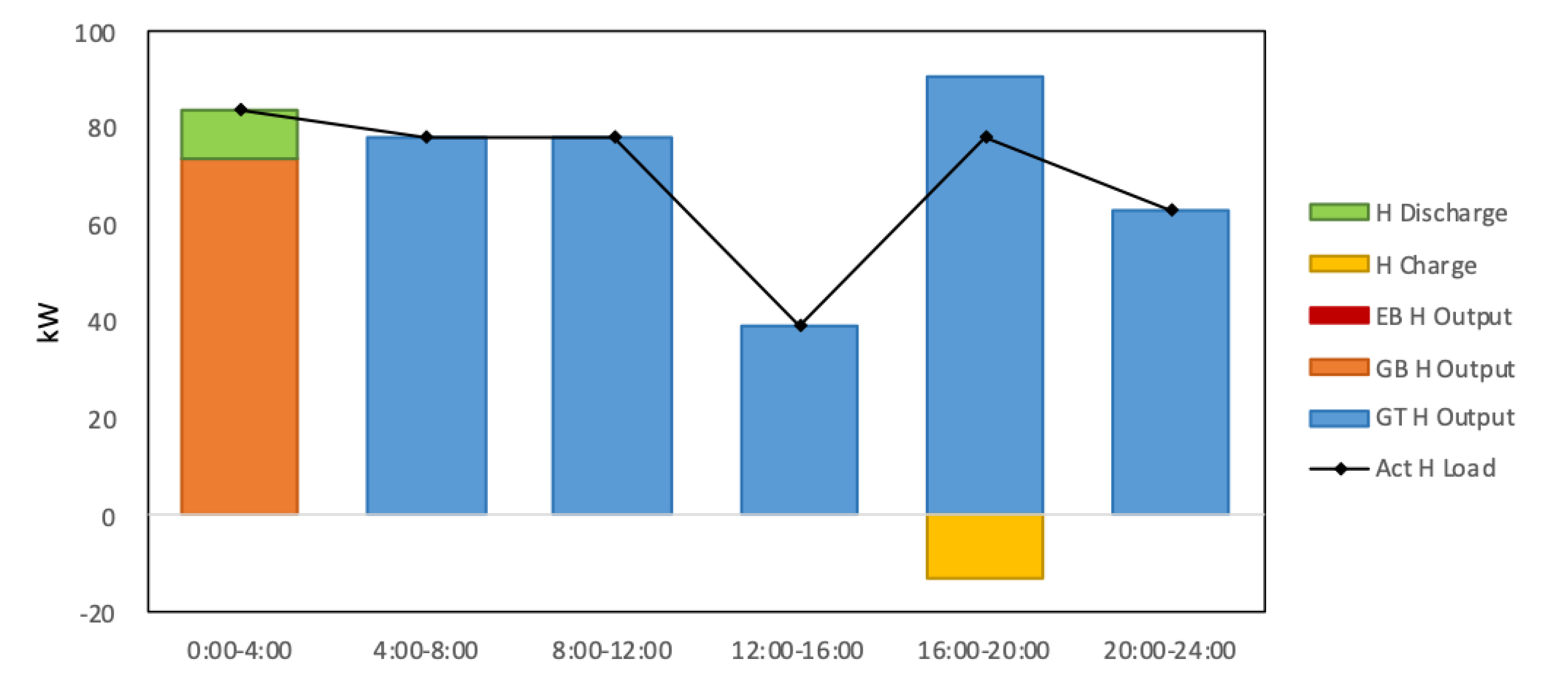
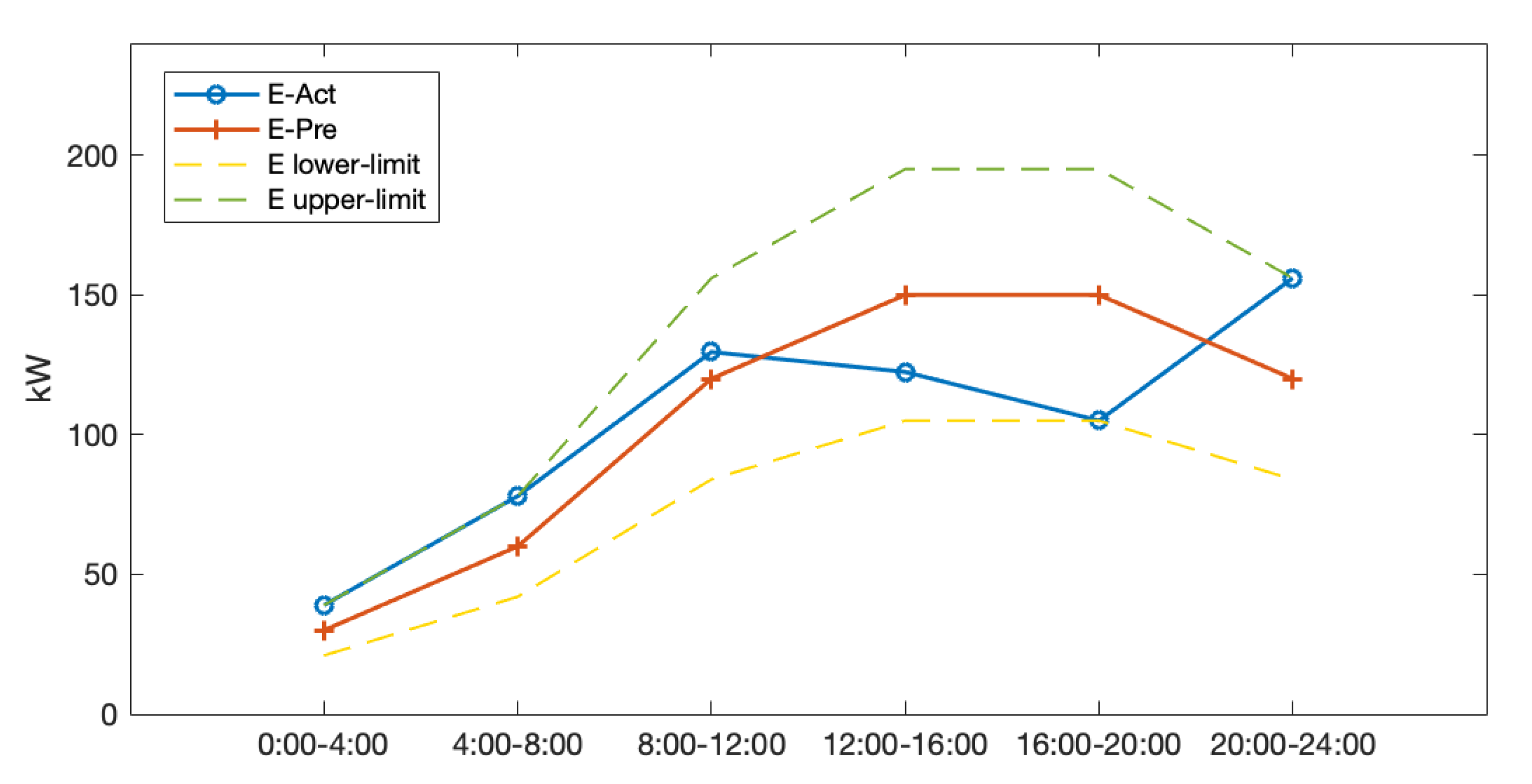
5.1. IES Service Provider Strategy Optimization Results
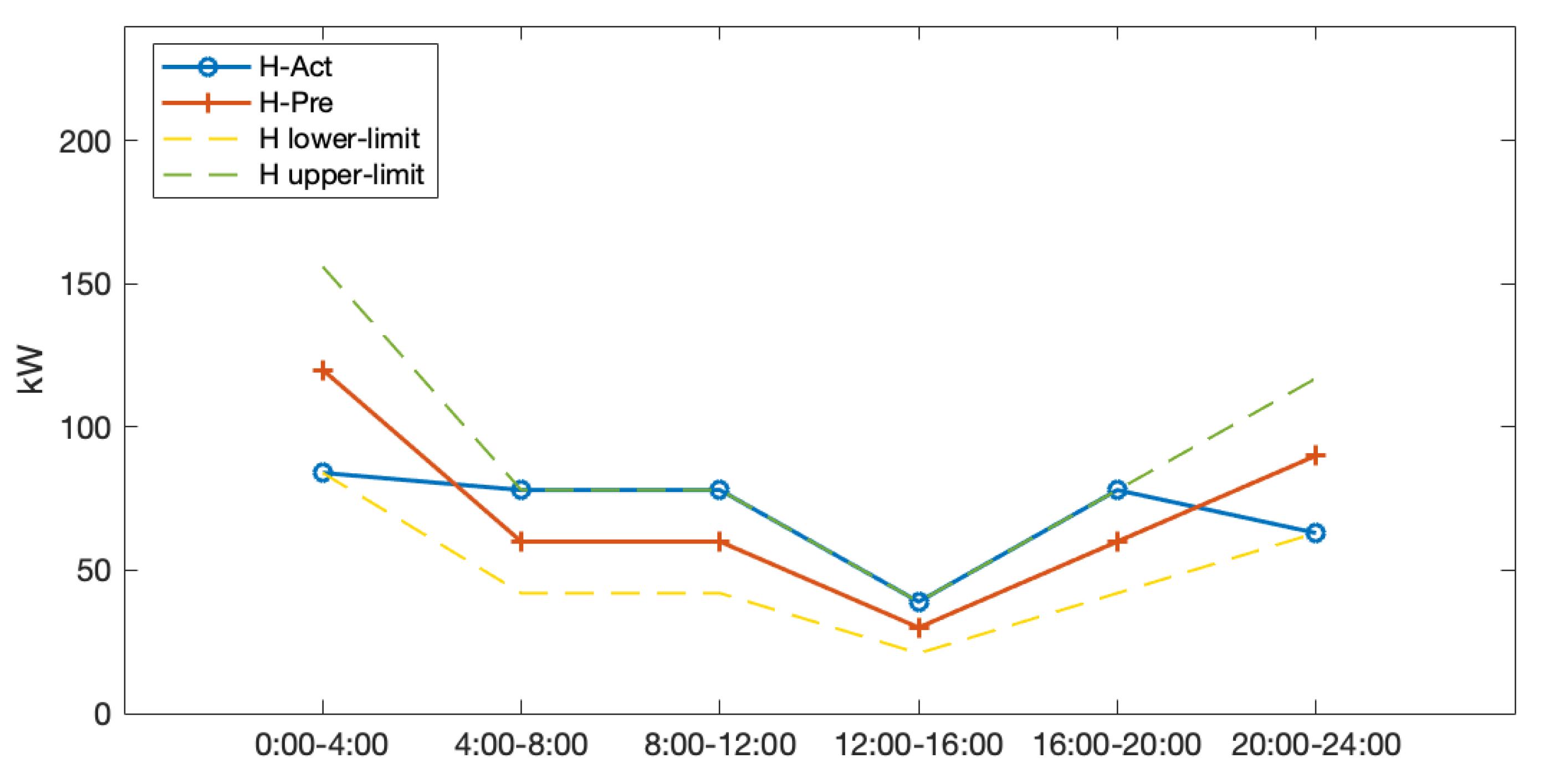
5.2. User-Side Policy Optimization Results
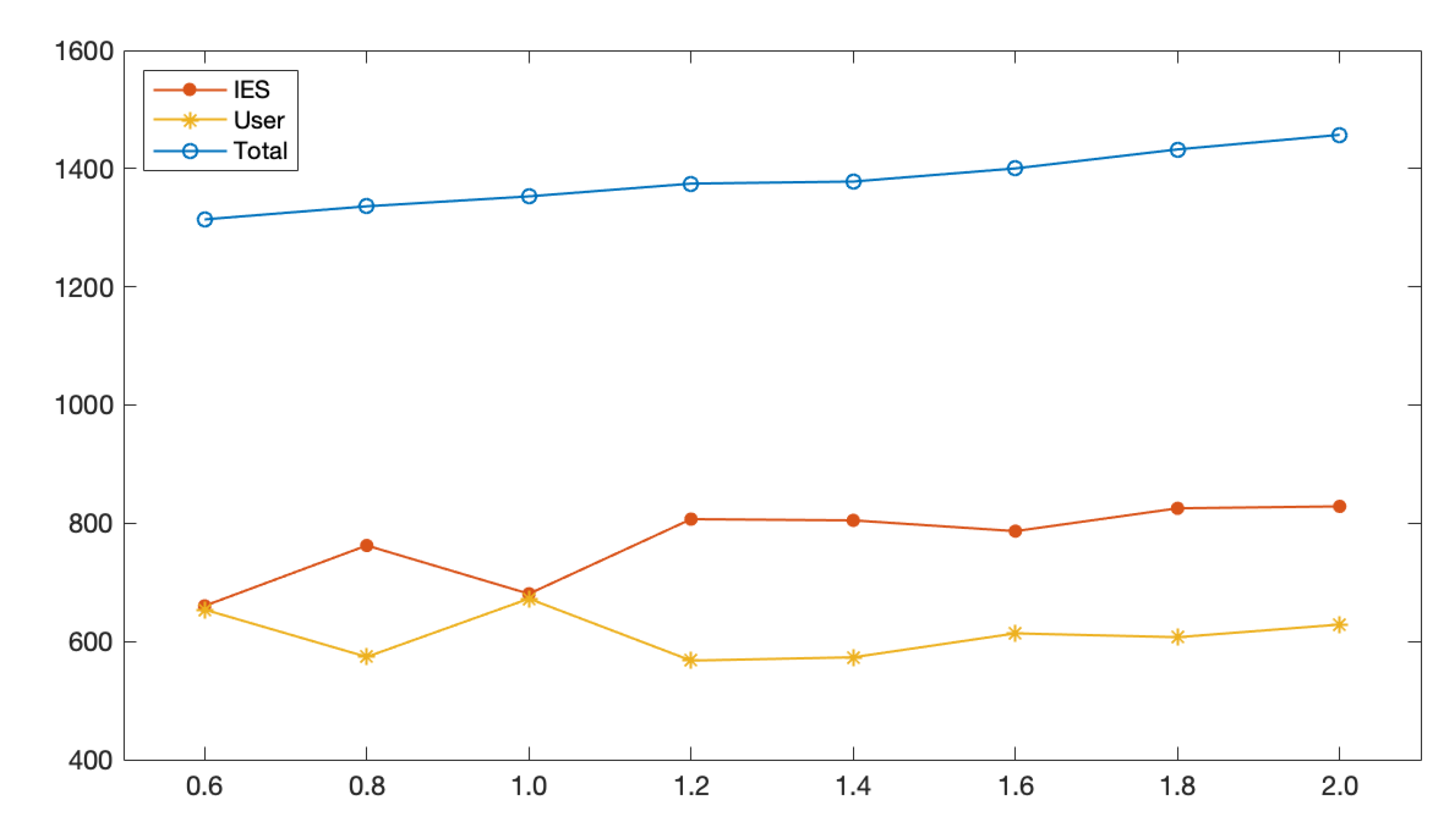
5.3. Sensitivity Analysis of Key Parameters
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Glossary
| Abbreviation | |
| IES | Integrated energy system |
| DSM | Demand-side management |
| TOU | Time of use |
| SDG | Sustainable Development Goals |
| CCHP | Combined cooling heating and power |
| P2G | Power to gas |
| PV | Photovoltaic |
| GT/GB | Gas turbine/gas boiler |
| EB | Electricity boiler |
| Indices and sets | |
| Set of indices of scheduling periods | |
| Input parameters | |
| Revenue from electricity and heat selling | |
| Production cost of electricity and heat | |
| Electricity and heat demand fluctuation cost | |
| Utility function for integrated energy system service providers | |
| Time-of-use electricity price of electricity/heat sold to users at time t | |
| Actual electricity/heat demand of users | |
| Baseline electrical/thermal load of users in the system at various times before the day | |
| Time-of-use electricity price of power grid | |
| Fixed natural gas prices in the market | |
| Excess electricity sold to the grid by the integrated energy system at time t | |
| Minimum and maximum electricity sales at any time | |
| Fuel cost (including electricity purchased from power grid) | |
| Operation and maintenance cost of equipment | |
| Carbon emission cost | |
| Electricity purchased from the power grid | |
| Minimum power purchase and maximum power purchase at any time | |
| Natural gas price at time t | |
| Natural gas consumption by gas turbine/gas boiler at time t | |
| Electricity output value of gas turbine at time t | |
| Heat output value of the gas turbine/gas boiler at time t | |
| Unit operational and maintenance cost of gas turbine, gas boiler | |
| Electricity conversion efficiency of gas turbine unit operation | |
| Heat conversion efficiency of the gas turbine/gas boiler unit operation | |
| Natural gas calorific value | |
| Minimum and maximum power output values of the gas turbine at any time | |
| Photovoltaic power generation/wind power generation at time t | |
| Unit operational and maintenance cost of PV, wind turbine | |
| Installed photovoltaic/wind turbine capacity | |
| Solar radiation density at time t | |
| Power generation efficiency of photovoltaic cells | |
| Carbon emission factor of natural gas | |
| Unit price of carbon emissions | |
| Cost parameters of electricity/heat supply fluctuation | |
| Average electrical load/average heat load of IES during the dispatch period T | |
| Wind speed at time t | |
| Cut-in/cut-out/rated wind speed of the wind turbine | |
| Minimum and maximum natural gas consumption of gas boilers at any time | |
| Heat output value/electricity consumption of electric boiler at time t | |
| Heating coefficient of electric boiler | |
| Heat loss of electric boiler | |
| Minimum and maximum electric power of the electric boiler at any time | |
| State of charge of the energy storage battery at time t | |
| Initial state/nT periodic states of charge of the energy storage battery | |
| Minimum state of charge/the maximum state of charge | |
| Charging/discharging power of the energy storage battery at time t | |
| Minimum and maximum charging power of energy storage battery at time t | |
| Minimum and maximum discharge power of energy storage battery at time t | |
| Self-discharge rate of the battery | |
| Charging/discharging efficiency of energy storage batteries | |
| Rated capacity of energy storage battery | |
| Heat storage state of the heat storage tank at time t | |
| Initial state/nT periodic states of the heat storage tank at time t | |
| Minimum/maximum heat storage state, | |
| Endothermic power and exothermic power of heat storage tank at time t | |
| Minimum and maximum heat absorb power of the heat storage tank at time t | |
| Minimum and maximum heat release power of the heat storage tank at time t | |
| Self-heat release rate of heat storage tank | |
| Charge and release efficiency of heat storage tank | |
| Rated capacity of heat storage tank | |
| Utility function of industrial users | |
| User’s utility through consuming energy | |
| User’s energy purchasing cost | |
| Marginal utility of electricity/heat used by industrial users | |
| User preferences | |
| Whether to charge/discharge power of energy storage battery at time t | |
| Whether to charge/discharge thermal energy at time t | |
| Whether to buy/sell electricity at time t | |
References
- Woon, K.S.; Phuang, Z.X.; Taler, J.; Varbanov, P.S.; Chong, C.T.; Klemeš, J.J.; Lee, C.T. Recent advances in urban green energy development towards carbon emissions neutrality. Energy 2023, 267, 126502, ISSN 0360-5442. [Google Scholar] [CrossRef]
- Fuso Nerini, F.; Tomei, J.; To, L.S.; Bisaga, I.; Parikh, P.; Black, M.; Borrion, A.; Spataru, C.; Castán Broto, V.; Anandarajah, G.; et al. Mapping synergies and trade-offs between energy and the Sustainable Development Goals. Nat. Energy 2018, 3, 10–15. [Google Scholar] [CrossRef]
- Salvia, M.; Reckien, D.; Pietrapertosa, F.; Eckersley, P.; Spyridaki, N.-A.; Krook-Riekkola, A.; Olazabal, M.; De Gregorio Hurtado, S.; Simoes, S.G.; Geneletti, D.; et al. Will climate mitigation ambitions lead to carbon neutrality? An analysis of the local-level plans of 327 cities in the EU. Renew. Sustain. Energy Rev. 2021, 135, 110253. [Google Scholar] [CrossRef]
- Aydin, M.; Guney, E.; Yigit, B.; Acikgoz, F.; Cakmak, B.Y. Regulatory pathways to green energy transition for sustainable environment: The fostering role of human rights, banking sector development, economic complexity, and economic freedom. J. Environ. Manag. 2024, 366, 121739. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Liu, Z. Low carbon economic scheduling model for a park integrated energy system considering integrated demand response, ladder-type carbon trading and fine utilization of hydrogen. Energy 2024, 290, 130311. [Google Scholar] [CrossRef]
- Li, F.; Sun, B.; Zhang, C.; Zhang, L. Operation optimization for combined cooling, heating, and power system with condensation heat recovery. Appl. Energy 2018, 230, 305–316. [Google Scholar] [CrossRef]
- Li, G.; Zhang, R.; Jiang, T.; Chen, H.; Bai, L.; Li, X. Security-constrained bi-level economic dispatch model for integrated natural gas and electricity systems considering wind power and power-to-gas process. Appl. Energy 2017, 194, 696–704. [Google Scholar] [CrossRef]
- Wang, C.; Lv, C.; Li, P.; Song, G.; Li, S.; Xu, X.; Wu, J. Modeling and optimal op-eration of community integrated energy systems: A case study from China. Appl. Energy 2018, 230, 1242–1254. [Google Scholar] [CrossRef]
- He, L.; Lu, Z.; Zhang, J.; Geng, L.; Zhao, H.; Li, X. Low-carbon economic dispatch for electricity and natural gas systems considering carbon capture systems and power-to-gas. Appl. Energy 2018, 224, 357–370. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, J.; Sun, Y.; Wei, C.; Wang, J.; Liao, S.; Ke, D.; Li, X.; Yang, J.; Peng, X. Coordinated operation of gas-electricity integrated distribution system with multi-CCHP and distributed renewable energy sources. Appl. Energy 2018, 211, 237–248. [Google Scholar] [CrossRef]
- Di Somma, M.; Yan, B.; Bianco, N.; Graditi, G.; Luh, P.; Mongibello, L.; Naso, V. Operation optimization of a distributed energy system considering energy costs and exergy efficiency. Energy Convers. Manag. 2015, 103, 739–751. [Google Scholar] [CrossRef]
- Di Somma, M.; Yan, B.; Bianco, N.; Luh, P.B.; Graditi, G.; Mongibello, L.; Naso, V. Multi-objective operation optimization of a Distributed Energy System for a large-scale utility customer. Appl. Therm. Eng. 2016, 101, 752–761. [Google Scholar] [CrossRef]
- Ma, W.; Fang, S.; Liu, G. Hybrid optimization method and seasonal operation strategy for distributed energy system integrating CCHP, photovoltaic and ground source heat pump. Energy 2017, 141, 1439–1455. [Google Scholar] [CrossRef]
- Wang, C.; Dong, S.; Xu, S.; Yang, M.; He, S.; Dong, X.; Liang, J. Impact of Power-to-Gas Cost Characteristics on Power-Gas-Heating Integrated System Scheduling. IEEE Access 2019, 7, 17654–17662. [Google Scholar] [CrossRef]
- Gao, M.; Yang, M.; Lu, Y.; Levin, V.A.; He, P.; Zhu, H. Mechanical characterization of uniaxial compression associated with lamination angles in shale. Adv. Geo-Energy Res. 2024, 13, 56–68. [Google Scholar] [CrossRef]
- Zhu, H.; Huang, C.; Ju, Y.; Bu, H.; Li, X.; Yang, M.; Chu, Q.; Feng, H.; Qiao, P.; Qi, Y.; et al. Multi-scale multi-dimensional characterization of clay-hosted pore networks of shale using FIBSEM, TEM, and X-ray micro-tomography: Implications for methane storage and migration. Appl. Clay Sci. 2021, 213, 106239, ISSN 0169-1317. [Google Scholar] [CrossRef]
- He, C.; Wu, L.; Liu, T.; Wei, W.; Wang, C. Co-optimization scheduling of interdependent power and gas systems with electricity and gas uncertainties. Energy 2018, 159, 1003–1015. [Google Scholar] [CrossRef]
- Gu, C.; Tang, C.; Xiang, Y.; Xie, D. Power-to-gas management using robust optimisation in integrated energy systems. Appl. Energy 2019, 236, 681–689. [Google Scholar] [CrossRef]
- Wang, C.; Wei, W.; Wang, J.; Bi, T. Convex optimization based adjustable robust dispatch for integrated elec-tric-gas systems considering gas delivery priority. Appl. Energy 2019, 239, 70–82. [Google Scholar] [CrossRef]
- Zhang, Y.; Le, J.; Zheng, F.; Zhang, Y.; Liu, K. Two-stage distributionally robust coordinated scheduling for gas-electricity integrated energy system considering wind power uncertainty and reserve capacity configuration. Renew. Energy 2019, 135, 122–135. [Google Scholar] [CrossRef]
- Zhou, Y.; Wei, Z.; Sun, G.; Cheung, K.W.; Zang, H.; Chen, S. A robust optimization approach for integrated community energy system in energy and ancillary service markets. Energy 2018, 148, 1–15. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, J.; Liu, P.; Li, Z.; Georgiadis, M.C.; Pistikopoulos, E.N. Pistikopoulos. A two-stage stochastic pro-gramming model for the optimal design of distributed energy systems. Appl. Energy 2013, 103, 135–144. [Google Scholar] [CrossRef]
- Yu, J.; Ryu, J.-H.; Lee, I.-B. A stochastic optimization approach to the design and operation planning of a hybrid renewable energy system. Appl. Energy 2019, 247, 212–220. [Google Scholar] [CrossRef]
- Maharjan, S.; Zhu, Q.; Zhang, Y.; Gjessing, S.; Basar, T. Dependable Demand Response Management in the Smart Grid: A Stackelberg Game Approach. IEEE Trans. Smart Grid 2013, 4, 120–132. [Google Scholar] [CrossRef]
- Yu, M.; Hong, S.H. Supply–demand balancing for power management in smart grid: A Stackelberg game approach. Appl. Energy 2016, 164, 702–710. [Google Scholar] [CrossRef]
- Yu, M.; Hong, S.H. A Real-Time Demand-Response Algorithm for Smart Grids: A Stackelberg Game Ap-proach. IEEE Trans. Smart Grid 2016, 7, 879–888. [Google Scholar] [CrossRef]
- Wu, C.; Gu, W.; Xu, Y.; Jiang, P.; Lu, S.; Zhao, B. Bi-level optimization model for integrated energy system considering the thermal comfort of heat customers. Appl. Energy 2018, 232, 607–616. [Google Scholar] [CrossRef]
- Tang, R.; Wang, S.; Li, H. Game theory based interactive demand side management responding to dynamic pricing in price-based demand response of smart grids. Appl. Energy 2019, 250, 118–130. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, Q. A Stackelberg Game Approach for Two-Level Distributed Energy Management in Smart Grids. IEEE Trans. Smart Grid 2018, 9, 6554–6565. [Google Scholar] [CrossRef]
- Moradi, M.H.; Abedini, M.; Hosseinian, S.M. A Combination of Evolutionary Algorithm and Game Theory for Optimal Location and Operation of DG from DG Owner Standpoints. IEEE Trans. Smart Grid 2016, 7, 608–616. [Google Scholar] [CrossRef]
- Chai, B.; Chen, J.; Yang, Z.; Zhang, Y. Demand Response Management with Multiple Utility Companies: A Two-Level Game Approach. IEEE Trans. Smart Grid 2014, 5, 722–731. [Google Scholar] [CrossRef]
- Lee, J.; Guo, J.; Choi, J.K.; Zukerman, M. Distributed Energy Trading in Microgrids: A Game-Theoretic Model and Its Equilibrium Analysis. IEEE Trans. Ind. Electron. 2015, 62, 3524–3533. [Google Scholar] [CrossRef]
- Wei, F.; Jing, Z.X.; Wu, P.Z.; Wu, Q.H. A Stackelberg game approach for multiple energies trading in integrated energy systems. Appl. Energy 2017, 200, 315–329. [Google Scholar] [CrossRef]
- Wan, Y.; Qin, J.; Shi, Y.; Fu, W.; Xiao, F. Stackelberg–Nash game approach for price-based demand response in retail electricity trading. Int. J. Electr. Power Energy Syst. 2024, 155, 109577, ISSN 0142-0615. [Google Scholar] [CrossRef]
- Wu, C.; Gu, W.; Yi, Z.; Lin, C.; Long, H. Non-cooperative differential game and feedback Nash equilib-rium analysis for real-time electricity markets. Int. J. Electr. Power Energy Syst. 2023, 144, 108561, ISSN 0142-0615. [Google Scholar] [CrossRef]
- Liu, X. Low-carbon scheduling research of integrated energy system based on Stackelberg game under sharing mode. Energy 2024, 303, 131928, ISSN 0360-5442. [Google Scholar] [CrossRef]
- Jeroslow, R.G. The polynomial hierarchy and a simple model for competitive analysis. Math. Program. 1985, 32, 146–164. [Google Scholar] [CrossRef]
- Gabriel, S.A.; Conejo, A.J.; Fuller, J.D.; Hobbs, B.F.; Ruiz, C. Complementarity Modeling in Energy Markets. In Volume 157 of International Series in Operations Research & Management Science; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
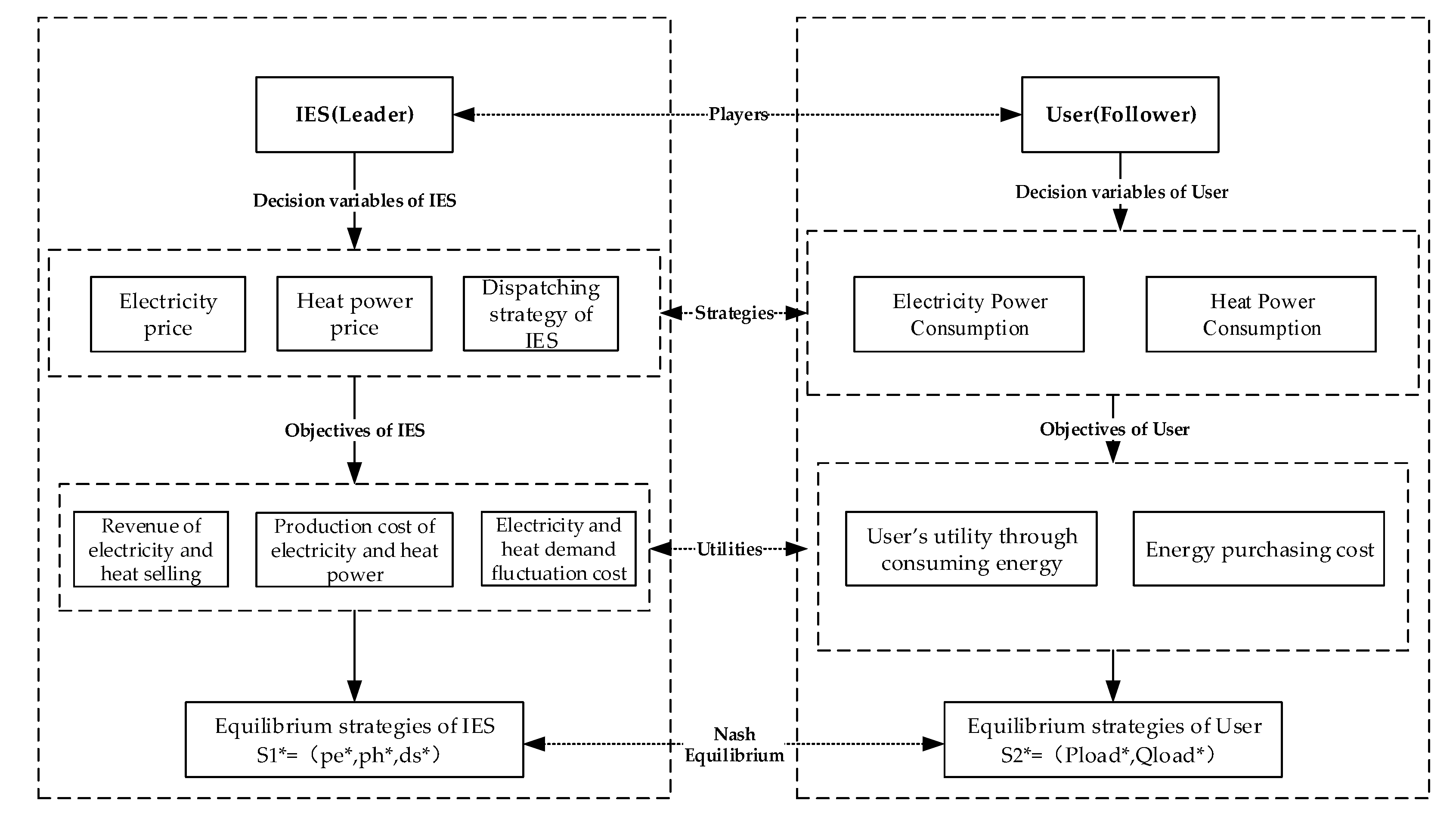



| Player (P) | IES (Leader) | User (Follower) |
|---|---|---|
| Decision variables (S) | ); ) | ) |
| Utility (U) | Equation (48) | Equation (49) |
| Equipment | Installed Capacity/kW | Unit Operation and Maintenance Cost/USD |
|---|---|---|
| Photovoltaic | 100 | 0.069 |
| Wind turbine | 100 | 0.069 |
| Gas turbine | 100 | 0.069 |
| Gas boiler | 100 | 0.069 |
| Electric boiler | 100 | 0.028 |
| Energy storage battery | 40 | 0.069 |
| Heat storage tank | 40 | 0.069 |
| Equipment | Electrical Efficiency | Thermal Efficiency |
|---|---|---|
| Gas turbine | 0.28 | 0.44 |
| Gas boiler | — | 0.85 |
| Electric boiler | — | 0.95 |
| Energy storage battery (charge/discharge) | 0.98 | — |
| Heat storage tank (charging/discharging) | — | 0.98 |
| Equipment | Minimum/Maximum Electrical Output (kW) | Minimum/Maximum Heat Output (kW) |
|---|---|---|
| Gas turbine | 0/100 | — |
| Gas boiler | — | 0/100 |
| Electric boiler | — | 0/100 |
| Energy storage battery (charge/discharge) | 8/36 | — |
| Heat storage tank (charging/discharging) | — | 8/36 |
| Power grid purchase and sale | 0/100 | — |
| Parameter | ||||||
|---|---|---|---|---|---|---|
| Value | −0.001 | −0.001 | 2 | 2 | 1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, K.; Chen, J.; Yang, L.; Wu, J.; Shi, P. Equilibrium Interaction Strategies for Integrated Energy System Incorporating Demand-Side Management Based on Stackelberg Game Approach. Energies 2024, 17, 3603. https://doi.org/10.3390/en17143603
Xiang K, Chen J, Yang L, Wu J, Shi P. Equilibrium Interaction Strategies for Integrated Energy System Incorporating Demand-Side Management Based on Stackelberg Game Approach. Energies. 2024; 17(14):3603. https://doi.org/10.3390/en17143603
Chicago/Turabian StyleXiang, Kangli, Jinyu Chen, Li Yang, Jianfa Wu, and Pengjia Shi. 2024. "Equilibrium Interaction Strategies for Integrated Energy System Incorporating Demand-Side Management Based on Stackelberg Game Approach" Energies 17, no. 14: 3603. https://doi.org/10.3390/en17143603
APA StyleXiang, K., Chen, J., Yang, L., Wu, J., & Shi, P. (2024). Equilibrium Interaction Strategies for Integrated Energy System Incorporating Demand-Side Management Based on Stackelberg Game Approach. Energies, 17(14), 3603. https://doi.org/10.3390/en17143603





