Abstract
Accurate parameters are crucial in modern energy systems to ensure the reliable operation of all components. Given the substantial volume of data in monitored systems, high-performance methods are necessary. This paper proposes a new Bayesian multi-output regressor for estimating the parameters of a three-phase transmission line. The presented approach achieves acceptable accuracy in parameter estimation using only one end of the line. The Bayesian regressor is developed using information derived from the data themselves, eliminating the need to explicitly model the system. This capability allows the method to estimate parameters while accommodating different noise models, even in the presence of systematic errors and non-Gaussian random noise. The methodology was validated on various systems, including a two-bus system, IEEE 14-bus, IEEE 39-bus, and IEEE 118-bus, under diverse conditions such as varying sample sizes, loads, and noise levels. These tests demonstrate the robustness of the proposed approach.
1. Introduction
Accurate estimation of power system parameters is a significant concern in modern systems, especially within the context of smart grids. Transmission line parameters, considering both positive and zero sequences, find application in various scenarios, including modeling of protection relays for distance protection [1], power system state estimation [2], and investigation of voltage stability [3]. Thus, evaluating these parameters with a high accuracy is imperative for ensuring the security and reliability of power system operations.
Studies in the literature have shown that the difference between the stored values of the transmission line parameters and the actual values can reach up to 30% [4,5]. These deviations directly affect the performance of the state estimators and the power flow solutions [6]. Therefore, a robust methodology to estimate the parameters of a given power system using the available noisy measurements is necessary.
Over the years, several papers have attempted to address transmission line parameter estimation [2,6,7,8,9,10,11,12,13]. Each of them focuses on a specific model of the transmission line or a different methodology to describe the observed data. In [6], a method to estimate the parameters of a three-phase transmission line employing robust linear regression in the presence of outliers was proposed. However, the methodology did not address the challenge of modeling random noise in measurements obtained from PMUs.
The authors of [7] presented a methodology to calculate the parameters of a short transmission line by developing a rigorous model for random noise based on an accurate noise covariance matrix, considering the realistic specifications of noise introduced by instrument transformers and PMUs. In this work, the solution is obtained using weighted least squares using the covariance matrix of the measurements. Nevertheless, systematic errors are neglected, and the projections are assumed to be Gaussian for all noise levels, which is not valid in general [11].
The work developed by [14] proposed a solution based on the Kalman filter, considering the presence of noise in voltage and current measurements. Additionally, the authors presented an analytical derivation for the covariance matrix for the lumped model of a transmission line. However, the authors ignored the presence of systematic errors and the possibility of non-Gaussian noise distributions. Moreover, the application of the method requires the presence of PMUs at both ends of the transmission lines.
In [12,13], the authors presented a multi-branch method to estimate the parameters of the transmission lines and the systematic errors present in the chain of measurements used to obtain a phasor measurement. The random errors are modeled as Gaussian distributions for both magnitude and phase, while the systematic error is assumed to follow a uniform distribution, i.e., it has the same contribution for each sample. The solution is calculated by applying a Tikhonov regularization framework.
The need for a method that requires measurements only from one side of a transmission line was introduced in [15]. This paper focused on identifying erroneous parameters and subsequently estimating them by applying the extended error function for state estimation in power systems. However, the authors did not address the problem of modeling noise in phasor measurements, although they heavily relied on it in the estimation process.
Additionally, it is important to highlight the work proposed by [8], where the authors developed a method to handle non-Gaussian random noise in voltage and current phasor measurements. This methodology was supported by recent studies that examined the Gaussian assumption of random errors [16,17], indicating that the process of obtaining phasors is multimodal and that the Gaussian assumption may not be the most suitable choice.
In this context, this work presents a novel, model-free methodology to estimate transmission line parameters. This approach does not rely on transmission line equations to evaluate parameters; instead, it is a data-centric solution. Moreover, the proposed method is capable of estimating parameters using only one-sided measurements with an acceptable performance. Additionally, the developed multi-output regressor can accommodate different noise models, including Gaussian random error, systematic errors, and non-Gaussian random noise, outperforming existing methods under the same studied conditions. Therefore, the main innovations introduced by this paper are as follows:
- A model-free methodology is developed to assess the parameters of a three-phase transmission line that does not necessitate measurements from both ends of the transmission line;
- The Bayesian regressor enables the construction of credible intervals for the estimation, thereby enhancing confidence in the results;
- The method is capable of handling various noise models, resulting in estimations with high performances across all cases;
- The method was tested on systems with varying dimensions, numbers of samples in the database, load conditions, and noise levels.
2. Description of the Employed Transmission Line Model
In this work, the model for long-transmission lines presented in [18] was studied. The multi-phase model, which includes consideration of ground effects, is depicted in Figure 1. In this figure, the parameters , , and represent the self-impedance per unit length (/km),while , , and represent the mutual inductances. As for capacitances, , , and denote the capacitances between phases per unit length (F/km), and denotes the ground capacitance.
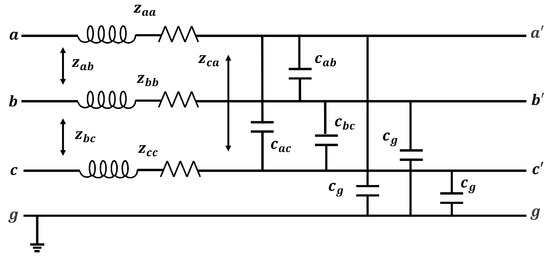
Figure 1.
Three-phase transmission line model with mutual coupling between phases used to obtain the sequence parameters.
The three-phase transmission lines are represented by the impedance matrix and the capacitance matrix . The parameters are shown in (1).
where , and f is the frequency of the power system.
Since we are assuming that the method deals with long transmission lines, it is reasonable to presume that the line is transposed. Thus, the model for the per-length parameters is represented by the matrices in (2):
Therefore, by applying symmetrical components, the sequence parameters are obtained while still considering the per-length units:
Using the parameters per length, it is possible to obtain the parameters using hyperbolic corrections [19] using the following equations:
where the index might be 1 for a positive sequence or 0 for a zero sequence.
The provided expressions delineate the circuit per sequence, as illustrated in Figure 2. Within this representation, and denote the phasors of voltage and current at the bus k for sequence s, while and represent the respective phasors at bus l. It is worth noting that each sequence needs its own circuit depiction. Notably, the negative sequence mirrors the positive sequence in terms of parameters, thereby rendering it unnecessary for the analysis.
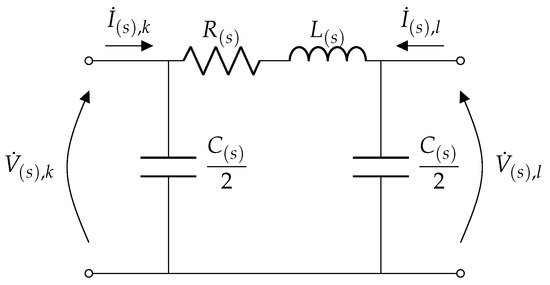
Figure 2.
-model of each sequence circuit of the transmission line used to generate the measurements at the sender and receiver ends.
To simplify the notation, the sequence notation will be omitted from this point forward, as the equations can be handled identically for positive and zero sequences. Any distinctions between sequences will be highlighted as needed.
3. Problem Formulation
In this section, we describe the methodology used to generate the database utilized for estimating the parameters, as well as the formulation of the problem concerning the supervised learning approach and the algorithm built to evaluate the parameters.
3.1. Building the Database
In a supervised learning framework, the methodology employed to construct the database holds significant importance in achieving a viable solution. Given the scarcity of literature addressing transmission line parameter estimation through a machine learning paradigm [20,21,22], this paper introduces a novel approach to generating the training data. This methodology takes into account the characteristics obtained from historical data documented in the technical literature.
According to studies in the literature, parameter errors typically fall within the range of approximately 10% to 30% of the true parameter value [4,15]. Consequently, it is anticipated that the database should encompass parameter values within this range. Thus, if represents the exact value of a specific parameter, then p, the parameter with inaccuracy, should fall within the following bounds:
Given that extreme parameter values are less frequently observed compared to those with smaller errors, the Gaussian distribution is suitable for data generation. By employing the empirical rule of [23], it is possible to establish a relationship between the maximum observed error and the standard deviation of the Gaussian distribution. This relationship can be succinctly expressed through the following rule:
where is the probability density function, X is a Gaussian random variable with mean and standard deviation . Using this rule with the formulation of the problem, we have the following:
Hence, to generate data for parameters with a mean value of and maximum observed values of and minimum values of , we use a truncated Gaussian distribution with a mean of and a standard deviation of , truncated in the interval .
For distribution lines, the approach of varying the parameters within a specific range of values was tested in [24]. However, in that work, the authors used a maximum variation of 5%, which simplifies the problem in terms of supervised learning because the target space is smaller. Additionally, for transmission lines, it is well-established that parameter values can vary by up to 30%.
Although this method for building the database is based on practical scenarios of transmission lines, it presents some concerns. If the parameter to be estimated falls outside the range of possible parameters, the algorithm needs to be retrained, considering the new range of possible values. Furthermore, the random generation of cases can lead to unfeasible values for the speed of signal propagation. To address this problem, an additional step was necessary to verify the generated speed of propagation. Regarding the speed of light in a vacuum , the values for the positive and zero sequences should be as follows:
The entire dataset consists of N samples or instances for valid cases, after the verification of both conditions. Before applying any machine learning algorithm, this dataset is split into 80% for training the algorithm and 20% for testing. It is important to note that this process ensures that the training process is completely blind to the test dataset.
3.2. Supervised Learning Setup
In modern power systems, advances in monitoring technology are increasing the use of Phasor Measurement Units in several buses of the system [25,26,27]. Additionally, the greater frequency reporting rate compared with common supervisory systems (SCADA) and the possibility to employ synchronized data in energy system problems make this device more suitable to deal with linear and nonlinear problems. Generally, the transmission line parameter estimation problem is nonlinear [11], requiring more sophisticated noise models [8].
Considering the presented context, this work presents a methodology to estimate the parameters based on a supervised learning approach. For such a task, initially, we have considered as features the voltage and current phasors for the sender (bus k) and receiver (bus l) ends in a three-phase transmission line. The goal is to estimate the parameters for positive and zero sequences. Mathematically, this is expressed as follows:
where the indices A, B, and C represent the system phases, and k and l are the indices of buses connected by a transmission line. Thus, the phasor measurements can be written as follows:
where both magnitude and angles are treated as features in the estimation process.
This way, each vector of features, denoted as , contains the information of the three-phase phasors in the sender and receiver ends. Each row in the matrix of features represents an instance or sample for a specific observation of the set of features . Additionally, each parameter is a different target t. A method to deal with multi-output regression is to perform one model per target [28]. Thus, the theory can be developed for a single target and applied for each desired parameter, ignoring the remaining parameters in the estimation.
3.3. Statistical Model
In this section, we describe the Bayesian ridge regression model [29] used to estimate the transmission line parameters. Even though this is a hierarchical Bayesian model, it assumes convenient prior distributions and approximates the posterior distributions of some parameters based on their maximum a posteriori estimates to produce low-complexity approximations of the transmission line parameters. As a Bayesian model, the output is a posterior distribution, with the mean serving as a point estimate and the standard deviation indicating the level of uncertainty.
To train the model, we use N pairs , where is the vector of features and is the label; that is, the value of the target for the n-th sample. We assume the measurement model is given by the following:
where and is an independent and identically distributed zero-mean Gaussian process with variance . Thus, , being is a Gaussian distribution with mean and variance .
Defining and assuming that each sample is independent and identically distributed [30], the likelihood of the observed data can be written as follows:
where , such that . The prior distribution for is chosen as a Gamma distribution; a common choice for scale parameters:
with
Following [29], we assume a hierarchical prior distribution for the parameter by defining a vector of hyperparameters representing the standard deviation of :
Instead of jointly estimating and , these hyperparameters are inferred using a maximum a posteriori (MAP) Bayesian inference approach; that is, we select
and calculate . The approach to numerically optimize the parameters and is presented in [29].
Because and are multivariate Gaussian distributions, the posterior distribution of is also Gaussian:
with the mean and covariance matrix given by:
where .
3.4. Inference
After the matrices and were computed, the model can predict a target given a new test point . The posterior distribution of the predicted target is as follows:
Since both terms in the integral are Gaussian functions, is a Gaussian distribution:
with the following parameters:
Therefore, the hierarchical Bayesian model learns , during the training step and use these estimates to calculate and . Unlike traditional machine learning models, this Bayesian framework produces as outputs both a central estimate (that is, the predicted mean value) and the variance of the prediction , given by (4).
The methodology used to generate the dataset and learn the parameters from the model, as well as the procedure used for inference, are summarized in Algorithm 1.
| Algorithm 1: Methodology used to generate the dataset, train the model, and infer the parameters. |
  |
4. Results
In the initial analysis, we studied a system with a non-ideal three-phase source connected to the transmission line, and at the end, an unbalanced three-phase load. The corresponding system is shown in Figure 3. The load was given as a percentage of the surge impedance loading (SIL) of the transmission line [18]. Using the lossless case, the SIL is given by:
where is the equivalent one-phase SIL, or the three-phase SIL divided by three, and is the phase–ground voltage of phase A.
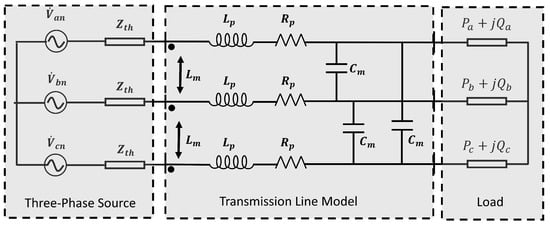
Figure 3.
Simplified 2-bus system used to obtain the measurements in the computational environment for different conditions.
Additionally, to estimate the zero-sequence parameters, an unbalance factor in the load was introduced, designated as . This way, we propose the following manner to generated different active powers for each phase:
Furthermore, to determine the influence of the reactive power, we fixed a power factor . The numerical values of the parameters for the studied system are presented in Appendix A.
The presented system was simulated using MATLAB/Simulink using a notebook equipped with an Intel Core i7-1165G7 2.8 GHz CPU and 8GB of memory. In the initial analysis, the dataset size was considered to be 10,000 samples, which were split into training and test sets in an 80/20 proportion.
In terms of practical applications, this approach aims to develop software for post-processing data obtained from transmission lines monitored by PMUs, even when monitoring is limited to one side. The assumption of monitoring a transmission line with at least one PMU is common in the literature [7,8,9]. However, many papers assume that PMUs are installed at both ends [15], which can increase system costs. In this work, our approach achieved satisfactory performance using measurements from only one side. The proposed methodology for estimating transmission line parameters leverages readily available data in transmission systems to enhance parameter monitoring, requiring only a computational environment for storing and processing the data used in the model.
Some studies in the literature have utilized practical systems to validate developed methods. Access to data from actual systems is often limited or restricted due to privacy concerns. For example, in [6], the method was tested using an experimental setup based on a simplified system. In contrast, [8] validated their solution for consistency using raw PMU data obtained from a U.S. power utility in the Eastern interconnection.
Using the approach of [6], it is possible to access the method performance directly, since the parameters of a simplified laboratory system can be calculated via offline techniques. Meanwhile, in [8], the consistency of the method can be tested by applying it to similar ambient temperature and loading conditions using different samples, but with the same length. This way, if the method produces the same results, it is possible to conclude that it is consistent.
Numerical Analysis
The model is built using a training database and evaluated on a test database that is completely excluded from the training process. To present the performance, it is necessary to use some metrics. For this purpose, consider the actual values of the target and the estimated values , where k is the size of the test database. In this work, we have adopted the root mean squared error (RMSE) and mean absolute percentage error (MAPE), defined as follows:
It is important to note that the RMSE is given in the unit of the parameter, e.g., for resistance, the RMSE is in , whereas the MAPE is given in % using the presented configurations. Additionally, it is relevant to note that the metric is taken considering different k values for the target in the test database. The result for the noiseless case is shown in Table 1. Regarding the computational time required to obtain the solution, we conducted an average time analysis based on running 100 realizations to train and test the algorithm, resulting in an average time of 0.0397 s. As a benchmark, we implemented a simple linear regression solution to that commonly employed in the literature [7,10,31], and we found an average computational time of 0.0213 s. Thus, our method exhibits a computational burden that is very similar to the standard methods used in the literature.

Table 1.
Performance metrics for the proposed approach considering a 2-bus system and the noiseless case.
The use of a Bayesian method to estimate the parameters presents another advantage compared to other machine learning-based solutions or even common maximum likelihood estimators. In (3), the developed method for prediction provides the estimator with the distribution of the target in the test database. Consequently, the mean value and the standard deviation of each sample in the test set are calculated. The mean value corresponds to the prediction used for a given set of features. Additionally, the standard deviations can be used to illustrate the possible variations in the estimation process. To demonstrate this behavior, we have performed the estimation for the parameters and , along with their error bars, considering a variation of . The obtained results are shown in Figure 4.

Figure 4.
Comparison between the estimated and true parameters for the noiseless case for (a) and (b).
The results depicted in Figure 4 reveal some important aspects of the solution. Firstly, the estimation performance is remarkably high, as the true values closely align with the estimated ones. Another noteworthy observation is the reliability of the estimations, evidenced by the small standard deviations. Consequently, the proposed method generates stable predictions with a high performance for estimating three-phase transmission line parameters.
An important influencing factor in a machine learning solution is the size of the dataset, i.e., the number of samples used to build the statistical model and obtain results. Some papers in the literature have employed various dataset sizes. In the context of data-based solutions in power systems, [32] used 5000 samples to train the model, whereas [33] employed 32,000 samples to develop the model used to address the problem. Generally, non-machine learning solutions utilize a day of PMU measurements considering a certain reporting rate for the device. For instance, in [7], a reporting rate of 50 samples per second was utilized, resulting in approximately samples.
The presented work initially employed 10,000 samples to obtain the results shown in Table 1. However, as shown in Figure 5, the required number of samples to achieve the best performance is considerably lower. By analyzing this figure, it is possible to conclude that, for the noiseless case, 200 samples are sufficient to produce results with a high performance.
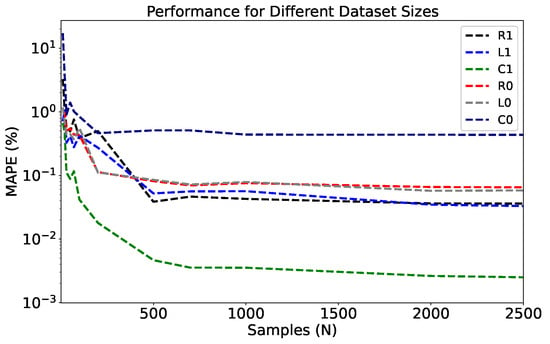
Figure 5.
Influence of the number of samples in the estimation method considering the noiseless case.
Another relevant aspect of the solution is the necessity of measurements at both ends. In real-world applications, obtaining PMUs to monitor each transmission line of the system is challenging due to the high cost of implementation [16]. Thus, it is expected that some non-critical lines may only be monitored using a single PMU. Consequently, we tested the proposed algorithm considering measurements from only one side. This process involves removing either the receiver or sender end measurement from the feature matrix and applying the method as described in Section 3.2. The results of this analysis are shown in Table 2.

Table 2.
Performance metrics of the proposed approach considering only one-sided measurement in the noiseless case.
The results presented in Table 2 confirm that, as expected, the method’s performance decreases when using measurements from only one side. However, the obtained values still demonstrate an acceptable performance [6], as it is desirable to achieve parameter values that are within 10% of the maximum values. It is worth highlighting that the worst-performing parameter is the zero-sequence susceptance. Generally, estimating zero-sequence parameters is more challenging due to their smaller magnitude compared to the positive sequence, which poses an additional barrier to achieving numerical stability in the estimation process.
Another relevant parameter in the estimation process is the active power carried through the line. In the initial analysis, we assumed that the active power was 1 SIL, equivalent to 100% of its value. To consider the influence of this parameter, the active power was varied in a range of of the 1 SIL. This range is a commonly observed value for the variation in the active power in a period of 24 h [34]. The results of this analysis are shown in Figure 6.
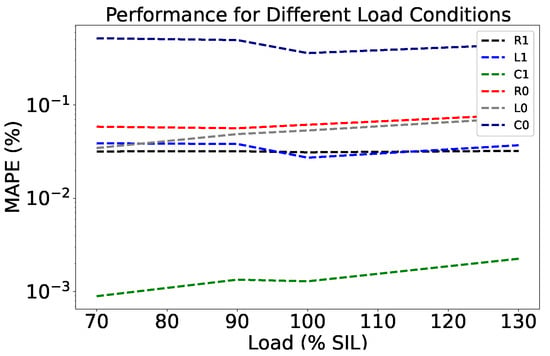
Figure 6.
Analysis of the MAPE of the solution under different load conditions and in the noiseless case.
The results presented in Figure 6 show that the proposed methodology is robust concerning the active power carried through the line. This way, the variation in the load did not have a significant influence on the performance of the method, since there was only a slight difference among the results for the studied loads. This is an interesting behavior of the proposed approach due to the fact that common methods in the literature [11], based on nonlinear optimization, present extreme variation in performance when the load is modified, especially for extreme values of load.
Another relevant scenario to test the performance of the algorithm is to estimate the parameters in a complete power system with the presence of other components, such as transformers, generators, loads, and transmission lines. To study the performance of the proposed method under this situation, we implemented the methodology to estimate the transmission line parameters in the IEEE 39-bus system. The IEEE 39-bus standard system is a widely used power network in the New England area of the United States [35], providing an extensive scope to evaluate power system solutions. The system consists of 10 generators, 39 bus bars, and 12 transformers, as illustrated in Figure 7. The methodology employed to generate the data is consistent with that presented in Section 3.1. It is important to note that the simulation was carried out for positive sequence analysis, which is the standard case for these test systems [36]. Thus, the results for several transmission lines of the system are presented in Table 3.

Figure 7.
The IEEE 39-bus system [37].

Table 3.
Performance metrics of the proposed solution considering the IEEE 39-bus system.
As observed for the simplified 2-bus system, Table 3 demonstrates that the method exhibits a high performance in estimating the positive sequence parameters of a three-phase transmission line. Particularly noteworthy is the fact that the worst parameter yielded a mean absolute percentage error (MAPE) smaller than 1%. Furthermore, it is relevant to emphasize that the parameters with the worst performances shared the characteristic of having one of their buses (sender or receiver) controlled, meaning that the voltage was constant in practical applications. This characteristic poses a challenge for conventional methods, which rely on algebraic solutions and often neglect such restrictions in their solutions. In contrast, the proposed methodology, based on statistical learning, is capable of handling this characteristic simply by ignoring this feature in the regression.
To directly compare different methods, it is necessary to perform the comparison using scenarios similar to those used to build and test the proposed methodology. In general, papers in the literature develop methods to address specific problems, such as considering the simplified model for the line in the dq domain [38] or in three-phase untransposed short transmission lines [7], which makes it difficult to propose a fair comparison. Additionally, the data models employed are generally different due to the use of other measurement resources, such as power measurements, or even due to the methods adopted to model the inaccuracies present in the data. However, it is possible to use references that present results using noiseless cases and some IEEE test systems. In [31,36], a method was implemented to estimate the parameters based on the extended vector of states in a power system. The comparison of the proposed solution with such references is shown in Table 4. Note that the works have calculated only the admittance branch parameters, which are simply obtained by inverting the elements .

Table 4.
Single line errors in the IEEE 14-bus system.
By observing the results presented in Table 4, it is possible to conclude that the developed methodology achieved better or at least comparable performance with the analyzed previous works in the literature. Furthermore, it is important to highlight that the methods developed in [31,36] may not work in some situations depending on the detection method used to evaluate the parameters. For example, for the branch 9–10, it was not possible to detect such a parameter as erroneous using the approach used in [39].
5. Estimation Considering Noise
The noise model for phasor measurements is a fundamental aspect of solutions utilizing data obtained from PMUs. In general, the chain of instruments and components introduces inaccuracies in the data. The instrument transformers (IT), namely voltage and current transformers associated with the PMU device, introduce both random and systematic errors in the temporal series generated by the sequence of obtained phasors.
Some papers in the literature have introduced the necessity of modeling the noise as a separated term for the magnitude and phase; i.e, the noise should be included in the polar coordinates and the distribution should be verified for the projections into the real and imaginary axes [7,9,11]. This model makes the solution more sophisticated, since it is not possible to obtain an analytical solution with a closed form. Instead, approximated numerical solutions are used to evaluate the parameters in different conditions.
In [16], the authors challenge the Gaussian assumption of random errors by arguing that the process of obtaining phasors is multimodal, time-variant, and characterized by non-stationary error statistics. Consequently, the central limit theorem is deemed inapplicable to this scenario, as the chosen sampling distribution may not accurately represent the actual random process underlying the measurement data generation, potentially leading to erroneous performance assessments. To address this challenge, the paper proposed modeling the errors using a Gaussian mixed model (GMM). Using this approach, the authors of [8] developed a solution by equating the statistical model and subsequently applying Newton’s method for solving nonlinear problems.
In summary, each different noise model leads to a specific solution, requiring algebraic work to formalize the cost function to optimize and the testing of different algorithms to obtain the parameters. In this work, we propose a solution that is able to deal with different noise models that do not require any algebraic work to equate the transmission line model. By employing a data-centric approach, it is possible to evaluate the parameters with acceptable performance considering several scenarios of the system.
5.1. Gaussian Random Noise with Uniform Systematic Error
Following recent papers in the literature that consider Gaussian models for the random errors [12,13], the field measurements can be simulated by using the following model:
where h represents the index of a specific bus, and represent the phasors corrupted by noise, the term “sys” denotes systematic error, while “random” pertains to the random errors inherent in the measurements. The terms , , , and are uncorrelated and separately modeled for each magnitude and phase in complex data. The key distinction between systematic and random errors lies in their behavior: systematic errors contribute consistently across all samples, whereas random errors fluctuate throughout the time series. As the errors are uncorrelated, it is possible to write the following:
for , where is the expected value of the random variable X.
This model relies on papers that deal with actual data from PMUs, and its design is based on the analyzed statistics of time series obtained from field applications. According to previous studies [40,41,42], a Gaussian distribution is often a meaningful choice, depending on the specific device, measured quantity, and considered channel. It is also important to highlight that the studies were conducted by fitting one model for the magnitude data and another for the phase data, as adopted in (5).
In terms of noise level, although the values vary significantly across the diverse data, a value of 0.5% is a good approximation for magnitude [40], and 0.52 degrees is a good approximation for the phase [13]. In this paper, we have used more conservative values for the noise: 1% for the magnitude noise level and 1.03 degrees for the phase, demonstrating that the developed methodology does not assume the availability of very high-quality data.
Concerning the values, the proposed approach considers that [13]:
- Instrument transformers, including both voltage and current transformers, are categorized as class 1.0 [11]. Systematic errors are modeled to follow a uniform distribution with a standard deviation equal to , where represents the maximum deviation. For example, in class 1.0, a systematic error of corresponds to the systematic error model.
- The random errors are assumed to be Gaussian based on the maximum total vector error (TVE) of 1% for the PMUs [13], which is decomposed into a maximum amplitude error of 1% and a maximum phase angle error of 0.57°.
It is worth highlighting that to evaluate the performance of the model under random noise, 1000 Monte Carlo simulations were carried out. This approach helps mitigate the bias introduced by a single numerically generated distribution and yields a more stable response that can be compared in a fairer manner with the proposed solutions in the literature.
When applying the presented model using the literature values, the results for the Gaussian random noise with uniform systematic errors are displayed in Table 5.

Table 5.
Performance metrics of the estimation for the 2-bus system considering Gaussian noise and systematic error in the measurements.
Similar to the noiseless case, it is possible to generate results with their corresponding error bars for . The obtained result is shown in Figure 8. Upon analyzing this figure, it is evident that the performance deteriorates when considering noise compared to the noiseless case, as expected since noise introduces complications in the parameter estimation problem. It is worth highlighting that the presented approach not only provides the estimated parameters but also presents the bounds for the expected error in a generic realization of the method. This represents an innovation in solutions dealing with transmission line parameter estimation.

Figure 8.
Comparison between the estimated and true parameters considering Gaussian noise and systematic errors for (a) and (b).
In order to demonstrate the robustness of the proposed solution under Gaussian noise compared with other works in the literature, the model presented in [9] was implemented. In this model, the authors developed a recursive least squares-based solution to estimate the transmission line parameters. In their paper, they used the IEEE 118-bus test system and applied Gaussian noise to phasor measurements using the errors in the instrument transformers shown in Table 6. To establish a fair comparison, we implemented the same system using the same noise model. It is important to emphasize that the authors of [9] used zero-mean Gaussian noise, neglecting the presence of systematic errors. Therefore, we adopted the same strategy to make a fair comparison of the methods. The results are shown in Table 7.

Table 6.
Standard deviations of measurement errors [9].

Table 7.
Errors in the IEEE 118-bus system.
The results presented in Table 7 demonstrate that the developed methodology is superior to the one in the literature for most of the analyzed lines of the IEEE 118-bus system. Some aspects are relevant in the comparison of the solutions. The largest observed deviations are in the resistance parameter, and the smallest deviations are in the susceptance parameter, which occurred in both solutions. Additionally, the highest encountered deviation in [9] was greater than 2%, while in the presented solution, it was less than 1.5%.
5.2. Non-Gaussian Random Noise
Recent papers in the literature have assessed the assumption that random errors in phasor measurements obtained from PMUs follow a Gaussian distribution. The authors of [16,17] used field data to demonstrate that phasor measurements, particularly for current measurements, do not conform to a Gaussian distribution [16]. In place of the Gaussian model, the authors in [16] propose a model based on GMMs for these measurements.
Using this model, let be a sample of the phasor measurements. The probability density function of this sample is given by:
where K is the number of clusters or Gaussian distributions and is the mixing coefficients of the normal distributions, such that:
Since is the multivariate normal distribution, it is possible to write the following:
An important parameter for modeling the Gaussian mixed model is the size of the window used to fit the centroids (average values) and the format of the distribution (covariance matrix). This parameter will be referred to as N. Thus, for N independent and identically distributed samples, the random vector is obtained using the following:
To accurately describe the noise model for the data, it is necessary to provide the number of clusters, the mean values for each measurement, their corresponding variances, and the vector of weights. In the model, it is assumed that each random variable is uncorrelated with the others; hence, the covariance matrix is diagonal.
In possession of real field data, these parameters could be estimated using a certain method. Initially, determining the optimal number of clusters is accomplished by employing the Bayesian information criterion (BIC). This approach aids in estimating the model that best fits the data while penalizing models with a high complexity. In the literature [8,16], the reported optimal number of clusters typically falls between 2 and 4. The means and variances can then be evaluated based on the maximization of the likelihood using the model outlined in Equation (6).
This way, to prove the robustness of the proposed methodology, we have investigated the performance of the method under two different conditions of Non-Gaussian noise for 2 and 4 clusters.
Utilizing the methodology elucidated in [8], the efficacy of the approach was explored for two clusters (Scenario 1) and four clusters (Scenario 2).
The subsequent parameters were employed for Scenarios 1 and 2:
where is the identity matrix of dimension n.
The corresponding results for both situations are presented in Table 8. By observing the results for the association between Gaussian and systematic noise and non-Gaussian noise, it is possible to conclude that, under the standard conditions of noise levels in both cases, the Gaussian noise associated with a uniform distribution is more difficult for the model to deal with. Generally speaking, this occurred because the former model introduced a greater bias value into the data, leading to a loss of accuracy in the method. However, in both cases, the proposed methodology was able to estimate the six parameters with acceptable performance, proving its robustness under different noise models.

Table 8.
Performance metrics the proposed method considering non-Gaussian noise in a 2-bus system.
According to [16], the noise level in GMM might vary in terms of the mean values and the variance of each Gaussian distribution. This way, following the approach presented in [8], it is possible to consider different values for the mean and variance by scaling using a factor expressed as a percentage. The magnitude of 1% noise closely resembles the GMM noise attributes employed in the previous study. For the remaining values, the GMM noise parameters were derived by appropriately adjusting the mean and standard deviations of the noise. For instance, to derive the GMM noise attributes for a 2% noise level, the GMM noise characteristics associated with a 1% noise level were doubled. The result is shown in Figure 9. This study proves that the method is robust under different noise levels. Particularly, for all the studied noise levels, the observed MAPE was less than 1%.
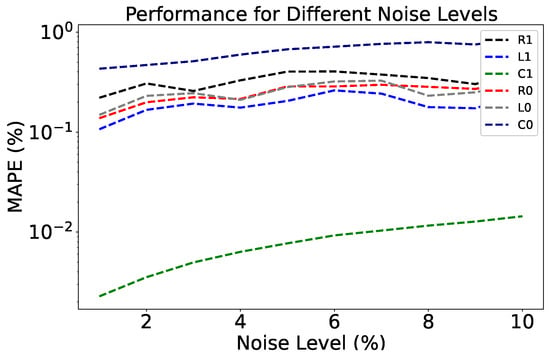
Figure 9.
Analysis of the MAPE of the solution under different noise levels using Gaussian mixed models.
6. Conclusions
This paper introduces a new Bayesian regression approach to estimate transmission line parameters. The proposed methodology is model-free, meaning that the estimation method does not rely on the transmission line equations to estimate the parameters. Instead, the developed method is data-centric, allowing for the evaluation of parameters even with measurements from only one side. Consequently, the method does not necessitate PMUs at both ends of the transmission lines, making it more realistic for real-world applications.
Furthermore, due to the nature of the proposed method, it was possible to obtain credible intervals for the solutions, providing bounds for the estimation of each parameter. This aspect is often overlooked in solutions dealing with transmission line parameter estimation. The performance of the solution was investigated under different noise models, considering the state-of-the-art noise modeling in phasor measurement units. In particular, it was concluded that the standard case of Gaussian random noise associated with systematic errors is more challenging to estimate compared to the model that employs GMMs. However, for all the studied models, our method achieved acceptable performance, outperforming solutions from the literature under the same studied conditions.
Finally, our methodology was tested across systems of varying scales, including several IEEE test systems of different sizes. This testing encompassed various load conditions, numbers of samples (size of the database), and noise levels. Therefore, the proposed solution remained stable under different conditions of the power system and data models.
Author Contributions
Conceptualization, F.P.d.A., R.N. and C.A.P.J.; methodology, F.P.d.A., R.N. and E.C.M.d.C.; software, F.P.d.A., R.N., E.C.M.d.C. and C.A.P.J.; validation, F.P.d.A., R.N. and C.A.P.J.; formal analysis, F.P.d.A., R.N. and E.C.M.d.C.; investigation, F.P.d.A., R.N. and C.A.P.J.; resources, F.P.d.A., R.N. and E.C.M.d.C.; data curation, F.P.d.A., R.N., C.A.P.J. and E.C.M.d.C.; writing—original draft preparation, F.P.d.A., R.N., C.A.P.J. and E.C.M.d.C.; writing—review and editing, F.P.d.A., R.N., C.A.P.J. and E.C.M.d.C.; visualization, F.P.d.A. and R.N.; supervision, R.N. and E.C.M.d.C. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financed by São Paulo Research Foundation (FAPESP)—Grant 2021/01325-7, 2024/00261-3 and 2019/21858-0.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have influenced the work reported in this paper.
Appendix A
Parameters of the System

Table A1.
Transmission system parameters used to simulate the measurements in a computational environment.
Table A1.
Transmission system parameters used to simulate the measurements in a computational environment.
| Parameter | Value |
|---|---|
| kV | |
| /km | |
| mH/km | |
| nF/km | |
| /km | |
| mH/km | |
| nF/km | |
| Rated frequency (f) | 60 Hz |
| Length | 200 km |
| Power factor | |
| Unbalance factor | |
| MW | |
References
- Patel, B.; Bera, P. A New Transmission Line Parameter Estimation Technique and Its Impact on Fault Localization. IEEE Trans. Instrum. Meas. 2023, 72. [Google Scholar] [CrossRef]
- Costa, E.C.M.; Kurokawa, S. Estimation of transmission line parameters using multiple methods. IET Gener. Transm. Distrib. 2015, 9, 2617–2624. [Google Scholar] [CrossRef]
- de Albuquerque, F.P.; Nascimento, R.; Liboni, L.H.; Pereira, R.F.R.; da Costa, E.C.M. Data-centric approach for online P-margin estimation from noisy phasor measurements. Energy Rep. 2023, 10, 2194–2205. [Google Scholar] [CrossRef]
- Kusic, G.; Garrison, D. Measurement of transmission line parameters from SCADA data. In Proceedings of the IEEE PES Power Systems Conference and Exposition, New York, NY, USA, 10–13 October 2004; pp. 440–445. [Google Scholar]
- Mansani, P.K.; Pal, A.; Rhodes, M.; Keel, B. Estimation of transmission line sequence impedances using real PMU data. In Proceedings of the 2018 North American Power Symposium (NAPS), Fargo, ND, USA, 9–11 September 2018; pp. 1–6. [Google Scholar]
- Milojević, V.; Čalija, S.; Rietveld, G.; Ačanski, M.V.; Colangelo, D. Utilization of PMU measurements for three-phase line parameter estimation in power systems. IEEE Trans. Instrum. Meas. 2018, 67, 2453–2462. [Google Scholar] [CrossRef]
- Wehenkel, A.; Mukhopadhyay, A.; Le Boudec, J.Y.; Paolone, M. Parameter estimation of three-phase untransposed short transmission lines from synchrophasor measurements. IEEE Trans. Instrum. Meas. 2020, 69, 6143–6154. [Google Scholar] [CrossRef]
- Varghese, A.C.; Pal, A.; Dasarathy, G. Transmission line parameter estimation under non-Gaussian measurement noise. IEEE Trans. Power Syst. 2022, 38, 3147–3162. [Google Scholar] [CrossRef]
- Lin, J.; Song, J.; Lu, C. Synchrophasor data analytics: Transmission line parameters online estimation for energy management. IEEE Trans. Eng. Manag. 2019, 69, 671–681. [Google Scholar] [CrossRef]
- Dobakhshari, A.S.; Abdolmaleki, M.; Terzija, V.; Azizi, S. Online non-iterative estimation of transmission line and transformer parameters by SCADA data. IEEE Trans. Power Syst. 2020, 36, 2632–2641. [Google Scholar] [CrossRef]
- De Albuquerque, F.P.; Da Costa, E.C.M.; Pereira, R.F.R.; Liboni, L.H.B.; De Oliveira, M.C. Nonlinear analysis on transmission line parameters estimation from noisy phasorial measurements. IEEE Access 2021, 10, 1720–1730. [Google Scholar] [CrossRef]
- Pegoraro, P.A.; Sitzia, C.; Solinas, A.V.; Sulis, S. Transmission line parameters estimation in the presence of realistic PMU measurement error models. Measurement 2023, 218, 113175. [Google Scholar] [CrossRef]
- Sitzia, C.; Muscas, C.; Pegoraro, P.A.; Solinas, A.V.; Sulis, S. Enhanced PMU-based line parameters estimation and compensation of systematic measurement errors in power grids considering multiple operating conditions. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Moghanian, M.; Dobakhshari, A.S. Accurate Kalman filter based estimation of transmission line parameters utilizing synchronized phasor measurements. Electr. Power Syst. Res. 2024, 230, 110218. [Google Scholar] [CrossRef]
- Khalili, R.; Abur, A. Transmission line parameter error identification and estimation in three-phase networks. IEEE Trans. Power Syst. 2021, 37, 2271–2282. [Google Scholar] [CrossRef]
- Ahmed, M.M.; Amjad, M.; Qureshi, M.A.; Imran, K.; Haider, Z.M.; Khan, M.O. A critical review of state-of-the-art optimal pmu placement techniques. Energies 2022, 15, 2125. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, J.; Huang, Z.; Diao, R. Assessing Gaussian assumption of PMU measurement error using field data. IEEE Trans. Power Deliv. 2017, 33, 3233–3236. [Google Scholar] [CrossRef]
- Kundur, P. Power system stability. Power Syst. Stab. Control 2007, 10, 7-1. [Google Scholar]
- Paul, C.R. Analysis of Multiconductor Transmission Lines; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Givaki, K.; Seyedzadeh, S. Machine learning based impedance estimation in power system. In Proceedings of the 8th Renewable Power Generation Conference (RPG 2019), Shanghai, China, 24–25 October 2019. [Google Scholar]
- Qin, C.; Vyakaranam, B.; Etingov, P.; Venetos, M.; Backhaus, S. Machine learning based network parameter estimation using AMI data. In Proceedings of the 2022 IEEE Power & Energy Society General Meeting (PESGM), Denver, CO, USA, 17–21 July 2022; pp. 1–5. [Google Scholar]
- Ramasamy, S.; Ganesan, K.; Arunachalam, V. Power Flow Parameter Estimation in Power System Using Machine Learning Techniques Under Varying Load Conditions. Int. J. Electr. Electron. Res. 2022, 10, 1299–1305. [Google Scholar] [CrossRef]
- Grafarend, E.W. Linear and Nonlinear Models: Fixed Effects, Random Effects, and Mixed Models; de Gruyter: Berlin, Germany, 2006. [Google Scholar]
- Yang, N.C.; Sen, A. Parameter estimation in unbalanced three-phase distribution lines using general regression neural networks with inconsistent data handling capacity. Appl. Soft Comput. 2023, 133, 109936. [Google Scholar] [CrossRef]
- Sun, L.; Chen, T.; Chen, X.; Ho, W.K.; Ling, K.V.; Tseng, K.J.; Amaratunga, G.A. Optimum placement of phasor measurement units in power systems. IEEE Trans. Instrum. Meas. 2018, 68, 421–429. [Google Scholar] [CrossRef]
- Monti, A.; Muscas, C.; Ponci, F. Phasor Measurement Units and Wide Area Monitoring Systems; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Johnson, T.; Moger, T. A critical review of methods for optimal placement of phasor measurement units. Int. Trans. Electr. Energy Syst. 2021, 31, e12698. [Google Scholar] [CrossRef]
- Borchani, H.; Varando, G.; Bielza, C.; Larranaga, P. A survey on multi-output regression. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2015, 5, 216–233. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Costa, L.F.; Giraldo, J.S.; Castro, C.A. Identification and correction of transmission line parameter errors using SCADA and synchrophasor measurements. Int. J. Electr. Power Energy Syst. 2022, 135, 107509. [Google Scholar] [CrossRef]
- Kumar, S.; Tyagi, B.; Kumar, V.; Chohan, S. PMU-based voltage stability measurement under contingency using ANN. IEEE Trans. Instrum. Meas. 2021, 71, 1–11. [Google Scholar] [CrossRef]
- Gao, H.; Wang, L.; Yang, D.; Cai, G.; Liu, C.; Yang, H.; Sun, Z.; Wang, B. Mechanism Enhanced Data-Driven Method for Reliability Improvement of Load Margin Estimation. IEEE Trans. Power Syst. 2023, 39, 3715–3724. [Google Scholar] [CrossRef]
- Zhou, D.Q.; Annakkage, U.D.; Rajapakse, A.D. Online monitoring of voltage stability margin using an artificial neural network. IEEE Trans. Power Syst. 2010, 25, 1566–1574. [Google Scholar] [CrossRef]
- Ghaedi, A.; Golshan, M.E.H.; Sanaye-Pasand, M. Transmission line fault location based on three-phase state estimation framework considering measurement chain error model. Electr. Power Syst. Res. 2020, 178, 106048. [Google Scholar] [CrossRef]
- Asprou, M.; Kyriakides, E. Identification and estimation of erroneous transmission line parameters using PMU measurements. IEEE Trans. Power Deliv. 2017, 32, 2510–2519. [Google Scholar] [CrossRef]
- Sahoo, B.; Samantaray, S.R.; Kamwa, I. Supervising Vulnerable Third Zone Distance Relay to Enhance Wide-Area Back-Up Protection Systems. IEEE Access 2022, 10, 49862–49872. [Google Scholar] [CrossRef]
- Pereira, R.F.R.; de Albuquerque, F.P.; Liboni, L.H.B.; Costa, E.C.M.; de Oliveira, M.C. Impedance Parameters Estimation of Transmission Lines by an Extended Kalman Filter-Based Algorithm. IEEE Trans. Instrum. Meas. 2022, 71, 1–10. [Google Scholar] [CrossRef]
- Asprou, M.; Kyriakides, E. Estimation of transmission line parameters using PMU measurements. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Brown, M.; Biswal, M.; Brahma, S.; Ranade, S.J.; Cao, H. Characterizing and quantifying noise in PMU data. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Castello, P.; Muscas, C.; Pegoraro, P.A. Statistical behavior of PMU measurement errors: An experimental characterization. IEEE Open J. Instrum. Meas. 2022, 1, 1–9. [Google Scholar] [CrossRef]
- Frigo, G.; Derviškadić, A.; Bach, A.; Paolone, M. Statistical model of measurement noise in real-world PMU-based acquisitions. In Proceedings of the 2019 International Conference on Smart Grid Synchronized Measurements and Analytics (SGSMA), College Station, TX, USA, 21–23 May 2019; pp. 1–8. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).