Investigation of the Optimal Operation Method of the Heat Recovery Ground Source Heat Pump System Installed in an Actual Building and Evaluation of Energy Saving Effect
Abstract
1. Introduction
2. Outlines of Subject Building and Heat Recovery Ground Source Heat Pump
2.1. Outlines of Subject Building
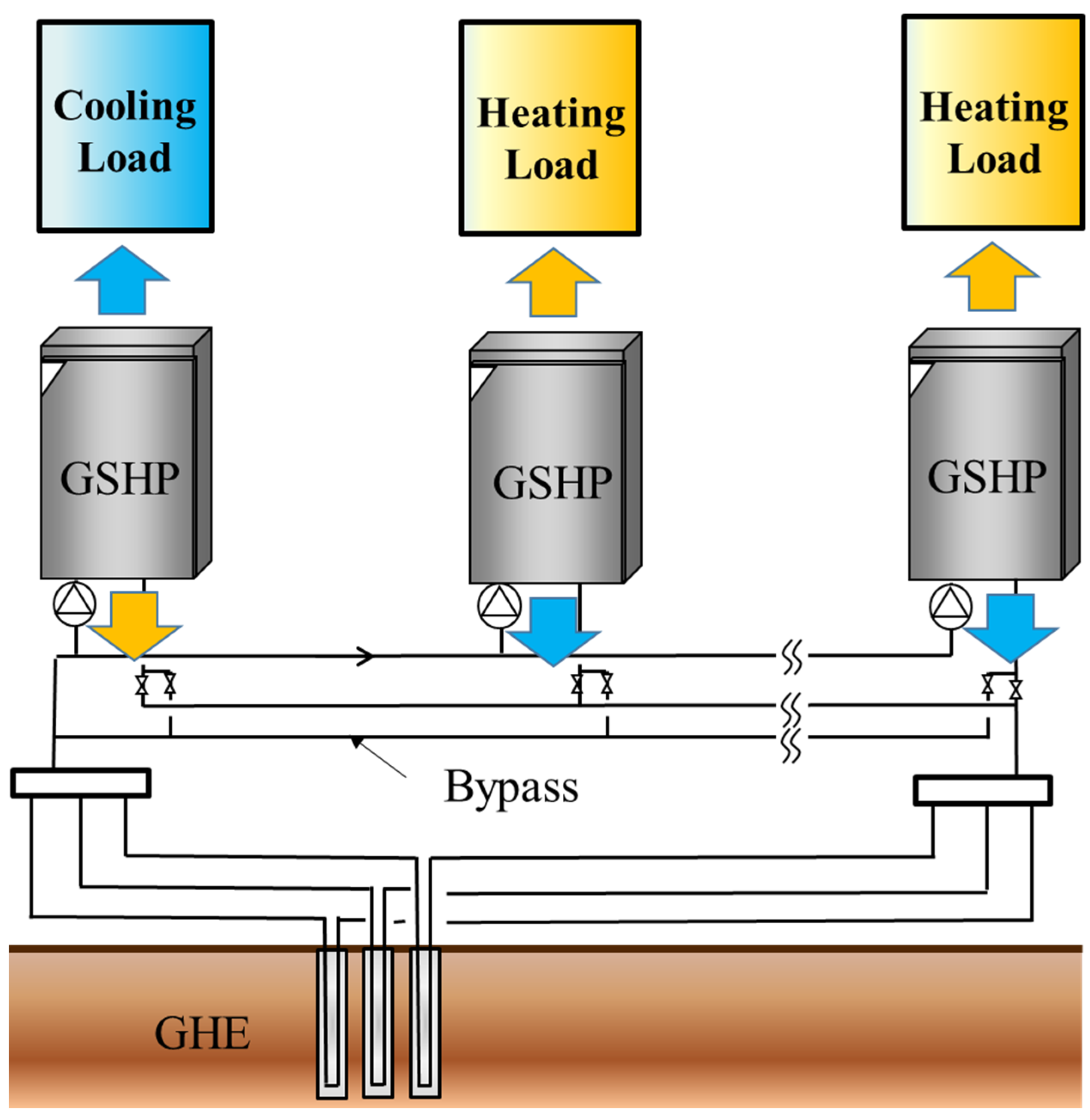
2.2. Outlines of Heat Recovery Ground Source Heat Pump
3. Method
3.1. Measurement
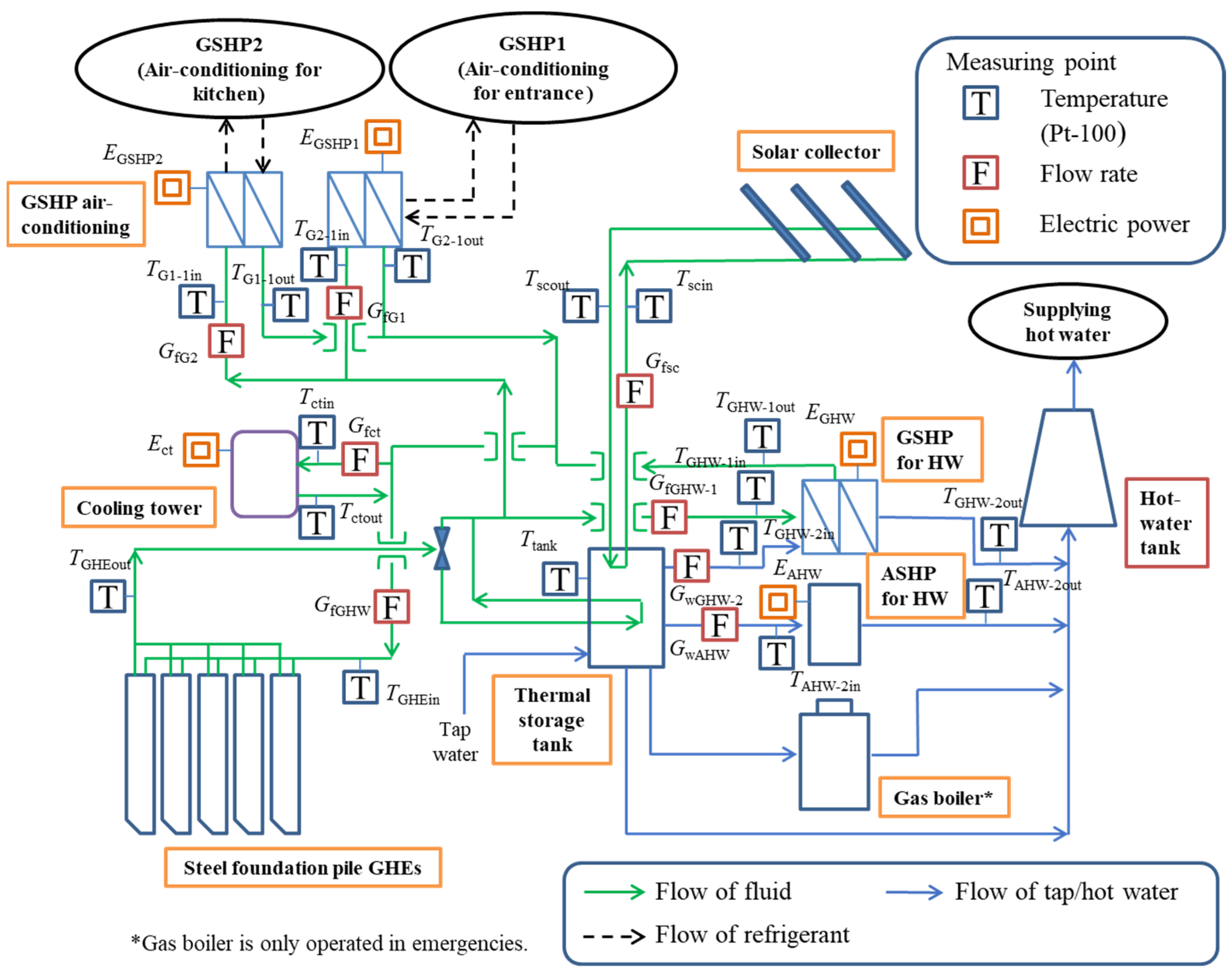
| Point (Indicated in Figure 4) | Measuring Items | Equipment | Unit |
|---|---|---|---|
| TG1-1in, TG1-1out | Inlet and outlet fluid temperature in the primary side of GSHP1 | Pt-100 | °C |
| TG2-1in, TG2-1out | Inlet and outlet fluid temperature in the primary side of GSHP2 | ||
| TGHW-1in, TGHW-1out | Inlet and outlet fluid temperature in the primary side of a GSHP for HW | ||
| TGHEin, TGHEout | Inlet and outlet fluid temperature of GHE | ||
| Tctin, Tctout | Inlet and outlet fluid temperature of cooling tower | ||
| Tscin, Tscout | Inlet and outlet fluid temperature of solar collector | ||
| Ttank | Water temperature in thermal storage tank | ||
| TGHW-2in, TGHW-2out | Inlet and outlet water temperature in the secondary side of a GSHP for HW | ||
| TAHWin, TAHWout | Inlet and outlet water temperature in the secondary side of an ASHP for HW | ||
| GfG1 | Flow rate of fluid in the primary side of GSHP1 | Electromagnetic flow meter | L/min |
| GfG2 | Flow rate of fluid in the primary side of GSHP2 | ||
| GfGHW-1 | Flow rate of fluid in the primary side of a GSHP for HW | ||
| GfGHE | Flow rate of fluid in GHEs | ||
| Gfct | Flow rate of fluid in cooling tower | ||
| Gfsc | Flow rate of fluid in solar collector | ||
| GwGHW-2 | Flow rate of water in the secondary side of a GSHP for HW | ||
| GwAHW | Flow rate of water in the secondary side of an ASHP for HW | ||
| EGSHP1 | Electric energy of GSHP1 | Power meter | W |
| EGSHP2 | Electric energy of GSHP2 | ||
| EGHW | Electric energy of a GSHP for HW | ||
| Ect | Electric energy of cooling tower |
| Parameters | Evaluated Items | Equation | Unit |
|---|---|---|---|
| QGSHP1-1 | Heat extraction/injection rate of GSHP1 | W | |
| QGSHP2-1 | Heat extraction/injection rate GSHP2 | ||
| QGSHP1-2 | Heating/Cooling output from GSHP1 | ||
| QGSHP2-2 | Heating/Cooling output from GSHP2 | ||
| QGSHP2 | Heating/Cooling output from GSHP (GSHP1 and GSHP2) | ||
| QGHW1 | Heat extraction/injection rate of a GSHP for HW | ||
| QGHW2 | Heating output from a GSHP for HW | ||
| QAHW | Heating output from an ASHP for HW | ||
| QGHE | Heating extraction/injection rate of ground heat exchangers | ||
| Qsc | Heating output from solar collector | ||
| Qct | Heating (cooling) output from cooling tower |
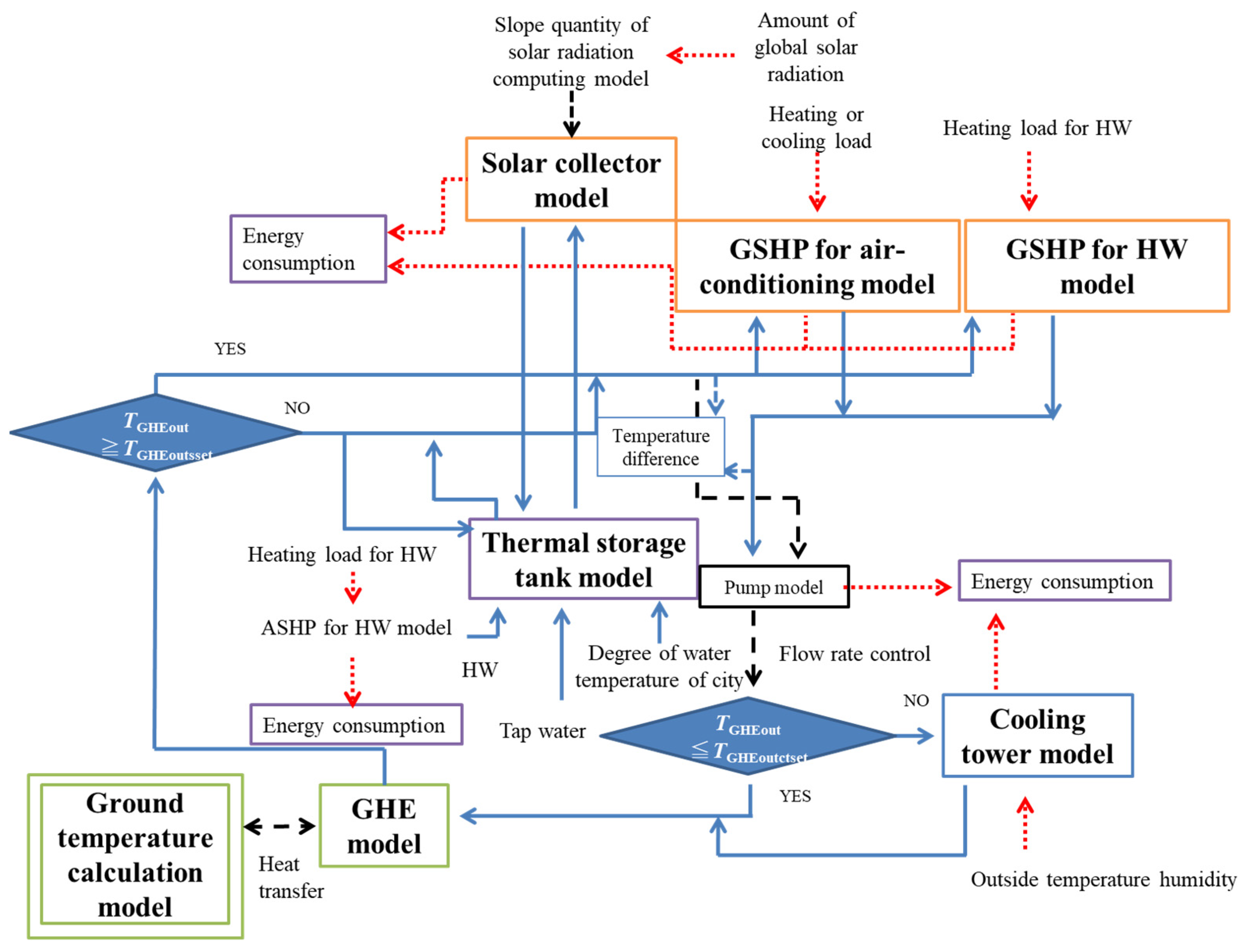
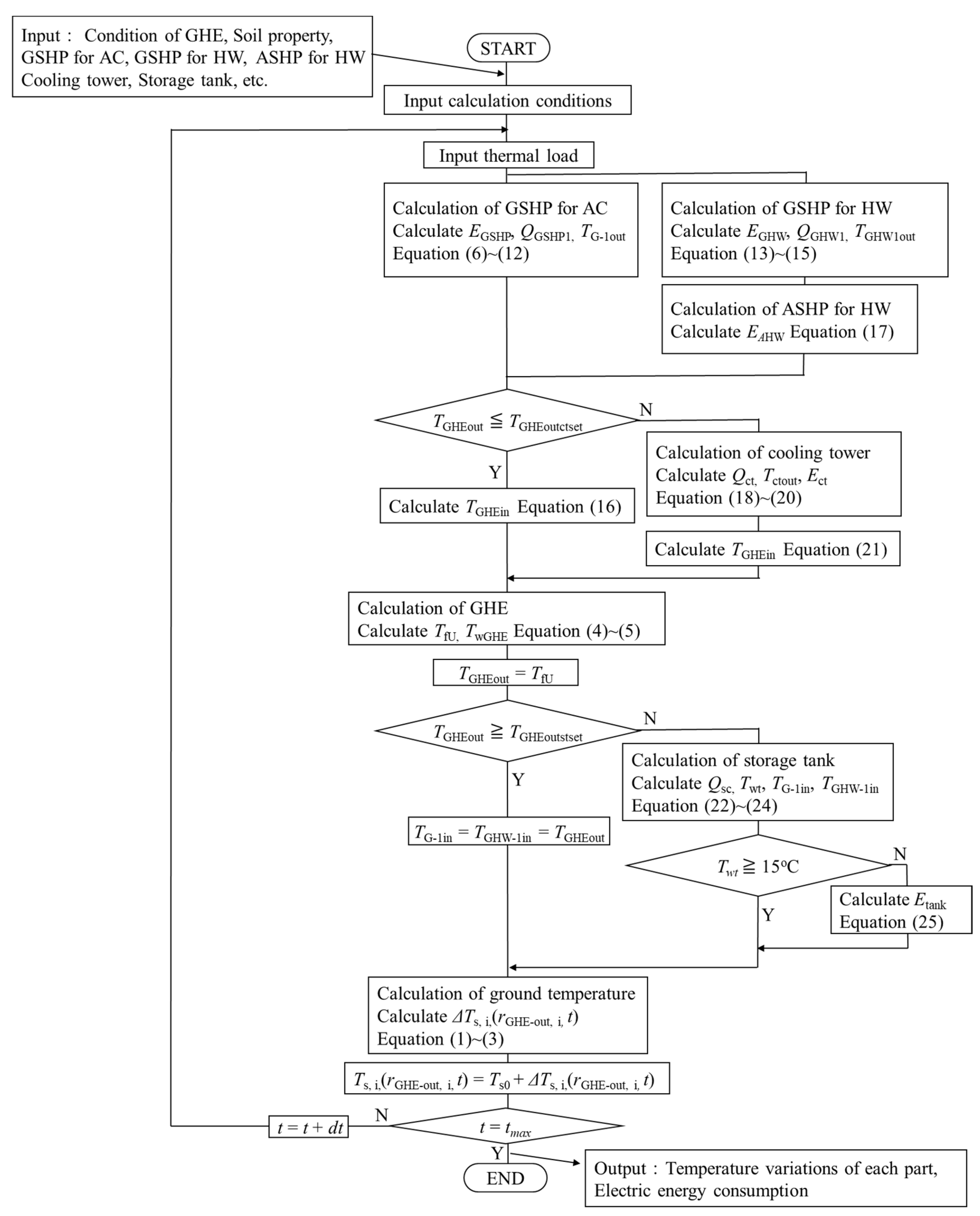
3.2. Establishment of Simulation Model
- (1)
- Ground temperature calculation model and GHE model
- (2)
- GSHP model and ASHP model
- (3)
- Cooling tower model
- (4)
- Solar collector and thermal storage tank model
3.3. Operation and Performance Evaluation of the HR-GSHP System
4. Results
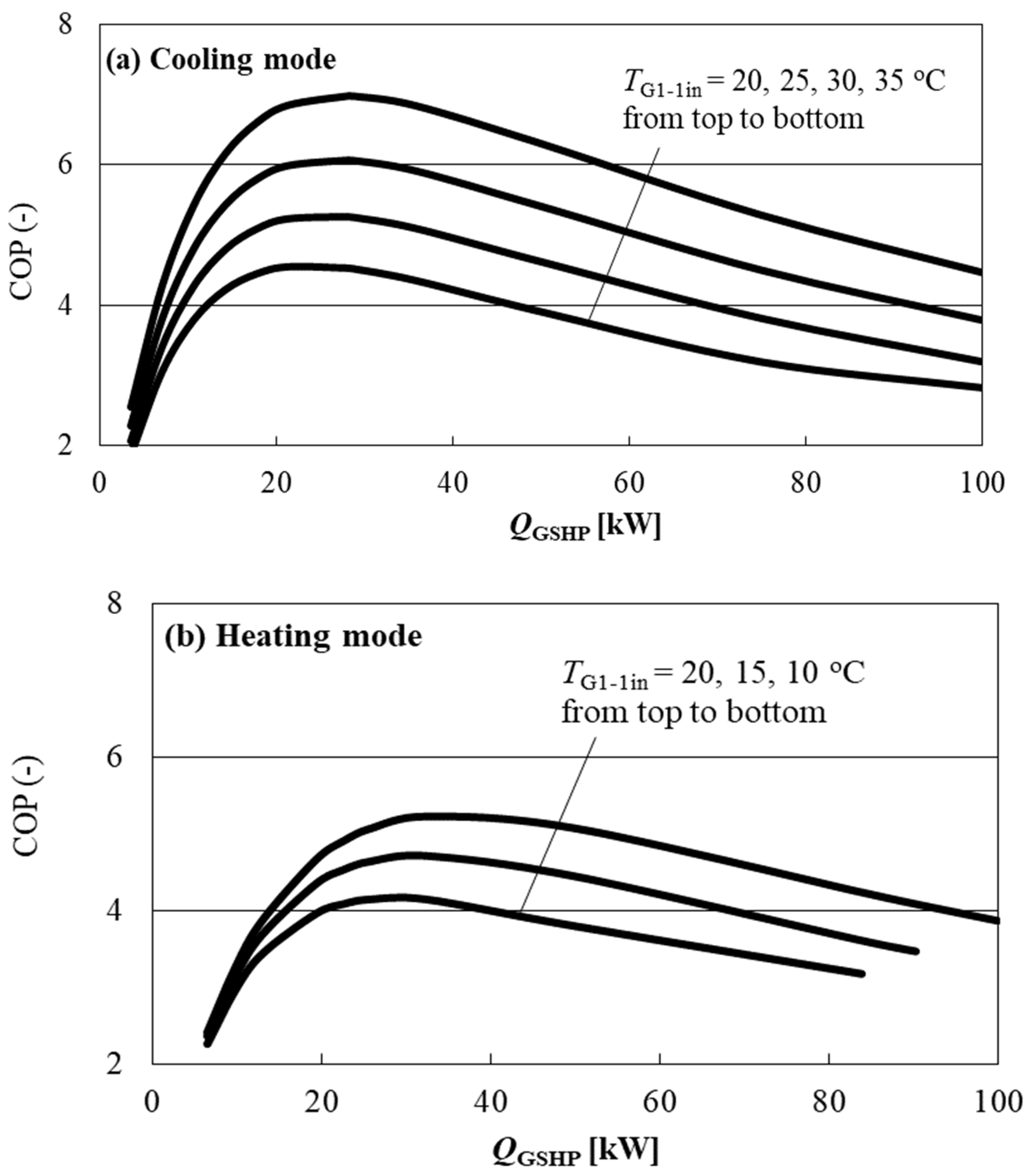
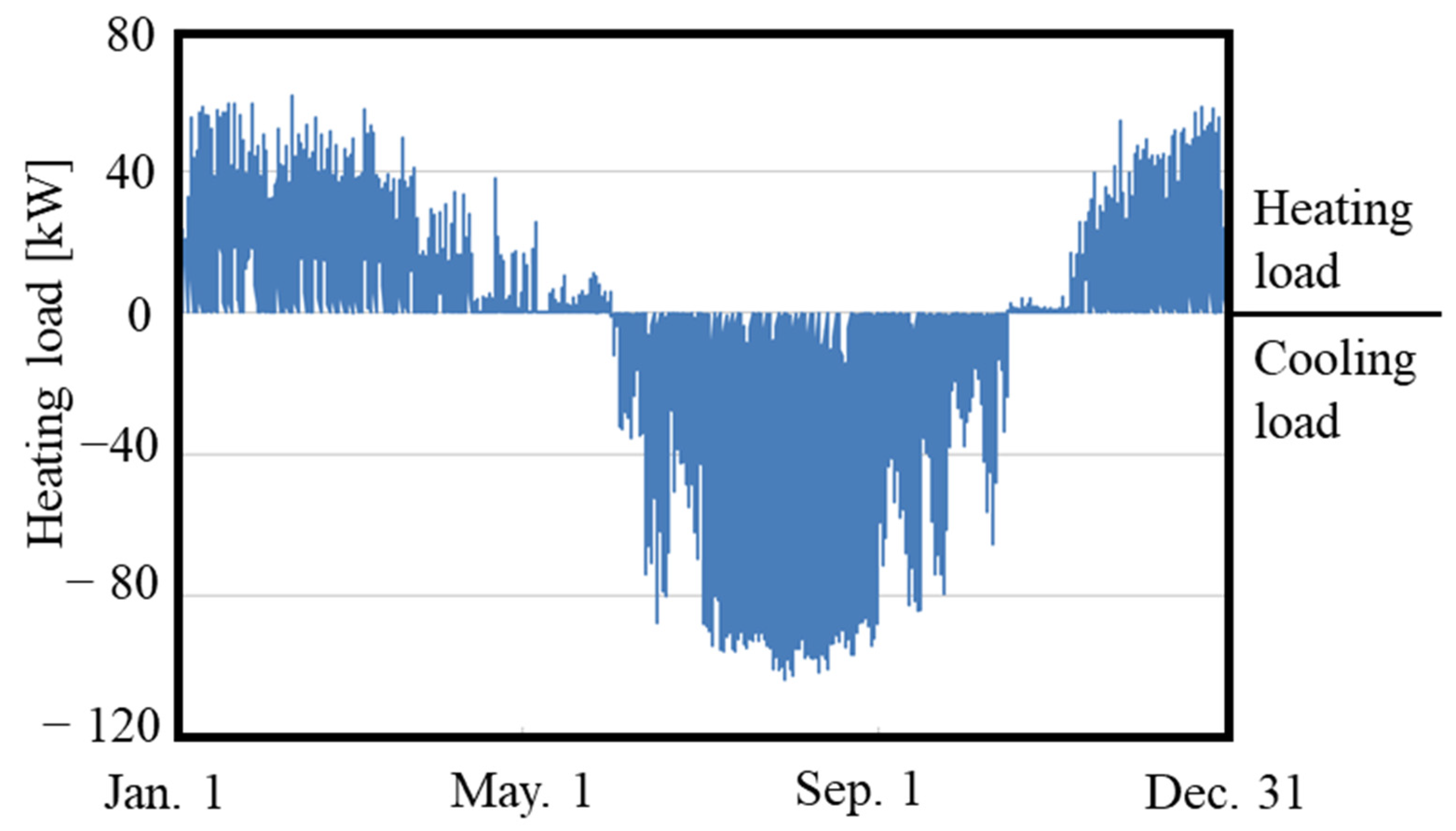
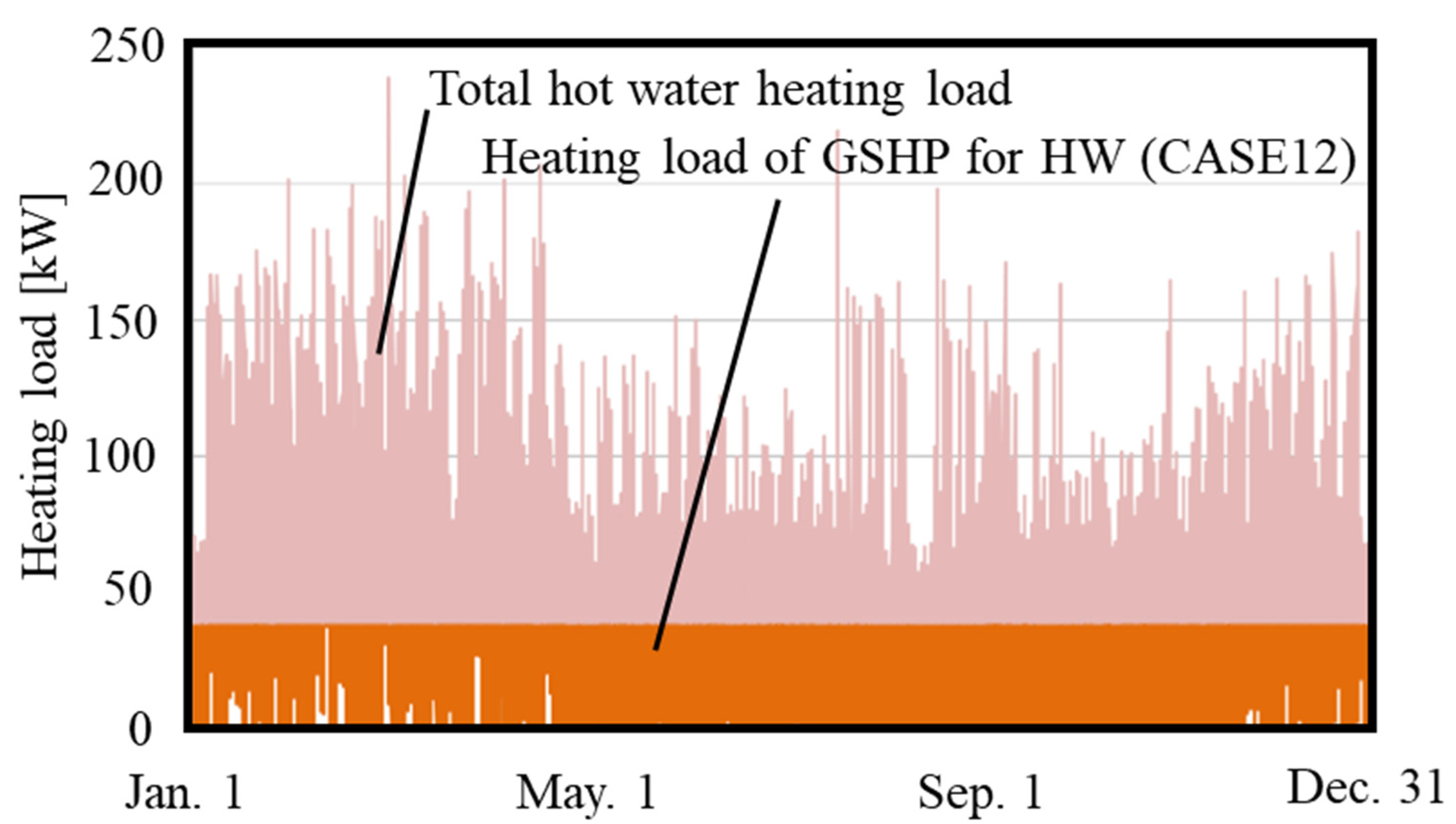
4.1. Investigation of Optimal Operation Method by Simulation Model
4.2. Performance Evaluation of the HR-GSHP System for Each Year
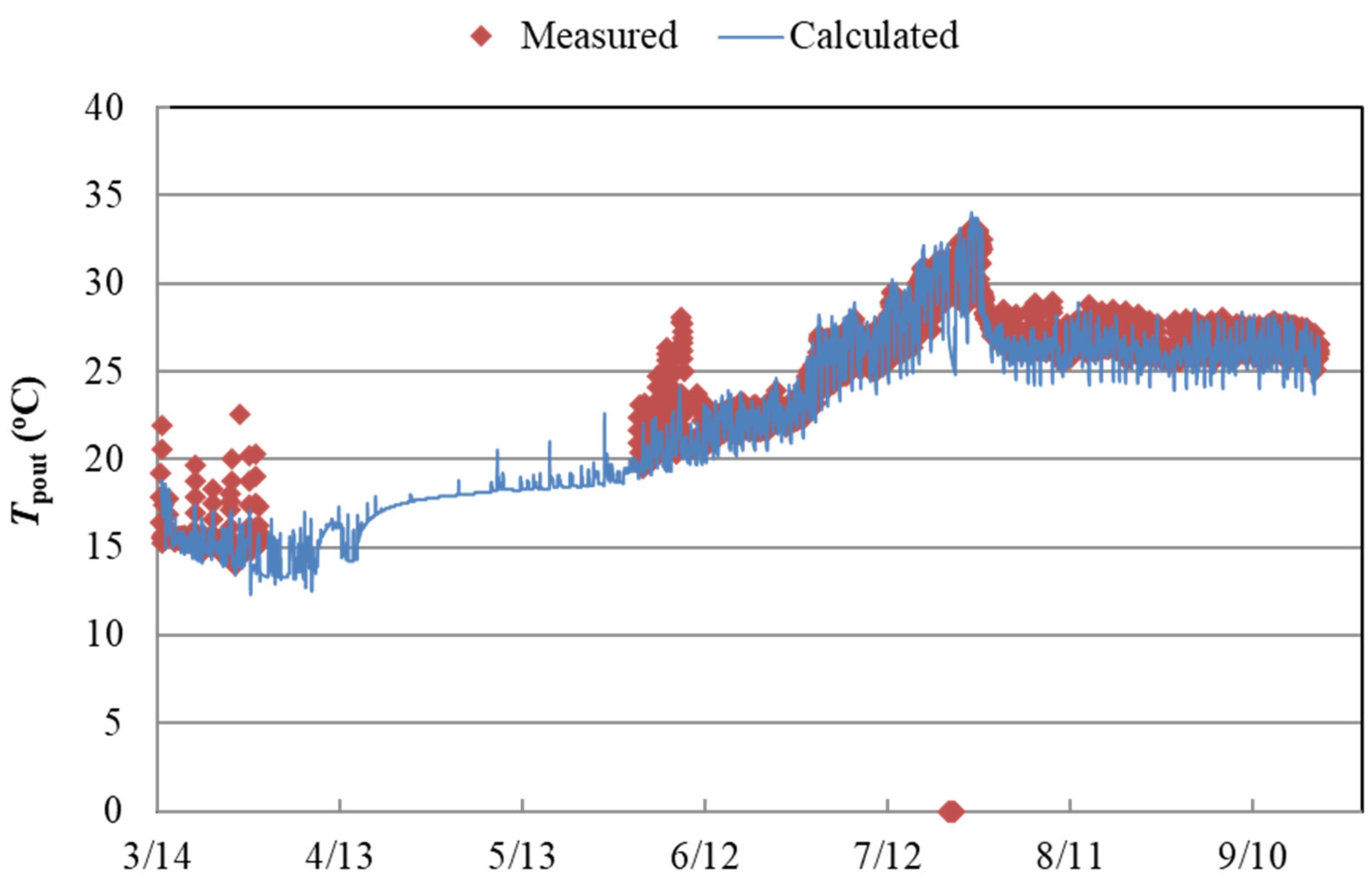
- (1)
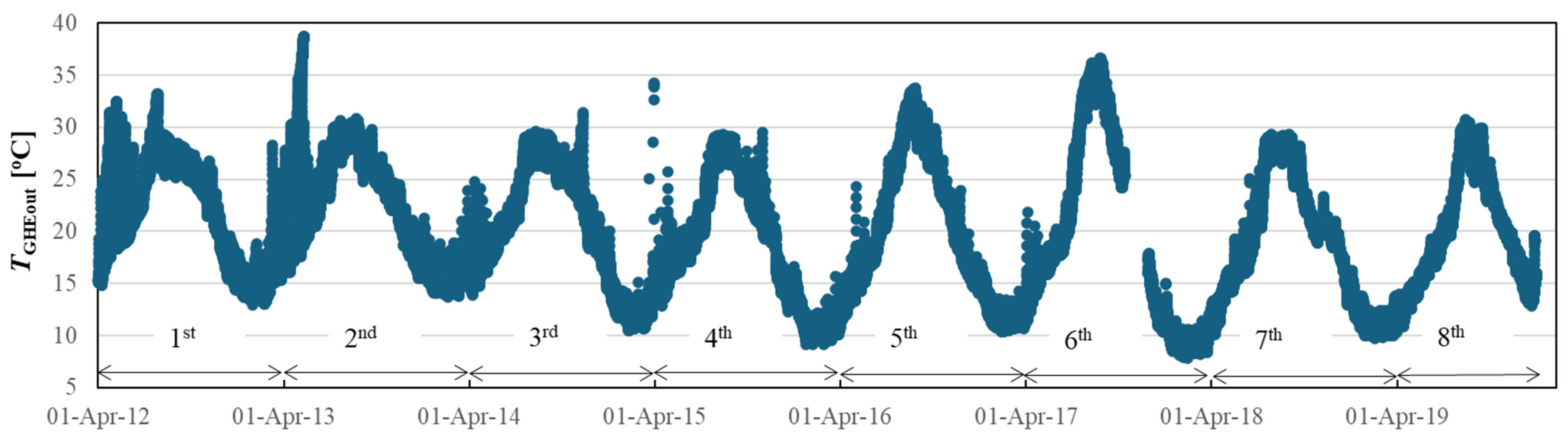
- Piping loop heat carrier fluid temperature.
- (2)
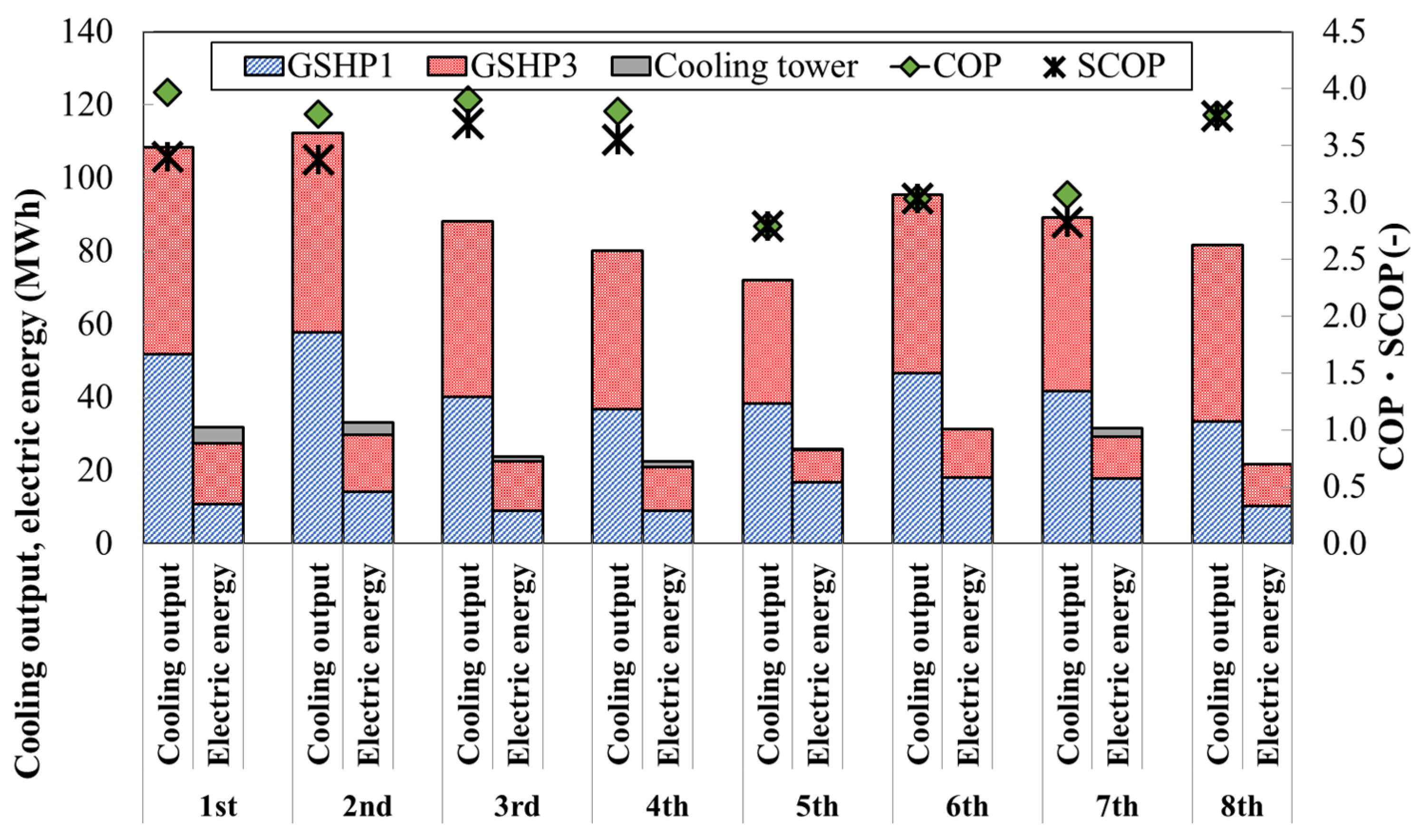
- GSHP for AC performance during the cooling period.
- (3)
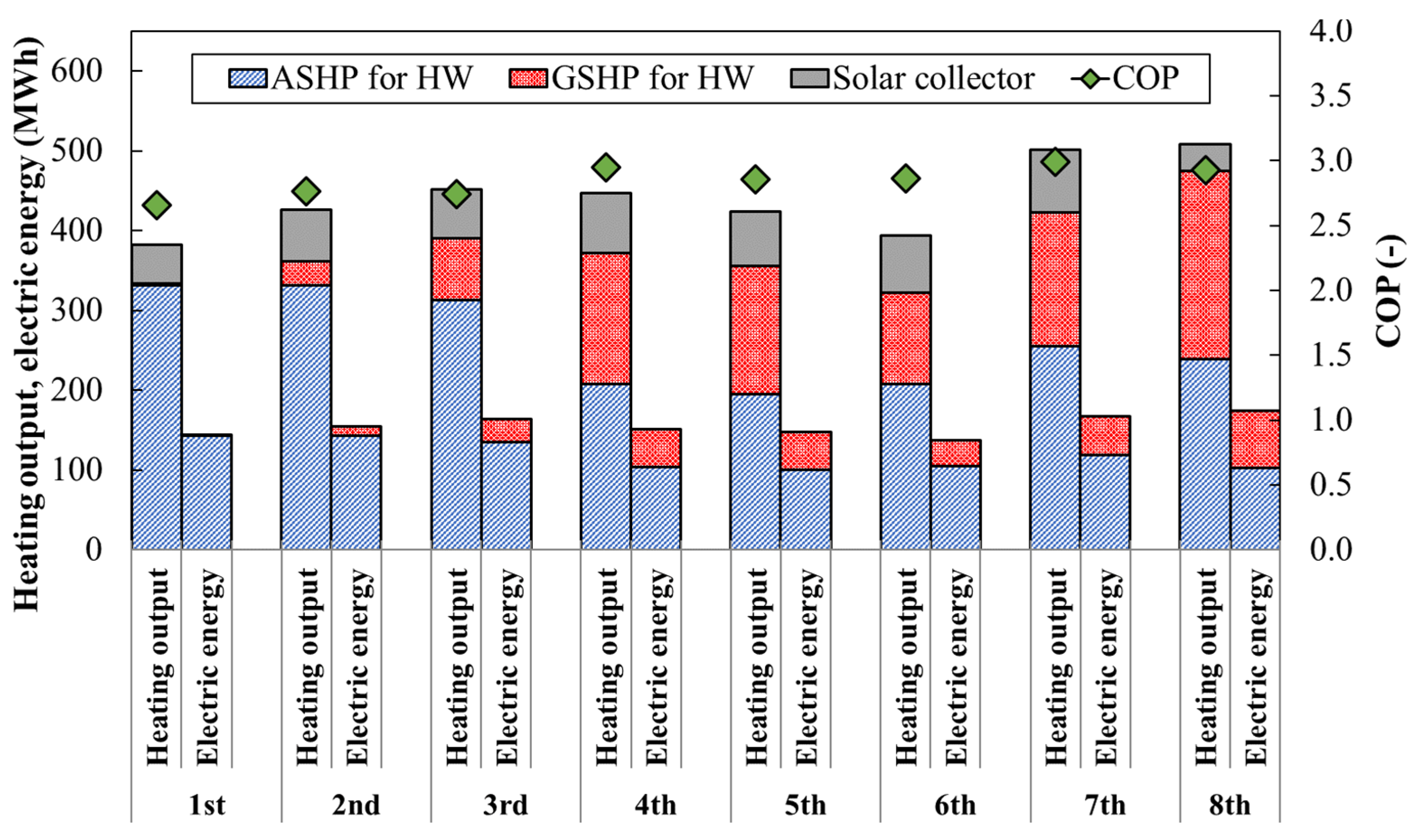
- Hot water system performance.
- (4)
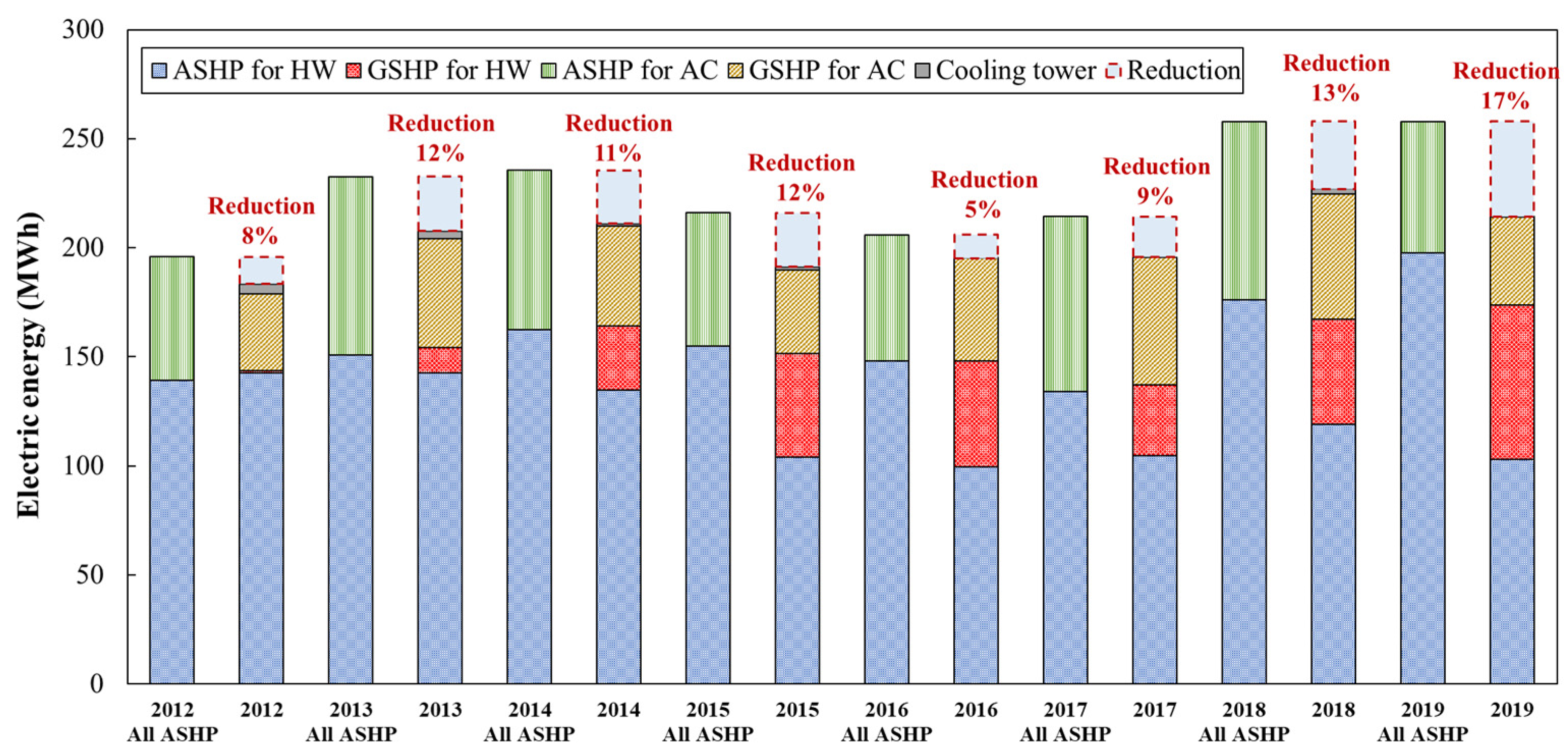
- Overall system energy consumption.
- (1)
- Piping loop heat carrier fluid temperature.
- (2)
- GSHP for AC performance during the cooling period
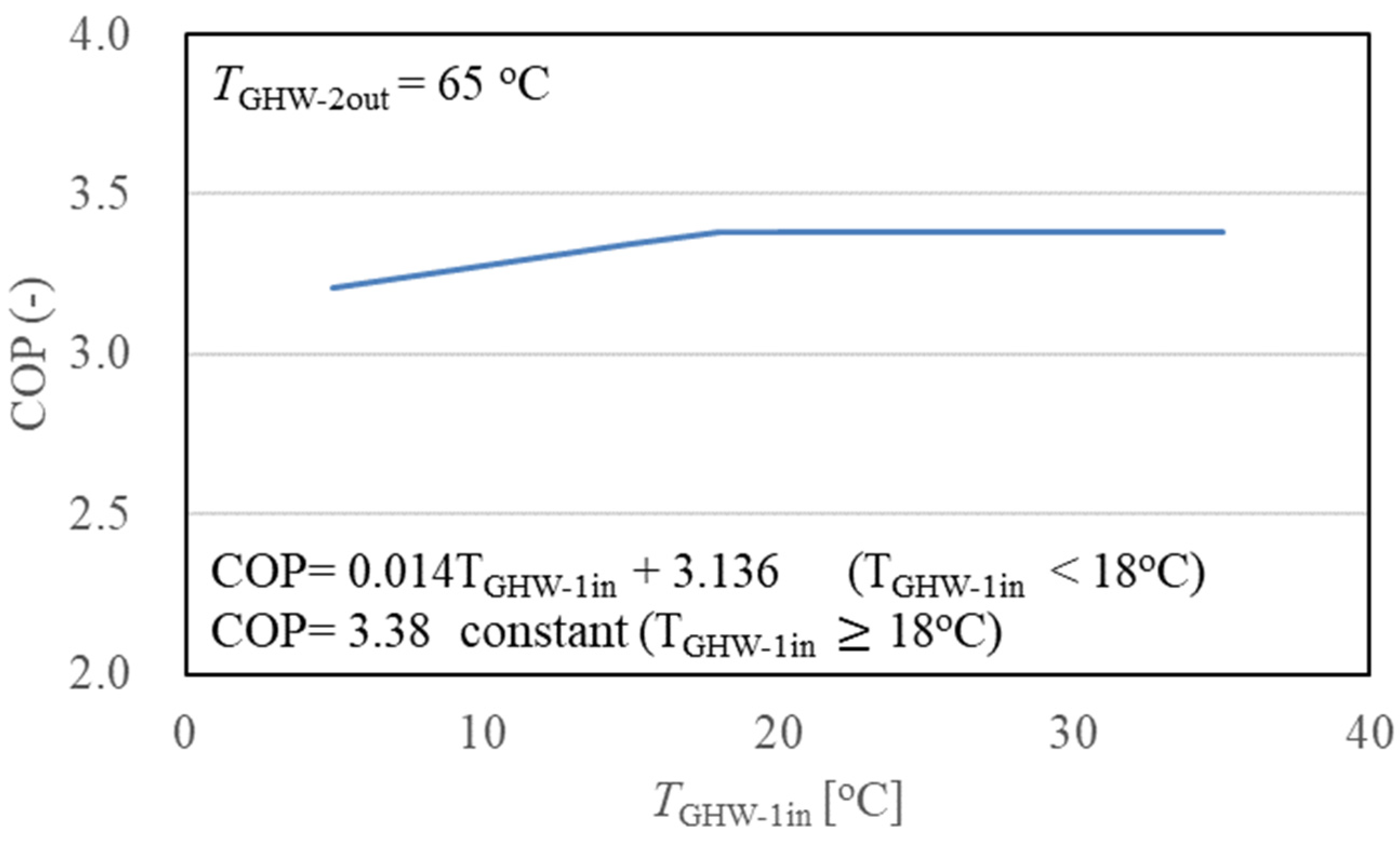
- (3)
- Hot water system performance
- (4)
- Overall system energy consumption
5. Discussion
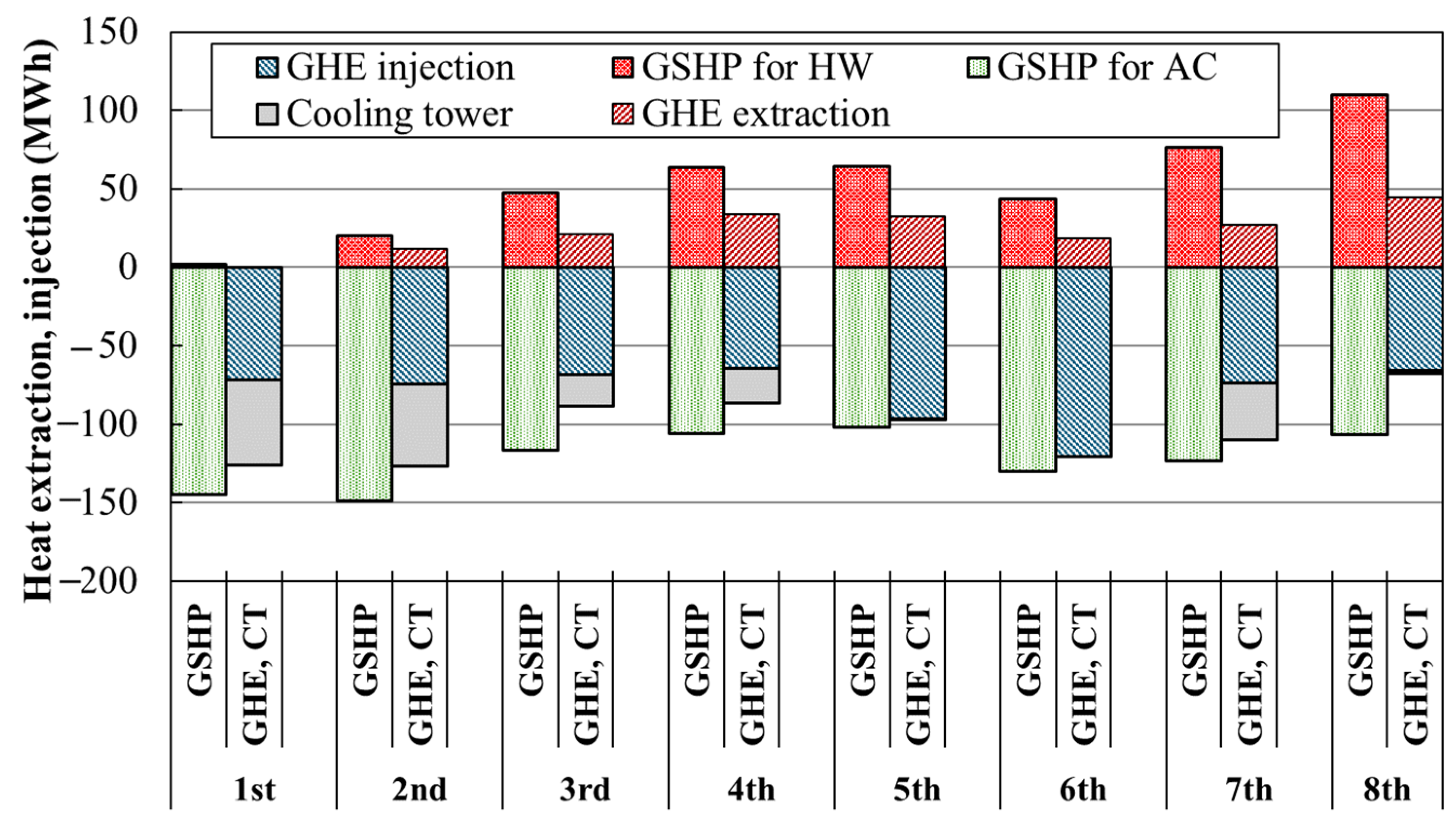
5.1. Heat Recovery Effect in the HR-GSHP System
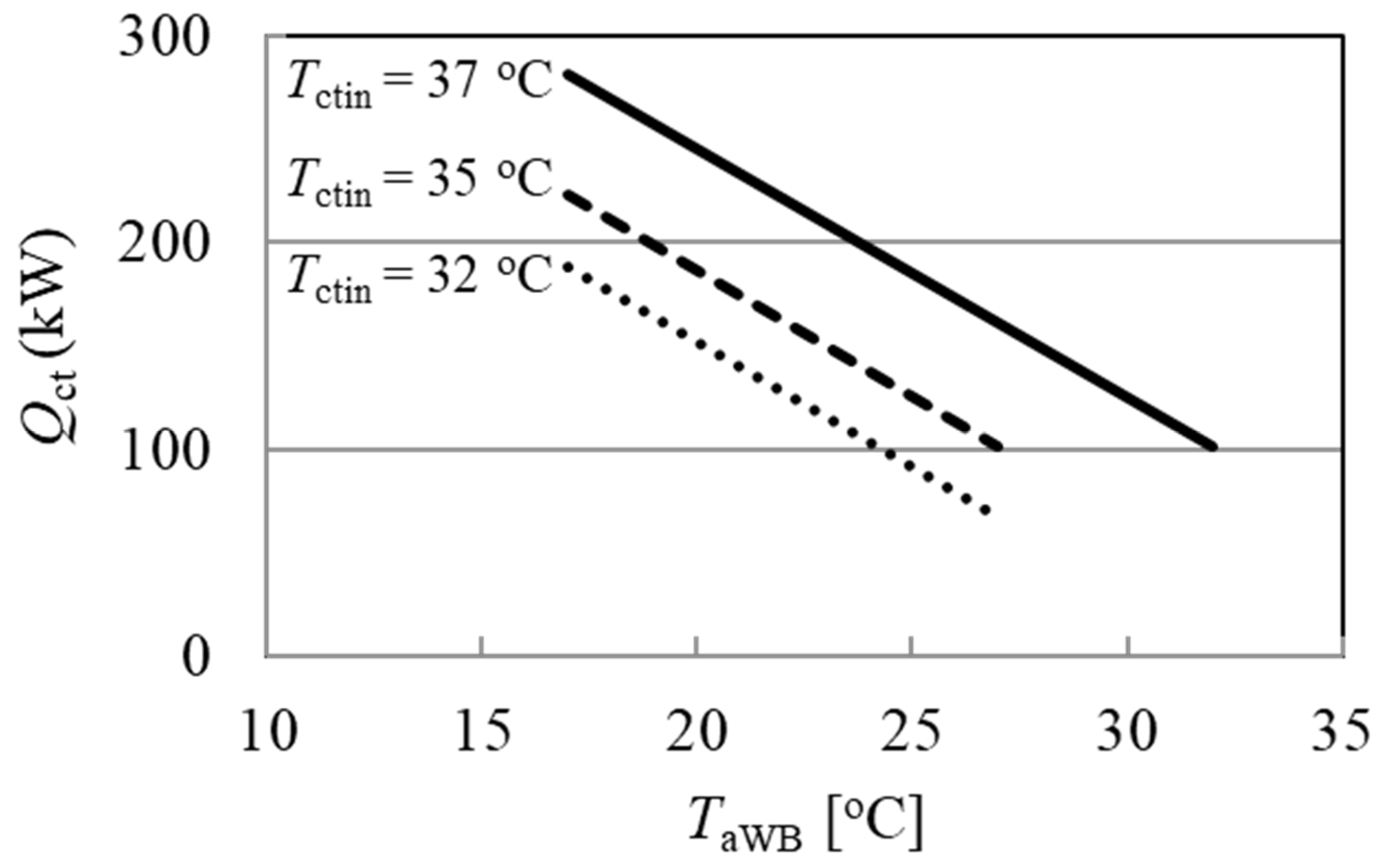
- (1)
- Heat recovery-related equipment (GSHP, GHE, and cooling tower) during the cooling period (April to November).
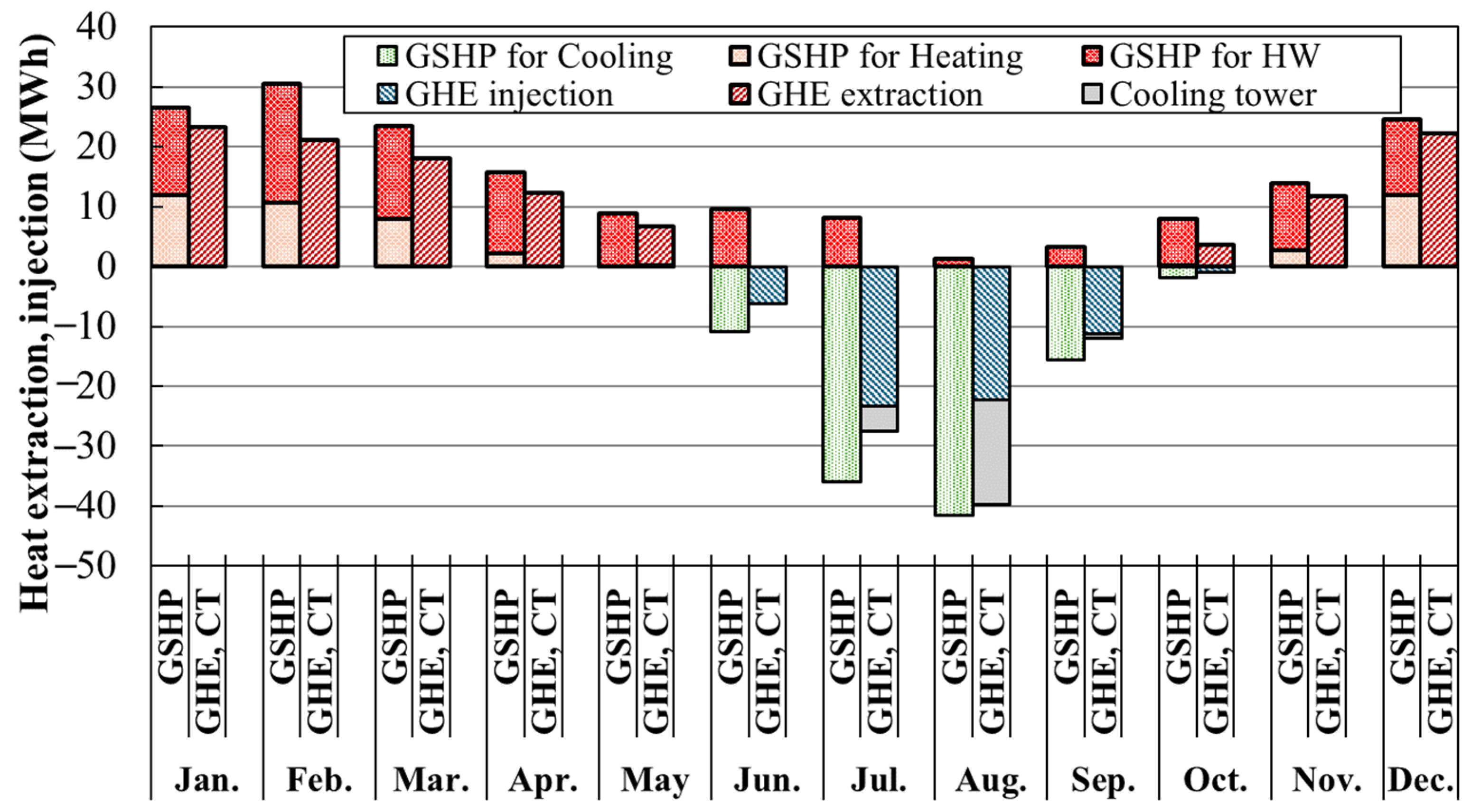
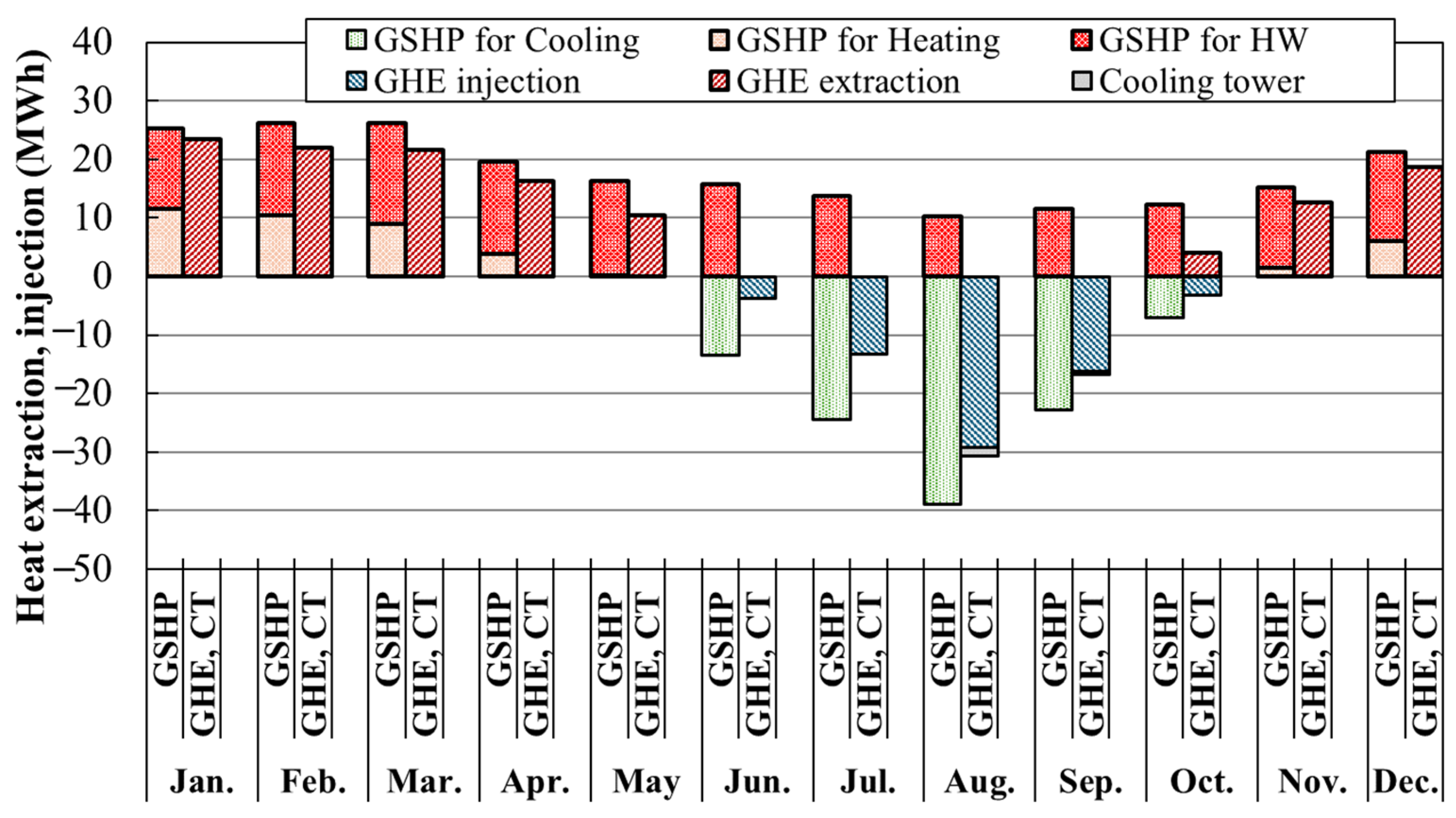
- (2)
- Monthly variation of heat extraction/injection rate
5.2. Shortcoming of the Study
6. Conclusions
- The operating period of the GSHP for hot water supply was changed, and the optimal operation method of the HR-GSHP system that minimizes the energy consumption of the system was studied using simulation. As a result, the operation period of the GSHP for HW that minimizes the energy consumption of the system is 8 months from April to November.
- Based on the operation results of the HR-GSHP system up to the second year, the temperature drop in the piping loop was 12~14 °C, which was smaller than the simulation. Therefore, the GSHP for HW was operated year-round after the third year. The minimum temperature of heat carrier fluid was about 10 °C and the maximum temperature was about 30 °C, except for the fifth and sixth years when the cooling tower failed, confirming that the system was being operated properly.
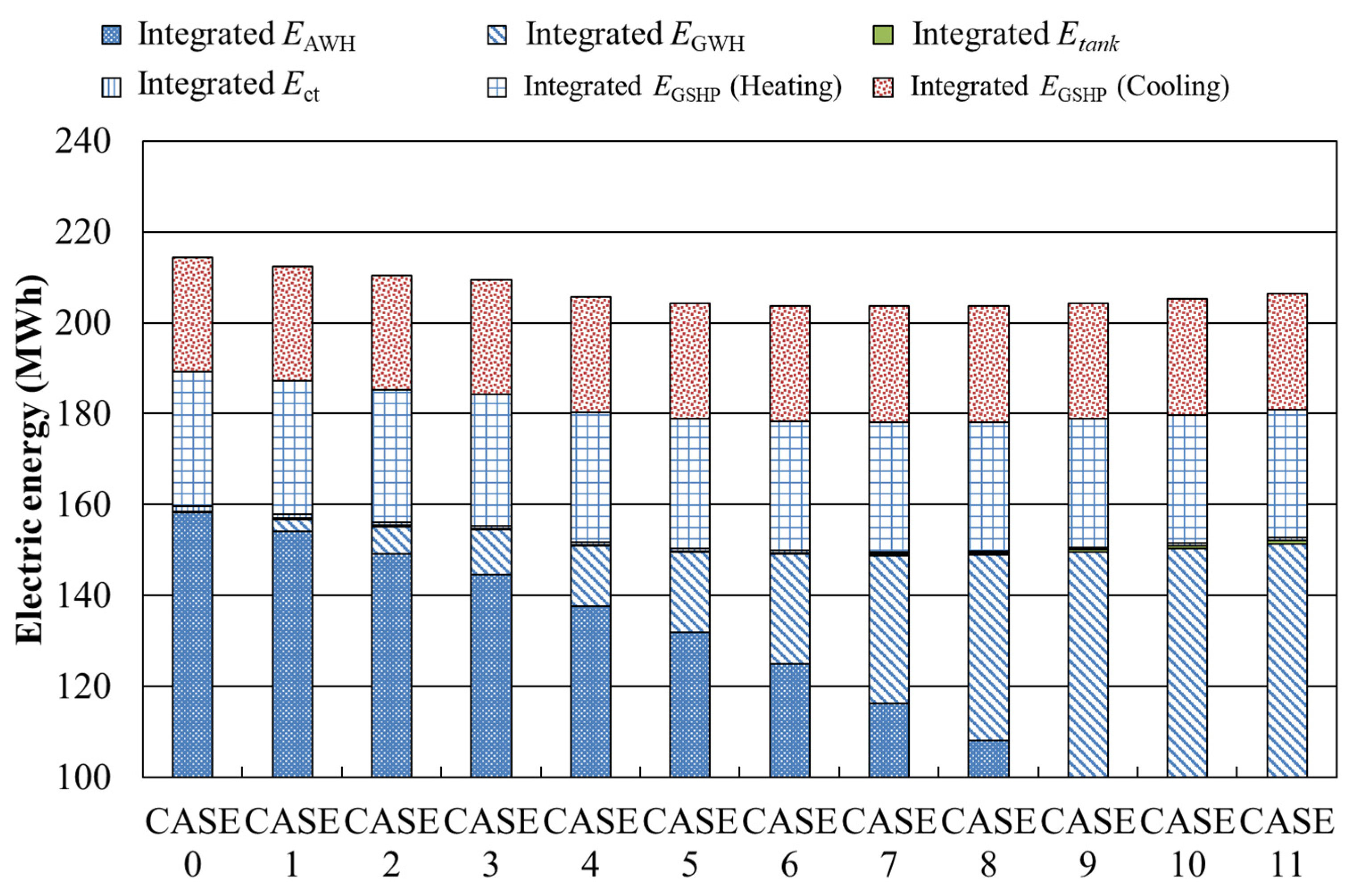
- Verification of the system performance based on the actual measurement results of the HR-GSHP system for 8 years showed that the SCOP for cooling in the eighth year of operation was the highest, and the COP for hot water supply was also the second highest. The reasons for this are that the GSHP for HW operated more in the summer in the eighth year, which reduced the operation of the cooling tower due to the heat extraction of the GSHP for HW, and that the GSHP for HW had a higher COP than the ASHP for HW. The reduction in power consumption compared to the case where air conditioning and hot water supply were operated only with the ASHP was also the largest in the eighth year, with a reduction of approximately 17%.
- Analysis of the amount of heat taken from the GSHP, the GHE, and the cooling tower during the cooling period in each year showed that the amount of heat taken from the GSHP for HW increased in the eighth year compared to the other years, thereby reducing the amount of heat released from the GHE and cooling tower relative to the amount of heat released by the GSHP for AC. In addition, it was also confirmed that the amount of heat extracted from the GSHP for HW increased from June to September, especially in the eighth year, and that when operating the HR-GSHP system, the ideal operation is to generate heat extraction and heat dissipation simultaneously, as much as possible, to suppress changes in the heat source water temperature and increase the system operation efficiency. The actual operation results confirm this.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | |
| A | area, m2 |
| a | thermal diffusivity, m2/s |
| c | specific heat capacity, J/(kg∙K) |
| cp | specific heat capacity at constant pressure, J/(kg∙K) |
| E | electric power consumption, W |
| EIR | energy input ratio, ND |
| G | flow rate, m3/s |
| g | gravitational acceleration, m/s2 |
| h | convective heat transfer coefficient, W/(m2∙K) |
| J | solar radiation, W/m2 |
| K | overall heat transfer coefficient, W/(m2 K) |
| l | length, m |
| n | model number of cooling tower, ND |
| PF | modifier for operation performance under part-load condition, ND |
| Q | heating/cooling output, heat extraction/injection, W |
| q | heat flux, W/m2 |
| r | radius, distance, m |
| T | temperature, °C |
| V | volume, m3 |
| v | velocity, m/s |
| η | efficiency of solar collector, ND |
| β | volume expansion coefficient, 1/K |
| ρ | density, kg/m3 |
| ν | kinematic viscosity, m2/s |
| Subscripts | |
| −1 | primary side |
| −2 | secondary side |
| a | ambient air |
| ai | indoor air |
| AHW | GSHP for HW |
| c | cooling |
| ct | cooling tower |
| d | distance (interval) |
| DB | dry bulb |
| f | circulating fluid |
| G, GSHP | GSHP |
| G1, GSHP1 | GSHP1 |
| G2, GSHP2 | GSHP2 |
| GHE | ground heat exchanger |
| GHW | GSHP for HW |
| h | heating |
| hw | hot water |
| in | inlet |
| out | outlet |
| -out | outside |
| p | pile |
| s | soil |
| s0 | undisturbed soil |
| sc | solar collector |
| sl | slope |
| system | system |
| t, tank | tank |
| tw | tap water |
| U | U-tube |
| w | water |
| wt | water tank |
| WB | wet bulb |
| Abbreviations | |
| COP | coefficient of performance |
| GHE | ground heat exchanger |
| GSHP | ground source heat pump |
| HR-GSHP | heat recovery ground source heat pump |
| HW | hot water |
| SCOP | system coefficient of performance |
| ICS | infinite cylindrical source |
| ILS | infinite line source |
Appendix A
Calculation of Overall Heat Transfer Coefficients and
References
- Luo, J.; Rohn, J.; Bayer, M.; Priess, A.; Wilkmann, L.; Xiang, W. Heating and cooling performance analysis of a ground source heat pump system in Southern Germany. Geothermics 2015, 53, 57–66. [Google Scholar] [CrossRef]
- Naicker, S.S.; Rees, S.J. Performance Analysis of a Large Geothermal Heating and Cooling System. Renew. Energy 2018, 122, 429–442. [Google Scholar] [CrossRef]
- Naicker, S.S.; Rees, S.J. Long-term high frequency monitoring of a large borehole heat exchanger array. Renew. Energy 2020, 145, 1528–1542. [Google Scholar] [CrossRef]
- Spitler, J.D.; Gehlin, S. Measured performance of a mixed-use commercial-building ground source heat pump system in Sweden. Energies 2019, 12, 2020. [Google Scholar] [CrossRef]
- Kindaichi, S.; Nishina, D. Simple index for onsite operation management of ground source heat pump systems in cooling-dominant regions. Renew. Energy 2018, 127, 182–194. [Google Scholar] [CrossRef]
- Todorov, O.; Alanne, K.; Virtanen, M.; Kosonen, R. A Novel Data Management Methodology and Case Study for Monitoring and Performance Analysis of Large-Scale Ground Source Heat Pump (GSHP) and Borehole Thermal Energy Storage (BTES) System. Energies 2021, 14, 1523. [Google Scholar] [CrossRef]
- Bockelmann, F.; Norbert Fisch, M. It Works—Long-Term Performance Measurement and Optimization of Six Ground Source Heat Pump Systems in Germany. Energies 2019, 12, 4691. [Google Scholar] [CrossRef]
- Hu, R.; Li, X.; Liang, J.; Wang, H.; Liu, G. Field study on cooling performance of a heat recovery ground source heat pump system coupled with thermally activated building systems (TABSs). Energy Convers. Manag. 2022, 262, 115678. [Google Scholar] [CrossRef]
- Kaneko, C.; Yoshinaga, M. Long-term operation analysis of a ground source heat pump with an air source heat pump as an auxiliary heat source in a warm region. Energy Build. 2023, 289, 113050. [Google Scholar] [CrossRef]
- Fan, R.; Gao, Y.; Huai, L.; Deng, X.; Shi, J. Thermal performance and operation strategy optimization for a practical hybrid ground-source heat-pump system. Energy Build. 2014, 78, 238–247. [Google Scholar] [CrossRef]
- Luo, J.; Zhao, H.; Jia, J.; Xiang, W.; Rohn, J.; Blum, P. Study on operation management of borehole heat exchangers for a large-scale hybrid ground source heat pump system in China. Energy 2017, 123, 340–352. [Google Scholar] [CrossRef]
- Weeratunge, H.; Narsilio, G.; Hoon, J.; Dunstall, S.; Halgamuge, S. Model predictive control for a solar assisted ground source heat pump system. Energy 2018, 152, 974–984. [Google Scholar] [CrossRef]
- Yoshinaga, M.; Kaneko, C. Operational control methods for a parallel system combining ground source and air source heat pumps in a warm region. J. Build. Eng. 2024, 86, 108712. [Google Scholar] [CrossRef]
- Yao, S.; Wu, J.; Qadrdan, M. A state-of-the-art analysis and perspectives on the 4th/5th generation district heating and cooling systems. Renew. Sustain. Energy Rev. 2024, 202, 114729. [Google Scholar] [CrossRef]
- Buffa, S.; Cozzini, M.; D’Antoni, M.; Baratieri, M.; Fedrizzi, R. 5th generation district heating and cooling systems: A review of existing cases in Europe. Renew. Sustain. Energy Rev. 2019, 104, 504–522. [Google Scholar] [CrossRef]
- Gjoka, K.; Rismanchi, B.; Crawford, R. Fifth-generation district heating and cooling systems: A review of recent advancements and implementation barriers. Renew. Sustain. Energy Rev. 2023, 171, 112997. [Google Scholar] [CrossRef]
- Garbrielli, P.; Acquilino, A.; Siri, S.; Bracco, S.; Sansavini, G.; Mazzotti, M. Optimization of low-carbon multi-energy systems with seasonal geothermal energy storage: The Anergy Grid of ETH Zurich. Energy Convers. Manag. 2020, 8, 100052. [Google Scholar] [CrossRef]
- Vetterli, N.; Sulzer, M.; Menti, U. Energy monitoring of a low temperature heating and cooling district network. Energy Procedia 2017, 122, 62–67. [Google Scholar] [CrossRef]
- Wang, Y.; Gillich, A.; Lu, D.; Saber, M.E.; Yebiyo, M.; Kang, R.; Ford, A.; Hewitt, M. Performance prediction and evaluation on the first balanced energy networks (BEN) part I: BEN and building internal factors. Energy 2021, 221, 119797. [Google Scholar] [CrossRef]
- Reiners, T.; Gross, M.; Altieri, L.; Wanger, H.; Bertsch, V. Heat pump efficiency in fifth generation ultra-low temperature district heating networks using a wastewater heat source. Energy 2021, 236, 121318. [Google Scholar] [CrossRef]
- Katsura, T.; Nagano, K.; Sakata, Y.; Wakayama, H. A design and simulation tool for ground source heat pump system using energy piles with large diameter. Int. J. Energy Res. 2019, 43, 1505–1520. [Google Scholar] [CrossRef]
- Katsura, T.; Nagano, K.; Narita, S.; Takeda, S.; Nakamura, Y.; Okamoto, A. Calculation Algorithm of the Temperatures for Pipe Arrangement of Multiple Ground Heat Exchangers. Appl. Therm. Eng. 2009, 28, 906–919. [Google Scholar] [CrossRef]
- Li, Y.; Wu, J.; Shiochi, S. Modeling and energy simulation of the variable refrigerant flow air conditioning system with water-cooled condenser under cooling condition. Energy Build. 2009, 41, 949–957. [Google Scholar] [CrossRef]

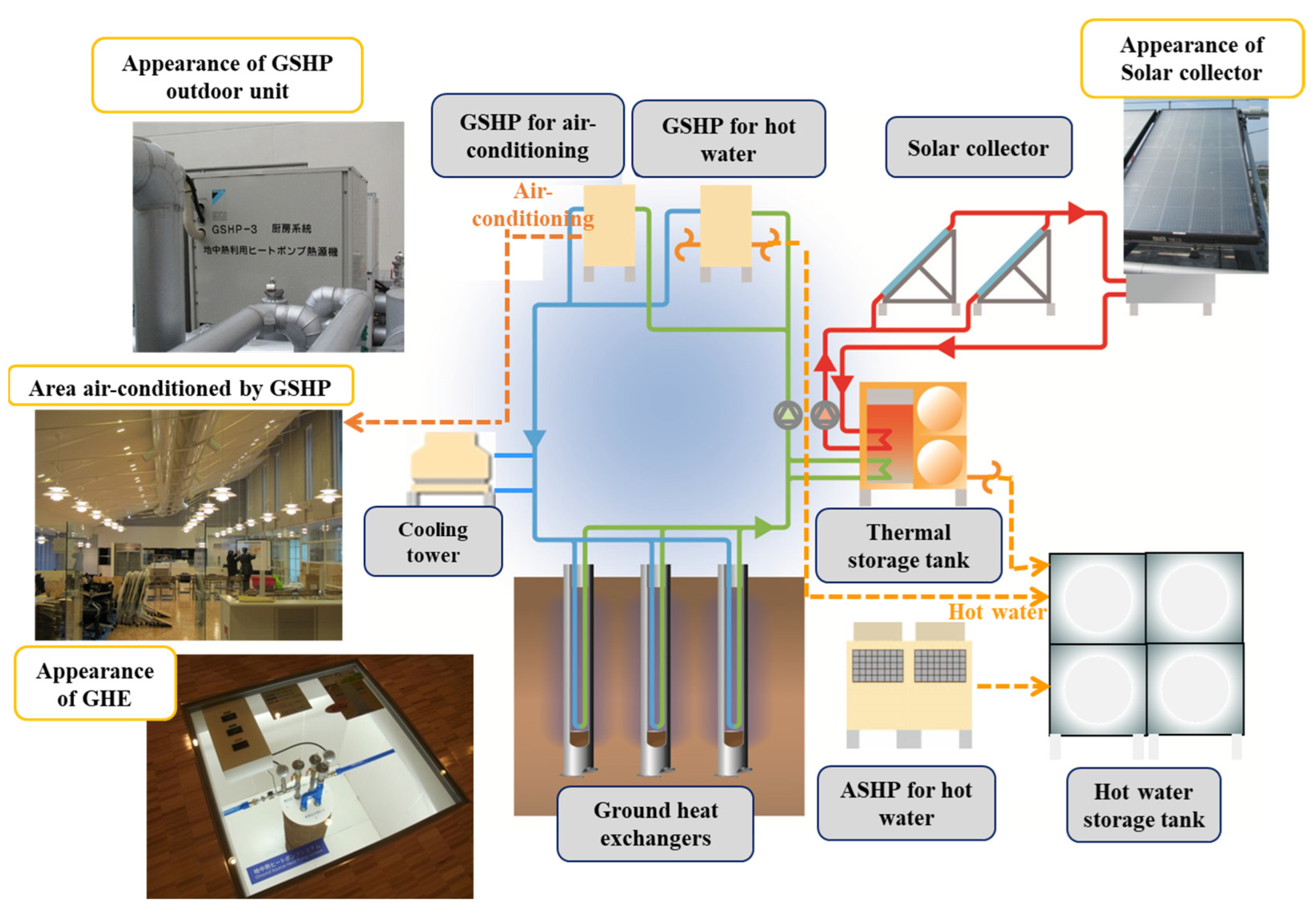
| Heat source equipment and subsystem | GSHP for air conditioning (×2) | Water source variable refrigerant flow (VRF) system |
| Rated cooling output: 50 kW; Rated electric power for cooling: 10.5 kW | ||
| Rated heating output: 56 kW; Rated electric power for heating: 10.5 kW | ||
| Circulation pump in the primary side of a GSHP for air conditioning | Rated flow rate: 384 L/min | |
| Rated power consumption: 3.7 kW | ||
| GSHP for hot water (×1) | Water source heat pump | |
| Rated heating output: 38.5 kW; Rated electric power: 11.5 kW | ||
| Circulation pump in the primary side of a GSHP for hot water | Rated flow rate: 76 L/min | |
| Rated power consumption: 0.75 kW | ||
| Cooling tower | Rated cooling output: 138.8 kW | |
| Rated electric power: 1.5 kW | ||
| Thermal storage tank | Capacity: 5 m3 | |
| Heat carrier fluid | Water | |
| Solar collector (×90) | Area: 1.91 m2 | |
| Rated heating output: 1.3 kW | ||
| ASHP for HW (×4) | Air source heat pump | |
| Rated heating output: 77 kW; Rated electric power: 20.7 kW | ||
| Steel pile GHE | Specification | Double U-tube in steel pile |
| Steel pile diameter | Outside diameter: 0.4~0.7 m | |
| Fluid | Water | |
| U-tube specification | HDPE25A (Outside diameter: 34 mm; inside diameter: 27 mm) | |
| Length and number | 5.9~12.4 m (Average 7.4 m), 68 piles (GHEs) | |
| Soil condition | Undisturbed temperature | 18.8 °C |
| Effective thermal conductivity | 3.3 W/(m·K) | |
| Density | 1500 kg/m3 | |
| Specific heat | 2.0 kJ/(kg·K) |
| Date | Details of the Changing the Operation |
|---|---|
| April 2013 | Operation of the GSHP for HW based on simulation results (April–November) |
| April 2014 | Extension of operation period of the GSHP for HW (all year round) |
| 2014, 2015 | GSHP for HW operation failure (August–September) |
| April 2016 | Suspension of cooling tower operation due to malfunction |
| April 2018 | Resumption of cooling tower operation |
| Electric Energy Consumption [kWh] | |||||||
|---|---|---|---|---|---|---|---|
| Storage Tank Heating | GSHP for AC | Cooling Tower | ASHP for HW | GSHP for HW | Total | ||
| Cooling | Heating | ||||||
| Measurement | 0 | 29,722 | 24,319 | 535 | 147,123 | 12,337 | 214,036 |
| Calculation | 259 | 29,244 | 25,235 | 797 | 144,689 | 12,166 | 212,390 |
| Relative error [%] | - | 1.6 | 3.8 | 49.0 | 1.7 | 1.4 | 0.8 |
| Operating Period of the GSHP for HW | Operating Period of the GSHP for HW | ||
|---|---|---|---|
| CASE0 | Nothing (0 month) | CASE6 | May~October (6 months) |
| CASE1 | August (1 month) | CASE7 | May~November (7 months) |
| CASE2 | July~August (2 months) | CASE8 | April~November (8 months) |
| CASE3 | July~September (3 months) | CASE9 | April~December (9 months) |
| CASE4 | June~September (4 months) | CASE10 | March~December (10 months) |
| CASE5 | June~October (5 months) | CASE11 | March~January (11 months) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katsura, T.; Nakamura, Y.; Ohara, T.; Kinouchi, K.; Nagano, K. Investigation of the Optimal Operation Method of the Heat Recovery Ground Source Heat Pump System Installed in an Actual Building and Evaluation of Energy Saving Effect. Energies 2024, 17, 3558. https://doi.org/10.3390/en17143558
Katsura T, Nakamura Y, Ohara T, Kinouchi K, Nagano K. Investigation of the Optimal Operation Method of the Heat Recovery Ground Source Heat Pump System Installed in an Actual Building and Evaluation of Energy Saving Effect. Energies. 2024; 17(14):3558. https://doi.org/10.3390/en17143558
Chicago/Turabian StyleKatsura, Takao, Yasushi Nakamura, Tomoya Ohara, Ken Kinouchi, and Katsunori Nagano. 2024. "Investigation of the Optimal Operation Method of the Heat Recovery Ground Source Heat Pump System Installed in an Actual Building and Evaluation of Energy Saving Effect" Energies 17, no. 14: 3558. https://doi.org/10.3390/en17143558
APA StyleKatsura, T., Nakamura, Y., Ohara, T., Kinouchi, K., & Nagano, K. (2024). Investigation of the Optimal Operation Method of the Heat Recovery Ground Source Heat Pump System Installed in an Actual Building and Evaluation of Energy Saving Effect. Energies, 17(14), 3558. https://doi.org/10.3390/en17143558








