Numerical and Experimental Analysis of Vortex Profiles in Gravitational Water Vortex Hydraulic Turbines
Abstract
1. Introduction
2. Materials and Methods
2.1. Gravitational Water Vortex Hydraulic Turbine (GWVHT)
2.2. Mass Flow Rate and Vortex Circulation
2.3. Numerical Analysis
2.3.1. Geometric Domain and Mesh Generation
2.3.2. Turbulence Model
2.4. Experimental Setup
3. Results and Discussion
3.1. Statistical Analysis
3.2. Experimental Test
4. Conclusions
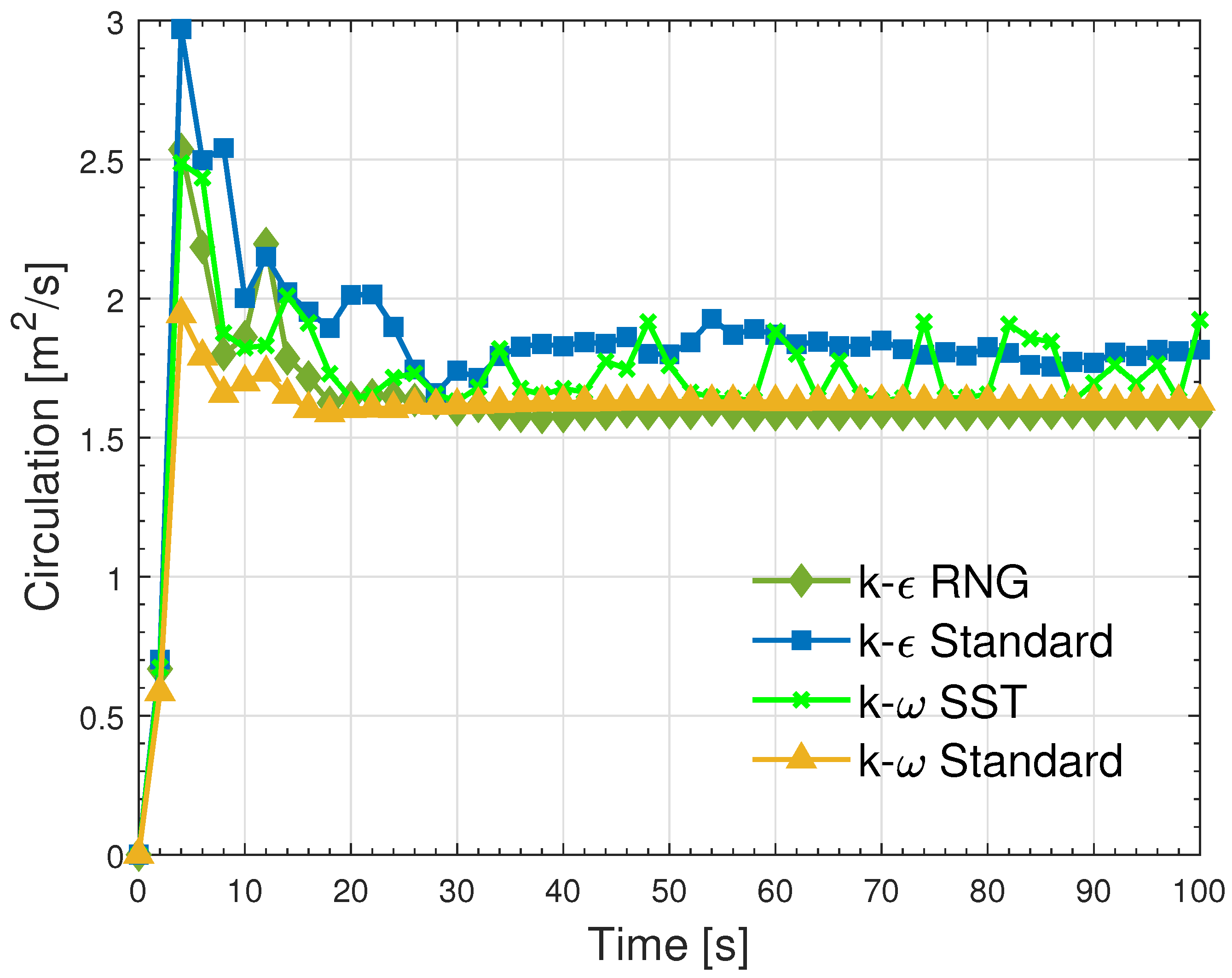
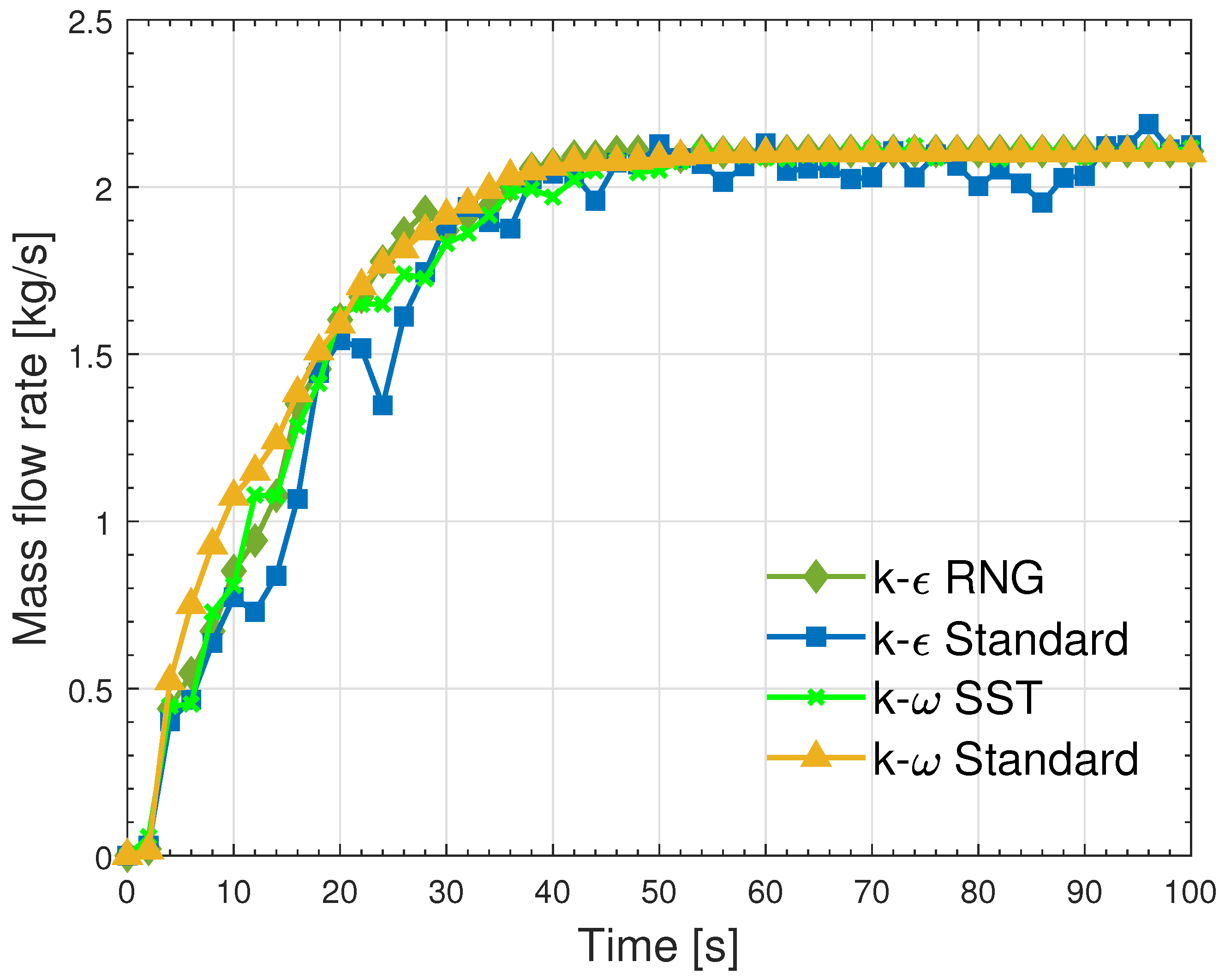
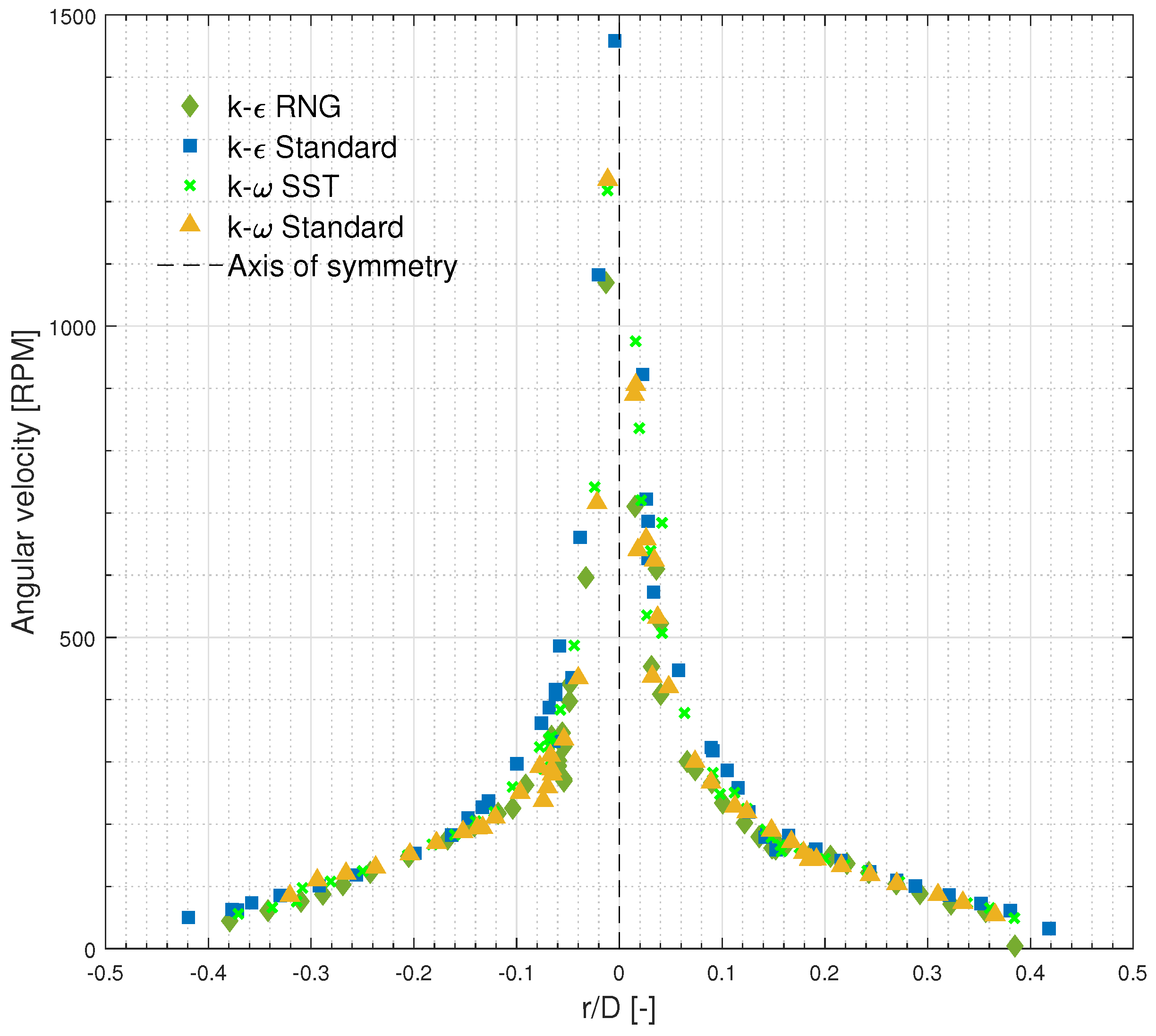
- It was observed that the behavior of the vortex circulation and the mass flow rate varied significantly between these models. This study revealed that the vortex circulation, which is a crucial parameter for understanding fluid dynamics, was dependent on the turbulence model used. While the k- RNG and standard k- models exhibited similar circulation behaviors, including maintaining a relatively constant circulation value, the k- standard model showed higher circulation values. In contrast, the k- SST model demonstrated an irregular circulation behavior, which fluctuated without evidence of stabilization during the analyzed time period. Similarly, the mass flow rate stabilization varied for each turbulence model. The k- RNG, k- SST, and k- standard models stabilized around a value of 2.1 kg/s after 40 s. However, the standard k- model exhibited fluctuations that ranged between 1.9 and 2.1 kg/s without being stabilized at the input mass flow rate value.
- Statistical analyses, including ANOVA and multiple comparison methods, confirmed the significant differences between the studied turbulence models for both the circulation and the mass flow rate. The obtained p-values indicate that the choice of the turbulence model significantly affected these variables, which reaffirmed the importance of the model selection in fluid dynamics simulations. Experimental tests were conducted to validate the numerical simulations.
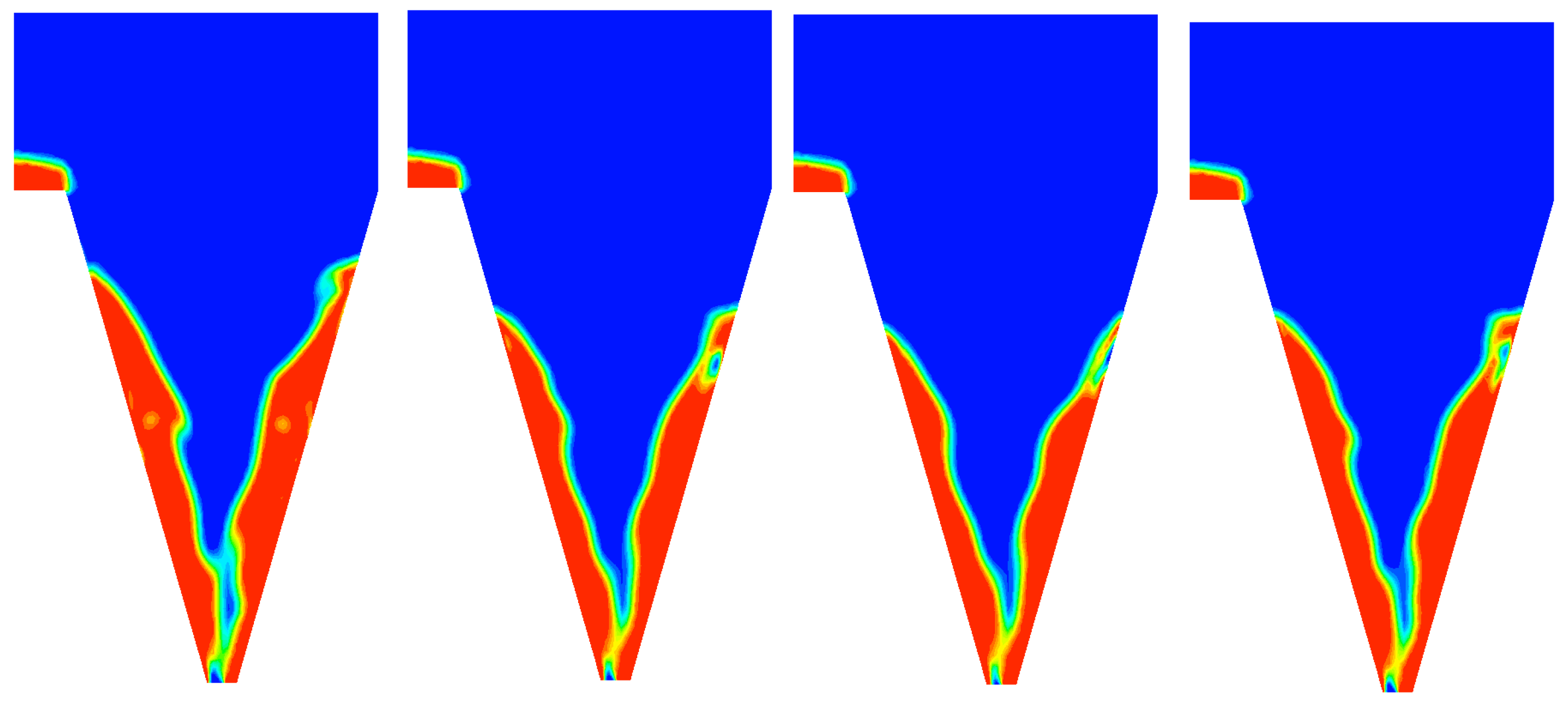
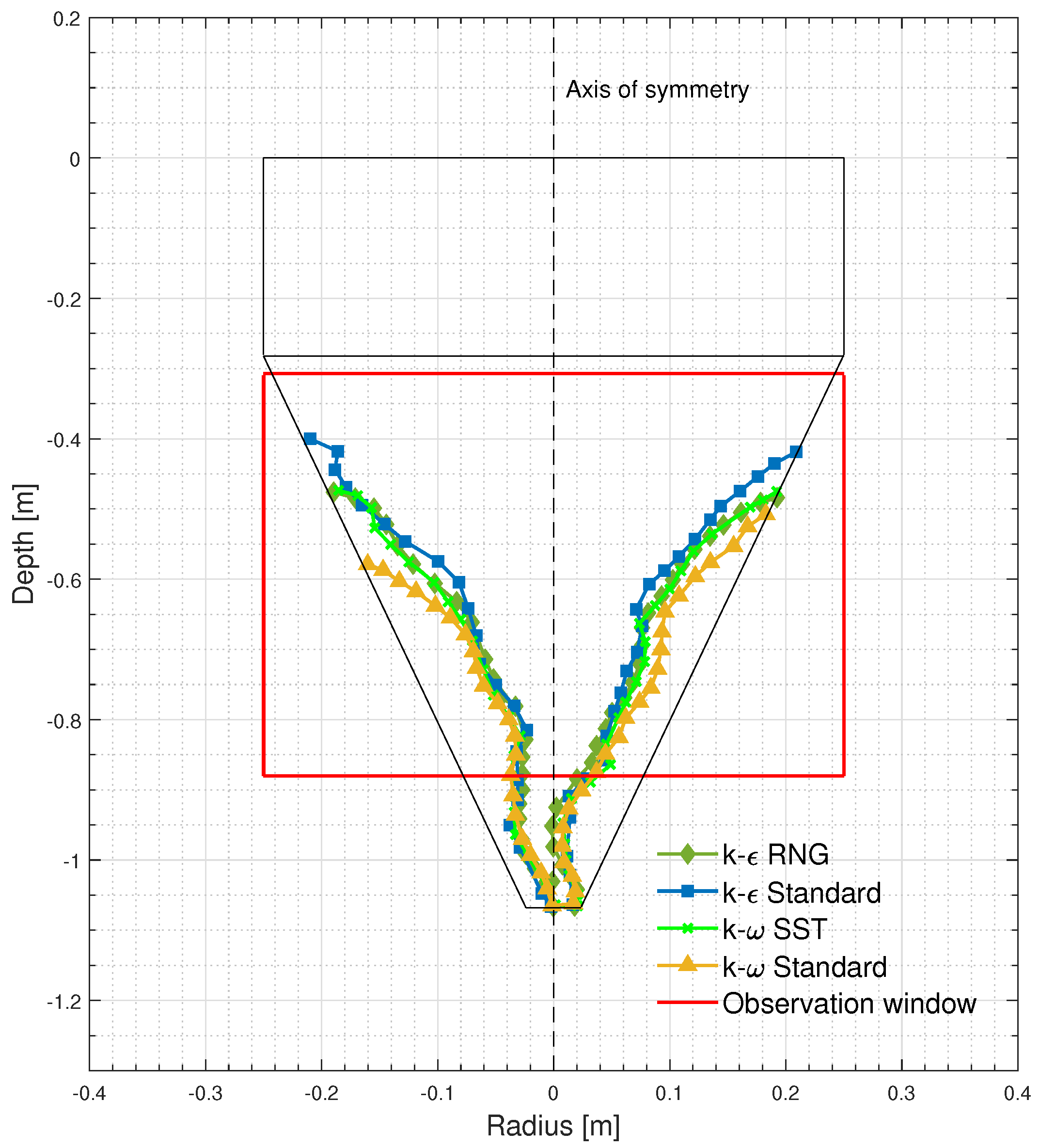
- By comparing the numerical vortex profiles with experimental results, it was confirmed that the k- SST model closely resembled the real vortex profile, followed by the k- RNG model. This experimental validation provided additional support to the numerical findings and highlighted the effectiveness of the chosen turbulence models in capturing real-world phenomena.
- Based on the various analyses conducted, the k- SST model is recommended as the most appropriate turbulence model for this type of turbine. This model had a better ability to capture and predict the turbulence behavior in the studied system.
- Continued efforts to optimize the turbine efficiency through advanced CFD simulations and experimental validations are crucial. This includes refining the turbulence models, such as further tuning the k- SST model, to improve the predictive accuracy under varying flow conditions. Optimization can also explore innovative designs and materials to enhance the turbine performance.
- Scaling up GWVHTs to larger capacities while maintaining efficiency is essential. Research could focus on modular designs or arrays of GWVHTs to harness energy from multiple low-head hydraulic sites effectively. Integration studies with existing water infrastructure, such as irrigation canals or urban drainage systems, could maximize energy recovery and sustainability benefits.
- Investigating the environmental impacts of GWVHT deployment by considering effects on aquatic ecosystems and local hydrology is critical. Research can explore mitigation strategies and sustainable practices to minimize the adverse effects and ensure long-term environmental stewardship. Additionally, assessing the socio-economic impacts of GWVHT projects on local communities, including job creation and energy access improvements, is essential for promoting equitable development.
- Conducting comprehensive techno-economic analyses to evaluate the cost-effectiveness of GWVHT installations compared with traditional hydropower and other renewable energy sources will play an important role. This includes assessing capital costs, operational and maintenance expenses, and the levelized cost of energy (LCOE). Such analyses can inform policy decisions and attract investment in GWVHT projects.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Velásquez, L.; Chica, E.; Posada, J. Advances in the Development of Gravitational Water Vortex Hydraulic Turbines. J. Eng. Sci. Technol. Rev. 2021, 14, 1–14. [Google Scholar] [CrossRef]
- Looney, B. Statistical Review of World Energy, 2020; BP: London, UK, 2020. [Google Scholar]
- Jogdand, O.K. Study on the effect of global warming and greenhouse gases on environmental system. In Green Chemistry and Sustainable Technology; Apple Academic Press: Cambridge, MA, USA, 2020; pp. 275–306. [Google Scholar]
- Soeder, D.J. Fossil fuels and climate change. In Fracking and the Environment: A Scientific Assessment of the Environmental Risks from Hydraulic Fracturing and Fossil Fuels; Springer: Cham, Switzerland, 2021; pp. 155–185. [Google Scholar]
- Singh, R.L.; Singh, P.K. Global environmental problems. In Principles and Applications of Environmental Biotechnology for a Sustainable Future; Springer: Cham, Switzerland, 2017; pp. 13–41. [Google Scholar]
- Upadhyay, R.K. Markers for global climate change and its impact on social, biological and ecological systems: A review. Am. J. Clim. Chang. 2020, 9, 102270. [Google Scholar] [CrossRef]
- Kushawaha, J.; Borra, S.; Kushawaha, A.K.; Singh, G.; Singh, P. Climate change and its impact on natural resources. In Water Conservation in the Era of Global Climate Change; Elsevier: Amsterdam, The Netherlands, 2021; pp. 333–346. [Google Scholar]
- Halkos, G.E.; Gkampoura, E.C. Reviewing usage, potentials, and limitations of renewable energy sources. Energies 2020, 13, 2906. [Google Scholar] [CrossRef]
- Holechek, J.L.; Geli, H.M.; Sawalhah, M.N.; Valdez, R. A global assessment: Can renewable energy replace fossil fuels by 2050? Sustainability 2022, 14, 4792. [Google Scholar] [CrossRef]
- Rahman, A.; Farrok, O.; Haque, M.M. Environmental impact of renewable energy source based electrical power plants: Solar, wind, hydroelectric, biomass, geothermal, tidal, ocean, and osmotic. Renew. Sustain. Energy Rev. 2022, 161, 112279. [Google Scholar] [CrossRef]
- Engeland, K.; Borga, M.; Creutin, J.D.; François, B.; Ramos, M.H.; Vidal, J.P. Space-time variability of climate variables and intermittent renewable electricity production—A review. Renew. Sustain. Energy Rev. 2017, 79, 600–617. [Google Scholar] [CrossRef]
- Twidell, J. Renewable Energy Resources; Routledge: London, UK, 2021. [Google Scholar]
- Timilsina, A.B.; Mulligan, S.; Bajracharya, T.R. Water vortex hydropower technology: A state-of-the-art review of developmental trends. Clean Technol. Environ. Policy 2018, 20, 1737–1760. [Google Scholar] [CrossRef]
- Marian, G.; Sajin, T.; Florescu, I.; Nedelcu, D.; Ostahie, C.; Bîrsan, C. The concept and theoretical study of micro hydropower plant with gravitational vortex and turbine with rapidity steps. Bul. AGIR 2012, 3, 219–226. [Google Scholar]
- Shabara, H.; Yaakob, O.; Ahmed, Y.M.; Elbatran, A.; Faddir, M.S. CFD validation for efficient gravitational vortex pool system. J. Teknol. 2015, 74. [Google Scholar] [CrossRef]
- Sreerag, S.; Raveendran, C.; Jinshah, B. Effect of outlet diameter on the performance of gravitational vortex turbine with conical basin. Int. J. Sci. Eng. Res. 2016, 7, 457–463. [Google Scholar]
- Velásquez, L.; Posada, A.; Chica, E. Optimization of the basin and inlet channel of a gravitational water vortex hydraulic turbine using the response surface methodology. Renew. Energy 2022, 187, 508–521. [Google Scholar] [CrossRef]
- Sritram, P.; Treedet, W.; Suntivarakorn, R. Effect of turbine materials on power generation efficiency from free water vortex hydro power plant. IOP Conf. Ser. Mater. Sci. Eng. 2015, 103, 012018. [Google Scholar] [CrossRef]
- Power, C.; McNabola, A.; Coughlan, P. A parametric experimental investigation of the operating conditions of gravitational vortex hydropower (GVHP). J. Clean Energy Technol. 2016, 4, 112–119. [Google Scholar] [CrossRef]
- Wichian, P.; Suntivarakorn, R. The effects of turbine baffle plates on the efficiency of water free vortex turbines. Energy Procedia 2016, 100, 198–202. [Google Scholar] [CrossRef]
- Betancour, J.; Romero-Menco, F.; Velásquez, L.; Rubio-Clemente, A.; Chica, E. Design and optimization of a runner for a gravitational vortex turbine using the response surface methodology and experimental tests. Renew. Energy 2023, 210, 306–320. [Google Scholar] [CrossRef]
- Velásquez, L.; Romero-Menco, F.; Rubio-Clemente, A.; Posada, A.; Chica, E. Numerical optimization and experimental validation of the runner of a gravitational water vortex hydraulic turbine with a spiral inlet channel and a conical basin. Renew. Energy 2024, 220, 119676. [Google Scholar] [CrossRef]
- Edirisinghe, D.S.; Yang, H.S.; Gunawardane, S.; Lee, Y.H. Enhancing the performance of gravitational water vortex turbine by flow simulation analysis. Renew. Energy 2022, 194, 163–180. [Google Scholar] [CrossRef]
- Tamiri, F.; Yeo, E.; Ismail, M. Vortex profile analysis under different diffuser size for inlet channel of gravitational water vortex power plant. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1217, 012014. [Google Scholar] [CrossRef]
- Abel, A.; Tamiri, F.; Ismail, M.; Bohari, N. An Experience with Simulation Modeling for Vortex Flow in Micro Hydropower Systems. In Proceedings of the 2022 International Conference on Green Energy, Computing and Sustainable Technology (GECOST), Miri Sarawak, Malaysia, 26–28 October 2022; pp. 365–370. [Google Scholar]
- Velásquez, L.; Posada, A.; Chica, E. Surrogate modeling method for multi-objective optimization of the inlet channel and the basin of a gravitational water vortex hydraulic turbine. Appl. Energy 2023, 330, 120357. [Google Scholar] [CrossRef]
- Kamal, M.M.; Abbas, A.; Prasad, V.; Kumar, R. A numerical study on the performance characteristics of low head Francis turbine with different turbulence models. Mater. Today Proc. 2022, 49, 349–353. [Google Scholar] [CrossRef]
- Mulligan, S. Experimental and Numerical Analysis of Three-Dimensional Free-Surface Turbulent Vortex Flows with Strong Circulation; Institute of Technology Sligo: Sligo, Ireland, 2015. [Google Scholar]
- Holton, J.R. An introduction to dynamic meteorology. Am. J. Phys. 1973, 41, 752–754. [Google Scholar] [CrossRef]
- Antuono, M.; Colagrossi, A.; Le Touzé, D.; Monaghan, J.J. Conservation of circulation in SPH for 2D free-surface flows. Int. J. Numer. Methods Fluids 2013, 72, 583–606. [Google Scholar] [CrossRef]
- Cengel, Y.A. Fluid Mechanics; Tata McGraw-Hill Education: New York, NY, USA, 2010. [Google Scholar]
- Zore, K.; Parkhi, G.; Sasanapuri, B.; Varghese, A. Ansys mosaic poly-hexcore mesh for high-lift aircraft configuration. In Proceedings of the 21th Annual CFD Symposium, Bangalore, India, 8–9 August 2019; pp. 1–11. [Google Scholar]
- Rakowitz, M. Grid refinement study with a uhca wing-body configuration using richardson extrapolation and grid convergence index gci. In New Results in Numerical and Experimental Fluid Mechanics III; Springer: Berlin/Heidelberg, Germany, 2002; pp. 297–303. [Google Scholar]
- Phillips, T.S.; Roy, C.J. Richardson extrapolation-based discretization uncertainty estimation for computational fluid dynamics. J. Fluids Eng. 2014, 136, 121401. [Google Scholar] [CrossRef]
- Baker, N.; Kelly, G.; O’Sullivan, P.D. A grid convergence index study of mesh style effect on the accuracy of the numerical results for an indoor airflow profile. Int. J. Vent. 2020, 19, 300–314. [Google Scholar] [CrossRef]
- Pope, S.B.; Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Maruzewski, P.; Hayashi, H.; Munch, C.; Yamaishi, K.; Hashii, T.; Mombelli, H.; Sugow, Y.; Avellan, F. Turbulence modeling for Francis turbine water passages simulation. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012070. [Google Scholar] [CrossRef]
- Dhakal, S.; Timilsina, A.B.; Dhakal, R.; Fuyal, D.; Bajracharya, T.R.; Pandit, H.P. Effect of dominant parameters for conical basin: Gravitational water vortex power plant. In Proceedings of the IOE Graduate Conference; Institute of Engineering, Tribhuvan University: Kathmandu, Nepal, 2014; p. 381. [Google Scholar]
- Dhakal, S.; Timilsina, A.B.; Dhakal, R.; Fuyal, D.; Bajracharya, T.R.; Pandit, H.P.; Amatya, N.; Nakarmi, A.M. Comparison of cylindrical and conical basins with optimum position of runner: Gravitational water vortex power plant. Renew. Sustain. Energy Rev. 2015, 48, 662–669. [Google Scholar] [CrossRef]
- Chattha, J.A.; Cheema, T.A.; Khan, N.H. Numerical investigation of basin geometries for vortex generation in a gravitational water vortex power plant. In Proceedings of the 2017 8th International Renewable Energy Congress (IREC), Amman, Jordan, 21–23 March 2017; pp. 1–5. [Google Scholar]
- Nishi, Y.; Inagaki, T. Performance and flow field of a gravitation vortex type water turbine. Int. J. Rotating Mach. 2017, 2017, 2610508. [Google Scholar] [CrossRef]
- Havaldar, S.; Gadekar, P.; Baviskar, S.; Jadhav, N.; Inamdar, S. Analyzing Geometries for Inlet Flow Channels to Gravitational Water Vortex Chamber. Int. J. Res. Eng. Appl. Manag. 2020, 5, 221–223. [Google Scholar]
- ANSYS Inc. ANSYS Fluent 12.0 Theory Guide; ANSYS FLUENT Release; ANSYS Inc.: Canonsburg, PA, USA, 2009. [Google Scholar]
- Chen, Q. Comparison of different k-ε models for indoor air flow computations. Numer. Heat Transf. Part B Fundam. 1995, 28, 353–369. [Google Scholar] [CrossRef]
- Toapanta-Ramos, L.F.; Zapata-Cautillo, J.A.; Cholango-Gavilanes, A.I.; Quitiaquez, W.; Nieto-Londoño, C.; Zapata-Benabithe, Z. Estudio numérico y comparativo del efecto de turbulencia en codos y dobleces para distribución de agua sanitaria. Rev. Fac. De Ing. 2019, 28, 101–118. [Google Scholar] [CrossRef]
- Monk, D.; Chadwick, E.A. Comparison of turbulence models effectiveness for a delta wing at low Reynolds numbers. In Proceedings of the 7th European Conference for Aeronautics and Space Sciences (EUCASS), Milan, Italy, 3–6 July 2017; Volume 1303. [Google Scholar]
- Argyropoulos, C.D.; Markatos, N. Recent advances on the numerical modelling of turbulent flows. Appl. Math. Model. 2015, 39, 693–732. [Google Scholar] [CrossRef]
- Notes, I.F. Introduction to CFD Analysis. Introductory FLUENT Training; ANSYS: Canonsburg, PA, USA, 2006. [Google Scholar]
- Nasution, S.B.S.; Adanta, D. A Comparison of Openflume Turbine Designs with Specific Speeds (Ns) Based on Power and Discharge Function. J. Adv. Res. Fluid Mech. Therm. Sci. 2018, 51, 53–60. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Potter, K.; Hagen, H.; Kerren, A.; Dannenmann, P. Methods for presenting statistical information: The box plot. Vis. Large Unstructured Data Sets 2006, 4, 97–106. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Rafter, J.A.; Abell, M.L.; Braselton, J.P. Multiple comparison methods for means. Siam Rev. 2002, 44, 259–278. [Google Scholar] [CrossRef]
- Huttenlocher, D.P.; Klanderman, G.A.; Rucklidge, W.J. Comparing images using the Hausdorff distance. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 850–863. [Google Scholar] [CrossRef]
- Taha, A.A.; Hanbury, A. An efficient algorithm for calculating the exact Hausdorff distance. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 2153–2163. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Shi, W.; Deng, Y. A new Hausdorff distance for image matching. Pattern Recognit. Lett. 2005, 26, 581–586. [Google Scholar] [CrossRef]
- Fischer, A.; Suen, C.Y.; Frinken, V.; Riesen, K.; Bunke, H. Approximation of graph edit distance based on Hausdorff matching. Pattern Recognit. 2015, 48, 331–343. [Google Scholar] [CrossRef]
- Kumar, K.S.; Manigandan, T.; Chitra, D.; Murali, L. Object recognition using Hausdorff distance for multimedia applications. Multimed. Tools Appl. 2020, 79, 4099–4114. [Google Scholar] [CrossRef]
- Kraft, D. Computing the Hausdorff distance of two sets from their distance functions. Int. J. Comput. Geom. Appl. 2020, 30, 19–49. [Google Scholar] [CrossRef]
- Wang, S.; Tan, J.; Yu, Z. Comparison and experimental validation of turbulence models for an axial flow blood pump. J. Mech. Med. Biol. 2019, 19, 1940063. [Google Scholar] [CrossRef]
- Muiruri, P.I.; Motsamai, O.S.; Ndeda, R. A comparative study of RANS-based turbulence models for an upscale wind turbine blade. SN Appl. Sci. 2019, 1, 237. [Google Scholar] [CrossRef]
- Meana-Fernández, A.; Fernández Oro, J.M.; Argüelles Díaz, K.M.; Velarde-Suárez, S. Turbulence-model comparison for aerodynamic-performance prediction of a typical vertical-axis wind-turbine airfoil. Energies 2019, 12, 488. [Google Scholar] [CrossRef]
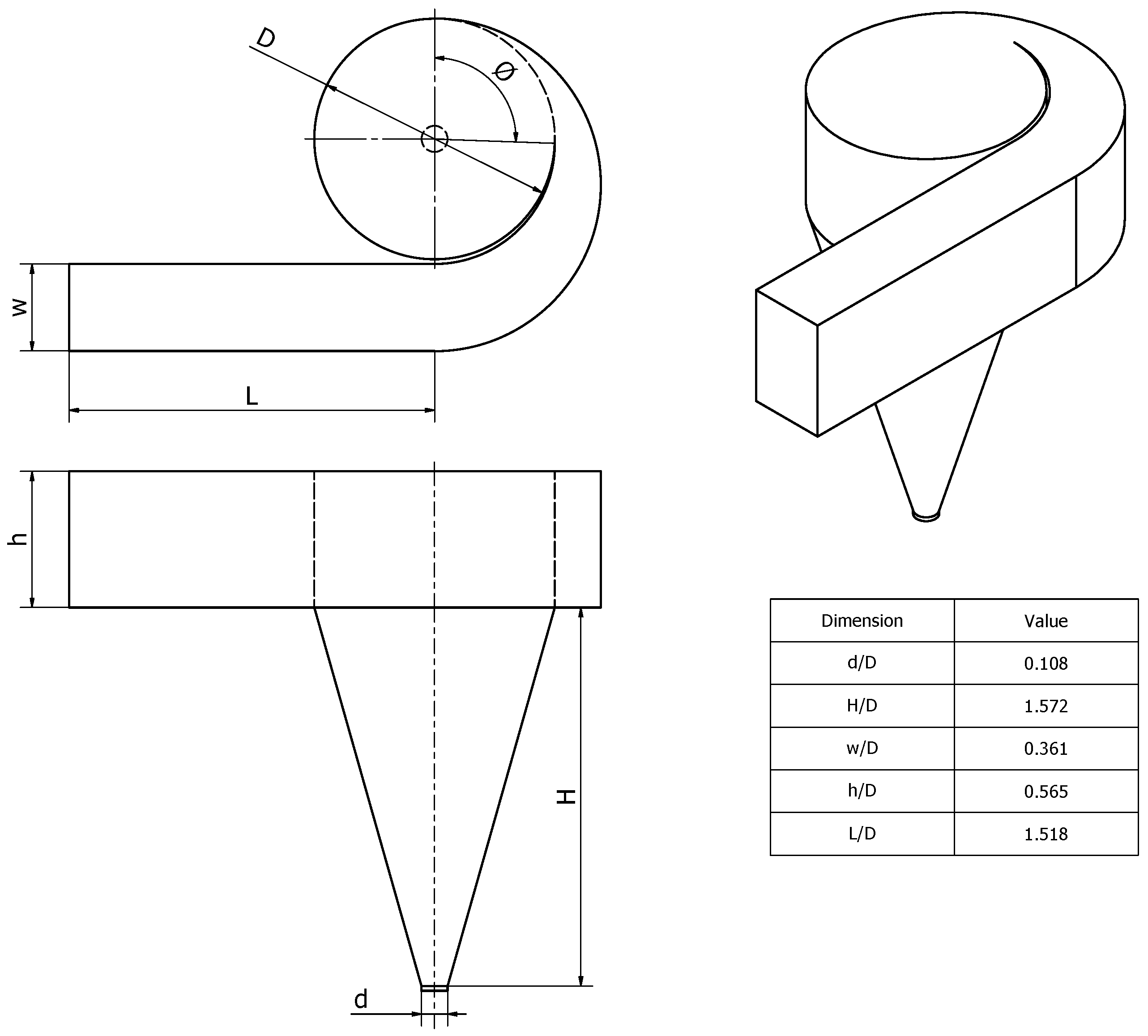
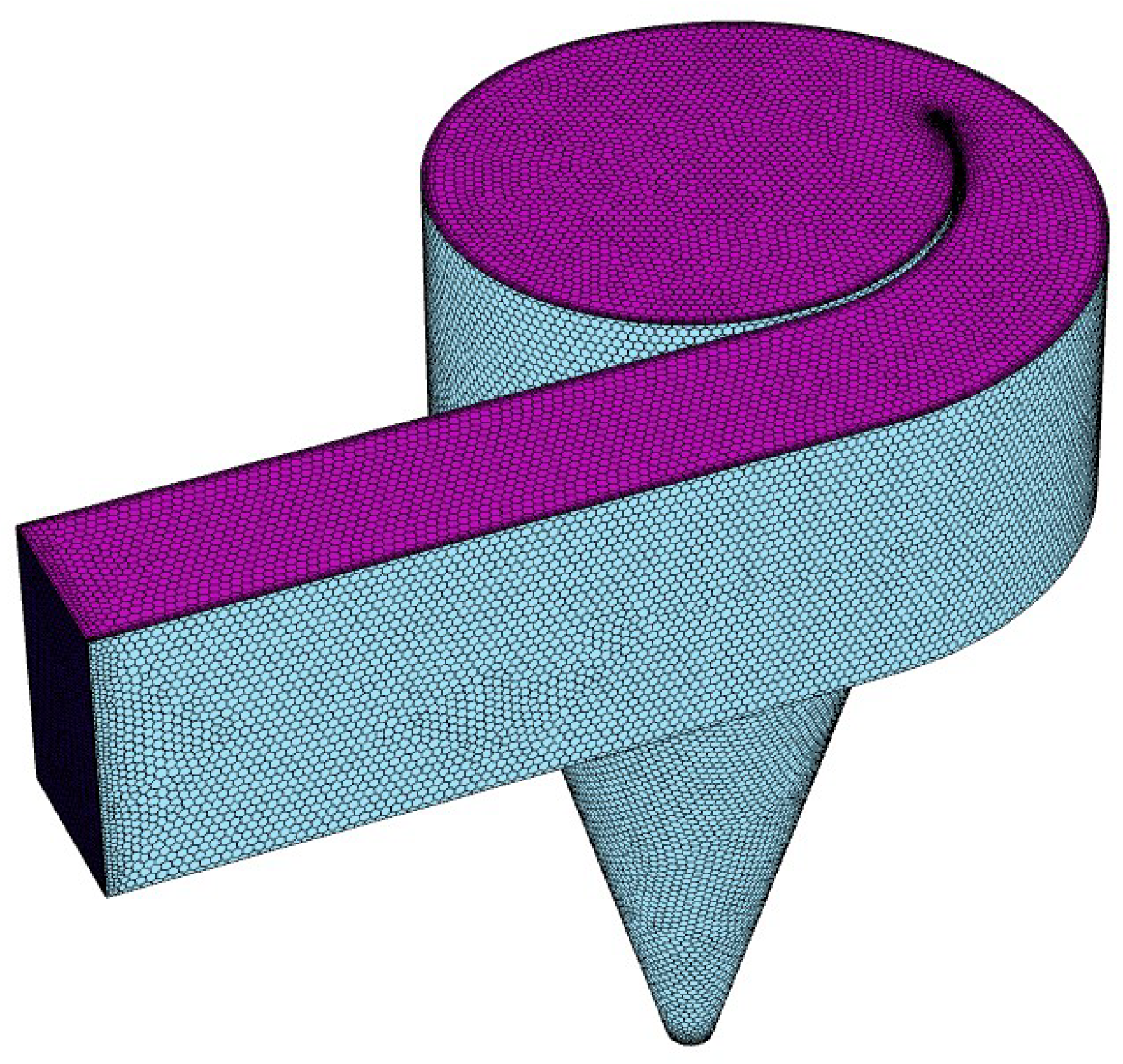
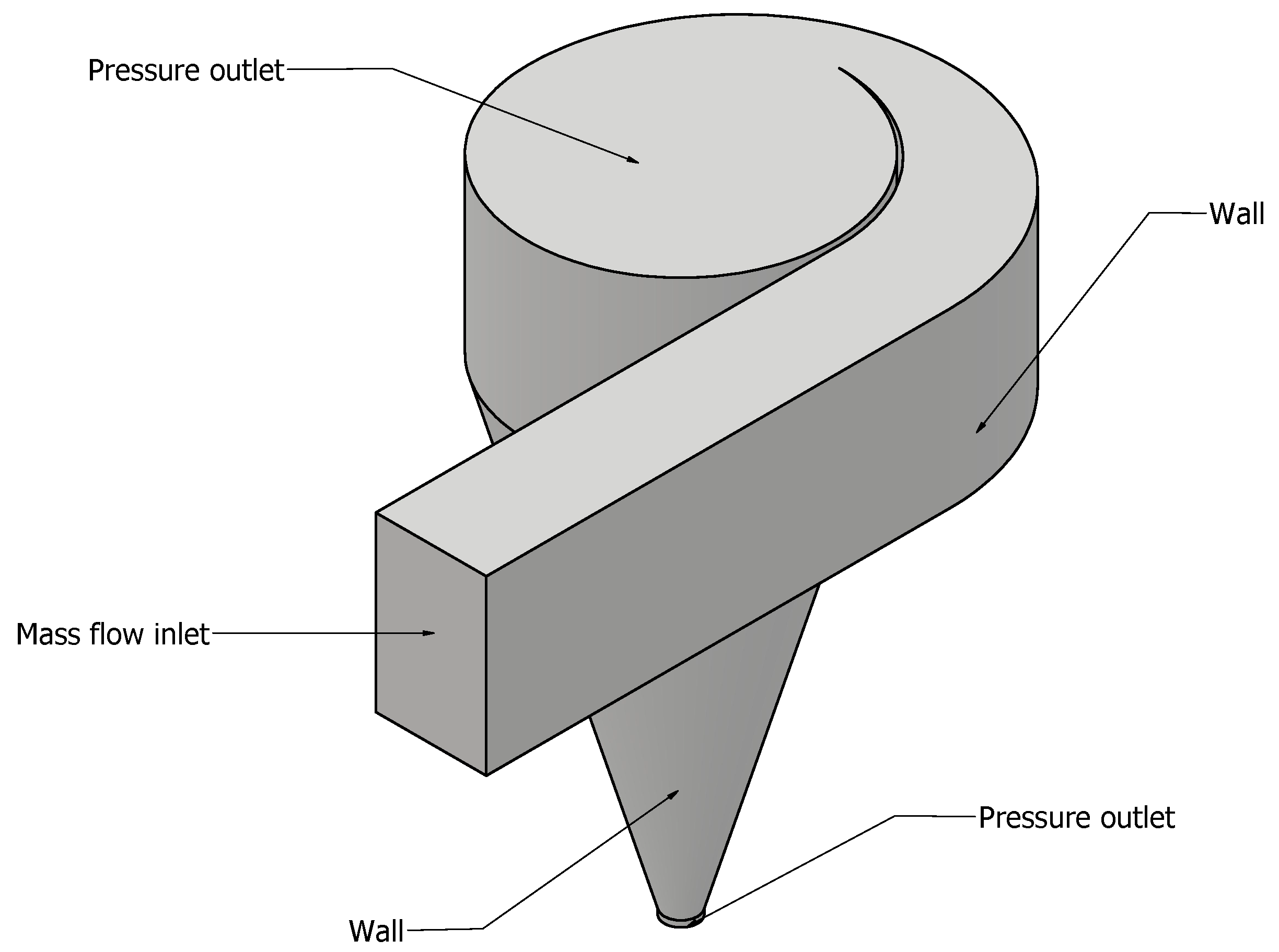
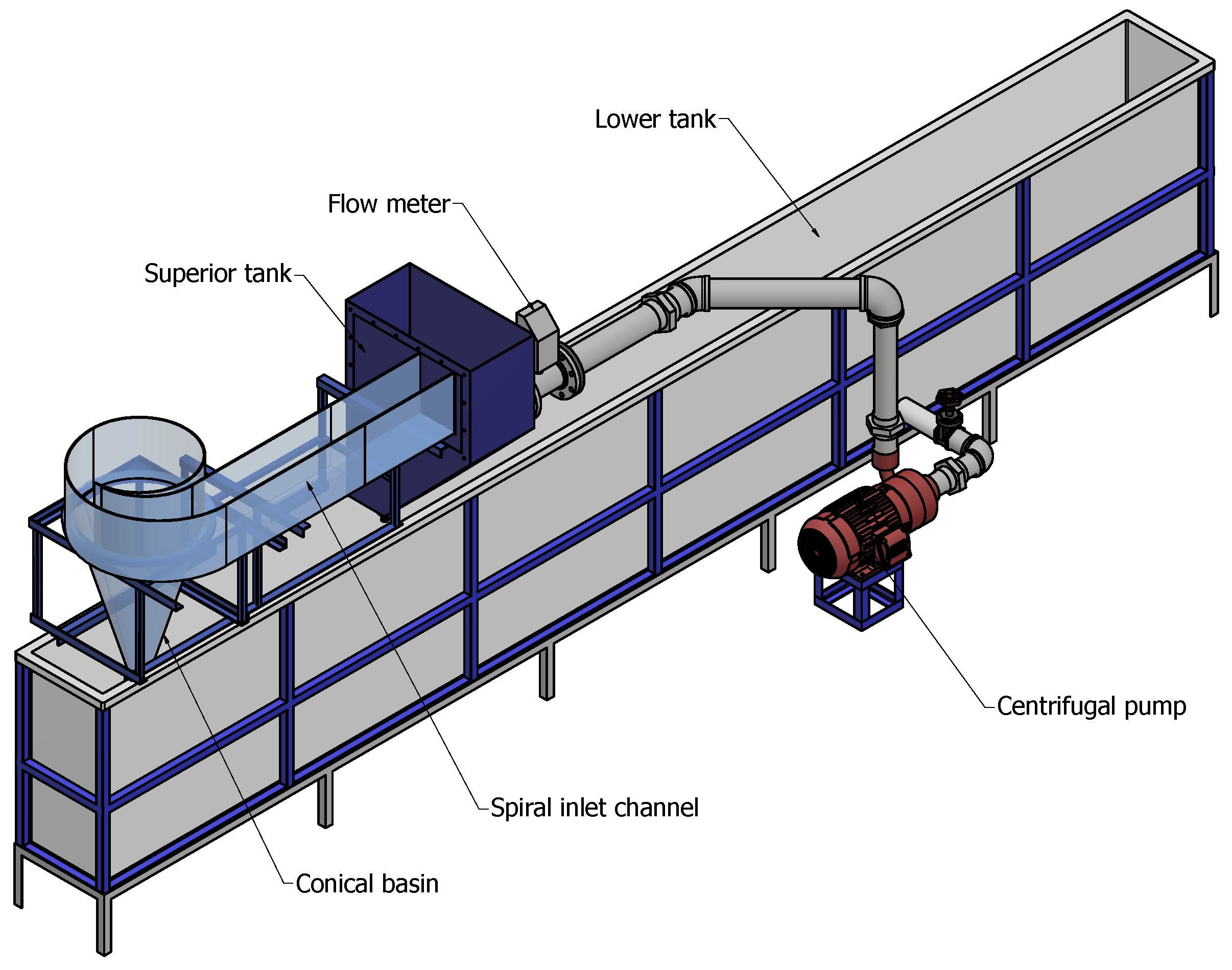




| Mesh | Number of Elements | (s) | |
|---|---|---|---|
| 1 | Coarse | 211,158 | 0.2 |
| 2 | Medium | 330,238 | 0.1 |
| 3 | Fine | 435,116 | 0.05 |
| GCI | 1.006 | 0.999 |
| Turbulence Model | Circulation [m2/s] | Mass Flow Rate [kg/s] | |
|---|---|---|---|
| T1 | k- RNG | 1.586830 | 2.104615 |
| T2 | k- standard | 1.818612 | 2.062747 |
| T3 | k- SST | 1.754791 | 2.102311 |
| T4 | Standard k- | 1.629372 | 2.100726 |
| Turbulence Model | Standard Deviation | Letter | UCL | LCL |
|---|---|---|---|---|
| T1 | 0.003829 | D | 1.589488 | 1.584173 |
| T2 | 0.039350 | A | 1.821269 | 1.815954 |
| T3 | 0.113385 | B | 1.757449 | 1.752134 |
| T4 | 0.000226 | C | 1.632029 | 1.626714 |
| Turbulence Model | Standard Deviation | Letter | UCL | LCL |
|---|---|---|---|---|
| T1 | 0.004893 | A | 2.105349 | 2.103880 |
| T2 | 0.053150 | D | 2.063482 | 2.062012 |
| T3 | 0.014400 | B | 2.103046 | 2.101576 |
| T4 | 0.003589 | C | 2.101460 | 2.099991 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velásquez, L.; Rubio-Clemente, A.; Chica, E. Numerical and Experimental Analysis of Vortex Profiles in Gravitational Water Vortex Hydraulic Turbines. Energies 2024, 17, 3543. https://doi.org/10.3390/en17143543
Velásquez L, Rubio-Clemente A, Chica E. Numerical and Experimental Analysis of Vortex Profiles in Gravitational Water Vortex Hydraulic Turbines. Energies. 2024; 17(14):3543. https://doi.org/10.3390/en17143543
Chicago/Turabian StyleVelásquez, Laura, Ainhoa Rubio-Clemente, and Edwin Chica. 2024. "Numerical and Experimental Analysis of Vortex Profiles in Gravitational Water Vortex Hydraulic Turbines" Energies 17, no. 14: 3543. https://doi.org/10.3390/en17143543
APA StyleVelásquez, L., Rubio-Clemente, A., & Chica, E. (2024). Numerical and Experimental Analysis of Vortex Profiles in Gravitational Water Vortex Hydraulic Turbines. Energies, 17(14), 3543. https://doi.org/10.3390/en17143543








