Systematic Design of Cathode Air Supply Systems for PEM Fuel Cells
Abstract
1. Introduction
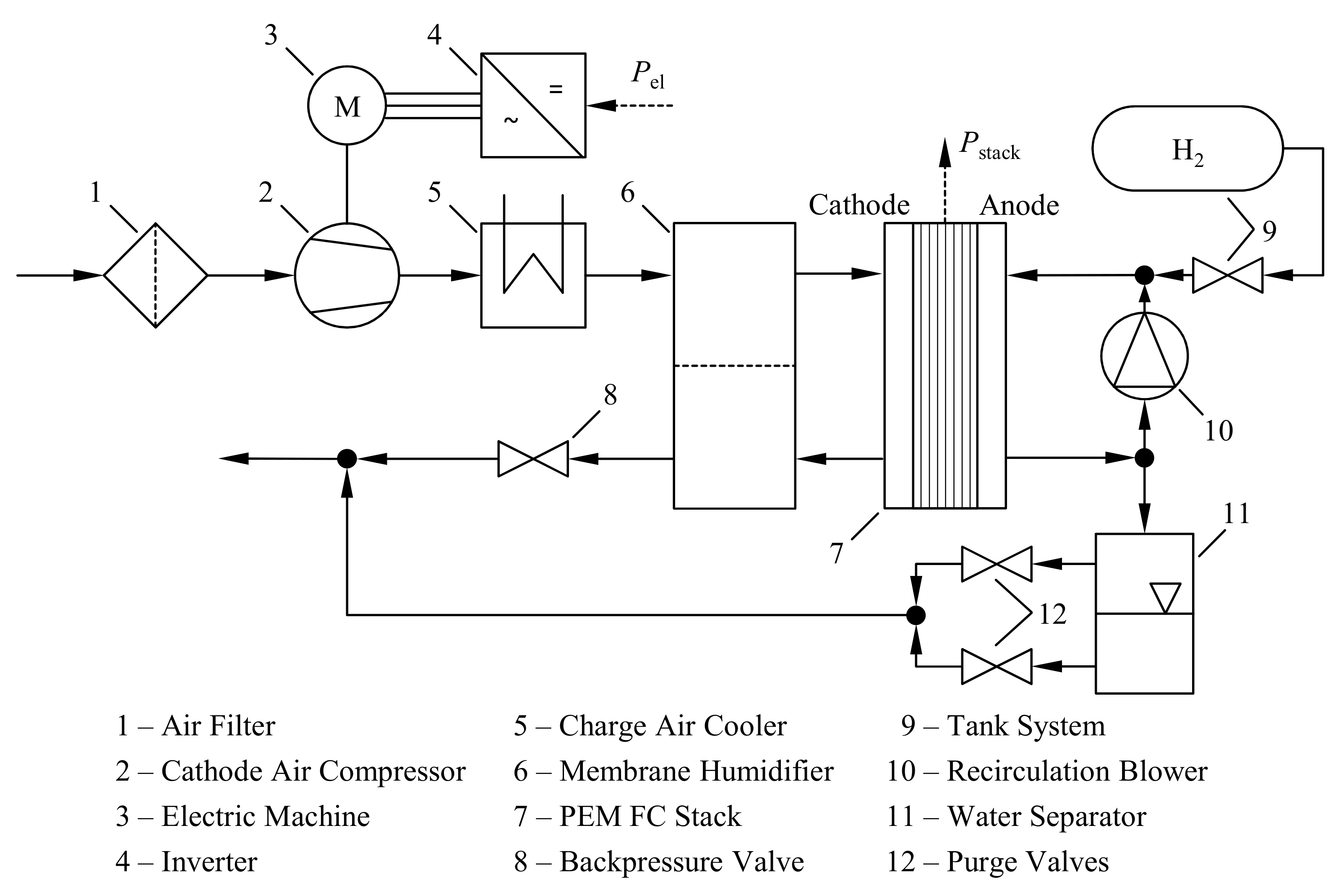
2. Fuel Cell System Simulation
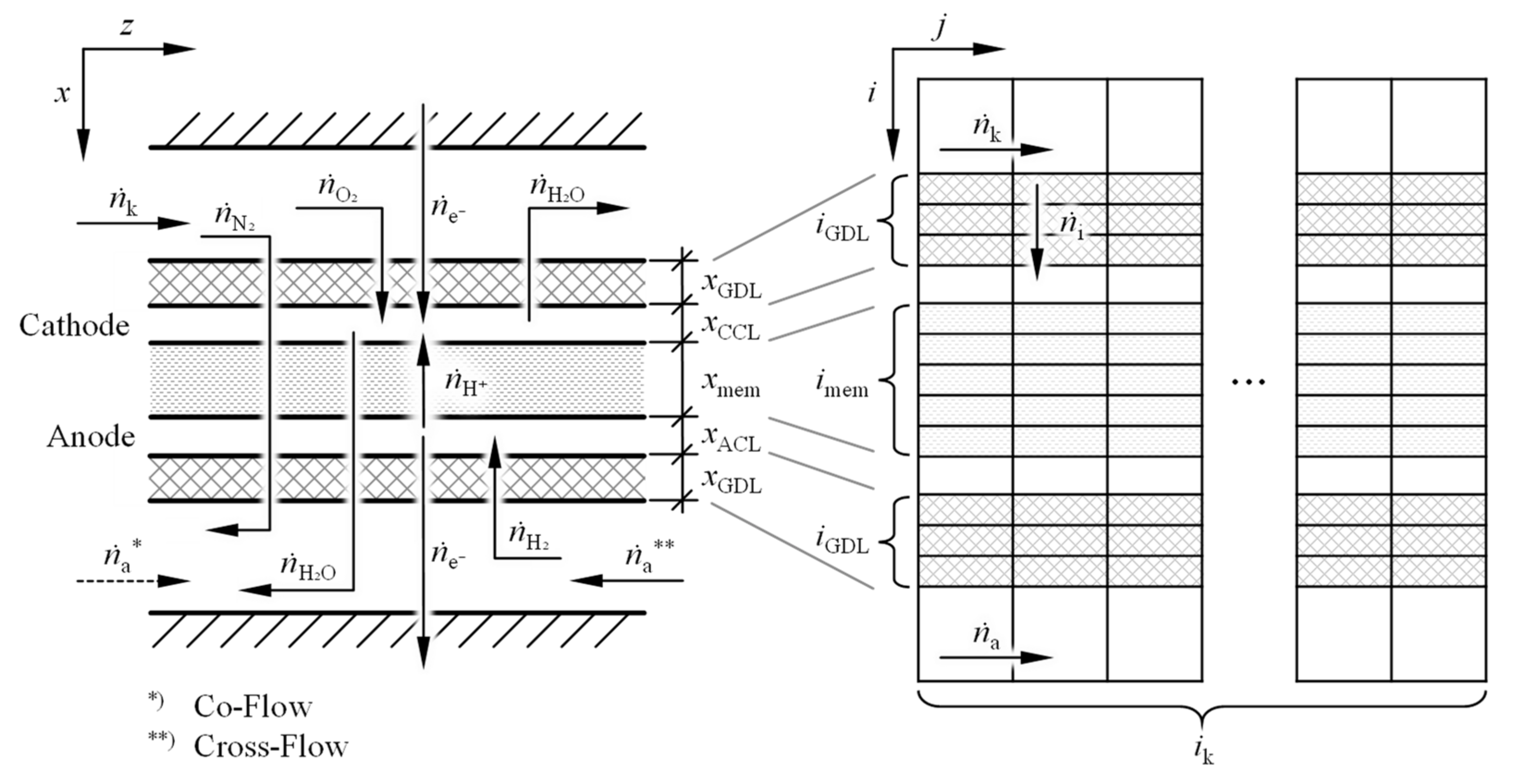
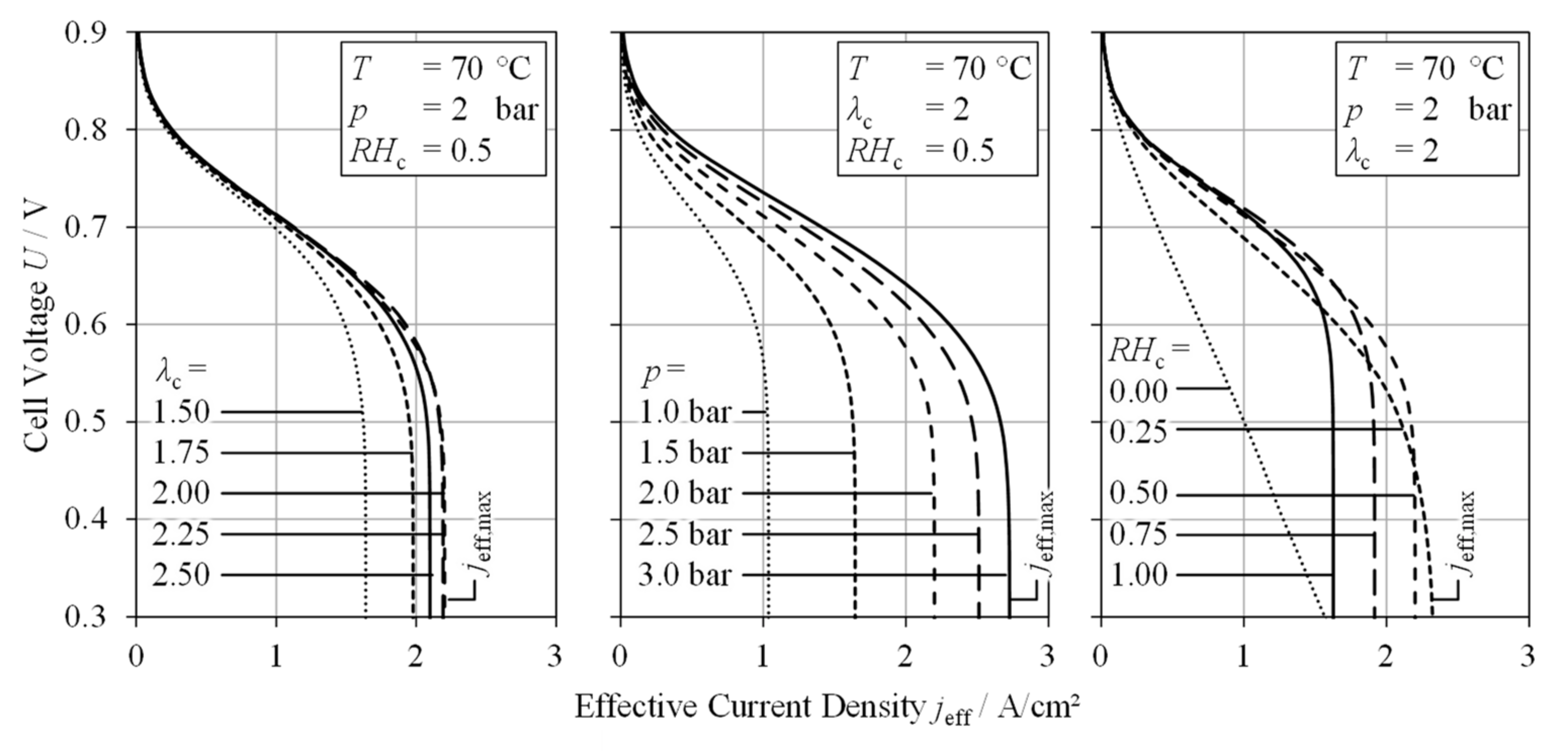
2.1. PEM FC Model
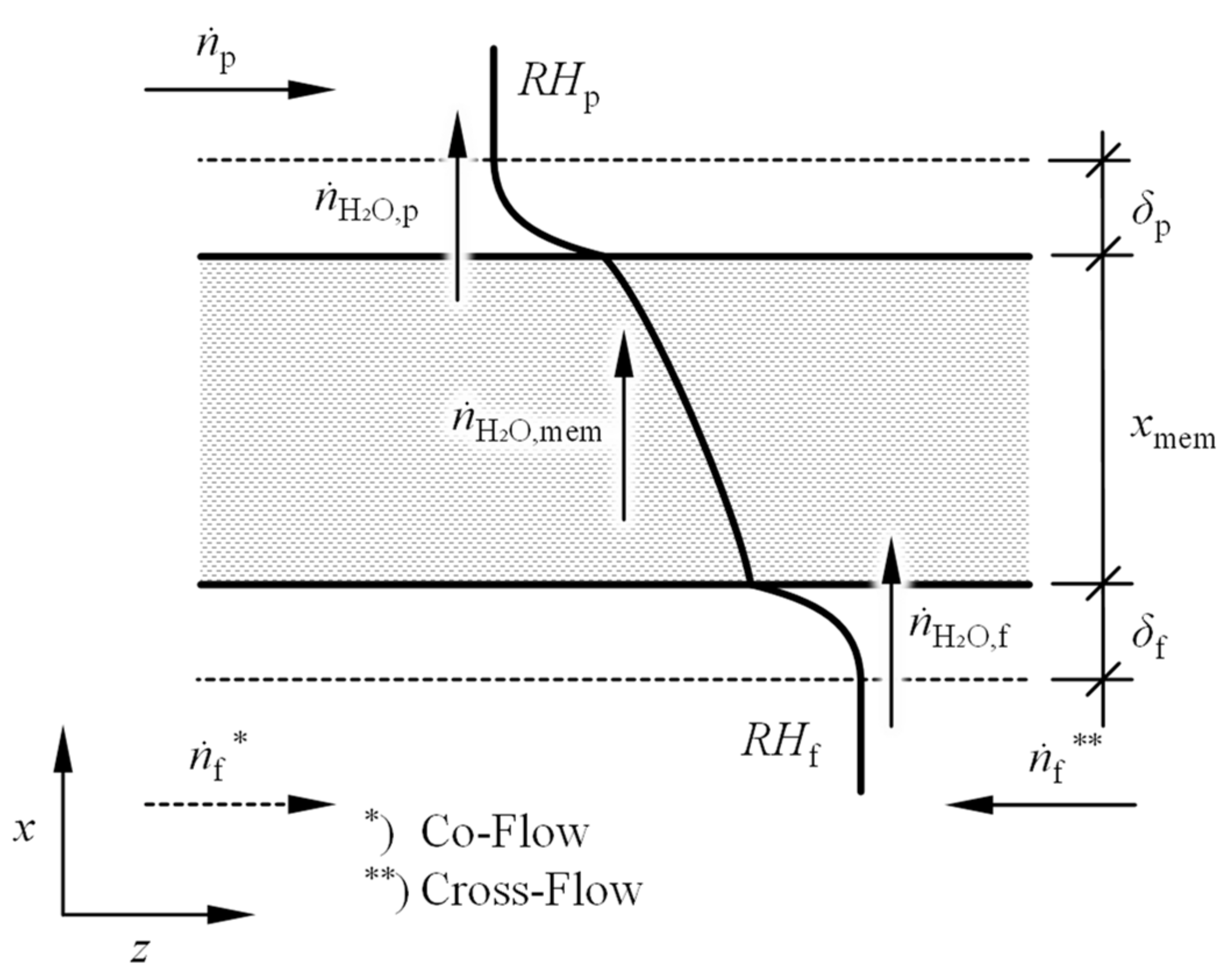
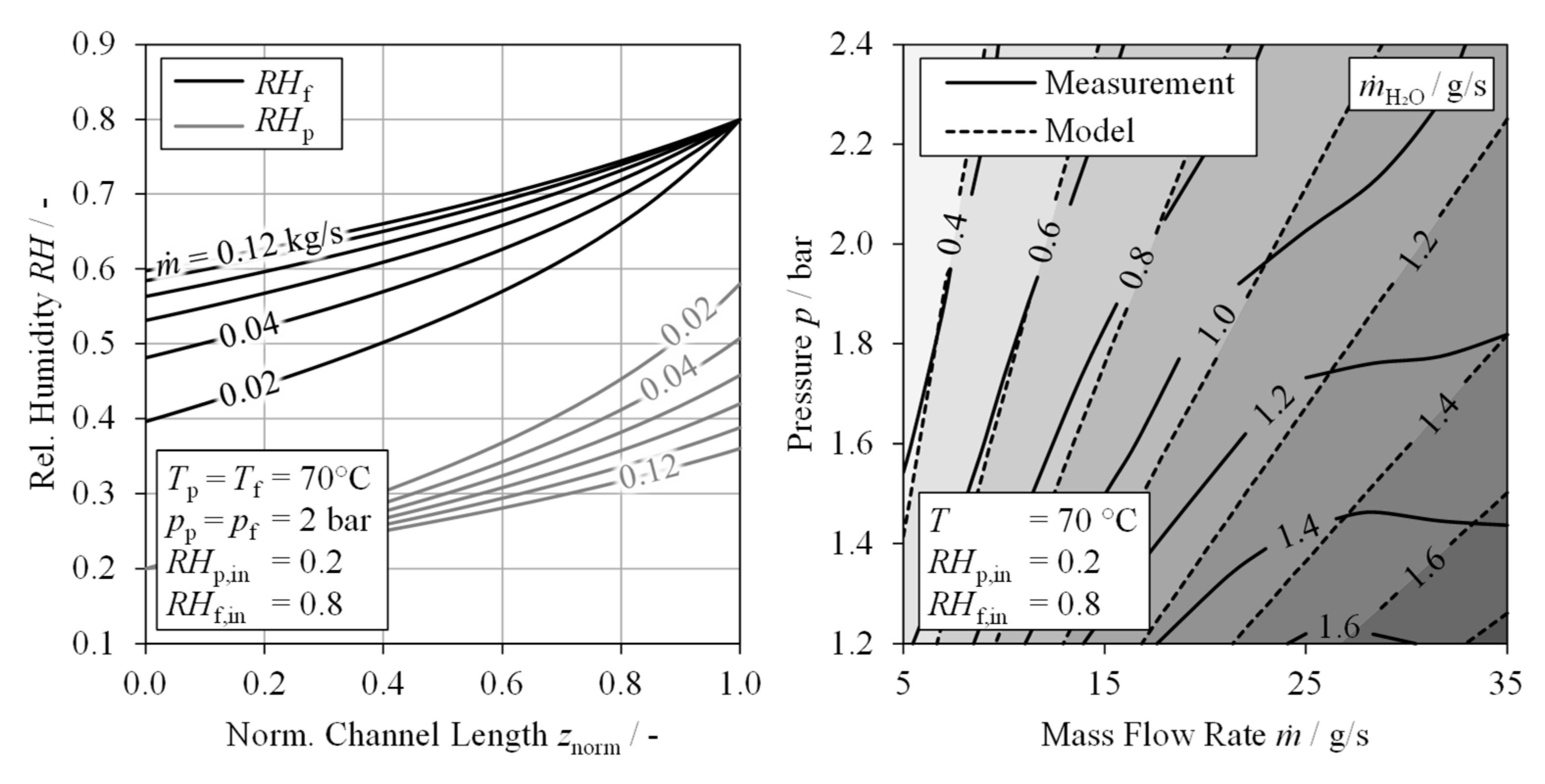
2.2. Membrane Humidifier Model
2.3. PEM FC System Model
3. Operating Strategy Optimization
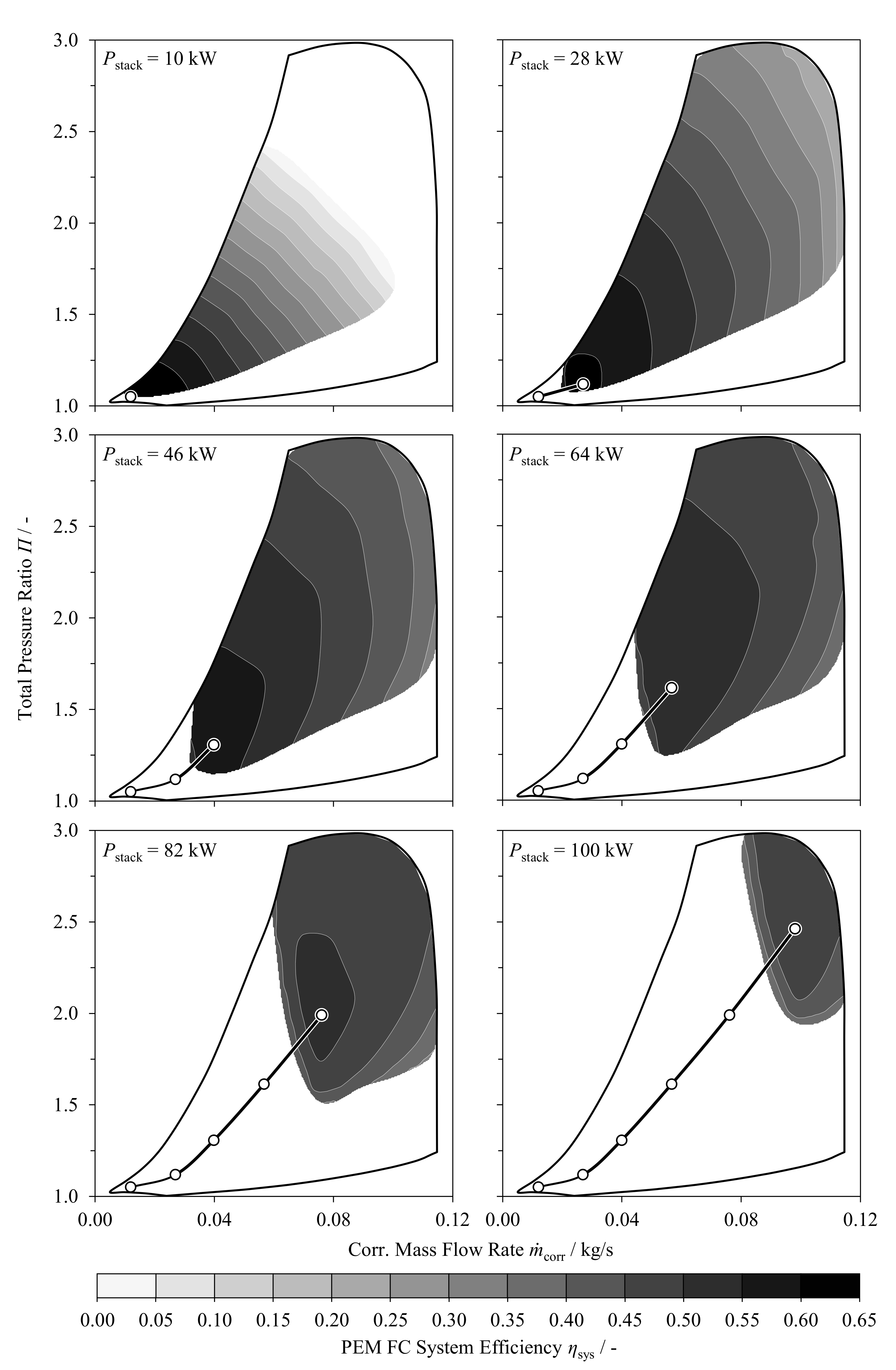
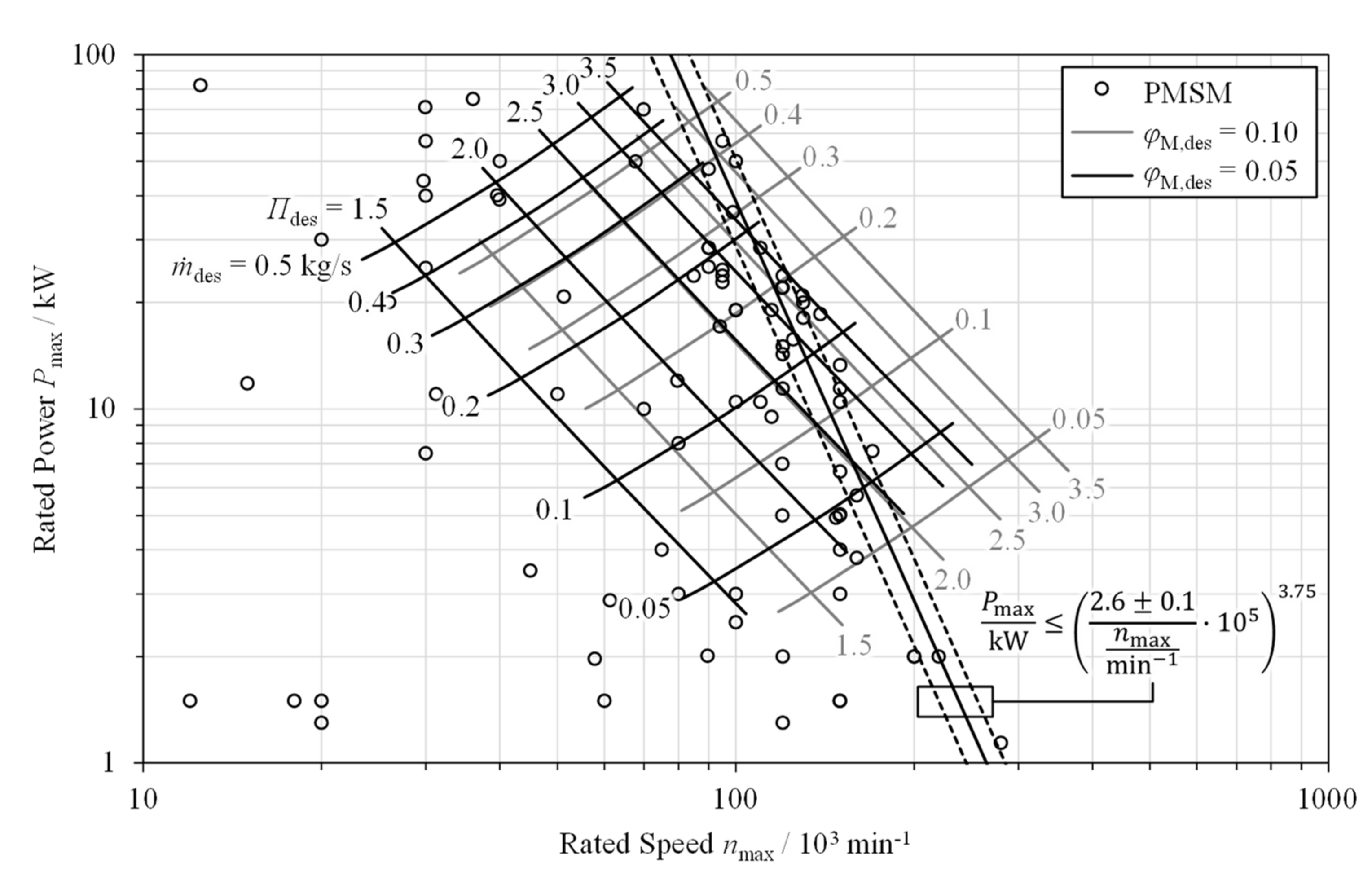
3.1. Component Sizing
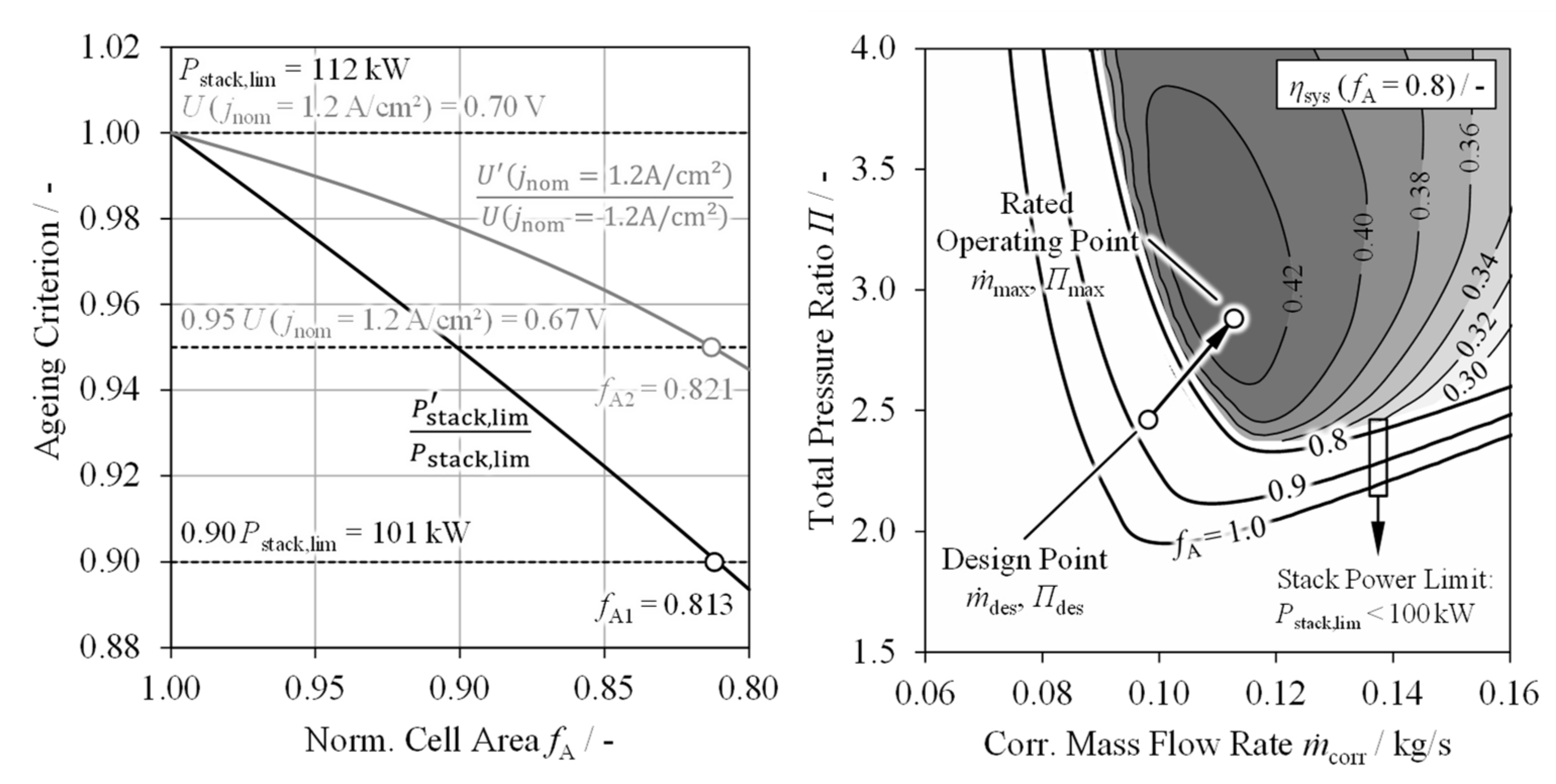
3.2. Cell Ageing
- A 10% reduction of the maximum stack power compared to the new system;
- A 5% reduction of the cell voltage at the nominal current density jnom = 1.2 A/cm2 compared to the new system.
4. Compressor Preliminary Design
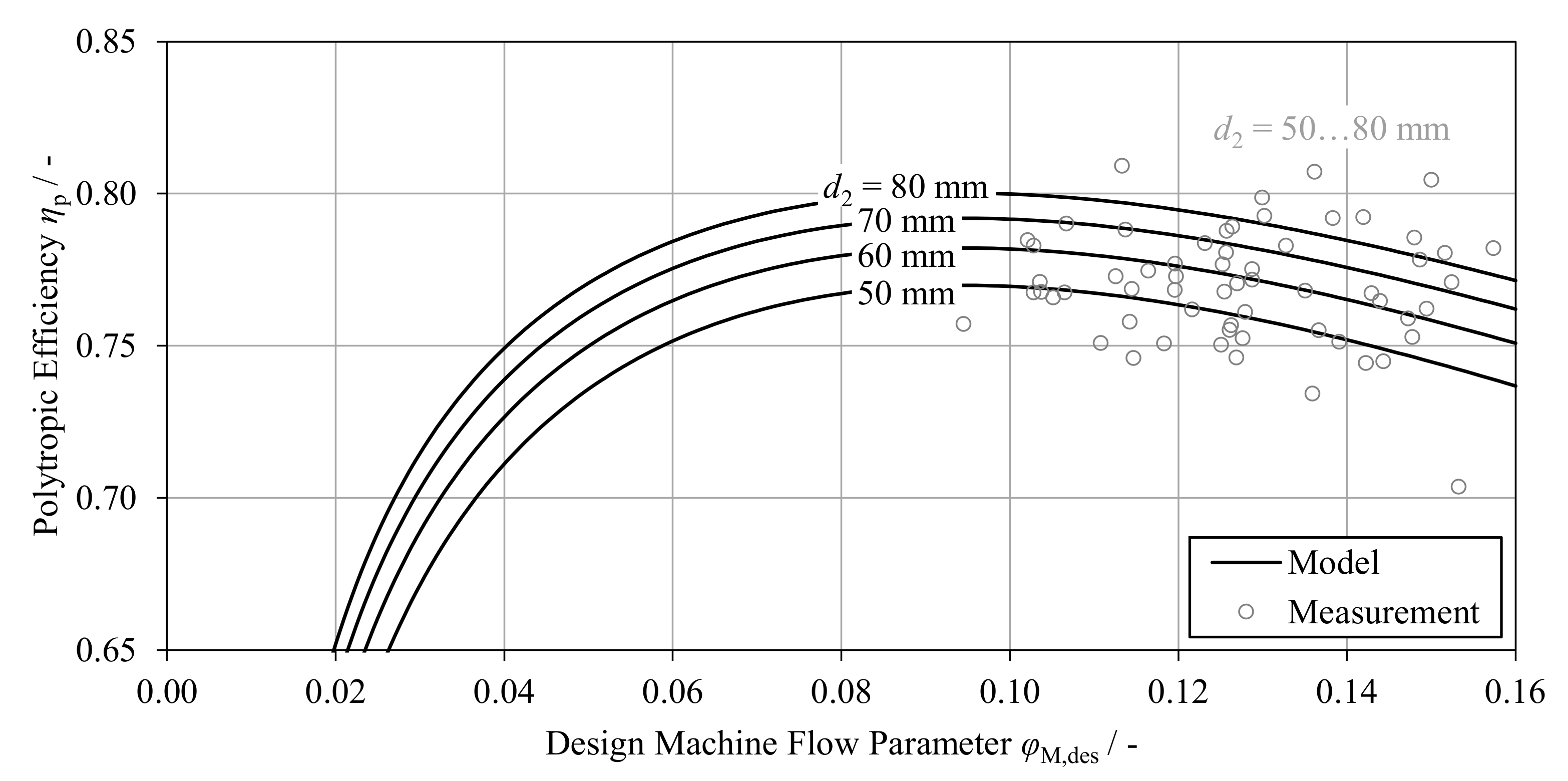
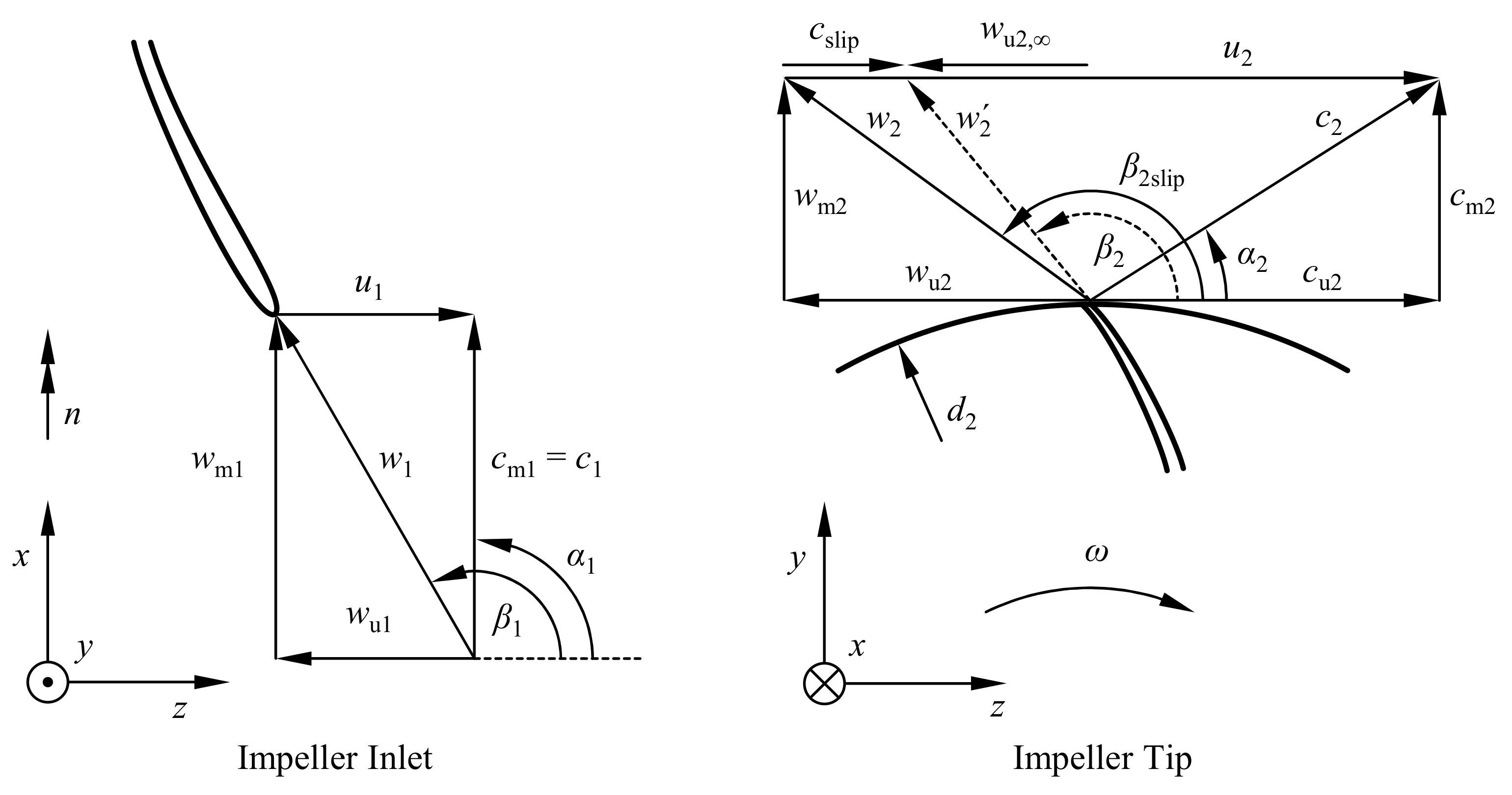
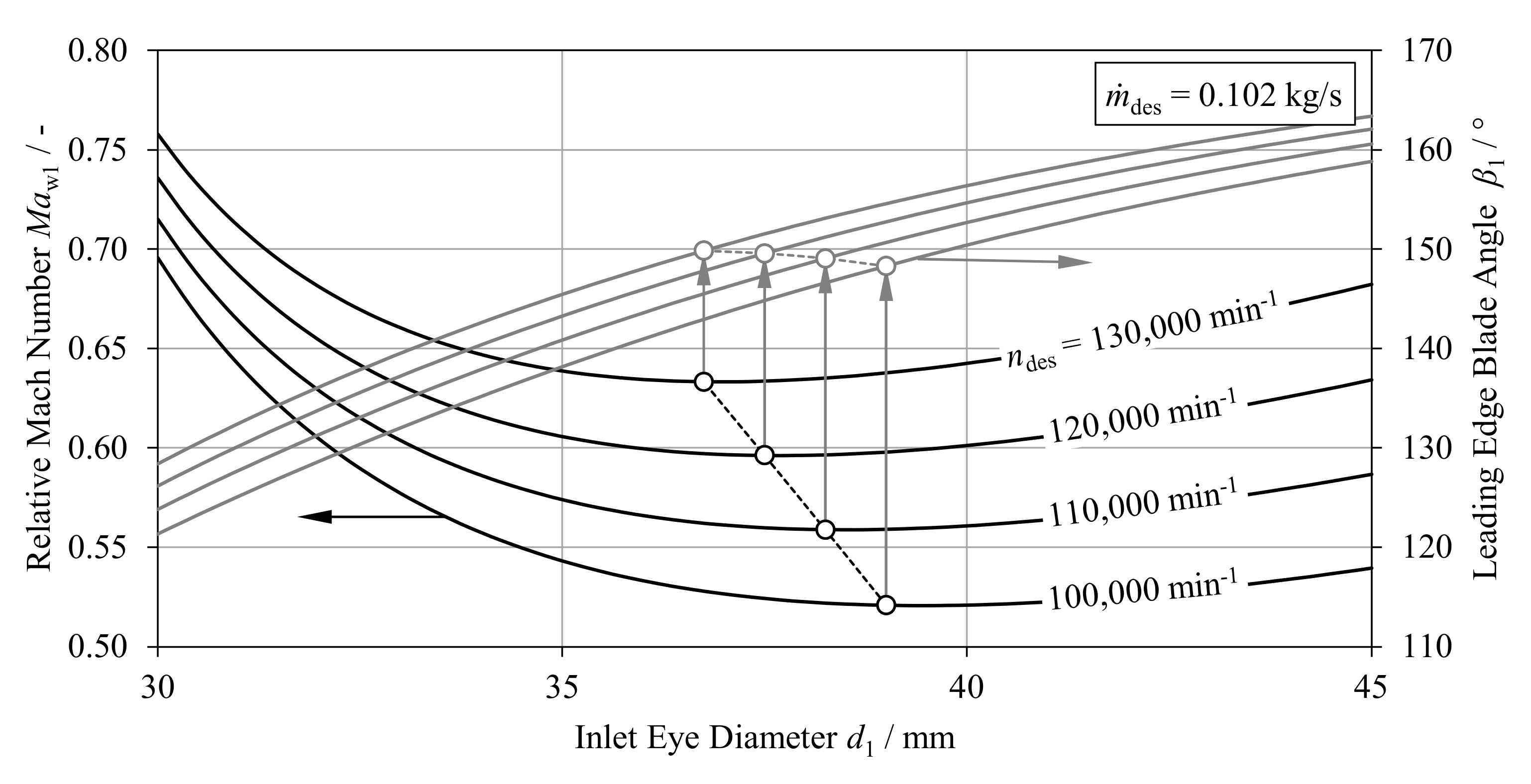
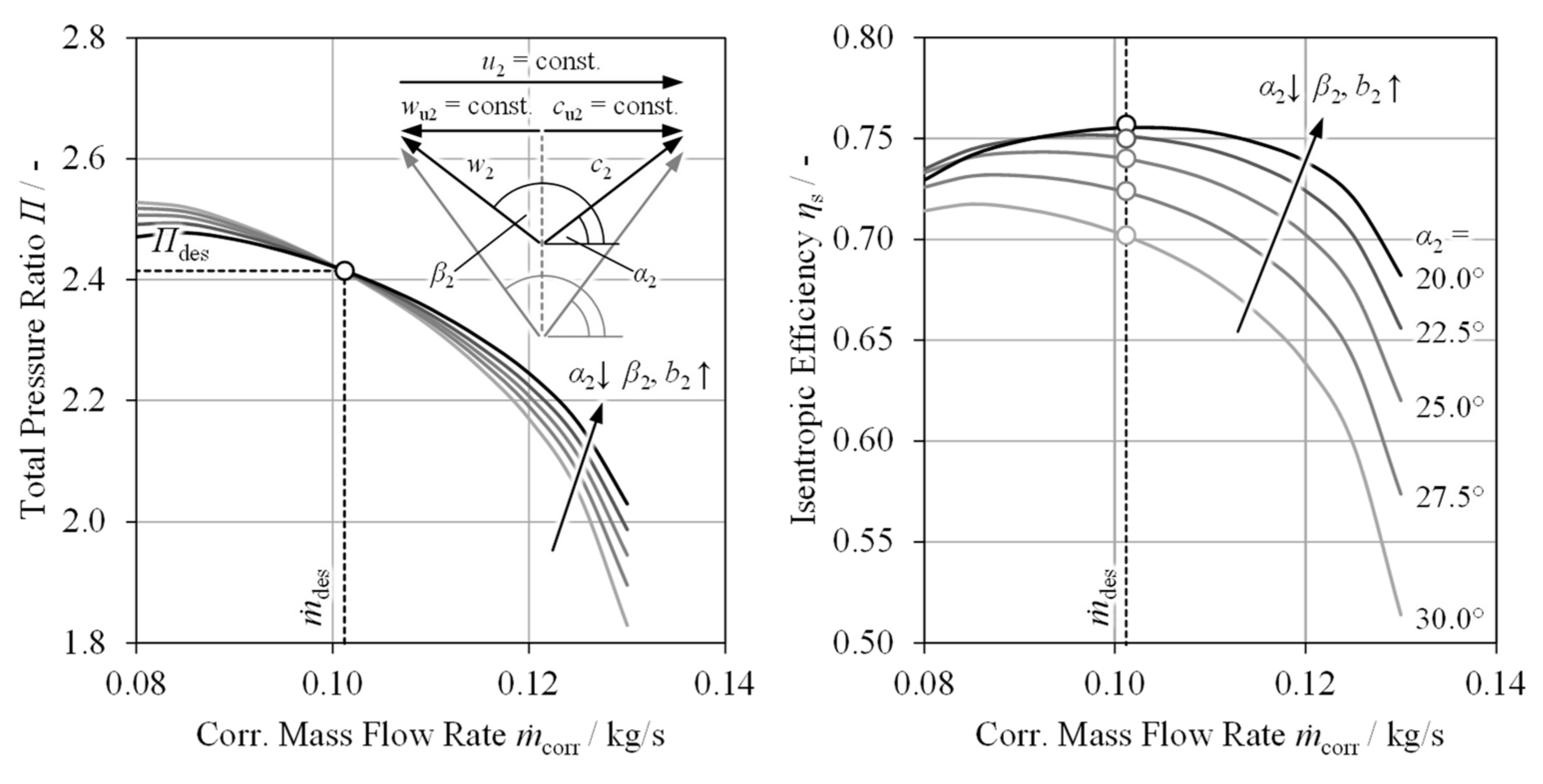
4.1. Compressor Stage Sizing
4.2. Electric Machine and Air Bearing Sizing
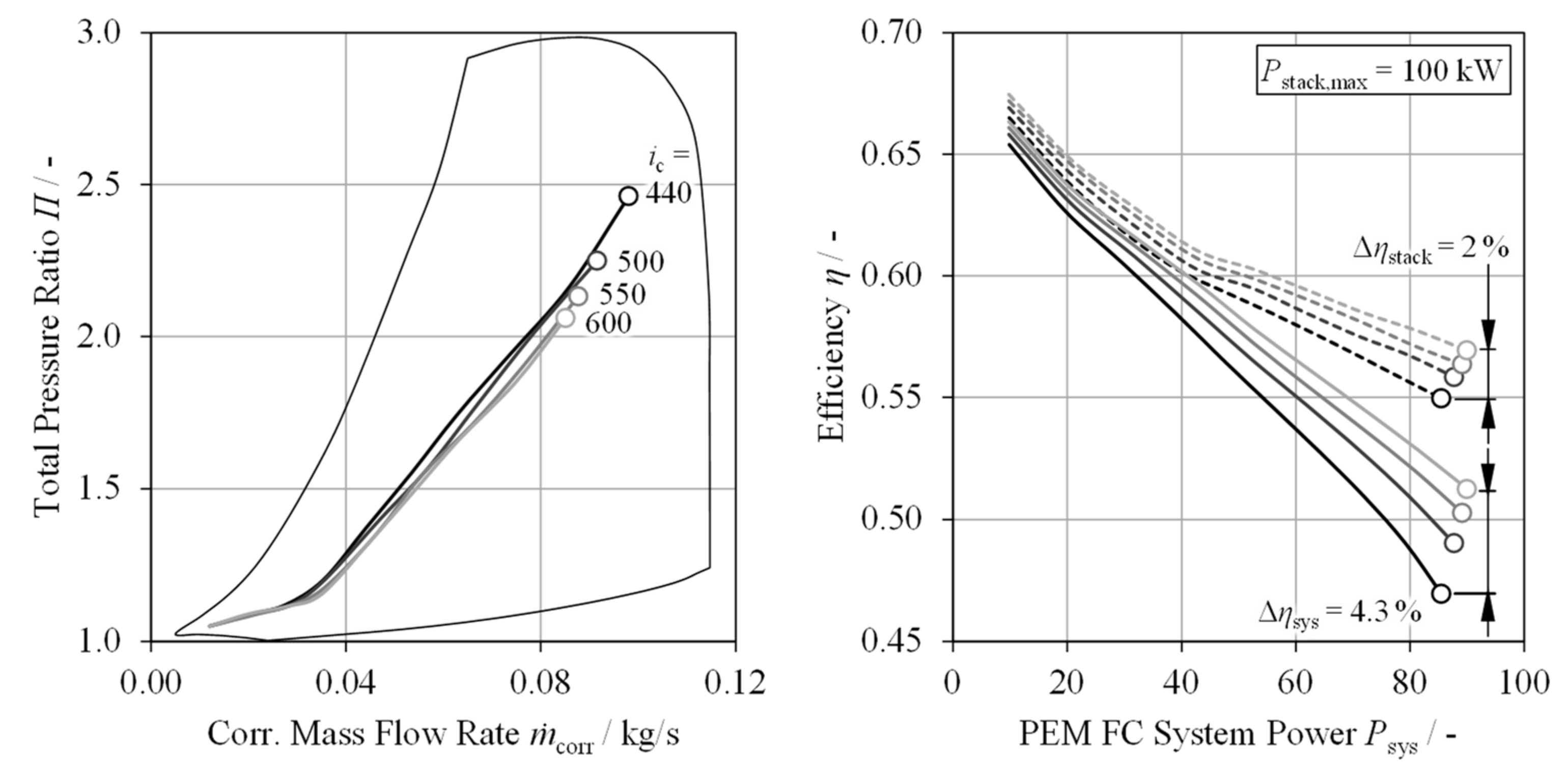
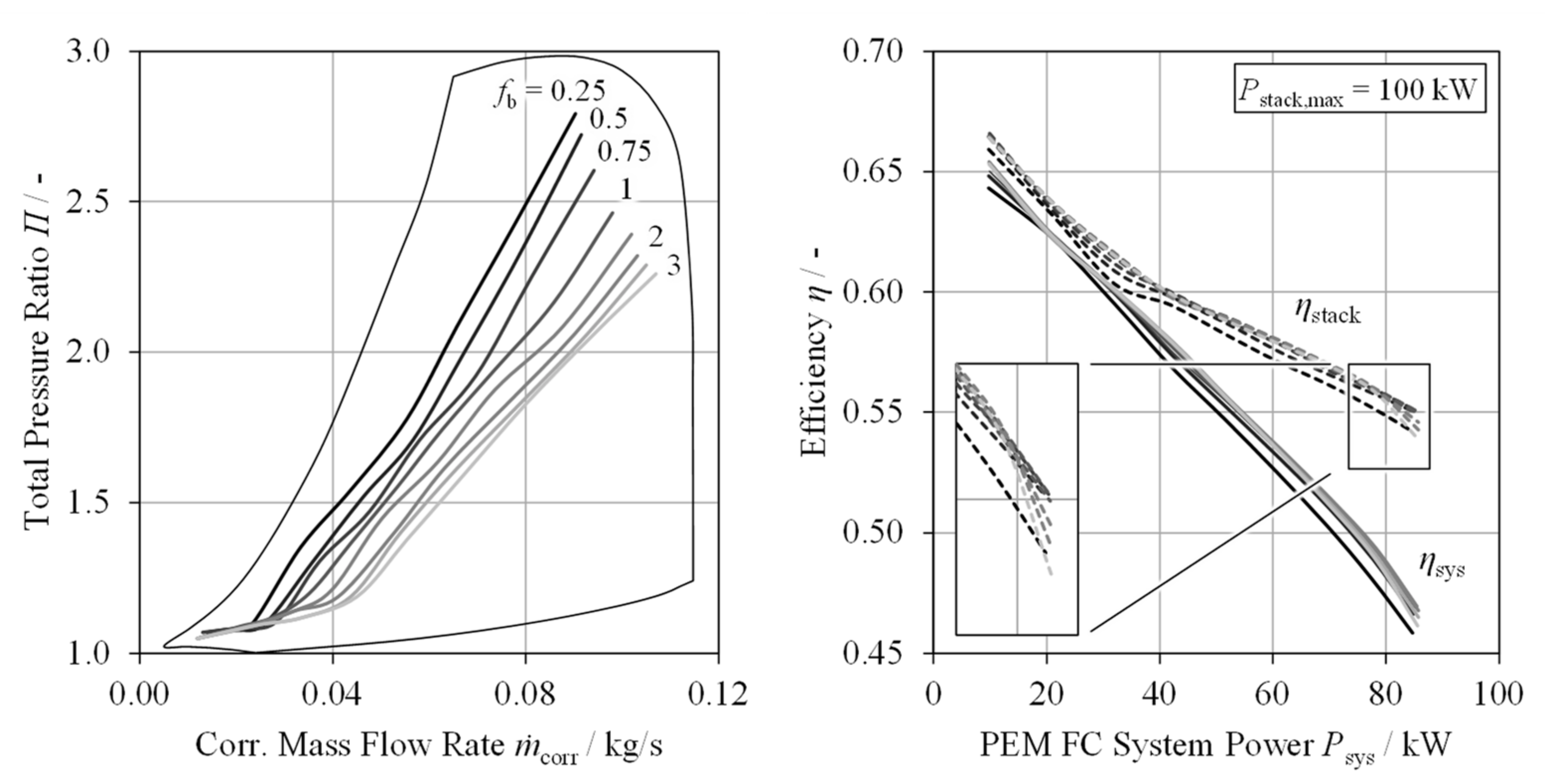
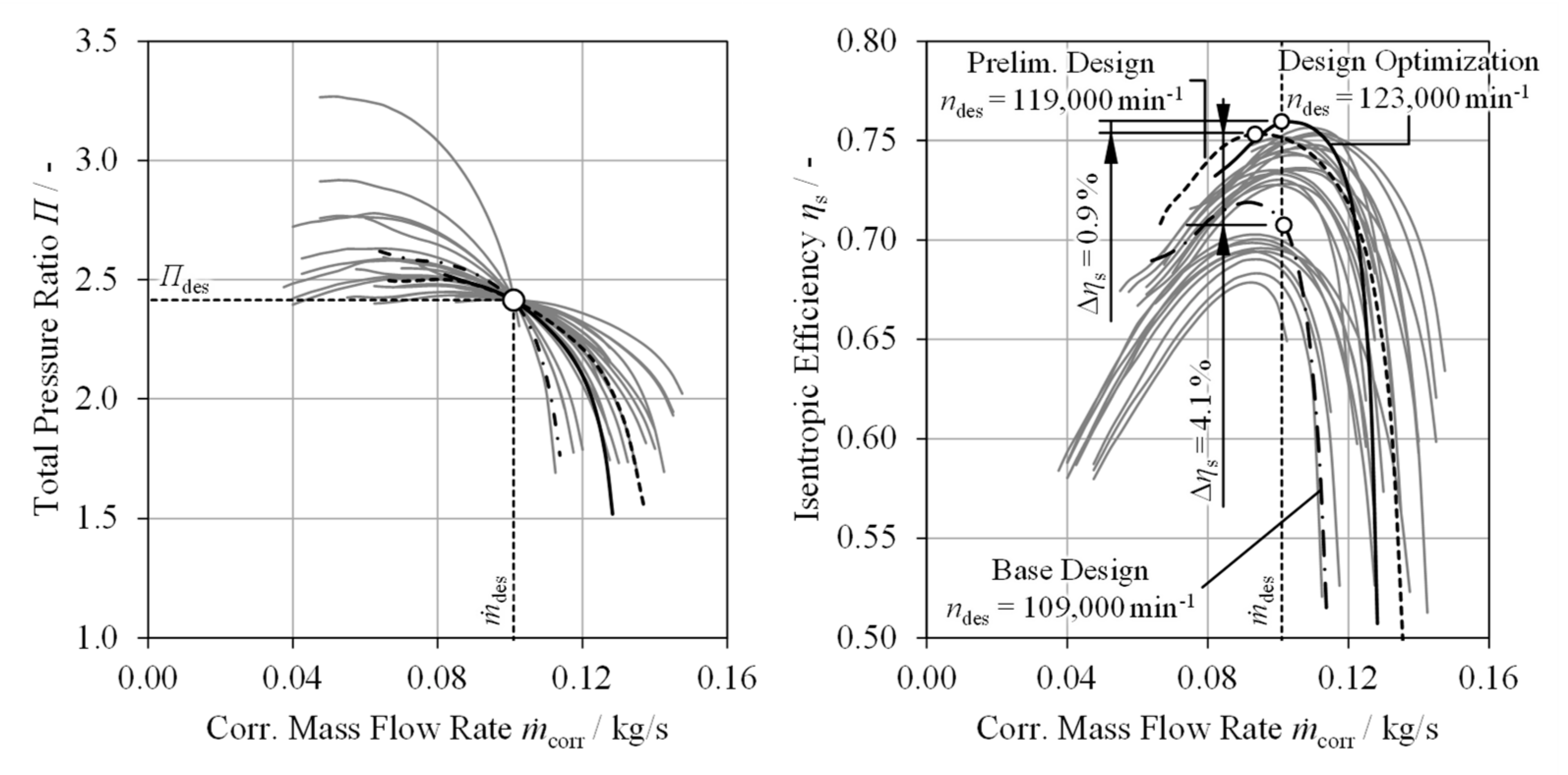
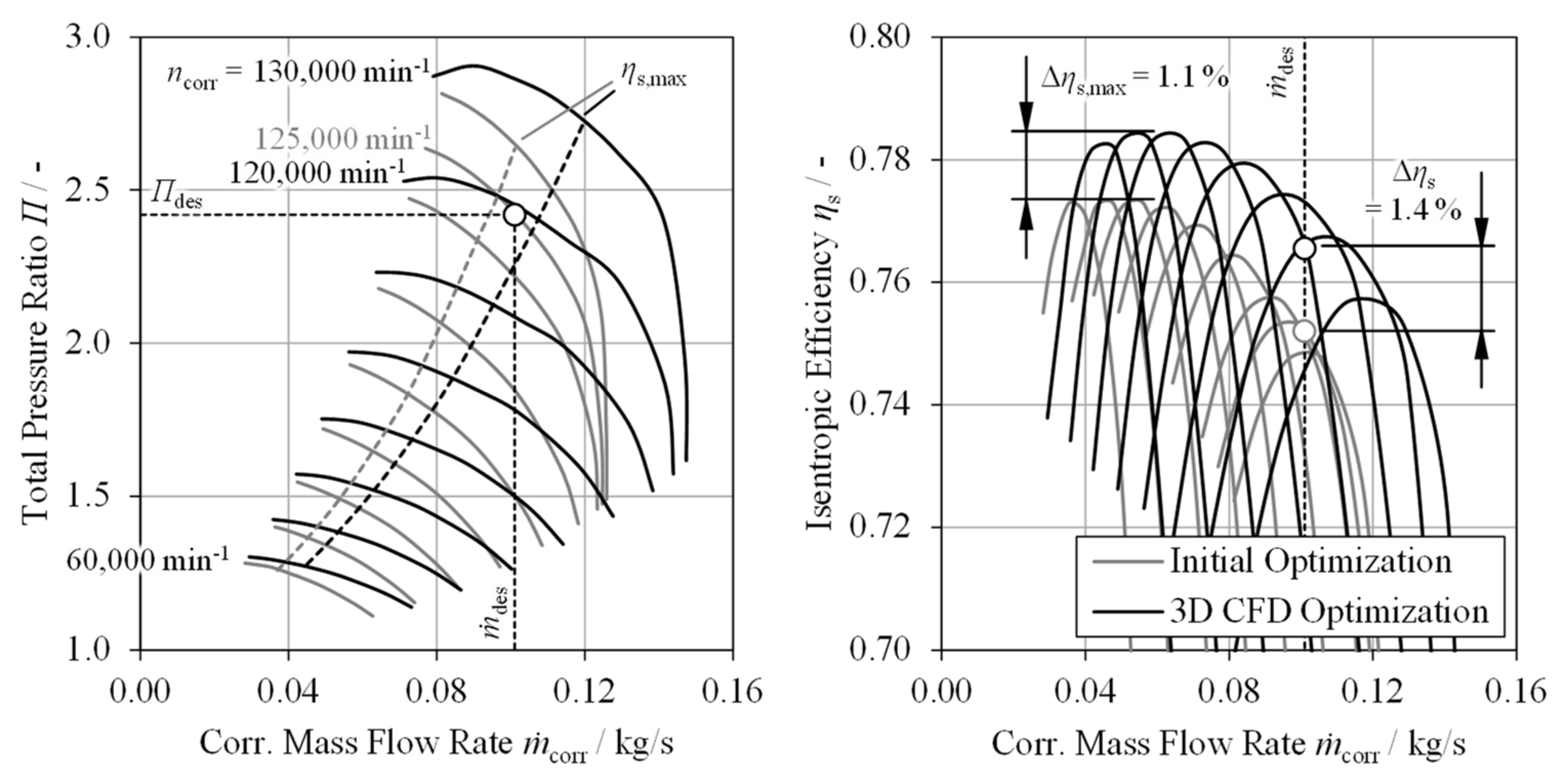
5. Compressor Design Optimization
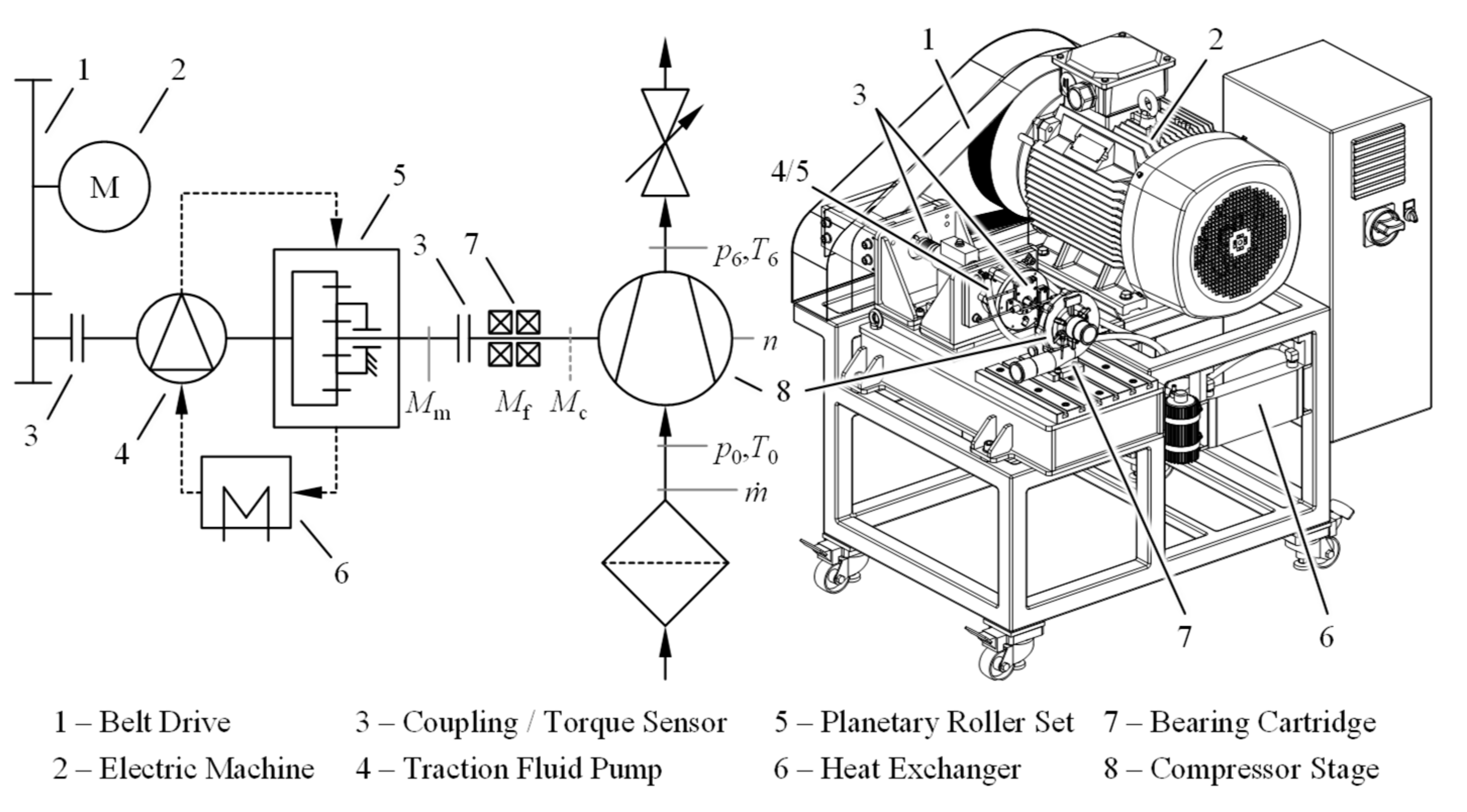
6. Experimental Validation
6.1. Test Setup and Measurement Equipment
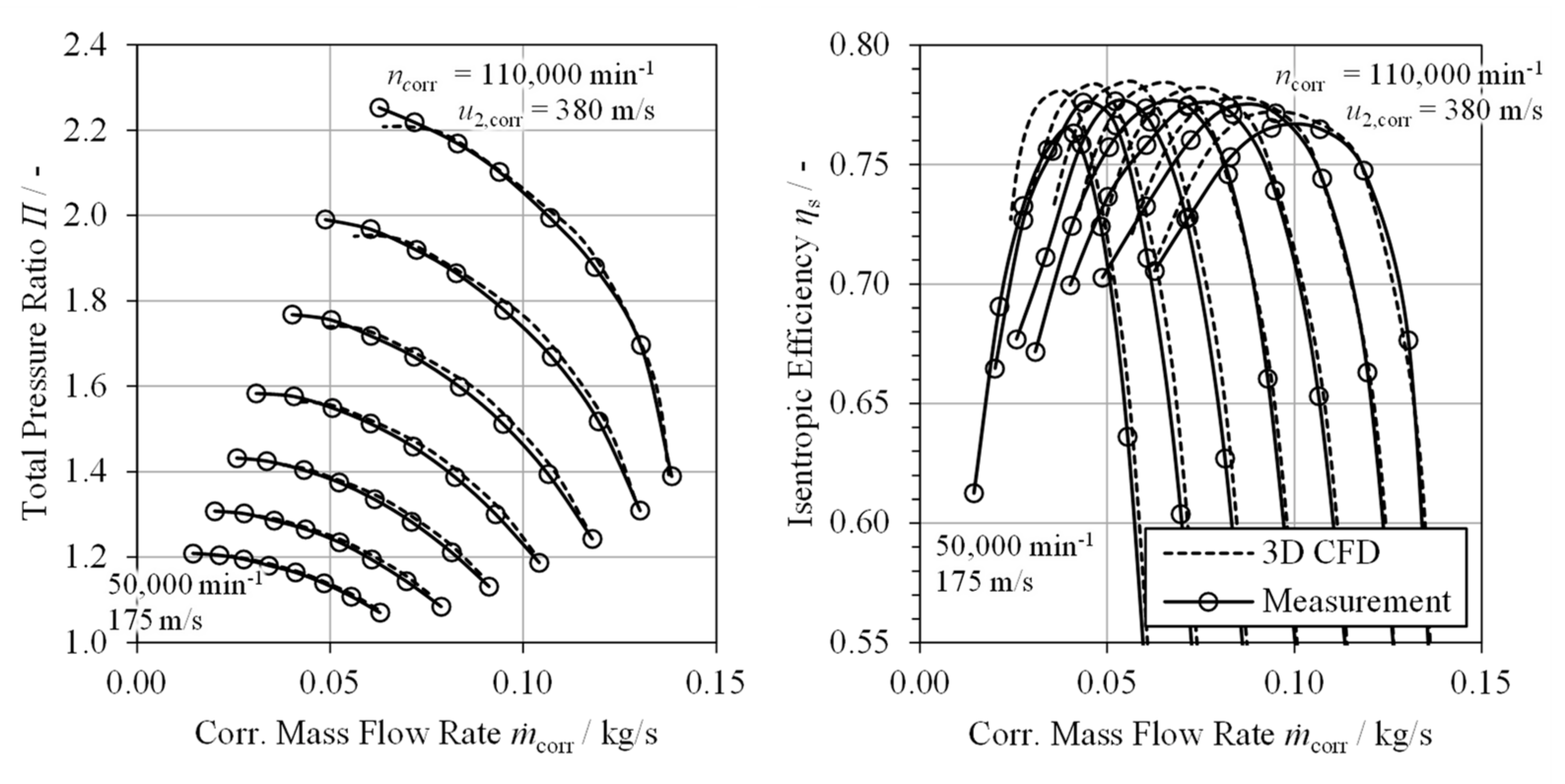
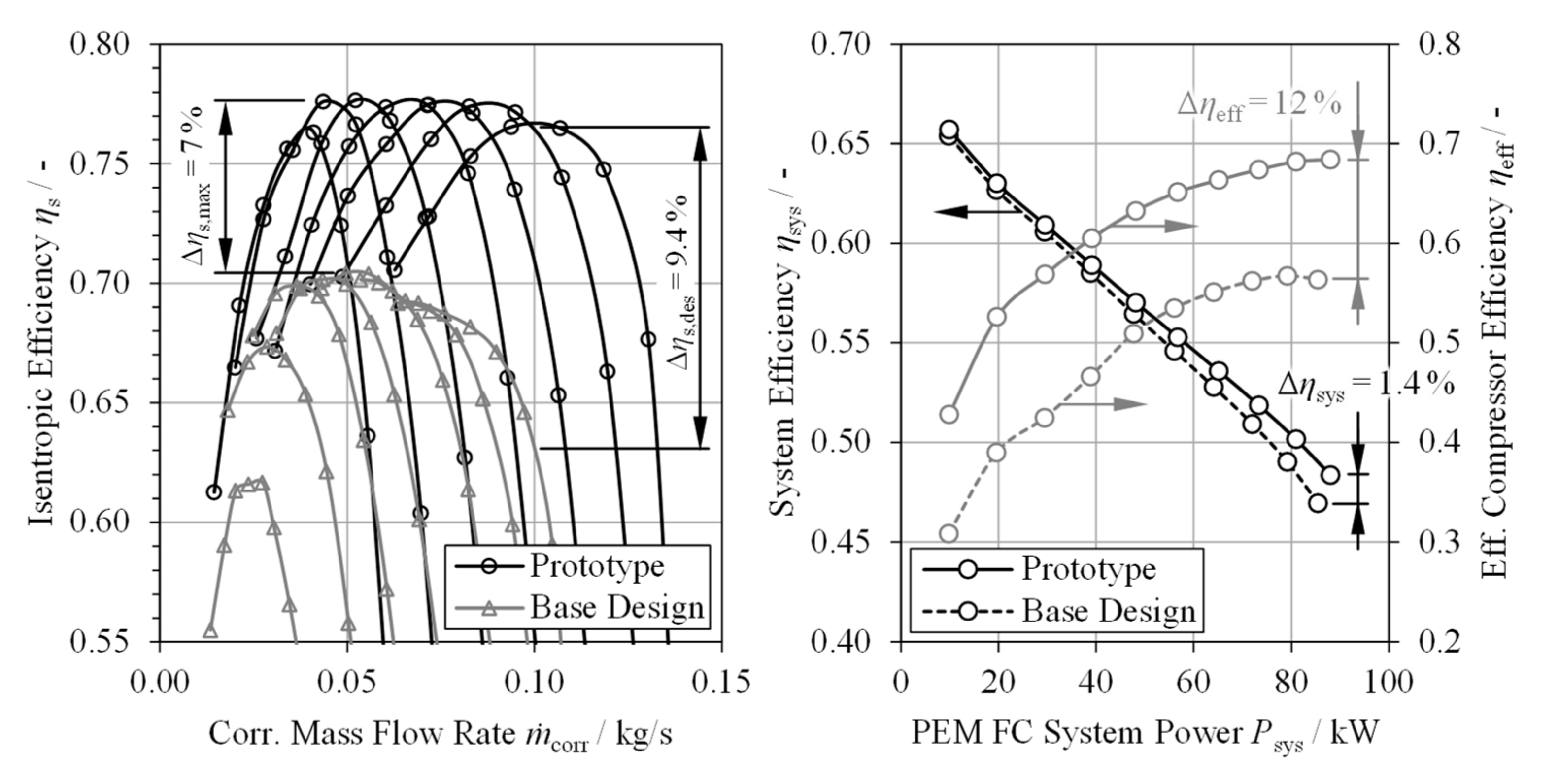
6.2. Experimental Results
7. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Thomas, C.E. Fuel cell and battery electric vehicles compared. Int. J. Hydrog. Energy 2009, 34, 6005–6020. [Google Scholar] [CrossRef]
- Dicks, L.; Rand, D.A.J. Fuel Cell Systems Explained, 3rd ed.; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Dixon, S.L.; Hall, C.A. Fluid Mechanics and Thermodynamics of Turbomachinery; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Schloßhauer. Erweiterung der Kennfeldbasierten Verdichtermodellierung für Sequentielle Aufladesysteme. Ph.D. Dissertation, RWTH Aachen University, Aachen, Germany, 2021. [Google Scholar]
- Luczynski, P.; Hohenberg, K.; Freytag, C.; Martinez-Botas, R. Integrated Design Optimisation and Engine Matching of a Turbocharger Radial Turbine. In Proceedings of the 14th International Conference on Turbochargers and Turbocharging; CRC Press: London, UK, 2021. [Google Scholar]
- Uhlmann, T. Vermessung und Modellierung von Abgasturboladern für Die Motorprozessrechnung. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2013. [Google Scholar]
- Lückmann, D. Interaktion Zweiflutiger Turbinen Mit Dem Verbrennungsmotor. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2016. [Google Scholar]
- Pfleiderer. Die Kreiselpumpen für Flüssigkeiten und Gase—Wasserpumpen, Ventilatoren, Turbogebläse—5. Neubearbeitete Auflage; Springer: Berlin/Göttingen/Heidelberg, Germany, 1961. [Google Scholar]
- Allard. Turbocharging & Supercharging; Cornell University: Ithaca, NY, USA, 1986. [Google Scholar]
- Giakoumis, E.G. Turbochargers and Turbocharging—Advancements, Applications and Research; Nova Science Publishers: Hauppauge, NY, USA, 2017. [Google Scholar]
- Klütsch, J.; Pischinger, S.; Lückmann, D.; Schloßhauer, A. Simulation-Driven Fuel Cell Compressor Design. MTZ Mot. Z. 2021, 82, 28–37. [Google Scholar] [CrossRef]
- Gerada, D.; Mebarki, A.; Brown, N.L.; Gerada, C.; Cavagnino, A.; Boglietti, A. High-Speed Electrical Machines: Technologies, Trends, and Developments. IEEE Trans. Ind. Electron. 2014, 61, 2946–2959. [Google Scholar] [CrossRef]
- Dellacorte, C.; Valco, M.J. Load Capacity Estimation of Foil Air Journal Bearings for Oil-Free Turbomachinery Applications. Tribol. Trans. 2000, 43, 795–801. [Google Scholar] [CrossRef]
- Klütsch, J.; Stadermann, M.; Lückmann, D.; Schloßhauer, A.; Walters, M. Fuel Cell Air Compressor Design for Mobile Applications. In Proceedings of the 26th Supercharging Conference, Dresden, Germany, 20–21 September 2022. [Google Scholar]
- Kim, J.; Lee, S.-M.; Srinivasan, S.; Chamberlin, C.E. Modeling of Proton Exchange Membrane Fuel Cell Performance with an Empirical Equation. J. Electrochem. Soc. 1995, 142, 2670. [Google Scholar] [CrossRef]
- Haslinger, M.; Lauer, T. Unsteady 3D-CFD Simulation of a Large Active Area PEM Fuel Cell under Automotive Operation Conditions—Efficient Parameterization and Simulation Using Numerically Reduced Models. Processes 2022, 10, 1605. [Google Scholar] [CrossRef]
- Houreh, N.B.; Afshari, E. Three-dimensional CFD modeling of a planar membrane humidifier for PEM fuel cell systems. Int. J. Hydrog. Energy 2014, 39, 14969–14979. [Google Scholar] [CrossRef]
- Oertel, H. Prandtl’s Essentials of Fluid Mechanics, 2nd ed.; Springer: New York, NY, USA; Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Moody, L.F. Friction Factors for Pipe Flow. Trans. ASME 1944, 66, 671–684. [Google Scholar] [CrossRef]
- Fick. Über Diffusion. Poggendorff’s Ann. Der Phys. 1855, 94, 59–86. [Google Scholar]
- Kulikovsky, A. Analytical Modelling of Fuel Cells; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Jamekhorshid, A.; Karimi, G.; Noshadi, I. Current Distribution and Cathode Flooding Prediction in a PEM Fuel Cell. Int. J. Chem. Mol. Energy 2010, 4, 157–165. [Google Scholar] [CrossRef]
- Liu, Z.; Mao, Z.; Wang, C. A two dimensional partial flooding model for PEMFC. J. Power Sources 2006, 158, 1229–1239. [Google Scholar] [CrossRef]
- Bakhtiar, A.; Kim, Y.-B.; You, J.-K.; Yoon, J.-I.; Choi, K.-H. A model and simulation of cathode flooding and drying on unsteady proton exchange membrane fuel cell. J. Cent. South Univ. 2012, 19, 2572–2577. [Google Scholar] [CrossRef]
- Springer, T.E.; Zawodzinski, T.A.; Gottesfeld, S. Polymer Electrolyte Fuel Cell Model. J. Electrochem. Soc. 1991, 138, 2334–2342. [Google Scholar] [CrossRef]
- Lee, J.S.; Quan, N.D.; Hwang, J.M.; Lee, S.D.; Kim, H.; Lee, H.; Kim, H.S. Polymer Electrolyte Membranes for Fuel Cells. J. Ind. Eng. Chem. 2006, 12, 175–183. [Google Scholar] [CrossRef]
- Zook, L.A.; Leddy, J. Density and Solubility of Nafion: Recast, Annealed, and Commercial Films. Anal. Chem. 1996, 68, 3793–3796. [Google Scholar] [CrossRef] [PubMed]
- Kulikovsky, A. Quasi-3D Modeling of Water Transport in Polymer Electrolyte Fuel Cells. J. Electrochem. Soc. 2003, 150, A1432–A1439. [Google Scholar] [CrossRef]
- Van Bussel, H.P.; Koene, F.G.; Mallant, R.K. Dynamic model of solid polymer fuel cell water management. J. Power Sources 1998, 71, 218–222. [Google Scholar] [CrossRef]
- FEV Europe GmbH. Vehicle Benchmark Hyundai Nexo, Final Report; FEV Europe GmbH: Aachen, Germany, 2020. [Google Scholar]
- FEV Europe GmbH. Vehicle Benchmark Toyota Mirai 2, Final Report; FEV Europe GmbH: Aachen, Germany, 2021. [Google Scholar]
- Tinz, S.N. Befeuchtungskonzepte für Brennstoffzellensysteme in Mobilen Anwendungen. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2022. [Google Scholar]
- Bird, R.B.; Steward, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Colburn, P. A Method of Correlating Forced Convection Heat Transfer Data and A Comparison with Fluid Friction. Int. J. Heat Mass Transf. 1933, 6, 1359–1384. [Google Scholar] [CrossRef]
- White, M. Viscous Fluid Flow, 2nd ed.; McGraw-Hill, Inc.: New York, NY, USA, 1991. [Google Scholar]
- Buhmann, M.D. Radial Basis Functions—Theory and Implementations; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Wick, M.; Klütsch, J.; Walters, M.; Zubel, M.; Jesser, M.; Ogrzewalla, J.; Schloßhauer, A.; Lückmann, D.; Uhlmann, T.; van der Put, D.; et al. 300+ kW Brennstoffzellensysteme für den Fernverkehr—Welche Verbesserungen sind mit dieser nächsten Generation von Brennstoffzellensystemen zu erwarten? In 44. Internationales Wiener Motorensymposium; Foreign Trade Center Budapest: Wien, NY, USA, 2023. [Google Scholar]
- Mayur, M.; Gerard, M.; Schott, P.; Bessler, W.G. Lifetime Prediction of a Polymer Electrolyte Membrane Fuel Cell under Automotive Load Cycling Using a Physically-Based Catalyst Degradation Model. Energies 2018, 11, 2054. [Google Scholar] [CrossRef]
- Wu, J.; Yuan, X.Z.; Martin, J.J.; Wang, H.; Zhang, J. A review of PEM fuel cell durability: Degradation mechanisms and mitigation strategies. J. Power Sources 2008, 184, 104–119. [Google Scholar] [CrossRef]
- Yousfi-Steiner, N.; Mocotéguy, P.; Candusso, D.; Hissel, D. A review on polymer electrolyte membrane fuel cell catalyst degradation and starvation issues: Causes, consequences and diagnostic for mitigation. J. Power Sources 2009, 194, 130–145. [Google Scholar] [CrossRef]
- US Department of Energy—Hydrogen and Fuel Cell Technologies Office. DOE Technical Targets for Polymer Electrolyte Membrane Fuel Cell Components. Available online: https://www.energy.gov/eere/fuelcells/doe-technical-targets-polymer-electrolyte-membrane-fuel-cell-components (accessed on 22 August 2022).
- Aungier, R.H. Centrifugal Compressors—A Strategy for Aerodynamic Design and Analysis; The American Society of Mechanical Engineers: New York, NY, USA, 2000. [Google Scholar]
- Rusch, D.; Casey, M. The Design Space Boundaries for High Flow Capacity Centrifugal Compressors. J. Turbomach. 2013, 135, 031035. [Google Scholar] [CrossRef]
- Casey, M.V.; Schlegel, M. Estimation of the performance of turbocharger compressors at extremely low pressure ratios. Proc. Inst. Mech. Eng. Part A J. Power Energy 2010, 224, 239–250. [Google Scholar] [CrossRef]
- Wiesner, J. A Review of Slip Factors for Centrifugal Impellers. J. Eng. Power 1967, 89, 558–566. [Google Scholar] [CrossRef]
- Stodola, A. Steam and Gas Turbines; McGraw-Hill: New York, NY, USA, 1927. [Google Scholar]
- Senoo, Y.; Kinoshita, Y. Limits of Rotating Stall and Stall in Vaneless Diffuser of Centrifugal Compressors. In ASME 1978 International Gas Turbine Conference and Products Show; American Society of Mechanical Engineers: London, UK, 1978. [Google Scholar]
- Wu, C.-H. A General Theory of Two- and Three-Dimensional Rotational Flow in Subsonic and Transonic Turbomachines, NASA Contractor Report 4496. In Nasa Scientific and Technical Information Program; NTRS—NASA Technical Reports Server: Cleveland, OH, USA, 1993. [Google Scholar]
- Japikse, D. Centrifugal Compressor Design and Performance, White River Junction; Concepts ETI: Wilder, TN, USA, 1996. [Google Scholar]
- Klütsch, J.; Wick, M.; Schloßhauer, A.; Lückmann, D.; Walters, M. Simulation-Driven PEM Fuel Cell Compressor Design. In Proceedings of the 30th Aachen Colloquium Sustainable Mobility 2021, Aachen, Germany, 4–6 October 2021. [Google Scholar]
- Müller, K.V.; Ponick, B. Berechnung Elektrischer Maschinen, 6. Auflage; Wiley-VCH: Berlin, Germany, 2007. [Google Scholar]
- Pyrhönen, J.; Jokinen, T.; Hrabovcova, V. Design of Rotating Electrical Machines, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Binder, A. Motor Development for Electrical Drive Systems—High Speed PM Machines; Institut für Elektrische Energiewandlung: Darmstadt, Germany, 2017. [Google Scholar]
- Dykas, B.; Bruckner, R.; DellaCorte, C.; Edmonds, B.; Prahl, J. Design, Fabrication, and Performance of Foil Gas Thrust Bearings for Microturbomachinery Applications; Nasa Technical Memo: Cleveland, OH, USA, 2008. [Google Scholar]
- DellaCorte, C.; Radil, K.C.; Bruckner, R.J.; Howard, S.A. Design, Fabrication, and Performance of Open Source Generation I and II Compliant Hydrodynamic Gas Foil Bearings. Tribol. Trans. 2008, 51, 254–264. [Google Scholar] [CrossRef]
- Kim, T.H.; Park, M.; Lee, T.W. Design Optimization of Gas Foil Thrust Bearings for Maximum Load Capacity. J. Tribol. 2017, 139, 031705. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, H.; Hu, L.; He, H. Fault Diagnosis and Failure Prediction by Thrust Load Analysis for a Turbocharger Thrust Bearing. In ASME Turbo Expo 2010: Power for Land, Sea and Air; ASME: Glasgow, UK, 2010. [Google Scholar]
- Bahm, F.U. Das Axialschubverhalten von Einstufigen Kreiselpumpen mit Spiralgehäuse. Ph.D. Thesis, Universität Hannover, Hannover, Germany, 2000. [Google Scholar]
- Honda, H.; Kanzaka, T.; Oka, N.; Verstraete, T.; Châtel, A.; Müller, L. Performance improvement of centrifugal compressors for automotive turbochargers using adjoint method. In 16th Asian International Conference on Fluid Machinery; IOP Publishing: Bristol, UK, 2021. [Google Scholar]
- Wang, X.-F.; Wang, G.; Wang, Z.H. Aerodynamic optimization design of centrifugal compressor’s impeller with Kriging model. Proc. Inst. Mech. Eng. Part A J. Power Energy 2006, 220, 589–597. [Google Scholar] [CrossRef]
- Siemens Digital Industries Software. Simcenter STAR-CCM+ Software. Available online: https://plm.sw.siemens.com/de-DE/simcenter/fluids-thermal-simulation/star-ccm/ (accessed on 29 June 2024).
- Rotrex A/S. C30 Technical Data Sheet, Rev. 6.0. 01 2022. Available online: https://www.rotrex.com/wp-content/uploads/2022/01/Rotrex-Technical-Datasheet-C30-Rev6.0.pdf (accessed on 8 May 2023).
- SAE Engine Power Test Code Committee, J1826-202204—Turbocharger Gas Stand Test Code; SAE International: Warrendale PA, USA, 2022.
- Björn, H. Analyse und Modellierung des thermischen Verhaltens von Pkw-Abgasturboladern. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2017. [Google Scholar]
- Klütsch, J.P.; Brodbeck, P.; Winkler, H. Bedatung von Modellen zur Beschreibung des Betriebsverhaltens von Abgasturboladern; FVV1314, Final Report; Forschungsvereinigung Verbrennungskraftmaschinen e. V.: Frankfurt am Main, Germany, 2020. [Google Scholar]
- Kistler Instrumente, A.G. Torque Sensor with Dual-Range-Option Type 4503B. Available online: https://kistler.cdn.celum.cloud/SAPCommerce_Download_original/000-767e.pdf (accessed on 3 May 2023).
- Manner Sensortelemetrie GmbH. Sensor Signal Amplifier Type RMC Samy-Flex—Technical Datasheet. Available online: https://www.sensortelemetrie.de/wp-content/uploads/technical_datasheet_signalverstrker_samy-flex.pdf (accessed on 3 May 2023).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klütsch, J.; Pischinger, S. Systematic Design of Cathode Air Supply Systems for PEM Fuel Cells. Energies 2024, 17, 3534. https://doi.org/10.3390/en17143534
Klütsch J, Pischinger S. Systematic Design of Cathode Air Supply Systems for PEM Fuel Cells. Energies. 2024; 17(14):3534. https://doi.org/10.3390/en17143534
Chicago/Turabian StyleKlütsch, Johannes, and Stefan Pischinger. 2024. "Systematic Design of Cathode Air Supply Systems for PEM Fuel Cells" Energies 17, no. 14: 3534. https://doi.org/10.3390/en17143534
APA StyleKlütsch, J., & Pischinger, S. (2024). Systematic Design of Cathode Air Supply Systems for PEM Fuel Cells. Energies, 17(14), 3534. https://doi.org/10.3390/en17143534



