Multiphase Flow’s Volume Fractions Intelligent Measurement by a Compound Method Employing Cesium-137, Photon Attenuation Sensor, and Capacitance-Based Sensor

Abstract

Multiphase fluids are common in many industries, such as oil and petrochemical, and volume fraction measurement of their phases is a vital subject. Hence, there are lots of scientists and researchers who have introduced many methods and equipment in this regard, for example, photon attenuation sensors, capacitance-based sensors, and so on. These approaches are non-invasive and for this reason, are very popular and widely used. In addition, nowadays, artificial neural networks (ANN) are very attractive in a lot of fields and this is because of their accuracy. Therefore, in this paper, to estimate volume proportion of a three-phase homogeneous fluid, a new system is proposed that contains an MLP ANN, standing for multilayer perceptron artificial neural network, a capacitance-based sensor, and a photon attenuation sensor. Through computational methods, capacities and mass attenuation coefficients are obtained, which act as inputs for the proposed network. All of these inputs were divided randomly in two main groups to train and test the presented model. To opt for a suitable network with the lowest rate of mean absolute error (MAE), a number of architectures with different factors were tested in MATLAB software R2023b. After receiving MAEs equal to 0.29, 1.60, and 1.67 for the water, gas, and oil phases, respectively, the network was chosen to be presented in the paper. Hence, based on outcomes, the proposed approach’s novelty is being able to predict all phases of a homogeneous flow with very low error.

1. Introduction

Multiphase fluids can be found in a number of industries, the most common of which are petrochemical, oil, water, and gas. These kind of flows are a mixture of different types of solid, liquid, or gas materials. Measuring volume fractions of phases is imperative in many subjects, such as economic matters, extraction, and so on. Previously, various phases of the fluid inside the pipe had to be separated and then measured. That manner was complex, time consuming, and expensive but was achieved by conventional tools. Hence, a multitude of either electrical or mechanical approaches have been introduced by researchers and scientists to overcome this important issue by utilizing turbo meters, vibrating densitometers, vortex meter, and sampling tubes, etc. [1,2]. One of the most seen multiphase fluids during transition is a combination of water, gas, and oil. For this reason, the importance of measuring volume fractions of such a fluid can be seen. Although there is lots of research related to the mentioned task, it can be considered as a challenge in the oil, petrochemical, and similar industries [3]. That is why a large number of methods and solutions have been introduced, to make it much better in comparison to previous manners. Take, for example, ANN, which stands for artificial neural networks. Due to its precision in many fields, ranging from engineering to medical-oriented concepts, it is one of the noteworthy tools for researchers in the measurement industry. On the other hand, to generate data as inputs for ANN, scientists are enthusiastic in utilizing a wide variety of prior valid sensors, such as capacitance-based sensors, photon attenuation sensors, electrical capacitance tomography (ECT), ultrasonic, and so on.

For instance, ECT as a useful approach in imaging has been used for over two decades [4,5]. The quality of this manner is good but when phases of a flow increases, ECT is faced with challenges. Due to this, it cannot be considered as a good way to investigate in multiphase flows [6]. Furthermore, in a separate investigation, wire-mesh sensors were deployed to assess gas–liquid–liquid flows, demonstrating the sensor’s efficacy in studying three-phase flow with some success. However, its capability was constrained as only a single electrical parameter was measured [7]. The calculation of liquid dielectric properties was often achieved by analyzing inductance, capacitance, or resistance, resulting in volume fraction measurements [8,9]. For instance, the authors of [10] utilized a flow meter based on correlation to determine water content, employing conductance measurement for the three-phase mixture. In [11], by utilizing a microcontroller, the authors have used several electrodes in order to monitor two-phase flows, while in [12], a capacitive sensor equipped with parallel plate (2 × 0.5 m) was used for this important task for a gas–solid flow. Extensive research has been dedicated to gamma radiation techniques for measuring volumes of gas, oil, and water. While many prior studies focused on specific fluids, the current investigation centers on a three-phase homogeneous system encompassing water, oil, and gas. In [13], Salgado and his colleagues employed a method based on gamma using dual-energy emitter radioisotopes to measure a multiphase fluid of gas, oil, and water.

Both capacitance-based sensors and photon attenuation sensors are non-invasive and that is why they are so attractive to use for not only direct measuring, but also producing inputs for ANN models. Authors in [14] measured both flow type and volume fractions by employing a gamma-based sensor along with an MLP ANN, standing for multilayer perceptron artificial neural network. For the proposed model, data were generated from a dual-energy photon source with two distinct detectors. This network could measure all three phases containing gas, water, and oil with an error rate of less than 5% for the former and the latter phases. In other research [15], radial basis function (RBF) network was used to estimate volume fractions of an annular flow containing gas, oil, and water. In this study, authors utilized a gamma-based sensor to generate data for three different RBF models. While the first one was employed to measure water and oil volumes, the second one was used to perform a similar task to that of the gas and water phases. This happened while volume fractions of gas and oil were measured by the third network. By comparing all of three models, the most accurate model was the first one to measure volume fractions of the mentioned flow. In addition, an ANN based on MLP architecture was developed [16] to assess volumetric proportions in homogeneous fluids, irrespective of the specific constitution of the liquid phase. Authors in [17] investigated measuring volume fractions of a two-phase homogeneous fluid regardless of the pressure factor changes along with considering temperature variations. Another study involved the potential of ANN tools and their intrinsic capabilities to uncover inventive strategies and methodologies to enhance a new kind of capacitive sensor’s efficacy [18]. Moreover, researchers in [19] scrutinized air–water and air–water–oil amalgamations with varying gas and liquid velocities. Additionally, feedforward backpropagation (FFBP) and MLP networks were employed to prognosticate pressure drop for both three-phase and two-phase flow scenarios.

In [20], researchers investigated measuring volume fractions of stratified and annular multiphase fluids by employing X-ray tubes along with a group method of data handling (GMDH). Moreover, the measuring of a three-phase fluid was performed by investigators in [21], who utilized a gamma backscatter technique and an MLP.

Utilizing just a capacitance-based sensor or a gamma-ray attenuation sensor with one detector and one source cannot result in measuring all phases of a multiphase fluid. This is because of the similar relative permittivity of oil and gas and the similar density of water and oil. To overcome this challenge, one of solutions is using multiple sensors relying on various physical characteristics. This manuscript introduces an innovative metering system crafted to independently gauge distinct phases. To apply such a great aim, there is need for employing cutting-edge methods. Hence, a new combination of two sensors along with an ANN was utilized to meet the goal. The presented metering system’s mean absolute error (MAE) for the all phases is under two. This underscores the remarkable precision of the proposed predictive approach. It is to be noted that, in homogeneous multiphase flows, all phases, including liquid and gas, move in the same velocity resulting in a slip ratio of 1, meaning the fluid is without bubble.

The following sections of this manuscript furnish a thorough narrative of the software, and mathematical expressions imperative for data generation in described Section 2. While the proposed network is investigated in Section 3, its results and discussion are shown in the next section. Ultimately, in Section 5, the presented metering system is concluded.

2. The Employed Sensors

It is an acknowledged truth that many types of equipment and methods exist to measure volume fractions of flows but among all of them, photon attenuation and capacitive sensors are so popular because they have shown a good accuracy in various applications. This is because of their non-invasive manner that can be installed easily without any kind of separation or interruption in the main process. For these reasons, both of them along with an optimized ANN are employed to estimate volume fractions of a multiphase fluid of water, oil, and gas. While many kind of flows exist, they can be considered in three main forms, named as homogeneous, stratified, and annular. These flows can be seen in Figure 1a–c. In these flows, the liquid with a yellow color presents a homogeneous fluid. While the blue color shows water phase, the oil phase is presented with orange. Eventually, the empty section stands for the gas phase.

The base of capacitive sensor is the measured capacities’ variation; that is because of altering in the material between its electrodes, which is called dielectric. When a capacitance-based sensor is utilized, the material inside the pipe is its dielectric. Hence, when there is a change in the proportion of materials and their ratio, the measured capacity of the sensor changes. This is because of materials’ dielectric properties, the most important of which is relative permittivity. This shows the dependence of a capacitive sensor to relative permittivity, which, due to very close relative permittivity of gas and oil, means that this sensor is unable to measure all three phases volume fractions [22]. Hence, there is a need for another sensor that relies on another physical parameter. Gamma-ray attenuation sensors, which rely on density factor, are a good choice but due to very close density of water and oil, measuring all three phases cannot be achieved. While the linear absorption coefficient of the gas phase is the lowest, the problem is other phases being liquids [23]. This way, a gamma sensor cannot measure these liquid phases all by itself. Hence, both sensors, capacitive and gamma, are used beside each other to complete the mission, which is measuring all three phases.

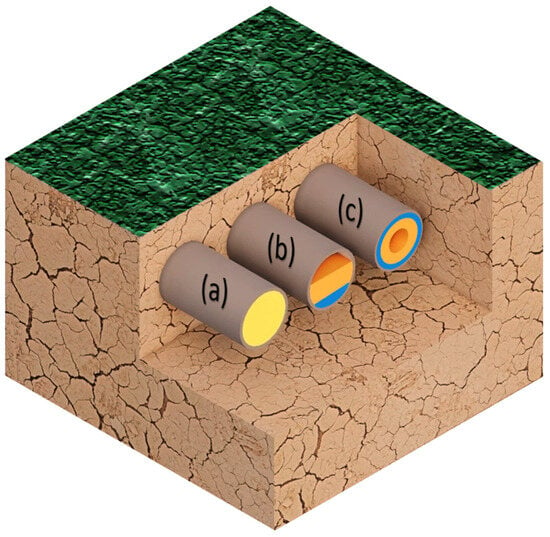
Figure 1. (a) Homogeneous fluid, (b) stratified fluid, and (c) annular fluid [24].

Opting for a sensor to measure volume fraction is a very important step in the measurement process. The main reason in selecting this kind of sensor in this study was its non-invasive behavior, meaning it can be used without performing separating or interruption in the process. Based on Equation (1), there is a definite link between measured capacity and the relative permittivity (ε_r) of the material between plates of the sensor. This parameter gives the amount of electrostatic energy related to the material that can be stored per unit after applying voltage. Whilst in the mentioned equation, C presents capacitance, D and A are the gap between two electrodes and area of electrodes, respectively. Finally, ε₀ is the relative permittivity of free space, being equal to 8.854 × 10⁻¹² F/m [25].

C = ε_r × ε₀ × A/D

(1)

Until today, many different kinds of geometrical shapes related to capacitive sensors have been introduced such as concave, ring, helix, and parallel plates, etc. In this paper, a special shape of capacitance-based sensors named twin rectangular fork-like capacitance sensor (TRFLC) [26] is chosen and simulated in the software. The software that is utilized is the COMSOL Multiphysics(version 6.2.339), which has a great level of precision in its calculations. This software was evaluated through experimental studies, which can be seen in the authors’ pervious work [27]. To benchmark this tool, a static experiment was built and its capacity was measured by an LCR meter. The model of the LCR meter utilized was GPS-3138C (GPS Ltd., London, UK) and the frequency of the measurement was 200 KHz. After that, both experimental and simulation results were compared and illustrated very close outcomes. Hence, this software was benchmarked and its data are completely valid.

To simulate the aforementioned sensor, the first step is separating other parts from the area with a stable condition and without any kind of noise that the sensor is supposed to create in it. After that, the main parts of the study are added, including a pipe with a relative permittivity equal to 3.4, electrode made from copper, and the liquid inside the pipe, which is shown as a yellow color in Figure 2. In the following steps, the liquid’s ε_r will be changed according to every ratio and combination of oil, Gas, and water. Next, as is clear in Figure 2, there are two different colors related to electrodes on the surface of the pipe. The red and gray electrodes define VCC and GND sections, respectively. Finally, the mesh and other settings are set and the process of simulating is started. Figure 2 shows a three-dimensional view of the simulated TRFLC sensor in the software. In Figure 3, various radiuses of the simulated sensor are presented. While R1 = 2.6 cm shows internal radius of the pipe, R2 = 3.3 cm shows external radius. The pipe has a thickness equal to 0.6 cm and the electrodes have a thickness equal to 0.1 cm that can be recognized by subtracting R3 = 3.2 cm from R2. About other sections, it is to be noted that the pipe has a length equal to 20 cm, labeled with L4 in Figure 4. This figure also shows each electrode’s length being L3 = 10.5 cm. L2, being the distance between the electrodes, and L1 are equal to 0.5 cm and 1 cm, respectively.

Figure 2. Three-dimensional view of the TRFLC sensor.

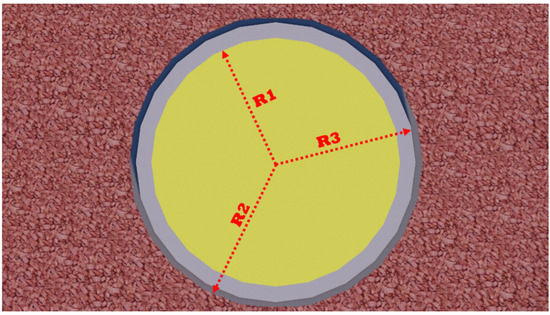
Figure 3. Different radiuses of the simulated TRFLC sensor.

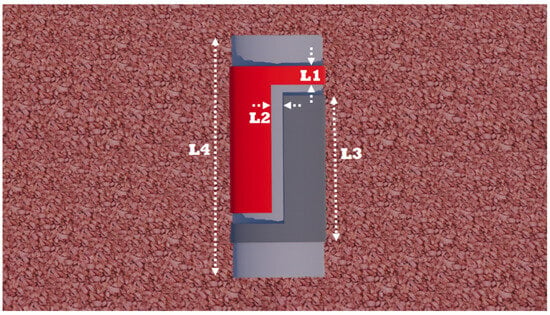
Figure 4. Different lengths of the simulated TRFLC sensor.

Simulations were performed 231 times because of the decision to select 5 percent change in the materials’ volume in every ratio. Mesh setting, which is a very important part. was set to “Fine” level to compute capacities with a great level of accuracy. After this simulation, the first input of the proposed network was generated and in the next step, gamma-ray attenuation sensor, the second input is produced.

Another critical determinant significantly influencing the gamma-ray attenuation sensor is density, denoting the mass of a material per unit volume. Essentially, higher particle concentration per unit volume results in a higher amount of density. This parameter plays a pivotal role in gamma-based sensor measurements. To gauge volumes using this approach, a ray traverses the liquid, and upon reaching the opposite side, the tally of received rays is recorded. Therefore, it becomes apparent that greater material density anticipates a lower count of rays due to a higher particles count.

Subsequent to material passage, interactions, notably photoelectric absorption, pair production, and Compton scattering, occur between the ray and the substance. These interactions underscore the density’s impact on this method, as depicted in Equation (2), recognized as the absorption law. Within this equation, I₀(E), I(E), η, E, Z, ρ, and L denote the emitted ray’s intensity, detected ray’s intensity, absorption coefficient, gamma-ray’s energy, atomic number, density, and liquid thickness, respectively [28]. Evidently, an inverse correlation exists between density and the number of rays reaching detectors. Equation (3) incorporates µ(E), the linear attenuation coefficients, into Equation (2), leading to the derivation of Equation (4), facilitating the calculation of I(E)/I₀(E), the second input for the network. Equation (5) provides a means to compute Equation (4) for the specified liquid, where α, β, and γ represent the volume fractions of oil, water, and gas, respectively, and the sum of them is equal to 1. While µ(E)_o is the linear attenuation coefficient of oil, µ(E)_w and µ(E)_g are the same parameters of water and gas, respectively. Equation (6) presents the main formula being used to generate data from the water–oil–gas flow for the network. It is to be noted that the length of the pipe is 5.2 cm.

The determination of the source gamma-ray type is essential for calculations, and this study employed Cesium-137 emitting 0.662 MeV. Figure 5 illustrates the process of the ray traversing the liquid and reaching the detector. Drawing from data in [29], the linear attenuation coefficients of gas, oil, and water were considered and applied to Equation (6) to generate the required data for the network’s second input.

I(E) = I₀(E)exp(−η(ZE)ρ × L)

(2)

µ(E) = η(ZE)ρ

(3)

I(E) = I₀(E)exp(−µ(E) × L)

(4)

µ(E) = α × µ(E)_o + β × µ(E)_w + γ × µ(E)_g

(5)

Ln (I/I₀) = −[α × µ(E)_o + β × µ(E)_w + γ × µ(E)_g] × L

(6)

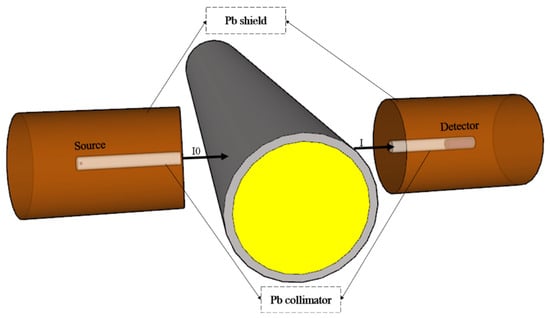
Figure 5. The way that a gamma-ray attenuation sensor counts.

3. Artificial Neural Network

In contemporary times, intelligent measurement finds applications across diverse fields, extending beyond electrical engineering and similar disciplines. Notably, research is evident in financial studies, medical investigations, transportation, and more [30]. Within the realm of artificial intelligence (AI), ANN encompass various types, including the MLP and radial basis function (RBF). The MLP ANN, distinguished by its simplicity, faithful precision, and significant capacity for accurate measurements, stands as a widely utilized variant [31]. Previous works in the measurement domain frequently employed MLP ANN [15,16,17,18,19]. The MLP ANN of the current study comprises the three following primary layers: the input layer, receiving data from the TRFLC sensor and gamma-ray sensor; the hidden layer, where calculations predominantly occur; and the output layer, presenting the predicted volume fractions. Data in this model are categorized into train and test sets, with the former facilitating network training and the latter assessing performance [32].

To identify the most accurate network configuration, extensive MATLAB coding and investigation of numerous networks with various hyperparameters led to the identification of the best network capable of accurately predicting the volume fractions of a water–oil–gas homogeneous flow. The main code incorporated several loops, each with varying different characteristics to find the network with the lowest mean absolute error (MAE) for all three phases. In each experiment, one hyperparameter was adjusted, such as the number of hidden layers, neurons in each hidden layer, activation functions, and the number of epochs. The model with the lowest error rate was selected and was explained in this paper. For the chosen model, 3 neurons are used in the output layer to represent gas, water, and oil amounts, with 11 neurons in the first hidden layer and 9 in the second hidden layer. Also, the network’s two inputs involve capacities generated by simulating the TRFLC sensor in COMSOL Multiphysics and counted Cs gamma rays from the gamma-ray sensor, obtained through various calculations. While 30% of all data was considered for testing the network, the rest of them (161 out of 231 data) were chosen for training. Additionally, a 5% material ratio change was applied across simulations and calculations. In Figure 6, all taken steps regarding the proposal of the best structure are shown. The activation function for input and output layers was “Purelin”, while “Tansig” served this crucial function for both hidden layers. The network’s learning method was based on Levenberg–Marquardt [33,34], utilizing 1600 epochs to achieve the desired outcome. In summary, the illustrated network in Figure 7 proficiently predicts volume fractions in a three-phase homogeneous fluid (gas, water, and oil) with minimal MAE across all phases.

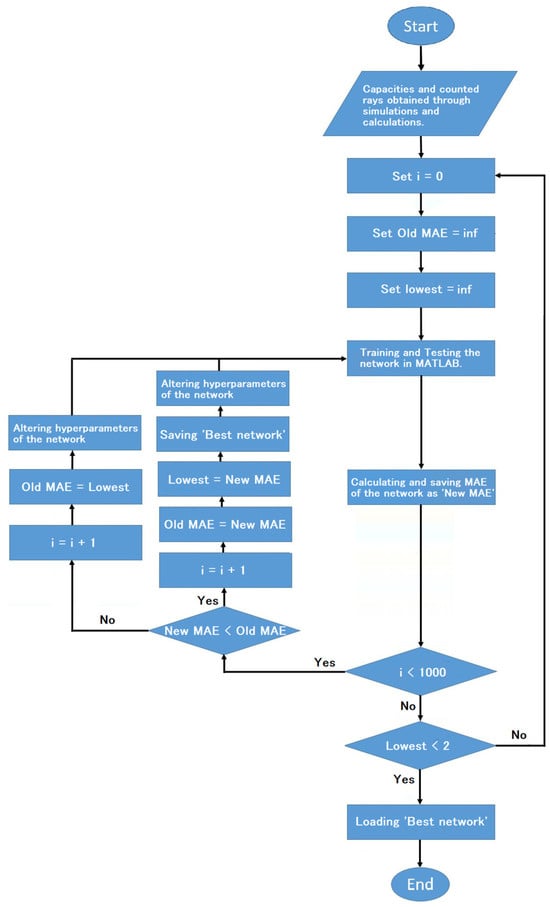
Figure 6. The way that the best network was chosen.

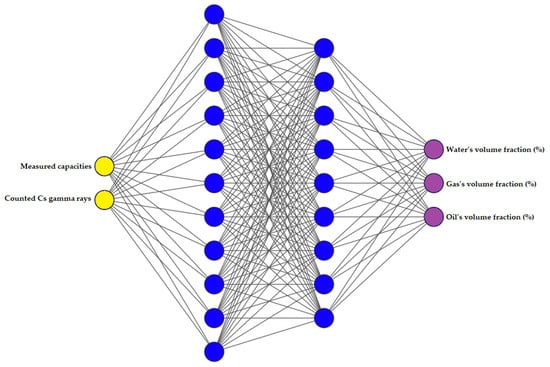
Figure 7. Architecture of the presented network.

4. Results and Discussion

In this section, the results from the implemented network are examined. The network used two inputs: one from simulations with the TRFLC sensor using COMSOL software, and the other from calculations based on equations related to the gamma-ray attenuation sensor. This resulted in 231 data points, each connected to a specific phase ratio. These data points were then divided for training and testing. Figure 8 shows the complete diagram of the new metering system, which includes the TRFLC sensor, a gamma-ray attenuation sensor, and an MLP ANN.

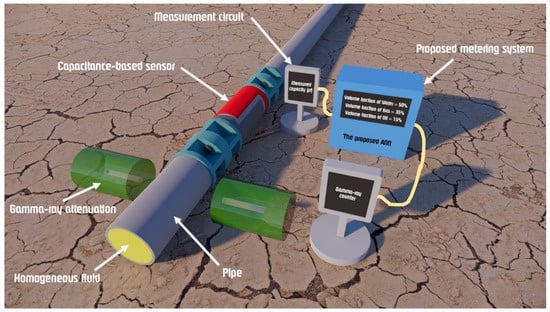
Figure 8. The schematic of the presented metering system.

There are different material ratios where the capacitance-based sensor generates very similar capacities, and this is because of the ε_r, which is the martial between its electrodes. Relative permittivity of water, gas, and oil is equal to 81, 1, and 2.2 [16], respectively, and due to this difference, this type of sensor can solely predict the volume fraction of water in diverse states. To address this limitation and propose a system being capable of predicting all three phases, another sensor relying on a different physical concept must be utilized. Hence, a gamma-ray attenuation sensor was incorporated because density exerts a significant influence on the measurement. This sensor adeptly measures the gas phase’s volume fraction due to the closely matched densities of water = 1 gr/cm³ and oil = 0.9 gr/cm³, which are much higher than that of gas, being 0.001 gr/cm³ [35].

Figure 9 depicts the train and test results produced by the implemented network, revealing accurate predictions for the water, gas, and oil phases without signs of overfitting or underfitting.

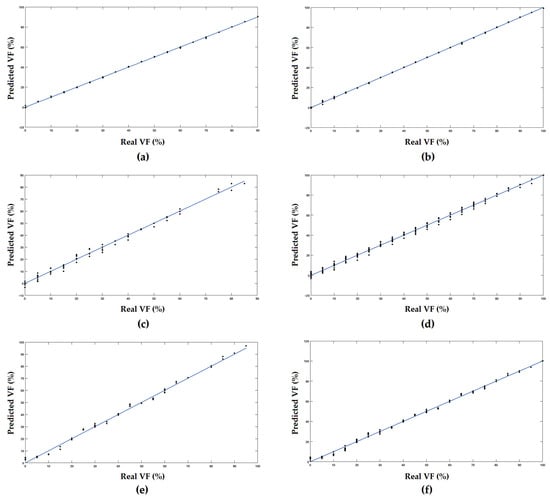
Figure 9. (a) Water’s test data regression diagram, (b) water’s train data regression diagram, (c) gas’s test data regression diagram, (d) gas’s train data regression diagram, (e) oil’s test data regression diagram, and (f) oil’s train data regression diagram.

In fluid flow, Prandtl and Reynolds dimensionless numbers are utilized to describe the flow characteristics. According to Equation (7), the Prandtl can be calculated, and the Reynolds number can be obtained by Equation (8) [36].

$$\mathrm{P}\mathrm{r}={\displaystyle \frac{{\mu }_{eff}{c}_{p·eff}}{k_{eff}}}$$

(7)

$$\mathrm{R}\mathrm{e}={\displaystyle \frac{{\rho }_{eff}ul}{{\mu }_{eff}}}$$

(8)

In these equations, Pr, Re, ${\mu }_{eff}$, $c_{p·eff}$, $k_{eff}$, ${\rho }_{eff}$, $u$, and $l$ are Prantdl number, Reynolds number, dynamic viscosity, specific heat capacity, thermal conductivity, density, characteristic velocity, and characteristic length, respectively. Due to the type of the fluid, which is a multiphase flow, effective values of each parameter were placed in equations. In Table 1, values of all of variables are presented except u and l, considered to be 10 m/s and 0.5 m, respectively. To calculate effective values, Equations (9) to (12) must be used [36]. Table 2 presents the obtained outputs and their disparities from the actual values. In Table 2, colors show the amount of error in each ratio and for each phase. Green shows the lowest error and yellow is the highest.

$${\rho }_{eff}={VF}_{Gas}\times {\rho }_{Gas}+{VF}_{Water}\times {\rho }_{Water}+{VF}_{Oil}\times {\rho }_{Oil}$$

(9)

$${\mu }_{eff}={VF}_{Gas}\times {\mu }_{Gas}+{VF}_{Water}\times {\mu }_{Water}+{VF}_{Oil}\times {\mu }_{Oil}$$

(10)

$$k_{eff}={VF}_{Gas}\times k_{Gas}+{VF}_{Water}\times k_{Water}+{VF}_{Oil}\times k_{Oil}$$

(11)

$$C_{p·eff} ={\displaystyle \frac{{VF}_{Gas}\times {\rho }_{Gas}\times c_{p·Gas}+{VF}_{Water}\times {\rho }_{Water}\times c_{p·Water}+{VF}_{Oil}\times {\rho }_{Oil}\times c_{p·Oil}}{{VF}_{Gas}\times {\rho }_{Gas}+{VF}_{Water}\times {\rho }_{Water}+{VF}_{Oil}\times {\rho }_{Oil}}}$$

(12)

Table 1. Various parameters for calculating Prandtl and Reynolds number at 20 degrees centigrade [36].

	Gas	Water	Oil
$\rho$ (kg/m3)	1.2	1000	900
$\mu$ (Pa·s)	1.8 × ${10}^{-5}$	0.001	0.5
$k$ (W/m·K)	0.025	0.6	0.15
$c_p$ (J/kg·K)	1005	4186	2000

Table 2. Predicted volume fractions of all three phases by the presented network in comparison with their real amounts.

Gas VF Real (%)	Water VF Real (%)	Oil VF Real (%)	Gas VF Predicted (%)	Water VF Predicted (%)	Oil VF Predicted (%)	Gas’s Absolute	Water’s Absolute	Oil’s Absolute
						Error	Error	Error
15	85	0	10.913387	85.172807	3.9137882	4.086613	0.172807	3.913788
25	65	10	27.831509	64.736502	7.4319771	2.831509	0.263498	2.568023
10	30	60	7.7712042	29.838744	62.390046	2.228796	0.161256	2.390046
25	10	65	26.572223	10.069296	63.35853	1.572223	0.069296	1.64147
50	25	25	49.243431	24.776412	25.980178	0.756569	0.223588	0.980178
15	75	10	11.285484	74.959631	13.754864	3.714516	0.040369	3.754864
65	10	25	66.884093	9.8224062	23.293635	1.884093	0.177594	1.706365
80	5	15	79.665931	6.5701996	13.76407	0.334069	1.5702	1.23593
35	25	40	33.933778	24.887602	41.178638	1.066222	0.112398	1.178638
5	50	45	5.0178017	50.138509	44.843658	0.017802	0.138509	0.156342
5	75	20	5.3384456	75.086652	19.574875	0.338446	0.086652	0.425125
5	65	30	5.0679691	64.860442	30.071558	0.067969	0.139558	0.071558
0	10	90	2.6335723	9.7371359	87.629322	2.633572	0.262864	2.370678
35	35	30	33.488231	35.269481	31.242289	1.511769	0.269481	1.242289
20	55	25	19.276919	55.168548	25.554513	0.723081	0.168548	0.554513
35	30	35	33.714687	30.08246	36.202862	1.285313	0.08246	1.202862
10	35	55	7.6975647	35.02615	57.276271	2.302435	0.02615	2.276271
70	15	15	69.620939	14.709692	15.669506	0.379061	0.290308	0.669506
35	15	50	33.890651	14.758431	51.350955	1.109349	0.241569	1.350955
85	5	10	87.404505	7.0362529	5.5594775	2.404505	2.036253	4.440522
35	45	20	33.344459	45.387005	21.268525	1.655541	0.387005	1.268525
10	85	5	6.876399	85.331049	7.7925308	3.123601	0.331049	2.792531
20	35	45	21.064888	35.260079	43.67503	1.064888	0.260079	1.32497
25	75	0	28.738268	74.392027	−3.1303018	3.738268	0.607973	3.130302
5	95	0	3.350574	94.952338	1.6970701	1.649426	0.047662	1.69707
80	0	20	81.056923	−0.5433485	19.486638	1.056923	0.543349	0.513363
100	0	0	100.25363	0.5660806	−0.8194028	0.253631	0.566081	0.819403
0	5	95	3.000451	5.3820733	91.617517	3.000451	0.382073	3.382483
5	5	90	4.3715126	5.3609461	90.267584	0.628487	0.360946	0.267584
10	40	50	7.5304801	40.15452	52.314979	2.46952	0.15452	2.314979
75	25	0	74.797941	24.062943	1.1392578	0.202059	0.937057	1.139258
15	10	75	13.620304	9.8520346	76.527701	1.379696	0.147965	1.527701
5	45	50	5.1056063	45.211362	49.683004	0.105606	0.211362	0.316996
45	5	50	46.677298	5.5768348	47.74592	1.677298	0.576835	2.25408
60	20	20	60.454517	19.662207	19.883359	0.454517	0.337793	0.116641
20	70	10	19.071512	69.797086	11.131384	0.928488	0.202914	1.131384
50	20	30	49.287898	19.646974	31.06516	0.712102	0.353026	1.06516
30	50	20	30.288257	50.342381	19.36935	0.288257	0.342381	0.63065
60	30	10	59.157734	29.953677	10.888646	0.842266	0.046323	0.888646
20	0	80	21.2667	−0.088374	78.821723	1.2667	0.088374	1.178277
10	90	0	6.2338835	90.251039	3.5150582	3.766117	0.251039	3.515058
40	30	30	39.879803	30.037108	30.083096	0.120198	0.037108	0.083096
65	20	15	67.472182	19.671555	12.85638	2.472182	0.328445	2.14362
5	0	95	4.4833565	−0.4718652	95.988546	0.516644	0.471865	0.988546
40	25	35	40.200223	24.853591	34.946202	0.200223	0.146409	0.053798
50	0	50	48.684902	−0.041292	51.35646	1.315098	0.041292	1.35646
45	25	30	46.440611	24.823834	28.73557	1.440611	0.176166	1.26443
20	30	50	21.610296	30.087453	48.302256	1.610296	0.087453	1.697744
40	0	60	41.383771	−0.0013561	58.617638	1.383771	0.001356	1.382362
0	50	50	4.1279189	50.192889	45.679161	4.127919	0.192889	4.320839
35	20	45	34.029008	19.763423	46.207596	0.970992	0.236577	1.207596
65	0	35	65.993002	−0.3015169	34.308578	0.993002	0.301517	0.691422
5	15	80	4.0333148	14.485203	81.481503	0.966685	0.514797	1.481503
10	50	40	7.140987	50.134776	42.724208	2.859013	0.134776	2.724208
20	20	60	22.287136	19.79164	57.921249	2.287136	0.20836	2.078751
20	5	75	20.807742	5.6544475	73.537867	0.807742	0.654447	1.462133
0	45	55	4.1698404	45.254529	50.575602	4.16984	0.254529	4.424398
95	5	0	93.89708	3.1089658	2.9942282	1.10292	1.891034	2.994228
0	30	70	3.9760036	29.884455	66.139532	3.976004	0.115545	3.860468
5	30	65	5.1096849	29.838898	65.051409	0.109685	0.161102	0.051409
40	5	55	40.472469	5.604083	53.923501	0.472469	0.604083	1.076499
5	55	40	4.9655444	55.024046	40.010377	0.034456	0.024046	0.010377
0	0	100	0.6871195	−0.520481	99.833396	0.68712	0.520481	0.166604
65	30	5	66.95703	29.848935	3.1941278	1.95703	0.151065	1.805872
55	40	5	52.472024	40.221586	7.3063942	2.527976	0.221586	2.306394
10	20	70	7.4783779	19.512368	73.009267	2.521622	0.487632	3.009267
0	75	25	4.5898371	75.17029	20.239845	4.589837	0.17029	4.760155
25	60	15	27.484312	59.98738	12.528295	2.484311	0.01262	2.471705
55	30	15	52.431476	29.942522	17.626027	2.568524	0.057478	2.626027
80	15	5	79.488386	15.435424	5.0763718	0.511614	0.435424	0.076372
35	55	10	33.771403	54.821706	11.406877	1.228597	0.178294	1.406877
85	10	5	86.032129	11.162328	2.8057639	1.032128	1.162328	2.194236
35	65	0	34.573681	63.405562	2.0207462	0.426319	1.594438	2.020746
20	60	20	19.097816	59.976573	20.92559	0.902184	0.023427	0.92559
50	15	35	49.343921	14.645025	36.011096	0.656079	0.354975	1.011096
45	20	35	46.57551	19.69299	33.731526	1.57551	0.30701	1.268474
50	45	5	50.79057	45.255732	3.9536846	0.79057	0.255732	1.046315
55	20	25	53.014921	19.627793	27.357335	1.985079	0.372207	2.357335
20	25	55	22.052018	24.913003	53.034994	2.052018	0.086997	1.965006
60	10	30	61.112744	9.8002161	29.087147	1.112744	0.199784	0.912853
20	80	0	19.087321	79.891236	1.0214298	0.912679	0.108764	1.02143
30	25	45	30.331617	24.946898	44.721505	0.331617	0.053102	0.278495
15	70	15	11.261024	69.83996	18.898992	3.738976	0.16004	3.898991
35	50	15	33.492018	50.207449	16.30052	1.507982	0.207449	1.30052
55	45	0	52.953531	45.200789	1.8456758	2.046469	0.200789	1.845676
20	45	35	19.997583	45.399897	34.602504	0.002417	0.399897	0.397496
15	50	35	11.742161	50.183911	38.073903	3.257839	0.183911	3.073903
0	65	35	4.2766986	64.914902	30.808368	4.276699	0.085098	4.191632
15	15	70	13.604106	14.617836	71.778087	1.395894	0.382164	1.778087
35	0	65	34.653616	−0.0221034	65.368539	0.346384	0.022103	0.368539
50	40	10	49.990271	40.264018	9.7457043	0.009729	0.264018	0.254296
25	70	5	28.27156	69.53906	2.1893708	3.27156	0.46094	2.810629
0	40	60	4.1957765	40.216457	55.587742	4.195776	0.216457	4.412258
55	10	35	53.529122	9.818305	36.652645	1.470878	0.181695	1.652645
45	45	10	47.09433	45.313222	7.5924329	2.09433	0.313222	2.407567
40	10	50	40.708367	9.9530206	49.338657	0.708367	0.046979	0.661343
0	90	10	3.7729887	90.43148	5.7955102	3.772989	0.43148	4.20449
55	0	45	53.543852	−0.1167825	46.573023	1.456148	0.116783	1.573023
75	0	25	75.055409	−0.1440884	25.085767	0.055409	0.144088	0.085767
0	35	65	4.1515115	35.079665	60.768806	4.151512	0.079665	4.231194
15	5	80	13.40098	5.5033959	81.095674	1.59902	0.503396	1.095674
10	45	45	7.3286369	45.191633	47.479705	2.671363	0.191633	2.479705
90	10	0	88.945006	8.8914744	2.163759	1.054994	1.108526	2.163759
45	10	45	46.773965	9.917948	43.308132	1.773965	0.082052	1.691868
15	35	50	12.911995	35.10617	51.981825	2.088005	0.10617	1.981825
90	0	10	90.183594	−0.1845679	10.001238	0.183594	0.184568	0.001238
10	60	30	6.9500862	59.886882	33.163002	3.049914	0.113118	3.163002
40	50	10	39.764107	50.139642	10.096234	0.235893	0.139642	0.096234
5	25	70	4.8424487	24.638456	70.519096	0.157551	0.361544	0.519096
0	55	45	4.1141159	55.073282	40.81257	4.114116	0.073282	4.18743
45	35	20	46.388204	35.190301	18.421492	1.388203	0.190301	1.578508
70	0	30	70.067518	−0.1067403	30.036693	0.067518	0.10674	0.036693
75	10	15	72.670752	10.290934	17.038475	2.329248	0.290934	2.038474
30	10	60	28.944183	10.019046	61.03682	1.055817	0.019046	1.03682
10	55	35	7.005809	55.006118	37.988043	2.994191	0.006118	2.988043
30	35	35	30.121086	35.321992	34.556924	0.121086	0.321992	0.443076
70	20	10	70.164516	19.585921	10.249692	0.164516	0.414079	0.249692
70	10	20	68.994425	9.9366292	21.069089	1.005575	0.063371	1.069089
30	5	65	27.474507	5.6495898	66.875961	2.525493	0.64959	1.875961
0	100	0	0.8694047	99.190353	−0.0597748	0.869405	0.809647	0.059775
35	10	55	33.448294	9.9785172	56.573236	1.551706	0.021483	1.573236
20	15	65	22.231111	14.792399	62.976525	2.231111	0.207601	2.023475
25	35	40	27.640928	35.368165	36.990908	2.640928	0.368165	3.009092
20	10	70	21.829486	10.017403	68.153157	1.829486	0.017403	1.846843
50	50	0	51.913795	50.07212	−1.9859327	1.913795	0.07212	1.985933
10	75	15	7.1584922	75.007937	17.833545	2.841508	0.007937	2.833545
10	25	65	7.6981281	24.645766	67.656109	2.301872	0.354234	2.656109
75	5	20	72.401343	5.8507274	21.748098	2.598657	0.850727	1.748098
0	95	5	2.642628	95.001645	2.355708	2.642628	0.001645	2.644292
15	55	30	11.473302	55.050149	33.476523	3.526698	0.050149	3.476523
45	0	55	45.871325	−0.0044087	54.133143	0.871325	0.004409	0.866857
75	20	5	74.102499	19.553661	6.343987	0.897501	0.446339	1.343987
25	30	45	27.897039	30.182151	41.92082	2.897039	0.182151	3.07918
15	20	65	13.619174	19.613427	66.767417	1.380826	0.386573	1.767417
50	10	40	49.389789	9.8636639	40.7466	0.610211	0.136336	0.7466
0	80	20	4.6167466	80.363665	15.019563	4.616747	0.363665	4.980437
5	85	10	5.1160617	85.417335	9.4665804	0.116062	0.417335	0.53342
15	0	85	16.012886	−0.1960515	84.183212	1.012886	0.196051	0.816788
30	45	25	30.089345	45.462118	24.448528	0.089345	0.462118	0.551473
5	10	85	4.0628973	9.7109687	86.226165	0.937103	0.289031	1.226165
15	45	40	12.09455	45.259268	42.64616	2.90545	0.259268	2.64616
30	0	70	28.834894	−0.0426017	71.20776	1.165106	0.042602	1.20776
30	65	5	31.796999	64.182091	4.0208999	1.796999	0.817909	0.9791
15	40	45	12.498867	40.226561	47.274555	2.501133	0.226561	2.274555
30	40	30	30.044455	40.451999	29.503542	0.044455	0.451999	0.496458
15	30	55	13.275546	29.922469	56.801984	1.724455	0.077531	1.801984
20	65	15	19.040246	64.841092	16.118642	0.959754	0.158908	1.118642
10	0	90	9.7842176	−0.3474061	90.56323	0.215782	0.347406	0.56323
70	5	25	68.345637	5.4968421	26.157671	1.654363	0.496842	1.157671
65	35	0	66.356377	34.915566	−1.2718627	1.356377	0.084434	1.271863
0	25	75	3.621414	24.686818	71.691767	3.621414	0.313182	3.308233
45	30	25	46.349887	30.006411	23.643707	1.349887	0.006411	1.356293
25	5	70	24.918156	5.6916129	69.390289	0.081844	0.691613	0.609711
40	35	25	39.62021	35.226099	25.15369	0.379791	0.226099	0.15369
25	0	75	24.77261	−0.0563324	75.283773	0.22739	0.056332	0.283773
65	15	20	67.290231	14.659834	18.05006	2.290231	0.340166	1.94994
75	15	10	73.311815	14.933888	11.75445	1.688185	0.066112	1.75445
40	20	40	40.48783	19.727364	39.784831	0.48783	0.272636	0.215169
60	5	35	61.04903	5.385587	33.565499	1.04903	0.385587	1.434501
35	40	25	33.346758	40.380947	26.272289	1.653242	0.380947	1.272289
10	5	85	7.4804784	5.3902283	87.129338	2.519522	0.390228	2.129338
25	45	30	27.226507	45.518504	27.254979	2.226507	0.518504	2.745021
45	55	0	48.652893	54.691393	−3.3443068	3.652893	0.308607	3.344307
40	60	0	40.527749	58.994486	0.4777477	0.527749	1.005514	0.477748
60	35	5	58.489183	35.097992	6.4128679	1.510817	0.097992	1.412868
65	25	10	67.3567	24.752476	7.89093	2.3567	0.247524	2.10907
60	15	25	60.875199	14.632202	24.492696	0.875199	0.367798	0.507304
30	30	40	30.252386	30.137817	39.609807	0.252386	0.137817	0.390193
65	5	30	66.22609	5.3807893	28.393261	1.22609	0.380789	1.606739
10	65	25	6.980261	64.826525	28.193184	3.019739	0.173475	3.193184
15	80	5	11.213203	80.108997	8.6777796	3.786797	0.108997	3.67778
0	85	15	4.3918155	85.491927	10.116234	4.391816	0.491927	4.883766
0	20	80	3.1092385	19.538914	77.351856	3.109239	0.461086	2.648144
10	70	20	7.0717233	69.87459	23.05366	2.928277	0.12541	3.053659
5	20	75	4.4231488	19.497036	76.079826	0.576851	0.502964	1.079826
5	60	35	4.9788773	59.902087	35.119004	0.021123	0.097913	0.119004
5	90	5	4.4921226	90.350521	5.1573363	0.507877	0.350521	0.157336
90	5	5	90.791574	5.6962448	3.5124352	0.791574	0.696245	1.487565
55	35	10	52.321102	35.111918	12.566994	2.678898	0.111918	2.566994
0	15	85	2.6377465	14.517448	82.844825	2.637746	0.482552	2.155175
45	40	15	46.62611	40.320226	13.053653	1.62611	0.320226	1.946347
5	40	55	5.1865054	40.171668	54.641804	0.186505	0.171668	0.358196
35	60	5	34.146151	59.217849	6.6359865	0.853849	0.782151	1.635986
80	20	0	80.344577	19.725399	−0.0698005	0.344577	0.274601	0.0698
55	25	20	52.699535	24.755926	22.544576	2.300465	0.244074	2.544576
55	15	30	53.298435	14.613616	32.088009	1.701565	0.386384	2.088009
30	15	55	29.796556	14.807679	55.395804	0.203444	0.192321	0.395804
25	55	20	27.262063	55.237417	17.500507	2.262063	0.237417	2.499493
15	65	20	11.244954	64.807927	23.947094	3.755046	0.192073	3.947094
85	15	0	85.884429	15.325745	−1.2099629	0.884429	0.325745	1.209963
70	30	0	70.52929	29.332831	0.1379894	0.52929	0.667169	0.137989
50	5	45	49.268047	5.5163266	45.215687	0.731953	0.516327	0.215687
30	70	0	32.548473	68.685149	−1.2336297	2.548473	1.314851	1.23363
40	55	5	40.114163	54.711524	5.1742955	0.114163	0.288476	0.174295
25	25	50	28.054286	24.993361	46.952373	3.054286	0.006639	3.047627
10	80	10	7.137932	80.197224	12.66482	2.862068	0.197224	2.66482
5	35	60	5.2080164	35.03693	59.755037	0.208016	0.03693	0.244963
50	35	15	49.504376	35.14967	15.345955	0.495624	0.14967	0.345955
20	75	5	19.121605	74.83041	6.0479691	0.878395	0.16959	1.047969
35	5	60	32.53335	5.6189468	61.847758	2.46665	0.618947	1.847758
60	40	0	57.986038	40.170488	1.8435046	2.013962	0.170488	1.843505
0	60	40	4.160284	59.964257	35.875426	4.160284	0.035743	4.124574
60	25	15	59.855633	24.793473	15.350964	0.144367	0.206527	0.350964
50	30	20	49.283128	29.96349	20.753393	0.716872	0.03651	0.753393
40	15	45	40.666732	14.727066	44.606237	0.666732	0.272934	0.393763
25	40	35	27.393874	40.487468	32.118653	2.393874	0.487468	2.881347
30	20	50	30.224041	19.812429	49.96356	0.224041	0.187571	0.036441
5	80	15	5.3512548	80.298256	14.350465	0.351255	0.298256	0.649535
60	0	40	61.12284	−0.2345656	39.111854	1.12284	0.234566	0.888146
70	25	5	70.483708	24.469902	5.0465107	0.483708	0.530098	0.046511
45	15	40	46.691662	14.69363	38.614744	1.691662	0.30637	1.385257
0	70	30	4.4418526	69.999031	25.559086	4.441853	0.000969	4.440914
80	10	10	79.121653	10.974562	9.9039736	0.878347	0.974562	0.096026
15	25	60	13.524677	24.740762	61.73457	1.475323	0.259238	1.734569
40	45	15	39.545089	45.334304	15.120594	0.454911	0.334304	0.120594
25	20	55	27.97571	19.865366	52.158954	2.97571	0.134634	2.841046
25	15	60	27.521049	14.859945	57.619045	2.521049	0.140055	2.380955
85	0	15	88.006425	−0.6523625	12.646192	3.006425	0.652362	2.353808
25	50	25	27.177003	50.429513	22.393471	2.177003	0.429513	2.606529
20	40	40	20.506066	40.385177	39.108747	0.506066	0.385177	0.891254
20	50	30	19.579689	50.316831	30.103462	0.420312	0.316831	0.103461
40	40	20	39.496094	40.34547	20.158428	0.503906	0.34547	0.158428
95	0	5	96.817879	1.6617942	1.5206177	1.817879	1.661794	3.479382
55	5	40	53.553033	5.4478845	40.999164	1.446967	0.447884	0.999164
30	60	10	31.155803	59.671021	9.1731646	1.155803	0.328979	0.826835
45	50	5	47.78669	50.126202	2.087088	2.78669	0.126202	2.912912
15	60	25	11.307241	59.903411	28.789321	3.692759	0.096589	3.789321
5	70	25	5.2095783	69.930228	24.860165	0.209578	0.069772	0.139835
10	10	80	7.317031	9.7366169	82.946386	2.682969	0.263383	2.946386
10	15	75	7.2494342	14.507154	78.243435	2.750566	0.492846	3.243435
30	55	15	30.645253	55.060041	14.294693	0.645253	0.060041	0.705307

As is clear, for every ratio of all three phases, both Pr and Re numbers can be calculated. For example, for the ratio when gas’s VF = 75%, water’s VF = 15%, and oil’s VF = 10%, Pr and Re numbers are equal to 1372 and 23510, respectively. The obtained Reynolds number indicates a highly turbulent flow regime, showing a uniformly distributed mixing, facilitating more accurate measurements and analysis.

Based on the outcomes, the accuracy of the proposed metering system can be observed because the MAE of the water, gas, and oil phases are equal to 0.29, 1.60, and 1.67, respectively. By solving Equations (13) and (14), MAE and root mean square error (RMSE) for the network can be calculated. In these equations n, X_i, and Y_i are the count of observations, the simulated (COMSOL Multiphysics), and predicted (MLP) values, respectively [24]. The errors of the proposed metering system are presented in Table 3.

Table 3. Obtained results of the proposed metering system including MAE and RMSE for all three phases.

	Gas	Water	Oil
MAE	1.60	0.29	1.67
RSME	2.02	0.43	2.06

To show the merits of the proposed metering approach, Table 4 acts as a comparison table, which compares the proposed metering approach with eight similar studies. In this table, green color is the lowest error and red is the highest.

$$MAE={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n|X_i-Y_i|$$

(13)

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{(X_i-Y_i)}^2}$$

(14)

Table 4. Comparing various details of the proposed method with that of other similar studies.

	Presented Volumes	Employed Sensors	Number of Source		Number of Detector	MAE
			Gamma	X-ray
[15]	Water	Radiation	2	0	2	1.79
	Oil					Not reported
	Gas					0.4
[21]	Water	Radiation	0	1	1	1.88
	Oil					Not reported
	Gas					1.87
[22]	Water	Capacitance	0	0	0	1.66
[24]	Water	Capacitance	1	0	1	0.33
	Oil	and				3.75
	Gas	Radiation				3.68
[37]	Gas	Radiation	1	0	1	7.72
[38]	Water	Radiation	0	1	2	2.02
	Oil					Not reported
	Gas					1.43
[39]	Gas	Radiation	1	0	2	1.47
	Water					Not reported
	Oil					5.17
[40]	Gas	Radiation	1	0	2	3
	Water					Not reported
	Oil					4.22
The proposed method	Water	Capacitance	1	0	1	0.29
	Oil	and				1.67
	Gas	radiation				1.6

The MAE is a crucial metric showing the accuracy of systems, and the approach detailed here outperforms others in measuring water, oil, and gas phases in comparison with some of them, particularly excelling in assessing water in water–oil–gas flows. All factors of a gamma ray attenuation sensor, such as its performance and accuracy, are influenced by the number of detectors and sources it contains. Hence, the more detectors and sources, the more accurate a measurement to be expected. On the other hand, increasing the number of detectors and sources raises some unwanted factors, such as the system’s complexity and cost and power consumption, etc. Additionally, by utilizing more gamma sources, a system becomes more dangerous in the aspect of safety risks and regularity challenges, because governing radioactive materials is a hard task to achieve. In the current study, the fewest number of detectors and sources was employed, being more cost-effective and easier to manage. All references, except [21,24,37], have utilized two detectors, but in the proposed approach there is just one detector and one source, which is one of the most important merits of it. In [22], which was just based on capacitive sensors, and [37], just one phase of a multiphase flow has been reported, but in this manuscript, all three phases, water, gas, and oil, have been reported, which is another advantage for it. Furthermore, in [21,38], an X-ray tube was used as the source. While X-ray tubes can adjust energy levels and beam intensity by accelerating electrons onto a metal target, they depend on a stable power supply and require regular maintenance and calibration. In contrast, the proposed approach uses gamma ray sensors with radioactive isotopes to emit gamma rays. These sensors are portable, have a long operational life, and do not need an external power source. In [24], a Baruim-133 source has been utilized, which in the presented metering system, means that there is a 0.04, 2.08, and 2.08 decrease for the MAE of the water, gas, and oil, respectively. This is because of the higher Cs gamma ray’s energy, which due to greater penetration. Compton scattering is the primary interaction for it, and makes the attenuation highly dependent on material’s density, but for Ba there is a lower level of energy and dependence on material’s atomic number. Photoelectric absorption is happening and it is less sensitive to the density of the material. Moreover, the utilized capacitance-based sensor in the current study was the TRFLC sensor and it has a higher rate of sensitivity in comparison to that of the concave sensor utilized in [24]. Consequently, the introduced combined approach, incorporating the gamma-ray attenuation sensor, capacitance-based sensor, and MLP ANN, emerges as a highly effective method in relevant fields. According to these comparisons, the presented metering system, which a conjunction of two sensors, capacitance-based and photon attenuation with one source and one detector, along with the optimized MLP model formed, is a great solution to measure volume fractions of a multiphase fluid.

5. Conclusions

Various industries encounter different types of fluids, such as oil and petroleum. The measurement of these fluids is a critical task in various sectors, including financial matters, and is often accompanied by numerous challenges. Many methods have been introduced to address this, each with its own advantages and disadvantages. The proposed metering system, containing photon attenuation and capacitive sensors along with an MLP, had two inputs; the first input, the TRFLC sensor, was simulated in COMSOL Multiphysics software, generating capacities related to various material volumes. The second input involved a gamma-ray sensor with Cesium-137, considering different situations and calculations using relevant equations. Obtained data were utilized to train and test data with 70% and 30% of all data, respectively. The proposed network, which was run in MATLAB software and was selected after considering many architectures, produced highly accurate outputs with a very low MAE for water, oil, and gas, recorded as 0.29, 1.67, and 1.60, respectively. These results highlight the system’s remarkable accuracy in measuring volume fractions in a three-phase water–oil–gas homogeneous regime.