Predictive Modeling of Solar PV Panel Operating Temperature over Water Bodies: Comparative Performance Analysis with Ground-Mounted Installations
Abstract
1. Introduction
- Identify the influencing factors and performance measures of Floating and ground-mounted solar PV installation;
- Develop mathematical Models by application of regression analysis with varying parameters;
- Apply Regression Model Analysis to predict the operating temperature of floating solar PV installation.
2. Existing Module Operating Temperature and Performance Models
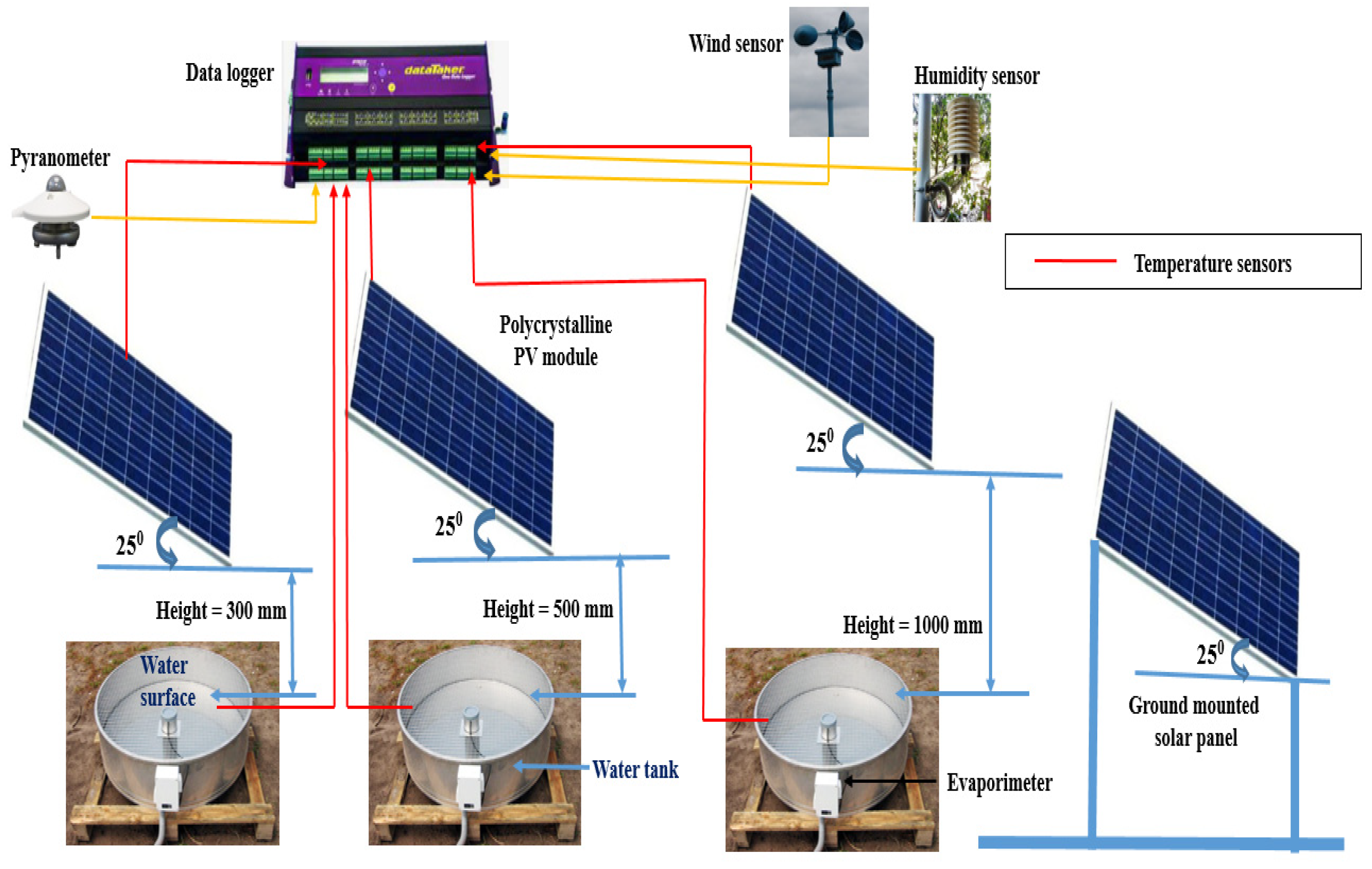
3. Experimental Setup in the Field
4. Modeling Procedure
4.1. Exponential Model Using Experimental Data
4.2. Linear and Quadratic Models Using Experimental Data
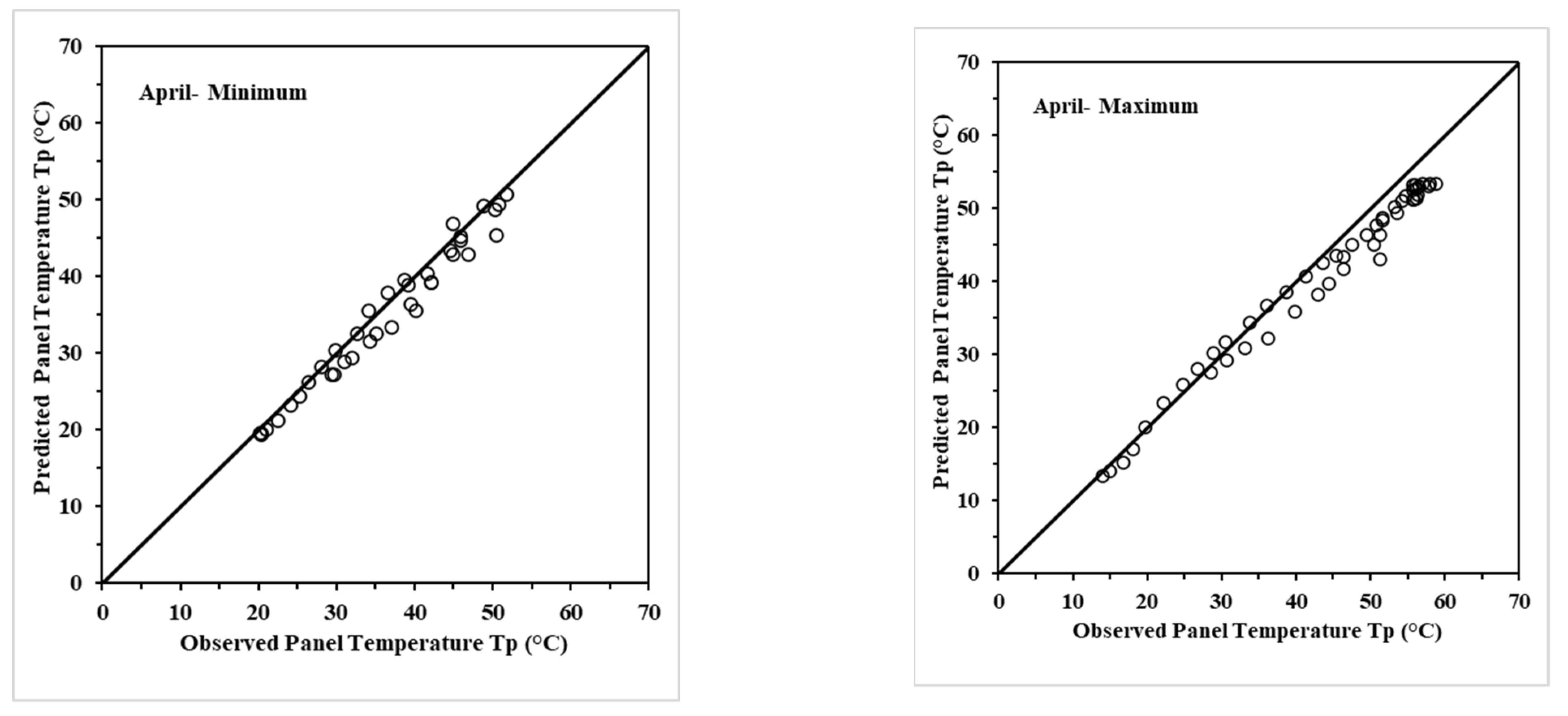
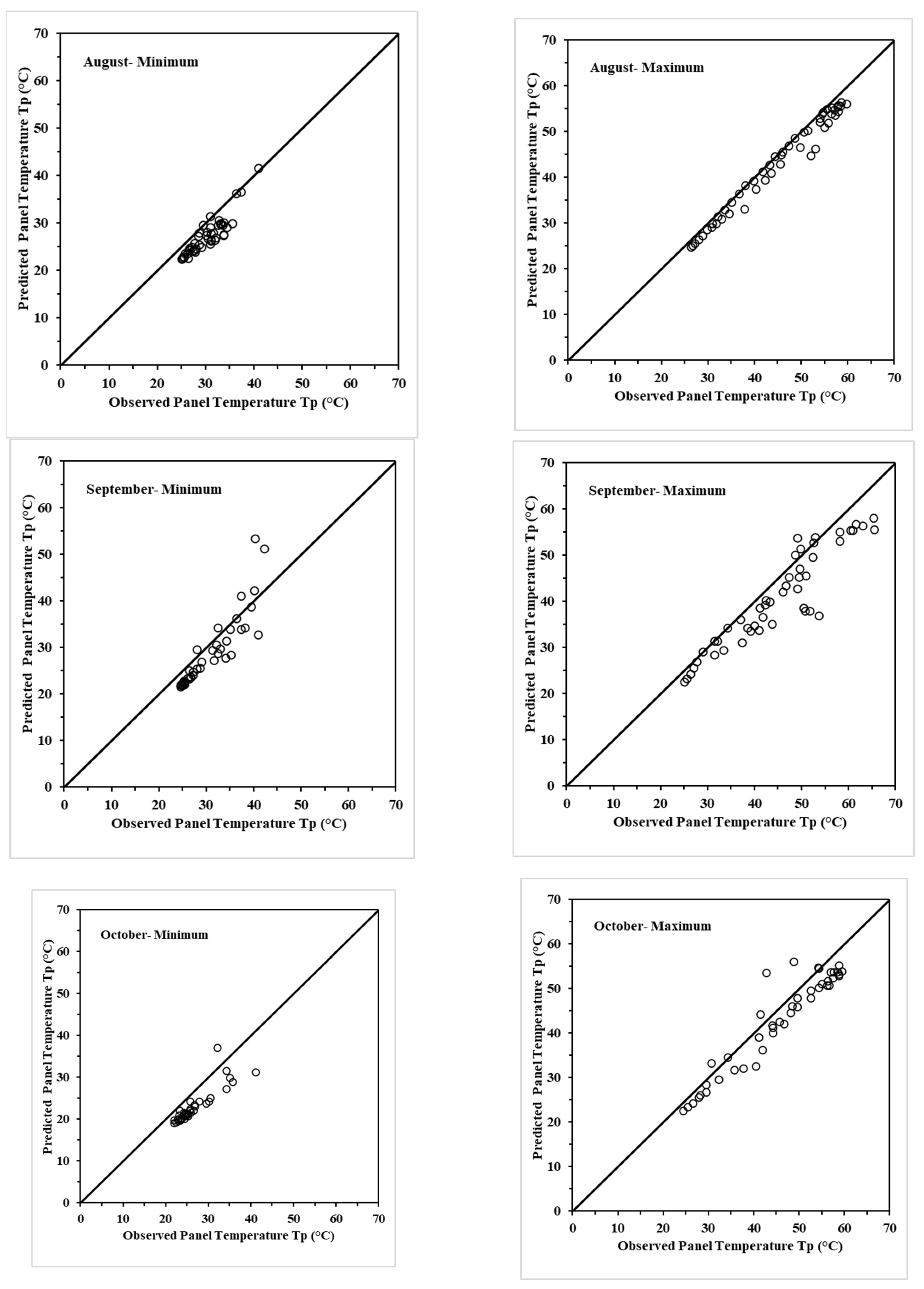
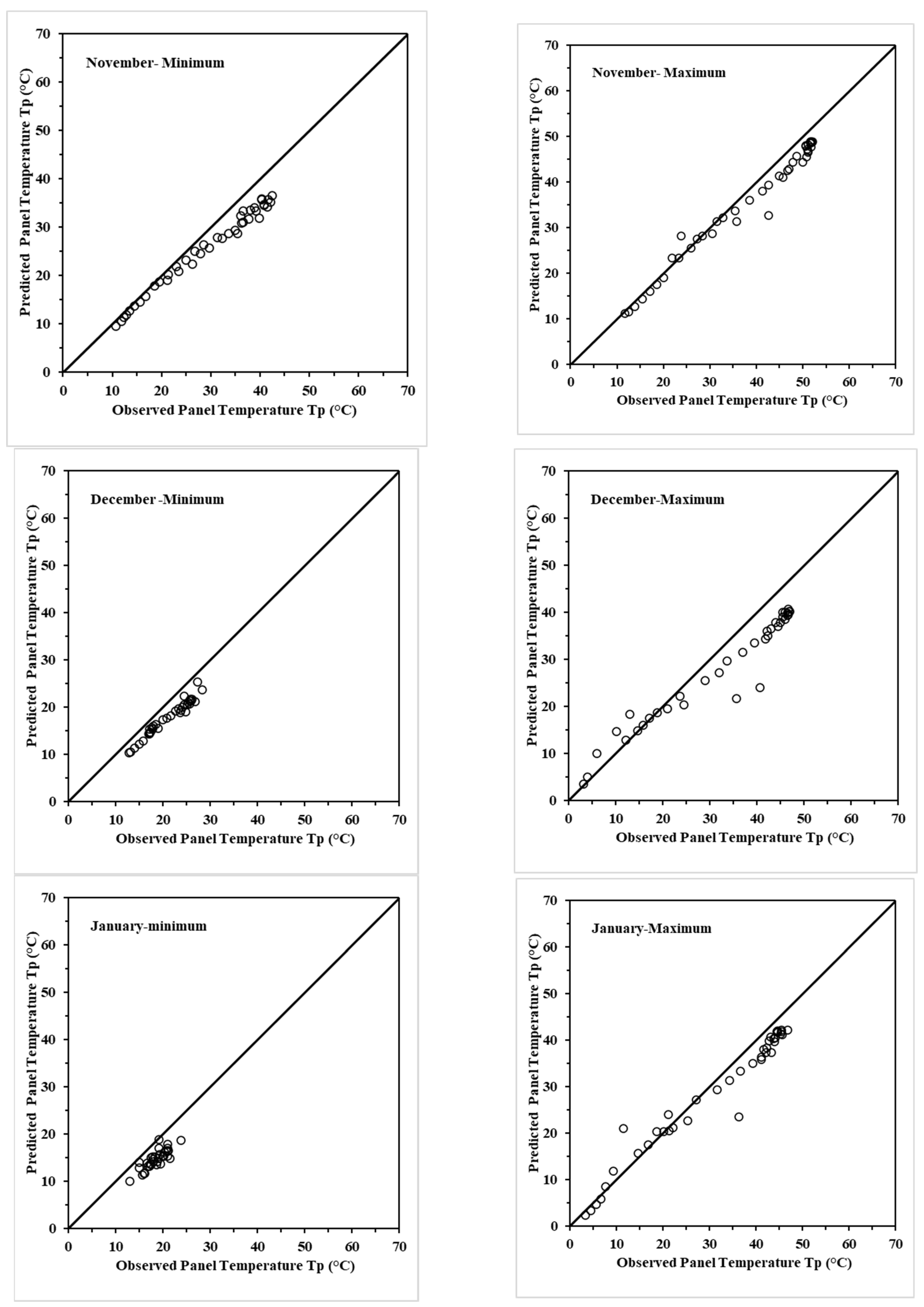
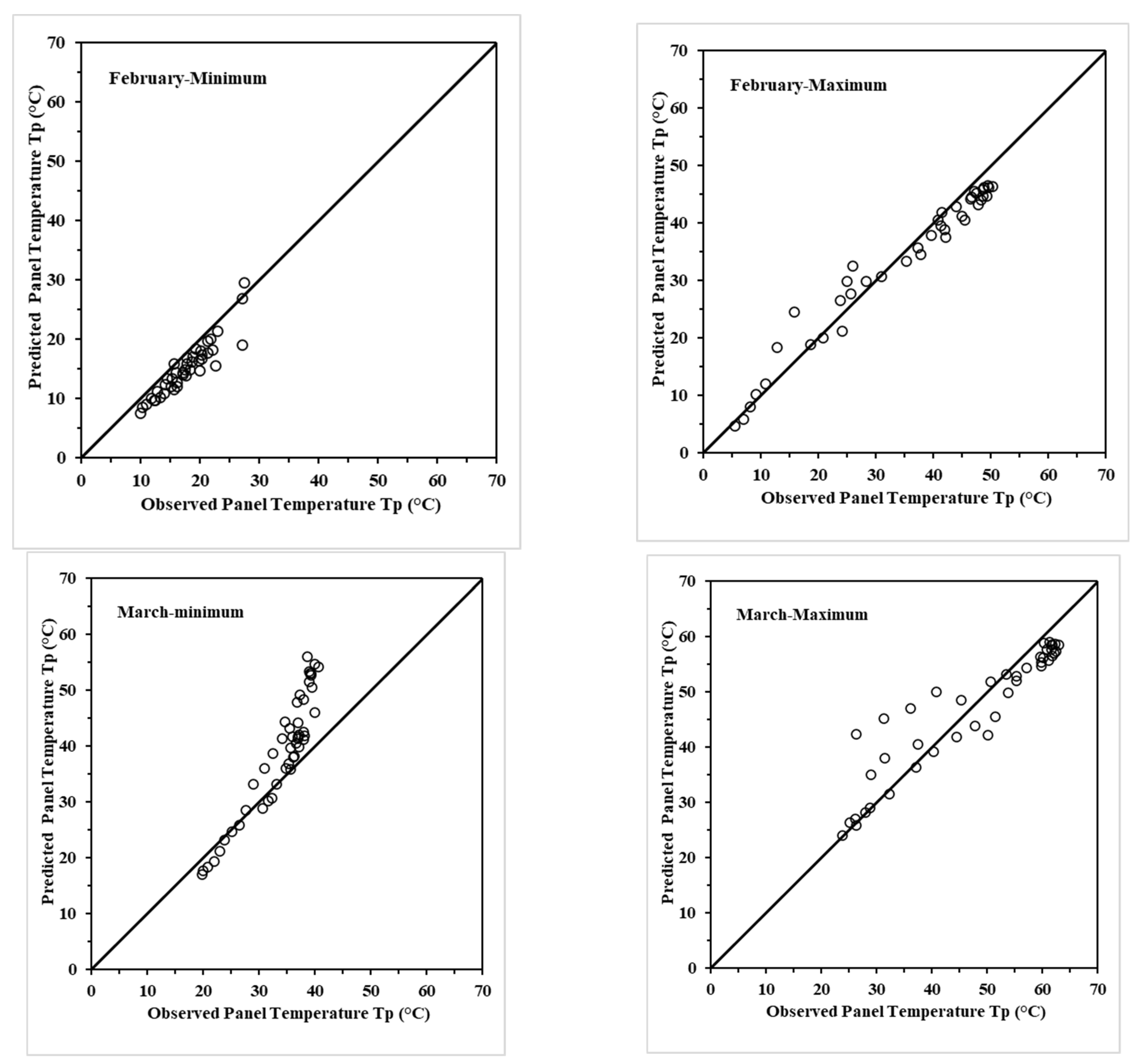
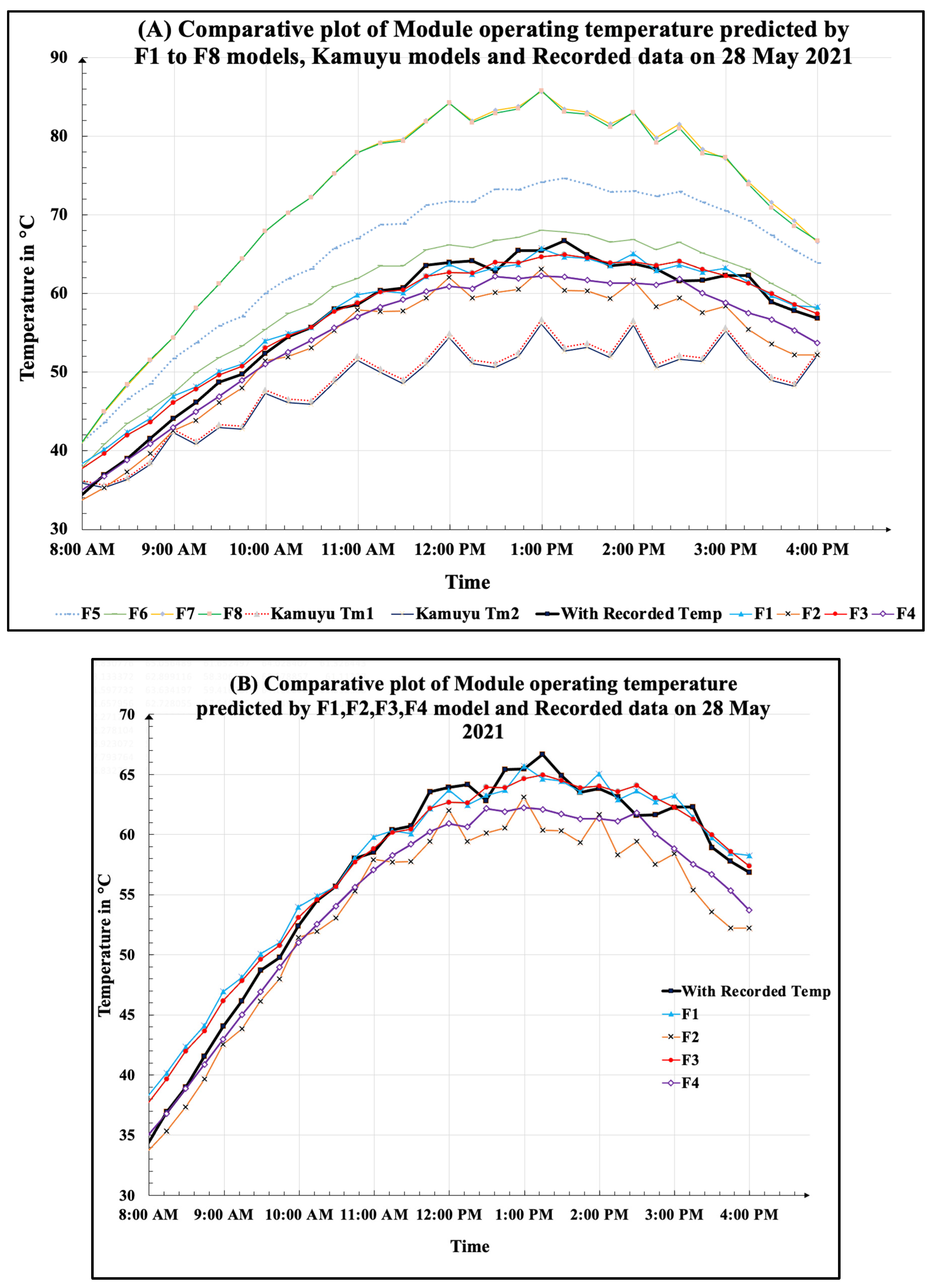
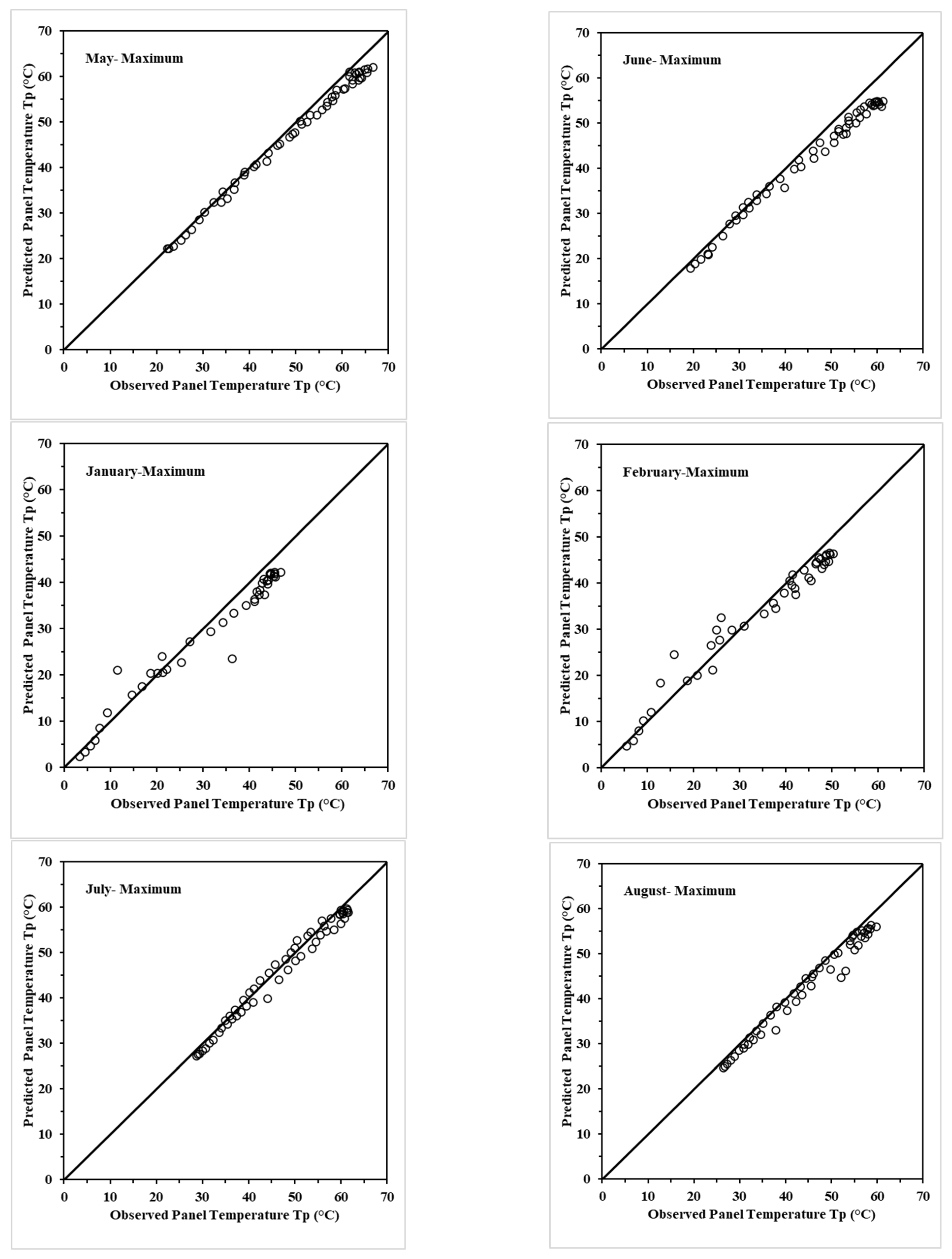
5. Testing the Models for Seasonal Adequacy
5.1. Seasonal Evaluation and Model Identification for Best Performance
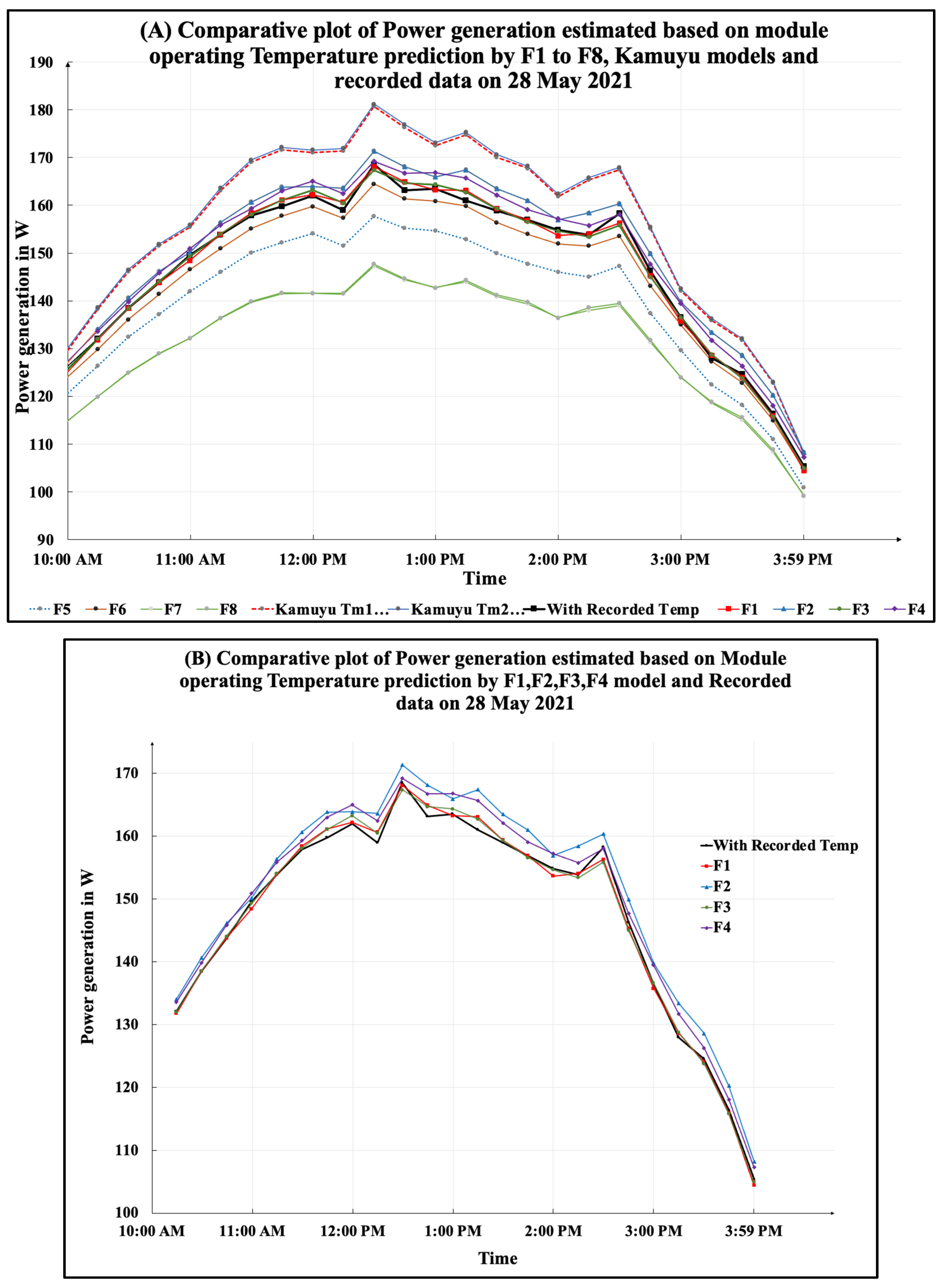
5.2. Evaluation of Energy Output from Developed Models
Assessment of Energy Output from Developed Models: Seasonal Variation
6. PV Panel Operating Temperature Variations: Comparison of Floating vs. Ground-Mounted PV Panels
7. Conclusions
- The three parametric models, F1 and F3, which utilized ambient temperature, solar insolation, and wind velocity, predicted panel operating temperature the best, with a maximum root mean square error (RMSE) of 5.64 °C and 5.50 °C, respectively. On the other hand, three parametric models replacing ambient temperature with water temperature, F2 and F4, predicted panel operating temperature less accurately, with a maximum RMSE of 8.26 °C and 9.43 °C, respectively;
- The study also found that the one-degree regression model with all five parameters did not add to the accuracy of the prediction model. However, the two-degree regression models were complex, with an RMSE of more than 20 °C;
- Finally, the study found that the best model is F3, which can be used to predict the operating temperature of the panel and power estimates, assessing the module’s overall performance;
- Floating solar PV systems should be preferred to ground-mounted ones due to the lowering of operating temperatures by 6 °C. The study found that floating solar PV installations consistently produced 2.59% more energy than ground-mounted solar PV installations.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

| Date and Time | Solar Panel Temp at Height 50 cm above Water Surface (°C) | Wind Speed (km/h) | Ambient Temperature (°C) | Humidity (%) | Solar Radiation (W/m2) | Water Temperature (°C) |
|---|---|---|---|---|---|---|
| 18/04/21 6:15 | 14.02 | 0.00 | 16.73 | 52.14 | 2.33 | 19.28 |
| 18/04/21 6:30 | 14.96 | 0.00 | 17.01 | 52.58 | 13.22 | 19.20 |
| 18/04/21 6:45 | 16.72 | 0.00 | 17.81 | 53.14 | 22.53 | 19.29 |
| 18/04/21 7:00 | 18.15 | 0.00 | 19.08 | 53.93 | 39.21 | 19.36 |
| 18/04/21 7:15 | 19.75 | 0.00 | 21.39 | 54.44 | 62.99 | 19.47 |
| 18/04/21 7:30 | 22.15 | 0.00 | 23.74 | 53.30 | 92.69 | 19.64 |
| 18/04/21 7:45 | 24.73 | 0.46 | 25.05 | 51.17 | 126.95 | 19.81 |
| 18/04/21 8:00 | 26.84 | 0.00 | 25.91 | 49.60 | 164.11 | 20.05 |
| 18/04/21 8:15 | 28.92 | 1.43 | 26.76 | 48.32 | 203.68 | 20.33 |
| 18/04/21 8:30 | 30.49 | 2.63 | 26.87 | 46.88 | 247.55 | 20.59 |
| 18/04/21 8:45 | 33.86 | 2.08 | 28.24 | 46.16 | 287.95 | 20.85 |
| 18/04/21 9:00 | 36.10 | 0.00 | 28.99 | 44.85 | 327.70 | 21.25 |
| 18/04/21 9:15 | 38.70 | 2.49 | 29.68 | 43.76 | 367.16 | 21.68 |
| 18/04/21 9:30 | 41.31 | 2.38 | 30.44 | 42.63 | 407.08 | 22.09 |
| 18/04/21 9:45 | 43.67 | 2.25 | 31.05 | 41.62 | 442.78 | 22.50 |
| 18/04/21 10:00 | 45.43 | 0.00 | 31.35 | 40.48 | 459.12 | 22.87 |
| 18/04/21 10:15 | 47.53 | 2.97 | 31.74 | 39.63 | 498.72 | 23.11 |
| 18/04/21 10:30 | 49.50 | 2.33 | 32.28 | 39.06 | 520.56 | 23.38 |
| 18/04/21 10:45 | 50.90 | 2.13 | 32.66 | 38.20 | 547.32 | 23.69 |
| 18/04/21 11:00 | 51.66 | 0.00 | 32.82 | 37.06 | 569.63 | 23.96 |
| 18/04/21 11:15 | 53.31 | 3.01 | 33.57 | 36.36 | 598.79 | 24.13 |
| 18/04/21 11:30 | 56.27 | 1.90 | 33.90 | 35.66 | 620.19 | 24.39 |
| 18/04/21 11:45 | 56.46 | 2.59 | 33.79 | 34.65 | 638.66 | 24.64 |
| 18/04/21 12:00 | 55.78 | 0.01 | 33.96 | 33.65 | 651.43 | 24.83 |
| 18/04/21 12:15 | 56.48 | 2.80 | 34.23 | 32.93 | 658.97 | 25.03 |
| 18/04/21 12:30 | 58.77 | 2.14 | 34.61 | 32.50 | 658.55 | 25.24 |
| 18/04/21 12:45 | 55.80 | 4.30 | 34.14 | 31.81 | 668.50 | 25.39 |
| 18/04/21 13:00 | 56.07 | 0.00 | 34.06 | 31.07 | 667.57 | 25.52 |
| 18/04/21 13:15 | 57.05 | 3.40 | 35.00 | 30.82 | 649.59 | 25.77 |
| 18/04/21 13:30 | 56.27 | 3.56 | 34.71 | 30.08 | 637.16 | 25.90 |
| 18/04/21 13:45 | 57.79 | 3.26 | 35.32 | 29.80 | 629.49 | 26.13 |
| 18/04/21 14:00 | 58.03 | 0.01 | 35.63 | 29.51 | 627.44 | 26.31 |
| 18/04/21 14:15 | 54.27 | 3.76 | 34.78 | 29.08 | 585.25 | 26.51 |
| 18/04/21 14:30 | 54.83 | 3.72 | 35.44 | 28.52 | 588.05 | 26.72 |
| 18/04/21 14:45 | 55.90 | 3.38 | 35.56 | 28.52 | 570.37 | 26.92 |
| 18/04/21 15:00 | 55.77 | 0.00 | 36.12 | 27.80 | 545.95 | 27.18 |
| 18/04/21 15:15 | 53.59 | 4.31 | 35.24 | 27.52 | 523.85 | 27.35 |
| 18/04/21 15:30 | 51.65 | 3.98 | 35.53 | 27.24 | 488.31 | 27.51 |
| 18/04/21 15:45 | 51.34 | 3.33 | 35.42 | 26.95 | 334.30 | 27.67 |
| 18/04/21 16:00 | 51.31 | 0.00 | 35.54 | 26.52 | 424.29 | 27.84 |
| 18/04/21 16:15 | 50.43 | 2.68 | 35.75 | 26.39 | 382.57 | 28.03 |
| 18/04/21 16:30 | 46.35 | 2.02 | 35.67 | 26.11 | 332.08 | 28.20 |
| 18/04/21 16:45 | 46.43 | 1.96 | 35.66 | 26.11 | 286.30 | 28.35 |
| 18/04/21 17:00 | 44.51 | 0.00 | 35.24 | 25.78 | 236.40 | 28.42 |
| 18/04/21 17:15 | 42.90 | 0.77 | 35.26 | 25.54 | 192.31 | 28.51 |
| 18/04/21 17:30 | 39.93 | 1.84 | 34.92 | 25.40 | 136.99 | 28.45 |
| 18/04/21 17:45 | 36.27 | 1.19 | 33.79 | 24.97 | 60.38 | 28.38 |
| 18/04/21 18:00 | 33.16 | 0.00 | 33.00 | 25.11 | 40.45 | 28.35 |
| 18/04/21 18:15 | 30.69 | 0.07 | 31.98 | 25.12 | 23.10 | 28.25 |
| 18/04/21 18:30 | 28.51 | 0.00 | 30.78 | 25.68 | 8.10 | 28.15 |
References
- Agrawal, K.K.; Jha, S.K.; Mittal, R.K.; Vashishtha, S. Assessment of floating solar PV (FSPV) potential and water conservation: Case study on Rajghat Dam in Uttar Pradesh, India. Energy Sustain. Dev. 2022, 66, 287–295. [Google Scholar] [CrossRef]
- Essak, L.; Ghosh, A. Floating photovoltaics: A review. Clean Technol. 2022, 4, 752–769. [Google Scholar] [CrossRef]
- Huang, G.; Tang, Y.; Chen, X.; Chen, M.; Jiang, Y. A comprehensive review of floating solar plants and potentials for offshore applications. J. Mar. Sci. Eng. 2023, 11, 2064. [Google Scholar] [CrossRef]
- Schott, T. Operation temperatures of PV modules: A theoretical and experimental approach. In Proceedings of the Sixth EC Photovoltaic Solar Energy Conference, London, UK, 15–19 April 1985. [Google Scholar]
- Servant, J.M. Calculation of the cell temperature for photovoltaic modules from climatic data. In Intersol Eighty Five; Pergamon: Cambridge, UK, 1986; pp. 1640–1643. [Google Scholar]
- Lasnier, F.; Ang, T.G. Photovoltaic Engineering Handbook; Adam Hilger: New York, NY, USA, 1990; p. 80. [Google Scholar]
- Mondol, J.D.; Yohanis, Y.G.; Smyth, M.; Norton, B. Long-term validated simulation of a building integrated photovoltaic system. Sol. Energy 2005, 78, 163–176. [Google Scholar] [CrossRef]
- Ross Jr, R.G.; Smokler, M.I. Flat-Plate Solar Array Project: Final Report: Volume 6, Engineering Sciences and Reliability; Jet Propulsion Lab.: Pasadena, CA, USA, 1986. [Google Scholar]
- Coskun, C.; Koçyiğit, N.; Oktay, Z. Estimation of pv module surface temperature using artificial neural networks. Mugla J. Sci. Technol. 2016, 2, 15–18. [Google Scholar] [CrossRef]
- Skoplaki, E.; Boudouvis, A.G.; Palyvos, J.A. A simple correlation for the operating temperature of photovoltaic modules of arbitrary mounting. Sol. Energy Mater. Sol. Cells 2008, 92, 1393–1402. [Google Scholar] [CrossRef]
- Skoplaki, E.; Palyvos, J.A. Operating temperature of photovoltaic modules: A survey of pertinent correlations. Renew. Energy 2009, 34, 23–29. [Google Scholar] [CrossRef]
- Muzathik, A.M. Photovoltaic modules operating temperature estimation using a simple correlation. Int. J. Energy Eng. 2014, 4, 151. [Google Scholar]
- Risser, V.V.; Fuentes, M.K. Linear regression analysis of flat-plate photovoltaic system performance data. In Proceedings of the 5th Photovoltaic Solar Energy Conference, Athens, Greece, 17–21 October 1983. [Google Scholar]
- Akyuz, E.; Coskun, C.; Oktay, Z.U.H.; Dincer, I. A novel approach for estimation of photovoltaic exergy efficiency. Energy 2012, 44, 1059–1066. [Google Scholar] [CrossRef]
- Chenni, R.; Makhlouf, M.; Kerbache, T.; Bouzid, A. A detailed modeling method for photovoltaic cells. Energy 2007, 32, 1724–1730. [Google Scholar] [CrossRef]
- King, D.L. Photovoltaic module and array performance characterization methods for all system operating conditions. AIP Conf. Proc. 1997, 394, 347–368. [Google Scholar] [CrossRef]
- Kurtz, S.; Whitfield, K.; Miller, D.; Joyce, J.; Wohlgemuth, J.; Kempe, M.; Dhere, N.; Bosco, N.; Zgonena, T. Evaluation of high-temperature exposure of rack-mounted photovoltaic modules. In Proceedings of the 34th IEEE Photovoltaic Specialists Conference (PVSC), Philadelphia, PA, USA, 7–12 June 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 2399–2404. [Google Scholar]
- Almaktar, M.; Rahman, H.A.; Hassan, M.Y.; Rahman, S. Climate-based empirical model for PV module temperature estimation in tropical environment. Appl. Sol. Energy 2013, 49, 192–201. [Google Scholar] [CrossRef]
- Irodionov, A.E.; Kurenkova, V.A.; Potapov, V.N.; Strebkov, D.S. Choice of resistance for elements of photovoltaic system’s external switching. Geliotechnika 1989, 25, 18–21. [Google Scholar]
- Kalogirou, S.A. Solar Energy Engineering: Processes and Systems; Elsevier: Amsterdam, The Netherlands, 2023. [Google Scholar]
- Mora Segado, P.; Carretero, J.; Sidrach-de-Cardona, M. Models to predict the operating temperature of different photovoltaic modules in outdoor conditions. Prog. Photovolt. Res. Appl. 2015, 23, 1267–1282. [Google Scholar] [CrossRef]
- Kaplani, E.; Kaplanis, S. PV module temperature prediction at any environmental conditions and mounting configurations. In Renewable Energy and Sustainable Buildings: Selected Papers from the World Renewable Energy Congress WREC 2018; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 921–933. [Google Scholar]
- Koehl, M.; Heck, M.; Wiesmeier, S.; Wirth, J. Modeling of the nominal operating cell temperature based on outdoor weathering. Sol. Energy Mater. Sol. Cells 2011, 95, 1638–1646. [Google Scholar] [CrossRef]
- Faiman, D. Assessing the outdoor operating temperature of photovoltaic modules. Prog. Photovolt. Res. Appl. 2008, 16, 307–315. [Google Scholar] [CrossRef]
- Barry, J.; Böttcher, D.; Pfeilsticker, K.; Herman-Czezuch, A.; Kimiaie, N.; Meilinger, S.; Schirrmeister, C.; Deneke, H.; Witthuhn, J.; Gödde, F. Dynamic model of photovoltaic module temperature as a function of atmospheric conditions. Adv. Sci. Res. 2020, 17, 165–173. [Google Scholar] [CrossRef]
- Du, Y.; Fell, C.J.; Duck, B.; Chen, D.; Liffman, K.; Zhang, Y.; Gu, M.; Zhu, Y. Evaluation of photovoltaic panel temperature in realistic scenarios. Energy Convers. Manag. 2016, 108, 60–67. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Energy of Processes, 3rd ed.; Wiley: Hoboken, NJ, USA, 2006; p. 3. [Google Scholar]
- Sohani, A.; Sayyaadi, H.; Cornaro, C.; Shahverdian, M.H.; Pierro, M.; Moser, D.; Karimi, N.; Doranehgard, M.H.; Li, L.K. Using machine learning in photovoltaics to create smarter and cleaner energy generation systems: A comprehensive review. J. Clean. Prod. 2022, 364, 132701. [Google Scholar] [CrossRef]
- Evans, D.L.; Florschuetz, L.W. Terrestrial concentrating photovoltaic power system studies. Sol. Energy 1978, 20, 37–43. [Google Scholar] [CrossRef]
- Evans, D.L. Simplified method for predicting photovoltaic array output. Sol. Energy 1981, 27, 555–560. [Google Scholar] [CrossRef]
- Notton, G.; Cristofari, C.; Mattei, M.; Poggi, P. Modelling of a double-glass photovoltaic module using finite differences. Appl. Therm. Eng. 2005, 25, 2854–2877. [Google Scholar] [CrossRef]
- Nordmann, T.; Clavadetscher, L. Understanding temperature effects on PV system performance. In Proceedings of the 3rd World Conference on Photovoltaic Energy Conversion, Osaka, Japan, 11–18 May 2003; IEEE: Piscataway, NJ, USA, 2003; pp. 2243–2246. [Google Scholar]
- Kamuyu, C.L.W.; Lim, J.R.; Won, C.S.; Ahn, H.K. Prediction Model of Photovoltaic Module Temperature for Power Performance of Floating PVs. Energies 2018, 11, 447. [Google Scholar] [CrossRef]
- Tina, G.M.; Bontempo Scavo, F.; Merlo, L.; Bizzarri, F. Analysis of water environment on the performances of floating photovoltaic plants. Renew. Energy 2021, 175, 281–295. [Google Scholar] [CrossRef]
- Florschuetz, L.W. Extension of the Hottel-Whillier model to the analysis of combined photovoltaic/thermal flat plate collectors. Sol. Energy 1979, 22, 361–366. [Google Scholar] [CrossRef]
- Ross, R.G. Interface design considerations for terrestrial solar cells modules. In Proceedings of the 12th IEEE Photovoltaic Specialist’s Conference, Baton Rouge, LA, USA, 7–10 January 1976; pp. 801–806. [Google Scholar]
- Rauschenbach, H.S. Solar Cell Array Design Handbook; Van Nosstrand Reinhold: New York, NY, USA, 1980; pp. 390–391. [Google Scholar]
- Markvart, T. (Ed.) Solar Electricity; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- King, D.L.; Kratochvil, J.A.; Boyson, W.E. Photovoltaic Array Performance Model. United States Department of Energy, 2004. Available online: http://prod.sandia.gov/techlib/access-control.cgi/2004/043535.pdf (accessed on 30 July 2022).
- Mattei, M.; Notton, G.; Cristofari, C.; Muselli, M.; Poggi, P. Calculation of the polycrystalline PV module temperature using a simple method of energy balance. Renew. Energy 2006, 31, 553–567. [Google Scholar] [CrossRef]
- Agrawal, K.K.; Mittal, R.K.; Jha, S.K.; Singh, A.P.; Vashishtha, S.; Soni, M.K. Experimental Studies and Analysis for Performance Assessment of Floating Solar Photovoltaic Systems. In Proceedings of the International Conference on Smart and Sustainable Energy Systems (ICSSES 2024), Bhimavaram, Andhra Pradesh, India, 16–17 February 2024; p. 47. [Google Scholar]


| Author | Year | Equation | Type of Mounting | Parameters |
|---|---|---|---|---|
| Ross [36] | 1976 | Ground Mounted | k—empirical constant | |
| Rauschenbach [37] | 1980 | Ground Mounted | TcNOCT Cell nominal operating temperature,°C TaNOCT Ambient temperature according to SRE, set at 20 °C GNOCT Total irradiance according to SRE, set at 800 W/m², Tc Cell Temperature in °C. = , —conversion efficiency of module. | |
| Risser and Fuentes [13] | 1983 | Ground Mounted | Tmod—module temperature in °C | |
| Schott [4] | 1985 | Ground Mounted | GT—Solar insolation in W/m2 | |
| Ross and Smokler [8] | 1986 | Ground Mounted | Vw—wind velocity in m/s | |
| Irodionov et al. [19] | 1989 | Ground Mounted | Ta—ambient temperature in °C | |
| Lasnier and Ang [6] | 1990 | Ground Mounted | TmodK—module temperature in K | |
| Markvart [38] | 2000 | Ground Mounted | TaK—ambient temperature in K | |
| King et al. [39] | 2004 | Ground Mounted | ||
| Mattei et al. [40] | 2006 | Ground Mounted | U—heat exchange coefficient of module —cell absorption coefficient τ—glass transmittance ηref—the module efficiency at reference temperature —25 °C —power variation coefficient | |
| Faiman [24] | 2008 | Ground Mounted | ||
| Skoplaki et al. [10] | 2008 | Ground Mounted | ||
| Muzathik [12] | 2014 | Ground Mounted | ||
| Coskun et al. [9] | 2016 | Ground Mounted | ||
| Kamuyu et al. [33] | 2018 | Tm1 = 2.0458 + 0.9458Ta + 0.0215 GT − 1.2376Vw Tm2 = 1.8081 + 0.9282Ta + 0.021GT − 1.2210Vw + 0.0246Tw | Water Mounted |
| Type of Mounting | R2 | Variables | Model Nomenclature |
|---|---|---|---|
| Ground-mounted | 0.737 | , v, | GM1 |
| Water mounted | 0.955 | , v, | F1 |
| Water mounted | 0.94 | , v, | F2 |
| Model | R2 | Variables | Model Nomenclature |
|---|---|---|---|
| Linear Regression Degree 01 | 0.956 | , v, | F3 |
| Linear Regression Degree 01 | 0.93 | , v,, | F4 |
| Linear Regression Degree 01 | 0.96 | , v,, | F5 |
| Linear Regression Degree 02 | 0.96 | , v, | F6 |
| Linear Regression Degree 02 | 0.944 | , v,, | F7 |
| Linear Regression Degree 02 | 0.963 | , v, | F8 |
| RMSE | Models | |||||||
|---|---|---|---|---|---|---|---|---|
| F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | |
| Maximum | 5.64 | 8.26 | 5.50 | 9.43 | 8.19 | 6.95 | 22.38 | 22.07 |
| Minimum | 1.96 | 2.65 | 1.67 | 2.34 | 5.49 | 2.54 | 11.35 | 11.90 |
| RMSE | Models | |||||||
|---|---|---|---|---|---|---|---|---|
| F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | |
| Summer | 7.42 | 7.21 | 7.30 | 8.27 | 10.81 | 8.99 | 20.21 | 20.07 |
| Monsoon | 2.61 | 3.66 | 2.74 | 3.36 | 5.31 | 3.31 | 13.50 | 13.34 |
| Winter | 3.11 | 4.19 | 3.07 | 3.95 | 5.28 | 3.74 | 11.58 | 13.04 |
| Correlation coefficient | ||||||||
| Summer | 0.90 | 0.89 | 0.90 | 0.90 | 0.87 | 0.89 | 0.88 | 0.87 |
| Monsoon | 0.97 | 0.95 | 0.97 | 0.96 | 0.97 | 0.97 | 0.93 | 0.92 |
| Winter | 0.98 | 0.95 | 0.97 | 0.96 | 0.97 | 0.97 | 0.95 | 0.93 |
| R2 | ||||||||
| Summer | 0.81 | 0.79 | 0.81 | 0.81 | 0.75 | 0.79 | 0.77 | 0.75 |
| Monsoon | 0.94 | 0.90 | 0.94 | 0.92 | 0.93 | 0.93 | 0.87 | 0.85 |
| Winter | 0.95 | 0.91 | 0.95 | 0.91 | 0.94 | 0.95 | 0.90 | 0.87 |
| Recorded Data | Model F1 | Model F2 | Model F3 | Model F4 | Model F5 | Model F6 | Model F7 | Model F8 | |
|---|---|---|---|---|---|---|---|---|---|
| Energy Estimated (Wh) | 20,372 | 20,293 | 20,303 | 20,362 | 20,309 | 19,639 | 19,999 | 18,435 | 18,410 |
| % above/below the Recorded data | −0.53 | −0.49 | −0.20 | −0.46 | −3.74 | −1.98 | −9.64 | −9.76 |
| Season | Energy Estimate with Recorded Panel Temperature Data | Energy Estimate with Modelled Panel Temperature Data | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model F1 | Model F2 | Model F3 | Model F4 | Model F5 | Model F6 | Model F7 | Model F8 | |||
| Summer | Power Estimated in Wh | 7809 | 7716 | 7723 | 7782 | 7724 | 7474 | 7604 | 6994 | 7000 |
| % above or below the Recorded data | −1.19 | −1.10 | −0.35 | −1.09 | −4.29 | −2.63 | −10.44 | −10.36 | ||
| Monsoon | Power Estimated in Wh | 5317 | 5296 | 5295 | 5261 | 5284 | 5125 | 5238 | 4785 | 4795 |
| % above or below the Recorded data | −0.39 | −0.41 | −1.05 | −0.62 | −3.61 | −1.49 | −10.00 | −9.82 | ||
| Winter | Power Estimated in Wh | 7276 | 7281 | 7285 | 7319 | 7301 | 7040 | 7157 | 6656 | 6615 |
| % above or below the Recorded data | 0.07 | 0.12 | 0.59 | 0.34 | −3.24 | −1.64 | −8.52 | −9.08 | ||
| Annual | Power Estimated in Wh | 20,402 | 20,293 | 20,303 | 20,362 | 20,309 | 19,639 | 19,999 | 18,435 | 18,410 |
| % above or below the Recorded data | −0.53 | −0.49 | −0.20 | −0.46 | −3.74 | −1.98 | −9.64 | −9.76 | ||
| Season | Summer | Winter | Monsoon | |||
|---|---|---|---|---|---|---|
| Panel over Water Bodies (°C) | Panel over Ground Mount (°C) | Panel over Water Bodies (°C) | Panel over Ground Mount (°C) | Panel over Water Bodies (°C) | Panel over Ground Mount (°C) | |
| Maximum Temperature | 66.68 | 70.86 | 59.57 | 63.73 | 65.55 | 70.87 |
| Minimum Temperature | 14.02 | 13.45 | −0.86 | −1.37 | 24.26 | 24.38 |
| Average Temperature | 39.50 | 46.77 | 25.71 | 29.06 | 38.33 | 39.77 |
| Month | Energy Generated (Floating) Maximum Insolation Day (Wh) | Energy Generated (Floating) Minimum Insolation Day (Wh) | Energy Generated (GM) Maximum Insolation Day (Wh) | Energy Generated (GM) Minimum Insolation Day (Wh) |
|---|---|---|---|---|
| Apr-21 | 1280.7 | 555.5 | 1238.4 | 541.0 |
| May-21 | 1258.1 | 188.7 | 1226.7 | 188.3 |
| Jun-21 | 1295.1 | 747.2 | 1258.6 | 758.2 |
| Jul-21 | 1261.7 | 462.5 | 1293.1 | 458.6 |
| Aug-21 | 1283.9 | 361.6 | 1248.5 | 355.8 |
| Sep-21 | 1120.9 | 504.2 | 1090.7 | 491.8 |
| Oct-21 | 1219.9 | 292.1 | 1194.3 | 288.6 |
| Nov-21 | 953.9 | 634.6 | 926.2 | 622.4 |
| Dec-21 | 981.7 | 203.1 | 952.1 | 201.7 |
| Jan-22 | 1105.3 | 213.1 | 1066.9 | 211.5 |
| Feb-22 | 1245.0 | 427.6 | 1198.2 | 422.9 |
| Mar-22 | 1307.4 | 1038.0 | 1256.7 | 946.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agrawal, K.K.; Jha, S.K.; Mittal, R.K.; Singh, A.P.; Vashishtha, S.; Gupta, S.; Soni, M.K. Predictive Modeling of Solar PV Panel Operating Temperature over Water Bodies: Comparative Performance Analysis with Ground-Mounted Installations. Energies 2024, 17, 3489. https://doi.org/10.3390/en17143489
Agrawal KK, Jha SK, Mittal RK, Singh AP, Vashishtha S, Gupta S, Soni MK. Predictive Modeling of Solar PV Panel Operating Temperature over Water Bodies: Comparative Performance Analysis with Ground-Mounted Installations. Energies. 2024; 17(14):3489. https://doi.org/10.3390/en17143489
Chicago/Turabian StyleAgrawal, Karmendra Kumar, Shibani Khanra Jha, Ravi Kant Mittal, Ajit Pratap Singh, Sanjay Vashishtha, Saurabh Gupta, and Manoj Kumar Soni. 2024. "Predictive Modeling of Solar PV Panel Operating Temperature over Water Bodies: Comparative Performance Analysis with Ground-Mounted Installations" Energies 17, no. 14: 3489. https://doi.org/10.3390/en17143489
APA StyleAgrawal, K. K., Jha, S. K., Mittal, R. K., Singh, A. P., Vashishtha, S., Gupta, S., & Soni, M. K. (2024). Predictive Modeling of Solar PV Panel Operating Temperature over Water Bodies: Comparative Performance Analysis with Ground-Mounted Installations. Energies, 17(14), 3489. https://doi.org/10.3390/en17143489









