Suitable Site Selection of Public Charging Stations: A Fuzzy TOPSIS MCDA Framework on Capacity Substation Assessment
Abstract
1. Introduction
1.1. Literature Review
| Method | City | Year | GIS-Based Method | Sustainable Criteria | Reference | ||||
|---|---|---|---|---|---|---|---|---|---|
| Technical | Economic | Social | Demographic | Environment | |||||
| Fuzzy TOPSIS | Beijing, China | 2015 | ✓ | ✓ | ✓ | [27] | |||
| Fuzzy Delphi method (FDM), combination weighting, and fuzzy grey relation analysis GRA-VIKOR | Tianjin, china | 2016 | ✓ | ✓ | ✓ | ✓ | [24] | ||
| Fuzzy analytical Hierarchy Process (FAHP) and TOPSIS | Ankara, Turkey | 2018 | ✓ | ✓ | ✓ | ✓ | [28] | ||
| FAHP technique and the traditional grey relational projection GRP method under a picture fuzzy environment | Beijing, China | 2019 | ✓ | ✓ | ✓ | ✓ | [31] | ||
| FAHP, PROMETHEE, and VIKOR | Anatolian, Turkey | 2020 | ✓ | ✓ | ✓ | ✓ | ✓ | [30] | |
| Decision-making trial and evaluation laboratory (DEMATEL), AHP, and TOPSIS | Istanbul, Turkey | 2020 | ✓ | ✓ | ✓ | ✓ | [32] | ||
| AHP, fuzzy AHP, Weighted Linear Combination (WLC), and TOPSIS | Istanbul, Turkey | 2020 | ✓ | ✓ | ✓ | ✓ | ✓ | [33] | |
| Linguistic entropy weight (LEW) method and fuzzy axiomatic design (FAD) | Chengdu, China | 2021 | ✓ | ✓ | ✓ | ✓ | [34] | ||
| AHP, TOPSIS | Istanbul, Turkey | 2021 | ✓ | ✓ | ✓ | ✓ | [25] | ||
| Integrated group aggregation techniques (GATs) with AHP, TOPSIS, and MOORA methods and sensitivity analysis results | Bursa, Turkey | 2022 | ✓ | ✓ | ✓ | ✓ | [35] | ||
| Machine learning frameworks (random forests, multinomial logistic regression, and support vector machines) | Orange, Southern California | 2022 | ✓ | ✓ | ✓ | ✓ | [36] | ||
| AHP, WLC | Winchester, UK | 2022 | ✓ | ✓ | [17] | ||||
| Combination weighting | Dublin, Ireland | 2023 | ✓ | ✓ | [37] | ||||
| Proposed work | Cuenca, Ecuador | 2024 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
1.2. Contributions
- Different from previous works, the proposed method simultaneously takes into account important criteria such as socio-demographics and environmental factors, which can play a decisive role in the massive increase of EVs as well as in the placement of EV charging stations.
- The density element in this analysis is important because it captures the strata of residential customers where an increase in EVs is most likely, consequently requiring greater dependence on public infrastructure. It uses high-resolution density electric load criteria in the analysis to determine suitable sites for EV charging stations.
- This work employs an adaptive TOPSIS MCDA approach to address uncertainties and imprecision in human judgment during decision-making. It employs linguistic membership functions and fuzzy sets in the criteria-weighting process, incorporating technical, economic, and social perspectives.
- The proposed GIS-based MCDA framework supports transformer capacity assessment in substations based on EV increase trends. It includes a charging station growth scenario to determine the expected electrical capabilities required to supply future EVs in the area.
2. Background
2.1. Criteria Definition
2.2. Geographically Weighted Regression
2.3. Geostatistical Interpolation
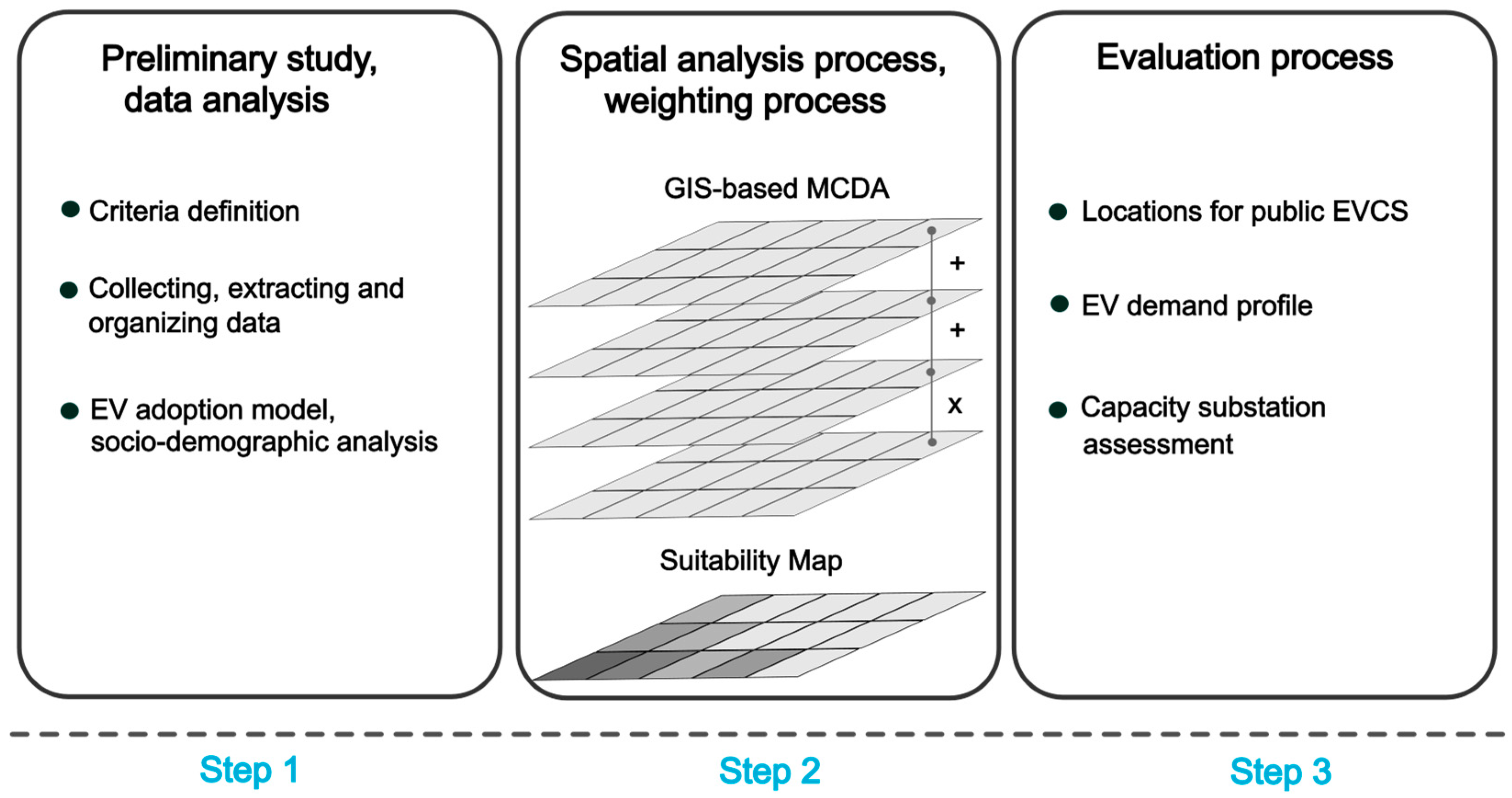
3. Proposed Method
3.1. Analytic Hierarchy Process
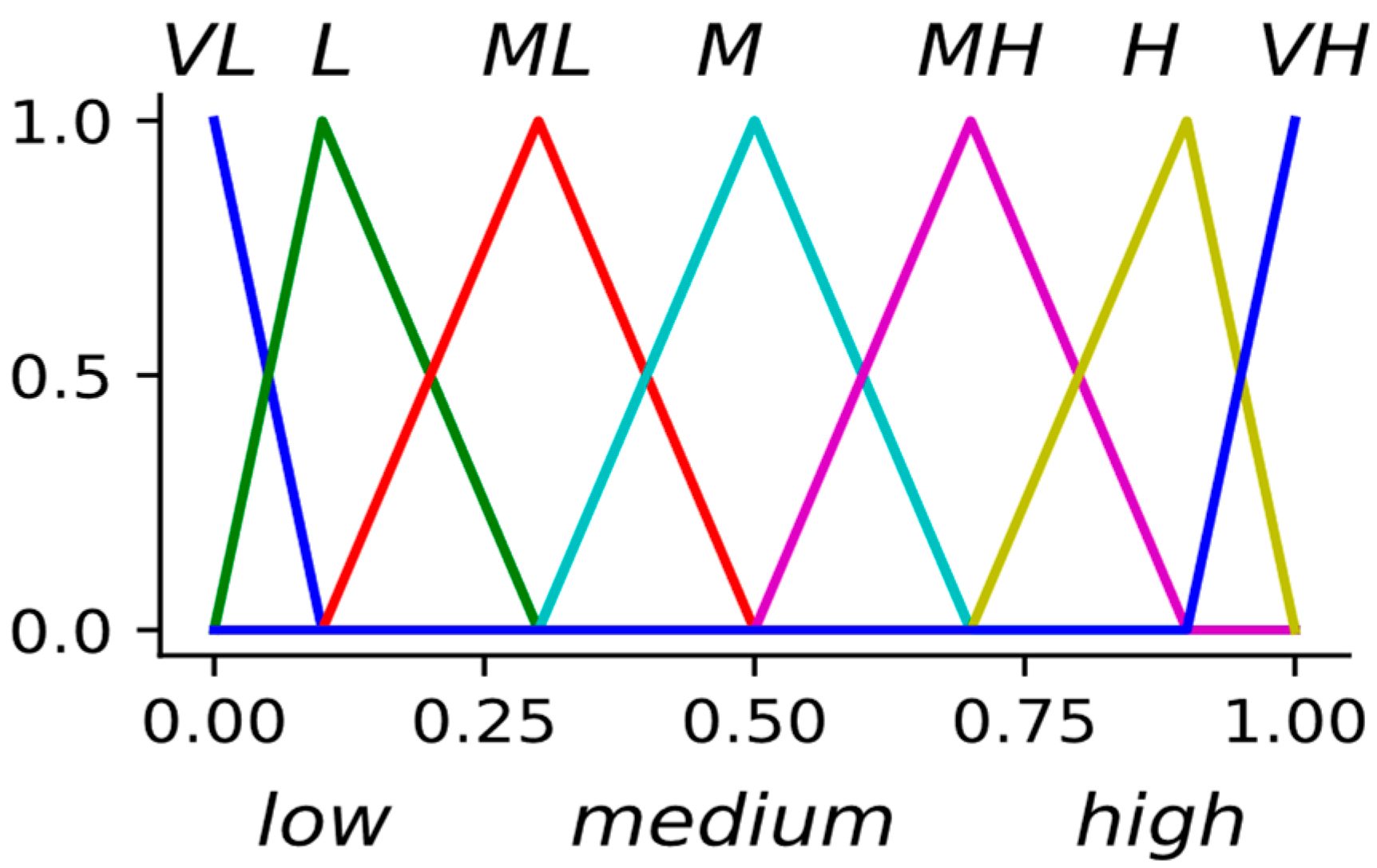
3.2. Fuzzy Logic
3.3. MCDM Framework
- Identify and define criteria for site suitability.
- Establish a hierarchy of criteria, conduct pairwise comparisons using AHP, and derive normalized weights.
- Assess candidate sites against criteria, assigning scores.
- Multiply scores by normalized weights and sum for each candidate site, and, for each candidate site, multiply the restricted condition.
- Rank candidate sites based on composite scores.
- Assess the impact of changes in criteria weights.
- Make the final decision.
- Normalize the decision matrix;
- Calculate the weighted normalized decision matrix;
- Determine the ideal and anti-ideal solutions;
- Calculate the separation measures;
- Calculate the relative closeness to the ideal solution;
- Rank the preferences in order.
- Determine the best and worst values of all criteria functions.
- Compute the values and , representing Separation Measure and Individual Regret, respectively.
- Compute the values named Maximum Group Utility.
- Rank the candidate sites.
- Propose a compromise solution.
- Determine the weight stability interval for each criterion.
- Determine the trade-offs.
- Adjust the trade-offs.
- Verify conditions for the algorithm’s termination.
- Form a committee of decision-makers, then identify the evaluation criteria.
- Choose the linguistic variables.
- Perform aggregations.
- Construct the fuzzy decision matrix and the normalized fuzzy decision matrix.
- Construct the fuzzy, weighted, normalized decision matrix.
- Determine the fuzzy positive ideal solution (FPIS) and the fuzzy negative ideal solution (FNIS).
- Calculate the distance for each candidate site from FPIS and FNIS.
- Calculate the closeness coefficient for each candidate site.
- Rank the candidate sites.
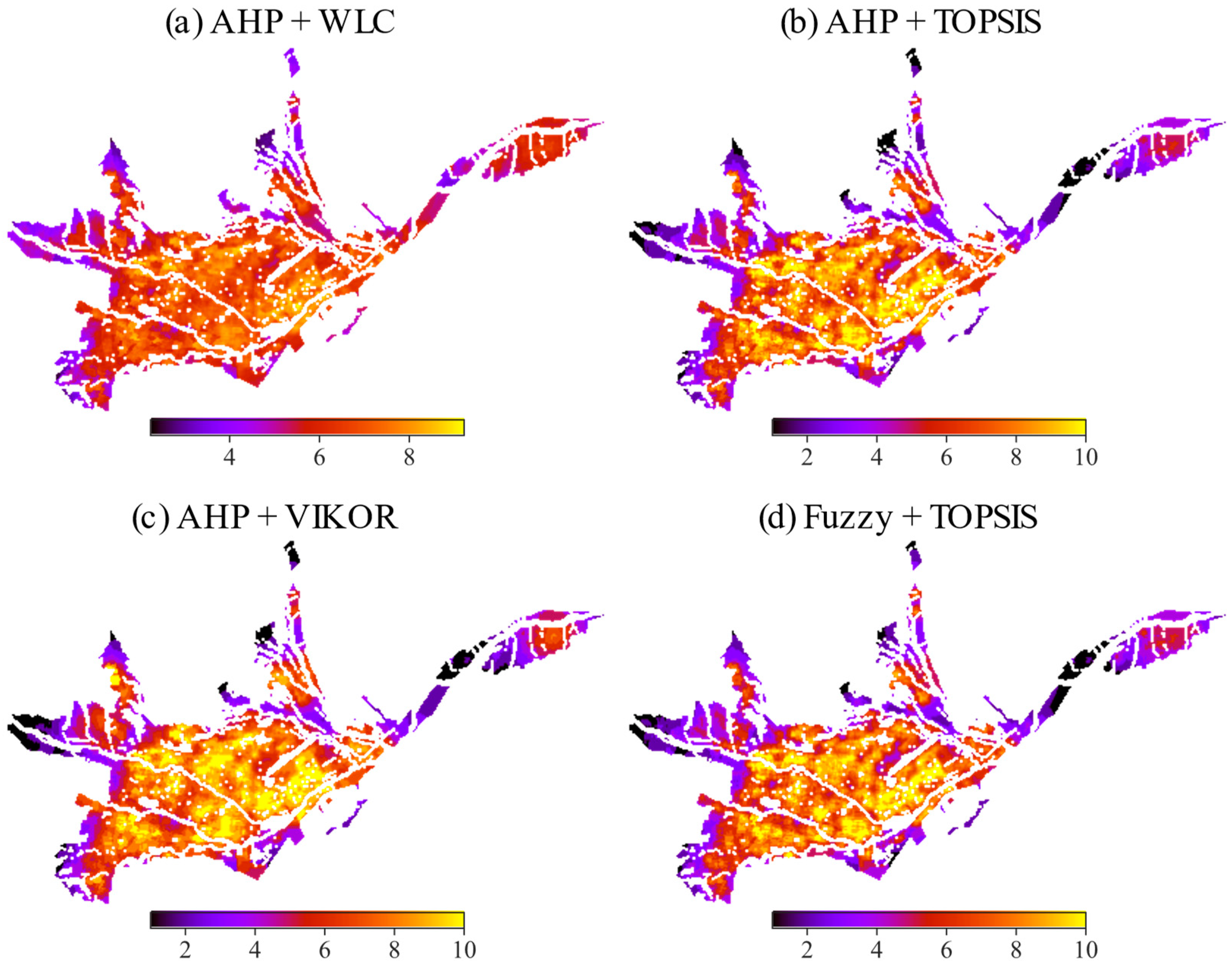
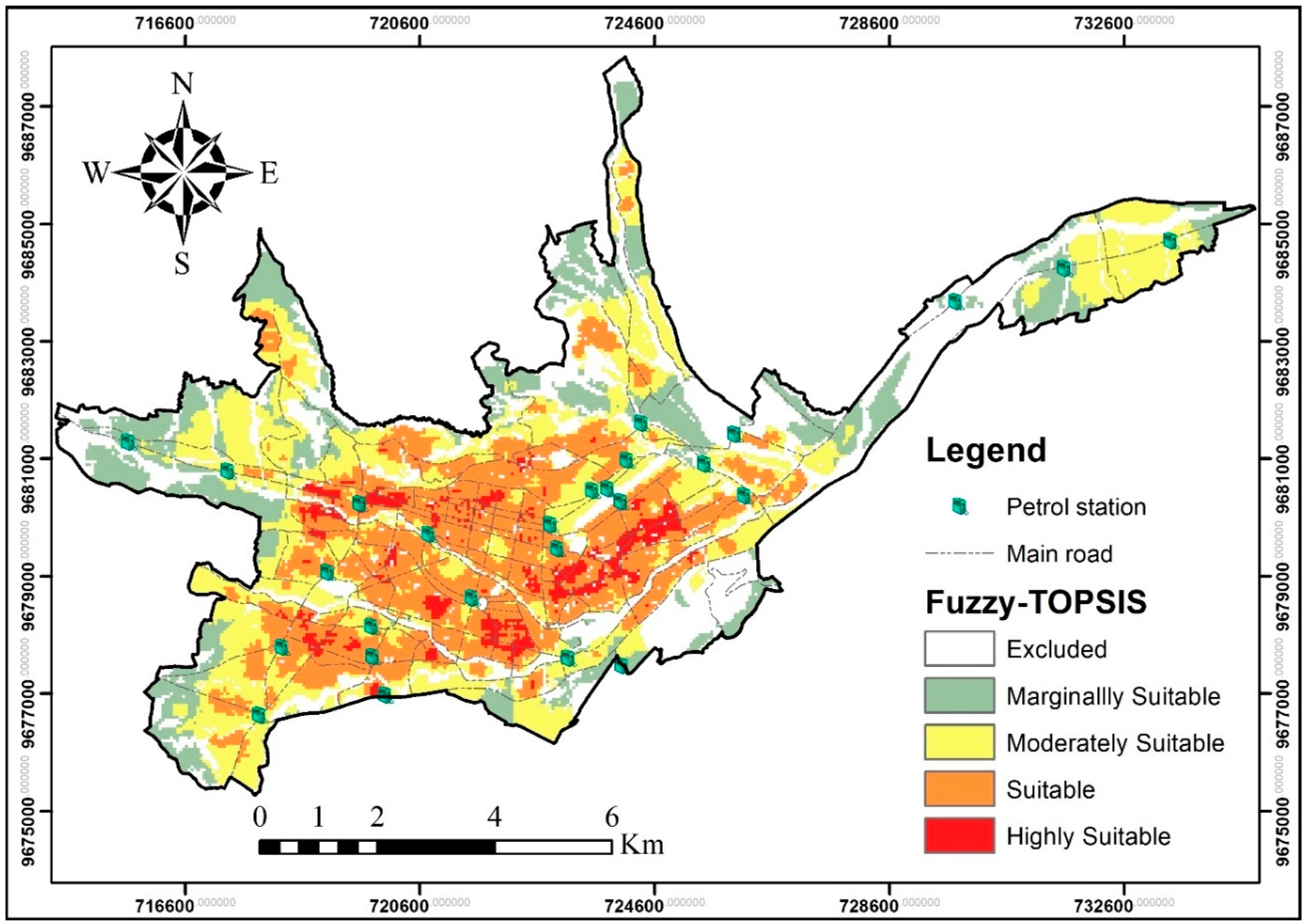
4. Results and Discussion
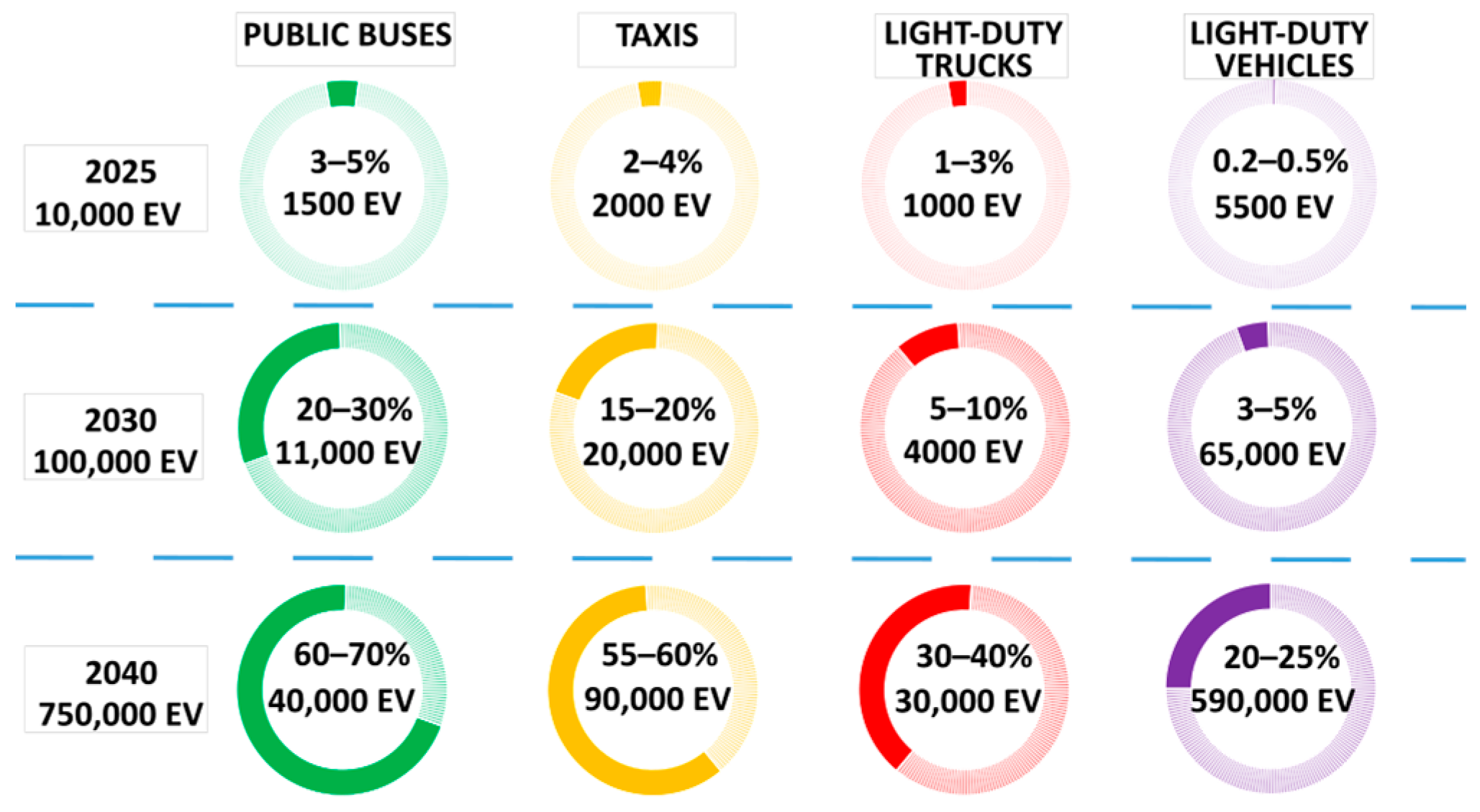
4.1. EV Adoption Model
4.2. Criteria and Restriction Analysis
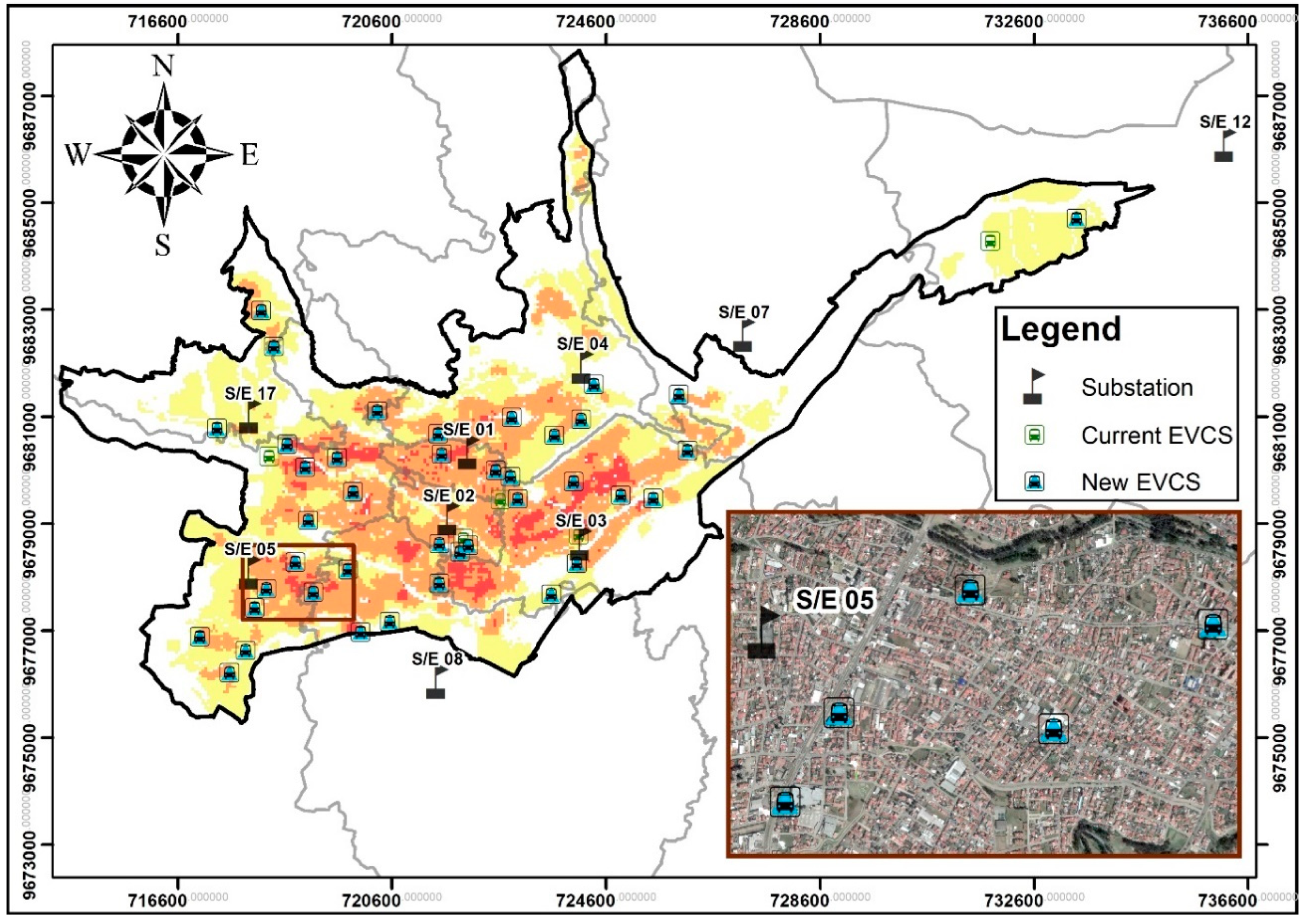
4.3. Suitability Locations
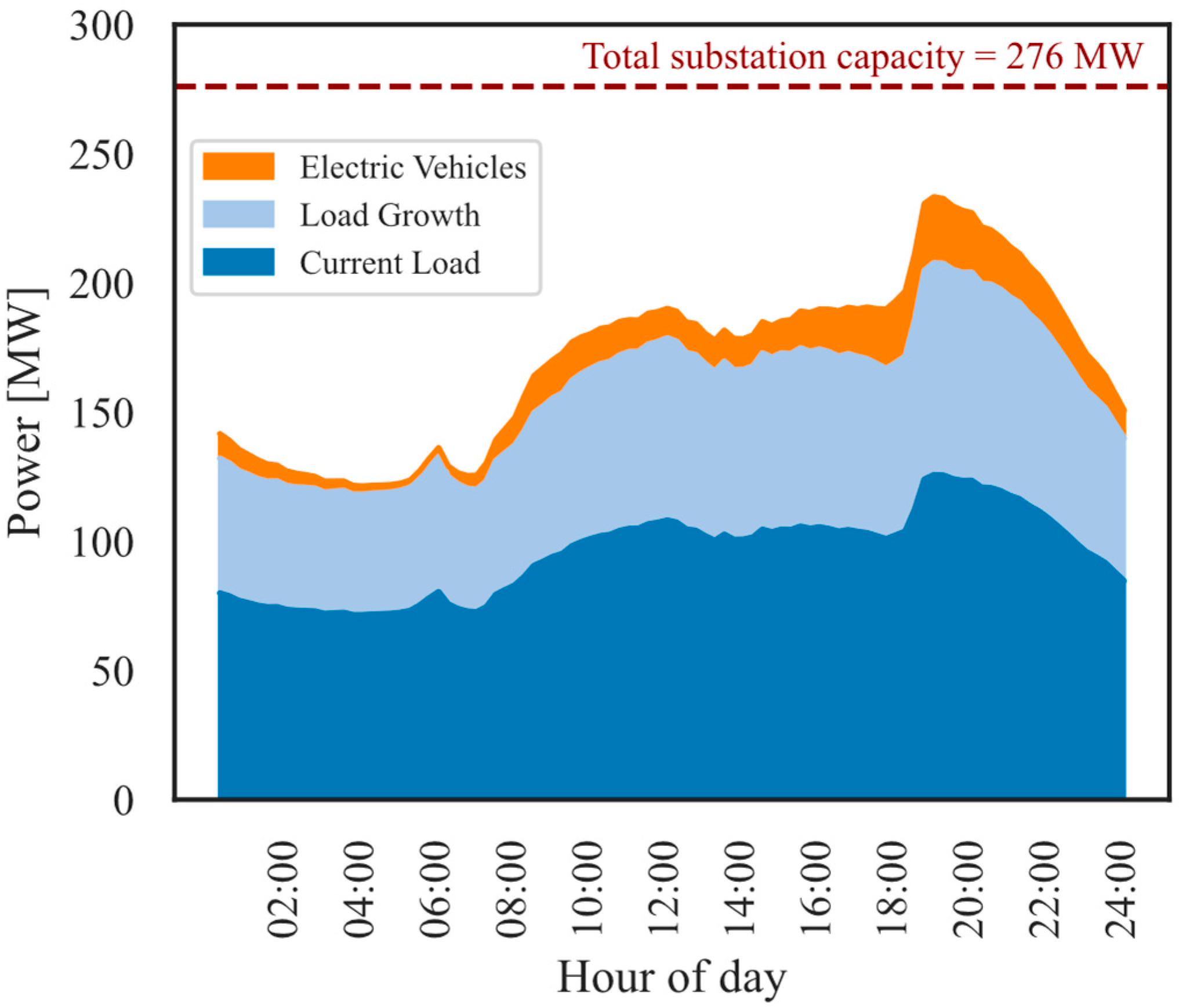
4.4. EV Charging Station Increase
4.5. Final Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- UNFCCC. Adoption of the Paris Agreement; United Nations Framework Convention on Climate Change: Paris, France, 2015; p. 32. [Google Scholar]
- International Energy Agency. World Energy Outlook; International Energy Agency: Paris, France, 2011; ISBN 2989264124134. [Google Scholar]
- International Organization of Motor Vehicle Manufacturers. Climate Change and CO2 Brochure; OICA: Paris, France, 2008; p. 9. [Google Scholar]
- Koch, N.; Ritter, N.; Rohlf, A.; Scarazzato, F. When Is the Electric Vehicle Market Self-Sustaining? Evidence from Norway. Energy Econ. 2022, 110, 105991. [Google Scholar] [CrossRef]
- International Energy Agency. Accelerating Ambitions Despite the Pandemic; Global EV Outlook; International Energy Agency: Paris, France, 2021; p. 100. [Google Scholar]
- Kheirkhah, A.R.; Meschini Almeida, C.F.; Kagan, N.; Leite, J.B. Optimal Probabilistic Allocation of Photovoltaic Distributed Generation: Proposing a Scenario-Based Stochastic Programming Model. Energies 2023, 16, 7261. [Google Scholar] [CrossRef]
- Global EV Data Explorer—Data Tools. Available online: https://www.iea.org/data-and-statistics/data-tools/global-ev-data-explorer (accessed on 1 February 2024).
- IEC 61851-1; Electric Vehicle Conductive Charging System—Part 1: General Requirements; Edition 3.0. International Electrotechnical Commission: Geneva, Switzerland, 2017; ISBN 978-2-8322-3766-3.
- Savari, G.F.; Sathik, M.J.; Raman, L.A.; El-Shahat, A.; Hasanien, H.M.; Almakhles, D.; Aleem, S.H.E.A.; Omar, A.I. Assessment of Charging Technologies, Infrastructure and Charging Station Recommendation Schemes of Electric Vehicles: A Review. Ain Shams Eng. J. 2023, 14, 101938. [Google Scholar] [CrossRef]
- Alternative Fuels Data Center: Electric Vehicle Charging Stations. Available online: https://afdc.energy.gov/fuels/electricity_stations.html#terms (accessed on 12 February 2024).
- Spendiff-Smith, M. The Different Levels of EV Charging Explained—EVESCO. Available online: https://www.power-sonic.com/blog/levels-of-ev-charging/ (accessed on 13 February 2024).
- US Department of Energy Alternative Fuels Data Center: Developing Infrastructure to Charge Electric Vehicles. Available online: https://afdc.energy.gov/fuels/electricity_infrastructure.html (accessed on 2 February 2024).
- PLUGNYC. NYC DOT Curbside Level 2 EV Charging Pilot; PLUGNYC: New York, NY, USA, 2023; p. 21. [Google Scholar]
- Lehrman, M. Electric Vehicle Charging Stations. Available online: https://bouldercolorado.gov/services/electric-vehicle-charging-stations (accessed on 2 February 2024).
- Slowik, P.; Lutsey, N. The Continued Transition to Electric Vehicles in U.S. Cities; ICCT: Washington, DC, USA, 2018; p. 42. [Google Scholar]
- Zhang, Q.; Li, H.; Zhu, L.; Campana, P.E.; Lu, H.; Wallin, F.; Sun, Q. Factors Influencing the Economics of Public Charging Infrastructures for EV—A Review. Renew. Sustain. Energy Rev. 2018, 94, 500–509. [Google Scholar] [CrossRef]
- Mahdy, M.; Bahaj, A.S.; Turner, P.; Wise, N.; Alghamdi, A.S.; Hamwi, H. Multi Criteria Decision Analysis to Optimise Siting of Electric Vehicle Charging Points—Case Study Winchester District, UK. Energies 2022, 15, 2497. [Google Scholar] [CrossRef]
- Xu, J.; Zhong, L.; Yao, L.; Wu, Z. An Interval Type-2 Fuzzy Analysis towards Electric Vehicle Charging Station Allocation from a Sustainable Perspective. Sustain. Cities Soc. 2018, 40, 335–351. [Google Scholar] [CrossRef]
- Saint, S.; Lawson, J.R. Rules for Reaching Consensus: A Modern Approach to Decision Making; Wiley: Hoboken, NJ, USA, 1994. [Google Scholar]
- Malczewski, J.; Rinner, C. Multicriteria Decision Analysis in Geographic Information Science; Springer: Berlin/Heidelberg, Germany, 2015; p. 331. [Google Scholar]
- Riemann, R.; Wang, D.Z.W.; Busch, F. Optimal Location of Wireless Charging Facilities for Electric Vehicles: Flow-Capturing Location Model with Stochastic User Equilibrium. Transp. Res. Part C Emerg. Technol. 2015, 58, 1–12. [Google Scholar] [CrossRef]
- Tu, W.; Li, Q.; Fang, Z.; Shaw, S.L.; Zhou, B.; Chang, X. Optimizing the Locations of Electric Taxi Charging Stations: A Spatial–Temporal Demand Coverage Approach. Transp. Res. Part C Emerg. Technol. 2016, 65, 172–189. [Google Scholar] [CrossRef]
- Funke, S.Á.; Gnann, T.; Plötz, P. Addressing the Different Needs for Charging Infrastructure: An Analysis of Some Criteria for Charging Infrastructure Set-Up. Green Energy Technol. 2015, 203, 73–90. [Google Scholar] [CrossRef]
- Zhao, H.; Li, N. Optimal Siting of Charging Stations for Electric Vehicles Based on Fuzzy Delphi and Hybrid Multi-Criteria Decision Making Approaches from an Extended Sustainability Perspective. Energies 2016, 9, 270. [Google Scholar] [CrossRef]
- Kaya, Ö.; Alemdar, K.D.; Campisi, T.; Tortum, A.; Çodur, M.K. The Development of Decarbonisation Strategies: A Three-Step Methodology for the Suitable Analysis of Current Evcs Locations Applied to Istanbul, Turkey. Energies 2021, 14, 2756. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, M.; Zhang, H.; Chen, K.; Wang, Y. Optimal Site Selection of Electric Vehicle Charging Stations Based on a Cloud Model and the PROMETHEE Method. Energies 2016, 9, 157. [Google Scholar] [CrossRef]
- Guo, S.; Zhao, H. Optimal Site Selection of Electric Vehicle Charging Station by Using Fuzzy TOPSIS Based on Sustainability Perspective. Appl. Energy 2015, 158, 390–402. [Google Scholar] [CrossRef]
- Erbaş, M.; Kabak, M.; Özceylan, E.; Çetinkaya, C. Optimal Siting of Electric Vehicle Charging Stations: A GIS-Based Fuzzy Multi-Criteria Decision Analysis. Energy 2018, 163, 1017–1031. [Google Scholar] [CrossRef]
- Zhou, J.; Wu, Y.; Wu, C.; He, F.; Zhang, B.; Liu, F. A Geographical Information System Based Multi-Criteria Decision-Making Approach for Location Analysis and Evaluation of Urban Photovoltaic Charging Station: A Case Study in Beijing. Energy Convers. Manag. 2020, 205, 112340. [Google Scholar] [CrossRef]
- Kaya, Ö.; Tortum, A.; Alemdar, K.D.; Çodur, M.Y. Site Selection for EVCS in Istanbul by GIS and Multi-Criteria Decision-Making. Transp. Res. Part D Transp. Environ. 2020, 80, 102271. [Google Scholar] [CrossRef]
- Ju, Y.; Ju, D.; Gonzalez, E.D.R.S.; Giannakis, M.; Wang, A. Study of Site Selection of Electric Vehicle Charging Station Based on Extended GRP Method under Picture Fuzzy Environment. Comput. Ind. Eng. 2019, 135, 1271–1285. [Google Scholar] [CrossRef]
- Karaşan, A.; Kaya, İ.; Erdoğan, M. Location Selection of Electric Vehicles Charging Stations by Using a Fuzzy MCDM Method: A Case Study in Turkey. Neural Comput. Appl. 2020, 32, 4553–4574. [Google Scholar] [CrossRef]
- Guler, D.; Yomralioglu, T. Suitable Location Selection for the Electric Vehicle Fast Charging Station with AHP and Fuzzy AHP Methods Using GIS. Ann. GIS 2020, 26, 169–189. [Google Scholar] [CrossRef]
- Feng, J.; Xu, S.X.; Li, M. A Novel Multi-Criteria Decision-Making Method for Selecting the Site of an Electric-Vehicle Charging Station from a Sustainable Perspective. Sustain. Cities Soc. 2021, 65, 102623. [Google Scholar] [CrossRef]
- Yagmahan, B.; Yılmaz, H. An Integrated Ranking Approach Based on Group Multi-Criteria Decision Making and Sensitivity Analysis to Evaluate Charging Stations under Sustainability. Environ. Dev. Sustain. 2022, 25, 96–121. [Google Scholar] [CrossRef]
- Roy, A.; Law, M. Examining Spatial Disparities in Electric Vehicle Charging Station Placements Using Machine Learning. Sustain. Cities Soc. 2022, 83, 103978. [Google Scholar] [CrossRef]
- Charly, A.; Thomas, N.J.; Foley, A.; Caulfield, B. Identifying Optimal Locations for Community Electric Vehicle Charging. Sustain. Cities Soc. 2023, 94, 104573. [Google Scholar] [CrossRef]
- Zambrano-Asanza, S.; Quiros-Tortos, J.; Franco, J.F. Optimal Site Selection for Photovoltaic Power Plants Using a GIS-Based Multi-Criteria Decision Making and Spatial Overlay with Electric Load. Renew. Sustain. Energy Rev. 2021, 143, 110853. [Google Scholar] [CrossRef]
- Zambrano-Asanza, S.; Chumbi, W.E.; Franco, J.F.; Padilha-Feltrin, A. Multicriteria Decision Analysis in Geographic Information Systems for Identifying Ideal Locations for New Substations. J. Control Autom. Electr. Syst. 2021, 32, 1305–1316. [Google Scholar] [CrossRef]
- Mejia, M.A.; Melo, J.D.; Zambrano-Asanza, S.; Padilha-Feltrin, A. Spatial-Temporal Growth Model to Estimate the Adoption of New End-Use Electric Technologies Encouraged by Energy-Efficiency Programs. Energy 2020, 191, 116531. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; Wiley: Chichester, UK; Hoboken, NJ, USA, 2002; ISBN 978-0-471-49616-8. [Google Scholar]
- Yang, D. Kriging for NSRDB PSM Version 3 Satellite-Derived Solar Irradiance. Sol. Energy 2018, 171, 876–883. [Google Scholar] [CrossRef]
- Oliver, M.A.; Webster, R. Kriging: A Method of Interpolation for Geographical Information Systems. Int. J. Geogr. Inf. Syst. 1990, 4, 313–332. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting. Resource Allocation, xiii ed.; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Yager, R.; Zadeh, L. An Introduction to Fuzzy Logic Applications in Intelligent Systems, 1st ed.; Springer: New York, NY, USA, 1992; ISBN 1-4613-6619-4. [Google Scholar]
- Bede, B. Mathematics of Fuzzy Sets and Fuzzy Logic; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Zadeh, L.A. The Concept of a Linguistic Variable and Its Application to Approximate Reasoning-I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Malczewski, J. On the Use of Weighted Linear Combination Method in GIS: Common and Best Practice Approaches. Trans. GIS 2000, 4, 5–22. [Google Scholar] [CrossRef]
- Papathanasiou, J.; Ploskas, N. Multiple Criteria Decision Aid: Methods Examples and Python Implementations; Springer: Cham, Switzerland, 2018. [Google Scholar]
- INEC Anuario de Estadísticas de Transporte. 2021. Available online: https://www.ecuadorencifras.gob.ec/transporte/ (accessed on 2 February 2024).
- Instituto Nacional de Estadística y Censos. Estadísticas de transporte (ESTRA); Instituto Nacional de Estadística y Censos: Quito, Ecuador, 2022.
- Mendieta, C.S. Hay 64.199 vehículos matriculados en Cuenca. Diario El Mercurio, 10 September 2022. [Google Scholar]
- Priessner, A.; Sposato, R.; Hampl, N. Predictors of Electric Vehicle Adoption: An Analysis of Potential Electric Vehicle Drivers in Austria. Energy Policy 2018, 122, 701–714. [Google Scholar] [CrossRef]
- Namdeo, A.; Tiwary, A.; Dziurla, R. Spatial Planning of Public Charging Points Using Multi-Dimensional Analysis of Early Adopters of Electric Vehicles for a City Region. Technol. Forecast. Soc. Change 2014, 89, 188–200. [Google Scholar] [CrossRef]
- MTOP Socializa La Estrategia Nacional de Electromovilidad Para Ecuador Con Sectores Estratégicos. Available online: https://www.obraspublicas.gob.ec/mtop-socializa-la-estrategia-nacional-de-electromovilidad-para-ecuador-con-sectores-estrategicos/ (accessed on 2 February 2024).
- Hinicio. Estrategia Nacional de Electromovilidad para Ecuador (ENEM); BID, MTOP, Hinicio: Quito, Ecuador, 2021; p. 88. [Google Scholar]
- Alternative Fuels Data Center: Electric Vehicle Infrastructure Projection Tool (EVI-Pro) Lite. Available online: https://afdc.energy.gov/evi-x-toolbox (accessed on 20 March 2024).

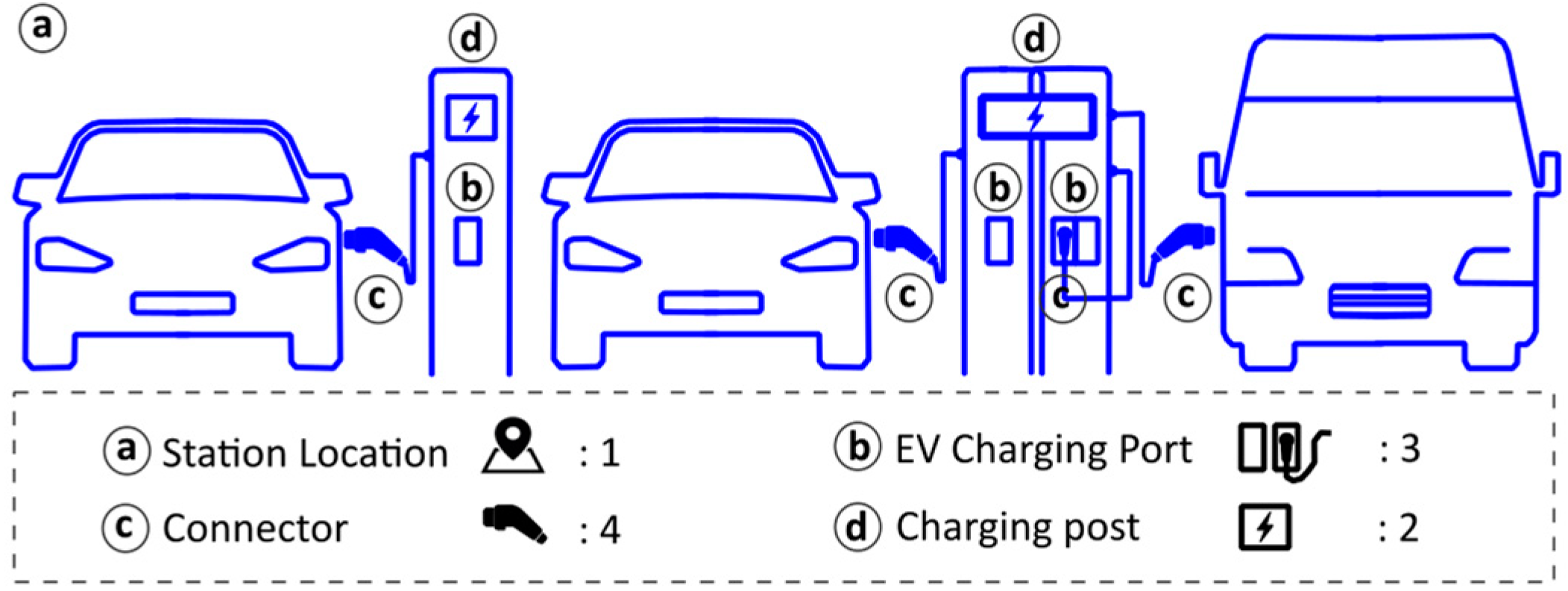

| Charging Level | Typical Use | Charging Power (kW) | Voltage | Current (A) | Charging Time (h) | Description |
|---|---|---|---|---|---|---|
| Level 1 | Home | 1.4 | 120 V AC | 15 | 4–11 | Basic charging from a standard electrical outlet |
| 1.9 | 20 | 11–36 | ||||
| Level 2 | Home, workplace | 4 | 240 V AC | 40 | 1–4 | Advanced charging at home or public stations |
| 8 | 400 V AC | 80 | 2–6 | |||
| 19.2 | 2–3 | |||||
| Level 3 (DC Fast Charging) | Public outlets | 30–150 | 480 V + DC | – | 0.2–1.5 | Rapid charging at specialized public stations |
| 250–350 | ||||||
| Extreme Fast Charging (XFC) | Highway | Over 350 kW | – | – | Up to 0.1 | Ultra-rapid charging technology for future infrastructure |
| Design | Number of Stations | Number of Ports | kW Station | kW Total | |
|---|---|---|---|---|---|
| L2 (7.2 kW) | DC Fast (150 kW) | ||||
| 1 | 15 | 2 | 0 | 38.4 | 576 |
| 2 | 3 | 4 | 0 | 76.8 | 230.4 |
| 3 | 1 | 4 | 4 | 676.8 | 676.8 |
| 19 | 46 | 4 | 1483.2 | ||
| Main Criteria | Sub Criteria | Description | Reference |
|---|---|---|---|
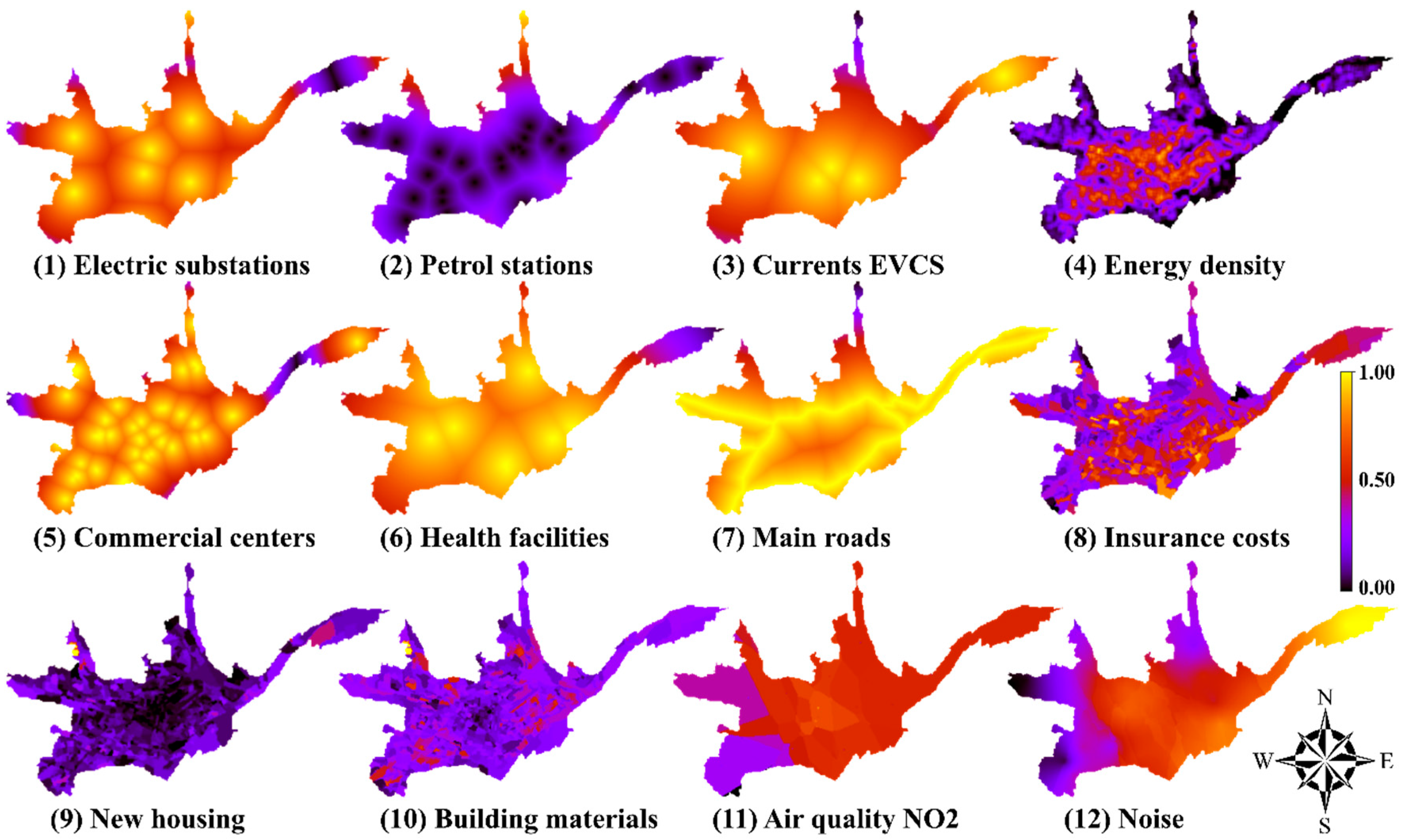
| C1: Energy criteria | Electric substations | Distance between the closest electrical substation and the candidate charging station location. | [25,28,30] |
| Petrol stations | Distance between the closest petrol station and the candidate charging station location. | [17,28,30,33] | |
| Current EV charging stations | Distance between the closest charging station and the candidate charging station location. | [17,28,30,36,37] | |
| Energy density | Spatial distribution of energy consumption, calculated by total energy/land area. | [38] | |
| C2: Economic and Social criteria | Commercial centers | Distance between the closest commercial center and the candidate charging station location. | [25,29,30,33] |
| Health facilities | Distance between the closest health facility and the candidate charging station location. | [39] | |
| C3: Transportation criteria | Main roads | Distance between the closest principal road and the candidate charging station location. | [17,25,28,29,30,33,37] |
| C4: Socio-demographics criteria | Insurance costs | Average household insurance cost. | [40] |
| New housing | Residential buildings’ age. | [40] | |
| Building materials | Households employing high-end building materials in their residences. | [40] | |
| C5: Environmental criteria | Air quality | Annual mean concentration of particulate matter level. Measures (NO2) recorded by monitoring stations. | [25,30] |
| Noise | The day-averaged noise level on a weekday. Traffic noise (dB) derived from the monitoring stations. | [39] |
| Main Criteria | Sub Criteria | GIS Analysis |
|---|---|---|
| C1: Energy criteria | Electric substations | Euclidean distance |
| Petrol stations | Euclidean distance | |
| Currents EVCS | Euclidean distance | |
| Energy density | Point density | |
| C2: Economic and Social criteria | Commercial centers | Euclidean distance |
| Health facilities | Euclidean distance | |
| C3: Transportation criteria | Main roads | Euclidean distance |
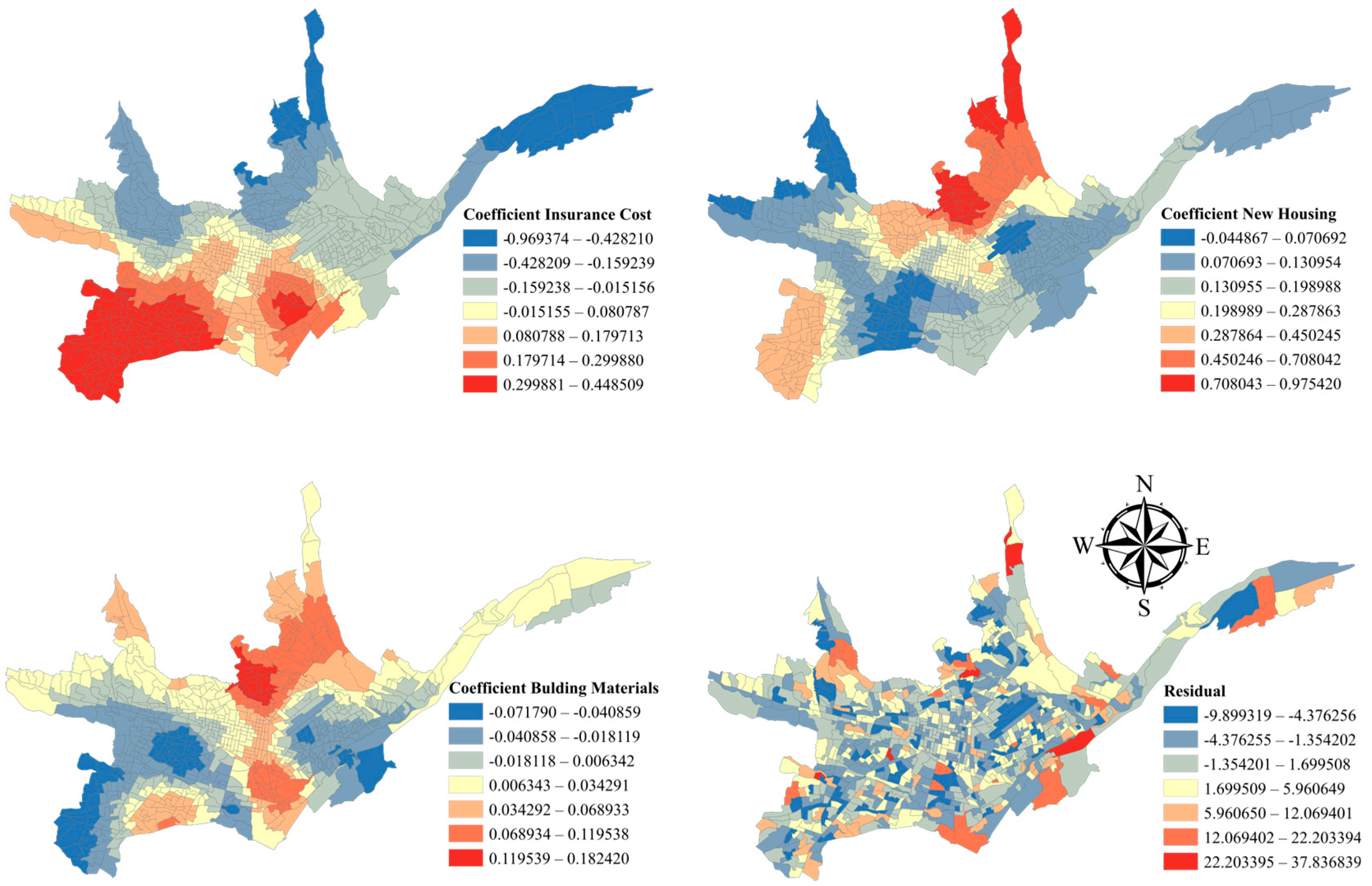
| C4: Socio-demographic criteria | Insurance costs | GWR |
| New housing | GWR | |
| Building materials | GWR | |
| C5: Environmental criteria | Air quality | Kriging interpolation |
| Noise | Kriging interpolation |
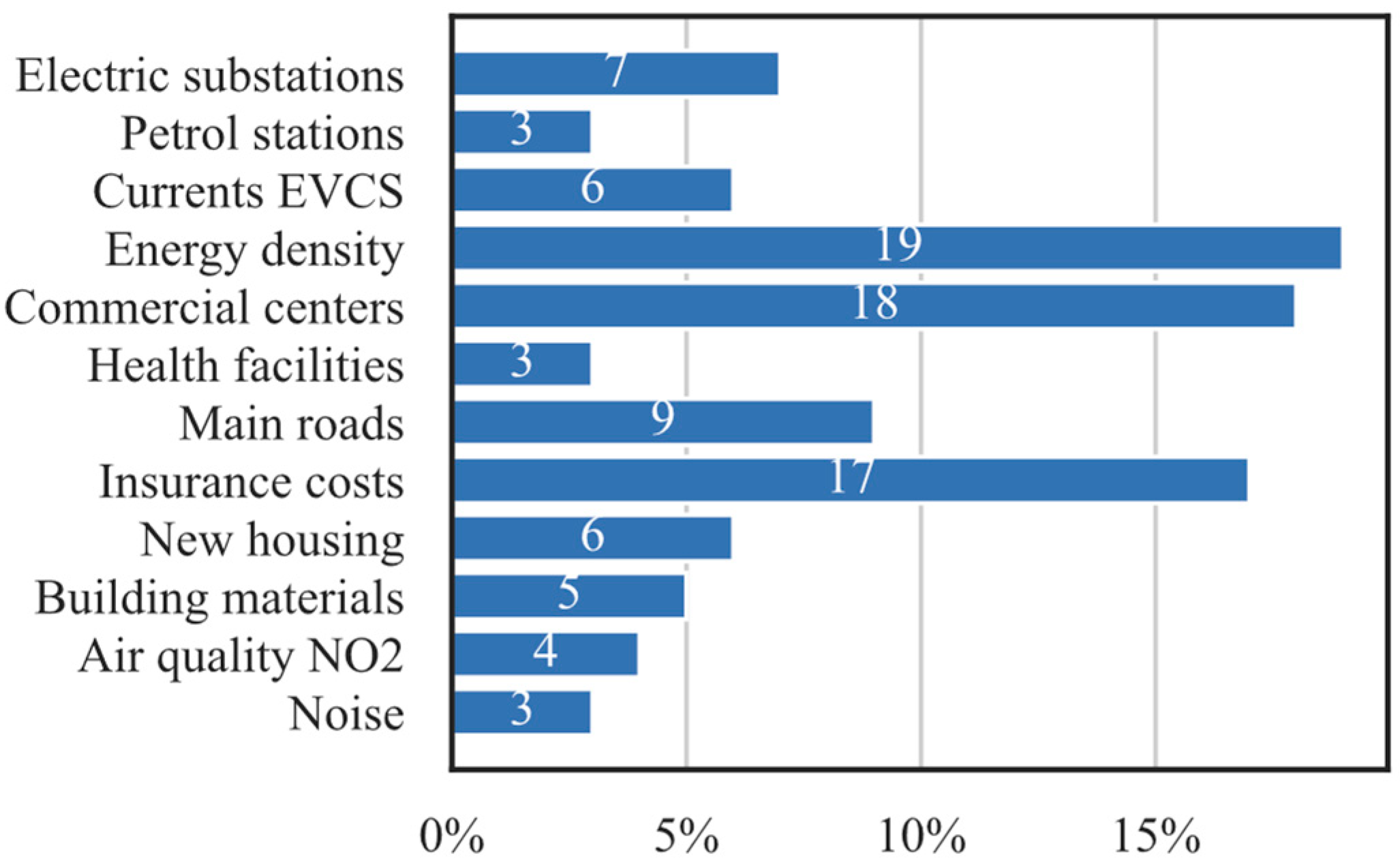
| Criteria | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1: Electric substations | 1 | 5 | 3 | 1/4 | 6 | 1/2 | 1/3 | 1/6 | 1/2 | 1/2 | 2 | 2 |
| 2: Petrol stations | 1 | 1/3 | 1/7 | 2 | 1/3 | 2 | 1/3 | 2 | 1/5 | 1/3 | 1/3 | |
| 3: Currents EVCS | 1 | 1/4 | 3 | 1/5 | 2 | 1/6 | 3 | 1/7 | 2 | 3 | ||
| 4: Commercial centers | 1 | 6 | 2 | 4 | 5 | 5 | 1/2 | 3 | 4 | |||
| 5: Health facilities | 1 | 1/4 | 1/2 | 1/8 | 1/3 | 1/4 | 3 | 2 | ||||
| 6: Main roads | 1 | 2 | 1/5 | 2 | 1/3 | 2 | 3 | |||||
| 7: New housing | 1 | 1/7 | 2 | 1/3 | 3 | 3 | ||||||
| 8: Insurance costs | 1 | 7 | 1/4 | 2 | 2 | |||||||
| 9: Building materials | 1 | 1/5 | 3 | 2 | ||||||||
| 10: Energy density | 1 | 4 | 3 | |||||||||
| 11: Air quality NO2 | 1 | 2 | ||||||||||
| 12: Noise | 1 |
| Decision Maker | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1: Technical | M | L | ML | VH | H | VL | M | H | L | L |
| 2: Economic | VH | M | L | L | VH | H | M | ML | H | L |
| 3: Social | M | H | L | ML | H | VH | VH | M | H | L |
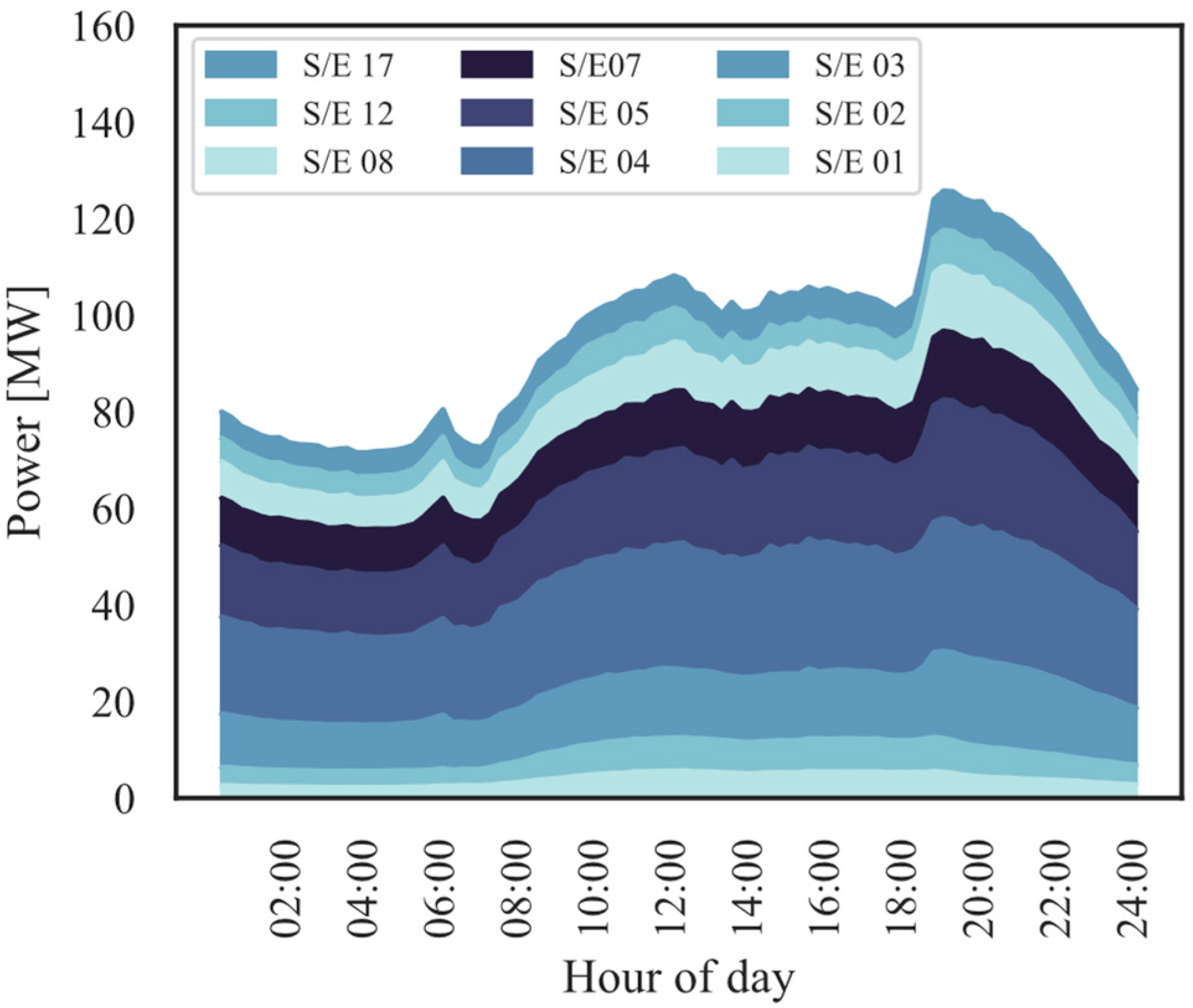
| Substation | Voltage (kV) | Peak Load (MW) | Rated Capacity ONAN (MW) | Reserve (MW) |
|---|---|---|---|---|
| S/E 01 | 22/6.3 | 5.57 | 15 | 9.43 |
| S/E 02 | 22/6.3 | 7.08 | 15 | 7.92 |
| S/E 03 | 69/22 | 18.23 | 48 | 29.77 |
| S/E 04 | 69/22 | 27.65 | 48 | 20.35 |
| S/E 05 | 69/22 | 24.71 | 48 | 23.29 |
| S/E 07 | 69/22 | 14.45 | 34 | 19.55 |
| S/E 08 | 69/22 | 13.47 | 24 | 10.53 |
| S/E 12 | 69/22 | 7.59 | 20 | 12.41 |
| S/E 17 | 69/22 | 8.35 | 24 | 15.65 |
| 125.70 | 276 |
| Design | No. of Stations | % | Number of Ports per Station | kW per Station | Total (kW) | |||
|---|---|---|---|---|---|---|---|---|
| Work L1 (4 kW) | Work L2 (8 kW) | Public L2 (19.2 kW) | DC Fast (150 kW) | |||||
| 1 | 8 | 20% | 11 | 34 | 5 | 0 | 412 | 3296 |
| 2 | 28 | 70% | 6 | 28 | 8 | 0 | 401.6 | 11,244.8 |
| 3 | 4 | 10% | 0 | 0 | 3 | 3 | 507.6 | 2030.4 |
| 40 | 256 | 1056 | 276 | 12 | 16,571.2 | |||
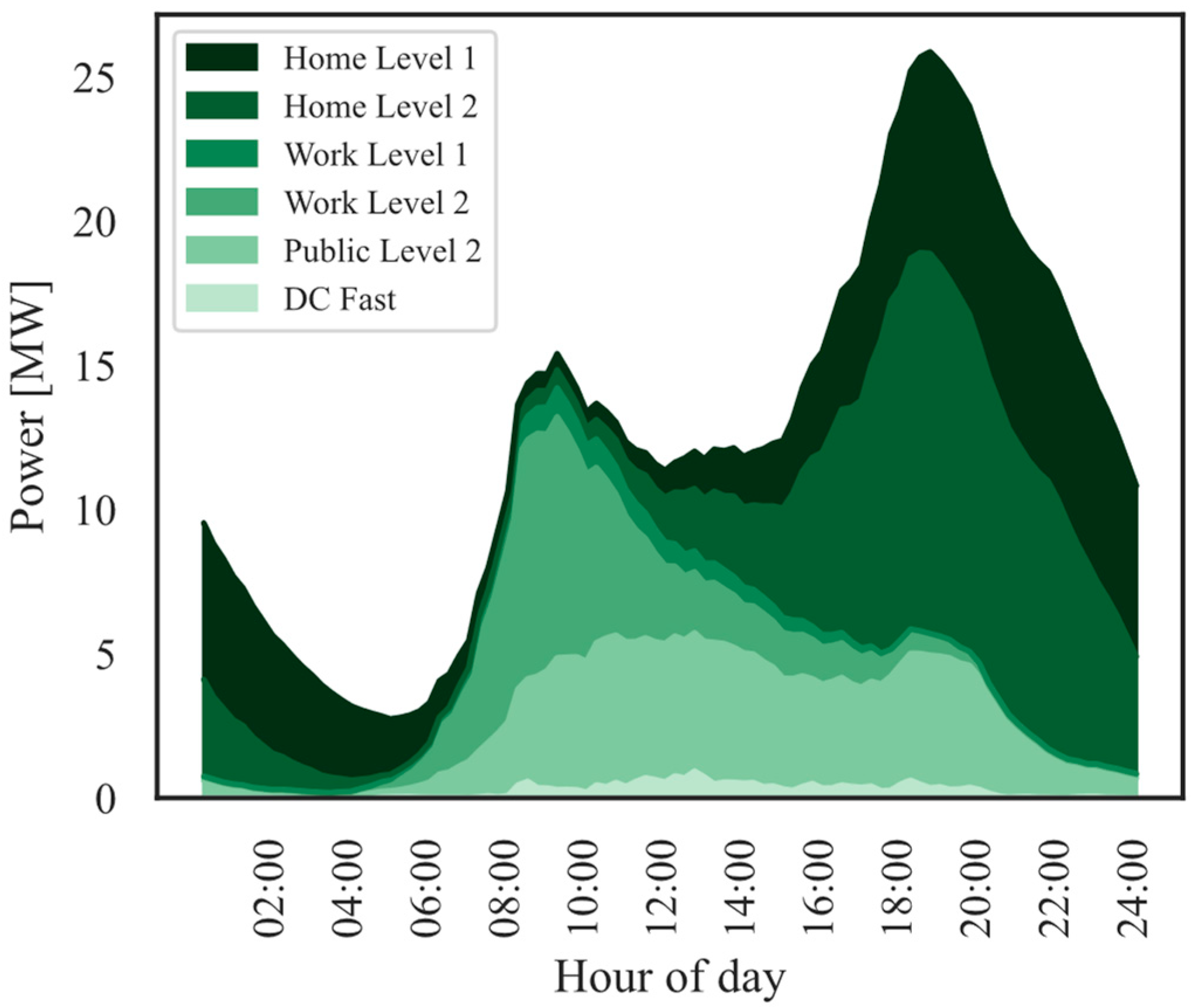
| Substation | Number of Ports | Total (MW) | |||
|---|---|---|---|---|---|
| Work Level 1 | Work Level 2 | Public Level 2 | DC Fast | ||
| S/E 01 | 12 | 56 | 16 | 0 | 0.80 |
| S/E 02 | 18 | 84 | 24 | 0 | 1.20 |
| S/E 03 | 57 | 214 | 50 | 3 | 3.35 |
| S/E 04 | 41 | 174 | 48 | 3 | 2.93 |
| S/E 05 | 86 | 332 | 79 | 3 | 4.97 |
| S/E07 | 6 | 28 | 8 | 0 | 0.40 |
| S/E 08 | 18 | 84 | 27 | 3 | 1.71 |
| S/E 12 | 6 | 28 | 8 | 0 | 0.40 |
| S/E 17 | 12 | 56 | 16 | 0 | 0.80 |
| Total | 256 | 1056 | 276 | 12 | 16.57 |
| Max Power (kW) | 4 | 8 | 19.2 | 150 | |
| Total (MW) | 1.024 | 8.448 | 5.30 | 1.80 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chumbi, W.E.; Martínez-Minga, R.; Zambrano-Asanza, S.; Leite, J.B.; Franco, J.F. Suitable Site Selection of Public Charging Stations: A Fuzzy TOPSIS MCDA Framework on Capacity Substation Assessment. Energies 2024, 17, 3452. https://doi.org/10.3390/en17143452
Chumbi WE, Martínez-Minga R, Zambrano-Asanza S, Leite JB, Franco JF. Suitable Site Selection of Public Charging Stations: A Fuzzy TOPSIS MCDA Framework on Capacity Substation Assessment. Energies. 2024; 17(14):3452. https://doi.org/10.3390/en17143452
Chicago/Turabian StyleChumbi, Wilson Enrique, Roger Martínez-Minga, Sergio Zambrano-Asanza, Jonatas B. Leite, and John Fredy Franco. 2024. "Suitable Site Selection of Public Charging Stations: A Fuzzy TOPSIS MCDA Framework on Capacity Substation Assessment" Energies 17, no. 14: 3452. https://doi.org/10.3390/en17143452
APA StyleChumbi, W. E., Martínez-Minga, R., Zambrano-Asanza, S., Leite, J. B., & Franco, J. F. (2024). Suitable Site Selection of Public Charging Stations: A Fuzzy TOPSIS MCDA Framework on Capacity Substation Assessment. Energies, 17(14), 3452. https://doi.org/10.3390/en17143452








