Abstract
A fault protection method is proposed for flexible direct-current (DC) power systems based on the cosine similarity of currents in current-limiting reactors. The typical characteristics of external and internal faults in a flexible DC power system were analyzed. The principles of cosine similarity and the fault current characteristics of current-limiting reactors were used to distinguish between internal and external faults. The ratio of the average positive and negative voltages of the current-limiting reactor was then used to distinguish the fault types and fault line. Finally, a simulation model of a circular flexible DC power system was constructed using MATLAB/Simulink software (2018b). The simulation results show that the proposed protection scheme can quickly and accurately identify the location and type of faults, and has a strong ability to withstand fault resistance and is less affected by distributed capacitance, noise, and communication delay.
1. Introduction
With the development of new energy generation technologies, direct-current (DC) distribution networks based on voltage source converters (VSCs) have become important components of new power systems [1,2,3]. However, owing to the low impedance characteristics of a DC distribution network based on VSCs, the fault current has a fast change rate and high amplitude when a short circuit or a grounding fault occurs, and there is no natural zero crossing in a DC distribution network [4]. Without timely protection measures, the power electronic equipment in a DC system can be easily damaged, and the reliable operation of the DC distribution network can be affected [5,6]. Therefore, a fast and reliable DC fault protection method is essential to the safe operation of a DC distribution network.
For DC distribution network line protection, fault current differential [7] and fault voltage differential [8] protection schemes were proposed. The use of fault current or voltage information in these schemes improves the protection speed. However, in multiterminal DC distribution network structures, the protection accuracy is easily affected. A DC fault protection method based on a zero-mode fault current initial traveling wave was proposed [9] that has the characteristics of high resistance to fault resistance and noise interference. However, its practicality in engineering is limited by an excessively high sampling rate. In other research [10], a new protection scheme was proposed that uses the first and second derivatives of the fault current as the protection criteria for DC faults. The accuracy of this scheme is easily affected by fault resistance. Zhou et al. [11] identified and determined faults based on the differences in voltage and direction characteristics of DC current-limiting reactors between faulty lines and nonfaulty lines, and their approach necessitates no communication and entails low hardware requirements. However, it exhibits low reliability and sensitivity when the transition resistance is high. Zhang et al. [12] detected faulty lines using the zero-crossing feature of current. Li et al. [13] proposed a full current direction longitudinal protection method. Nonetheless, it proves challenging to meet rapidity requirements when the transition resistance is significant. The authors of [14] utilized the traveling waves of two rectilinear positive-sequence voltages of a current-limiting inductor for fault location and protection. However, the setting value of this protection method is susceptible to the influence of system harmonics. Jia et al. [15] proposed a line protection method for a flexible DC distribution system based on the cosine similarity principle of the fault transient current. A DC fault protection scheme based on the fault current change rate of a current-limiting reactor was developed [16] to achieve fast fault identification. However, its protection threshold is easily affected by the fault resistance. Current-limiting reactors were installed at both ends of the DC distribution network line. This limited the peak value of the fault current. Moreover, it possessed strong boundary characteristics that made it possible to use relevant electrical quantities to identify the fault area accurately. Considering that cosine similarity is less affected by amplitude and has a high evaluation accuracy [17], it can be used for power system fault protection. Based on this, a fault protection method for a DC distribution network based on the cosine similarity of the transient current of the current-limiting reactor is proposed, which has great significance for the safe operation of DC distribution networks.
In this study, a method for identifying faults based on cosine similarity is proposed, the fault characteristics of the current-limiting reactor currents at both ends of the DC line under typical faults are discussed, the principle of cosine similarity is introduced, and a new protection scheme is proposed on this basis. The main contributions of this paper are summarized as follows:
(1) Based on the transient current characteristics of DC systems during internal or external faults, and combined with the principle of cosine similarity, a fault identification method satisfying the requirements of speed and selectivity of DC systems is proposed. Through simulation verification, it is shown that this method exhibits good anti-interference capabilities and has certain engineering application prospects.
(2) A comprehensive fault protection scheme is designed. Firstly, a five-point criterion is used to determine whether a fault has occurred. If a fault is detected, the protection is activated. Then, the cosine similarity value of the DC line current is utilized to determine whether the fault occurs internally or externally. If it occurs externally, the protection remains inactive; if it occurs internally, the fault location is determined based on the ratio of positive and negative pole voltages. This new protection scheme enables rapid and accurate fault location determination.
The remainder of this article is organized as follows. In Section 2, the basic topology of a DC distribution network is introduced. The internal/external fault characteristics of DC distribution networks are analyzed. In Section 3, a fault protection criterion for DC distribution networks based on the current cosine similarity of the current-limiting reactors is proposed. The simulation results for DC distribution network fault protection based on the proposed method are presented in Section 4. Finally, the most important conclusions are summarized in Section 5.
2. Fault Analysis of Flexible DC Power System
2.1. Topology of Flexible DC Power System
In this study, a flexible DC power system based on two-level VSCs was taken as the research object, and its topology is illustrated in Figure 1. In the figure, Lines 1, 2, 3, and 4 are DC lines; M, N, E, and F are DC buses; F1, F2, F3, and F4 represent DC faults in different lines; L1–L8 represent the equivalent inductances of the current-limiting reactors installed on both sides of each DC line. The flexible DC power system can be integrated into the alternating-current (AC) grid through converters VSC1 and VSC2. The DC load, energy storage device, and photovoltaic power generation system are connected to the DC bus E using a DC/DC converter. The AC load is connected from the DC/AC to the DC bus F.
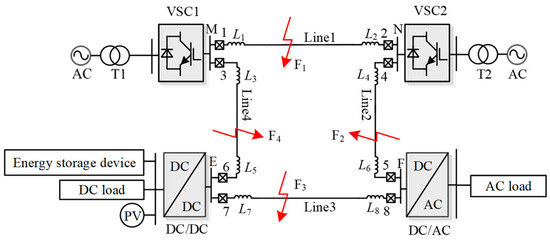
Figure 1.
Topology of a typical flexible DC power system.
2.2. Fault Analysis
Fault types in flexible DC power systems primarily include line-to-line short-circuit faults and single line-to-ground faults. In Figure 1, when a line-to-line short-circuit fault occurs in the DC lines of the distribution network, the fault characteristics undergo the following three fault stages [18]: bus capacitor discharge, diode-on, and fault stabilization stages. When a single line-to-ground fault occurs in a DC line, the fault characteristics are mainly manifested in the faulted pole bus capacitor discharge stage, nonfaulted pole capacitor charging stage, and fault stabilization stage [19,20]. The equivalent discharge circuits for line-to-line short-circuit faults and single line-to-ground faults are illustrated in Figure 2. Loops 1 and 2 correspond to the line-to-line short-circuit fault circuit and the single line-to-ground fault circuit, respectively.
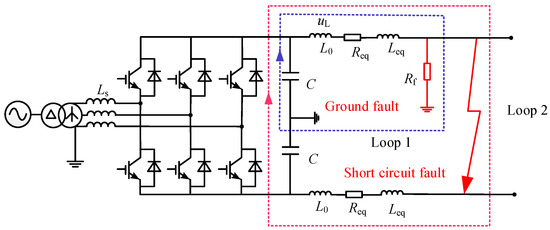
Figure 2.
Capacitor discharge circuits in the case of DC line faults.
When a single line-to-ground fault or line-to-line short-circuit fault occurs in a flexible DC power system, the high-amplitude fault current threatens the safe operation of the DC system. The fault protection device must accurately identify the fault types and take corresponding protective measures within a few milliseconds. Therefore, it is important to analyze the fault characteristics of a single line-to-ground fault and line-to-line short-circuit fault in a flexible DC power system. A fast and reliable fault identification and protection method for the stable operation of flexible DC power systems is presented in this article.
2.2.1. Internal Fault Analysis
Considering fault F1 in Figure 1 as an example, the faulted circuit for the internal line-to-line short-circuit fault in DC Line 1 is shown in Figure 3. In the figure, P and N represent the positive and negative DC lines, respectively; LP1, LP2, LN1, and LN2 represent the current-limiting reactor inductances on both sides of the positive and negative DC lines; uP1, uP2, uN1, and uN2 indicate the instantaneous voltages at both ends of the positive and negative current-limiting reactors after the fault occurs; ip1, ip2, in1, and in2 are the fault currents flowing through the positive and negative lines. Furthermore, f2, f4, and f6 indicate the line-to-line short-circuit faults of the DC line that occur at different locations, and f1, f3, and f5 indicate the single line-to-ground faults of the DC line that occur at different locations. The positive pole current is referenced in the direction from the bus to the line. The negative pole current is referenced in the direction from the line to the bus.
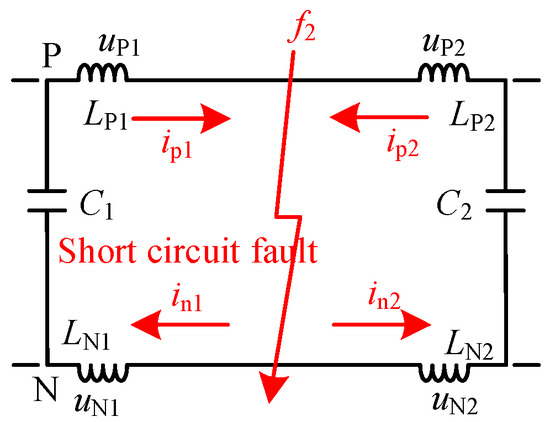
Figure 3.
Equivalent circuit of an internal line-to-line short-circuit fault at F1.
As shown in Figure 3, when an internal line-to-line short-circuit fault occurs in the DC line, converters VSC1 and VSC2 inject a fault current toward the fault point at both ends of the DC line. At this time, the fault current increases instantaneously, and the reference direction of the sudden current change is the same as the current flow direction, as shown in Figure 3. At this point, the fault current direction is positive, ∆ip1 and ∆ip2 are the sudden current changes in the positive line, ∆in1 and ∆in2 are the sudden current changes in the negative line, and the sudden current change is the same as the current reference direction. Hence, the sudden fault current change can be expressed as follows:
Therefore, the voltage–current relationships in a current-limiting reactor can be obtained as follows:
The equivalent fault circuit when an internal single line-to-ground fault occurs in the DC line is shown in Figure 4; in the figure, Rf represents the fault resistance. It can be seen from the figure that, when a single line-to-ground fault occurs, the fault current sudden-change in the DC line can be expressed as follows:
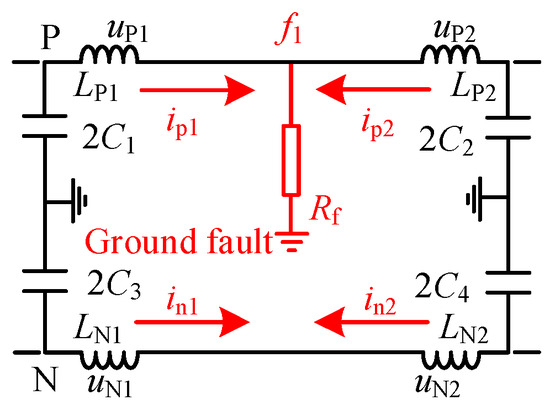
Figure 4.
Equivalent circuit of an internal single line-to-ground fault at F1.
According to Equations (1) and (2), regardless of whether an internal single line-to-ground fault or an internal line-to-line short-circuit fault occurs in the flexible DC power system, the direction of the sudden current change is the same as that of the fault current—that is, the direction of the sudden current change is positive, and the value is greater than zero.
2.2.2. External Fault Analysis
The equivalent fault circuit when an external line-to-line short-circuit fault occurs in the DC line is shown in Figure 5. The figure shows that, when a line-to-line short-circuit fault occurs in Lines 2, 3, and 4, the directions of currents ip1 and ip2, as well as in1 and in2, are opposite. At this time, the sudden current change can be expressed as follows:
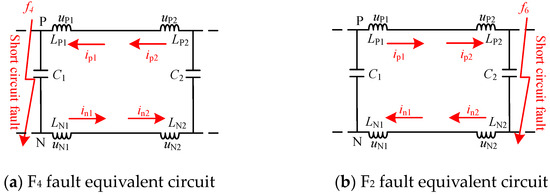
Figure 5.
Equivalent circuit of an external line-to-line short-circuit fault.
The equivalent fault circuit when an external single line-to-ground fault occurs in the DC line is shown in Figure 6. The expressions of sudden current change are consistent with Equation (4).
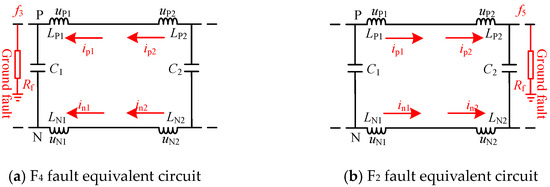
Figure 6.
Equivalent circuit of an external single line-to-ground fault.
In summary, when an internal fault occurs in the DC line, the direction of the sudden current change in the current-limiting reactors on both sides of the line is consistent. When an external fault occurs in the DC line, the direction of the sudden current change in the current-limiting reactors on both sides of the line is inconsistent. Therefore, it can be inferred that the variation trend of the fault region is closely related to the sudden fault current change in the current-limiting reactors of the DC line. Based on this characteristic, a fault protection method was developed using the transient current cosine similarity of current-limiting reactors.
3. Principle of Breakage Protection
3.1. Principle of Cosine Similarity
Cosine similarity is the extension and application of the cosine concept of the angle between two vectors in analytical geometry. It is used in multivariate space and emphasizes the differences in the directions of the independent variables. Moreover, it is not influenced by the amplitude and provides a high accuracy. When there are two discrete signals with independent change laws in space, the cosine similarity [15] can be expressed as follows:
This shows that, in the case of internal faults, the change directions of ∆ip1 and ∆ip2, as well as ∆in1 and ∆in2, are consistent. Therefore, the cosine angle between ∆ip1 and ∆ip2, as well as between ∆in1 and ∆in2, is less than 90°. At this time, cos (∆ip1, ∆ip2) > 0 and cos (∆in1, ∆in2) > 0 are satisfied. When an external fault occurs, the change directions of ∆ip1 and ∆ip2, as well as ∆in1 and ∆in2, are opposite. Therefore, the cosine angle between ∆ip1 and ∆ip2, as well as between ∆in1 and ∆in2, is greater than 90°. In addition, cos (∆ip1, ∆ip2) < 0 and cos (∆in1, ∆in2) < 0 are satisfied. Combining the cosine similarity method with the transient current of the current-limiting reactors can accurately distinguish the similarities and differences in fault characteristics when an internal or an external fault occurs. This is helpful for improving the protection accuracy.
3.2. Fault Detection Criterion
To avoid frequent start-ups of protection, it is necessary to set a fault detection criterion. In this study, the voltage change rate of the current-limiting reactors was used to set the fault detection criterion. The fault detection criterion is expressed as follows:
where Kset is the maximum value of the rate of voltage change in the positive and negative current-limiting reactors, duP/dt and duN/dt are the voltage change rates of the current-limiting reactors for the positive and negative lines, respectively, and ∆1 is the protection starting threshold. When the maximum value of the voltage change rate of the current-limiting reactors of the positive and negative lines is greater than ∆1, the protection starts.
In engineering, this difference is often used to calculate the voltage change rate in current-limiting reactors. However, there are some problems with this method, such as poor accuracy and the ease of disturbance caused by noise. Therefore, a five-point numerical differentiation algorithm for the first derivative was used to calculate the voltage change rate in current-limiting reactors [21]. The calculation formulae are as follows:
where ∆t is the sampling time interval, up1–up5 are the data of five consecutive voltage sampling points for the positive current-limiting reactors, and un1–un5 are the data of five consecutive voltage sampling points for the negative current-limiting reactors.
3.3. Broken Pole Selection and Fault Identification
The fault identification criteria are based on the cosine similarity of the current-limiting reactors. The equations are as follows:
According to Equation (8), and in combination with the characteristics of the internal faults and external faults, the cosine values of the current angle between the current-limiting reactors at both ends of the line are 1 and −1, respectively. Hence, the cosine values 1 and −1 of the current angle are used to build the protection criterion. However, in practical engineering applications, factors such as fault resistance, measurement errors, and communication delays may affect the accuracy of the protection criterion. Hence, considering the above factors, the identification conditions for the internal and external faults are as follows:
When a line fault of the flexible DC power system occurs, the cosine similarity value is calculated according to Equation (8) and satisfies Equation (9), which can be judged as an internal fault, and vice versa for an external fault.
In this study, the absolute ratio HL of the average voltage of the current-limiting reactor of the positive and negative pole lines was used to determine the fault pole. The time window was set to 0.2 ms. The broken pole selection criteria are defined as follows:
where n is the total number of sampling points in the 0.2 ms time window, uL+(h) and uL−(h) represent the sampled voltage values of the positive and negative current-limiting reactors, respectively, and HL is the absolute ratio of the average voltages of the positive and negative current-limiting reactors. When an internal single line-to-ground fault occurs, the voltage ratio of the fault pole to the nonfault current-limiting reactor is approximately the coupling coefficient between the bipolar lines (maximum of 0.6) [17]. When an internal line-to-line short-circuit fault occurs, the voltage ratio of the two current-limiting reactors is approximately 1. To distinguish between different types of faults, hset = 0.6 is set. The broken pole selection criteria for the DC line are as follows:
When Equation (11) is satisfied, the fault is determined as a line-to-line short-circuit fault. If Equation (12) is satisfied, the fault is determined to be a positive grounding fault. Similarly, if Equation (13) is satisfied, it is a negative grounding fault.
3.4. Breakage Protection Flow Chart
A flowchart of the proposed fault protection method is presented in Figure 7. Protection is initiated when the sampled data satisfy the fault detection criterion in Equation (6). After the protection device is started, the current in the current-limiting reactor is calculated to determine whether Equation (9) is satisfied according to the current cosine similarity. Hence, internal and external faults can be identified. A continuous judgment calculation is performed three times to avoid protection misoperation. If the protection criterion is satisfied three consecutive times, the internal faults of the DC line are determined. Finally, the types and locations of DC faults are determined using Equations (11)–(13).
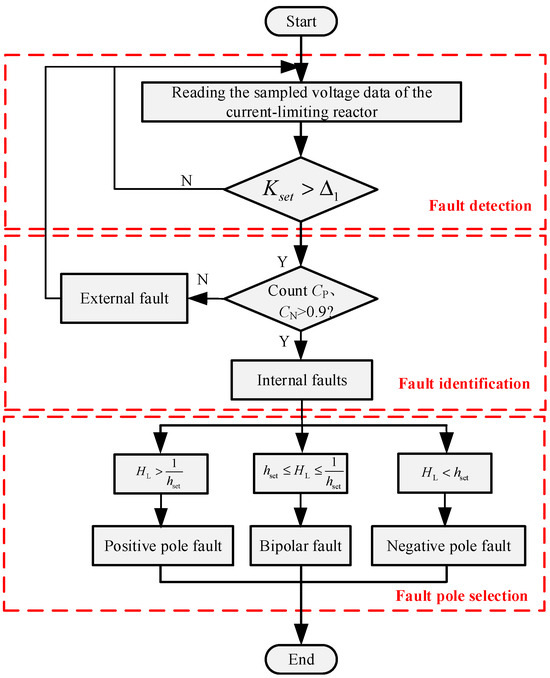
Figure 7.
Flowchart of the proposed fault protection method.
4. Simulation Results
The ±10 kV flexible DC power system shown in Figure 1 was built using MATLAB/Simulink simulation software (2018b) to verify the effectiveness of the proposed fault protection method. The primary system parameters are listed in Table 1. Assuming that a DC line fault occurs at t = 1 s, the sampling frequency is 10 kHz. The maximum time between protection startup and recovery is approximately 4 ms. The data window length of the protection method is 0.3 ms, the time used for three consecutive calculations is approximately 1 ms, the protection start time is about 0.3 ms, the communication delay is 1 ms, and the circuit breaker operation time is 2 ms. The simulation takes the measurement points 1 and 2 in Figure 1 as the fault test points, in which f1 and f2 are the internal faults, and f3–f6 are the external faults.

Table 1.
Main parameters of the simulation system.
4.1. Simulation Results of Internal Fault
4.1.1. Internal Line-to-Line Short-Circuit Fault
A line-to-line short-circuit fault occurs at fault point F1 (t = 1 s) in the flexible DC power system. The current variation diagrams of the current-limiting reactors at both ends of the positive and negative lines are shown in Figure 8. Before the failure, the value of ip1 was 3.194 A, the value of ip2 was −2.987 A, the value of in1 was 2.093 A, and the value of in2 was –1.893 A. The figure shows that the directions of currents ip1 and ip2, as well as in1 and in2, are the same. The current waveforms of the current-limiting reactors at both ends of the line are highly similar. Meanwhile, the cosine similarity calculation value of the current-limiting reactors at both ends of the positive and negative lines is 0.999, which is greater than the set value of 0.9 in Equation (9). Therefore, it satisfies the criteria for fault protection action.
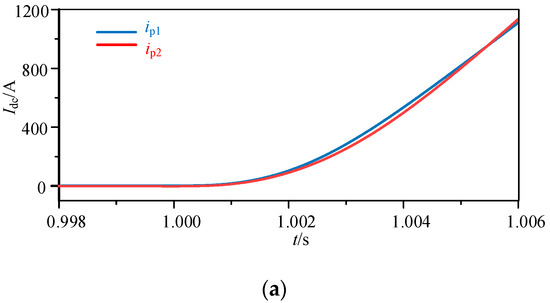
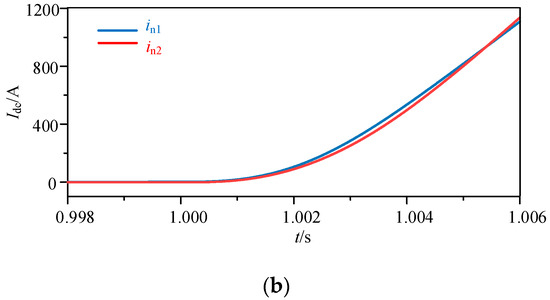
Figure 8.
Current waveforms of the current-limiting reactors when an internal line-to-line short-circuit fault in F1 occurs. (a) Current waveforms of the current-limiting reactors at both ends of the positive line. (b) Current waveforms of the current-limiting reactors at both ends of the negative line.
4.1.2. Internal Single Line-to-Ground Fault
A single line-to-ground fault occurs at fault point F1 (t = 1 s) in the flexible DC power system. The current variation diagram is shown in Figure 9. Before the failure, the value of ip1 was 1.411 A, the value of ip2 was −1.312 A, the value of in1 was 1.265 A, and the value of in2 was −1.265 A, At the moment of the internal single line-to-ground fault, the directions of currents ip1 and ip2 are the same, and the sudden current change waveform has high similarity. At 0.3 ms after the fault occurs, the current cosine similarity of the current-limiting reactor at both ends of the line is calculated to be 0.998 using Equation (5). When a negative grounding fault occurs, the current cosine similarity is 0.998. The calculated values of the current cosine similarity of the current-limiting reactor in the above two cases of grounding faults are greater than the set value of 0.9 in Equation (9). Therefore, regardless of whether a positive or negative grounding fault occurs, the protection action criterion conditions are satisfied.
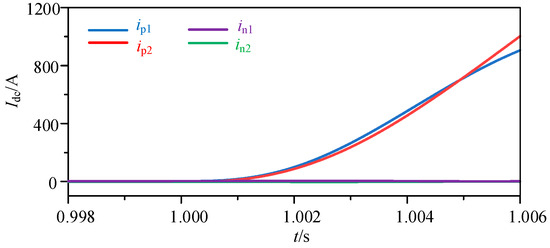
Figure 9.
Current waveforms of the current-limiting reactors when an internal single line-to-ground fault in positive line (F1) occurs.
4.2. Simulation Results of External Fault
A single line-to-ground fault and a line-to-line short-circuit fault occur at fault points f3–f6 (t = 1 s) in the flexible DC power system. The current change in the current-limiting reactors at both ends of the positive line is considered as an example, and the current change trends are shown in Figure 10 and Figure 11. When an external fault occurs, whether it is a line-to-line short-circuit fault or a single line-to-ground fault, the directions of currents ip1 and ip2 are opposite. Moreover, the similarity between the current waveforms of the current-limiting reactor is low. By sampling the current data of the current-limiting reactor and calculating its cosine similarity value, the calculated cosine similarity value is −0.999 in the case of an external line-to-line short-circuit fault. The calculated value is −0.996 in the case of an external single line-to-ground fault. The above conditions are close to −1, which satisfies the criteria for an external fault. Hence, the proposed protection method can reliably identify the internal and external faults.
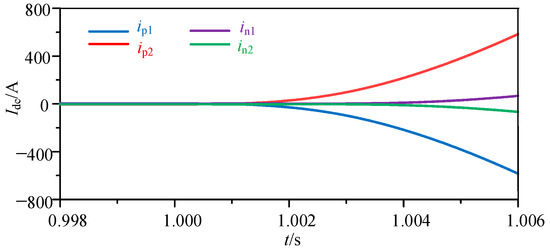
Figure 10.
Current waveforms of the current-limiting reactors when an external single line-to-ground fault in positive line (F4) occurs.
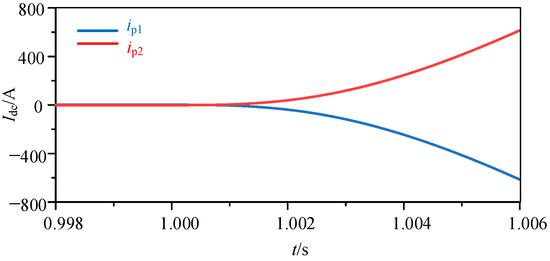
Figure 11.
Current waveforms of the current-limiting reactors when an external line-to-line short-circuit fault in F4 occurs.
4.3. Influences of Fault Resistance
To verify the influence of fault resistance on the accuracy of the proposed protection method, when the fault resistance is set to 5 Ω, 15 Ω, 30 Ω, and 50 Ω, respectively, the current mutation waveform of the current-limiting reactors at both ends of the DC line in the case of an internal line-to-line short-circuit fault and internal single line-to-ground fault at fault point F1 (t = 1 s) is shown in Figure 12. It can be seen from the figure that, with the increase in the fault resistance, the current mutation direction of the current-limiting reactors at both ends of the DC line is positive regardless of the occurrence of the internal line-to-line short-circuit fault and internal single line-to-ground fault. And the cosine similarity value can be calculated by using Equation (5), as shown in Table 2. It can be seen from the table that, when an internal fault occurs, the theoretical calculation value of the current cosine similarity of the current-limiting reactor decreases with the increase in the fault resistance, and the theoretical calculation value of the current cosine similarity is greater than 0.99. Therefore, the above four fault resistances can meet the fault criterion conditions, and the discrimination results are accurate and have good fault resistance ability.
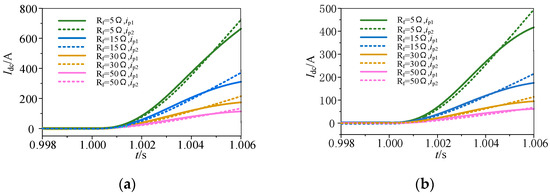
Figure 12.
Current waveforms of the current-limiting reactors at both ends of the line under different transition resistances. (a) Current waveforms of the current-limiting reactors when an internal line-to-line short-circuit fault in F1 occurs. (b) Current waveforms of the current-limiting reactors when an internal single line-to-ground fault in F1 occurs.

Table 2.
Calculation results of cosine similarity of current-limiting reactors at both ends of the line with different fault resistors.
4.4. Influences of Communication Delays
The proposed pilot protection scheme needs to transmit the transient current data signals on both sides of the line to the central processing unit for cosine similarity calculation after the protection is started. Therefore, it is necessary to consider the influence of signal transmission delay on protection performance. Considering different communication delays, the theoretical calculation value of the current cosine similarity is shown in Table 3 when an internal line-to-line short-circuit fault and an internal single line-to-ground fault occur at fault point F1 (t = 1 s). It can be seen from the table that, with the increase in the communication delay, the theoretical calculation value of the current cosine similarity of the current-limiting reactors at both ends of the DC line is greater than 0.9 in the case of the internal line-to-line short-circuit fault and the internal single line-to-ground fault. Therefore, the protection method can accurately identify the fault within the signal delay time of 0.3 ms.

Table 3.
Calculation results of cosine similarity of current-limiting reactors at both ends of the line with different communication delays.
4.5. Influences of Distributed Capacitance
The distributed capacitance in the DC line will cause the transient fluctuation of the fault current after the fault occurs, which may affect the sudden change in direction of the transient current. When the distributed capacitance in the DC line increases to 2 times, 5 times, and 10 times of the original, there is a sudden change in the waveform of the current-limiting reactor at both ends of the DC line when there is an internal line-to-line short-circuit fault and an internal single line-to-ground fault at fault point F1 (t = 1 s), as shown in Figure 13. It can be seen from the figure that the current mutation direction of the current-limiting reactor is positive with the increase in the line-distributed capacitance after the fault occurs. It can be seen from Table 4 that the theoretical calculation values of current cosine similarity are greater than 0.99, meeting the fault criterion conditions. Therefore, the above three kinds of distributed capacitance can still reliably identify the internal and external faults, which is less affected by the distributed capacitance of the line.
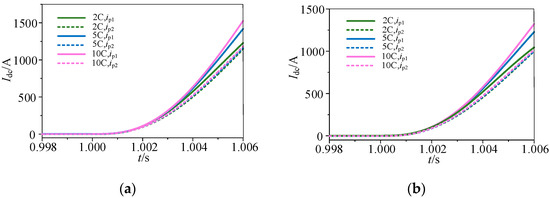
Figure 13.
Current waveforms of the current-limiting reactors at both ends of the line under different distributed capacitance. (a) Current waveforms of the current-limiting reactors when an internal line-to-line short-circuit fault in F1 occurs. (b) Current waveforms of the current-limiting reactors when an internal single line-to-ground fault in F1 occurs.

Table 4.
Calculation results of cosine similarity of current-limiting reactors at both ends of the line with different distributed capacitance.
4.6. Influences of Noise
In practical engineering, noise usually affects the sampling of data signals, affecting the reliability of protection methods. To verify the influence of noise on the reliability of the proposed protection scheme when Gaussian noise with signal-to-noise ratios of 20, 30, and 40 dB are added to the fault current when an internal line-to-line short-circuit fault and an internal single line-to-ground fault occur at fault point F1 (t = 1 s), the current cosine similarity calculation results are shown in Table 5. It can be seen from the table that, with the increase in the signal-to-noise ratio, the theoretical calculation value of the current cosine similarity of the current-limiting reactors at both ends of the DC line is greater than 0.99 regardless of the occurrence of the internal line-to-line short-circuit fault and internal single line-to-ground fault, which meets the fault criterion conditions. Therefore, noise has little effect on the reliability of the proposed protection method.

Table 5.
Calculation results of cosine similarity of current-limiting reactors at both ends of the line with different signal-to-noise ratios.
4.7. Comparison of Protection Schemes
Comparative analysis is conducted between the proposed protection scheme and typical protection schemes from the existing literature. Reference [12] discriminates fault regions by utilizing the zero-crossing feature of DC line currents at both ends and the polarity of fault currents. However, in cases of high transition resistance, the slow zero-crossing speed of fault currents may compromise its speediness. Reference [13] discriminates fault regions based on the polarity of fault currents, but this method requires waiting for polarity changes, resulting in reduced speediness when transition resistance is high. Both of these protection schemes focus on double-pole grounded faults and cannot identify single-pole grounded faults with low fault currents. As illustrated in the simulation results in Figure 12, the proposed fault identification method based on cosine similarity of the current in line-limiting reactors remains reliable even when the fault resistance reaches 50Ω. Based on the aforementioned analysis, the performance comparison between the proposed protection scheme and typical protection schemes is presented in Table 6. In the table, “√” indicates the fulfillment of technical requirements, while “×” indicates the failure to meet the technical requirements. The assessment of the noise performance is conducted under 20 dB white noise.

Table 6.
Comparative analysis of the protection schemes.
5. Conclusions
A novel fault protection method was proposed for flexible DC power systems based on the cosine similarity of the transient current of current-limiting reactors. It can quickly identify internal and external faults by obtaining only a 1 ms data window. The proposed protection method meets the protection speed requirements of a flexible DC power system. For a high fault resistance of 20 Ω, the current cosine similarity of the current-limiting reactor at both ends of the line is greater than 0.9, which satisfies the criteria of protection action. In addition, the proposed method is less affected by communication delay, line distributed capacitance, and noise interference, and can be applied to other DC system topologies, with the effect of the grid operation mode minimized. This method promotes the development of DC protection. However, this method relies on communication, and there could be misjudgments in the event of communication interruptions or significant delays. Enhancing communication solutions in the future would represent a promising direction for development.
Author Contributions
G.C.: Conceptualization, Investigation, and Writing—review and editing. Q.D.: Writing—review and editing, Methodology, and Formal Analysis. C.Z.: Writing an original draft and Writing—review and editing. H.W.: Methodology, Supervision, and Validation. G.S.: Writing—review and editing. J.G.: Methodology, Supervision, and Validation. Y.L.: Writing—review and editing. S.Z.: Supervision and Validation. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the State Grid Technology Project, grant number 5400-202255484A-2-0-KJ.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
Authors Genqi Chen, Yong Li and Shuiliang Zhou were employed by the company State Grid Zhejiang Electric Power Company. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Wang, Y.; Yang, L.; Wu, Q.; Chen, S.; Yu, Z.; Guan, Y.; Zhang, Y. A hybrid isolated bidirectional DC/DC solid-state transformer for DC distribution network. IEEE Access 2021, 9, 159059–159070. [Google Scholar] [CrossRef]
- Liu, Y.; Guan, L.; Chen, J.; Shi, G.; Zheng, J.; Wei, T.; Guo, F. Over-current mechanism and suppression strategy of DC transformer in multiterminal interconnected flexible DC distribution network. IEEE Syst. J. 2023, 17, 1785–1796. [Google Scholar] [CrossRef]
- Zheng, T.; Lv, W.; Wu, Q.; Li, R.; Liu, X.; Zhang, C.; Xu, L. An integrated control and protection scheme based on FBSM-MMC active current limiting strategy for DC distribution network. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 2632–2642. [Google Scholar] [CrossRef]
- Shuai, Z.; He, D.; Xiong, Z.; Lei, Z.; John Shen, Z. Comparative study of short-circuit fault characteristics for VSC-based DC distribution networks with different distributed generators. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 528–540. [Google Scholar] [CrossRef]
- Li, M.; Jia, K.; Bi, T.; Zhu, R.; Wang, C.; Yang, Q. Full-current-based directional pilot protection for VSC-DC distribution systems. IET Generation. Transm. Distrib. 2019, 13, 3713–3724. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, S.; Wang, Z.; Zhu, L.; Guan, Y.; Zhang, G.; Yang, L.; Zhang, Y. A Multiple modular isolated DC/DC converter with bidirectional fault handling and efficient energy conversion for DC distribution network. IEEE Trans. Power Electron. 2020, 35, 11502–11517. [Google Scholar] [CrossRef]
- Dambhare, S.; Soma, S.A.; Chandorkar, M.C. Adaptive current differential protection schemes for transmission-line protection. IEEE Trans. Power Deliv. 2009, 24, 1832–1841. [Google Scholar] [CrossRef]
- Sneath, J.; Rajapakse, A.D. Fault detection and interruption in an earthed HVDC grid using ROCOV and hybrid DC breakers. IEEE Trans. Power Deliv. 2014, 31, 973–981. [Google Scholar] [CrossRef]
- Zhang, C.; Song, G.; Dong, X. A novel traveling wave protection method for DC transmission lines using current fitting. IEEE Trans. Power Deliv. 2019, 35, 2980–2991. [Google Scholar] [CrossRef]
- Meghwani, A.; Srivastava, S.C.; Chakrabarti, S. A non-unit protection scheme for DC microgrid based on local measurements. IEEE Trans. Power Deliv. 2016, 32, 172–181. [Google Scholar] [CrossRef]
- Zhou, J.; Zhao, C.; Li, C.; Xu, J.; An, T. Boundary protection scheme of multi-terminal flexible DC power grid based on DC reactor voltage. Autom. Electr. Power Syst. 2017, 41, 89–94. [Google Scholar]
- Zheng, T.; Wu, Q.; Lü, W.; Wang, X.; Cao, H. Research on protection scheme of flexible DC distribution grids based on DC current zero-crossing characteristics. Power Syst. Technol. 2020, 44, 1806–1815. [Google Scholar]
- Li, M.; Jia, K.; Zhang, Q.; Liu, Y.; Bi, T. Directional pilot protection for flexible DC distribution network based on directional characteristics of instantaneous current. Autom. Electr. Power Syst. 2019, 43, 116–122. [Google Scholar]
- Zhang, S.; Zou, G.; Huang, Q.; Xu, B.; Li, J. Single-ended line protection for MMC-MTDC grids. IET Gener. Transm. Distrib. 2019, 13, 4331–4338. [Google Scholar] [CrossRef]
- Jia, K.; Wang, C.; Bi, T.; Feng, T.; Zhu, R. Transient current correlation based protection for DC distribution system. IEEE Trans. Ind. Electron. 2019, 67, 9927–9936. [Google Scholar] [CrossRef]
- Li, R.; Xu, L.; Yao, L. DC fault detection and location in meshed multiterminal HVDC systems based on DC reactor voltage change rate. IEEE Trans. Power Deliv. 2016, 32, 1516–1526. [Google Scholar] [CrossRef]
- Li, S.; Chen, W.; Yin, X.; Chen, D.; Teng, Y. A Novel integrated protection for VSC-HVDC transmission line based on current limiting reactor power. IEEE Trans. Power Deliv. 2020, 35, 226–233. [Google Scholar] [CrossRef]
- Bi, T.; Yang, B.; Jia, K.; Zheng, L.; Liu, Q.; Yang, Q. Review on renewable energy source fault characteristics analysis. CSEE J. Power Energy Syst. 2022, 8, 963–972. [Google Scholar]
- Li, Z.; Duan, J.; Lu, W.; Du, X.; Yang, W.; Tu, S. Non-permanent Pole-to-pole fault restoration strategy for flexible DC distribution network. J. Mod. Power Syst. Clean Energy 2021, 9, 1339–1351. [Google Scholar] [CrossRef]
- Fei, K.; Song, Z.; Zhiguo, H.; Baohui, Z. Development of a novel protection device for bipolar HVDC transmission Lines. IEEE Trans. Power Deliv. 2014, 29, 2270–2278. [Google Scholar]
- Li, B.; Liao, K.; Zhu, Y.; He, Z. Single-terminal protection of DC distribution network based on current-limiting reactor voltage. High Volt. Technol. 2023, 2, 1–23. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).