Numerical Investigation of Flow Field Distributions and Water and Thermal Management for a Proton Exchange Membrane Electrolysis Cell
Abstract
1. Introduction
2. Experimental Tests and Numerical Model
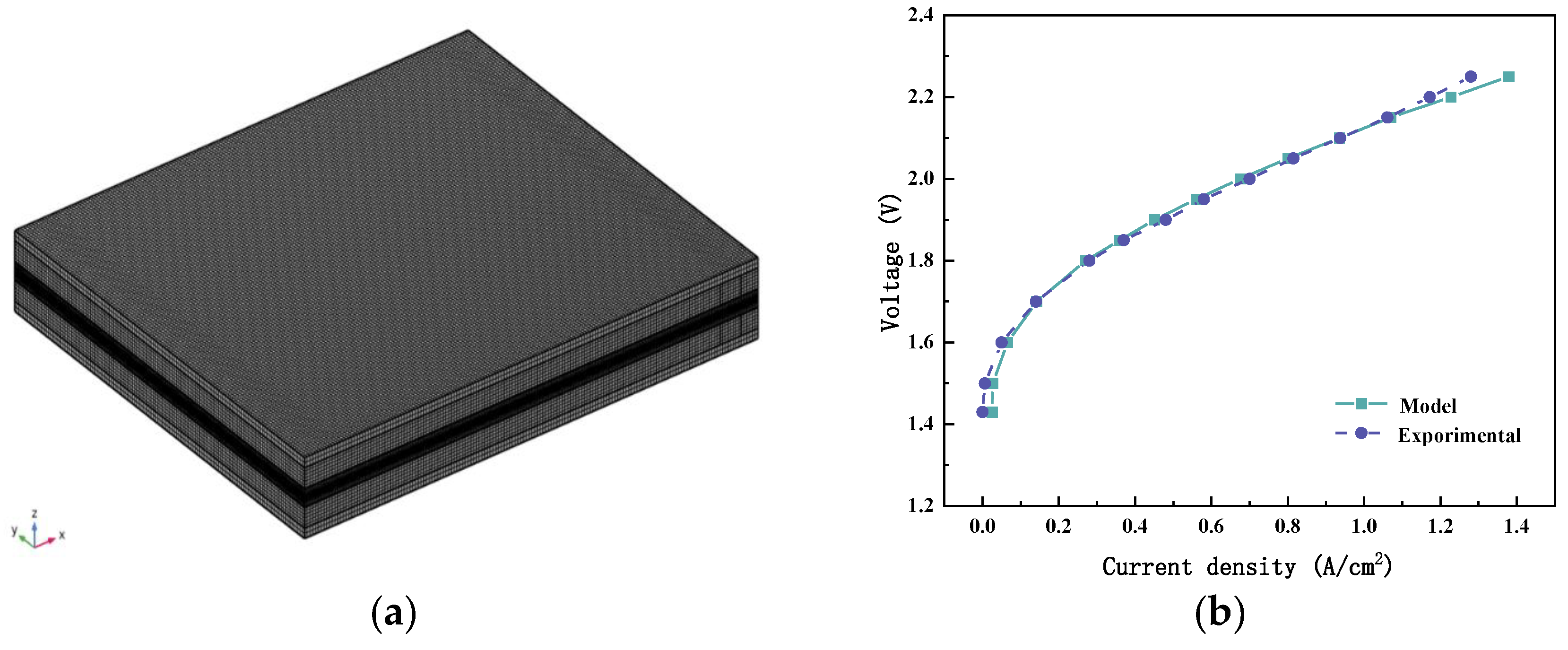
2.1. Experimental Tests
2.2. Numerical Model
- (1)
- The gas phase was considered as an compressible ideal gas;
- (2)
- The membrane was considered liquid-water-permeable and gas-impermeable;
- (3)
- The phase transition process of liquid water was neglected;
- (4)
- The material was homogeneous and isotropic;
- (5)
- Contact resistance between adjacent components was neglected.
2.2.1. Charge Transport and Conservation
2.2.2. Transport of Multicomponent Mass Transfer
2.2.3. Thermal Transport
3. Boundary Conditions and Model Validation
4. Results and Discussion
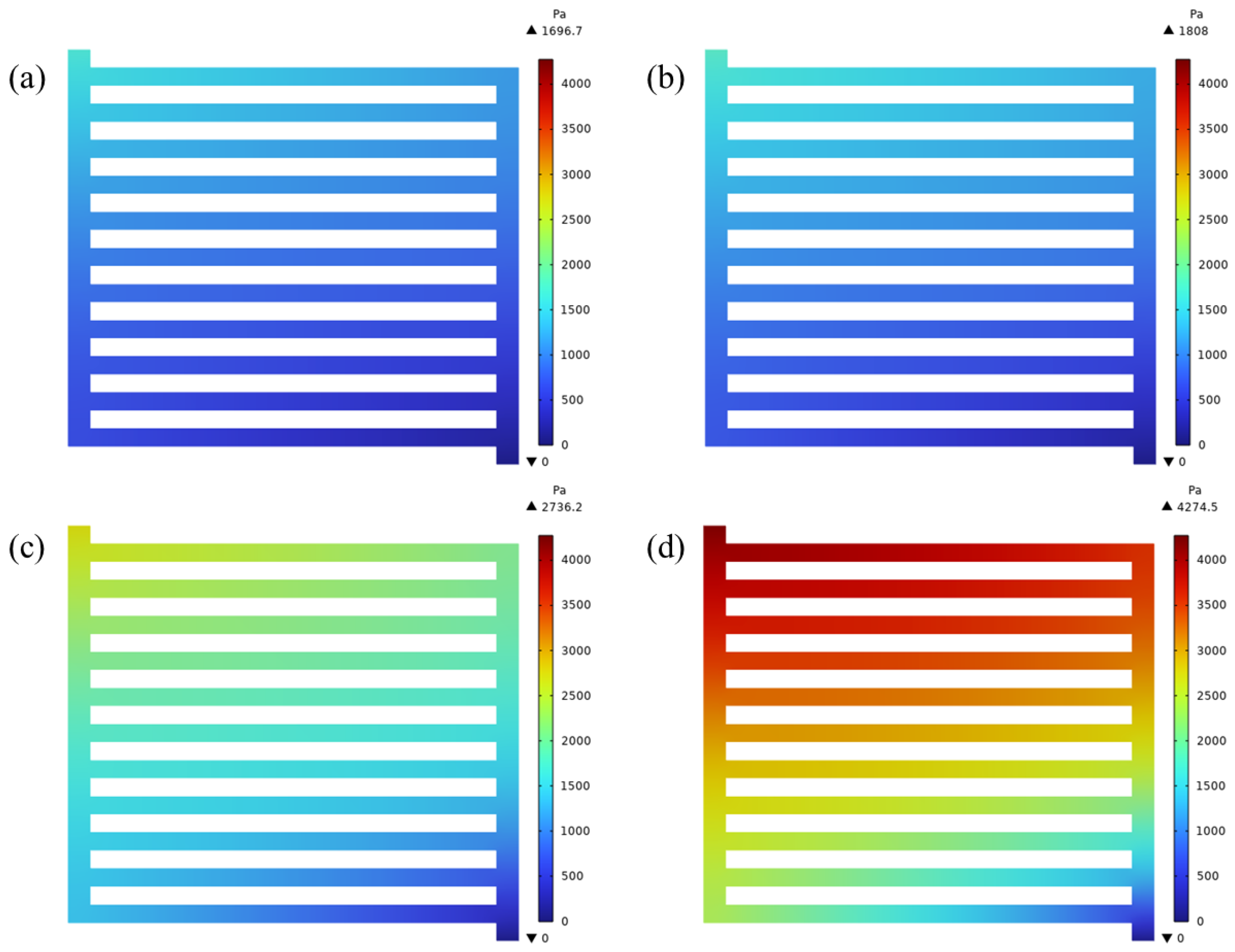
4.1. Pressure and Velocity Distributions at Different Voltages
4.2. Oxygen Flux and Liquid Water Flux at Different Voltages
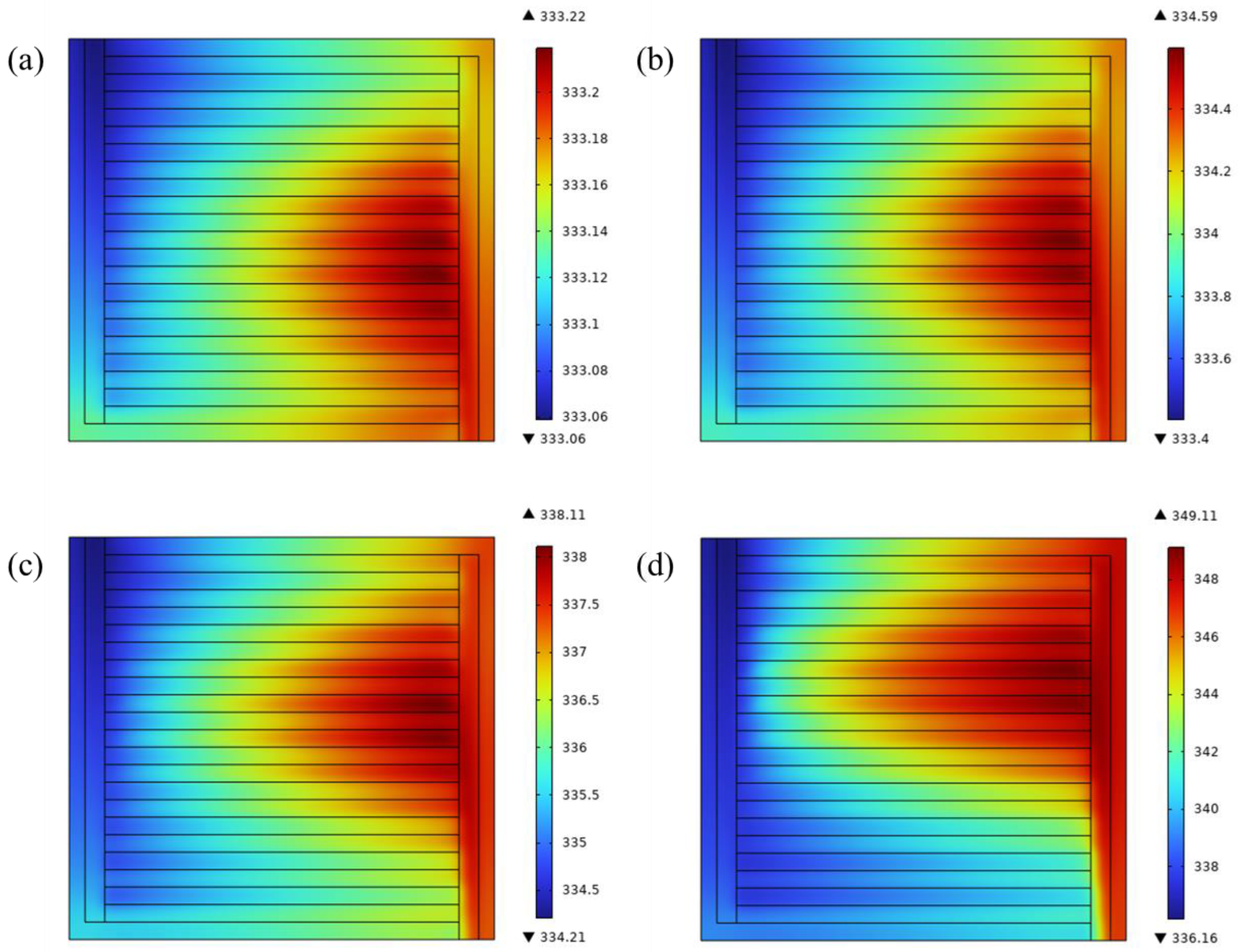
4.3. Temperature Distribution at Different Voltages
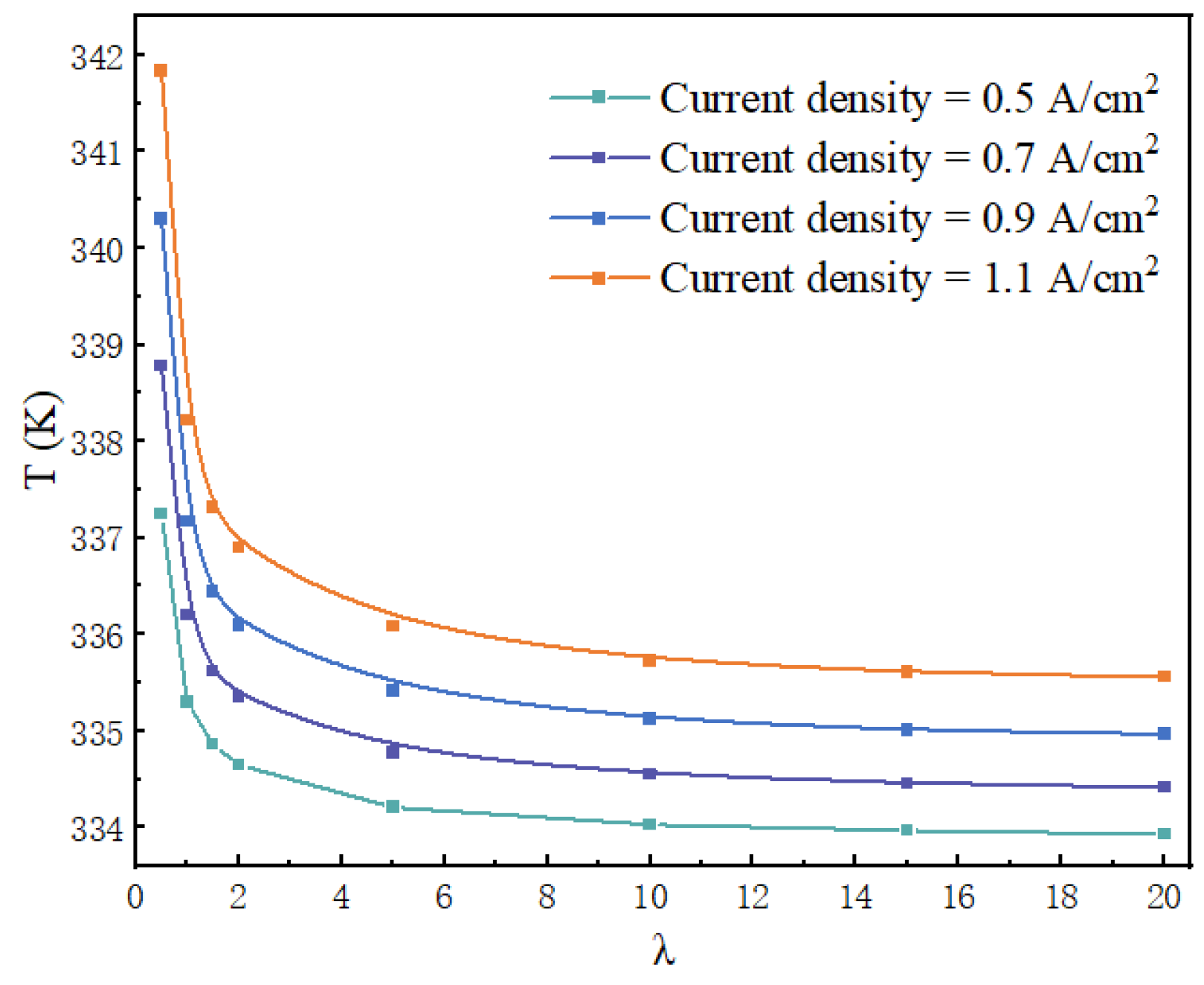
4.4. Water and Thermal Management Performance at Different Water Flow Rates
4.5. The Changes in Velocity and Mass Transfer Characteristics at Different Water Flow Rates
5. Conclusions
- (1)
- The mass flux of oxygen and water in the channel was lower in the middle region. The oxygen mass flux of channel_11 was always higher than that of channel_1. The relative velocity of channel_1 and channel_11 was determined by the inlet water flow.
- (2)
- The pressure distribution decreased diagonally from the inlet to the outlet. The pressure difference at 2.2 V was 2.5 times that at 1.6 V at the same inlet flow rate. Because of the flow characteristics of parallel flow field, the mass flux and pressure difference of the middle channel were smaller than others.
- (3)
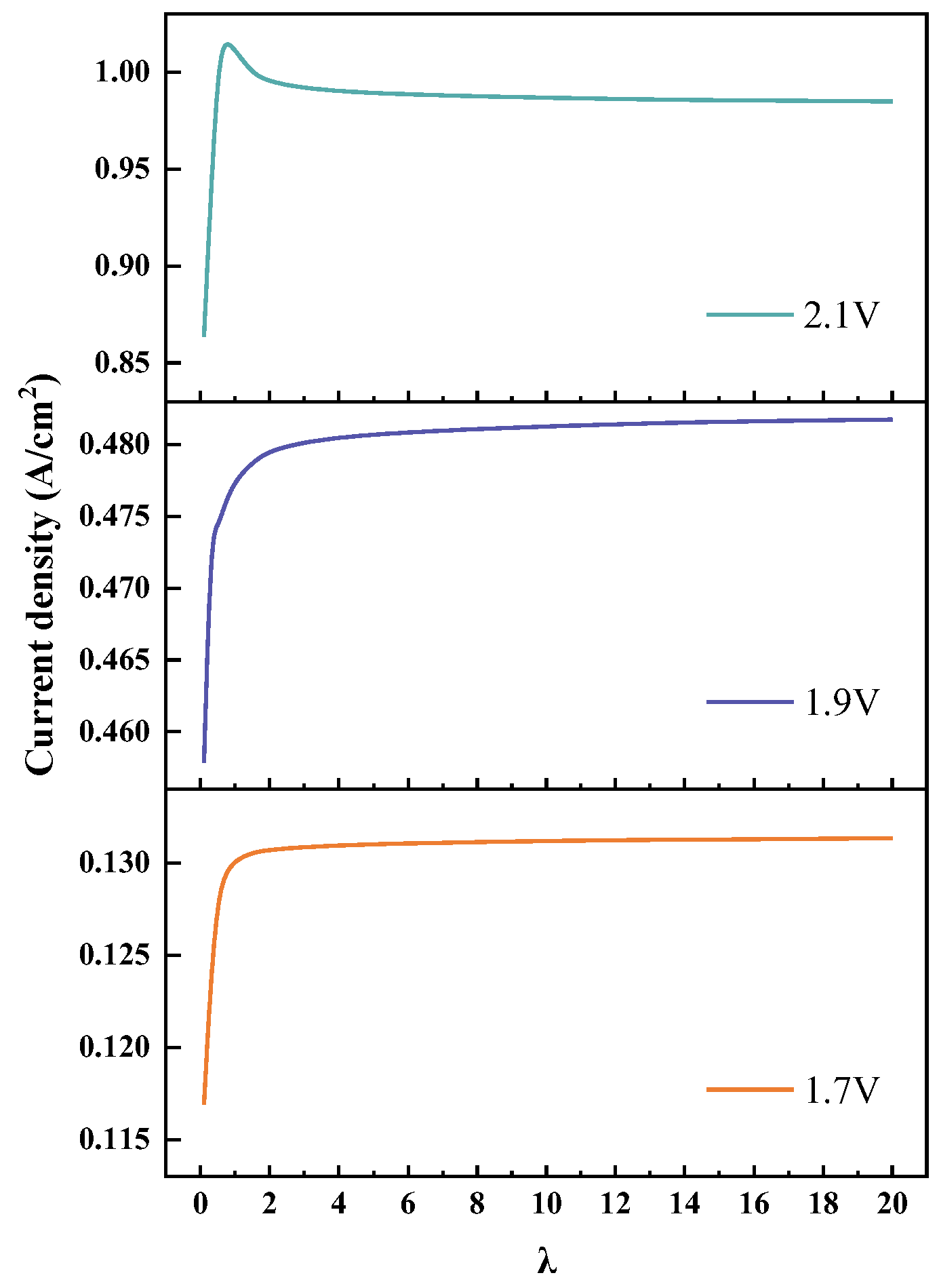
- The average temperature and average current density of the CL decreased rapidly and then gradually stabilized with the increase in the water flow rate. When the voltage was 2.1 V, the current density came to the highest value at a stoichiometry of 0.7, and then gradually decreased until stable. When λ was greater than five, the temperature and current density of the CL changed slowly.
- (4)
- Electrolysis performance and water and thermal management characteristics could be estimated according to the flow velocity distribution features. When the average temperature and current density of the CL were less affected by the inlet flow rate, the velocity of channel_1 was higher than that of channel_11.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Guo, C.H.; Chen, X.-J.; Jia, L.-Q.; Guo, X.-N.; Chen, R.-S.; Zhang, M.-S.; Chen, Z.-Y.; Wang, H.-D. Carbon peak and carbon neutrality in China: Goals, implementation path and prospects. China Geol. 2021, 4, 720–746. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, X.J.; Chen, R.; Mao, X.; Qi, X. The United States and China on the paths and policies to carbon neutrality. J. Environ. Manag. 2022, 320, 115785. [Google Scholar] [CrossRef] [PubMed]
- Alexander, B.; Hartmut, S. Current status of water electrolysis for energy storage, grid balancing and sector coupling via power-to-gas and power-to-liquids: A review. Renew. Sustain. Energy Rev. 2018, 82, 2440–2454. [Google Scholar]
- Kumar, S.S.; Himabindu, V. Hydrogen Production by PEM Water Electrolysis—A Review. Mater. Sci. Energy Technol. 2019, 2, 442–454. [Google Scholar]
- Ahmad Kamaroddin, M.F.; Sabli, N.; Tuan Abdullah, T.A.; Siajam, S.I.; Abdullah, L.C.; Abdul Jalil, A.; Ahmad, A. Membrane-Based Electrolysis for Hydrogen Production: A Review. Membranes 2021, 11, 810. [Google Scholar] [CrossRef] [PubMed]
- Grigoriev, S.; Fateev, V.; Bessarabov, D.; Millet, P. Current status, research trends, and challenges in water electrolysis science and technology. Int. J. Hydrogen Energy 2020, 45, 26036–26058. [Google Scholar] [CrossRef]
- García-Salaberri, P.A. 1D two-phase, non-isothermal modeling of a proton exchange membrane water electrolyzer: An optimization perspective. J. Power Sources 2022, 521, 230915. [Google Scholar] [CrossRef]
- Lopata, J.; Kang, Z.; Young, J.; Bender, G.; Weidner, J.W.; Cho, H.S.; Shimpalee, S. Resolving Anodic Current and Temperature Distributions in a Polymer Electrolyte Membrane Water Electrolysis Cell Using a Pseudo-Two-Phase Computational Fluid Dynamics Model. J. Electrochem. Soc. 2021, 168, 054518. [Google Scholar] [CrossRef]
- Sönke, G.; Sebastian, S.; Matthias, B.; Oberschachtsiek, B.; Heinzel, A. Proton Exchange Membrane Water Electrolysis Modeling for System Simulation and Degradation Analysis. Chem. Ing. Tech. 2018, 90, 1437–1442. [Google Scholar]
- Upadhyay, M.; Kim, A.; Paramanantham, S.S.; Kim, H.; Lim, D.; Lee, S.; Moon, S.; Lim, H. Three-dimensional CFD simulation of proton exchange membrane water electrolyser: Performance assessment under different condition. Appl. Energy 2022, 306, 118016. [Google Scholar] [CrossRef]
- Toghyani, S.; Afshari, E.; Baniasadi, E.; Atyabi, S.; Naterer, G. Thermal and electrochemical performance assessment of a high temperature PEM electrolyzer. Energy 2018, 152, 237–246. [Google Scholar] [CrossRef]
- Toghyani, S.; Afshari, E.; Baniasadi, E.; Atyabi, S.A. Thermal and electrochemical analysis of different flow field patterns in a PEM electrolyzer. Electrochim. Acta 2018, 267, 234–245. [Google Scholar] [CrossRef]
- Toghyani, S.; Afshari, E.; Baniasadi, E. Metal foams as flow distributors in comparison with serpentine and parallel flow fields in proton exchange membrane electrolyzer cells. Electrochim. Acta 2018, 290, 506–519. [Google Scholar] [CrossRef]
- Toghyani, S.; Afshari, E.; Baniasadi, E. Three-dimensional computational fluid dynamics modeling of proton exchange membrane electrolyzer with new flow field pattern. J. Therm. Anal. Calorim. 2019, 135, 1911–1919. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, G.; Wu, L.; Bao, Z.; Zu, B.; Jiao, K. A 3-D multiphase model of proton exchange membrane electrolyzer based on open-source CFD. Digit. Chem. Eng. 2021, 1, 100004. [Google Scholar] [CrossRef]
- Nie, J.H.; Chen, Y.T. Numerical modeling of three-dimensional two-phase gas–liquid flow in the flow field plate of a PEM electrolysis cell. Int. J. Hydrogen Energy 2010, 35, 3183–3197. [Google Scholar] [CrossRef]
- Jia, Y.; Zeng, M.; Barnoon, P.; Toghraie, D. CFD simulation of time-dependent oxygen production in a manifold electrolyzer using a two-phase model. Int. Commun. Heat Mass Transf. 2021, 126, 105446. [Google Scholar] [CrossRef]
- Lafmejani, S.S.; Olesen, A.C.; Kær, S.K. VOF modelling of gas–liquid flow in PEM water electrolysis cell micro-channels. Int. J. Hydrogen Energy 2017, 42, 16333–16344. [Google Scholar] [CrossRef]
- Aubras, F.; Deseure, J.; Kadjo, J.J.A.; Dedigama, I.; Majasan, J.; Grondin-Perez, B.; Chabriat, J.-P.; Brett, D. Two-dimensional model of low-pressure PEM electrolyser: Two-phase flow regime, electrochemical modelling and experimental validation. Int. J. Hydrogen Energy 2017, 42, 26203–26216. [Google Scholar] [CrossRef]
- Wu, L.Z.; Zhang, G.B.; Xie, B.; Tongsh, C.; Jiao, K. Integration of the detailed channel two-phase flow into three-dimensional multi-phase simulation of proton exchange membrane electrolyzer cell. Int. J. Green Energy 2021, 18, 541–555. [Google Scholar] [CrossRef]
- Olesen, A.C.; Rømer, C.; Kær, S.K. A numerical study of the gas-liquid, two-phase flow maldistribution in the anode of a high pressure PEM water electrolysis cell. Int. J. Hydrogen Energy 2016, 41, 52–68. [Google Scholar] [CrossRef]
- Toghyani, S.; Baniasadi, E.; Afshari, E. Numerical simulation and exergoeconomic analysis of a high temperature polymer exchange membrane electrolyzer. Int. J. Hydrogen Energy 2019, 44, 31731–31744. [Google Scholar] [CrossRef]
- Nagy, E. Basic Equations of Mass Transport through a Membrane Layer, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2019; 68p. [Google Scholar]
- Coker, A.K. Physical Properties of Liquids and Gases—ScienceDirect. In Ludwig’s Applied Process Design for Chemical and Petrochemical Plants, 4th ed.; Gulf Professional Publishing: Houston, TX, USA, 2007; Volume 17, pp. 103–132. [Google Scholar]
- Weber, A.Z.; Newman, J. Transport in Polymer-Electrolyte Membranes II. Mathematical Model. J. Electrochem. Soc. 2004, 151, A311–A325. [Google Scholar] [CrossRef]
- Maier, M.; Meyer, Q.; Majasan, J.; Tan, C.; Dedigama, I.; Robinson, J.; Dodwell, J.; Wu, Y.; Castanheira, L.; Hinds, G.; et al. Brett. Operando flow regime diagnosis using acoustic emission in a polymer electrolyte membrane water electrolyser. J. Power Sources 2019, 424, 138–149. [Google Scholar] [CrossRef]
- Xing, L.; Liu, X.; Alaje, T.; Kumar, R.; Mamlouk, M.; Scott, K. A two-phase flow and non-isothermal agglomerate model for a proton exchange membrane (PEM) fuel cell. Energy 2014, 73, 618–634. [Google Scholar] [CrossRef]
- Wrubel, J.A.; Kang, Z.Y.; Witteman, L.; Zhang, F.-Y.; Ma, Z.; Bender, G. Mathematical modeling of novel porous transport layer architectures for proton exchange membrane electrolysis cells. Int. J. Hydrogen Energy 2021, 46, 25341–25354. [Google Scholar] [CrossRef]
- Fan, L.H.; Zhang, G.B.; Jiao, K. Characteristics of PEMFC operating at high current density with low external humidification. Energy Convers. Manag. 2017, 150, 763–774. [Google Scholar] [CrossRef]
- Olesen, A.C.; Frensch, S.H.; Kær, S.K. Towards uniformly distributed heat, mass and charge: A flow field design study for high pressure and high current density operation of PEM electrolysis cells. Electrochim. Acta 2018, 293, 476–495. [Google Scholar] [CrossRef]
- Nie, J.H.; Chen, Y.T.; Cohen, S.; Carter, B.D.; Boehm, R.F. Numerical and experimental study of three-dimensional fluid flow in the bipolar plate of a PEM electrolysis cell. Int. J. Therm. Sci. 2009, 48, 1914–1922. [Google Scholar] [CrossRef]
- Chandesris, M.; Médeau, V.; Guillet, N.; Chelghoum, S.; Thoby, D.; Fouda-Onana, F. Membrane degradation in PEM water electrolyzer: Numerical modeling and experimental evidence of the influence of temperature and current density. Int. J. Hydrogen Energy 2015, 40, 1353–1366. [Google Scholar] [CrossRef]





| Instrument | Specifications | Accuracy |
|---|---|---|
| Water bath | WB100-1 | ±0.5 °C |
| Peristaltic pump | BT100 | ±2% |
| Stable DC power supply | KXN-1530D | ±0.5% |
| Temperature control | Mainz-TC | ±0.01 °C |
| Flowmeter | KD800 | ±4% |
| Parameters | Symbol | Value |
|---|---|---|
| GDL porosity | εgdl | 0.6 [20] |
| CL porosity | εcl | 0.2 [20] |
| GDL intrinsic permeability | κgdl | 1 × 10−12 |
| CL intrinsic permeability | κcl | 1 × 10−13 |
| Anode transfer coefficient | αa | 0.3 |
| Cathode transfer coefficient | αc | 0.5 |
| Electrical conductivity of the BP (S/m) | 20,000 [26] | |
| Electrical conductivity of the GDL (S/m) | 10,000 [26] | |
| Electrical conductivity of the CL (S/m) | 5000 [26] | |
| Heat capacity of oxygen (J/(mol·K)) | CO2 | [27] |
| Heat capacity of hydrogen (J/(mol·K)) | CH2 | [27] |
| Water content in the membrane | mem | [28] |
| Dynamic viscosity of water (Pa·m) | [29] | |
| Thermal conductivity of O2 (W/(m·K)) | kO2 | [27] |
| Thermal conductivity of H2 (W/(m·K)) | kH2 | [27] |
| Thermal conductivity of H2O (W/(m·K)) | kH2O | [27] |
| Electrical conductivity of the membrane (S/m) | ||
| Electro-osmotic drag coefficient | [20] |
| Parameter | Value |
|---|---|
| Channel width (mm) | 0.8 |
| Channel height (mm) | 0.8 |
| Channel length (mm) | 18 |
| Rib width (mm) | 0.4 |
| Bipolar plate height (mm) | 1.2 |
| GDL thickness (μm) | 300 |
| Catalyst thickness (μm) | 10 |
| Membrane thickness (μm) | 127 |
| Active surface area (cm2) | 4 |
| Channel number | 11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, D.; Hu, L.; Zhang, G.; Hu, K.; Zhang, J.; Liu, J.; Peng, K.; Jiang, L.; Jiang, W.; Wen, Y. Numerical Investigation of Flow Field Distributions and Water and Thermal Management for a Proton Exchange Membrane Electrolysis Cell. Energies 2024, 17, 3428. https://doi.org/10.3390/en17143428
Shao D, Hu L, Zhang G, Hu K, Zhang J, Liu J, Peng K, Jiang L, Jiang W, Wen Y. Numerical Investigation of Flow Field Distributions and Water and Thermal Management for a Proton Exchange Membrane Electrolysis Cell. Energies. 2024; 17(14):3428. https://doi.org/10.3390/en17143428
Chicago/Turabian StyleShao, Dan, Liangyong Hu, Guoqing Zhang, Kaicheng Hu, Jiangyun Zhang, Jun Liu, Kang Peng, Liqin Jiang, Wenzhao Jiang, and Yuliang Wen. 2024. "Numerical Investigation of Flow Field Distributions and Water and Thermal Management for a Proton Exchange Membrane Electrolysis Cell" Energies 17, no. 14: 3428. https://doi.org/10.3390/en17143428
APA StyleShao, D., Hu, L., Zhang, G., Hu, K., Zhang, J., Liu, J., Peng, K., Jiang, L., Jiang, W., & Wen, Y. (2024). Numerical Investigation of Flow Field Distributions and Water and Thermal Management for a Proton Exchange Membrane Electrolysis Cell. Energies, 17(14), 3428. https://doi.org/10.3390/en17143428






