Optimal Scheduling for Increased Satisfaction of Both Electric Vehicle Users and Grid Fast-Charging Stations by SOR&KANO and MVO in PV-Connected Distribution Network
Abstract
1. Introduction
- A novel CNN prediction model based on the SSA is proposed to enhance the accuracy of PV prediction;
- An EV driving model is developed to capture various scenarios, such as weekdays, weekends, and holidays, with the introduction of Monte Carlo simulation to estimate the charging load distribution of EVs;
- A spatial–temporal model of EVs is constructed to comprehensively simulate the charging process, covering the stages of entering, queuing, charging, staying, and exiting, thus providing insights into the spatial–temporal status of EVs;
- An SOR&KANO decision model is introduced to consider the charging scheduling of EVs and GFCSs by taking into account both subjective and objective factors;
- An MVO is proposed to guide NREVs and REVs in optimizing their charging and discharging behaviors based on TOU, resulting in the determination of scheduled spatial–temporal charging and discharging loads for NREVs and REVs.
2. Prediction of PV Output
2.1. Convolutional Neural Network
2.2. Salp Swarm Algorithm
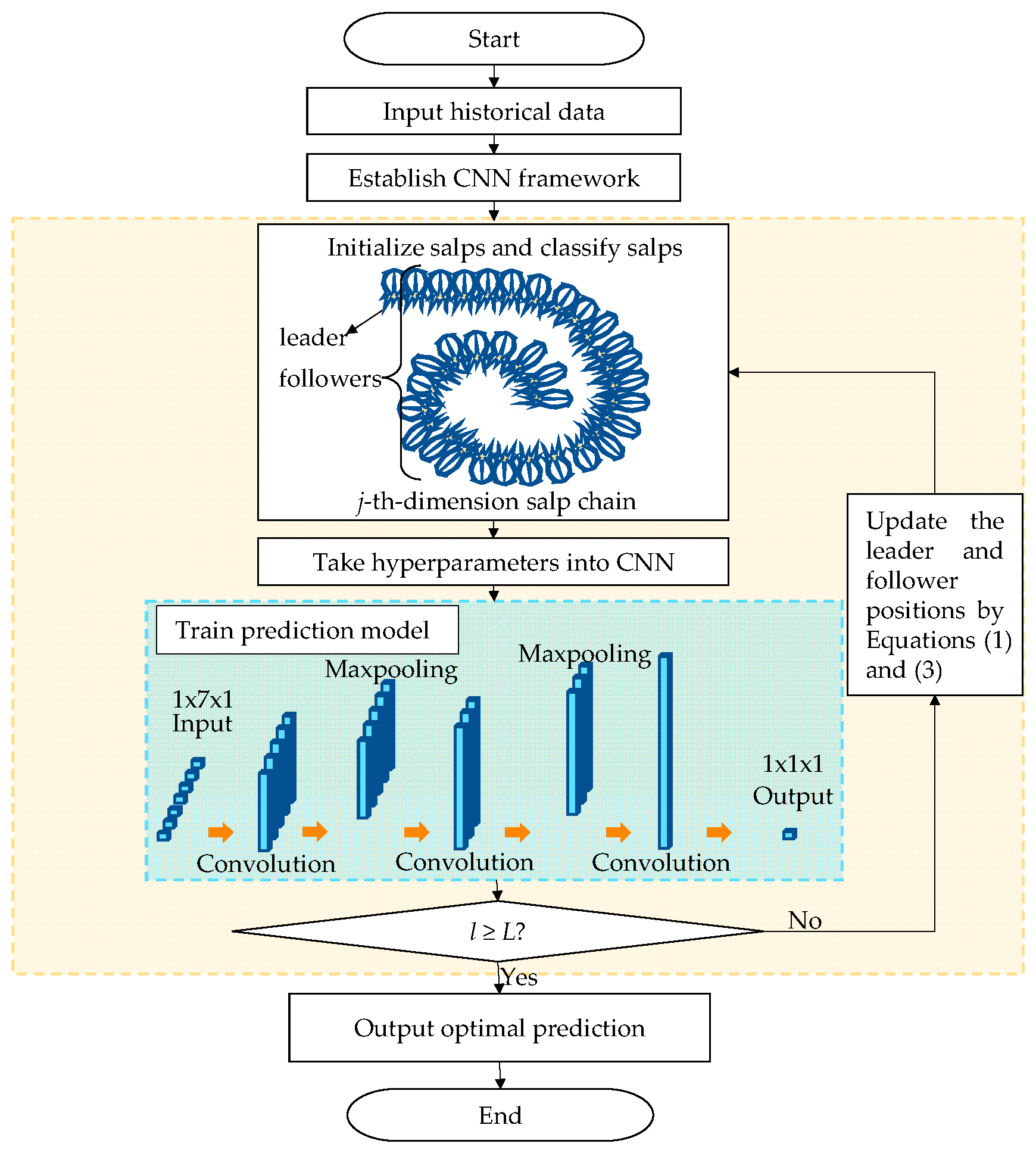
2.3. Salp Swarm Algorithm–Convolutional Neural Network
- Step 1
- Input the historical data;
- Step 2
- Establish the basic structure of the CNN;
- Step 3
- Set , , , , and of the SSA;
- Step 4
- Initialize the locations of salps;
- Step 5
- Calculate salp fitness and classify the leader and followers (hyperparameters);
- Step 6
- Input hyperparameters into the CNN and predict PV output to obtain the loss and accuracy;
- Step 7
- Repeat Steps 4–6 and update the positions of salps in Equations (1) and (3) until the current iteration reaches the maximum iteration number;
- Step 8
- Output the optimal prediction.
3. EVs’ Spatial–Temporal Distribution
3.1. Trip Chain
3.1.1. Initial Departure Time
3.1.2. Initial Departure/Destination
3.1.3. Parking Time
3.1.4. Initial SOC
3.2. EV Energy Consumption
3.2.1. Temperature Model
3.2.2. Traveling Speed Model
3.2.3. Status of Charge
- Charging Status
- Discharging Status
- Driving Status
- Idle Status
3.3. EV Queuing Model
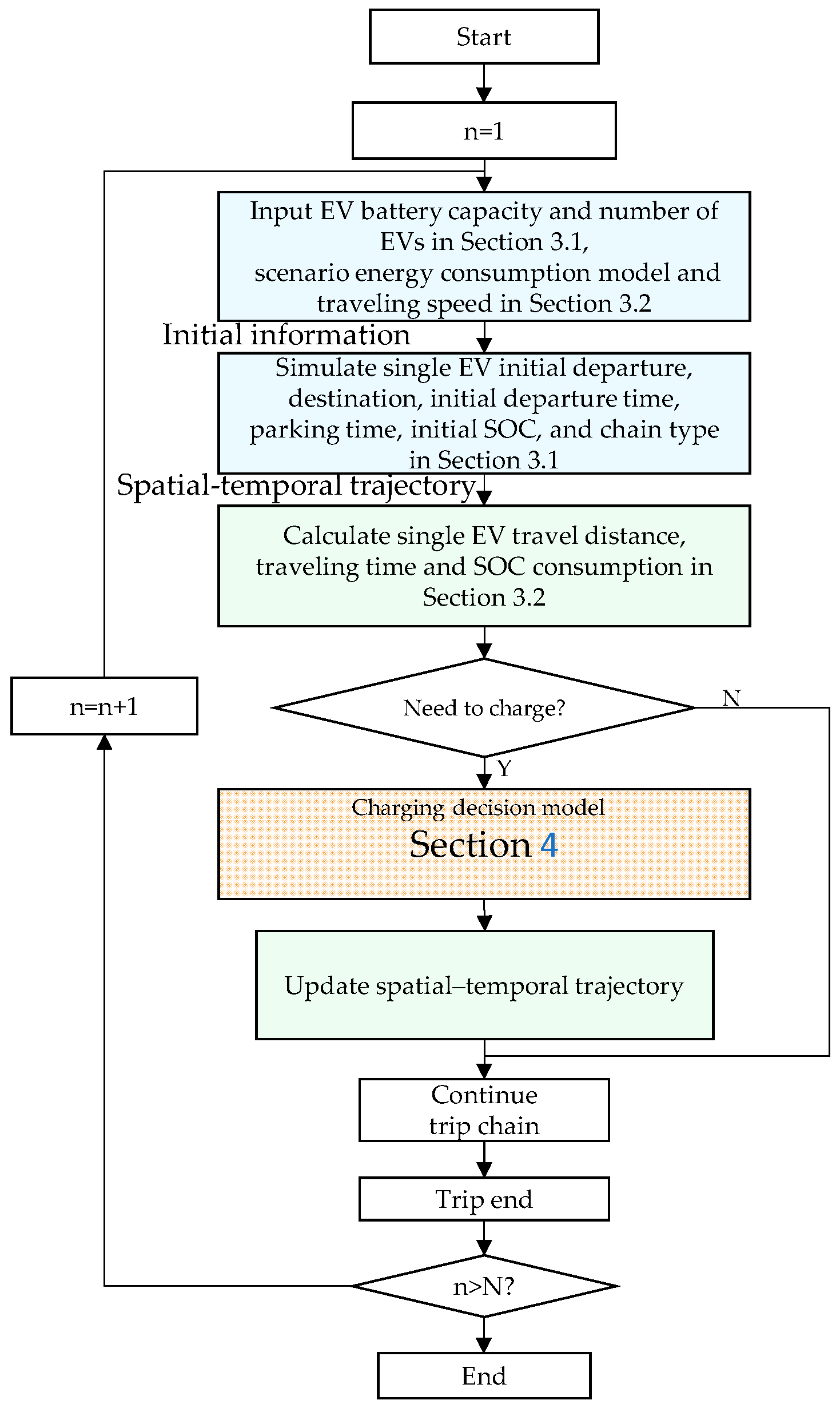
3.4. Monte Carlo Simulation
- Step 1
- Input the EV battery capacity and the number of EVs, as described in Section 3.1, and the scenario energy consumption model and traveling speed, as described in Section 3.2;
- Step 2
- Simulate a single EV’s initial departure, destination, initial departure time, parking time, initial SOC, and chain type, as described in Section 3.1;
- Step 3
- Calculate a single EV’s travel distance, traveling time, and SOC consumption, as described in Section 3.2;
- Step 4
- Judge whether the EV is charged, as described in Section 4. If so, update spatial–temporal trajectories; if not, continue the trip until completion;
- Step 5
- Update the initial trip chain of each EV;
- Step 6
- Repeat Steps 2–5 for the next EV until all EVs are simulated.
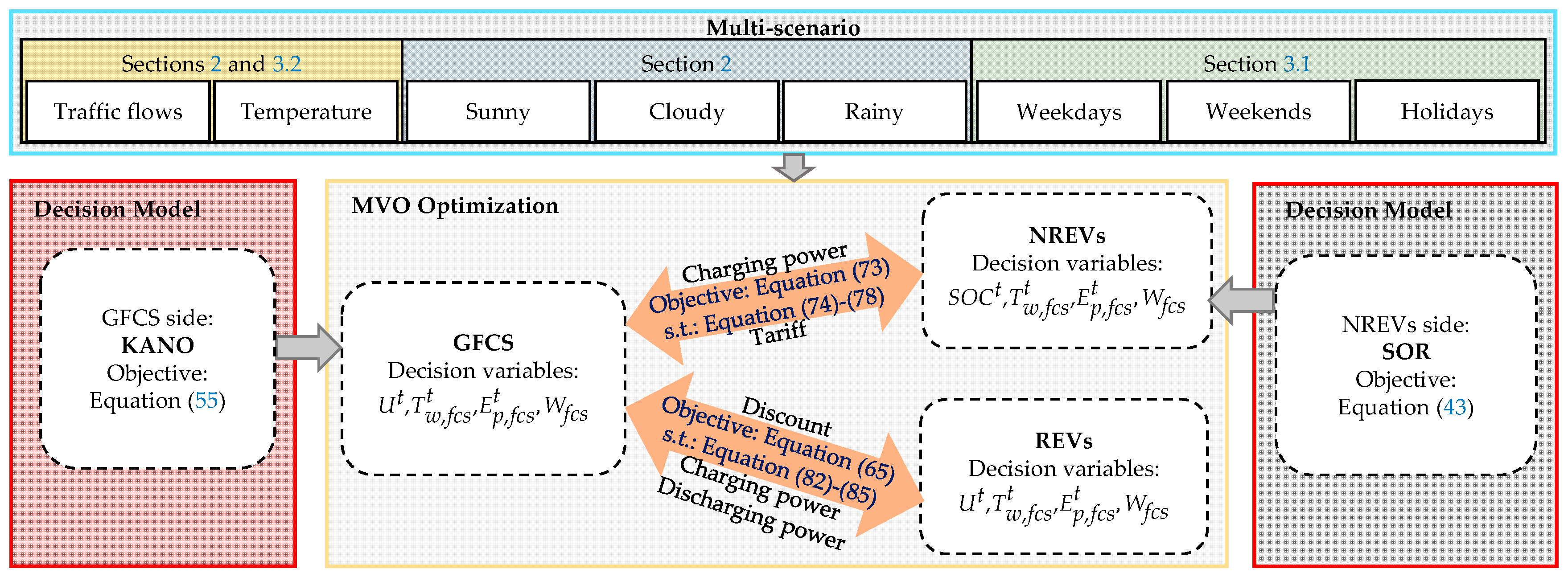
4. SOR&KANO for Charging/Discharging Decision-Making of EVs and GFCSs
4.1. Disordered Decision-Making
4.2. SO(TPB)R Decision-Making
- S
- O
- R
4.3. KANO Decision-Making
- Attractive Quality
- One-dimensional Quality
- Must-be Quality
4.4. SOR&KANO Decision-Making
5. Objective Function in Optimal Scheduling for Increased Satisfaction of GFCSs and NREV/REV Users
5.1. EVs’ Objective Function
5.2. GFCSs’ Objective Function
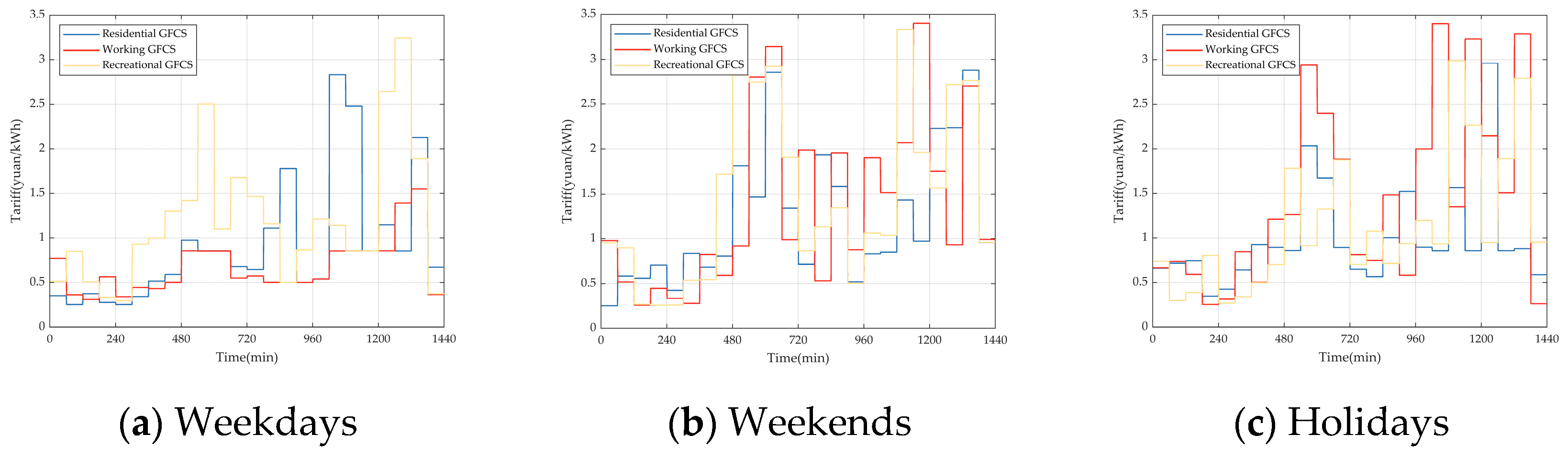
5.3. Optimal Scheduling of NREVs and REVs
5.3.1. Optimal Scheduling of NREVs
5.3.2. Optimal Scheduling of REVs
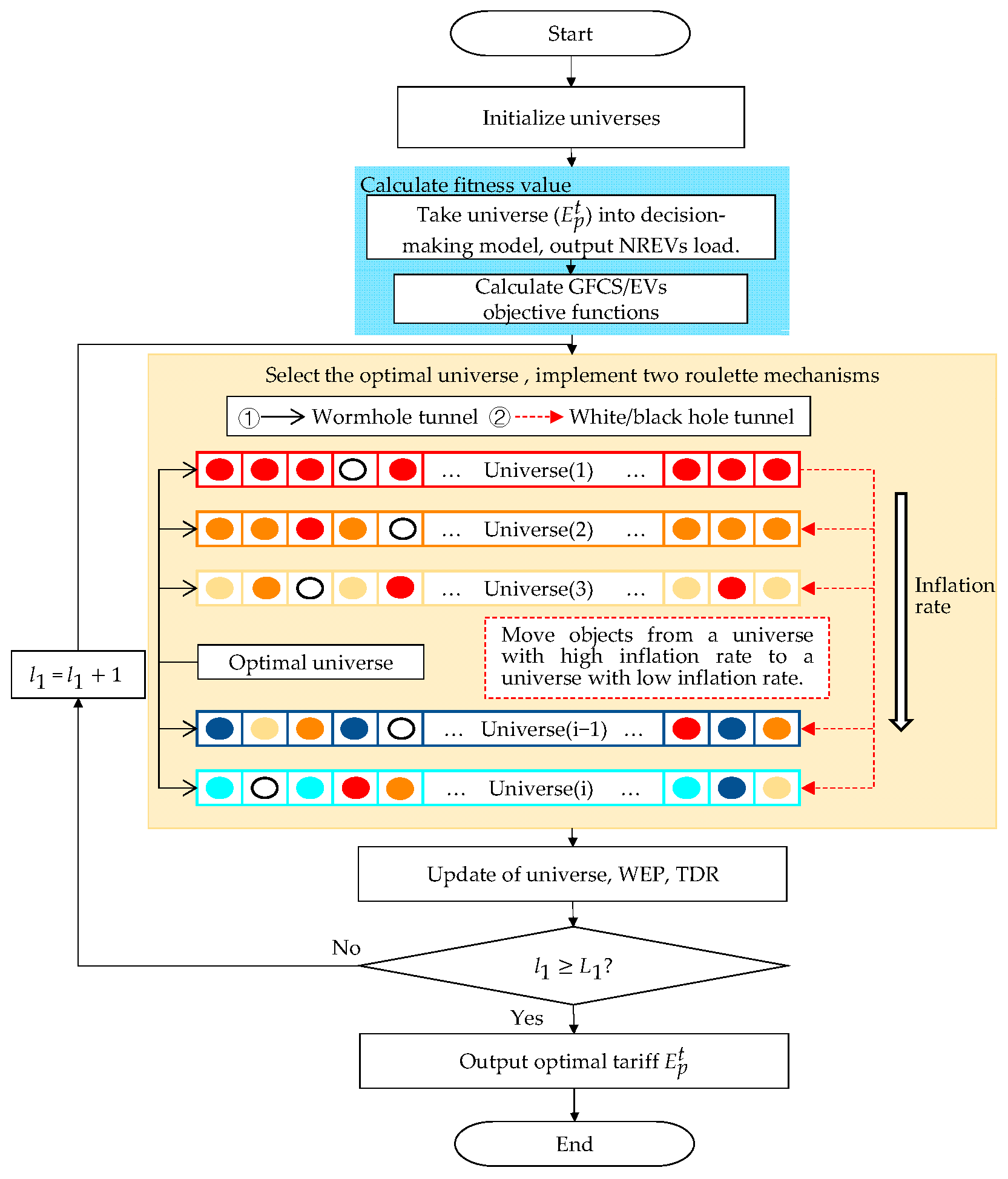
5.4. Multi-Verse Optimizer
- Step 1
- Set the MVO parameters, the maximum number of objects and universes , and iterations , where the upper and lower limits of are and , respectively;
- Step 2
- Initialize the universes, output each universe in turn, and calculate the initial value of the objective function;
- Step 3
- Input the universe (tariffs) and simulate the NREV charging load in that universe;
- Step 4
- Input the NREV charging load to calculate the value of the EV side’s objective function, as described in Section 5.1, and the value of the GFCS side’s objective function, as described in Section 5.2;
- Step 5
- According to the function value, to obtain the expansion rate of the universe, select the optimal universe and execute the roulette mechanism;
- Step 6
- Update the universes, the wormhole existence rate , and the travel distance rate ;
- Step 7
- Determine whether the abort condition is reached or not, and if not, repeat Steps 3–6;
- Step 8
- Output the optimal tariffs.
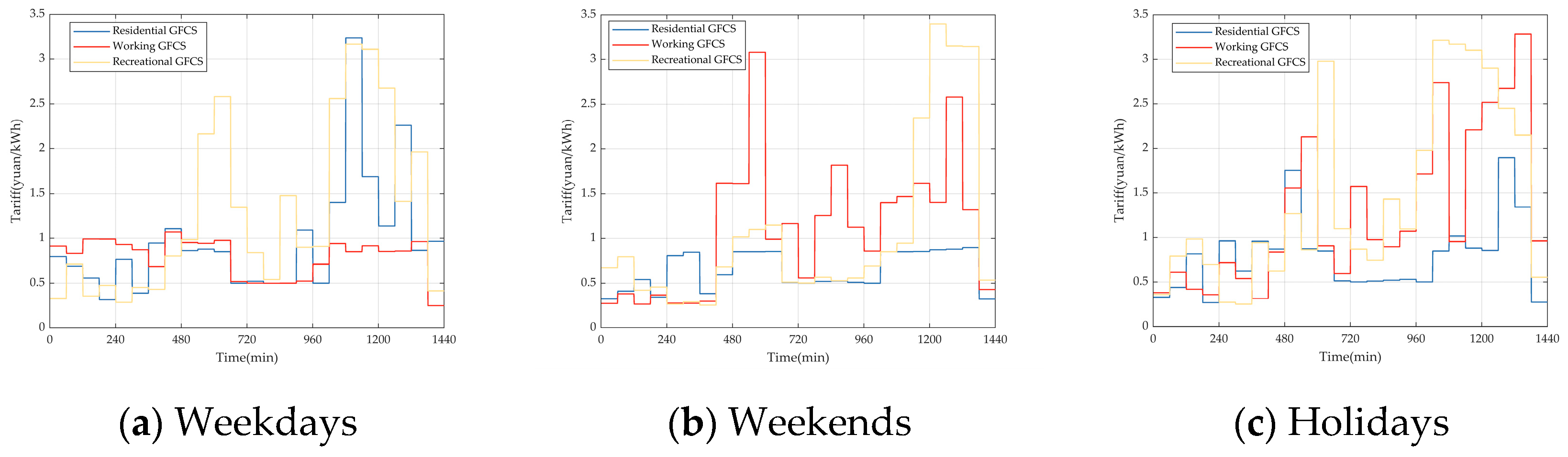
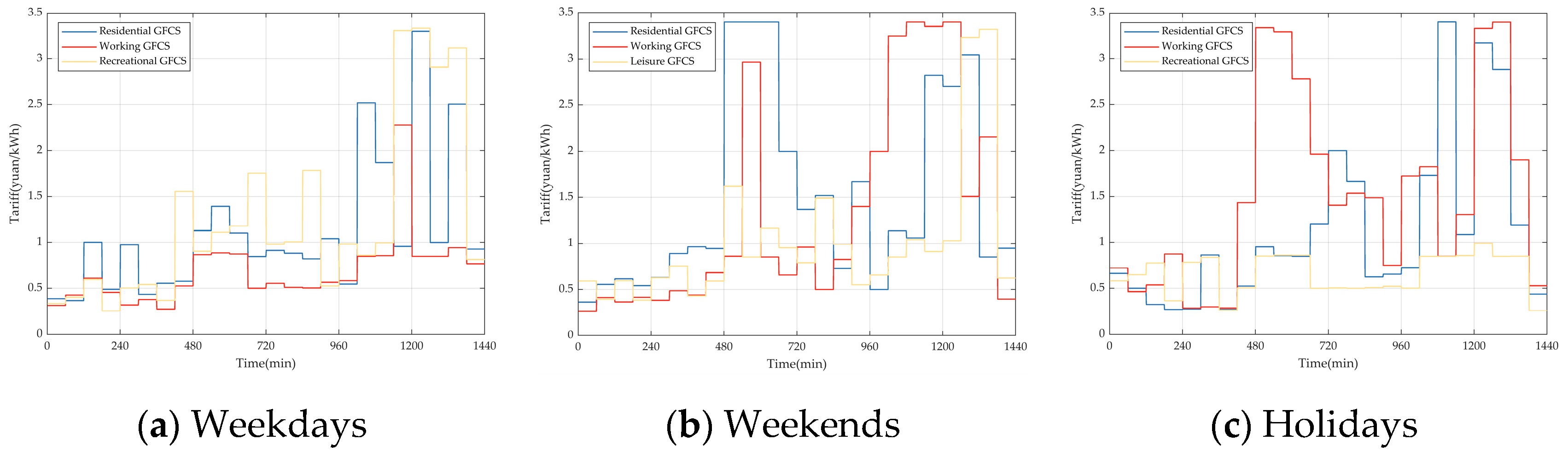
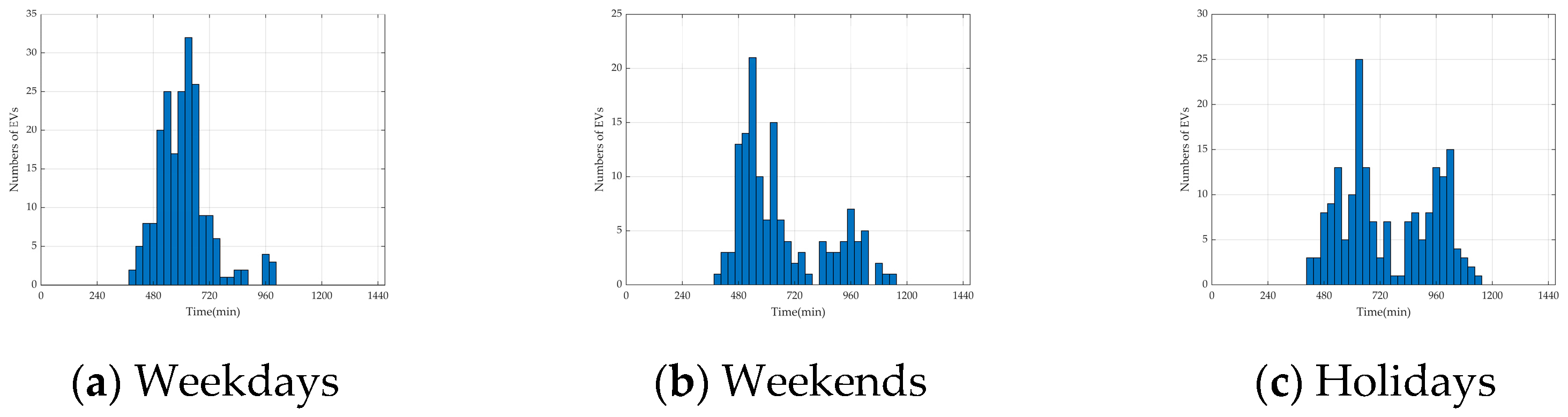
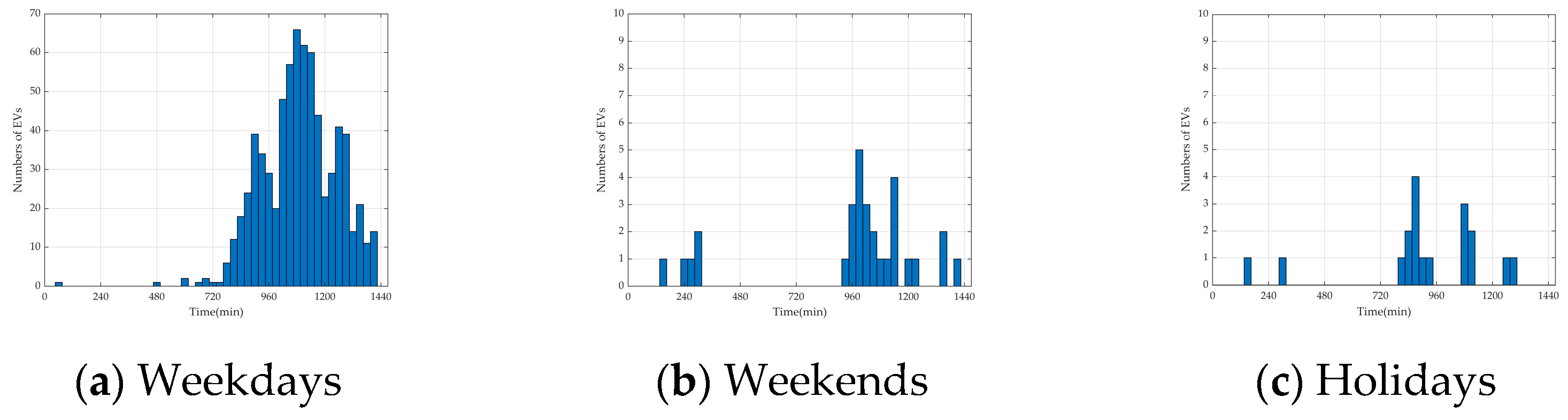
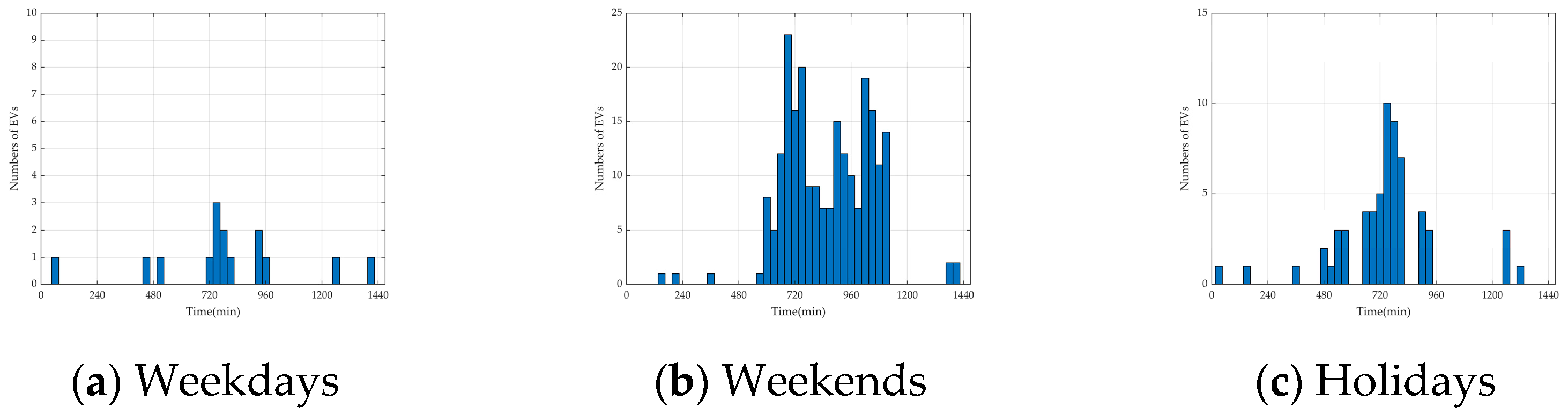
6. Case Study
6.1. Simulation System
6.2. Case Settings
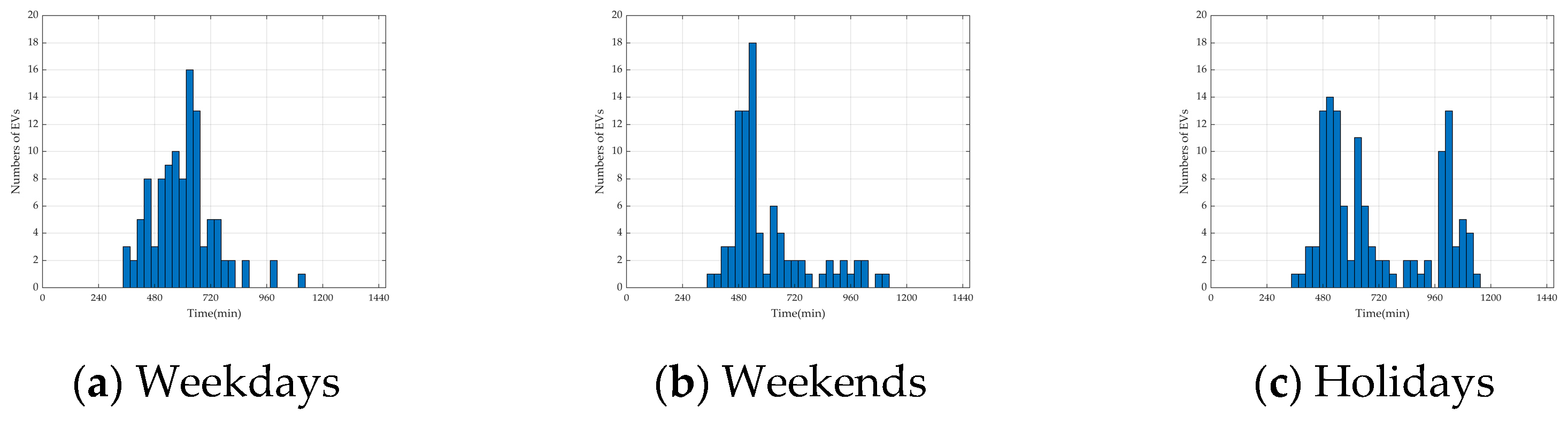
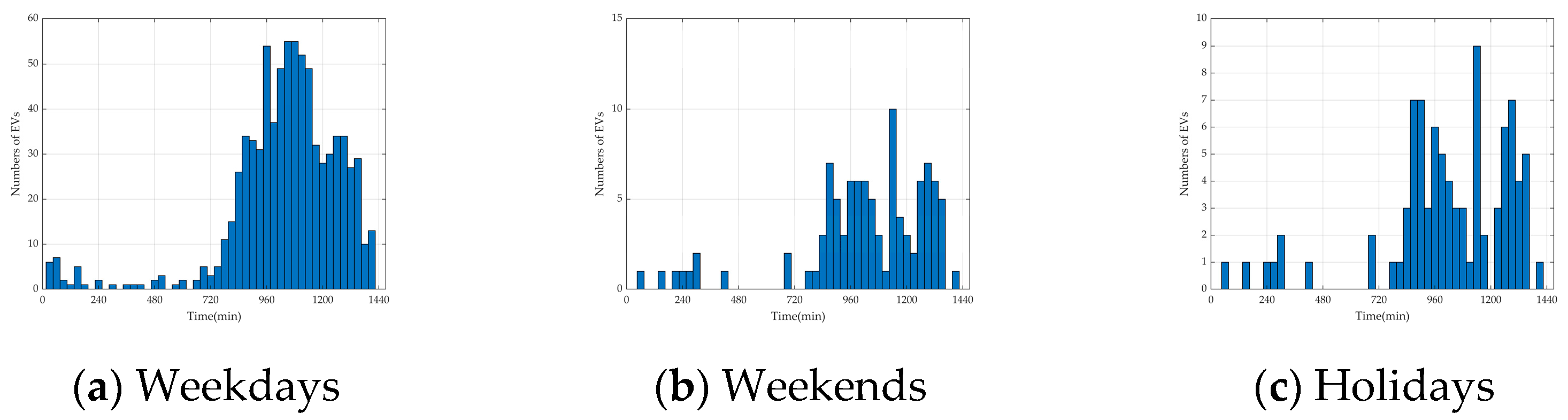
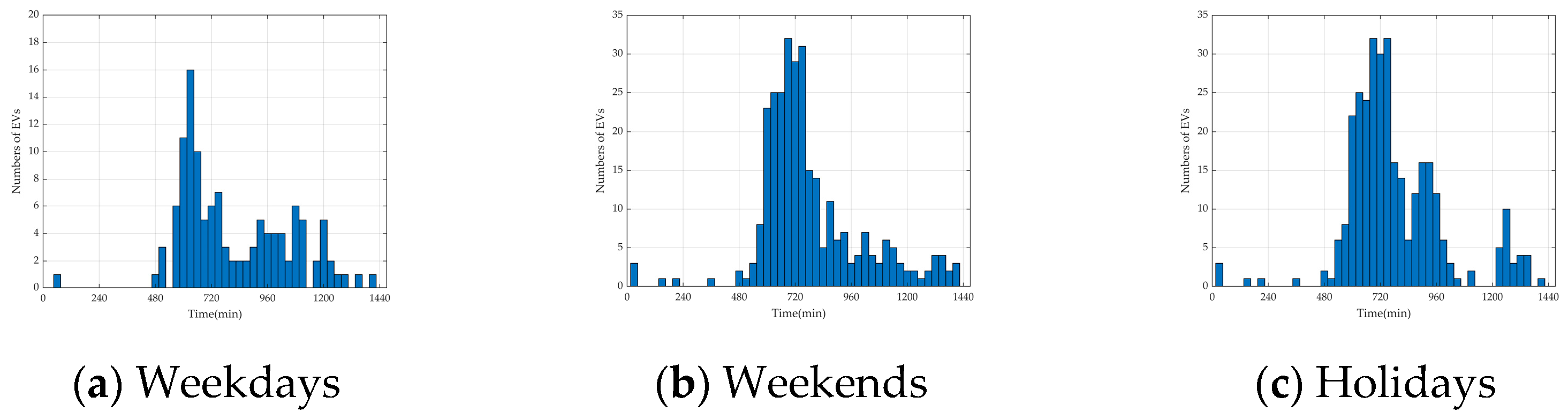
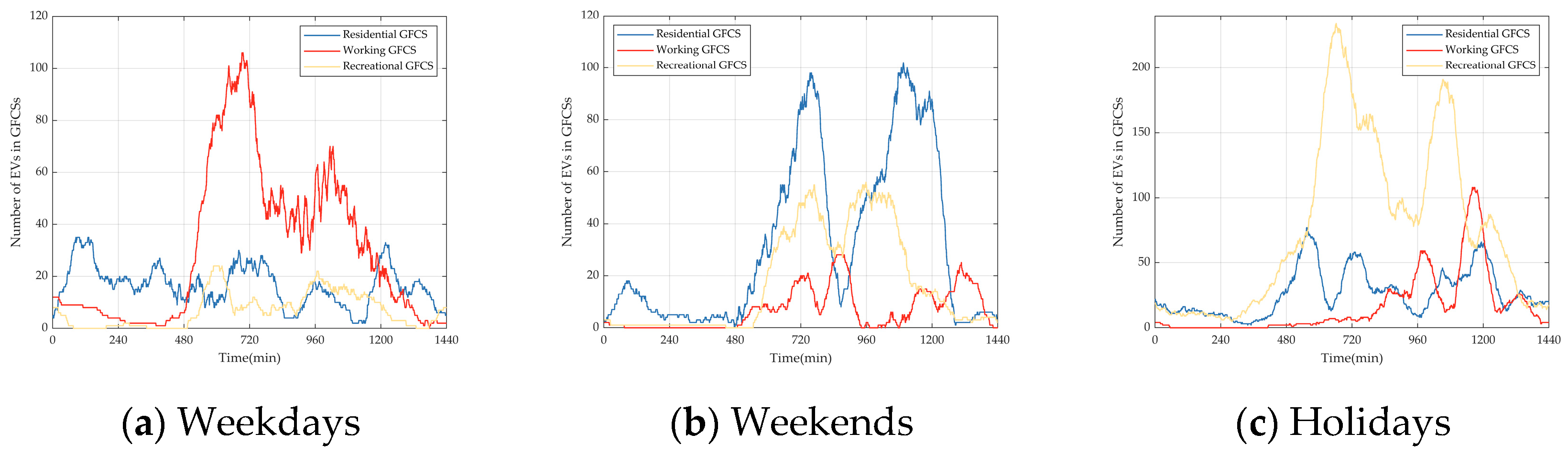
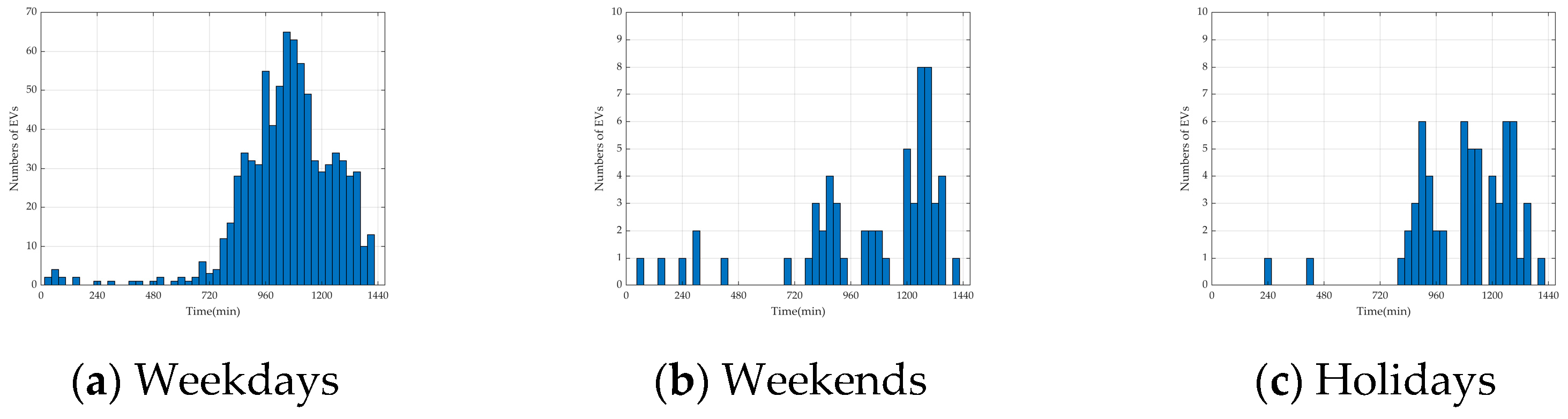
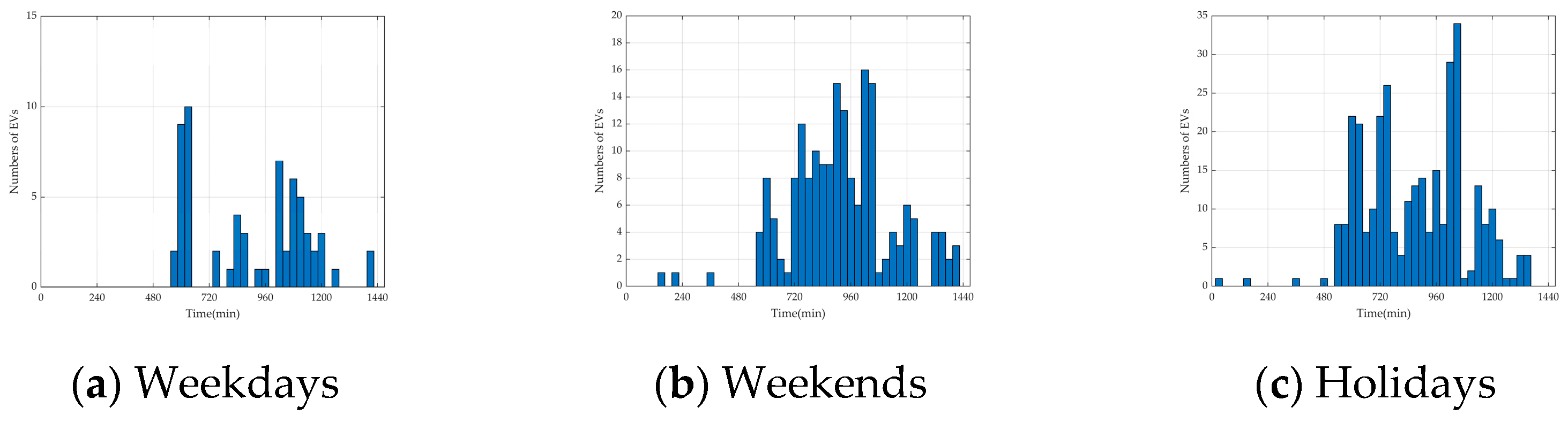
- In the weekday scenario, which is dominated by the commuting chain, the number of total EVs is set to 15,000, of which 3000 are REVs and 12,000 are NREVs. The proportion of NREVs is set to 9600 in the commuting chain, 1200 in the recreational chain for morning trips, and 1200 in the recreational chain for afternoon trips.
- In the weekend scenario, which is dominated by the recreational chain, the number of total EVs is set to 10,000, with 2000 REVs and 8000 NREVs. The proportion of NREVs is set to 1600 in the commuting chain, 3200 in the recreational chain for morning trips, and 3200 in the recreational chain for afternoon trips.
- In the holiday scenario, which is dominated by local EVs in the recreational chain and an extra influx of tourist EVs, the number of total EVs is set to 20,000, with 2000 REVs, 8000 NREVs, and 10,000 tourist NREVs. The proportion of NREVs is set to 1600 in the commuting chain, 9200 in the recreational chain for morning trips, and 7200 in the recreational chain for afternoon trips.
- is 10 and is 1.5 in morning trip; is 16 and is 1.5 in afternoon trip.
- , , and are set to 439, 168, and 0.234 for parking time in the working zone, respectively; , , and are set to 69, 45, and 0.644 for parking time in the recreational zone.
- is set to 0.5, and is set to 0.1 for the initial SOC.
- Scenario parameters: the temperature is set to 25 °C, and the weather is set to sunny.
- The load is 46 MW, and PV is 65.7 MW. EVs’ fast-charging power is 70 kW. The charging and discharging efficiency are both 0.9. The residential GFCS has 45 charging piles, the working GFCS has 65 charging piles, and the recreational GFCS has 80 charging piles.
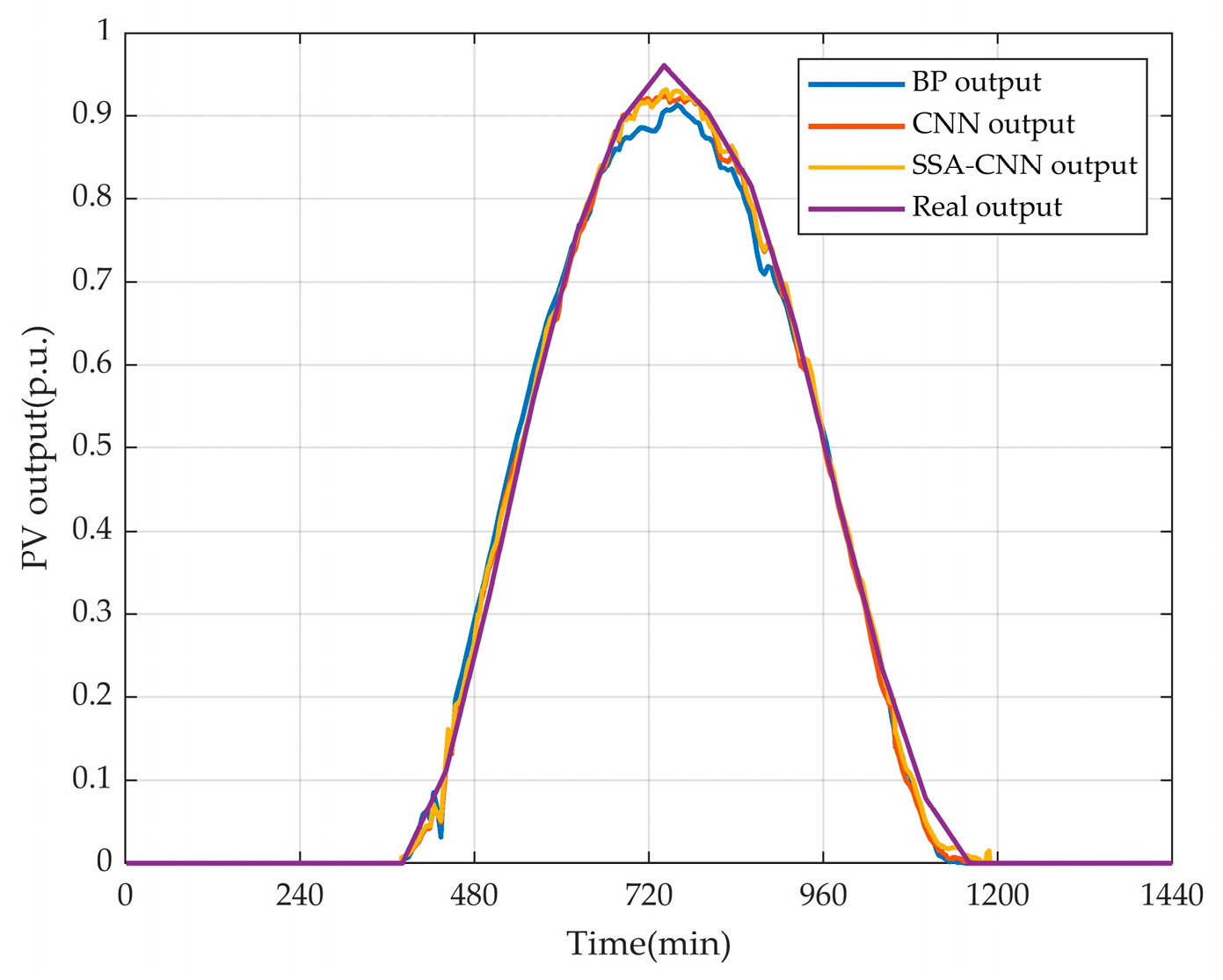
6.3. The Result of PV Output Prediction
6.4. Comparison of Optimization Algorithms
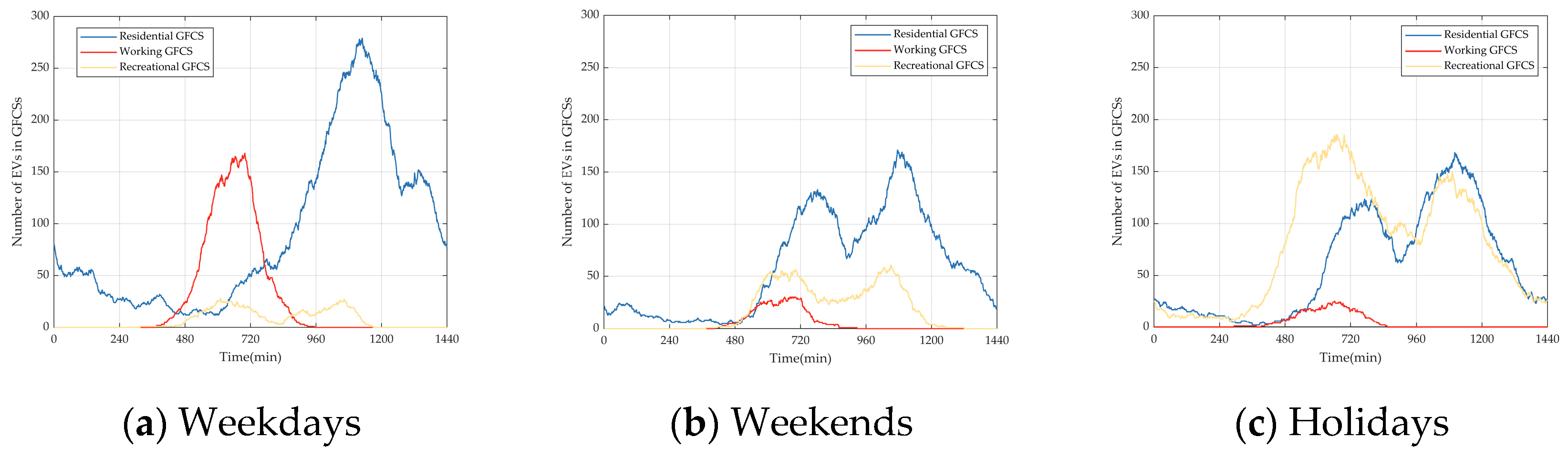
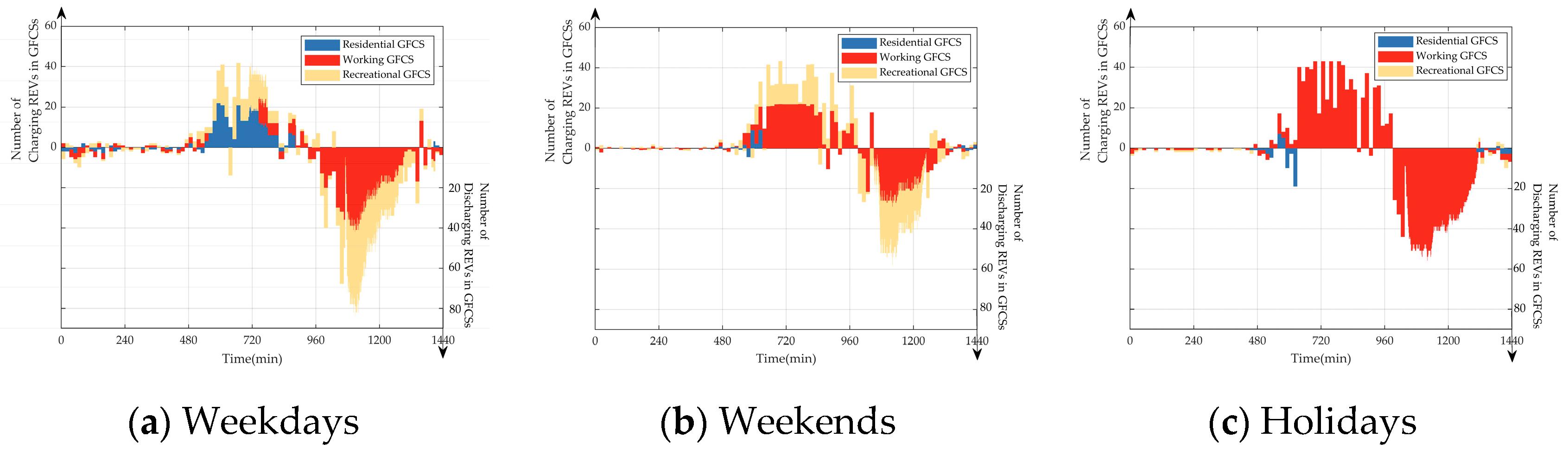
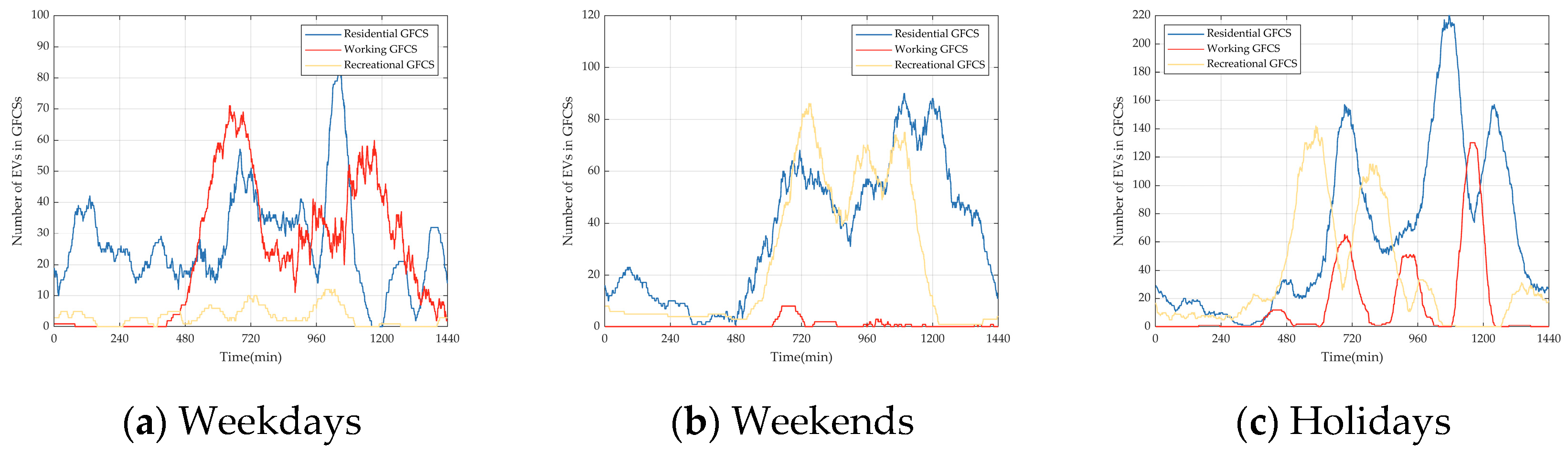
6.5. Case Study
6.5.1. Case 1: NREVs with No Scheduling and REVs with No Scheduling
6.5.2. Case 2: NREVs with No Scheduling and REVs with Scheduling
6.5.3. Case 3: NREV Scheduling by SOR and REV Scheduling
6.5.4. Case 4: NREV Scheduling by KANO and REV Scheduling
6.5.5. Case 5: NREV Scheduling by SOR&KANO and REV Scheduling
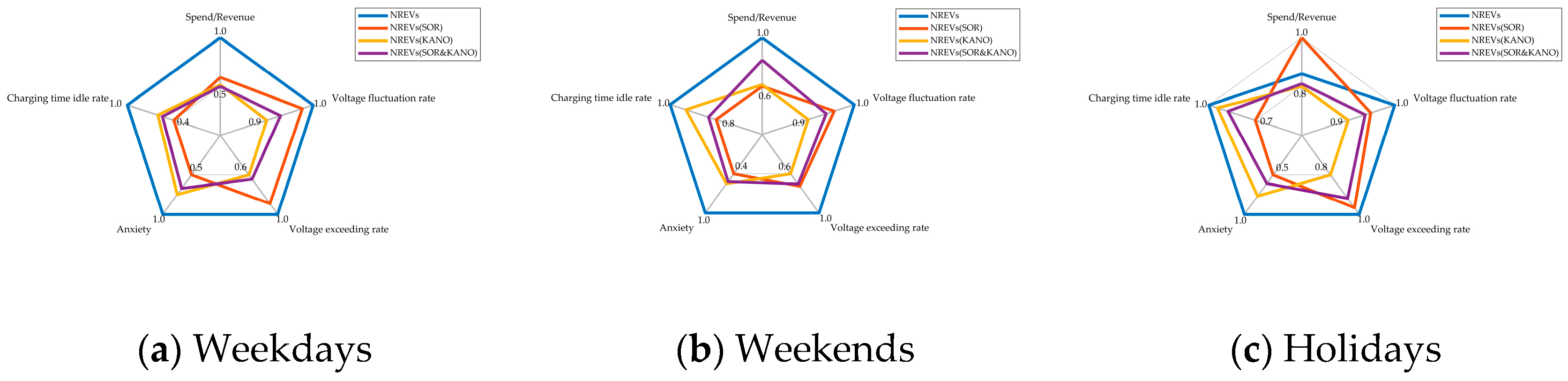
6.5.6. Case Evaluation
- The GFCS side’s voltage fluctuation rate and voltage exceedance rate are ranked as NREVs> NREVs (SOR) > NREVs (SOR&KANO) > NREVs (KANO);
- The EV side’s mileage anxiety and charging time idle rate are ranked as NREVs > NREVs (KANO) > NREVs (SOR&KANO) > NREVs (SOR).
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, R.; Cai, T.; Xu, W. Exploring the Technology Changes of New Energy Vehicles in China: Evolution and Trends. Comput. Ind. Eng. 2024, 191, 110178. [Google Scholar] [CrossRef]
- Chen, X.H.; Tee, K.; Elnahass, M.; Ahmed, R. Assessing the Environmental Impacts of Renewable Energy Sources: A Case Study on Air Pollution and Carbon Emissions in China. J. Environ. Manag. 2023, 345, 118525. [Google Scholar] [CrossRef]
- Wu, J.; Su, H.; Meng, J.; Lin, M. Electric Vehicle Charging Scheduling Considering Infrastructure Constraints. Energy 2023, 278, 127806. [Google Scholar] [CrossRef]
- National Energy Administration. Transcript of the National Energy Administration’s Q1 2024 Press Conference. Available online: https://www.nea.gov.cn/2024-01/25/c_1310762019.htm (accessed on 25 January 2024).
- Fachrizal, R.; Shepero, M.; Van Der Meer, D.; Munkhammar, J.; Widén, J. Smart Charging of Electric Vehicles Considering Photovoltaic Power Production and Electricity Consumption: A Review. eTransportation 2020, 4, 100056. [Google Scholar] [CrossRef]
- Secchi, M.; Barchi, G.; Macii, D.; Petri, D. Smart Electric Vehicles Charging with Centralised Vehicle-to-Grid Capability for Net-Load Variance Minimisation under Increasing EV and PV Penetration Levels. Sustain. Energy Grids Netw. 2023, 35, 101120. [Google Scholar] [CrossRef]
- Gaboitaolelwe, J.; Zungeru, A.M.; Yahya, A.; Lebekwe, C.K.; Vinod, D.N.; Salau, A.O. Machine Learning Based Solar Photovoltaic Power Forecasting: A Review and Comparison. IEEE Access 2023, 11, 40820–40845. [Google Scholar] [CrossRef]
- Huang, Q.; Wei, S. Improved Quantile Convolutional Neural Network with Two-Stage Training for Daily-Ahead Probabilistic Forecasting of Photovoltaic Power. Energy Convers. Manag. 2020, 220, 113085. [Google Scholar] [CrossRef]
- Suresh, V.; Janik, P.; Rezmer, J.; Leonowicz, Z. Forecasting Solar PV Output Using Convolutional Neural Networks with a Sliding Window Algorithm. Energies 2020, 13, 723. [Google Scholar] [CrossRef]
- Wang, F.; Xuan, Z.; Zhen, Z.; Li, K.; Wang, T.; Shi, M. A Day-Ahead PV Power Forecasting Method Based on LSTM-RNN Model and Time Correlation Modification under Partial Daily Pattern Prediction Framework. Energy Convers. Manag. 2020, 212, 112766. [Google Scholar] [CrossRef]
- Dong, N.; Chang, J.-F.; Wu, A.-G.; Gao, Z.-K. A Novel Convolutional Neural Network Framework Based Solar Irradiance Prediction Method. Int. J. Electr. Power Energy Syst. 2020, 114, 105411. [Google Scholar] [CrossRef]
- Han, X.; Wei, Z.; Hong, Z.; Zhao, S. Ordered Charge Control Considering the Uncertainty of Charging Load of Electric Vehicles Based on Markov Chain. Renew. Energy 2020, 161, 419–434. [Google Scholar] [CrossRef]
- Anand, M.P.; Bagen, B.; Rajapakse, A. Probabilistic Reliability Evaluation of Distribution Systems Considering the Spatial and Temporal Distribution of Electric Vehicles. Int. J. Electr. Power Energy Syst. 2020, 117, 105609. [Google Scholar] [CrossRef]
- Hafeez, G.; Alimgeer, K.S.; Khan, I. Electric Load Forecasting Based on Deep Learning and Optimized by Heuristic Algorithm in Smart Grid. Appl. Energy 2020, 269, 114915. [Google Scholar] [CrossRef]
- Li, H.; Yu, L.; Chen, Y.; Tu, H.; Zhang, J. Uncertainty of Available Range in Explaining the Charging Choice Behavior of BEV Users. Transp. Res. Part A Policy Pract. 2023, 170, 103624. [Google Scholar] [CrossRef]
- Yi, T.; Zhang, C.; Lin, T.; Liu, J. Research on the Spatial-Temporal Distribution of Electric Vehicle Charging Load Demand: A Case Study in China. J. Clean. Prod. 2020, 242, 118457. [Google Scholar] [CrossRef]
- Li, B.; Chen, M.; Kammen, D.M. Electric vehicle’s impacts on China’s electricity load profiles based on driving patterns and demographics. Energy Rep. 2022, 8, 26–35. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, J.; Liu, Y. Daily electric vehicle charging load profiles considering demographics of vehicle users. Appl. Energy 2020, 274, 115063. [Google Scholar] [CrossRef]
- Fischer, D.; Harbrecht, A.; Surmann, A.; McKenna, R. Electric Vehicles’ Impacts on Residential Electric Local Profiles—A Stochastic Modelling Approach Considering Socio-Economic, Behavioural and Spatial Factors. Appl. Energy 2019, 233–234, 644–658. [Google Scholar] [CrossRef]
- Gschwendtner, C.; Knoeri, C.; Stephan, A. The Impact of Plug-in Behavior on the Spatial–Temporal Flexibility of Electric Vehicle Charging Load. Sustain. Cities Soc. 2023, 88, 104263. [Google Scholar] [CrossRef]
- Zhang, Z.; Lv, L. Status and Development of Research on Orderly Charging and Discharging of Electric Vehicles. Electronics 2023, 12, 2041. [Google Scholar] [CrossRef]
- Zhou, C.; Qi, S.; Zhang, J.; Tang, S. Potential Co-Benefit Effect Analysis of Orderly Charging and Discharging of Electric Vehicles in China. Energy 2021, 226, 120352. [Google Scholar] [CrossRef]
- Li, Z.; Wu, L.; Xu, Y.; Zheng, X. Stochastic-Weighted Robust Optimization Based Bilayer Operation of a Multi-Energy Building Microgrid Considering Practical Thermal Loads and Battery Degradation. IEEE Trans. Sustain. Energy 2022, 13, 668–682. [Google Scholar] [CrossRef]
- Shang, Y.; Li, S. FedPT-V2G: Security Enhanced Federated Transformer Learning for Real-Time V2G Dispatch with Non-IID Data. Appl. Energy 2024, 358, 122626. [Google Scholar] [CrossRef]
- Shang, Y.; Shang, Y.; Yu, H.; Shao, Z.; Jian, L. Achieving Efficient and Adaptable Dispatching for Vehicle-to-Grid Using Distributed Edge Computing and Attention-Based LSTM. IEEE Trans. Ind. Inform. 2022, 18, 6915–6926. [Google Scholar] [CrossRef]
- Yan, D.; Yin, H.; Li, T.; Ma, C. A Two-Stage Scheme for Both Power Allocation and EV Charging Coordination in a Grid-Tied PV–Battery Charging Station. IEEE Trans. Ind. Inf. 2021, 17, 6994–7004. [Google Scholar] [CrossRef]
- Firouzjah, K.G. Profit-based electric vehicle charging scheduling: Comparison with different strategies and impact assessment on distribution networks. Int. J. Electr. Power Energy Syst. 2022, 138, 107977. [Google Scholar] [CrossRef]
- Xiang, Y.; Yang, J.; Li, X.; Gu, C.; Zhang, S. Routing Optimization of Electric Vehicles for Charging with Event-Driven Pricing Strategy. IEEE Trans. Automat. Sci. Eng. 2022, 19, 7–20. [Google Scholar] [CrossRef]
- Cui, Y.; Hu, Z.; Duan, X. Optimal Pricing of Public Electric Vehicle Charging Stations Considering Operations of Coupled Transportation and Power Systems. IEEE Trans. Smart Grid 2021, 12, 3278–3288. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Li, Y.; Gooi, H.B.; Xin, H. Multi-Agent Based Optimal Scheduling and Trading for Multi-Microgrids Integrated with Urban Transportation Networks. IEEE Trans. Power Syst. 2021, 36, 2197–2210. [Google Scholar] [CrossRef]
- Zhang, Y. Estimating charging demand from the perspective of choice behavior: A Framework combining rule-based algorithm and Hybrid Choice Model. J. Clean. Prod. 2022, 376, 134262. [Google Scholar] [CrossRef]
- Fazeli, S.S.; Venkatachalam, S.; Chinnam, R.B.; Murat, A. Two-Stage Stochastic Choice Modeling Approach for Electric Vehicle Charging Station Network Design in Urban Communities. IEEE Trans. Intell. Transport. Syst. 2021, 22, 3038–3053. [Google Scholar] [CrossRef]
- Zhao, H.; Hao, X. Location Decision of Electric Vehicle Charging Station Based on a Novel Grey Correlation Comprehensive Evaluation Multi-Criteria Decision Method. Energy 2024, 299, 131356. [Google Scholar] [CrossRef]
- Dai, Y.; Qi, Y.; Li, L.; Wang, B.; Gao, H. A Dynamic Pricing Scheme for Electric Vehicle in Photovoltaic Charging Station Based on Stackelberg Game Considering User Satisfaction. Comput. Ind. Eng. 2021, 154, 107117. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; El-Shahat, D.; Faris, H.; Mirjalili, S. A Binary Multi-Verse Optimizer for 0-1 Multidimensional Knapsack Problems with Application in Interactive Multimedia Systems. Comput. Ind. Eng. 2019, 132, 187–206. [Google Scholar] [CrossRef]
- Sundaram, A. Multiobjective Multi-Verse Optimization Algorithm to Solve Combined Economic, Heat and Power Emission Dispatch Problems. Appl. Soft Comput. 2020, 91, 106195. [Google Scholar] [CrossRef]
- Xu, W.; Yu, X. A Multi-Objective Multi-Verse Optimizer Algorithm to Solve Environmental and Economic Dispatch. Appl. Soft Comput. 2023, 146, 110650. [Google Scholar] [CrossRef]
- Fu, Y.; Zhou, M.; Guo, X.; Qi, L.; Sedraoui, K. Multiverse Optimization Algorithm for Stochastic Biobjective Disassembly Sequence Planning Subject to Operation Failures. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1041–1051. [Google Scholar] [CrossRef]
- Sultan, H.M.; Menesy, A.S.; Kamel, S.; Selim, A.; Jurado, F. Parameter Identification of Proton Exchange Membrane Fuel Cells Using an Improved Salp Swarm Algorithm. Energy Convers. Manag. 2020, 224, 113341. [Google Scholar] [CrossRef]
- Tayab, U.B.; Lu, J.; Yang, F.; AlGarni, T.S.; Kashif, M. Energy Management System for Microgrids Using Weighted Salp Swarm Algorithm and Hybrid Forecasting Approach. Renew. Energy 2021, 180, 467–481. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A Bio-Inspired Optimizer for Engineering Design Problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Beijing Transport Institute. The Beijing Transport Development Annual Report of 2023. Available online: https://www.bjtrc.org.cn/List/index/cid/7.html (accessed on 1 August 2023).
- U.S. Department of Transportation. Summary of Travel Trends: 2022 National Household Travel Survey. Available online: https://nhts.ornl.gov/ (accessed on 1 January 2024).
- Sun, X.; Fu, J. Experiment Investigation for Interconnected Effects of Driving Cycle and Ambient Temperature on Bidirectional Energy Flows in an Electric Sport Utility Vehicle. Energy 2024, 300, 131594. [Google Scholar] [CrossRef]
- Lee, G.; Song, J.; Lim, Y.; Park, S. Energy Consumption Evaluation of Passenger Electric Vehicle Based on Ambient Temperature under Real-World Driving Conditions. Energy Convers. Manag. 2024, 306, 118289. [Google Scholar] [CrossRef]
- Hao, X.; Wang, H.; Lin, Z.; Ouyang, M. Seasonal Effects on Electric Vehicle Energy Consumption and Driving Range: A Case Study on Personal, Taxi, and Ridesharing Vehicles. J. Clean. Prod. 2020, 249, 119403. [Google Scholar] [CrossRef]
- Temelcan, G.; Kocken, H.G.; Albayrak, I. Fuzzy Modelling of Static System Optimum Traffic Assignment Problem Having Multi Origin-Destination Pair. Socio-Econ. Plan. Sci. 2021, 77, 101024. [Google Scholar] [CrossRef]
- Modeling the Effect of Autonomous Vehicles (AVs) on the Accessibility of the Transportation Network|Scientific Reports. Available online: https://www.nature.com/articles/s41598-024-60069-8 (accessed on 24 June 2024).
- The People’s Government of Henan Province. Implementation Plan for Accelerating the Development of New Energy Vehicles in Henan Province. Available online: https://www.henan.gov.cn/2022/05-19/2451587.html (accessed on 19 May 2022).
- Abdel-Aal, M.M.M. Survey-Based Calibration of a Parking Entry as a Single-Server Mathematical Queuing Model: A Case Study. Alex. Eng. J. 2020, 59, 829–838. [Google Scholar] [CrossRef]
- Gnedenko, B.V.; Kovalenko, I.N. Introduction to Queueing Theory; Birkhauser Boston Inc.: Boston, MA, USA, 1989. [Google Scholar]
- Sørensen, Å.L.; Sartori, I.; Lindberg, K.B.; Andresen, I. A Method for Generating Complete EV Charging Datasets and Analysis of Residential Charging Behaviour in a Large Norwegian Case Study. Sustain. Energy Grids Netw. 2023, 36, 101195. [Google Scholar] [CrossRef]
- Liu, F.; Lai, K.-H.; Wu, J.; Duan, W. Listening to Online Reviews: A Mixed-Methods Investigation of Customer Experience in the Sharing Economy. Decis. Support Syst. 2021, 149, 113609. [Google Scholar] [CrossRef]
- Sultan, P.; Wong, H.Y.; Azam, M.S. How Perceived Communication Source and Food Value Stimulate Purchase Intention of Organic Food: An Examination of the Stimulus-Organism-Response (SOR) Model. J. Clean. Prod. 2021, 312, 127807. [Google Scholar] [CrossRef]
- Shi, R.; Wang, M.; Liu, C.; Gull, N. The Influence of Short Video Platform Characteristics on Users’ Willingness to Share Marketing Information: Based on the SOR Model. Sustainability 2023, 15, 2448. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, X.; Fan, Y.; Zhang, J. Utilizing the Theory of Planned Behavior to Predict Willingness to Pay for Urban Heat Island Effect Mitigation. Build. Environ. 2021, 204, 108136. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Q.-C.; Jian, I.Y.; Chi, H.-L.; Yang, D.; Chan, E.H.-W. Are You an Energy Saver at Home? The Personality Insights of Household Energy Conservation Behaviors Based on Theory of Planned Behavior. Resour. Conserv. Recycl. 2021, 174, 105823. [Google Scholar] [CrossRef]
- Bai, S.; Li, F.; Xie, W. Green but Unpopular? Analysis on Purchase Intention of Heat Pump Water Heaters in China. Energies 2022, 15, 2464. [Google Scholar] [CrossRef]
- State Administration for Market Regulation; Standardization Administration of the People’s Republic of China. Conversion Methods for Energy Consumption of Electric Vehicles (GB/T37340—2019); Ministry of Health of the People’s Republic of China: Beijing, China, 2019. (In Chinese)
- Wang, X.; Wang, X.; Liang, L.; Yue, X.; Van Wassenhove, L.N. Estimation of Deprivation Level Functions Using a Numerical Rating Scale. Prod. Oper. Manag. 2017, 26, 2137–2150. [Google Scholar] [CrossRef]
- Slevitch, L. Kano Model Categorization Methods: Typology and Systematic Critical Overview for Hospitality and Tourism Academics and Practitioners. J. Hosp. Tour. Res. 2024. [Google Scholar] [CrossRef]
- Li, X.; Zhu, S.; Yüksel, S.; Dinçer, H.; Ubay, G.G. Kano-Based Mapping of Innovation Strategies for Renewable Energy Alternatives Using Hybrid Interval Type-2 Fuzzy Decision-Making Approach. Energy 2020, 211, 118679. [Google Scholar] [CrossRef]
- Encinas, F.; Marmolejo-Duarte, C.; Aguirre-Nuñez, C.; Vergara-Perucich, F. When Residential Energy Labeling Becomes Irrelevant: Sustainability vs. Profitability in the Liberalized Chilean Property Market. Sustainability 2020, 12, 9638. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-Verse Optimizer: A Nature-Inspired Algorithm for Global Optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]























| Case | REV No Scheduling | NREV No Scheduling | REV Scheduling | NREV Scheduling |
|---|---|---|---|---|
| Case 1 | √ | √ | ||
| Case 2 | √ | √ | ||
| Case 3 | √ | √ | ||
| Case 4 | √ | √ | ||
| Case 5 | √ | √ |
| Scenario | Case | Residential GFCS Utilization | Working GFCS Utilization | Recreational GFCS Utilization |
|---|---|---|---|---|
| Weekdays | Case 2 | 80.7% | 33.0% | 16.3% |
| Case 3 (No-REVs) | 56.7% | 35.0% | 4.1% | |
| Case 4 (No-REVs) | 36.1% | 34.6% | 14.8% | |
| Case 5 (No-REVs) | 36.5% | 41.8% | 8.5% | |
| Weekends | Case 2 | 66.3% | 18.3% | 25.9% |
| Case 3 (No-REVs) | 65.5% | 1.1% | 31.6% | |
| Case 4 (No-REVs) | 40.5% | 25.5% | 12.0% | |
| Case 5 (No-REVs) | 50.4% | 10.6% | 21.6% | |
| Holidays | Case 2 | 65.6% | 30.0% | 68.5% |
| Case 3 (No-REVs) | 70.5% | 21.1% | 36.8% | |
| Case 4 (No-REVs) | 46.8% | 23.3% | 63.5% | |
| Case 5 (No-REVs) | 54.4% | 22.7% | 63.7% |
| Scenario | Case Compared with Case 1 | Node-18 Voltage Fluctuation Rate Improvement | Node-18 Voltage Exceedance Rate Improvement |
|---|---|---|---|
| Weekdays | Case 2 | 5.4% | 44.9% |
| Case 3 (No-REVs) | 3.5% | 11.2% | |
| Case 4 (No-REVs) | 15.0% | 41.4% | |
| Case 5 (No-REVs) | 10.5% | 36.9% | |
| Weekends | Case 2 | 7.3% | 56.0% |
| Case 3 (No-REVs) | 3.2% | 23.7% | |
| Case 4 (No-REVs) | 7.4% | 35.1% | |
| Case 5 (No-REVs) | 4.5% | 25.8% | |
| Holidays | Case 2 | 25.1% | 6.7% |
| Case 3 (No-REVs) | 5.9% | 3.6% | |
| Case 4 (No-REVs) | 11.3% | 21.8% | |
| Case 5 (No-REVs) | 7.3% | 8.9% |
| Scenario | Case Compared with Case 1 | Mileage Anxiety Improvement | Fatigue Index Improvement | Charging Time Idle Rate Improvement |
|---|---|---|---|---|
| Weekdays | Case 3 | 51.2% | 68.8% | 63.3% |
| Case 4 | 25.6% | 60.6% | 41.7% | |
| Case 5 | 33.6% | 63.2% | 47.9% | |
| Weekends | Case 3 | 58.6% | 48.5% | 22.5% |
| Case 4 | 43.6% | 23.2% | 7.7% | |
| Case 5 | 46.9% | 31.2% | 18.9% | |
| Holidays | Case 3 | 45.5% | 29.9% | 34.9% |
| Case 4 | 20.9% | 9.3% | 6.5% | |
| Case 3 | 51.2% | 68.8% | 63.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Q.; Gao, Y.; Xing, L.; Xu, B.; Li, Y.; Chen, W. Optimal Scheduling for Increased Satisfaction of Both Electric Vehicle Users and Grid Fast-Charging Stations by SOR&KANO and MVO in PV-Connected Distribution Network. Energies 2024, 17, 3413. https://doi.org/10.3390/en17143413
Yan Q, Gao Y, Xing L, Xu B, Li Y, Chen W. Optimal Scheduling for Increased Satisfaction of Both Electric Vehicle Users and Grid Fast-Charging Stations by SOR&KANO and MVO in PV-Connected Distribution Network. Energies. 2024; 17(14):3413. https://doi.org/10.3390/en17143413
Chicago/Turabian StyleYan, Qingyuan, Yang Gao, Ling Xing, Binrui Xu, Yanxue Li, and Weili Chen. 2024. "Optimal Scheduling for Increased Satisfaction of Both Electric Vehicle Users and Grid Fast-Charging Stations by SOR&KANO and MVO in PV-Connected Distribution Network" Energies 17, no. 14: 3413. https://doi.org/10.3390/en17143413
APA StyleYan, Q., Gao, Y., Xing, L., Xu, B., Li, Y., & Chen, W. (2024). Optimal Scheduling for Increased Satisfaction of Both Electric Vehicle Users and Grid Fast-Charging Stations by SOR&KANO and MVO in PV-Connected Distribution Network. Energies, 17(14), 3413. https://doi.org/10.3390/en17143413






