A Reliability Assessment Method for Natural Gas Pipelines with Corroded Defects That Considers Detection Cycles

Abstract

With the development of natural gas pipelines, the proportion of aged pipelines in service has been increasing, and corrosion remains a primary cause of pipeline failure. Regular inspections and reliability assessments are crucial to ensure the safe operation of pipelines. This study investigated an efficient reliability assessment method for corroded pipelines that considers in-line inspection intervals. First, this study compared the commonly used limit state equations for corrosion defects to select one suitable for X80-grade steel pipelines. Additionally, a Tail-Fit Monte Carlo Simulation (TF-MCS) algorithm was proposed to improve the computational speed by 30 times compared to traditional Monte Carlo simulations. Then, this study explored the inspection intervals used for reliability assessments of corroded pipelines. Finally, the parameter sensitivity was analyzed considering the yield strength, maximum operating pressure, and pipe diameter. This study ensures the reliable operation of corroded gas pipelines.

1. Introduction

As of 2022, there are about 135 × 10⁴ km of onshore natural gas pipelines in service around the world [1]. With the increase in pipeline service time and the complex environments of pipeline operation, pipeline structure failures continue to occur with serious consequences. The statistics indicate that corrosion-induced pipeline failures are one of the primary causes of these incidents [2,3]. As far as corrosion defects are concerned, these defects grow over time, making pipelines less resistant than their internal pressures, which leads to pipeline failures [4]. If the maximum depth of a corrosion defect reaches the pipeline wall thickness, a small leak will occur [5]. When a defect reaches a critical size, defined by the maximum axial length and average depth, it can cause a rupture, resulting in a leak through a pipe. If the length of the resulting crack exceeds a critical value, the crack will propagate unstably and rupture; otherwise, it will result in a large leak [6].

With the miniaturization of inspection components and the diversified development of application principles, in-line inspection has been widely employed as an effective means of ensuring pipeline integrity [7,8], which involves considering all maintenance and protective activities that may affect limit states. Pipeline operators utilize high-resolution inspection tools (such as those based on magnetic flux leakage technology) to conduct in-line inspections (ILIs), enabling the regular detection, localization, and characterization of corrosion defects [9]. Regular inspections and maintenance are crucial for reducing pipeline failure probability and ensuring safe operation [10]. However, in-line inspections are expensive and come with operational risks. In current engineering practice, fixed inspection intervals are used, which means a schedule with a fixed inspection cycle is adopted. Intervals that are too short waste resources, while those that are too long increase safety risks. Moreover, the accuracy of the inspection tools plays a significant role. Therefore, selecting appropriate inspection tools and setting optimal inspection intervals are essential for balancing pipeline safety and economic efficiency.

The occurrence and growth of corrosion defects are highly stochastic. Reliability analysis of natural gas pipelines can address inherent uncertainties and predict the probability of pipeline failure [11,12]. However, pipeline failures caused by corrosion defects are low-probability events. Traditional Monte Carlo simulation exhibits low computational efficiency and is prone to issues such as stochastic convergence in such scenarios [13]. Caleyo et al. [14] adopted the First-Order Second-Moment (FOSM) iterative reliability method, the Monte Carlo (MC) integration technique, and the first-order Taylor series expansion of Limit State Functions (LSFs) to determine the reliability and remaining lives of underground pipelines with corrosion. To improve the calculation efficiency, advanced methods such as Importance Sampling (IS) [15], Latin Hypercube Sampling (LHS) [16], and Subset Simulation (SS) [17] have been developed. These methods aim to minimize the number of samples in the MCS algorithm by altering the sampling method. Different sampling methods can enhance the computational speed by reducing the number of samples. However, more advanced and efficient methods are required to accurately calculate failure rates at the E-7 level.

Besides the randomness of the corrosion parameters, ILI tools have their own accuracy errors (Probability of Detection, PoD), in addition to measurement errors, during inspections. Determining the inspection period requires consideration of both the inherent randomness of pipeline defects and the stochastic nature of the inspection process itself. Due to the extreme randomness in the generation and degradation of pipeline corrosion defects, determining the optimal inspection interval poses a significant challenge [18]. Gomes et al. [19] utilized a simulation-based approach to investigate the optimal inspection interval for buried pressurized pipelines subjected to external corrosion. Although they incorporated the PoD of the inspection tools into their analysis, they overlooked measurement errors. Provan [20] developed a model based on Markov processes to determine corrosion defect growth with the optimal inspection time but also neglected measurement errors within the inspection interval. Zhou et al. [21] considered both PoD and measurement errors in their study. Their determination of the optimal inspection interval was based on economic considerations. However, their approach relied on traditional Monte Carlo simulation, which cannot guarantee computational efficiency.

To accommodate the application of high-precision in-line inspection tools to pipelines with high steel grades and large pressures, this paper proposes a reliability-based method for determining the inspection intervals of natural gas pipelines. Considering the low-probability characteristics of corrosion defects, this paper proposes a Monte Carlo simulation method based on tail fitting to improve the computational efficiency of reliability calculations from a data perspective. Based on this, an efficient and reliable evaluation method for corroded pipelines that considers inspection intervals is constructed. This serves as a reference for further investigations into reliability assessments of corroded pipelines.

This article is organized as follows: In Section 2, a suitable algorithm for X80-grade steel pipelines is selected through comparisons and a Tail-Fit Monte Carlo Simulation (TF-MCS) algorithm is proposed, considering the impacts of inspection intervals on the calculation results. Section 3 demonstrates the model’s accuracy and effectiveness by examining three cases and performing a sensitivity analysis. Section 4 provides a summary of this paper and outlines areas for future research and development.

2. Methodology

This paper proposes a reliability assessment method for natural gas pipelines with corroded defects that considers detection cycles for determining the corrosion limit states of X80 pipelines. The specific process is illustrated in Figure 1.

2.1. Comparison of Limit State Equations

The failure modes of corrosion defects, represented by nonlinear equations, include small leaks, large leaks, and ruptures, indicating a pipeline’s states under extreme conditions. Standards have been established for evaluating corrosion defects in pipelines regarding remaining strength and fatigue failure mechanisms, such as ASME-B31G, modified-B31G, PCORRC, C-Fer, DNV-RP-F101, SHELL-92, RSTRENG, and CSA Z662 [22,23,24]. In order to adapt to the development of pipeline steel grades, appropriate limit state equations suitable for high-grade steels were selected. This study compared the classic corrosion defect rupture limit state equations based on the years they were developed, their development institutions, and their basic equations. A comparison was conducted based on their equation forms, applicable materials, defect shapes, corrosion depth definitions, representations of flow stress, and types of loads. The details are listed in

Table 1. Comparison of eight corrosion defect rupture limit state equations.

-	ASME-B31G	Modified-B31G	PCORRC	C-Fer
Institution	The American Institute of Mechanical Engineers	The American Institute of Mechanical Engineers	Battle Laboratory	Nessim and Zhou
Year	1984	2012	1999	2012
Equation	$p_b={\sigma }_{flow}\frac{2t}{D}\left[\frac{1-A/A_0}{1-(A/A_0)(M_t^{-1})}\right]$	$M=\left\{\begin{array}{l}{\left[1+0.6275\frac{L^2}{D_t}-0.003375\frac{L^4}{D^2{t}^2}\right]}^{\frac{1}{2}}\\ 0.032\frac{L^2}{Dt}+3.3\end{array}\right.$	$p_b={\sigma }_{\mu }\frac{2t}{D}\left[1-\frac{d_{\max }}{t}\left(1-\exp \left(-0.157\frac{L}{\sqrt{R\left(t-d_{\max }\right)}}\right)\right)\right]$	$p_b={\sigma }_{flow}\frac{2t}{D}\left[\frac{1-A/A_0}{1-(A/A_0)(M_t^{-1})}\right]$
Basic Equation	NG-18	NG-18	Finite element	NG-18
Material Range	Low- and medium-strength steel	Low- and medium-strength steel	Medium- and high-strength steel	Medium- and high-strength steel
Defect Shape	Parabolic curve (2/3 × d/t) Rectangle (d/t)	Arbitrary shape (0.85 d/t)	Rectangle (d/t)	Rectangle (d/t)
Corrosion Depth Definition	Maximum corrosion depth	Maximum corrosion depth	Maximum corrosion depth	Average corrosion depth
Flow Stress	1.1SMYS (SMYS + SMTS)/2	SMYS + 68.95 (SMYS + SMTS)/2	SMTS	1.8SMYS
Load Type	Internal pressure	Internal pressure	Internal pressure	Internal pressure
-	DNV-RP-F101	SHELL-92	RSTRENG	CSA Z662
Institution	British Gas Corporation Norwegian Register	Ritchie and Last	Kiefner and Viet	Canadian standard association
Year	1999	1995	1989	2007
Equation	$P_c=\frac{2t{\sigma }_b}{D-t}\left[\frac{1-(d/t)}{1-(d/t)/Q}\right]$	$P_f=\frac{1.8{\sigma }_{uts}t}{D}\left(\frac{1-\frac{d(t)}{t}}{1-\frac{d(t)}{t}{R}^{-1}}\right)$	$P_b=\frac{2t{\sigma }_{flow}}{D}\left(\frac{1-A_d/A_0}{1-A_d/A_0{M}_t}\right)$	$P_{b6}=\frac{2t{\sigma }_f}{D}\frac{1-\frac{d_{ave}}{t}}{1-\frac{d_{ave}}{t{M}_2}}$
Basic Equation	NG-18	NG-18	NG-18	NG-18
Material Range	<X80	Low- and mediumstrength steel	Low- and medium-strength steel	Medium- and high-strength steel
Defect Shape	Rectangle (d/t)	Rectangle (d/t)	0.85 dL/Actual shape	Rectangle (d/t)
Corrosion Depth Definition	Corrosion depth	Corrosion depth	Maximum corrosion depth/Effective area	Average corrosion depth
Flow Stress	SMTS	0.9SMTS	SMYS + 68.95 (SMYS + SMTS)/2	1.15SMYS X80:0.9SMTS
Load Type	Internal pressure, axial pressure	Internal pressure	Internal pressure	Internal pressure, axial pressure

.

These common forms of corrosion limit state equations are quite similar, with the main differences lying in the definitions of flow stress and corrosion defect depth. The eight corroded pipeline rupture limit state equations were compared and analyzed, and the failure probabilities of the equations were calculated for high-grade steel. To compare the performances of the equations under high-grade steel conditions, the eight rupture limit state equations were calculated via Monte Carlo simulation using the data in

Table 2. Distribution and parameters of random variables in the rupture state of a certain X80 pipeline.

X80	Mean Value (E)	Standard Deviation (Std)	Distribution
Pressure (MPa)	10	0.6	Normal distribution
Thickness (mm)	11.4	0.35	Normal distribution
Diameter (mm)	1216	15.7	Normal distribution
Yield Strength (MPa)	653	31.8	Normal distribution
Defect Length (mm)	500	30	Normal distribution

, and the results are shown in Figure 2.

The performances of the different equations under high-grade steel conditions is compared in Figure 2. After 22 years, the results of the equations other than PCORRC were relatively consistent. This arose because the basic equations utilized in PCORRC differ from the others, suggesting it is unsuitable for calculating failure probabilities in high-grade steel pipelines during service. However, there were significant differences in the calculation results of each equation before 22 years. Many equations failed to calculate the failure probability in the first few years. Notably, the C-Fer equation outperformed the others by accurately predicting the failure probabilities, even for pipelines in operation for 18 years. Therefore, the C-Fer equation exhibited better calculation performance compared with the other equations. It can provide better calculation results in the initial years while ensuring accuracy. Hence, the C-Fer equation was selected for the reliability assessments of corroded pipelines. The specific formulas are shown in Equations (1)–(8):

$$g_1=t-d_{\max }$$

(1)

$$g_2=r_a-P$$

(2)

$$g_3=\frac{2.3\cdot t\cdot {\sigma }_y}{m\cdot D}-P$$

(3)

$$r_a=e_1\cdot r_c+(1-e_1)\cdot r_0-e_2\cdot {\sigma }_y$$

(4)

$$r_0=2.3\frac{t\cdot {\sigma }_y}{D}$$

(5)

$$r_c=r_0\left(\frac{1-\frac{d_a}{t}}{1-\frac{d_a}{m\cdot t}}\right)$$

(6)

$$m=\left\{\begin{array}{l}\sqrt{1+0.6275\frac{l^2}{D\cdot t}}\frac{l^2}{D\cdot t}\le 50 \\ 0.032\frac{l^2}{D\cdot t}+3.3\frac{l^2}{D\cdot t}>50\end{array}\right.$$

(7)

$$\begin{array}{l}{P}_{sl}=\mathrm{Pr}ob\left[\left(g_1\le 0\right)\cap \left(g_2>0\right)\right]\\ P_{bl}=\mathrm{Pr}ob\left[\left(g_1>0\right)\cap \left(g_2\le 0\right)\cap \left(g_3>0\right)\right]\\ P_{ll}=\mathrm{Pr}ob\left[\left(g_1>0\right)\cap \left(g_2\le 0\right)\cap \left(g_3\le 0\right)\right]\end{array}$$

(8)

In the equations, g₁, g₂, and g₃ represent the pipeline limit states, and failure occurs when g₁, g₂, and g₃ < 0. t denotes the pipeline wall thickness in millimeters (mm), d_max stands for the maximum corrosion depth in mm, r_a signifies the circumferential stress at pipeline failure in MPa, P represents the internal pressure of the pipeline in Mpa, σ_y denotes the yield strength in MPa, m indicates the expansion coefficient, D represents the pipeline diameter in mm, e₁ and e₂ denote model errors, d_a stands for the average corrosion depth in mm, and l signifies the length of the corrosion defect in mm. P_sl, P_bl, and P_ll represent the calculation methods for the three limit states of small leaks, large leaks, and ruptures, respectively.

2.2. Tail-Fitting Monte Carlo Simulation (TF-MCS)

Reliability (R) is defined as the probability that a pipeline satisfies all its design requirements within a specified time period. It is calculated using Equation (9):

R = 1 − P_f

(9)

The probability of failure (P_f) is calculated from the probability distributions of the load effects and resistance. Since reliability is typically close to 1, it is often difficult to express and distinguish using decimal numbers. Therefore, failure probability is commonly calculated, and reliability is then defined as 1 minus the failure probability.

The Monte Carlo simulation method is the most commonly used and accurate method for reliability calculations. It allows for straightforward simulation of the probability solutions of limit state equations using statistical analysis methods. This approach helps to avoid mathematical difficulties in pipeline reliability calculations, as there is no need to worry about the complexity of equation functions or the time-dependence of reliability issues. It possesses the capability to directly address problems. However, Monte Carlo simulation requires a large number of repeated calculations that are not interrelated. Therefore, a sufficient number of statistical quantities are needed to ensure that the simulation results closely approximate the true values, especially for calculations involving extremely low probabilities. In order to ensure computational accuracy, an extremely large number of samples is required. This poses many challenges during the computational process, leading to low computational efficiency. It limits the application of quantitative reliability methods in the industry. Hence, this paper discusses the improvement of the Monte Carlo simulation algorithm using the tail-fitting method for extremely low-probability events such as pipeline failure caused by corrosion defects. This enhancement provides accurate and reliable estimates of failure probabilities.

Tail fitting is a concept in statistics and data analysis that is typically used to describe the tail portions of a distribution, which are the extreme values. It involves modeling or fitting the tail portion of a distribution to understand the probability distributions and characteristics of extreme events. The probability of pipeline failure, being the most extreme value in the distribution of the limit state equation calculation results, generally contains relatively few extreme data points in the tail. Therefore, employing tail-fitting algorithms can effectively improve the computational efficiency of Monte Carlo simulations for events with low probabilities. The quality and reliability of tail-fitting analysis depend on the selected fitting distribution and the quality of the data. Therefore, before conducting tail-fitting calculations, it is essential to ensure appropriate processing and validation of the data to ensure the reliability of the analysis. The mathematical expressions corresponding to the probabilities of pipeline failures due to corrosion defects, such as small leak failures, large leak failures, and rupture failures, are given in Equation (8). Based on this, this paper proposes a Monte Carlo rapid calculation process using tail fitting, and a flowchart is illustrated in Figure 3. Before conducting reliability calculations, the years of failure for each limit state are determined. Then, based on the conditions of Equation (8), the data points are classified, and the tail data points are selected for fitting. The mean and variance of the tail points are determined using goodness-of-fit tests. Then, the algorithm is fitted and applied to calculate the failure probabilities of various corrosion limit state equations.

During calculations, utilizing failure times for tail fitting to compute the failure probabilities of corroded pipelines yields more accurate results. The selection of data points for tail fitting is crucial, as too many points can lead to overfitting, while too few points may result in less precise outcomes. Additionally, due to the uncertainty associated with corrosion defects, there is no uniform selection criterion for the number of fitting points. In this study, the selection of tail data points followed the criteria established by C-Fer: when the maximum cumulative probability density of the tail data points reached 0.01, these accumulated data points were considered for tail fitting. However, if the cumulative data points reached 100 before the cumulative probability density reached 0.01, those 100 points were directly chosen for subsequent calculations. Notably, at the point of reaching a maximum cumulative probability density of 0.01, if there were fewer than 100 accumulated data points, tail fitting was not employed for calculations to avoid inaccuracies due to insufficient fitting data. Moreover, since the number of points in the tail region is limited, it indicates that Monte Carlo simulation can be utilized to rapidly obtain precise results.

2.3. Reliability Evaluation Method That Considers the Detection Cycle

As the occurrence of a corrosion defect is an extremely low-probability event, it is imperative to accurately calculate the failure probability and reliability of pipelines containing corrosion defects using the various methods mentioned above. However, the pipeline operation process is a continuously degrading system. To ensure the safe operation of pipelines, regular internal inspections are necessary. Corrosion is one of the primary defects threatening pipeline safety. After quantitatively assessing the reliability of a pipeline, the actual conditions during pipeline operation and management necessitate internal inspections. Based on the corrosion defect information obtained from internal inspections, an assessment can be made, and maintenance strategies for the pipeline system can be formulated. Taking effective measures before pipeline failure occurs can minimize the risks and losses associated with pipeline operation. Given the high economic costs and operational risks associated with internal inspections, as well as the impacts of internal inspection results on reliability assessments, research on reliability analysis and evaluation methods incorporating internal inspection devices is crucial.

Based on the defect information obtained from internal pipeline inspections, a corrosion growth model can be established to predict the growth of corrosion defects, assess the failure probabilities of pipeline systems, and make maintenance decisions. Regarding corrosion defects, there are two maintenance criteria for the detection of pipelines containing corrosion defects [25]:

$$LS{F}_1\left(d\right)=0.5w_t-d_{\max }\left(t\right)\le 0orLS{F}_1\left(P_f\right)=P_f-1.39P_{op}\le 0$$

(10)

$$LS{F}_2\left(d\right)=0.75w_t-d_{\max }\left(t\right)\le 0orLS{F}_2\left(P_f\right)=P_f-1.1P_{op}\le 0$$

(11)

If a corrosion defect meets criterion one, excavation and the addition of a coating are required for maintenance; if both criteria are met simultaneously, sleeve installation is needed for repair. Since internal inspection tools themselves also have dimensional errors, when conducting reliability assessment calculations for pipelines with corrosion defects and internal inspection tools, the main consideration is how to screen corrosion defects that meet the maintenance criteria and handle them accordingly. For corroded pipelines, incorporating reliability calculations for internal inspection tools is highly beneficial for safe operation, as it allows for more accurate simulation of actual pipeline operation scenarios. Conversely, the calculation results can assist in determining internal inspection intervals and maintenance plans. The reliability calculation process for corroded pipelines with internal inspection tools is illustrated in Figure 4. Initially, corrosion defect values are sampled, assuming linear defect growth, with a detection cycle of 5 years, meaning the first inspection starts in the fifth year. The internal inspection tool has a size accuracy of 0.01, meaning the detection results fall within ±10% of a probability of 90%, and a roulette wheel selection method is used to assess whether defects can be detected. At this point, the calculated values are theoretical detection values. However, the internal inspection tool itself has instrument errors that follow a normal distribution. After calculation, the theoretical detection values are transformed into actual detection values. These actual detection values are used to determine whether defects are detected and repaired. If a defect is repaired, its value becomes 0; if not, the defect value continues to grow, awaiting the next inspection. This process continues in a dynamic calculation loop.

3. Case Study

3.1. Reliability Calculation of Pipeline with Corrosion Defect Based on Tail Fitting

In this paper, the failure data of a natural gas pipeline were used for reliability calculations. It is worth noting that the assessment did not take into account changes in operating conditions or related gas storage facilities. The parameters are shown in

Table 3. Parameter distribution types and values.

Parameter	Distribution Function	Mean Value (E)	Standard Deviation (Std)
External Diameter (mm)	Constant	711.0
Thickness (mm)	Normal distribution	8.0	0.131
Pressure (MPa)	Geng Bell distribution	6.3	0.08
Yield Strength (MPa)	Normal distribution	471.0	32.0
Tensile Strength (MPa)	Normal distribution	587.0	25.0
Defect Density (/km)	Constant	1.0
Defect Depth (mm)	Weibull distribution	2.5	1.25
Defect Length (mm)	Logarithmic normal distribution	31.0	13.0
Defect Depth Growth Velocity (mm/year)	Weibull distribution	0.06	0.04
Defect Length Growth Velocity (mm/year)	Logarithmic normal distribution	0.085	0.68

.

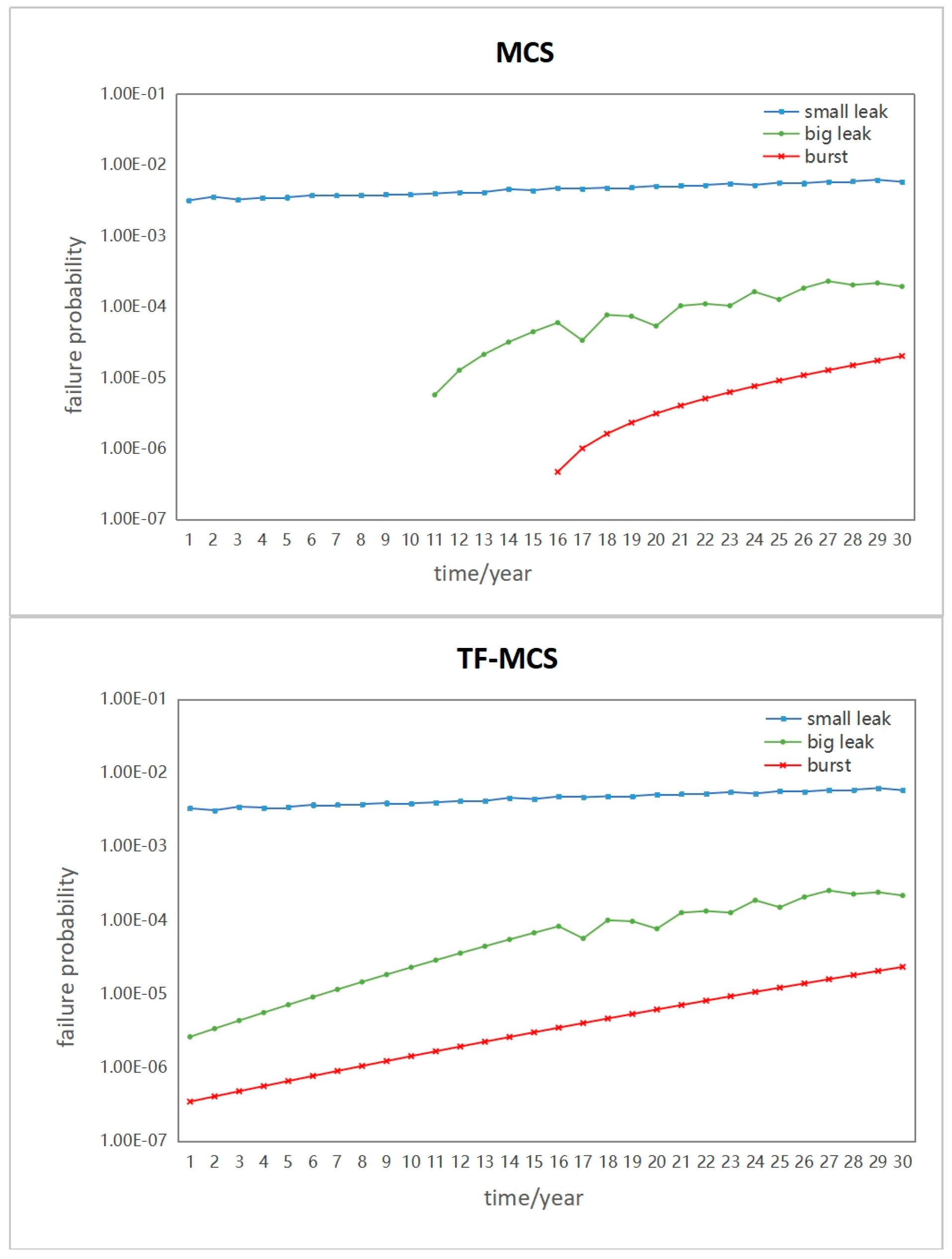
In this study, a pipeline lifespan of 30 years was selected for the calculations. Comparing the results with those of the Monte Carlo simulations, it was observed that the proposed method’s results were comparable to the failure probabilities calculated by the Monte Carlo simulations after approximately 15 years of operation, as Figure 5. This was because the corrosion defects became more pronounced as the pipeline operated for a period of time, allowing the Monte Carlo simulations to generate more samples and calculate the failure probability more accurately. The results of the TF-MCS indicate that using the tail-fitting method, especially during the initial years of corrosion defect occurrence, allowed the TF-MCS to perform better when predicting the failure probability results. Additionally, while the Monte Carlo simulation algorithm took 30 min to compute specific results, using TF-MCS required only 1 min and 28 s. In terms of computational speed, TF-MCS was 30 times faster than the regular Monte Carlo method.

3.2. Reliability Calculation of Corroded Pipeline with Internal Detector

On the basis of corroded pipeline failure probability calculations incorporating inspection and maintenance tools, calculations were conducted by investigating the detection probabilities and size accuracies of inspection tools categorized as high-, medium-, and low-precision detectors. The parameters of the medium-precision detectors are shown in

Table 4. Parameters of internal detector accuracy.

Testing Precision	Detection Probability (%)	Maximum Corrosion Depth (%)
High	95	70
Medium	90	60
Low	85	50

.

The calculation results are shown in Figure 6, Figure 7 and Figure 8.

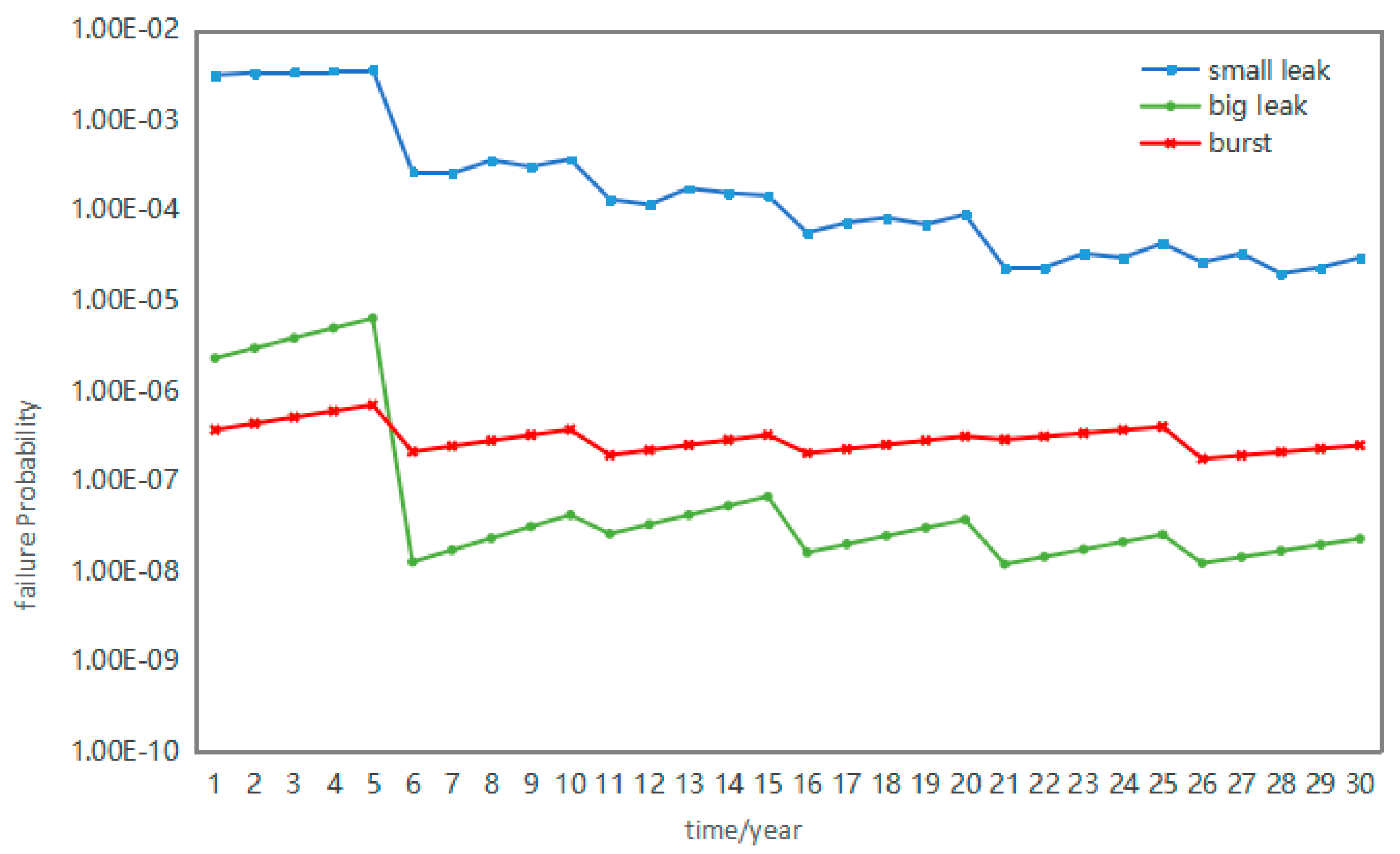
The figures above illustrate significant reductions in the failure probabilities of corroded pipelines after each in-line inspection, especially regarding the limit state of large leaks. In order to better compare the effects of different inspection accuracies, this study used a common inspection cycle for the calculations. For high-, medium-, and low-precision detectors, the failure probabilities of the large leak limit state noticeably decreased after each inspection cycle. When using high-precision detectors, the failure probability of the large leak limit state decreased from 1 × 10⁻⁵ to below 1 × 10⁻⁸ after the first inspection cycle, while for medium-precision detectors, it decreased to above 1 × 10⁻⁸. Low-precision detectors only reduced it to around 1 × 10⁻⁷. Moreover, after several inspection cycles, high-precision detectors could ensure that the failure probability of the large leak state did not exceed 1 × 10⁻⁷. Medium-precision detectors showed failure probabilities exceeding 1 × 10⁻⁷ after approximately 15 to 20 years of pipeline operation, while low-precision detectors could only maintain failure probabilities between 1 × 10⁻⁶ and 1 × 10⁻⁷. In summary, the higher the accuracy of a detector, the lower the failure probability of the large leak state that it can maintain.

However, in-line inspection is a costly detection method, and detectors with higher accuracy correspond to higher costs. Therefore, considering the overall cost, using medium-precision detectors can meet detection requirements and ensure the normal operation of a pipeline. Additionally, the determination of inspection cycles is crucial. In the past, pipelines were inspected according to fixed inspection cycles, which may have led to unnecessary waste. According to the corroded pipeline reliability calculation method proposed in this paper, inspection cycles can be determined based on reliability, which is of great significance for maintaining pipeline operations.

3.3. Sensitivity Analysis

Sensitivity analysis was conducted to explore the influences of various parameters on the failure probability calculation results of corroded pipelines with internal detectors. To make the analysis more practical, the defect depth, defect length, defect depth growth rate, and yield strength parameters corresponding to the pipeline steel grades X52, X60, X65, X70, X80, and X90 from the ‘Oil and Gas Pipeline Engineering Design Code’ standard were compared. The sensitivity analysis conducted in this study focused on different steel grades, and each was influenced by specific factors. These relationships were integrated into the standards. They can be found in Appendix A for reference and are shown in Figure 9, Figure 10 and Figure 11.

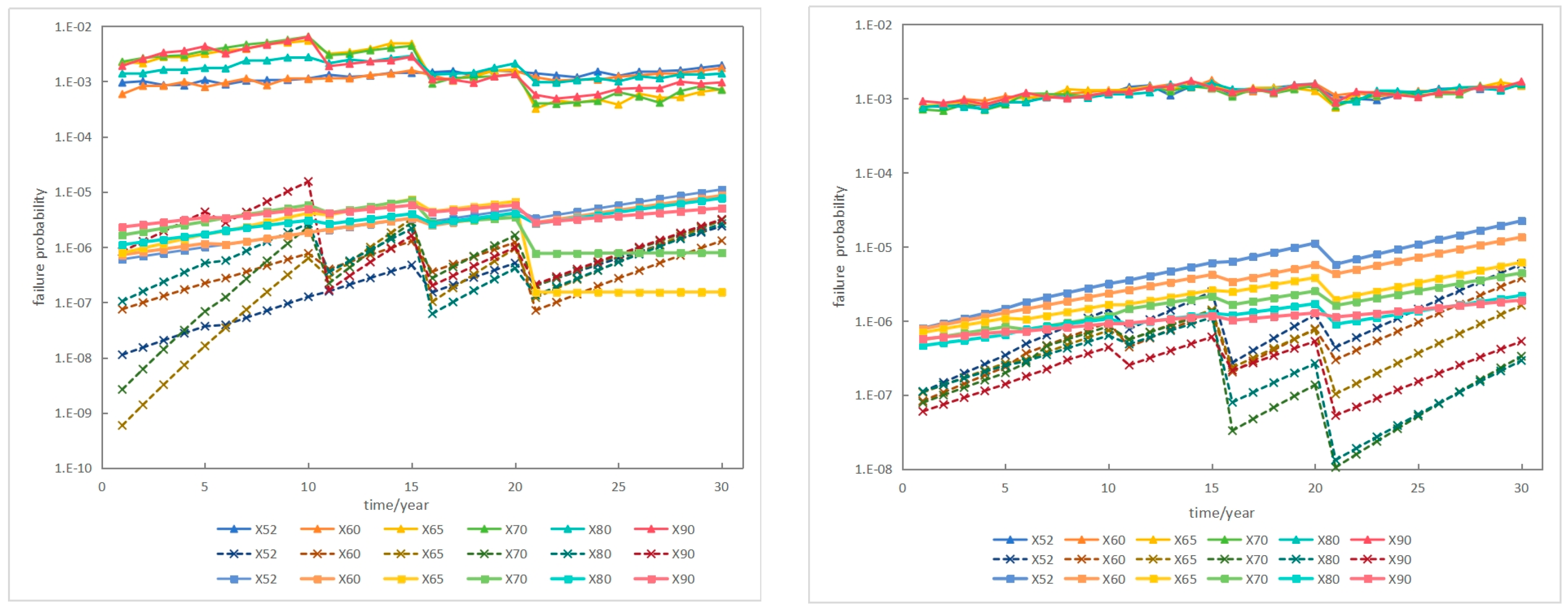
Figure 9 shows the influences of defect depth and defect length on the failure probability. It can be observed that the variation in defect depth affected the failure probabilities of small leaks, large leaks, and ruptures in corroded pipelines. The impact was more significant during the first 5 years of operation, and as the operating years increased, the effect of defect depth on failure probability diminished. On the other hand, defect length only affected the failure probabilities of large leaks and ruptures because the limit state equations for small leaks do not involve defect length. For the large leak and rupture limit state equations, defect length serves as a parameter for calculating the expansion coefficient (M). Therefore, based on Figure 9, it can be inferred that the impact of defect length on the failure probabilities of corroded pipelines is around 0.5 × 10⁻¹.

Figure 10 illustrates the impacts of the defect depth growth rate and yield strength on the failure probability. The defect depth growth rate had a significant effect on the pipeline failure probability during the first 10 years of operation, with an influence of around 1 × 10⁻³. As the operating years increased, this impact decreased to approximately 0.5 × 10⁻¹. In addition, it can be observed that lower steel grades and smaller yield strengths led to higher pipeline failure probabilities. And with increasing pipeline operating times, the yield strength had a greater impact on the failure probabilities of large leaks and ruptures, reaching a maximum of 1 × 10⁻².

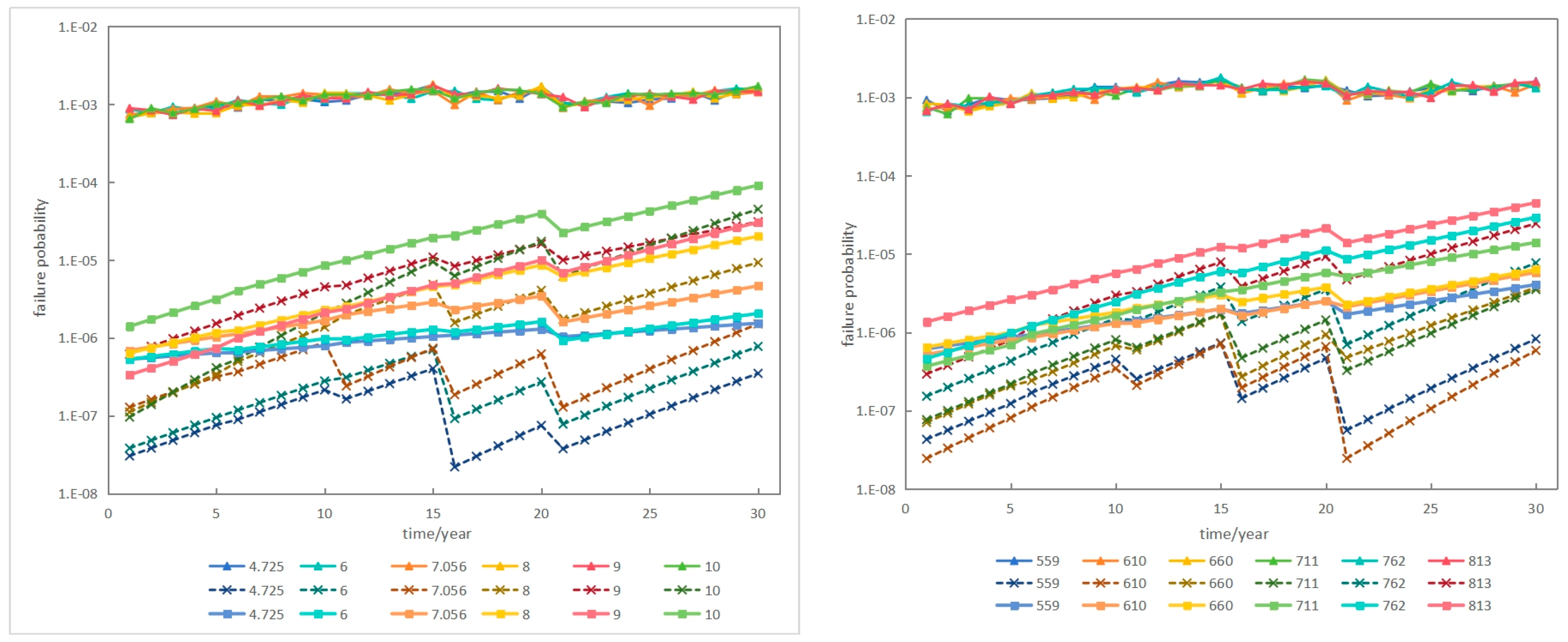
Additionally, the maximum operating pressure and pipe diameter also affected the failure probabilities of corroded pipelines, as shown in the sensitivity analysis presented in Figure 11. Higher operating pressures and larger pipe diameters corresponded to higher failure probabilities. Both parameters had significant and relatively uniform effects on large leak failures. For rupture failures, the influences of these two parameters increased with longer operating times.

In summary, the depths and growth rates of defects have certain impacts on failure, while the effects of defect length and its growth rate on failure probability are relatively minor. The major influencing factors are primarily the yield strength, maximum operating pressure, and pipe diameter.

4. Conclusions

This paper compared several common corrosion limit state equations and identified C-Fer as the most suitable equation for high-grade steel pipelines. Additionally, a Monte Carlo algorithm based on tail fitting was proposed, effectively enhancing the computational efficiency of Monte Carlo simulations. Subsequently, a reliability algorithm for corroded pipelines that considers inspection cycles was investigated. Feasibility verification was conducted on an actual pipeline, and the following conclusions were drawn:

(1)

The main differences among the limit state equations lie in the calculation form of the burst pressure and the definition of flow stress. In high-grade steel pipelines, the C-Fer equation can compute the failure probability during the early stage of pipeline operation (18 years), which is a capability not possessed by other equations.

(2)

Due to the low computational efficiency of Monte Carlo simulation, this study adopted tail fitting to enhance its computational efficiency. Through computational comparisons, it was observed that TF-MCS achieves results comparable to MCS during the later stages of pipeline operation (beyond 20 years) and can also calculate the failure probabilities of pipelines during the earlier stages (before 10 years). Additionally, the computational speed of TF-MCS is 30 times faster than MCS, indicating that TF-MCS improves the efficiency of calculating corroded pipeline failure probabilities while ensuring accuracy. Based on this, this study also investigated an efficient reliability calculation method that considers the inspection period, providing assurance for the normal operation of corroded pipelines.

(3)

For the time-dependent reliability calculation method that considers the inspection periods of corroded pipelines, sensitivity analysis was conducted on seven aspects: defect depth, defect length, defect depth growth rate, defect length growth rate, yield strength, maximum operating pressure of the pipeline, and pipeline diameter. The main influencing factors were the yield strength, maximum operating pressure, and pipeline diameter.

This study investigated an efficient computational method for time-dependent reliability assessments of corroded pipelines that considers inspection intervals, which is significant for subsequent research and the application of reliability in the pipeline industry. With the advancement of technology, detectors are expected to evolve, and future research should focus on further studying the variations in detector accuracy and inspection intervals.