Influence of Ambient Temperature on the Reliability of Overhead LV Power Lines with Bare Conductors
Abstract
1. Introduction
2. Materials and Methods
2.1. Influence of Ambient Temperature on Overhead Power Lines Operation
2.2. Method of Analysis
2.3. Statistical Data
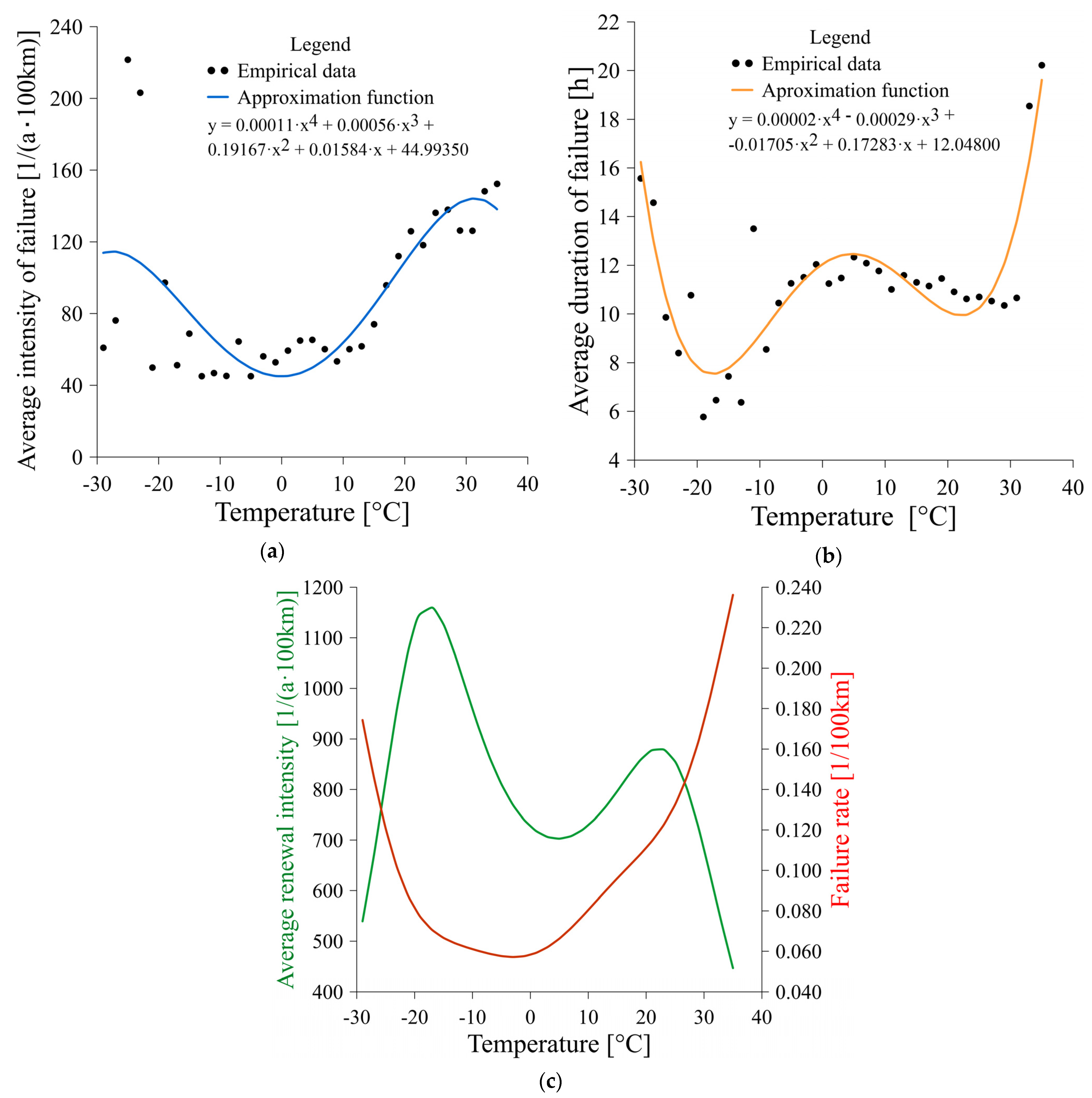
3. Results
Analysis of the Influence of Ambient Temperature on the Reliability of Overhead LV Lines with Bare Conductors
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bartáková, B.; Rychtera, M. Tropikalizacja Urządzeń Elektrycznych; Wydawnictwo Naukowo-Techniczne: Warszawa, Poland, 1960. [Google Scholar]
- Chojnacki, A.Ł. Analiza Niezawodności Eksploatacyjnej Elektroenergetycznych Sieci Dystrybucyjnych-Rozprawa Habilitacyjna; Wydawnictwo Politechniki Świętokrzyskiej: Kielce, Poland, 2013. [Google Scholar]
- Chojnacki, A.Ł.; Chojnacka, K.J. Niezawodność Elektroenergetycznych Sieci Dystrybucyjnych; Wydawnictwo Politechniki Świętokrzyskiej: Kielce, Poland, 2018. [Google Scholar]
- Chojnacki, A.Ł. Assessment of the Risk of Damage to 110 kV Overhead Lines Due to Wind. Energies 2021, 14, 556. [Google Scholar] [CrossRef]
- Jakušenoks, A.; Laizāns, A. Weather impact on the household electric energy consumption. Res. Rural Dev. 2016, 1, 248–253. [Google Scholar]
- Marzecki, J. Terenowe Sieci Elektroenergetyczne; Wydawnictwo Instytutu Elektroenergetyki Politechniki Warszawskiej: Warszawa, Poland, 2007. [Google Scholar]
- Sroka, K.; Złotecka, D. The risk of large blackout failures in power systems. Arch. Electr. Eng. 2019, 68, 411–426. [Google Scholar]
- Habrych, M.; Staszewski, Ł. Zwiększenie możliwości przesyłowych napowietrznych linii elektroenergetycznych z zachowaniem wymaganego poziomu bezpieczeństwa. Mech. I Autom. Górnictwa 2014, 5, 28–35. [Google Scholar]
- Kabir, E.; Guikema, S.D.; Quiring, S.M. Power outage prediction using data streams: An adaptive esemble learning approach with a feature- and performance-basen weighting mechanism. Risk Anal. 2024, 44, 686–704. [Google Scholar] [CrossRef] [PubMed]
- Do, V.; McBrien, H.; Flores, N.M.; Northrop, A.J.; Schlegelmilch, J.; Kiang, M.V.; Casey, J.A. Spatiotemporal distribution of power outages with climate events and social vulnerability in the USA. Nat. Commun. 2023, 14, 2470. [Google Scholar] [CrossRef] [PubMed]
- Sozański, J. Niezawodność i Jakość Pracy Systemu Elektroenergetycznego; WNT: Warszawa, Poland, 1990. [Google Scholar]
- Schrijver, C.J.; Dobbins, R.; Murtagh, W.; Petrinec, S.M. Assessing the impact of space weather on the electric power grid based on insurance claims for industrial electrical equipment. Space Weather 2014, 12, 487–498. [Google Scholar] [CrossRef]
- Mideksa, T.K.; Kallbekken, S. The impact of climate change on the electricity market: A review. Energy Policy 2010, 38, 3579–3585. [Google Scholar] [CrossRef]
- Stobiecki, A.; Majcherczyk, A. Ocena parametrów zawodnościowych terenowej sieci elektroenergetycznej średniego napięcia. Wiadomości Elektrotec. 2010, 3, 25–29. [Google Scholar]
- Stobiecki, A.; Chojnacki, A.Ł.; Majcherczyk, A. Ocena własności niezawodnościowych transformatorów rozdzielczych w wiejskich sieciach elektroenergetycznych. In Proceedings of the V Ogólnopolska Konferencja Naukowa, Modelowanie i Symulacja”, Kościelisko, Poland, 23–27 June 2008; pp. 145–148. [Google Scholar]
- Mukherjee, S.; Nateghi, R.; Hastak, M. A multi-hazard approach to assess severe weather-induced major power outage risks in the U.S. Reliab. Eng. Syst. Saf. 2018, 175, 283–305. [Google Scholar] [CrossRef]
- Kankanala, P.; Das, S.; Pahwa, A. Adaboost+: An ensemble learning approach for estimating weather-related outages in distribution systems. IEEE Trans. Power Syst. 2014, 29, 359–367. [Google Scholar] [CrossRef]
- Chojnacki, A.Ł.; Kaźmierczyk, A.; Stobiecki, A. Właściwości niezawodnościowe napowietrznych linii dystrybucyjnych 110 kV. Wiadomości Elektrotechniczne 2017, 7, 15–19. [Google Scholar] [CrossRef]
- Rübbelke, D.; Vögele, S. Impacts of climate change on European critical infrastructures: The case of the power sector. Environ. Sci. Policy 2011, 14, 53–65. [Google Scholar] [CrossRef]
- Sathaye, J.A.; Dale, L.L.; Larsen, P.H.; Fitts, G.A.; Koy, K.; Lewis, S.M.; Frossard Pereira de Lucena, A. Estimating impacts of Warming temperatures on California’s electricity system. Glob. Environ. Chang. 2013, 23, 499–511. [Google Scholar] [CrossRef]
- Acharya, J.R. Weather Effect Considerations in Reliability Evaluation of Electrical Transmission and Distribution Systems. Ph.D. Dissertation, University of Saskatchewan, Saskatoon, SK, Canada, 2005. [Google Scholar]
- Sanyal, J.; Dumas, M.; Lee, S.; Chinthavali, S.; King, J.; Mukherjee, S. Understanding the Computing and Analysis Needs for Resiliency of Power Systems from Severe Weather Impacts. In Proceedings of the PASC’23: Proceedings of the Platform for Advanced Scientific Computing Conference, Davos, Switzerland, 26–28 June 2023; pp. 1–10. [Google Scholar]
- Arciszewski, A.; Zawodniak, J. Linie średniego napięcia w aspekcie awaryjności oraz problemów formalno-technicznych. In Prace Instytutu Elektrotechniki Politechniki Poznańskiej; Sieć Badawcza Łukasiewicz-Instytut Elektrotechniki: Warszawa, Poland, 2010; Volume 247. [Google Scholar]
- PN-E 05100-1:1998; Elektroenergetyczne Linie Napowietrzne. Projektowanie i budowa. Linie Prądu Przemiennego z Przewodami Roboczymi Gołymi. Polish Committee for Standardization: Warsaw, Poland, 1998.
- Gkika, A.V.; Zacharis, E.A.; Lekkas, E.L.; Lizios, S.G.; Parcharidis, I.A. Climate Change Adaptation Management Pathway for Overhead Electricity Pole Systems of Distribution Networks. In Proceedings of the 2nd World Conference on Sustainability, Energy and Environment, Berlin, Germany, 9–11 December 2022; pp. 49–83. [Google Scholar]
- Złotecka, D. Wpływ ekstremalnych zjawisk atmosferycznych na system elektroenergetyczny. Electr. Eng. 2018, 94, 87–98. [Google Scholar] [CrossRef]
- Apadula, F.; Bassini, A.; Elli, A.; Scapin, S. Relationship between meteorological variables and monthly electricity demand. Appl. Energy 2012, 98, 346–356. [Google Scholar] [CrossRef]
- Chojnacki, A.Ł.; Kaźmierczyk, A. Influence of ambient temperature on the intensity of failures of MV/LV power distribution substations. Logistic 2014, 6, 2610–2618. [Google Scholar]
- Migdalski, J. (Ed.) Inżynieria Niezawodności–Poradnik; ATR Bydgoszcz i Zetom Warszawa: Warszawa, Poland, 1992. [Google Scholar]
- Czapp, S.; Szultka, S.; Tomaszewski, A. Design of power cable lines partially exposed to direct solar radiation–special aspects. Energies 2020, 13, 2650. [Google Scholar] [CrossRef]
- Hanif, S.; Mukherjee, M.; Poudel, S.; Yu, M.G.; Jinsiwale, R.A.; Hardy, T.D.; Reeve, H.M. Analyzing at-scale distribution grid response to extreme temperatures. Appl. Energy 2023, 337, 120886. [Google Scholar] [CrossRef]
- Banasik, K.; Chojnacki, A.Ł.; Gębczyk, K.; Grąkowski, Ł. Influence of wind speed on the reliability of low-voltage overhead power lines. In Proceedings of the 2019 Progress in Applied Electrical Engineering (PAEE)–IEEE, Koscielisko, Poland, 17–21 June 2019; pp. 1–5. [Google Scholar]
- Dołęga, W. Wymagania środowiskowe dla urządzeń i instalacji elektroenergetycznych. Elektro Info 2017, 4, 68–72. [Google Scholar]
- Potts, J.; Tiedmann, H.R.; Syephens, K.K.; Faust, K.M.; Castellanos, S. Enhancing power system resilience to extreme weather events: A qualitative assessment of winter storm Uri. Int. J. Disaster Risk Reduct. 2024, 103, 104309. [Google Scholar] [CrossRef]
- Ahmed, T.; Muttaqi, K.M.; Agalgaonkar, A.P. Climate change impacts on electricity demand in the State of New South Wales, Australia. Appl. Energy 2012, 98, 376–383. [Google Scholar] [CrossRef]
- Santágata, D.M.; Castesana, P.; Rössler, C.E.; Gómez, D.R. Extreme temperature events affecting the electricity distribution system of the metropolitan area of Buenos Aires (1971–2013). Energy Policy 2017, 106, 404–414. [Google Scholar] [CrossRef]
- De Felice, M.; Alessandri, A.; Ruti, P.M. Electricity demand forecasting over Italy: Potential benefits using numerical weather prediction models. Electr. Power Syst. Res. 2013, 104, 71–79. [Google Scholar] [CrossRef]
- Son, H.; Kim, C. Short-term forecasting of electricity demand for the residential sector using weather and social variables. Resour. Conserv. Recycl. 2017, 123, 200–207. [Google Scholar] [CrossRef]
- Zhou, Y.; Pahwa, A.; Yang, S.S. Modeling weather-related failures of overhead distribution lines. IEEE Trans. Power Syst. 2006, 21, 1683–1690. [Google Scholar] [CrossRef]
- Akeel, R. Predicting Weather-Related Transmission Line Failures Using Machine Learning. Ph.D. Dissertation, Reykjavík University, Reykjavík, Iceland, 2019. [Google Scholar]
- Banasik, K. Analysis of the Impact of Weather Conditions on the Operational Reliability of Equipment and Facilities in Electric Power Distribution Networks. Ph.D. Dissertation, Wydawnictwo Politechniki Świętokrzyskiej, Kielce, Poland, 2023. [Google Scholar]
- EN 50160:2023-10; Supply Voltage Parameters in Public Power Grids. Polish Committee for Standardization: Warsaw, Poland, 2023.
| Year of Observation | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Overhead LV lines with bare conductors [km] | 1494.9 | 1495 | 1447 | 1447 | 1444 | 1432 | 1421 | 1408 | 1401 | 1383 |
| An average failure intensity on ambient temperature [1/(a⋅100 km)] | |||||
| Multiple correlation coefficient | Coefficient of determination | Coefficient of convergence | Coefficient of random variation | Sign test | Series test |
| 0.72 | 0.52 | 0.48 | 0.37 | ||
| Average failure duration on ambient temperature [h] | |||||
| Multiple correlation coefficient | Coefficient of determination | Coefficient of convergence | Coefficient of random variation | Sign test | Series test |
| 0.87 | 0.76 | 0.24 | 0.13 | ||
| Temperature Range [°C] | [1/(a⋅100 km)] | [h] | [1/100 km] | [1/(a⋅100 km)] | |||||
|---|---|---|---|---|---|---|---|---|---|
| Number of Failures | Empiric | Theoretic | Empiric | Theoretic | Empiric | Theoretic | Empiric | Theoretic | |
| (−30,−28> | 1 | 60.93 | 113.87 | 15.57 | 16.24 | 0.097693 | 0.174314 | 562.74 | 539.38 |
| (−28,−26> | 1 | 76.16 | 114.52 | 14.57 | 13.04 | 0.112407 | 0.145616 | 601.37 | 671.91 |
| (−26,−24> | 4 | 221.56 | 112.46 | 9.86 | 10.70 | 0.199641 | 0.120781 | 888.21 | 818.64 |
| (−24,−22> | 15 | 203.09 | 108.28 | 8.39 | 9.10 | 0.162894 | 0.101113 | 1043.69 | 962.57 |
| (−22,−20> | 5 | 49.94 | 102.51 | 10.76 | 8.12 | 0.057814 | 0.086734 | 813.87 | 1079.34 |
| (−20,−18> | 15 | 97.23 | 95.64 | 5.76 | 7.63 | 0.060131 | 0.076944 | 1519.66 | 1147.38 |
| (−18,−16> | 11 | 51.16 | 88.14 | 6.46 | 7.55 | 0.036368 | 0.070631 | 1355.59 | 1159.72 |
| (−16,−14> | 26 | 68.87 | 80.40 | 7.44 | 7.78 | 0.055244 | 0.066630 | 1177.87 | 1126.26 |
| (−14,−12> | 28 | 45.01 | 72.80 | 6.37 | 8.22 | 0.031673 | 0.063960 | 1376.17 | 1065.35 |
| (−12,−10> | 55 | 46.80 | 65.65 | 13.50 | 8.81 | 0.067297 | 0.061943 | 648.66 | 994.20 |
| (−10,−8> | 63 | 45.16 | 59.24 | 8.55 | 9.48 | 0.042202 | 0.060226 | 1024.88 | 924.46 |
| (−8,−6> | 159 | 64.37 | 53.82 | 10.45 | 10.16 | 0.071300 | 0.058742 | 838.42 | 862.36 |
| (−6,−4> | 185 | 45.14 | 49.57 | 11.26 | 10.81 | 0.054826 | 0.057633 | 778.20 | 810.48 |
| (−4,−2> | 411 | 56.18 | 46.65 | 11.51 | 11.39 | 0.068755 | 0.057163 | 760.99 | 769.38 |
| (−2,0> | 574 | 52.79 | 45.17 | 12.03 | 11.86 | 0.067608 | 0.057622 | 728.01 | 738.71 |
| (0,2> | 724 | 59.31 | 45.20 | 11.24 | 12.20 | 0.070745 | 0.059240 | 779.10 | 717.83 |
| (2,4> | 659 | 64.91 | 46.77 | 11.47 | 12.41 | 0.078355 | 0.062129 | 763.46 | 706.05 |
| (4,6> | 653 | 65.36 | 49.87 | 12.34 | 12.46 | 0.084315 | 0.066249 | 709.85 | 702.83 |
| (6,8> | 601 | 60.21 | 54.42 | 12.09 | 12.38 | 0.076710 | 0.071408 | 724.65 | 707.71 |
| (8,10> | 548 | 53.35 | 60.34 | 11.76 | 12.16 | 0.066858 | 0.077301 | 744.66 | 720.27 |
| (10,12> | 607 | 60.09 | 67.48 | 11.00 | 11.84 | 0.070183 | 0.083572 | 796.06 | 739.98 |
| (12,14> | 648 | 61.74 | 75.66 | 11.59 | 11.44 | 0.075508 | 0.089892 | 755.89 | 765.97 |
| (14,16> | 750 | 74.09 | 84.64 | 11.30 | 11.00 | 0.087215 | 0.096044 | 775.37 | 796.58 |
| (16,18> | 881 | 95.82 | 94.15 | 11.14 | 10.57 | 0.108657 | 0.101998 | 786.02 | 828.92 |
| (18,20> | 791 | 112.03 | 103.89 | 11.46 | 10.21 | 0.127784 | 0.107979 | 764.66 | 858.23 |
| (20,22> | 689 | 125.91 | 113.49 | 10.91 | 9.98 | 0.135566 | 0.114500 | 802.88 | 877.71 |
| (22,24> | 487 | 118.12 | 122.56 | 10.62 | 9.96 | 0.125233 | 0.122350 | 825.09 | 879.19 |
| (24,26> | 392 | 136.24 | 130.66 | 10.70 | 10.24 | 0.142662 | 0.132511 | 818.77 | 855.39 |
| (26,28> | 243 | 137.85 | 137.31 | 10.53 | 10.91 | 0.142108 | 0.145979 | 832.21 | 803.28 |
| (28,30> | 97 | 126.28 | 141.97 | 10.35 | 12.06 | 0.129845 | 0.163480 | 846.28 | 726.44 |
| (30,32> | 41 | 126.16 | 144.08 | 10.65 | 13.81 | 0.133017 | 0.185125 | 822.32 | 634.20 |
| (32,34> | 9 | 148.2 | 143.03 | 18.54 | 16.29 | 0.238794 | 0.210064 | 472.43 | 537.86 |
| (34,36> | 1 | 152.32 | 138.17 | 20.22 | 19.61 | 0.260097 | 0.236234 | 433.31 | 446.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banasik, K. Influence of Ambient Temperature on the Reliability of Overhead LV Power Lines with Bare Conductors. Energies 2024, 17, 3062. https://doi.org/10.3390/en17133062
Banasik K. Influence of Ambient Temperature on the Reliability of Overhead LV Power Lines with Bare Conductors. Energies. 2024; 17(13):3062. https://doi.org/10.3390/en17133062
Chicago/Turabian StyleBanasik, Kornelia. 2024. "Influence of Ambient Temperature on the Reliability of Overhead LV Power Lines with Bare Conductors" Energies 17, no. 13: 3062. https://doi.org/10.3390/en17133062
APA StyleBanasik, K. (2024). Influence of Ambient Temperature on the Reliability of Overhead LV Power Lines with Bare Conductors. Energies, 17(13), 3062. https://doi.org/10.3390/en17133062






